Perturbation theory of scattering for grazing-incidence fast-atom diffraction
Received
1st March 2022
, Accepted 16th June 2022
First published on 17th June 2022
Abstract
Recent grazing-incidence, fast atom diffraction (GIFAD) experiments have highlighted the well known observation that the distance between classical rainbow angles depends on the incident energy. The GIFAD experiments imply an incident vertical scattering angle, facilitating an analytic analysis using classical perturbation theory, which leads to the conclusion that the so called “dynamic corrugation” amplitude, as defined by Bocan et al., Phys. Rev. Lett., 2020 125, 096101 is, within first-order perturbation theory, proportional to the tangent of the rainbow angle. Therefore it provides no further information about the interaction than is gleaned from the rainbow angle and its energy dependence. Perhaps more importantly, the resulting analytic theory reveals how the energy dependence of rainbow angles may be inverted into information on the force field governing the interaction of the incident projectile with the surface.
1 Introduction
Grazing Incidence Fast Atom Diffraction (GIFAD) has recently been developed as a technique for the study of surfaces and 2-D materials.1,2 When compared to conventional, low-energy atom scattering,3,4 the fast-atom method,5–7 and specifically the use of a geometry with grazing incidence, gives technical benefits such as the ease with which the energy can be varied and the opportunity for instrumental access to the surface during the experiment.8,9 There are also benefits from the perspective of analysis. The scattering problem at high incident energy is, in principle, a formidable one since there are a huge number of open diffraction-channels even in the case of purely elastic scattering. Only a tiny number of these open-channels carry any significant intensity. The grazing trajectory averages the interaction along the incident azimuth so that most of the scattering is confined to a single diffraction-plane that contains the specular direction.1,2 Thus, a complex 1 + 2-D scattering problem is reduced to that of scattering from a simpler, 1 + 1-D corrugated potential, with a limited number of open channels. In the following, we take x as the coordinate parallel to the surface and z perpendicular to the surface.
In recent work on He scattering from a KCl(001) surface,10,11 the theoretical analysis of experimental data and the implications for classical scattering indicated an “unexpected” energy dependence in that both the corrugation of an “effective hard-wall” potential, and the corresponding rainbow angle increased as the experiment came closer to grazing incidence. As we show below, the energy dependence of the rainbow angle is not unexpected theoretically12 and has been observed experimentally in the scattering of Ar on a 2H-W(100) surface13 and most notably in the case of scattering of Ar on a LiF(100) surface.14
Surface corrugation is an appealing concept but it is not as simple as appearances suggest, and defining a unique corrugation is not at all trivial.15 The simplest scattering model, that of a hard-wall potential has been used extensively.1,16 It has the merit of a simple relationship between the corrugation function and the classical rainbow angles. However, an energy dependent hard wall parameterization fails to describe the full details of the atom-surface potential and is not a faithful description of the true potential. A hard-wall is of limited value as an interpretive tool and the notion of a “corrugation” obtained from an energy dependent hard wall model is only helpful in a highly qualitative sense. With more realistic potentials there is no simple relationship between a parameterised “experimental” potential and the underlying corrugation in the electronic properties of the surface.15,17 In any quantitative discussion it is essential to distinguish clearly between these different “corrugations”.
A strongly corrugated surface will have a different morphology and correspondingly very different scattering pattern from a weakly corrugated surface. However, making that notion more quantitative is not trivial. For example, the “corrugation” of a potential may be identified as the iso-potential contour at the classical turning point. It may alternatively be calculated in the semi-classical picture from the action along classical trajectories, a quantity Bocan et al. call the “dynamic corrugation”.10,11 These two definitions are not the same and to compare them directly is unhelpful. In the present work, we clarify the dynamics by discussing a simple model of the interaction, which allows the phenomenology in the scattering to be attributed directly to features of the potential. The model is used to explain why the observed energy dependence of the classical rainbow angle in the scattering of He/KCl(001)10,11 is not at all “unexpected”. Not less important is our observation that the action-derived corrugation amplitude and the rainbow angle are, to first order in perturbation theory, proportional to each other and therefore provide the same information on particular aspects of the potential morphology.
In Section 2 we describe a parameterised Morse potential that is flexible enough to represent a variety of surfaces while being sufficiently simple to identify the features leading to the observed phenomenology. In Section 3 the scattering is treated with first and second order perturbation theory for the resulting classical dynamics. These are then used to derive results for the energy dependence of the classical rainbow angles. We stress here the terminology “classical”, since, strictly speaking, in quantum mechanics, due to the discreteness of the angular distribution, there is no divergence related to a rainbow angle. The general theory is applied to normal incidence in the plane perpendicular to the incident direction, which is relevant for the GIFAD experimental setup. In Section 4 we present an application of the perturbation theory to the Morse potential model. We end with a discussion of the results, paying special attention to the possibility of inferring information on the static potential energy surface from energy dependent scattering measurements.
In the present work, we provide simple analytic results that are directly applicable to GIFAD experiments. The formulae, insights and conclusions are generally applicable. However, since raw experimental data is not generally in the public domain, and the data that is available has been pre-processed using a hard-wall analysis, we have avoided direct quantitative comparisons with existing experiments.
2 A Morse potential for GIFAD scattering
We seek a functional form for the potential that delivers analytical results, while providing sufficient flexibility to represent a range of realistic surfaces with an acceptable degree of accuracy. The Morse potential has been applied successfully to low energy collisions of heavy particles for many years (see for example)18,19. Following previous practice, we take the variation, perpendicular to the surface, to have the Morse form,| | | VM(z) = V0[exp(−2αz) − 2exp(−αz)], | (2.1) |
where V0 is the depth of the attractive well and α is the “softness parameter”. Lateral corrugation is introduced by a rigid displacement, in z, as a function of the coordinate parallel to the surface.18, 20 An appropriate displacement function having the simplest symmetry needed to describe recent grazing-incidence experiments11 is| | 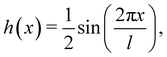 | (2.2) |
where the surface has a periodicity of l.
In the present work we aim to reproduce the essential features of recent experiments and numerical calculations of the potential.10,11 Specifically, we adopt an approach that corrugates the depth of the adsorption well by allowing the amplitude of the displacement, h(x), to be different for the attractive and the repulsive terms in eqn (2.1). Thus,
| | | VM(z, x) = V0[exp(−2α(z − hrh(x))) − 2exp(−α(z− hah(x)))], | (2.3) |
where
hr and
ha respectively give the amplitude of the displacement in the repulsive and attractive terms. Four parameters define the potential:
V0 gives the overall depth of the attractive well;
α is the softness; while
hr and
ha define the displacement amplitudes. Of most concern in the remaining discussion is the ratio
ha/
hr.
Fig. 1 illustrates the flexibility offered by varying the ratio ha/hr. In Fig. 1(a), ha/hr > 1, and the deepest well (dashed purple curve) is situated above the maximum of h(x), top-site, whereas in panel (c), ha/hr < 1, and the well is deepest for the solid red curve, which is above the minimum of h(x), hollow-site. The figure illustrates why it is not helpful, in the present context, to think of h(x) as a “corrugation function” since it only represents the iso-potential corrugation deep in the repulsive region. Iso-potential contours have a corrugation whose energy dependence is complex, but that complexity can be rendered in a simple and quantitative form through the ratio ha/hr. Only in the case ha/hr = 1 (Fig. 1(b)) is there a single, well-defined value for the iso-potential corrugation.
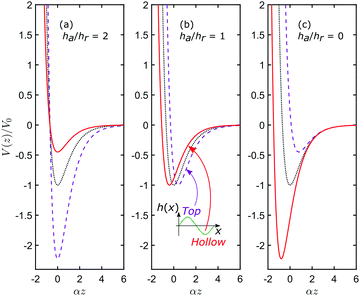 |
| | Fig. 1 Examples of potentials with different values of the parameter ha/hr. The plots show the z-dependence at high-symmetry values of ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) : the dashed purple curves correspond to the potential at : the dashed purple curves correspond to the potential at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = π/2, which we call the top-site (see inset in the central panel); the solid red curves are for = π/2, which we call the top-site (see inset in the central panel); the solid red curves are for ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 3π/2, the hollow-site; and the dotted black curves are at = 3π/2, the hollow-site; and the dotted black curves are at ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) =π. (a) ha/hr = 2, generates a potential where the well is deepest at the top-site; (b) ha/hr = 1, corresponds to the case where the well-depth is the same at all values of =π. (a) ha/hr = 2, generates a potential where the well is deepest at the top-site; (b) ha/hr = 1, corresponds to the case where the well-depth is the same at all values of ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ; (c) ha/hr = 2, gives a potential with the deepest well at the hollow site. ; (c) ha/hr = 2, gives a potential with the deepest well at the hollow site. | |
Parameter values in Fig. 1 are chosen to demonstrate the variety of surface interactions that are possible. For example, panel (c), ha/hr = 0, corresponds to the conventional “corrugated-Morse” potential that has been in use for many years.18 Panel (b), ha/hr = 1, is the form used more recently in classical and semi-classical descriptions of thermal-energy scattering,20,21,22 while panel (a) illustrates that when ha/hr > 1, the site of the deepest well can be shifted from hollow to top.
It is important to note that the extreme variations in well-depth generated by the illustrations in Fig. 1 are unlikely to be observed in practice. The subtle variations in well depth calculated, for example in ref. 11, are reasonably well reproduced by choosing ha/hr ≈ 1. However, as we will show, the behaviour expected in experiment depends critically on whether ha/hr > 1, or ha/hr < 1.
3 Classical perturbation theory for rainbow scattering
3.1 The perturbation expansion
A derivation of the classical theory of elastic scattering from surfaces, using second order perturbation theory may be found in some detail elsewhere.21,22 The basis for the perturbation approach is to expand the potential as a power series in ha and hr, assuming that these displacements are small compared to the unit cell length. In the case of a Morse potential with ha/hr = 1, the result is a simple Taylor series.20 More generally, the expansion becomes| | 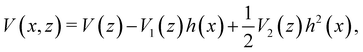 | (3.1) |
where, for the particular choice of potential, eqn (2.3), expansion to second order in the corrugation function h (x) gives| | VM(z, x) = VM(z) + 2V0α[hr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2αz) − ha exp(−2αz) − ha![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αz)]h(x) + V0α2[2hr2 exp(−αz)]h(x) + V0α2[2hr2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2αz) −ha2 exp(−2αz) −ha2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αz)]h2(x), exp(−αz)]h2(x), | (3.2) |
which identifies the functions V1 and V2 appearing in eqn (3.1).
3.2 A short review of classical elastic scattering
The particle is incident on the surface with initial momenta pzi, pxi, the incident vertical momentum is assumed to be negative. The (negative) angle of incidence is by definition| | 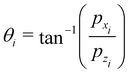 | (3.3) |
and we note that it vanishes for vertical incidence defined by pxi = 0. The final angular distribution is by definition| | 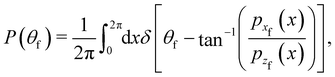 | (3.4) |
where the initial horizontal coordinate x may be considered as an “impact parameter” and the final momenta are functions of it. The angular distribution may be rewritten as| | 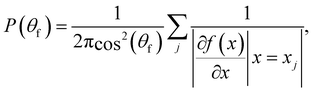 | (3.5) |
where by definition| | 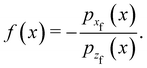 | (3.6) |
The xj 's are functions of the final scattering angle and are all the possible solutions of
| | | θf(x) = tan−1[−f(x)]. | (3.7) |
θf(
x) is known as the classical deflection function (CDF) and the rainbow angles are given by the condition that
| | 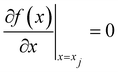 | (3.8) |
at which the classical angular distribution diverges.
It cannot be over-stressed that the rainbow angles are precisely defined only in classical mechanics. In quantum mechanics, due to the discrete structure of the angular distribution in terms of discrete diffraction peaks, the angular distribution is no longer a continuous function of the impact parameter and therefore the derivative with respect to it is ill defined. In quantum mechanics one cannot “know” in advance both the incident horizontal momentum and the impact parameter x due to the uncertainty principle and therefore one should be careful with the notion of “experimental rainbow angles”. They are “experimental” only when the diffraction peaks are sufficiently dense so that effectively the scattering is well approximated as classical scattering. Only if by accident the final rainbow angle is a Bragg angle, one should attribute the corresponding diffraction peak to a rainbow.23
3.3 A short review of classical perturbation theory
In zero-th order perturbation theory only the vertical potential V(z) is considered and the higher order terms in h(x) are set to zero. The zero-th order horizontal motion x0,t is then free motion with momentum pxi such that| | 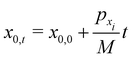 | (3.9) |
and the vertical motion is the solution of| | 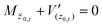 | (3.10) |
with the initial condition ż0,−∞ = Mpzi. The initial vertical distance from the surface is taken to be sufficiently large such that the potential vanishes. To provide symmetric formulae, we assume that the scattering is initiated at t = −∞ and ends at t = +∞ such that the zero-th order vertical trajectory reaches the turning point at time t = 0.
Taking the corrugation into consideration, the first order equation of motion for the vertical distance is
| | 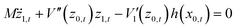 | (3.11) |
and for the horizontal distance it is
| | 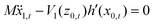 | (3.12) |
The second order equation of motion for the horizontal distance is
| | 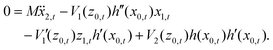 | (3.13) |
The classical angular distribution is obtained by solving for the final momenta. To first order one readily finds for the time dependent horizontal momentum
| | 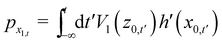 | (3.14) |
while the second order contribution is
| | 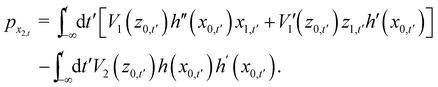 | (3.15) |
For the vertical motion we note that to first order, the final (denoted by the subscript f) vertical momentum may be obtained through the first order energy conservation equation
| | 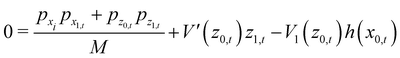 | (3.16) |
so that asymptotically, after the collision is over and the potential terms vanish, we find that the final first order vertical momentum is given in terms of the first order final horizontal momentum
| | 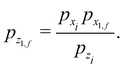 | (3.17) |
Similarly, the second order vertical momentum may be obtained from energy conservation and knowledge of the second order horizontal momentum:
| | 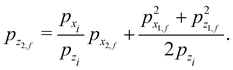 | (3.18) |
However, as seen from eqn (3.15) this entails solution of the first order horizontal equation of motion (3.12) and the first order vertical equation of motion which is derived from the first order energy conservation relation
| | 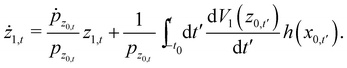 | (3.19) |
The solution of eqn (3.12) and (3.19) is straightforward, but long and tedious, the details may be found in ref. 22. Using the displacement function given in eqn (2.2) and the symmetry in time of the zero-th order vertical motion, one finds that the first order contribution to the horizontal momentum may be written as
| | | px1, f = pziKhwKcos(x) | (3.20) |
where
| | 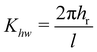 | (3.21) |
is termed the hard wall rainbow angle parameter;
hr being related to the repulsive part of the potential. The coefficient
K is given by
| | 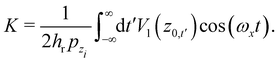 | (3.22) |
The horizontal frequency ωx is defined as
| | 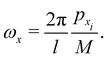 | (3.23) |
The second order contribution to the final horizontal momentum may be written as22
| | | px2,f = pxiKcc + pziKhwsin(2x)K2. | (3.24) |
The explicit expressions for the parameter Kcc are given in eqn (2.33) and (2.34) of ref. 22, and we note that pxiKcc vanishes when the scattering is vertical. The expression for the parameter K2 is given in eqn (2.35) and (2.36) of ref. 22.
3.4 The rainbow angle in GIFAD
The general expressions for the rainbow angles have been derived elsewhere.22 Here we specify them for our purpose of studying the GIFAD experiments which correspond to normal incidence in the plane perpendicular to the incident plane, that is the initial horizontal momentum vanishes. This simplifies the theory. From the definition of the function f (x) in eqn (3.6) and the second order perturbation theory results for the final momenta we find that, for vertical scattering to second order, the CDF is| | 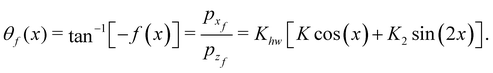 | (3.25) |
The important point for our purposes is that with our simplified model, the first order contribution to the horizontal momentum goes as cos(x) while the second order contribution goes as sin(2x). The rainbow angles are determined by the condition that 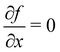 (see eqn (3.8)) and from eqn (3.25), we find that the rainbow solutions for the x's are the solutions of the equation
(see eqn (3.8)) and from eqn (3.25), we find that the rainbow solutions for the x's are the solutions of the equation
| | K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(x) = 2K2 sin(x) = 2K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2x). cos(2x). | (3.26) |
This is already an instructive result. In first order perturbation theory, the second order parameter K2 would be neglected, the solutions for x would be 0 and π such that f(x = 0, π) = ± KhwK. If the function V1(z0,t) = hrV′(z0,t) (which is the case if hr = ha), then K = 1 and the first order solution for vertical scattering would become independent of the energy and just equal to the hard wall scattering rainbow angle. Since, however, we do not make this assumption, we find that even to first order the rainbow angle will become energy dependent and this is demonstrated explicitly for the Morse potential model presented in the next Section.
But we do not want to neglect the second order term K2. Using the variable y = sin(x) we note that eqn (3.26) is a quadratic equation. One of its two solutions will give a value of y which is much larger than unity and unphysical since the second order parameter is typically much smaller than the first order one. The other solution is
| | 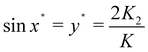 | (3.27) |
from which we deduce that the two possible solutions for the rainbow value
x* are
| | 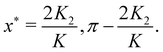 | (3.28) |
From eqn (3.6), we then find that the two vertical rainbow angles are given by
| | 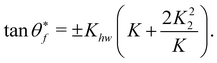 | (3.29) |
Notably, the parameter K2 is dependent on the vertical energy. The two rainbow angles are symmetrically located about the surface normal as they should be for a structureless particle, with vertical incidence and a surface containing a mirror plane.
3.5 A corrugation amplitude derived from the semi-classical action
The action along a classical trajectory is related to the phase induced by the scattering potential and when, multiple trajectories contribute to the scattered intensity, interference oscillations and their energy dependence provide direct and quantitative information about the potential.24 The information in such oscillations arises from the different spatial regions explored by different trajectories. Bocan et al.,11 motivated by the semiclassical theory of surface scattering, use the action of the trajectories to give a definition of a corrugation amplitude.25, 26 As it is based on the scattered phases, it is difficult to make direct comparison with an experiment that measures intensity, not phase. Within the realm of the perturbation theory used here, their definition implies considering the action that appears in the semiclassical first order perturbation theory for elastic scattering of Hubbard and Miller27, 28 and its generalization to second order by Pollak and Miret-Artés.12
The action A(x) of a trajectory as the particle undergoes scattering by the surface is naturally a function of the impact parameter x. Bocan et al.11 define a corrugation amplitude by considering the points of the impact parameter xmax and xmin which respectively maximize and minimize the action. The quantity
| | 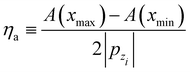 | (3.30) |
has the dimensions of length and the factor two arises from the symmetry of the vertically incident trajectories, the action difference includes the added motion in the maximal action both coming in and going out. Bocan
et al.11 refer to this quantity as a dynamical corrugation, since the action depends on the motion of the particle. The value of
ηa is energy dependent, as the magnitude of the phase shifts contributing to the scattering are themselves functions of the incident energy. For a hard wall potential,
ηa is independent of the energy. In the present context, we note that the use of the word “corrugation” is problematic, and therefore, we refrain from using the concept, except when expressly referring to the work of others such as Bocan
et al. who gave a specific definition.
As shown in ref. 12 within second order perturbation theory, for vertical scattering, with the potential as given in eqn (2.2) and (2.3), the action is given by the general form
| | 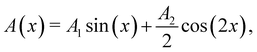 | (3.31) |
where, as may be seen from eqn (2.12) of ref.
12, the first order action
A1 is determined by the relation
| | 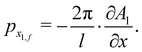 | (3.32) |
While, from eqn (2.16), one sees that the second order action A2 is determined by the relation
| | 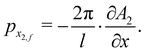 | (3.33) |
The condition for the maximum and minimum of the action with respect to the impact parameter is
| | 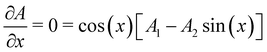 | (3.34) |
from which we note that the solutions are
| | 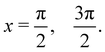 | (3.35) |
The term in the square brackets cannot vanish if perturbation theory is valid, that is we know that A1/A2 ≥ 1. But this means that
| | 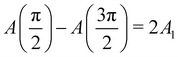 | (3.36) |
so that to second order, the “corrugation amplitude” is
| | 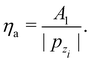 | (3.37) |
This is an interesting observation. The amplitude ηa is obtained by trajectories that maximize and minimize the action. By symmetry, these are straight line trajectories with the x coordinate unchanging in time. Therefore, ηa includes only information from the vertical motion, since there is no contribution from the motion along the horizontal coordinate.
Interestingly, as shown by Hubbard and Miller,27,28 and as may be verified from eqn (3.20) and (3.32), the first order action is given by the expression
| | 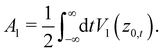 | (3.38) |
Note then the relationship between ηa and the first order expression for the rainbow angle. Using eqn (3.22), (3.29), (3.37) and (3.38), we find the illuminating result
| | 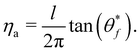 | (3.39) |
The corrugation amplitude derived from the action, ηa, and the tangent of the vertical rainbow angle are proportional to each other. The proportionality factor is an energy independent constant. In other words, any energy dependence in the SIVR-corrugation of Bocan et al.,11 or equivalently ηa, will be manifested in the energy dependence of the rainbow angle and vice versa. The information content of both of these at least within first order perturbation theory is identical and the result will be valid whenever the second order term is sufficiently small.
4 Scattering phenomenology from a Morse potential model
As detailed in the Appendix, one readily finds that, for the Morse potential model, defined in Section 2, the first order coefficient K defined in eqn (3.22) is| | 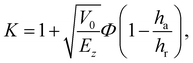 | (4.1) |
where Φ is defined by| | 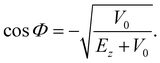 | (4.2) |
To first order the distance between the tangents of the rainbow angles (see eqn (3.29)) is
| | 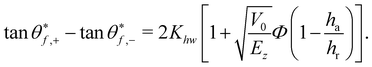 | (4.3) |
This is a central result. If the well depth vanishes, or alternatively if the well depth has no lateral variation, that is, if ha/hr = 1, Fig. 1b, the parameter K becomes a constant (K = 1) independent of the energy and the rainbow angles are identical to the hard wall result. On the other hand, if ha/hr ≠ 1, the distance between the vertical rainbow angles changes as the energy is lowered. At high energy, the slight change in potential energy due to the corrugation amplitudes becomes negligible, and the distance between the rainbow angles becomes energy independent.
These conclusions are illustrated in Fig. 2, which shows the dependence of the classical rainbow angle on the incident energy, in first-order perturbation theory. Variation with the incident energy is seen to depend critically on the potential in the region of the well. It is not the depth of the well, per se, that causes the variation but the way that depth is modulated parallel to the surface. In cases where the well is deepest above the hollow site (see Fig. 1c), ha/hr < 1 the rainbow angle increases at low-energy (solid red and dash-dot blue curves), whereas when the deepest well is located above the top-site, ha/hr < 1, the rainbow angle decreases with energy (purple, dashed curve). A measurement showing an increase in the rainbow angle as the energy is lowered immediately reveals that ha < hr. As noted in the previous section, a corrugation amplitude derived from the semi-classical action has, to first order, the same energy dependence as that of the rainbow angle, eqn (3.39), and is therefore also given by eqn (4.1).
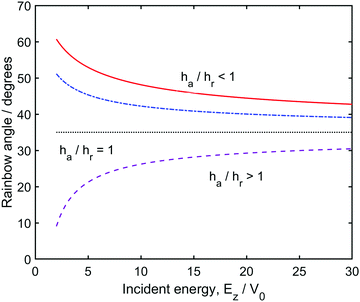 |
| | Fig. 2 First-order contribution to the energy-dependence of the rainbow angle, from eqn (4.3). Examples show corrugated potentials with different values of the parameter ha/hr. The dotted black curve shows the case for ha/hr = 1, where the potential is uniformly corrugated. It is the only case where there is no variation with incident energy. For cases where the deepest-well is located above a hollow-site (see Fig. 1) the rainbow angle increases, to first-order, as the energy is lowered: solid red-curve ha/hr = 0; dash-dotted blue-curve ha/hr = 0.5. For cases where the deepest-well is located above a top-site (see Fig. 1) the rainbow angle decreases: dashed purple-curve ha/hr = 1.5. In all cases the hard-wall parameter, Khw, is chosen to be close to the value seen in recent work.11 It corresponds to a rainbow-angle of 35°, and the repulsive corrugation parameter, hr, can be determined through eqn (3.21). | |
To complete the picture, we also estimate the contribution coming from the second order perturbation theory term. If hr = ha, one readily finds an analytic result as shown in the Appendix
| | 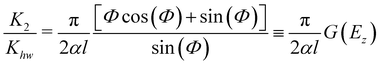 | (4.4) |
and therefore, the rainbow angles are given by
| | 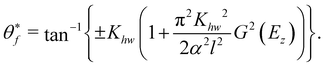 | (4.5) |
Fig. 3 shows the second order contribution to the rainbow angle for various values of the potential softness (defined through the parameter π/αl, with ha/hr = 1, so that the first order contribution is zero). In Fig. 3 there is a minimum in all curves when Ez ≈ 4V0. Here, G(Ez) = 0 so that tan(Φ) = −Φ. The minimum near Ez ≈ 4V0 gives an immediate indication of the energy range where these effects will be observed. Fig. 3 also demonstrates how the softness of the potential determines the magnitude of the shift in rainbow-angle. Softer potentials exhibit greater shift, at low and high energy and, as noted above, there is no shift in the hard-wall limit.
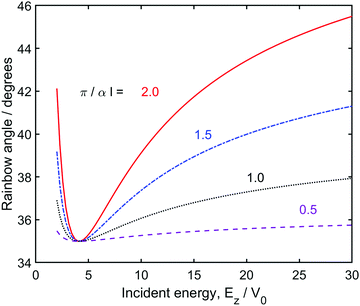 |
| | Fig. 3 Second-order effect on the rainbow angles calculated with ha/hr = 1 and eqn (4.5). Note that the first-order shift from the hard-wall result is zero for ha/hr = 1. Curves, from top to bottom have π/αl = 2, 1.56, 1.0, 0.5. Softer potentials show greater effects at all energies. In all cases the hard-wall parameter, Khw, is chosen to be close to the value seen in recent work.11 It corresponds to a rainbow-angle of 35°, and the repulsive corrugation parameter, hr, can be determined through eqn (3.21). | |
Finally, we note that if the well depth vanishes or equivalently as the energy goes to infinity
| | 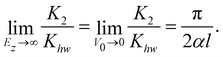 | (4.6) |
The result implies that, even at high energy, the softness of the potential affects the rainbow angle.
5 Summary and conclusions
The GIFAD experiments open up new tools for exploring surfaces and the interaction of atoms and molecules with surfaces. This is especially facilitated in the classical limit, so that a proviso for the following discussion is that the diffraction pattern is sufficiently dense such that one may identify with some certainty for example the rainbow angles and their energy dependence. Using classical perturbation theory, we demonstrated how the energy dependence of the rainbow angles can be inverted into information on the force field governing the scattering.
Here, we make a few central observations. One is that energy dependence of the rainbow angle can be attributed mainly to the existence of an attractive well as the projectile approaches the surface. The depth of the well may be assessed with reasonable accuracy from the quantitatively measured energy dependence. Secondly, in principle, the distance between the rainbow angles may increase or decrease with decreasing energy. An increase immediately implies that the variation of the periodic potential with the impact parameter is larger in the repulsive region of the potential as compared to the long ranged attractive region and vice versa.
From a theoretical point of view, the perturbation theory is much richer than a hard wall model. Due to this richness we recommend that henceforth one replaces the hard wall model with the analytic model presented in the present paper. Or course, the Morse model used has its limitations. We know that the long range potential decays as a power law in the distance and not exponentially as in the Morse potential mode. Yet, the fact that the Morse potential is amenable to analytic solution is a huge advantage and the results are at least qualitatively correct and, in any case, give a much more reliable account of the scattering as compared to hard wall potential models. We note that there is much more to be done; for example, we limited ourselves mainly to the low vertical energy scattering regime. Especially the second order perturbation theory results should be useful for an analysis of the scattering in the high energy regime as reported for example in ref. 1. Moreover, we described the variation of the potential in the horizontal direction using a single sine function. One may use the perturbation theory approach to analyse the scattering with more complicated x dependent potentials, however, this might just obfuscate some of the clear qualitative conclusions that may be reached by using a single sine (or cosine) function.
The concept of corrugation is an old one, yet not precisely defined. On purpose, we have limited the use of the word “corrugation” here to stress this fact. Typically one has used the hard wall model to extract a height parameter which is then considered to be the “corrugation amplitude”. The analysis presented here should be sufficient to show that it is, at best, a highly qualitative way of describing properties of the surface. As one may learn from the work of Bocan et al.,11 a hard wall corrugation that is energy dependent, loses its simplistic meaning. Moreover, we showed that the energy dependent “dynamic corrugation” as defined by Bocan et al. is the same (up to a trivial constant) as the energy dependence of the tangent of the rainbow angles. In other words, it adds little or no information about the scattering that cannot be gleaned from the experimentally measured energy dependent rainbow angle.
It is then of interest to analyse the results of Bocan et al.10,11 in view of the tools and insight obtained in our work. They considered the scattering of a He atom on a KCl(001) surface. Their experiment is carried out with fast He atoms, incident at grazing angles such that the scattering is reduced to two dimensional scattering in the plane perpendicular to the direction of the incident atom. Their normal-energy corresponds to our energy Ez and their y direction corresponds to our horizontal motion along the x axis.
Since they are using a light atom (He), and as also may be noted from the supplementary material of their ref. 10, the measured diffraction pattern shows only a few well defined diffraction peaks. It is in the quantum regime and therefore there is no well defined rainbow angle. Indeed, their “experimental” “dynamic corrugation” and rainbow-angles are obtained indirectly from the experiment by fitting an effective hard-wall potential to the data at each value of the normal-energy, Ez. This inversion then shows a clear increase in the rainbow-angle as the scattering energy is decreased from 40 to 20 meV. It follows from our Fig. 2 that the scattering potential has ha/hr < 1 so the well is somewhat deeper above the hollow-site than the top-site. The onset of the increase in the inferred rainbow angle seen in their Fig. 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 is more marked than suggested by the first-order contribution (Fig. 2), and this suggests that second-order contributions cannot be neglected. Our Fig. 3 indicates that, at high energies, the second-order contribution will tend to cancel that of a first-order contribution, given ha/hr < 1. The extent of the cancellation will depend on the softness of the potential and thus the observed energy dependence could lead to an inferred softness in the potential. Furthermore, from the position of the minimum in Fig. 3, a well-depth of 5–10 meV is indicated in the scattering of He on the KCl(001) surface. These very qualitative conclusions are in accord with comparisons with the various DFT potentials presented in ref. 11 and suggest that a more forensic analysis of features in the potential would be beneficial.
11 is more marked than suggested by the first-order contribution (Fig. 2), and this suggests that second-order contributions cannot be neglected. Our Fig. 3 indicates that, at high energies, the second-order contribution will tend to cancel that of a first-order contribution, given ha/hr < 1. The extent of the cancellation will depend on the softness of the potential and thus the observed energy dependence could lead to an inferred softness in the potential. Furthermore, from the position of the minimum in Fig. 3, a well-depth of 5–10 meV is indicated in the scattering of He on the KCl(001) surface. These very qualitative conclusions are in accord with comparisons with the various DFT potentials presented in ref. 11 and suggest that a more forensic analysis of features in the potential would be beneficial.
A more quantitative analysis would be possible if the raw data at all measured energies were available; however, pursuing an approach, where the experiment is discussed in the context of an effective, energy-dependent hard-wall model is not very illuminating. In the semi-classical picture, intensity variations in the diffraction data arise from interference between trajectories leading to the same final state. These classical trajectories accumulate phase-shifts depending on the potential in the regions of space that they explore1,24 and the interference effects could be a more informative source for a quantitative analysis. There is a possible analogy with tomographic methods here. As the energy is varied, the classical paths scan systematically through real-space and the accumulated phase is directly related to the spatial variation of the potential. Thus, a more quantitative, albeit numerical, view of the full potential could be elucidated.
Finally, we note that the analysis given above is entirely elastic. Inelastic effects could been included, to first and second order, using classical and semi-classical perturbation theory methods.20,29 These may also offer the opportunity to explore the role of surface temperature and frictional coupling in the scattering.
Author contributions
All authors contributed equally to this work.
Conflicts of interest
There are no conflicts to declare.
Appendix
A Analytic details for the Morse potential model
For the Morse potential, the zero-th order trajectory is known analytically (eqn (4.16) of ref. 22)| | 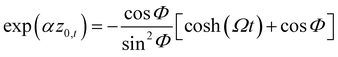 | (A.1) |
with| | 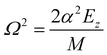 | (A.2) |
and| | 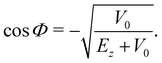 | (A.3) |
From eqn (4.6) of Zhou et al. we note the integral
| | 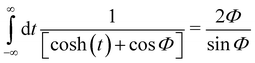 | (A.4) |
so that by taking the derivative we also find
| | 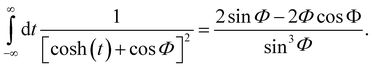 | (A.5) |
Using the definition of V1 in eqn (3.22) one readily finds that
| | 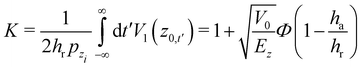 | (A.6) |
and this is the result given in
eqn (4.1).
When hr = ha = h one readily sees that| | | V1 (z) = hV′(z), V2(z) = h2V′′(z) | (A.7) |
and this enables one to obtain an analytic form for the second order parameter K2 when V(z) is a Morse potential. From eqn (3.34) and (3.35) of ref. 22 one readily finds that| | 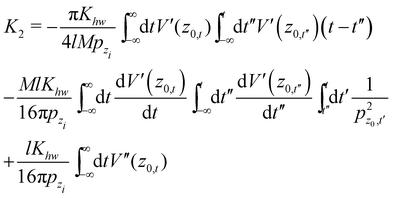 | (A.8) |
In general, even without specifying the Morse potential, due to the vertical scattering condition, the second and third terms cancel each other. Using the fact that 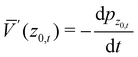 and integrating by parts we note that
and integrating by parts we note that
| | 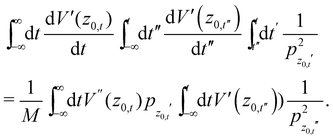 | (A.9) |
Then with a further integration by parts we have that
| | 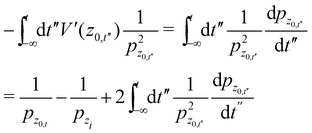 | (A.10) |
from which we infer that
| | 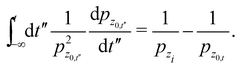 | (A.11) |
Using the fact that ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ′′(z0,t)pz0,t' is an antisymmetric function with respect to time, we readily find
′′(z0,t)pz0,t' is an antisymmetric function with respect to time, we readily find
| | 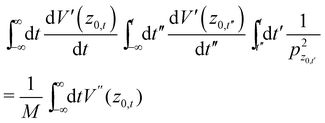 | (A.12) |
so that indeed the second and third integrals in
eqn (A.8) cancel each other. The remaining integral may be further simplified. Using the zero-th order trajectory and following the usual manipulations we find
| | 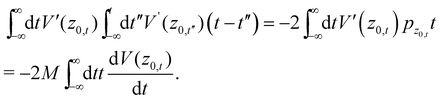 | (A.13) |
Specifying to the Morse potential where the zero-th order trajectory is known analytically (eqn (A.1)) and integrating by parts remembering the known integrals as in eqn (A.4) and (A.5) and manipulating we find
| | 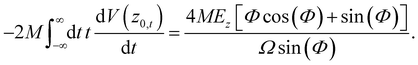 | (A.14) |
Inserting this into the expression for K2 (eqn (A.8)) one finds the desired answer
| | 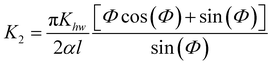 | (A.15) |
and this is the result given in
eqn (4.4).
Acknowledgements
In this Festschrift devoted to Giorgio Benedek, we would like to thank him for being an important referent in low dimensional systems, surface related phenomena and material science. His outstanding contributions have served as a fundamental guide to us personally as well as different communities. SMA would like to thank support from Ministerio de Ciencia e Innovación (Spain) with Project PID2021-125735NB-I00 and Fundación Humanismo y Ciencia. EP thanks the Israel Science Foundation (grant no. 408/19) for its generous support. WA acknowledges support from the Cambridge Atom Scattering Facility (https://atomscattering.phy.cam.ac.uk) and EPSRC award EP/T00634X/1.
References
- H. Winter and A. Schüller, Prog. Surf. Sci., 2011, 86, 169–221 CrossRef CAS.
- M. Debiossac, P. Pan and P. Roncin, Phys. Chem. Chem. Phys., 2021, 23, 7615–7636 RSC.
- B. Holst and G. Bracco, Springer Series in Surface Sciences, 2013, 51, 333–365 CAS.
-
G. Benedek and J. P. Toennies, Atomic Scale Dynamics at Surfaces, Springer Berlin Heidelberg, 2018, vol. 63, pp. 1-30 Search PubMed.
- P. Rousseau, H. Khemliche, A. G. Borisov and P. Roncin, Phys. Rev. Lett., 2007, 98, 016104 CrossRef CAS PubMed.
- A. Schüller, S. Wethekam and H. Winter, Phys. Rev. Lett., 2007, 98, 016103 CrossRef PubMed.
- M. Debiossac, P. Roncin and A. G. Borisov, J. Phys. Chem. Lett., 2020, 11, 4564–4569 CrossRef CAS PubMed.
- P. Atkinson, M. Eddrief, V. H. Etgens, H. Khemliche, M. Debiossac, A. Momeni, M. Mulier, B. Lalmi and P. Roncin, Appl. Phys. Lett., 2014, 105, 021602 CrossRef.
- A. Momeni, E. M. S. Casagrande, A. Dechaux and H. Khemliche, J. Phys. Chem. Lett., 2018, 9, 908–913 CrossRef CAS PubMed.
- G. A. Bocan, H. Breiss, S. Szilasi, A. Momeni, E. M. Casagrande, M. S. Gravielle, E. A. Sánchez and H. Khemliche, Phys. Rev. Lett., 2020, 125, 096101 CrossRef CAS PubMed.
- G. A. Bocan, H. Breiss, S. Szilasi, A. Momeni, E. M. S. Casagrande, E. A. Sánchez, M. S. Gravielle and H. Khemliche, Phys. Rev. B, 2021, 104, 235401 CrossRef CAS.
- E. Pollak and S. Miret-Artés, J. Phys. Chem. C, 2015, 119, 14532–14541 CrossRef CAS.
- E. Schweizer, C. Rettner and S. Holloway, Surf. Sci., 1991, 249, 335–349 CrossRef CAS.
- T. Kondo, H. S. Kato, T. Yamada, S. Yamamoto and M. Kawai, Eur. Phys. J. D, 2006, 38, 129–138 CrossRef CAS.
- A. M. Lahee, W. Allison and R. F. Willis, Surf. Sci., 1984, 147, L630–L636 CrossRef CAS.
- D. Farías and K. H. Rieder, Rep. Prog. Phys., 1998, 61, 1575–1664 CrossRef.
- S. J. Schmutzler, A. Ruckhofer, W. E. Ernst and A. Tamtögl, Phys. Chem. Chem. Phys., 2022, 24, 9146 RSC.
- A. S. Sanz and S. Miret-Artés, Phys. Rep., 2007, 451, 37–154 CrossRef.
- P. Pan, M. Debiossac and P. Roncin, Phys. Rev. B, 2021, 104, 165415 CrossRef CAS.
- S. Miret-Artés and E. Pollak, Surf. Sci. Rep., 2012, 67, 161–200 CrossRef.
- S. Miret-Artés, S. Daon and E. Pollak, J. Chem. Phys., 2012, 136, 204707 CrossRef PubMed.
- Y. Zhou, E. Pollak and S. Miret-Artés, J. Chem. Phys., 2014, 140, 024709 CrossRef PubMed.
- M. Hernández, S. Miret-Artés, P. Villarreal and G. Delgado-Barrio, Surf. Sci., 1993, 290, L693–L698 CrossRef.
- C. Huang, D. A. MacLaren, J. Ellis and W. Allison, Phys. Rev. Lett., 2006, 96, 126102 CrossRef CAS PubMed.
- M. S. Gravielle and J. E. Miraglia, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 052718 CrossRef.
- M. S. Gravielle and J. E. Miraglia, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 062709 CrossRef.
- L. M. Hubbard and W. H. Miller, J. Chem. Phys., 1983, 78, 1801 CrossRef CAS.
- L. M. Hubbard and W. H. Miller, J. Chem. Phys., 1984, 80, 5827–5831 CrossRef CAS.
- S. Daon and E. Pollak, J. Chem. Phys., 2015, 142, 174102 CrossRef PubMed.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b and
Eli
Pollak
b and
Eli
Pollak
 c
c
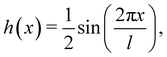
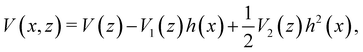
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2αz) − ha
exp(−2αz) − ha![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αz)]h(x) + V0α2[2hr2
exp(−αz)]h(x) + V0α2[2hr2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2αz) −ha2
exp(−2αz) −ha2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αz)]h2(x),
exp(−αz)]h2(x),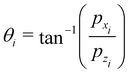
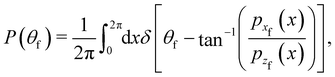
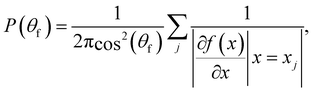
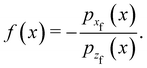
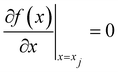
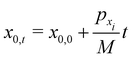
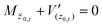
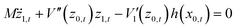
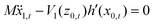
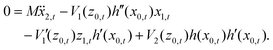
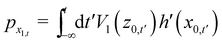
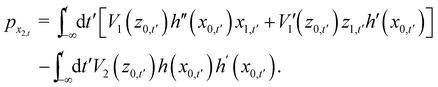
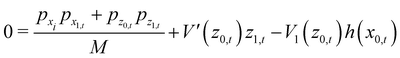
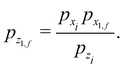
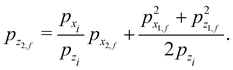
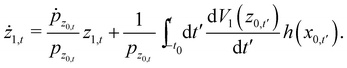
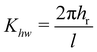
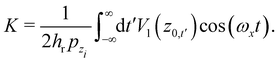
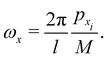
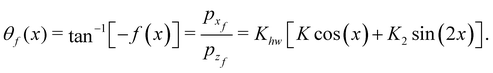
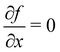 (see eqn (3.8)) and from eqn (3.25), we find that the rainbow solutions for the x's are the solutions of the equation
(see eqn (3.8)) and from eqn (3.25), we find that the rainbow solutions for the x's are the solutions of the equation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(x) = 2K2
sin(x) = 2K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2x).
cos(2x).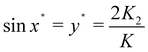
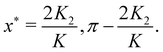
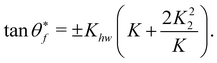
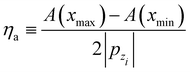
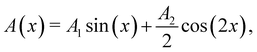
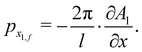
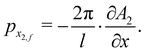
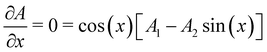
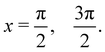
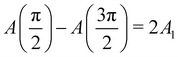
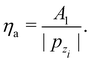
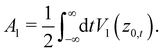
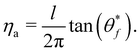
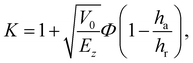
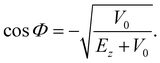
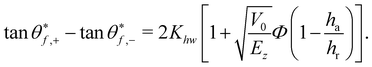

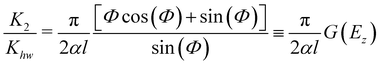
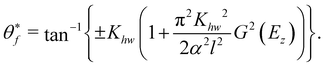

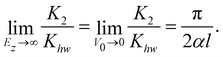
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 is more marked than suggested by the first-order contribution (Fig. 2), and this suggests that second-order contributions cannot be neglected. Our Fig. 3 indicates that, at high energies, the second-order contribution will tend to cancel that of a first-order contribution, given ha/hr < 1. The extent of the cancellation will depend on the softness of the potential and thus the observed energy dependence could lead to an inferred softness in the potential. Furthermore, from the position of the minimum in Fig. 3, a well-depth of 5–10 meV is indicated in the scattering of He on the KCl(001) surface. These very qualitative conclusions are in accord with comparisons with the various DFT potentials presented in ref. 11 and suggest that a more forensic analysis of features in the potential would be beneficial.
11 is more marked than suggested by the first-order contribution (Fig. 2), and this suggests that second-order contributions cannot be neglected. Our Fig. 3 indicates that, at high energies, the second-order contribution will tend to cancel that of a first-order contribution, given ha/hr < 1. The extent of the cancellation will depend on the softness of the potential and thus the observed energy dependence could lead to an inferred softness in the potential. Furthermore, from the position of the minimum in Fig. 3, a well-depth of 5–10 meV is indicated in the scattering of He on the KCl(001) surface. These very qualitative conclusions are in accord with comparisons with the various DFT potentials presented in ref. 11 and suggest that a more forensic analysis of features in the potential would be beneficial.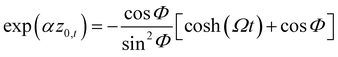
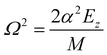
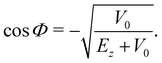
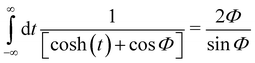
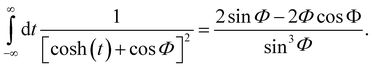
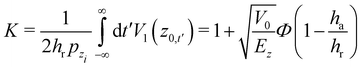
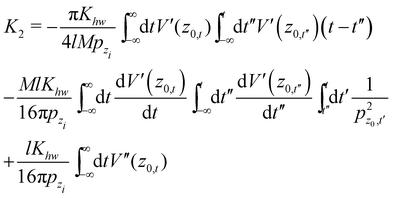
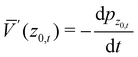 and integrating by parts we note that
and integrating by parts we note that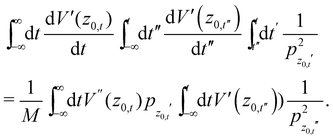
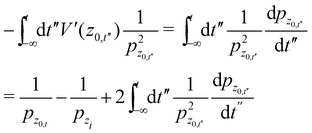
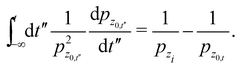
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ′′(z0,t)pz0,t' is an antisymmetric function with respect to time, we readily find
′′(z0,t)pz0,t' is an antisymmetric function with respect to time, we readily find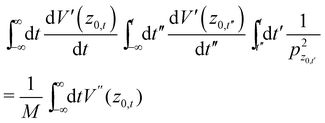
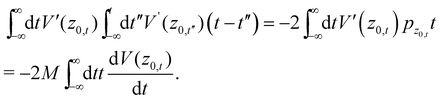
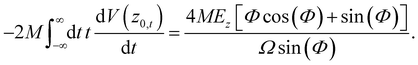
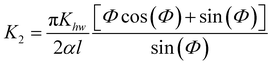


![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)