Accounting for molecular flexibility in photoionization: case of tert-butyl hydroperoxide†
Jérémy
Bourgalais
 *a,
Zhongming
Jiang
*a,
Zhongming
Jiang
 b,
Julien
Bloino
b,
Julien
Bloino
 b,
Olivier
Herbinet
b,
Olivier
Herbinet
 a,
Hans-Heinrich
Carstensen
a,
Hans-Heinrich
Carstensen
 cd,
Gustavo A.
Garcia
cd,
Gustavo A.
Garcia
 e,
Philippe
Arnoux
a,
Luc-Sy
Tran
f,
Guillaume
Vanhove
e,
Philippe
Arnoux
a,
Luc-Sy
Tran
f,
Guillaume
Vanhove
 f,
Laurent
Nahon
f,
Laurent
Nahon
 e,
Frédérique
Battin-Leclerc
e,
Frédérique
Battin-Leclerc
 a and
Majdi
Hochlaf
a and
Majdi
Hochlaf
 *g
*g
aUniversité de Lorraine, CNRS, LRGP, F-54000 Nancy, France. E-mail: jeremy.bourgalais@univ-lorraine.fr
bSMART Laboratory, Scuola Normale Superiore, Pisa, Italy
cThermochemical Processes Group (GPT), Department of Chemical and Environmental Engineering, Engineering and Architecture School, University of Zaragoza, Spain
dFundacion Agencia Aragonesa para la Investigacion y el Desarrollo (ARAID), Zagaroza, Spain
eSynchrotron SOLEIL, L’Orme des Merisiers, Saint-Aubin-BP 48, 91192 Gif-sur-Yvette Cedex, France
fPC2A, Université de Lille, CNRS, Avenue Mendeleiev, 59650 Villeneuve-d'Ascq, France
gUniversité Gustave Eiffel, COSYS/LISIS, 5 Bd Descartes 77454, Champs sur Marne, France. E-mail: majdi.hochlaf@univ-eiffel.fr
First published on 14th April 2022
Abstract
tert-Butyl hydroperoxide (tBuOOH) is a common intermediate in the oxidation of organic compounds that needs to be accurately quantified in complex gas mixtures for the development of chemical kinetic models of low temperature combustion. This work presents a combined theoretical and experimental investigation on the synchrotron-based VUV single photon ionization of gas-phase tBuOOH in the 9.0 - 11.0 eV energy range, including dissociative ionization processes. Computations consist of the determination of the structures, vibrational frequencies and the energetics of neutral and ionic tBuOOH. The Franck–Condon spectrum for the tBuOOH+ (X+) + e− ← tBuOOH (X) + hν transition is computed, where special treatment is undertaken because of the flexibility of tBuOOH, in particular regarding the OOH group. Through comparison of the experimental mass-selected threshold photoelectron spectra with explicitly correlated coupled cluster calculations and Franck–Condon simulations that account for the flexibility of the molecule, an estimation of the ionization energy is given. The appearance energy of the only fragment observed within the above-mentioned energy range, identified as the tert-butyl C4H9+, is also reported. Finally, the signal branching ratio between the parent and the fragment ions is provided as a function of photon energy, essential to quantify tBuOOH in gas-phase oxidation/combustion experiments via advanced mass spectrometry techniques.
I. Introduction
Organic hydroperoxides (R–OOH) are key compounds in the atmospheric oxidation of volatile organic compounds (∼300 K) and play an important role in the formation and evolution of secondary organic aerosols in the atmosphere.1,2 They are present in the liquid/gas phase oxidation of fuels at higher temperatures (∼400–1000 K) as well, and are responsible for the two-stage autoignition of fuel components in internal combustion engines.3 An in-depth knowledge of the elementary reactions involving hydroperoxides is necessary to develop predictive kinetic models that are essential to improve and develop combustion processes, or to understand the impact of emissions on the Earth's radiation balance. This requires quantitative information on hydroperoxides to confront the predictions of kinetic models with laboratory experiments, but such kinetic investigations remain scarce in the literature.Molecular-beam sampling coupled to an advanced mass spectrometer using a tunable photon ionization source is one of the suitable analytical tools for the study of hydroperoxides in complex mixtures.4 The combination of photoelectron spectroscopy with mass spectrometry, in the so-called photoelectron photoion coincidence spectroscopy (PEPICO) scheme, is a powerful multiplex analysis technique that allows the sensitive detection and identification of species in complex mixtures. However, the signal conversion to quantification remains a challenging process subject to significant uncertainty. For instance, to achieve a rigorous quantification of R—OOH by photoionization-based mass spectrometry in oxidation and combustion experiments,5,6 the absolute ionization cross-sections of all species involved are needed. In addition, although tunable sources lead to soft ionization, greatly simplifying species detection, fragmentation cannot always be avoided and some cations are unstable even in their ground state. Therefore, the measurements of the photoionization cross-sections (PICS) of species that tend to fragment upon ionization require the knowledge of the fragmentation pattern because the total PICS arises from the total ion count corresponding to the parent plus daughters contributions.7
Hydroperoxides belong to the group of species whose cations strongly fragment, which makes quantification of their concentration as neutrals in gas mixtures a challenging task, further complicated by their limited commercial availability. The synthesis and purification of hydroperoxides is difficult because of their tendency to spontaneously decompose exothermically.8tert-Butyl hydroperoxide (tBuOOH), a tertiary hydroperoxide, is one of the most stable hydroperoxides,9 with many interesting industrial applications (see Willms et al.10 and references therein). tBuOOH is also a widely used radical precursor for OH kinetic measurements with organic species.11–14
This work is centered onto the photoionization and dissociative photoionization of tBuOOH and also on the main tBuOOH cation possible fragment ions. In the literature, only a single study on tBuOOH cation fragmentation can be found, to our knowledge: the work of Stevens et al.15 who investigated the dissociation dynamics of energy-selected tBuOOH ions using threshold photoelectron-photoion coincidence (TPEPICO) spectrometry forming the t-butyl (C4H9+) cation + HO2. This channel was compared with the dissociative ionization of the neo-pentane cation, whose main dissociation pathway also leads to the t-butyl (C4H9+) cation. However, in the work of Stevens et al.15 the photoelectron spectra (PES) of the parent and daughter species were not provided, nor was the parent survival ratio as a function of the photon energy reported.
The present work makes use of double imaging photoion photoelectron coincidence (i2PEPICO) spectroscopy coupled to VUV synchrotron radiation to fully characterize the dissociative single photon ionization of tBuOOH. The interpretation of the spectra is supported by high-level quantum chemical calculations. In addition to the structural, spectroscopic and energetic properties of tBuOOH cation, the Franck–Condon (FC) simulated spectrum for the tBuOOH+ (X+) + e− ← tBuOOH (X) + hν transition is provided. In the latter calculations, special care was taken to treat the low-frequency modes, in particular the C–OOH torsional mode, accurately. Indeed, this work shows that the standard treatment may lead to erroneous FC envelops for this class of flexible organic compounds.16
II. Experimental procedure, methodology and materials
The experiments were performed at the DESIRS VUV beamline with the i2PEPICO spectrometer DELICIOUS III at the SOLEIL synchrotron facility located in Saint-Aubin, France. The configurations of the beamline, the SAPHIRS molecular beam chamber and the i2PEPICO spectrometer, have already been presented in detail before and only a description related to the parameters used in the present experiments are given hereafter.17–19 The VUV photons were delivered by a variable polarization undulator, which was set to linear, and monochromatized by a 200 gr mm−1 6.65 m radius spherical normal incidence grating, before being focused on a spot of ∼200 × 200 μm in the ionization region. The used 200 μm slit led to a photon energy resolution of ∼12 meV at 10 eV. Only photon energies below 14 eV were used, so the gas filter located upstream the monochromator was filled with Kr to suppress high-order harmonics from the undulator.20 The photon energy was calibrated using the 5s and 5s′ Kr autoionization lines,21 to a precision of 3 meV.A He flow at about 800 mbar was passed through a bubbler containing ≃12 mL of a solution of tert-butyl hydroperoxide diluted in n-decane (≃5.0–6.0 mol L−1), supplied by Sigma-Aldrich. The resulting vapor was adiabatically expanded through a 70 μm nozzle into the expansion chamber (Pexp ≃ 6.2 × 10−6 mbar) and traversed a first skimmer (ϕ = 1 mm) leading to a differentially pumped chamber (Pdiff ≃ 7.7 × 10−7 mbar) and then a second skimmer (ϕ = 2 mm) leading to the ionization chamber (Pion ≃ 7.0 × 10−8 mbar). The molecular beam crossed the synchrotron radiation at the center of the DELICIOUS III double imaging photoelectron/photoion coincidence (i2PEPICO) spectrometer.22 Electrons and ions are accelerated perpendicularly by a constant 88 V cm−1 electric field, towards a velocity map imaging device and a modified Wiley–McLaren time of flight 3D-momentum imaging analyzer respectively.23,24 The coincidence scheme yields mass-selected photoelectron images which are then Abel inverted25 to obtain photoelectron spectra for each mass of interest. The coincidence signal can then be plotted as a function of electron and photon energy, from which the slow photoelectron spectrum (SPES) can be obtained by integration along constant ionic state lines.26,27 The SPES have been corrected by the beamline's flux as measured with a dedicated photodiode, and the error bars shown in the following mass-selected SPES have been obtained assuming a Poisson distribution in the photoelectron images, which is then carried through the Abel inversion operations using standard error propagation formulas. The total (photon + electron) energy resolution of the SPES in this work is ∼20 meV.
III. Theoretical methods
Computations started by optimizing the ground state of neutral and cationic tBuOOH equilibrium structures. These computations are done using the density functional theory (DFT) PBE0 exchange–correlation functional, where the atoms are described using the aug-cc-pVDZ basis set, as implemented in GAUSSIAN 16.28 No constraints were applied (i.e. C1 point group computations, where all coordinates were relaxed). Afterwards, the PBE0/aug-cc-pVDZ geometries were used for post-Hartree–Fock computations to deduce an accurate adiabatic ionization energy (AIE) of tBuOOH. Indeed, we performed single point computations using the explicitly correlated coupled clusters single and double with perturbative treatment of triple excitations (i.e. (R)CCSD(T)-F12 (approximation b)29–31) approach as implemented in MOLPRO,32 where the atoms were described using the aug-cc-pVXZ (X = D,T) basis sets and the corresponding density fitting and resolution-of-identity (RI) functions as implemented in MOLPRO.33–36 Then, the tBuOOH AIE is deduced using a composite scheme,37 namely the PBE0/aug-cc-pVDZ(Optg)//(R)CCSD(T)-F12(b)/aug-cc-pVXZ (X = D,T) (+ΔZPE), where ΔZPE stands for the zero-point vibrational energy correction. Optg refers to full geometry optimisation.Vibrationally-resolved electronic spectra were computed within the Franck–Condon approximation, using the implementation and protocol described in Bloino et al.38 The FC spectrum should correspond to a direct photoionization process, i.e. to the photoelectron spectrum (PES) of tBuOOH. To generate the full PES band-shape with full account of potential temperature effects, the time-dependent (TD) formalism was used. The required quantities, that is, the initial- and final-state equilibrium geometries, normal coordinates and harmonic frequencies, were obtained by optimizing the neutral and cationic forms of tBuOOH at the DFT level using the PBE0 exchange correlation functional in conjunction with the aug-cc-pVTZ basis set and then by computing the analytic force constants, as implemented in GAUSSIAN 16, where normal coordinates are defines with respect to Cartesian displacements. Very tight criteria were used for the optimization, which means that the convergence was reached when the maximum force was smaller than 5 × 10−6 Hartrees Bohr−1 and the maximum displacement lower than 2 × 10−5 Å. The electronic transition dipole moment was assumed constant and set to unity, an approach justified by the fact that the ground electronic state of tBuOOH is the only interest here. Although the procedure implemented in GAUSSIAN 16 is straightforward to generate such spectra for rigid molecules, the flexibility of tBuOOH leads to some significant structural changes upon photoionizing this molecule, in particular with respect to the vibrational modes involving the OOH group (e.g. torsional mode along the OO bond). Therefore, a special treatment was adopted here to derive the FC spectrum for the tBuOOH+ (X+) + e− ← tBuOOH (X) + hν transition (vide infra).
For anharmonic calculations, the second-order vibrational perturbation theory (VPT2) was used, as implemented in GAUSSIAN 16. The necessary third and semi-diagonal fourth derivatives of the potential energy were generated by numerical differentiation of analytic second derivatives obtained at displaced geometries by moving from the equilibrium geometry along each mass-weighted coordinate with a fixed step of 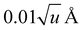 , u refers the atomic mass unit. VPT2 is known to perform poorly in presence of large amplitude motions, like hindered rotors. For this reason, all the modes previously identified as hindered rotors were set to be passive, which means that the anharmonic correction on their fundamentals was ignored, and all anharmonic constants involving those modes were nullified. Fermi resonances and Darling–Dennison couplings were automatically identified using the default parameters in GAUSSIAN 16.
, u refers the atomic mass unit. VPT2 is known to perform poorly in presence of large amplitude motions, like hindered rotors. For this reason, all the modes previously identified as hindered rotors were set to be passive, which means that the anharmonic correction on their fundamentals was ignored, and all anharmonic constants involving those modes were nullified. Fermi resonances and Darling–Dennison couplings were automatically identified using the default parameters in GAUSSIAN 16.
IV. Results and discussion
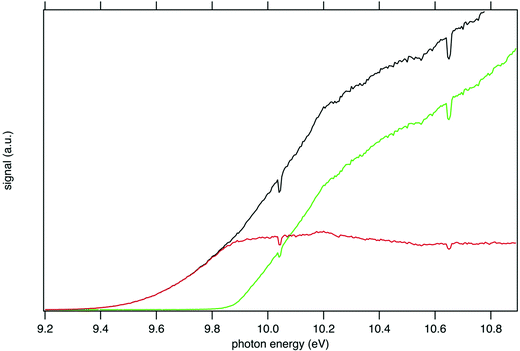
Fig. 1 presents the recorded mass spectrum of a tBuOOH/n-decane mixture in helium after single photon ionization by synchrotron radiation. The mass spectrum is integrated over the 9.0–11.0 eV photon energy range. Fig. 1 shows that the most important signals measured are m/z 57, 58, 59, 90, 142, and 146. m/z 90 and 142 are the parent species of the bubbled sample, tBuOOH and n-decane with their 13C natural counterpart at m/z 91 and 143 respectively. Minor peaks between m/z 72, 74, and 76 are noticed. The total signal is about 20% of that of m/z 59. These peaks have been identified as methyl ethyl ketone, tert-butanol, and isopropyl hydroperoxide respectively (see the right panel in Fig. S1 and S2, ESI†). These species likely originate from the decomposition of tBuOOH and subsequent reactions upstream of the ionization zone (mixing tank, sampling lines) in agreement with the literature.39–42tBuOOH is among the most stable hydroperoxides but relatively unstable and sensitive to temperature and pressure conditions, contaminations or frictions.10 The signal at m/z 58 also originates from an impurity of the sample, in this case acetone (see left panel of Fig. S1, ESI†), another characteristic product of tBuOOH decomposition.43 The peaks of m/z 57 and 59 shown in Fig. 1 are broad compared to the others and attributed to ions produced by dissociative ionization processes. The kinetic energy release (KER) in the dissociation step is carried by the ionic fragments and causes the visible Doppler broadening. Indeed, the extraction field used in the present work is low enough so that the broad velocity distribution of the fragment cations in the time-of-flight direction leads to wide characteristic peak shapes.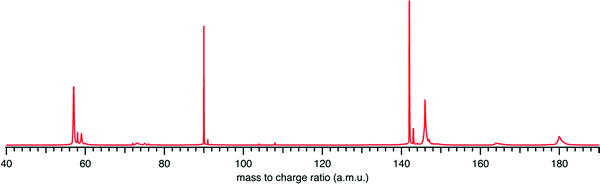 | ||
| Fig. 1 Mass spectrum recorded by synchrotron photoionization of a tBuOOH/n-decane mixture in helium integrated over the 9.0–11.0 eV photon energy range. | ||
The mass-selected total ion yields (TIY) of m/z 57 and 90 are shown in Fig. 2, along with the sum of both TIY. The curves are obtained by considering all coincidence events, independently of the electron kinetic energy, and are proportional to the photoionization cross section of the species. Note that with the extraction field used in this work, all photoelectrons are detected up to 3.5 eV kinetic energy, so that 100% transmission is achieved for all ions and electrons in the current photon energy range. Fig. 2 shows a correlation between the TIY of m/z 57 and 90, as the TIY of m/z 90 stops rising around 9.8–9.9 eV where the TIY of m/z 57 starts rising. No other correlation between the parent signal and another potential fragment mass has been found, so that m/z 57 appears as the only product of dissociative photoionization of tBuOOH within the photon energy range explored in this work. Fig. 2 shows that at a photon energy of 10.6 eV, which is currently used for the quantification by VUV photoionization mass spectrometry,3,44 the ratio of the fragment to the parent is 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3. Note that, to extract the tBuOOH molar fraction in complex mixtures, the absolute ionization cross-sections of all products involved are needed. Although this value is not known for tBuOOH, Ashmore and Burgess showed that hydroperoxide cross-sections resemble those of alcohols,45 and could therefore be estimated from that of tert-butanol (9.14 Mb at 10.6 eV for instance).46
0.3. Note that, to extract the tBuOOH molar fraction in complex mixtures, the absolute ionization cross-sections of all products involved are needed. Although this value is not known for tBuOOH, Ashmore and Burgess showed that hydroperoxide cross-sections resemble those of alcohols,45 and could therefore be estimated from that of tert-butanol (9.14 Mb at 10.6 eV for instance).46
Consistently with the previous analysis of TIY, the SPES of m/z 57 and 90 are displayed in Fig. 3 showing a clear correlation between the two masses, with the SPES of m/z 90 dropping to zero abruptly around 9.8 eV while at the same energy the SPES of m/z 57 is rising. Within the single electronic transition in this energy range, the lowest vibrational states of the tBuOOH+ ground state are stable, but beyond 9.8 eV, vibrational excitations lead to predissociation to give the m/z 57 fragment. The m/z 57 corresponds to the C4H9+ ion, which is likely formed through the C–OOH bond rupture of tBuOOH+ in agreement with the interpretation by Stevens et al.15 The CBS–QB3 calculated enthalpy of reaction:
| tBuOOH+ → (CH3)3C+ + HO2 ΔRH298 = 18.2 kcal mol−1 (0.79 eV) |
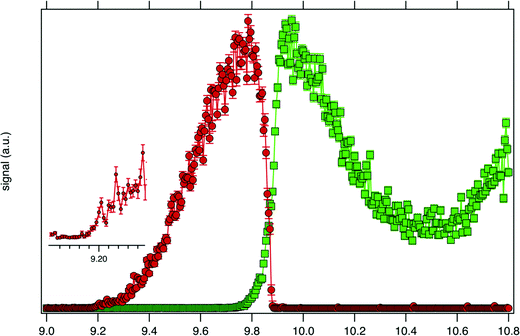 | ||
| Fig. 3 SPES of m/z 57 (green squares) and 90 (red dots) recorded by synchrotron photoionization of a tBuOOH/n-decane mixture in helium. The inset shows a blown-up view around the ionization onset. | ||
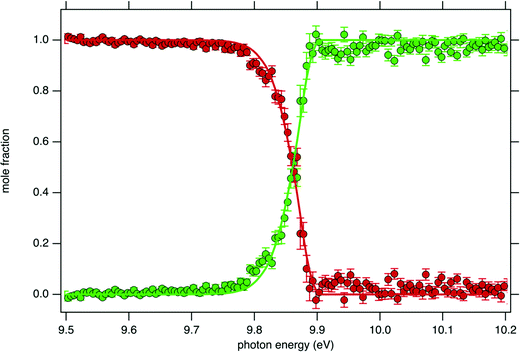
Fig. 4 displays the ion mole fraction as a function of the energy deposited into the cation, i.e., as a function of photon energy but selecting events correlated only with photoelectrons close to 0 eV, commonly called breakdown diagram. The curves in the figure can be fitted with a unimolecular statistical fragmentation model47 to extract an accurate appearance energy for the m/z 57 fragment. Here, we have assumed that the fragmentation is fast with respect to the fragment detection time of a few μs, and only the initial thermal energy of the neutral parent molecule is considered. The temperature and the appearance energy at 0 K (AE0K) of the fragment are varied within a least-square fit and were thus determined at T = 130 K and AE0K = 9.906 ± 0.005 eV. The latter is in excellent agreement with the AE0k obtained by Stevens et al. (9.904 ± 0.012 eV).15
Although the breakdown diagram in Fig. 4 is perfectly modelled with a single fragmentation and shows no contributions from other parents, additional energetics arguments can also be given to rule them out. n-Decane which is the most abundant species in the gas mixture has a fragmentation threshold of 10.4 eV, thus the analysis of the tBuOOH fragmentation can safely be done below this threshold without interference from the solvent, i.e. n-decane.48
Another potential contribution for the fragment m/z 57 could come from di-tBuO which can originate from a reaction sequence from tBuOOH decomposition (see the signal at m/z 146 in Fig. 1). Shuman et al.49 studied the dissociation of selected ions by TPEPICO spectroscopy, suggesting that di-tBuO ions dissociate via two exit channels, a methyl loss followed by a sequential dissociation to produce tBuO+ (m/z 73) and a direct detachment of the tBu+ ion (m/z 57). The formation of di-tBuO could not be addressed since its AIE is 8.32 eV,49 1 eV below the energy scan acquisition in this work. However, the comparison between the PES of di-tBuO from the literature50 and the SPES of m/z 146 recorded in this work shows no agreement (see left panel in Fig. S3, ESI†). One would note the good agreement of the simulated spectrum from this work and the reference spectrum from the literature. An additional small peak is noticed at m/z 73 (see Fig. 1) and could correspond to a dissociative ionization fragment of di-tBuO, but the appearance energy of tBuO+ is estimated to be 9.6 eV which does not agree with the ionization threshold of the SPES of m/z 73 (see the right panel in Fig. S3, ESI†). As a conclusion, the identification of the species at m/z 146 remains unknown in this work but is not correlated with m/z 57 signal.
The SPES of m/z 59 shows an ionization threshold close to the one of m/z 57 (see Fig. S4, ESI†) suggesting m/z 59 can be a second dissociation channel from the same unstable cation. The formation of the daughter ion at m/z 59 would correspond to a hydroxypropanyl (C3H6–OH+) cation. However, its formation from tBuOOH seems unlikely since a potential formation mechanism would require the migration of a methyl group to the terminal oxygen. This is confirmed by the lack of correlation between the SPES of m/z 59 and 90 and the formation of m/z 59 would be more likely originating from the tBuOOH dimer (see the signal at m/z 180 in Fig. 1), both SPES exhibiting a correlation (see Fig. S4, ESI†). However, the m/z 180 peak is broad and likely to be itself a fragment from a larger unstable cation, like a bigger oligomer. Additionally, no other expected fragments from the dissociative ionization of dimer, like a protonated monomer [(tBuOOH)2+ → tBuOO + (tBuOOH)H+] have been detected. A more thorough study of this system would be needed to assign signals from the dimer.
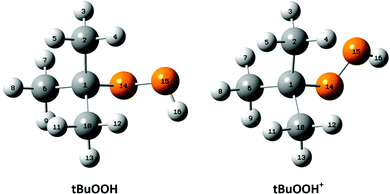
For the interpretation of the experimental SPES spectrum of tBuOOH recorded in this work, theoretical computations treating neutral and cationic tBuOOH were carried out. Table S1 (ESI†) presents the optimized equilibrium structures of tBuOOH and of tBuOOH+ as computed at the PBE0/aug-cc-pVTZ level. These equilibrium structures, defined as local or global minima of a potential energy surface, are displayed in Fig. 5. After optimization, the cation is of C1 symmetry as well as the neutral species. Since the neutral and the ion have relatively close equilibrium structures, very few modes are expected to be active upon single photon ionization.
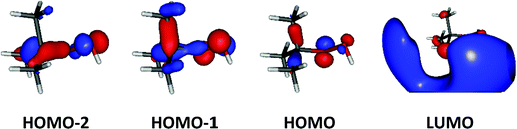
Upon ionization the main geometrical changes occur in the vicinity of the central carbon atom and the OOH group linked to it. Indeed, the Table S1 (ESI†) shows that the C1–O14 distance is lengthened from 1.438 to 1.546 Å, whereas the OO distance is shortened from 1.427 to 1.307 Å. The shortening of the OO bond is due to the removal of an electron from the HOMO orbital of tBuOOH. Indeed, Fig. 6 shows that this HOMO is π* antibonding in nature, and mainly located on the O14–O15 bond. This figure shows also that this MO extends over the CC bonds around the C1 atom. Ejection of an electron from this orbital affects thus the in-plane angles and the dihedral angles involving the C1 and O14 atoms, where one can observe up to 4–5° differences in these in-plane angles between neutral and ionic tBuOOH and even larger differences in the dihedral angles as shown in Table S1 (ESI†) and illustrated in Fig. S5 (ESI†). Therefore, the photoelectron spectrum should correspond to a long vibrational progression populating the C1–O14 and the O14–O15 stretching modes, in addition to the population of the bending and torsional modes involving these 3 atoms. Moreover, Table S2 (ESI†) lists the anharmonic frequencies of tBuOOH+ as computed at the PBE0/aug-cc-pVTZ level together with their tentative assignment in terms of normal modes.
Table 1 lists the total energies of tBuOOH and of tBuOOH+ as computed at different levels of theory. The AIE of tBuOOH is also given since there is no data in the literature, only a vertical ionization energy (VIE) of 10.24 eV is referenced in the NIST database.50 The AIE of tBuOOH increases while accounting better for electron correlation either by going from DFT to (R)CCSD(T)-F12 computations and/or by describing the atoms with larger basis sets. This is due to the better description of the OO bond in this compound as discussed for other peroxides.51,52 At the highest level of theory adopted in the present work i.e., PBE0/aug-cc-pVDZ (Optg + ΔZPE)//(R)CCSD-F12(T)/aug-cc-pVTZ (SP), we compute an AIE of tBuOOH of 9.254 eV. Experimentally, obtaining a precise measurement of the AIE is challenging due to the low FC factors (see below). Nevertheless, the onset at 9.2 eV observed in the SPES (see the blow-up view in Fig. 3) is consistent with the above-mentioned calculated value. A difference of a few tens of meV between the experimental and calculated values can be explained by the missing core-valence correction (contribution of several tenths of meVs) and to a less extent by the scalar-relativistic correction (contribution of several meVs).53,54 Such complete computations are extremely costly for polyatomic molecules as large as tBuOOH and tBuOOH+ and are beyond the scope of this work.
| Method | tBuOOH | tBuOOH+ |
|---|---|---|
| a Full optimization. b Anharmonic computations at the PBE0/aug-cc-pVDZ level. c Single point computations at the PBE0/aug-cc-pVDZ optimized geometry. | ||
| PBE0/aug-cc-pVDZ (Optg)a | −308.4945384 | −308.1698072 |
| ZPEb | 3.731 | 3.714 |
| PBE0/aug-cc-pVTZ (Optg)a | −308.5687141 | −308.2436817 |
| (R)CCSD(T)-F12b/aug-cc-pVDZ (SP)c | −308.3803927 | −308.0412898 |
| (R)CCSD(T)-F12b/aug-cc-pVTZ (SP)c | −308.4342040 | −308.0934975 |
| Method | AIE |
|---|---|
| PBE0/aug-cc-pVDZ (Optg + ΔZPE) | 8.819 |
| PBE0/aug-cc-pVTZ (Optg + ΔZPE) | 8.827 |
| PBE0/aug-cc-pVDZ (Optg + ΔZPE)//(R)CCSD-F12(T)/aug-cc-pVDZ (SP) | 9.210 |
| PBE0/aug-cc-pVDZ (Optg + ΔZPE)//(R)CCSD-F12(T)/aug-cc-pVTZ (SP) | 9.254 |
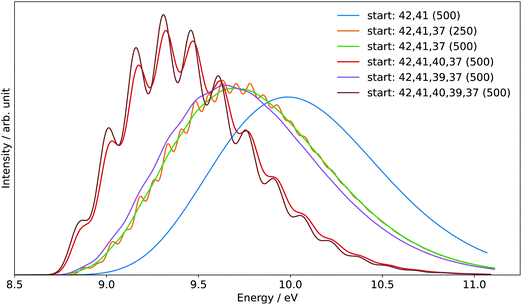
The generation of the FC spectrum for the tBuOOH+ (X+) + e− ← tBuOOH (X) + hν transition is not straightforward because of the flexibility of tBuOOH in particular along the vibrational modes involving the C–OOH group. Indeed, this flexibility induces strong structural changes between the minima of the neutral and ionic states. The consequences of such flexibility are often an important shift of some normal modes, especially those at low frequencies, and a larger mode mixing. Because of the underlying harmonic approximation of the potential energy surfaces used to compute the FC integrals, this commonly results in an overestimation of those shifted modes and their coupling, and consequently an excessive broadening of the theoretical spectra. To mitigate this problem, internal coordinates were used to describe the vibrations in the vibronic calculations, using a locally modified version of GAUSSIAN 16.55 The aim here is to decouple the strongly shifted modes from those of smaller amplitudes, so that combination bands involving the former will have a far lower intensity, closer to reality, and can be isolated and removed if their respective contributions are excessive.56 To do so, an initial set of redundant coordinates was automatically generated from the primitive internal coordinates, which comprise bonds, in-plane angles and dihedrals. First, the topology was built by considering two atoms bonded if their distance was inferior to 130% of their average bond length based on B3LYP/6-31G(d) following the GAUSSIAN standard. Then, a non-redundant set of delocalized internal coordinates was generated. While an improvement of the band-shape can be noted (see Fig. S6, ESI†), the broadening remains excessive, which means that the contributions of some lower-frequency modes to the overall band-shape are improperly estimated. As a consequence, they must be removed from the simulation. To identify the modes to remove, two protocols were followed. First, strongly shifted modes, i.e., with a corresponding value of the shift vector of at least 100 atomic units (see bottom left panel in Fig. S7, ESI† and the caption for details) were initially selected for removal. This is the case for modes 42 and 41 of tBuOOH (numbering by decreasing energies, see Table S2, ESI†). Next, a hindered-rotor analysis was carried out to identify possible large amplitude motions. Modes 42, 41, 40, 39, and 37 were found for the neutral species (42, 41, 40, 39, and 31 for the cation). Mode 37 is the third most shifted mode overall.
To build the smallest set of modes to remove, an iterative process was followed, by removing sequentially each mode identified as hindered rotor and by analyzing their impact on the overall Franck–Condon calculations. This was measured through two criteria, the form and width of the spectral TD band-shape, and the convergence of time-independent (TI) calculations. Regarding the latter, an alternative way to generate FC spectra is to compute the band-shape as an ensemble of transitions connecting the manifold of vibrational states belonging to the electronic states of interest. The practical difficulty for this sum-over-state approach is that it involves in theory an infinity of initial and final states. However, only a limited number of transitions contribute to the total intensity of the spectrum. As a result, truncation methods have been proposed in the literature, often based on a-priori estimates of the intensity of groups of transitions (see Biczysko et al.57 for a review of such schemes), to make such calculations tractable. It is noteworthy that the total intensity can be known analytically, so it is possible to check if all relevant transitions have been included by comparing the calculated intensity, obtained by summing the contribution of each treated transition, with this reference value. This ratio is sometimes referred to as the progression or convergence. Very low convergences are often indicative of an excessively large number of transitions with very small intensity, and thus a breakdown of the FC principle. Indeed, the latter assumes that the structural changes induced by an electronic transition are minimal, which should correspond to a relatively low mode mixing. This is the case if mode 37 is included, with a progression below 1% using the prescreening implemented in GAUSSIAN 16 with the following parameters: C1max = 40, C2max = 20, Imax = 1010 (see Santoro et al.58 for details). The TD formalism does not suffer from the issue of the truncation because of the automatic inclusion of all transitions by construction. However, the main band of the final spectrum shown in Fig. 7 is excessively broad. This confirms the fact that mode 37 must be excluded. A good progression with TI is obtained by keeping modes 40 and 39 (>97%). However, an analysis of the prescreening algorithm shows that the vibrational progression of the former is too high compared to the other modes, resulting in intense overtones and combination bands involving mode 40. This is consistent with the broad band observed at the TD level (Fig. 7). The influence of mode 39 is very limited and can be safely included. As a result, modes 42, 41, 40, and 37 from tBuOOH were selected in the initial state to be removed. Starting from this set, an automated procedure is used to build two ensembles of modes to remove, one for each state, with the same number of elements. This is done by looking at the overlap of each mode to be removed onto the other state through the Duschinsky matrix. More details on the procedure can be found in Bloino et al.38 In total, 12 modes were removed. The final Duschinsky matrix and shift vector for the model system are shown in Fig. S8 (ESI†). Finally, the band-shape origin was shifted by using the (R)CCSD(T)-F12 adiabatic ionization energy instead of the DFT one.
The sum of the SPES of m/z 57 and 90 (daughter and parent ions, respectively) in Fig. 8 is in fairly good agreement with the reference PES of tBuOOH from Nagaoka et al. within the energy range 9.0 to 10.4 eV.59 In Nagaoka et al.,59 the measurements were performed at room temperature using a photoelectron spectrometer coupled to a VUV He discharge lamp (total resolution = 40 meV). Deviations are observed, which might be caused by the presence of autoionization in the SPES, or from the contribution of side products since the PES of Nagaoka et al.59 was obtained by photoionization of a custom-made synthesized tBuOOH sample without any means to remove the possible contribution of spurious compounds by PEPICO filtering. Note that the maximum of the SPES in Fig. 8, i.e. 10.0 eV can be compared with the VIE of 10.24 eV referenced in the NIST database for tBuOOH.50 Beyond 10.4 eV, another band is observed corresponding to the excited states of the cation.
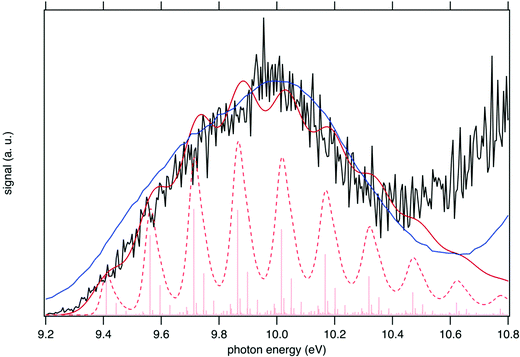 | ||
| Fig. 8 Sum of the SPES of m/z 57 and 90 (black line) compared to a reference PES of tBuOOH (blue line) from Nagaoka et al.59 and two simulated spectra of tBuOOH using the current FC simulation. The simulations are based on the computed stick spectrum (light red sticks) convoluted with 20 meV (dashed red line) and 60 meV (dark red line) HWHM Gaussians. The latter corresponds to the spectrum in Fig. 7 in which modes 42, 41, 40, and 37 have been removed. The simulations have been shifted by 156 meV from the calculated AIE by CC calculations. | ||
In addition to the experimental SPES and the reference PES from the literature, Fig. 8 displays two simulated spectra of tBuOOH using the current FC simulations. The simulations are based on the computed stick spectrum convoluted with two HWHM Gaussians. One corresponds to the red spectrum in Fig. 7 in which modes 42, 41, 40, and 37 have been removed while the other one still corresponds to the red spectrum in Fig. 7 but using a HWHM of 20 meV (160 cm−1) i.e. close to the experimental resolution. Note those spectra are obtained with fixing T = 130 K (=temperature in the cooled molecular jet). Using a HWHM of 20 meV for the empirical broadening, as derived from experiment, produces narrow bands. This is expected, as part of the flexibility of tBuOOH is missing in the model system. By increasing the HWHM to 60 meV to compensate this limitation, a closer agreement with the experimental band-shape is reached. A fairly good agreement is observed between the simulated and measured spectra. Indeed, the FC spectrum accounts only for direct single photon ionization whereas indirect photoionization processes (i.e. t-BuOOH + hν → t-BuOOH* → t-BuOOH+ + e−) may contribute. The latter may be in action at the rotational and/or vibrational and/or electronic levels, where an enhancement of respective bands is observed.60,61 However, it should be noted that in Fig. 8 the simulated spectra had to be shifted by 156 meV from the coupled cluster AIE value to fit the experimental spectrum, meaning that the FC simulations rather support an AIE of ∼9.4 eV.
The SPES spectrum exhibits a long vibrational progression with a spacing of about 1180 cm−1, which corresponds to the population of mode 23 of the cation. This mode corresponds to the OO stretching vibration in the cation (see Table S2, ESI†). Looking in more detail at the stick spectrum in Fig. 8, sub-patterns can be observed with regular spacing. The first one corresponds to the cationic fundamental of mode 39. (CH3 torsion coupled with the COO in-plane bending) and its combination with the fundamental and overtones of cationic mode 23 (139 + n23). The second pattern of significantly lower intensity regards the combination of the fundamental of cationic mode 21 (C–C stretching) with overtones of cationic mode 23.
V. Conclusion
The photoionization of tBuOOH was studied with the VUV DESIRS beamline of the SOLEIL synchrotron using i2PEPICO techniques. Commercially available tBuOOH as a 5% solution in n-decane was used. The objectives were to measure the spectroscopy and fragmentation pattern of the tBuOOH+ cation, and to benchmark the predictive abilities of theoretical methods in the case of R—OOH systems. The results can then be used as future reference for its detection in combustion/oxidation reactions via advanced mass spectrometry techniques.62 Besides, the signal branching ratio between the parent and fragment ions is also provided for the first time in this work for an accurate quantification of tBuOOH in combustion/oxidation experiments and show that a corrective factor of 3.3 needs to be applied to quantify tBuOOH at 10.6 eV. The current work shows that tBuOOH produces a signal at m/z 90 at 9.8 eV that is only a factor of 2–2.5 weaker than the fragment signal at m/z 57 at 10.6 eV. This points to the opportunity to quantify tBuOOH at 9.8 eV using its parent ion, completely avoiding problems due to fragmentation. In this context, tBuOOH differs from ketohydroperoxides, which have been shown to more heavily photodissociate. For example, in low temperature n-pentane oxidation, accounting for dissociative ionization of ketohydroperoxides increases their mole fraction by more than a factor of 107. This work reinforces the need to study the fragmentation mechanisms of these low-temperature combustion intermediates to strengthen the quantitative predictions of chemical kinetic models.The instability of tBuOOH leads to a relatively complex mass spectrum, but all observed signals could be attributed to known or plausible tBuOOH decomposition products. The broad signal shape of m/z 57 allows easy identification as a fragment. In line with the work of Stevens et al., the data clearly point to the formation of only one fragment, the tert-butyl (C4H9+, m/z 57) ion through a barrierless bond scission which releases HO2 as second product.15 Both presently computed and measured 0 K appearance energies of the C4H9+ fragment are also in agreement with the literature.
Based on the threshold photoelectron spectrum using the SPES method and the theoretical data it is not possible accurately measure the AIE value. Low FC factors and lack of vibrational structure in the experimental spectrum only allow constraining of the AIE to the region 9.2–9.4 eV. The simulated PES is consistent with the experimental one and shows a long vibrational progression due to the population of the cationic vibrational levels associated with the OO stretching mode. While a direct application of the FC principle gives unsatisfactory results due to the marked geometry changes primarily connected to the OOH group, tailored models that remove selectively floppy modes can help reach very good agreement with experiment, making it possible to elucidate the important features of the experimental spectrum. Indeed, this particular example shows a complicated case for computations where the system of interest exhibits some significant level of flexibility. For rigid or semi-rigid molecules, the approach is straightforward and can be used in fully automated procedures as we recently showed for methyl adenine and pyruvic acid.53,61 For such flexible species, the choice of a suitable coordinate system remains a difficult challenge, even done manually. An interesting aspect highlighted in this work is that instruments/gauges exist to assess quantitatively the validity of the representation adopted for the description of the vibrational motions. This could pave the way to more automated procedures, an aspect on which some of us are working on. More generally, such procedure is promising for the simulation of photoionization spectra of organic compounds, where large amplitude motions are often in action. Enhancing the predictive capabilities of theoretical methods is critical for species identification since most often their experimental photoelectron spectrum is not known and detection is solely based on simulated spectra.
Author contributions
Je. B., O. H., H.-H. C., P. A., L.-S. T., G. V., and F. B.-L. collected the experimental data. G. A. G. and L. H. provided support for the analysis; Z. J., Ju. B., and M. H. performed the theoretical calculations and analyzed the results; Je. B. analyzed the experimental data and wrote the original draft. All the authors contributed to review the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to the whole SOLEIL staff for smoothly running the facility under project 20180021. We warmly thank J.-F. Gil for his technical help around the SAPHIRS experiment. H.-H. C. acknowledges I3A for the use of its HPC cluster HERMES and the funding from the Aragón Government (Ref. T22_20R), co-funded by FEDER 2014-2020 “Construyendo Europa desde Aragón”. Ju. B. thanks the Italian Ministry of University and Research for the financial support (PRIN Grant num. 2020HTSXMA). Z. J. and Ju. B. thank Marco Fusè for useful discussions.References
- M. Krapf, I. El Haddad, E. A. Bruns, U. Molteni, K. R. Daellenbach, A. S. H. Prévôt, U. Baltensperger and J. Dommen, Labile Peroxides in Secondary Organic Aerosol, Chem, 2016, 1, 603–616, DOI:10.1016/j.chempr.2016.09.007.
- M. Lee, B. G. Heikes and D. W. O’Sullivan, Hydrogen peroxide and organic hydroperoxide in the troposphere: a review, Atmos. Environ., 2000, 34, 3475–3494, DOI:10.1016/S1352-2310(99)00432-X.
- Z. Wang, O. Herbinet, N. Hansen and F. Battin-Leclerc, Exploring hydroperoxides in combustion: History, recent advances and perspectives, Prog. Energy Combust. Sci., 2019, 73, 132–181, DOI:10.1016/j.pecs.2019.02.003.
- R. Zimmermann and L. Hanley, Photoionization and Photo-Induced Processes in Mass Spectrometry: Fundamentals and Applications, John Wiley & Sons, 2021 Search PubMed.
- T. Bierkandt, P. Oßwald, N. Gaiser, D. Krüger, M. Köhler, M. Hoener, S. Shaqiri, D. Kaczmarek, Y. Karakaya, P. Hemberger and T. Kasper, Observation of low-temperature chemistry products in laminar premixed low-pressure flames by molecular-beam mass spectrometry, Int. J. Chem. Kinet., 2021, 53, 1063–1081, DOI:10.1002/kin.21503.
- F. Battin-Leclerc, O. Herbinet, P.-A. Glaude, R. Fournet, Z. Zhou, L. Deng, H. Guo, M. Xie and F. Qi, Experimental Confirmation of the Low-Temperature Oxidation Scheme of Alkanes, Angew. Chem., 2010, 122, 3237–3240, DOI:10.1002/ange.200906850.
- F. Battin-Leclerc, J. Bourgalais, Z. Gouid, O. Herbinet, G. Garcia, P. Arnoux, Z. Wang, L.-S. Tran, G. Vanhove, L. Nahon and M. Hochlaf, Chemistry deriving from OOQOOH radicals in alkane low-temperature oxidation: A first combined theoretical and electron-ion coincidence mass spectrometry study, Proc. Combust. Inst., 2021, 38, 309–319, DOI:10.1016/j.proci.2020.06.159.
- S. Kyasa, B. W. Puffer and P. H. Dussault, Synthesis of Alkyl Hydroperoxides via Alkylation of gem-Dihydroperoxides, J. Org. Chem., 2013, 78, 3452–3456, DOI:10.1021/jo4001564.
- N. A. Milas and D. M. Surgenor, Studies in Organic Peroxides. VIII. t-Butyl Hydroperoxide and Di-t-Butyl Peroxide1, J. Am. Chem. Soc., 1946, 68, 205–208, DOI:10.1021/ja01206a017.
- T. Willms, H. Kryk, J. Oertel, C. Hempel, F. Knitt and U. Hampel, On the thermal decomposition of tert.-butyl hydroperoxide, its sensitivity to metals and its kinetics, studied by thermoanalytic methods, Thermochim. Acta, 2019, 672, 25–42, DOI:10.1016/j.tca.2018.12.007.
- S. Wang, S. Li, D. F. Davidson and R. K. Hanson, Shock Tube Measurement of the High-Temperature Rate Constant for OH + CH3 → Products, J. Phys. Chem. A, 2015, 119, 8799–8805, DOI:10.1021/acs.jpca.5b05725.
- G. A. Pang, R. K. Hanson, D. M. Golden and C. T. Bowman, Rate Constant Measurements for the Overall Reaction of OH + 1-Butanol → Products from 900 to 1200 K, J. Phys. Chem. A, 2012, 116, 2475–2483, DOI:10.1021/jp211885p.
- D. Liu, F. Khaled, B. R. Giri, E. Assaf, C. Fittschen and A. Farooq, H-Abstraction by OH from Large Branched Alkanes: Overall Rate Measurements and Site-Specific Tertiary Rate Calculations, J. Phys. Chem. A, 2017, 121, 927–937, DOI:10.1021/acs.jpca.6b10576.
- S. Li, E. Dames, D. F. Davidson and R. K. Hanson, High-Temperature Measurements of the Reactions of OH with Ethylamine and Dimethylamine, J. Phys. Chem. A, 2014, 118, 70–77, DOI:10.1021/jp411141w.
- W. R. Stevens, S. H. Walker, N. S. Shuman and T. Baer, Dissociative Photoionization Study of Neopentane: A Path to an Accurate Heat of Formation of the t-Butyl Ion, t-Butyl Iodide, and t-Butyl Hydroperoxide, J. Phys. Chem. A, 2010, 114, 804–810, DOI:10.1021/jp908583j.
- X. Tang, X. Lin, G. A. Garcia, J.-C. Loison, Z. Gouid, H. H. Abdallah, C. Fittschen, M. Hochlaf, X. Gu, W. Zhang and L. Nahon, Identifying isomers of peroxy radicals in the gas phase: 1-C3H7O2vs. 2-C3H7O2, Chem. Commun., 2020, 56, 15525–15528, 10.1039/D0CC06516A.
- G. A. Garcia, X. Tang, J.-F. Gil, L. Nahon, M. Ward, S. Batut, C. Fittschen, C. A. Taatjes, D. L. Osborn and J.-C. Loison, Synchrotron-based double imaging photoelectron/photoion coincidence spectroscopy of radicals produced in a flow tube: OH and OD, J. Chem. Phys., 2015, 142, 164201, DOI:10.1063/1.4918634.
- L. Nahon, N. de Oliveira, G. A. Garcia, J.-F. Gil, B. Pilette, O. Marcouillé, B. Lagarde and F. Polack, DESIRS: a state-of-the-art VUV beamline featuring high resolution and variable polarization for spectroscopy and dichroism at SOLEIL, J. Synchrotron Rad., 2012, 19, 508–520, DOI:10.1107/S0909049512010588.
- X. Tang, G. A. Garcia, J.-F. Gil and L. Nahon, Vacuum upgrade and enhanced performances of the double imaging electron/ion coincidence end-station at the vacuum ultraviolet beamline DESIRS, Rev. Sci. Instrum., 2015, 86, 123108, DOI:10.1063/1.4937624.
- B. Mercier, M. Compin, C. Prevost, G. Bellec, R. Thissen, O. Dutuit and L. Nahon, Experimental and theoretical study of a differentially pumped absorption gas cell used as a low energy-pass filter in the vacuum ultraviolet photon energy range, J. Vac. Sci. Technol., A, 2000, 18, 2533–2541, DOI:10.1116/1.1288196.
- K. Yoshino and Y. Tanaka, Absorption spectrum of krypton in the vacuum uv region, J. Opt. Soc. Am., 1979, 69, 159, DOI:10.1364/JOSA.69.000159.
- G. A. Garcia, B. K. Cunha de Miranda, M. Tia, S. Daly and L. Nahon, DELICIOUS III: A multipurpose double imaging particle coincidence spectrometer for gas phase vacuum ultraviolet photodynamics studies, Rev. Sci. Instrum., 2013, 84, 053112, DOI:10.1063/1.4807751.
- D. H. Parker and A. T. J. B. Eppink, Photoelectron and photofragment velocity map imaging of state-selected molecular oxygen dissociation/ionization dynamics, J. Chem. Phys., 1997, 107, 2357–2362, DOI:10.1063/1.474624.
- W. C. Wiley and I. H. McLaren, Time-of-Flight Mass Spectrometer with Improved Resolution, Rev. Sci. Instrum., 1955, 26, 1150–1157, DOI:10.1063/1.1715212.
- G. A. Garcia, L. Nahon and I. Powis, Two-dimensional charged particle image inversion using a polar basis function expansion, Rev. Sci. Instrum., 2004, 75, 4989–4996, DOI:10.1063/1.1807578.
- J. C. Poully, J. P. Schermann, N. Nieuwjaer, F. Lecomte, G. Grégoire, C. Desfrançois, G. A. Garcia, L. Nahon, D. Nandi, L. Poisson and M. Hochlaf, Photoionization of 2-pyridone and 2-hydroxypyridine, Phys. Chem. Chem. Phys., 2010, 12, 3566–3572, 10.1039/B923630A.
- M. Briant, L. Poisson, M. Hochlaf, P. de Pujo, M.-A. Gaveau and B. Soep, Ar2 Photoelectron Spectroscopy Mediated by Autoionizing States, Phys. Rev. Lett., 2012, 109, 193401, DOI:10.1103/PhysRevLett.109.193401.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- T. B. Adler, G. Knizia and H.-J. Werner, A simple and efficient CCSD(T)-F12 approximation, J. Chem. Phys., 2007, 127, 221106, DOI:10.1063/1.2817618.
- G. Knizia, T. B. Adler and H.-J. Werner, Simplified CCSD(T)-F12 methods: Theory and benchmarks, J. Chem. Phys., 2009, 130, 054104, DOI:10.1063/1.3054300.
- H.-J. Werner, G. Knizia and F. R. Manby, Explicitly correlated coupled cluster methods with pair-specific geminals, Mol. Phys., 2011, 109, 407–417, DOI:10.1080/00268976.2010.526641.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a general-purpose quantum chemistry program package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253, DOI:10.1002/wcms.82.
- F. Weigend, A fully direct RI-HF algorithm: Implementation, optimised auxiliary basis sets, demonstration of accuracy and efficiency, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291, 10.1039/B204199P.
- C. Hättig, Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations: Core–valence and quintuple- ζ basis sets for H to Ar and QZVPP basis sets for Li to Kr, Phys. Chem. Chem. Phys., 2005, 7, 59–66, 10.1039/B415208E.
- W. Klopper, Highly accurate coupled-cluster singlet and triplet pair energies from explicitly correlated calculations in comparison with extrapolation techniques, Mol. Phys., 2001, 99, 481–507, DOI:10.1080/00268970010017315.
- K. E. Yousaf and K. A. Peterson, Optimized auxiliary basis sets for explicitly correlated methods, J. Chem. Phys., 2008, 129, 184108, DOI:10.1063/1.3009271.
- M. Hochlaf, Advances in spectroscopy and dynamics of small and medium sized molecules and clusters, Phys. Chem. Chem. Phys., 2017, 19, 21236–21261, 10.1039/C7CP01980G.
- J. Bloino, Aiming at an accurate prediction of vibrational and electronic spectra for medium-to-large molecules: An overview - Bloino - 2016 - International Journal of Quantum Chemistry - Wiley Online Library, (2016). https://onlinelibrary.wiley.com/doi/full/10.1002/qua.25188 (accessed June 7, 2021).
- D. L. Allara, T. Mill, D. G. Hendry and F. R. Mayo, Low Temperature Gas- and Liquid-Phase Oxidations of Isobutane, Oxidation of Organic Compounds, American Chemical Society, 1968, pp. 40–57. DOI:10.1021/ba-1968-0076.ch029.
- U. Shah, S. M. Mahajani, M. M. Sharma and T. Sridhar, Effect of supercritical conditions on the oxidation of isobutane, Chem. Eng. Sci., 2000, 55, 25–35, DOI:10.1016/S0009-2509(99)00185-2.
- T. Willms, H. Kryk and U. Hampel, The gas chromatographic analysis of the reaction products of the partial isobutane oxidation as a two phase process, J. Chromatogr. A, 2016, 1458, 126–135, DOI:10.1016/j.chroma.2016.06.052.
- D. E. Winkler and G. W. Hearne, Liquid Phase Oxidation of Isobutane, Ind. Eng. Chem., 1961, 53, 655–658, DOI:10.1021/ie50620a030.
- V. Vasudevan, D. F. Davidson and R. K. Hanson, Direct measurements of the reaction OH + CH2O → HCO + H2O at high temperatures, Int. J. Chem. Kinet., 2005, 37, 98–109, DOI:10.1002/kin.20056.
- A. Rodriguez, O. Herbinet, Z. Wang, F. Qi, C. Fittschen, P. R. Westmoreland and F. Battin-Leclerc, Measuring hydroperoxide chain-branching agents during n-pentane low-temperature oxidation, Proc. Combust. Inst., 2017, 36, 333–342, DOI:10.1016/j.proci.2016.05.044.
- F. S. Ashmore and A. R. Burgess, Study of some medium size alcohols and hydroperoxides by photoelectron spectroscopy, J. Chem. Soc., Faraday Trans. 2, 1977, 73, 1247, 10.1039/f29777301247.
- M. Xie, Z. Zhou, Z. Wang, D. Chen and F. Qi, Determination of absolute photoionization cross-sections of oxygenated hydrocarbons, Int. J. Mass Spectrom., 2010, 293, 28–33, DOI:10.1016/j.ijms.2010.03.007.
- B. Sztáray, A. Bodi and T. Baer, Modeling unimolecular reactions in photoelectron photoion coincidence experiments, J. Mass Spectrom., 2010, 45, 1233–1245, DOI:10.1002/jms.1813.
- Z. Zhou, L. Zhang, M. Xie, Z. Wang, D. Chen and F. Qi, Determination of absolute photoionization cross-sections of alkanes and cyclo-alkanes, Rapid Commun. Mass Spectrom., 2010, 24, 1335–1342, DOI:10.1002/rcm.4523.
- N. S. Shuman, A. Bodi and T. Baer, Heats of Formation of t-Butyl Peroxy Radical and t-Butyl Diazyl Ion: RRKM vs. SSACM Rate Theories in Systems with Kinetic and Competitive Shifts, J. Phys. Chem. A, 2010, 114, 232–240, DOI:10.1021/jp907767c.
- C. Batich and W. Adam, The photoelectron spectra of alkylperoxides, Tetrahedron Lett., 1974, 15, 1467–1470, DOI:10.1016/S0040-4039(01)93112-0.
- D. J. Carmona, D. R. Contreras, O. A. Douglas-Gallardo, S. Vogt-Geisse, P. Jaque and E. Vöhringer-Martinez, A systematic electronic structure study of the O–O bond dissociation energy of hydrogen peroxide and the electron affinity of the hydroxyl radical, Theor. Chem. Acc., 2018, 137, 126, DOI:10.1007/s00214-018-2307-z.
- D. J. Carmona, P. Jaque and E. Vöhringer-Martinez, DFT benchmark study of the O–O bond dissociation energy in peroxides validated with high-level ab initio calculations, Theor. Chem. Acc., 2020, 139, 102, DOI:10.1007/s00214-020-02607-x.
- K. Laamiri, G. A. Garcia, L. Nahon, A. B. Houria, R. Feifel and M. Hochlaf, Threshold photoelectron spectroscopy of 9-methyladenine: theory and experiment, Phys. Chem. Chem. Phys., 2022, 24, 3523–3531, 10.1039/D1CP03729C.
- H. Yan Zhao, K.-C. Lau, G. A. Garcia, L. Nahon, S. Carniato, L. Poisson, M. Schwell, M. Mogren Al-Mogren and M. Hochlaf, Unveiling the complex vibronic structure of the canonical adenine cation, Phys. Chem. Chem. Phys., 2018, 20, 20756–20765, 10.1039/C8CP02930J.
- A. Baiardi, J. Bloino and V. Barone, General formulation of vibronic spectroscopy in internal coordinates, J. Chem. Phys., 2016, 144, 084114, DOI:10.1063/1.4942165.
- H. A. Frank, J. A. Bautista, J. S. Josue and A. J. Young, Mechanism of Nonphotochemical Quenching in Green Plants:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Energies of the Lowest Excited Singlet States of Violaxanthin and Zeaxanthin, Biochemistry, 2000, 39, 2831–2837, DOI:10.1021/bi9924664.
Energies of the Lowest Excited Singlet States of Violaxanthin and Zeaxanthin, Biochemistry, 2000, 39, 2831–2837, DOI:10.1021/bi9924664. - M. Biczysko, J. Bloino, F. Santoro and V. Barone, Time-Independent Approaches to Simulate Electronic Spectra Lineshapes: From Small Molecules to Macrosystems, Computational Strategies for Spectroscopy, John Wiley & Sons, Ltd, 2011, pp. 361–443. DOI:10.1002/9781118008720.ch8.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, Effective method to compute Franck-Condon integrals for optical spectra of large molecules in solution, J. Chem. Phys., 2007, 126, 084509, DOI:10.1063/1.2437197.
- S. Nagaoka, K. Sawada, Y. Fukumoto, U. Nagashima, S. Katsumata and K. Mukai, Mechanism of prooxidant reaction of vitamin E: kinetic, spectroscopic, and ab initio study of proton-transfer reaction, J. Phys. Chem., 1992, 96, 6663–6668, DOI:10.1021/j100195a027.
- T. Baer and R. P. Tuckett, Advances in threshold photoelectron spectroscopy (TPES) and threshold photoelectron photoion coincidence (TPEPICO), Phys. Chem. Chem. Phys., 2017, 19, 9698–9723, 10.1039/C7CP00144D.
- M. Jarraya, A. Bellili, L. Barreau, D. Cubaynes, G. A. Garcia, L. Poisson and M. Hochlaf, Probing the dynamics of the photo-induced decarboxylation of neutral and ionic pyruvic acid, Faraday Discuss., 2022 10.1039/D2FD00023G.
- J. Bourgalais, O. Herbinet, H.-H. Carstensen, J. Debleza, G. A. Garcia, P. Arnoux, L. S. Tran, G. Vanhove, B. Liu, Z. Wang, M. Hochlaf, L. Nahon and F. Battin-Leclerc, Jet-Stirred Reactor Study of Low-Temperature Neopentane Oxidation: A Combined Theoretical, Chromatographic, Mass Spectrometric, and PEPICO Analysis, Energy Fuels, 2021, 35, 19689–19704, DOI:10.1021/acs.energyfuels.1c02080.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00929c |
| This journal is © the Owner Societies 2022 |