Probing the presence and absence of metal-fullerene electron transfer reactions in helium nanodroplets by deflection measurements†
John W.
Niman
 a,
Benjamin S.
Kamerin
a,
Benjamin S.
Kamerin
 a,
Thomas H.
Villers
a,
Thomas M.
Linker
b,
Aiichiro
Nakano
b and
Vitaly V.
Kresin
a,
Thomas H.
Villers
a,
Thomas M.
Linker
b,
Aiichiro
Nakano
b and
Vitaly V.
Kresin
 *a
*a
aDepartment of Physics and Astronomy, University of Southern California, Los Angeles, CA 90089-0484, USA. E-mail: kresin@usc.edu
bCollaboratory for Advanced Computing and Simulations, University of Southern California, Los Angeles, CA 90089-0242, USA
First published on 12th April 2022
Abstract
Metal-fullerene compounds are characterized by significant electron transfer to the fullerene cage, giving rise to an electric dipole moment. We use the method of electrostatic beam deflection to verify whether such reactions take place within superfluid helium nanodroplets between an embedded C60 molecule and either alkali (heliophobic) or rare-earth (heliophilic) atoms. The two cases lead to distinctly different outcomes: C60Nan (n = 1–4) display no discernable dipole moment, while C60Yb is strongly polar. This suggests that the fullerene and small alkali clusters fail to form a charge-transfer bond in the helium matrix despite their strong van der Waals attraction. The C60Yb dipole moment, on the other hand, is in agreement with the value expected for an ionic complex.
1 Introduction
Since the discovery of alkali-doped fullerides and their superconductivity,1,2 it has been known that metal atom-fullerene structures with significant charge transfer are readily formed in the bulk, surface,3 and gas phases.4–6 Gas-phase studies are informative because they permit a molecular-level analysis of the charge transfer process.The formation of an ion pair implies the appearance of a large dipole moment, and indeed studies of fullerene-alkali systems by molecular beam electric deflection7 have demonstrated high electric susceptibilities related to extremely large (∼10–20 D) dipole moments in these systems. Interestingly, these experiments showed that at higher temperatures the alkali metal atoms and clusters appear to skate about the surface of the fullerene. Analogously, complexes of C60 with transition metals were found to have dipole moments of 6–10 D.8
Helium nanodroplet embedding offers a method to assemble and study such systems at very low temperatures and within a superfluid environment.9 Rotational and vibrational motion are greatly suppressed at the nanodroplet temperature of 0.37 K, and polar complexes can be strongly oriented by an external electric field and interrogated by pendular spectroscopy10,11 and electrostatic deflection.12
However, there is a hurdle: alkali atoms are strongly heliophobic and are not wetted by the helium medium.13 As a result, alkali atoms and small clusters do not submerge into helium nanodroplets and instead reside in surface dimples.14–17 On the other hand, recent work by Renzler et al.18 provided evidence, based on electron ionization mass spectrometry, that co-doping helium nanodroplets with the highly polarizable C60 molecule induces Na atoms, as well as small clusters of Na and Cs, to submerge into the nanodroplet. It was suggested that this could derive from the strong long-range van der Waals attraction between the partners,19 or from electron transfer via a harpoon reaction. A follow-up computational study20 concluded that harpoon-type charge transfer may take place between Cs2 and fullerene dopants.
The presence or absence of an ion pair within a nanodroplet can be directly established by the electrostatic deflection method. In this work we apply it to the sodium-C60 system and demonstrate that for C60Nan=1–4 there is in fact no evidence of a strong electric dipole appearing in the system, and hence of the partners approaching closely enough to form an ionic bond.
For a comparative measurement, we performed a deflection measurement for nanodroplets doped with C60 and ytterbium atoms. Yb was chosen due to the combination of a favorable ionization energy and vapor pressure. It is also pertinent that ytterbium-intercalated fulleride conductors have been synthesized21 and were found to exhibit superconductivity. While to the best of our knowledge Yb previously has not been used as a nanodroplet dopant, it is unambiguously expected to solvate, analogously to Eu, another rare-earth atom.22 Here we observe a sizable deflection indicative of the formation of a large electric dipole. The magnitude of the dipole is in very good agreement with the computed dipole moment for a Yb atom positioned on a pentagonal face of the fullerene, implying that an electron is readily transferred and a bound C60Yb system is formed.
2 Experiment
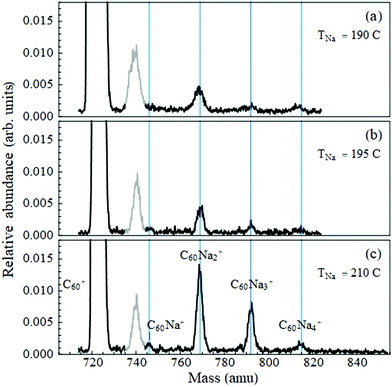
As described in ref. 12 and 23, a supersonic beam of helium nanodroplets is generated by expansion of ultrahigh purity grade helium gas at 80 bar stagnation pressure through a 5 micron nozzle held at a temperature of 15 K. The beam is skimmed, and chopped by a rotating wheel; the beam velocity is measured to be ≈375 m s−1. It then passes through two heated stainless steel pick-up cells, with the first containing C60 powder (99.9%) and the second a small lump of Na (99.99%, loaded under hexane to combat oxidation) or of Yb chips (99.95%). The dopants are picked up by sequential collisions with the droplet beam and their thermal energy is promptly dissipated by partial evaporation of the droplet.9The pick-up process follows Poisson statistics. The cell temperatures were stabilized to optimize the signal to a desired average number of dopants. The temperature of C60 was fixed to a value between 370 °C and 380 °C. This yielded sufficient intensity in the mass spectrum at the single C60+ mass while keeping the intensity of the C60 dimer to a negligible level. (At this temperature many of the fullerene's vibrational modes24 are activated, hence pick-up of one molecule results in the nanodroplet shrinking by ∼9000 He atoms.) Deflection measurements of C60Nan were taken with the metal-containing cell temperature ranging from 190 °C to 210 °C, and of C60Yb with this cell at 360 °C.
The beam then travels to the deflection chamber where it is collimated by a 0.25 mm × 1.25 mm slit, and passes between two 15 cm-long high voltage electrodes which create an electric field and a collinear field gradient directed perpendicular to the beam axis. With an applied voltage of 20 kV, a field strength of 82 kV cm−1 with a gradient of 338 kV cm−2 is achieved.25 The nanodroplets then traverse a 1.25 m free-flight region and enter the aperture of a quadrupole mass spectrometer (Ardara Technologies), where they are ionized by electron impact with an electron energy of 70 eV and detected using a pulse-counting channeltron multiplier with a digital counter system synchronized to the chopper.26 With this arrangement, deflection profiles can be acquired even with counting rates as low as a few per second.
Among the peaks in the mass spectrum there are those which correspond to bare C60M+ ions, where M is a metal atom or cluster. These ions are ejected from the droplet following charge exchange with a He+ hole generated by electron-impact ionization.15 Note that they may derive either from post-ionization encounters between C60+ and M (or between C60 and M+), or from the ionization of bound C60M complexes preformed in the nanodroplets. The aim of the measurement is to ascertain whether nanodroplets contain any polar complexes of the latter type, formed by a charge transfer reaction. It is worth reiterating that the deflection step occurs before ionization of the beam, and therefore the reactants and the complexes are electrically neutral.
Deflection profiles were collected by setting the mass spectrometer to these peaks and translating the detection chamber on a precision linear slide, controlled by a stepper motor, under two conditions: “field-off” and “field-on.” The former establishes the original cross section of the beam, and the latter determines the magnitude of beam deviation under the influence of the electric field. As mentioned above, the very low temperature of the helium nanodroplets allows for nearly complete orientation of the permanent dipole of the embedded dopant along the electric field. This permits the force from the electric field gradient on the dipole to become so strong as to deflect the entire heavy nanodroplet on the scale of millimeters.
The initial nanodroplet size distribution in the beam is calibrated by deflections using a dopant with a known dipole moment, in this case CsI. For the conditions employed in the present measurements, the mean size was found to be ≈2 × 104 helium atoms per droplet. Based on this information, we can solve for the dipole moment of a polar embedded complex by fitting its “field-on” profile to a Monte Carlo simulation of the deflection process. Using the “field-off” profile as input, it simulates the beam's path by accounting for the dopants’ pick-up probabilities, post-pickup droplet shrinkage by evaporation, dipole orientation in the electric field region, a correction for the polarization of the helium matrix, the deflection angle induced by the field gradient, and finally the size dependence of the probabilities of droplet ionization and subsequent charge transfer to the dopant. This procedure is described in our previous publications.12,23,27,28
3 Results
3.1 Sodium
Fig. 1 displays the C60Nan mass spectra over the temperature range used for deflection measurements. The peak widths are partially due to the presence of 13C isotopes in the fullerene. Note that the ion signals are quite weak compared to the intensity of the bare fullerene peak. The C60Na+ signal is the weakest of all, including at cell temperatures outside of the range shown. Thus, sodium has a low propensity for forming bound complexes with C60. To determine whether they ever establish direct contact as neutral dopants, we look for evidence of the formation of a dipole moment.Electrostatic beam deflections were performed at the temperatures shown in Fig. 1. At these settings a given mass peak acquires sufficient intensity for a profile measurement, while the larger ones remain weak, minimizing the likelihood of their fragmentation contaminating the peak of interest. This strategy could not be adopted for C60Na due to its low peak intensity but was followed for C60Na2–4.
Fig. 2 shows the undeflected and deflected beam profiles acquired with the mass spectrometer set to the C60Nan+ peaks. For all measured n the deflection is essentially negligible within the accuracy of the measurement. This is in striking contrast with the 14–16 D dipole moment of the ionic C60Na molecule,8,29 which would have resulted in deflections on the order of several millimeters,30 and confirms that no charge-transfer bound complexes between the fullerene cluster and the sodium atom form within the nanodroplet.
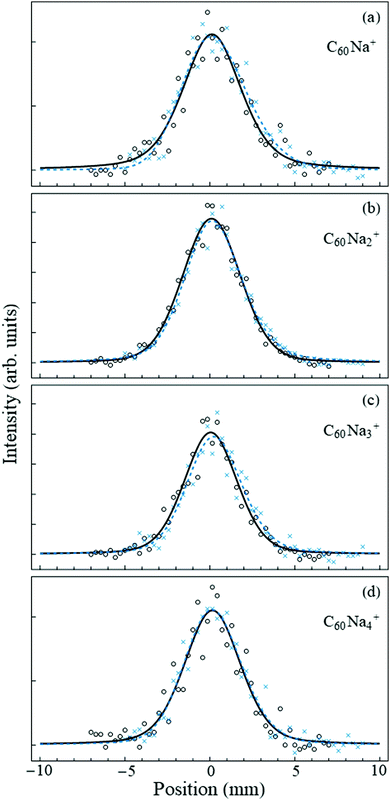 | ||
| Fig. 2 Beam deflection measurements for nanodroplets containing C60Nan=1–4. Circles (crosses) denote data points with the electric field turned off (on). The counting rates of selected ions in the strongly collimated beam were on the order of a few per second. The solid-line profiles are smoothing fits to the “field-off” data points using a symmetric pseudo-Voigt function,31 while the dashed lines are asymmetric pseudo-Voigt smoothing fits to the “field-on” data. In all cases the deflection is negligible. | ||
Note that the average nanodroplet size in this work is approximately 25 times smaller than in ref. 18, and the average radius is therefore almost three times smaller9 (≈60 Å vs. ≈175 Å). It is evident that this decrease in separation does not facilitate a charge-transfer reaction.
3.2 Ytterbium
The case for fullerenes and Yb atoms is qualitatively different. This was already hinted at by the mass spectra, where the ratio of the C60Yb+:C60+ peak intensities was an order of magnitude higher than for C60Nan+:C60+. (The C60Yb mass spectrum is shown in the ESI†). Deflection measurements made the distinction apparent. Fig. 3(a) shows the “field-off” and “field-on” profiles of the C60Yb mass peak. A very sizable deviation is immediately evident, in contrast with the results for sodium, and establishes that the embedded complex has a large permanent electric dipole moment.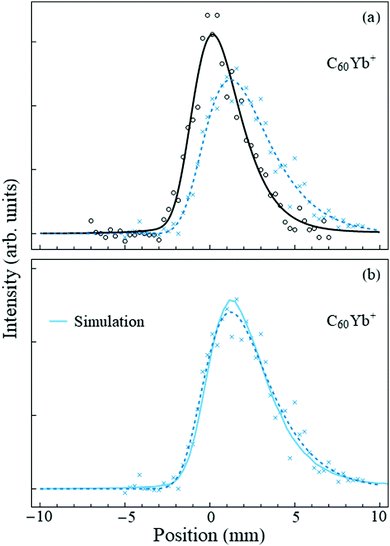 | ||
| Fig. 3 Panel (a) shows the beam deflection measurements of nanodroplets containing C60Yb with the same notation as Fig. 2. A slight offset of the second pick-up cell added minor skewness to the profiles, hence in this figure both the “field-off” and the “field-on” data were fit to an asymmetric pseudo-Voigt profile. The shift of the profile centroid is ≈1.4 mm. Panel (b) shows the same “field-on” profile (dashed line) and data points, together with the Monte Carlo simulation (solid line) for the optimized dipole moment value of 8 D. | ||
Following the fitting procedure described in Section 2, we deduce the magnitude of this dipole moment. The deflecting force is proportional to the degree of orientation induced by the applied electric field onto the molecular dipole. Since the rotational constant of the C60Yb complex is small, it is accurate to use the classical Langevin-Debye expression for the orientation cosine.32,33 Indeed, the fullerene rotational constant is34 0.003 cm−1 and that of the surface-bound Yb atom can be estimated by approximating its radial coordinate by the radius of C60. The result for the complex is ≈0.024 cm−1 = 3.5 mK, which is two orders of magnitude lower than the nanodroplet temperature, and therefore many rotational states are occupied. For the given electric field strength, nanodroplet temperature, and the dipole moment quoted below, the orientation cosine is 0.98, i.e., the complex becomes essentially completely oriented along the field.
Fig. 3(b) displays the result of the optimized fit and demonstrates good agreement with the experimental data. Based on this procedure we assign a dipole moment of 8 ± 1.5 D to the C60Yb complex. The estimated error bar, discussed in the ESI,† derives partially from the data fit and partially from the uncertainty in the branching ratio involved in the charge exchange between He+ and the dopant.12 The result unambiguously demonstrates that the rare earth metal atom contacts and donates charge to the fullerene.
As shown in the next section, the experimentally deduced value of the dipole moment is in good agreement with a calculation of the C60Yb complex, in particular for Yb atoms positioned at the pentagonal face of the fullerene. According to the computation, this situation has a marginally advantageous binding energy (although it is known that systems embedded in helium nanodroplets are not always able to reach their lowest energy geometries). Measurements of crystalline fullerene-ytterbium compounds suggest that the pentagonal face is indeed preferred for charge transfer,35,36 supporting our results.
4 Calculations
To further validate the result for C60Yb, the dipole moments and binding energies of free-space molecules were computed by plane-wave based Density Functional Theory (DFT). Calculations were performed in the Vienna Ab Initio Software Package (VASP).37,38 Electronic states were computed within the frozen core approximation using the projected augmented wave-vector (PAW) method39,40 with projectors generated for the C 2s and 2p states and the Yb 6s and 5p states. The strongly correlated Yb f electrons were assumed not to be involved in bonding and were kept within the core of the pseudopotential. A plane wave cut-off energy of 500 eV and the Perdew–Burke–Ernzerhof (PBE)41 styled generalized gradient approximation (GGA) for the exchange–correlation functional were used. The C60 and C60Yb molecules were placed in the center of a non-cubic 15 Å × 18 Å × 20 Å box to remove spurious image interactions. Optimization was first performed on the C60 molecule to obtain its ground state structure. For computation of the binding energies and dipole moment the ground state C60 structure was kept frozen during the optimization of C60Yb. Linear dipole corrections were used to correct the errors introduced by the periodic boundary conditions.42The results of these calculations are presented in Table 1 alongside similar ones for the dipole moment of isolated C60Na. The latter are in reasonable agreement with previous computations29 and partially validate the present results for C60Yb. As mentioned in the preceding section, it is found that settling the Yb atom on the pentagonal face yields a marginally higher binding energy and a noticeably lower dipole moment.
| Dipole moment (D) | Binding energy (eV) | |||
|---|---|---|---|---|
| Pentagon | Hexagon | Pentagon | Hexagon | |
| C60Yb | 8.5 | 13.0 | 0.58 | 0.54 |
| C60Na | 13.4 | 12.8 | 1.16 | 1.21 |
5 Summary
The experiments detect no sizable electric dipole moment appearing when a fullerene molecule, followed by between one and several sodium atoms, is embedded in helium nanodroplets. Therefore even if a heliophobic alkali atom is pulled inside the nanodroplet by the presence of C60,18 it appears that they continue to be separated by a helium barrier and neither short-range electron transfer nor a longer-range harpoon reaction takes place.The measurement does not provide information about the size of this separation barrier, and therefore an interesting question for further theoretical and experimental analysis is whether the Na atom and C60 form a weakly bound van der Waals-type complex, and how far apart they remain.
As for the absence of an electric dipole moment for C60Na2–4, one can envision two scenarios. One is that the sequentially picked up atoms assemble into a small sodium cluster on or near the droplet surface but still fail to approach the fullerene within the droplet sufficiently to transfer charge and form a bond. This contrasts with C60Nan agglomerates forming in neat molecular beams.43 An alternative possibility is that multiple sodium atoms do attach to the fullerene but arrange themselves in symmetric configurations, as calculated for lowest-energy structures due to Coulomb repulsion between positive sodium ions.29 This cannot be excluded, but would require either a sequence of individual atom-C60 agglomeration events (which appear unlikely within the nanodroplets in view of the data), or attachment of a Na cluster followed by its separation into individual atoms and their subsequent rearrangement around the cage (which, however, would need to proceed in the very low-temperature nanodroplet environment). Consequently, the data do not support the theoretical picture20 of an alkali dimer undergoing a harpoon reaction with C60 and settling into an ionic arrangement with the latter.
In contrast to sodium, we observe that a very strong permanent dipole moment is formed between ytterbium atoms (which are wetted by helium) and C60, revealing successful electron transfer and bond formation in this system. Comparison with modeling of the C60Yb molecule suggests that the ytterbium atom prefers to locate above the pentagonal face of the fullerene. Interestingly, while the harpoon reaction is suppressed in binary collisions in the gas phase19 due to unfavorable Franck–Condon factors,44 in the present case the strong reactive channel is kept open thanks to removal of the accompanying vibrational excitation by the helium matrix.
It would be interesting to extend such measurements to larger alkali clusters, because above a certain critical size they begin to submerge into the nanodroplet by themselves.45,46 This should promote charge transfer and dipole formation, analogous to observations on C60-alkali cluster complexes in free space.7 Interesting complementary information also could be derived from spectroscopic experiments, since near-IR absorption peaks of the fullerenes have been shown47 to be sensitive to the oxidation state of C60n−.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to express our appreciation to Prof. G. Benedek for his eminent contributions to research on helium nanodroplets, fullerenes, and nanoclusters. We would like to thank L. Kranabetter and P. Scheier for productive discussions and R. E. Pedder for advice on sensitivity calibration of the quadrupole mass spectrometer. The research of J. W. N, B. S. K., T. H. V. and V. V. K. was supported by the U. S. National Science Foundation, Division of Chemistry under Grants No. CHE-1664601 and CHE-2153255. T. M. L. and A. N. were supported by the National Science Foundation, Award OAC-2118061. Simulations were performed at the Center for Advanced Research Computing of the University of Southern California. The figures for this article were generated using the SciDraw scientific figure preparation system.48References
- A. F. Hebard, Annu. Rev. Mater. Sci., 1993, 23, 159–191 CrossRef CAS.
- O. Gunnarsson, Alkali-Doped Fullerides: Narrow-Band Solids with Unusual Properties, World Scientific, Singapore, 2004 Search PubMed.
- M. R. C. Hunt, S. Modesti, P. Rudolf and R. E. Palmer, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 10039 CrossRef CAS PubMed.
- L. S. Wang, O. Cheshnovsky, R. E. Smalley, J. P. Carpenter and S. J. Hwu, J. Chem. Phys., 1992, 96, 4028 CrossRef CAS.
- T. P. Martin, N. Malinowski, U. Zimmermann, U. Näher and H. Schaber, J. Chem. Phys., 1993, 99, 4210 CrossRef CAS.
- M. Pellarin, E. Cottancin, J. Lermé, J. L. Vialle, M. Broyer, F. Tournus, B. Masenelli and P. Mélinon, Eur. Phys. J. D, 2003, 25, 31–40 CrossRef CAS.
- M. Broyer, R. Antoine, I. Compagnon, D. Rayane and P. Dugourd, Phys. Scr., 2007, 76, C135 CrossRef CAS.
- D. Rayane, A. R. Allouche, R. Antoine, I. Compagnon, M. Broyer and P. Dugourd, Eur. Phys. J. D, 2003, 24, 9–13 CrossRef CAS.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed.
- M. Y. Choi, G. E. Douberly, T. M. Falconer, W. K. Lewis, C. M. Lindsay, J. M. Merritt, P. L. Stiles and R. E. Miller, Int. Rev. Phys. Chem., 2006, 25, 15–75 Search PubMed.
- D. Verma, R. M. P. Tanyag, S. M. O. O’Connell and A. F. Vilesov, Adv. Phys.: X, 2019, 4, 1553569 Search PubMed.
- J. W. Niman, B. S. Kamerin, D. J. Merthe, L. Kranabetter and V. V. Kresin, Phys. Rev. Lett., 2019, 123, 043203 CrossRef CAS PubMed.
- F. Ancilotto, E. Cheng, M. W. Cole and F. Tiogo, Z. Phys. B: Condens. Matter, 1995, 98, 323–329 CrossRef CAS.
- J. Tiggesbäumker and F. Stienkemeier, Phys. Chem. Chem. Phys., 2007, 9, 4748–4770 RSC.
- A. Mauracher, O. Echt, A. M. Ellis, S. Yang, D. K. Bohme, J. Postler, A. Kaiser, S. Denifl and P. Scheier, Phys. Rep., 2018, 751, 1–90 CrossRef CAS.
- F. Stienkemeier and K. K. Lehmann, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, R127 CrossRef CAS.
- C. Callegari and W. E. Ernst, Helium Droplets as Nanocryostats for Molecular Spectroscopy – from the Vacuum Ultraviolet to the Microwave Regime, in Handbook of High Resolution Spectroscopy, ed. M. Quack and F. Merkt, John Wiley & Sons, Chichester, 2011, vol. 1, pp. 1551–1594 Search PubMed.
- M. Renzler, M. Daxner, L. Kranabetter, A. Kaiser, A. W. Hauser, W. E. Ernst, A. Lindinger, R. Zillich, P. Scheier and A. M. Ellis, J. Chem. Phys., 2016, 145, 181101 CrossRef PubMed.
- V. V. Kresin, V. Kasperovich, G. Tikhonov and K. Wong, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 57, 383–387 CrossRef.
- M. P. de Lara-Castells, A. W. Hauser and O. Mitrushchenkov, J. Phys. Chem. Lett., 2017, 8, 4284–4288 CrossRef CAS PubMed.
- E. Özdaş, A. R. Kortan, N. Kopylov, A. P. Ramirez, T. Siegrist, K. M. Rabe, H. E. Bair, S. Schuppler and P. H. Citrin, Nature, 1995, 375, 126–129 CrossRef.
- A. Bartelt, J. D. Close, F. Federmann, K. Hoffmann, N. Quaas and J. P. Toennies, Z. Phys. D: At., Mol. Clusters, 1997, 39, 1–2 CrossRef CAS.
- D. J. Merthe and V. V. Kresin, J. Phys. Chem. Lett., 2016, 7, 4879–4883 CrossRef CAS PubMed.
- J. Menéndez and J. B. Page, Vibrational Spectroscopy of C60, in Light Scattering in Solids VIII, ed. M. Cardona and G. Güntherodt, Springer; Berlin, 2006, 1, 27–95 Search PubMed.
- G. Tikhonov, K. Wong, V. Kasperovich and V. V. Kresin, Rev. Sci. Instrum., 2002, 73, 1204–1211 CrossRef CAS.
- N. Guggemos, P. Slavíček and V. V. Kresin, Phys. Rev. Lett., 2015, 114, 043401 CrossRef PubMed.
- J. W. Niman, B. S. Kamerin, L. Kranabetter, D. J. Merthe, J. Suchan, P. Slavíček and V. V. Kresin, Phys. Chem. Chem. Phys., 2019, 21, 20764–20769 RSC.
- B. S. Kamerin, J. W. Niman and V. V. Kresin, J. Chem. Phys., 2020, 153, 081101 CrossRef PubMed.
- J. Roques, F. Calvo, F. Spiegelman and C. Mijoule, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 205412 CrossRef.
- While Fig. 1 shows that water, which is a ubiquitous contaminant in vacuum systems, is also present in the beam, the fact that there are no noticeable C60NanH2O peaks indicates that the deflection profiles are uncontaminated. Furthermore, even the adsorption of a water molecule would not be able to extinguish such a big dipole moment.
- A. L. Stancik and E. B. Brauns, Vib. Spectrosc., 2008, 47, 66–69 CrossRef CAS.
- B. Friedrich and D. Herschbach, Int. Rev. Phys. Chem., 1996, 15, 325–344 Search PubMed.
- J. Bulthuis, J. A. Becker, R. Moro and V. V. Kresin, J. Chem. Phys., 2008, 129, 024101 CrossRef CAS PubMed.
- P. B. Changala, M. L. Weichman, K. F. Lee, M. E. Fermann and J. Ye, Science, 2019, 363, 49–54 CrossRef CAS PubMed.
- P. H. Citrin, E. Özdaş, S. Schuppler, A. R. Kortan and K. B. Lyons, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 5213–5227 CrossRef CAS.
- X. Cao, Y. Wang, J. Hao, J. Liu, S. Hu and G. Lan, J. Raman Spectrosc., 2000, 31, 461–463 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558(R) CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067 CrossRef CAS PubMed.
- P. Dugourd, R. Antoine, D. Rayane, I. Compagnon and M. Broyer, J. Chem. Phys., 2001, 114, 1970–1973 CrossRef CAS.
- V. V. Kresin and V. Z. Kresin, Z. Phys. D: At., Mol. Clusters, 1997, 40, 381–384 CrossRef CAS.
- C. Stark and V. V. Kresin, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085401 CrossRef.
- L. An der Lan, P. Bartl, C. Leidlmair, H. Schöbel, R. Jochum, S. Denifl, T. D. Märk, A. M. Ellis and P. Scheier, J. Chem. Phys., 2011, 135, 044309 CrossRef PubMed.
- D. R. Lawson, D. L. Feldheim, C. A. Foss, P. K. Dorhout, C. M. Elliott, C. R. Martin and B. Parkinson, J. Electrochem. Soc., 1992, 139, L68–L71 CrossRef CAS.
- M. A. Caprio, Comput. Phys. Commun., 2005, 171, 107–118 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00751g |
| This journal is © the Owner Societies 2022 |