Open Access Article
Open Access ArticleDelving into guest-free and He-filled sI and sII clathrate hydrates: a first-principles computational study†
Raquel
Yanes-Rodríguez
 ab,
Adriana
Cabrera-Ramírez
ab and
Rita
Prosmiti
ab,
Adriana
Cabrera-Ramírez
ab and
Rita
Prosmiti
 *a
*a
aInstitute of Fundamental Physics (IFF-CSIC), CSIC, Serrano 123, 28006 Madrid, Spain. E-mail: rita@iff.csic.es; Tel: +34 915616800
bDoctoral Programme in Theoretical Chemistry and Computational Modelling, Doctoral School, Universidad Autónoma de Madrid, Spain
First published on 13th May 2022
Abstract
The dynamics of the formation of a specific clathrate hydrate as well as its thermodynamic transitions depend on the interactions between the trapped molecules and the host water lattice. The molecular-level understanding of the different underlying processes benefits not only the description of the properties of the system, but also allows the development of multiple technological applications such as gas storage, gas separation, energy transport, etc. In this work we investigate the stability of periodic crystalline structures, such as He@sI and He@sII clathrate hydrates by first-principles computations. We consider such host water networks interacting with a guest He atom using selected density functional theory approaches, in order to explore the effects on the encapsulation of a light atom in the sI/sII crystals, by deriving all energy components (guest–water, water–water, guest–guest). Structural properties and energies were first computed by structural relaxations of the He-filled and empty sI/sII unit cells, yielding lattice and compressibility parameters comparable to experimental and theoretical values available for those hydrates. According to the results obtained, the He enclathration in the sI/sII unit cells is a stabilizing process, and both He@sI and He@sII clathrates, considering single cage occupancy, are predicted to be stable whatever the XDM or D4 dispersion correction applied. Our results further reveal that despite the weak underlying interactions the He encapsulation has a rather notable effect on both lattice parameters and energetics, with the He@sII being the most energetically favorable in accord with recent experimental observations.
1 Introduction
Clathrate hydrates are crystalline compounds formed by a host water skeleton containing polyhedral cavities of different size and shape, which can be occupied, fully or partially, by diverse guest molecules (noble gases, H2, N2, CH4, CO2, H2S,…) depending mostly on the thermodynamic conditions (low temperature and high pressure).1–3 These ice-like lattices are naturally occurring in the ocean depths, as well as in permafrost regions of Earth.4,5 Moreover, they are also likely to exist in other planetary bodies, such as Pluto's ocean,6 Mars’ ice caps7 or Titan's surface.8 The stability of these complexes arises from the hydrogen bonds established between water molecules and the van der Waals (vdW) dispersion forces between host and guest species.9,10The three most common clathrate hydrates structures adopted naturally are the cubic sI and sII lattices and the hexagonal sH. What distinguishes them is the size, shape and number of water cages present in each of the structures, as well as the periodic crystal structure. Thus, the cubic sI host lattice consists of 46 water molecules per unit cell, forming two pentagonal dodecahedron (small cavity formed by 20 water molecules, 512) and six ellipsoidal-shaped tetrakaidecahedron cages (large cavity formed by 24 water molecules, 51262). The cubic sII unit cell comprises 136 water molecules located in sixteen small 512 cages and eight hexakaidecahedron large cages (composed by 28 water molecules, 51264). Finally, the hexagonal sH unit cell is made up of 34 water molecules distributed in three 512, two irregular dodecahedra 435663 (with 20 water molecules) small cages and one large icosahedron 51268 (with 36 water molecules) cage.5,11,12 Less common clathrate hydrates structures, such as the C0, C1, C2, etc. have been also reported.13–18 Generally, there is only one guest atom/molecule within each small cage, whereas two or more species can be encapsulated in the larger cages as reported in different multiple-occupancy studies.19–25
Due to the flexible character of the H-bonds, water presents a rich phase diagram with a great diversity of crystalline phases, both clathrate-like and ice-like. The formation of one structure or another strongly depends, among other things, on the conditions of pressure (P) and temperature (T). Therefore, transitions between different phases can occur or even several structures can coexist.3 Is it important to emphasize the need to understand the stability of these systems, taking into account nuclear quantum effects,26,27 as well as the mechanisms involved in their formation/dissociation,28 since new structures can be found by both filling with guest molecules23 or by emptying16,29 the corresponding hydrate cavities or even the inter-cage molecule migration of one cage to the neighboring ones,30–32 under certain P–T conditions.33 This may be useful and relevant, not only from a fundamental point of view, given that new regimes of the phase diagram of water can be investigated, such as low-density ice structures,34,35 but also from a practical point of view, since promising applications of gas hydrates can be further explored, such as gas storage materials,36–38 potential energy sources,39,40 gas separation,41–43 energy transport44,45 and desalination techniques.46–48
So far, a great number of clathrate hydrates filled with different guest species have already been studied.49–55 In this context, noble gas hydrates are a valuable target due to the simple electronic structure of these inert atoms, together with their unique stability and properties.10,56 These features make them perfect to create prototype models which may serve to study, for example, the energy variation with the guest size or with the cage occupancy, as well as to predict the stability of other similar systems.57,58 In this regard, the clathrate hydrates of Ar, Kr, and Xe were discovered long time ago,59–63 whereas the clathrate hydrates of the lighter noble gases (He and Ne) have been synthesized more recently.23,29 Focusing our attention on the He atom, it has been observed that it is more likely to form ice-like structures.64–67 However, as mentioned before, Falenty et al. were able to stabilize the eagerly awaited He@sII clathrate hydrate.23 Helium also forms binary hydrates with molecules such as hydrogen or tetrahydrofuran in sII clathrate structure.68,69 Recently, valuable information on benchmark data,10,70 as well as on the stability of each of the clathrate cavities of the sI, sII structures70 have been reported, indicating that the reactions associated with the encapsulation of the He atom inside the 512, 51262 and 51264 cages are thermodynamically favored in the range of experimental conditions.23 Therefore, given the shortage of information available on these systems, and following our previous studies on He–water complexes of different size, in this work we aim to go one step further by studying from a theoretical point of view the stability of periodic crystalline structures of the He@sI and He@sII clathrate hydrates from first-principles approaches.
Since its inception, computational chemistry has made remarkable progress, becoming a useful tool in the study of diverse chemical species, from simple atoms and molecules to complex systems. It yields valuable information about understanding and predicting trends in structures and properties of compounds, as well as about reaction mechanisms or dynamics.71 The continuous development of quantum theories combined with progressing technology steadily increases the variety of chemical problems that can be treated computationally in terms of reasonable accuracy and affordable computational time.72,73 Moreover, the recent advances in data science techniques, such as in machine-learning,74–79 offer new opportunities to efficiently evaluate the properties of molecular systems by successfully accelerating computational algorithms and amplifying the knowledge available from computational chemistry techniques.80 Most of the theoretical investigations on noble gas clathrate hydrates have been reported from molecular dynamics simulations, and ab initio quantum chemical approaches.10,13,56,58 In this context, density functional theory (DFT) is nowadays a suitable and an appropriate tool for studying molecular interactions in condensed phase systems. Modern DFT-D approaches including dispersion corrections improve the description of the nonstandard, non-covalent guest–host interactions, and such schemes are important when one is dealing with gas hydrates. Thus, in this work we performed DFT-D calculations on He-filled and empty sI and sII clathrate hydrates in order to obtain valuable structural and energetic insights, by evaluating their binding through the computation of the two main, host–host and guest–host, interactions. Comparisons with the individual cages,70 as well as with experimental and previous theoretical data available in the literature for similar systems are also considered and discussed.
2 Computational details
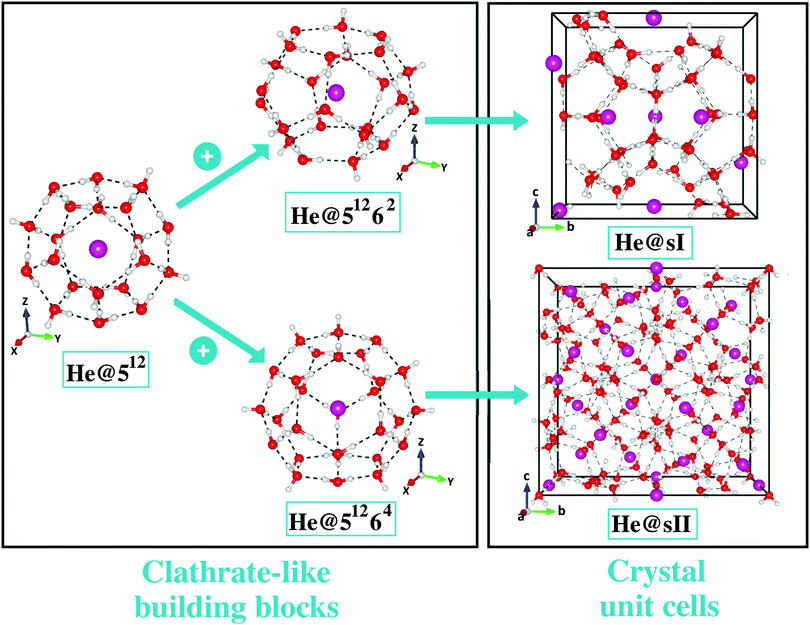
In Fig. 1 the He@sI and He@sII crystal unit cells together with their corresponding building block cages are shown. Both sI and sII empty crystal structure was initially taken from the 3D crystalline framework given in ref. 81. The oxygen atoms positions have been extracted from the X-ray diffraction experiments, while the hydrogen atoms orientations have been determined from TIP4P water model optimizations, satisfying both the ice rules and give a net zero dipole moment for the unit cell configuration.81 The cubic sI unit cell has 46 water molecules and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n space group symmetry, while the cubic sII hydrate unit cell has 136 water molecules and Fd
n space group symmetry, while the cubic sII hydrate unit cell has 136 water molecules and Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group symmetry. The He atoms are positioned at the center of each cages in the cell, with a H2O
m space group symmetry. The He atoms are positioned at the center of each cages in the cell, with a H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He ratio, called hydration number, of 46
He ratio, called hydration number, of 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 and 136
8 and 136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 in the He@sI and He@sII structures, respectively, using the DENEB software package.82
24 in the He@sI and He@sII structures, respectively, using the DENEB software package.82
Electronic structure DFT calculations were performed for both the empty and He-filled sI and sII periodic structures, using the PW86PBE functional as implemented in the LIBXC library83 of the Quantum Espresso (QE) code.84–86 Dispersion corrections were also considered using the exchange dipole moment (XDM) scheme,87,88 as implemented in QE, and the D4 term89,90 as a postprocessing through the DFTD491 program. The selection of the PW86PBE functional and the specific dispersion correction schemes is made on the basis of previous investigations on the assessment of various GGA, meta-GGA and hybrid DFT functionals for finite-size clathrate-like cages,3,10,70,92 as well as on similar gas hydrate systems,3,12,93 in comparison with benchmark data from DF-MP2, DLPNO-MP2 and DLPNO-CCSD(T) approaches, taking into consideration the computational resources available and the cost of the calculations. Further, we should also note that non-local dispersion effects are also explored through the vdW-DF and vdW-DF2 functionals,94,95 as implemented in the QE code, although we found an expansion in the lattice parameter for both He-filled sI and sII structures, observed previously in similar clathrate systems,2,51 and thus they were not considered any further.
The plane-wave/pseudopotential approach within the projector-augmented-waves (PAW) method96 was employed using the standard PAW pseudopotentials supplied within QE, with PBE-based pseudopotentials used for the PW86PBE97,98 computations. Several single-point runs were carried out to check the convergence for the energy cutoff for the plane-wave expansion of the wavefunctions, Ecut_wfc, and for the charge density, Ecut_rho, (see Fig. S1–S4 of the ESI†), as well as the number of k-points in the DFT calculations using the PW86PBE without and with XDM and D4 dispersion corrections for each He-filled and empty sI and sII structures. In this way the Ecut_wfc was selected at 90/80 Ry (1224/1088 eV) and for the Ecut_rho at 480/360 Ry (6530/4898 eV) for the empty and He-filled sI/sII structures, respectively, while a Monkhorst–Pack 2 × 2 × 2/1 × 1 × 1 k-point grid99 in the reciprocal space was used per unit cell in the sI/sII systems. As regards the DFT calculations for the isolated H2O molecule and He atom, they were performed at the Γ-point, in a cubic simulation cell of volume 20 × 20 × 20 Å3. Regarding the structure optimizations, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-newton algorithm was chosen to perform the corresponding geometry relaxation until components of energies and forces on all atoms are below 10−4 Ry and 10−3 Ry bohr−1, respectively.
The cohesive energies per water molecule for the fully occupied He@sI/He@sII structures and the empty sI/sII hydrates were computed as:
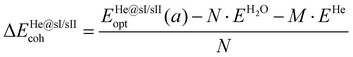 | (1) |
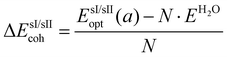 | (2) |
Thus, the binding energy per He atom encaged in the empty sI/sII systems is given by,
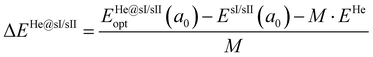 | (3) |
Finally, the saturation energy corresponding to the total energy difference when the sI/sII hydrates are fully occupied, with one helium per cage, is given by
| ΔEsat = EHe@sI/sIIopt(a0) − EsI/sIIopt(a0) − EM·Heopt(a0) | (4) |
3 Results and discussion
3.1 Structural empty and He-filled sI/sII lattice properties
We started by carrying out full geometry optimizations on the fully He-filled and empty sI/sII periodic structures, at a variety of lattice constant, a, values. Total energies EHe@sI/sIIopt and EsI/sIIopt as a function of a are shown in in Fig. S5 of the ESI,† while the resulting cohesive energies per water molecule as a function of a using the PW86PBE functional with the D4 and XDM dispersion correction schemes (see Tables S1 and S2 for numerical results, ESI†) are plotted in Fig. 2.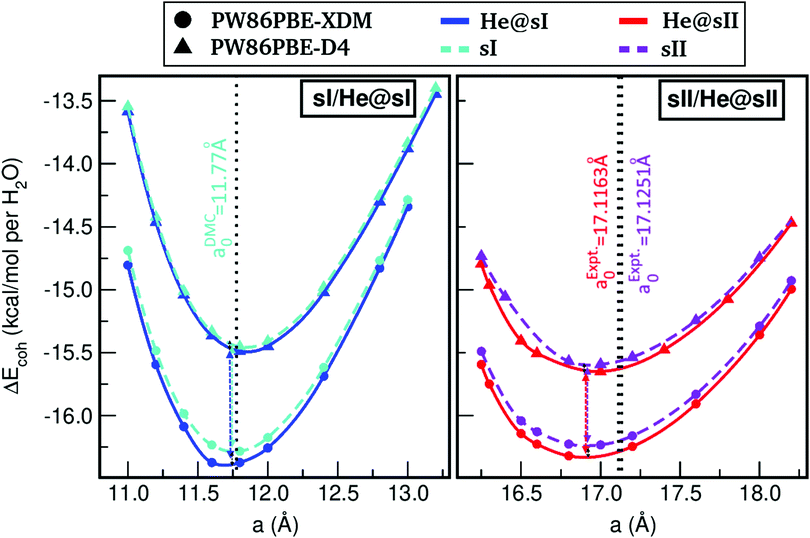 | ||
| Fig. 2 Cohesive energies, in kcal per mol per water molecule, of the fully occupied He@sI clathrate and the empty sI hydrate (left panel), and of the fully occupied He@sII clathrate and the empty sII hydrate (right panel), as a function of the lattice constant a in Å. Solid lines corresponds to the MEOS fits, while the values of equilibrium lattice constants are drawn with dashed (this work) and dotted (DMC value from ref. 51 for sI, and experimental ones from ref. 23 and 29 for He@sII and sII) lines. | ||
The curves present similar behavior in both panels, although there are certain differences that should be mentioned. First of all, the lattice parameters associated with the sI crystal are smaller than those corresponding to the sII crystal, as a consequence of the smaller size of the sI lattice. In both systems, the PW86PBE-XDM functional predicts more energetically favorable lattices than the same functional with the D4 dispersion correction. Nevertheless, the energy difference between the He-filled (He@sI/He@sII) and empty (sI/sII) systems, when considering both D4 and XDM schemes, is higher for the sI crystals than for the sII ones. For example, at a = 11.8 Å (sI/He@sI systems) and 16.8 Å (sII/He@sII systems) this difference is around 0.88 and 0.83 kcal mol−1 for the He@sI and sI curves, respectively, and 0.67 and 0.66 kcal mol−1 for the He@sII and sII, respectively. Therefore, we can extract two conclusions from this analysis: on the one hand, the energy difference between the D4 and XDM energies is higher for the He-filled and empty sI systems, and on the other hand, the curves corresponding to the empty structures for both sI and sII systems are energetically closer than those of the corresponding He-filled lattices. Another interesting feature that should be mentioned is that the inclusion of the He atom in both sI and sII lattices generates full He-filled structures with lower energy than the sI and sII ones. In particular, an energy lowering by around 0.09 kcal per mol per H2O molecule is obtained for both He@sI and He@sII from the PW86PBE-XDM calculations, while smaller values of around 0.03–0.06 kcal per mol per H2O molecule is estimated from the PW86PBE-D4 ones. Thus, such energy differences (per water molecule) between the He-filled and empty systems curves are approximately equal when one considers the XDM dispersion scheme, but higher for the sII–He@sII curves when the D4 correction is included.
The next step in our analysis consists in obtaining the equilibrium lattice constants, a0, and the corresponding ΔEHe@sI/sIIcoh(a0) and ΔEsI/sIIcoh(a0) energies. The calculated total EHe@sI/sII(a) and EsI/sII(a) energies as a function of the lattice parameter are fitted to the Murnaghan's (see solid and dashed lines in Fig. 2) and Vinet's equations of state (MEOS, VEOS).100,101 Similar trends are found for both MEOS and VEOS fits, with the resulting equilibrium lattice parameters, as well as the bulk moduli (bulk modulus, B0, and bulk modulus pressure derivative, 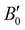 , at zero pressure) listed in Table 1.
, at zero pressure) listed in Table 1.
In the present DFT calculations, the a0 values are computed through potential energy optimizations for the empty and fully filled He@sI/He@sII crystal cells, and thus temperature or pressure, as well as vibrational zero-point effects are not taken into account. However, since the experimental data available in the literature reported at specific P–T conditions, we should only consider comparisons with those results at zero pressure and temperature. Thus, for the empty sI clathrate we compare the a0 obtained from the present MEOS fits with the recent theoretical value of a0 = 11.77 Å reported from MEOS fits to diffusion Monte Carlo (DMC) calculations, while for the empty sII hydrate an equilibrium lattice parameter a0 = 17.1251 Å has been obtained by fitting to a polynomial T-dependence expression the data from the neutron diffraction experiments on the deuterated hydrate.29 If we compare these results with the present values, we get relative errors of 0.144% and 0.578% at PW86PBE-XDM and PW86PBE-D4 levels, respectively, for the empty sI system; whereas the error increases to 1.244% and 1.063%, respectively, for the sII crystal. We should note that the deuterated hydrates have somewhat weaker D-bonds that could result to slightly longer cell parameters than those of the H-bonding ones, as one can observe such isotopic H/D effect between the calculated and experimentally measured a0 value for the sII hydrates. As we can also see, the equilibrium lattice parameter computed including XDM dispersion correction is closer to the reference theoretical value for the sI hydrate, while the calculated value with the D4 dispersion has the smallest relative error for the sII structure.
Regarding the case of the He-filled sI and sII crystals, until recently studies were limited to He atom encapsulation in ice-frameworks. Nevertheless, in 2018 the He@sII structure has been synthesized in the laboratory,23 and for such partially filled clathrates an a0 value of 17.0763 Å has been reported for samples at 100 MPa, and a0 = 17.1163 Å at ambient pressure for a temperature of 80 K. We should highlight here that the changes reported23 in the lattice parameters of the empty sII and partially filled He@sII count 0.01 Å, at the same P–T conditions (both structures with deuterated water framework). Unfortunately, there is no more information on lattice parameters at low temperatures for such He clathrates, although an extrapolation by considering the analytical expression of the thermal expansivity is available for the Ne@sII in ref. 29. The polynomial, a(T) = A0 + A1T + A2T2 + A3T3 + A4T4, expression29 extrapolates the measured lattice parameter from 145 K to 0 K, and estimates of a0 = 17.1025 and 17.1251 Å have been reported for the Ne@sII and sII, respectively. The a0 value for the Ne@sII is shorter by less than 0.1% from the experimental value at 80 K, thus we may suggest that a similar change might be expected for the He@sII system. Indeed, such experimental value is very close to the 16.903/16.950 Å obtained from the PW86PBE-XDM/D4 calculations for the He@sII, and it is by 0.01 Å smaller than those of the empty sII at the PW86PBE-XDM level of calculation and 0.01 Å larger at the PW86PBE-D4 (see Table 1), with the XDM predicting the lattice changes in the same direction with the experimental data. However, we should be rather cautious as multiple or partial occupancy observed in the experimental study, as well as deuterated effects could also affect these results.
In the absence of further He data, we also compare our results with those reported in the literature for similar systems. For example, values of a0 = 17.103 Å for Ne@sII,29 and a0 = 11.835 Å for Xe@sI102 for rare-gas clathrates. Continuing with small molecules clathrates, a0 = 17.083 and 11.811 Å for the N2@sII29 and N2@sI,103 respectively, while for systems encapsulating CO, such as CO@sI/sII a0 = 11.819/17.063 Å have been reported2 from neutron powder diffraction experiments. We can also compare our outcomes with those available for larger encapsulated molecules, such as a0 = 11.835 Å for ethylene oxide sI hydrate, and a0 = 17.130 Å for tetrahydrofuran sII hydrate.104,105 In most cases, the difference with respect to the computed He@sI and He@sII lattice parameters is less than 0.08 and 0.17 Å, respectively. One can see that all these lattice parameters are larger than those of He-filled systems, as expected from species with stronger interactions.
In turn, we have studied the effects of pressure on both empty sI/sII and fully filled He@sI/sII structures. The corresponding MEOS of each structure are displayed in the a–P diagrams of Fig. 3. The bulk moduli, both B0 and 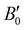 were initially estimated from the corresponding MEOS fits, assuming linear dependence of the bulk modulus with pressure,
were initially estimated from the corresponding MEOS fits, assuming linear dependence of the bulk modulus with pressure, 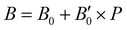 , with B0 being constant and valid for the range
, with B0 being constant and valid for the range 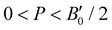 . Using an initial guess of
. Using an initial guess of 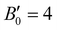 , the B0 values listed in Table 1 are obtained. The PW86PBE-XDM predicts higher values of B0 and
, the B0 values listed in Table 1 are obtained. The PW86PBE-XDM predicts higher values of B0 and 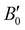 for the He-filled structures compared with empty hydrates, thus indicating that the crystal without guest molecules is more compressible, whereas the PW86PBE-D4 predicts lower values for the same parameters in the He-filled structures, concluding that the empty systems are more resistant to compression. Therefore, the PW86PBE functional with XDM and D4 dispersion corrections produces opposite results. To clarify the results related to the structural parameters, we have also fitted the values of the total EHe@sI/sIIopt(a) and EsI/sIIopt(a) energies considering the VEOS, which is applicable for all classes of solids in compression.101 With this idea, we have found that PW86PBE-XDM predicts that empty systems (sI and sII) are more compressible than fully occupied clathrates (He@sI/sII) having a smaller bulk modulus, while, PW86PBE-D4 predicts that filled systems have higher compressibility than empty hydrates. Although, the trend observed using the MEOS is confirmed by using the VEOS (see corresponding values in the Table 1), it should be noted that such overall claims on the bulk modulus are weakened by accuracy issues in the theoretical bulk modulus, as testified by the fact that by changing the EOS form their value difference is larger that the differences obtained between filled and empty hydrates systems employing XDM or D4 dispersion corrections. Next, in Fig. 3, one can see that the higher the pressure, the shorter the lattice parameter or what is the same, the He-filled and empty sI and sII hydrates suffer greater compression as pressure increases. The curves corresponding to He-filled and empty clathrates are almost overlapped when XDM or D4 dispersion corrections are applied.
for the He-filled structures compared with empty hydrates, thus indicating that the crystal without guest molecules is more compressible, whereas the PW86PBE-D4 predicts lower values for the same parameters in the He-filled structures, concluding that the empty systems are more resistant to compression. Therefore, the PW86PBE functional with XDM and D4 dispersion corrections produces opposite results. To clarify the results related to the structural parameters, we have also fitted the values of the total EHe@sI/sIIopt(a) and EsI/sIIopt(a) energies considering the VEOS, which is applicable for all classes of solids in compression.101 With this idea, we have found that PW86PBE-XDM predicts that empty systems (sI and sII) are more compressible than fully occupied clathrates (He@sI/sII) having a smaller bulk modulus, while, PW86PBE-D4 predicts that filled systems have higher compressibility than empty hydrates. Although, the trend observed using the MEOS is confirmed by using the VEOS (see corresponding values in the Table 1), it should be noted that such overall claims on the bulk modulus are weakened by accuracy issues in the theoretical bulk modulus, as testified by the fact that by changing the EOS form their value difference is larger that the differences obtained between filled and empty hydrates systems employing XDM or D4 dispersion corrections. Next, in Fig. 3, one can see that the higher the pressure, the shorter the lattice parameter or what is the same, the He-filled and empty sI and sII hydrates suffer greater compression as pressure increases. The curves corresponding to He-filled and empty clathrates are almost overlapped when XDM or D4 dispersion corrections are applied.
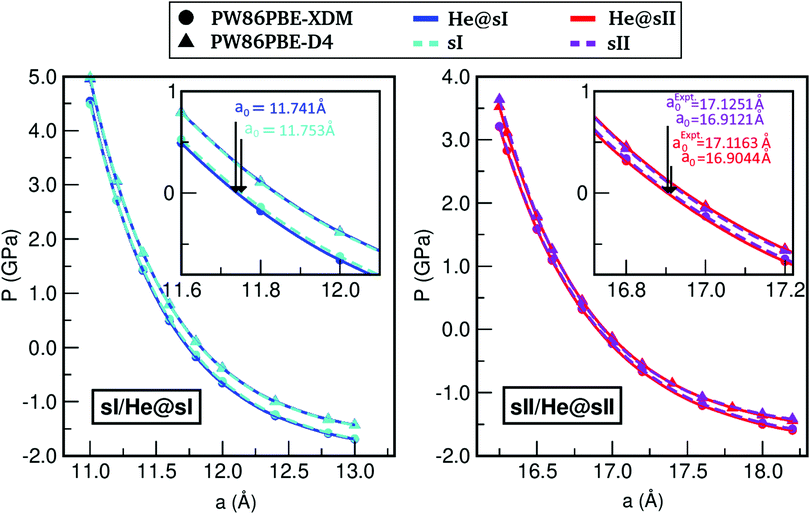 | ||
| Fig. 3 Pressure effects on the lattice constant a of the He-filled and empty sI (left panel) and sII clathrate hydrates (right panel). Solid lines correspond to the MEOS fits (see Table 1). The zero-pressure lattice parameter values are indicated for the sI/He@sI, while the values at ambient pressure (10−4 GPa) are reported for the sII/He@sII. | ||
The bulk modulus obtained for the He@sI/sII clathrates at PW86PBE-XDM/D4 level (Table 1) are smaller than those obtained for other systems.3,12 For example, for the CO2@sI hydrate values of 13.64/12.53 GPa for the bulk modulus have been recently reported, while in the He@sI the values obtained are 12.140/10.632 GPa for the same functionals. In the case of CO2@sII, these values are 17.149/16.053 GPa, whereas for the He@sII hydrate we obtained 15.851/15.084 GPa. According to this, it is possible to see that for both structures (sI and sII), the bulk modulus values for the clathrate hydrates with helium encapsulated are smaller than in the cases with the larger CO2 molecule, that indicates the higher compressibility of the He@sI/sII clathrates compared to the CO2@sI/sII ones. We should note that all comparisons of the structure parameters and compressibility of He clathrates with experimental data on other clathrates is informative on the strength of the cage–host interaction, it is not meant as a validation of the calculations.
3.2 Stability of the He@sI and He@sII clathrates
The He clathrate hydrate has been recently observed only in the sII structure,23 and prediction of stability issues involves the calculation of guest–host and host–host interactions in the such crystal lattices. All energies were computed for a single occupancy of all cages with hydration number of 5.75 and 5.67 for the He@sI and He@sII clathrates, respectively, using the PW86-XDM/D4 DFT-D functionals.Total and cohesive energy values are reported above, and in order to better understand these results, we have decomposed the total cohesive energy into contributions arising from the He atom binding to the empty sI or sII hydrate (see eqn (3)), ΔEHe@sI/sII, the guest–host interaction part, and the cohesive energy of the empty sI and sII hydrate (see eqn (2)), ΔEsI/sIIcoh, corresponding to the host–host interaction component. In Fig. 4 these binding energy values of He to the sI/sII hydrates, as well as the cohesive energies of the empty sI/sII crystals at their corresponding equilibrium lattice constant, a0, obtained from the present DFT-D computations, are displayed. The binding energies (per He atom) characterizing the guest–host interactions, and the cohesive energies per water molecule are consistent with energies previously reported for the individual He-filled and empty 512 (present in sI and sII), 51262 (present in sI) and 51264 (present in sII) cages from DLPNO-CCSD(T)/AVTZ reference calculations,70 and are plotted in Fig. 4 (see vertical dashed and dashed-dotted lines), together with the reference DMC value for the bulk sI hydrate, ΔEsIcoh, (see vertical solid line) available in the literature.51
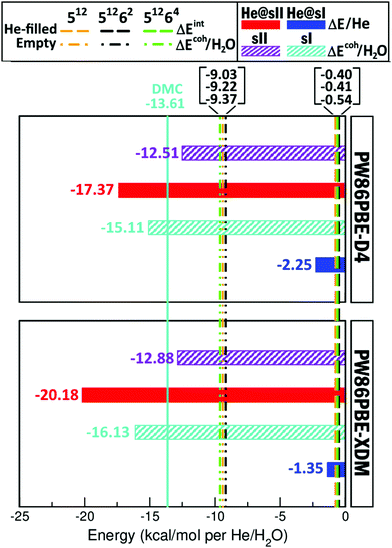 | ||
| Fig. 4 Binding (per He atom) and cohesive (per water molecule) energies, in kcal mol−1, of the He-filled and empty sI and sII clathrate hydrates, respectively, obtained from the present PW86PBE-XDM/D4 computations. Vertical dashed/dashed-dotted lines correspond to interaction and cohesive (per water molecule) energies, in kcal mol−1, of the individual He-filled/empty sI and sII clathrate-like cages, respectively, computed at DLPNO-CCSD(T)/AVTZ level,70 while the reference DMC value from ref. 51 for the empty sI hydrate is displayed by a solid color (cyan) line. | ||
One can see that the PW86PBE-XDM/D4 values underestimate the bulk sI formation energies compared to the references DMC data,51 while the DLPNO-CCSD(T) values for finite-size cages should be considered as lower energy limits in all bulk hydrates studied here. The PW86PBE-XDM calculations overestimate binding energies of the He@sII clathrates, as well as formation energies of empty sI and sII hydrates, and underestimate binding of the He@sI structure compared to the PW86PBE-D4 results. Another aspect which stands out is the fact that for the He@sII crystal the binding is stronger than for the He@sI one by approximately 17 kcal mol−1, whatever the dispersion correction is. On the contrary, the empty sI hydrate is predicted to have lower cohesive energy than the sII one by approximately 3 kcal mol−1. Although the difference in the cohesive energies of the water framework is smaller on a per molecule basis, compared to those in the He binding energies, apparently the H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He ratio means that small errors/differences in water–water interactions are much affected compared to the larger values in binding per He atom. Nevertheless, one can see that the PW86PBE functional with both XDM and D4 dispersion schemes exhibit the same qualitative behavior.
He ratio means that small errors/differences in water–water interactions are much affected compared to the larger values in binding per He atom. Nevertheless, one can see that the PW86PBE functional with both XDM and D4 dispersion schemes exhibit the same qualitative behavior.
In turn we also present the results of energetics involved in the total energy release after saturation of all 8 and 24 cages in the bulk sI and sII hydrates. The saturation energy, ΔEsat, is obtained as the total energy difference between the empty sI/sII and free He atoms to full occupied He@sI/sII clathrate (see eqn (4)). We found that single He filling of all 24 sII cages is energetically more favorable than filling all 8 cavities of the sI structure. The values of the corresponding saturation energies are −3.99/−1.45 and −11.95/−7.22 kcal mol−1 for He@sI and He@sII, respectively, calculated at PW86PBE-XDM/D4 (see Fig. 5). Again we can see that results obtained from both XDM and D4 dispersion energies are qualitatively similar, predicting that the full single He occupation stabilizes the sII and sI structures, He@sII is clearly more stable than He@sI, although the XDM saturation energies being much lower than those obtained from the D4 scheme.
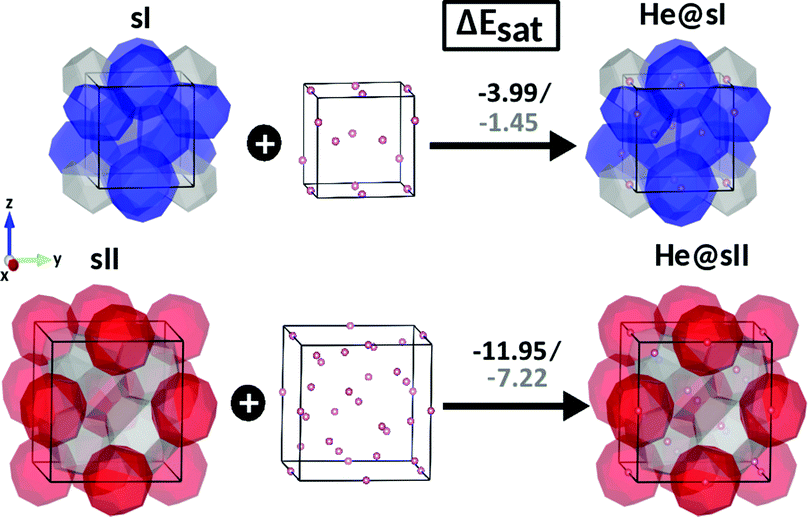 | ||
| Fig. 5 Saturation energies, ΔEsat, in kcal mol−1, for fully single cage occupation He@sI and He@sII clathrate hydrates, as computed from the present PW86PBE-XDM/D4 calculations. | ||
Such conclusion could be supported by considering the size and number of cages forming the bulk sI and sII unit cells. The fact that the sII unit cell has a larger number of small 512 than the sI one, and further the size of the 51262 and 51264 cages forming the sI and sII clathrates, respectively, could affect the He binding in these cages, as have been also found from the DLPNO-CCSD(T) calculations of these individual cages70 (see also Fig. 4). Similar results have been also reported for the CO and CO2 molecules and their stabilizing role in the sII and sI structures,2,3,12 considering both single and multiple cages occupancy. Overall, our calculations show that the full single He occupation of the sII hydrate is energetically more favorable than the sI one, although entropy and enthalpy effects need to be considered too.
4 Summary and conclusions
By performing first-principles DFT-D calculations, we study the effects on the encapsulation of a He atom in sI/sII clathrate hydrates considering the entire periodic 3D crystal lattices. Such light rare-gas@hydrate are challenging targets, as they are suitable for checking the accuracy of computational quantum chemistry approaches on nonstandard non-covalent interactions, and at the same time, the output could contribute to the current emerging research on stabilization of new low-density ice polymorphs, such as ice-XVI or sIII. Thus, on the basis of previous benchmark studies, we have employed the PW86PBE functional with the XDM and D4 schemes for describing the water–water (host–host) and He–water (guest–host) interactions, and evaluating the role of dispersion forces in the complete periodic lattices. Cohesive and binding energies, through structural geometry relaxation DFT-D calculations of the fully He-filled and empty sI/sII unit cells were determined, and their structural properties and stability were discussed. Our results show that the stability could be properly determined by taking into account dispersion corrected schemes such as D4 or XDM ones, with the PW86PBE-D4/XDM functional yielding lattice constants and compressibility parameters comparable to recent experimental and previous theoretical values available for the bulk sII/He@sII and sI structures, respectively. We have highlighted that for an overall reasonable description both the H-bonded water framework and the vdW bound He interactions should be accurately represented, emphasizing the importance of H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He ratio in the error analysis of water–water/He–water interactions.
He ratio in the error analysis of water–water/He–water interactions.
The present computations reveal that both processes for full He occupation of the sI and sII hydrates cages are energetically favored, with the encapsulation of a single He atom per cage playing a stabilizing role in the formation of He@sI and He@sII clathrates, whatever XDM or D4 dispersion scheme used. As shown, guest–host interactions are far from being negligible contributing to the stabilization of such He-filled structures. Total saturation energies of −3.99/−1.45 and −11.95/−7.22 kcal mol−1 were obtained from the present PW86PBE-XDM/D4 calculations for the He@sI and He@sII crystal structures, respectively.
A complete description of the formation of He clathrate structures requires taking into account thermodynamic factors, such as temperature and pressure, as well as nuclear quantum effects.26,27 The incorporation of enthalpy and entropy effects could determine whether the calculated stabilization energies are related to observed phase diagram transformations.13,33,67,70,106,107 Understanding the underlying factors involved in the stability of such hydrates allows the extension of this work in this direction. Thus the next step consists to consider multiple cage occupancy similar to those established by diffraction experiments23 with up to 4 He atoms in the large sII cages and one guest in the small ones, for a more direct comparison with measurements on structural properties. Admittedly, the large sII unit cell of the He clathrate structure as the number of guests increases could become computationally expensive, although tractable for few of them. Moreover, investigations involving the filling with heavier rare-gas, such as Ne, atoms, as well as the stability of other clathrate structures (e.g. He@sH, He@C0,…) or ice-polymorphs could further contribute to delve deeper into the subject, and will be addressed in future studies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Raúl Rodríguez-Segundo for assistance with DENEB-Atelgraphics software. The authors thank to Centro de Cálculo del IFF, SGAI (CSIC) and CESGA for allocation of computer time. This work has been supported by MINECO grant no. FIS2017-83157-P, MICINN grant no. PID2020-114654GB-I00, Comunidad de Madrid grant no. IND2018/TIC-9467, and COST Action CA18212(MD-GAS).Notes and references
- S. Patchkovskii and J. S. Tse, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14645–14650 CrossRef CAS PubMed.
- C. Pétuya, L. Martin-Gondre, P. Aurel, F. Damay and A. Desmedt, J. Chem. Phys., 2019, 150, 184705 CrossRef PubMed.
- A. Cabrera-Ramírez, R. Yanes-Rodríguez and R. Prosmiti, J. Chem. Phys., 2021, 154, 044301 CrossRef PubMed.
- F. J.-A. L. Cruz and J. P.-B. Mota, Phys. Chem. Chem. Phys., 2021, 23, 16033 RSC.
- J. P. Heindel, K. M. Herman, E. Aprá and S. S. Xantheas, J. Phys. Chem. Lett., 2021, 12, 7574–7582 CrossRef CAS PubMed.
- S. Kamata, F. Nimmo, Y. Sekine, K. Kuramoto, N. Noguchi, J. Kimura and A. Tani, Nat. Geosci., 2019, 12, 407–410 CrossRef CAS.
- D. Ambuehl and M. E. Madden, Icarus, 2014, 234, 45–52 CrossRef CAS.
- T. H. Vu, M. Choukroun, C. Sotin, Y. Muñoz Iglesias and H. E. Maynard-Casely, Geophys. Res. Lett., 2020, 47, e2019GL086265 CrossRef.
- J. Lee and J. W. Kenney III, in Solidification, ed. A. E. Ares, IntechOpen, Rijeka, 2018, ch. 7 Search PubMed.
- R. Yanes-Rodríguez, D. J. Arismendi-Arrieta and R. Prosmiti, J. Chem. Inf. Model., 2020, 60, 3043–3056 CrossRef PubMed.
- E. Kim and Y. Seo, Chem. Eng. Sci., 2019, 359, 775–778 CrossRef CAS.
- A. Cabrera-Ramírez, D. J. Arismendi-Arrieta, A. Valdés and R. Prosmiti, ChemPhysChem, 2021, 22, 359–369 CrossRef PubMed.
- P. Teeratchanan and A. Hermann, J. Chem. Phys., 2015, 143, 154507 CrossRef PubMed.
- D. Londono, J. L. Finney and W. F. Kuhs, J. Chem. Phys., 1992, 97, 547–552 CrossRef CAS.
- J. S. Loveday and R. J. Nelmes, Phys. Chem. Chem. Phys., 2008, 10, 913–1068 RSC.
- L. del Rosso, M. Celli and L. Ulivi, Nat. Commun., 2016, 7, 13394 CrossRef CAS PubMed.
- T. A. Strobel, M. Somayazulu, S. V. Sinogeikin, P. Dera and R. J. Hemley, J. Am. Chem. Soc., 2016, 138, 13786–13789 CrossRef CAS PubMed.
- D. Amos, M.-E. Donelly, P. Teeratchanan, C. Bull, A. Falenty, W. Kuhs, A. Hermann and J. Loveday, J. Phys. Chem. Lett., 2017, 8, 4295–4299 CrossRef CAS PubMed.
- H. Itoh and J. S. Tse, J. Chem. Phys., 2001, 115, 9414 CrossRef CAS.
- W. L. Mao, H.-k Mao, A. F. Goncharov, V. V. Struzhkin, Q. Guo, J. Hu, J. Shu, R. J. Hemley, M. Somayazulu and Y. Zhao, Science, 2002, 297, 2247–2249 CrossRef CAS PubMed.
- H. Lu, J. Wang, C. Liu, C. I. Ratcliffe, U. Becker, R. Kumar and J. Ripmeester, J. Am. Chem. Soc., 2012, 134, 9160–9162 CrossRef CAS PubMed.
- X. Cao, Y. Su, Y. Liu, J. Zhao and C. Liu, J. Phys. Chem. A, 2014, 118, 215–222 CrossRef CAS PubMed.
- W. F. Kuhs, T. C. Hansen and A. Falenty, J. Phys. Chem. Lett., 2018, 9, 3194–3198 CrossRef CAS PubMed.
- R. Ma, H. Zhong, J. Liu, J. Zhong, Y. Yan, J. Zhang and J. Xu, Processes, 2019, 7, 699 CrossRef CAS.
- C. Métais, C. Petuya, S. Espert, J. Ollivier, L. Martin-Gondre and A. Desmedt, J. Phys. Chem. C, 2021, 125, 6433–6441 CrossRef.
- A. Witt, F. Sebastianelli, M. E. Tuckerman and Z. Bacić, J. Phys. Chem. C, 2010, 114, 20775–20782 CrossRef CAS.
- A. Valdés, D. J. Arismendi-Arrieta and R. Prosmiti, J. Phys. Chem. C, 2015, 119, 3945–3956 CrossRef.
- J. R. Zhong, X. Y. Zeng, F. H. Zhou, Q. D. Ran, C. Y. Sun, R. Q. Zhong, L. Y. Yang, G. J. Chen and C. A. Koh, Sci. Rep., 2016, 6, 38855 CrossRef CAS PubMed.
- A. Falenty, T. C. Hansen and W. F. Kuhs, Nature, 2014, 516, 231–233 CrossRef CAS PubMed.
- H. Cao, N. J. English and J. M.-D. MacElroy, J. Chem. Phys., 2013, 138, 094507 CrossRef PubMed.
- C. Burnham and N. J. English, J. Phys. Chem. C, 2016, 120, 16561–16567 CrossRef CAS.
- J. R. Cendagorta, A. Powers, T. J.-H. Hele, O. Marsalek, Z. Bacić and M. E. Tuckerman, Phys. Chem. Chem. Phys., 2016, 18, 32169–32177 RSC.
- K. V. Gets, R. K. Zhdanov, Y. Y. Bozhko and V. R. Belosludov, J. Phys. Chem. C, 2021, 125, 15659–15663 CrossRef CAS.
- Y. Liu and L. Ojamäe, Phys. Chem. Chem. Phys., 2018, 20, 8333–8340 RSC.
- Y. Huang, C. Zhu, L. Wang, X. Cao, Y. Su, X. Jiang, S. Meng, J. Zhao and X. C. Zeng, Sci. Adv., 2016, 2, e1501010 CrossRef PubMed.
- V. R. Belosludov, Y. Y. Bozhko, O. S. Gets, K. V. Subbotin and Y. Kawazoe, J. Phys.: Conf. Ser., 2018, 1128, 012031 CrossRef.
- C. Cheng, F. Wang, Y. Tian, X. Wu, J. Zheng, J. Zhang, L. Li, P. Yang and J. Zhao, Renewable Sustainable Energy Rev., 2020, 117, 109492 CrossRef CAS.
- A. K. Both, Y. Gao, X. C. Zeng and C. L. Cheung, Nanoscale, 2021, 13, 7447 RSC.
- Z. R. Chong, S. H.-B. Yang, P. Babu, P. Linga and X. S. Li, Appl. Energy, 2016, 162, 1633–1652 CrossRef.
- Y. H. Ahn, S. Moon, D. Y. Koh, S. Hong, H. Lee, J. W. Lee and Y. Park, Energy Storage Mater., 2020, 24, 655–661 CrossRef.
- V. R. Avula, P. Gupta, R. L. Gardas and J. S. Sangwai, Asia-Pac. J. Chem. Eng., 2017, 12, 709–722 CrossRef CAS.
- P. Linga, R. Kumar and P. Englezos, J. Hazard. Mater., 2007, 149, 625–629 CrossRef CAS PubMed.
- P. Babu, P. Linga, R. Kumar and P. Englezos, Energy, 2015, 85, 261–279 CrossRef CAS.
- J. S. Gudmundsson, Method for production of gas hydrates for transportation and storage, US Pat., 5536893, 1996 Search PubMed.
- N.-J. Kim, J. H. Lee, Y. S. Cho and W. Chun, Energy, 2010, 35, 2717–2722 CrossRef CAS.
- P. Babu, A. Nambiar, T. He, I. A. Karimi, J. D. Lee, P. Englezos and P. Linga, ACS Sustainable Chem. Eng., 2018, 6, 8093–8107 CrossRef CAS.
- J. Lee and Y. Seo, Chem. Eng. J., 2019, 375, 121974 CrossRef CAS.
- N. Thakre and A. K. Jana, Renewable Sustainable Energy Rev., 2021, 135, 110150 CrossRef CAS.
- S. Y. Willow and S. S. Xantheas, Chem. Phys. Lett., 2012, 525–526, 13–18 CrossRef CAS.
- J. Zhu, S. Du, X. Yu, J. Zhang, H. Xu, S. C. Vogel, T. C. Germann, J. S. Francisco, F. Izumi, K. Momma, Y. Kawamura, C. Jin and Y. Zhao, Nat. Commun., 2014, 5, 4128 CrossRef CAS PubMed.
- S. J. Cox, M. D. Towler, D. Alfè and A. Michaelides, J. Chem. Phys., 2014, 140, 174703 CrossRef PubMed.
- S. Alavi and J. A. Ripmeester, Mol. Simul., 2017, 43, 808–820 CrossRef CAS.
- U. Ranieri, M. M. Koza, W. F. Kuhs, S. Klotz, A. Falenty, P. Gillet and L. E. Bove, Nat. Commun., 2017, 8, 1076 CrossRef PubMed.
- J. Ghosh, R. R.-J. Methikkalam, R. G. Bhuin, G. Ragupathy, N. Choudhary, R. Kumar and T. Pradeep, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1526–1531 CrossRef CAS PubMed.
- J. Zheng, Z. R. Chong, M. F. Qureshi and P. Linga, Energy Fuels, 2020, 34, 10529–10546 CrossRef CAS.
- S. Mondal and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2014, 16, 17943–17954 RSC.
- S. P. Kaur and C. N. Ramachandran, Mol. Phys., 2018, 116, 54–63 CrossRef CAS.
- P. H.-B. Brant Carvalho, A. Mace, O. Andersson, C. A. Tulk, J. Molaison, A. P. Lyubartsev, I. M. Nangoi, A. A. Leitão and U. Häussermann, Phys. Rev. B, 2021, 103, 064205 CrossRef CAS.
- P. Villard, C. R. Hebd. Seances Acad. Sci., 1896, 123, 377–379 CAS.
- P. Villard, C. R. Hebd. Seances Acad. Sci., 1896, 123, 377–379 CAS.
- R. de Forcrand, C. R. Hebd. Seances Acad. Sci., 1923, 176, 355–358 CAS.
- R. M. Barrer and A. V.-J. Edge, Proc. R. Soc. London, Ser. A, 1967, 300, 1–24 CAS.
- Y. A. Dyadin, E. Y. Aladko, A. Y. Manakov, F. V. Zhurko, T. V. Mikina, V. Y. Komarov and E. V. Grachev, J. Struct. Chem., 1999, 40, 790–795 CrossRef CAS.
- D. Londono, W. F. Kuhs and J. L. Finney, Nature, 1998, 332, 141–142 CrossRef.
- C. Lobban and J. L. Finney, J. Chem. Phys., 2002, 117, 3928 CrossRef CAS.
- A. V. Ildyakov, A. Y. Manakov, E. Y. Aladko, V. I. Kosyakov and V. A. Shestakov, J. Phys. Chem. B, 2013, 117, 7756–7762 CrossRef CAS PubMed.
- R. V. Belosludov, Y. Y. Bozhko, O. S. Subbotin, V. R. Belosludov, H. Mizuseki, Y. Kawazoe and V. M. Fomin, J. Phys. Chem. C, 2014, 118, 2587–2593 CrossRef CAS.
- N. I. Papadimitriou, I. N. Tsimpanogiannis, A. K. Stubos, A. Martin, L. J. Rovetto and C. J. Peters, J. Phys. Chem. Lett., 2010, 1, 1014–1017 CrossRef CAS.
- U. Ranieri, M. M. Koza, W. F. Kuhs, R. Gaal, S. Klotz, A. Falenty, D. Wallacher, J. Ollivier, P. Gillet and L. E. Bove, J. Phys. Chem. C, 2019, 123, 1888–1903 CrossRef CAS.
- R. Yanes-Rodríguez and R. Prosmiti, Phys. Chem. Chem. Phys., 2022, 24, 1475–1485 RSC.
- R. A. Friesner and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6648–6653 CrossRef CAS PubMed.
- Y. Ozaki, K. B. Beć, Y. Morisawa, S. Yamamoto, I. Tanabe, C. W. Huck and T. S. Hofer, Chem. Soc. Rev., 2021, 50, 10917–10954 RSC.
- I. Tuvi-Arad, Isr. J. Chem., 2021, 61, 1–10 CrossRef.
- M. Gastegger, J. Behler and P. Marquetand, Chem. Sci., 2017, 8, 6924–6935 RSC.
- G. Carleo, Y. Nomura and M. Imada, Nat. Commun., 2018, 9, 5322 CrossRef CAS PubMed.
- F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Annu. Rev. Phys. Chem., 2020, 71, 361–390 CrossRef PubMed.
- J. Westermayr and P. Marquetand, Chem. Rev., 2021, 121, 9873–9926 CrossRef CAS PubMed.
- Q. Ai, V. Bhat, S. M. Ryno, K. Jarolimek, P. Sornberger, A. Smith, M. M. Haley, J. E. Anthony and C. Risko, J. Chem. Phys., 2021, 154, 174705 CrossRef CAS PubMed.
- M. Ceriotti, C. Clementi and O. A. von Lilienfeld, Chem. Rev., 2021, 121, 9719–9721 CrossRef CAS PubMed.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K. R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed.
- F. Takeuchi, M. Hiratsuka, R. Ohmura, S. Alavi, A. K. Sum and K. Yasuoka, J. Chem. Phys., 2013, 138, 124504 CrossRef PubMed.
- DENEB 1.30 beta: the Nanotechnology Software by Atelgraphics, 2021, https://www.atelgraphics.com.
- M. A.-L. Marques, M. J.-T. Oliveira and T. Burnus, Comput. Phys. Commun., 2012, 183, 2272–2281 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Kücükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- P. Giannozzi, O. Baseggio, P. Bonfá, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105 CrossRef CAS PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108 CrossRef PubMed.
- A. Otero de la Roza and E. R. Johnson, J. Chem. Phys., 2012, 136, 174109 CrossRef CAS PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- Universität-Bonn, D4- A Generally Applicable Atomic-Charge Dependent London Dispersion Correction, https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/dftd4.
- A. Cabrera-Ramírez, D. J. Arismendi-Arrieta, A. Valdés and R. Prosmiti, Chem. Phys. Chem., 2020, 21, 2618–2628 CrossRef PubMed.
- F. Izquierdo-Ruiz, A. Otero-de-la Roza, J. Contreras-Garciía, O. Prieto-Ballesteros and J. M. Recio, Materials, 2016, 9, 777 CrossRef PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- K. Lee, E. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247 CrossRef CAS PubMed.
- P. Vinet, J. Ferrante, J. Smith and J. Rose, J. Phys. C: Solid State Phys., 1986, 19, L467 CrossRef CAS.
- T. C. Hansen, A. Falenty and W. F. Kuhs, J. Chem. Phys., 2016, 144, 054301 CrossRef CAS PubMed.
- V. Vins, A. Jäger, S. Hielscher, R. Span, J. Hrubý and C. Breitkopf, EPJ Web Conf., 2017, 143, 02141 CrossRef.
- J. S. Tse, W. R. McKinnon and M. Marchi, J. Phys. Chem., 1987, 91, 4188–4193 CrossRef CAS.
- J. S. Tse, J. Phys., Colloq., 1987, 48, 543–549 CrossRef.
- A. Vítek, D. J. Arismendi-Arrieta, R. Rodríguez-Cantano, R. Prosmiti, P. Villarreal, R. Kalus and G. Delgado-Barrio, Phys. Chem. Chem. Phys., 2015, 17, 8792–8801 RSC.
- A. Vítek, D. J. Arismendi-Arrieta, M. Sarmanová, R. Kalus and R. Prosmiti, J. Phys. Chem. A, 2020, 124, 4036–4047 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00701k |
| This journal is © the Owner Societies 2022 |