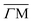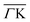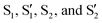Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electron–phonon coupling and superconductivity in a 2D Tl–Pb compound on Si(111)
I. Yu
Sklyadneva
 *ab,
R.
Heid
*ab,
R.
Heid
 b,
P. M.
Echenique
ac and
E. V.
Chulkov
b,
P. M.
Echenique
ac and
E. V.
Chulkov
 acd
acd
aDonostia International Physics Center (DIPC), 20018 San Sebastián/Donostia, Basque Country, Spain
bInstitute for Quantum Materials and Technologies, Karlsruhe Institute of Technology, D-76021 Karlsruhe, Germany. E-mail: rolf.heid@kit.edu
cDepartamento de Polímeros y Materiales Avanzados: Física, Química y Tecnología, Facultad de Ciencias Químicas, Universidad del País Vasco UPV/EHU 20080, San Sebastián/Donostia, Basque Country, Spain
dHSE University, 101000, Moscow, Russia
First published on 14th April 2022
Abstract
Electron–phonon interaction in a single-layer Tl–Pb compound on Si(111) is investigated within the density-functional theory and linear-response approach in the mixed-basis pseudopotential representation. It is found that phonon-induced scattering of electrons at the Fermi level is primarily determined by surface electronic states responsible for bonding at the interface and by low-energy, predominantly shear-vertical vibrations of adatoms. The contribution of substrate-localized vibrations involved in the electron–phonon scattering turns out to be small. We have also estimated the superconducting transition temperature Tc by solving the linearized gap equation of the Eliashberg theory. An analysis of phonon-mediated transitions for a number of electronic states in the Tl–Pb surface bands showed that the strength of the coupling varies with the binding energy, increasing as it approaches the Fermi level, and significantly depends on the surface band to which the state belongs.
1 Introduction
Advances in nanotechnology have stimulated an active interest in two-dimensional 2D metallic films grown on semiconductor substrates due to their potentially advanced properties such as the discovered two-dimensional superconductivity.1–13 For example, two-dimensional superconductivity was found for the striped incommensurate (SIC) phase of Pb on Si(111) and for the quasi-rectangular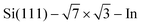 reconstruction.5 The scanning tunneling spectroscopy measurements (STS) demonstrated that one (two) atomic layers of Pb (In) were quite enough to retain superconductivity and showed that the structures become superconducting at Tc = 1.83 K and Tc = 3.18 K, respectively. The discovery of superconductivity was followed by a number of theoretical works which focused on the strength of the electron–phonon (e–ph) interaction and the critical temperature of superconductivity in Pb/Si(111) and In/Si(111) systems.9,14–17
reconstruction.5 The scanning tunneling spectroscopy measurements (STS) demonstrated that one (two) atomic layers of Pb (In) were quite enough to retain superconductivity and showed that the structures become superconducting at Tc = 1.83 K and Tc = 3.18 K, respectively. The discovery of superconductivity was followed by a number of theoretical works which focused on the strength of the electron–phonon (e–ph) interaction and the critical temperature of superconductivity in Pb/Si(111) and In/Si(111) systems.9,14–17
The experimental findings have also stimulated research activity on exploring other ultrathin superconductors, among them, a surface compound formed by metallic adsorbates, Tl and Pb, on Si(111) and Ge(111) surfaces.11–13,18–20 Both heavy metals are bulk superconductors with strong spin–orbit coupling. When alloying one monolayer (ML) of Tl with 1/3 ML of Pb a single atomic layer Tl–Pb compound with 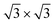 periodicity is formed. The surface metal phase exhibits both a noticeable Rashba-type spin splitting of surface electronic bands and 2D superconducting transport properties.12,19 The low-temperature conductivity measurements12 showed that the
periodicity is formed. The surface metal phase exhibits both a noticeable Rashba-type spin splitting of surface electronic bands and 2D superconducting transport properties.12,19 The low-temperature conductivity measurements12 showed that the 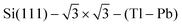 becomes superconducting at the critical temperature of 2.25 K.
becomes superconducting at the critical temperature of 2.25 K.
Since the atomic arrangement and the electronic band structure of the compound have already been experimentally established,11,13 the available information can be used as a basis for further theoretical investigations. First of all, it seems useful to study the phonon-mediated scattering of electrons in the surface metallic bands of the Si(111)-supported Tl–Pb compound to obtain an accurate quantitative description and analysis of the e–ph interaction, which is still missing.
Here we present the results of a first-principles study focusing on the pairing strength of phonon-induced scattering processes in the 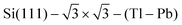 compound. We calculated both the e–ph coupling parameter and Eliashberg spectral function, averaged over electron momentum at the Fermi energy, EF. Then, the superconducting transition temperature was estimated by solving the linearized gap equation. We also analyzed the strength of e–ph interaction in a number of fixed electronic states in the surface Tl–Pb bands.
compound. We calculated both the e–ph coupling parameter and Eliashberg spectral function, averaged over electron momentum at the Fermi energy, EF. Then, the superconducting transition temperature was estimated by solving the linearized gap equation. We also analyzed the strength of e–ph interaction in a number of fixed electronic states in the surface Tl–Pb bands.
2 Calculation details
The Eliashberg spectral function averaged over electron momentum at the Fermi level can be expressed as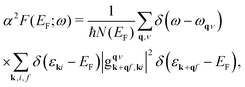 | (1) |
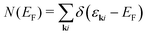 is the density of electronic states at the Fermi energy. The summation is carried out over (i) all combinations of electronic states (ki) and (k + qf) and (ii) all phonon modes (q,ν). Because of the slow convergence of Fermi-surface averages we used a dense mesh21 of k-points (48 × 48 × 1) corresponding to 217 special points in the irreducible part of the surface Brillouin zone (SBZ).
is the density of electronic states at the Fermi energy. The summation is carried out over (i) all combinations of electronic states (ki) and (k + qf) and (ii) all phonon modes (q,ν). Because of the slow convergence of Fermi-surface averages we used a dense mesh21 of k-points (48 × 48 × 1) corresponding to 217 special points in the irreducible part of the surface Brillouin zone (SBZ).
The averaged strength of electron–phonon interaction is related to the Eliashberg function by22
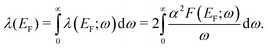 | (2) |
All calculations were carried out within the density-functional formalism (DFT) and the generalized gradient approximation (GGA-PBE) for the exchange–correlation functional23 using the mixed-basis pseudopotential approach.24,25 The scheme employs a combination of local functions and plane waves for representing valence states.24 For ground state calculations we used an implementation of the mixed-basis method by Meyer et al.26 The norm-conserving pseudopotentials were constructed following the scheme of Vanderbilt.27 For Tl, the semicore 5d states were treated explicitly as valence states for greater accuracy.28 By using d-type local functions at each atomic site of Tl, the cutoff energy for plane waves is reduced to 20 Ry without loss of accuracy. Dynamical properties were calculated using the linear response theory29 adapted to the mixed-basis pseudopotential approach.25 In the self-consistent calculations the integrations over the SBZ were performed by sampling a uniform (12 × 12 × 1) k-point mesh in combination with a Gaussian broadening with a smearing parameter of 0.05 eV.
Due to the strong influence of spin–orbit coupling (SOC) on the two-dimensional electronic bands (spin splitting) of the 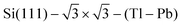 compound,12 spin–orbit interaction was taken into account. The inclusion of SOC improves the agreement of the calculated bulk phonon dispersion with experiment for both Tl and Pb.28 Details of the spin–orbit coupling implementation within the mixed-basis method can be found in ref. 28.
compound,12 spin–orbit interaction was taken into account. The inclusion of SOC improves the agreement of the calculated bulk phonon dispersion with experiment for both Tl and Pb.28 Details of the spin–orbit coupling implementation within the mixed-basis method can be found in ref. 28.
In our calculation we did not use the +U correction to resolve the band-gap problem. As it is known the DFT may underestimate the bulk band gap but the reduction is not important for analyzing the e–ph interaction in the system of interest. The main point is the position of EF relative to the substrate valence band edge and the surface band dispersion around EF.
3 Results and discussion
3.1 Structural parameters
We simulate the system by considering a single-layer-compound on top of periodically repeating six Si(111) layers (a three-bilayer film) separated by a vacuum gap of 12 Å. The imitation of the substrate by three Si bilayers provides practically convergent results on the structural parameters of the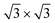 phase and, most importantly, is sufficient to reproduce the band dispersion in good agreement with the data obtained for 12 bilayers of Si(111).11 The bottom silicon dangling bonds are saturated with hydrogen atoms.
phase and, most importantly, is sufficient to reproduce the band dispersion in good agreement with the data obtained for 12 bilayers of Si(111).11 The bottom silicon dangling bonds are saturated with hydrogen atoms.
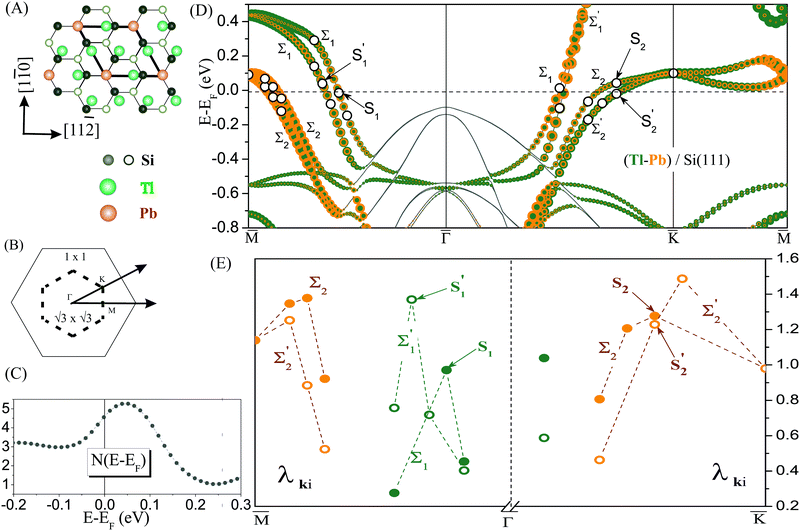
The lattice constant is first fixed at the theoretical bulk Si lattice parameter a = 5.402 Å obtained by total-energy minimization. It is a bit smaller than the experimental value,30aexp = 5.43 Å. A single-layer Tl–Pb compound is then deposited on the top of the substrate according to the 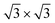 periodicity12 (see Fig. 1(A)). The superstructure contains three Tl atoms and one Pb atom per unit cell: Tl atoms form a chained-trimer structure and are equivalent with respect to the underlying Si substrate, while 1/3 ML of Pb atoms occupy T1 (on-top) sites where the Tl trimers are centered.12 Essentially, the 2D Tl–Pb compound is confined to a single atomic layer, which is slightly buckled because Pb is 0.37 Å (0.34 Å in ref. 18) above the Tl atoms.
periodicity12 (see Fig. 1(A)). The superstructure contains three Tl atoms and one Pb atom per unit cell: Tl atoms form a chained-trimer structure and are equivalent with respect to the underlying Si substrate, while 1/3 ML of Pb atoms occupy T1 (on-top) sites where the Tl trimers are centered.12 Essentially, the 2D Tl–Pb compound is confined to a single atomic layer, which is slightly buckled because Pb is 0.37 Å (0.34 Å in ref. 18) above the Tl atoms.
The bottom Si bilayer is held fixed to simulate the bulk environment. All other atoms are allowed to move both in-plane and along the stacking direction. The force criterion was chosen so as to ensure complete convergence of bond lengths with an accuracy of less than 0.01 Å. The H–Si distance was determined in the calculation of a Si(111) film saturated by H on both sides. The optimized structural parameters, namely, the bond length dTl–Tl and the difference in the heights of atoms at the interface are given in Table 1. Also shown are available experimental data from ref. 18. The optimized Tl–Si1 hight spacing is a bit shorter than the interlayer distance for the Tl(0001) surface,31hTl–Tl = 2.74 Å. We note that the structural parameters are hardly influenced by the spin–orbit coupling.
| d Tl–Tl | h Tl–Si1 | h Pb–Si1 | h Pb–Tl | ||
|---|---|---|---|---|---|
| Si(111) | 3.31 | 2.48 | 2.86 | 0.37 | Present calc. |
| 3.34 | 2.50 | 2.85 | 0.34 | Expt |
3.2 Electron–phonon coupling
Superconducting properties can be associated with enhanced electron–phonon scattering whose strength is described by the e–ph coupling constant. Therefore, we estimated the momentum-averaged strength of the e–ph interaction at EF. The calculated value λ(EF) = 1.06 is close to the e–ph coupling strength obtained at the Fermi level of the Tl(0001) surface, λsurf (EF) = 1.01,32 and both values are larger than the bulk thallium parameter, λbulktheory (EF) = 0.8728 and λbulkexpt (EF) = 0.795.33In what follows, we will address two main factors that have a significant effect on phonon-mediated electronic transitions. One of the factors determining λ is the phase space, that is, the electronic states available for scattering processes. The calculated density of electronic states at the Fermi level, N(EF) = 2.3 states/(eV unit cell spin), is close to the value at the Fermi energy of the Tl(0001) surface, NT1(0001)(EF)) = 2.12 states/(eV unit cell spin), the difference is ∼8%.
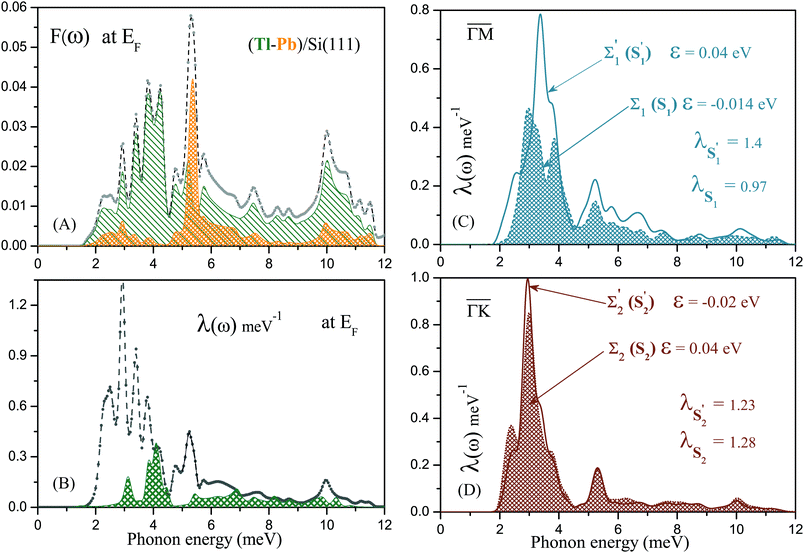
To clarify the role of Pb in the formation of the electronic structure of the compound and in the e–ph coupling, we considered the same structure, replacing Pb with Tl. The “hypothetical” (4/3) ML of Tl on Si(111) has a very similar band structure, but when Pb is replaced by Tl, the number of valence electrons in the unit cell decreases and, accordingly, the Fermi level drops. At the new position of EF, the density of electronic states N (EF) = 1.14 states/(eV unit cell spin) is more than 2 times less than for the Tl–Pb compound. The structure remains dynamically stable, but the e–ph coupling weakens by as much as a factor of 4 to λ(EF) = 0.28. Therefore, the reduction of N (EF) is not the only relevant factor in this case. Fig. 2(B) shows spectral decompositions of the e–ph coupling parameter at the Fermi level, λ(EF;ω), calculated for the Tl–Pb compound on Si(111) and for the “hypothetical” (4/3) ML of Tl on Si(111). It turns out that at the new position of the Fermi level, long-wavelength lattice vibrations (small-wave-vector phonons) hardly contribute to the scattering of electrons due to a lack of final electronic states. As a result, the spectral e–ph function is strongly suppressed in the low-frequency part up to ∼3 meV, which drastically weakens the e–ph coupling due to the weighting factor 1/ω in eqn (2). Thus, the role of Pb is twofold: (i) adding valence electrons, which increases the number of available electronic states for the pairing, and (ii) as a consequence of the new position of the Fermi level, activating low-frequency phonons for the pairing by greatly enhancing the probability of transitions mediated by these modes. Both effects lead to a fourfold increase in λ(EF) compared to the “hypothetical” (4/3) ML Tl on Si(111).
Another question is how the different surface bands are involved in the e–ph coupling. Fig. 1(D) shows the calculated band structure around EF. The SBZ symmetry points are given in Fig. 1(B). The band structure has a metallic character with two spin-split metallic surface bands 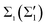 and
and 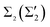 , which form the Fermi surface. The spin degeneracy is lifted in the entire SBZ, except for the high-symmetry points. On the one hand, the electronic bands participating in the e–ph interaction are formed by Tl and Pb states of px, py character (mainly
, which form the Fermi surface. The spin degeneracy is lifted in the entire SBZ, except for the high-symmetry points. On the one hand, the electronic bands participating in the e–ph interaction are formed by Tl and Pb states of px, py character (mainly 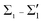 ), which indicates an in-plane metallic Tl–Pb bonding. Note that the electronic states localized on Pb atoms are exclusively of the character px, py within the band gap of the substrate. On the other hand, the bands (mainly
), which indicates an in-plane metallic Tl–Pb bonding. Note that the electronic states localized on Pb atoms are exclusively of the character px, py within the band gap of the substrate. On the other hand, the bands (mainly 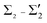 ) show a coupling of Tl pz orbitals to pz and dxz, yz orbitals of Si atoms from the topmost valence band. Moreover, these states dominate the density of states at the Fermi level, as they contribute ∼87% to the total N(EF). A detailed description of the surface band structure can be found in ref. 11–13.
) show a coupling of Tl pz orbitals to pz and dxz, yz orbitals of Si atoms from the topmost valence band. Moreover, these states dominate the density of states at the Fermi level, as they contribute ∼87% to the total N(EF). A detailed description of the surface band structure can be found in ref. 11–13.
On the Tl(0001) surface, an analysis of electronic states with a predominant contribution to the e–ph scattering also revealed that these states partially or completely are of pz symmetry.32 Thus, the e–ph scattering is dominated by states that build interface bonds in the 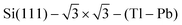 compound or interlayer bonds of the Tl(0001) surface, respectively. In contrast, for the “hypothetical” (4/3) ML of Tl on Si(111), the Tl-induced electronic states prevailing in the e–ph coupling are of px,py and s types.
compound or interlayer bonds of the Tl(0001) surface, respectively. In contrast, for the “hypothetical” (4/3) ML of Tl on Si(111), the Tl-induced electronic states prevailing in the e–ph coupling are of px,py and s types.
The participation of each electronic band in the e–ph scattering turns out to be proportional to its contribution to the density of states at EF. The 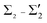 bands make the largest contribution to λ(EF), ∼83%, according to their density of states at EF, 2.0 states/(eV unit cell). The share of bands
bands make the largest contribution to λ(EF), ∼83%, according to their density of states at EF, 2.0 states/(eV unit cell). The share of bands 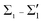 is only ∼11% and ∼6% falls on the substrate.
is only ∼11% and ∼6% falls on the substrate.
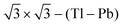 compound on Si(111) is shown in Fig. 2(A). The phonon modes associated with vibrations of Tl and Pb atoms lie below 12 meV, while the vibrations of substrate atoms occupy the high-frequency region extending up to 75 meV. In the energy region up to 5.6 meV, most of the modes are predominantly shear-vertical (SV) with displacements of adatoms along the normal to the surface. The only exception is the lowest broad peak (around 2.4 meV) in F (ω), associated with both in-plane and out-of-plane shear surface vibrations.
compound on Si(111) is shown in Fig. 2(A). The phonon modes associated with vibrations of Tl and Pb atoms lie below 12 meV, while the vibrations of substrate atoms occupy the high-frequency region extending up to 75 meV. In the energy region up to 5.6 meV, most of the modes are predominantly shear-vertical (SV) with displacements of adatoms along the normal to the surface. The only exception is the lowest broad peak (around 2.4 meV) in F (ω), associated with both in-plane and out-of-plane shear surface vibrations.
From the spectral decomposition of λ(EF) shown in Fig. 2(B), it is obvious that the phonon-mediated scattering of electrons at the Fermi level is determined by vibrations of Tl and Pb adatoms. In the first place, these are low-energy, predominantly shear-vertical displacements. These modes form a multi-peak structure in λ(EF;ω) between 2 and 4.5 meV, although some SV vibrations of Tl atoms are coupled to the longitudinal motion of Pb atoms (the highest peak, at about 3 meV). Contribution of shear-vertical Pb modes to λ(EF) shows a peak at ∼5–5.5 meV. Since the position of Tl adatoms relative to the underlying Si surface layer is the same, the contributions to λ(EF) from vibrations of different Tl atoms are identical.
Thus, the vibrations dominating in the phonon-mediated scattering of electrons are concentrated up to ∼6 meV. The adlayer-localized modes provide ∼93% of λ(EF), while the substrate vibrations involved in the scattering of electrons contribute little. The reason is that these vibrations are predominantly high-frequency and, as a consequence, turn out to be much less important in the e–ph interaction because of the definition of λ as proportional to 1/ω.
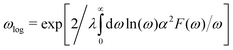 . The resulting transition temperature Tc = 3.5 K is higher than the value obtained from transport measurements,12Tc = 2.25 K.
. The resulting transition temperature Tc = 3.5 K is higher than the value obtained from transport measurements,12Tc = 2.25 K.
However, transport measurements at a surface always show a lower value of Tc than that obtained by opening of the superconducting energy gap (STS), due to fluctuation effects inherent in low-dimensional superconductors38 and which can only be detected by STS.7 So, for a (4/3)-monolayer of Pb on Si(111), a dense SIC phase, STS measurements5 give Tc = 1.83 K, while conductivity measurements7 showed the superconductivity transition at 1.1 K. The theoretical estimate16 gives the value Tc for the SIC phase of Pb on Si(111) which is closer to the STS data: Tc = 1.84 K with μ* = 0.11.
The calculated transition temperature for the 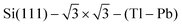 compound exceeds Tc = ∼2.4 K for bulk thallium.22 However, the strength of e–ph interaction in the bulk33 (∼0.8) is also noticeably less than on the surface, both for Tl(0001) and
compound exceeds Tc = ∼2.4 K for bulk thallium.22 However, the strength of e–ph interaction in the bulk33 (∼0.8) is also noticeably less than on the surface, both for Tl(0001) and 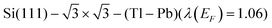 . Therefore, it is not surprising that Tbulkc < Tsurfc.
. Therefore, it is not surprising that Tbulkc < Tsurfc.
3.3 Band-resolved electron–phonon coupling
Besides the e-ph coupling parameter averaged over electron momentum at the Fermi level, we also analyzed phonon-mediated transitions for a number of electronic states in the Tl–Pb surface bands. The states are marked by open circles in Fig. 1(D).To calculate the strength of the e–ph interaction for a fixed electron state with momentum k and band index i, the state-dependent Eliashberg spectral function
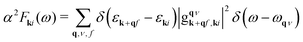 | (3) |
The strength of e–ph interaction for all states marked with open circles is shown in Fig. 1(E). All these states are located near the Fermi level: their energies are in the range (−0.2)–(+0.3) eV. Nevertheless, there is a significant variation in λki's from 0.3 to 1.5. Spectral decompositions of λki for four surface electronic states 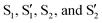 are shown in Fig. 2(C and D).
are shown in Fig. 2(C and D).
On the whole, for all considered states with the same electron momentum in a pair of neighboring subbands, the e–ph interaction is stronger for the electronic state, the energy of which is closer to the Fermi level. This is due to an increase in the density of electronic states as the Fermi level is approached (Fig. 1(C)). At energies very close to EF or slightly higher, surface bands at the SBZ boundary come into play, sharply increasing the phase space for the scattering of electrons. For states in a pair of neighboring subbands with close binding energies, but different electron moments, the strength of e–ph interaction depends markedly on the surface band to which the states belong.
Both S1 (band Σ1) and  (band
(band 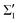 ) are surface states of s, px,y symmetry. The only difference between them is that in
) are surface states of s, px,y symmetry. The only difference between them is that in 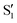 the contribution of Tl pz-type orbitals becomes noticeable. λki's differ in these two subbands, namely,
the contribution of Tl pz-type orbitals becomes noticeable. λki's differ in these two subbands, namely, 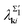 is substantially larger than
is substantially larger than 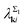 , as the spectral functions in Fig. 2(C) reveal. The calculated λki's show the same trend as the values roughly estimated experimentally for the
, as the spectral functions in Fig. 2(C) reveal. The calculated λki's show the same trend as the values roughly estimated experimentally for the 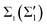 bands from the slope of the temperature-depended linewidth:12
bands from the slope of the temperature-depended linewidth:12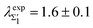 and
and 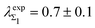 .
.
As for the states 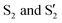 , they do not differ in symmetry and both are characterized by the presence of a significant fraction of Tl pz orbitals responsible for the coupling to the topmost valence band Si states. As a result, the corresponding λki's are equally large. At binding energies of about 60–200 meV, the calculated strength of the e–ph interaction in the
, they do not differ in symmetry and both are characterized by the presence of a significant fraction of Tl pz orbitals responsible for the coupling to the topmost valence band Si states. As a result, the corresponding λki's are equally large. At binding energies of about 60–200 meV, the calculated strength of the e–ph interaction in the 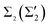 bands varies from 0.46 to 0.8, and the averaged value of λki ≈ 0.65 is close to the value extracted for the same bands from the ARPES data,12λexp = 0.6± 0.05. However, when approaching the Fermi level, the e–ph interaction in these two neighboring subbands with opposite spin orientations enhances drastically and λki → 1.4–1.5 depending on electron momentum.
bands varies from 0.46 to 0.8, and the averaged value of λki ≈ 0.65 is close to the value extracted for the same bands from the ARPES data,12λexp = 0.6± 0.05. However, when approaching the Fermi level, the e–ph interaction in these two neighboring subbands with opposite spin orientations enhances drastically and λki → 1.4–1.5 depending on electron momentum.
4 Conclusions
We have presented the results of an ab initio study of the electron–phonon coupling in the two-dimensional Tl–Pb compound on Si(111). The calculated λ(EF) = 1.06 coincides with the e–ph coupling strength at the Fermi level of the Tl(0001) surface and both values are larger than the bulk thallium parameter. It is found that bands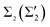 make a decisive contribution (∼83%) to λ(EF), proportional to their large density of states at EF compared to the
make a decisive contribution (∼83%) to λ(EF), proportional to their large density of states at EF compared to the 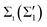 bands. The phonon-mediated scattering of electrons at the Fermi level is almost completely controlled by the vibrations of Tl and Pb atoms, predominantly by low-energy shear-vertical modes. Much less important are the high-frequency substrate-localized phonons participating in the scattering of electrons. The calculated superconducting transition temperature Tc = 3.5 K is higher than the value extracted from transport measurements.12 An analysis of phonon-mediated transitions for a number of electronic states in the Tl–Pb surface bands showed that λki varies with the binding energy, increasing as the Fermi level is approached, and at the same binding energy the strength of e–ph interaction depends on the surface band.
bands. The phonon-mediated scattering of electrons at the Fermi level is almost completely controlled by the vibrations of Tl and Pb atoms, predominantly by low-energy shear-vertical modes. Much less important are the high-frequency substrate-localized phonons participating in the scattering of electrons. The calculated superconducting transition temperature Tc = 3.5 K is higher than the value extracted from transport measurements.12 An analysis of phonon-mediated transitions for a number of electronic states in the Tl–Pb surface bands showed that λki varies with the binding energy, increasing as the Fermi level is approached, and at the same binding energy the strength of e–ph interaction depends on the surface band.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the University of the Basque Country (Grants no. GIC07-IT-366-07 and No. IT-756-13) and the Spanish Ministry of Science and Innovation (Grant no. FIS2016-75862-P). The authors acknowledge support by the state of Baden–Württemberg through bwHPC.References
- T. Hirahara, T. Nagao, I. Matsuda, G. Bihlmayer, E. V. Chulkov, Yu. M. Koroteev and S. Hasegawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 035422 CrossRef.
- P. S. Kirchmann and U. Bovensiepen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035437 CrossRef.
- S. Qin, J. Kim, Q. Niu and C.-K. Shih, Science, 2009, 324, 1314–1317 CrossRef CAS PubMed.
- C. Brun, I.-P. Hong, F. Patthey, I. Y. Sklyadneva, R. Heid, P. M. Echenique, K.-P. Bohnen, E. V. Chulkov and W.-D. Schneider, Phys. Rev. Lett., 2009, 102, 207002 CrossRef PubMed.
- T. Zhang, P. Cheng, W.-J. Li, Y.-J. Sun, G. Wang, X.-G. Zhu, K. He, L. Wang, X. Ma, X. Chen, Y. Wang, Y. Liu, H.-Q. Lin, J.-F. Jia and Q.-K. Xue, Nat. Phys., 2010, 6, 104–108 Search PubMed.
- T. Uchihashi, P. Mishra, M. Aono and T. Nakayama, Phys. Rev. Lett., 2011, 107, 207001 CrossRef PubMed.
- M. Yamada, T. Hirahara and S. Hasegawa, Phys. Rev. Lett., 2013, 110, 237001 CrossRef PubMed.
- G. Benedek, M. Bernasconi, K.-P. Bohnen, D. Campi, E. V. Chulkov, P. M. Echenique, R. Heid, I. Y. Sklyadneva and J. P. Toennies, Phys. Chem. Chem. Phys., 2014, 16, 7159–7172 RSC.
- I. Y. Sklyadneva, G. Benedek, R. Heid, P. M. Echenique, J. P. Toennies and E. V. Chulkov, J. Phys. Chem. C, 2018, 122, 29039–29043 CrossRef CAS.
- S. Yoshizawa, H. Kim, T. Kawakami, Y. Nagai, T. Nakayama, X. Hu, Y. Hasegawa and T. Uchihashi, Phys. Rev. Lett., 2014, 113, 237004 CrossRef PubMed.
- D. V. Gruznev, L. V. Bondarenko, A. V. Matetskiy, A. A. Yakovlev, A. Y. Tupchaya, S. V. Eremeev, E. V. Chulkov, J. P. Chou, C. M. Wei, M. Y. Lai, Y. L. Wang, A. V. Zotov and A. A. Saranin, Sci. Rep., 2014, 4, 04742 CrossRef PubMed.
- A. V. Matetskiy, S. Ichinokura, L. V. Bondarenko, A. Y. Tupchaya, D. V. Gruznev, A. V. Zotov, A. A. Saranin, R. Hobara, A. Takayama and S. Hasegawa, Phys. Rev. Lett., 2015, 115, 147003 CrossRef CAS PubMed.
- D. V. Gruznev, A. V. Zotov and A. A. Saranin, Jpn. J. Appl. Phys., 2017, 56, 08LA01 CrossRef.
- J. Noffsinger and M. L. Cohen, Solid State Commun., 2011, 151, 421–424 CrossRef CAS.
- G. Q. Huang, New J. Phys., 2011, 13, 093023 CrossRef.
- I. Y. Sklyadneva, R. Heid, K.-P. Bohnen, P. M. Echenique and E. V. Chulkov, Phys. Rev. B, 2018, 97, 195409 CrossRef CAS.
- I. Y. Sklyadneva, R. Heid, P. M. Echenique and E. V. Chulkov, Phys. Chem. Chem. Phys., 2021, 23, 7955–7960 RSC.
- D. V. Gruznev, L. V. Bondarenko, A. Y. Tupchaya, S. V. Eremeev, A. N. Mihalyuk, J. P. Chou, C. M. Wei, A. V. Zotov and A. A. Saranin, J. Phys.: Condens. Matter, 2017, 29, 035001 CrossRef CAS PubMed.
- T. Nakamura, A. Takayama, R. Hobara, D. V. Gruznev, A. V. Zotov, A. A. Saranin and S. Hasegawa, Appl. Surf. Sci., 2019, 479, 679–684 CrossRef CAS.
- A. N. Mihalyuk, C. R. Hsing, C. M. Wei, D. V. Gruznev, L. V. Bondarenko, A. Y. Tupchaya, A. V. Zotov and A. A. Saranin, Surf. Sci., 2017, 657, 63–68 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- P. B. Allen and M. L. Cohen, Phys. Rev., 1969, 187, 525–538 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. G. Louie, K.-M. Ho and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 1774–1782 CrossRef CAS.
- R. Heid and K. P. Bohnen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, R3709–R3712 CrossRef CAS.
- B. Meyer, C. Elsässer, F. Lechermann and M. Fähnle, FORTRAN90 Program for Mixed-Basis Pseudopotential Calculations for Crystals (Max-Planck-Institut für Metallforschung).
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 8412–8415 CrossRef CAS PubMed.
- R. Heid, K.-P. Bohnen, I. Y. Sklyadneva and E. V. Chulkov, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174527 CrossRef.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- A. G. Beattie and J. E. Schirber, Phys. Rev. B: Solid State, 1970, 1, 1548–1551 CrossRef.
- C. S. Barrett, Phys. Rev., 1958, 110, 1071–1072 CrossRef CAS.
- I. Y. Sklyadneva, R. Heid, K.-P. Bohnen, P. M. Echenique, G. Benedek and E. V. Chulkov, J. Phys. Chem. A, 2011, 115, 7352–7355 CrossRef CAS PubMed.
- R. C. Dynes, Phys. Rev. B, 1958, 2, 644–656 CrossRef.
- G. Grimvall, The Electron-phonon Interaction in Metals, New York, North-Holland, 1981 Search PubMed.
- G. Bergmann and D. Rainer, Z. Phys., 1973, 263, 59–68 CrossRef CAS.
- W. L. McMillan, Phys. Rev., 1968, 167, 331–344 CrossRef CAS.
- G. P. Carbotte, Rev. Mod. Phys., 1990, 62, 1027–1157 CrossRef.
- L. G. Aslamasov and A. I. Larkin, Phys. Lett. A, 1968, 26, 238–239 CrossRef.
| This journal is © the Owner Societies 2022 |