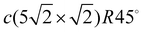Surface dynamics on submonolayer Pb/Cu(001) surfaces
S. D.
Borisova
 a,
S. V.
Eremeev
a,
S. V.
Eremeev
 *a,
G. G.
Rusina
*a,
G. G.
Rusina
 a and
E. V.
Chulkov
a and
E. V.
Chulkov
 bc
bc
aInstitute of Strength Physics and Materials Science, 634055, Tomsk, Russia. E-mail: eremeev@ispms.tsc.ru
bDonostia International Physics Center (DIPC), 20018 San Sebastián/Donostia, Basque Country, Spain
cDepartamento de Polímeros y Materiales Avanzados, Física, Química y Tecnología, Facultad de Ciencias Químicas, Universidad del País Vasco UPV/EHU, 20080 San Sebastián/Donostia, Basque Country, Spain
First published on 3rd February 2022
Abstract
The interplay of the atomic structure and phonon spectra in a variety of two dimensional phases forming during submonolayer Pb adsorption on a Cu(001) surface has been investigated using embedded atom method interatomic interaction potentials. Complementary calculations of the equilibrium atomic structure of these phases were performed using density functional theory. It has been shown that the dynamic stability of the Pb/Cu(001) structures increases with increasing the coverage from 0.375 ML to ultimately 0.6 ML, when a dense Pb layer is formed. The increase of the coverage also results in progressive shift of the Rayleigh mode of the copper surface to higher energy and the appearance of new mixed adsorbate–substrate vibration modes.
1 Introduction
Lead thin films have attracted much attention due to their two-dimensional physical properties. Due to their simplicity, the physics of low-dimensional systems provides a fundamental understanding of complex processes. In particular, the superconductivity of supported lead films with a thickness of a few monolayers1–5 and even of a single Pb atomic layer on silicon6 has stimulated an active interest in the electronic and phonon structure of thin Pb films, especially Pb/Cu(111) structures.7–12 Another interesting property of Pb films is the formation of a charge density wave. The particular case of submonolayer amounts of Pb grown on Cu(001) has received ample attention.13,14Pb on Cu(001) is a lattice-mismatched system exhibiting a rich and complex phenomenology. Several different surface structures with complex properties and phase transitions are observed in the submonolayer coverage range.15,16 The growth mode of Pb on Cu(100) is Stranski–Krastanov, so that a dense Pb layer is formed by 0.6 monolayers (MLs) and further Pb deposition gives rise to island formation. There are different surface structures for coverages below 0.6 ML: c(4 × 4) (for 0.375 ML), c(2 × 2) (for 0.5ML) and 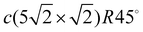 (for 0.6 ML). The c(4 × 4) structure is a Cu–Pb surface alloy with Cu4Pb3 composition,17 while the c(2 × 2) structure is interpreted as a simple arrangement of Pb atoms occupying one half of all available Cu(001) hollow sites.17,18 Above 0.5 ML and below 0.6 ML, a c(2 × 2) phase with split superstructure spots is observed. The spot splitting is due to antiphase domain boundaries inserted into the c(2 × 2) structure.19 For a critical coverage of 0.6 ML, a regular distribution of linear domain boundaries is observed. This domain boundary arrangement is characterized by the regular succession of three rows of Pb atoms occupying the same kind of hollow site. The long-range order of this structure corresponds to a
(for 0.6 ML). The c(4 × 4) structure is a Cu–Pb surface alloy with Cu4Pb3 composition,17 while the c(2 × 2) structure is interpreted as a simple arrangement of Pb atoms occupying one half of all available Cu(001) hollow sites.17,18 Above 0.5 ML and below 0.6 ML, a c(2 × 2) phase with split superstructure spots is observed. The spot splitting is due to antiphase domain boundaries inserted into the c(2 × 2) structure.19 For a critical coverage of 0.6 ML, a regular distribution of linear domain boundaries is observed. This domain boundary arrangement is characterized by the regular succession of three rows of Pb atoms occupying the same kind of hollow site. The long-range order of this structure corresponds to a 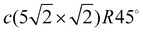 conventional unit cell18,20 that can be described as a periodic sequence of long-range ordered linear antiphase domain boundaries defining Pb stripes with a width of three atomic rows. The formation of antiphase domain boundaries permits the accommodation of extra Pb atoms with respect to the c(2 × 2) phase. Indeed, the formation of the domain boundaries is a way to compress the c(2 × 2) structure. In contrast to the well studied film growth mechanism and electronic structure of Pb/Cu(001) systems,14,21,22 a detailed description of their dynamics is absent up until today.
conventional unit cell18,20 that can be described as a periodic sequence of long-range ordered linear antiphase domain boundaries defining Pb stripes with a width of three atomic rows. The formation of antiphase domain boundaries permits the accommodation of extra Pb atoms with respect to the c(2 × 2) phase. Indeed, the formation of the domain boundaries is a way to compress the c(2 × 2) structure. In contrast to the well studied film growth mechanism and electronic structure of Pb/Cu(001) systems,14,21,22 a detailed description of their dynamics is absent up until today.
In the present work, we address the interplay of atomic structure and vibration characteristics of the Pb/Cu(001) adsorbed systems from 0.375 ML to 0.6 ML coverages using embedded atom method interatomic interaction potentials, which we employed earlier for the calculation of the vibration properties of Pb/Cu(111) systems.12 We discuss the dependence of the vibration spectra on the adlayer structures.
2 Calculation methods
The calculations are performed using the embedded atom method (EAM) to construct the interatomic interaction potentials Cu–Cu and Pb–Pb.23 The parameters of the method are determined by fitting to experimental data, such as the equilibrium lattice constant, elastic constants, sublimation energy, and vacancy formation energy of the Cu and Pb bulk metals. The Cu–Cu interatomic potentials were successfully applied before to the calculation of phonons on the clean metal surfaces24,25 and on the surfaces covered by adsorbates.12,24,26,27The interaction between Cu and Pb atoms is described by a pair potential constructed in the form proposed by Johnson.28 A two-dimensional periodic slab consisting of 31 atomic layers of Cu(001) is used for calculating the structure and phonons. To obtain the equilibrium configuration of the system at zero temperature, the atomic positions of both adsorbates and substrate atoms were relaxed using a standard molecular dynamics technique based on the constructed EAM interaction potentials. Since experimental data for the crystal structure of Pb/Cu surface phases is limited at the atomic level or only average Pb–Cu distances for complex structures are known, we additionally performed DFT relaxation of these structures. Total energy calculations were performed with the Vienna ab initio simulation package (VASP).29,30
The calculations of the vibration spectra were carried out using EAM potentials by the dynamical matrix method. Diagonalizing the matrix gives the eigenfrequencies and the polarization vectors of the vibrations. The local vibration densities of states were obtained by projecting eigenmodes onto the atoms of interest in a given X, Y or Z direction.
3 Results and discussion
3.1 Pb/Cu(001)-c(4 × 4): Pb–Cu surface alloy
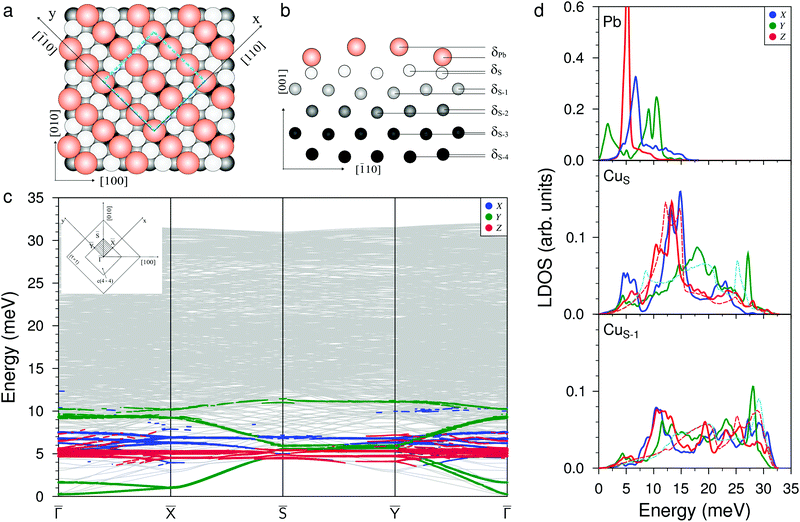
Fig. 1(a and b) show the atomic structure of the c(4 × 4) surface alloy formed at Θ = 0.375 ML of Pb adsorption from the top and side view, respectively. The unit cell contains three equidistant (3.38 Å) Pb atoms in the missing row of the four surface copper atoms. One of the three atoms in the Pb chain is situated in the ideal hollow (Pbh) position, while two others are located in the distorted (Pbd) non-symmetric positions with respect to the atoms of the second Cu layer (CuS−1). The former atoms are located δPb = 0.13 Å higher than the Pb atom in the hollow position. The heights of the Pb atoms with respect to the nearest CuS atoms are also different: it is 1.2 Å for Pb in the hollow site and 1.3 Å for Pb atoms in the distorted positions; both are close to the average experimental value hPb = 1.41 Å.31 The difference in the positions of the Pb atoms leads to the appearance of rippling in the copper layers, up to the depth of the fifth layer. As can be seen from Fig. 1(b), the largest rippling is observed in the CuS−1 and CuS−2 atomic layers: δS−1 = 0.05 Å and δS−2 = 0.04 Å. Note that in the DFT relaxed structure, the heights of the Pbh and Pbd are smaller at 0.70 and 0.78 Å, respectively. This is due to the larger Pb–Pb distance of 3.42 Å in the row, which is a consequence of the larger equilibrium lattice parameter of copper in the DFT calculation (3.633 vs. the experimental parameter of 3.615 Å used in the EAM calculation).For clean Cu(001), the EAM relaxation leads to a reduction in the interlayer distances Δ12 and Δ23 by 1.0% and 0.3%, respectively. These data are in good agreement with the experiments32 and other theoretical calculations.33 For deeper atomic layers, the relaxation shifts are almost absent. For the surface alloy, the relaxation of the copper substrate changes significantly. The large rippling in the CuS−1 and CuS−2 atomic layers results in different reductions in the distance between the substrate atoms located under the Pb atoms in the hollow and distorted positions and the local relaxations are equal to Δ12 = −7.0% and Δ12 = −4.1%, respectively. The relaxations of the second interlayer distance Δ23 also vary from −0.1% to −2.9%. At the same time, an expansion of the next two interlayer distances Δ34 ≈ +1.2% and Δ45 ≈ +0.3% was found, and thus, in general, Pb/Cu(001)-c(4 × 4) shows a surface relaxation character similar to that of Na and K adsorbed structures on the reconstructed Cu(110) surface.34,35
Fig. 1(c) shows the phonon spectrum of the Pb–Cu surface alloy calculated along the high-symmetry directions of the (4 × 4) surface Brillouin zone (see the inset). A characteristic feature of the phonon spectrum is the presence of the two localized low-frequency modes of Y-polarized vibrations in the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) −
− ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) and
and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) − Ȳ directions. The lower mode is determined by the inphase vibrations of the Pb rows in the [
− Ȳ directions. The lower mode is determined by the inphase vibrations of the Pb rows in the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] direction, while the second mode has an antiphase character of displacements of Pb atomic rows in the same direction. At the
10] direction, while the second mode has an antiphase character of displacements of Pb atomic rows in the same direction. At the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) point, these vibration modes have very low energies (0.3 and 1.6 meV, respectively). In the local density of states (LDOS), shown in Fig. 1(d), the first Y peak with a maximum at ≈1.6 meV is determined by these states. In the high-frequency region, the localized symmetric (upper, almost dispersionless over the whole SBZ) and antisymmetric (lower) Y-polarized vibrations of Pb atoms within the row are found. In the LDOS, these vibration states correspond to the peaks at 9.0 meV and 10.5 meV, respectively. The phonon spectrum and LDOS show that the X-polarized vibrations of Pb atoms (perpendicular to the rows) are located in the energy range from 4.5 meV to 8.0 meV. The maximum peak in the Pb LDOS is observed at ≈6.8 meV and corresponds to the mode representing the antisymmetric vibrations of Pb atoms which mix with XZ-polarized vibrations of the CuS and CuS−1 substrate atoms and propagate perpendicularly to the adatom's rows. In the phonon spectrum, along all high-symmetry directions of the two-dimensional BZ, almost dispersionless Z-polarized states, strongly localized on Pb adatoms, are observed. In the Pb LDOS, they correspond to a narrow peak with a maximum at 5.2 meV. These perpendicular Pb vibrations give rise to the emergence of longitudinal vibrations in the CuS layer and, to a lesser extent, in the CuS−1 layer (see the corresponding panels in Fig. 1(d)). In addition, the presence of Pb rows in the surface layer also results in the shift down of high-frequency longitudinal vibrations of the CuS atoms. In addition, two localized X-peaks in CuS LDOS appear in the energy range of the Rayleigh wave vibration mode (12.0–15.0 meV). The first peak is determined to the maximum extent by the hybridization of the X-polarized vibrations of Pb adatoms with the X, Z vibrations of the substrate atoms. The second peak is the result of antisymmetric X-polarized vibrations of the CuS layer atoms. The large width of these peaks is due to different positions of adsorption of the Pbh and Pbd atoms. It can be seen from the CuS LDOS that the peak corresponding to the Rayleigh mode shifts to higher energies by ≈1.3 meV with respect to that on the clean surface (red dashed line).
point, these vibration modes have very low energies (0.3 and 1.6 meV, respectively). In the local density of states (LDOS), shown in Fig. 1(d), the first Y peak with a maximum at ≈1.6 meV is determined by these states. In the high-frequency region, the localized symmetric (upper, almost dispersionless over the whole SBZ) and antisymmetric (lower) Y-polarized vibrations of Pb atoms within the row are found. In the LDOS, these vibration states correspond to the peaks at 9.0 meV and 10.5 meV, respectively. The phonon spectrum and LDOS show that the X-polarized vibrations of Pb atoms (perpendicular to the rows) are located in the energy range from 4.5 meV to 8.0 meV. The maximum peak in the Pb LDOS is observed at ≈6.8 meV and corresponds to the mode representing the antisymmetric vibrations of Pb atoms which mix with XZ-polarized vibrations of the CuS and CuS−1 substrate atoms and propagate perpendicularly to the adatom's rows. In the phonon spectrum, along all high-symmetry directions of the two-dimensional BZ, almost dispersionless Z-polarized states, strongly localized on Pb adatoms, are observed. In the Pb LDOS, they correspond to a narrow peak with a maximum at 5.2 meV. These perpendicular Pb vibrations give rise to the emergence of longitudinal vibrations in the CuS layer and, to a lesser extent, in the CuS−1 layer (see the corresponding panels in Fig. 1(d)). In addition, the presence of Pb rows in the surface layer also results in the shift down of high-frequency longitudinal vibrations of the CuS atoms. In addition, two localized X-peaks in CuS LDOS appear in the energy range of the Rayleigh wave vibration mode (12.0–15.0 meV). The first peak is determined to the maximum extent by the hybridization of the X-polarized vibrations of Pb adatoms with the X, Z vibrations of the substrate atoms. The second peak is the result of antisymmetric X-polarized vibrations of the CuS layer atoms. The large width of these peaks is due to different positions of adsorption of the Pbh and Pbd atoms. It can be seen from the CuS LDOS that the peak corresponding to the Rayleigh mode shifts to higher energies by ≈1.3 meV with respect to that on the clean surface (red dashed line).
3.2 Pb/Cu(001)-c(2 × 2) reconstruction
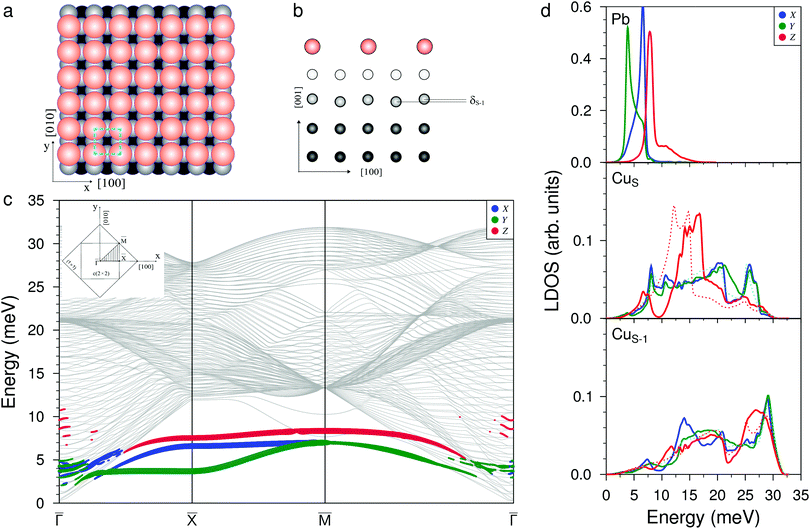
The structure of the c(2 × 2) adsorption phase formed at Θ = 0.5 ML of Pb coverage is highly symmetric (Fig. 2(a and b)). The Pb atoms are located at a height of 2.40 Å above the CuS layer. This distance is in a good agreement with both the LEED data (2.29 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18) and our DFT calculation (2.29 Å). Negligible rippling is found only in the CuS−1 layer and its value δS−1 = 0.002 Å. The deposition of Pb reduces the relaxation contraction of the interlayer distances of the copper surface from −1% (inherent to clean Cu(001)) to −0.4% for atoms underneath Pb atoms for the first interlayer distance of copper, and it completely removes relaxation for the other copper atoms. There is no lateral relaxation in this structure.
18) and our DFT calculation (2.29 Å). Negligible rippling is found only in the CuS−1 layer and its value δS−1 = 0.002 Å. The deposition of Pb reduces the relaxation contraction of the interlayer distances of the copper surface from −1% (inherent to clean Cu(001)) to −0.4% for atoms underneath Pb atoms for the first interlayer distance of copper, and it completely removes relaxation for the other copper atoms. There is no lateral relaxation in this structure.
The phonon spectrum contains three vibration modes localized on Pb adatoms (Fig. 2(c)). The shear horizontal mode is provided by Y-polarized vibrations propagating along all the high-symmetry directions of the surface BZ. At the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) point, this mode degenerates with the frustrated translation mode determined by the X-polarized vibrations. In the Pb LDOS, the peaks corresponding to these modes are observed at energies of 3.8 and 6.6 meV (Fig. 2(d), top panel). The third mode is determined by the Z-polarized vibrations of Pb atoms, which are mixed with the XZ vibrations of the substrate atoms from both the CuS and CuS−1 layers. In the Pb LDOS, this gives rise to a peak at 7.9 meV. The presence of half a monolayer of lead on the surface leads to a high-frequency shift of the RW mode of Cu(001) by ≈2.0 meV and to the appearance of new vibration states with XY and Z polarization in the low-frequency region of the phonon spectrum of the substrate. This is clearly seen from the LDOSs of CuS and CuS−1 shown in Fig. 2(d).
point, this mode degenerates with the frustrated translation mode determined by the X-polarized vibrations. In the Pb LDOS, the peaks corresponding to these modes are observed at energies of 3.8 and 6.6 meV (Fig. 2(d), top panel). The third mode is determined by the Z-polarized vibrations of Pb atoms, which are mixed with the XZ vibrations of the substrate atoms from both the CuS and CuS−1 layers. In the Pb LDOS, this gives rise to a peak at 7.9 meV. The presence of half a monolayer of lead on the surface leads to a high-frequency shift of the RW mode of Cu(001) by ≈2.0 meV and to the appearance of new vibration states with XY and Z polarization in the low-frequency region of the phonon spectrum of the substrate. This is clearly seen from the LDOSs of CuS and CuS−1 shown in Fig. 2(d).
3.3 Pb/Cu(001)-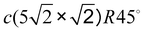 : ultimate 0.6 ML coverage
: ultimate 0.6 ML coverage
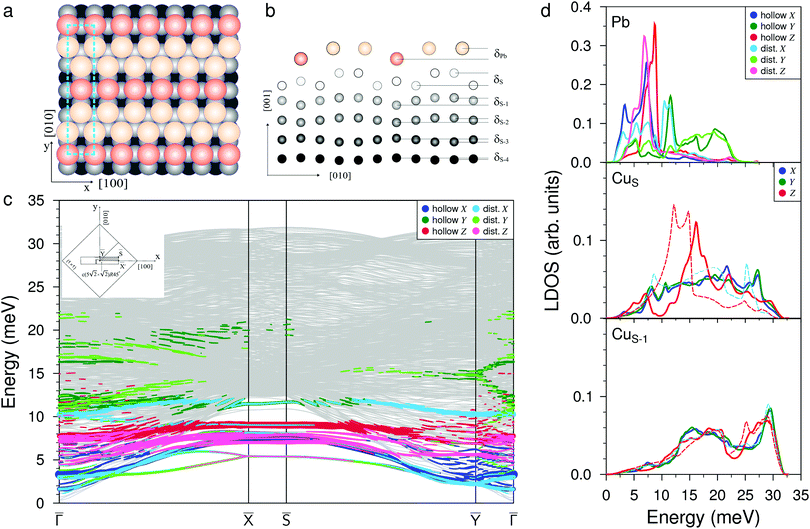
When increasing the coverage from Θ = 0.5 ML, corresponding to the Pb/Cu(001)-c(2 × 2) superstructure, to Θ = 0.6 ML, a continuous phase transition occurs. This phase transition proceeds by the insertion of antiphase domain boundaries into the c(2 × 2) until at Θ = 0.6 ML a regular sequence of domain boundaries, which are separating three rows of Pb atoms in c(2 × 2) positions, is formed (Fig. 3(a)). In this Pb/Cu(001)-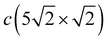 structure, the Pb atoms occupy different positions relative to the copper atoms of the CuS layer (Fig. 3(b)): the first position is ideal hollow (Pbh), like in the c(2 × 2) structure, and the second one is a distorted position (Pbd) at the domain boundaries. Due to the displacement of Pb atoms from hollow positions, the distance between Pbh and Pbd in the y direction decreases to 3.19 Å within a domain (it is 3.615 Å in the x direction), while the distance between the Pbd of neighboring domains is 3.22 Å. The DFT relaxation of the Pb/Cu(001)-
structure, the Pb atoms occupy different positions relative to the copper atoms of the CuS layer (Fig. 3(b)): the first position is ideal hollow (Pbh), like in the c(2 × 2) structure, and the second one is a distorted position (Pbd) at the domain boundaries. Due to the displacement of Pb atoms from hollow positions, the distance between Pbh and Pbd in the y direction decreases to 3.19 Å within a domain (it is 3.615 Å in the x direction), while the distance between the Pbd of neighboring domains is 3.22 Å. The DFT relaxation of the Pb/Cu(001)-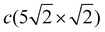 structure gives 3.23 and 3.19 Å for the Pbh–Pbd and Pbd–Pbd distances, respectively. The compression of domains in the y direction is also in agreement with the LEED data,19 which have shown the displacements of Pbd atoms towards Pbh by 0.4 Å. The formation of domain boundaries also leads to the rippling of the Pb layer so that the Pbd atoms are located by δPb = 0.13 Å (the same as in the c(4 × 4) surface alloy) above Pbh and distances between Pbh and Pbd and their nearest neighbor Cu atoms are 2.73 and 2.61 Å, respectively. These distances are also in a good agreement with the DFT-derived values of 2.88 and 2.78 Å, respectively. The rippling in the Pb layer causes corresponding rippling in the substrate layers that decreases with a depth. The rippling in the CuS layer δS = 0.15 Å, almost the same as in the Pb layer, while it is two times smaller in the next layer, δS−1 = 0.08 Å. Like in the Pb/Cu(001)-c(4 × 4) alloy, for the Pb/Cu(001)-
structure gives 3.23 and 3.19 Å for the Pbh–Pbd and Pbd–Pbd distances, respectively. The compression of domains in the y direction is also in agreement with the LEED data,19 which have shown the displacements of Pbd atoms towards Pbh by 0.4 Å. The formation of domain boundaries also leads to the rippling of the Pb layer so that the Pbd atoms are located by δPb = 0.13 Å (the same as in the c(4 × 4) surface alloy) above Pbh and distances between Pbh and Pbd and their nearest neighbor Cu atoms are 2.73 and 2.61 Å, respectively. These distances are also in a good agreement with the DFT-derived values of 2.88 and 2.78 Å, respectively. The rippling in the Pb layer causes corresponding rippling in the substrate layers that decreases with a depth. The rippling in the CuS layer δS = 0.15 Å, almost the same as in the Pb layer, while it is two times smaller in the next layer, δS−1 = 0.08 Å. Like in the Pb/Cu(001)-c(4 × 4) alloy, for the Pb/Cu(001)-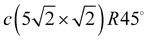 structure, the lateral relaxation of substrate atoms is also observed, but the copper atoms are displaced only in the y direction and the relaxation displacements is an order of magnitude smaller than in the former case. In the CuS layer, only copper atoms closest to Pbh move away from each other by 0.06 Å (the shifts of ±0.03 Å along y). In the CuS−1 and CuS−2 layers, all the copper atoms are displaced by ∼±0.02 Å from their ideal positions, while in deeper layers, the lateral relaxation is almost absent.
structure, the lateral relaxation of substrate atoms is also observed, but the copper atoms are displaced only in the y direction and the relaxation displacements is an order of magnitude smaller than in the former case. In the CuS layer, only copper atoms closest to Pbh move away from each other by 0.06 Å (the shifts of ±0.03 Å along y). In the CuS−1 and CuS−2 layers, all the copper atoms are displaced by ∼±0.02 Å from their ideal positions, while in deeper layers, the lateral relaxation is almost absent.
The complication of the atomic structure due to the appearance of domain boundaries leads to significant modification of the phonon spectrum in comparison with that of the single domain Pb/Cu(001)-c(2 × 2) structure. In Fig. 3(c) and (d) the spectrum and local density of vibration states projected onto Pbh and Pbd separately are shown. Let us consider first the modes localized on Pb atoms residing in the same hollow positions as in the c(2 × 2) structure (Pbh). Since the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) direction of SBZ is the same for both the c(2 × 2) and
direction of SBZ is the same for both the c(2 × 2) and 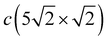 structures, we will focus mostly on this high-symmetry direction. The lowest, almost dispersionless, along the
structures, we will focus mostly on this high-symmetry direction. The lowest, almost dispersionless, along the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) Y-polarized mode of the c(2 × 2) structure splits in two branches in the case of
Y-polarized mode of the c(2 × 2) structure splits in two branches in the case of 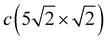 , among which the lower one is determined by the symmetric and the upper one by the antisymmetric vibrations of Pbh atoms. These two branches are degenerate at
, among which the lower one is determined by the symmetric and the upper one by the antisymmetric vibrations of Pbh atoms. These two branches are degenerate at ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) at energy that is 1.7 meV higher than the corresponding Y-polarized mode of c(2 × 2). However, these vibrations of Pbh atoms are not independent; they are accompanied by the complicated, mostly in-plane vibrations of the Pbd atoms. In particular, at the
at energy that is 1.7 meV higher than the corresponding Y-polarized mode of c(2 × 2). However, these vibrations of Pbh atoms are not independent; they are accompanied by the complicated, mostly in-plane vibrations of the Pbd atoms. In particular, at the ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point, the degenerate state is characterized by an alternating displacement of Pbh atoms in the Y direction, while Pbd atoms located on both sides of the domain boundary have different displacements: along and perpendicular to the boundary. Moreover, the last displacements are also accompanied by the vibrations of Pbd atoms in the z direction. In the Pb LDOS (Fig. 3(d)), this complicated Y-polarized mode gives rise to a broad Y-peak in the region of 3–5 meV.
point, the degenerate state is characterized by an alternating displacement of Pbh atoms in the Y direction, while Pbd atoms located on both sides of the domain boundary have different displacements: along and perpendicular to the boundary. Moreover, the last displacements are also accompanied by the vibrations of Pbd atoms in the z direction. In the Pb LDOS (Fig. 3(d)), this complicated Y-polarized mode gives rise to a broad Y-peak in the region of 3–5 meV.
The X-polarized Pb vibration mode of the c(2 × 2) structure, which generates a narrow peak in the LDOS at 6.6 meV, can also be identified in the Pbh LDOS for the 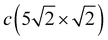 structure at 7.2 meV. In the phonon spectrum, this mode is characterized by noticeable broadening, even at the
structure at 7.2 meV. In the phonon spectrum, this mode is characterized by noticeable broadening, even at the ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point (below the bulk phonon spectrum), due to complicated mixing with the vibrations of the Pbd atoms. Three branches appear between 7.0 and 8.1 meV at the
point (below the bulk phonon spectrum), due to complicated mixing with the vibrations of the Pbd atoms. Three branches appear between 7.0 and 8.1 meV at the ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point. Among them, the two lower states at 7.0 and 7.5 meV come from the X-polarized Pbh vibrations accompanied by the XZ displacements of neighboring Pbd atoms, whereas the upper state in this range represents the even more complex collective XZ-polarized vibrations of Pbh and Pbd atoms. The Rayleigh wave Z-polarized vibration mode localized on Pbh atoms can be found at an energy 1.5 meV higher than that in c(2 × 2), moreover it is accompanied by the displacement of Pbd atoms along the x direction. In contrast to the Z-polarized vibrations of Pbh located at ≈9.2 meV, the Z-polarized state highly localized on Pbd atoms is observed at 7.8 meV, i.e. almost at the same energy as in the c(2 × 2) structure. This localized Z mode contributes to the LDOS peak, which is determined by XZ mixed states discussed above.
point. Among them, the two lower states at 7.0 and 7.5 meV come from the X-polarized Pbh vibrations accompanied by the XZ displacements of neighboring Pbd atoms, whereas the upper state in this range represents the even more complex collective XZ-polarized vibrations of Pbh and Pbd atoms. The Rayleigh wave Z-polarized vibration mode localized on Pbh atoms can be found at an energy 1.5 meV higher than that in c(2 × 2), moreover it is accompanied by the displacement of Pbd atoms along the x direction. In contrast to the Z-polarized vibrations of Pbh located at ≈9.2 meV, the Z-polarized state highly localized on Pbd atoms is observed at 7.8 meV, i.e. almost at the same energy as in the c(2 × 2) structure. This localized Z mode contributes to the LDOS peak, which is determined by XZ mixed states discussed above.
In addition to vibrational states that are inherited from a less dense c(2 × 2) structure and which are significantly modified when domain boundaries appear, new longitudinal states also appear in the spectrum of the 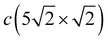 structure. At low frequencies, in the vicinity of the
structure. At low frequencies, in the vicinity of the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) and Ȳ points, the X-polarized collective vibrations of both Pbh and Pbd atoms are observed. In the Pb LDOS, these vibrations give rise to a peak at 3.3 meV. Also, in the region of ∼10 meV, an almost dispersionless mode, determined by the mixed vibrations of Pbh and Pbh atoms along the y and x directions, respectively, appears in the spectrum. These vibrations are manifested as well localized peaks at about of 11.5 meV in the Pb LDOS. Even higher in energy, up to 22 meV, pure Y-polarized resonant states localized on both Pbh and Pbd atoms are observed. Their appearance is caused by a contraction in the distances between the nearest Pb atoms in the y direction which are decreased to ∼3.2 Å, compared to the distance of 3.615 Å in the c(2 × 2) structure.
and Ȳ points, the X-polarized collective vibrations of both Pbh and Pbd atoms are observed. In the Pb LDOS, these vibrations give rise to a peak at 3.3 meV. Also, in the region of ∼10 meV, an almost dispersionless mode, determined by the mixed vibrations of Pbh and Pbh atoms along the y and x directions, respectively, appears in the spectrum. These vibrations are manifested as well localized peaks at about of 11.5 meV in the Pb LDOS. Even higher in energy, up to 22 meV, pure Y-polarized resonant states localized on both Pbh and Pbd atoms are observed. Their appearance is caused by a contraction in the distances between the nearest Pb atoms in the y direction which are decreased to ∼3.2 Å, compared to the distance of 3.615 Å in the c(2 × 2) structure.
Despite strong modification of the Pb vibration spectrum in the 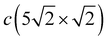 structure as opposed to that of c(2 × 2), in the CuS LDOS a significant change is observed only in the RW mode peak, which demonstrates a larger high-frequency shift of ≈3.0 meV with respect to that on the clean Cu(001) surface (red dashed line in Fig. 3(d), middle panel). The LDOS of the second Cu layer (Fig. 3(d), bottom panel) and of deeper layers practically does not feel the presence of the Pb adlayer.
structure as opposed to that of c(2 × 2), in the CuS LDOS a significant change is observed only in the RW mode peak, which demonstrates a larger high-frequency shift of ≈3.0 meV with respect to that on the clean Cu(001) surface (red dashed line in Fig. 3(d), middle panel). The LDOS of the second Cu layer (Fig. 3(d), bottom panel) and of deeper layers practically does not feel the presence of the Pb adlayer.
4 Conclusions
In summary, we have studied the dynamics of Pb/Cu(001) structures formed at various submonolayer Pb coverages from 0.375 ML to 0.6 ML. The following conclusions can be drawn. The surface Pb–Cu alloy with a c(4 × 4) structure forming at Θ = 0.375 ML is characterized by the vibrations of Pb atomic rows along the row direction. These vibrations, which are antiphase and inphase, lead to the appearance of soft modes in the![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) direction in the phonon spectrum, which indicate the instability of this structure to external influences. An increase in the Pb coverage to Θ = 0.5 ML is accompanied by a phase transition to a highly symmetric c(2 × 2) structure, where Pb adatoms form an adlayer instead of a surface alloy. The phonon spectrum of this adlayer is similar to the spectra of clean (001) surfaces of fcc metals.33 Vibrations of the Pb adlayer only slightly change the phonon spectrum of the substrate, which is expressed mainly in the high-frequency shift of the RW mode, which, however, retains its localization. Such behavior signifies relatively weak interactions between the Pb adlayer and the Cu(001) substrate. A further increase in the coverage leads to the formation of the
direction in the phonon spectrum, which indicate the instability of this structure to external influences. An increase in the Pb coverage to Θ = 0.5 ML is accompanied by a phase transition to a highly symmetric c(2 × 2) structure, where Pb adatoms form an adlayer instead of a surface alloy. The phonon spectrum of this adlayer is similar to the spectra of clean (001) surfaces of fcc metals.33 Vibrations of the Pb adlayer only slightly change the phonon spectrum of the substrate, which is expressed mainly in the high-frequency shift of the RW mode, which, however, retains its localization. Such behavior signifies relatively weak interactions between the Pb adlayer and the Cu(001) substrate. A further increase in the coverage leads to the formation of the 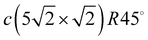 structure at Θ = 0.6 ML. This structure is characterised by a regular sequence of domain boundaries due to the compression of the c(2 × 2) structure along the direction perpendicular to the boundaries and demonstrates higher dynamic stability. This is due to the deep penetration of longitudinal vibrations of Pb adatoms into the region of bulk vibrations of the substrate, leading to the stronger interatomic interactions of the adatoms.
structure at Θ = 0.6 ML. This structure is characterised by a regular sequence of domain boundaries due to the compression of the c(2 × 2) structure along the direction perpendicular to the boundaries and demonstrates higher dynamic stability. This is due to the deep penetration of longitudinal vibrations of Pb adatoms into the region of bulk vibrations of the substrate, leading to the stronger interatomic interactions of the adatoms.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the government research assignment for ISPMS SB RAS (project FWRW-2022-0001).References
- Y. Guo, Y.-F. Zhang, X.-Y. Bao, T.-Z. Han, Z. Tang, L.-X. Zhang, W.-G. Zhu, E. G. Wang, Q. Niu, Z. Q. Qiu, J.-F. Jia, Z.-X. Zhao and Q.-K. Xue, Science, 2004, 306, 1915 CrossRef CAS PubMed.
- M. M. Özer, J. R. Thompson and H. H. Weitering, Nat. Phys., 2006, 2, 173–176 Search PubMed.
- D. Eom, S. Qin, M.-Y. Chou and C. K. Shih, Phys. Rev. Lett., 2006, 96, 027005 CrossRef PubMed.
- S. Qin, J. Kim, Q. Niu and C.-K. Shih, Science, 2009, 324, 1314 CrossRef CAS PubMed.
- C. Brun, I.-P. Hong, F. M. C. Patthey, I. Y. Sklyadneva, R. Heid, P. M. Echenique, K. P. Bohnen, E. V. Chulkov and W.-D. Schneider, Phys. Rev. Lett., 2009, 102, 207002 CrossRef PubMed.
- T. Zhang, P. Cheng, W.-J. Li, Y.-J. Sun, G. Wang, X.-G. Zhu, K. He, L. Wang, X. Ma, X. Chen, Y. Wang, Y. Liu, H.-Q. Lin, J.-F. Jia and Q.-K. Xue, Nat. Phys., 2010, 6, 104–108 Search PubMed.
- J. H. Dil, J. W. Kim, S. Gokhale, M. Tallarida and K. Horn, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 045405 CrossRef.
- J. Braun, P. Ruggerone, G. Zhang, J. P. Toennies and G. Benedek, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205423 CrossRef.
- S. Mathias, A. Ruffing, F. Deicke, M. Wiesenmayer, M. Aeschlimann and M. Bauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155429 CrossRef.
- I. Y. Sklyadneva, G. Benedek, E. V. Chulkov, P. M. Echenique, R. Heid, K.-P. Bohnen and J. P. Toennies, Phys. Rev. Lett., 2011, 107, 095502 CrossRef PubMed.
- G. Benedek, M. Bernasconi, K.-P. Bohnen, D. Campi, E. V. Chulkov, P. M. Echenique, R. Heid, I. Y. Sklyadneva and J. P. Toennies, Phys. Chem. Chem. Phys., 2014, 16, 7159–7172 RSC.
- G. G. Rusina, S. D. Borisova, S. V. Eremeev, I. Y. Sklyadneva, E. V. Chulkov, G. Benedek and J. P. Toennies, J. Phys. Chem. C, 2016, 120, 22304–22317 CrossRef CAS.
- T. Aruga, Surf. Sci. Rep., 2006, 61, 283–302 CrossRef CAS.
- T. Ohto, A. Nojima, K. Yamashita and H. Nakamura, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155415 CrossRef.
- G. L. Kellogg and R. Plass, Surf. Sci., 2000, 465, L777–L782 CrossRef CAS.
- G. L. Kellogg and R. A. Plass, Surf. Rev. Lett., 2000, 07, 649–655 CrossRef CAS.
- C. Nagl, E. Platzgummer, O. Haller, M. Schmid and P. Varga, Surf. Sci., 1995, 331–333, 831–837 CrossRef CAS.
- W. Hösler, W. Moritz, E. Tamura and R. Feder, Surf. Sci., 1986, 171, 55–68 CrossRef.
- W. Hoesler and W. Moritz, Surf. Sci., 1982, 117, 196–203 CrossRef CAS.
- A. Sánchez and S. Ferrer, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5778–5786 CrossRef PubMed.
- V. Joco, J. Martínez-Blanco, P. Segovia, T. Balasubramanian, J. Fujii and E. G. Michel, Surf. Sci., 2006, 600, 3851–3855 CrossRef CAS.
- V. Joco, J. Martínez-Blanco, P. Segovia, I. Vobornik and E. G. Michel, J. Phys.: Condens. Matter, 2009, 21, 474216 CrossRef CAS PubMed.
- S. M. Foiles, M. I. Baskes and M. S. Daw, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7983–7991 CrossRef CAS PubMed.
- G. G. Rusina and E. V. Chulkov, Russ. Chem. Rev., 2013, 82, 483 CrossRef.
- I. Sklyadneva, G. Rusina and E. Chulkov, Surf. Sci., 1998, 416, 17–36 CrossRef CAS.
- G. G. Rusina, S. V. Eremeev, P. M. Echenique, G. Benedek, S. D. Borisova and E. V. Chulkov, J. Phys.: Condens. Matter, 2008, 20, 224007 CrossRef.
- S. V. Eremeev, I. Y. Sklyadneva, P. M. Echenique, S. D. Borisova, G. Benedek, G. G. Rusina and E. V. Chulkov, Surf. Sci., 2007, 601, 4553–4556 CrossRef CAS.
- R. A. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 12554–12559 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- S. Robert, C. Cohen, A. L’Hoir, J. Moulin, D. Schmaus and M. G. Barthes-Labrousse, Surf. Sci., 1996, 365, 285–296 CrossRef CAS.
- D. M. Lind, F. B. Dunning, G. K. Walters and H. L. Davis, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 9037–9044 CrossRef CAS PubMed.
- R. Heid and K.-P. Bohnen, Phys. Rep., 2003, 387, 151–213 CrossRef CAS.
- G. G. Rusina, S. D. Borisova and E. V. Chulkov, J. Exp. Theor. Phys., 2017, 125, 278–289 CrossRef CAS.
- S. D. Borisova, G. G. Rusina, S. V. Eremeev and E. V. Chulkov, J. Phys. Chem. C, 2017, 121, 22969–22976 CrossRef CAS.
| This journal is © the Owner Societies 2022 |