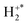Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bimolecular reactions of S2+ with Ar, H2 and N2: reactivity and dynamics†
Sam
Armenta Butt
* and
Stephen D.
Price
 *
*
Department of Chemistry, University College London, 20 Gordon Street, London, WC1H 0AJ, UK. E-mail: sam.butt.16@ucl.ac.uk; s.d.price@ucl.ac.uk; Fax: +44 (0)20 7679 7463; Tel: +44 (0)20 7679 4600 Tel: +44 (0)20 7679 4606
First published on 22nd March 2022
Abstract
The reactivity, energetics and dynamics of bimolecular reactions between S2+ and three neutral species (Ar, H2 and N2) have been studied using a position-sensitive coincidence methodology at centre-of-mass collision energies below 6 eV. This is the first study of bimolecular reactions involving S2+, a species detected in planetary ionospheres, the interstellar medium, and in anthropogenic manufacturing processes. The reactant dication beam employed consists predominantly of S2+ in the ground 3P state, but some excited states are also present. Most of the observed reactions involve the ground state of S2+, but the dissociative electron transfer reactions appear to exclusively involve excited states of this atomic dication. We observe exclusively single electron-transfer between S2+ and Ar, a process which exhibits strong forward scatting typical of the Landau–Zener style dynamics observed for other dicationic electron transfer reactions. Following collisions between S2+ + H2, non-dissociative and dissociative single electron-transfer reactions were detected. The dynamics here show evidence for the formation of a long-lived collision complex, [SH2]2+, in the dissociative single electron-transfer channel. The formation of SH+ was not observed. In contrast, the collisions of S2+ + N2 result in the formation of SN+ + N+ in addition to the products of single electron-transfer reactions.
Introduction
Doubly charged positive ions (dications) can be found in energised environments such as the ionospheres of planets and their satellites,1–8 the interstellar medium,9–11 and in anthropogenic plasmas.12–14 Significant bimolecular reactivity is shown following collisions of both atomic and molecular dications with neutral species in the gas-phase.15–20 The lifetimes of atomic dications in planetary ionospheres are expected to be primarily determined by such collisional processes.21 In addition, despite their usual inherent thermodynamic instability, the metastable electronic states of molecular dications have been shown to possess lifetimes sufficient to allow collisions with other species in ionospheres and elsewhere.15 Given the above lifetimes, the demonstrated bimolecular reactivity of these dications strongly suggests that dication chemistry can play a role in ionospheric processes;22 for example, dications could be involved in the chemistry of complex molecule formation through reactions involving carbon chain-growth.21,23–26There are numerous examples of the detection of atomic dications in planetary ionospheres.27 However, it is difficult to unambiguously detect molecular dications in ionospheres using simple mass spectrometry, the usual sampling technique. This difficulty arises because these environments often contain monocations with the same mass to charge ratio as the target dication.15 The historical absence of a definitive detection of ionospheric molecular dications may account for the relative neglect of these species in models of ionosphere chemistry.21 Encouragingly, the presence of the CO22+ dication in the ionosphere of Mars has been recently confirmed, the first detection of a molecular dication in such an environment.28 In order to identify dication reactions of ionospheric interest, laboratory-based experiments to probe dicationic reactivity, along with further in situ detection of dications in ionospheres, are vital.29 Indeed, recognition of the presence of molecular dications in planetary atmospheres has led to the identification of the role these species can play in atmospheric erosion.30–33 To develop further our understanding of dicationic processes, this paper presents an investigation of the reactions of S2+ with Ar, H2 and N2. This work reveals the reactivity, reaction mechanisms and reaction energetics of S2+, extending and enhancing our understanding of the chemistry of dications in environments such as planetary atmospheres.
Sulfur-containing species are found in a wide variety of astrophysical environments34–37 and on Earth, where they are ubiquitous both in nature and from anthropogenic activities.38,39 The S2+ ion has been observed in both terrestrial and non-terrestrial environments. For example, when plasmas involving SF6 are used for etching, S2+ can be formed.40,41 In interstellar clouds, organic compounds containing sulfur have been detected, including species with S–X bonds where X = O, C, N, H,34 and S2+ has been observed in nebulae close to sources of high energy photons.42–44 Indeed, the reactions of the sulfur dication are thought to be important in the ionosphere of Io, the satellite of Jupiter, where S2+ has been detected by the Galileo27 and Voyager I45,46 spacecraft, as well as by the Hubble telescope.47 Io's sulfur-rich atmosphere is derived from this moon's intense volcanic activity which results in the expulsion of SO2.48,49 Hence, S2+ is thought to be one of the major species in the Io torus,50 a region of the Jovian system where charged species generated in Io's ionosphere, such as S2+, are transferred to Jupiter, dominating both the planets magnetosphere49,51 and the torus of Europa.52 Despite this clear relevance of S2+ to astrophysical and anthropogenic environments, and the longevity of the atomic dication, there are no reports in the literature (to the authors’ knowledge) of the bimolecular reactivity of S2+ dications in the gas phase. Therefore, the investigation of the collisions of S2+ with neutral molecules presented in this study provides the first experimental information on the reactivity of this ion; that information is particularly pertinent to the chemistry of a number of astrophysical and terrestrial environments.
As a first investigation of the chemistry of S2+, we have chosen to study the reactions with three neutral gases that are important in interstellar and atmospheric chemistry: Ar, H2 and N2. Argon is often present in significant concentrations in planetary atmospheres.53–55 H2 is the most abundant molecule in the universe and is the dominant species making up the gaseous planets, including Jupiter.56–58 Molecular nitrogen (N2) is important in the atmospheres of terrestrial bodies in the solar system, especially the Earth and Titan where it is the dominant species.21,22,54,55,59–63
The reactions resulting from dication collisions with argon have been well studied. Single electron-transfer (SET) was observed in collisions with rare gas dications: Ne2+, Ar2+, Kr2+ or Xe2+.64–69 Collisions between N22+ and Ar also resulted in the observation of SET reactions.70 Collisions between Ar and hydrogen-containing dications, such as CHX2+ (X = F, Cl, Br, I), often result in SET and proton-transfer (PT) reactions; the latter, for example, forming ArH+.71–73 Interactions between Ar and SFx2+ (x = 2–4) or CFy2+ (y = 1–3) have been the subject of several studies, with SET and collision-induced dissociation (CID) channels being observed.74–78 Additionally, some dication reactions with Ar have been shown to generate product dications involving new chemical bonds. For example, HCCAr2+ and ArCF22+ are detected following collisions of Ar with C2H22+ and CF32+ respectively.79,80
A variety of dication reactions with H2 have been studied at low collision energies, often resulting in SET reactions. Reactions between Ar2+ and H2 resulted in non-dissociative and dissociative SET (NDSET and DSET respectively).64,66,81 With some H-containing dications (for example CHCl2+) H+ transfer to the neutral H2 is observed, producing H3+via the formation of collision complexes.82–84 Direct hydride (H−) transfer from the H2 to the dication is also seen in some systems.83,85 Many other bond-forming channels have been observed in dication reactions with H2, often with evidence that the reactions proceed via complexation.17,86–89 Some of the new bonds formed in this class of reaction include N–H,89 H–H,84 C–H,82,83,85–88 F–H,17,87,88 Cl–H,83 and Br–H.82 The ubiquity of bond-forming reactions in dication/H2 collision systems, and the prevalence of S–H bonds in nature, marks out the S2+ + H2 collision system as a candidate for the generation of new bonds.
The reactions following dication collisions with N2 have been the subject of several previous studies, including recent work by the current authors.90 In the Ar2+ + N2 collision system, SET, double electron-transfer (DET) and bond-forming pathways were observed.64,66–68,81,90–92 SET channels were also reported following the interactions of N2 with CO2+ and N22+.93,94 DSET resulting from the collisions of Ne2+ + N2 was shown to occur via two mechanisms, one involving a collision complex.95 Bond-forming reactions have been observed following the interactions of N2 with C4H32+ and O22+, resulting in the formation of N–H and N–O bonds.84,96 Additionally, S–N bond-formation has been observed following the gas-phase collisions of S+ ions with ammonia.97
In our experiments, we collide S2+ ions with the selected neutral species using a Position-Sensitive Coincidence Mass Spectrometer (PSCO-MS), at centre-of-mass (CM) collision energies of less than 6 eV. The PSCO-MS combines coincident detection of product cations with a crossed-beam methodology. The results from our experiments give a detailed insight into the reactivity and dynamics of dication–neutral interactions. For example, SET reactions are observed following the interactions of S2+ with Ar, N2 and H2, including both non-dissociative and dissociative channels with the molecular targets. The collisions of S2+ with N2 also result in the formation of SN+ + N+via a collision complex. The dynamics of the DSET channel in the S2+ + H2 system also shows evidence for the formation of a collision complex, [SH2]2+.
Experimental
Coincidence techniques involve the simultaneous detection of two or more products from a single reactive event. Dication interactions with neutrals often generate pairs of monocations, and these pairs of ions are detected in coincidence in our PSCO-MS experiment, which has been described in detail in the literature.76,98,99 In brief, a pulsed beam of dications is directed into the field-free source region of a time-of-flight mass spectrometer (TOF-MS). In this region the dications interact with a jet of the neutral reactant. Subsequent application of an extraction voltage to the source region allows the TOF-MS to detect the cation pairs generated from the dication-neutral interactions. The detection of these ions involves recording their arrival time, and position, at a large microchannel-plate detector. From this raw data, a list of flight times and arrival positions of the ions detected in pairs, a two-dimensional mass spectrum, can be generated revealing the different reactive channels. The positional data accompanying the ionic detections yields the relative motion of the products of each reactive event, providing a detailed insight into the mechanisms of each reactive channel.99The S2+ ions used in the experiments described in this paper were generated via electron ionization of H2S (CKgas, 99.5%) by 100 eV electrons in a custom-built ion source. Previous investigations show that S2+ (m/z = 16), HS2+ (m/z = 16.5), and H2S2+ (m/z = 17) dications are all formed following the bombardment of H2S with electrons.100 The positively charged ions are extracted from the ion source and pass through a hemispherical energy analyser to restrict the translational energy spread of the final S2+ beam to ∼0.3 eV. The continuous beam of ions exiting the hemispherical analyser is then pulsed, using a set of electrostatic deflectors, before being accelerated and focussed into a commercial velocity filter. The velocity filter is set to transmit just the 32S2+ (m/z = 16) ions. O+ ions, generated from the ionization of background gases in the ion source, may also be present in our dication beam because O+ has the same m/z ratio as 32S2+. However, reactions involving O+ ions will not result in the generation of two cationic products. Therefore, the products of reactions involving these contaminant O+ ions will not contribute to our coincidence spectra. The resulting pulsed beam of energy-constrained S2+ ions is then decelerated to <10 eV in the laboratory frame before entering the source region of the TOF-MS. In the TOF-MS source region the beam of dications is crossed with an effusive jet of the appropriate neutral species: Ar (BOC, 99.998%), H2 (BOC, >99.995%), or N2 (BOC, >99.998%). Single-collision conditions101 are achieved by employing an appropriately low pressure of the neutral collision partner. Under these conditions most dications do not undergo a collision and only a small percentage experience one collision. Such a pressure regime ensures no secondary reactions, due to successive collisions with two neutral species, influence the S2+ reactivity we observe. An electric field is applied across the TOF-MS source when the dication pulse reaches the centre of this region. This electric field accelerates positively charged species into the second electric field (acceleration region) of the TOF-MS and then on into the flight tube. At the end of the flight tube, the cations are detected by the position-sensitive detector which comprises a chevron-pair of microchannel plates (diameter = 12.7 cm) located in front of a dual delay-line anode.98 The voltage pulse applied to the source region also starts the ion timing circuitry, to which the signals from the detector provide stop pulses. The experiments in this work employed TOF-MS source fields of 183 V cm−1. The electrostatic fields employed in the TOF region are homogeneous in order to achieve high mass resolution, therefore our PSCO technique is distinct from ‘velocity map imaging’.
Signals from the detector are amplified and discriminated before being passed to a PC-based time-to-digital converter. If two ions are observed in the same TOF cycle, a coincidence event is recorded and each ion's arrival time and impact position on the detector are stored for off-line analysis. The use of single-collision conditions ensures ‘false’ coincidences are kept to a minimum in our spectra. The ion pairs data can be plotted as a 2D histogram, a ‘pairs spectrum’, where the time of flights (t1, t2) of each ion in the pair are used as the (x, y) co-ordinates. Peaks in the pairs spectrum readily identify bimolecular reaction channels that form a pair of positively-charged product ions. The subset of events associated with each such peak, events corresponding to an individual reaction channel, can then be selected for further off-line analysis.
As shown in previous work, the positional and time of flight information for each ion of a pair can be used to generate their x, y and z velocity vectors in the laboratory frame; here the z-axis is defined by the principal axis of the TOF-MS.98 The x and y velocity vectors of an ion are determined from the positional information and flight time; the z vector is determined from the deviation of the observed TOF from the expected TOF of an identical ion with zero initial kinetic energy. The laboratory frame velocities are then converted into the CM frame using the initial dication velocity.98 Often the pair of monocations resulting from the reaction between a dication and a neutral are accompanied by a neutral species: a three-body reaction. A powerful feature of the PSCO-MS experiment is that the CM velocity of such a neutral product can be determined from the CM velocities of the detected ionic products via conservation of momentum.98
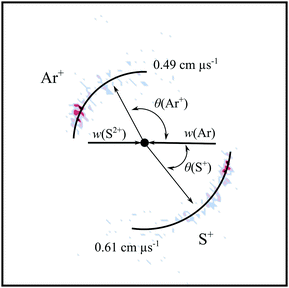
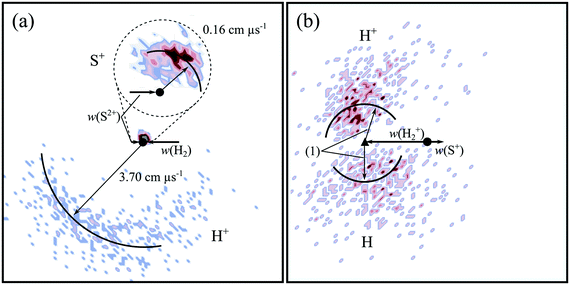
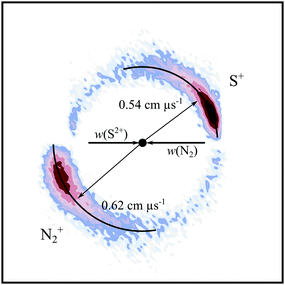
To reveal the dynamics of a given reaction channel, a CM scattering diagram (Fig. 1) can be generated from the velocities of the product ions. Such CM scattering diagrams are radial histograms that, for each event collected for a given reaction channel, plot the magnitude of the products’ CM velocity |wi| as the radial co-ordinate and the scattering angle θ between wi and the CM velocity of the incident dication as the angular coordinate. In the kinematics that apply in our experiment, where the dication has significantly more momentum than the neutrals, the velocity of the incident dication is closely oriented with the velocity of the centre of mass. In our CM scattering diagrams, since 0° ≤ θ ≤ 180°, the data for one product can be shown in the upper semi-circle of the figure and the data for another product in the lower semi-circle, as the scattering of each ion is azimuthally symmetric. The typical angular resolution of the scattering data achieved by the PSCO apparatus operating with a high source field is 4°.69 It should be noted that in our data treatment, to enable presentation in a two-dimensional figure on the page, we are integrating over the azimuthal angle (in which the scattering is cylindrically symmetric). That is, we are binning events according to their value of θ irrespective of the azimuthal scattering angle. This integration over the azimuthal angle results in an isotropic scattering distribution giving a sin(θ) intensity distribution in our scattering diagrams, giving our experimental arrangement a lower relative detection efficiency at values of θ very close to 0° or 180°. This phenomenon is ubiquitous where integration over the azimuthal angle occurs and is clearly visible in the scattering diagrams, where even strongly forward scattered reactions exhibit a peak in θ away from θ = 0.
In all the scattering diagrams presented in this work, a logarithmic scale is used for the scattering intensity. Such scales allow the diagrams to reveal subtleties of the low intensity scattering. However, we should be aware that such logarithmic scales can, at first glance, overemphasise the importance of the areas in the scattering diagrams with low intensities. In the ESI† (Fig. SI 1) we contrast scattering diagrams with linear and logarithmic intensity scales.
For three-body reactions, internal-frame scattering diagrams can be a powerful aid in interpreting the reaction dynamics. In this class of scattering diagram |wi| is again the radial coordinate, but the angular coordinate is now the CM scattering angle with respect to CM velocity of one of the other product species.
From the CM velocities of the product species the total kinetic energy release (KER) T for a given reactive event can also be determined using the individual CM velocities of the products.98 The exoergicity of the reaction ΔE can then be determined from T and the CM collision energy, Ecom:
| ΔE = T − Ecom = −(Eproducts − Ereactants) | (1) |
To interpret the experimental exoergicity spectra presented below we need to consider the electronic states of S2+ populated in our dication beam. Beams of S2+ ions generated by EI are not well characterised, but electronic state information is, of course, available for the S2+ dication from atomic spectroscopy.103,104 Experiments studying the electron ionization of H2S have previously reported the formation of S2+, but provide little information on the S2+ states populated.100,105,106 In our experiments, after the formation of S2+ from H2S via electron ionization in the source region, the S2+ dications must travel through the apparatus to the interaction region where they can collide with the appropriate neutral species. In the time taken to travel to the interaction region (∼100 μs), one would expect S2+ formed in higher lying excited states to radiatively decay to lower energy, metastable, states, where such a decay is ‘allowed’. Hence, it seems reasonable that the S2+ ions in our beam predominantly exist in one of the [Ne]3s23p2 states (3P, 1D or 1S) from the ground configuration. Such a deduction is in strong accord with experimental determination of the dication states populated when generating the analogous (p4) states of rare gas dications.107 Here, electronic states from the ground configuration dominate the dication beam, with the associated electronic states having populations approximately in accord with their degeneracy 9[3P]:5[1D]:1[1S].
Ground state S2+(3P) has an energy of 33.7 eV relative to a neutral S atom in its ground (1S) state. The excited 1D and 1S states lie 35.1 and 37.1 eV above the ground state of S respectively. S2+ also has some higher energy states which are potentially long-lived and could therefore also be present in our dication beam: the 5S state derived from the [Ne]3s13p3 configuration, which lies 41.0 eV above the ground state of S, and the 3F state, derived from the [Ne]3s23p13d1 configuration, lies 48.8 eV above the ground state of S. Emission lines attributed to decay from the 5S state of S2+ have been observed experimentally, including in the atmosphere Io.108–110 These investigations reveal the 5S state is metastable, with estimated lifetimes on the order of ∼100 μs, and therefore is possibly a minority species in our S2+ beam.111 The 3F state has a shorter lifetime than 5S, but could also be present in the dication beam.103,111 Given the above, and also noting that the cross section for formation of the various S2+ electronic states will increase with excess energy in this ionizing energy regime favouring the population of the p2 states, we expect our dication beam to be dominated by ions in the ground 3P state (60%) with the next most abundant state 1D (30%), with minor contribution (10%) from the 1S state. Small quantities of the excited 5S and 3F states may be present, but likely with a markedly lower abundance than the 1S state. We will see below that our experimental exoergicity spectra strongly support this deduced beam composition, with literature exoergicities associated with reactions of the 3P state accounting for the only observed reaction with Ar, the dominant reaction with H2 and 98% of the product flux with N2.
Results and discussion
The collisions of S2+ with Ar
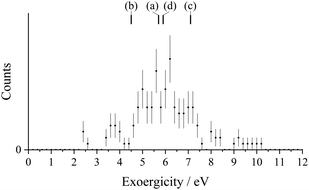
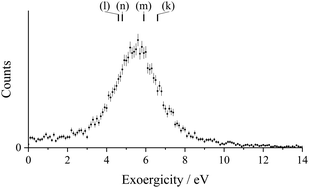
PSCO-MS spectra were recorded following the collisions of S2+ with Ar at Ecm = 5.3 eV. As with all reactions of S2+, there is no prior literature with which to compare our results. The only peak in the coincidence pairs spectrum, S+ + Ar+, results from single electron-transfer (SET). Fig. 1 shows the scattering of the S+ and Ar+ product ions from this SET reaction, revealing strong ‘forward’ scattering, where the velocity of the S+ product is oriented in the same direction as the velocity of the reactant dication, w(S2+). This forward scattering has been commonly observed for other dicationic SET processes and arises from a direct electron-transfer, where the electron is transferred at a significant interspecies separation (3–6 Å, the so-called reaction window). Such processes are typically well described, for a wide range of collision partners by a Landau–Zener (LZ) formalism.69,99,112,113 This LZ approach, and the general applicability of the concept of the reaction window, has been established by studies involving a wide range of different ions and targets.112,114Fig. 2 shows a histogram of the event exoergicities recorded in this SET channel. The bulk of the structure in this spectrum is between 4.8 eV and 7.2 eV. In order to interpret the experimental exoergicity distribution, we must consider the possible reactant and product electronic states involved. We discussed above the fact our beam is primarily composed of dications in the p2 configuration, and likely dominated by the ground S2+(3P) state. It should be noted that in dication-neutral reactions, in this energy regime, the collision energy (Ecm) generally does not couple efficiently to the potential energy surface.15,112 Therefore, Ecm does not usually need to be included when considering the energetics of these reactions. In the ESI,† we present in detail the accessible reactant and product states for this reaction and their associated literature exoergicities, a significant number of which lie in the reaction window (2–7 eV). However, given the arguments above, we see that pathways (a)–(d) of the 3P and 1D states of S2+ populating the ground state of Ar+ and the ground and first excited states of S+, correlate well with the experimental exoergicity distribution (Fig. 2). These dication states are expected to dominate our beam and the product states involved are readily accessible. Thus, pathways (a)–(d) contributing the bulk of the signals seems highly probable.
Pathways (a)–(d) are all spin allowed and their resulting literature exoergicities are marked in Fig. 2. The range of experimental exoergicities observed in this channel is typical for a LZ governed process (2–7 eV).112,114
| S2+(3P) + Ar(1S) → Ar+(2P) + S+(2D) ΔE = 5.7 eV | (a) |
| S2+(3P) + Ar(1S) → Ar+(2P) + S+(2P) ΔE = 4.5 eV | (b) |
| S2+(1D) + Ar(1S) → Ar+(2P) + S+(2D) ΔE = 7.1 eV | (c) |
| S2+(1D) + Ar(1S) → Ar+(2P) + S+(2P) ΔE = 5.9 eV | (d) |
In summary, the above analysis shows that reactions between S2+ and Ar are dominated by single electron-transfer with dynamics and energetics that conform well with the established models of dicationic electron transfer. The exoergicities observed support the arguments that our S2+ beam is primarily composed of ions from the ground (p2) configuration. Of course, small contributions from the higher excited states of S2+ may be present but would be swamped by the signals from the 3P and 1D states.
The collisions of S2+ with H2
PSCO-MS spectra were recorded following the collisions of S2+ and H2 at Ecm = 0.71 eV. Two reaction channels were observed in the coincidence pairs spectrum (Table 1). The dominant channel, Rxn I, is non-dissociative single electron-transfer (NDSET), producing S+ + H2+. A dissociative single electron-transfer (DSET) reaction is also observed (Rxn II), resulting in the formation of S+ + H+ + H. We note, in passing, that the pairs count rate for the S2+/H2 collision system was markedly lower than the experiments involving Ar or N2.| Reaction | Products | Relative intensity/% | Modal experimental ΔE/eV |
|---|---|---|---|
| I | S+ + H2+ | 61 | 5.6 |
| II | S+ + H+ + H | 39 | 12.0 |
There is no peak in the coincidence spectrum resulting from the transfer of two electrons from H2 to S2+, resulting in the formation of H+ + H+. Previous work has shown that in dication-neutral systems, facile double electron-transfer (DET) involves a concerted mechanism in which the reactant and product asymptotes have to lie close in energy (<1 eV).115 Whilst the recombination energy from S2+ gaining two electrons is enough (>31.7 eV) to form H+ + H+ sequentially from H2, the (vertical) double ionization potential of H2 is ∼51 eV, significantly higher in energy than is accessible from even the 3F state of S2+.103,116 Therefore, we would not expect the S2+ + H2 collisions in our experiment to result in DET via a concerted mechanism, in agreement with the experimental data. Hence, the absence of a DET channel in this collision system, despite the accessibility of a step-wise mechanism, adds to the increasing evidence that, in dication-neutral systems, DET reactions occur via a concerted two-electron transfer.115
We note that there is no peak in the coincidence spectrum corresponding to SH+ + H+, the products of a bond-forming reaction. SH+ is observed in star-forming regions117 and diffuse interstellar clouds where it is thought to be involved in ion-neutral chemistry resulting in the formation of a range of sulfur containing species.118 The formation of SH+ + H+ from S2+ + H2 is exothermic by ∼9 eV, therefore we might expect to observe SH+ + H+ in our experiment,103,119,120 especially considering the ubiquity of the S–H bond in biological systems, and the propensity of dication + H2 reactions to result in bond-formation.17,82–89 The fact we do not observe the formation of SH+ + H+ could be because in order to transition to the SH+ + H+ asymptote, the S2+ + H2 system has to traverse a region of the potential energy surface with ready access to SET channels. Indeed, the model developed by Herman et al.,86 to explain the competition between SET and bond-forming reactivity in dication-neutral collision systems, shows that the presence of favourable curve crossings that result in SET reduce the probability of bond-forming reactions occurring. The fact we do not observe SH+ following the collisions of S2+ with H2 suggests that this route is unlikely to contribute to the formation of SH+ observed in astrophysical environments.
Non-dissociative single electron-transfer (NDSET)
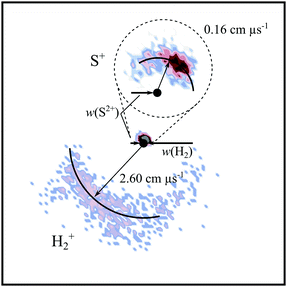
The most intense product channel we observe following collisions between S2+ and H2 is NDSET, forming S+ and H2+. Fig. 3 shows the CM scattering of the S+ and H2+ products in this NDSET channel. It should be noted that because the H2+ is significantly lighter than the S+ fragment, it carries away a large part of the energy release, and the low S+ velocity leads to increased uncertainty in the scattering angles and velocity of the S+ product. Fig. 3 shows that the velocity of the S+ product ion is broadly oriented with the velocity of the incident dication, w(S2+). Conversely, the scattering of the H2+ product ion is broadly oriented with w(H2), anti-parallel to w(S2+). This form of scattering was also noted in the S2+ + Ar SET reaction, and, as mentioned in the discussion of that channel, such kinematics are consistent with direct electron-transfer occurring at a significant interspecies separation (3–6 Å). Such scattering patterns are commonly observed for other NDSET processes and are generally well represented by a LZ formalism.69,99,112,113The experimental exoergicity distribution of this NDSET channel, shown in Fig. 4, is centred at ∼6.7 eV, with a full width at half maximum (FWHM) from 4.8–8.6 eV. To rationalise the experimental exoergicity spectrum in this NDSET reaction we must again consider the possible electronic states of the reactant and product species. For this collision system, energetic data are readily available. Given the evidence from the S2+ + Ar reaction, and the arguments presented in the experimental section, we would expect the reactions to involve S2+ in the 3s2 3p2 states.103 The H2, emitted as an effusive beam, will be in its ground vibronic state, X1Σg+v = 0. The ground state of H2+ (X2Σg+) lies ∼15.4 eV in energy above H2(X1Σg+).121–123 The lowest energy dissociation asymptote of H2+, the energy at which H2+ can dissociate and form H+ + H, is at ∼18.1 eV.124,125 If H2+ is formed with energy above this dissociation asymptote it is expected to dissociate within the timescale of our experiment.121 Therefore, H2+ formed above 18.1 eV would not contribute to the H2+ counts in this NDSET channel. Photoelectron spectra show that formation of H2+(X2Σg+) from the neutral moelcule involves populating vibrational states up to the dissociation asymptote at ∼18.1 eV.126,127 There are also metastable electronic excited states of H2+ to consider; however experimental data here are limited.128 For example, there are three bound vibrational levels of H2+(A2Σu+), lying at ∼18 eV above the ground state of neutral H2, just below the H+ + H dissociation asymptote. However, the large equilibrium internuclear separation means that H2+(A2Σu+) is not directly accessible from the H2 ground state.129,130 There are also the B and C states of H2+, with energies of ∼27.1 eV and ∼28.2 eV above H2.103 These excited states of H2+ are not well characterised, as they cannot be accessed by traditional PES. However, any involvement of these excited electronic states of H2+ would require a two-electron transition from H2(X1Σg+) and, in dication + neutral collision systems, ET processes involving the movement of two electrons are seen to be significantly less favoured.131 Therefore, the involvement of excited electronic H2+ states in this channel is unlikely.
From energetic considerations, we see that there are many possible reaction pathways that result in literature exoergicities that fall within the range of the observed experimental exoergicities. The reactant dication, S2+, could be in any of the S2+ 3s2 3p2 electronic states (3P, 1D and 1S). The H2+ product ion can be formed in ground state, X2Σg+, with a wide range of vibrational excitation: with an energy of anywhere from 15.4 eV (X2Σg+v = 0) to the dissociation limit at ∼18.1 eV relative to H2(X1Σg+). The S+ product ion can be formed in its three lowest energy states: 4S, 2D and 2P.
Previous studies have shown that the vibrational state distribution of product molecular monocations, formed in dication-neutral SET reactions, are dominated by vertical (Frank–Condon style) transitions from the relevant reactant (dication or neutral molecule).93 Photoelectron spectra of H2 show that H2+ is primarily populated from H2 with an energy of <∼17.5 eV with respect to the neutral ground state, and it is likely that the H2+ formed from H2 in this NDSET channel will also be formed in this energy range.121,122,126,127 Given this H2+ energy range, and the likely dominance of S2+(3P) states in the beam, we propose that pathways (e) and (f) involving the 3P state are primarily involved in this NDSET channel. The listed literature exoergicities for these pathways assume the population of H2+(2Σg+) v = 0. However, as noted above, it is likely that a spread of H2+ vibrational states will be formed. The population of excited vibrational levels of H2+ will, of course, spread the observed experimental exoergicity to lower values. The literature exoergicities resulting from pathways (e) and (f) are marked on Fig. 4, with arrows showing the energy spread due to the potential vibrational excitation of H2+, and provide a good match to the observed experimental exoergicity distribution (Fig. 4). Of course, analogous channels associated with the other states (1D,1S) from the 3p2 configuration of S2+, which we expect to be minor components in the S2+ beam are also likely to contribute here. Indeed, analogous channels to (e) and (f) for these S2+ excited states nicely account for the lower intensity signals up to 11.3 eV in the experimental exoergicity spectrum. However, as for the reaction with Ar, we can easily account for the bulk of the observed exoergicities in terms of the S2+ states we argue dominate the dication beam populating readily accessible states of the product ions.
| S2+(3P) + H2(X1Σg+) → H2+(2Σg+) + S+(4S) ΔE = 7.9 eV | (e) |
| S2+(3P) + H2(X1Σg+) → H2+(2Σg+) + S+(2D) ΔE = 6.1 eV | (f) |
Dissociative single electron-transfer (DSET)
The dynamics we extract from each pair of ions making up the S+ + H+ peak in the coincidence spectrum reveal that the reaction proceeds via DSET. The established mechanism for dication + neutral DSET reactions is that an initial LZ style electron-transfer generates one (or both) of the product monocations in a dissociative state.15 The nascent dissociative states subsequently fragment to yield the observed products. Fig. 5a shows the CM scattering diagram for the S+ and H+ products from this DSET channel. As with the NDSET channel discussed above, it should be noted that the relatively low S+ velocity leads to increased uncertainty in the scattering angles of the S+. The S+ is broadly forward scattered but with a tail towards higher angles when compared with the NDSET reaction (Fig. 3), scattering mirrored in the H+ signals. This scattering pattern is indicative of a longer-lived association between the reactant species than in the standard NDSET process: a [SH2]2+ collision complex. Therefore, this DSET reaction appears not to follow the standard model of dication + neutral electron-transfer where an initial LZ style (long-distance) electron-transfer populates one of the products in a dissociative electronic state.95,132,133 As discussed, such an LZ style electron-transfer reaction should lead to a more prominent forward scattering pattern than is observed here. Indeed, although not common, SET involving complexation has been observed before in dication/neutral reactions.90,95,132,133 Electron ionization experiments studying H2S show evidence for H2S2+ states that are energetically accessible to the S2+ + H2 reactants in this system, and that dissociate to form S+ + H2+.100 These H2S2+ states could be involved as a short-lived intermediates in this DSET channel.
Fig. 5b shows the scattering of the H+ and H fragments relative to the velocity of the S+ product ion. We refer the reader back to Section 3 for information on the construction of these internal frame scattering diagrams. The H+ and H fragments are both clearly backward scattered, away from the S+ ion and their scattering is distributed about a clear 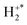 precursor velocity which is indicated in Fig. 5b. This scattering motif, which has been observed before for many DSET reactions,112,114,115,134 clearly shows the [SH2]2+ complex dissociates into S+ +
precursor velocity which is indicated in Fig. 5b. This scattering motif, which has been observed before for many DSET reactions,112,114,115,134 clearly shows the [SH2]2+ complex dissociates into S+ + 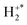 before the fragmentation of
before the fragmentation of 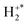 . The H+ fragment ion distribution is slightly more energetically backward scattered than that of the H fragment, likely because the
. The H+ fragment ion distribution is slightly more energetically backward scattered than that of the H fragment, likely because the 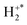 ion fragments within the electric field of the S+ ion, resulting in the H+ experiencing an additional acceleration.
ion fragments within the electric field of the S+ ion, resulting in the H+ experiencing an additional acceleration.
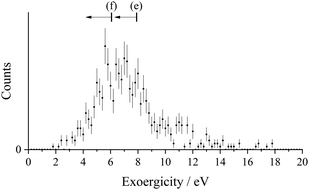
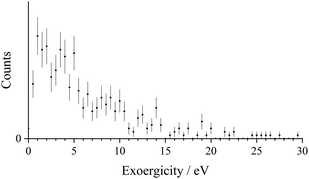
The experimental exoergicity observed from this DSET channel is shown in Fig. 6. The experimental exoergicity distribution has a broad maximum, centred at ∼10 eV, with a FWHM from 6.5–15.5 eV. In order to give the exoergicities observed in this channel, the S2+ dication must be in an electronically excited state, thus the dominant species we expect in the dication beam S2+(3P) cannot contribute and the experimental exoergicity spectrum reveals the excited S2+ states in the beam. Even the coupling of the collision energy (0.71 eV) into the energetics does not allow reactions of S2+(3P) to generate the observed exoergicities. Representative reactions of the relevant S2+ excited states (g)–(j) which fit the observed experimental exoergicity distribution are given below. Variations on these processes are also compatible with the exoergicity data (Fig. 6) involving, for example, the formation of excited states of S+. The literature exoergicities resulting from pathways (g)–(j) are marked on the experimental exoergicity spectrum in Fig. 6. There is an exoergic channel for the 1D state (Fig. 6, (g)), but the maximum exoergicity possible for the highest energy state of the p2 configuration (1S) is 8.6 eV (marked by (h) in Fig. 6) and there are clearly events with experimental exoergicities markedly above this value; such exoergicities can only be generated by electronic states of S2+ from excited configurations. That is, the demanding energetics allow the contribution of these minor beam components to be distinguished from that of the p2 configuration. Above we considered a minor beam component as comprising the metastable 5S and 3F states. Reaction of S2+(5S) can give exoergicities up to ∼12.5 eV, and the involvement of 3F can give exoergicities of up to ∼20.4 eV. These exoergicities nicely encompass the higher end of the observed experimental exoergicity distribution (Fig. 6, (i)–(j)) and indeed the reaction of the 3F state correlates nicely with a weak high exoergicity feature in the spectrum (Fig. 6, (j)).
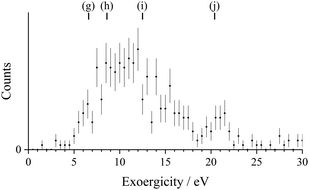 | ||
| Fig. 6 Experimental exoergicity spectrum for the reaction S2+ + H2 → S+ + H+ + H. The error bars represent two standard deviations of the associated counts. | ||
Despite the assignments of the product states not being definitive, it is clear that the DSET reaction with H2 involves the excited states of S2+ we predicted to be present in the dication beam. The contribution of these excited states dominates the product flux in this reaction channel as the demanding energetics mean the dominant dication state in the ion beam, the 3P ground state of S2+, cannot contribute. Given our deductions concerning the dominance of the 3P state in the beam, the involvement of excited S2+ in this channel explains the low signal rate noted above.
| S2+(1D) + H2(X1Σg+) → S+(4S) + H(2S) + H+ ΔE = 6.6 eV | (g) |
| S2+(1S) + H2(X1Σg+) → S+(4S) + H(2S) + H+ ΔE = 8.6 eV | (h) |
| S2+(5S) + H2(X1Σg+) → S+(4S) + H(2S) + H+ ΔE = 12.5 eV | (i) |
| S2+(3F) + H2(X1−Σg+) → S+(4S) + H(2S) + H+ ΔE = 20.4 eV | (j) |
Applying a powerful approach we have used in previous work to study the energetics of DSET reactions we can, on an event-by-event basis, determine the velocity of the precursor 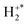 ion from the measured velocity of the S+ ion using conservation of momentum. The S+ and
ion from the measured velocity of the S+ ion using conservation of momentum. The S+ and 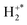 velocities then allow us to construct an exoergicity spectrum for the initial electron transfer step to reveal the electronic states involved. Subsequently, again on an event by event basis we can examine the velocities of the H and H+ products in the frame of the
velocities then allow us to construct an exoergicity spectrum for the initial electron transfer step to reveal the electronic states involved. Subsequently, again on an event by event basis we can examine the velocities of the H and H+ products in the frame of the 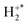 precursor velocity to derive a spectrum representing the energies involved in the dissociation of the
precursor velocity to derive a spectrum representing the energies involved in the dissociation of the 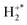 ion. This analysis assumes the formation of S+ +
ion. This analysis assumes the formation of S+ + 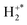 can be treated as a two-body reaction, dynamically distinct from the subsequent dissociation of the
can be treated as a two-body reaction, dynamically distinct from the subsequent dissociation of the 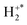 . Given the observed scattering dynamics (Fig. 5b) this is clearly a good, but not perfect approximation. Applying this approach yields the experimental exoergicity distribution for dissociation of
. Given the observed scattering dynamics (Fig. 5b) this is clearly a good, but not perfect approximation. Applying this approach yields the experimental exoergicity distribution for dissociation of 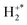 to H+ + H shown in Fig. 7.
to H+ + H shown in Fig. 7.
In 1986, Cordaro et al.125 studied the dissociation of H2+generated by electron ionization, observing experimental exoergicities from 2–8 eV. Strathdee and Browning135 observed similar kinetic energy releases, ranging from 4–10 eV, using 26.9 eV photoionization. In their study of H2 electron ionization, Köllmann136 reported H+ kinetic energy distributions that correspond to kinetic energy releases ranging from 0–24 eV resulting from H2+ dissociation. The electronic states attributed to these kinetic energy releases were the high vibrational states of H2+(X2Σg+) and H2+(A2Σu+). Other experiments studying photo- and electron-ionization of H2 also resulted in the observation of kinetic energy releases from H2+ dissociation of up to ∼20 eV.137–139 The bulk of the experimental exoergicity distribution resulting from H2+ dissociation observed in our experiment (Fig. 7) matches well with Cordaro et al.125 and Strathdee and Browning,135 and the shoulder towards higher experimental exoergicities is in agreement with the distributions observed by Köllmann and others.136–139 The agreement between the exoergicity release resulting from H2+ dissociation observed in our experiment and those previously reported confirms that the mechanism responsible for the formation of S+ + H+ in this channel is DSET via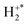 .
.
As mentioned, if H2+ is formed at energies over ∼18.1 eV above the ground state of the neutral H2 molecule, it will dissociate.124,125 Our analysis of the experimental exoergicity (Fig. 6) above suggests that only the lowest energy H state (2S) is formed in this dissociation. To yield experimental exoergicities in the range observed in Figure 7, H2+ therefore needs to be primarily formed with energies between 19–24 eV relative to H2(X1Σg+). Thus, the H2+ ion could be populated in the A2Σu+ state. As noted above, the geometry of the A2Σu+ state in the 19–24 eV energy range is significantly different to the neutral molecule and would therefore not be expected to be efficiently formed in a vertical ionizing transition. Moreover, the formation of H2+(A2Σu+) from H2(X1Σg+) is a two-electron transition, which, as discussed above, is thought to be significantly less likely than a one-electron process.131 However, both forming the H2+ ion with a markedly different geometry to the neutral species, and the movement of two electrons are more feasible if the reaction proceeds via a collision complex, as suggested by the scattering we observe. Alternatively, H2+ could be formed in the continuum of the X2Σg+ state, above the 18.1 eV dissociation asymptote. The involement of either the H2+(A2Σu+) or H2+(X2Σg+) states is in good agreement with the H2+ dissociation studies discussed above.125,136
As discussed above, the exoergicity of the initial electron-transfer step of this DSET reaction can also be evaluated using the precursor velocity of the H2+ ion and w(S+). Using this method, an estimate of the experimental exoergicity distribution for the initial electron-transfer step (S2+ + H2 → S+ + 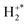 ) was determined and is shown in Fig. 8. The experimental exoergicity distribution has a broad peak centred at ∼7 eV with a FWHM from 1–12 eV. The observed experimental exoergicity distribution exceeds the typical range for LZ style processes (2–7 eV),112,114 providing further indirect evidence that this DSET reaction proceeds via a collision complex, as suggested by the scattering.
) was determined and is shown in Fig. 8. The experimental exoergicity distribution has a broad peak centred at ∼7 eV with a FWHM from 1–12 eV. The observed experimental exoergicity distribution exceeds the typical range for LZ style processes (2–7 eV),112,114 providing further indirect evidence that this DSET reaction proceeds via a collision complex, as suggested by the scattering.
The experimental exoergicity distribution determined for the initial electron-transfer step (Fig. 8) aligns satisfyingly with the literature exoergicities expected from our above assessment of the likely electronic states involved in this channel. These include the excited states of S2+ (1D, 1S, 5S and 3F), the lowest three energy states of S+ (4S, 2D and 2P), and H2+(A2Σu+) or the continuum of the H2+(X2Σg+) state. The possible involvement of this large number of states, and the range of vibrational excitation available for H2+, results in too many accessible pathways to determine which specific states are involved.
In summary, DSET occurs following the collisions of S2+ + H2, resulting in the formation of S+ + H+ (+ H). This channel involves S2+ in its electronically excited states derived from the 3s23p2 electron configuration (1D, 1S) and also shows evidence for the presence of higher energy S2+ states in the beam: 5S and 3F, resulting from the 3s13p3 and 3s23p13d1 configurations respectively. This DSET channel involves the formation of S+ primarily in its lowest electronic state (4S), with contributions from the first two excited states, 2D and 2P. The nascent H2+ ion is generated at initial energies of between 19 eV and 24 eV relative to H2(X1Σg+) before dissociating to the lowest energy asymptote: H+ + H(2S).
The collisions of S2+ + N2
PSCO-MS spectra were recorded following the collisions of S2+ and N2 at Ecm = 4.7 eV. In the coincidence pairs spectrum three reaction channels which produce pairs of product ions were observed, and are shown in Table 2. The dominant channel, Rxn III, is NDSET, producing S+ + N2+. A DSET reaction (Rxn IV), results in the formation of S+ + N+ + N. Finally, a bond-forming channel (Rxn V), producing SN+ + N+, is detected.Whilst the PSCO-MS apparatus is optimised for the detection of pairs of ions, we also record a simple mass spectrum of single ion arrivals. We do not detect any structures present in this mass spectrum ions in the m/z = 23 region that could be indicative of SN2+ or the m/z = 30 region that could be indicative of SN22+. However, we note that the sensitivity of our experiment is optimised for detecting ion pairs involving energetic monocations, not product dications.
It is notable that there is no peak in the coincidence spectrum corresponding to N+ + N+, the products of a dissociative DET reaction. However, the absence of a DET reaction is not surprising as the polarisability of S (2.9 × 10−24 cm3) is greater than N2 (1.7403 × 10−24 cm3).140 In this situation, under the concerted model of DET,115,133 we would not expect the S2+ + N2 and S + N22+ curves to cross even if the S2+ + N2 → S + N22+ reaction was exothermic; this situation has been shown before to strongly disfavour DET. Added to this, DET between S2+ and N2 would be endothermic for S2+ states with energies below S2+(3F), the states that we have deduced make up the bulk of our S2+ beam.
Non-dissociative single electron-transfer (NDSET)
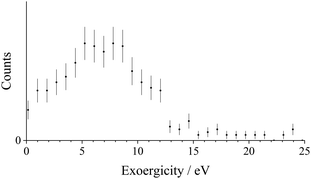
Fig. 9 shows the CM scattering diagram for the S+ + N2+ product ions of the NDSET reaction, S2+ + N2 → S+ + N2+. A strong forward scattering pattern is observed, where the S+ is oriented in the same direction as w(S2+), whilst the N2+ product is oriented in the same direction as w(N2). Note the peaking of the signals in Fig. 9 slightly away from θ = 0° and 180° as discussed in the experimental section. This scattering pattern is typical of a direct electron-transfer process, occurring at a relatively large interspecies separation (3–6 Å) as discussed above. These electron-transfer dynamics are well represented by a Landau–Zener formalism.69,99,112,113Fig. 10 shows a histogram for the experimental exoergicities recorded in this NDSET reaction channel. The spectrum shows a structure with a maximum at 5.6 eV, and a FWHM from 4.3–6.9 eV. The observed experimental exoergicities are typical for such a LZ style SET reaction.112,114 As discussed above, we have good evidence that the dication beam is primarily comprised of S2+ in the 3s23p2 configuration, dominated by the 3P state. The N2 reactant will be in its ground vibronic state, X1Σg+v = 0. The ground state of N2+, X2Σg+, has an energy of 15.58 eV relative to N2(X1Σg+).141,142 If N2+ is formed with energies above ∼24.3 eV relative to N2(X1Σg+) (corresponding to N2+(C2Σu+v = 3)), it will be unstable to dissociation to the N+(3P) + N(4S) asymptote.103,143 Photoionization studies have shown that N2+ states generated with more than 24.3 eV, relative to N2(X1Σg+), have dissociation lifetimes less than the timescale of our experiment. Therefore, we do not expect any contribution to the N2+ counts observed in this channel from N2+ states formed with more than 24.3 eV of energy with respect to N2.143–146 Electron-transfer occurring between N2 and any of the 3P, 1D and 1S electronic states of S2+ can result in the formation of S+ in any of the states from the ground state (4S) up to the 4F state, derived from the [Ne] 3s2 3p2 3d1 configuration.
Considering the above constraints, we find that there are many possible electronic pathways that could be involved in the formation of S+ + N2+. However, as discussed above we expect the major component of our S2+ beam to be ions in the 3P state. Possible pathways involving the 3P state are shown by (k)–(n), and their resulting literature exoergicities are shown on Fig. 10. These channels show N2+ is likely formed in one of the stable X2Σg+, A2Πu or B2Σu+ states, which reassuringly are those which dominate photoelectron spectra,141 and the S+ products are primarily the lowest two electronic states: 4S and 2D. Although these contributions from the dication 3P state (pathways (k)–(n)) can account for the signals we observe, especially when varying degrees of vibrational excitation of the product N2+ ion is considered which will broaden the observed exoergicities, excited S2+ states could also be contributing to the product flux in this NDSET channel. However, given energetically favourable channels for the reaction of the 3P state, which lie in the reaction window, and the expected dominance of this state in the ion beam, we feel confident that pathways (k)–(n) account for the bulk of the events we detect in this reactive channel.
| S2+(3P) + N2(X1Σg+) → S+(4S) + N2+(A2Πu) ΔE = 6.6 eV | (k) |
| S2+(3P) + N2(X1Σg+) → S+(4S) + N2+(B2Σu+) ΔE = 4.6 eV | (l) |
| S2+(3P) + N2(X1Σg+) → S+(2D) + N2+(X2Σg+) ΔE = 5.9 eV | (m) |
| S2+(3P) + N2(X1Σg+) → S+(2D) + N2+(A2Πu) ΔE = 4.8 eV | (n) |
Dissociative single electron-transfer (DSET)
The peak in the coincidence pairs spectrum corresponding to the detection of ions with m/z = 32 and m/z = 14 is due to the formation of S+ and N+. The peak is weak, so it is only possible to probe the dynamics and exoergicities in an indicative manner. In order to discriminate against some of the stray counts arising from background noise, which become problematic in this channel due to the low number of counts, any events that gave unrealistic experimental exoergicities were removed before the analysis.
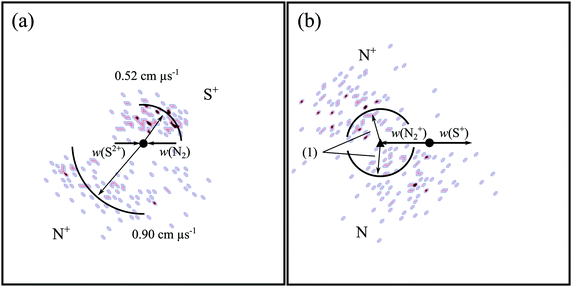
Fig. 11a shows the CM scattering diagram for the S+ and N+ products resulting from this channel. The S+ ions are broadly forward scattered, however, there is scattering to higher angles. Conversely, the N+ ions are broadly backscattered, with some ions scattered towards lower angles. One might expect a higher propensity of forward scattering if this channel resulted from a direct, LZ style electron-transfer. The presence of scattering to higher angles could be evidence of the involvement of a collision complex, however, due to the low intensity signal in this channel, it is difficult to be conclusive. Fig. 11b shows the internal frame scattering of the N+ and N products relative to the S+ product ion. The N+ and N ions are scattered around the expected precursor velocity of an 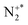 intermediate, confirming the mechanism of this channel as DSET. SET occurs, producing
intermediate, confirming the mechanism of this channel as DSET. SET occurs, producing 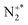 in a dissociative state (and S+), which then dissociates to form N+ + N. In Fig. 11b the N+ is scattered away from the S+ with a higher velocity than the N fragment. This asymmetric scattering of the N+ and N fragments is because the
in a dissociative state (and S+), which then dissociates to form N+ + N. In Fig. 11b the N+ is scattered away from the S+ with a higher velocity than the N fragment. This asymmetric scattering of the N+ and N fragments is because the  species dissociates within the electric field of the S+ ion, and Coulomb repulsion then accelerates only the N+ species. Such behaviour has been noted before for DSET channels in other dicationic collision systems.90,115,133
species dissociates within the electric field of the S+ ion, and Coulomb repulsion then accelerates only the N+ species. Such behaviour has been noted before for DSET channels in other dicationic collision systems.90,115,133
The experimental exoergicity distribution resulting from this DSET channel reveals a broad structure between 0.5 eV and 11.0 eV. Note that due to the low intensity, the energy resolution is low, and hence any conclusions we draw from this data must be tentative. It is not common to see energy releases of less than 2 eV for reactions involving LZ style ET, however, as discussed above, the scattering hints that a more complicated reaction mechanism is involved. The formation of N+ + S+ + N resulting from the ground state of S2+(3P) is endothermic, therefore the occurrence of this channel again confirms the existence of electronically excited states of S2+ in the dication beam. Indeed, the exclusive involvement of higher energy S2+ states undoubtedly accounts for the low intensity of this DSET channel. The involvement of S2+(1S) can result in exoergicities in this DSET channel of up to 2.4 eV, significantly lower than the bulk of the observed experimental exoergicity distribution. However, the involvement of the 5S and 3F states of S2+ allows events with exoergicities of up to 6.3 eV and 14.1 eV respectively. Given the high experimental exoergicities observed in this DSET channel, the S+, N+ and N fragments are likely all formed in their ground or lower energy excited electronic states.
The experimental exoergicity of the  dissociation, calculated from the N2+ precursor velocity, has structure from 0.3–4.0 eV. This range of experimental exoergicities is comparable to those observed from N2+ dissociation in the DSET channel in our previous investigation of Ar2+ + N2 collisions.90 As mentioned above, N2+ states generated with more than 24.3 eV above N2(X1Σg+) are unstable to dissociation and will dissociate within the lifetime of our experiment. Considering the experimental exoergicity of the complete reaction and the N2+ dissociation exoergicity, N2+ is likely formed with energies of 25–29 eV above N2(X1Σg+) and primarily dissociates to the lowest energy N+ + N asymptote, with both N+ and N in their ground electronic states.
dissociation, calculated from the N2+ precursor velocity, has structure from 0.3–4.0 eV. This range of experimental exoergicities is comparable to those observed from N2+ dissociation in the DSET channel in our previous investigation of Ar2+ + N2 collisions.90 As mentioned above, N2+ states generated with more than 24.3 eV above N2(X1Σg+) are unstable to dissociation and will dissociate within the lifetime of our experiment. Considering the experimental exoergicity of the complete reaction and the N2+ dissociation exoergicity, N2+ is likely formed with energies of 25–29 eV above N2(X1Σg+) and primarily dissociates to the lowest energy N+ + N asymptote, with both N+ and N in their ground electronic states.
Chemical bond-formation
The peak in the pairs spectrum corresponding to the ions m/z = 46 and m/z = 14 is due to the detection of SN+ and N+: a bond-forming reaction (Rxn V). The SN+ molecular ion is relevant to a range of astrophysical environments, including in comets and nebulae.147–151 SN+ is also important terrestrially, in man-made plasmas.152Fig. 12 shows the CM scattering for the SN+ and N+ product ions in this channel, revealing an isotropic scattering pattern. Such scattering is strong evidence for the involvement of an intermediate, long-lived, collision complex, [SN2]2+. The collision complex exists for at least several rotations, before fragmenting into SN+ and N+, as shown in (o).
| S2+ + N2 → [SN2]2+ → SN+ + N+ | (o) |
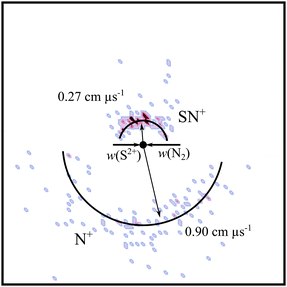 | ||
| Fig. 12 CM scattering diagram for the reaction S2+ + N2 → SN+ + N+ at a CM collision energy of 4.7 eV. The black dot indicates the position of the CM. See text for details. | ||
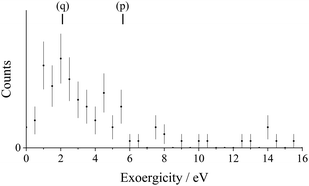
The experimental exoergicity of Rxn V, determined from the product ion velocities, is shown in Fig. 13. The experimental exoergicity distribution has a maximum at 2.0 eV with a FWHM from 0.5–4.5 eV. In order to rationalise the observed experimental exoergicities, we must again consider the possible electronic states of the reactant and product species. Due to its astrophysical relevance, the SN+ species has been the subject of experimental study,150,153,154 and several theoretical investigations have probed the electronic states of SN+.151,155–157 In this work we use the electronic state structure calculated by Ben Yaghlane & Hochlaf (2009),151 as it provides the most comprehensive data. The SN+ ground state (X1Σ+) lies ∼6.3 eV below the lowest energy dissociation asymptote of S+(4S) + N(4S), and ∼8.3 eV below the second lowest energy dissociation asymptote of S+(2D) + N(4S). There are also many other bound SN+ electronic states lying below these dissociation asymptotes, several with well depths sufficient to sustain vibrational excitation. Again, we assume that the dication beam is primarily comprised of the ground configuration, dominated by the 3P state, and N2 is in its ground vibronic state (1Σg+). These energetics mean that N+ can therefore be formed in any of its four lowest energy electronic states.
Considering the above, there are a large number of pathways that match the observed experimental exoergicity distribution of this bond-forming channel. Two likely pathways which match well with the exoergicity spectrum and involve the ground state of S2+, the dominant ion in our beam, are shown by (p) and (q):
| S2+(3P) + N2(1Σg+) → SN+(X1Σ+) + N+(3P) ΔE = 5.6 eV | (p) |
| S2+(3P) + N2(1Σg+) → SN+(13Σ+) + N+(3P) ΔE = 2.1 eV | (q) |
The 1D and 1S states of S2+ could also be involved, as well as the first three excited states of N+ (1D, 1S and 5S). Moreover, it is possible that a number of the electronic states of SN+ that are stable to dissociation could be populated in this channel.
To summarise, this channel involves a chemical bond-forming reaction between S2+ + N2, producing SN+ + N+. An isotropic scattering pattern is observed, clearly showing the involvement of a collision complex, [SN2]2+, typical for a dicationic bond-forming reaction. The observed experimental exoergicity distribution is in good agreement with the population of known electronic states of SN+,151 and the involvement of the S2+ states that we know dominate our S2+ beam.
Conclusions
In this work we have studied the gas-phase reactivity of S2+ with Ar, N2 and H2. This, to our knowledge, is the first study of the bimolecular reactivity of S2+. The experiments indicate that the dication beam is composed predominantly of S2+ ions resulting from the 3s23p2 ground electronic configuration. Most of the observed reaction channels can be accounted for by the involvement of S2+ in its ground state, 3P. However, the dissociative electron transfer reactivity reveals the involvement of higher energy S2+ states.The SET reaction between S2+ and Ar displays dynamics and energetics typical of a Landau–Zener style electron transfer reaction. In the reactions between S2+ + H2, NDSET and DSET were observed. The dynamics here show evidence for the formation of a long-lived association between the reactants, a collision complex [SH2]2+. Perhaps surprisingly, the formation of SH+, the potential product of a chemical bond-forming channel, was not observed. The reactions of S2+ + H2 are especially relevant as S2+ has been observed in the outer atmosphere of Jupiter, where H2 is the dominant chemical species. The collisions of S2+ + N2 result in both dissociative and non-dissociative SET reactions as well as a bond-forming channel, the latter resulting in the formation of SN+ + N+. This bond-forming reaction proceeds via a collision complex.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support of the EPSRC (EP/J010839/1), the Leverhulme Trust (RPG-2017-309), the Royal Society of Chemistry (E21-4679591105) and UCL.References
- C. Simon, J. Lilensten, O. Dutuit, R. Thissen, O. Witasse, C. Alcaraz and H. Soldi-Lose, Ann. Geophys., 2005, 23, 781–797 CrossRef CAS.
- H. S. Bridge, J. W. Belcher, A. J. Lazarus, J. D. Sullivan, R. L. McNutt, F. Bagenal, J. D. Scudder, E. C. Sittler, G. L. Siscoe, V. M. Vasyliunas, C. K. Goertz and C. M. Yeates, Science, 1979, 204, 987–991 CrossRef CAS PubMed.
- S. Ghosh, K. K. Mahajan, J. M. Grebowsky and N. Nath, J. Geophys. Res., 1995, 100, 23983–23991 CrossRef CAS.
- J. H. Hoffman, C. Y. Johnson, J. C. Holmes and J. M. Young, J. Geophys. Res., 1969, 74, 6281–6290 CrossRef CAS.
- E. Dubinin, R. Modolo, M. Fraenz, J. Woch, G. Chanteur, F. Duru, F. Akalin, D. Gurnett, R. Lundin, S. Barabash, J. D. Winningham, R. Frahm, J. J. Plaut and G. Picardi, J. Geophys. Res.: Space Phys., 2008, 113, A10217 CrossRef.
- J. Lilensten, O. Witasse, C. Simon, H. Soldi-Lose, O. Dutuit, R. Thissen and C. Alcaraz, Geophys. Res. Lett., 2005, 32, L03203 CrossRef.
- J. Lilensten, C. Simon, O. Witasse, O. Dutuit, R. Thissen and C. Alcaraz, Icarus, 2005, 174, 285–288 CrossRef CAS.
- O. Witasse, O. Dutuit, J. Lilensten, R. Thissen, J. Zabka, C. Alcaraz, P.-L. Blelly, S. W. Bougher, S. Engel, L. H. Andersen and K. Seiersen, Geophys. Res. Lett., 2002, 29, 104 CrossRef.
- B. J. Wilkes, G. J. Ferland, D. Hanes and J. W. Truran, Mon. Not. R. Astron. Soc., 1981, 197, 1–6 CrossRef CAS.
- D. K. Böhme, Phys. Chem. Chem. Phys., 2011, 13, 18253–18263 RSC.
- J. P. Simpson, R. H. Rubin, E. F. Erickson and M. R. Haas, Astrophys. J., 1986, 311, 895–908 CrossRef CAS.
- R. S. Houk, Anal. Chem., 1980, 52, 2283–2289 CrossRef CAS.
- A. Bogaerts and R. Gijbels, J. Appl. Phys., 1999, 86, 4124–4133 CrossRef CAS.
- J. S. Becker, G. Seifert, A. I. Saprykin and H.-J. Dietze, J. Anal. At. Spectrom., 1996, 11, 643–648 RSC.
- S. D. Price, J. D. Fletcher, F. E. Gossan and M. A. Parkes, Int. Rev. Phys. Chem., 2017, 36, 145–183 Search PubMed.
- D. Ascenzi, J. Aysina, E. L. Zins, D. Schröder, J. Žabka, C. Alcaraz, S. D. Price and J. Roithová, Phys. Chem. Chem. Phys., 2011, 13, 18330–18338 RSC.
- J. Roithová, H. Schwarz and D. Schröder, Chem. – Eur. J., 2009, 15, 9995–9999 CrossRef.
- W. Wolff, H. Luna, R. Schuch, N. D. Cariatore, S. Otranto, F. Turco, D. Fregenal, G. Bernardi and S. Suárez, Phys. Rev. A, 2016, 94, 022712 CrossRef.
- P. Bhatt, T. Sairam, A. Kumar, H. Kumar and C. P. Safvan, Phys. Rev. A, 2017, 96, 022710 CrossRef.
- R. Plašil, S. Rednyk, A. Kovalenko, T. D. Tran, Š. Roučka, P. Dohnal, O. Novotný and J. Glosík, Astrophys. J., 2021, 910, 155 CrossRef.
- R. Thissen, O. Witasse, O. Dutuit, C. S. Wedlund, G. Gronoff and J. Lilensten, Phys. Chem. Chem. Phys., 2011, 13, 18264–18287 RSC.
- O. Dutuit, N. Carrasco, R. Thissen, V. Vuitton, C. Alcaraz, P. Pernot, N. Balucani, P. Casavecchia, A. Canosa, S. Le Picard, J.-C. Loison, Z. Herman, J. Zabka, D. Ascenzi, P. Tosi, P. Franceschi, S. D. Price and P. Lavvas, Astrophys. J., Suppl. Ser., 2013, 204, 20 CrossRef.
- C. L. Ricketts, D. Schröder, C. Alcaraz and J. Roithová, Chem. – Eur. J., 2008, 14, 4779–4783 CrossRef.
- E.-L. Zins and D. Schröder, J. Phys. Chem. A, 2010, 114, 5989–5996 CAS.
- J. Roithová and D. Schröder, Chem. – Eur. J., 2007, 13, 2893–2902 CrossRef.
- J. Roithová and D. Schröder, Phys. Chem. Chem. Phys., 2007, 9, 731–738 RSC.
- L. A. Frank, W. R. Paterson, K. L. Ackerson, V. M. Vasyliunas, F. V. Coroniti and S. J. Bolton, Science, 1996, 274, 394–395 CrossRef CAS PubMed.
- H. Gu, J. Cui, D. Niu, L. Dai, J. Huang, X. Wu, Y. Hao and Y. Wei, Earth Planet. Phys., 2020, 4, 396–402 Search PubMed.
- H. Sabzyan, E. Keshavarz and Z. Noorisafa, J. Iran. Chem. Soc., 2014, 11, 871–945 CrossRef CAS.
- S. Falcinelli, F. Pirani, M. Alagia, L. Schio, R. Richter, S. Stranges, N. Balucani and F. Vecchiocattivi, Atmosphere, 2016, 7, 112 CrossRef.
- S. Falcinelli, M. Rosi, P. Candori, F. Vecchiocattivi, J. M. Farrar, F. Pirani, N. Balucani, M. Alagia, R. Richter and S. Stranges, Planet. Space Sci., 2014, 99, 149–157 CrossRef CAS.
- J. Lilensten, C. Simon Wedlund, M. Barthélémy, R. Thissen, D. Ehrenreich, G. Gronoff and O. Witasse, Icarus, 2013, 222, 169–187 CrossRef CAS.
- M. Alagia, N. Balucani, P. Candori, S. Falcinelli, F. Pirani, R. Richter, M. Rosi, S. Stranges and F. Vecchiocattivi, Rend. Lincei, 2013, 24, 53–65 CrossRef.
- J. C. Laas and P. Caselli, Astron. Astrophys., 2019, 624, A108 CrossRef CAS.
- C. T. Russell and M. G. Kivelson, Science, 2000, 287, 1998–1999 CrossRef CAS PubMed.
- M. Kumar and J. S. Francisco, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 864–869 CrossRef CAS.
- X. Zhang, M. C. Liang, F. Montmessin, J. L. Bertaux, C. Parkinson and Y. L. Yung, Nat. Geosci., 2010, 3, 834–837 CrossRef CAS.
- W. W. Kellogg, R. D. Cadle, E. R. Allen, A. L. Lazrus and E. A. Martell, Science, 1972, 175, 587–596 CrossRef CAS.
- L. A. Komarnisky, R. J. Christopherson and T. K. Basu, Nutrition, 2003, 19, 54–61 CrossRef CAS PubMed.
- J. N. Bull, J. W. L. Lee and C. Vallance, Phys. Rev. A, 2017, 96, 042704 CrossRef.
- M. Hochlaf, R. Linguerri, M. Cheraki, T. Ayari, R. Ben Said, R. Feifel and G. Chambaud, J. Phys. Chem. A, 2021, 125, 1958–1971 CrossRef CAS.
- T. Barker, Astrophys. J., 1980, 240, 99–104 CrossRef CAS.
- S. Rappaport, E. Chiang, T. Kallman and R. Malina, Astrophys. J., 1994, 431, 237–246 CrossRef CAS.
- L. T. Greenberg, P. Dyal and T. R. Geballe, Astrophys. J., Lett., 1977, 213, L71–L74 CrossRef CAS.
- D. E. Shemansky and G. R. Smith, J. Geophys. Res., 1981, 86, 9179–9192 CrossRef CAS.
- F. Bagenal and J. D. Sullivan, J. Geophys. Res.: Space Phys., 1981, 86, 8447–8466 CrossRef CAS.
- F. Herbert, N. M. Schneider, A. R. Hendrix and F. Bagenal, J. Geophys. Res.: Space Phys., 2003, 108, 1167 CrossRef.
- S. Kumar, Icarus, 1985, 61, 101–123 CrossRef CAS.
- J. R. Spencer and N. M. Schneider, Annu. Rev. Earth Planet. Sci., 1996, 24, 125–190 CrossRef CAS.
- P. A. Delamere and F. Bagenal, J. Geophys. Res., 2003, 108, 1276 CrossRef.
- R. C. Allen, C. P. Paranicas, F. Bagenal, S. K. Vines, D. C. Hamilton, F. Allegrini, G. Clark, P. A. Delamere, T. K. Kim, S. M. Krimigis, D. G. Mitchell, T. H. Smith and R. J. Wilson, Geophys. Res. Lett., 2019, 46, 11709–11717 CrossRef CAS PubMed.
- G. Clark, B. H. Mauk, C. Paranicas, P. Kollmann and H. T. Smith, J. Geophys. Res.: Space Phys., 2016, 121, 2264–2273 CrossRef CAS.
- D. F. Mark, F. M. Stuart and M. de Podesta, Geochim. Cosmochim. Acta, 2011, 75, 7494–7501 CrossRef CAS.
- S. A. Stern, Rev. Geophys., 1999, 37, 453–491 CrossRef CAS.
- A. O. Nier, W. B. Hanson, A. Seiff, M. B. McElroy, N. W. Spencer, R. J. Duckett, T. C. Knight and W. S. Cook, Science, 1976, 193, 786–788 CrossRef CAS.
- H. B. Niemann, S. K. Atreya, G. R. Carignan, T. M. Donahue, J. A. Haberman, D. N. Harpold, R. E. Hartle, D. M. Hunten, W. T. Kasprzak, P. R. Mahaffy, T. C. Owen, N. W. Spencer and S. H. Way, Science, 1996, 272, 846–849 CrossRef CAS PubMed.
- W. B. Hubbard and M. S. Marley, Icarus, 1989, 78, 102–118 CrossRef CAS.
- L. Wallace, Icarus, 1980, 43, 231–259 CrossRef CAS.
- A. G. W. Cameron, Space Sci. Rev., 1973, 15, 121–146 CrossRef CAS.
- D. D. Bogard, R. N. Clayton, K. Marti, T. Owen and G. Turner, in Space Science Reviews, ed. R. Kallenbach, J. Geiss and W. K. Hartmann, Springer, Dordrecht, 2001, vol. 12, pp. 425–458 Search PubMed.
- H. B. Niemann, S. K. Atreya, J. E. Demick, D. Gautier, J. A. Haberman, D. N. Harpold, W. T. Kasprzak, J. I. Lunine, T. C. Owen and F. Raulin, J. Geophys. Res., 2010, 115, E12006 CrossRef.
- O. Badr and S. D. Probert, Appl. Energy, 1993, 46, 1–67 CrossRef CAS.
- E. W. Schwieterman, T. D. Robinson, V. S. Meadows, A. Misra and S. Domagal-Goldman, Astrophys. J., 2015, 810, 57 CrossRef.
- D. Smith, D. Grief and N. G. Adams, Int. J. Mass Spectrom. Ion Phys., 1979, 30, 271–283 CrossRef CAS.
- D. Smith, N. G. Adams, E. Alge, H. Villinger and W. Lindinger, J. Phys. B: At. Mol. Phys., 1980, 13, 2787–2799 CrossRef CAS.
- G. Dupeyrat, J. B. Marquette, B. R. Rowe and C. Rebrion, Int. J. Mass Spectrom. Ion Processes, 1991, 103, 149–156 CrossRef CAS.
- G. C. Shields and T. F. Moran, J. Phys. B: At. Mol. Phys., 1983, 16, 3591–3607 CrossRef CAS.
- E. Y. Kamber, P. Jonathan, A. G. Brenton and J. H. Beynon, J. Phys. B: At. Mol. Phys., 1987, 20, 4129–4142 CrossRef CAS.
- S. M. Harper, W.-P. Hu and S. D. Price, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 4409–4423 CrossRef CAS.
- H. R. Koslowski, H. Lebius, V. Staemmler, R. Fink, K. Wiesemann and B. A. Huber, J. Phys. B: At., Mol. Opt. Phys., 1991, 24, 5023–5034 CrossRef CAS.
- E. L. Zins and D. Schröder, Int. J. Mass Spectrom., 2011, 299, 53–58 CrossRef CAS.
- J. Roithová, Z. Herman, D. Schröder and H. Schwarz, Chem. – Eur. J., 2006, 12, 2465–2471 CrossRef.
- J. Roithová, R. Thissen, J. Žabka, P. Franceschi, O. Dutuit and Z. Herman, Int. J. Mass Spectrom., 2003, 228, 487–495 CrossRef.
- N. Tafadar, N. Kaltsoyannis and S. D. Price, Int. J. Mass Spectrom., 1999, 192, 205–214 CrossRef CAS.
- P. W. Burnside and S. D. Price, Int. J. Mass Spectrom., 2006, 249–250, 279–288 CrossRef.
- W.-P. Hu, S. M. Harper and S. D. Price, Mol. Phys., 2005, 103, 1809–1819 CrossRef CAS.
- M. Manning, S. D. Price and S. R. Leone, J. Chem. Phys., 1993, 99, 8695–8704 CrossRef CAS.
- S. D. Price, M. Manning and S. R. Leone, Chem. Phys. Lett., 1993, 214, 553–558 CrossRef CAS.
- D. Ascenzi, P. Tosi, J. Roithová, C. L. Ricketts, D. Schröder, J. F. Lockyear, M. A. Parkes and S. D. Price, Phys. Chem. Chem. Phys., 2008, 10, 7121–7128 RSC.
- J. F. Lockyear, K. Douglas, S. D. Price, M. Karwowska, K. J. Fijalkowski, W. Grochala, M. Remeš, J. Roithová and D. Schröder, J. Phys. Chem. Lett., 2010, 1, 358–362 CrossRef CAS.
- H. Störi, E. Alge, H. Villinger, F. Egger and W. Lindinger, Int. J. Mass Spectrom. Ion Phys., 1979, 30, 263–270 CrossRef.
- J. Roithová, J. Žabka, Z. Herman, R. Thissen, D. Schröder and H. Schwarz, J. Phys. Chem. A, 2006, 110, 6447–6453 CrossRef PubMed.
- J. Roithová, J. Žabka, J. Hrušák, R. Thissen and Z. Herman, J. Phys. Chem. A, 2003, 107, 7347–7354 CrossRef.
- J. Jašik, J. Roithová, J. Žabka, R. Thissen, I. Ipolyi and Z. Herman, Int. J. Mass Spectrom., 2006, 255–256, 150–163 CrossRef.
- K. A. Newson and S. D. Price, Chem. Phys. Lett., 1997, 269, 93–98 CrossRef CAS.
- Z. Herman, J. Žabka, Z. Dolejšek, M. Fárník and M. Fárník, Int. J. Mass Spectrom., 1999, 192, 191–203 CrossRef CAS.
- N. Lambert, N. Kaltsoyannis, S. D. Price, J. Žabka and Z. Herman, J. Phys. Chem. A, 2006, 110, 2898–2905 CrossRef CAS.
- N. Tafadar and S. D. Price, Int. J. Mass Spectrom., 2003, 223–224, 547–560 CrossRef CAS.
- J. F. Lockyear, C. L. Ricketts, M. A. Parkes and S. D. Price, Chem. Sci., 2011, 2, 150–156 RSC.
- S. Armenta Butt and S. D. Price, Phys. Chem. Chem. Phys., 2021, 23, 11287–11299 RSC.
- H. M. Holzscheiter and D. A. Church, J. Chem. Phys., 1981, 74, 2313–2318 CrossRef CAS.
- P. Tosi, R. Correale, W. Lu, S. Falcinelli and D. Bassi, Phys. Rev. Lett., 1999, 82, 450–452 CrossRef CAS.
- A. Ehbrecht, N. Mustafa, C. Ottinger and Z. Herman, J. Chem. Phys., 1996, 105, 9833–9846 CrossRef CAS.
- J. H. Agee, J. B. Wilcox, L. E. Abbey and T. F. Moran, Chem. Phys., 1981, 61, 171–179 CrossRef CAS.
- S. M. Harper, S. W.-P. Hu and S. D. Price, J. Chem. Phys., 2004, 120, 7245–7248 CrossRef CAS PubMed.
- B. K. Chatterjee and R. Johnsen, J. Chem. Phys., 1989, 91, 1378–1379 CrossRef CAS.
- G. Niedner-Schatteburg, T. Schindler, C. Berg, D. Wössner and V. E. Bondybey, J. Chem. Phys., 1993, 99, 9664–9669 CrossRef CAS.
- W.-P. Hu, S. M. Harper and S. D. Price, Meas. Sci. Technol., 2002, 13, 1512–1522 CrossRef CAS.
- S. D. Price, Int. J. Mass Spectrom., 2007, 260, 1–19 CrossRef CAS.
- K. M. Douglas and S. D. Price, Int. J. Mass Spectrom., 2011, 303, 147–153 CrossRef CAS.
- K. Yamasaki and S. R. Leone, J. Chem. Phys., 1989, 90, 964–976 CrossRef CAS.
- J. F. Lockyear, M. A. Parkes and S. D. Price, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 145201 CrossRef.
- NIST Atomic Spectra Database (version 5.6.1), ed. A. Kramida, Y. Ralchenko, J. Reader and NIST ASD Team, National Institute of Standards and Technology, Gaithersburg, MD, 2020 Search PubMed.
- W. C. Martin, R. Zalubas and A. Musgrove, J. Phys. Chem. Ref. Data, 1990, 19, 821–880 CrossRef CAS.
- N. Imadouchene, H. Aouchiche and C. Champion, J. Electron Spectrosc. Relat. Phenom., 2016, 210, 36–48 CrossRef CAS.
- M. V. V. S. Rao and S. K. Srivastava, J. Geophys. Res., 1993, 98, 13137–13145 CrossRef CAS.
- T. Nakamura, N. Kobayashi and Y. Kaneko, J. Phys. Soc. Jpn., 1985, 54, 2774–2775 CrossRef CAS.
- S. J. Smith, J. B. Greenwood, A. Chutjian and S. S. Tayal, Astrophys. J., 2000, 541, 501–505 CrossRef CAS.
- H. W. Moos, S. T. Durrance, T. E. Skinner, P. D. Feldman, J.-L. Bertaux and M. C. Festou, Astrophys. J., 1983, 275, L19–L23 CrossRef CAS.
- P. L. Smith, C. E. Magnusson and P. O. Zetterberg, Astrophys. J., 1984, 277, L79 CrossRef CAS.
- L. I. Podobedova, D. E. Kelleher and W. L. Wiese, J. Phys. Chem. Ref. Data, 2009, 38, 171–439 CrossRef CAS.
- Z. Herman, Int. Rev. Phys. Chem., 1996, 15, 299–324 Search PubMed.
- S. A. Rogers, S. D. Price and S. R. Leone, J. Chem. Phys., 1993, 98, 280–289 CrossRef CAS.
- S. D. Price, J. Chem. Soc., Faraday Trans., 1997, 93, 2451–2460 RSC.
- M. A. Parkes, J. F. Lockyear and S. D. Price, Int. J. Mass Spectrom., 2009, 280, 85–92 CrossRef CAS.
- G. Dujardin, M. J. Besnard, L. Hellner and Y. Malinovitch, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 35, 5012–5019 CrossRef CAS PubMed.
- B. Godard, E. Falgarone, M. Gerin, D. C. Lis, M. De Luca, J. H. Black, J. R. Goicoechea, J. Cernicharo, D. A. Neufeld, K. M. Menten and M. Emprechtinger, Astron. Astrophys., 2012, 540, A87 CrossRef.
- F. Lique, A. Zanchet, N. Bulut, J. R. Goicoechea and O. Roncero, Astron. Astrophys., 2020, 638, A72 CrossRef CAS.
- D. O. Kashinski, D. Talbi, A. P. Hickman, O. E. Di Nallo, F. Colboc, K. Chakrabarti, I. F. Schneider and J. Z. Mezei, J. Chem. Phys., 2017, 146, 204109 CrossRef CAS PubMed.
- P. J. Dagdigian, J. Chem. Phys., 2019, 150, 84308 CrossRef.
- P. Bolognesi, L. Avaldi, M. A. MacDonald, C. M. A. Lopes, G. Dawber, C. E. Brion, Y. Zheng and G. C. King, Chem. Phys. Lett., 1999, 309, 171–176 CrossRef CAS.
- L. Åsbrink, Chem. Phys. Lett., 1970, 7, 549–552 CrossRef.
- F. Merkt and T. P. Softley, J. Chem. Phys., 1992, 96, 4149–4156 CrossRef CAS.
- K. M. Weitzel, J. Mähnert and M. Penno, Chem. Phys. Lett., 1994, 224, 371–380 CrossRef CAS.
- R. B. Cordaro, K. C. Hsieh and L. C. McIntyre Jr, J. Phys. B: At. Mol. Phys., 1986, 19, 1863–1872 CrossRef CAS.
- R. Stockbauer, J. Chem. Phys., 1979, 70, 2108–2114 CrossRef CAS.
- J. L. Gardner and J. A. R. Samson, J. Electron Spectrosc. Relat. Phenom., 1976, 8, 123–127 CrossRef CAS.
- T. E. Sharp, At. Data Nucl. Data Tables, 1970, 2, 119–169 CrossRef.
- M. Beyer and F. Merkt, J. Mol. Spectrosc., 2016, 330, 147–157 CrossRef CAS.
- M. Beyer and F. Merkt, Phys. Rev. Lett., 2016, 116, 093001 CrossRef PubMed.
- M. A. Parkes, J. F. Lockyear, S. D. Price, D. Schröder, J. Roithová and Z. Herman, Phys. Chem. Chem. Phys., 2010, 12, 6233–6243 RSC.
- C. L. Ricketts, D. Schröder, J. Roithová, H. Schwarz, R. Thissen, O. Dutuit, J. Žabka, Z. Herman and S. D. Price, Phys. Chem. Chem. Phys., 2008, 10, 5135–5143 RSC.
- S. Armenta Butt and S. D. Price, Phys. Chem. Chem. Phys., 2020, 22, 8391–8400 RSC.
- M. A. Parkes, J. F. Lockyear, D. Schröder, J. Roithová and S. D. Price, Phys. Chem. Chem. Phys., 2011, 13, 18386–18392 RSC.
- S. Strathdee and R. Browning, J. Phys. B: At. Mol. Phys., 1979, 12, 1789–1804 CrossRef CAS.
- K. Köllmann, Int. J. Mass Spectrom. Ion Phys., 1975, 17, 261–285 CrossRef.
- K. Ito, R. I. Hall and M. Ukai, J. Chem. Phys., 1996, 104, 8449–8457 CrossRef CAS.
- C. Bottcher, J. Phys. B: At. Mol. Phys., 1974, 7, L352 CrossRef CAS.
- C. J. Latimer, J. Geddes, M. A. MacDonald, N. Kouchi and K. F. Dunn, J. Phys. B: At., Mol. Opt. Phys., 1996, 29, 6113–6121 CrossRef CAS.
- In CRC Handbook of Chemistry and Physics, ed. J. R. Rumble, CRC Press/Taylor & Francis, Boca Raton, FL, 100th edn, 2020 Search PubMed.
- A. J. Yencha, K. Ellis and G. C. King, J. Electron Spectrosc. Relat. Phenom., 2014, 195, 160–173 CrossRef CAS.
- P. Baltzer, M. Larsson, L. Karlsson, B. Wannberg and M. Carlsson Göthe, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 5545–5553 CrossRef CAS PubMed.
- H. R. Hrodmarsson, R. Thissen, D. Dowek, G. A. Garcia, L. Nahon and T. R. Govers, Front. Chem., 2019, 7, 222 CrossRef CAS.
- E. M. Bahati, J. J. Jureta, D. S. Belic, H. Cherkani-Hassani, M. O. Abdellahi and P. Defrance, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 2963–2973 CrossRef CAS.
- X. Tang, Y. Hou, C. Y. Ng and B. Ruscic, J. Chem. Phys., 2005, 123, 074330 CrossRef PubMed.
- L. Åsbrink and C. Fridh, Phys. Scr., 1974, 9, 338–340 CrossRef.
- P. Rivière-Marichalar, A. Fuente, J. R. Goicoechea, J. Pety, R. Le Gal, P. Gratier, V. Guzmán, E. Roueff, J. C. Loison, V. Wakelam and M. Gerin, Astron. Astrophys., 2019, 628, A16 CrossRef PubMed.
- T. Trabelsi, S. Ben Yaghlane, M. M. Al Mogren, J. S. Francisco and M. Hochlaf, J. Chem. Phys., 2016, 145, 084307 CrossRef PubMed.
- M. Canaves, A. A. De Almeida, D. C. Boice and G. C. Sanzovo, Earth, Moon, Planets, 2002, 90, 335–347 CrossRef CAS.
- J. Cernicharo, B. Lefloch, M. Agúndez, S. Bailleux, L. Margulès, E. Roueff, R. Bachiller, N. Marcelino, B. Tercero, C. Vastel and E. Caux, Astrophys. J., Lett., 2018, 853, L22 CrossRef PubMed.
- S. Ben Yaghlane and M. Hochlaf, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 015101 CrossRef.
- J. Czernek and O. Živný, Chem. Phys., 2004, 303, 137–142 CrossRef CAS.
- J. M. Dyke, A. Morris and I. R. Trickle, J. Chem. Soc., Faraday Trans. 2, 1977, 73, 147–151 RSC.
- P. A. G. O’Hare, J. Chem. Phys., 1970, 52, 2992–2996 CrossRef.
- A. Karpfen, P. Schuster, J. Petkov and H. Lischka, J. Chem. Phys., 1978, 68, 3884–3890 CrossRef CAS.
- K. A. Peterson and R. C. Woods, J. Chem. Phys., 1988, 89, 4929–4944 CrossRef CAS.
- D. Zhou, D. Shi, Z. Zhu and J. Sun, J. Quant. Spectrosc. Radiat. Transfer, 2019, 224, 1–8 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp05397c |
| This journal is © the Owner Societies 2022 |