Threshold photoelectron spectroscopy of 9-methyladenine: theory and experiment†
K.
Laamiri
ab,
G. A.
Garcia
 c,
L.
Nahon
c,
L.
Nahon
 c,
A.
Ben Houria
c,
A.
Ben Houria
 b,
R.
Feifel
b,
R.
Feifel
 d and
M.
Hochlaf
d and
M.
Hochlaf
 *a
*a
aUniversité Gustave Eiffel, COSYS/LISIS, 5 Bd Descartes 77454, Champs-sur-Marne, France. E-mail: hochlaf@univ-mlv.fr
bLaboratoire de Spectroscopie Atomique, Moléculaire et Applications – LSAMA, Université de Tunis El Manar, Tunis, Tunisia
cSynchrotron SOLEIL, L’orme des Merisiers, Saint-Aubin – BP 48 – 91192 Gif-sur-Yvette Cedex, France
dUniversity of Gothenburg, Department of Physics, 412 58 Gothenburg, Sweden
First published on 4th October 2021
Abstract
We present a combined experimental and theoretical study of single-photon ionization of 9-methyladenine (9MA) in the gas phase. In addition to tautomerism, several rotamers due to the rotation of the methyl group may exist. Computations show, however, that solely one rotamer contributes because of low population in the molecular beam and/or unfavorable Franck–Condon factors upon ionization. Experimentally, we used VUV radiation available at the DESIRS beamline of the synchrotron radiation facility SOLEIL to record the threshold photoelectron spectrum of this molecule between 8 and 11 eV. This spectrum consists of a well-resolved band assigned mainly to vibronic levels of the D0 cationic state, plus a contribution from the D1 state, and two large bands corresponding to the D1, D2 and D3 electronically excited states. The adiabatic ionization energy of 9MA is measured at 8.097 ± 0.005 eV in close agreement with the computed value using the explicitly correlated coupled cluster approach including core valence, scalar relativistic and zero-point vibrational energy corrections. This work sheds light on the complex pattern of the lowest doublet electronic states of 9MA+. The comparison to canonical adenine reveals that methylation induces further electronic structure complication that may be important to understand the effects of ionizing radiation and the charge distribution in these biological entities at different time scales.
I. Introduction
Methylation occurs in DNA (adenine and cytosine) and changes the gene transcription without changing the sequence, and it is associated with natural processes such as ageing and cancer onsets. Indeed, methylation at some specific positions of the DNA bases may alter their pairing and subsequently induce mutagenesis and genotoxicity. There has been recent interest because of its potential effects in targeted cancer therapy,1 epigenomics,2 and genetic analysis3 and for the development of new therapies.4,5 Moreover, studying methylated DNA bases is important to investigate the damage produced by ionizing radiation, which leads not only to different dynamics from their non-substituted DNA bases but also to changes in their biological activities, thermodynamic and kinetic behaviors. Such studies helped thus to understand the structural and functional changes upon ionization and induced effects, as well as the intrinsic processes occurring when these biological entities interact with ionizing radiation.In order to shed light on the effects induced by methylation, a common strategy consists of comparing the spectra of canonical DNA bases to those of their methylated counterparts. Different experimental methodologies were used to investigate these species either isolated or embedded into clusters or interacting with metallic nanoparticles. These include standard IR, Raman and UV spectroscopies and also time-resolved spectroscopy and photoelectron spectroscopy.6–14 These studies are complemented by theoretical computations on the structures and the electronic properties of DNA bases and their methylated entities, which highlight the complex electronic structure and the radiationless ultrafast deexcitation dynamics of electronically excited DNA bases, and the corresponding methylation effects.
Adenine has several tautomers in its amino and imino forms, where the most stable form (i.e. 9H adenine, 9HA) is known as canonical adenine.15 Methylation of the purine ring of the canonical adenine may occur in “1”, “3”, “7” and “9” positions resulting in 1-methyladenine (1MA), 3-methyladenine (3MA), 7-methyladenine (7MA), and 9-methyladenine (9MA), respectively. Previous studies showed that the most stable isomer is 9-methyladenine,16 which is the subject of the present work.
LeBreton and co-workers17,18 recorded the He I photoelectron spectra of 9MA and 9HA in the 7.5–14 eV energy range. These spectra are composed of six large bands associated with the removal of one electron from the π and n outermost orbitals of 9MA and of 9HA. Based on CNDO/2, HAM/3 and ab initio 4-31G SCF calculations, D0(π−1) was attributed to the first band, D1(n−1) and D2(π−1) to the second band since these states are found close in energy and then D3(n−1) and D4(π−1) to the third band. Later on, Stolow and co-workers19,20 obtained time-resolved photoelectron spectroscopy results and reassigned the electronic character and ionization energies of the low lying cationic states of 9HA and 9MA. For both cations, they proposed the following state ordering: D0(π−1) (first band), D1(n−1) (second band) and then D2(π−1) & D3(n−1) (third band) where the energies of the bands were lower for 9MA compared to 9HA. In 2020, Tureček and co-workers21 carried out UV-vis photodissociation action spectroscopy and collision induced dissociation (CID) mass spectrometry on gas phase 9MA trapped cations. Through density functional theory and coupled clusters computations, they identified a unique form of the 9MA cation (denoted in what follows as 9MA+). After analysis of the recorded vibronic bands in the 210–700 nm wavelength region with respect to the ground cationic state, these authors underlined the complexity of the 9MA+ electronic states’ pattern due to vibronic couplings, as already noticed by Stolow and co-workers. In sum, these experimental studies revealed the complexity of the electronic structures of the 9MA and 9HA cations because of electronic excited state interactions leading to spectral congestion. Moreover, different shapes of 9MA+ and 9HA+ spectra were recorded, due to the methylation-induced changes in the electronic structure. Besides, there is a lack of resolution leading to spectral congestion, which is made even worse by the fact that the trapped ions are at room temperature. It was not sufficiently high to disentangle such effects.
In 2018, some of us studied canonical adenine using threshold photoelectron spectroscopy and post Hartree–Fock explicitly correlated coupled clusters and multireference configuration interaction techniques.22 Experimentally, we obtained a vibrationally resolved spectrum for the ground electronic state of the canonical adenine cation and some broad bands for the electronic excited states. The computations allowed assigning these features and understanding the complex vibronic structure of the canonical adenine cation. In the present study, we use similar theoretical and experimental approaches to investigate the 9-methyladenine cation, formed upon VUV single-photon ionization of the neutral species. A priori, the present spectra could be more complex because of the possible contribution of several neutral rotamers (linked to the methylation of adenine) in the gas phase prior to ionization and because of the vibronic coupling induced interaction between the cationic electronic states pointed out above.
II. Methods
a. Experimental
The experiments were performed at the VUV DESIRS beamline of the French synchrotron facility SOLEIL.23 A commercial 9-methyladenine sample was placed into an in-vacuum oven and heated to 200/220 °C (body/nozzle). The resulting vapor was expanded through a 70 µm pinhole using 1.5 bars of Ar as the carrier gas. The molecular beam traversed two consecutive skimmers (1 mm and 2 mm diameter) before being ionized at the center of the double imaging photoelectron-photoion coincidence (i2PEPICO) DELICIOUS3 spectrometer.24 This spectrometer is composed of a velocity map imaging (VMI) electron analyzer25 and a photoion momentum imager that are operated in coincidence, so that photoelectron images can be filtered by ion mass and translational energy in a multiplex manner. These images were then Abel inverted to derive the corresponding photoelectron spectra.26For the energy scans, the monochromator was set to a resolution of 9 meV, while a pressure of 0.15 mbars of Kr was fed into the gas filter upstream to suppress the high harmonics emitted by the undulator.27 The energy steps were set to 5 meV, except for the threshold region of 9MA, where 3 meV steps were selected. The signal was corrected for molecular beam instabilities by recording fast scans for 9MA and using them to normalize the signal. The photon flux, recorded with a calibrated AXUV photodiode, was used to correct all the energy scans. The krypton 5s and 5s′ absorption lines documented by Yoshino et al.,28 appearing at 10.032 eV and 10.644 eV respectively, served as the energy reference for a final absolute precision of ± 3 meV on the energy scales.
The threshold photoelectron spectrum (TPES) was obtained using a method called slow photoelectron spectroscopy (SPES).29,30 Briefly, it involves obtaining the mass-selected photoelectron spectrum as a function of photon energy, and integrating the signal along the constant ionic state lines up to a given electron kinetic energy (here 100 meV), resulting in an overall resolution of 20 meV including the photon bandwidth. No fragmentation was observed in the TPES, although in the PES spectra recorded at a higher photon energy, 13.9 eV (see Fig. S1, ESI†); the hydrogen loss channel is observed above ∼11.7 eV binding energy.
b. Computations
The main goal of the present computations is to provide an interpretation of the experimental TPES spectra. First we performed geometry optimizations (optg) of the neutral and cationic 9MA and their tautomers in their electronic ground states using GAUSSIAN 16.31 These optimizations were carried out, in the C1 point group, at the PBE0/aug-cc-pVDZ level,32–34 where we relaxed all internal coordinates and used the default options. Then, we checked the minimal nature of the stationary points by frequency calculations using the VPT2 approach. Only molecular species with all >0 frequencies were considered. Then, we evaluated the zero-point vibrational energy correction (ZPVE) after scaling the harmonic frequencies, to obtain the anharmonic ones. We used a scaling factor of 0.9698 for the frequencies <1000 cm−1 and 0.9592 for those >1000 cm−1 as recommended by Laury et al.35 Furthermore, we carried out single point (SP) computations at the PBE0/aug-cc-pVDZ equilibrium structures, where we make use of the explicitly correlated and the standard versions of the coupled clusters single and double with perturbative treatment of triples (i.e. (R)CCSD(T)36–38 or (R)CCSD(T)-F12 (approximation b)39–41) techniques as implemented in MOLPRO.42 For (R)CCSD(T)-F12, we described the atoms with the aug-cc-pVDZ basis set and the corresponding density fitting and RI functions as implemented in MOLPRO.43–46 Afterwards, we adopted composite schemes to deduce accurate energetics.47 These schemes correspond to the PBE0/aug-cc-pVDZ(optg)//(R)CCSD(T)-F12(b)/aug-cc-pVDZ (+ΔZPVE) composite scheme for 9MA tautomers and their cations, and the more computationally demanding, though more accurate, PBE0/aug-cc-pVDZ(optg)//(R)CCSD(T)-F12(b)/aug-cc-pVDZ (+ΔCV + ΔSR + ΔZPVE) scheme for the 9MA conformers and their cations. ΔCV, ΔSR and ΔZPVE stand for the core-valence, scalar relativistic and the zero-point vibrational energy corrections, respectively. ΔCV was evaluated as the energy difference between the (R)CCSD(T)/cc-pwCVTZ48 energies with and without considering core electron correlation. ΔSR is obtained as the energy difference between (R)CCSD(T)/cc-pVTZ-DK49–51 and (R)CCSD(T)/cc-pVTZ energies. Moreover, we carried out a Franck–Condon (FC) analysis for the neutral-cation ionization transitions as implemented in GAUSSIAN 16 following the time-independent adiabatic Hessian FC (TI-AH|FC) model.52–55 The resulting FC factors were convoluted with a Gaussian with FWHM = 20 meV to match the experimental spectra. The simulated spectra were positioned on an absolute photon energy scale by matching the 0–0 transition with the computed adiabatic ionization energy (AIE) at the PBE0/aug-cc-pVDZ(optg)//(R)CCSD(T)-F12(b)/aug-cc-pVDZ (+ΔCV + ΔSR + ΔZPVE) level. For the validation of these approaches, we refer to our previous studies where we present direct comparisons between the theoretical and experimental data for similar molecular systems.22,47,56–60The second set of computations corresponds to the investigation of the electronic excited states of the 9MA cation using the MOLPRO package, where the atoms were described by the aug-cc-pVDZ basis sets in conjunction with the corresponding fitting and RI auxiliary basis sets as implemented in MOLPRO. These computations consisted of the optimization of the equilibrium geometries of the four lowest electronic states of 9MA+ using the state-averaged complete active space self-consistent field (SA-CASSCF) method.61,62 All internal coordinates were relaxed (C1 point group). The CASSCF active space was constructed with 8 molecular orbitals ranging from HOMO−3 to LUMO+3 (Fig. S2, ESI†); the core orbitals and the valence orbitals up to HOMO−4 were considered as closed. All valence electrons were considered. Then, we performed single point computations at the optimized structures using the newly implemented, explicitly correlated, internally contracted multi-reference configuration interaction MRCI-F1263–65 approach. The MRCI-F12 active space includes all configurations having a weight ≥0.05 in the CI expansion of the CASSCF wave functions. While computing the doublet cation states, this results in >6.8 × 107 (2 × 109) contracted (uncontracted) configuration state functions to be treated. As discussed in ref. 65, the MRCI-F12/aug-cc-pVDZ level should lead to a similar accuracy to standard MRCI in conjunction with the aug-cc-pVQZ basis set, but the computational costs (both CPU and disk occupancy) are strongly reduced.
III. Results and discussion
The TPES spectrum of 9MA as a function of the photon energy is shown in Fig. 1. Three main photoionization bands are seen in the spectrum, with the first one exhibiting rich structures akin to the spectrum of canonical adenine.22 We also show in Fig. S1 (ESI†) the fixed photon energy VMI-PES spectra of 9MA recorded at hν = 13.9 eV. Apart from the three bands already seen in Fig. 1, there are two bands located at higher binding energies, ∼11.2 eV and ∼11.9 eV, in the parent channel. In the corresponding TOF-MS (not shown), there is a clear, broader peak at m/z 148, which can be attributed to dissociative ionization leading to H loss. In the fragment photoelectron spectrum shown in Fig. S1 (ESI†), the onset for fragmentation is seen at about 11.7 eV. Above 12.2 eV binding energy, no parent signal can be discerned.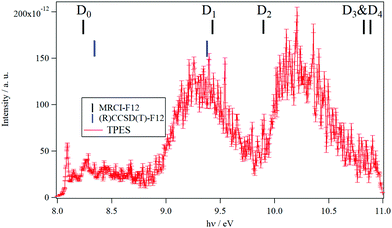 | ||
| Fig. 1 TPES spectrum of 9MA taking into account all electrons with kinetic energies between 0 and 100 meV, leading to a total resolution of 20 meV. The photon energy step is 5 meV. The vertical combs correspond to the vertical ionization energies of 9MA as computed at the MRCI-F12/aug-cc-pVDZ (in black) and (R)CCSD(T)-F12/aug-cc-pVDZ (in blue) levels of theory in the present work. The theoretical data are summarized in Table 3. | ||
According to the exploratory DFT work of Nguyen et al.,14 9MA possesses 5 tautomers (cf.Scheme 1). The most stable form has an amino function at the N6 position whereas the 4 other forms present an imino group instead. The present PBE0/aug-cc-pVDZ (+ΔZPVE) computations confirm these findings. Indeed, we give in Tables S1 and S2 of the ESI† the PBE0/aug-cc-pVDZ total energies and optimized geometries in Cartesian coordinates. More accurate relative energies are obtained using the PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (SP) (+ΔZPVE) composite scheme. These energies confirm this ordering and show that most likely only 9MA or its rotamers, more stable by more than 0.5 eV as compared to the imino tautomers, are present in our molecular beam of the present experiments irrespective of the cooling achieved in the adiabatic expansion. Table 1 shows that the relative energies of the cations follow the ordering of the neutral species. Afterwards, we deduced the adiabatic ionization energies (AIEs) of these species at the PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (+ΔZPVE) (SP) as listed in Table 2. This table shows that the first peak of the TPES spectrum (at ∼8.09 eV) corresponds to the AIE of 9MA whereas the AIE of the I1(1H) imino form is 0.3 eV lower in energy, excluding thus the contribution of such forms and of the even less stable other imino tautomers in the present experiment. Therefore, from now on, we will only consider the contribution from the 9MA/9MA′ most stable species.
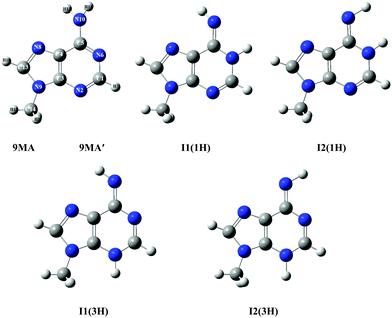 | ||
| Scheme 1 Structures of 9MA and its four imino tautomers/rotamers. 9MA and 9MA′ are rotamers differing by the relative position of the methyl group (cf. Table S3, ESI†). The imino rotamer types I1 and I2 correspond to different C4–C5–N10–H11 dihedral angles, while the two types of tautomers (1H) and (3H) are labelled according to the imino hydrogen. We followed the denomination given by Nguyen et al.14 We give also the numbering of atoms used presently. | ||
| Method | 9MA′ | 9MA | I1(1H) | I2(1H) | I1(3H) | I2(3H) | 9MA+ | I1(1H)+ | I2(1H)+ | I1(3H)+ | I2(3H)+ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Full optimization computations. b Single point computations at the optimized PBE0/aug-cc-pVDZ geometry. c Used as the reference for neutral species. d Used as the reference for ionic species. e B3LYP/6-31G++(d,p). | |||||||||||
| PBE0a | 0.000c | 0.000 | 0.553 | 0.819 | 1.362 | 1.364 | 0.000d | 0.183 | 0.428 | 0.904 | 0.859 |
| (R)CCSD(T)-F12b | 0.000c | 0.006 | 0.548 | 0.812 | 1.322 | 1.330 | 0.000d | 0.190 | 0.907 | 0.869 | 0.890 |
| Ref. 14e | 0.000c | 0.528 | 0.829 | 1.389 | 1.388 | ||||||
| Method | 9MA′ | 9MA | I1(1H) | I2(1H) | I1(3H) | I2(3H) |
|---|---|---|---|---|---|---|
| PBE0/aug-cc-pVDZ (optg) (+ΔZPVE) | 7.876 | 7.876 | 7.507 | 7.486 | 7.419 | 7.371 |
| PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (SP) | 8.072 | 8.067 | 7.753 | 8.202 | 7.655 | 7.663 |
| PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (+ΔZPVE) (SP) | 8.086 | 8.079 | 7.727 | 8.180 | 7.632 | 7.642 |
| PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (+ΔCV) (SP) | 8.089 | 8.084 | ||||
| PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (+ΔSR) (SP) | 8.072 | 8.067 | ||||
| PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (+ΔCV + ΔSR + ΔZPVE) (SP) | 8.102 | 8.097 | ||||
| TPES | 8.090 ± 0.005 |
In the case of 9MA, further complications may arise from the existence of several rotamers due to the rotation of the methyl group around the N9–C14 (methyl) bond. We thus searched for the stable conformers of 9MA performing several geometry optimizations where the H15–C14–N9–C3 dihedral angle was rotated from −180° to +180° with 30° steps. For the neutral, two stable forms are found, where one CH of the methyl group is in the plane of the purine ring either in cis (denoted as 9MA, Table S3, ESI†) or in trans (denoted as 9MA′, Table S3, ESI†) configuration with respect to C3–N9 bonds. Both possess a planar structure (Cs point group) and all positive frequencies (Table S5, ESI†). We also computed the barrier potential along the H15–C14–N9–C3 dihedral angle as displayed in Fig. S3 (ESI†). This figure shows that this barrier amounts to 82.7 cm−1. Since the temperature of the jet cooled 9-methyladenine gas is ∼60 K in the present experiments, this barrier is relatively high and does not allow the conversion of one rotamer into another. Therefore, 9MA and 9MA′ can be considered as distinct isomers.
While 9MA was already identified in previous studies,14,66–68 9MA′ is found here for the first time. The relative energy of both rotamers depends on the theoretical level. Indeed, 9MA is slightly more stable than 9MA′ using the PBE0/aug-cc-pVDZ method, whereas it turns out that 9MA′ is the most stable by ∼50 cm−1, when using the costlier explicitly correlated coupled cluster (R)CCSD(T)-F12 approach. For 9MA, Table S3 (ESI†) shows that the presently computed bond lengths and bond angles differ by <0.03 Å and <3° degrees from previous studies. When comparing 9MA and 9MA′, the bond distances and angles are quite similar, except those connecting the N9 atom because of the N lone pair induced repulsion upon methyl rotation along the N9–C14 (methyl) bond.
In 2020, Tureček and co-workers21 identified a stable form for the cationic species, 9MA+, which has Cs symmetry. In the present work we found also a unique stable form similar to their structure, where the CH of the methyl is in trans with respect to the C3–N9 bond. The geometrically optimized parameters of 9MA+ are listed in Tables S2 and S3 (ESI†), which are close to those determined by Tureček and co-workers.21 Obviously, the Franck–Condon factors (FCFs) for the 9MA X + hν → 9MA+ X+ + e− photoionization transition should be close to zero whereas non-zero FCFs are expected for 9MA′ X + hν → 9MA+ X+ + e− because of the trans → cis change at the N9–C14 (methyl) bond in the former as illustrated in Fig. 2. Therefore, only the later conformer is expected to contribute in our experiments although both rotamers are a priori present with similar abundance in our molecular beam since they have similar stabilities with an energy difference of ∼50 cm−1, which is within the uncertainty of the calculations. In what follows we will concentrate on the single photon ionization processes occurring from the 9MA′ ground state only, where ionization mainly affects the purine five and six membered aromatic ring distances, although these changes remain relatively small with bond lengths differing by less than 0.05 Å while the angles are weakly affected. Nevertheless, we cannot fully exclude the contribution of the cis form for the population of the Dn (n ≥1) states. The experimental spectra correspond to unresolved large bands.
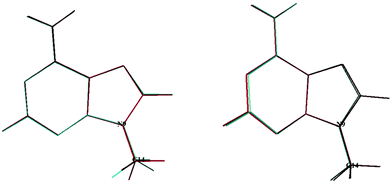 | ||
| Fig. 2 Superposition of the 9MA and 9MA+ (left) structures and that of 9MA′ and 9MA+ (right). See Scheme 1 for the numbering of the other atoms. | ||
In the 8–11 eV energy range covered in Fig. 1, previous studies located the D0, D1, D2, D3 and D4 doublet states of the 9MA+ cation. As mentioned in the Introduction section, LeBreton and co-workers17,18 assigned the first band in the PES spectra to the D0(π−1) state, the D1(n−1) and D2(π−1) states to the second band and then the D3(n−1) and D4(π−1) states to the third band. In contrast, Stolow and co-workers19,20 proposed the following attribution: D0(π−1) (first band), D1(n−1) (second band) and then D2(π−1) & D3(n−1) (third band). Our investigations on these electronic states using multiconfigurational approaches (CASSCF followed by MRCI-F12) show that the situation is even more complicated. Indeed, we located a conical intersection between the D0 and D1 states resulting in the mixing of their electronic wave functions. At the equilibrium geometry of 9MA′ (X1A′), we found that the wave function of the electronic ground state of 9MA+ is mainly described by the ejection of an electron from the (7a″) outermost molecular orbital (MO) (π type) with however non negligible contributions from the (5a″)−1 and (6a″)−1 configurations. Therefore, the D0 (i.e. X+2A″) and D1 (i.e. 12A) states are coupled vibronically. Besides, the D1 state is associated with a π−1 configuration and not n−1. And instead, the n−1 configuration is that of the D2 state, which is monoconfigurational in nature. D3 and D4 are of π−1 and n−1 types. Both are coupled vibronically with a strong mixing character. Our work confirms thus the assumptions of Tureček and co-workers.21 We would like to note that we locate the lowest quartet state (14A (Q1)) in the vicinity of D5. Although the single photoionization of neutral 9-methyladenine does not populate the quartet cationic state, the latter may couple to the close lying doublets (e.g. D5) via spin–orbit and may participate in their unimolecular dynamics.
At the CASSCF/aug-cc-pVDZ level, we computed an adiabatic excitation energy of 0.23 eV for the D0–D1 separation. Therefore, the first experimental band corresponds to the population of the D0 and D1 states and not only of the D0 as stated previously. Moreover, the MRCI-F12/aug-cc-pVDZ and the (R)CCSD(T)-F12/aug-cc-pVDZ vertical ionization energies (VIEs) from 9MA′ (X1A′) to reach these cationic states (Table 3) reveal that the second band is due to the population of the high vibrational levels of the D1 state solely. The second band is also found corresponding to the 9MA′ (X1A′) + hν → 9MA+ (D2) + e− ionization transition. The contribution of the D3 and D4 states starts in the right part of the spectrum of Fig. 1. Although we propose a new assignment of the PES/SPES bands, we notice that the computed VIEs are close to those previously determined experimentally (Table 3). Indeed, the measured VIE(D0) = 8.39–8.42 eV is close to the MRCI-F12/aug-cc-pVDZ and the (R)CCSD(T)-F12/aug-cc-pVDZ VIEs of 8.24 eV and 8.34 eV. For D1, both theoretical values coincide with the PES VIE (of ∼9.4 eV) with a better agreement between the (R)CCSD(T)-F12/aug-cc-pVDZ (of ∼9.37 eV) and TPES (of 9.34 eV), both considered as the most accurate determinations. For D3, D4 and D5, deviations of ∼ 0.4 eV are found between PES and MRCI-F12/aug-cc-pVDZ, which may be due to the difficulties to derive such quantities in this spectral range due to the complicated cationic electronic state pattern and the subsequent congestion. When compared to the canonical adenine spectrum,22 the situation is more complicated when this DNA basis is methylated in the N9 position. For instance, the D0–D1 adiabatic excitation energy is reduced from ∼0.9 eV to ∼0.2 eV complicating the spectroscopy of both cationic states. The D2–D5 states are also closer in energy resulting in larger experimental bands.
| State | This work | |||||
|---|---|---|---|---|---|---|
| Calc. | Exp. | Exp.g | Exp.h | |||
| MRCI-F12a | (R)CCSD(T)-F12c | PESe | TPESf | PES | TRPES | |
| a We added the vertical ionization energy as computed at the MRCI-F12/aug-cc-pVDZ level of theory. b MRCI-F12 total energies: 9MA(X1A′): −505.138558212355 a.u. 9MA+(X+2A″): −504.835645114 a.u. c We added the vertical ionization energy as computed at the (R)CCSD(T)-F12/aug-cc-pVDZ level of theory in the Cs point group and at the equilibrium geometry of 9MA(X1A′). d (R)CCSD(T)-F12 total energies: 9MA(X1A′): −505.882537959939 a.u. 9MA+(X+2A″): −505.575967035432 a.u. 9MA+(22A): −505.538160867854 a.u. e Cf. Fig. S1 (ESI). f Cf. Fig. 1. g Photoelectron spectroscopy. Ref. 18 h Time-resolved photoelectron spectroscopy. Ref. 19 | ||||||
| X+ 2A″ (D0) | 8.24b | 8.34d | 8.42 | — | 8.39 | 8.4 |
| 22A (D1) | 9.42 | 9.37d | 9.41 | 9.34 | 9.4 | 9.4 |
| 32A (D2) | 9.90 | 10.25 | 10.23 | 10.2 | 10.2 | |
| 42A (D3) | 10.82 | 11.19 | 10.2 | 10.2 | ||
| 52A (D4) | 10.87 | 11.6 | ||||
| 62A (D5) | 12.13 | 11.84 | 11.6 | |||
| 14A (Q1) | 12.14 | |||||
Fig. 3 shows the TPES spectrum of 9MA′ in the 8–9 eV range. This spectrum exhibits a rich structure which is related to the population of vibronic levels of 9MA+. The first peak in both the experimental and in silico spectra corresponds to the adiabatic ionization energy (AIE) of 9MA′. Theoretically, this AIE is determined at 8.102 eV at the highest computational level (i.e. PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (+ΔCV + ΔSR + ΔZPVE) (SP)), which includes the core-valence, the scalar relativistic and the zero-point vibrational energy corrections as given in Table 2. This value is very close to the experimental AIE (9MA′) of 8.097 ± 0.005 eV, obtained after adding the 7 meV Stark shift expected from the 88 V cm−1 experimental extraction field.69 This is the first determination of the AIE of this molecule. Note that the inclusion of the core-valence correction is mandatory to reach such accuracy, whereas the scalar relativistic effects may be omitted. For instance, Table 2 shows that the AIE computed at the PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (+ΔCV) (SP) level is 8.089 eV, which differs by 1 meV from the TPES AIE, whereas the PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (+ΔSR) (SP) (of 8.072 eV) is far from the experimental value by 18 meV i.e. out of the range of the experimental error bars.
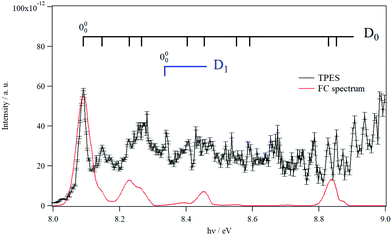 | ||
| Fig. 3 TPES spectrum of 9MA in the 8–9 eV region. Also shown is a Franck–Condon simulated spectrum set to an absolute scale via high level computations’-determined AIE. The vertical combs correspond to the peak positions reported in Table 4. | ||
In Fig. 3, we also superpose the FC spectrum for the 9MA′ (X1A′) + hν → 9MA+ (D0) + e− ionization transition, where the first peak is positioned to coincide with the computed AIE at the PBE0/aug-cc-pVDZ (optg)//(R)CCSD(T)-F12 (+ΔCV + ΔSR + ΔZPVE) (SP) level. The comparison of the experimental and the simulated spectra shows that several bands in the TPES spectrum remain unreproducible by the simulated one. This might be due to the contribution of resonant autoionization processes70 and to photoionization transitions populating the low vibronic levels of the D1 cationic state. Indeed, the strong D0–D1 vibronic coupling pointed out above participated in the congestion of the spectrum via the trading of the intensities between the D0 and D1 bands. The simulation of such features is challenging and goes beyond the scope of the present work.
To facilitate in the assignment of D0 bands, we estimated the anharmonic frequencies of 9MA+ (X+ 2A″/D0) at the PBE0/aug-cc-pVDZ level. These data are listed in Table S7 (ESI†). This ion has 48 vibrational modes: 32 a′ and 16 a″. Since both the neutral and the cation are planar in their electronic ground states, only the a′ vibrational modes are allowed upon single photon ionization. These correspond to the 32 a′ vibrational modes, those having even quanta of a″ and to any multiple and combination modes of these levels. Nevertheless, the geometries of the cation and the neutral species are very close, resulting in a short vibrational progression upon photoionization, as seen in the simulated FC spectrum (cf.Fig. 3). In Table 4, we list the tentative assignment of the bands of 9MA+ (D0). They correspond mainly to the population of ν1+, ν6+, ν17+, ν22+, ν30+ and some of their combination modes. This allows determining the respective fundamentals: ν1+ = 3703, ν6+ = 2953, ν17+ = 1380, and ν22+ = 1114, ν30+ = 460 (all values in cm−1). These values should be considered with caution because of the abovementioned D0–D1 vibronic couplings.
| Band origin (eV) | Relative energy (cm−1) | Assignment |
|---|---|---|
| a Used as reference. | ||
| 8.0904 | 0a | 000 |
| 8.1475 | 460 | 3010 or 4410 + 4610 |
| 8.2285 | 1114 | 2210 |
| 8.2615 | 1380 | 1710 |
| 8.3395 | 2009 | 22A/D1000 |
| 8.4024 | 2516 | 1710 + 2210 |
| 8.4565 | 2953 | 610 |
| 8.5495 | 3703 | 110 |
| 8.5915 | 4042 | 610 + 2210 |
| 8.8275 | 5945 | 620 |
| 8.8524 | 6146 | 110 + 1710 + 2210 or 610 + 2220 |
IV. Conclusions
Using a combination of advanced theoretical and experimental approaches, we investigated the single photon ionization spectrum of 9-methyladenine. Imino-tautomers cannot be present in our experimental conditions and have therefore been discarded in our spectral analysis. However, two rotamers could be expected, while a single one is found to be contributing to the spectrum in practice. This is either due to the cooling in the molecular beam or because of unfavorable Franck–Condon factors upon single-photon ionization. Upon methylation, the adiabatic ionization energy reduces by ∼0.2 eV as compared to the canonical adenine base.The experimental spectrum is thus fully assigned to photoionization transitions populating the D0, D1, D2, D3 and D4 9MA+ states. Moreover, our work shows that the pattern of the electronic states is dense, resulting in more complicated features because of congestion. Indeed, the electronic states of 9MA+, as those of canonical adenine cation, are coupled vibronically, and Koopmans’ correlations and monoconfigurational approaches are not sufficient to model the electronic structure of such a cation. For instance, our work reveals that the band structure only loosely corresponds to the photoionization transitions because of the possible large or small geometry change and the resulting Franck–Condon gaps. Also, the dynamics of photoionization of this biological entity should be very complex, more so than in canonical adenine, because of the higher density of states of 9MA+ and the subsequent interactions and couplings. This may explain the different dynamics observed on ultrashort time scales for the highly excited electronic states of 9MA as compared to its non-substituted base.8
Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
This study was carried out while M. H. was the Waernska Guest Professor at the University of Gothenburg, Sweden. The support of this Guest Professorship is hereby gratefully acknowledged. Some of the computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at the Chalmers Centre for Computational Science and Engineering (C3SE) partially funded by the Swedish Research Council through grant agreement no. 2018–05973. K. A. thanks the Tunisian Ministry for Higher Education and Research for a fellowship for the preparation of this work. R. F. and M. H. acknowledge financial support from the Swedish Research Council (VR) – grant number 2018–03731. We are indebted to the general technical staff of Synchrotron Soleil for running the facility under proposal #20181477. We would also like to thank H. Mouhib, M. Schwell and L. Poisson for their help while collecting the data and J.-F. Gil for his technical help on the SAPHIRS molecular beam chamber.References
- K. D. Rasmussen and K. Helin, Role of TET enzymes in DNA methylation, development, and cancer, Genes Dev., 2016, 30, 733e750, DOI:10.1101/gad.276568.115.
- C. H. Vinkers, A. L. Kalafateli, B. P. F. Rutten, M. J. Kas, Z. Kaminsky, J. D. Turner and M. P. M. Boks, Traumatic stress and human DNA methylation: a critical review, Epigenomics, 2015, 7, 593e608, DOI:10.2217/epi.15.11.
- H. Heyn and M. Esteller, An adenine code for DNA: a second life for N6-methyladenine, Cell, 2015, 161, 710e713, DOI:10.1016/j.cell.2015.04.021.
- J. C. Delaney and J. M. Essigmann, Mutagenesis, genotoxicity, and repair of 1-methyladenine, 3-alkylcytosines, 1-methylguanine, and 3-methylthymine in alkB Escherichia coli, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14051e14056 Search PubMed.
- Y. T. Wu, H. L. Tan, G. Shui, C. Bauvy, Q. Huang, M. R. Wenk, C. N. Ong, P. Codogno and H. M. Shen, Dual role of 3-methyladenine in modulation of autophagy via different temporal patterns of inhibition on class I and III phosphoinositide 3-kinase, J. Biol. Chem., 2010, 285, 10850e10861, DOI:10.1074/jbc.M109.080796.
- D. C. Lührs, J. Viallon and I. Fischer, Excited state spectroscopy and dynamics of isolated adenine and 9-methyladenine, Phys. Chem. Chem. Phys., 2001, 3, 1827–1831 RSC.
- S. Smolarek, A. M. Rijs, W. J. Buma and M. Drabbels, Absorption spectroscopy of adenine, 9-methyladenine, and 2-aminopurine in helium nanodroplets, Phys. Chem. Chem. Phys., 2010, 12, 15600–15606 RSC.
- C. Canuel, M. Elhanine, M. Mons, F. Piuzzi, B. Tardivel and I. Dimicoli, Time-resolved photoelectron and photoion fragmentation spectroscopy study of 9-methyladenine and its hydrates: a contribution to the understanding of the ultrafast radiationless decay of excited DNA bases, Phys. Chem. Chem. Phys., 2006, 8, 3978 RSC.
- Y. Xue, D. Xie and G. Yan, Density functional theory studies on molecular structure and IR spectra of 9-methyladenine: A scaled quantum mechanical force field approach, Int. J. Quantum Chem., 2000, 76, 686–699 CrossRef CAS.
- S. G. Stepanian, G. G. Sheina, E. D. Radchenko and Y. P. Blagoi, Theoretical and experimental studies of adenine, purine and pyrimidine isolated molecule structure, J. Mol. Struct., 1985, 131, 333–346 CrossRef.
- R. Savoie, D. Poirier, L. Prizant and A. L. Beauchamp, Raman and infrared spectra of crystalline 9-methyladenine and its methylmercury complexes, J. Raman Spectrosc., 1981, 11, 481–486 CrossRef CAS.
- Y. Kyogoku, S. Higuchi and M. Tsuboi, Intra-red absorption spectra of the single crystals of 1-methyl-thymine, 9-methyladenine and their 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, Spectrochim. Acta, Part A, 1967, 23, 969–983 CrossRef CAS.
1 complex, Spectrochim. Acta, Part A, 1967, 23, 969–983 CrossRef CAS. - T. Gustavsson, N. Sarkar, I. Vayá, M. Consuelo Jiménez, D. Markovitsi and R. Improta, A joint experimental/theoretical study of the ultrafast excited state deactivation of deoxyadenosine and 9-methyladenine in water and acetonitrile, Photochem. Photobiol. Sci., 2013, 12, 1375 CrossRef CAS.
- D. B. Nguyen, S. W. Joo and J. Choo, Interfacial structures of 1-methyladenine, 3-methyladenine, 7-methyladenine, and 9-methyladenine on gold nanoparticles by Raman spectroscopy, J. Mol. Struct., 2017, 1128, 215–220 CrossRef CAS.
- M. Hanus, M. Kabelac, J. Rejnek, F. Ryjacek and P. Hobza, Correlated ab initio studyof nucleic acid bases and their tautomers in the gas phase, in a microhydrated environment, and in aqueous solution. Part 3. Adenine, J. Phys. Chem. B, 2004, 108, 2087e2097 CrossRef.
- M. Kabel, C. Plützer, K. Kleinermanns and P. Hobza, Isomer selective IR experiments and correlated ab initio quantum chemical calculations support planar H-bonded structure of the 7-methyl adenine/adenine and stacked structure of the 9-methyl adenine/adenine base pairs, Phys. Chem. Chem. Phys., 2004, 6, 2781e2785 Search PubMed.
- S. Peng, A. Pavda and P. R. LeBreton, Ultraviolet photoelectron studies of biological purines: the valence electronic structure of adenine, Proc. Natl. Acad. Sci. U. S. A., 1976, 73, 2966–2968 CrossRef CAS.
- J. Lin, C. Yu, S. Peng, I. Akiyama, K. Li, K. L. Li and P. R. LeBreton, Ultraviolet photoelectron studies of the ground-state electronic structure and gas-phase tautomerism of purine and adenine, J. Am. Chem. Soc., 1980, 102, 4627–4631 CrossRef CAS.
- H. Satzger, D. Townsend and A. Stolow, Reassignment of the low lying cationic states in gas phase adenine and 9-methyl adenine, Chem. Phys. Lett., 2006, 430, 144–148 CrossRef CAS.
- H. Satzger, D. Townsend, M. Z. Zgierski, S. Patchkovskii, S. Ullrich and A. Stolow, Primary processes underlying the photostability of isolated DNA bases: Adenine, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10196–10201 CrossRef CAS.
- S. R. Huang, A. Dang and F. Turecek, Ground and Excited States of Gas-Phase DNA Nucleobase Cation-Radicals. A UV-vis Photodisociation Action Spectroscopy and Computational Study of Adenine and 9-Methyladenine, J. Am. Soc. Mass Spectrom., 2020, 31, 1271–1281 CrossRef CAS PubMed.
- H. Y. Zhao, K.-C. Lau, G. A. Garcia, L. Nahon, S. Carniato, L. Poisson, M. Schwell and M. Hochlaf, Unveiling the complex vibronic structure of the canonical adenine cation, Phys. Chem. Chem. Phys., 2018, 20, 20756–20765 RSC.
- L. Nahon, N. de Oliveira, G. A. Garcia, J.-F. Gil, B. Pilette, O. Marcouillé, B. Lagarde and F. Polack, DESIRS: a state-of-the-art VUV beamline featuring high resolution and variable polarization for spectroscopy and dichroism at SOLEIL, J. Synchrotron Radiat., 2012, 19, 508–520 CrossRef CAS PubMed.
- G. A. Garcia, B. K. Cunha de Miranda, M. Tia, S. Daly and L. Nahon, DELICIOUS III: a multipurpose double imaging particle coincidence spectrometer for gas phase vacuum ultraviolet photodynamics studies, Rev. Sci. Instrum., 2013, 84, 053112 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, Velocity map imaging of ions and electrons using electrostatic lenses: Application in photoelectron and photofragment ion imaging of molecular oxygen, Rev. Sci. Instrum., 1997, 68, 3477 CrossRef CAS.
- G. A. Garcia, L. Nahon and I. Powis, Two-dimensional charged particle image inversion using a polar basis function expansion, Rev. Sci. Instrum., 2004, 75, 4989 CrossRef CAS.
- B. Mercier, M. Compin, C. Prevost, G. Bellec, R. Thissen, O. Dutuit and L. Nahon, Experimental and theoretical study of a differentially pumped absorption gas cell used as a low energy-pass filter in the vacuum ultraviolet photon energy range, J. Vac. Sci. Technol., A, 2000, 18, 2533 CrossRef CAS.
- K. Yoshino and Y. Tanaka, Absorption spectrum of krypton in the vacuum UV region, J. Opt. Soc. Am., 1979, 69, 159 CrossRef CAS.
- J. C. Poully, J. P. Schermann, N. Nieuwjaer, F. Lecomte, G. Grégoire, C. Desfrançois, G. A. Garcia, L. Nahon, D. Nandi, L. Poisson and M. Hochlaf, Photoionization of 2-pyridone and 2-hydroxypyridine, Phys. Chem. Chem. Phys., 2010, 12, 3566–3572 RSC.
- M. Briant, L. Poisson, M. Hochlaf, P. de Pujo, M.-A. Gaveau and B. Soep, Ar2 Photoelectron Spectroscopy Mediated by Autoionizing States, Phys. Rev. Lett., 2012, 109, 193401 CrossRef PubMed.
- M. J. Frisch, et al., Gaussian 16, revision A.02, Gaussian, Inc., Wallingford, CT, 2016.
- C. Adamo and V. Barone, Toward Reliable Density Functional Methods Without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- T. H. Dunning, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- M. L. Laury, M. J. Carlson and A. K. Wilson, Vibrational frequency scale factors for density functional theory and the polarization consistent basis sets, J. Comput. Chem., 2012, 33, 2380–2387 CrossRef CAS.
- P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 1993, 99, 5219 CrossRef CAS.
- P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 2000, 112, 3106 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- T. B. Adler, G. Knizia and H.-J. Werner, A simple and efficient CCSD(T)-F12 approximation, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- H.-J. Werner, G. Knizia and F. R. Manby, Explicitly correlated coupled cluster methods with pair-specific geminals, Mol. Phys., 2011, 109, 407–417 CrossRef CAS.
- G. Knizia, T. B. Adler and H.-J. Werner, Simplified CCSD(T)-F12 methods: Theory and benchmarks, J. Chem. Phys., 2009, 130, 054104 CrossRef CAS PubMed.
- H. J. Werner and P. J. Knowles, et al., MOLPRO version 2015 is a package of ab initio programs, See http://www.molpro.net, University of Cardiff Chemistry Consultants (UC3), Cardiff, Wales, UK, 2015.
- F. A. Weigend, A fully direct RI-HF algorithm: Implementation, optimised auxiliary basis sets, demonstration of accuracy and efficiency, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC.
- C. Hättig, Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations: Core–valence and quintuple-ζ basis sets for H to Ar and QZVPP basis sets for Li to Kr, Phys. Chem. Chem. Phys., 2005, 7, 59–66 RSC.
- W. Klopper, Highly accurate coupled-cluster singlet and triplet pair energies from explicitly correlated calculations in comparison with extrapolation techniques, Mol. Phys., 2001, 99, 481–507 CrossRef CAS.
- K. E. Yousaf and K. A. Peterson, Auxiliary RI Basis Sets (OptRI) matched to cc-pVnZ-F12: H, B–Ne, Al–Ar, J. Chem. Phys., 2008, 129, 184108 CrossRef.
- M. Hochlaf, Advances in spectroscopy and dynamics of small and medium sized molecules and clusters, Phys. Chem. Chem. Phys., 2017, 19, 21236–21261 RSC.
- K. A. Peterson and T. H. Dunning, Accurate correlation consistent basis sets for molecular core–valence correlation effects: The second row atoms Al–Ar, and the first row atoms B–Ne revisited, J. Chem. Phys., 2002, 117, 10548 CrossRef CAS.
- M. Douglas and N. M. Kroll, Quantum electrodynamical corrections to the fine structure of helium, Ann. Phys., 1974, 82, 89–155 CAS.
- G. Jansen and B. A. Hess, Revision of the Douglas-Kroll transformation, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 6016–6017 CrossRef.
- W. A. de Jong, R. J. Harrison and D. A. Dixon, Parallel Douglas–Kroll energy and gradients in NWChem: Estimating scalar relativistic effects using Douglas–Kroll contracted basis sets, J. Chem. Phys., 2001, 114, 48 CrossRef CAS.
- M. Lax, The Franck–Condon Principle and Its Application to Crystals, J. Chem. Phys., 1952, 20, 1752 CrossRef CAS.
- V. Barone, J. Bloino, M. Biczysko and F. Santoro, Fully Integrated Approach to Compute Vibrationally Resolved Optical Spectra: From Small Molecules to Macrosystems, J. Chem. Theory Comput., 2009, 5, 540–554 CrossRef CAS PubMed.
- J. Bloino, M. Biczysko, F. Santoro and V. Barone, General Approach to Compute Vibrationally Resolved One-Photon Electronic Spectra, J. Chem. Theory Comput., 2010, 6, 1256–1274 CrossRef CAS.
- J. Bloino, A. Baiardi and M. Biczysko, Aiming at an Accurate Prediction of Vibrational and Electronic Spectra for Medium-to-Large Molecules: An Overview, Int. J. Quantum Chem., 2016, 116, 1543–1574 CrossRef CAS.
- Y. Pan, K.-C. Lau, L. Poisson, G. A. Garcia, L. Nahon and M. Hochlaf, J. Phys. Chem. A, 2013, 117, 8095 CrossRef CAS PubMed.
- Y. Pan, K.-C. Lau, M. M. Al-Mogren, A. Mahjoub and M. Hochlaf, Chem. Phys. Lett., 2014, 613, 29 CrossRef CAS.
- Z. Chen, K.-C. Lau, G. A. Garcia, L. Nahon, D. K. Božanić, L. Poisson, M. Mogren Al-Mogren, M. Schwell, J. S. Francisco, A. Bellili and M. Hochlaf, Identifying cytosine-specific isomers via high-accuracy single photon ionization, J. Am. Chem. Soc., 2016, 138, 16596–16599 CrossRef CAS.
- I. Derbali, H. R. Hrodmarsson, M. Schwell, Y. Bénilan, L. Poisson, M. Hochlaf, M. E. Alikhani, J.-C. Guillemin and E.-L. Zins, Unimolecular decomposition of methyl ketene and its dimer in the gas phase: theory and experiment, Phys. Chem. Chem. Phys., 2020, 22, 20394–20408 RSC.
- I. Derbali, H. R. Hrodmarsson, Z. Gouid, M. Schwell, M.-C. Gazeau, J.-C. Guillemin, M. Hochlaf, M. E. Alikhani and E.-L. Zins, Photoionization and Dissociative Photoionization of Propynal in the Gas Phase: Theory and Experiment, Phys. Chem. Chem. Phys., 2019, 21(26), 14053–14062 RSC.
- P. J. Knowles and H.-J. Werner, An efficient second-order MC SCF method for long configuration expansions, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, A second order multiconfiguration SCF procedure with optimum convergence, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- T. Shiozaki, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 134, 034113 CrossRef PubMed.
- T. Shiozaki and H.-J. Werner, J. Chem. Phys., 2011, 134, 184104 CrossRef PubMed.
- T. Shiozaki and H.-J. Werner, Mol. Phys., 2013, 111, 607 CrossRef CAS.
- J. Wiorkiewicz-Kuczer and M. Karplus, Ab initio study of the vibrational spectra of N9–H and N7–H adenine and 9-methyladenine, J. Am. Chem. Soc., 1990, 112, 5324–5340 CrossRef.
- Y. Xue, D. Xie and G. Yan, Density functional theory studies on molecular structure and IR spectra of 9-methyladenine: A scaled quantum mechanical force field approach, Int. J. Quantum Chem., 2000, 76, 686–699 CrossRef CAS.
- E. L. Stewart, C. K. Foley, L. Allinger and J. P. Bowen, Ab Initio Calculations with Electronic Correlation (MP2) on the Nucleic Acid Bases and Their Methyl Derivatives, J. Am. Chem. Soc., 1994, 116, 7282 CrossRef CAS.
- F. Merkt, A. Osterwalder, R. Seiler, R. Signorel, H. Palm, H. Schmutz and R. Gunzinger, High Rydberg states of argon: Stark effect and field-ionization properties, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, 1705 CrossRef CAS.
- T. Baer, Vacuum UV Photophysics and Photoionization Spectroscopy, Annu. Rev. Phys. Chem., 1989, 40, 637–669 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The full set of theoretical data, including optimized equilibrium structures of the neutral and ionic 9-methyladenine species and of their energetics. See DOI: 10.1039/d1cp03729c |
| This journal is © the Owner Societies 2022 |
