Open Access Article
Open Access ArticleOn the underestimated influence of synthetic conditions in solid ionic conductors
Ananya
Banik
a,
Theodosios
Famprikis
 b,
Michael
Ghidiu
c,
Saneyuki
Ohno
b,
Michael
Ghidiu
c,
Saneyuki
Ohno
 d,
Marvin A.
Kraft
a and
Wolfgang G.
Zeier
d,
Marvin A.
Kraft
a and
Wolfgang G.
Zeier
 *ae
*ae
aInstitute for Inorganic and Analytical Chemistry, University of Muenster, Corrensstr. 30, 48149 Münster, Germany. E-mail: wzeier@uni-muenster.de
bDepartment of Radiation Science and Technology, Delft University of Technology, Mekelweg 15, Delft, 2629 JB, Netherlands
cInstitute of Physical Chemistry, Justus-Liebig-University Giessen, Heinrich-Buff-Ring 17, D-35392 Giessen, Germany
dDepartment of Applied Chemistry, Graduate School of Engineering, Kyushu University, 744 Motooka, Nishi-ku, 819-0395 Fukuoka, Japan
eHelmholtz Institute Münster (IEK-12), Forschungszentrum Jülich GmbH, Corrensstr. 46, 48149 Münster, Germany
First published on 29th March 2021
Abstract
The development of high-performance inorganic solid electrolytes is central to achieving high-energy- density solid-state batteries. Whereas these solid-state materials are often prepared via classic solid-state syntheses, recent efforts in the community have shown that mechanochemical reactions, solution syntheses, microwave syntheses, and various post-synthetic heat treatment routines can drastically affect the structure and microstructure, and with it, the transport properties of the materials. On the one hand, these are important considerations for the upscaling of a materials processing route for industrial applications and industrial production. On the other hand, it shows that the influence of the different syntheses on the materials' properties is neither well understood fundamentally nor broadly internalized well. Here we aim to review the recent efforts on understanding the influence of the synthetic procedure on the synthesis – (micro)structure – transport correlations in superionic conductors. Our aim is to provide the field of solid-state research a direction for future efforts to better understand current materials properties based on synthetic routes, rather than having an overly simplistic idea of any given composition having an intrinsic conductivity. We hope this review will shed light on the underestimated influence of synthesis on the transport properties of solid electrolytes toward the design of syntheses of future solid electrolytes and help guide industrial efforts of known materials.
1. Introduction
Since their commercial introduction,1,2 rechargeable lithium-ion batteries have become necessary parts of our daily lives, especially in the realms of transportation and mobile electronics. In these areas, demands for smaller, safer, and more energy-dense batteries are only expected to increase in the coming years.3 By far the most used architecture to date involves solid electrodes and a liquid electrolyte (generally a lithium salt dissolved in organic solvents).2 Problems with the liquid electrolyte systems involve flammability (in the case of cell short-circuits or rupture),4 lowered transference numbers,5,6 and prevalence of dendrite growth leading to shorting, disallowing use of higher-energy-density lithium metal anodes.7 Though dendrite formation and cell short-circuiting is intrinsic to the use of lithium metal electrode irrespective of the nature of an electrolyte,8 the ease of growth of dendrites is especially a problem for liquid electrolyte cell when combined with flammability concerns. Engineering solutions have been proposed for these issues,7 but a more promising path altogether is the use of solid electrolytes.9 Due to understandably poorer conduction, many solids were not initially thought of as viable, with some focus on polymers or supported gels.7 However, the emergence of superionic solids that could conduct lithium and sodium nearly as well as some liquids brought extreme interest to the concept of the all-solid-state battery.10–12 These materials offer excellent ionic conductivities,11,13–15 low electronic conductivity saving the cell from self-discharge,16 a transference number near unity which further can boost the power density of the cells.11Typical solid ionic conductors include polymeric materials;17 oxides such as LISICON (lithium superionic conductor)18,19 and NASICON (sodium superionic conductor and Li-ion conducting sodium superionic conductor)20 – type phosphates and garnets such as Li7La3Zr2O12 (LLZO);21 sulfides such as thio-LISICONs22 and thiophosphates, including the argyrodites Li6PS5X (X = Cl, Br, I),13,14,23 Li10MP2S12 (LMPS) (M = Si, Ge, Sn)11,15,24,25 or Na3MS4 (M = P, Sb)26,27 and its substituted analogues.12 Other materials such as the ternary halides, lithium hydride, and lithium nitride also garner interest.28–30 All these materials have been reviewed in-depth in the literature so we suffice it to say here that each class spans a wide range of advantages and disadvantages in various properties: ionic and electronic conductivity, electrochemical stability windows, mechanical softness or brittleness, the energy required for synthesis and processing, cost of materials.30–32 Ionic conductivity, however, retains a high focus as a key property for determining whether a candidate material will be acceptable for battery application.33,34 Especially, considering the solid composite nature in absence of liquids, these solid-state batteries require fast ionic transport with ionic conductivities of cold-pressed materials ideally exceeding 10 mS cm−1 in order to achieve high materials loading and high partial ionic conductivities.34,35
In this review we will focus on the inorganic ion conductors, which exhibit a large range of conductivities for similar or identical materials based on synthetic protocol. To illustrate how much of an effect is possible, Fig. 1 shows a graphical summary of a number of selected materials from the literature. The spread within a single class can be as much as five orders of magnitude, with differences arising from the ways the materials were made or treated; it is important to note, however, that these effects are attributable to the produced materials themselves and cannot be explained solely on the basis of differences in the conductivity measurement protocols.36
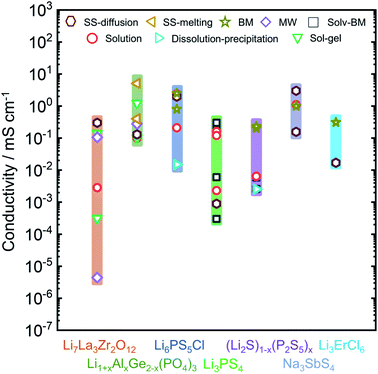 | ||
| Fig. 1 Overview of the observed ionic conductivities for well-known Li-ion and Na-ion conducting electrolytes including Li7La3Zr2O12,37–43 Li1+xAlxGe2−x(PO4)3,44–51 Li6PS5Cl,14,52–55 Li3PS4,56–61 (Li2S)x–(P2S5)100−x,62–65 Na3SbS4,12,66–68 and Li3ErCl6 (ref. 69) as a function of synthetic condition. Conductivity can vary over orders of magnitude, based on the adopted synthesis route. Li1+xAlxGe2−x(PO4)3 column represents the conductivities for Li1+xAlxGe2−x(PO4)3 with x = 0.4, 0.5. (Li2S)x(P2S5)100−x column consists of conductivities data from non-crystalline phases of (Li2S)x(P2S5)100−x with x = 75, 80. | ||
Tailoring structures to optimize ionic conductivity in solids is becoming better understood. Body-centred-cube-like structures with face-sharing tetrahedra are ideal to avail low ion-diffusion barrier and high conductivity.16,33 Recent discoveries have reestablished the correlation between lattice dynamics and ionic transport.70–72 The presence of soft, polarizable anionic frameworks is responsible for widening of ion-diffusion pathway and low activation barrier.70 However, because measurements on or implementation in batteries of solid electrolytes generally involve polycrystalline materials, a myriad of other phenomena can influence performance; these can be in turn very sensitive to the synthesis and treatment of the materials. Some of these phenomena include:
Densification
Higher contact area and more percolation pathways not only lead to higher ion conductance but also allow complete electrochemical utilization of active materials.73 Densification can result from e.g. sintering, or from pressure applied either prior to a measurement or during measurement.13,74,75 For applied pressure, the elastic modulus, fracture toughness of the material are important. By use of softer materials, like the thiophosphates better connectivity with the adjacent phases like electrode materials can be achieved by allowing elastic-deformation as opposed to oxides; nevertheless, both the materials are prone to crack formation under stress due to low fracture toughness.70,73,76–78Particle morphology, orientation and grain size
Some materials are ionic conductors only in one or two dimensions.79 Hence, changes in bulk conductivity can arise if there are differences in grain orientation, aspect ratio, or size.48,80 Grain boundaries can also influence conductivity due to impurity segregation and, therefore, formation of space charge layer.Change in crystalline and amorphous content
Bulk materials with a fixed chemical composition often contain changing percentages of crystalline and amorphous regions.81 These can have very different transport properties, with no general rule governing which has the higher conductivity. For instance, amorphous Li–thiophosphates are faster conductors than their crystalline counterparts, but for argyrodites, the crystalline phase has the higher conductivity.82–84 Some phases, such as Li7P3S11, may always inherently exist as mixture of glassy and crystalline phases (or glass–ceramics).83,85 This theme can also include local structural changes that are not reflected in the bulk crystal structure, as well as phase changes into different polymorphs, e.g. between β and γ forms of Li3PS4.86Change in local or bulk chemical composition
A bulk material of a given chemical composition can, under some circumstances, experience local changes in composition. Li7P3S11, for example, can undergo decomposition into the poor conductor Li4P2S6 by reduction of PV to PIV with additional sulfur segregating to another phase.87Strain
Structures can, through various pathways, have strain that may lead to change in the lattice volume and thus differences in the ability to conduct ions.81,88 It is worth mentioning here that use of solid electrolytes in lithium ion battery does not solve the problem of lithium dendrite formation and cell short circuiting. Due to the lower density of the solid electrolyte, the presence of a porous network or internal cracking. Recent studies have predicted beneficial role of compressive force as an electrolyte processing parameter to prevent lithium penetration and dendritic degration.89Structural disorder
A relatively new direction of exploration, some compositions contain atoms on different crystallographic sites that can be exchanged; a prime example is Li6PS5Br or the ternary lithium halides.69,84,90 Disorder between the exchangeable sites can alter the activation barriers of ionic movement.In this review, we wish to show how all these factors can be extremely important in determining the overall usefulness of a solid electrolyte material, and that synthesis and processing conditions can lead to such changes occurring, sometimes in combination. Understanding what will happen to a solid electrolyte throughout its production and how to control the processes is critical in producing optimized solid-state batteries.
2. Overview of possible synthetic conditions
In this section, common techniques of synthesis of ionic conductors will be reviewed in order to provide a baseline for the reader to follow the subsequent discussions of how synthesis parameters influence structures, chemistry, and transport. This will include high-temperature, mechanochemical, solvent-based, and microwave techniques, with discussion on variable parameters such as precursor routes, temperature programming, mechanical energy input, and solvent selection. Table 1 summarizes the advantages and drawbacks of these synthesis techniques for solid electrolyte preparation.| Method | Advantage | Disadvantage |
|---|---|---|
| Classical high-temperature solid-state syntheses | Well-explored; much background knowledge | Bulk material production is time and energy consuming and not suitable for practical use |
| Not suitable for non-equilibrium phase formation | ||
| Mechanochemical syntheses | Scalable material production; synthesis of non-equilibrium phases, reduced post synthesis processing time and temperature | Difficult to control the particle morphology. Optimization of processing parameters is needed |
| Solution syntheses | Scalable, cost-effective approach; synthesis of non-equilibrium phases, reduced post-synthesis processing time and temperature. Possibility controlled particle morphology | Underlying reaction chemistry sometimes poorly understood, as well as interactions between reagents and solvent |
| Solvent choice can be critical but is nontrivial. Solvent residue or carbonized solvent can remain in product | ||
| Sol–gel syntheses | Scalable; non-equilibrium phases attainable | Expensive alkoxide routes. Not universally applicable since it is difficult to choose the right alkoxide reagents having similar reactivity for a given stoichiometry |
| Microwave syntheses | Energy-efficient and cost-effective synthesis process | Not well-optimized; influence on phase formation is not well understood yet |
| Post-synthetic treatments | Controlled material density, particle size and morphology, crystallinity and associated conductivity | Materials decomposition if the conditions are not carefully monitored |
2.1 Solid-state synthesis
One of the most accessible and straightforward routes to obtaining solid electrolytes is by mixing solid precursors and applying heat to drive their reaction. Such synthesis is referred to as “solid-state-”, “high-temperature-” or “ceramic-” synthesis91 and has led to the synthesis of some of the most highly conducting Li+ and Na+ solid electrolytes in recent literature. For example, the Li6.6Si0.4Sb0.6S5I, synthesized from binary reagents via solid-state routes, shows Li+ conductivity of 14.8 mS cm−1.92 Similarly, the synthesis of the W-doped Na2.9Sb0.9W0.1S4 with a Na+ conductivity of ∼40 mS cm−1 was also achieved by solid-state synthesis.12,27The first step in any solid-state synthesis is ensuring the intimate mixing of the reagent powders, which is crucial given the limited diffusivity of atoms in the solid-state. Since the reactivity of a material varies significantly with particle size, selection of the starting materials itself plays a dominant role. Further, grinding helps to reduce the particle sizes, prepare a homogenous precursor mixture and generate interfaces of physical contact between the reagent powders, all of which help to overcome diffusion limited product particle growth. Such grinding can be performed manually, using a mortar and pestle, or mechanically using a milling machine, typically a ball-mill. In certain cases, mechanical milling alone can drive reactions to completion, referred to as mechanochemical synthesis, which will be discussed specifically in Section 2.2. After grinding, the powder mixtures are typically densified into pellets through mechanical pressing to reduce porosity and thus maximize physical contact between the reagent particles.
The subsequent control of the sample environment can decisively affect the results of solid-state synthesis. The reaction vessel must be chosen to eliminate the possibility of reactivity with the reagents, with typical choices being alumina, silica (quartz), and glassy carbon. Still, either unintended incorporation of chemical species from the vessel or change in stoichiometry of the product due to loss of reagents by reaction on the vessel surface can occur; for example, synthesis of Li7La3Zr2O12 garnet in alumina crucibles leads to Al-doping, which in itself was the reason for the success of Li7La3Zr2O12 early on, as it stabilizes the fast conducting cubic phase.93 For cases of extreme reactivity, refractory materials such as tungsten, tantalum and boron nitride can also be used. For solid electrolytes, noble metal crucibles (e.g. gold, silver, platinum) are not preferred due to their reactivity/alloying with the alkali metals and their preferred reaction with sulfides. For example, the synthesis of Na3PS4 in Au crucibles leads to the formation of Na3AuS2 side-phase.94 The ambient atmosphere can be manipulated to promote oxidizing or reducing conditions, typically by introducing O2 or H2 gases, respectively. For reagents or products that are prone to reaction with ambient air (O2, N2, H2O and/or CO2), reactions must be carried out under controlled atmosphere, typically under inert gas (N2, He, Ne, Ar) or vacuum. For example, most sulfides will hydrolyze producing H2S upon exposure to air,95 and oxides such as the Li7La3Zr2O12 garnet are prone to protonation by Li+/H+ exchange and surface carbonation by Li2CO3 formation,96–99 which can decrease ionic conductivity by one or more orders of magnitude.100 Thus, in practice, such manipulations typically involve a glove-box, either featuring a furnace or in combination with a sealable reaction vessel. For Li-ion conducting sulfides, a typical setup involves the sample placed in an evacuated silica ampoule whose interior walls have been coated with carbon through pyrolysis of a solvent such as acetone, or the use of glassy-carbon crucibles.13,81
The reaction temperature profile refers to the change of the furnace (and by extension, sample) temperature over time. This includes target temperature(s), annealing time(s) as well as heating and cooling rates. The temperature(s) dictate the state(s) that the reactants and products will pass through, depending on the phase diagrams of the constituent elements. The effects of temperature can be simply understood through the concept of entropy. Higher temperatures tend to favor symmetric, single-phase (i.e. solid solution) behavior by promoting disorder and reactant atom diffusivity. This is especially relevant to ion conductors for which disorder is often desirable. In contrast, lower temperatures tend to favor phase separation through ordering of the atomic constituents. For example, heating a heterogeneous equimolar mixture of Li3PO4 and Li4SiO4 will result in a single phase Li3.5P0.5Si0.5O4, where the PO43− and SiO44− are randomly distributed, increasing the ionic conductivity by at least three orders of magnitude compared to the end-members.101 Manipulating such solid solutions is a key strategy in controlling the concentration of charge carriers in an solid and as such tailoring ionic conductivity.18,101
In the absence of accurate phase diagrams, important temperatures to consider are phase transitions (typically melting) of the reactants and products. Melting of a reaction mixture can strongly increase reaction rates and facilitate homogeneous mixing of elemental constituents, owing to the much faster diffusion rates in the liquid phase. Nevertheless, melting is not always desirable owing to various possible complications, e.g. reactivity with the reaction container, volatilization of the reaction mixture, and incongruent solidification. For example, the high-performance quaternary phase Li10GeP2S12 will melt incongruently above ∼600 °C into a phosphorus-rich liquid, from which it is almost impossible to recover a pure phase.102 Regrettably, construction of phase diagrams and accurate melting point determination are not commonplace in recent solid-electrolyte-related work. The case of Li10GeP2S12 provides a notable exception; the careful determination of the Li3PS4–Li4GeS4 phase diagram,102 has enabled the rational synthesis optimization as well as the growth of single crystals of this seminal material for in-depth structural and dynamic studies.103
The cooling and heating rates can be used to control kinetic effects that might affect a given synthesis. Generally, if the reaction product is thermodynamically favored, low rates and long annealing time are preferred. Lower heating rates also practically help to alleviate the overshoot of temperature that might be experienced by the sample. Long annealing times and slower cooling rates result in better crystallinity by allowing for grain growth (sintering) and the release of mechanical strain induced by lattice contraction during cooling (thermal shock) which can have a severe impact on crystal structure and ion transport. A notable example is that of the Li7La3Zr2O12-type garnets104 and NASICONs105 that present high intrinsic ionic conductivities of the order of mS cm−1 in the bulk but typically blocking grain boundaries that decrease the conductivity in polycrystalline pellets. Here, the parameters of the thermal treatment greatly affect the resulting microstructural features (grain size, grain boundaries, phase impurities) which in turn control the final ionic conductivity.48 In another example, variation of the grain-size of the Li0.3La0.57TiO3 perovskite in the range 860 to 25 nm through sintering was shown to decrease its ionic conductivity by four orders of magnitude, likely again due to the presence of more blocking grain boundaries.106
If the desired product is not thermodynamically favored at temperatures below the reaction temperature, a fast cooling rate can help kinetically stabilizing it, a procedure commonly referred to as quenching. The desired product can be a distinct crystallographic polymorph or a more disordered arrangement of constituents in a given crystal structure, often quantified by partial occupation of shared sites. While a slow cooling might allow for the ordering of constituents with decreasing temperature, quenching can “freeze” the high temperature configuration if the necessary atomic rearrangements are too slow to occur at lower temperature, even if they are thermodynamically favored. In practice, quenching is typically performed by submerging the reaction container in a cold fluid, typically water, but also oil or liquid nitrogen; even room-temperature air can sometimes be used depending on the reaction kinetics. The higher the heat capacity and thermal conductivity of the quenching fluid, the higher the cooling rate. Such effects have recently been demonstrated for the argyrodite Li6PS5Br, in which the S2−/Br− site disorder decisively affects ion transport by affecting the dynamics of Li+ diffusion.84 By cooling at different rates and from different temperatures the authors showed that the degree of site disorder could be controlled, with quenching increasing the resulting ionic conductivity fourfold compared to slower cooling.84 The ability of the reaction vessel to withstand thermal shock is critical; quartz can remain intact through rapid changes over hundreds of degrees, while a quenched ampoule of borosilicate glass might have quite undesirable results.
A final comment that is especially relevant to the solid-state synthesis of ion conductors pertains to the common volatilization of the reagents at high temperature, leading to deviations from the intended stoichiometry of the final product. Typical culprits involve S, O2, and Li/Na-precursors, which tend to develop non-negligible vapor pressures. This is prevalent, e.g. in the synthesis of Li7La3Zr2O12-type garnets where volatilization of Li leads to decrease the final Li content of the material.104 Such problems are typically empirically alleviated through the addition of excess, “sacrificial” amounts of these reagents, which however requires careful trial and error for stoichiometric control.
2.2. Mechanochemical synthesis
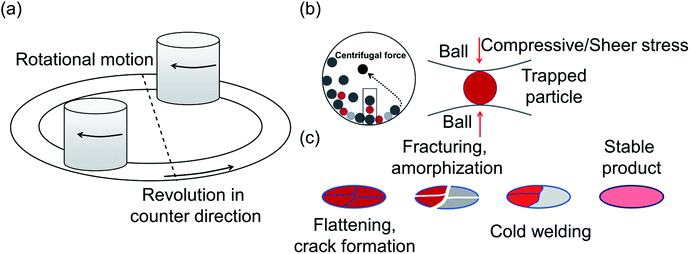
Another common synthetic route for the successful production of pure ion conductors is the use of mechanochemistry, which deals with the influence of mechanical energy like compression, shear or friction in chemical and physicochemical transformations.69,107–110 Though mechanochemical synthesis (often mentioned as ‘ball milling’) was discovered as a subsection of solid-state synthesis, in recent days it is a widely used synthetic technique in various fields including metal–organic frameworks, biomaterials, catalysts, organics, and pharmaceuticals.111 The hallmark of this method includes the application of mechanical force controlling the reactivity of solids by the evolution of crystal defects, interphases, and tuning the relaxation phenomena, where materials can be effectively ground, amorphized, and mixed. Thus, it facilitates the reactions to occur under non-equilibrium conditions.107,112,113 This brings several technological successes including synthesis of non-equilibrium phases with the desired dimension, enhanced concentration of vacancies, formation of crystal defects, a striking reduction of crystallization temperature and post-synthetic annealing time duration which ultimately gives the choice to tune their transport, reproducibility, high production yield and efficient utilization of energy and materials under basic operating conditions.69,84,114 For Li-ion conductors, defects are required for long-range ion conduction. Thus, mechanochemical synthesis is a well-known route used for the synthesis of Li-ion conducting sulfide glass electrolytes. The synthesis of crystallized ion conductors involves amorphous phase formation via ball milling followed by an additional annealing step.15,115,116 The mechanochemical synthesis of garnet-like Li-ion conductors offers a significant reduction of annealing temperature and time.113 The synthesis of superionic argyrodites (Li6PS5X, X = Cl, Br, I) requires much lower crystallization time as compared to material synthesized by usual diffusion-mediated solid-state synthesis.117,118 Furthermore, it is a common route to prepare nano-dimensional heterostructured ion conductors.119 Improved interfacial ion diffusion has been realized in nanocrystalline Li2O–X2O3 heterostructure when Li2O, an ion conductor and ionic insulator X2O3 (X = Al, B) were mechanochemically mixed.120 Mechanochemically-synthesized halide-substituted LiBH4 (Li4(BH4)3I) has shown superior conductivity.121 Recently, ternary metal halides have been rediscovered as promising solid electrolyte candidate when prepared via mechanochemical route.69,122The important variables which influence the milling process include type of the mill, nature of milling media (size, mass, mechanical strength and chemical composition), milling media-to-sample ratio, filling extent of the milling chamber, milling atmosphere, milling speed at a constant speed ratio, milling time, etc. These variables can alter the nature of impacts like the stress frequency, the stress energy and also the amount of trapped powder in-between colliding bodies, which eventually control the energy transfer by varying these above mention parameters. The total amount of energy transferred to the product particles during the milling process can be estimated based on the following expression, where ΔSFj is the frequency of stress events at interval j, SEj is the average stress energy and t is the processing time. Hence, the total energy can be represented as the product of the total number of stress events SN and the average stress energy 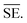 The specific energy Ei is the ratio of the total energy to the total mass of the powder, mp.108
The specific energy Ei is the ratio of the total energy to the total mass of the powder, mp.108
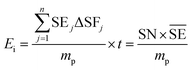 | (1) |
The stress energy SE is the maximum amount of energy that can be transferred to the product particles during single collision. This can be calculated from the relative impact velocity ϑj and the masses of the colliding bodies m1 and m2 as given below:108
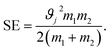 | (2) |
The choice of the material used in milling balls is governed by its thermal stability, nature of interaction with the sample powder to prevent product degradation via secondary reactions or cause abrasion and damage the milling vessel.108 Agate, silicon nitride, sintered corundum, zirconia, chrome steel, Cr–Ni steel, tungsten carbide, or polyamide are the typical materials used in the mechanochemical vessels and milling media. Use of zirconia milling balls has proven to be more effective for the synthesis of sulfur based glass-ceramic electrolytes.123 Furthermore, it is recommended to use milling media with a uniform diameter to avoid a random motion of the balls without well-defined trajectories in the vessels. Milling balls with a large diameter and/or larger mass provide higher impact energy during the collision and, therefore, are suitable for reactions where particle refinement can enhance the surface activity.108 In addition, a larger milling vessel leads to higher kinetic energy being transferred.108 However, a higher density of milling media can generate high stress which can cause degradation of the reaction product because of the local heating.
Milling media-to-sample ratio and the degree of filling of the milling vessel play a critical role in the milling process. At a constant density and diameter, the quantity of milling media controls the reaction rate by altering the stress number, SN. Thus, to obtain a specific reaction yield, the required amounts of milling media depends on both the diameter and number. Although the reaction yield and quantity of milling media shows a linearly proportional behavior for any chemical synthesis upto a certain limit, the use of an excessive amount of milling media will result in a poor yield due to their constrained movement inside the loaded vessel.
One of the essential parameters for synthesis optimization is the milling speed that determines the amount of energy transfer for given masses of the colliding bodies during the milling process.107 The energy is supplied to the particles due to collisions with the milling balls. Although it is difficult to gauge the actual mechanism of ball milling because of its complex nature, the internal process can be visualized as follows: during high-energy milling, the particle size of the materials decreases to a critical value; an additional supply of energy to these materials of limiting size seeds crystals deformation, enhanced surface reactivity, and subsequently amorphization. It eventually leads to change in the surface area, particle size, reaction kinetics, phase transformations, atomic defects formation and non-equillibrium product formation. For instance, in order to synthesize the argyrodite Li6PS5X, the use of mechanical milling as a preliminary step allows rapid reactions of Li2S with P4S10 to form ortho-thiophosphate and probable nucleation clusters of Li6PS5X; this bypasses the normally long diffusion-mediated reaction.84
The primary nature of responses to mechanical action are (a) redistribution of cations/anions over non-equivalent crystallographic sites,69,84 (b) changes in the geometry of constitutive polyhedra which significantly alter the ion migration entropy69 and activation energy of transport, further discussed in Section 3.3, (c) formation of crystal defect112 and (d) the mechanically induced phase transformation.81 During the high-energy ball milling process, a material undergoes a continuous fragmentation and deformation process, resulting in the reduction of their crystallite size. By this comminution, many nanocrystalline ion conductors were prepared, which showed improved transport properties, for example ternary fluorides show greatly enhanced ionic conductivity.124 Recent studies show an effective change in conductivity of c-Na3PS4, which can be attributed to a combination of crystal defect formation and its nanocrystalline nature as (discussed in Section 3.1).75
Another important parameter is milling time. The yield increases with milling time due to the gradual rise in the collision number and the total energy transfer. Wagemaker's group reports significant impact of milling time on the Li-ion mobility of Li6PS5Br, which is associated with distribution of Br− ion over different crystallographic sites.125 Meng and coworkers have thoroughly studied the influence of milling time on the ionic conductivity of Na3PS4.126 With increasing milling time conductivity increases and reaches a maximum value of ∼0.2 mS cm−1 within 1 hour; the ionic conductivity does not increase further with additional milling process indicating completion of the reaction. Rapid production of high conducting Na3PS4 confirms the role of ball milling as a promising alternative to other existing energy-intensive multiple-step methods. However, prolonged ball milling can lead to formation of undesired material due to the decomposition the reaction product.127
2.3. Solution-assisted synthesis
Solvent processes are attractive, whether as a synthetic medium (alone or in conjunction with other techniques such as milling), or as processing medium such as suspension/dissolution and infiltration of electrolyte.65 Solvents are sought according to a number of criteria. We have categorized solution mediated synthesis of solid electrolyte in two sections. This section will be focused on thiophosphate materials whereas in the next section, we will briefly discuss oxide electrolyte processing. For the syntheses of lithium-ion conducting thiophosphate solid electrolytes, the paradigm to date is typically reaction of Li2S with P4S10 at varied stoichiometry, with the possible addition of extra Li2S and lithium halides (LiX; X = Cl, Br, I) for more complex compositions.65,83,128,129 For the purpose of this summary, the formula P2S5, due to its prominence in the literature, is sometimes used interchangeably with P4S10, although the compound actually consists of isolated cage-like molecules of P4S10;130 further, it should be noted that commercial P4S10 is generally high in impurities of P4S9 and possibly polysulfidic species, which are much higher in reactivity.131 The reactants typically do not fully dissolve and a heterogeneous reaction system is the norm.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P4S10. Small changes can result in large differences of the species distribution present: PS43−, P2S62−, P2S74−, P2S64−, S0/S–S.65,87,123,132,133 This can also apply locally; 75
P4S10. Small changes can result in large differences of the species distribution present: PS43−, P2S62−, P2S74−, P2S64−, S0/S–S.65,87,123,132,133 This can also apply locally; 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 Li2S
25 Li2S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P2S5 (typical stoichiometry for Li3PS4) under certain conditions in acetonitrile (ACN) resulted in Li7P3S11 with Li2S, likely the result of local stoichiometry closer to 70
P2S5 (typical stoichiometry for Li3PS4) under certain conditions in acetonitrile (ACN) resulted in Li7P3S11 with Li2S, likely the result of local stoichiometry closer to 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 due to unreacted Li2S.134 Thus incomplete reaction and uncontrolled heterogeneous distribution of reactants can be a potential pitfall in synthesis. There seems to be no ideal solvent that fully dissolves starting materials and/or products without inducing unwanted reactions (thus making isolation of products difficult) – alcohols such as ethanol may dissolve Li2S and LiX, but may tend to attack and decompose P4S10.130 This may also be a problem with N-methyl formamide (NMF), as suggested by Tatsumisago and coworkers; in this case the reaction was performed in a mixture of NMF and hexane to mitigate undesired reactivity.57 Further, some compositions are difficult to synthesize in a single solvent. Argyrodites, e.g. Li6PS5X (X = Cl, Br, I), do not form in tetrahydrofuran (THF) from binary precursors due to the stability of precipitated Li3PS4 and insolubility of other reactants, and the overall reaction also does not proceed satisfactorily in ethanol alone, likely due to the aforementioned restrictions. Therefore, an approach of first forming Li3PS4 (to eliminate the possibility of attack of P4S10) and subsequent addition of Li2S and LiX was utilized; either by initial reaction in solvent to produce Li3PS4,135,136 or by starting with Li3PS4 produced by solid-state means.55 Later, some success was realized with Li6PS5Cl in ethanol alone using Li2S, LiCl and P2S5, albeit with a conductivity lower than expected.54 Li3PS4 was shown to first crystallize as a complex with solvents it was synthesized in, such as THF and acetonitrile; this will be discussed later in Section 3.3. On a final note, there is clearly chemistry that is not yet fully understood, as there are reports of mixtures of 1
30 due to unreacted Li2S.134 Thus incomplete reaction and uncontrolled heterogeneous distribution of reactants can be a potential pitfall in synthesis. There seems to be no ideal solvent that fully dissolves starting materials and/or products without inducing unwanted reactions (thus making isolation of products difficult) – alcohols such as ethanol may dissolve Li2S and LiX, but may tend to attack and decompose P4S10.130 This may also be a problem with N-methyl formamide (NMF), as suggested by Tatsumisago and coworkers; in this case the reaction was performed in a mixture of NMF and hexane to mitigate undesired reactivity.57 Further, some compositions are difficult to synthesize in a single solvent. Argyrodites, e.g. Li6PS5X (X = Cl, Br, I), do not form in tetrahydrofuran (THF) from binary precursors due to the stability of precipitated Li3PS4 and insolubility of other reactants, and the overall reaction also does not proceed satisfactorily in ethanol alone, likely due to the aforementioned restrictions. Therefore, an approach of first forming Li3PS4 (to eliminate the possibility of attack of P4S10) and subsequent addition of Li2S and LiX was utilized; either by initial reaction in solvent to produce Li3PS4,135,136 or by starting with Li3PS4 produced by solid-state means.55 Later, some success was realized with Li6PS5Cl in ethanol alone using Li2S, LiCl and P2S5, albeit with a conductivity lower than expected.54 Li3PS4 was shown to first crystallize as a complex with solvents it was synthesized in, such as THF and acetonitrile; this will be discussed later in Section 3.3. On a final note, there is clearly chemistry that is not yet fully understood, as there are reports of mixtures of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Li2S
1 Li2S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P2S5 dissolving in solvents that neither reactant dissolves in.65Fig. 3 summarizes a generalized reactivity trend in the Li2S–P2S5–(LiX) system in solution.
P2S5 dissolving in solvents that neither reactant dissolves in.65Fig. 3 summarizes a generalized reactivity trend in the Li2S–P2S5–(LiX) system in solution.
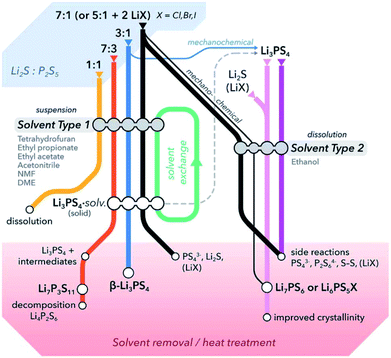 | ||
| Fig. 3 A general overview of literature reported solution routes for the synthesis of common thiophosphate solid electrolytes. Based on the choice of solvents, reaction steps, and post-synthetic heat treatments, it is possible to prepare thiophosphates with different compositions, structures or morphologies using Li2S, P2S5 and/or LiX as preliminary precursors. Solvents are differentiated into two types based on their properties such as polarity, donor number, etc.; DME stands for dimethyl ether. This figure is adopted from ref. 65. | ||
2.4 Sol gel syntheses
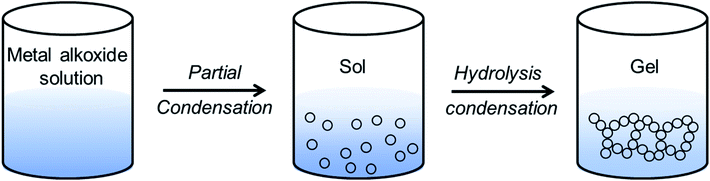
Sol–gel routes have emerged as an energy efficient alternative of solid-state synthetic technique to prepare inorganic ceramics from homogenized solution via formation of a network structure called ‘gel’.137 The advantage of sol–gel synthesis relies on the successful preparation of solid-state compounds from a chemically homogeneous precursor solutions. It is a well-established route to prepare oxide- and phosphate-based ionic conductors such as the garnets, LISICONs, and NASICONs.The major limitation of alkoxide-based sol–gel chemistry is that it is difficult to get a stable metal-alkoxide.137 To overcome this drawback, an alternative method has been developed that uses aqueous metal salts precursor and small molecules as chelating agents to tune the aqueous hydrolysis process of metal alkoxide. One of the most common chelating agents used in sol–gel chemistry is citric acid. In a modified sol–gel synthesis, the homogenized solution of aqueous metal salts (mostly nitrates) and citric acid is heated to form gel. Murugan's group prepared Al-doped cubic phase of LLZO, Li6.16Al0.28La3Zr2O12 (Al-LLZO) by a modified sol–gel technique.140
When carboxylic acids (like citric acid, tartaric acid, polyacrylic acid, etc.) are used as chelating agents along with polyhydroxy alcohol (such as ethylene glycol, glycerol, polyvinyl alcohol, etc.), the modified sol–gel method is termed as Pechini process.137 Here, the metal carboxylates undergo polyesterification upon heating and form a three-dimensional network of polymeric resin. The cations are then homogeneously dispersed all over the polymeric resin, thus inhibiting the precipitation. The low temperature calcination of resin yields nano dimensional oxide. Fang's group prepared nanocrystalline cubic phase of lithium garnets, Li5La3Ta2O12 and Li5La3Bi2O12via the Pechini sol–gel method by calcining the gels at 700 °C and 650 °C, respectively.141,142
2.5 Microwave synthesis
Microwave syntheses of solid-state inorganic materials have emerged with the goal of energy-efficient and cost-effective synthesis by reducing the reaction time and heating temperature.143 It offers potential solutions for industrial applications and also a means to access metastable materials, which draws the attention of materials chemists. In the case of battery materials, numerous electrode materials, e.g. intercalation-type cathodes144–146 and carbon-based anodes,147,148 have been synthesized via microwave methods.149 Despite the emerging use of the microwave synthesis in various fields, there are only a few reports on the successful synthesis of solid electrolytes. In this section, we briefly summarize the technical requirements and unique nature of microwave-assisted synthesis and applications to the synthesis of solid electrolytes.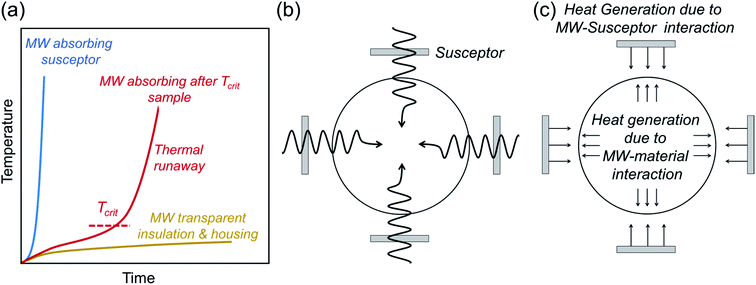 | ||
| Fig. 5 (a) Schematic of the heating profile of microwave (MW) susceptors, insulators, and the materials possessing critical temperature (Tcrit) where the microwaves start coupling with the target sample.153 (b and c) show schematics of heating mechanisms of microwave-assisted synthesis. Whereas only the susceptors are heated up below Tcrit, the heat generation also occurs within the sample above Tcrit due to the coupling with microwave radiation, homogenizing the temperature profile throughout the sample.154 Figures are redrawn after ref. 153 and 154 respectively with permission. Copyright 2019 American Chemical Society; Copyright 2016 Elsevier. | ||
The first few successful uses of microwave-assisted synthesis for solid electrolytes have been demonstrated with Li-ion conducting oxides. Amores et al. synthesized Li+ conducting garnets (Li6.5Al0.25La2.92Zr2O12) with a microwave method for the first time in 2016.42 The SiC walls of the microwave furnace can absorb microwaves and initially heat the precursors and ZrO2 in the powder as a precursor absorbs microwave above 800 °C.155 Later Gao et al. compared the garnets prepared by microwave-assisted synthesis with those prepared via conventional sintering, confirming the lower loss of volatile materials during microwave synthesis.43 Another Li-ion conducting oxide, Li1.3Al0.3Ti1.7(PO4)3, was synthesized with a microwave-assisted reactive sintering by Hallopeau et al.156 This work demonstrated a successful preparation of dense pellets within 10 minutes at 890 °C exhibiting over 0.3 mS cm−1, which highlight the energy-efficient sintering with a microwave method.
Microwave methods also enable energy-efficient synthesis of Li-ion conducting sulfides e.g. β-Li3PS4 and Li7P3S11. Whereas the synthesis of Li-thiophosphate glass and glass-ceramics via mechano-chemical alloying or melt quenching often takes 1–3 days,87,157,158 Suto et al. prepared β-Li3PS4 within 3 hours by applying microwave radiation during solution processing.159 The significant reduction in the reaction time with a microwave-assisted synthesis without solvent was demonstrated by Preefer et al. In their work, a successful synthesis of glass and glass-ceramic Li7P3S11 was achieved within 18 and 28 min, respectively, with only a minimal amount of the undesirable Li4P2S6 phase.160 Activated charcoal was employed as a microwave susceptor for the initial heating step. The glass-ceramic Li7P3S11 phase is metastable and typically obtainable only through annealing the amorphous 70Li2S–30P2S5 glass phase at around 260 °C; thus the direct one-step synthesis of this glass-ceramic Li7P3S11 is remarkable.161 Although the sulfide electrolytes synthesized via microwave-assisted synthesis exhibit slightly lower conductivity (0.1 and 1 mS cm−1 for β-Li3PS4 and glass-ceramic Li7P3S11),159,160 this energy-efficient and rapid synthesis method may pave the way for the cost-effective production of highly conductive Li–thiophosphate phases.
3. Case studies of the influence of synthesis on the structure and ionic transport
In the previous section we summarized synthesis routes typically employed for the production of solid ionic conductors. In this section we will delve deeper into the influence of these different synthesis conditions on structure and ionic transport properties with specific examples, used as case studies, of several inorganic solid electrolytes. We have chosen some of the most well-known solid electrolytes including electrochemically stable garnets and phosphates, Na/Li-conducting thiophosphates, and the recently rediscovered ionically conducting ternary halides. These case studies will highlight the need to understand the influence of synthetic procedures on the local structure, defect formation, phase stability and ultimately the ionic transport properties, in order to tailor production methods to obtain the desired results.3.1 Milling induced defect introduction and structural stabilization of Na3PS4
Sodium thio-ortho-phosphate, Na3PS4, is an archetypal Na ion conductor, defining a structural family that includes multiple other notable members such as Na3SbS4 (ref. 66–68 and 162) and the highly conductive tungsten-doped Na3−xSb1−xWxS4.12,27 Compounds of the Na3PS4 archetype exhibit a tetragonal ground state and transformation to a closely related cubic polymorph at elevated temperature,163 owing to convergence of the a and c lattice parameters and a slight tilting of the constituent PS43− tetrahedra. For Na3PS4 this tetragonal-to-cubic transition normally occurs at approximately 250 °C.164Interest in this material family as solid electrolytes boomed after the seminal reports of Hayashi et al. showing that the conductivity of Na3PS4 could reach the order of 0.1 mS cm−1 through a mechanochemical synthesis route.26,165 This was a significant improvement over the previous reports of solid-state-synthesized t-Na3PS4 (HT-Na3PS4), showing Na+ conductivity of the order of 10−3 mS cm−1.164 Most interestingly, the mechanochemically-synthesized sample exhibited a cubic average structure of the high-temperature polymorph, as evident from Bragg X-ray diffraction (XRD) shown in Fig. 6a (BM-Na3PS4). Naturally, the hypothesis was put forward that the stabilization of the high-temperature polymorph through mechanochemistry was responsible for the stark increase in ionic conductivity.
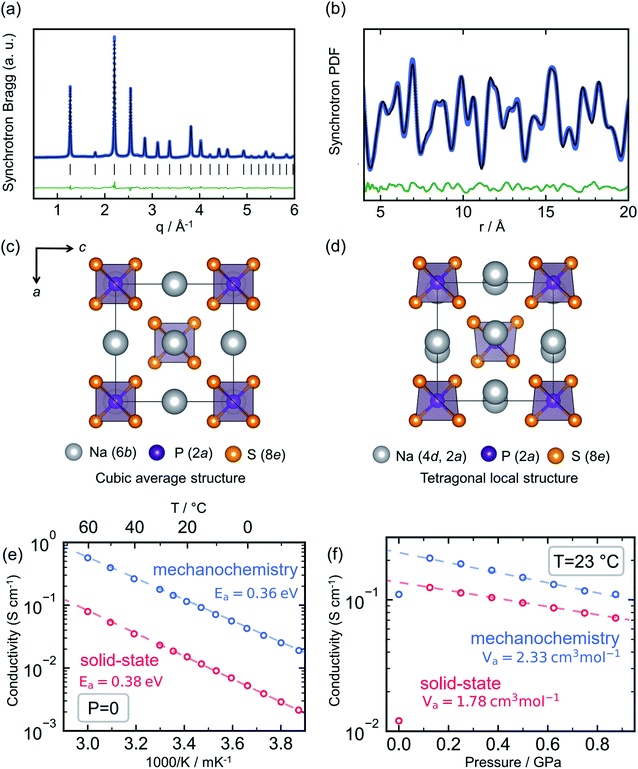 | ||
| Fig. 6 Mechanochemistry induced local structural distortion in Na3PS4 and its influence on the ionic conductivity. (a) Powder X-ray diffraction pattern for Na3PS4 synthesized via ball milling suggests a cubic structure, whereas (b) a local tetragonal distortion was observed in the pair distribution function analyses. Representation of the resulting structural models (c) cubic and (d) tetragonal showing the difference in Na-sublattice. Variation of ionic conductivity for ball-milled cubic- and high temperature-tetragonal phase of Na3PS4 with temperature and pressure, quantified by their respective activation energy, Ea and volumes, Va are given in (e and f), respectively. Data digitized from ref. 70 and 75. | ||
Nevertheless, subsequent theoretical investigations of the ion migration mechanism in the two polymorphs showed that the differences in ion diffusion imposed by the crystal structure alone should be negligible.94,166–169 On the contrary, these simulations performed by multiple groups indicated that the ion conductivity in the Na3PS4 structure can be severely affected by the presence of extrinsic defects, such as sodium vacancies and interstitials. Investigations of the local structure by means of total scattering experiments were needed to bring full clarity; studies of BM-Na3PS4 through pair distribution function analysis showed that it possesses the same local tetragonal distortion as HT-Na3PS4, despite its average cubic symmetry (Fig. 6b).75,112 The samples are indistinguishable through Raman spectroscopy, due to the same distortions of the PS43− tetrahedra (which should not be observable in a truly cubic local structure).75 The 23Na NMR resonance of BM-Na3PS4 shows clear signs of isotropy and motional narrowing, indicating higher Na+ mobility compared to HT-Na3PS4.75,168 Through the aforementioned observations it has been reasoned that the mechanochemical synthesis significantly impacts the sodium sublattice with a positive effect on ion migration. One hypothesis is that the harsh ball-milling conditions induce defects into the crystal structure, possibly Na+ vacancies and/or interstitials, along with microstructural strain, which could explain the observed increase in ionic conductivity.75,112
Recent experimental results have shown that HT-Na3PS4 can reach a similar order of magnitude in conductivity to BM-Na3PS4, through application of external uniaxial pressure, as seen in Fig. 6f.75 This would indicate that the beneficial effect of ball-milling on the resulting ionic conductivity of Na3PS4 is related to the mechanical strain generated during the mechanochemical synthesis. Ab initio calculations as a function of pressure show that the stabilization of the cubic polymorph can be explained through residual strain. Further, from diffraction experiments, it is evident that BM-Na3PS4 possesses a distinct micro- and macro-strained local structure and minute crystallite size of the order of 25 nm, in stark contrast to the well-crystallized HT-Na3PS4.70,75 Such microstructural effects have been hypothesized to aid ion conduction in other mechanically soft solid electrolytes, e.g. LiBH4 (ref. 170) and Li3PS4.56 It can further be assumed that the microstructure of the resulting samples affects the measured ionic conductivity and that the strained, nanocrystalline nature of the BM-Na3PS4 is beneficial to macroscopic ion transport.
In conclusion, ball-milling has been shown to have a clearly beneficial effect on the macroscopic ionic conductivity of Na3PS4. Although the high-temperature cubic polymorph is stabilized, probably due to the applied stresses during milling, this average structure cannot fully explain the increase in conductivity given that the resulting local structures show the same tetragonal distortions. It is believed that one or a combination of the following is at the origin of the enhanced ion transport:75 (a) Na+ defect introduction, (b) a strained local structure (c) nanocrystalline structure. Overall, the efficacy of mechanochemistry in increasing the conductivity of ion conductors is a promising route for future development and merits further study, and local structural changes must not be ignored and need to be exploited.
3.2 Mechanochemically synthesized fluorides: local structures and ion transport
Another class of solid electrolyte from which we can understand the difference between conventional solid-state and mechanochemical routes are fluoride ion conductors. Because of the small size and monovalent nature of F−, these materials have drawn the attention of the battery community.171,172 A major breakthrough happened when a mechanochemical route was introduced to create nanostructured fluorides benefiting from crystal defects and space charge layer formation at the grain interface. Fluoride ion conductors mostly crystallize in two different structure types: fluorite-type MF2 with M = Ca, Ba, Sr, Sn and tysonite-type MF3 with M = La, Ce, Pr, Nd.124 The binary halide SnF2 (monoclinic structure) shows a drastic rise in ionic conductivity from 4 × 10−3 mS cm−1 to 0.2 mS cm−1 at 100 °C when ball milled for several hours, which is associated with reduction of crystallites to nanoscale dimensions and resulting microstrain.173 The ternary layered heterostructured halides, MF2–SnF2 (M = Pb, Ba) show the highest conductivity among the fluoride ion conductors.174–177 PbSnF4 and BaSnF4 can be synthesized via both high temperature solid-state routes and mechanochemical milling. The mechanochemically-synthesized BaSnF4 is considered as one of the fastest conducting fluoride electrolytes, with a room temperature ionic conductivity of 0.7 mS cm−1.174 The higher ionic conductivity is the result of a small crystallite size (∼25 nm), crystal defects, and large interfacial areas beneficially influencing F− ion diffusion.As discussed earlier, the mechanochemical synthesis is a well-known route to prepare metastable phases. As an example, BaF2–CaF2 solid solutions cannot be prepared via high temperature solid-state route because of the cationic radius difference (Ba2+: 1.42 Å; Ca2+: 1.12 Å).178 However, successful synthesis of BaxCa1−xF2 was reported via a high energy ball-milling process, which decomposes upon heat treatment confirming the metastable nature of the solid solution.179 The ionic conductivity values for Ba0.5Ca0.5F2 amounts to ∼1.4 mS cm−1 at 281 °C, which is almost two orders of magnitude higher than that of nanocrystalline BaF2. Mixtures of BaF2 and LaF3 have been extensively studied over the past few years to understand the influence of aliovalent substitution on F− ion transport.180,181 In contrast to BaF2–CaF2, the BaF2–LaF3 solid solution can be prepared via both high temperature solid-state route as well as mechanochemical syntheses routes. The benefit of mechanochemistry, however, is the defect formation which is required to achieve higher conductivities compared to their highly ordered, crystalline counterparts in BaF2–LaF3. For instance, Ba0.6La0.4F2.4 shows the highest conductivity of 0.19 mS cm−1 at 160 °C.180
3.3 Cooling routines affecting disorder and ionic transport in Li6PS5X
Lithium argyrodite superionic conductors with high ionic conductivity and mechanically soft nature are promising candidates for commercially viable solid electrolytes.10,14,23,55,182 A high ionic conductivity that directly correlates with structural disorder raises intense scientific interest in terms of structure-composition-transport relationships.14,53,183–185 The crystal structure of the halide containing Li-argyrodites Li6PS5X (X = Cl, Br, I) (shown in Fig. 7a) is cubic at room temperature, consisting of X− forming a face-centered cubic sublattice with ortho-thiophosphate PS43− units on the octahedral voids and so-called “free sulfur”, S2− not bound to P, in half of the tetrahedral voids. Li+ resides on three distinct sites and forms a cage-like structure around the 4d site.186 A high degree of intrinsic X−/S2− site-disorder (between this site and 4a, as seen in Fig. 7b) is responsible for fast ion conduction, particularly in Li6PS5Cl1−xBrx solid solutions. This disorder is drastically reduced with increasing iodine content in Li6PS5Br1−xIx, accompanied by stark reduction in the ionic conductivity (Fig. 7c).14 As the structure becomes ordered, the activation barriers for ionic motion increases, and with it, the conductivity drastically decreases. The X−/S2− site-disorder can be re-introduced in the intrinsically ordered Li6PS5I structure through aliovalent substitutions e.g. Li6+xP1−xGexS5I, Li6+xP1−xSixS5I, and Li6+xSb1−xSixS5I.13,32,92 Despite an evident structure–composition–transport relationship, it has been challenging to experimentally deconvolute individual factors influencing ionic transport, e.g. lattice polarizability, number of carriers, and structural disorder. To overcome this complication, recent work has varied the reaction kinetics with a systematically modified synthesis conditions, enabling isolation of the impact of the structural disorder.84 Li6PS5Br was pre-synthesized mechanochemically, followed by heat treatment, with various reaction times (soaking times) and cooling speeds. The variation in the soaking time showed little end effect, revealing rapid reaction kinetics, achieving a crystalline Li6PS5Br within one minute of annealing. However, it was the variation in cooling speed after the reaction that severely impacted the resulting structural disorder and, with it, ionic conductivity, as shown in Fig. 7d. Thermodynamically, entropy stabilizes the disorder formation at elevated temperature. Upon cooling, the amount of those entropically introduced disorders can be kinetically frozen depending upon the rate of cooling compared to the rate at which the disorder is able to relax. As a consequence, a higher disorder can be trapped in the structure by a rapid quenching with liquid nitrogen. Subsequent work showed that a precise control of the disorder can be made by heating a minimally-disordered, slow-cooled sample to various temperatures followed by quenching, with an achievable range of X−/S2− disorder of 10–40%.187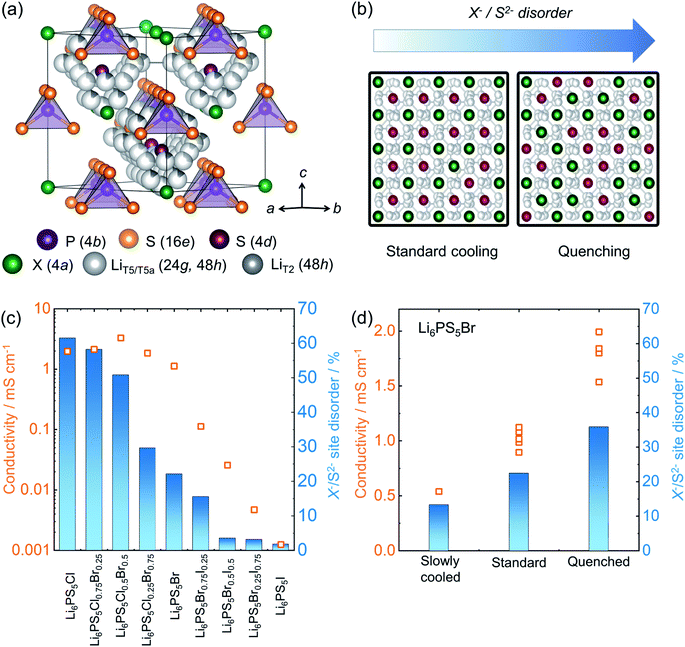 | ||
| Fig. 7 Structure of lithium-argyrodites and a structure–transport relationship. (a) A unit cell structure of room temperature lithium argyrodite Li6PS5X (X = Cl, Br, I) phase. (b) The schematic represents lowering of Li+ diffusion barrier upon enhanced site-disorder resulting in an enhanced ionic conductivity. (c) A correlation between site-disorder percentage and the resulting conductivity. The more the structure is ordered, the lower the conductivity becomes. (d) The fraction of site disorder X−/S2− can be kinetically engineered by systematically altering synthesis conditions, corroborating the disorder–transport relationship. Data digitized from ref. 14 and 84. | ||
Clearly synthesis protocols affect the disorder and local structure and with it the ionic transport in solid electrolytes. In case of the lithium argyrodites, the structural disorder, tailorable by a systematic control over the synthesis conditions, play a vital role in transport as it directly affects the Li+ distribution and diffusion energy landscape; this could likely be applicable to many other materials as well.
3.4 Milling and crystallization effects in Li3MCl6
The development of halide based solid ionic conductors started in 1930 with lithium halide salts (LiX; X = Cl, Br, I).188 To improve the conductivity of these materials, substituent metals have been introduced: divalent189 (mainly the first row transition metals and Mg, Pb, etc.) and trivalent (mainly Group 3 elements Sc, Y; rare earth elements, La–Lu;69,190–194 Group 13 elements, especially In29). Nevertheless, these halide materials were initially characterized as poor ion conductors until 2018 when Asano et al. achieved ∼1 mS cm−1 in conductivity from Li3YX6 (X = Cl, Br), by employing mechanical milling.28 From these materials, Li3YCl6 (isostructural to Li3ErCl6) crystallizes in a trigonal cell with an hexagonal close packed (hcp) anion sublattice, whereas Li3YBr6 has a monoclinic structure with cubic closed pack (ccp) anion framework. Both Li and Y occupy the octahedral voids. In Li3YCl6, the yttrium can occupy three distinct crystallographic sites (M1 at Wyckoff position 1a and M2, M3 at Wyckoff positions 2d) as shown in Fig. 8a. The edge shared LiCl65− octahedra forms a honeycomb-like arrangement (Fig. 8b).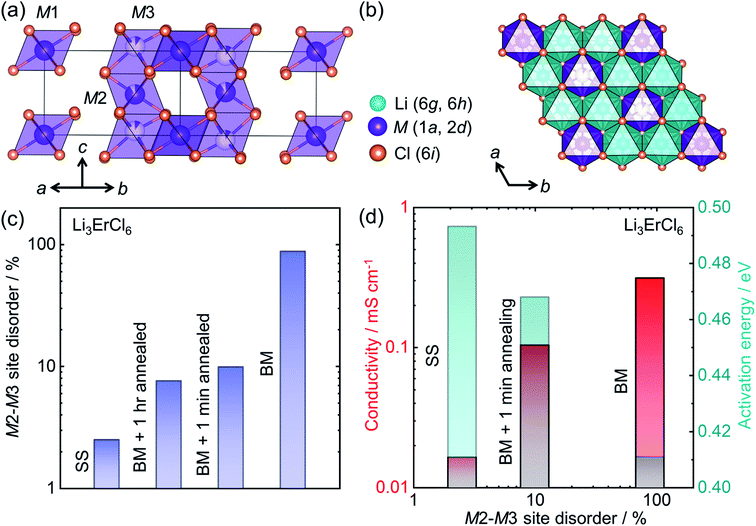 | ||
| Fig. 8 Structure–transport correlation in Li3MCl6 (M = Er, Y) (a) MCl63− octahedra form a trigonal unit cell in Li3MCl6 where M occupies three different crystallographic sites. (b) Lithium occupies octahedral voids forming edge-shared LiCl65− octahedra which surround each ErCl63− octahedron in a honeycomb arrangement in the a–b plane. (c) Evolution of the M2–M3 site-disorder as a function of synthetic conditions (‘solid-state synthesis’ corresponding to SS, BM = ‘ball milling’), (d) correlation of ionic conductivity and activation energy with M2–M3 site disorder. Data digitized from ref. 69. | ||
Recent work has shown the large influence of synthesis parameters on the crystal structure and resulting ionic transport of these materials.28 The lower crystallinity of Li3YCl6 and Li3YBr6 when synthesized by ball-milling leads to room temperature ionic conductivities of 0.51 mS cm−1 and 0.72 mS cm−1, respectively. A significant difference in the conductivity has been observed when the crystallinity of the ball milled product was improved through high temperature annealing. Whereas the crystalline Li3YCl6 has a reduced ionic conductivity of ∼0.03 mS cm−1, the Li3YBr6 shows superior conductivity of 1.7 mS cm−1 after the annealing process. The plausible explanation for this contrasting result is the difference in the anion sublattice structures. Schlem et al. have recently investigated the influence of the synthesis methods on Li3MCl6 (M = Er, Y) showing an M2–M3 site disordering, which results in different ionic transport properties.69 Li3ErCl6 and Li3YCl6 were synthesized by high temperature solid-state reaction and mechanochemical synthesis. To understand the impact of crystallization on the structure and ionic conductivity, mechanochemically synthesized samples were subjected to an additional crystallization step, which further tunes M2–M3 site-disorder and thus lithium ion transport. Even though mechanochemical synthesis causes a high M2–M3 site-disorder (up to almost 100%, or a complete site-inversion), the classic high-temperature ampoule syntheses result in only a low degree of disorder as seen in Fig. 8c. The cation site disorder induces a Li-redistribution in the Li-substructure which itself leads to significant change in the structural windows of the Li-ion jump and hence the activation barriers for Li-ion migration as depicted in Fig. 8d. Even in other compositions in these halide conductors, mechanochemical syntheses affect the ionic transport significantly.28,195,196
3.5 Solvent influence on crystallization, phase formation and ionic conductivity in Li–P–S phases
Most superionic thiophosphates share the predominant structural motif of PS43− tetrahedra (e.g. Li3PS4, Li7PS6, Li6PS5X, Li4PS4I, Li7P3S11, and many amorphous Li2S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P2S5 compositions). Reports seem to indicate that after the formation of PS43− units in solution (typically from Li2S and P4S10 starting materials), solvent molecules strongly complex to form Li3PS4·nsolv; the number of solvent molecules per unit varies but is typically 2–3.56,86,197 The stability of these units seem to be such that, even when additional Li2S or LiX (X = Cl, Br, I) are present, the predominant initial product contains the crystalline solvent complex, and stoichiometric products such as Li7P3S11 or Li6PS5X are only achieved after higher-temperature heat treatments in the solid-state.65 This is to say that the “solution synthesis” aspects of thiophosphates are only part of the story; the specific effects of solvents offer deeper complexity than simply a reaction medium, and what happens after treatment in solution can be just as important to the resulting product.
P2S5 compositions). Reports seem to indicate that after the formation of PS43− units in solution (typically from Li2S and P4S10 starting materials), solvent molecules strongly complex to form Li3PS4·nsolv; the number of solvent molecules per unit varies but is typically 2–3.56,86,197 The stability of these units seem to be such that, even when additional Li2S or LiX (X = Cl, Br, I) are present, the predominant initial product contains the crystalline solvent complex, and stoichiometric products such as Li7P3S11 or Li6PS5X are only achieved after higher-temperature heat treatments in the solid-state.65 This is to say that the “solution synthesis” aspects of thiophosphates are only part of the story; the specific effects of solvents offer deeper complexity than simply a reaction medium, and what happens after treatment in solution can be just as important to the resulting product.
For the synthesis in acetonitrile of Li7P3S11, composed of both PS43− and P2S74− units, it is clear that in solution processes, only the highly stable PS43− units form; the additional P2S74− units are only formed at elevated temperatures of 200–260 °C.200 Higher temperatures decompose the Li7P3S11.201 As Li3PS4 was determined to be an important intermediate in the overall synthesis from Li2S and P4S10,200 careful scrutiny of the solvent chemistry with this compound, and what effects arise as solvent molecules leave at higher temperatures, may be of high importance in the synthesis of Li7P3S11.
In the case of argyrodites Li6PS5X (using the higher-conducting phases with X = Br, Cl, as examples), either by synthesis or dissolution in ethanol, crystalline argyrodite (rather than a crystalline or amorphous solvato complex, as evidenced by X-ray diffraction) can be recovered by removal of solvent at as little as 80 °C; however, the conductivity remains low, even in the range of 10−2 mS cm−1.202 Heat treatment up to 150–200 °C improves the conductivity to 0.1 mS cm−1, but ultimately heating to 550 °C fully recovers conductivity to the expected mS cm−1 range.135 So far, these high heat treatments are needed, which partially alleviates the beneficial approach of solution synthesis in argyrodites, and future work for low temperature syntheses is needed. A generalized schematic representing the influence of processing temperature on phase formation, its stability and ionic conductivity is shown in Fig. 9a.
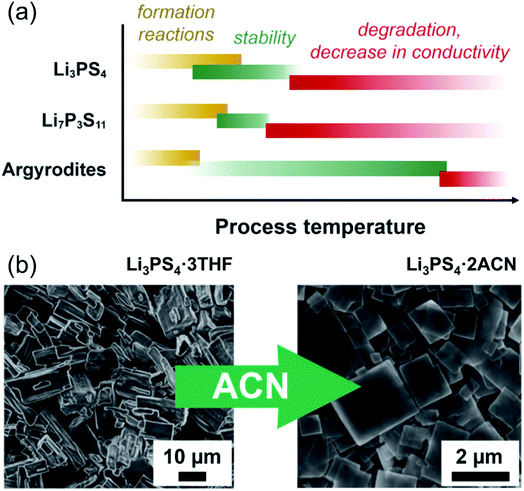 | ||
| Fig. 9 (a) A simplification showing the effect of temperature throughout processing of three types of lithium thiophosphates. Li3PS4, due to the diversity of solvents used to produce it, shows a wide span of temperatures over which the material forms and solvent is removed (roughly 60 to 200 °C); it is stable, with some decrease in conductivity, until at higher temperatures the phase changes. Li7P3S11 does not form until a higher temperature solid-state reaction (above 200 °C) occurs, but decomposes to Li4P2S6 above roughly 300 °C. For the argyrodites, the formation is generally complete after solvent removal below 100 °C. The conductivity gradually increases with heat treatment. (b) An example of morphological change with the same composition (adapted from ref. 198). Li3PS4 produced with THF shows block-like crystals of Li3PS4·3THF; after stirring in acetonitrile, the composition changes to Li3PS4·2ACN, and the morphology changes to flat plate-like squares. This figure is adopted with permission from ref. 198. Copyright 2018 John Wiley and Sons. | ||
Through these case studies, producing PS43− units from precursors in solution seems at this point fairly straightforward. However, though this is a dominant structural moiety in thiophosphate superionic conductors, the solution-based synthesis (and post-synthetic processing) of more complex compositions and structures requires much deeper attention. To properly synthesize desired compounds may require multiple solvents, either mixed or selected at various stages, as well as carefully controlled heat treatments. In the selection of solvents, undesired reactivity of solvent with precursors and products must be monitored and mitigated.
3.6 Synthesis of high performing metastable phases – Li10GeP2S12 and Na10Sn2PS12
Quaternary chalcogenides are some of the best performing solid electrolytes in terms of ionic conductivity.11,15,25 The discovery of Li10Ge2PS12, which first demonstrated solid-state lithium ionic conductivity as fast as in liquids, jumpstarted the development of room temperature lithium solid-state batteries.15 Most of such known quaternary phases can be considered as mixtures of (usually lower ion-conducting) ternary phases. Their structures are based on the arrangement of isolated MCh4 (M = P, Sb, Si, Ge, Sn; Ch = S, Se) tetrahedra coordinating Li+ (in mixed tetrahedral and octahedral sites) or Na+ (in mainly octahedral sites) to form diffusion pathways. The sodium compositional analogues follow a distinct structural motif exemplified in the Na11SnP2S12 archetype.204–206 Due to their quaternary nature, these phases exist in phase equilibrium with multiple ternary and binary compounds which complicates their synthesis. This case study aims to discuss the challenges and opportunities relating to the synthesis of these high-performance compounds.
Ab initio calculations have played a key role in understanding the behavior of ternary chalcogenides, since their discovery.207–209 The Li10Ge2PS12 compounds are enthalpically unstable against decomposition at 0 K. Consequently, their successful synthesis hinges on entropic stabilizing effects at finite temperature that favor mixing of the MCh4 tetrahedra and disorder of mobile cations as well as single-phase formation. For example, Li10Ge2PS12 (LGPS) is enthalpically less stable than a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of Li4GeS4 and Li3PS4,207 which can thus appear as synthesis side-products under non-optimized conditions, with negative consequences on the ion transport properties of the resulting material. For Na11SnP2S12-type compounds, comparably smaller decomposition energies towards ternary products or even thermodynamic stability at 0 K is reported. Here, the stability of compounds with different immobile cationic ratios M′:M′′ (M′ = P, Sb; M′′ = Sn) are currently subject to investigation.210 Nevertheless, it seems that a lot of these quaternary materials are metastable and rely on specific synthesis conditions such as ball-milling, or control of synthesis according to the phase diagram.
1 mixture of Li4GeS4 and Li3PS4,207 which can thus appear as synthesis side-products under non-optimized conditions, with negative consequences on the ion transport properties of the resulting material. For Na11SnP2S12-type compounds, comparably smaller decomposition energies towards ternary products or even thermodynamic stability at 0 K is reported. Here, the stability of compounds with different immobile cationic ratios M′:M′′ (M′ = P, Sb; M′′ = Sn) are currently subject to investigation.210 Nevertheless, it seems that a lot of these quaternary materials are metastable and rely on specific synthesis conditions such as ball-milling, or control of synthesis according to the phase diagram.
Arguably the most important, but hitherto underused, tool in optimizing the synthesis of such ternary phases is a phase diagram describing phase equilibria at finite temperatures. Such phase diagrams are practically only accessible experimentally due to the difficulties of ab initio calculation methodologies to accurately capture the effects of temperature.211 As discussed in the solid-state synthesis section (Section 2.1), high temperature tends to favor single-phase behavior, which is key in synthesizing pure quaternary phases. Still, excessive heating can also lead to (partial and/or incongruent) melting, which is counterproductive. A successful phase diagram identifies the temperature and composition ranges of single-phase domain(s) and characterizes the melting behavior of the system, allowing for the rational tailoring of the synthesis parameters to the desired product.
Fig. 10a shows the Li4GeS4–Li3PS4 quasi-binary phase diagram containing Li10Ge2PS12 constructed by Hori et al.102 Five unique solid phases are accessible in this composition-temperature space: Li4GeS4 (β′) in the germanium-rich end; α-, β-, and γ-Li3PS4 in the phosphorus-rich end; and the highly ion conductive Li10Ge2PS12 in between. It is evident from the phase diagram that a Li10Ge2PS12 composition will start partially melting at ∼550 °C into a phosphorus-rich melt which would crystallize as Li3PS4 upon subsequent cooling. Further heating will cause a phase transition of the remaining Li10Ge2PS12 phase to Li4GeS4, which would persist after cooling.212 Altogether, this phase diagram suggests that the material should be synthesized at around 500 °C, which is the maximum temperature possible while avoiding incongruent melting and crystallization of the ternaries; and indeed, the temperature range 500–550 °C is utilized in most reports (Fig. 10b).
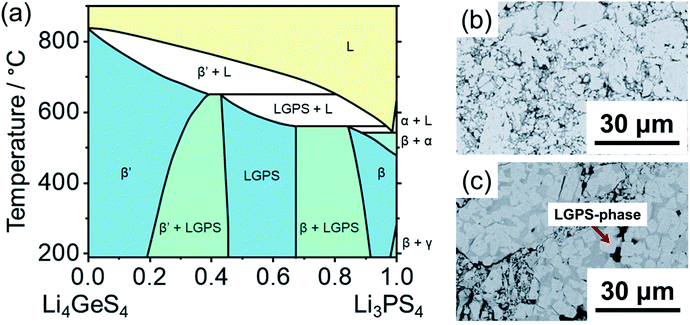 | ||
| Fig. 10 (a) Li4GeS4–Li3PS4 quasi-binary phase diagram proposed by Hori et al.102 As suggested by the phase diagram, variation of synthesis temperature and cooling controls on the phase formation and microstructures. Scanning electron micrographs (SEM) for the composition [(1 − x) Li4GeS4 + x Li3PS4] with x = 0.65 cooled under different condition: slowly cooled synthesis from 550 °C (b) and quenched from 650 °C (c). Uniform contrast in the roughout matrix indicates formation of pure LGPS (b); sample quenched from 650 °C shows rectangular brighter crystalline area surrounded by darker areas corresponding to LGPS-type and Li3PS4-rich solid phases, respectively (c). The phase diagram is digitized from ref. 102. SEM images were adopted from ref. 102 with permission. Copyright 2015 John Wiley and Sons. | ||
In addition, there exists a compositional window of approximately 0.5 < x < 0.67 at room temperature (0.45 < x < 0.67 at 500 °C) of phase stability for an Li10Ge2PS12-type phase. In other words, an LGPS-type structure can crystallize in compositions richer in Ge than the nominal Li10GeP2S12, up to approximately Li10.5Ge1.5P1.5S12.213 In contrast, any excess of phosphorus beyond the nominal composition would cause crystallization of Li3PS4. As such, if a single Li10Ge2PS12 phase is intended, a slightly Ge-rich composition should be targeted to account for experimental error in the weighing of reagents. In fact, the Ge-rich composition of the archetypical Li10Ge2PS12 stoichiometry shows increased ionic conductivity.213
Overall, knowledge of relevant phase diagrams has enabled the synthesis of pure phases and single crystals103 to build on the fundamental understanding of Li10Ge2PS12. Furthermore, the phase diagram can allow for the synthesis of phase mixtures with controlled microstructures. For example, Li10Ge2PS12 crystals in an amorphous LPS matrix can be produced by quenching (Fig. 10c) which could alleviate so called “grain-boundary” resistances of such quaternary compounds.102 Others have examined the crystallization of Li10GeP2S12 starting from mechanochemically prepared amorphous precursors.214,215 It was shown that annealing these precursors at moderate temperatures (260 °C < T < 410 °C) resulted in crystallization of the two end-member phases Li4GeS4 and Li3PS4, indicating a kinetic barrier to forming the single Li10Ge2PS12 phase, even in temperatures where according to the phase diagram of Fig. 10a it should be thermodynamically favored.214 This can be understood by the need for mobility of the PS43− and GeS43− moieties which are statistically mixed in the Li10Ge2PS12 phase. In this study, temperatures 450 °C < T < 550 °C were required to crystallize Li10GeP2S12 and such increase the ionic conductivity of the resulting powder.
From a local structure point of view, the building blocks of (a) the amorphous precursor, (b) a two-phase mixture of Li4GeS4 and Li3PS4, and (c) single-phase Li10GeP2S12, are always the same: Li+, GeS44− and PS43−; the arrangement in the quaternary Li10GeP2S12 phase yields the most facile local pathways for Li+-ion transport and maximizes ionic conductivity. It is noteworthy that even after the heat treatment, no full crystallization is obtained, giving rise to the possibility to create such Li10GeP2S12 precipitates in a glassy matrix as by the quenching approach. Similarly in related compounds such as Li7SiPS8 the synthesis conditions strongly affect the phase formation of lower and faster conducting polymorphs alongside an amorphous side phase limiting the ionic transport.81
In Na11SnP2S12 such a detailed phase diagram and/or the effect of mechanochemical synthesis on structure and transport have yet to be explored. However, the phase width (and thereby a similar two-phase region) of Na11SnP2S12 + Na3PS4 (analogous to Li10GeP2S12 + Li3PS4) has been investigated in mixtures of Na4SnS4 and Na3PS4 yielding the pure Na11Sn2PS12 structure at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Additionally, Na11SnP2S12-isostructural Na12−x(Sn2Si)1−xPxS12 and Na11Sn2PSe12 have been produced by mechanochemical synthesis routes,216 indicating the likelihood to synthesize Na11SnP2S12 in a related way. In the Na-quaternary phases grain boundary contributions to the total impedance are often observed making the above-mentioned possibilities worthwhile to explore in the Na based system.204,217
1 ratio. Additionally, Na11SnP2S12-isostructural Na12−x(Sn2Si)1−xPxS12 and Na11Sn2PSe12 have been produced by mechanochemical synthesis routes,216 indicating the likelihood to synthesize Na11SnP2S12 in a related way. In the Na-quaternary phases grain boundary contributions to the total impedance are often observed making the above-mentioned possibilities worthwhile to explore in the Na based system.204,217
3.7 Solid-state vs. solution synthesis for Li7La2Zr3O12 and Li1+xAlxGe2−x(PO4)3
Garnets (LixA2B3O12)21,218–220 and Li-NASICONS (LiM2(PO4)3)105 are typical representatives of solid ion conductors. The conventional synthesis route follows solid-state reaction of the oxide precursors, which usually require high temperatures (900–1230 °C), and long dwelling times (>12 h). Furthermore, high-temperature annealing is the additional necessary step to achieve maximum densification to reduce grain boundary resistance. This produces highly crystalline materials with large grain size and low grain boundary density, resulting in a high density and good ionic conductivity. However, lithium loss and secondary phase formation are two detrimental effects associated with high temperature heat treatment, both of which have a negative impact on the Li-ion conductivity.21,105 Thus, optimization of the heat treatment parameters such as synthesis temperature and time has become crucial for viable application of these material classes. In addition to the optimization of known synthesis processes, alternative synthesis approaches have been adopted in order to achieve a more cost-effective production. This includes sol–gel methods, thin film processing techniques (radio-frequency magnetron sputtering, pulsed laser deposition, metal–organic chemical vapor deposition and sol–gel spin coating), spray pyrolysis and electrospinning techniques.21,105,221 In the following section we compare ionic transport properties of Li7La2Zr3O12 and Li1+xAlxGe2−x(PO4)3 synthesized via solid-state and sol–gel routes.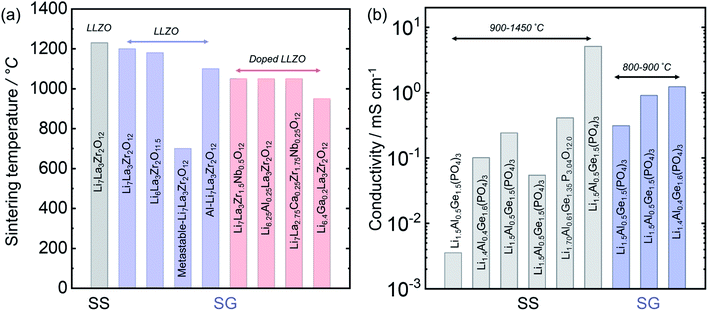 | ||
| Fig. 11 Influence of synthesis route on the sintering temperature and conductivity of cubic Li7La2Zr3O12 and Li1+xAlxGe2−x(PO4)3. (a) The sintering temperature for sol–gel (SG) route41,140,219,226 is lower than solid-state (SS) synthesis,37 which further decreases with substitution.224–227 (b) Ionic conductivities of Li1+xAlxGe2−x(PO4)3 synthesized via SS139,231–234 and SG methods.45,49,235 | ||
Room temperature ionic conductivity of sol–gel and solid-state synthesized Li7La3Zr2O12 is comparable to values reported previously, which further shows possible improvements of a sol–gel route over a solid-state one.226 Although sol–gel syntheses can offer lower sintering temperatures, they do not improve the atmospheric stability of Li7La3Zr2O12.226,229 Further, the reduction of grain boundary resistance still remains as an open challenge for this material class. Studies on the Li-site disorder are also rare; these could pave the way to achieving higher conducting Li7La3Zr2O12 derivatives.229,230
Despite these challenges and the promising possibility of different synthetic techniques, in-depth studies on how the synthesis conditions can further increase disorder and affect conductivities and even the microstructure and grain boundaries are lacking so far.
One of the most well-known ionic conductors from this family is Li1+xAlxGe2−x(PO4)3, where substitution of tetravalent Ge4+ ions by trivalent Al3+ leads to incorporation of additional Li+ in the structure, resulting in higher conductivity. High temperature melt-quenching and sol–gel processes are the common synthesis routes to prepare these materials.44 Because of the very high synthesis temperature (∼1500 °C), lithium loss by vaporization is a common problem associated with the melt quenching reaction. On the contrary, sol–gel methods offer syntheses of phase pure Li1+xAlxGe2−x(PO4)3 at much lower temperatures, without Li-loss (Fig. 11b).45,236 Weiss et al. recently reported a simple one-pot solution-phase synthesis of Li1+xAlxGe2−x(PO4)3 using GeO2 as the replacement of expensive precursor Ge(OC2H5)4.50
The properties of Li1+xAlxGe2−x(PO4)3 are highly dependent on the purity of the phase and the Al incorporation into the structure, which often deviates based on synthetic inputs specially different sintering conditions. Hence, optimization of the sintering temperature is key to achieving desirable phases and hence optimized properties. It has been observed that sol–gel synthesis can produce phase pure Li1+xAlxGe2−x(PO4)3 up to x = 0.5, which was not the case for solid-state reactions.236 The highest total conductivity of 1.22 mS cm−1 at 25 °C was observed for the sample Li1+xAlxGe2−x(PO4)3 with x = 0.4, which was higher than that of the Li1+xAlxGe2−x(PO4)3 (x = 0.5) glass-ceramic reported by Xu et al. (0.725 mS cm−1), and those of the Li1+xAlxGe2−x(PO4)3 (x = 0.5) prepared using a solid-state reaction precursor (0.0035 mS cm−1). In situ synchrotron X-ray powder diffraction, nuclear magnetic resonance studies, and neutron diffraction confirmed successful synthesis of Al-substituted Li1+xAlxGe2−x(PO4)3 structure when the reaction temperature was above 800 °C. Accumulation of additional phases on the grain boundaries causes a significant reduction in the grain boundary conductivity and detrimentally increases the activation energy.236
From the above-mentioned studies it is clear that sol–gel syntheses can offer a more cost-effective production of garnet and NASICON over solid-state synthesis. However, the underlying structural and, more so, microstructural modifications associated with these approaches are not entirely clear. Further, work using sol–gel approaches shows that even metastable polymorphs can be stabilized.237 In summary, the use of sol–gel methods provides a viable approach to reduce the synthesis temperatures of the oxides; however, the deeper understanding of how it influences the structure, the microstructure and grain boundaries as well as the ionic transport still needs to be developed.
4. Conclusion and future outlook
Throughout this review we have highlighted the fact that the real-world properties of materials used as electrolytes in all-solid-state batteries are not just a function of their chemical formulae, but of a host of other factors that are not always obvious or easily predictable, using case studies to make specific points. Quite often in the literature there is focus on specific achievements or effects without a broad understanding of the minutiae during synthesis and processing that lead there; this review is intended to start to fill those gaps with a sampling of case studies, showcasing effects on the scale of unit cells up to bulk materials. This was achieved by highlighting combinations of specific synthesis techniques and selected materials, with the important caveat that it is difficult to judge which technique is best for each situation, as what is beneficial for optimizing properties in one material may be detrimental in another. Some of the results of this scrutiny are shown in Fig. 12, intended to show the complexity of considerations that must be taken into account. Materials reported in the literature may not always be comparable if synthesized differently; synthetic procedures should therefore be reported clearly and in detail to aid in consistency of synthesis.Clearly the choice of a synthesis route should revolve around the target chemistry and bulk material properties, but it may also need to transcend simple laboratory needs and involve additional factors such as feasibility, scalability, costs, and environmental impact; trade-offs often need to be made, but they should be approached with a deeper understanding. Further development is necessary for characterization and modelling techniques, which play a crucial role to probe chemical structures, ion conduction mechanisms as well as the interfacial chemistry. Since syntheses can tune a material's structure and composition, one may also envision a change in chemical and electrochemical stability. It is therefore important to study the influence of synthesis on the chemical, thermal and electrochemical stability of solid electrolyte materials. Furthermore, interfacial (in)stability can be strongly affected based on the processing route, all of which needs special attention. We hope this review stimulates further thought into what may seem like minutiae during production that can lead to large differences in the resulting product, and how to better control outcomes.
Author contributions
W. G. Z. has proposed the out-line. All the authors have contributed to literature review, discussions, manuscript preparation, and revisions leading to the final format of the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The research was supported by the Federal Ministry of Education and Research (BMBF) within the project FESTBATT under grant number 03XP0177A. A. B. gratefully acknowledges the Alexander von Humboldt Foundation for financial support through a Postdoctoral Fellowship. T. F. gratefully acknowledges the German Academic Exchange Service (DAAD) for financial support through a short-term research grant.References
- Y. Nishi, Electrochem. Soc. Interface, 2016, 25, 71 CrossRef.
- J. B. Goodenough and K. S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264 CrossRef CAS.
- E. P. Roth and C. J. Orendorff, Interface Mag, 2012, 21, 45–49 CrossRef CAS.
- K. Xu, Chem. Rev., 2004, 104, 4303–4418 CrossRef CAS.
- S. Zugmann, M. Fleischmann, M. Amereller, R. M. Gschwind, H. D. Wiemhöfer and H. J. Gores, Electrochim. Acta, 2011, 56, 3926–3933 CrossRef CAS.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 16103 CrossRef CAS.
- L. Porz, T. Swamy, B. W. Sheldon, D. Rettenwander, T. Frömling, H. L. Thaman, S. Berendts, R. Uecker, W. C. Carter and Y.-M. Chiang, Adv. Energy Mater., 2017, 7, 1701003 CrossRef.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141 CrossRef.
- S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Prog. Energy, 2020, 2, 022001 CrossRef.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- T. Fuchs, S. P. Culver, P. Till and W. G. Zeier, ACS Energy Lett, 2020, 5, 146–151 CrossRef CAS.
- M. A. Kraft, S. Ohno, T. Zinkevich, R. Koerver, S. P. Culver, T. Fuchs, A. Senyshyn, S. Indris, B. J. Morgan and W. G. Zeier, J. Am. Chem. Soc., 2018, 140, 16330–16339 CrossRef CAS PubMed.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef CAS PubMed.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- S. P. Culver, R. Koerver, T. Krauskopf and W. G. Zeier, Chem. Mater., 2018, 30, 4179–4192 CrossRef CAS.
- F. Croce, G. B. Appetecchi, L. Persi and B. Scrosati, Nature, 1998, 394, 456–458 CrossRef CAS.
- Y. Deng, C. Eames, B. Fleutot, R. David, J. N. Chotard, E. Suard, C. Masquelier and M. S. Islam, ACS Appl. Mater. Interfaces, 2017, 9, 7050–7058 CrossRef CAS PubMed.
- S. Muy, J. C. Bachman, H.-H. Chang, L. Giordano, F. Maglia, S. Lupart, P. Lamp, W. G. Zeier and Y. Shao-Horn, Chem. Mater., 2018, 30, 5573–5582 CrossRef CAS.
- A. Rossbach, F. Tietz and S. Grieshammer, J. Power Sources, 2018, 391, 1–9 CrossRef CAS.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC.
- N. Minafra, S. P. Culver, C. Li, A. Senyshyn and W. G. Zeier, Chem. Mater., 2019, 31, 3794–3802 CrossRef CAS.
- P. Adeli, J. D. Bazak, K. H. Park, I. Kochetkov, A. Huq, G. R. Goward and L. F. Nazar, Angew. Chem., Int. Ed., 2019, 58, 8681–8686 CrossRef CAS PubMed.
- A. Kuhn, V. Duppel and B. V Lotsch, Energy Environ. Sci., 2013, 6, 3548–3552 RSC.
- A. Kuhn, O. Gerbig, C. Zhu, F. Falkenberg, J. Maier and B. V. Lotsch, Phys. Chem. Chem. Phys., 2014, 16, 14669–14674 RSC.
- A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Nat. Commun., 2012, 3, 856 CrossRef PubMed.
- A. Hayashi, N. Masuzawa, S. Yubuchi, F. Tsuji, C. Hotehama, A. Sakuda and M. Tatsumisago, Nat. Commun., 2019, 10, 5266 CrossRef CAS PubMed.
- T. Asano, A. Sakai, S. Ouchi, M. Sakaida, A. Miyazaki and S. Hasegawa, Adv. Mater., 2018, 30, 1803075 CrossRef PubMed.
- X. Li, J. Liang, X. Yang, K. R. Adair, C. Wang, F. Zhao and X. Sun, Energy Environ. Sci., 2020, 13, 1429–1461 RSC.
- J. C. Bachman, S. Muy, A. Grimaud, H. H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- Y. Zhu, X. He and Y. Mo, ACS Appl. Mater. Interfaces, 2015, 7, 23685–23693 CrossRef CAS PubMed.
- G. F. Dewald, S. Ohno, M. A. Kraft, R. Koerver, P. Till, N. M. Vargas-Barbosa, J. Janek and W. G. Zeier, Chem. Mater., 2019, 31, 8328–8337 CrossRef CAS.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS PubMed.
- Y. Kato, S. Shiotani, K. Morita, K. Suzuki, M. Hirayama and R. Kanno, J. Phys. Chem. Lett., 2018, 9, 607–613 CrossRef CAS PubMed.
- S. Ohno, C. Rosenbach, G. F. Dewald, J. Janek and W. G. Zeier, Adv. Funct. Mater., 2021, 2010620 CrossRef.
- S. Ohno, T. Bernges, J. Buchheim, M. Duchardt, A.-K. Hatz, M. A. Kraft, H. Kwak, A. L. Santhosha, Z. Liu, N. Minafra, F. Tsuji, A. Sakuda, R. Schlem, S. Xiong, Z. Zhang, P. Adelhelm, H. Chen, A. Hayashi, Y. S. Jung, B. V Lotsch, B. Roling, N. M. Vargas-Barbosa and W. G. Zeier, ACS Energy Lett, 2020, 5, 910–915 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781 CrossRef CAS PubMed.
- H. Xie, Y. Li and J. B. Goodenough, Mater. Res. Bull., 2012, 47, 1229–1232 CrossRef CAS.
- I. Kokal, M. Somer, P. H. L. Notten and H. T. Hintzen, Solid State Ionics, 2011, 185, 42–46 CrossRef CAS.
- J. Awaka, N. Kijima, H. Hayakawa and J. Akimoto, J. Solid State Chem., 2009, 182, 2046–2052 CrossRef CAS.
- Y. Li, J.-T. Han, C.-A. Wang, S. C. Vogel, H. Xie, M. Xu and J. B. Goodenough, J. Power Sources, 2012, 209, 278–281 CrossRef CAS.
- M. Amores, T. E. Ashton, P. J. Baker, E. J. Cussen and S. A. Corr, J. Mater. Chem. A, 2016, 4, 1729–1736 RSC.
- D. Gao, R. Wu, P. Chen, T. Hong and J. Cheng, Mater. Res. Express, 2020, 6, 125539 CrossRef.
- J. Fu, Solid State Ionics, 1997, 104, 191–194 CrossRef CAS.
- M. Zhang, K. Takahashi, N. Imanishi, Y. Takeda, O. Yamamoto, B. Chi, J. Pu and J. Li, J. Electrochem. Soc., 2012, 159, A1114–A1119 CrossRef CAS.
- J. S. Thokchom, N. Gupta and B. Kumar, J. Electrochem. Soc., 2008, 155, A915 CrossRef CAS.
- P. D. Kichambare, T. Howell and S. Rodrigues, Energy Technol, 2014, 2, 391–396 CrossRef CAS.
- C. R. Mariappan, C. Yada, F. Rosciano and B. Roling, J. Power Sources, 2011, 196, 6456–6464 CrossRef CAS.
- Y. Liu, J. Chen and J. Gao, Solid State Ionics, 2018, 318, 27–34 CrossRef CAS.
- M. Weiss, D. A. Weber, A. Senyshyn, J. Janek and W. G. Zeier, ACS Appl. Mater. Interfaces, 2018, 10, 10935–10944 CrossRef CAS PubMed.
- M. M. Mahmoud, Y. Cui, M. Rohde, C. Ziebert, G. Link and H. J. Seifert, Materials, 2016, 9, 506 CrossRef PubMed.
- S. Yubuchi, S. Teragawa, K. Aso, K. Tadanaga, A. Hayashi and M. Tatsumisago, J. Power Sources, 2015, 293, 941–945 CrossRef CAS.
- H. Wang, C. Yu, S. Ganapathy, E. R. H. van Eck, L. van Eijck and M. Wagemaker, J. Power Sources, 2019, 412, 29–36 CrossRef CAS.
- Z. Zhang, L. Zhang, Y. Liu, X. Yan, B. Xu and L. min Wang, J. Alloys Compd., 2020, 812, 152103 CrossRef CAS.
- L. Zhou, K. H. Park, X. Sun, F. Lalère, T. Adermann, P. Hartmann and L. F. Nazar, ACS Energy Lett, 2019, 4, 265–270 CrossRef CAS.
- Z. Liu, W. Fu, E. A. Payzant, X. Yu, Z. Wu, N. J. Dudney, J. Kiggans, K. Hong, A. J. Rondinone and C. Liang, J. Am. Chem. Soc., 2013, 135, 975–978 CrossRef CAS.
- S. Teragawa, K. Aso, K. Tadanaga, A. Hayashi and M. Tatsumisago, J. Mater. Chem. A, 2014, 2, 5095–5099 RSC.
- H. Wang, Z. D. Hood, Y. Xia and C. Liang, J. Mater. Chem. A, 2016, 4, 8091–8096 RSC.
- N. H. H. Phuc, K. Morikawa, T. Mitsuhiro, H. Muto and A. Matsuda, Ionics, 2017, 23, 2061–2067 CrossRef.
- A. Matsuda, H. Muto and N. H. H. Phuc, J. Japan Soc. Powder Powder Metall., 2016, 63, 976–980 CrossRef CAS.
- N. H. H. Phuc, K. Morikawa, M. Totani, H. Muto and A. Matsuda, Solid State Ionics, 2016, 285, 2–5 CrossRef CAS.
- S. Teragawa, K. Aso, K. Tadanaga, A. Hayashi and M. Tatsumisago, Chem. Lett., 2013, 42, 1435–1437 CrossRef CAS.
- S. Teragawa, K. Aso, K. Tadanaga, A. Hayashi and M. Tatsumisago, J. Power Sources, 2014, 248, 939–942 CrossRef CAS.
- M. Tatsumisago, F. Mizuno and A. Hayashi, J. Power Sources, 2006, 159, 193–199 CrossRef CAS.
- M. Ghidiu, J. Ruhl, S. P. Culver and W. G. Zeier, J. Mater. Chem. A, 2019, 7, 17735–17753 RSC.
- H. Wang, Y. Chen, Z. D. Hood, G. Sahu, A. S. Pandian, J. K. Keum, K. An and C. Liang, Angew. Chem., Int. Ed., 2016, 55, 8551–8555 CrossRef CAS PubMed.
- A. Banerjee, K. H. Park, J. W. Heo, Y. J. Nam, C. K. Moon, S. M. Oh, S.-T. Hong and Y. S. Jung, Angew. Chem., Int. Ed., 2016, 55, 9634–9638 CrossRef CAS PubMed.
- L. Zhang, D. Zhang, K. Yang, X. Yan, L. Wang, J. Mi, B. Xu and Y. Li, Adv. Sci., 2016, 3, 1600089 CrossRef PubMed.
- R. Schlem, S. Muy, N. Prinz, A. Banik, Y. Shao-Horn, M. Zobel and W. G. Zeier, Adv. Energy Mater., 2020, 10, 1903719 CrossRef CAS.
- T. Krauskopf, C. Pompe, M. A. Kraft and W. G. Zeier, Chem. Mater., 2017, 29, 8859–8869 CrossRef CAS.
- T. Krauskopf, S. Muy, S. P. Culver, S. Ohno, O. Delaire, Y. Shao-Horn and W. G. Zeier, J. Am. Chem. Soc., 2018, 140, 14464–14473 CrossRef CAS PubMed.
- S. Muy, J. C. Bachman, L. Giordano, H.-H. Chang, D. L. Abernathy, D. Bansal, O. Delaire, S. Hori, R. Kanno, F. Maglia, S. Lupart, P. Lamp and Y. Shao-Horn, Energy Environ. Sci., 2018, 11, 850–859 RSC.
- W. Zhang, D. A. Weber, H. Weigand, T. Arlt, I. Manke, D. Schröder, R. Koerver, T. Leichtweiss, P. Hartmann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2017, 9, 17835–17845 CrossRef CAS PubMed.
- Y. Wang, X. Guo, Z. Lin, Y. Yang, L. Wu, H. Liu and H. Yu, Chem. Res. Chinese Univ., 2020, 36, 439–446 CrossRef CAS.
- T. Famprikis, O. U. Kudu, J. Dawson, P. Canepa, F. Fauth, E. Suard, M. Zbiri, D. Dambournet, O. Borkiewicz, H. Bouyanfif, S. Emge, C. Grey, S. Cretu, J.-N. Chotard, W. Zeier, S. Islam and C. Masquelier, J. Am. Chem. Soc., 2020, 142, 18422–18436 CrossRef CAS PubMed.
- J. Lau, R. H. DeBlock, D. M. Butts, D. S. Ashby, C. S. Choi and B. S. Dunn, Adv. Energy Mater., 2018, 8, 1602011 Search PubMed.
- A. Sakuda, A. Hayashi and M. Tatsumisago, Sci. Rep., 2013, 3, 2261 CrossRef PubMed.
- Y.-H. Cho, J. Wolfenstine, E. Rangasamy, H. Kim, H. Choe and J. Sakamoto, J. Mater. Sci., 2012, 47, 5970–5977 CrossRef CAS.
- T. Holzmann, L. M. Schoop, M. N. Ali, I. Moudrakovski, G. Gregori, J. Maier, R. J. Cava and B. V Lotsch, Energy Environ. Sci., 2016, 9, 2578–2585 RSC.
- L. Ladenstein, S. Lunghammer, E. Y. Wang, L. J. Miara, H. M. R. Wilkening, G. J. Redhammer and D. Rettenwander, J. Phys. Energy, 2020, 2, 35003 CrossRef CAS.
- S. Harm, A.-K. Hatz, I. Moudrakovski, R. Eger, A. Kuhn, C. Hoch and B. V Lotsch, Chem. Mater., 2019, 31, 1280–1288 CrossRef CAS.
- H. Tsukasaki, S. Mori, H. Morimoto, A. Hayashi and M. Tatsumisago, Sci. Rep., 2017, 7, 4142 CrossRef PubMed.
- Ö. U. Kudu, T. Famprikis, B. Fleutot, M. D. Braida, T. Le Mercier, M. S. Islam and C. Masquelier, J. Power Sources, 2018, 407, 31–43 CrossRef.
- A. Gautam, M. Sadowski, N. Prinz, H. Eickhoff, N. Minafra, M. Ghidiu, S. P. Culver, K. Albe, T. F. Fässler, M. Zobel and W. G. Zeier, Chem. Mater., 2019, 31, 10178–10185 CrossRef CAS.
- Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, Energy Environ. Sci., 2014, 7, 627–631 RSC.
- Z. D. Hood, H. Wang, A. S. Pandian, R. Peng, K. D. Gilroy, M. Chi, C. Liang and Y. Xia, Adv. Energy Mater., 2018, 8, 1800014 CrossRef.
- C. Dietrich, D. A. Weber, S. J. Sedlmaier, S. Indris, S. P. Culver, D. Walter, J. J. Janek and W. G. Zeier, J. Mater. Chem. A, 2017, 5, 18111–18119 RSC.
- C. Korte, J. Keppner, A. Peters, N. Schichtel, H. Aydin and J. Janek, Phys. Chem. Chem. Phys., 2014, 16, 24575–24591 RSC.
- Y. Qi, C. Ban and S. J. Harris, Joule, 2020, 4, 2599–2608 CrossRef CAS.
- N. J. J. De Klerk, I. Rosłoń and M. Wagemaker, Chem. Mater., 2016, 28, 7955–7963 CrossRef CAS.
- A. R. West, Solid state chemistry and its applications, Wiley, 2014 Search PubMed.
- L. Zhou, A. Assoud, Q. Zhang, X. Wu and L. F. Nazar, J. Am. Chem. Soc., 2019, 141, 19002–19013 CrossRef CAS PubMed.
- C. A. Geiger, E. Alekseev, B. Lazic, M. Fisch, T. Armbruster, R. Langner, M. Fechtelkord, N. Kim, T. Pettke and W. Weppner, Inorg. Chem., 2011, 50, 1089–1097 CrossRef CAS PubMed.
- S.-H. Bo, Y. Wang and G. Ceder, J. Mater. Chem. A, 2016, 4, 9044–9053 RSC.
- H. Muramatsu, A. Hayashi, T. Ohtomo, S. Hama and M. Tatsumisago, Solid State Ionics, 2011, 182, 116–119 CrossRef CAS.
- A. Sharafi, S. Yu, M. Naguib, M. Lee, C. Ma, H. M. Meyer, J. Nanda, M. Chi, D. J. Siegel and J. Sakamoto, J. Mater. Chem. A, 2017, 5, 13475–13487 RSC.
- W. G. Zeier, S. Zhou, B. Lopez-Bermudez, K. Page and B. C. Melot, ACS Appl. Mater. Interfaces, 2014, 6, 10900–10907 CrossRef CAS.
- L. Truong and V. Thangadurai, Chem. Mater., 2011, 23, 3970–3977 CrossRef CAS.
- C. Galven, J.-L. Fourquet, M.-P. Crosnier-Lopez and F. Le Berre, Chem. Mater., 2011, 23, 1892–1900 CrossRef CAS.
- W. Xia, B. Xu, H. Duan, Y. Guo, H. Kang, H. Li and H. Liu, ACS Appl. Mater. Interfaces, 2016, 8, 5335–5342 CrossRef CAS PubMed.
- Y. Deng, C. Eames, J.-N. Chotard, F. Lalère, V. Seznec, S. Emge, O. Pecher, C. P. Grey, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2015, 137, 9136–9145 CrossRef CAS PubMed.
- S. Hori, M. Kato, K. Suzuki, M. Hirayama, Y. Kato and R. Kanno, J. Am. Ceram. Soc., 2015, 98, 3352–3360 CrossRef CAS.
- R. Iwasaki, S. Hori, R. Kanno, T. Yajima, D. Hirai, Y. Kato and Z. Hiroi, Chem. Mater., 2019, 31, 3694–3699 CrossRef CAS.
- Q. Liu, Z. Geng, C. Han, Y. Fu, S. Li, Y. bing He, F. Kang and B. Li, J. Power Sources, 2018, 389, 120–134 CrossRef CAS.
- R. DeWees and H. Wang, ChemSusChem, 2019, 12, 3713–3725 CrossRef CAS PubMed.
- J.-F. Wu and X. Guo, Solid State Ionics, 2017, 310, 38–43 CrossRef CAS.
- P. Baláž, M. Achimovicová, M. Baláž, P. Billik, C. Z. Zara, J. M. Criado, F. Delogu, E. Dutková, E. Gaffet, F. J. Gotor, R. Kumar, I. Mitov, T. Rojac, M. Senna, A. Streletskii and W. C. Krystyna, Chem. Soc. Rev., 2013, 42, 7571–7637 RSC.
- C. F. Burmeister and A. Kwade, Chem. Soc. Rev., 2013, 42, 7660–7667 RSC.
- S. Boulineau, M. Courty, J. M. Tarascon and V. Viallet, Solid State Ionics, 2012, 221, 1–5 CrossRef CAS.
- A. Hayashi, S. Hama, H. Morimoto, M. Tatsumisago and T. Minami, J. Am. Ceram. Soc., 2001, 84, 477–479 CrossRef CAS.
- S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Frišcic, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447 RSC.
- T. Krauskopf, S. P. Culver and W. G. Zeier, Inorg. Chem., 2018, 57, 4739–4744 CrossRef CAS.
- A. Düvel, A. Kuhn, L. Robben, M. Wilkening and P. Heitjans, J. Phys. Chem. C, 2012, 116, 15192–15202 CrossRef.
- V. Šepelák, A. Düvel, M. Wilkening, K. D. Becker and P. Heitjans, Chem. Soc. Rev., 2013, 42, 7507–7520 RSC.
- K. Homma, M. Yonemura, T. Kobayashi, M. Nagao, M. Hirayama and R. Kanno, Solid State Ionics, 2011, 182, 53–58 CrossRef CAS.
- S. Y. Jung, R. Rajagopal and K. S. Ryu, J. Energy Chem., 2020, 47, 307–316 CrossRef.
- R. P. Rao and S. Adams, Phys. Status Solidi Appl. Mater. Sci., 2011, 208, 1804–1807 CrossRef CAS.
- H.-J. Deiseroth, S.-T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiß and M. Schlosser, Angew. Chem., Int. Ed., 2008, 47, 755–758 CrossRef CAS PubMed.
- N. Sata, K. Eberman, K. Eberl and J. Maier, Nature, 2000, 408, 946–949 CrossRef CAS PubMed.
- M. Wilkening, S. Indris and P. Heitjans, Phys. Chem. Chem. Phys., 2003, 5, 2225–2231 RSC.
- K. Kisu, S. Kim, R. Yoshida, H. Oguchi, N. Toyama and S. ichi Orimo, J. Energy Chem., 2020, 50, 424–429 CrossRef.
- X. Li, J. Liang, J. Luo, M. Norouzi Banis, C. Wang, W. Li, S. Deng, C. Yu, F. Zhao, Y. Hu, T. K. Sham, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li, K. R. Adair and X. Sun, Energy Environ. Sci., 2019, 12, 2665–2671 RSC.
- A. Hayashi, K. Minami, S. Ujiie and M. Tatsumisago, J. Non. Cryst. Solids, 2010, 356, 2670–2673 CrossRef CAS.
- F. Preishuber-Pflügl and M. Wilkening, Dalt. Trans., 2016, 45, 8675–8687 RSC.
- C. Yu, S. Ganapathy, E. R. H. Van Eck, L. Van Eijck, S. Basak, Y. Liu, L. Zhang, H. W. Zandbergen and M. Wagemaker, J. Mater. Chem. A, 2017, 5, 21178–21188 RSC.
- H. Nguyen, A. Banerjee, X. Wang, D. Tan, E. A. Wu, J.-M. Doux, R. Stephens, G. Verbist and Y. S. Meng, J. Power Sources, 2019, 435, 126623 CrossRef CAS.
- K. Suzuki, D. Kato, K. Hara, T. Yano, M. Hirayama, M. Hara and R. Kanno, Electrochemistry, 2018, 86, 1–5 CrossRef CAS.
- A. Miura, N. C. Rosero-Navarro, A. Sakuda, K. Tadanaga, N. H. H. Phuc, A. Matsuda, N. Machida, A. Hayashi and M. Tatsumisago, Nat. Rev. Chem., 2019, 3, 189–198 CrossRef CAS.
- K. H. Park, Q. Bai, D. H. Kim, D. Y. Oh, Y. Zhu, Y. Mo and Y. S. Jung, Adv. Energy Mater., 2018, 8, 1800035 CrossRef.
- T. Ozturk, E. Ertas and O. Mert, Chem. Rev., 2010, 110, 3419–3478 CrossRef CAS PubMed.
- M. C. Démarcq, Ind. Eng. Chem. Res., 1991, 30, 1906–1911 CrossRef.
- Y. Seino, M. Nakagawa, M. Senga, H. Higuchi, K. Takada and T. Sasaki, J. Mater. Chem. A, 2015, 3, 2756–2761 RSC.
- M. Calpa, N. C. Rosero-Navarro, A. Miura, K. Terai, F. Utsuno and K. Tadanaga, Chem. Mater., 2020, 32, 9627–9632 CrossRef CAS.
- M. Calpa, N. C. Rosero-Navarro, A. Miura and K. Tadanaga, Inorg. Chem. Front., 2018, 5, 501–508 RSC.
- S. Yubuchi, M. Uematsu, C. Hotehama, A. Sakuda, A. Hayashi and M. Tatsumisago, J. Mater. Chem. A, 2018, 7, 558–566 RSC.
- S. Chida, A. Miura, N. C. Rosero-Navarro, M. Higuchi, N. H. H. Phuc, H. Muto, A. Matsuda and K. Tadanaga, Ceram. Int., 2018, 44, 742–746 CrossRef CAS.
- A. E. Danks, S. R. Hall and Z. Schnepp, Mater. Horizons, 2016, 3, 91–112 RSC.
- J. Livage, M. Henry and C. Sanchez, Prog. Solid State Chem., 1988, 18, 259–341 CrossRef CAS.
- M. Kotobuki and M. Koishi, Ceram. Int., 2013, 39, 4645–4649 CrossRef CAS.
- N. Janani, S. Ramakumar, L. Dhivya, C. Deviannapoorani, K. Saranya and R. Murugan, Ionics, 2011, 17, 575–580 CrossRef CAS.
- Y. X. Gao, X. P. Wang, W. G. Wang and Q. F. Fang, Solid State Ionics, 2010, 181, 33–36 CrossRef CAS.
- Y. X. Gao, X. P. Wang, W. G. Wang, Z. Zhuang, D. M. Zhang and Q. F. Fang, Solid State Ionics, 2010, 181, 1415–1419 CrossRef CAS.
- M. Oghbaei and O. Mirzaee, J. Alloys Compd., 2010, 494, 175–189 CrossRef CAS.
- C. J. Jafta, M. K. Mathe, N. Manyala, W. D. Roos and K. I. Ozoemena, ACS Appl. Mater. Interfaces, 2013, 5, 7592–7598 CrossRef CAS PubMed.
- A. K. Mondal, D. Su, S. Chen, K. Kretschmer, X. Xie, H. J. Ahn and G. Wang, ChemPhysChem, 2015, 16, 169–175 CrossRef CAS PubMed.
- J. V. Laveda, V. Chandhok, C. A. Murray, G. W. Paterson and S. A. Corr, Chem. Commun., 2016, 52, 9028–9031 RSC.
- Q. Shi, D. Liu, Y. Wang, Y. Zhao, X. Yang and J. Huang, Small, 2019, 15, 1901724 CrossRef CAS PubMed.
- J. Xiang, D. Dong, F. Wen, J. Zhao, X. Zhang, L. Wang and Z. Liu, J. Alloys Compd., 2016, 660, 11–16 CrossRef CAS.
- S. Balaji, D. Mutharasu, N. S. Subramanian and K. Ramanathan, Ionics, 2009, 15, 765–777 CrossRef CAS.
- D. R. Baghurst and D. M. P. Mingos, J. Chem. Soc. Chem. Commun., 1988, 829–830 RSC.
- J. B. Hasted, in The Physics and Physical Chemistry of Water, Springer, New York, 1972, pp. 255–309 Search PubMed.
- H. J. Kitchen, S. R. Vallance, J. L. Kennedy, N. Tapia-Ruiz, L. Carassiti, A. Harrison, A. G. Whittaker, T. D. Drysdale, S. W. Kingman and D. H. Gregory, Chem. Rev., 2014, 114, 1170–1206 CrossRef CAS PubMed.
- E. E. Levin, J. H. Grebenkemper, T. M. Pollock and R. Seshadri, Chem. Mater., 2019, 31, 7151–7159 CrossRef CAS.
- M. Bhattacharya and T. Basak, Energy, 2016, 97, 306–338 CrossRef.
- J. Lasri, P. D. Ramesh and L. Schächter, J. Am. Ceram. Soc., 2000, 83, 1465–1468 CrossRef CAS.
- L. Hallopeau, D. Bregiroux, G. Rousse, D. Portehault, P. Stevens, G. Toussaint and C. Laberty-Robert, J. Power Sources, 2018, 378, 48–52 CrossRef CAS.
- K. Ohara, A. Mitsui, M. Mori, Y. Onodera, S. Shiotani, Y. Koyama, Y. Orikasa, M. Murakami, K. Shimoda, K. Mori, T. Fukunaga, H. Arai, Y. Uchimoto and Z. Ogumi, Sci. Rep., 2016, 6, 21302 CrossRef CAS PubMed.
- A. Hayashi, K. Minami, F. Mizuno and M. Tatsumisago, J. Mater. Sci., 2008, 43, 1885–1889 CrossRef CAS.
- K. Suto, P. Bonnick, E. Nagai, K. Niitani, T. S. Arthur and J. Muldoon, J. Mater. Chem. A, 2018, 6, 21261–21265 RSC.
- M. B. Preefer, J. H. Grebenkemper, F. Schroeder, J. D. Bocarsly, K. Pilar, J. A. Cooley, W. Zhang, J. Hu, S. Misra, F. Seeler, K. Schierle-Arndt and R. Seshadri, ACS Appl. Mater. Interfaces, 2019, 11, 42280–42287 CrossRef CAS PubMed.
- M. R. Busche, D. A. Weber, Y. Schneider, C. Dietrich, S. Wenzel, T. Leichtweiss, D. Schröder, W. Zhang, H. Weigand, D. Walter, S. J. Sedlmaier, D. Houtarde, L. F. Nazar and J. Janek, Chem. Mater., 2016, 28, 6152–6165 CrossRef CAS.
- L. E. Rush, Z. D. Hood and N. A. W. Holzwarth, Phys. Rev. Mater., 2017, 1, 075405 CrossRef.
- S. Seidel, W. G. Zeier and R. Pöttgen, Zeitschrift für Krist. – Cryst. Mater., 2020, 235, 1–6 CrossRef CAS.
- M. Jansen and U. Henseler, J. Solid State Chem., 1992, 99, 110–119 CrossRef CAS.
- A. Hayashi, K. Noi, N. Tanibata, M. Nagao and M. Tatsumisago, J. Power Sources, 2014, 258, 420–423 CrossRef CAS.
- Z. Zhu, I.-H. Chu, Z. Deng and S. P. Ong, Chem. Mater., 2015, 27, 8318–8325 CrossRef CAS.
- N. J. J. De Klerk and M. Wagemaker, Chem. Mater., 2016, 28, 3122–3130 CrossRef CAS.
- C. Yu, S. Ganapathy, N. J. J. de Klerk, E. R. H. van Eck and M. Wagemaker, J. Mater. Chem. A, 2016, 4, 15095–15105 RSC.
- I.-H. Chu, C. S. Kompella, H. Nguyen, Z. Zhu, S. Hy, Z. Deng, Y. S. Meng and S. P. Ong, Sci. Rep., 2016, 6, 33733 CrossRef CAS PubMed.
- S. Breuer, M. Uitz and H. M. R. Wilkening, J. Phys. Chem. Lett., 2018, 9, 2093–2097 CrossRef CAS PubMed.
- J. Schoonman, J. Electrochem. Soc., 1976, 123, 1772–1775 CrossRef CAS.
- M. Anji Reddy and M. Fichtner, J. Mater. Chem., 2011, 21, 17059–17062 RSC.
- L. N. Patro and K. Hariharan, Mater. Lett., 2012, 80, 26–28 CrossRef CAS.
- F. Preishuber-Pflügl, V. Epp, S. Nakhal, M. Lerch and M. Wilkening, Phys. status solidi c, 2015, 12, 10–14 CrossRef.
- M. M. Ahmad, Y. Yamane and K. Yamada, J. Appl. Phys., 2009, 106, 074106 CrossRef.
- R. Kanno, K. Ohno, H. Izumi, Y. Kawamoto, T. Kamiyama, H. Asano and F. Izumi, Solid State Ionics, 1994, 70–71, 253–258 CrossRef CAS.
- G. Denes, Y. H. Yu, T. Tyliszczak and A. P. Hitchcock, J. Solid State Chem., 1991, 15, 1–15 CrossRef.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- A. Düvel, B. Ruprecht, P. Heitjans and M. Wilkening, J. Phys. Chem. C, 2011, 115, 23784–23789 CrossRef.
- F. Preishuber-Pflügl, P. Bottke, V. Pregartner, B. Bitschnau and M. Wilkening, Phys. Chem. Chem. Phys., 2014, 16, 9580–9590 RSC.
- C. Rongeat, M. A. Reddy, R. Witter and M. Fichtner, J. Phys. Chem. C, 2013, 117, 4943–4950 CrossRef CAS.
- S. Randau, D. A. Weber, O. Kötz, R. Koerver, P. Braun, A. Weber, E. Ivers-Tiffée, T. Adermann, J. Kulisch, W. G. Zeier, F. H. Richter and J. Janek, Nat. Energy, 2020, 5, 259–270 CrossRef CAS.
- I. Hanghofer, B. Gadermaier and H. M. R. Wilkening, Chem. Mater., 2019, 31, 4591–4597 CrossRef CAS.
- P. R. Rayavarapu, N. Sharma, V. K. Peterson and S. Adams, J. Solid State Electrochem., 2012, 16, 1807–1813 CrossRef CAS.
- H. J. Deiseroth, J. Maier, K. Weichert, V. Nickel, S. T. Kong and C. Reiner, Z. Anorg. Allg. Chem., 2011, 637, 1287–1294 CrossRef CAS.
- N. Minafra, M. A. Kraft, T. Bernges, C. Li, R. Schlem, B. J. Morgan and W. G. Zeier, Inorg. Chem., 2020, 59, 11009–11019 CrossRef CAS.
- A. Gautam, M. Sadowski, M. Ghidiu, N. Minafra, A. Senyshyn, K. Albe and W. Zeier, Adv. Energy Mater., 2021, 2003369 CrossRef CAS.
- D. C. Ginnings and T. E. Phipps, J. Am. Chem. Soc., 1930, 52, 1340–1345 CrossRef CAS.
- R. Kanno, J. Electrochem. Soc., 1984, 131, 469 CrossRef CAS.
- H. J. Seifert, J. Therm. Anal. Calorim., 2006, 83, 479–505 CrossRef CAS.
- Z. Xu, X. Chen, K. Liu, R. Chen, X. Zeng and H. Zhu, Chem. Mater., 2019, 31, 7425–7433 CrossRef CAS.
- K. H. Park, K. Kaup, A. Assoud, Q. Zhang, X. Wu and L. F. Nazar, ACS Energy Lett, 2020, 533–539 CrossRef CAS.
- J. Liang, X. Li, S. Wang, K. R. Adair, W. Li, Y. Zhao, C. Wang, Y. Hu, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li, Y. Mo and X. Sun, J. Am. Chem. Soc., 2020, 142, 7012–7022 CrossRef CAS.
- L. Zhou, C. Y. Kwok, A. Shyamsunder, Q. Zhang, X. Wu and L. F. Nazar, Energy Environ. Sci., 2020, 13, 2056–2063 RSC.
- R. Schlem, A. Banik, M. Eckardt, M. Zobel and W. G. Zeier, ACS Appl. Energy Mater., 2020, 3, 10164–10173 CrossRef CAS.
- S. Muy, J. Voss, R. Schlem, R. Koerver, S. J. Sedlmaier, F. Maglia, P. Lamp, W. G. Zeier and Y. Shao-Horn, iScience, 2019, 16, 270–282 CrossRef CAS.
- N. H. H. Phuc, M. Totani, K. Morikawa, H. Muto and A. Matsuda, Solid State Ionics, 2016, 288, 240–243 CrossRef CAS.
- Z. D. Hood, H. Wang, A. S. Pandian, R. Peng, K. D. Gilroy, M. Chi, C. Liang and Y. Xia, Adv. Energy Mater., 2018, 8, 1870096 CrossRef.
- Z. Liu, W. Fu, E. A. Payzant, X. Yu, Z. Wu, N. J. Dudney, J. Kiggans, K. Hong, A. J. Rondinone and C. Liang, J. Am. Chem. Soc., 2013, 135, 975–978 CrossRef CAS PubMed.
- Y. Wang, D. Lu, M. Bowden, P. Z. El Khoury, K. S. Han, Z. D. Deng, J. Xiao, J. G. Zhang and J. Liu, Chem. Mater., 2018, 30, 990–997 CrossRef CAS.
- S. Ito, M. Nakakita, Y. Aihara, T. Uehara and N. Machida, J. Power Sources, 2014, 271, 342–345 CrossRef CAS.
- S. Yubuchi, M. Uematsu, M. Deguchi, A. Hayashi and M. Tatsumisago, ACS Appl. Energy Mater., 2018, 1, 3622–3629 CrossRef CAS.
- R. C. Xu, X. H. Xia, Z. J. Yao, X. L. Wang, C. D. Gu and J. P. Tu, Electrochim. Acta, 2016, 219, 235–240 CrossRef CAS.
- M. Duchardt, U. Ruschewitz, S. Adams, S. Dehnen and B. Roling, Angew. Chem., Int. Ed., 2018, 57, 1351–1355 CrossRef CAS PubMed.
- Z. Zhang, E. Ramos, F. Lalère, A. Assoud, K. Kaup, P. Hartman and L. F. Nazar, Energy Environ. Sci., 2018, 11, 87–93 RSC.
- Z. Yu, S.-L. Shang, Y. Gao, D. Wang, X. Li, Z.-K. Liu and D. Wang, Nano Energy, 2018, 47, 325–330 CrossRef CAS.
- S. P. Ong, Y. Mo, W. D. Richards, L. Miara, H. S. Lee and G. Ceder, Energy Environ. Sci., 2013, 6, 148–156 RSC.
- S. Adams and R. Prasada Rao, J. Mater. Chem., 2012, 22, 7687–7691 RSC.
- Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2012, 24, 15–17 CrossRef CAS.
- A. Sorkin and S. Adams, Mater. Adv., 2020, 1, 184–196 RSC.
- Z. Yu, S.-L. Shang, D. Wang, Y. C. Li, H. P. Yennawar, G. Li, H.-T. Huang, Y. Gao, T. E. Mallouk, Z.-K. Liu and D. Wang, Energy Storage Materials, 2019, 17, 70–77 CrossRef.
- R. Kanno and M. Murayama, J. Electrochem. Soc., 2001, 148, A742 CrossRef CAS.
- O. Kwon, M. Hirayama, K. Suzuki, Y. Kato, T. Saito, M. Yonemura, T. Kamiyama and R. Kanno, J. Mater. Chem. A, 2015, 3, 438–446 RSC.
- H. Tsukasaki, S. Mori, S. Shiotani, H. Yamamura and H. Iba, J. Power Sources, 2017, 369, 57–64 CrossRef CAS.
- K. Mori, T. Kasai, K. Iwase, F. Fujisaki, Y. Onodera and T. Fukunaga, Solid State Ionics, 2017, 301, 163–169 CrossRef CAS.
- R. P. Rao, X. Zhang, K. C. Phuah and S. Adams, J. Mater. Chem. A, 2019, 7, 20790–20798 RSC.
- M. A. Kraft, L. M. Gronych, T. Famprikis, S. Ohno and W. G. Zeier, Chem. Mater., 2020, 32, 6566–6576 CrossRef CAS.
- E. J. Cussen, J. Mater. Chem., 2010, 20, 5167–5173 RSC.
- S. Afyon, F. Krumeich and J. L. M. Rupp, J. Mater. Chem. A, 2015, 3, 18636–18648 RSC.
- S. Ramakumar, C. Deviannapoorani, L. Dhivya, L. S. Shankar and R. Murugan, Prog. Mater. Sci., 2017, 88, 325–411 CrossRef CAS.
- S. Y. Li, W. P. Wang, S. Xin, J. Zhang and Y. G. Guo, Energy Storage Materials, 2020, 32, 458–464 CrossRef.
- R. P. Rao, W. Gu, N. Sharma, V. K. Peterson, M. Avdeev and S. Adams, Chem. Mater., 2015, 27, 2903–2910 CrossRef CAS.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378–19392 RSC.
- L. Cheng, C. H. Wu, A. Jarry, W. Chen, Y. Ye, J. Zhu, R. Kostecki, K. Persson, J. Guo, M. Salmeron, G. Chen and M. Doeff, ACS Appl. Mater. Interfaces, 2015, 7, 17649–17655 CrossRef CAS PubMed.
- T. Krauskopf, R. Dippel, H. Hartmann, K. Peppler, B. Mogwitz, F. H. Richter, W. G. Zeier and J. Janek, Joule, 2019, 3, 2030–2049 CrossRef CAS.
- Y. Shimonishi, A. Toda, T. Zhang, A. Hirano, N. Imanishi, O. Yamamoto and Y. Takeda, Solid State Ionics, 2011, 183, 48–53 CrossRef CAS.
- A. Paolella, W. Zhu, G. Bertoni, S. Savoie, Z. Feng, H. Demers, V. Gariepy, G. Girard, E. Rivard, N. Delaporte, A. Guerfi, H. Lorrmann, C. George and K. Zaghib, ACS Appl. Energy Mater., 2020, 3, 3415–3424 CrossRef CAS.
- P. J. Kumar, K. Nishimura, M. Senna, A. Düvel, P. Heitjans, T. Kawaguchi, N. Sakamoto, N. Wakiya and H. Suzuki, RSC Adv., 2016, 6, 62656–62667 RSC.
- R. H. Brugge, A. K. O. Hekselman, A. Cavallaro, F. M. Pesci, R. J. Chater, J. A. Kilner and A. Aguadero, Chem. Mater., 2018, 30, 3704–3713 CrossRef CAS.
- C. Bernuy-Lopez, W. Manalastas, J. M. Lopez del Amo, A. Aguadero, F. Aguesse and J. A. Kilner, Chem. Mater., 2014, 26, 3610–3617 CrossRef CAS.
- J. K. Feng, L. Lu and M. O. Lai, J. Alloys Compd., 2010, 501, 255–258 CrossRef CAS.
- P. Maldonado-Manso, M. C. Martín-Sedeño, S. Bruque, J. Sanz and E. R. Losilla, Solid State Ionics, 2007, 178, 43–52 CrossRef CAS.
- H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G. Adachi, Bull. Chem. Soc. Jpn., 1992, 65, 2200–2204 CrossRef CAS.
- Y. Cui, M. M. Mahmoud, M. Rohde, C. Ziebert and H. J. Seifert, Solid State Ionics, 2016, 289, 125–132 CrossRef CAS.
- B. E. Francisco, C. R. Stoldt and J.-C. M'Peko, J. Phys. Chem. C, 2015, 119, 16432–16442 CrossRef CAS.
- Z. Liu, S. Venkatachalam and L. Van Wüllen, Solid State Ionics, 2015, 276, 47–55 CrossRef CAS.
- H. El-Shinawi, C. Greaves and J. Janek, RSC Adv., 2015, 5, 17054–17059 RSC.
| This journal is © The Royal Society of Chemistry 2021 |