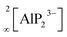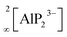Supertetrahedral polyanionic network in the first lithium phosphidoindate Li₃InP₂ – structural similarity to Li₂SiP₂ and Li₂GeP₂ and dissimilarity to Li₃AlP₂ and Li₃GaP₂

Abstract

Phosphide-based materials have been investigated as promising candidates for solid electrolytes, among which the recently reported Li₉AlP₄ displays an ionic conductivity of 3 mS cm⁻¹. While the phases Li–Al–P and Li–Ga–P have already been investigated, no ternary indium-based phosphide has been reported up to now. Here, we describe the synthesis and characterization of the first lithium phosphidoindate Li₃InP₂, which is easily accessible via ball milling of the elements and subsequent annealing. Li₃InP₂ crystallizes in the tetragonal space group I4₁/acd with lattice parameters of a = 12.0007(2) and c = 23.917(5) Å, featuring a supertetrahedral polyanionic framework of interconnected InP₄ tetrahedra. All lithium atoms occupy tetrahedral voids with no partial occupation. Remarkably, Li₃InP₂ is not isotypic to the previously reported homologues Li₃AlP₂ and Li₃GaP₂, which both crystallize in the space group Cmce and feature 2D layers of connected tetrahedra but no supertetrahedral framework. DFT computations support the observed stability of Li₃InP₂. A detailed geometrical analysis leads to a more general insight into the structural factors governing lithium ion mobility in phosphide-based materials: in the non-ionic conducting Li₃InP₂ the Li ions exclusively occupy tetrahedral voids in the distorted close packing of P atoms, whereas partially filled octahedral voids are present in the moderate ionic conductors Li₂SiP₂ and Li₂GeP₂.

---

Introduction

All-solid-state batteries (ASSB) have recently become the focus of research as an attractive alternative to state-of-the-art liquid-based batteries due to their enhanced safety combined with high energy/power density and mechanical stability.^1–7 One of the main obstacles for the commercialization of ASSBs is the difficulty to develop superionic solid conductors, which are crucial for fast ionic diffusion in ASSBs. Recently, our group investigated new classes of lithium ion conductors based on phosphides. Starting with Li₈SiP₄ in 2016, we introduced phosphidosilicates with an ionic conductivity of 4.5 × 10⁻⁵ S cm⁻¹.⁸ Lately, in the Li-richer compound Li₁₄SiP₆ the conductivity was even higher with up to 1 × 10⁻³ S cm⁻¹.⁹ Furthermore, we extended the system to the heavier tetrel (group-14) homologues, phosphidogermanates, with two Li-ion conducting modifications of Li₈GeP₄ that show ionic conductivities of up to 8.6 × 10⁻⁵ S cm⁻¹ and with Li₁₄GeP₆, which achieves an ionic conductivity of 1.7 × 10⁻³ S cm⁻¹.^10,11 The structural building units in these phosphides are [TtP₄]⁸⁻ tetrahedra surrounded by lithium atoms (Tt = Si, Ge). They exhibit a huge structural variety, and by decreasing the amount of lithium, condensed and covalently connected tetrahedra are formed, thereby offering different polyanionic networks: Li₁₀Si₂P₆ features pairs of edge-sharing SiP₄ tetrahedra,¹² in Li₂SiP₂/Li₂GeP₂ and LiSi₂P₃, respectively, SiP₄ and GeP₄ tetrahedra are condensed to networks of supertetrahedra.^8,13,14 Layered structures have been reported as well: in Li₃Si₃P₇, vertex-sharing SiP₄ tetrahedra form double layers,¹² and LiGe₃P₃ is built up by a two dimensionally extended polyanion comprising GeP₄ and Ge(P₃Ge) tetrahedra.¹³

Phosphide-based materials as lithium ionic conductors originated from the aliovalent substitution of [TtS₄]⁴⁻ tetrahedra, which are the main building block in sulfide-based conductors. This leads to analogous structures with more negatively charged [TtP₄]⁸⁻ tetrahedra, which can therefore accommodate more lithium than the well-known sulfur-based analogues. In recent investigations we expanded this class of compound further to phosphidoaluminates, which contain tetrahedral AlP₄ building units, and we discovered the fast lithium ion conductor Li₉AlP₄, which shows ionic conductivities of 3 × 10⁻³ S cm⁻¹.¹⁵ In addition, we also obtained Li₃AlP₂, which is built up by 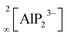layers of corner- and edge-sharing AlP₄ tetrahedra,¹⁶ and we then also introduced the isotypic gallium compound Li₃GaP₂ as the first phosphidogallate.¹⁶ Both trielate (Tr = Al, Ga) compounds do not show moderate lithium ion conductivity but unexpectedly turned out to be direct band gap semiconductors with optical band gaps of 3.1 and 2.8 eV, respectively.

Prior to the present work, no ternary Li–In–P phase has been described in the literature, and only one ternary Na–In–P phase was mentioned: Na₃InP₂ is built up by a distorted hcp of P atoms with all octahedral voids filled by Na, whereas the tetrahedral voids are occupied by Na and In, giving rise to a polyanionic network of corner-sharing InP₄ tetrahedra.¹⁷

In the present work, we report the first lithium phosphidoindate, Li₃InP₂, synthesized via ball milling of the elements and subsequent annealing. The compound retains the principal structural building unit of TrP₄ tetrahedra, but their arrangement is notably different from that of Li₃AlP₂ and Li₃GaP₂. In Li₃InP₂, the InP₄ tetrahedra are condensed to supertetrahedra in a three-dimensional framework. The structure is determined by single crystal X-ray diffraction and analyzed by complementary solid-state NMR experiments and first-principles computations. The knowledge of the lithium ion mobilities of the now-completed series of phosphidotrielates allows us to suggest a structural design rule linked to ionic conductivity, namely, the presence (or absence) of partially occupied Li-containing octahedral sites between which the ions can move rapidly.

Results and discussion

Synthesis and structure of Li₃InP₂

Li₃InP₂ was synthesized from the elements via a two-step procedure. At first, stoichiometric amounts of lithium, indium and phosphorus were ball milled resulting in a reactive mixture. Besides small amounts of the desired phase, Li₃InP₂, the polycrystalline powder contains considerable amounts of InP and Li_0.3In_1.7 (see Fig. S4†). Subsequently, pellets of the mixture were annealed in sealed niobium ampules at 1023 K for 22 h. Afterwards, the ampoules were rapidly cooled to room temperature by quenching in an ice-water mixture yielding almost phase-pure Li₃InP₂ with 3.3(1) % Li_0.3In_1.7 as an impurity according to Rietveld analysis (Fig. S3†). Annealing at lower temperatures such as 673 K or slow cooling rates led to impurities such as InP. Powdered Li₃InP₂ is brick-red. Complete data of the Rietveld refinement are given in the ESI; Tables S5 and S6.†

Red single crystals of Li₃InP₂ were obtained after reacting the elements with the formal stoichiometry “Li₃In₂P₃” at 1073 K in tantalum ampoules. Besides Li₃InP₂, the resulting product contains InP and at least one more, so far unknown phase according to unassigned reflections in the powder X-ray diffractogram (see Fig. S5†). Details of the structure refinement of the single crystal X-ray diffraction data of Li₃InP₂ are listed in the ESI in Tables S1–S4.†

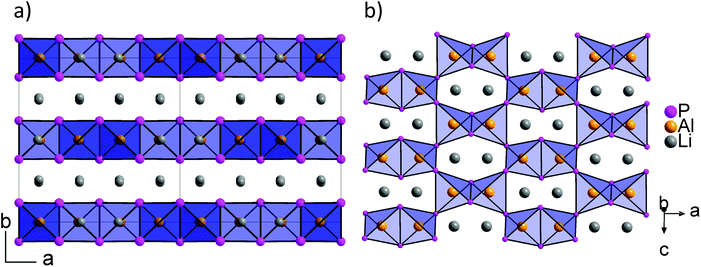
According to the single crystal structure determination, Li₃InP₂ crystallizes in the tetragonal space group I4₁/acd (no. 142) with seven independent crystallographic positions (one for In, three each for Li and P; Table S2†). Considering that the crystal structure is based on a tetragonally distorted cubic close packing of phosphorus atoms, the multiplicity of the phosphorus Wyckoff positions (32g + 16e + 16e) leads to a total of 128 tetrahedral voids and 64 octahedral voids. One quarter of these tetrahedral voids is filled by the indium atoms (Wyckoff position 32g). The remaining 96 tetrahedral voids are occupied by lithium (3 × 32g). Hence, the tetrahedral voids are fully occupied, whereas all octahedral voids are empty. The unit cell determined by single crystal X-ray diffraction is displayed in Fig. 1a.

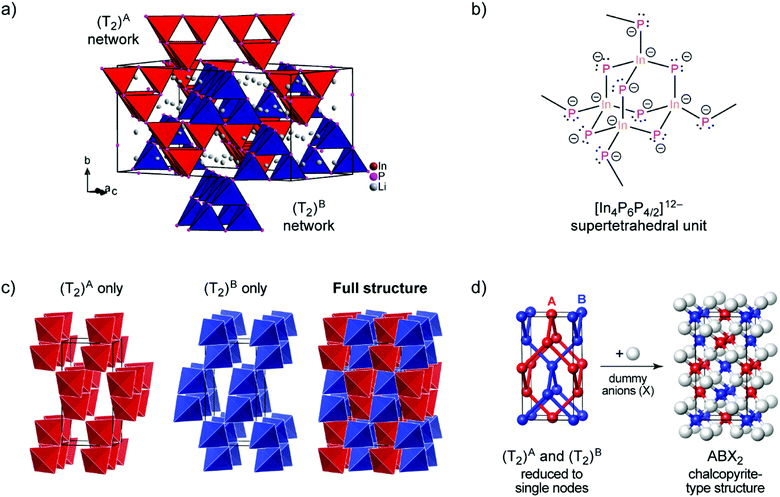Fig. 1 (a) The crystal structure of Li₃InP₂. The T2-supertetrahedra consist of four InP₄ tetrahedra and form two independent adamantane-like networks (the two networks, denoted as (T₂)^A and (T₂)^B, are shown in red and blue color, respectively). Li⁺ ions are located in tetrahedral voids of the distorted ccp of P atoms. Li, In and P atoms are depicted in grey, brown and purple color, respectively (displacement ellipsoids set at 90% at 150 K). Crystal data and structure refinement are shown in Tables S1–S4 in the ESI.† CSD 2026514 contains the ESI crystallographic data for this paper.† (b) Lewis structure with formal charges of the atoms. (c) The two independent adamantane-like supertetrahedral networks (T₂)^A and (T₂)^B and the penetration of the two networks (each T₂ unit is represented by a tetrahedron). (d) A simplified view of the structure, in which the center of gravity of each T₂ unit is represented by a colored sphere (“node”), inspired by ref. 18 Notice: the ABX₂ chalcopyrite structure type is formed by the formal insertion of X atoms shown as grey spheres. Structural drawings in panels (c and d) were created using VESTA.¹⁹

Indium and phosphorus form InP₄ tetrahedra, and four corner-sharing InP₄ tetrahedra build a T2-supertetrahedron. These T2-supertetrahedra are interconnected via corners, yielding two independent adamantane-like networks, which are shown in red and blue colors in Fig. 1a and c.

The In and P atoms are covalently connected to four and two atoms, respectively, resulting in a formal negative charge for both In and P of (−1). Since the P atoms at the corner of the supertetrahedron are shared with the next supertetrahedron, one such unit can be written as [In₄P₆P_4/2]¹²⁻ (Fig. 1b), which leads to an electronically balanced formula Li₃InP₂ (≡(Li⁺)₁₂[In₄P₆P_4/2]¹²⁻ or Li₁₂In₄P₈).

The InP₄ units slightly deviate from an ideal tetrahedron with P–In–P angles ranging from 107.20(1) to 111.55(1)°. The bond lengths within the InP₄ tetrahedra are in the narrow range between 2.5676(5) and 2.5899(5) Å and are very similar to those in compounds with strong In–P interactions like InP (2.5412(1) Å)²⁰ and Na₃InP₂ (2.592(3)–2.682(3) Å)¹⁷ and in excellent agreement with DFT computations after full structural optimization (2.57–2.58 Å). The Li–P bonds in Li₃InP₂ range from 2.526(2) to 2.673(2) Å and are in good agreement with those in other binary or ternary phases containing Li and P.^{8–10,12,13,15} DFT optimization yields 2.51–2.67 Å, again practically superimposable with the experimental results.

Considering each center of gravity of the supertetrahedra, the arrangement of the independent networks of the T2-supertetrahedra corresponds in a hierarchical relationship to the arrangement of the Cu and Fe cations in the chalcopyrite structure, which is highlighted in Fig. 1d. The concept of supertetrahedra is already known in the literature, including supertetrahedral sulfides,^21,22 which show structures with huge cavities, and also phosphidosilicates.^8,23

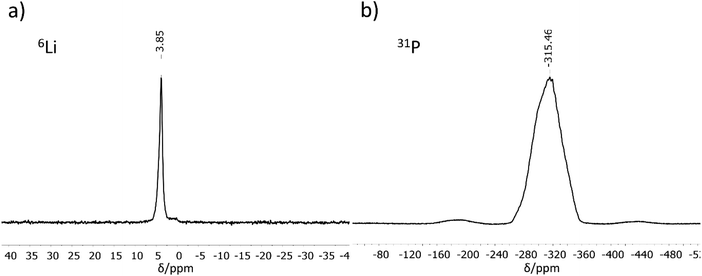
MAS-NMR spectroscopy

⁶Li and ³¹P MAS-NMR measurements (Fig. 2) support the results of the crystal structure determination. The ⁶Li NMR spectrum shows only one signal with a chemical shift of 3.85 ppm. As expected, the NMR experiment cannot distinguish between the three crystallographically different lithium atoms, all of which are tetrahedrally coordinated by phosphorus in a very similar chemical environment. The chemical shift of the Li atoms is in the same range as those for related compounds like Li₉AlP₄ (4.2 ppm), Li₃AlP₂ (4.0 and 3.0 ppm), Li₃GaP₂ (4.1 and 3.4 ppm), Li₂SiP₂ (2.1 ppm from ⁷Li MAS-NMR spectroscopy), and Li₂GeP₂ (3.6 and 2.4 ppm).^8,13,15,16 Compared to the above-mentioned compounds with two signals in the ⁶Li NMR spectrum, the difference in local coordination, which is expressed by the P–Li–P angles, is the lowest for Li₃InP₂ (Li₃InP₂: 104.99(8)–113.25(8)°, Li₃AlP₂: 100.0(3)–116.647(1)°, Li₃GaP₂: 102.258(1)–115.2(3)°, Li₂GeP₂: 84.68(1)–158.89(2)°). The ³¹P NMR spectrum displays a very broad, asymmetric signal in the range of −260 to −360 ppm. This range is typical for chemical shifts of two-fold connected P¹⁻ atoms such as in Li₃AlP₂ (−300 and −308.7 ppm) or Li₃GaP₂ (−234.8 and −280.5 ppm).¹⁶ However, the signals of two-fold connected P¹⁻ atoms in the related phosphidotetrelates are much more downfield shifted (Li₂SiP₂: −129.1 and −241.5 ppm and Li₂GeP₂: −59.9, −164.8 and −178.4 ppm) due to the deshielding of the more electronegative tetrel elements compared to indium.^8,13

Fig. 2 ⁶Li (a) and ³¹P (b) MAS-NMR measurements performed for Li₃InP₂.

Interestingly, only one ³¹P NMR signal is observed for Li₃InP₂, whereas two signals are obtained for all other related compounds. This correlates with the fact that the smallest distortion of the E–P–E bond angles is observed for Li₃InP₂ [106.411(9)–111.41(1)°] if compared to the others with E = Al, Ga, In, Si, Ge such as Li₃AlP₂ [78.298(1)–111.709(1)°], Li₃GaP₂ [79.943(1)–110.253(1)°], Li₂SiP₂ [102.669(9)–114.937(9)°], and Li₂GeP₂ [101.726(7)–112.609(7)°].

Comparison of Li₃InP₂ with the lighter homologues Li₃AlP₂ and Li₃GaP₂

Recently, we described the two isotypic phases Li₃AlP₂ and Li₃GaP₂,¹⁶ which crystallize in a distorted orthorhombic packing of phosphorus atoms in the space group Cmce (no. 64) with lattice parameters a = 11.5138(2), b = 11.7634(2), c = 5.8202(1) Å and a = 11.5839(2), b = 11.7809(2), c = 5.8129(2) Å, respectively, both determined by Rietveld refinement at room temperature. The crystal structures are built up by corner- and edge-sharing TrP₄ (Tr = Al, Ga) tetrahedra in two-dimensional layers. Based on a close packing of P atoms, the lithium atoms are located in all tetrahedral voids (Fig. 3). By contrast, Li₃InP₂ crystallizes in a tetragonal distorted phosphorus lattice in the space group I4₁/acd (no. 142) with lattice parameters of a = 12.03049(8) and c = 23.9641(3) Å, determined by Rietveld refinement at room temperature, and as mentioned above, the single crystal structure determination reveals a three-dimensional structure with exclusively corner-sharing InP₄ tetrahedra for t-Li₃InP₂ (Fig. 1).

Fig. 3 Structural details of Li₃AlP₂: (a) layers of polyanions are separated by lithium ions. (b) Top view of one layer of dimers of two edge-sharing AlP₄ tetrahedra that are interconnected by vertex-sharing. Unfilled voids within the layer are filled with additional Li ions. AlP₄ tetrahedra are shown as blue polyhedra. Al, P and Li atoms are drawn in orange, purple and grey, respectively.

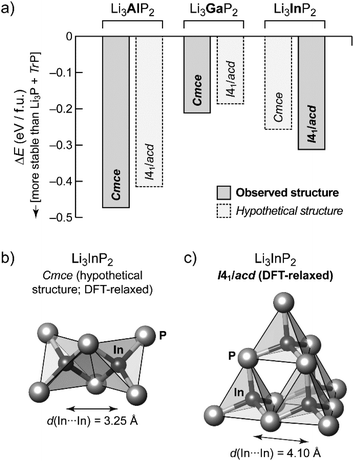
In order to gain additional insight into the experimentally observed structure types, we performed DFT-based structural optimizations for the Al, Ga and In compounds using the PBEsol functional²⁴ as implemented in CASTEP²⁵ (computational details are given in the ESI†). In addition to the experimentally determined unit cells we performed a substitutional “cross-check”: both modifications, orthorhombic o-Li₃TrP₂ and tetragonal t-Li₃TrP₂, were used for Tr = Al, Ga and In, starting either from the experimentally determined structure or from a hypothetical one obtained by substituting the Tr species. The DFT-optimized cell parameters are in excellent agreement with the experiment for the title compound (we obtained a_DFT = 11.96 Å and c_DFT = 23.74 Å); full results are listed in Table S7.†Fig. 4a shows the resulting energies, relative to the respective binary phosphides similar in spirit to our recent work on Li₉AlP₄.¹⁵ We compute the DFT electronic energy, E, for the relaxed ternary structure as well as for Li₃P and the respective zinc blende-type phase of AlP, GaP or InP; the difference (in the sense of a “reaction energy”) then allows us to estimate the stability of the ternary phase:

ΔE = E(Li₃TrP₂) − [E(Li₃P) + E(TrP)]

Fig. 4 First-principles DFT computations for Li₃AlP₂, Li₃GaP₂ and Li₃InP₂. (a) Computed total energies for DFT-relaxed structural models of the Li₃TrP₂ (Tr = Al, Ga, or In). Results are given relative to the respective binary phases; negative values indicate that the formation of the ternary compound is favorable. Results for experimentally observed structures correspond to solid lines and darker shading. Hypothetical structures, generated by cation substitution and DFT relaxation, are shown by dashed lines and lighter shading, and in all three cases these are less favorable than their respective counterpart, in agreement with experimental observations. (b) Structural fragment from a hypothetical, DFT-generated, Cmce Li₃InP₂ structure, emphasizing the edge-sharing [InP₄] tetrahedra, which may be compared to (c) the DFT-optimized I4₁/acd Li₃InP₂ structure, from which a supertetrahedral fragment is shown.

Negative values of ΔE therefore indicate that the ternary phase is stable with respect to the binaries (Fig. 4a).

The compounds Li₃TrP₂ are energetically favored over their respective binary components Li₃P and AlP, GaP and InP. The latter all adapt the cubic zinc blende type. The energy gain is significant considering the known stability of the zinc blende type that is most frequent among III–V semiconductors. More importantly, the difference in pairs of ΔE values allows us to compare the tendency for assuming either the Cmce or the I4₁/acd structure for all of the Li₃TrP₂ phases. For the Al and Ga compounds, the Cmce structure is favored by about 0.06 and 0.03 eV per formula unit (f.u.), respectively; by contrast, the I4₁/acd structure is preferred for Li₃InP₂ (by about 0.06 eV f.u.⁻¹), all in agreement with experiments. The stabilization of the title compound compared to the constituent binary phosphides is computed to be 0.31 eV f.u.⁻¹ (indicated by a negative sign in the convention of Fig. 4a), which represents a significant gain in stability and explains the synthetic accessibility of the ternary compound. Whilst there will always remain a certain error due to the DFT approximation and the neglect of thermal effects, we do trust that the computed trends shown in Fig. 4a are robust, and we note that they are fully consistent with the experimental observations.

As expected, the unit cell volume for the heavier homologues increases, however the In compound shows a much stronger increase: 788.30 ų for Al and 793.28 ų for Ga if compared to 867.10 ų (=3468.39 ų:4) for In. This correlates with a larger increase of the size of the InP₄ tetrahedron (8.8857 ų) compared to AlP₄ (7.0897 ų) and GaP₄ (7.1334 ų).

The trends of the interatomic Tr–Tr (Tr = Al, Ga, In) distances in Li₃AlP₂, Li₃GaP₂ and Li₃InP₂ are listed in Table 1. Regarding the different orthorhombic (Li₃AlP₂, Li₃GaP₂) and tetragonal structures (Li₃InP₂), the interatomic distances of the metal atoms are shorter in the orthorhombic structures, where edge-sharing tetrahedra occur compared to the tetragonal structure, where only corner-sharing tetrahedra are present. One may ask for the origin of the preference of one structure type over the other when comparing all three phosphidotrielates side-by-side. Interestingly, the results of the calculations are in agreement with Pauling's third rule. At least qualitatively and within the limits of such empirical concepts,²⁶ edge-sharing tetrahedra are disfavored on account of the repulsion of positively charged central atoms (Fig. 4b and c). This effect might be expected to be strongest in the In compound, where not only the ionic radius is the largest of the three, but the computed Mulliken charges for the series of Cmce structures (Al: +0.42e, Ga: +0.57e, hypothetical In structure: +0.65e) appear to be consistent with an increasing repulsion of Tr atoms in the case of edge-sharing tetrahedra. Note that the Mulliken charges, derived from quantum-mechanical computation, are not to the same as the formal negative charge of the Tr atom using the Lewis valence model (Fig. 1b). Accordingly, a structure containing edge-sharing tetrahedra is observed for Li₃AlP₂ and Li₃GaP₂, but not for Li₃InP₂ (Fig. 4c). This trend of the differences of the different metal to metal distances by DFT calculation is confirmed by the experimental interatomic Tr–Tr (Tr = Al, Ga, In) distances (Table 1). The experimental In–In distance is significantly longer than the Al–Al or Ga–Ga distances (4.116(3) Å (In) vs. 3.028(5) Å (Al) and 3.089(2) Å (Ga)).

Table 1 Comparison of the shortest interatomic Tr–Tr (Tr = Al, Ga, In) distances, the cell volume and the volume per formula unit in Li₃AlP₂, Li₃GaP₂ and Li₃InP₂ from Rietveld refinements at room temperature¹⁶

	o-Li3AlP2	o-Li3GaP2	t-Li3InP2
Cell volume/Å^3	788.29(2)	793.28(2)	3468.39(6) (3468.39:4 = 867.10)
Volume per formula unit/Å^3	98.54	99.16	108.38
Tetrahedron volume/Å^3	7.0897	7.1334	8.8857
Tr–Tr distances/Å	3.028(5)	3.089(2)	4.116(3)

---

Comparison of Li₃InP₂ with the phosphidotetrelates Li₂SiP₂ and Li₂GeP₂

The crystal structure of Li₃InP₂ is related to the structure of Li₂SiP₂ and Li₂GeP₂.^8,13 The two latter isotypic phases also crystallize in the space group I4₁/acd (no. 142), with lattice parameters of a = 12.1111(1) and c = 18.6299(4) Å for Li₂SiP₂ and a = 12.3070(1) and c = 19.0307(4) Å for Li₂GeP₂ and a slightly longer a, but much shorter c parameter as compared to Li₃InP₂. A full comparison of the lattice parameters and the tetrahedral volumes in Li₃InP₂, Li₂SiP₂ and Li₂GeP₂ is given in Table 2.

Table 2 Comparison of the tetrahedral volumes of InP₄, SiP₄ and GeP₄, the distances and angles between the supertetrahedra and the lithium coordination in Li₃InP₂, Li₂SiP₂ and Li₂GeP₂ obtained from single crystal structure determination. The values for Li₂SiP₂ and Li₂GeP₂ are taken from the literature^8,13

	Li3InP2	Li2SiP2	Li2GeP2
a/Å	12.0007(2)	12.1111(1)	12.3070(1)
c/Å	23.917(5)	18.6299(4)	19.0307(4)
V/Å^3	3447.7(1)	2732.61(7)	2882.42(9)
V (Tr/Tt)P4 tetrahedra/Å^3	8.7944	5.8042	6.4083
Distances (Å) between the centers of the T2-supertetrahedra	8.4729(1), 8.4899(9)	7.6395(1), 8.5638(1)	7.7782(1), 8.7023(1)

---

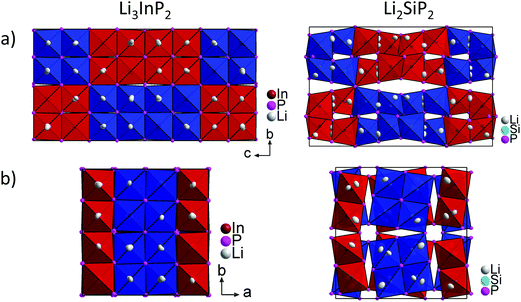
Assuming an average volume of 18 ų per heavy atom, the increase in cell volume corresponds approximately to the volume of 32 additional lithium atoms in the unit cell of Li₂SiP₂. Besides the change in the number of Li atoms, also the larger volume of the InP₄ tetrahedra compared to SiP₄/GeP₄ (see Table 2) contributes to an overall increase of the volume. However, this increase is highly anisotropic, since in Li₃InP₂ the lattice parameter c increases strongly, whereas the lattice parameter a is even slightly shorter compared to the one in Li₂SiP₂ and Li₂GeP₂.

Fig. 5 shows a comparison of the structures of Li₃InP₂ and Li₂SiP₂ viewed along the a and c direction. In Li₃InP₂ the InP₄ tetrahedra respectively the T2-supertetrahedra are aligned in an almost parallel fashion, whereas in Li₂SiP₂ the T2-supertetrahedra are rotated along the tetragonal axes. Interestingly, the parallel alignment in Li₃InP₂ leads to a slight decrease of the a and b axes despite the higher lithium content, but to a significant increase of the c axes.

Fig. 5 Comparison of the crystal structures of Li₃InP₂ (left) and Li₂SiP₂ (right). (a) The unit cell in a direction. (b) The unit cell in c direction. The InP₄ and SiP₄ tetrahedra are shown in blue and red. Both structures exhibit two independent diamond-like networks of T2-supertetrahedra. The different networks are drawn in blue and red, respectively.

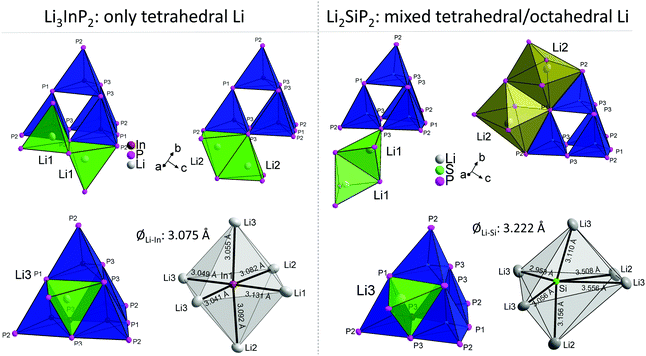
In Table 3 the Wyckoff positions in Li₃InP₂ and Li₂SiP₂ are compared (Li₂GeP₂ is omitted since it is isotypic to Li₂SiP₂). The higher Li content of the In compound arises from the occupation of two 32g Wyckoff sites instead of two 16f sites in the tetrelates. As a consequence, the coordination environments of the lithium atoms in the structures are different. The coordination of the lithium atoms in Li₃InP₂ and Li₂SiP₂ by phosphorus is illustrated in Fig. S2 and S8,† respectively. The positions Li1 and Li3 are similarly coordinated by four phosphorus atoms forming a distorted tetrahedron. By contrast, Li2 fills a strongly distorted octahedral void of phosphorus atoms with significant longer Li–P distances compared to Li1 and Li3. Here, the lithium atom Li2 is not located in the center of gravity of the octahedron but shows two much longer distances to neighboring P atoms of the distorted octahedron, resulting in a butterfly-type coordination of four P atoms. Interestingly, despite the smaller amount of Li atoms in Li₂SiP₂, not all the tetrahedral voids are occupied. In both compounds 25% of the tetrahedral voids are occupied by In or Si. Whereas all of the remaining 75% tetrahedral voids in Li₃InP₂ are filled with Li, only 37.5% are occupied by Li in Li₂SiP₂. In the latter, however, Li atoms occupy 25% of the distorted octahedral voids.

Table 3 Comparison of Wyckoff positions and atomic coordinates in Li₃InP₂ and Li₂SiP₂

Atom	Li3InP2				Li2SiP2
	Wyck.	x	y	z	Wyck.	x	y	z
In1/Si	32g	0.11730(2)	0.12523(2)	0.31365(2)	32g	0.08345(2)	0.12967(2)	0.30710(1)
P1	16d	0	1/4	0.00065(2)	16d	0	1/4	0.23093(2)
P2	16e	0.23884(3)	0	1/4	16e	0.18335(3)	0	1/4
P3	32g	0.25031(2)	0.25604(2)	0.12516(2)	32g	0.21330(2)	0.21711(2)	0.37222(2)
Li1	32g	0.1279(2)	0.3720(2)	0.0615(1)	16f	0.0946(2)	0.3446(2)	1/8
Li2	32g	0.1179(2)	0.1250(2)	0.0651(1)	16f	0.1506(2)	0.0995(2)	1/8
Li3	32g	0.3635(2)	0.1212(2)	0.19053(9)	32g	0.3426(2)	0.1271(2)	0.2173(1)

---

The different occupation of voids in Li₃InP₂ and Li₂SiP₂ also results in a different coordination of the supertetrahedra by lithium, which is shown in Fig. 6.

Fig. 6 Comparison of the different lithium atoms and how they are connected to the T2-supertetrahedra in Li₃InP₂ (left) and Li₂SiP₂ (right). For clarity, just one or two polyhedra are shown for the lithium atoms, respectively. In Li₃InP₂, all lithium atoms (Li1, Li2 and Li3) are in tetrahedral voids. The tetrahedra of Li1 and Li2 are connected via one edge or one corner to the supertetrahedron. The tetrahedron of Li3 is connected via one face to the center of the supertetrahedron's face. In Li₂SiP₂, Li1 and Li3 are placed in tetrahedral voids (green) whereas Li2 resides in an octahedral void (orange). As in Li₃InP₂, the tetrahedron of Li3 is connected via one face to the center of the supertetrahedron's face. By contrast, the strongly distorted tetrahedron of Li1 is only connected via one corner to the supertetrahedron. The strongly distorted octahedra of Li2 are connected via edges to the supertetrahedron. In Li₃InP₂, the indium atoms are octahedrally coordinated by lithium atoms with an average Li–In distance of 3.075 Å. In Li₂SiP₂, the silicon atoms are coordinated by a strongly distorted octahedron of lithium atoms with an average Li–Si distance of 3.222 Å.

The different Li coordination arises from the different charges of the supertetrahedra Si₄P₈⁸⁻/Ge₄P₈⁸⁻ and In₄P₈¹²⁻ (Fig. 1b). In Li₃InP₂ the lithium atoms form an almost regular octahedron around the indium atom with In–Li distances in the narrow range of 3.041 to 3.131 Å with an average of 3.075 Å, whereas in Li₂SiP₂ the octahedron formed by lithium atoms around silicon is strongly distorted with longer average distances of 3.222 Å and values between 2.958 and 3.556 Å. As a consequence, also octahedral voids of P atoms are filled with Li ions in Li₂SiP₂.

Impedance spectroscopy

For Li₃InP₂ two impedance measurements were performed to determine the ionic conductivity. The results are shown in Fig. S10.† The semi-circle can be described as parallel circuit element of a resistor and a constant phase element (R/Q). For the constant phase element the fit of the data acquired at 298 K resulted in α values of ≈0.99 and Q parameters of ≈2 × 10⁻⁸ F s^{(α − 1)}; the conductivity was determined to σ(Li₃InP₂) = 2.8(2) × 10⁻⁹ S cm⁻¹ at 298 K (obtained from two independently measured cells). DC polarization measurements in the range from 50 to 150 mV reveal an electronic conductivity of 2.7(3) × 10⁻⁹ S cm⁻¹ at 298 K (based on the standard deviation of two cells). The conductivity value obtained by DC polarization measurements is in the same range as the value obtained by PEIS measurements. Hence, the Nyquist plot shows only the semi-circle of the electronic conductivity, and no semi-circle for the ionic conductivity appears.

Conclusions

Li₃InP₂ is the first lithium phosphidoindate and can be described as a tetragonally distorted fcc lattice of P atoms (space group I4₁/acd), in which the In atoms occupy tetrahedral voids, thus forming a polyanionic framework of InP₄ supertetrahedra. The lithium atoms occupy the remaining tetrahedral voids. The structure of the compound is not isotypic to the previously reported ones of the lighter homologues, the orthorhombic compounds Li₃AlP₂ and Li₃GaP₂ (space group Cmce), which feature 2D layers of connected tetrahedra. First-principles DFT computations confirm the trend for the Al and Ga (In) compounds to crystallize in the orthorhombic (tetragonal) structure, respectively, which might originate in the different repulsive cation⋯cation interactions in both structures. Impedance spectroscopy reveals a very low electronic, but no ionic conductivity, whereas Li₂SiP₂ and Li₂GeP₂ show a moderate ionic mobility (2.2(3) × 10⁻⁷ S cm⁻¹ at 293 K and 1.5(3) × 10⁻⁷ S cm⁻¹ at 300 K, respectively).^8,13 The geometrical analysis of the Li positions shows that in Li₃InP₂ all tetrahedral voids are fully occupied by lithium, whereas in Li₂SiP₂ and Li₂GeP₂ tetrahedral voids remain empty, and especially strongly distorted octahedral voids are filled. In accordance with the observations in fcc phosphide-based lithium ion conductors such as Li₉AlP₄,¹⁵ lithium diffusion preferably appears on pathways via partially occupied octahedral sites.

Overall, these results demonstrate that even though crystal structures of phosphide compounds can contain complex polyanionic networks, a relatively simple description in terms of distorted close-packed arrangements of phosphorus atoms gives better insight for the description of lithium ion mobility. The title compound Li₃InP₂ provides a missing link in two respects: (i) it shows the structure changes in the series Li₃TrP₂ for Tr = Al, Ga, In, and (ii) it shows changes in lithium ion mobility in the series Li₃InP₂, Li₂SiP₂ and Li₂GeP₂.

Author contributions

TMFR carried out the crystal structure determination by single crystal and powder X-ray diffraction, performed the impedance spectroscopy measurements and wrote the manuscript draft. VLD carried out the DFT computations and provided discussion. JM contributed to the synthesis and data evaluation. GRS performed NMR experiments. TF designed research, provided guidance, and critically reviewed the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The work was carried out as part of the research project ASSB coordinated by ZAE Bayern. The project is funded by the Bavarian Ministry of Economic Affairs, Regional Development and Energy. V. L. D. acknowledges a Leverhulme Early Career Fellowship. The authors would like to acknowledge the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out this work (see DOI: 10.5281/zenodo.22558).

References

1. P. Knauth, Solid State Ionics, 2009, 180, 911–916.
2. Y.-S. Hu, Nat. Energy, 2016, 1, 16042.
3. J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141.
4. Z. Gao, H. Sun, L. Fu, F. Ye, Y. Zhang, W. Luo and Y. Huang, Adv. Mater., 2018, 30, 1705702.
5. J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162.
6. Y. Meesala, A. Jena, H. Chang and R.-S. Liu, ACS Energy Lett., 2017, 2, 2734–2751.
7. Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945–1976.
8. L. Toffoletti, H. Kirchhain, J. Landesfeind, W. Klein, L. van Wüllen, H. A. Gasteiger and T. F. Fässler, Chem.–Eur. J., 2016, 22, 17635–17645.
9. S. Strangmüller, H. Eickhoff, D. Müller, W. Klein, G. Raudaschl-Sieber, H. Kirchhain, C. Sedlmeier, V. Baran, A. Senyshyn, V. L. Deringer, L. van Wüllen, H. A. Gasteiger and T. F. Fässler, J. Am. Chem. Soc., 2019, 141, 14200–14209.
10. H. Eickhoff, S. Strangmüller, W. Klein, H. Kirchhain, C. Dietrich, W. G. Zeier, L. van Wüllen and T. F. Fässler, Chem. Mater., 2018, 30, 6440–6448.
11. S. Strangmüller, H. Eickhoff, G. Raudaschl-Sieber, H. Kirchhain, C. Sedlmeier, L. van Wüllen, H. A. Gasteiger and T. F. Fässler, Chem. Mater., 2020, 32, 6925–6934.
12. H. Eickhoff, L. Toffoletti, W. Klein, G. Raudaschl-Sieber and T. F. Fässler, Inorg. Chem., 2017, 56, 6688–6694.
13. H. Eickhoff, C. Sedlmeier, W. Klein, G. Raudaschl-Sieber, H. A. Gasteiger and T. F. Fässler, Z. Anorg. Allg. Chem., 2020, 646, 95–102.
14. A. Haffner, T. Bräuniger and D. Johrendt, Angew. Chem., 2016, 128, 13783–13786.
15. T. M. F. Restle, C. Sedlmeier, H. Kirchhain, W. Klein, G. Raudaschl-Sieber, V. L. Deringer, L. v. Wüllen, H. A. Gasteiger and T. F. Fässler, Angew. Chem., Int. Ed., 2020, 59, 5665–5674.
16. T. M. F. Restle, J. V. Dums, G. Raudaschl-Sieber and T. F. Fässler, Chem.–Eur. J., 2020, 26, 6812–6819.
17. W. Blase, G. Cordier and M. Somer, Z. Kristallogr., 1991, 195, 119–120.
18. V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576–3586.
19. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
20. A. Addamiano, J. Am. Chem. Soc., 1960, 82, 1537–1540.
21. H. Li, A. Laine, M. O'Keeffe and O. M. Yaghi, Science, 1999, 283, 1145–1147.
22. N. Zheng, X. Bu, B. Wang and P. Feng, Science, 2002, 298, 2366–2369.
23. A. Haffner, A.-K. Hatz, I. Moudrakovski, B. V. Lotsch and D. Johrendt, Angew. Chem., Int. Ed., 2018, 57, 6155–6160.
24. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
25. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. Cryst. Mater., 2005, 220, 567–570.
26. J. George, D. Waroquiers, D. Di Stefano, G. Petretto, G.-M. Rignanese and G. Hautier, Angew. Chem., Int. Ed., 2020, 59, 7569.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, details of the crystal structure determination, experimental powder X-ray diffraction pattern, coordination polyhedra, differential scanning calorimetry thermogram, Nyquist plot. CSD 2026514. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc05851c

---