Open Access Article
Open Access ArticleWhen are two hydrogen bonds better than one? Accurate first-principles models explain the balance of hydrogen bond donors and acceptors found in proteins†
Vyshnavi
Vennelakanti
 ab,
Helena W.
Qi
ab,
Rimsha
Mehmood
ab and
Heather J.
Kulik
ab,
Helena W.
Qi
ab,
Rimsha
Mehmood
ab and
Heather J.
Kulik
 *a
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: hjkulik@mit.edu; Tel: +1-617-253-4584
bDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 19th November 2020
Abstract
Hydrogen bonds (HBs) play an essential role in the structure and catalytic action of enzymes, but a complete understanding of HBs in proteins challenges the resolution of modern structural (i.e., X-ray diffraction) techniques and mandates computationally demanding electronic structure methods from correlated wavefunction theory for predictive accuracy. Numerous amino acid sidechains contain functional groups (e.g., hydroxyls in Ser/Thr or Tyr and amides in Asn/Gln) that can act as either HB acceptors or donors (HBA/HBD) and even form simultaneous, ambifunctional HB interactions. To understand the relative energetic benefit of each interaction, we characterize the potential energy surfaces of representative model systems with accurate coupled cluster theory calculations. To reveal the relationship of these energetics to the balance of these interactions in proteins, we curate a set of 4000 HBs, of which >500 are ambifunctional HBs, in high-resolution protein structures. We show that our model systems accurately predict the favored HB structural properties. Differences are apparent in HBA/HBD preference for aromatic Tyr versus aliphatic Ser/Thr hydroxyls because Tyr forms significantly stronger O–H⋯O HBs than N–H⋯O HBs in contrast to comparable strengths of the two for Ser/Thr. Despite this residue-specific distinction, all models of residue pairs indicate an energetic benefit for simultaneous HBA and HBD interactions in an ambifunctional HB. Although the stabilization is less than the additive maximum due both to geometric constraints and many-body electronic effects, a wide range of ambifunctional HB geometries are more favorable than any single HB interaction.
1. Introduction
Noncovalent interactions are ubiquitous in biological systems, playing essential roles in both enzyme catalysis1 and the structural properties of both DNA2 and proteins.3–6 Over the years, an increasing array of interactions including noncovalent carbon bonds,7,8 n to π* interactions,9–11 protein–ligand cation–π, aromatic, salt bridges,12 and other interactions13–19 have been studied to understand their potential roles in biomolecular structure and function. Among these, hydrogen bonds (HBs) are a particularly critical class of noncovalent interactions for biological function. The definition of the HB has become more encompassing over the years,20 expanding to include a range of interactions such as N–H⋯N,21–24 sulfur-containing,25–27 X–H π,28,29 and C–H⋯O,30–34 among others. Nevertheless, the HB is generally distinguished from other noncovalent interactions by its fairly strong electrostatic component35 with evidence of some covalent36–38 bond formation,20,39 as supported by the interaction being directional in nature.40Given the inherently quantum mechanical (QM) nature of the HB, care must be taken in defining and observing it in structural or computational studies. Use of geometric considerations (i.e., van der Waals radii) alone to determine the presence or absence of HBs can lead to erroneous conclusions.39,41,42 Some classical electrostatic models or empirical correlations43–45 have been developed along with first-principles investigations46–50 to understand the strength and nature of hydrogen bonding. Nevertheless, HBs can challenge conventional modeling methods, including approximate density functional theory (DFT) treatments51–53 that fail to accurately model long-range electron correlation. Although protein structures can be used to validate DFT and more accurate correlated wavefunction theory (WFT) methods,15,54–57 challenges remain. For example, short hydrogen bonds are ubiquitous in proteins, but they are often penalized during structural refinement.58 Many noncovalent distances in a range of 2.6–2.8 Å that would be deemed to be unfavorable in crystal structures are instead observed to be favorable and weakly stabilizing when evaluated with correlated wavefunction theory.59 These interactions cannot be captured with the classical force fields predominantly used to simulate proteins.59 Similar observations have recently been made in noncovalent interactions in DNA.60 Although force fields have been noted in recent years to be broadly improving in agreement with experiment,61 they can fail to describe noncovalent interactions essential for modeling protein structure in globular55,62 or intrinsically disordered proteins63 due to inherent limitations in the physics that can be captured by their functional forms.64,65
Cooperative, strong hydrogen bonds are an exemplary subset of HBs where modeling beyond the force field level is essential. In low-barrier hydrogen bonds (LBHBs),1,66 the barrier to hydrogen transfer is similar to the zero-point vibrational energy.67,68 These HBs are typically69 characterized by O⋯O separations around 2.6 Å or lower, and similarly short interactions are observed in charge-assisted hydrogen bonds and salt bridges.67,70–73 These functionally important interactions1,66,68,74 would be missed by standard force fields that do not treat charge transfer or polarization and disfavor short non-covalent distances.
The same assumptions that limit the modeling of LBHBs give rise to uncertainty about the interplay and balance of sidechain–sidechain,5,6 sidechain–backbone23 and intraresidue HBs75 in protein structure and function. For instance, it is poorly understood, given the number of potential hydrogen-bonding partners that a sidechain can form, the extent to which single or multiple hydrogen bonds are observed for a particular sidechain.76 Part of this challenge arises from the fact that the structure of most amino acids will require some compromise of the preferred linear and directional nature of the HB to form multiple interactions. This is in contrast to the lack of compromise required for base pairing interactions comprising simultaneous short, linear N–H⋯O and N–H⋯N HBs in RNA77,78 and DNA.79,80 As an example of the potential functionality offered by multiple, compromised interactions, we recently observed that simultaneous donor and acceptor HB interactions between the aliphatic hydroxyl of a Thr sidechain and a neighboring Asn played an essential role in native substrate recognition of a non-heme iron halogenase.81 This interaction, validated by experimental mutagenesis,82 was revealed with QM modeling but was challenging to replicate with force fields. Similarly, a large-scale screen of protein interactions suggests that many simultaneous donor/acceptor interactions can form between the aromatic Tyr and Asn or Gln residues.59
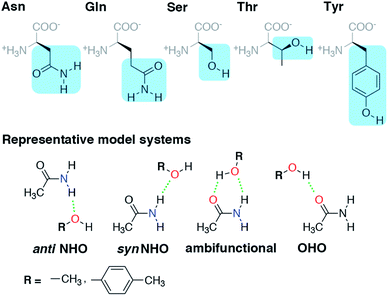
In this work, we thus investigate the balance of hydrogen bond acceptor (HBA) and donor (HBD) interactions in representative models of amino acid sidechains (i.e., Tyr/Ser/Thr with Asn/Gln) that can act simultaneously as HBAs and HBDs. Because the ability of charged residues (e.g., Arg, Lys, His, or Glu/Asp) to form multiple HBDs/HBAs depends upon their protonation state, we focus on a subset of neutral residues capable of forming multiple interactions. Given the challenges with ensuring the accuracy of computational models of HBs, we first carry out careful coupled cluster theory modeling of individual HBA or HBD interactions. The WFT-level analysis carried out here is critical, as force-field modeling fails to reproduce essential differences between aromatic and aliphatic amino acids. We confirm the suitability of our models and level of theory for capturing the structures favored in a curated set of 4000 HBs obtained from high-resolution (<1.5 Å) X-ray crystal structures of proteins. Using this analysis, we quantify the degree and nature of the benefit observed in the formation of ambifunctional (i.e., simultaneous HBA/HBD) HB interactions.
2. Curation approach
We curated a data set of candidate hydrogen-bonding residues from the protein data bank (PDB)83 following a refinement of the procedure introduced in prior work.59 Candidate HBs between Tyr, Ser, or Thr and Asn or Gln were extracted from X-ray crystal structures with resolution < 1.5 Å, which was selected to ensure low positional uncertainty (ca. 0.03 Å) of heavy atoms.84,85 In accordance with prior work, all residues were both required to not be within close (i.e., hydrogen-bonding) distance of nonstandard residues or ligands and were taken from a subset of unique structures that had less than 90% sequence identity deposited in the PDB as of October 29, 2017. Residues were selected for the data set if the heavy-atom distances between O and N HB donors or acceptors from the relevant residue sidechains were within 120% of the sum of van der Waals (vdW) radii, which was longer by design than the cutoff for close contacts targeted in ref. 59. To confirm that HB interactions were not an artifact of poorly solved structures, we retained residues following our prior approach59 using constraints on the difference of calculated and experimental structure factor amplitudes (i.e., R factor ≤ 20%), good agreement on the held out set (i.e., Rfree – R ≤ 0.07), and a good Z-score of the real-space R-value (i.e., RSRZ ≤ 20%), which is evaluated against proteins of similar resolution. In addition to prior constraints, we confirmed density support86 (i.e., electron density support for individual atoms, EDIA, scores > 0.8) for the atoms of both residues in curated HB pairs. We subsequently refined the set based on quantum mechanical criteria (ESI Table S1†).From the resulting set of 6114 residue pairs, we carried out further refinements to identify a subset for which HBs were most likely to be present. A wide range of HB distance (2.2–4.0 Å) and angle criteria (90–180°) have been proposed87–89 in the literature. Because consensus about HB distances and angles is not established, and the optimal HB distance or angle is strongly species dependent, we developed a quantum-mechanically derived approach to selecting distance and angle cutoffs. The presence of bond critical points (BCPs90) from the quantum theory of atoms in molecules (QTAIM)91 and the potential energy density evaluated at that point provides a heuristic estimate of HB strength.92 After adding and optimizing hydrogen atoms on representative (ca. 10%) residue pairs from PDB structures, we quantified the presence of BCPs and the potential energy density at the BCP using Multiwfn93 (ESI Text S1 and Table S2†). Our final range of HBA/HBD distances (N⋯O: 2.5–3.2 Å, O⋯O Ser/Thr: 2.4–3.1 Å, and O⋯O Tyr: 2.4–3.2 Å) and angles (N–H⋯O: 105–180° and O–H⋯O: 110–180°) was selected based on structures where BCPs were detected for N–H⋯O and O–H⋯O HBs. Our definition of an ambifunctional HB requires at least one of the O⋯O and N⋯O HB distances to fall within their specified HB distance criteria, whereas the second must only be within the 120% vdW radii sum criteria. Using these distance criteria, the refined protein data set consists of 3908 residue pairs. HB angle distributions were evaluated over all of these residues by an automated procedure that added hydrogen atoms, evaluated HB angles, and also classified N–H⋯O HBs as syn or anti (ESI Text S2†).
3. Results and discussion
3.1. N–H⋯O hydrogen bonds
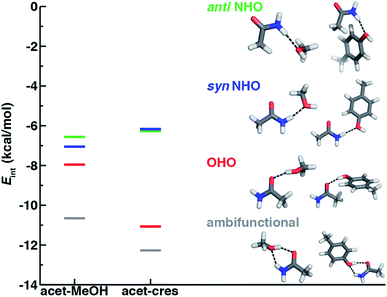
Before we can evaluate the relative stabilization of the ambifunctional HB configuration, we first determine the strength of single HB (i.e., N–H⋯O or O–H⋯O) interactions with model system potential energy curves and compare these observations to geometries observed in X-ray crystal structures of analogous protein residues. Sidechain-based N–H⋯O HBs are formed when the sidechain amide hydrogen atoms of Asn/Gln act as HB donors to the HB acceptor sidechain hydroxyl oxygen of Ser, Thr, or Tyr (Fig. 1). The aliphatic hydroxyl in Ser/Thr is expected94 to form stronger N–H⋯O HBs than the aromatic hydroxyl in Tyr because in the latter the resonance with the tolyl group induces less negative partial charge on the oxygen (Fig. 1). We employ truncated models for these residues, i.e., acetamide for Asn/Gln and methanol for Ser/Thr or p-cresol for Tyr, which facilitates the use of high-accuracy methods95,96 with larger basis sets (i.e., DLPNO-CCSD(T)/CBS, see Section 5) and simplifies the study of the HB interaction.In both the protein residues and their truncated models, the planar amide hydrogen atoms can be either syn or anti with respect to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond (Fig. 1 and ESI Fig. S1†). The WFT N–H⋯O HB interaction energies of syn and anti N–H⋯O HBs agree within 1 kcal mol−1 for both models, so we select syn as the representative case for further comparison (Fig. 2 and ESI Table S3†). Between models, the interaction energies of N–H⋯O HBs in acetamide–p-cresol are smaller for both conformations (−6.1 kcal mol−1) than in the acetamide–methanol model (syn: −7.0 kcal mol−1), consistent with our expectations (Fig. 2 and ESI Table S3†). Although the aromatic p-cresol hydroxyl exhibits weaker interaction energies than the aliphatic hydroxyl in methanol, the difference remains modest (<1 kcal mol−1, Fig. 2 and ESI Table S3†). The optimized geometries support energetic observations; longer N⋯O HB distances (∼0.1 Å) and larger HB angles (∼6.3°) are observed for p-cresol than methanol N–H⋯O HBs (ESI Tables S4 and S5†).
O bond (Fig. 1 and ESI Fig. S1†). The WFT N–H⋯O HB interaction energies of syn and anti N–H⋯O HBs agree within 1 kcal mol−1 for both models, so we select syn as the representative case for further comparison (Fig. 2 and ESI Table S3†). Between models, the interaction energies of N–H⋯O HBs in acetamide–p-cresol are smaller for both conformations (−6.1 kcal mol−1) than in the acetamide–methanol model (syn: −7.0 kcal mol−1), consistent with our expectations (Fig. 2 and ESI Table S3†). Although the aromatic p-cresol hydroxyl exhibits weaker interaction energies than the aliphatic hydroxyl in methanol, the difference remains modest (<1 kcal mol−1, Fig. 2 and ESI Table S3†). The optimized geometries support energetic observations; longer N⋯O HB distances (∼0.1 Å) and larger HB angles (∼6.3°) are observed for p-cresol than methanol N–H⋯O HBs (ESI Tables S4 and S5†).
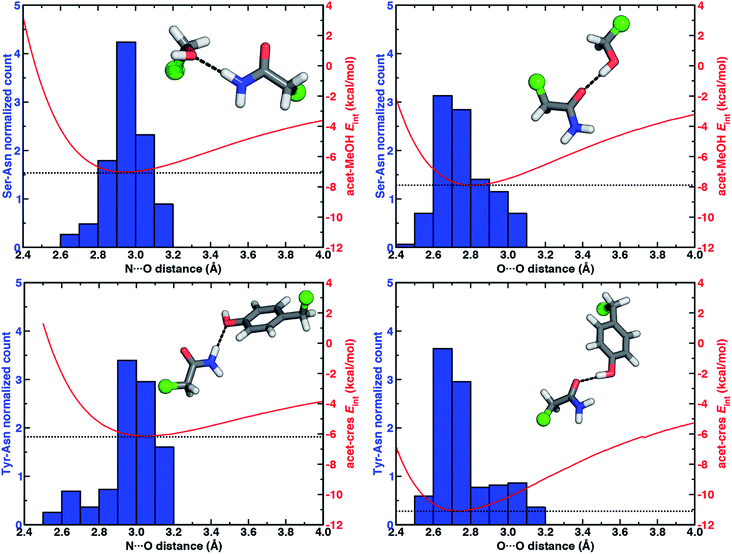
To quantify how well our energetic models reproduce the N⋯O HB distances in high-resolution crystal structures, we calculated one-dimensional (1D) potential energy curves (PECs) (see Section 5) as a function of the N⋯O HB distance and compared distances in the protein data set to the representative model systems (Fig. 1 and see Section 2). Features of the 1D PECs for the representative syn N–H⋯O HB conformation in both models are broadly consistent with the freely optimized model structures, both in terms of a deeper energy minimum for the methanol model (by ca. 0.9 kcal mol−1) and a shorter (methanol: 2.94 Å vs. p-cresol: 3.06 Å) N⋯O HB distance (Fig. 3, ESI Fig. S2 and S3†).
Despite differences in the hydroxyl placement on Ser or Thr, the most frequently observed N⋯O HB distances in Ser/Thr–Asn/Gln pairs agree well with the 1D PEC minimum for the acetamide–methanol model (Fig. 3, ESI Fig. S2 and S3†). This good agreement further supports the choice of truncated models (i.e., methanol for both Ser and Thr) to represent the protein residues. Although a range of distances are observed over the full protein set, only a small fraction of structures have distances different from the value at the minimum of the acetamide–methanol N⋯O HB 1D PEC (Fig. 3). Consistent trends hold for HBs with Tyr, where the shallower 1D PEC model coincides with both the slightly wider range and longer distances of X-ray crystal structures (Fig. 3). Overall, our truncated models capture key interactions from protein crystal structures whether in syn or anti N–H⋯O HB conformations, but sub-kcal mol−1 energetic differences (e.g., relative preference for syn or anti) in the models can be expected to be affected by competing backbone and environmental stabilization in the crystal structures (Fig. 1, 2, and ESI Text S3, Tables S3, S6 and S7, Fig. S4 and S5†).
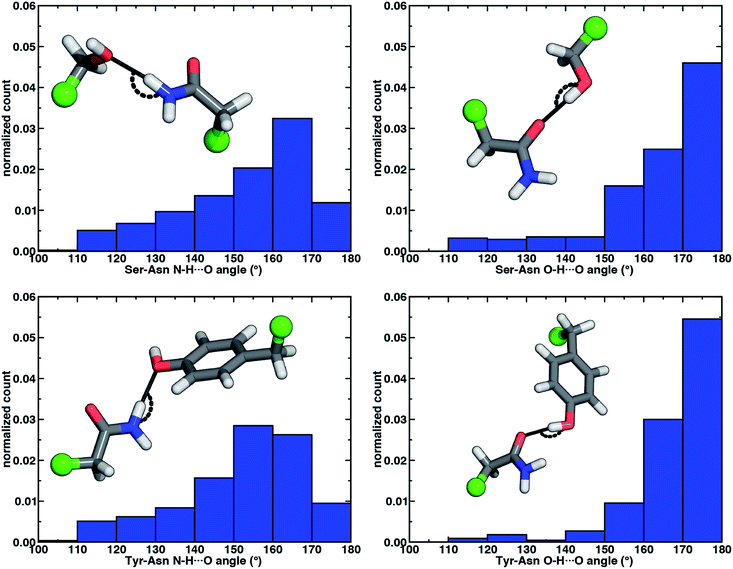
The directionality of HBs provides a key indicator of their strength and character. We thus evaluated N–H⋯O HB angle distributions over the X-ray crystal structures (see Section 2). Ser/Thr and Tyr N–H⋯O angle distributions exhibit similar trends, with the highest angle probability between 150 and 170° and a rapid decay outside of that range (Fig. 4, ESI Fig. S6 and S7†). In our model systems, we had observed more obtuse N–H⋯O angles, with the acetamide–p-cresol angle (178°) larger than acetamide–methanol (171°), both of which exceed many of the angles observed in our X-ray structure data set (Fig. 4). Because we approximate the placement of hydrogen atoms to compute angles in the X-ray structures (see Section 2), this additional uncertainty limits determination of the relative directionality of Tyr versus Ser/Thr N–H⋯O HBs with Asn/Gln amino acid pairs (Fig. 4). For the N–H⋯O HB angles for X-ray structures of all amino acid pairs, average values (154°) are reduced by ca. 20° with respect to the model systems, suggesting a possible effect of the protein environment on favored HB angles (see Section 2 and ESI Table S6†). In the extended X-ray crystal structures of amino acid pairs with reduced HB angles, interactions with solvent molecules, backbone (i.e., N–H hydrogen or carbonyl oxygen) atoms of nearby residues or other interactions in the greater environment absent from the models are present to varying degrees (ESI Fig. S8†). We also optimized our small models in a dielectric medium (ε = 10) to capture the screening effect of the protein environment (ESI Table S8†). This approximate incorporation of environment effects leads to only small changes in HB distances (ca. 0.02 Å in both directions) and angles (ca. 2–5° increase) for either model (ESI Table S8†).
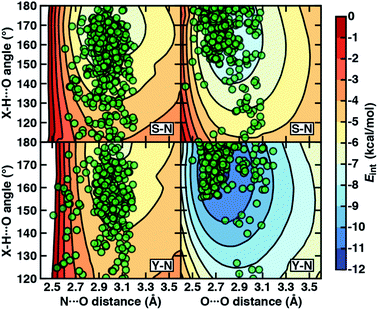
To examine the interplay of optimal HB distances and angles, we computed two-dimensional potential energy surfaces (PESs) of the N–H⋯O HB interaction. Qualitatively similar PES shapes are obtained for the acetamide–methanol and acetamide–p-cresol model systems (Fig. 5). The main difference between the two arises from the less favorable minimum in p-cresol that corresponds to a shallower overall PES, leading to more comparable interaction energies for the two models when the angles or distances are displaced from the minimum (Fig. 5, ESI Fig. S9 and S10†). Although in both cases, the strongest interaction energies are at the expected HB distances (i.e., between 2.8 and 3.2 Å) and HB angles (i.e., between 160° and 180°), structures over a wide 140–180° angle range are within 1–2 kcal mol−1 of the minimum (Fig. 5). In both cases, structures at a fixed distance always favor larger HB angles, but displacement from the equilibrium angle incurs considerably less penalty than distance displacement (Fig. 5).
Comparing protein structures to our model systems, the majority (i.e., over 85%) of Ser/Thr–Asn/Gln structures reside within 2 kcal mol−1 of the minimum on the computed model 2D PES (Fig. 5 and ESI Table S9†). Results for Tyr–Asn/Gln are consistent, but the shallower nature of the 2D PES for p-cresol leads to a smaller fraction (70%) residing within 2 kcal mol−1 of the model global minimum (Fig. 5 and ESI Table S9†). Over all amino acid pairs, a minority (10%) of X-ray structures sample smaller than expected HB angles (i.e., between 110° and 130°) that correspond to less favorable model interaction energies due to a short N⋯O distance but relatively long HBD to HBA (i.e., H⋯O) distance (ESI Table S9†). Examining the full protein in representative cases reveals competing HB interactions in the surrounding protein environment with alternative HB partners (e.g., solvent or other amino acids) that likely compensate for the formation of these weaker N–H⋯O HBs (ESI Fig. S11†).
3.2. O–H⋯O hydrogen bonds
When the sidechain hydroxyls of Ser, Thr, or Tyr act as HBDs to the sidechain amide oxygen HBA of Asn or Gln, O–H⋯O HBs are formed instead of N–H⋯O HBs (Fig. 1). In this case, an aromatic hydroxyl (e.g., Tyr or p-cresol) is expected97 to form stronger O–H⋯O HBs than the aliphatic hydroxyl (e.g., Ser/Thr or methanol) due to the resonance delocalization of the nonbonded electron pair of the hydroxyl oxygen into the aromatic ring that enhances O–H bond polarity. As expected, the interaction energy of the O–H⋯O HB in acetamide–p-cresol is stronger (ca. 3 kcal mol−1) than in acetamide–methanol (−11.0 kcal mol−1vs. −7.9 kcal mol−1, Fig. 2). Consistent with energetic trends, modest geometric differences (i.e., 0.05 Å shorter O⋯O HB distances for p-cresol than for methanol) are observed between the two models of O–H⋯O HBs (ESI Tables S4 and S5†). These geometric differences are similar to those we observed for N–H⋯O HBs despite the higher energetic differences for the two model systems' O–H⋯O HBs (ESI Tables S4 and S5†).While the 1D PEC O⋯O HB energetics are largely consistent with those of the freely optimized structures, some minor differences are apparent due to differences in the level of theory used (see Section 5, Fig. 3, ESI Fig. S2 and S3†). The 1D PEC acetamide–p-cresol O⋯O heavy-atom HB distance is further reduced (2.73 Å vs. 2.81 Å) with respect to methanol (Fig. 3, ESI Tables S4 and S5†). Overlaying X-ray crystal structure O⋯O distances on these 1D PECs confirms the suitability of the model systems for O–H⋯O HBs, with a significant fraction of Tyr–Asn/Gln O⋯O distances that are shorter than those for Ser/Thr–Asn/Gln (Fig. 3, ESI Fig. S2 and S3†). The distribution of X-ray crystal structure O⋯O HB distances is especially narrow for Tyr HBs, consistent with the steeper 1D PEC for Tyr in comparison to Ser/Thr (Fig. 3, ESI Fig. S2 and S3†). The most frequently observed O⋯O distances in X-ray crystal structures are slightly shorter (by ca. 0.1 Å) than the 1D PEC minima for both methanol and p-cresol (Fig. 3, ESI Fig. S2 and S3†). This effect is relatively modest, as it corresponds to interaction energies approximately 0.3 kcal mol−1 above the model 1D PEC minimum. Both the omission of the protein environment and our neglect of quantum nuclear effects58,68 particularly relevant at short HB distances could explain this discrepancy. Indeed, incorporation of a dielectric during optimization of our model systems leads to shorter (0.06–0.07 Å) HB distances (ESI Table S8†).
Analyzing the O–H⋯O HB angle distribution over the X-ray crystal structure data set highlights a greater preference for near-linear (i.e., 170–180°) angles in comparison to N–H⋯O HB angles, especially for the Tyr residue pairs (Fig. 4, ESI Fig. S6 and S7†). The greater strength of Tyr O–H⋯O HBs is consistent with a slightly higher fraction of the most linear angles in comparison to Ser or Thr (Fig. 4, ESI Fig. S6 and S7†). Average O–H⋯O HB angles (ca. 165°) are comparable for all residue pairs and higher than those for N–H⋯O HB angles by around 11° (ESI Table S10†). This increase in favored angles in the X-ray crystal structures suggests greater consistency with the O–H⋯O HB angles of fully optimized models in comparison to the N–H⋯O HB case (ESI Tables S4 and S5†).
Evaluation of the O–H⋯O HB 2D PESs highlights good agreement between the optimal model structures and observed X-ray crystal structures for all amino acid pairs (Fig. 5, ESI Fig. S9 and S10†). In comparison to N–H⋯O HBs, the joint distribution of X-ray crystal structure distances and angles is both more compact and more aligned with the lowest-energy regions of the model systems for both aromatic (i.e., Tyr or p-cresol) and aliphatic (i.e., Ser/Thr or methanol) hydroxyl HBDs (Fig. 5, ESI Fig. S9 and S10†). Almost all (ca. 95%) of the Ser/Thr X-ray crystal structures sample distances and angles within 2 kcal mol−1 of the O–H⋯O model minimum (Fig. 5 and ESI Table S9†). The percentage of Tyr–Asn/Gln O–H⋯O HB X-ray structures (ca. 85%) within 2 kcal mol−1 of the model 2D PES minimum is also increased (Fig. 5 and ESI Table S9†). Thus, the steeper PES and greater directionality of O–H⋯O HBs is likely due to local interactions that are well described in gas-phase models.
Of the four HBs considered thus far, the acetamide–p-cresol O–H⋯O HB is significantly (∼4.9 kcal mol−1) stronger than the acetamide–p-cresol N–H⋯O HB as well as the HBs in the acetamide–methanol model (Fig. 5 and ESI Table S3†). Displacements of the acetamide–p-cresol O–H⋯O HB distance by ca. 0.7 Å or angle by ca. 60° lead to interaction energies still as strong as the alternative N–H⋯O HB (Fig. 5, ESI Fig. S9 and S10†). The differentiation of HB strength for aromatic hydroxyls diverges from the aliphatic hydroxyl (i.e., the methanol model) where the O–H⋯O HB is only slightly stronger (0.9–1.4 kcal mol−1) than the N–H⋯O HB (ESI Table S3†).
We used energy decomposition analysis (i.e., at the SAPT2+3 level of theory98) to understand the origins of the O–H⋯O HB interaction being more favorable than the N–H⋯O HB (see Fig. 2 and ESI Table S11†). In the acetamide–p-cresol model, stronger electrostatic attraction (by 8 kcal mol−1) and induction (by 3 kcal mol−1) terms both contribute to the stronger O–H⋯O HB, and similar but smaller effects are observed for acetamide–methanol (ESI Table S11†). Although the shorter O–H⋯O HB distances expectedly give rise to more destabilizing exchange repulsion, this effect is outweighed by the other factors, including greater dispersion stabilization for the O–H⋯O HB especially for acetamide–p-cresol (by ca. 3 kcal mol−1) that contributes to the overall more favorable O–H⋯O HB (ESI Table S11†).
Given the greater favorability of O–H⋯O over N–H⋯O HBs, we expected to observe a significantly larger number of O–H⋯O HBs especially for interactions with Tyr. Contrary to both our expectations and prior observations over a larger data set,59 a greater number of N–H⋯O HBs is observed in our data set than O–H⋯O HBs for either Ser/Thr or Tyr with Asn/Gln (ESI Table S12†). Supporting our choice of the methanol model to represent either Ser or Thr, we also observe that these trends are consistent when comparing the relative number of O–H⋯O and N–H⋯O HBs for Ser or Thr with Asn or Gln individually (ESI Table S12†). Of all 3908 HBs in the curated set, slightly more are observed for Thr than Ser (1332 vs. 1174), but both residues have a similar relative percentage of N–H⋯O HBs with Gln (63%) that exceeds those with Asn (54–57%, ESI Table S12†). One potential source of this counterintuitive difference in HB abundance is the compensation of weaker N–H⋯O sidechain–sidechain HBs by additional sidechain–backbone or sidechain–solvent interactions. Indeed, inspection of the protein around representative N–H⋯O HBs reveals simultaneous formation of sidechain–backbone HBs and additional sidechain (i.e., Ser/Thr/Tyr hydroxyl or Asn/Gln carbonyl) to solvent HB interactions that could not form in O–H⋯O HB conformations (ESI Fig. S8 and S12†). Additionally, Asn/Gln can form two N–H⋯O HBs per sidechain, which we also observe in our data set (ESI Fig. S13†). Thus, raw counts in a limited data set likely capture the relative favorability of globally compensated HB interactions, whereas the relative strengths of the individual HBs appear better captured by comparison of the distributions of X-ray structures and model systems.
3.3. Energetic stabilization from ambifunctional hydrogen bonds
If oriented appropriately, the sidechain hydroxyl (i.e., of Ser, Thr, or Tyr) can simultaneously act as an HBD to the amide oxygen and an HBA to the amide nitrogen of Asn or Gln, forming a conformation we refer to as an ambifunctional59 HB. Because this arrangement involves the combined formation of an O–H⋯O and syn N–H⋯O HB, its interaction strength could be as large as the sum of the two individual HBs (see Section 3.1 and 3.2). Unlike other noncovalent interactions in biological systems (e.g., RNA/DNA) where multiple HBA/HBDs can form in near-linear configurations,79 we can expect this sidechain–sidechain interaction to involve some compromise. Such a compromise in the ambifunctional HB can arise from differences of the distances/angles of the two HBs with respect to optimal values for individual HBs as well as from the electronic properties that dictate the participating atoms' abilities to act as HBAs/HBDs (Fig. 1). If these effects are modest, the ambifunctional HB interaction energy should by higher than either individual HB, and this conformation should be observed in protein structures.At its upper limit, the ambifunctional HB would correspond to the sum of the two single HBs (methanol: −14.9 kcal mol−1 and p-cresol: −17.1 kcal mol−1), with a more favorable acetamide–p-cresol ambifunctional HB expected due to its strong constituent O–H⋯O HB (ESI Table S13†). The acetamide–p-cresol ambifunctional HB (−12.2 kcal mol−1) is indeed stronger by ca. 2 kcal mol−1 than that in acetamide–methanol (−10.6 kcal mol−1), but both are weaker than their theoretical limit by a comparable 4–5 kcal mol−1 (Fig. 2 and ESI Table S13†). Despite the overall weaker interaction energy for methanol, its ambifunctional HB is significantly (ca. 3–4 kcal mol−1) more favorable than its individual O–H⋯O or N–H⋯O HBs (Fig. 2 and ESI Table S3†). Conversely, the acetamide–p-cresol ambifunctional HB provides a limited (ca. 1 kcal mol−1) benefit over the O–H⋯O HB conformation, suggesting the dominant role of the O–H⋯O HB even in the ambifunctional conformation (Fig. 2 and ESI Table S3†). Beyond this purely electronic interaction energy picture, the ambifunctional HB could be expected to incur a relative entropic penalty in comparison to the individual HBs. While relative free energies do disfavor the ambifunctional HB very slightly (ca. 0.2–0.5 kcal mol−1) with respect to the single O–H⋯O HB, this difference is significantly smaller than the free energy penalty increase from the single N–H⋯O to O–H⋯O HB (ESI Table S14†).
To understand if the reduced interaction energies in the ambifunctional HB arise due to a geometric compromise, we compared the geometry of the constituent HBs with the corresponding single O–H⋯O and syn N–H⋯O HBs. In both model system ambifunctional conformations, the N⋯O and O⋯O HB distances are mostly unchanged (shortened by ca. 0.05 Å and 0.1 Å, ESI Tables S4, S5 and S13†). Comparing interaction energies at these shortened HB distances from the individual 1D PECs, we determine that no significant energy penalty is incurred (ESI Table S15†). The ambifunctional HB angles are more distinct, being significantly reduced (O–H⋯O: ca. 10° and N–H⋯O: ca. 30–40°) with respect to their near-linear values in single HBs (ESI Tables S4, S5 and S13†). In contrast to the negligible distance penalties, the penalty for displacing both HB angles from their optimal values comes at an energetic cost of 1.5 kcal mol−1 in both model systems (ESI Tables S13 and S15†). The remaining difference between the ambifunctional HB interaction energy and the additive sum of the single HBs (ca. 3 kcal mol−1) is thus likely due to many-body, electronic effects such as those that limit the simultaneous HBA/HBD strength of the hydroxyl oxygen. Indeed, if we had used a typical force field for biomolecular simulations (i.e., the generalized amber force field, or GAFF99) we would have failed to distinguish differences between the aromatic and aliphatic hydroxyls, resulting in underestimation of the higher O–H⋯O HB strength in p-cresol and failure to predict the relatively high benefit of the ambifunctional HB in the methanol model (ESI Table S16†).
To quantify energetic relationships among the syn N–H⋯O HB, O–H⋯O HB, and ambifunctional HB conformations, we identified an approximate reaction coordinate for the minimal structural rearrangement that describes the transition between these conformations (see Section 5 and ESI Text S4†). A suitable approximate reaction coordinate to capture this transition is the rotation of the alcohol (i.e., methanol or p-cresol) with respect to the amide, a quantity well described by the (H)O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N intermolecular angle (ESI Fig. S14†). Although the intermolecular angle was constrained during optimization, the remaining degrees of freedom (e.g., HB distance and angle) were fully relaxed. We made this choice rather than obtaining explicit free energies and minimum energy pathways because the reaction coordinate energetics are evaluated at a higher level of theory (i.e., local coupled cluster at the complete basis set limit) than is feasible for geometry optimization and vibrational characterization (see Section 5). This approximation introduces at most one small rotational imaginary mode, typically corresponding to rotation about the O–H⋯O HB axis (ESI Tables S17 and S18†). This approximate reaction coordinate can be transformed to the N–H⋯O angle between acetamide and the alcohol, a quantity more intuitively linked to the hydrogen bond (ESI Text S4 and Fig. S15†).
N intermolecular angle (ESI Fig. S14†). Although the intermolecular angle was constrained during optimization, the remaining degrees of freedom (e.g., HB distance and angle) were fully relaxed. We made this choice rather than obtaining explicit free energies and minimum energy pathways because the reaction coordinate energetics are evaluated at a higher level of theory (i.e., local coupled cluster at the complete basis set limit) than is feasible for geometry optimization and vibrational characterization (see Section 5). This approximation introduces at most one small rotational imaginary mode, typically corresponding to rotation about the O–H⋯O HB axis (ESI Tables S17 and S18†). This approximate reaction coordinate can be transformed to the N–H⋯O angle between acetamide and the alcohol, a quantity more intuitively linked to the hydrogen bond (ESI Text S4 and Fig. S15†).
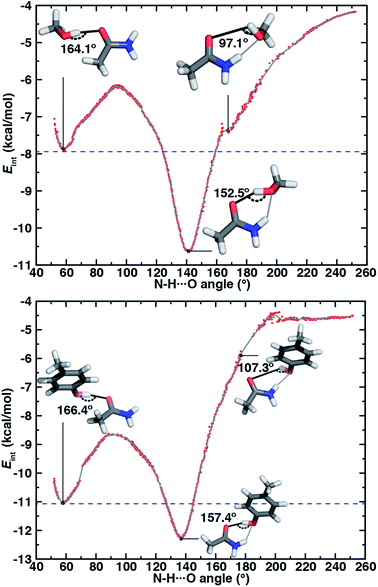
Along the approximate reaction coordinate, increasing N–H⋯O angles correspond to the transformation from a single O–H⋯O HB to the formation of an additional N–H⋯O interaction in the ambifunctional HB until the O–H⋯O HB interaction is lost and only the N–H⋯O HB remains (Fig. 6). The hydroxyl group of the alcohol in either model rotates freely along the chosen reaction coordinate, making it difficult to map the approximate reaction coordinate to the O–H⋯O angle. Still, the O–H⋯O angle generally behaves as expected with changing N–H⋯O angle: a near-linear O–H⋯O angle must coincide with an acute N–H⋯O angle or vice versa (ESI Fig. S16†).
For both model systems, the N–H⋯O HB conformation appears only as a shoulder along the approximate reaction coordinate and thus the transition to the lowest-energy ambifunctional HB conformation is barrierless (Fig. 6). This is consistent with vibrational analysis along the reaction coordinate, which shows an imaginary mode toward the ambifunctional basin (ESI Tables S17 and S18†). Conversely, while the O–H⋯O HB is a local minimum along the approximate reaction coordinate, the transition from the O–H⋯O HB conformation to the ambifunctional HB conformation has a small (methanol: 1.7 kcal mol−1, p-cresol: 2.3 kcal mol−1) approximate barrier in both model systems (Fig. 6 and ESI Table S19†). For the acetamide–methanol model, it is apparent that this approximate barrier can be partly attributed to the reduction of the O–H⋯O HB angle from its ideal value (180° to 160°) before the N–H⋯O angle approaches the larger values (ca. 120–140°) near the ambifunctional HB global minimum (Fig. 6 and ESI Fig. S16†). However, no such geometric distortion is observed for the acetamide–p-cresol case (ESI Fig. S16†). The thermodynamic driving force for forming the ambifunctional HB (e.g., with respect to a single O–H⋯O HB) on the approximate reaction coordinate is lower for p-cresol than methanol, despite both p-cresol conformations having stronger overall interaction energies (Fig. 6). Exiting the ambifunctional HB global minimum requires 4–5 kcal mol−1 for both model systems to break the ambifunctional N–H⋯O interaction and reform a single O–H⋯O HB, with the greater stability of the ambifunctional HB in acetamide–methanol leading to a slightly higher energetic cost than for acetamide–p-cresol (Fig. 6).
Although geometric arguments can partly explain the significant barrier on the acetamide–methanol approximate reaction coordinate for rearranging from the single O–H⋯O HB to the ambifunctional HB, it does not explain the equally large approximate barrier for the p-cresol model. To understand the electronic origins of the barrier for rearrangement, we used symmetry-adapted perturbation theory (i.e., at the SAPT2+3 level of theory98) to decompose relative electrostatic and dispersion contributions in both minima on the approximate reaction coordinate as well as at the peak of the DLPNO-CCSD(T) approximate barrier (ESI Table S11†). This energy decomposition reveals that a loss of dispersion and induction stabilization occurs equivalently (by ca. 2 kcal mol−1) for both model systems at the maximum energy point between the O–H⋯O and ambifunctional HB configurations (ESI Table S11†). At this energetic peak on both approximate reaction coordinates, dispersion stabilization is also weaker than at the N–H⋯O HB geometry (ESI Table S11†). Although favorable electrostatic interactions also weaken at the barrier maximum, this effect is counteracted by a reduction in the exchange repulsion (ESI Table S11†). Thus, a delicate interplay of electronic effects can be expected to govern rearrangement between single and ambifunctional HB configurations. It is therefore unsurprising that using a standard biomolecular force field (e.g., GAFF99) fails to capture this approximate barrier for rearrangement in addition to underestimating the stabilization of the ambifunctional HB (ESI Fig. S17 and Table S16†).
In both model systems, we identify an ambifunctional HB basin as the range of approximate reaction coordinate geometries around the global minimum that remain stabilized with respect to the most stable single HB (i.e., O–H⋯O) conformation (Fig. 6). Due to the greater relative stability of the methanol ambifunctional HB with respect to the constituent HBs, its basin corresponds to a larger, nearly 3 kcal mol−1 energy window instead of approximately 1.5 kcal mol−1 for p-cresol (Fig. 6). These differences are reflected in the geometric properties of structures within the basin: methanol N–H⋯O angles span a nearly 40° range (123 to 160°), whereas favorable p-cresol N–H⋯O angles span only 20° (126 to 146°, Fig. 6, ESI Fig. S18 and S19†). An even wider range of O–H⋯O angles is observed for methanol (135–167°), whereas the favored O–H⋯O angles for p-cresol (151–168°) are more restrictive (Fig. 6, ESI Fig. S18 and S19†). This observation confirms that for the aromatic hydroxyls in p-cresol or Tyr residues, the O–H⋯O interactions dominate and an ambifunctional HB provides limited additional stabilization.
Nevertheless, structural variations in the ambifunctional HB basin are comparable for both models, with the higher, productive O–H⋯O angles compensated by a monotonic linear reduction to less productive N–H⋯O angles or vice versa (ESI Fig. S18 and S19†). Approaching the ambifunctional HB global minimum from either side of the basin corresponds to a shortening of the heavy-atom distance for the forming HB (i.e., N⋯O or O⋯O) while the other HB distance changes minimally (ESI Fig. S18 and S19†). As a result, the sum of the two HB distances is lowest in the ambifunctional HB global minimum and rises in either direction (ESI Fig. S20†). The basin O⋯O distances span a significantly narrower 0.18 Å range for p-cresol (2.72–2.90 Å) than the 0.55 Å range for methanol (2.75–3.30 Å, ESI Fig. S18 and S19†).
Given the increased favorability of ambifunctional HBs over both O–H⋯O and N–H⋯O HBs for model systems, we expect to observe them in protein crystal structures. Indeed, we observe ambifunctional HBs between all pairs of amino acids, corresponding to around 15% (559 of 3908) of all HBs in our data set (ESI Table S12†). Although one may expect a more significant fraction of Ser/Thr HBs to be ambifunctional than Tyr HBs due to the enhanced relative benefit for the aliphatic hydroxyl, the difference in relative abundance is modest (ca. 15–18% vs. 11–12%, ESI Table S12†). This relative abundance in crystal structures is likely dictated by a combination of both geometric constraints for ambifunctional HB formation as well as competition with other interactions as previously observed for single HBs (see Section 3.2).
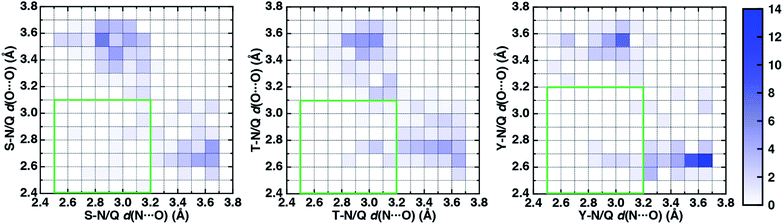
To characterize the geometries of X-ray crystal structure ambifunctional HBs, we computed their joint N⋯O and O⋯O HB distance distributions (Fig. 7 and ESI Fig. S21†). In this set, one of the HB distances is typically closer to its optimal value than the other, with a small (ca. 10%) fraction consisting of two HB distances close to their optimal values in single N–H⋯O or O–H⋯O HBs (Fig. 7, ESI Fig. S21 and S22 and Table S20†). While competing interactions with solvent molecules or other residues can partially rationalize why symmetric ambifunctional HB interactions are infrequently observed, such competing interactions are also observed simultaneously with highly symmetric ambifunctional HBs (Fig. 8). For the asymmetric Ser/Thr pairs with Asn or Gln, a slight majority (57%) has shorter N⋯O than O⋯O HB distances, whereas for Tyr this subset represents a minority (43%), consistent with differences in relative O–H⋯O HB strength (Fig. 7 and ESI Fig. S21†). We also observe lengthening of the N–H⋯O HB distance when the protein environment is incorporated as a dielectric during our optimizations, which could also support the reduced number of symmetric ambifunctional HBs in the X-ray crystal structure set (ESI Table S8†). Although the HB distances in many cases are asymmetric, the positioning of the residue pairs still orients both sets of HBAs and HBDs in sufficient proximity for two simultaneous interactions that are each characterized by the presence of a BCP (Fig. 8 and ESI Table S21†).
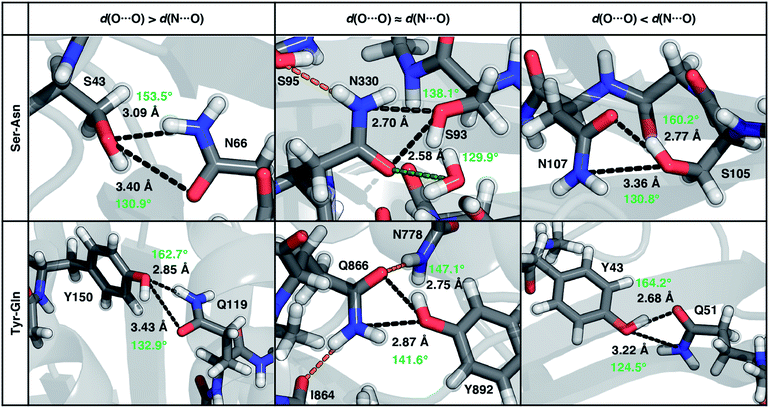 | ||
| Fig. 8 Representative proteins showing the three different types of ambifunctional HBs in Ser–Asn (top) and Tyr–Gln (bottom) residue pairs in our data set: shorter d(N⋯O) (left), equivalent length d(N⋯O) and d(O⋯O) (middle), and shorter d(O⋯O) (right). The Ser–Asn pairs correspond to PDB IDs (left to right): 1SFS, 2VOV, and 1O4Y, and the Tyr–Gln pairs to PDB IDs (left to right): 3EPW, 3BVU, and 4B9F. Specific HBs are indicated by black dashed lines between the heavy atoms in residue pairs with annotated distances (black, in Å) and N/O–H⋯O angles (light green, in °). Hydrogen atoms added for all proteins and relaxed with constrained heavy atoms are shown as translucent spheres. The orange and green dashed lines indicate additional stabilizing interactions observed with respect to the residue pair with nearby residues and solvent molecules, respectively. All residues are labeled by one-letter amino acid codes and residue numbers. | ||
In the model systems, we attributed lower than expected interaction energies to the difficulties associated with simultaneous formation of two productive HB angles. In the X-ray structure set, more ambifunctional HBs have near-linear (i.e., 170–180°) O–H⋯O angles and small (i.e., 110–130°) N–H⋯O angles than the reverse, but average angles differ only by around 5° from the average values of the single HB angles in X-ray structures (Fig. 8, ESI Fig. S23 and Tables S4, S5 and S22†). Consistent with the HB distance analysis, a minority of all Tyr (9%) and Ser/Thr (20%) ambifunctional HBs simultaneously form relatively obtuse O–H⋯O and N–H⋯O angles as high as those observed in the model systems (Fig. 8 and ESI Fig. S23†). This small fraction overlaps significantly with the minority of strong, symmetric ambifunctional HBs that nearly all have two obtuse angles (Fig. 8 and ESI Fig. S23†). Analyzing the secondary structure motifs in proteins with symmetric ambifunctional HBs reveals the two residues are most commonly located on adjacent strands of β-sheets, on the same β-sheet strand but separated by a single residue, or on a flexible loop. These symmetric ambifunctional HBs are less frequently observed on α-helices. When these are observed, it is typically between an α-helix and an adjacent loop or when two α-helices are oriented perpendicular to each other. Consistent with observations on protein structures, model system ambifunctional HB geometries also exhibit a greater reduction of the N–H⋯O angle than the O–H⋯O angle, especially for p-cresol (20°) versus methanol (10°, ESI Tables S4 and S5†).
While ambifunctional HBs are apparent in protein structures, the benefit of a near-linear O–H⋯O angle especially in interactions with Tyr can be expected to dominate. Thus we can expect the Tyr hydroxyl to act as a simultaneous HBA and HBD only when limited deviation of HB angles is necessary. Conversely, we should anticipate this motif to be apparent in proteins with Ser or Thr in close proximity to Gln or Asn. We expect more such structures could be uncovered with even larger-scale and more inclusive examination of proteins from crystal structures, molecular dynamics, or with other (e.g., NMR) spectroscopic techniques.
4. Conclusions
We combined accurate correlated wavefunction theory energetics of model systems and analysis of high-resolution X-ray crystal structures of proteins to understand the balance of individual or simultaneous hydrogen bond donor and acceptor interactions between sidechains in proteins. Using representative models of aliphatic hydroxyl (i.e., Ser/Thr) or aromatic hydroxyl (i.e., Tyr) groups with the amide sidechains of Asn/Gln, we obtained accurate potential energy curves that defined these hydrogen-bonding interactions. Analysis of the model systems confirmed expectations that aromatic hydroxyl groups form the strongest O–H⋯O HBs but considerably weaker N–H⋯O HBs, whereas these interactions were balanced for aliphatic hydroxyl groups. The model systems were deemed to be suitable representations of residue–residue interactions in proteins thanks to the good agreement of gas-phase optimized and crystal structure geometries. Almost all HB distances obtained from protein crystal structures resided within 1–2 kcal mol−1 of the favored gas-phase minimum energy structure. Nevertheless, we observed limited correspondence between energetic favorability (i.e., O–H⋯O > N–H⋯O) and relative abundance in the data set, which we attributed partly to compensating intermolecular HBs that are more plentiful in N–H⋯O HB configurations. In future work, larger models of the explicit protein environment in combination with geometric and bond critical point analysis could be used to better understand competing factors that influence HB formation and abundance.We showed that simultaneous O–H⋯O and N–H⋯O interactions are stabilizing in an ambifunctional HB. While this energetic benefit was most significant for aliphatic hydroxyl groups, it was less than the theoretical limit (i.e., sum of two individual HBs) and only slightly more favorable than the O–H⋯O HB alone for aromatic hydroxyls. We determined this reduction in interaction strength was due both to geometric constraints on the formation of two productive HB angles and distances along with the reduced ability of a single hydroxyl to act as a simultaneous HBA/HBD. These many-body effects could not be captured by conventional force fields widely used to study proteins. While evaluating the reaction coordinate that ccaptured the transformation between HB conformations revealed rearrangement from the N–H⋯O to ambifunctional HB to be approximately barrierless, the basin of stable ambifunctional HB structures accommodated a wide range of distances and angles especially for Ser/Thr–Asn/Gln. Consistent with model system observations, we observed a range of ambifunctional HB structures in X-ray crystal structures, especially for Ser/Thr over Tyr. These studies set the stage for systematic100–102 and quantitative study of representative models to illuminate mechanistic roles for ambifunctional HBs that may have been missed when studied with conventional force fields. It is expected that the unique energetic and geometric properties of these hydrogen bonds could play an important role in substrate recognition and in controlling enzyme selectivity through substrate positioning.
5. Computational details
Representative models of protein hydrogen-bonding interactions were studied using methanol and p-cresol as hydrogen bond donor or acceptor (HBD or HBA) models of Ser/Thr and Tyr, respectively, and acetamide as an HBD or HBA model of Asn/Gln (Fig. 1). These choices were made to minimize the effect of sidechain truncation on interaction energies in comparison to the full residues while minimizing computational cost (ESI Table S23†). Initial structures were built by hand and optimized with the MMFF94 force field103 using Avogadro v1.2.0.104 Geometries were prepared in four configurations containing up to two candidate hydrogen bonds for both unconstrained and constrained geometry optimizations on acetamide–methanol and acetamide–p-cresol model systems (Fig. 1).Unconstrained and constrained geometry optimizations were performed using both hybrid (i.e., B3LYP105–107) density functional theory (DFT) and Møller–Plesset second-order perturbation theory (MP2). All optimizations were carried out using the 6-31G* basis set,108 followed by single-point energies evaluated using larger basis sets (ESI Tables S4 and S5†). Semi-empirical D3 (ref. 109) dispersion with Becke–Johnson110 damping was incorporated in the B3LYP optimizations, although its effect on geometries was limited (ESI Tables S4 and S5†). B3LYP-D3 DFT geometry optimizations were carried out in a developer version of TeraChem111 v1.9 in Cartesian coordinates using L-BFGS algorithm, as implemented in DL-FIND.112 Default thresholds of 4.5 × 10−4 hartree per bohr for the maximum gradient and 1 × 10−6 hartree for self-consistent field (SCF) convergence were employed. Geometry optimizations with MP2 in ORCA113 v.4.0.1.2 were carried out in redundant internal coordinates using the BFGS method with default thresholds of 3 × 10−4 hartree per bohr for the maximum gradient and 5 × 10−6 hartree for SCF convergence. The MP2 and B3LYP-D3 HB distances and angles as well as intramolecular bonds were comparable, with only equilibrium O⋯O distances exhibiting a slight dependence on basis set or method choice (ESI Tables S4, S5 and S24†). Comparisons of single-point energies at higher levels of theory on MP2 and B3LYP-D3 geometries revealed very limited differences (≤0.1 kcal mol−1) on evaluated interaction energies (ESI Table S25†). All initial and optimized structures are provided in the ESI.†
For the acetamide–methanol model system, single-point energy calculations were carried out on MP2/6-31G* geometries with both canonical coupled cluster singles doubles with perturbative triples (i.e., CCSD(T)) and domain-localized pair natural orbital CCSD(T) (i.e., DLPNO-CCSD(T)114,115). Dunning-style correlation consistent double-ζ and triple-ζ (i.e., aug-cc-pVDZ and aug-cc-pVTZ) basis sets were employed to enable two-point116–118 extrapolation to the complete basis set (CBS) limit. Given the larger size (i.e., 25 atoms) of the acetamide–p-cresol system, only DLPNO-CCSD(T) single-point energies were evaluated on MP2/6-31G* structures with aug-cc-pVXZ (X = D, T) basis sets to enable extrapolation to the CBS limit (ESI Table S3†). All reported DLPNO-CCSD(T) energies correspond to those obtained from Tight PNO thresholds, after testing the effect of threshold choice on interaction energies (ESI Table S3†). For the acetamide–methanol model system where canonical CCSD(T) could be carried out, interaction energies obtained from DLPNO-CCSD(T)/CBS with Tight PNO thresholds and CCSD(T)/CBS agreed to within 0.3 kcal mol−1, with relative interaction trends in even closer agreement (ESI Table S3†).
One-dimensional (1D) potential energy curves (PECs) and two-dimensional (2D) potential energy surfaces (PESs) were obtained by generating initial geometries for constrained geometry optimizations. Constrained optimizations were all carried out in ORCA v4.0.1.2 at the MP2/6-31G* level of theory, followed by single-point energies evaluated with DLPNO-CCSD(T)/CBS or with the generalized amber force field (GAFF99). We select this protocol to ensure we are predictive across full HB potential energy curves, but B3LYP-D3/aug-cc-pVTZ interaction energies underestimate the DLPNO-CCSD(T)/aug-cc-pVTZ values by only ca. 1 kcal mol−1, indicating limited method sensitivity of some properties (ESI Table S26†). The 1D PECs were obtained for syn N–H⋯O HBs and O–H⋯O HBs in acetamide–methanol and acetamide–p-cresol systems by varying the constrained HB distance (i.e., N⋯O or O⋯O) in steps of 0.01 Å from 2.4 Å to 4.0 Å. The 2D PESs were obtained for the syn N–H⋯O HB and O–H⋯O HB of acetamide–methanol and acetamide–p-cresol by varying the constrained HB distance from 2.40 up to 5.00 Å in steps of 0.05 Å and simultaneously varying the angle from 110° to 180° in steps of 5°. Reaction coordinates for the transformation between N–H⋯O, ambifunctional, and O–H⋯O HBs for the acetamide–methanol and acetamide–p-cresol model systems were sampled from initial geometries in which HB partners were translated and rotated with respect to each other using an in-house Python script. The reaction coordinate corresponded to an intermolecular angle, which was selected by trial and error, and initial geometries for constrained optimizations were generated by rotation of this angle in 0.1° increments (ESI Text S4†).
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge primary support by the National Science Foundation under grant number CBET-1704266 (to V. V. and R. M.) as well as partial support from the Department of Energy under grant number DE-SC0018096 (to V. V.). H.J.K. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund, which supported this work (to V. V. and R. M.). H. W. Q. was supported in part by a Department of Energy Computational Science Graduate Fellowship (DOE-CSGF). The authors acknowledge Adam H. Steeves for providing a critical reading of the manuscript.References
- W. W. Cleland and M. M. Kreevoy, Low-Barrier Hydrogen Bonds and Enzymic Catalysis, Science, 1994, 264, 1887–1890 CrossRef CAS
.
- J. D. Watson and F. H. C. Crick, Molecular Structure of Nucleic Acids - a Structure for Deoxyribose Nucleic Acid, Nature, 1953, 171, 737–738 CrossRef CAS
.
- L. Pauling, R. B. Corey and H. R. Branson, The Structure of Proteins - 2 Hydrogen-Bonded Helical Configurations of the Polypeptide Chain, Proc. Natl. Acad. Sci. U.S.A., 1951, 37, 205–211 CrossRef CAS
.
- L. Pauling and R. B. Corey, Configurations of Polypeptide Chains with Favored Orientations around Single Bonds - 2 New Pleated Sheets, Proc. Natl. Acad. Sci. U.S.A., 1951, 37, 729–740 CrossRef CAS
.
- M. G. Grutter, R. B. Hawkes and B. W. Matthews, Molecular-Basis of Thermostability in the Lysozyme from Bacteriophage-T4, Nature, 1979, 277, 667–669 CrossRef CAS
.
- M. F. Perutz and H. Raidt, Stereochemical Basis of Heat-Stability in Bacterial Ferredoxins and in Hemoglobin-A2, Nature, 1975, 255, 256–259 CrossRef CAS
.
- A. Bauzá and A. Frontera, Rch3⋯O Interactions in Biological Systems: Are They Trifurcated H-Bonds or Noncovalent Carbon Bonds?, Crystals, 2016, 6, 26 CrossRef
.
- V. R. Mundlapati, D. K. Sahoo, S. Bhaumik, S. Jena, A. Chandrakar and H. S. Biswal, Noncovalent Carbon-Bonding Interactions in Proteins, Angew. Chem., Int. Ed., 2018, 57, 16496–16500 CrossRef CAS
.
- R. W. Newberry and R. T. Raines, The N→π* Interaction, Acc. Chem. Res., 2017, 50, 1838–1846 CrossRef CAS
.
- G. J. Bartlett and D. N. Woolfson, On the Satisfaction of Backbone-Carbonyl Lone Pairs of Electrons in Protein Structures, Protein Sci., 2016, 25, 887–897 CrossRef CAS
.
- G. J. Bartlett, R. W. Newberry, B. VanVeller, R. T. Raines and D. N. Woolfson, Interplay of Hydrogen Bonds and N→π* Interactions in Proteins, J. Am. Chem. Soc., 2013, 135, 18682–18688 CrossRef CAS
.
- R. Kurczab, P. Śliwa, K. Rataj, R. Kafel and A. J. Bojarski, Salt Bridge in Ligand–Protein Complexes—Systematic Theoretical and Statistical Investigations, J. Chem. Inf. Model., 2018, 58, 2224–2238 CrossRef CAS
.
- Y. An, J. W. Bloom and S. E. Wheeler, Quantifying the π-Stacking Interactions in Nitroarene Binding Sites of Proteins, J. Phys. Chem. B, 2015, 119, 14441–14450 CrossRef CAS
.
- K. L. Hudson, G. J. Bartlett, R. C. Diehl, J. Agirre, T. Gallagher, L. L. Kiessling and D. N. Woolfson, Carbohydrate–Aromatic Interactions in Proteins, J. Am. Chem. Soc., 2015, 137, 15152–15160 CrossRef CAS
.
- K. Kumar, S. M. Woo, T. Siu, W. A. Cortopassi, F. Duarte and R. S. Paton, Cation–π Interactions in Protein–Ligand Binding: Theory and Data-Mining Reveal Different Roles for Lysine and Arginine, Chem. Sci., 2018, 9, 2655–2665 RSC
.
- J. Liebeschuetz, J. Hennemann, T. Olsson and C. R. Groom, The Good, the Bad and the Twisted: A Survey of Ligand Geometry in Protein Crystal Structures, J. Comput.-Aided Mol. Des., 2012, 26, 169–183 CrossRef CAS
.
- L. M. Salonen, M. Ellermann and F. Diederich, Aromatic Rings in Chemical and Biological Recognition: Energetics and Structures, Angew. Chem., Int. Ed., 2011, 50, 4808–4842 CrossRef CAS
.
- J. P. Gallivan and D. A. Dougherty, Cation-π Interactions in Structural Biology, Proc. Natl. Acad. Sci. U.S.A., 1999, 96, 9459–9464 CrossRef CAS
.
- A. N. Bootsma, A. C. Doney and S. E. Wheeler, Predicting the Strength of Stacking Interactions between Heterocycles and Aromatic Amino Acid Side Chains, J. Am. Chem. Soc., 2019, 141, 11027–11035 CrossRef CAS
.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg and P. Hobza,
et al., Definition of the Hydrogen Bond (IUPAC Recommendations 2011), Pure Appl. Chem., 2011, 83, 1637–1641 CAS
.
- A. H. Iyer, R. N. V. Krishna Deepak and R. Sankararamakrishnan, Imidazole Nitrogens of Two Histidine Residues Participating in N–H⋯N Hydrogen Bonds in Protein Structures: Structural Bioinformatics Approach Combined with Quantum Chemical Calculations, J. Phys. Chem. B, 2018, 122, 1205–1212 CrossRef CAS
.
- M. Holcomb, R. Adhikary, J. Zimmermann and F. E. Romesberg, Topological Evidence of Previously Overlooked Ni+1–H⋯Ni H-Bonds and Their Contribution to Protein Structure and Stability, J. Phys. Chem. A, 2018, 122, 446–450 CrossRef CAS
.
- R. N. V. K. Deepak and R. Sankararamakrishnan, Unconventional N–H⋯N Hydrogen Bonds Involving Proline Backbone Nitrogen in Protein Structures, Biophys. J., 2016, 110, 1967–1979 CrossRef CAS
.
- B. Luisi, M. Orozco, J. Sponer, F. J. Luque and Z. Shakked, On the Potential Role of the Amino Nitrogen Atom as a Hydrogen Bond Acceptor in Macromolecules, J. Mol. Biol., 1998, 279, 1123–1136 CrossRef CAS
.
- K. Mazmanian, K. Sargsyan, C. Grauffel, T. Dudev and C. Lim, Preferred Hydrogen-Bonding Partners of Cysteine: Implications for Regulating Cys Functions, J. Phys. Chem. B, 2016, 120, 10288–10296 CrossRef CAS
.
- P. Zhou, F. Tian, F. Lv and Z. Shang, Geometric Characteristics of Hydrogen Bonds Involving Sulfur Atoms in Proteins, Proteins: Struct., Funct., Bioinf., 2009, 76, 151–163 CrossRef CAS
.
- V. R. Mundlapati, S. Gautam, D. K. Sahoo, A. Ghosh and H. S. Biswal, Thioamide, a Hydrogen Bond Acceptor in Proteins and Nucleic Acids, J. Phys. Chem. Lett., 2017, 8, 4573–4579 CrossRef CAS
.
- M. Nishio, Y. Umezawa, J. Fantini, M. S. Weiss and P. Chakrabarti, CH–π Hydrogen Bonds in Biological Macromolecules, Phys. Chem. Chem. Phys., 2014, 16, 12648–12683 RSC
.
- T. Steiner and G. Koellner, Hydrogen Bonds with π-Acceptors in Proteins: Frequencies and Role in Stabilizing Local 3D Structures, J. Mol. Biol., 2001, 305, 535–557 CrossRef CAS
.
- J. D. Yesselman, S. Horowitz, C. L. Brooks and R. C. Trievel, Frequent Side Chain Methyl Carbon-Oxygen Hydrogen Bonding in Proteins Revealed by Computational and Stereochemical Analysis of Neutron Structures, Proteins: Struct., Funct., Bioinf., 2014, 83, 403–410 CrossRef
.
- T. Steiner and W. Saenger, The Ordered Water Cluster in Vitamin-B-12 Coenzyme at 15 K Is Stabilized by C-H⋯O Hydrogen-Bonds, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1993, 49, 592–593 CrossRef CAS
.
- T. Steiner and W. Saenger, Role of C-H⋯O Hydrogen-Bonds in the Coordination of Water-Molecules - Analysis of Neutron-Diffraction Data, J. Am. Chem. Soc., 1993, 115, 4540–4547 CrossRef CAS
.
- Z. S. Derewenda, U. Derewenda and P. M. Kobos, (His)C-Epsilon-H⋯O=C Hydrogen-Bond in the Active-Sites of Serine Hydrolases, J. Mol. Biol., 1994, 241, 83–93 CrossRef CAS
.
- Z. S. Derewenda, L. Lee and U. Derewenda, The Occurrence of C-H⋯O Hydrogen-Bonds in Proteins, J. Mol. Biol., 1995, 252, 248–262 CrossRef CAS
.
- P. Muller, Glossary of Terms Used in Physical Organic-Chemistry, Pure Appl. Chem., 1994, 66, 1077–1184 Search PubMed
.
- C. A. Coulson and U. Danielsson, Ionic and Covalent Contributions to the Hydrogen Bond .2, Ark. Fys., 1954, 8, 245–255 CAS
.
- G. Gilli and P. Gilli, Towards an Unified Hydrogen-Bond Theory, J. Mol. Struct., 2000, 552, 1–15 CrossRef CAS
.
- P. Gilli, V. Bertolasi, L. Pretto and G. Gilli, Outline of a Transition-State Hydrogen-Bond Theory, J. Mol. Struct., 2006, 790, 40–49 CrossRef CAS
.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg and P. Hobza,
et al., Defining the Hydrogen Bond: An Account (IUPAC Technical Report), Pure Appl. Chem., 2011, 83, 1619–1636 CAS
.
- A. Shahi and E. Arunan, Why Are Hydrogen Bonds Directional?, J. Chem. Sci., 2016, 128, 1571–1577 CrossRef CAS
.
- R. A. Klein, Modified Van Der Waals Atomic Radii for Hydrogen Bonding Based on Electron Density Topology, Chem. Phys. Lett., 2006, 425, 128–133 CrossRef CAS
.
- B. Raghavendra, P. K. Mandal and E. Arunan, Ab Initio and Aim Theoretical Analysis of Hydrogen-Bond Radius of Hd (D = F, Cl, Br, Cn, HO, Hs and Cch) Donors and Some Acceptors, Phys. Chem. Chem. Phys., 2006, 8, 5276–5286 RSC
.
- M. H. Abraham and J. A. Platts, Hydrogen Bond Structural Group Constants, J. Org. Chem., 2001, 66, 3484–3491 CrossRef CAS
.
- C. A. Hunter, Quantifying Intermolecular Interactions: Guidelines for the Molecular Recognition Toolbox, Angew. Chem., Int. Ed., 2004, 43, 5310–5324 CrossRef CAS
.
- M. H. Abraham, W. E. Acree, C. E. Earp, A. Vladimirova and W. L. Whaley, Studies on the Hydrogen Bond Acidity, and Other Descriptors and Properties for Hydroxyflavones and Hydroxyisoflavones, J. Mol. Liq., 2015, 208, 363–372 CrossRef CAS
.
-
G. Gilli and P. GilliThe Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory, OUP Oxford, 2009 Search PubMed
.
- F. Weinhold and R. A. Klein, What Is a Hydrogen Bond? Mutually Consistent Theoretical and Experimental Criteria for Characterizing H-Bonding Interactions, Mol. Phys., 2012, 110, 565–579 CrossRef CAS
.
- F. Weinhold and R. A. Klein, Anti-Electrostatic Hydrogen Bonds, Angew. Chem., Int. Ed., 2014, 53, 11214–11217 CrossRef CAS
.
- Z. Yang, F. Liu, A. H. Steeves and H. J. Kulik, Quantum Mechanical Description of Electrostatics Provides a Unified Picture of Catalytic Action across Methyltransferases, J. Phys. Chem. Lett., 2019, 10, 3779–3787 CrossRef CAS
.
- K. B. Moore III, K. Sadeghian, C. D. Sherrill, C. Ochsenfeld and H. F. Schaefer III, C–H⋯O Hydrogen Bonding. The Prototypical Methane-Formaldehyde System: A Critical Assessment, J. Chem. Theory Comput., 2017, 13, 5379–5395 CrossRef
.
- A. D. Boese, Density Functional Theory and Hydrogen Bonds: Are We There Yet?, ChemPhysChem, 2015, 16, 978–985 CrossRef CAS
.
- S. Kristyan and P. Pulay, Can (Semi)Local Density-Functional Theory Account for the London Dispersion Forces, Chem. Phys. Lett., 1994, 229, 175–180 CrossRef CAS
.
- E. J. Meijer and M. Sprik, A Density-Functional Study of the Intermolecular Interactions of Benzene, J. Chem. Phys., 1996, 105, 8684–8689 CrossRef CAS
.
- L. A. Burns, J. C. Faver, Z. Zheng, M. S. Marshall, D. G. A. Smith, K. Vanommeslaeghe, A. D. MacKerell, K. M. Merz and C. D. Sherrill, The Biofragment Database (BFDb): An Open-Data Platform for Computational Chemistry Analysis of Noncovalent Interactions, J. Chem. Phys., 2017, 147, 161727 CrossRef
.
- H. J. Kulik, N. Luehr, I. S. Ufimtsev and T. J. Martinez, Ab Initio Quantum Chemistry for Protein Structure, J. Phys. Chem. B, 2012, 116, 12501–12509 CrossRef CAS
.
- K. E. Riley, M. Pitoňák, P. Jurečka and P. Hobza, Stabilization and Structure Calculations for Noncovalent Interactions in Extended Molecular Systems Based on Wave Function and Density Functional Theories, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS
.
- H. J. Kulik, Large-Scale QM/MM Free Energy Simulations of Enzyme Catalysis Reveal the Influence of Charge Transfer, Phys. Chem. Chem. Phys., 2018, 20, 20650–20660 RSC
.
- S. M. Zhou and L. Wang, Unraveling the Structural and Chemical Features of Biological Short Hydrogen Bonds, Chem. Sci., 2019, 10, 7734–7745 RSC
.
- H. W. Qi and H. J. Kulik, Evaluating Unexpectedly Short Non-Covalent Distances in X-Ray Crystal Structures of Proteins with Electronic Structure Analysis, J. Chem. Inf. Model., 2019, 59, 2199–2211 CrossRef CAS
.
- H. Kruse, K. Mrazikova, L. D'Ascenzo, J. Sponer and P. Auffinger, Short but Weak: The Z-DNA Lone-Pair⋯π
Conundrum Challenges Standard Carbon Van Der Waals Radii, Angew. Chem., Int. Ed., 2020, 59, 16553–16560 CrossRef CAS
.
- K. A. Beauchamp, Y.-S. Lin, R. Das and V. S. Pande, Are Protein Force Fields Getting Better? A Systematic Benchmark on 524 Diverse NMR Measurements, J. Chem. Theory Comput., 2012, 8, 1409–1414 CrossRef CAS
.
- Z. Jiang, M. Biczysko and N. W. Moriarty, Accurate Geometries for “Mountain Pass” Regions of the Ramachandran Plot Using Quantum Chemical Calculations, Proteins: Struct., Funct., Bioinf., 2018, 86, 273–278 CrossRef CAS
.
- S. Rauscher, V. Gapsys, M. J. Gajda, M. Zweckstetter, B. L. de Groot and H. Grubmüller, Structural Ensembles of Intrinsically Disordered Proteins Depend Strongly on Force Field: A Comparison to Experiment, J. Chem. Theory Comput., 2015, 11, 5513–5524 CrossRef CAS
.
- S. Riniker, Fixed-Charge Atomistic Force Fields for Molecular Dynamics Simulations in the Condensed Phase: An Overview, J. Chem. Inf. Model., 2018, 58, 565–578 CrossRef CAS
.
- Z. Yang, R. Mehmood, M. Wang, H. W. Qi, A. H. Steeves and H. J. Kulik, Revealing Quantum Mechanical Effects in Enzyme Catalysis with Large-Scale Electronic Structure Simulation, React. Chem. Eng., 2019, 4, 298–315 RSC
.
- P. Frey, S. Whitt and J. Tobin, A Low-Barrier Hydrogen Bond in the Catalytic Triad of Serine Proteases, Science, 1994, 264, 1927–1930 CrossRef CAS
.
- C. L. Perrin and J. B. Nielson, “Strong” Hydrogen Bonds in Chemistry and Biology, Annu. Rev. Phys. Chem., 1997, 48, 511–544 CrossRef CAS
.
- L. Wang, S. D. Fried, S. G. Boxer and T. E. Markland, Quantum Delocalization of Protons in the Hydrogen-Bond Network of an Enzyme Active Site, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 18454–18459 CrossRef CAS
.
- H. Ishikita and K. Saito, Proton Transfer Reactions and Hydrogen-Bond Networks in Protein Environments, J. R. Soc. Interface, 2014, 11, 20130518 CrossRef
.
- G. R. Desiraju, A Bond by Any Other Name, Angew. Chem., Int. Ed., 2011, 50, 52–59 CrossRef CAS
.
- P. Gilli, L. Pretto, V. Bertolasi and G. Gilli, Predicting Hydrogen-Bond Strengths from Acid−Base Molecular Properties. The pKa Slide Rule: Toward the Solution of a Long-Lasting Problem, Acc. Chem. Res., 2009, 42, 33–44 CrossRef CAS
.
- P. Gilli and G. Gilli, Hydrogen Bond Models and Theories: The Dual Hydrogen Bond Model and Its Consequences, J. Mol. Struct., 2010, 972, 2–10 CrossRef CAS
.
- P. Gilli, L. Pretto and G. Gilli, Pa/pKa Equalization and the Prediction of the Hydrogen-Bond Strength: A Synergism of Classical Thermodynamics and Structural Crystallography, J. Mol. Struct., 2007, 844, 328–339 CrossRef
.
- S. Dai, L.-M. Funk, F. R. von Pappenheim, V. Sautner, M. Paulikat, B. Schröder, J. Uranga, R. A. Mata and K. Tittmann, Low-Barrier Hydrogen Bonds in Enzyme Cooperativity, Nature, 2019, 573, 609–613 CrossRef CAS
.
- R. W. Newberry and R. T. Raines, A Prevalent Intraresidue Hydrogen Bond Stabilizes Proteins, Nat. Chem. Biol., 2016, 12, 1084–1088 CrossRef CAS
.
- E. N. Baker and R. E. Hubbard, Hydrogen-Bonding in Globular-Proteins, Prog. Biophys. Mol. Biol., 1984, 44, 97–179 CrossRef CAS
.
- N. C. Seeman, J. M. Rosenberg, F. L. Suddath, J. J. Parkkim and A. Rich, Rna Double-Helical Fragments at Atomic Resolution - .1. Crystal and Molecular-Structure of Sodium Adenylyl-3',5'-Uridine Hexahydrate, J. Mol. Biol., 1976, 104, 109–144 CrossRef CAS
.
- J. M. Rosenberg, N. C. Seeman, R. O. Day and A. Rich, Rna Double-Helical Fragments at Atomic Resolution - Crystal-Structure of Sodium Guanylyl-3',5'-Cytidine Nonahydrate, J. Mol. Biol., 1976, 104, 145–167 CrossRef CAS
.
- C. F. Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, Hydrogen Bonding in DNA Base Pairs: Reconciliation of Theory and Experiment, J. Am. Chem. Soc., 2000, 122, 4117–4128 CrossRef CAS
.
- J. Sponer and P. Hobza, Bifurcated Hydrogen Bonds in DNA Crystal Structures. An Ab Initio Quantum Chemical Study, J. Am. Chem. Soc., 1994, 116, 709–714 CrossRef CAS
.
- R. Mehmood, H. W. Qi, A. H. Steeves and H. J. Kulik, The Protein's Role in Substrate Positioning and Reactivity for Biosynthetic Enzyme Complexes: The Case of SyrB2/SyrB1, ACS Catal., 2019, 9, 4930–4943 CrossRef CAS
.
- M. R. Fullone, A. Paiardini, R. Miele, S. Marsango, D. C. Gross, S. Omura, E. Ros-Herrera, M. C. B. di Patti, A. Lagana and S. Pascarella, Insight into the Structure–Function Relationship of the Nonheme Iron Halogenases Involved in the Biosynthesis of 4-Chlorothreonine–Thr3 from Streptomyces Sp. OH-5093 and SyrB2 from Pseudomonas Syringae Pv. Syringae B301DR, FEBS J., 2012, 279, 4269–4282 CrossRef CAS
.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, The Protein Data Bank, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS
.
- A. Wlodawer, W. Minor, Z. Dauter and M. Jaskolski, Protein Crystallography for Non-Crystallographers, or How to Get the Best (but Not More) from Published Macromolecular Structures, FEBS J., 2008, 275, 1–21 CrossRef CAS
.
- K. S. Wilson, S. Butterworth, Z. Dauter, V. S. Lamzin, M. Walsh, S. Wodak, J. Pontius, J. Richelle, A. Vaguine, C. Sander, R. W. W. Hooft, G. Vriend, J. M. Thornton, R. A. Laskowski, M. W. MacArthur, E. J. Dodson, G. Murshudov, T. J. Oldfield, R. Kaptein and J. A. C. Rullmann, Who Checks the Checkers? Four Validation Tools Applied to Eight Atomic Resolution Structures., J. Mol. Biol., 1998, 276, 417–436 CrossRef
.
- A. Meyder, E. Nittinger, G. Lange, R. Klein and M. Rarey, Estimating Electron Density Support for Individual Atoms and Molecular Fragments in X-Ray Structures, J. Chem. Inf. Model., 2017, 57, 2437–2447 CrossRef CAS
.
- D. R. Roe and T. E. Cheatham, Ptraj and Cpptraj: Software for Processing and Analysis of Molecular Dynamics Trajectory Data, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS
.
- P. Smith, R. M. Ziolek, E. Gazzarrini, D. M. Owen and C. D. Lorenz, On the Interaction of Hyaluronic Acid with Synovial Fluid Lipid Membranes, Phys. Chem. Chem. Phys., 2019, 21, 9845–9857 RSC
.
-
G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, New York, N.Y, 1997 Search PubMed
.
- R. F. W. A. Bader, Quantum-Theory of Molecular-Structure and Its Applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS
.
- R. F. Bader, Atoms in Molecules, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS
.
- E. Espinosa, E. Molins and C. Lecomte, Hydrogen Bond Strengths Revealed by Topological Analyses of Experimentally Observed Electron Densities, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS
.
- T. Lu and F. W. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS
.
- C. Laurence, K. A. Brameld, J. Graton, J. Y. Le Questel and E. Renault, The pK(Bhx) Database: Toward a Better Understanding of Hydrogen-Bond Basicity for Medicinal Chemists, J. Med. Chem., 2009, 52, 4073–4086 CrossRef CAS
.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. Martin and F. Neese, Exploring the Accuracy Limits of Local Pair Natural Orbital Coupled-Cluster Theory, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS
.
- J. Rezac and P. Hobza, Describing Noncovalent Interactions Beyond the Common Approximations: How Accurate Is the “Gold Standard,” CCSD (T) at the Complete Basis Set Limit?, J. Chem. Theory Comput., 2013, 9, 2151–2155 CrossRef CAS
.
- J. Graton, F. Besseau, A. M. Brossard, E. Charpentier, A. Deroche and J. Y. Le Questel, Hydrogen-Bond Acidity of Oh Groups in Various Molecular Environments (Phenols, Alcohols, Steroid Derivatives, and Amino Acids Structures): Experimental Measurements and Density Functional Theory Calculations, J. Phys. Chem. A, 2013, 117, 13184–13193 CrossRef CAS
.
- E. G. Hohenstein and C. D. Sherrill, Density Fitting of Intramonomer Correlation Effects in Symmetry-Adapted Perturbation Theory, J. Chem. Phys., 2010, 133, 014101 CrossRef
.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and Testing of a General Amber Force Field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS
.
- M. Karelina and H. J. Kulik, Systematic Quantum Mechanical Region Determination in QM/MM Simulation, J. Chem. Theory Comput., 2017, 13, 563–576 CrossRef CAS
.
- H. W. Qi, M. Karelina and H. J. Kulik, Quantifying Electronic Effects in QM and QM/MM Biomolecular Modeling with the Fukui Function, Acta Phys.-Chim. Sin., 2018, 34, 81–91 CAS
.
- R. Mehmood and H. J. Kulik, Both Configuration and QM Region Size Matter: Zinc Stability in QM/MM Models of DNA Methyltransferase, J. Chem. Theory Comput., 2020, 16, 3121–3134 CrossRef CAS
.
- T. A. Halgren, Merck Molecular Force Field .3. Molecular Geometries and Vibrational Frequencies for MMFF94, J. Comput. Chem., 1996, 17, 553–586 CrossRef CAS
.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: An Advanced Semantic Chemical Editor, Visualization, and Analysis Platform, J. Cheminf., 2012, 4, 17 CAS
.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS
.
- A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS
.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods .9. Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54, 724 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef
.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS
.
- I. S. Ufimtsev and T. J. Martinez, Quantum Chemistry on Graphical Processing Units. 3. Analytical Energy Gradients, Geometry Optimization, and First Principles Molecular Dynamics, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS
.
- J. Kastner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, DL-FIND: An Open-Source Geometry Optimizer for Atomistic Simulations, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef CAS
.
- F. Neese, Software Update: The ORCA Program System, Version 4.0. Wiley Inderdiscip. Rev., Comput. Mol. Sci., 2018, 8, e1327 Search PubMed
.
- C. Riplinger and F. Neese, An Efficient and near Linear Scaling Pair Natural Orbital Based Local Coupled Cluster Method, J. Chem. Phys., 2013, 138, 034106 CrossRef
.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, Natural Triple Excitations in Local Coupled Cluster Calculations with Pair Natural Orbitals, J. Chem. Phys., 2013, 139, 134101 CrossRef
.
- S. J. Zhong, E. C. Barnes and G. A. Petersson, Uniformly Convergent N-Tuple-Zeta Augmented Polarized (nZaP) Basis Sets for Complete Basis Set Extrapolations. I. Self-Consistent Field Energies, J. Chem. Phys., 2008, 129, 184116 CrossRef
.
- F. Neese and E. F. Valeev, Revisiting the Atomic Natural Orbital Approach for Basis Sets: Robust Systematic Basis Sets for Explicitly Correlated and Conventional Correlated Ab Initio Methods?, J. Chem. Theory Comput., 2011, 7, 33–43 CrossRef CAS
.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-Set Convergence of Correlated Calculations on Water, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05084a |
| This journal is © The Royal Society of Chemistry 2021 |