Lithium nickel borides: evolution of [NiB] layers driven by Li pressure

Abstract

Here we show the effect of Li chemical pressure on the structure of layered polymorphs with LiNiB composition: RT-LiNiB (room temperature polymorph) and HT-LiNiB (high temperature polymorph), resulting in stabilization of the novel RT-Li_1+xNiB (x ∼ 0.17) and HT-Li_1+yNiB (y ∼ 0.06) phases. Depending on the synthesis temperature and initial Li content, precisely controlled via hydride route synthesis, [NiB] layers undergo structural deformations, allowing for extra Li atoms to be accommodated between the layers. In situ variable temperature synchrotron and time-dependent laboratory powder X-ray diffraction studies suggest Li step-wise deintercalation processes: RT-Li_1+xNiB → RT-LiNiB (high temp.) → LiNi₃B_1.8 → binary Ni borides and HT-Li_1+yNiB → HT-LiNiB (high temp.) → LiNi₃B_1.8 → binary Ni borides. Quantum chemistry calculations and solid state ⁷Li and ¹¹B NMR spectroscopy shed light on the complexity of real superstructures of these compounds determined from high resolution synchrotron powder diffraction data.

---

Introduction

The story of lithium nickel borides began in 1976 when four ternary phases were identified in the Li–Ni–B system.^1–3 Crystal structures were reported for three of these compounds, LiNi₃B_1.8 (MgNi₃B₂ structure type, P6₂22 space group), Li₃Ni₂₀B₆ (Cr₂₃C₆, Fm3̄m), and Li_2.8Ni₁₆B₈ (Li₃Ni₁₆B₈, P4/mbm). Only a tentative composition of 1 : 1 : 1 was assigned for the fourth compound, a phase with the richest Li content. To the best of our knowledge, no other ternary compounds in all A–T–B systems (A = alkali metal, T = Ti–Zn) have been reported. The lack of the ternary A–T–B compounds can be due to the drastically different reactivity of refractory boron (melting point 2348 K) and alkali metals (boiling point 944–1615 K) making traditional synthesis methods (e.g. arc melting) non-applicable.

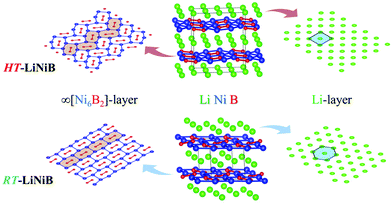
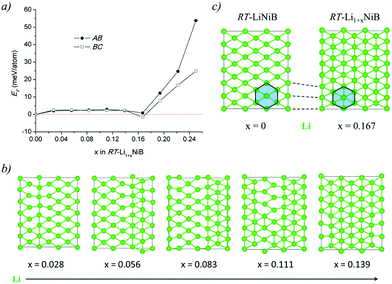
The hydride synthesis route, where salt-like alkali metal hydrides are used as a source of alkali metals, has been successfully utilized for the preparation of alkali/alkali-earth antimonides, arsenides, germanides, and silicides.^4–10 Application of this method for the Li–Ni–B system significantly shortened the synthesis time of ternary phases. For instance, LiNi₃B_1.8 can be synthesized in a span of ∼24 hours compared with the previously reported 3-month annealing for the reaction of elements.⁹ The hydride route also permitted the compositional control and comprehensive screening of unknown compounds. This way, two lithium nickel boride polymorphs RT-LiNiB (room temperature polymorph) and HT-LiNiB (high temperature polymorph), with unique layered crystal structures, were discovered.¹¹ In these polymorphic compounds, Li layers, featuring hexagonal-like or squared motif, alternate with nearly planar [NiB] layers, whose structure differs depending on the polymorph (Fig. 1). A structural relationship between the RT-LiNiB and HT-LiNiB polymorphs, Li-depleted phase LiNi₃B_1.8, Ni₂B, and Li has been found,¹¹ indicating on the _∞[NiB] framework evolves with the changing of Li content and/or temperature variation (Fig. S1†).

Fig. 1 Crystal structure of RT-LiNiB and HT-LiNiB polymorphs.

Layered lithium nickel borides are of interest from the functional materials perspective. Firstly, ∼33 at% of Li is stored between [NiB] layers in RT- and HT-LiNiB (9.1 wt% of Li as compared to 8.8 wt% of Li in LiC₆ anode material) gives these compounds potential for applications in Li-ion batteries. Secondly, due to the unique arrangement of Li and [NiB] layers in their structures, exfoliation of these materials can open a pathway to novel two-dimensional (2D) nickel borides.^11,12 The search for 2D borides or MBene has been accelerated after successful preparation of the 2D transition metal carbides or MXene.^13,14 MXenes are extensively studied due to their attractive thermal, magnetic, mechanical and electric properties.^15–20 MBenes were predicted to have similarly fascinating properties^21–24 but have not yet been obtained experimentally, despite several prominent attempts.^24–28

Recent theoretical investigation of the Li–Ni–B system²⁹ revealed a new Li-rich layered compound Li₂NiB, whose structure is derived from RT-LiNiB. According to the calculations, only a little extra energy is needed to accommodate an additional Li layer in the structure of the LiNiB parent phase. Here, we have experimentally explored the Li-rich compositions of the Li–Ni–B phase diagram and discovered two compounds that are Li-enriched versions of RT-LiNiB and HT-LiNiB polymorphs. Both RT-Li_1+xNiB (x ∼ 0.17) and HT-Li_1+yNiB (y ∼ 0.06) phases feature layered crystal structures with the original topology of the [NiB] layers modified due to the incorporation of extra Li between the layers. We use in situ synchrotron and laboratory powder X-ray diffraction, solid state NMR spectroscopy, and quantum chemical calculations to study structural relationships, reactivity, and phase transformations upon heating or exposure to air of these lithium-rich layered nickel borides.

Results and discussion

Synthesis and composition

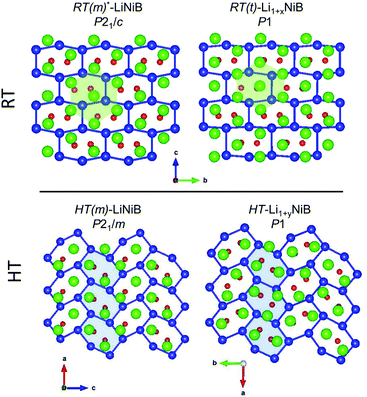
In our recent study,¹¹ the Li–Ni–B ternary system was evaluated using an adaptive genetic algorithm (AGA) search for potentially stable ternary phases. As a result, a RT-LiNiB compound with a unique layered structure was computationally predicted and further synthesized experimentally using the hydride route. The structure of RT-LiNiB can be represented as almost planar [NiB] layers alternating with Li layers (Fig. 1).

However, as evident from high-resolution synchrotron data, the real structure is more complex and includes intergrowth of two polytypes (Table 1). Above 1173 K RT-LiNiB transforms to its high-temperature polymorph HT-LiNiB featuring different topology of [NiB] and Li layers (Fig. 1).

Table 1 Family of layered lithium nickel borides

Phase (space group)	a, Å	b, Å	c, Å	α, °	β, °	γ, °	V, Å^3	V/Z,^e Å^3	Ref.
a Different polytypes of RT-LiNiB compound. b Superstructure of two polytypes of RT-LiNiB. c Idealized structure of RT-Li1+xNiB compound. d Idealized structure of HT-Li1+yNiB compound. e Volume normalized per formula units.
RT(m)-LiNiB (P21/c)^a	4.6114	4.8333	6.156	90	109.607	90	129.26	32.32	11
RT*(m)-LiNiB (P21/c)^b	18.451	4.8336	6.1573	90	109.636	90	517.21	32.33	11
RT(o)-LiNiB (Cmc21)^a	4.8341	6.1573	8.6888	90	90	90	258.62	32.33	11
RT(m)-Li1+xNiB (P21/c)^c	18.277(1)	4.86606(5)	6.1818(2)	90	107.623(1)	90	524.00(2)	32.75	This work
RT(t)-Li1+xNiB (P1)	18.2763(4)	4.86589(3)	18.5447(5)	89.9810(6)	107.6202(9)	90.056(2)	1571.82(3)	32.75	This work
HT-LiNiB (P21/m)	3.9095	8.8087	7.5234	90	90.070	90	259.08	32.39	11
HT(m)-Li1+yNiB (P21/c)^d	3.92591(7)	7.5593(1)	8.8181(2)	90	92.6245(7)	90	261.42(1)	32.68	This work
HT(t)-Li1+yNiB (P1)	7.85184(9)	15.1183(2)	8.8179(1)	89.9079(7)	92.6271(5)	90.0008(5)	1045.63(3)	32.68	This work

---

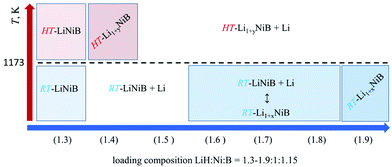
Previously we showed^10,11 the hydride route is feasible for preparation of ternary lithium nickel borides providing fast reactions and accurate compositional control. The experimentally determined, LiH : Ni : B = 1.3 : 1 : 1.15, molar ratio results in phase-pure samples of LiNiB phases with minimal excess of LiH and B needed.¹¹ A further increase of the LiH ratio to values of 1.4 to 1.9 leads to stabilization of two new phases RT-Li_1+xNiB and HT-Li_1+yNiB (Table 1, Fig. 2). A slight excess of lithium hydride (LiH : Ni : B = 1.4 : 1 : 1.15) is necessary for the synthesis of the HT-Li_1+yNiB compound. For stabilization of the RT-Li_1+xNiB phase, a considerable excess of LiH must be used (LiH : Ni : B = 1.9 : 1 : 1.15). Moreover, we found that synthesis of RT-Li_1+xNiB compound requires that the sample be ground and annealed following the initial heating of precursors. After the first annealing, samples always comprise the RT-LiNiB phase. RT-LiNiB was the major phase and only a small amount of RT-Li_1+xNiB compound was detected experimentally in the sample synthesized with loading composition LiH : Ni : B = 1.6 : 1 : 1.15. With a further increase in Li content, the fraction of RT-Li_1+xNiB increases accordingly (Fig. S2†), while loading composition LiH : Ni : B = 1.9 : 1 : 1.15 gives phase pure RT-Li_1+xNiB samples.

Fig. 2 Temperature-composition diagram for the synthesis of layered lithium nickel borides.

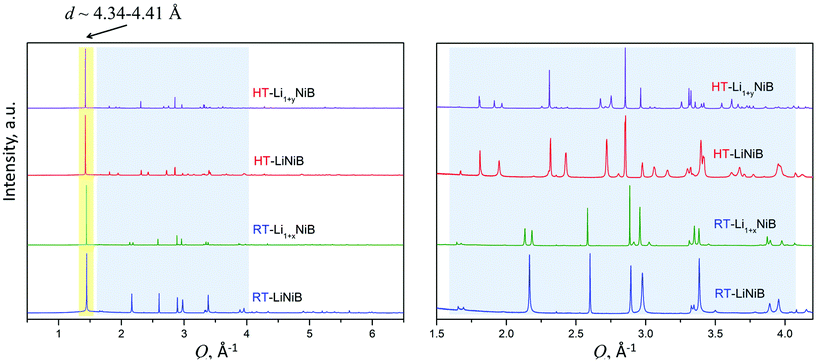
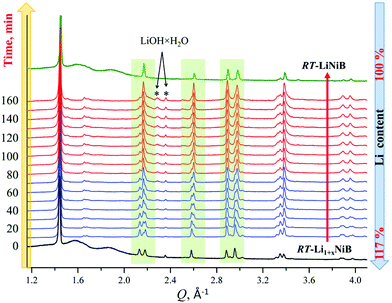
As evident from the high-resolution synchrotron powder X-ray diffraction (PXRD) data (Fig. 3), experimental PXRD patterns of RT-Li_1+xNiB and HT-Li_1+yNiB compounds are similar. Both feature an intensive peak corresponding to the interlayer distance of d ∼ 4.34–4.41 Å between the [NiB] layers (yellow-shaded, Fig. 3). In contrast, the structure of [NiB] layers in two phases is different, resulting in the difference in PXRD patterns (blue-shaded, Fig. 3).

Fig. 3 Experimental synchrotron powder X-ray diffraction patterns of RT-LiNiB [11], HT-LiNiB [11], RT-Li_1+xNiB and HT-Li_1+yNiB. The most intense characteristic peak d ∼ 4.34–4.41 Å corresponds to the distance between [NiB] layers and is common for all phases. However, compounds have different atomic arrangement within the [NiB] layers, as indicated by the different sequence of the diffraction peaks in the blue-shadowed region, an enlarged view is shown on the right.

Crystal structures

Determination of RT-Li_1+xNiB and HT-Li_1+yNiB crystal structures is challenging for several reasons: (1) extreme air-sensitivity (vide infra), (2) hydride synthesis did not yield large enough crystals suitable for laboratory single crystal X-ray diffraction; (3) the presence of light elements, Li and B, which makes X-ray data less informative, since heavier Ni atoms dominate X-ray scattering. Therefore, we used a synergistic combination of PXRD data refinement and theoretical calculations to elucidate crystal structures of RT-Li_1+xNiB and HT-Li_1+yNiB. Solving structures from PXRD data yields the positions of Ni atoms, thus the [NiB] layers (Tables S1–S6†). The structure of Li layers, including the atomic coordinates of extra-Li atoms in RT-Li_1+xNiB and HT-Li_1+yNiB, was determined using theoretical calculations.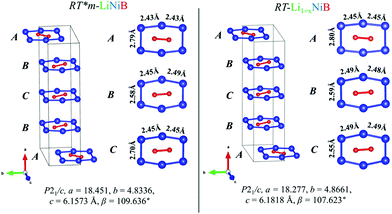

Variations of [NiB] layers. Comparison of RT-Li_1+xNiB and HT-Li_1+yNiB crystal structures with their respective parent phases RT*(m)-LiNiB and HT-LiNiB are shown in Fig. 4 and 5. Additional Li atoms neither change the topology of [NiB] layers in the case of RT-Li_1+xNiB nor the stacking sequence of [NiB] layers (Tables S1–S3†). Thus, RT-Li_1+xNiB exhibits the same space group and Wyckoff sequence of the atomic sites as RT*(m)-LiNiB (Tables 1, S1–S3†), while variation in the monoclinic β-angle is responsible for variations in the PXRD pattern (Fig. 3 and 4). The stacking sequence of [NiB] layers for both RT-Li_1+xNiB and RT-LiNiB is ABCB (Fig. 4).

Fig. 4 Comparison between [NiB] layers (ABCB stacking sequence) of RT-LiNiB and RT-Li_1+xNiB compounds. Bond distances between Ni atoms in the [Ni₆B₂] units are highlighted.

Fig. 5 Comparison between [NiB] layers in the structures of HT-LiNiB and HT-Li_1+yNiB compounds. The lower panel shows a relative shift between two adjacent [NiB] layers in the structures of HT-LiNiB and HT-Li_1+yNiB.

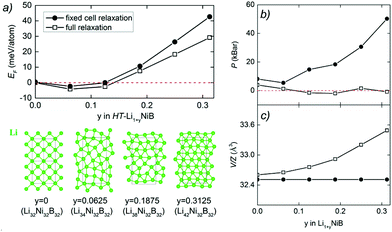
The unit cell volume of RT-Li_1+xNiB is larger than that of RT*(m)-LiNiB, consistent with the incorporation of extra Li atoms (Table 1). This increased volume is due to the longer Ni–Ni distances within the Ni₆B₂ units leading to the slightly longer b and c parameters in the structure of RT-Li_1+xNiB compared to RT*(m)-LiNiB.

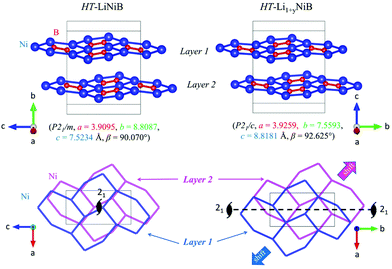
The topology of the [NiB] layers in HT-LiNiB and HT-Li_1+yNiB compounds is similar. Here the fused Ni₆B₂ units form zig-zag chains within the layers. However, the stacking of [NiB] layers differs between the two compounds, resulting in the respective change of the space group from P2₁/m to P2₁/c, as well as in a swap of the b- and c-axes (Fig. 5 and Tables 1, S4–S6†). The [NiB] planar layers in HT-LiNiB are stacked along the two-fold screw axis 2₁, e.g. b axis is a stacking direction. On the contrary, for the HT-Li_1+xNiB phase the c axis is a stacking direction, thus perpendicular to the axis 2₁. The change in the space group arises from the more pronounced relative shift between the two adjacent [NiB] layers in structure of HT-Li_1+yNiB as compared to the HT-LiNiB structure (Fig. 5).

Li chemical pressure as a driving force for structural variation. The distance between [NiB] layers in the structures of RT-Li_1+xNiB and HT-Li_1+yNiB increases only slightly compared to the parent RT-LiNiB and HT-LiNiB, d ∼ 4.34–4.41 Å, as evident from the high resolution synchrotron powder X-ray diffraction data (Fig. 3). The normalized volume per formula unit (V/Z) increases by 0.43 ų for RT-Li_1+xNiB and by 0.29 ų for HT-Li_1+yNiB compared to the respective parent compounds (Table 1). The increase of only ∼1.3% is not sufficient to presume double Li-layers in the structure of RT-Li_1+xNiB or HT-Li_1+yNiB, as in the structure of theoretically predicted Li₂NiB compound.²⁹ Since the intensity of the PXRD peaks is dominated by scattering from Ni atoms, we utilized a constrained GA (genetic algorithm) search^30,31 to shed light on the structure of Li layer in the RT-Li_1+xNiB and HT-Li_1+xNiB compounds.

Li layers in RT-Li_1+xNiB phase. A constrained GA search for the structure of the Li layers was performed while fixing the positions of Ni and B atoms to those in the experimentally determined structure (P2₁/c space group, Table 1). Since the complex “Li_1+x” packing can only be modeled by a superlattice, we performed the search on the supercell of the current lattice. The structure searching is very challenging for RT-Li_1+xNiB structure, because it already contains 48 atoms for x = 0 (i.e. Li₁₆Ni₁₆B₁₆). On the other hand, as indicated in Fig. 4, the layered structure of RT-Li_1+xNiB contains only AB- and BC-types of [NiB] stacking. Therefore, we searched for the Li layers between the AB and BC stacking types of [NiB] layers separately to reduce the computational cost. We built a smaller Li₈Ni₈B₈ lattice with only AB- or BC-type NiB layers. Two different searches with the lattices extended along b and c direction by 1 × 2 × 2 (i.e. Li_32+mNi₃₂B₃₂ with m = 1, 2, 3, 4) and 1 × 3 × 3 (i.e. Li_72+nNi₇₂B₇₂ with n = 2, 4, 6, 8,…, 18) were performed. With 1 × 2 × 2 supercell, no energetically favored structures were found. Interestingly, as shown in Fig. 6a, the search with 1 × 3 × 3 supercell revealed an energetically stable Li packing with 16.7% excess of Li compared to the RT-LiNiB parent phase.

Fig. 6 (a) Energetics of RT-Li_1+xNiB structure as a function of x. Formation energies are calculated as E_F = [E(Li_1+yNiB) − x × E(Li) − E(LiNiB)]/(3 + x), where the P2₁/c structure is used for x = 0. (b) Top views of the Li layers in the selected optimized structures are plotted. (c) Comparison of Li layer in RT-LiNiB and RT-Li_1+xNiB.

The Li layer configuration with x = 0.167 is stable in both AB-type and BC stacking types since they have the same formation energy as RT-LiNiB. Incorporation of extra Li atoms into the Li layer is accomplished by shortening of Li–Li distances to 2.6–2.8 Å, resulting in the denser hexagonal lattice (Fig. 6c) compared to RT-LiNiB (Li–Li distances ∼2.8–3.1 Å). The configurations with intermediate Li excess 0 < x < 0.167 form combinations of loose (x = 0) and dense (x = 0.167) hexagonal lattices, resulting in a locally disordered packing motif and have an excess in the formation energy in a range of 3 meV (Fig. 6a).

Li layers in HT-Li_1+yNiB phase. We performed a similar GA search of the Li layers by implementing constraints to fix the positions of Ni and B atoms as those in the experimentally determined structure of HT-Li_1+yNiB (space group P2₁/c). Only Li positions were optimized during the structure searches. The 2 × 2 × 1 supercell was used in the search with 32 Li atoms for x = 0. The number of excessive Li atoms ranges from 2 to 10, i.e. Li_32+kNi₃₂B₃₂ with k = 0, 2, 4,…10. In the constraint searches, EAM (embedded atom method³²) classical potential selected from the AGA searches was used to screen the structures, and the final structures were then relaxed by DFT. For y = 0, Li atoms form a square lattice as plotted in the lower panel of the Fig. 7. The Li layer is similar to that experimentally found for HT-LiNiB.¹¹ With the increase of Li content, Li atoms tend to have coordination numbers larger than 4, e.g. 5 or 6 (Fig. 7a). Eventually, after adding enough Li atoms, such as in Li₄₂Ni₃₂B₃₂, Li atoms form a modulated hexagonal lattice. The addition of a small amounts of Li atoms lowers the formation energy of HT-Li_1+yNiB at first (Fig. 7a), while for y > 0.125, the structure becomes less stable, even though with positive formation energies. The internal pressure induced by incorporating more Li atoms inside the structure as the function of y is plotted in Fig. 7b. If the unit cell is not allowed to expand (solid points), adding more Li atoms significantly increases this pressure for y > 0.1, again indicating the possible structural instability of HT-Li_1+yNiB with large y. Therefore, we estimate the upper limit for y in HT-Li_1+yNiB to be 0.125.

Fig. 7 (a) Energetics of HT-Li_1+yNiB structure as a function of y. Formation energies are calculated as E_F = [E(Li_1+yNiB) − y × E(Li) − E(LiNiB)]/(3 + y), where the P2₁/m structure is used for y = 0. Top views of the Li layers in the optimized structures are plotted in the lower panel of (a). (b) Pressure of the HT-Li_1+yNiB structure calculated as the function of y. (c) Volume per formula unit of the HT-Li_1+yNiB generated structure calculated as the function of y. Note that here a 2 × 2 × 1 supercell was used. Structure relaxations were carried out for two scenarios: unit cell fixed to the 2 × 2 × 1 supercell during relaxation (solid circles) and full relaxation (hollow squares).

Overall structure. Careful analysis of synchrotron powder XRD patterns of the RT-Li_1+xNiB or HT-Li_1+yNiB compounds reveals the plethora of the low-intensity Bragg peaks (Fig. S3†). Part of these diffraction peaks can be accounted by superstructures, obtained by multiplying of the unit cell parameters by a factor of 2 or 3 and simultaneous lowering of the symmetry to triclinic: a_superstr = a, b_superstr = b, c_superstr = 3 × c, Z_superstr = 3 × Z for RT-Li_1+xNiB; a_superstr = 2 × a, b_superstr = 2 × b, c_superstr = c, Z_superstr = 4 × Z for HT-Li_1+yNiB (Tables 1 and S1–S6, cif files are provided in ESI†). We utilized these unit cells and created the structural models with [NiB] layers obtained from the PXRD data and Li layers found computationally, as described above. Rietveld refinement of these models resulted in a satisfactory fit (Tables S1, S4, Fig. S4–S11†), allowing for fitting of low intensity diffraction peaks while accounting for additional Li atoms between [NiB] layers. The obtained structural models are consistent with denser packing of Li atoms within the layer. As it is highlighted in Fig. 8, the denser packing of Li atoms results in 2 or 3 Li atoms per each Ni₆B₂ hexagonal unit, while solely 2 Li atoms per Ni₆B₂ are present in RT-LiNiB and HT-LiNiB parent structures (Fig. 8). This is accompanied by shortening of the interatomic distances between Li atoms. We also note that not all low intensity diffraction peaks can be accounted by the triclinic supercell (Fig. S3†), and the real structure of RT-Li_1+xNiB or HT-Li_1+yNiB might be even more complex (modulated or even larger cell), however the present model agrees fairly well with PXRD data, has reasonable bond distances and accounts for extra Li atoms in the structures. Most Li–B bonds in the structures of RT-Li_1+xNiB and HT-Li_1+yNiB compounds have the same length as in the parent compounds (d_Li–B ∼ 2.3–2.4 Å) (Fig. S12†). However, due to the distortion of Li-layers in the Li-enriched RT-Li_1+xNiB and HT-Li_1+yNiB compounds (Fig. 6 and 7), some of the Li atoms have longer distances to the nearest B atoms (2.4–2.6 Å).

Fig. 8 Comparison of RT-Li_1+xNiB and HT-Li_1+yNiB with the RT-LiNiB and HT-LiNiB parents. Light green and blue highlighted areas emphasizes denser packing of Li atoms in the case of RT-Li_1+xNiB and HT-Li_1+yNiB, leading to 3 Li atoms per each Ni₆B₂ distorted hexagon.

Temperature stability, reactivity and phase transformations

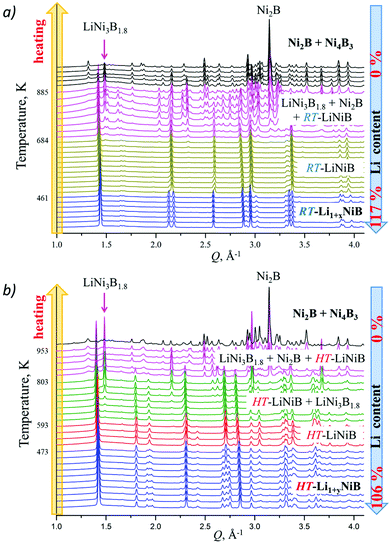
High-temperature synchrotron powder X-ray diffraction (HT-PXRD) was used to study the thermal stability of RT-Li_1+xNiB and HT-Li_1+yNiB. Samples were vacuum-sealed into silica capillaries for high temperature PXRD experiments. Upon heating Li is gradually “leached” from the structure, presumably reacting with silica. This leads to RT-Li_1+xNiB and HT-Li_1+yNiB transformation into RT-LiNiB and HT-LiNiB at 461 and 473 K, respectively (Fig. 9a and b). This again confirms the presence of extra Li atoms in RT-Li_1+xNiB and HT-Li_1+yNiB compared to their parent compounds. With a further increase in temperature above 684 K, RT-LiNiB transforms to Li-depleted LiNi₃B_1.8 phase¹⁰ and binary Ni₂B. Between 684 K and 885 K, all three phases, RT-LiNiB, LiNi₃B_1.8 and binary Ni₂B, are present. Above ∼885 K, binary nickel borides Ni₂B, Ni₄B₃, Ni₃B are the major products.

Fig. 9 High-temperature in situ powder X-ray diffraction patterns showing the equilibria in the Li–Ni–B system. With the increase of temperature Li is gradually “leached” from the compounds because of reaction with capillary material (SiO₂) involving (a) RT-Li_1+xNiB → RT-LiNiB → LiNi₃B_1.8 → Ni₂B and Ni₄B₃ transformations; (b) HT-Li_1+yNiB → HT-LiNiB → LiNi₃B_1.8 → Ni₂B and Ni₄B₃ transformations.

Interestingly, HT-PXRD data of the HT-LiNiB polymorph (Fig. S13b†) shows considerable structural distortion, which was refined in the same structure type (same space group P2₁/m and Wyckoff sequence) (Table S7†). The distorted structure features substantially deformed Ni₆B₂ units within [NiB] layers and the relative shift of [NiB] layers (Fig. S13c and d†). This distorted structure was only observed in in situ PXRD experiments, while attempts to quench it from ∼620 K were not successful. With further increase in temperature, the HT-LiNiB phase decomposes into Li-depleted LiNi₃B_1.8, and finally, binary Ni borides similarly to RT-LiNiB polymorph (Fig. S13†).

Air stability of RT-Li_1+xNiB and HT-Li_1+yNiB. In addition to the temperature, the transition between RT-Li_1+xNiB and HT-Li_1+yNiB compounds and their respective parents RT-LiNiB and HT-LiNiB can be driven by oxidation with oxygen in air. HT-Li_1+xNiB, if exposed to air, rapidly transforms to the HT-LiNiB phase (Fig. S14†). However, decomposition of the RT-Li_1+xNiB phase in air is considerably slower (Fig. 10). The higher reactivity of HT-Li_1+xNiB might originate from the considerably distorted Li-layer in the structure as well longer Li–B bonds, compared to the RT-Li_1+xNiB (Fig. 6, 7 and Fig. S12†). Powder X-ray diffraction patterns of RT-Li_1+xNiB show its evolution in air is completed within 160 min (Fig. 10). The process is relatively fast during the first ∼1 hour (patterns in blue) and slows down afterwards. The last acquired powder pattern (at 160 min) contains mostly the RT-LiNiB compound with traces of the initial RT-Li_1+xNiB. Also, the fraction of LiOH·H₂O increases with the exposure time, suggesting that the overall process can be described as follows: Li_1+xNiB + O₂ + H₂O → LiNiB + xLiOH·H₂O, which again confirms the presence of extra-Li in RT-Li_1+xNiB and HT-Li_1+yNiB compounds.

Fig. 10 X-ray diffraction patterns showing evolution of RT-Li_1+xNiB phase (bottom, black) upon expose to air in 0–160 min range. Reference powder pattern of RT-LiNiB compound (top, green) is provided for comparison.

Solid-state NMR spectroscopy

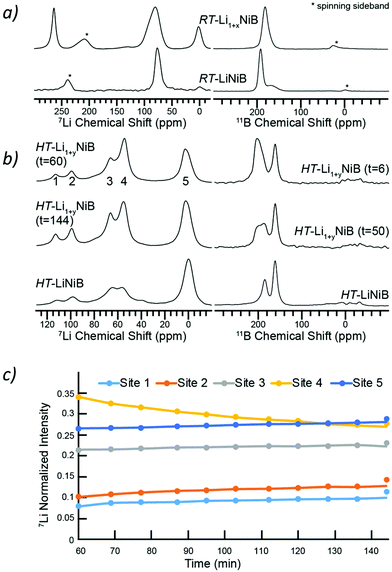
To further shed light on the evolution of Li and B coordination environment upon incorporation of extra-Li in the structures of RT-Li_1+xNiB and HT-Li_1+yNiB compounds, ⁷Li and ¹¹B solid-state magic angle spinning (MAS) NMR spectra were collected (Fig. 11a). The ⁷Li MAS NMR spectra of RT-Li_1+xNiB compound have two major peaks at ∼265 and ∼80 ppm and a minor one at ∼0 ppm. The peak at 0 ppm originates from diamagnetic impurity phases, such as Li₂O (2.8 ppm), LiOH·H₂O (0.4 ppm), or LiOH (1.3 ppm), and is also present in ⁷Li MAS NMR spectrum of RT-LiNiB phase.¹¹ The peak at 265 ppm is most likely due to a Li metal impurity,³³ as a result of the significant excess of LiH required for synthesis and its further decomposition upon heating. The peak at ∼80 ppm is attributed to the RT-Li_1+xNiB phase and is consistent with a single type of Li site expected in the structure. It is slightly positively shifted compared to the peak at ∼75 ppm for RT-LiNiB phase but within the range of ⁷Li chemical shifts in other Li-containing intermetallics.^9,11 The slight increase in the ⁷Li chemical shift for RT-Li_1+xNiB as compared to RT-LiNiB can likely be attributed to the subtle differences in the Li coordination environment in the two compounds. The increased width of the ⁷Li peak may be a result of the increased complexity of RT-Li_1+xNiB structure, where extra Li atoms are incorporated between the [NiB] layers, leading to a variety of local ⁷Li environments and distribution of shifts. The peak at ∼80 pm is shifted to higher frequencies compared to the diamagnetic signal, indicative of Knight shift from conduction electrons, and thus metallic behavior is expected for RT-Li_1+xNiB phase. The ⁷Li MAS NMR spectra of HT-Li_1+yNiB is akin to HT-LiNiB and is distinctive from that of RT-Li_1+xNiB and RT-LiNiB. There are two intense peaks at ∼55–65 ppm and two peaks with lower intensity at ∼95 and 110 ppm, in addition to the peak at ∼0 ppm (diamagnetic impurity, e.g. Li₂O). Multiple peaks with positive chemical shifts are expected for HT-Li_1+xNiB, since it would be consistent with its metallic nature and a structure model with three Li sites (2a, 2c, 4e, P2₁/c).

Fig. 11 (a) ⁷Li and ¹¹B MAS solid-state NMR spectra of RT-Li_1+xNiB in comparison to RT-LiNiB phase. (b) ⁷Li and ¹¹B MAS solid-state NMR spectra of HT-Li_1+yNiB in comparison to HT-LiNiB phase. The time in minutes after starting the magic angle spinning is indicated. (c) Variation in intensities of characteristic peaks (1, 2, 3, 4, 5) with time.

The NMR spectroscopy data also confirms the high reactivity of HT-Li_1+yNiB compound, which rapidly transforms in the air to HT-LiNiB compound (Fig. S14†). Fig. 11b shows the evolution of NMR spectra of a HT-Li_1+xNiB sample with time while the sample is undergoing magic angle spinning in a 2.5 mm rotor. The nitrogen gas used for spinning is approximately 99.9% pure and the 2.5 mm rotors are not gas-tight. Hence the reaction is likely driven by the slow diffusion of residual oxygen and water in the MAS gas into the sample. There are clear variations in intensities of five observed ⁷Li peaks, likely because of the changes in Li local environment between the layers. Li is also partly deintercalated and forms Li₂O, explaining the increased intensity of the 5^th peak. During the course of MAS experiments, the ¹¹B solid-state NMR spectra of HT-Li_1+yNiB become more similar in appearance to HT-LiNiB.

The ¹¹B solid-state NMR spectrum for RT-Li_1+xNiB and HT-Li_1+yNiB is consistent with their metallic behavior. The 150–220 ppm range of ¹¹B chemical shifts is similar to the chemical shift observed for RT-LiNiB and HT-LiNiB compounds¹¹ and other metallic borides and borocarbides.^9,34,35 Boron atoms in all RT-Li_1+xNiB, RT-LiNiB, HT-LiNiB, HT-Li_1+yNiB layered phases form B–B pairs, which are further surrounded by 6 Ni atoms (Fig. 1, 4 and 5). However, the different topology of the layers, as well as differences in boron coordination by Li, likely explains the observed differences in the ¹¹B solid-state NMR spectra.

Magnetic properties

Temperature dependence of the molar magnetic susceptibility in the range 5–300 K of RT-Li_1+xNiB and HT-Li_1+yNiB (Fig. S15†) is consistent with both phases being temperature-independent Pauli paramagnets. No magnetic ordering was observed down to 5 K. The field dependence of the magnetization in the same temperature range (Fig. S15†) at high magnetic field (10 000 Oe–50 000 Oe) is linear with no tendency for saturation, which is again consistent with temperature independent paramagnetism. Small deviation from linearity of the field dependence of the magnetization at low magnetic field (0–10 000 Oe, see Fig. S15†) could be attributed to some magnetic moment bearing impurity, concentration of which is under the detection limit of X-ray analysis (below 1%). The intrinsic susceptibility values were estimated to be in the range of 0.7–1.2 × 10⁻⁴ emu mol⁻¹ (Fig. S15†). The parent compounds RT-LiNiB and HT-LiNiB also exhibit temperature-independent paramagnetism.¹¹ Thus, incorporation of additional Li atoms does not affect the magnetic properties. This is in stark contrast to the partial deintercalation of Li from paramagnetic LiNiB, inducing magnetic ordering in Li_1−δNiB.¹²

Experimental

Synthesis

Starting materials for the synthesis were powders of lithium hydride (AlfaAesar, 99.4%), nickel (AlfaAesar, 99.996%), and boron (AlfaAesar, amorphous & crystalline, 98%). All manipulations of the starting materials and samples were performed in an argon-filled glovebox with p(O₂) < 1 ppm. Powders of the starting materials (total mass = 0.3 g) were weighted in LiH : Ni : B = 1.9 : 1 : 1.15 (RT-Li_1+xNiB) and 1.4 : 1 : 1.15 (HT-Li_1+yNiB) molar ratios and loaded into polystyrene grinding vial set with slip-on cap. These loading compositions were determined empirically to get the highest yield of the target phases. The vials were then sealed into double-sided polypropylene bag under argon atmosphere and brought out for the powder mixing/milling using ball-mill (8000M MIXER/MILL) for 18 min (vials were enclosed in poly-bags during the process to ensure O₂-free environment). Afterward, freshly prepared fine powders were loaded in Ta tubes inside argon-filled glovebox. The metal containers were sealed by arc-melting and placed into silica reactors equipped with Swagelok safety check valves to prevent over-pressurization of the reactors due to the release of hydrogen gas during the heat treatment. The silica reactors were evacuated down to 4 × 10⁻⁵ Bar and slowly (1.25 K min⁻¹) heated from room temperature to 1173 K, held at that temperature for 12 hours and quenched into cold water for the preparation of HT-Li_1+yNiB phase or cooled to room temperature by switching off furnace in the case of RT-Li_1+xNiB phase. The second annealing of the manually ground sample loaded to the Ta tube using the same temperature profile was necessary to obtain RT-Li_1+xNiB, otherwise RT-LiNiB compound forms. The synthesized compounds are air and moisture sensitive.

Powder X-ray diffraction

The purity of polycrystalline samples was checked using Rigaku MiniFlex600 powder diffractometer with Cu Kα radiation (λ = 1.54051 Å) and Ni-K_β filter. Data were collected in zero-background plate holder for air-sensitive samples at room temperature. Phase analysis was performed using the PDF-2 database incorporated into PDXL2 program software.³⁶ Powder diffractograms during controlled samples oxidation in the air were collected using open zero-background plate holder with ∼10 min time intervals.

Crystal structure determination from synchrotron powder X-ray diffraction data

High-resolution synchrotron powder diffraction data were collected at beamline 11-BM-B Advanced Photon Source (APS), Argonne National Laboratory at 295 K and 100 K and λ = 0.412815 Å for a sample of RT-Li_1+xNiB and λ = 0.412818 Å for a sample of HT-Li_1+yNiB. Data were collected at ambient pressure.

The unit cell symmetry, metrics, and atomic arrangement in the structures of RT-Li_1+xNiB and HT-Li_1+yNiB were obtained using program FOX for the ab initio structure determination from powder diffraction.³⁷ After indexing, positions of heavy Ni atoms were determined and further refined in the triclinic space group P1. After the atomic coordinates of heavy Ni atoms were found, the structure was analyzed with the program Platon,³⁸ and the correct space group was determined. The residual electron density peaks were assigned to tentative B and Li atomic positions based on the analysis of interatomic distances.

RT-Li_1+xNiB. Indexing of the high-resolution synchrotron powder X-ray diffraction data using program FOX³⁷ resulted the P-monoclinic unit cell (space group P2₁/c, a = 18.277, b = 4.8660, c = 6.1818 Å, β = 107.623°, V = 524.00 ų at 295 K, Z = 16). Ni atoms occupy four 4e sites. Further refinements showed residual electron density peaks, which were assigned to be B in four 4e sites and Li in four 4e sites based on the analysis of interatomic distances.

HT-Li_1+yNiB. Indexing of the high-resolution synchrotron powder X-ray diffraction data using program FOX³⁷ resulted in P-monoclinic unit cell (space group P2₁/c, Z = 8, a = 3.92591, b = 7.5593, c = 8.8181 Å, β = 92.6245, V = 261.42 ų). Ni atoms occupy two 4e sites. Further refinements showed residual electron density peaks assigned to be B in 4e, 4e, and Li occupying 2a, 2c, 4e sites based on the analysis of interatomic distances.

Rietveld refinement with the GSAS II software package³⁹ was further performed using the derived structural models. The profile parameters, background parameters, zero shift, and cell parameters were refined first. The background was fitted using a shifted 24-points linear interpolation function, a pseudo-Voigt function was applied to generate the profile shape. Atomic coordinates of Ni atoms were refined, while atomic coordinates of light B and Li atoms were fixed to the values obtained computationally. Experimental details and crystallographic data are compiled in Tables S1–S3, Fig. S4–S7† (RT-Li_1+xNiB), and Tables S4–S6, Fig. S8–S11† (HT-Li_1+yNiB). The final refinements of the structures were performed with isotropic displacement parameters for all atoms. Crystal structures were visualized using the program VESTA 3.⁴⁰

In situ high-temperature synchrotron powder X-ray diffraction (HT-PXRD). Transformation of the RT-LiNiB, HT-LiNiB, RT-Li_1+xNiB, and HT-Li_1+yNiB compounds at elevated temperatures was evaluated from in situ high-temperature synchrotron X-ray powder diffraction data collected at beamline 17-BM-B APS (λ = 0.24158 Å). Powdered samples were filled into 0.7 mm outer diameter thick-walled (0.1 mm) silica capillaries and sealed under vacuum. Capillaries were mounted on a standard base equipped with two coiled resistance heaters. The further details of experimental setup can be found elsewhere.⁴¹ High energy synchrotron X-ray diffraction spectra were collected in the temperature range 295–1000 K.

Solid-state NMR spectroscopy. ⁷Li and ¹¹B solid state NMR spectra were measured on a Bruker widebore 9.4 T (v_1H = 400 MHz) NMR magnet equipped with a Bruker Avance III HD spectrometer. All spectra were acquired using a 2.5 mm triple resonance MAS probe. Samples were diluted to approximately 50 weight% in powdered polyfluoroethylene to minimize conductivity effects and packed into MAS rotors while still under inert atmosphere. The MAS rate was 25 kHz in all cases.

Magnetic properties. Magnetic measurements were performed on polycrystalline samples (m = 50 mg), which were loaded under an inert atmosphere in EPR quartz tubes and sealed under vacuum. The data were collected using a Quantum Design MPMS XL and MPMS3 SQUID Magnetometer DC. Magnetic susceptibility was measured in an applied field of 1000 Oe, in the 5–300 K range. Field-dependent measurements were carried out at 2 K, 5 K and 300 K.

Computational methods. The crystal structure searches were performed using the adaptive genetic algorithm (AGA).^30,31 AGA integrates auxiliary interatomic potentials and first-principles calculations in an adaptive manner to ensure high efficiency and accuracy. Interatomic potentials based on the embedded-atom method (EAM)³² were chosen as the auxiliary classical potentials to describe the Li–Ni–B system (see ref. 11 for more details). The packing of Li atoms in RT-Li_1+xNiB and HT-Li_1+yNiB were determined using constraint genetic algorithm (GA) searches by fixing the atomic positions on the NiB layers. During the searches, no symmetry constraint was applied. The EAM potential obtained from the AGA search was also used to screen the high-energy structures, the final structures from constraint GA were relaxed and evaluated by first-principles calculations.

First-principles calculations were carried out using the density functional theory (DFT) within a generalized gradient approximation (GGA) of the exchange–correlation functional as implemented in the VASP code.^42,43 The projector augmented-wave method⁴⁴ was used to describe the valence configuration: 1s²2s¹ for Li, 3d⁸4s² for Ni, and 2s²2p¹ for B. The GGA exchange–correlation energy functional parametrized by Perdew, Burke, and Ernzerhof was used.⁴⁵ A plane-wave basis was used with a kinetic energy cutoff of 650 eV. The Monkhorst–Pack's scheme⁴⁶ was adopted for Brillouin zone sampling using a k-point grid with a spacing of 2π × 0.033 Å⁻¹, and the ionic relaxations stopped when the forces on every atom became smaller than 0.01 eV Å⁻¹.

Conclusions

Li chemical pressure is a driving force for the formation of RT-Li_1+xNiB and HT-Li_1+yNiB, which accommodate up to 16.7% and 12.5% excess Li into their structure compared to their parent compounds RT-LiNiB and HT-LiNiB. The crystal structures of RT-Li_1+xNiB and HT-Li_1+yNiB compounds are similar to that of RT-LiNiB and HT-LiNiB, built up from alternating Li layers with hexagonal or squared motif respectively, and [NiB] layers. The complex Li environments in layers of these two new compounds were determined using DFT methods, while subtle variations in the [NiB] layers were elucidated from synchrotron powder X-ray diffraction. Deintercalation of Li from the [NiB] layers was observed at elevated temperatures resulting in the gradual “leaching” of Li from the layers of these Li-enriched compounds and their subsequent transformation into their parent phases: RT-Li_1+xNiB → RT-LiNiB at 461 K and HT-Li_1+yNiB → HT-LiNiB at 473 K. Upon further heating decomposition into LiNi₃B_1.8 and finally, into binary nickel borides (∼900 K) takes place. Upon oxidation in air at room temperature, both RT-Li_1+xNiB and HT-Li_1+yNiB phases slowly release Li and transform to RT-LiNiB and HT-LiNiB compounds, respectively. Controlled oxidation and deintercalation as a route of further modification of layered LiNiB structures is a subject of future investigation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the National Science Foundation (DMR-1944551) CAREER award is gratefully acknowledged. A. J. R. and S. L. C. (NMR spectroscopy) and P. C. C. were supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. The Ames Laboratory is operated for the U.S. Department of Energy by Iowa State University under contract #DE-AC02-07CH11358. X. Z., F. Z., and C. Z. W. were supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division including a grant of computer time at the National Energy Research Scientific Computing Centre (NERSC) in Berkeley, CA. Y. S. was supported by NSF Awards No. EAR-1918134 and No. EAR-1918126. K. M. H. was supported by NSF Awards No. EAR-1918134. R. A. R was supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF4411. Use of the Advanced Photon Source at Argonne National Laboratory was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under contract no. DE-AC02-06CH11357.

References

1. W. Jung, Ternäre Phasen im System Lithium-Nickel-Bor, Naturwissenschaften, 1976, 63, 246.
2. W. Jung, Die Kristallstrukturen von Li₃Ni₂₀B₆ und Li∼₃Ni₁₆B∼₈, Z. Kristallogr., 1980, 151, 113–120.
3. W. Jung, Darstellung und Kristallstruktur von MgNi_2.5B₂ und Li_1.2Ni_2.5B₂, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1977, 32, 1371–1374.
4. T. Yi, S. Chen, S. Li, H. Yang, S. Bux, Z. Bian, N. A. Katcho, A. Shakouri, N. Mingo, J. P. Fleurial, N. D. Browning and S. M. Kauzlarich, Synthesis and characterization of Mg₂Si/Si nanocomposites prepared from MgH₂ and silicon, and their thermoelectric properties, J. Mater. Chem., 2012, 22, 24805–24813.
5. X. Ma, F. Xu, T. M. Atkins, A. M. Goforth, D. Neiner, A. Navrotsky and S. M. Kauzlarich, A versatile low temperature synthetic route to Zintl phase precursors: Na₄Si₄, Na₄Ge₄ and K₄Ge₄ as examples, Dalton Trans., 2009, 10250–10255.
6. J. V. Zaikina, M. Batuk, A. M. Abakumov, A. Navrotsky and S. M. Kauzlarich, Facile synthesis of Ba_1−xK_xFe₂As₂ superconductors via hydride route, J. Am. Chem. Soc., 2014, 136, 16932–16939.
7. T. Cox, V. Gvozdetskyi, B. Owens-Baird and J. Zaikina, Rapid phase screening via hydride route: A discovery of K_8−x,Zn_18+3xSb₁₆, Chem. Mater., 2018, 30, 8707–8715.
8. V. Gvozdetskyi, B. Owens-Baird, S. Hong and J. Zaikina, Materials, 2019, 30, 2–14.
9. V. Gvozdetskyi, M. P. Hanrahan, R. A. Ribeiro, T. Kim, L. Zhou, A. J. Rossini, P. C. Canfield and J. V. Zaikina, A hydride route to ternary alkali metal borides: a case study of lithium nickel borides, Chem. – Eur. J., 2019, 25, 4123–4135.
10. V. Gvozdetskyi, B. Owens-Baird, S. Hong, T. Cox, G. Bhaskar, C. Harmer, Y. Sun, F. Zhang, C. Zh. Wang, K.-M. Ho and J. V. Zaikina, From NaZn₄Sb₃ to HT-Na_1−xZn_4−ySb₃: Panoramic hydride synthesis, structural diversity, and thermoelectric properties, Chem. Mater., 2019, 31, 8695–8707.
11. V. Gvozdetskyi, G. Bhaskar, M. Batuk, X. Zhao, R. Wang, S. Carnahan, M. Hanrahan, R. Ribeiro, P. Canfield, A. Rossini, C.-Z. Wang, K.-M. Ho, J. Hadermann and J. V. Zaikina, Computationally driven discovery of a family of layered LiNiB polymorphs, Angew. Chem., Int. Ed., 2019, 58, 15855–15862.
12. G. Bhaskar, V. Gvozdetskyi, M. Batuk, K. Wiaderek, Y. Sun, R. Wang, C. Zhang, S. L. Carnahan, X. Wu, R. A. Ribeiro, S. L. Bud'ko, P. C. Canfield, W. Huang, A. J. Rossini, C.-Zh. Wang, K.-M. Ho, J. Hadermann and J. V. Zaikina, Topochemical deintercalation of Li from layered LiNiB: towards 2D MBene, manuscriptunder review, 2020.
13. M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Two–Dimensional Nanocrystals Produced by Exfoliation of Ti₃AlC₂, Adv. Mater., 2011, 23, 4248–4253.
14. M. Alhabeb, K. Maleski, B. Anasori, P. Lelyukh, L. Clark, S. Sin and Y. Gogotsi, Guidelines for synthesis and processing of two-dimensional titanium carbide (Ti₃C₂T_x MXene), Chem. Mater., 2017, 29, 7633–7644.
15. Y. Zhang, W. Tang, R. Zhan, H. Liu, H. Chen, J. Yang and M. Xu, An N-doped porous carbon/MXene composite as a sulfur host for lithium–sulfur batteries, Inorg. Chem. Front., 2019, 6, 2894–2899.
16. J. L. Hart, K. Hantanasirisakul, A. C. Lang, B. Anasori, D. Pinto, Y. Pivak, J. T. van Omme, S. J. May, Y. Gogotsi and M. L. Taheri, Control of MXenes electronic properties through termination and intercalation, Nat. Commun., 2019, 10, 522.
17. M. Zhang, X. Chen, J. Sui, B. S. Abraha, Y. Li, W. Peng, G. L. Zhang, F. Zhang and X. Fan, Improving the performance of a titanium carbide MXene in supercapacitors by partial oxidation treatment, Inorg. Chem. Front., 2020, 7, 1205–1211.
18. J. Pang, R. G. Mendes, A. Bachmatiuk, L. Zhao, H. Q. Ta, T. Gemming, H. Liu, Z. Liu and M. Rummeli, 3D flexible, conductive, and recyclable Ti₃C₂T_x MXene-Melamine foam for high-areal-capacity and long-lifetime alkali-metal anode, Chem. Soc., 2019, 48/1, 1–408.
19. G. Du, M. Tao, W. Gao, Y. Zhang, R. Zhan, S. Bao and M. Xugg, TiS₂ nanosheets for efficient electrocatalytic N₂ fixation to NH₃ under ambient conditions, Inorg. Chem. Front., 2019, 6, 1986–1989.
20. S. Chen, Y. Xiang, W. Xu and C. Peng, A novel MnO₂/MXene composite prepared by electrostatic self-assembly and its use as an electrode for enhanced supercapacitive performance, Inorg. Chem. Front., 2019, 6, 199–208.
21. M. Khazaei, J. Wang, M. Estili, A. Ranjbar, S. Suehara, S. Arai, K. Esfarjani and S. Yunoki, Novel MAB phases and insights into their exfoliation into 2D MBenes, Nanoscale, 2019, 11, 11305–11314.
22. Z. Jiang, P. Wang, X. Jiang and J. Zhao, MBene (MnB): a new type of 2D metallic ferromagnet with high Curie temperature, Nanoscale Horiz., 2018, 3, 335–341.
23. Z. Guo, J. Zhou and Z. Sun, New two-dimensional transition metal borides for Li ion batteries and electrocatalysis, J. Mater. Chem. A, 2017, 5, 23530–23535.
24. T. Bo, P. F. Liu, J. Zhang, F. Wang and B. T. Wang, Tetragonal and trigonal Mo₂B₂ monolayers: two new low-dimensional materials for Li-ion and Na-ion batteries, Phys. Chem. Chem. Phys., 2019, 21, 5178–5188.
25. H. Nishino, T. Fujita, N. Cuong, S. Tominaka, M. Miyauchi, S. Limura, A. Hirata, N. Umezawa, S. Okada, E. Nishibori, A. Fujino, T. Fujimori, S. Ito, J. Nakamura, H. Hosono and T. Kondo, Formation and Characterization of Hydrogen Boride Sheets Derived from MgB₂ by Cation Exchange, J. Am. Chem. Soc., 2017, 139, 13761–13769.
26. L. T. Alameda, P. Moradifar, Z. P. Metzger, N. Alem and R. E. Schaak, Topochemical deintercalation of Al from MoAlB: stepwise etching pathway, layered intergrowth structures, and two-dimensional MBene, J. Am. Chem. Soc., 2018, 140, 8833–8840.
27. L. T. Alameda, R. W. Lord, J. A. Barr, P. Moradifar, Z. P. Metzger, B. C. Steimle, C. F. Holder, N. Alem, S. B. Sinnott and R. E. Schaak, Multi-Step Topochemical pathway to metastable Mo₂AlB₂ and related two-dimensional nanosheet heterostructures, J. Am. Chem. Soc., 2019, 141, 10852–10861.
28. J. Wang, T. N. Ye, Y. Gong, J. Wu, N. Miao, T. Tada and H. Hosono, Discovery of hexagonal ternary phase Ti₂InB₂ and its evolution to layered boride TiB, Nat. Commun., 2019, 10, 2284.
29. R. Wang, Y. Sun, V. Gvozdetskyi, X. Zhao, F. Zhang, L.-H. Xu, J. V. Zaikina, Z. Lin, C.-Z. Wang and K.-M. Ho, Theoretical search for possible Li–Ni–B crystal structures using an adaptive genetic algorithm, J. Appl. Phys., 2020, 127, 094902.
30. S. Q. Wu, M. Ji, C. Z. Wang, M. C. Nguyen, X. Zhao, K. Umemoto, R. M. Wentzcovitch and K. M. Ho, An adaptive genetic algorithm for crystal structure prediction, J. Phys.: Condens. Matter, 2014, 26, 035402.
31. X. Zhao, M. C. Nguyen, W. Y. Zhang, C. Z. Wang, M. J. Kramer, D. J. Sellmyer, X. Z. Li, F. Zhang, L. Q. Ke, V. P. Antropov and K. M. Ho, Exploring the Structural Complexity of Intermetallic Compounds by an Adaptive Genetic Algorithm, Phys. Rev. Lett., 2014, 112, 045502.
32. M. S. Daw and M. I. Baskes, Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals, Phys. Rev. Lett., 1983, 50, 1285–1288.
33. R. Bhattacharyya, B. Key, H. Chen, A. S. Best, A. F. Hollenkamp and C. P. Grey, In situ NMR observation of the formation of metallic lithium microstructures in lithium batteries, Nat. Mater., 2010, 9, 504–510.
34. D. Koumoulis, J. P. Scheifers, R. S. Touzani, B. P. T. Fokwa and L. S. Bouchard, Pseudogap formation and vacancy ordering in the new perovskite boride Zr₂Ir₆B, Acta Mater., 2016, 120, 32–39.
35. R. E. J. Sears, ¹¹B chemical shifts and quadrupole coupling constants in the alkaline–earth hexaborides, J. Chem. Phys., 1982, 76, 5651–5652.
36. PDXL: Integrated X-ray powder diffraction software, Version 2.8.1.1, Rigaku, 2018.
37. V. Favre-Nicolin and R. Cerny, FOX, “free objects for crystallography”: a modular approach to ab initio structure determination from powder diffraction, J. Appl. Crystallogr., 2002, 35, 734–743.
38. A. L. Spek, Structure validation in chemical crystallography, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155.
39. B. H. Toby and R. B. Von Dreele, GSAS-II: the genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46, 544–549.
40. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.
41. P. J. Chupas, K. W. Chapman, C. Kurtz, J. C. Hanson, P. L. Lee and C. P. Grey, A versatile sample-environment cell for non-ambient X-ray scattering experiments, J. Appl. Crystallogr., 2008, 41, 822–824.
42. G. Kresse and J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
43. G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
45. P. E. Bloechl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
46. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.

---

Footnote

† Electronic supplementary information (ESI) available: Tables with crystallographic information, figures with PXRD patterns, Rietveld refinements plots, magnetic susceptibility plots. CCDC 2031377, 2031379, 2031381, 2031382, 2031386, 2031387, 2031389, 2031390. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0qi01150a

---