Charge-storage mechanism of highly defective NiO nanostructures on carbon nanofibers in electrochemical supercapacitors†
Willian G.
Nunes
 a,
Andre N.
Miranda
a,
Andre N.
Miranda
 b,
Bruno
Freitas
b,
Bruno
Freitas
 a,
Rafael
Vicentini
a,
Rafael
Vicentini
 a,
Aline C.
Oliveira
c,
Gustavo
Doubek
a,
Aline C.
Oliveira
c,
Gustavo
Doubek
 b,
Renato G.
Freitas
*c,
Leonardo M.
Da Silva
b,
Renato G.
Freitas
*c,
Leonardo M.
Da Silva
 *d and
Hudson
Zanin
*d and
Hudson
Zanin
 *a
*a
aAdvanced Energy Storage Division, Center for Innovation on New Energies, Carbon Sci-Tech Labs, School of Electrical and Computer Engineering, University of Campinas, Av. Albert Einstein 400, Campinas, SP 13083-852, Brazil. E-mail: hzanin@unicamp.br
bAdvanced Energy Storage Division, Center for Innovation on New Energies, Laboratory of Advanced Batteries, University of Campinas, School of Chemical Engineering, Av. Albert Einstein 500, Campinas, SP 13083-852, Brazil
cDepartment of Chemistry, Laboratory of Computational Materials, Federal University of Mato Grosso, ICET-UFMT, 78060-900, Cuiabá, MT, Brazil. E-mail: rgfreitas@ufmt.br
dDepartment of Chemistry, Laboratory of Fundamental and Applied Electrochemistry, Federal University of Jequitinhonha e Mucuri's Valley, Rodovia MGT 367, km 583, 5000, Alto da Jacuba, 39100-000, Diamantina, MG, Brazil. E-mail: lsilvamorais@hotmail.com
First published on 1st April 2021
Abstract
An electrode composed of highly defective nickel oxide (NiO) nanostructures supported on carbon nanofibers (CNFs) and immersed in an Li+-based aqueous electrolyte is studied using Raman spectroscopy under dynamic polarization conditions to address the charge-storage phenomenon. By this operando technique, the formation of Li2SO4·H2O during the discharge process is verified. At the same time, we observed the phase transformation of NiO to NiOOH. The Ni(OH)2/NiOOH redox couple is responsible for the pseudocapacitive behavior with intercalation of cationic species in the different Ni structures. A ‘substitutive solid-state redox reaction’ is proposed to represent the amphoteric nature of the oxide, resulting in proton intercalation, while the insertion of Li+ occurs to a less extent. The electrode material exhibits outstanding stability with 98% coulombic efficiency after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 charge–discharge cycles. The excellent electrode properties can be ascribed to a synergism between CNFs and NiO, where the carbon nanostructures ensured rapid electron transport from the hydrated nickel nanoparticles. The NiO@CNF composite material is a promising candidate for future applications in aqueous-based supercapacitors. DFT simulation elucidates that compressive stress and Ni-site displacement lead to a decrease up-to 3.5-fold on the electron density map located onto the Ni-atom, which promotes NiO/Ni(OH)2/NiOOH transition.
000 charge–discharge cycles. The excellent electrode properties can be ascribed to a synergism between CNFs and NiO, where the carbon nanostructures ensured rapid electron transport from the hydrated nickel nanoparticles. The NiO@CNF composite material is a promising candidate for future applications in aqueous-based supercapacitors. DFT simulation elucidates that compressive stress and Ni-site displacement lead to a decrease up-to 3.5-fold on the electron density map located onto the Ni-atom, which promotes NiO/Ni(OH)2/NiOOH transition.
1. Introduction
Modern batteries show a high specific energy (A h g−1), while supercapacitors (SCs) are mainly characterized by their high specific power (W kg−1). Therefore, these devices complement each other in several different applications, i.e., the cooperation between supercapacitors and batteries results in the desired power and energy demanded in practical applications.1–5 Electric double-layer capacitors (EDLCs) are devices characterized by the presence of an interface separating the electronic and ionic charges in the solid and liquid phases, respectively. Thus, the high specific capacitances of EDLCs are due to electrode materials with a high specific surface area (e.g., activated carbons) and the quick charge accumulation in the electrical double-layer (EDL) structure (e.g., ≈1–2 nm). In contrast, in the case of pseudocapacitors (PSCs), the charge-storage mechanism at the interface involves the additional contribution of solid-state faradaic reactions (SSFRs) characterized by electron transfer at the electrode/electrolyte interface. Intrinsic conducting polymers and transition metal oxides (TMOs) are the classic ‘redox-active’ electrode materials used in PSCs.6–8An excellent strategy to boost the characteristics of SCs is the use of composite electrode materials to improve the electrochemically active surface area and the areal pseudocapacitance (F cm−2). In this scenario, good results can be obtained using, for example, two different materials, where one provides a highly porous electrode structure containing a high surface area accessible to the ionic species from the electrolyte and, the other feature to enhance the pseudocapacitance.9–13 It is worth mentioning that several papers in the literature reports involving composite electrodes containing TMOs are entirely speculative. Several studies reported unrealistic values for the specific capacitance, energy, and power due to the inadequate treatment of battery-like electrode systems, as they were real supercapacitors. Therefore, a premise regarding the development of SCs is to maintain the well-established electrochemical properties expected from well-behaved devices (e.g., high capacitance, high power density, high energy density and long lifespan).
As can be seen elsewhere,14–18 impressive composite materials for well-behaved SCs can be synthesized using different porous carbons and some TMOs (e.g., RuO2, NiO, Co3O4, NiCo2O4, and MnO2). In the case of hybrid supercapacitors (HSCs), a carbon-based material is applied as the cathode i.e. EDLC type electrode and a redox-active material is applied as the anode (pseudocapacitor (PSC) like electrode for boosting specific capacitance and energy).
From the above considerations, the use of electrodes composed of nickel oxide/hydroxide as the redox-active material is inspiring for developing PSCs and HSCs. The redox couple involving nickel (Ni(OH)2/NiOOH: Ni2+ ↔ Ni3+ + e−) is extensively used in alkaline batteries. Commonly, their electrochemical properties depend on the structure and electronic characteristics, which are affected by the synthesis processes.19 The NiO particles in the near-surface regions spontaneously transform into the α-Ni(OH)2 hydrous form in alkaline solutions.20
A significant challenge involving NiO-based PSCs is concerned with elucidating the fundamental processes occurring at the electrode/electrolyte interface during the charge-storage process involving surface charge accumulation in a strong electric field (≈10−9 V m−1) with the occurrence of intercalation/deintercalation of some species from the electrolyte in the porous electrode structure. The situation is further complicated for TMOs, where the basic or amphoteric oxide properties cause a strong interaction with water leading to different hydroxylation degrees. In the case of the NiO electrode in Li2SO4 aqueous electrolytes, three possible processes may occur at the electrode/electrolyte interface: (i) adsorption/desorption of ions, (ii) electrochemical activity of the Ni(OH)2/NiOOH redox couple, and (iii) Li+ intercalation/deintercalation processes. As a result, the overall charge-storage mechanism is rather complicated. In this scenario, operando Raman analysis can help obtain in-depth knowledge about the charge-storage fundamental processes occurring in NiO-based PSCs.
Laboratory strategies, which combine several different electrode materials and electrolytes, have been adopted by several researchers to improve the overall charge-storage capabilities in SCs. In addition to alkaline electrolytes, neutral aqueous solutions have also been used in batteries and supercapacitors with excellent advantages (e.g., corrosion inhibition, greater safety, and wide working voltage window).21 In this sense, the improvement of environmentally friendly aqueous-based electrolytes to obtain a wider working voltage window (WVW) and the long-term charge–discharge cyclability comprises a critical issue from the technological viewpoint. Good candidates as quasi neutral electrolytes for different SCs are aqueous solutions composed of lithium sulfate (Li2SO4). The conductivity and viscosity of the Li2SO4 solutions do not differ remarkably from the other aqueous-based electrolytes used in SCs,22i.e., these solutions are very beneficial for the rapid ionic transport in the hierarchically interconnected porous structures present in AC-based electrodes. As a result, high specific capacitance values, power, energy, cyclability, and low equivalent series resistance (ESR) can be achieved.21,22
There is some evidence that the Li2SO4 aqueous electrolytes facilitate near-surface SSFRs in TMOs, resulting in excellent pseudocapacitive characteristics. Some authors also proposed the occurrence of surface-to-bulk intercalation/deintercalation processes in TMOs using aqueous electrolytes.23 To quote, Misnon et al.24 and Yuan et al.25 suggested that the Li+, Na+, and K+ species can undergo intercalation/deintercalation during the charge–discharge processes occurring in the hydrated MnO2 structure. Similarly, Inamdar et al.26 proposed the intercalation/deintercalation of Na+ and K+ ions in NiO. In common, these authors claimed that the reduced unsolvated ion sizes of those alkali metal ions increase the specific capacitance and energy in SCs. Xu et al.27 proposed the intercalation of some monovalent (e.g., Li+, Na+, and K+) and bivalent (e.g., Mg2+, Ca2+, and Ba2+) cations into MnO2 structures. The importance of the bivalent ions to the monovalent electrolyte species for the charge-balance during the SSFRs involving the different manganese oxidation states was emphasized (e.g., Mn3+ → Mn4+ + e−).21,27
To further investigate the role of Li2SO4 aqueous electrolytes in NiO near-surface SSFRs, we perform a Raman operando study supported by in situ electrochemistry experiments. Contextualizing, the Raman spectrum of nonstoichiometric NiO shows several bands located at wavenumbers above 410 cm−1.28,29 The prominent band centered at ∼498 cm−1 is commonly assigned to a lack of symmetry due to high nickel vacancies affecting the one-phonon vibration of the TO (transversal) and LO (longitudinal) optical modes.29 Visually, single crystal and stoichiometric NiO is green while its nonstoichiometric counterpart is black. The redox state of Ni in the hydroxide (e.g., Ni(OH)2) can be identified in the Raman spectrum as two bands around 465 and 545 cm−1, assigned to the Eg and A1g phonon modes, respectively. Some Raman bands are more pronounced in the in situ surface-enhanced Raman spectra (SERS). However, in this case, we may have the inconvenient interference of ultra-sensitive electrochemical processes.19,30–32 The Raman spectrum obtained for the mixed lithium-nickel oxides (e.g., LixNi1−xO2) has similar characteristics of the NiOOH spectrum with two significant bands due to the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group.33,34 Julien and Massot33 and Flores et al.34 observed similar results that supported that the deintercalation of Li+-ion may affect the band intensity at ∼545 cm−1 and predicted a Raman effect at 572 cm−1. In this sense, with unmodified electrodes, one can verify the redox states and also the possible intercalation of Li+-ion in the Ni structures formed in the aqueous medium (e.g., NiO/Ni(OH)2/NiOOH).
m space group.33,34 Julien and Massot33 and Flores et al.34 observed similar results that supported that the deintercalation of Li+-ion may affect the band intensity at ∼545 cm−1 and predicted a Raman effect at 572 cm−1. In this sense, with unmodified electrodes, one can verify the redox states and also the possible intercalation of Li+-ion in the Ni structures formed in the aqueous medium (e.g., NiO/Ni(OH)2/NiOOH).
During the synthesis of TMOs, nonstoichiometric crystalline structures and electrochemical cycling (charging–discharging) processes can lead to cation disorder along the crystalline lattices.35 From a theoretical point of view, the effect of cation disorder on a crystalline structure can significantly affect the average Li+-ion intercalation average voltage and alter the voltammetric profile. Ceder et al.,36 using density functional theory (DFT), observed that cation disorder could increase or reduce the average Li+-ion intercalation voltage of lithium transition-metal oxides depending on the transition metal species. The authors observed that redox transitions in nickel oxides were high, suggesting that it is likely to be preceded by oxygen activity in disordered compounds. Ji et al.37 studied the Li-ion intercalation into bilayer graphene using DFT to describe the fundamental aspects of the energy-storage process in the presence of structural defects. According to these authors,37 lithium atoms can be inserted only in the graphene interlayer, thus proposing the first planar lithium-intercalation model for graphene-like carbons. In brief, the Li+-ion entering the graphene interlayer by diffusion and migration (polarization conditions) can undergo a redox reaction (e.g., Li+ + e− → Li) in those reaction sites with the most balanced electronic cloud density.
Moreover, the importance of the balanced electronic cloud density was studied by Freitas et al.,38 probing the O-site displacement, i.e., the induced lattice-defects in the TiO2 nanostructure. The authors observed that the O-displacement decreases the band gap values by about 1.12-fold, increasing the water-splitting reaction and modifying the charge density maps. Therefore, electronic structure calculation is an essential tool in order to study the role of structural disorders along with energy storage materials.
In this work, we used time-resolved Raman analyses of electrode/electrolyte interface under dynamic polarization conditions to obtain information of the charge-storage process in the NiO@CNF structures in the absence of the surface enhancement effects, which is indicative of the presence of substantial Raman scattering cross sections for metal oxides and carbon materials. To the best of our knowledge, this is the first study devoted to elucidating the correlation between the charge-storage phenomenon and the operando Raman scattering for nickel oxide nanoparticles anchored on carbon nanofibers as a composite material for applications in aqueous-based supercapacitors. Electronic structure calculation evidenced lattice strain and tuning along the electron density map located onto the Ni-atom along the crystalline structure.
2. Experimental
2.1. Synthesis and characterization of the composite electrode material
Carbon nanofibers (CNFs) were grown onto the microfibers of a carbon cloth substrate from Hexcel Co. used as the current collector. First, the carbon cloth was previously cleaned in an HNO3 63% (v/v) solution for 1.0 h to remove the fabrication residues. After drying at 110 °C for 12 h, the carbon cloth was immersed in a 10 g L−1 (NO3)2·6H2O (Acros, 98%) alcoholic solution containing 50% (v/v) of water and ethanol for impregnating the metallic species, used in this step as the catalyst, and subsequently dried for 12 h at 110 °C. The carbon cloth substrate was then calcined at 350 °C using a solvothermal treatment for 1.0 h. An Jung LT93010 model CVD reactor was used to synthesize the CNF structures on the carbon substrate's microfibers. In this sense, the carbon cloth was purged with argon gas using 100 cm3 min−1 volumetric flow rate for 10 min to remove the oxygen gas present. The reactor was then filled with an argon/10% H2 gas mixture using a volumetric flow rate of 200 cm3 min−1. During this procedure, the reactor temperature was gradually increased up to 700 °C. Afterward, ethane gas, used as the carbon source, was applied using a volumetric flow rate of 50 cm3 min−1 for 30 min to grow the CNF onto the carbon cloth's microfibers. A cooling step was accomplished using an argon flow at room temperature. The as-prepared carbon samples were cut into 10 mm diameter discs and decorated with NiO nanostructures using the incipient wetness impregnation method,39i.e., the CNF discs were soaked in a 0.1 mol L−1 Ni(NO3)2 alcoholic solution for 48 h and the impregnated carbon samples were washed and dried in an evacuated oven at 80 °C for 1.0 h. Finally, the impregnated carbon cloth discs were annealed at 350 °C for 2.0 h in an ambient atmosphere to obtain the NiO@CNF composite nanostructures.The surface and structural properties of the as-prepared composite were characterized using different ex situ techniques. SEM micrographs were taken using an Inspect F50 microscope from FEI (5 to 30 kV and collected with ETD), while the TEM analyses were performed using a model 2100 MSC microscope from JEOL. In the latter case, the composite samples were dispersed in isopropanol using an ultrasonic bath and dropped on a TEM lacey carbon film supported on a copper mesh. TEM data were analyzed by Gatan & Image J software40 to measure the particle size and its distribution.
The crystalline structure was characterized by X-ray diffraction performed with a model X'Pert PRO X-ray diffractometer from PANalytical using Co-Kα radiation (λ = 1.7890 Å) in a Bragg–Brentano θ/2θ configuration (Goniometer PW3050/65) for ex situ characterization. The diffraction patterns were collected with steps of 0.04° using an accumulation time of 5 s per step for the entire 2θ-scale range of 20° to 80°.
Raman sample spectra were recorded using a Renishaw inVia spectrometer using 633 nm laser wavelength, with an integration time of 60 s, 1.0 accumulation, and a 50× LWD objective lens for the 100 to 1800 cm−1 range. Spectral analyses were accomplished by proper baseline subtraction while the curve fitting was obtained using Lorentzian and Gaussian functions with software Fityk41 in the region from 300 to 1750 cm−1. The operando Raman measurements were carried out using a model ECC-Opto-Std electrochemical test cell from EL-CELL through a glass window, as showed in the schematic representation in Fig. S2.†
2.2. Electrochemical characterization studies
Different symmetric coin cells, using identical cathodes and anodes, were assembled using two identical CNF (for the sake of contrast) or NiO@CNF electrodes. Filter paper mesoporous cellulosic membranes (containing a small central hole for ECC-Opto-Std electrochemical test) were used as the separator soaked in 80 μL of a 1.0 mol L−1 Li2SO4 aqueous solution. The electrodes were assembled face-to-face and close enough to propitiate an almost uniform distribution of the electric field. All electrochemical tests were performed at 25 °C using a model VersaSTAT 4 potentiostat–galvanostat from Ametek.Cyclic voltammetry (CV) experiments were accomplished with 0.1 to 50 mV s−1 scan rate on a maximum cell voltage of 1.8 V. Galvanostatic charge–discharge (GCD) curves were recorded by applying currents in the 0.1 to 50 mA range using a voltage window of 1.0 V. The correct working voltage window (WVW) in the total absence of the water-splitting reaction was defined using the protocol based on the single-step chronoamperometry (SSC) technique reported elsewhere.42 The galvanostatic cyclability test was composed of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. For each electrode, the mass considered in the normalization of the electrochemical findings was 6.4 mg and 6.7 mg for the CNF and NiO@CNF materials, respectively. By using a model MYA 11.4Y microbalance from Radwag, we measured for each sample a NiO mass of 0.15 ± 0.03 mg.
000 cycles. For each electrode, the mass considered in the normalization of the electrochemical findings was 6.4 mg and 6.7 mg for the CNF and NiO@CNF materials, respectively. By using a model MYA 11.4Y microbalance from Radwag, we measured for each sample a NiO mass of 0.15 ± 0.03 mg.
The voltammetric capacitance was defined according to eqn (1):
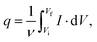 | (1) |
The calculation of the specific integral capacitance (Cesp(cv)) is defined from the voltammetric charge (q) using eqn (2):
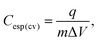 | (2) |
The calculation of the differential capacitance can also be obtained through the GCD curves of the discharge to determine the specific differential capacitance (C(gcd)) using eqn (3):
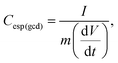 | (3) |
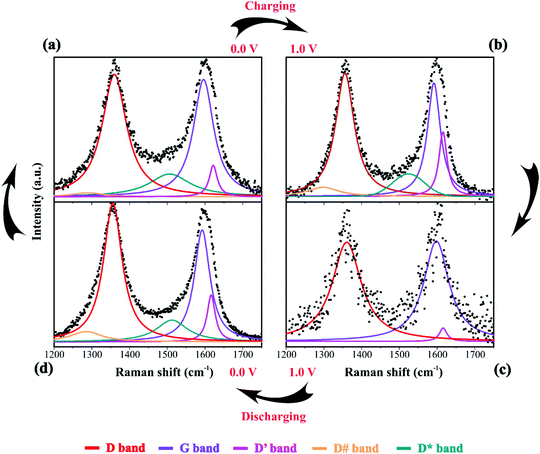
For the equivalent series resistance (ESR) calculation, the ΔV defined previously was divided by the current applied during the charge–discharge process and by factor 2 as defined in previously published studies.43 Therefore, we have the following equation:
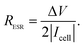 | (4) |
2.3. Computational details
All spin-polarized electronic structure calculations were carried out using a DFT+U approach with the Hubbard U correction (SGGA+U).44,45 In the present calculations, the strong on-site Coulomb repulsion parameter U and the screened exchange interaction parameter J were used to describe the localized Ni-3d electrons of NiO. We used the value of Ueff = U − J = 5.3 eV, which is consistent with the previously reported DFT+U calculations.45–48All calculations were performed using density functional theory (DFT)49,50 within the plane wave-pseudopotential framework, as implemented in the quantum-ESPRESSO51 package within the spin-polarized generalized gradient approximation (SGGA). Electronic interactions were described by the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional52 with the Vanderbilt ultrasoft pseudopotential. The latter include explicitly calculating the electrons from Ni 3s, 3p, 3d and 4s, and O 2s, 2p shells. We performed the optimization convergence test of the system, and the plane-wave basis set cutoff for the smooth part of the wave functions was 100 Ry and 8 × 8 × 8 k-points for NiO mesh sampling based on the Monkhorst–Pack53 scheme, which are sufficient to provide satisfactory accuracy of the DFT calculations. The (a, b, c) lattice parameters and the (x, y, z) internal coordinates were fully optimized, and any significant difference was compared to atomic positions obtained from the refinement procedure. Based on NiO's crystallographic information file (CIF ICSD 9866), the equation of state, strain, and total electron density maps were calculated.
3. Results and discussion
3.1. Material and electrode characterization studies
To better understand the morphological and structural properties of CNF and NiO@CNF nanostructures, SEM & TEM micrographs, XRD pattern, and Raman spectrum results are shown in Fig. 1. | ||
| Fig. 1 Material characterization: (a) SEM and (b) TEM micrographs, (c) XRD pattern, and (d) Raman spectrum from the NiO@CNF composite material. | ||
It is possible to observe in Fig. 1a the hierarchical porous structure of the CNFs. TEM data in Fig. 1b revealed for CNFs a diameter range from 20 to 90 nm with a lattice spacing of 3.2 ± 0.1 Å. NiO nanoparticles exhibited a quasi-spherical shape with diameters ranging from 1.0 to 5.0 nm and a lattice spacing of 2.08 ± 0.05 Å. Using the same synthesis procedure, our research group has recently verified11 similar diameter values of 90 and 5.0 nm for CNFs and NiO structures, respectively. This comparison evidences the reproducibility of the proposed synthesis procedure.
The crystallinity and crystal phases of the CNF and NiO@CNF nanostructures were further investigated, as presented in Fig. 1c. XRD patterns showed the NiO prominent peaks at 43.76°, 50.94°, and 74.96° in the 2θ-scale, which correspond to (1 1 1), (2 0 0), and (2 2 0) hkl-planes, respectively. According to the JCPDS card (PDF# 00-001-1239), these findings confirmed that NiO is a cubic crystal system of spatial group FM![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Crystallographic analysis of NiO nanostructures presented a lattice parameter of a = 4.1470(6) Å, lattice strain of 0.231%, and lattice spacing d200 = 2.0761(2) Å. The following statistics were verified for this analysis: σ = 0.00016, res(d) = 0.00323, tStudent = 4.32, and SD = 0.0456. As can be observed in Fig. 1b, an agreement for lattice spacing was noticed using the present data of HRTEM (2.08 Å), XRD (2.07 Å), and with the literature54 whose value of 2.4 Å was related to the (2 0 0) hkl-plane. Wu et al.54 observed a 2.4 Å value for lattice spacing using HRTEM for the NiO nanosheet assembles prepared using the hydrothermal method. Moreover, it was possible to obtain the (1 1 1)/(2 0 0) ratio values of 5.13 and 1.63 by comparing the relative intensity between the (1 1 1) and (2 0 0) hkl-planes obtained from the literature (e.g., ICSD CIF # 9866) with those referring to NiO@CNFs. This preferred orientation can lead to tuning and structural properties, i.e., texture, anisotropy, and lattice strain.55 The NiO@CNF lattice strain of 0.231% agreed with the literature referring to different synthesis method,56–58i.e., similar values of the lattice strain for NiO nanoparticles were reported (e.g., 0.23%,56 0.20%,57 and 0.17%58). Awad et al.56 studied the dielectric properties of NiO and NiO (doped-Y and Gd) nanoparticles and also verified that the charge-transfer resistance and activation energy decreased (Ni0.98Gd0.02O < Ni0.98Y0.02O < NiO) as a function of lattice strain (0.11% < 0.12% < 0.23%).
m. Crystallographic analysis of NiO nanostructures presented a lattice parameter of a = 4.1470(6) Å, lattice strain of 0.231%, and lattice spacing d200 = 2.0761(2) Å. The following statistics were verified for this analysis: σ = 0.00016, res(d) = 0.00323, tStudent = 4.32, and SD = 0.0456. As can be observed in Fig. 1b, an agreement for lattice spacing was noticed using the present data of HRTEM (2.08 Å), XRD (2.07 Å), and with the literature54 whose value of 2.4 Å was related to the (2 0 0) hkl-plane. Wu et al.54 observed a 2.4 Å value for lattice spacing using HRTEM for the NiO nanosheet assembles prepared using the hydrothermal method. Moreover, it was possible to obtain the (1 1 1)/(2 0 0) ratio values of 5.13 and 1.63 by comparing the relative intensity between the (1 1 1) and (2 0 0) hkl-planes obtained from the literature (e.g., ICSD CIF # 9866) with those referring to NiO@CNFs. This preferred orientation can lead to tuning and structural properties, i.e., texture, anisotropy, and lattice strain.55 The NiO@CNF lattice strain of 0.231% agreed with the literature referring to different synthesis method,56–58i.e., similar values of the lattice strain for NiO nanoparticles were reported (e.g., 0.23%,56 0.20%,57 and 0.17%58). Awad et al.56 studied the dielectric properties of NiO and NiO (doped-Y and Gd) nanoparticles and also verified that the charge-transfer resistance and activation energy decreased (Ni0.98Gd0.02O < Ni0.98Y0.02O < NiO) as a function of lattice strain (0.11% < 0.12% < 0.23%).
In this sense, the investigation of the lattice parameter of NiO@CNFs is fundamental from the theoretical and technological viewpoints. The lattice parameter reported in the literature (ICSD CIF # 9866) was a = 4.178(1) Å, while that verified in this work (NiO@CNFs) is a = 4.1470(6) Å. Other studies reported values of a = 4.178(0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56 and a = 4.206(0)
56 and a = 4.206(0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 for NiO nanostructures, which are also higher than a = 4.178(1) Å. Based on that, it is possible to recognize compressive stress for NiO@CNF nanoparticles reported in the current work. Finally, the broad peak corresponding to the carbon phase was observed around 30°, according to the PDF# 01-089-8487 file. Also, it is important to emphasize that the reflection plane located at 30.85° related to CNF alone was shifted to a new position of 28.82° in the presence of NiO (e.g., NiO@CNF) (please see Fig. S3†). These findings evidenced an increase in the lattice parameter with a lattice strain in the carbon structures in the presence of NiO nanoparticles.
58 for NiO nanostructures, which are also higher than a = 4.178(1) Å. Based on that, it is possible to recognize compressive stress for NiO@CNF nanoparticles reported in the current work. Finally, the broad peak corresponding to the carbon phase was observed around 30°, according to the PDF# 01-089-8487 file. Also, it is important to emphasize that the reflection plane located at 30.85° related to CNF alone was shifted to a new position of 28.82° in the presence of NiO (e.g., NiO@CNF) (please see Fig. S3†). These findings evidenced an increase in the lattice parameter with a lattice strain in the carbon structures in the presence of NiO nanoparticles.
The Raman spectrum of NiO@CNFs shown in Fig. 1d was deconvoluted into three prominent bands and five shoulders/adjacent bands. The prominent band centered at ∼498 cm−1, and the two adjacent bands at ∼370 cm−1 and ∼740 cm−1 were assigned to the 1LO mode. The 498 cm−1 band is assigned to a lack of symmetry caused by defects, including the high concentration of nickel vacancy. These findings corroborate the lattice strain observed in the XRD study. It is known that the first-order Raman scattering of 1TO and 1LO is generally absent for the face-centered cubic NiO structure with perfect stoichiometry.59,60 Therefore, our Raman spectra study indicates structural disorders with the presence of the nickel vacancies61,62 in the as-grown NiO@CNF composite.
The band assigned to the lack of symmetry (498 cm−1) is not present in the NiO single crystal.63 The 370 cm−1 band is attributed to TO and 740 cm−1 is the harmonic of 2TO modes.11,29,63–65 From this analysis, it is possible to conclude that nickel oxide nanoparticles are highly defective according to the intensity of the 498 cm−1 band.46 Tripathi et al.58 also studied the role of oxygen vacancy and lattice defects on NiO nanostructures using Raman spectroscopy. These authors also observed bands in similar wavenumber positions, as discussed above. However, a new band was found in the NiO sample near (1400 cm−1) to the magnon mode (2 M). This latter signal generally comes from the antiferromagnetic interactions between Ni ions such as Ni2+–O2−–Ni2+. This band was not evidenced in the present data due to the strong intensity band related to the D-mode (1359 cm−1) in CNFs (please see further discussion). Han et al.66 studied the interaction and ordering of the Ni vacancy (VNi) defects in NiO using DFT+U theoretical methods. According to these authors,66 NiO is deficient in cations for a typical growth condition, which explains its p-type conducting behavior. In addition, it was verified that the observed vacancies (VNi) might be replaced by other foreigner atoms (e.g., Fe or Li).66 This behavior can be related to the Raman shifts observed and further discussed in the operando Raman section of this work.
To study the Ni vacancy, some authors66 used a face-centered-cubic supercell in the absence of one Ni atom. It was verified in the relax computation analysis that nearby oxygen atoms around the defect site relax outward by 0.17 Å. These findings can be explained based on the electrostatic interaction between the defect site and nearby atoms, i.e., with the loosely bound holes since the net charge of VNi is negative, which is identical to those of oxygen species (O2−–VNi–O2−). Therefore, oxygen atoms are repelled from the defect site, accounting for the observed relaxation pattern.
From the data in Fig. 1d, it is also possible to evidence the G and D prominent bands related to the G (1598 cm−1) and D (1359 cm−1) modes, respectively, of CNFs and other less pronounced signals (e.g., D# (∼1248 cm−1) and D* (∼1509 cm−1)) ascribed to a degenerate vibrational mode of iLO and iTO phonon branches crossing the Γ point in the graphite-like material at the first Brillouin zone.23,24 The G-band corresponds to the high-frequency E2g phonon at the Γ point, and D-bands originate from the breathing modes of six-atom rings, associated with the LO phonon at the K point of the Brillouin zone. Since this band originated from a phonon mode at the edge of the Brillouin zone, a defect is required in the scattering process for the momentum conservation. Thus, the graphite-like materials’ D-band is activated by the structural disorder commonly located at the edge regions.22,25 As discussed previously, it is worth mentioning that the diffraction (reflection) related to CNFs verified at 2θ = 30.85° decreases to 2θ = 28.82° for the NiO@CNF composite, suggesting an increase in the lattice parameter with a lattice strain for CNFs in the presence of the NiO nanoparticles. Comins et al.67 also studied carbon-based materials and observed micro-Raman and XRD stress in polycrystalline diamond discs. According to these authors,67 the Raman technique showed a progressive shift of the residual stress state from a compressive one to an average tensile stress state as a cycling number function. In this sense, D-bands appeared when the lattice vibrational (e.g., Raman-inactive process) hits a defect, causing the breaking of symmetry and affecting the selection rule (q = 0) required for the first-order Raman bands. Finally, as seen in Fig. S3,† defects in CNFs were not only caused by the NiO synthesis, but they are also presented in the as-prepared CNF materials.
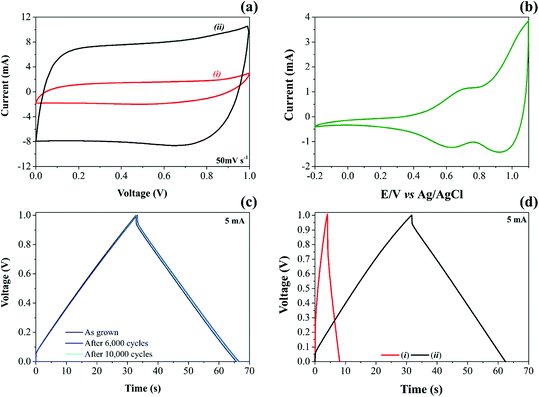
High-surface area carbon-based electrode materials usually are chemically stable in different electrolytes, exhibiting high electrical and ionic conductivities and excellent charge-transfer properties. These features make these materials exciting candidates for EDLCs and PCs.68 By adding NiO nanoparticles onto CNFs, it is possible to increase considerably the energy stored due to the vital contribution of the reversible solid-state faradaic reactions (e.g., pseudocapacitive effects). Therefore, after a careful evaluation of the electrode materials, NiO@CNF electrodes were subjected to dynamic polarization conditions during the operando Raman studies. Fig. 2 presents the electrochemical properties of CNF and NiO@CNF nanostructured electrode materials in SCs.
The analysis of cyclic voltammogram data in Fig. 2a, contrasting the different specific capacitances obtained for the (i) CNF and (ii) NiO@CNF electrode materials assembled in the symmetric configuration, revealed a ∼7-fold improvement (e.g., ∼6.7 to ∼47.2 F g−1 per electrode calculated using eqn (1) and (2)) in the charge-storage capability of the coin-cell after the decoration process using the NiO nanoparticles. In addition, the composite electrode material exhibited the almost rectangular “mirror-like” voltammetric profile expected for well-behaved SCs. In contrast, the analysis of Fig. 2b revealed a battery-like voltammetric behavior at very low scan rates for the symmetric coin-cell having only the NiO electrodes, i.e., the desired supercapacitor characteristics practically disappear.11 In any case, is it worth mentioning that the well-known battery-like properties exhibited by pure NiO electrodes in aqueous solutions can be verified even at medium and high scan rates. In contrast, one has the case of the NiO electrode immersed in aprotic (organic) electrolytes, where the cyclic voltammograms must be recorded at very low scan rates (≤1 mV s−1) to verify the narrow (“needle-like”) redox peaks characterizing the intercalation/deintercalation of Li+-ion species. Since the proton intercalation reaction does not occur in the absence of water, the charge-storage process is exclusively due to a prolonged Li+-ion intercalation process controlled by mass transport inside the host material (D ≈ 10−8 to 10−11 cm2 s−1).
NiO nanoparticles in aqueous media spontaneously transform into Ni(OH)2. This hydrated form is amorphous, forming a nonstoichiometric intermediate compound.19 As verified in the study using the XRD technique (please see Fig. S3†), the diffraction pattern related to NiO@CNFs in the dry form is entirely different from that obtained for the wetted material (e.g., α-Ni(OH)2).
In neutral solutions, the hydration of NiO and the redox activity of the Ni-species under anodic polarization conditions can be represented by the following mechanism adapted from Bode's model:69,70
| NiO + H2O ↔ Ni(OH)2 | (A) |
| α-Ni(OH)2 → γ-NiOOH + H+ + e− | (B1) |
| β-Ni(OH)2 → β-NiOOH + H+ + e− | (B2) |
| α-Ni(OH)2 → β-Ni(OH)2 | (B3) |
| γ-NiOOH → β-NiOOH. | (B4) |
The basic or amphoteric chemical nature exhibited by some transition metal oxides (TMOs) in aqueous solutions is characterized by a negative change in the Gibbs’ free energy during the hydration process resulting in the formation of an insoluble acidic substance (please see step (A)). In the other steps of the mechanism, the different forms (α and β) of the hydrated nickel oxide can undergo charge-transfer (faradaic) reactions (steps (B1) and (B2)) or spontaneous structural changes involving the additional γ-phase (steps (B3) and (B4)).
In Fig. 2b during the anodic sweep a voltammetric peak at 0.69 V can be observed, which, in principle, can be attributed to the Ni(OH)2/NiOOH redox couple. The corresponding cathodic peak is verified at 0.63 V, i.e., we observed a peak separation potential of 60 mV as predicted for Nernstian redox processes.
The electrochemical steps (B1) and (B2) represent the pseudocapacitive or battery-like behaviors where electrons are transferred at the electrode/solution interface during the anodic polarization with the concomitant deintercalation of protons. The occurrence of battery-like or pseudocapacitive behaviors depends on the synergism between the different species present in the composite electrode.
Depending on the proton transport behavior in the porous carbon structure, the Ni-sites’ electron transfer can occur in the near-surface or surface-to-bulk regions of the composite electrode material. An example of a fast and reversible near-surface “pseudocapacitive process” consists of a porous carbon-based scaffold containing finely dispersed metal–oxide nanoparticles on its surface in intimate contact with the electrolyte. In this case, the proton deintercalation process is not mass-transport controlled.71,72 As a result, the cyclic voltammogram profiles are featureless (e.g., almost rectangular), resembling the electrochemical response of EDLCs governed by a purely charge-separation (electrostatic) process.
By contrast, in the case of a surface-to-bulk “battery-like process”, the electron transfer mainly resides in the inner regions of the porous composite material where the proton deintercalation is more challenging to occur since the active Ni-sites are not in intimate contact with the aqueous electrolyte. In this sense, considering the concept of a Nernst's stagnant layer for the proton transport, the overall surface-to-bulk faradaic process is characterized by a voltage in the cyclic voltammograms similar to that in batteries.
For convenience, the intercalation/deintercalation of protons can be represented as follows:
| Ni(OH)2 ↔ NiOx(OH)(2−x) + xH+ + xe−, | (C) |
Although the NiOOH/Ni(OH)2 redox couple's formation is mostly reported in the literature,74–76 other reaction steps can be taken into account involving the water mobility into and leaving the electrode material. This reaction would lead to empty spaces (vacancies) that Li+-ion may occupy. For example, the Li–Ni mixed-oxide (LiNiO2) comprises Li+-ion between the adjacent NiO slabs or occupying the Ni vacancies.77
Therefore, at least in principle, we can consider a pseudocapacitive phenomenon due to the intercalation/deintercalation of Li+-ion in aqueous solutions. However, this type of pseudocapacitance is commonly verified only in concentrated LiOH aqueous solution or in anhydrous electrolytes (e.g., LiClO4 + PC (propylene carbonate)).78 Even so, Faria et al.79 proposed an ‘exchange reaction’ to describe the proton intercalation in aqueous solutions with a small contribution of the intercalation process involving different monovalent cations. Therefore, one can consider in the present study the following ‘substitutive solid-state redox’ reaction:
| Ni(OH)OxHy + zLi+ ↔ Ni(OH)OxLi(y−g) + gH+ + e− | (D) |
As a result, we are considering in the current work the occurrence of a mixed pseudocapacitive process represented by the pertinent solid-state reactions (eqn (C) and (D)) (please see further discussion).
The experimental findings regarding the galvanostatic charge–discharge (GCD) tests for both CNF and NiO@CNF symmetric coin cells are presented in Fig. 2c and d. The analysis of these findings revealed the typical “triangular galvanostatic profile” predicted for well-behaved SCs. By contrast, for battery-like systems, the GCD profile is characterized by a “voltage plateau”. Unfortunately, in several reports, the battery-like behavior is incorrectly interpreted to determine the specific capacitance (F g−1), while the relevant parameter, in this case, is the specific capacity (A h g−1). This incorrect analysis of the GCD data commonly results in absurd (illusory) pseudocapacitances.
Excellent electrode stability keeping at the same time the well-established capacitive properties was verified for the NiO@CNF composite where even after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GCD cycles, the triangular profile remained unaffected (Fig. 2c). To the best of our knowledge, these findings are by far more reliable than those of several literature reports where even for short-term GCD tests (e.g., ≈1000–5000 cycles), the experimental results give strong evidence of the electrode instability.80–83
000 GCD cycles, the triangular profile remained unaffected (Fig. 2c). To the best of our knowledge, these findings are by far more reliable than those of several literature reports where even for short-term GCD tests (e.g., ≈1000–5000 cycles), the experimental results give strong evidence of the electrode instability.80–83
As recently discussed by Nunes et al.,11 when the specific capacitance values are determined considering only the redox-active material, we can verify high values of ∼1200 to 3152 F g−1 for NiO electrodes. In contrast, smaller capacitances (e.g., ≈50–600 F g−1) can be found for practical devices when the different masses of the cell components are considered in the calculation. Also, the specific capacitance obtained for the symmetric electrodes housed in a two-electrode cell is ¼ of that obtained for the isolated (individual) electrode.
From the above considerations, the different normalization conditions used to calculate the specific (gravimetric) quantities referring to the different material components were specified in the current work to avoid ambiguity. Table 1 shows the figures-of-merit representing the electrochemical performance of the different materials. The values of the specific capacitance and the ESR in Table 1 were obtained using eqn (3) and eqn (4):
As seen, a small “electrostatic capacitance” of 3.1 F g−1 was verified for the carbon-based (EDLC) scaffold. At the same time, the composite electrode (NiO@CNFs) exhibited an “overall capacitance” of 23.1 F g−1. Finally, considering only the redox-active material (NiO), we identified a very high “pseudocapacitance” of 1033 F g−1. Unfortunately, in several literature reports, the crucial details involving the normalization of the relevant parameters for SCs are not unambiguously specified, resulting in speculative statements.
| Material | Cell capacitance and ESR values | Electrode capacitances | ||||
|---|---|---|---|---|---|---|
| Normalized values [F g−1] and [Ω g] | Non-normalized [mF] and [Ω] | Normalized values [F g−1] | Non-normalized [mF] | |||
| CNFs | 0.8 | 0.13 | 5.0 | 0.02 | 3.1 | 20 |
| NiO@CNFs | 5.8 | 0.04 | 38.8 | 0.01 | 23.1 | 155 |
| NiO | 258.3 | 0.00 | — | — | 1033.3 | — |
3.2. Raman operando study during dynamic electrode polarization
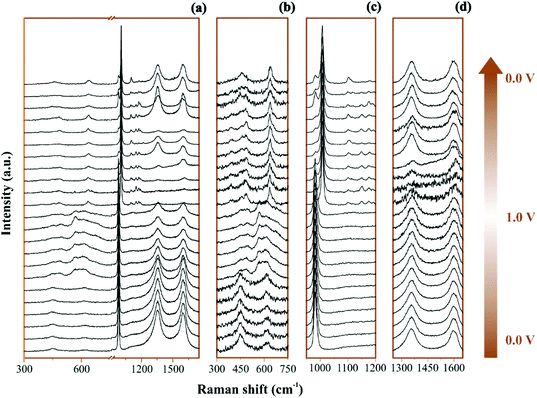
The Raman operando spectra for NiO@CNFs nanostructured during polarization of the working electrode are shown in Fig. 3.In Fig. 3a and 3b–d the broad spectral range and selected regions can be noticed, respectively. Fig. 3b focuses on the range from 300 to 750 cm−1, where it is possible to notice the presence of Ni and O bonding. The selected spectral regions will be discussed separately due to the distinct vibrational Raman modes (please see Fig. 4–6 and the discussion thereof).
 | ||
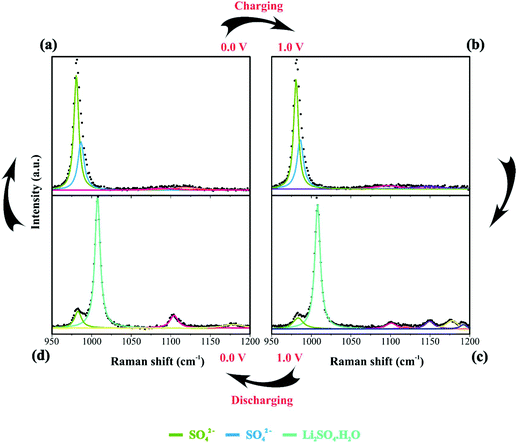
| Fig. 6 Raman spectra of the electrode/electrolyte interface under cyclic voltammetry at scan rate 0.15 mV s−1 from (a) 0 V to (b) 1 V during charge and from (c) 1 V to (d) 0 V during discharge. Spectra intensities are normalized from 0 to 1 in the 1200 to 1750 cm−1. Electrodes were housed in an El Cell filled with 80 μL of a 1 M Li2SO4 aqueous solution. Deconvolution considered five bands as described in Fig. 1(d). | ||
All spectra ranges were normalized relative to the maximum peak intensity value of each region. It is possible to observe in Fig. 4 the operando Raman spectra recorded during dynamic polarization conditions (charge: 0 V → 1.0 V & discharge: 1.0 V → 0 V) accomplished using cyclic voltammetry.
By analyzing Fig. 4 and Fig. S6(a and b),† we have Raman spectra of the as-prepared electrode and the wetted one. It can be concluded from the electrode spectral changes that other Raman bands are necessary for fitting the experimental findings. Fig. S6(a)† shows that by adding water or Li2SO4 aqueous solution, the SO42− species spontaneously accumulate/adsorb at the electrode/electrolyte interface. Fig. S7–S9† show significant findings that permitted us to propose the formation of Li2SO4·H2O during the discharge step occurring in the cathodic scan. Fig. S7† shows the full spectral Raman interval for CNFs. Fig. S8 and S9† show the magnification of the 300–800 cm−1 and 950–1200 cm−1 spectral region, respectively. Deconvolution permitted us to separate the individual spectral information due to NiO and SO42− species.
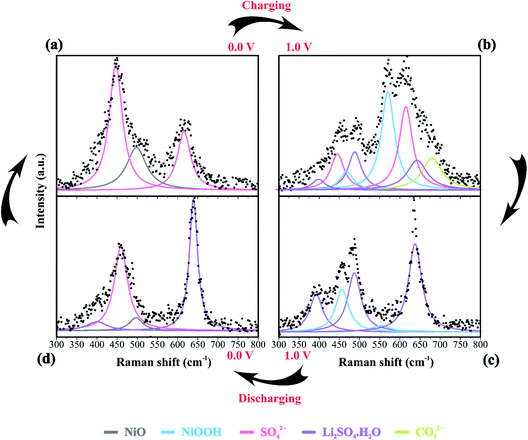
Table 2 summarizes the Raman information extracted from Fig. 3b, c, 4a–d and 5. In this case, we also considered the ESI (Fig. S6–S9†) and the literature reports.19,21,22,30–32,77,84–86,87,88 At 0 V (Fig. 4a), it is possible to observe three prominent bands that were assigned to the symmetric (449 cm−1) and anti-symmetric (615 cm−1) deformation modes incurred by the presence of SO42− in the electrical double-layer structure,85,86,89 and to the NiO lattice mode (498 cm−1).74 Fig. S6† shows the Raman spectra of the as-prepared NiO@CNF nanostructured material (Fig. S6i†) and that after hydration (wetted conditions) (Fig. S6ii†). The analysis of Fig. S6i† revealed the absence of Raman signals at 449 and 615 cm−1 related to SO42−. Finally, the analysis of the Raman band at 498 cm−1 (NiO lattice mode) revealed an intensity decrease due to the influence of the electrolyte and the formation of Ni(OH)2 species.
| Assignment | 0 V (charge) | 1.0 V (charge) | 1.0 V (discharge) | 0 V (discharge) |
|---|---|---|---|---|
| Band position (cm−1) | ||||
| NiO | 498 | — | — | 497 |
| NiOOH | — | 468; 550 | 465; 545 | — |
| SO42− | 449; 616 | 446; 615; 980.7;986; 1096;1147 | 986 | 460; 982 |
| Li2SO4·H2O | — | 398; 487; 643; | 391; 487; 638; 1008; 1104; 1149; 1189 | 400; 635; 1008; 1104; 1149; 1189 |
| CO32− | — | 680 | — | — |
We continued to verify sulfate bands at 449 and 615 cm−1 during the charging process. At 1.0 V (Fig. 4b), the prominent band centered at ∼550 cm−1 was ascribed to NiOOH, i.e., the O–Ni–O stretching vibration of NiO6 units due to the A1g vibration mode about the D3d5 space group77,88 is followed by the band at 468 cm−1 assigned to Eg symmetry of NiOOH.19,30–32 The intensity ratio of the NiOOH bands at the end of the charging process (anodic sweep) was IA1g/IEg ≈ 5. Besides, we also verified a Raman band related to the bending in-plane vibrations of carbonate species at 680 cm−1. In principle, these findings indicate an upper cell voltage limit incurred by the faradaic reaction involving the dissolved O2 from the atmosphere and the carbon structures present in the working electrode to form the CO32− anionic species characterized by the D3h space group.21,22,87 Also, cell voltages higher than 1.0 V might induce the evolution of CO2 and CO due to the oxidation of the carbon-based electrode.21
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 84 species during electrode polarization accomplished using cyclic voltammetry were observed. The analysis of Fig. 4c indicates that the Raman band at 550 cm−1 with a reduced intensity is related to Li+-ion intercalation while the bands at 460 cm−1 and 550 cm−1 correspond to the presence of the NiOOH structure. In particular, the Raman findings in Fig. 5 indicated that in the anodic sweep, the SO42− ions accumulated at the interface. During the cathodic process, these species moved towards the bulk region. As a result, hydrated lithium sulfate (Li2SO4·H2O) was formed at the interface under forced saturation conditions imposed by the applied electric field.
84 species during electrode polarization accomplished using cyclic voltammetry were observed. The analysis of Fig. 4c indicates that the Raman band at 550 cm−1 with a reduced intensity is related to Li+-ion intercalation while the bands at 460 cm−1 and 550 cm−1 correspond to the presence of the NiOOH structure. In particular, the Raman findings in Fig. 5 indicated that in the anodic sweep, the SO42− ions accumulated at the interface. During the cathodic process, these species moved towards the bulk region. As a result, hydrated lithium sulfate (Li2SO4·H2O) was formed at the interface under forced saturation conditions imposed by the applied electric field.
More specifically, as the working electrode was progressively polarized in the anodic (positive) direction, the surface excess (Γ) of SO42− is drastically increased. In this sense, to satisfy the local electroneutrality principle, a considerable amount of solvated Li+-ions were dragged to the anionic clusters’ immediate vicinity. As verified in the operando Raman study, the band located at 498 cm−1 is no longer detected. Besides, we also observed a strong band at 550 cm−1 assigned to the presence of NiOOH structures.34 Another plausible explanation for the verified Raman behavior is that Li+-ions might enter the composite material to occupy the Ni vacancies and/or penetrate the NiO slabs. Generally, this proposal agrees with the substitutive solid-state redox reaction (please see eqn (D)) where the redox-active material is oxidized, resulting in the intercalation of Li+ and deintercalation of H+ species.
During the discharge process, an inversion in the band intensity ratio was verified (e.g., IA1g/IEg ≈ 0.2). The A1g vibrational mode was more pronounced in the cathodic scan, while the bands at ∼398, 487, and 637 cm−1 indicated the presence of Li2SO4·H2O. During the reversal voltage scan in the cathodic (negative) direction, the Li2SO4·H2O species previously accumulated at the interface are progressively dissolved due to contact with bulk water (e.g., [H2O] ≈ 55 mol L−1) entering the stagnant Nernst's layer in the opposite direction, i.e., in this case, the dissolution process is thermodynamically favored due to entropic factors. Simultaneously, the redox-active sites undergo a reduction (e.g., Ni(OH)OxLi(y−g) + gH+ + e− ↔ Ni(OH)OxHy + zLi+) where the Li+-ions are deintercalated while the intercalation of H+ species also proceeds. Generally, the operando Raman findings shown in Fig. 5, 6 and Fig. S5–S8† support the above theoretical proposals. Additionally, Fig. 6 shows that the accumulation of ionic species at the interface promoted blue shifts (e.g., Δω ≈ 3.0–4.0 cm−1) regarding the D and G bands referring to graphite-like structures.12,30,90Table 3 shows the D and G band positions. We attributed these Raman shifts to changes in the local electrical field, which affects the phonon vibrations of the c-lattice.
| Assignment | 0 V (charge) | 1 V (charge) | 1 V (discharge) | 0 V (discharge) |
|---|---|---|---|---|
| Band position (cm−1) | ||||
| D | 1357 | 1360 | 1361 | 1356 |
| G | 1592 | 1596 | 1598 | 1591 |
| D′ | 1616 | 1622 | 1616 | 1616 |
| D# | 1285 | 1290 | — | 1298 |
| D* | 1512 | 1506 | — | 1515 |
In summary, the operando Raman study accomplished under dynamic polarization conditions in electrochemical cells gives relevant information regarding the chemical and structural changes of the different species present at the electrode/solution interface.
3.3. DFT analysis: structural and electronic properties of the composite material
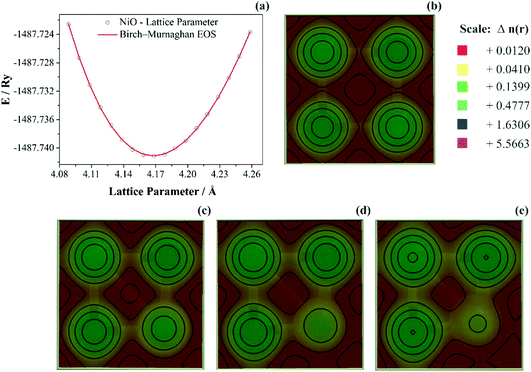
As discussed previously, the operando Raman study evidenced defects related to the Ni-sites along the lattice of the NiO phase obtained in NiO@CNF nanostructures, i.e., the Raman band was assigned to the lack of symmetry, as a result of the lattice strain observed in the XRD analysis. Also, it was observed that such lattice-strain is a compressive-type. We accomplished a DFT study in order to model the equation of state (EOS) and compare it to the experimental data from this experimental information.Crystallographic analysis of NiO@CNF nanostructures presented lattice parameter a = 4.1470(6) Å and a lattice strain of 0.231%. As previously mentioned, this lattice strain observed was a compressive-type. However, lattice strain can be observed as tensile and compressive. In this sense, it is possible to induce lattice parameter modification from full relax geometry towards compressive and tensile strains. It results in a parabola-like profile (energy vs. lattice parameter), fitted using proper functions well-described as the EoS. The equation of state is more attractive if parameters for specific materials are made available from properties determined at or near ambient conditions. In this sense, the equation of state can be an energy–volume relationship describing a solid's behavior under compression or expansion. The simplest isothermal EOS for a solid is the bulk modulus, which is a measure of the material's ability to resist changes in volume under uniform compression or expansion. The equilibrium bulk modulus B0 of a crystal can be defined as follows:91
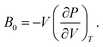 | (5) |
A dimensionless parameter B′0 can then be defined as its first derivative with respect to the pressure, at constant temperature (T):
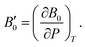 | (6) |
Let us recall that the pressure P may be written as a function of the volume V as:
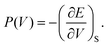 | (7) |
According to eqn (7) we can redefine the bulk modulus in terms of eqn (5) as the second energy derivative concerning the volume (V):
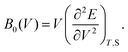 | (8) |
The third-order Birch–Murnaghan isothermal equation of state91 is given as:
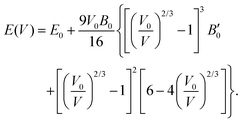 | (9) |
To study anisotropic strain causing a NiO lattice strain, structural parameters such as bulk modulus are worth studying, as shown in Fig. 7.
In Fig. 7a the bulk modulus values of 210 GPa for NiO are shown. Moreover, the lattice parameter obtained using DFT+U computations was aNiO = 4.1842(5) Å. This value agrees with those obtained using the refinement presented previously (aNiO = 4.1470(6) Å) and diverges only 0.88% for NiO. Prakapenka et al.92 studied the high-pressure effects on the NiO oxygen fugacity buffers. These authors experimentally measured the NiO bulk modulus using a diamond anvil cell apparatus. They92 also used the Birch–Murnaghan equation of state to fit experimental values and obtained a value of 190 GPa for NiO. However, Panero et al.93 also used the Birch–Murnaghan equation of state to fit experimental values using the diamond-anvil cell methodology; the authors93 obtained 201 GPa for the NiO crystal structure. This difference can be related to the samples’ nature, once that Panero et al.93 studied high-pressure, high-temperature equations of state using nanofabricated controlled-geometry samples into a hot-plate.
The SGGA+U computation level improves the calculations largely by including correlation effects and other properties such as lattice constants and bulk modulus. Using SGGA+U several authors obtained NiO bulk modulus values of 177 GPa (U = 0 eV),94 182 GPa (U = 6.2 eV),95 203 GPa (U = 6.3 eV),96 and 248 GPa (U = 8.0 eV).94 As observed, the present SGGA+U calculations were reasonable, which are also in good agreement with other similar SGGA+U calculations. These differences were related to XC-pseudopotential (PBE, PW91), type-pseudopotential (USPP or PAW), and Hubbard values. The experimental values for the NiO bulk modulus was reported as 205 GPa.96,97 Based on the results presented above, in general, NiO presented an average experimental bulk modulus B0-NiO = 205 GPa. In this sense, bulk modulus values obtained herein of B0-NiO = 210 GPa agreed with the literature data. Moreover, the computation level presented herein (SGGA/PBE U = 6.0 eV) is in agreement with the lattice parameter obtained using refinement, as discussed previously.
The computation of bulk modulus values is essential as a significant loss in energy conversion for the battery/supercapacitor is related to the increase of the electrode material's molar volume and, consequently, fracture of the nanostructured material. For example, graphite, which is mostly used as energy conversion material, presents B0-Graphite = 0.0229 GPa,98 which is significantly lower than that obtained for the NiO nanostructures discussed above. Understanding the relationships between the microstructure and mechanical properties is fundamental for improving and tuning properties related to a better energy-storage device. As a result, Dai et al.99 studied the intrinsic correlation between fragility and bulk modulus in metallic glasses. The authors observed a linear relation for both properties (fragility and bulk modulus) for 26 metallic glasses.
When the probability density distribution is multiplied by the total number of electrons in the molecule, N, it becomes known as the electron density distribution or simply the electron density and is given the symbol ρ(x,y,z). It represents the probability of finding any one of the N electrons in an infinitesimal volume of space surrounding the point (x,y,z). Therefore, it yields the total number of electrons when the overall space is integrated. The electron density can be conveniently thought of as a cloud or gas of negative charge that varies in density throughout the molecule. Once the lattice strain was a compressive-type and related to Ni-site defects, 0.01, 0.02, and 0.03 Å displacement were induced along with the (2 0 0) hkl-plane towards a compressive volume variation as observed in Fig. 7b–e, respectively. The most intriguing features in Fig. 7b–e are that ρ is very large in an almost spherical region around each nucleus while assuming relatively minimal values; at first sight, a featureless topology between these nuclear regions. The high electron density in the nearly spherical region around each nucleus arises from the tightly held core electrons; the relatively minimal and more diffuse density between these regions arises from the more weakly held bonding electrons. The calculated electron density shows that charge density lines are spherical and the plane structure shows the sign of the ionic bond of Ni and O atoms.
It is possible to notice that, as the Ni-site displacement increase from 0.01 up to 0.03 Å, the electron density map located onto the Ni-atom decreases 3.5-fold and the charge densities accumulated homogeneously near the Ni and O atom. This decrease in Ni-site charge density is significant to obtain a deeper understanding of the charge/discharge dynamic movement of ions. It was discussed previously that NiO nanoparticles in aqueous media spontaneously transform into α-Ni(OH)2. However, the increase in the compressive lattice strain and decreasing charge density onto Ni-site atoms decrease the promotion and dynamic equilibrium between NiO and α-Ni(OH)2. The saturation of charge/discharge species is probably related to the decrease of the electron density distribution.
4. Conclusions
We have reported nickel oxide nanoparticles’ characterization supported on carbon nanofibers grown on a carbon-cloth substrate's microfibers as a material and operando electrode. Several characterization studies using traditional techniques and the innovative operando Raman analysis were accomplished for studying the fundamentals involving the charge-storage process in supercapacitors. Raman spectra of the electrode/solution interface were obtained under dynamic polarization conditions, deconvoluted, and contrasted with the NiO system's literature data. Blank experiments were also carried out using the carbon nanofiber (CNF) scaffold. The ionic adsorption process was pronounced and relatively easy to detect using Raman spectroscopy. We observed spontaneous sulfate adsorption/desorption during the anodic and cathodic scans, respectively, with the formation of Li2SO4·H2O at the electrode/electrolyte interface due to an enormous surface excess of the ionic species. The electrochemical activity of the Ni(OH)2/NiOOH redox couple previously verified in the cyclic voltammetry study carried out in an aqueous medium was verified using the Raman technique. We believe that the intercalation/deintercalation of H+ and, to a minor extent, the Li+ ions can occur during polarization in aqueous solutions according to the ‘substitutive solid-state redox reaction’.Additionally, our electrochemical system shows outstanding stability with 98% coulombic efficiency after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 charge–discharge cycles. We believe it is possible that a synergism exists between the carbon scaffold and NiO, where the former extracts electrons very quickly. At the same time, the latter is responsible for the pronounced pseudocapacitive behavior. As a result, passivation was strongly suppressed, while the voltammetric charge increased in the presence of NiO. The NiO@CNF composite exhibited excellent electron and ionic conductivities and, consequently, reversible and fast charge-transfer than bulky materials. We believe that this novel composite material is auspicious for future applications as an electrode in practical supercapacitors. Finally, the combination of Raman spectroscopy and cyclic voltammetry comprised a powerful tool to investigate the actual events occurring during the energy-storage process at the electrode/solution interface.
000 charge–discharge cycles. We believe it is possible that a synergism exists between the carbon scaffold and NiO, where the former extracts electrons very quickly. At the same time, the latter is responsible for the pronounced pseudocapacitive behavior. As a result, passivation was strongly suppressed, while the voltammetric charge increased in the presence of NiO. The NiO@CNF composite exhibited excellent electron and ionic conductivities and, consequently, reversible and fast charge-transfer than bulky materials. We believe that this novel composite material is auspicious for future applications as an electrode in practical supercapacitors. Finally, the combination of Raman spectroscopy and cyclic voltammetry comprised a powerful tool to investigate the actual events occurring during the energy-storage process at the electrode/solution interface.
The electronic structure calculation shows that CNFs lead to a stabilization of NiO nanoparticles, which present a compressive strain and large bulk modulus values. Also it was observed that as the Ni-site displacement increases, the electron density map located onto the Ni-atom decreases up-to 3.5-fold and the charge densities accumulated homogeneously near the Ni and O atom. This electronic structure evidence can lead to a conversion between NiO/Ni(OH)2 with similar Ni2+-redox values and further to Ni(OH)2/NiOOH (Ni2+/Ni3+-redox) energy-storage materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are very grateful to LNNano/CNPEM for SEM and to the financial support from the Brazilian funding agencies CNPq (301486/2016-6 and 427350/2016-6), FAPESP (2014/02163-7, 2017/11958-1, and 2018/20756-6). L. M. Da Silva wishes to thank FAPEMIG (Financial support for the LMMA/UFVJM Laboratory) and CNPq (PQ-2 grant: Process 301095/2018-3). A. C. Oliveira wishes to thank FAPEMAT (Financial support for the LCM/UFMT Laboratory 0259310/2017). R. G. Freitas wishes to thank CNPq (PQ-2 grant: Process 304442/2019-4) and CENAPAD/SP (Proj650) for providing the computational time. The authors gratefully acknowledge the support from Shell and the strategic importance of the support given by ANP (Brazil's National Oil, Natural Gas and Biofuels Agency) through the R&D levy regulation.References
- D. Lin, Y. Liu and Y. Cui, Nat. Nanotechnol., 2017, 12, 194–206 CrossRef CAS PubMed.
- V. Viallet and B. Fleutot, Inorganic massive batteries, 2017 Search PubMed.
- N. Kularatna, Energy Storage Devices for Electronic Systems: Rechargeable Batteries and Supercapacitors, 2014 Search PubMed.
- K. E. Aifantis, S. A. Hackney and R. V. Kumar, High Energy Density Lithium Batteries: Materials, Engineering, Applications, 2010 Search PubMed.
- V. S. Bagotsky, A. M. Skundin and Y. M. Volfkovich, Electrochemical Power Sources: Batteries, Fuel Cells, and Supercapacitors, 2015 Search PubMed.
- F. Béguin and E. Frackowiak, Supercapacitors: Materials, Systems, and Applications, 2013 Search PubMed.
- P. Simon, T. Brousse and F. Favier, Supercapacitors based on carbon or pseudocapacitive materials, 2017 Search PubMed.
- G. Wang, L. Zhang and J. Zhang, Chem. Soc. Rev., 2012, 41, 797–828 RSC.
- Y. Y. Horng, Y. C. Lu, Y. K. Hsu, C. C. Chen, L. C. Chen and K. H. Chen, J. Power Sources, 2010, 195, 4418–4422 CrossRef CAS.
- L. L. Zhang, T. Wei, W. Wang and X. S. Zhao, Microporous Mesoporous Mater., 2009, 123, 260–267 CrossRef CAS.
- W. G. Nunes, L. M. Da Silva, R. Vicentini, B. G. A. Freitas, L. H. Costa, A. M. Pascon and H. Zanin, Electrochim. Acta, 2019, 298, 468–483 CrossRef CAS.
- R. Vicentini, W. Nunes, B. G. A. Freitas, L. M. Da Silva, D. M. Soares, R. Cesar, C. B. Rodella and H. Zanin, Energy Storage Mater., 2019, 22, 311–322 CrossRef.
- L. M. Da Silva, R. Cesar, C. M. R. Moreira, J. H. M. Santos, L. G. De Souza, B. M. Pires, R. Vicentini, W. Nunes and H. Zanin, Energy Storage Mater., 2019, 27, 555–590 CrossRef.
- W. Wei, X. Cui, W. Chen and D. G. Ivey, Chem. Soc. Rev., 2011, 40, 1697–1721 RSC.
- H. Xia, Y. Shirley Meng, G. Yuan, C. Cui and L. Lu, Electrochem. Solid-State Lett., 2012, 15, 60 CrossRef.
- S. Vijayakumar, S. Nagamuthu and G. Muralidharan, ACS Appl. Mater. Interfaces, 2013, 5, 2188–2196 CrossRef CAS PubMed.
- B. Çakıroğlu and M. Özacar, Biosens. Bioelectron., 2018, 119, 34–41 CrossRef PubMed.
- C. Guan, X. Liu, W. Ren, X. Li, C. Cheng and J. Wang, Adv. Energy Mater., 2017, 7, 1602391 CrossRef.
- Y. L. Lo and B. J. Hwang, Langmuir, 1998, 14, 944–950 CrossRef CAS.
- B. S. Yeo and A. T. Bell, J. Phys. Chem. C, 2012, 116, 8394–8400 CrossRef CAS.
- C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, Chem. Soc. Rev., 2015, 44, 7484–7539 RSC.
- K. Fic, A. Płatek, J. Piwek, J. Menzel, A. Ślesiński, P. Bujewska, P. Galek and E. Frąckowiak, Energy Storage Mater., 2019, 22, 1–14 CrossRef.
- S. Passerini and B. Scrosati, Solid State Ionics, 1992, 53–56, 520–524 CrossRef CAS.
- I. I. Misnon, R. A. Aziz, N. K. M. Zain, B. Vidhyadharan, S. G. Krishnan and R. Jose, Mater. Res. Bull., 2014, 57, 221–230 CrossRef CAS.
- A. Yuan and Q. Zhang, Electrochem. Commun., 2006, 8, 1173–1178 CrossRef CAS.
- A. I. Inamdar, Y. Kim, S. M. Pawar, J. H. Kim, H. Im and H. Kim, J. Power Sources, 2011, 196, 2393–2397 CrossRef CAS.
- C. Xu, C. Wei, B. Li, F. Kang and Z. Guan, J. Power Sources, 2011, 196, 7854–7859 CrossRef CAS.
- P. Dubey, K. K. Choudhary and N. Kaurav, in AIP Conference Proceedings, 2018 Search PubMed.
- G. George and S. Anandhan, RSC Adv., 2014, 4, 62009–62020 RSC.
- B. M. Pires, W. G. Nunes, B. G. Freitas, F. E. R. Oliveira, V. Katic, C. B. Rodella, L. M. Da Silva and H. Zanin, J. Energy Chem., 2020, 54, 53–62 CrossRef.
- B. C. Cornilsen, P. J. Karjala and P. L. Loyselle, J. Power Sources, 1988, 22, 351–357 CrossRef CAS.
- J. Desilvestro, D. A. Corrigan and M. J. Weaver, J. Electrochem. Soc., 1988, 135, 885 CrossRef CAS.
- C. Julien and M. Massot, Phys. Chem. Chem. Phys., 2002, 4, 4226–4235 RSC.
- E. Flores, P. Novák and E. J. Berg, Front. Energy Res., 2018, 6 DOI:10.3389/fenrg.2018.00082.
- P. Dubey, N. Kaurav, R. S. Devan, G. S. Okram and Y. K. Kuo, RSC Adv., 2018, 8, 5882–5890 RSC.
- A. Abdellahi, A. Urban, S. Dacek and G. Ceder, Chem. Mater., 2016, 28, 3659–3665 CrossRef CAS.
- K. Ji, J. Han, A. Hirata, T. Fujita, Y. Shen, S. Ning, P. Liu, H. Kashani, Y. Tian, Y. Ito, J. ichi Fujita and Y. Oyama, Nat. Commun., 2019, 10, 275 CrossRef PubMed.
- M. A. Santanna, W. T. Menezes, Y. V. B. Santana, M. M. Ferrer, A. F. Gouveia, A. D. Faceto, A. J. Terezo, A. J. A. Oliveira, E. Longo, R. G. Freitas and E. C. Pereira, Int. J. Hydrogen Energy, 2018, 43, 6838–6850 CrossRef CAS.
- B. A. T. Mehrabadi, S. Eskandari, U. Khan, R. D. White and J. R. Regalbuto, Adv. Catal., 2017, 61, 1–35 CAS.
- M. D. Abràmoff, P. J. Magalhães and S. J. Ram, Biophotonics Int., 2004, 11, 36–42 Search PubMed.
- M. Wojdyr, J. Appl. Crystallogr., 2010, 43, 1126–1128 CrossRef CAS.
- W. G. Nunes, B. G. A. Freitas, R. M. Beraldo, R. M. Filho, L. M. Da Silva and H. Zanin, Sci. Rep., 2020, 10, 19195 CrossRef CAS.
- R. Vicentini, L. M. Da Silva, E. P. Cecilio, T. A. Alves, W. G. Nunes and H. Zanin, Molecules, 2019, 24, 1452 CrossRef CAS PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B, 1991, 44, 943 CrossRef CAS.
- S. Dudarev and G. Botton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- G. Rohrbach, J. Hafner and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 64, 075413 CrossRef.
- W. B. Zhang, Y. L. Hu, K. L. Han and B. Y. Tang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 054421 CrossRef.
- W. B. Zhang, Y. L. Hu, K. L. Han and B. Y. Tang, J. Phys.: Condens. Matter, 2006, 18, 9691–9701 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864–871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- H. Xiao, S. Yao, H. Liu, F. Qu, X. Zhang and X. Wu, Prog. Nat. Sci.: Mater. Int., 2016, 26, 271–275 CrossRef CAS.
- B. D. Cullity and S. R. Stock, Elements of X-ray Diffraction, Prentice-Hall, New York, 3rd edn, 2001, p. 3998040 Search PubMed.
- J. Al Boukhari, A. Khalaf and R. Awad, J. Alloys Compd., 2020, 820, 153381 CrossRef CAS.
- N. S. Gonçalves, J. A. Carvalho, Z. M. Lima and J. M. Sasaki, Mater. Lett., 2012, 76, 36–38 CrossRef.
- M. N. Siddique and P. Tripathi, J. Alloys Compd., 2020, 825, 154071 CrossRef CAS.
- P. Ravikumar, B. Kisan and A. Perumal, AIP Adv., 2015, 5, 087116 CrossRef.
- S. Liu, J. Jia, J. Wang, S. Liu, X. Wang, H. Song and X. Hu, J. Magn. Magn. Mater., 2012, 324, 2070–2074 CrossRef CAS.
- Z. Wang, H. Zhou, D. Han and F. Gu, J. Mater. Chem. C, 2017, 5, 3247–3253 RSC.
- M. H. Mamat, N. Parimon, A. S. Ismail, I. B. Shameem Banu, S. Sathik Basha, R. A. Rani, A. S. Zoolfakar, M. F. Malek, A. B. Suriani, M. K. Ahmad and M. Rusop, Mater. Res. Bull., 2020, 682, 012070 Search PubMed.
- R. E. Dietz, G. I. Parisot and A. E. Meixner, Phys. Rev. B, 1971, 4, 2302 CrossRef.
- H. Ramachandran, M. M. Jahanara, N. M. Nair and P. Swaminathan, 10.1039/c9ra08466e.
- N. Mironova-Ulmane, A. Kuzmin, I. Steins, J. Grabis, I. Sildos and M. Pärs, J. Phys.: Conf. Ser., 2007, 93, 012039 CrossRef.
- S. Park, H. S. Ahn, C. K. Lee, H. Kim, H. Jin, H. S. Lee, S. Seo, J. Yu and S. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 134103 CrossRef.
- M. Vhareta, R. M. Erasmus and J. D. Comins, Int. J. Refract. Met. Hard Mater., 2020, 88, 105176 CrossRef CAS.
- R. Vicentini, L. M. Da Silva, L. H. Costa, H. Zanin, T. Tadeu and W. G. Nunes, J. Electrochem. Soc., 2018, 165, A3684–A3696 CrossRef.
- S. L. Medway, C. A. Lucas, A. Kowal, R. J. Nichols and D. Johnson, J. Electroanal. Chem., 2006, 587, 172–181 CrossRef CAS.
- P. Oliva, J. Leonardi, J. F. Laurent, C. Delmas, J. J. Braconnier, M. Figlarz, F. Fievet and A. de Guibert, J. Power Sources, 1982, 8, 229–255 CrossRef CAS.
- D. S. Hall, C. Bock and B. R. MacDougall, J. Electrochem. Soc., 2014, 161, 787–795 CrossRef.
- J. van Drunen, A. F. B. Barbosa and G. Tremiliosi-Filho, Electrocatalysis, 2015, 6, 481–491 CrossRef CAS.
- M. Wehrens-Dijksma and P. H. L. Notten, Electrochim. Acta, 2006, 51, 3609–3621 CrossRef CAS.
- D. S. Hall, D. J. Lockwood, S. Poirier, C. Bock and B. R. MacDougall, J. Phys. Chem. A, 2012, 116, 6771–6784 CrossRef CAS PubMed.
- S. Deabate, F. Fourgeot and F. Henn, Electrochim. Acta, 2006, 51, 5430–5437 CrossRef CAS.
- B. S. Yeo and A. T. Bell, J. Phys. Chem. C, 2012, 116, 8394–8400 CrossRef CAS.
- C. Julien and M. Massot, Solid State Ionics, 2002, 148, 53–59 CrossRef CAS.
- M. V. Rama Krishna and R. A. Friesner, J. Chem. Phys., 1991, 95, 8309 CrossRef.
- I. C. Faria, R. Torresi and A. Gorenstein, Electrochim. Acta, 1993, 38, 2765–2771 CrossRef CAS.
- W. Q. Chen, J. Wang, K. Y. Ma, M. Li, S. H. Guo, F. Liu and J. P. Cheng, Appl. Surf. Sci., 2018, 451, 280–288 CrossRef CAS.
- K. Xu, J. Yang and J. Hu, J. Colloid Interface Sci., 2018, 511, 456–462 CrossRef CAS.
- H. Chen, C. Huang and J. Jiang, J. Electrochem. Soc., 2018 DOI:10.1149/2.0241803jes.
- X. Sun, G. Wang, J. Y. Hwang and J. Lian, J. Mater. Chem., 2011, 21, 16581 RSC.
- I. A. Degen and G. A. Newman, Spectrochim. Acta, Part A, 1993, 49, 859–887 CrossRef.
- C. C. Pye and W. W. Rudolph, J. Phys. Chem. A, 2001, 105, 905–912 CrossRef CAS.
- T. S. Pacheco, S. Ghosh, M. de Oliveira, A. A. Barbosa, G. J. Perpétuo and C. J. Franco, J. Sci.: Adv. Mater. Devices, 2017, 2, 354–359 Search PubMed.
- P. Pasierb, S. Komornicki, M. Rokita and M. RÈ©kas, J. Mol. Struct., 2001, 596, 151–156 CrossRef CAS.
- P. Kalyani and N. Kalaiselvi, Sci. Technol. Adv. Mater., 2005, 6, 689–703 CrossRef CAS.
- T. S. Pacheco, S. Ghosh, M. de Oliveira, A. A. Barbosa, G. J. Perpétuo and C. J. Franco, J. Sci.: Adv. Mater. Devices, 2017, 2, 354–359 Search PubMed.
- W. G. Nunes, R. Vicentini, B. G. A. Freitas, F. E. R. Oliveira, A. M. P. Marque, R. M. Filho, G. Doubek, L. M. Da Silva and H. Zanin, J. Energy Storage, 2020, 31, 101583 CrossRef.
- R. Bini and V. Schettino, Materials under extreme conditions: Molecular crystals at high pressure, 2013 Search PubMed.
- A. J. Campbell, L. Danielson, K. Righter, C. T. Seagle, Y. Wang and V. B. Prakapenka, Earth Planet. Sci. Lett., 2009, 286, 556–564 CrossRef CAS.
- J. S. Pigott, D. A. Ditmer, R. A. Fischer, D. M. Reaman, R. Hrubiak, Y. Meng, R. J. Davis and W. R. Panero, Geophys. Res. Lett., 2015, 42, 10239–10247 CrossRef CAS.
- A. J. Cinthia, R. Rajeswarapalanichamy and K. Iyakutti, Z. Naturforsch., A: Phys. Sci., 2015, 70, 797–804 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505–1509 CrossRef CAS.
- N. Yu, W. B. Zhang, N. Wang, Y. F. Wang and B. Y. Tang, J. Phys. Chem. C, 2008, 112, 452–457 CrossRef CAS.
- W. A. N. G. Jifang, E. S. Fisher and M. H. Manghnzmi, Chin. Phys. Lett., 1991, 8, 153–156 CrossRef.
- J. R. Cost, K. R. Janowski and R. C. Rossi, Philos. Mag., 1968, 17, 851–854 CrossRef CAS.
- M. Jiang and L. Dai, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054204 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr00065a |
| This journal is © The Royal Society of Chemistry 2021 |