Prediction of room-temperature ferromagnetism and large perpendicular magnetic anisotropy in a planar hypercoordinate FeB₃ monolayer

Abstract

Two-dimensional (2D) magnets simultaneously possessing a high transition temperature and large perpendicular magnetic anisotropy are extremely rare, but essential for highly efficient spintronic applications. By using ab initio and global minimization approaches, we for the first time report a completely planar hypercoordinate metalloborophene (α-FeB₃) with high stability, unusual stoichiometry and exceptional magnetoelectronic properties. The α-FeB₃ monolayer exhibits room-temperature ferromagnetism (T_c = 480 K), whose origin is first revealed by the B-mediated RKKY interaction in the 2D regime. Its perpendicular magnetic anisotropy is almost six times larger than that of the experimentally realized 2D CrI₃ and Fe₃GeTe₂. Moreover, metallic α-FeB₃ shows n- and p-type Dirac transport with a high Fermi velocity in both spin channels. Our results not only highlight a promising 2D ferromagnet for advanced spintronics, but also pave the way for exploring novel 2D magnetism in boron-based magnetic allotropes.

---

New concepts

The discovery of two-dimensional (2D) magnetism opens the gate for advanced spintronic nanodevices. However, the practical application of 2D magnets is limited by their own disadvantages, such as low Cuire temperature and/or moderate magnetic anisotropy. In this work, by combining comprehensive PSO and first-principles approaches, we present a new type of metalloborophene (α-FeB₃) monolayer with a planar hypercoordinate structure, high stability and novel magnetoelectronic properties. α-FeB₃ exhibits out-of-plane ferromagnetism with a Curie temperature of 480 K. The magnetic anisotropy energy is almost six-times larger than that of 2D CrI₃ and Fe₃GeTe₂. Such novel magnetism in α-FeB₃ originates from the B-mediated RKKY interaction, which is first revealed in the 2D regime. Furthermore, metallic α-FeB₃ shows n- and p-type Dirac transport with a high Fermi velocity in both spin channels. Our findings highlight the α-FeB₃ monolayer with novel magnetoelectronic properties for highly efficient spintronic applications and pave the way for exploring new 2D magnets among boron-based allotropes.

Introduction

The realization of two-dimensional (2D) magnetism provides unprecedented opportunities for future magnetoelectronic and magneto-optic applications.^1–4 However, the long-range 2D ferromagnetic (FM) order is limited by its instability originating from short-range interactions and weak anisotropy, as established in the Mermin–Wagner theorem.⁵ After unremitting efforts, a few 2D magnets were experimentally fabricated.^6–10 Herein, the sizable magnetocrystalline anisotropy plays the critical role in lifting the Mermin–Wagner restriction, thus stabilizing the 2D magnetic order. Among them, the CrI₃ and Fe₃GeTe₂ monolayers exhibit persistent ferromagnetism and large perpendicular magnetic anisotropy (∼0.70 meV per magnetic atom).^7,9 However, the Curie temperatures of these monolayers remain well below room temperature, imposing great limitations on practical applications.¹¹ The exception is the room-temperature 2D magnet VSe₂, which, however, can only be synthesized on metal substrates.¹² Its wide application is then limited by the unstable magnetic order in the free-standing form.¹³ In addition, a very limited number of single-layer magnets have been theoretically predicted, all with a magnetic anisotropy significantly lower than that of the CrI₃ monolayer.^14–21 Hence, the exploration of new 2D magnets with high transition temperatures and large perpendicular magnetic anisotropy remains a huge challenge and is of great importance for both fundamental research and future applications.

Boron, B, is electron deficient and can form diverse compounds with metals. These span a range of different stoichiometry and present rich electrochemical properties.^22,23 Recently, 2D boron nanosheets, i.e. borophene, have been experimentally realized in abundant allotropes^24,25 with novel Dirac dispersion, superconductivity and high thermal conductivity.^26–28 Going beyond borophene, metalloborophene (MB) could be a promising platform for the exploration of a new family of 2D compounds with hypercoordinate metal–boron bonds.²⁹ However, unlike the rich stoichiometries in the bulk compounds and planar structures in clusters, to date theoretically investigated MB nanosheets are limited to the MB_2n composition, rarely possessing a completely planar geometry.^30–34 Particularly, MB monolayers with transition metal centred boron rings promise great potential in stabilizing 2D magnetism since the intrinsic magnetic coupling is likely induced by the unpaired d or f electrons.³⁵ Nevertheless, current studies have been mainly focused on their electronic and optical properties.^30–34 Therefore, the study of the origin of the magnetism in 2D hypercoordinate MB is still urgent and significant. If it displays novel 2D magnetism, the MB monolayer might offer hope for applications toward high-speed, low dissipation spintronic nanodevices.

In this work, we investigate 2D MB allotropes by departing from the conventional MB_2n configurations. Herein, Fe is chosen as the magnetic element, simply because its multiple oxidation states can facilitate the coordination with B. By combining a global structure search and density functional theory (DFT) calculations, we have discovered a completely planar α-FeB₃ monolayer with an unusual hypercoordinate structure, high stability, and novel magnetic and electronic properties. In such a planar structure, hexacoordinate and pentacoordinate B coexist around the Fe centre. Electron transfer from Fe to B atoms in the Fe©B₆ ring endows the 2D FeB₃ structure with significant dynamical and thermal stability.³¹ Remarkably, the α-FeB₃ sheet possesses perpendicular FM with a high Curie temperature of 480 K. Its high magnetic anisotropy energy (MAE) also suggests great potentials for applications in low energy spintronics. The origin of the 2D magnetism in the MB monolayer is first realized in terms of the B-mediated Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions. Furthermore, n- and p-type Dirac dispersions with high Fermi velocities are discovered in both spin channels. This work provides new insights into the chemical bonding in 2D boron-based hypercoordinate materials and aims at stimulating experimental efforts towards magnetic α-FeB₃ for novel spintronic devices.

Results and discussion

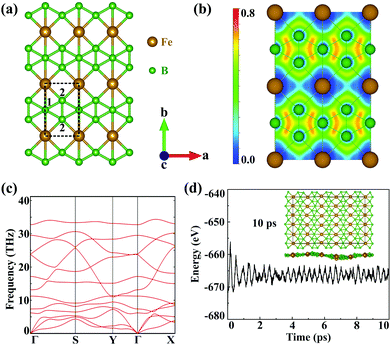
The geometric structures of 2D unconventional iron borides including FeB, FeB₃ and FeB₅ are first generated and then filtered by comprehensive particle swarm optimization (PSO) and DFT calculations. Among thousands of generated structures, iron triboride, FeB₃, possesses the lower relative energy and the completely planar structure is expected to exhibit high stability and unique properties. Fig. S1 (ESI†) shows the convex hull diagram of the predicted FeB_x monolayers. Compared to the discovered FeB_2n monolayers, FeB₃ nanosheets are more energetically favourable. Accordingly, five FeB₃ monolayers with relatively lower energies are plotted in Fig. S2 (ESI†). The first two planar structures are named α- and β-FeB₃. The α-FeB₃ monolayer (space group Pmmm) possesses a rectangular lattice with parameters a = 2.90 and b = 4.49 Å, while β-FeB₃ with a space group of P6/mmm presents a hexagonal lattice with a = 3.89 Å, and contains kagome B and trigonal Fe sublattices. Since a large total energy gap (−0.37 eV per atom) exists between these two structures, we mainly focus on the α-FeB₃ monolayer, with the details for β-FeB₃ in the ESI.† In Fig. 1(a), each iron atom is coordinated by 6 boron ones, forming planar iron-centred boron wheels (Fe©B₆). Here, the Fe©B₆ unit is composed of hexacoordinate (B1) and pentacoordinate (B2) boron atoms with bond lengths of 2.25 Å for Fe–B1 and 2.04 Å for Fe–B2. Notably, the bond angle of Fe–B2–Fe is near to 90° along the a direction, while the Fe–B1–Fe one is linear along the b direction. In addition, the B–B bond length (1.66 Å) is comparable to that in borophene (∼1.67 Å),^24,36 suggesting the stability of α-FeB₃. To understand the bonding nature, we calculate the electron localization function (ELF) of the FeB₃ monolayer. As shown in Fig. 1(b), the electrons are mainly delocalized around Fe atoms, and an electron gas with an ELF value of around 0.5 is distributed between Fe and B. These indicate ionic Fe–B bonds and electron transfer from Fe to B. Bader charge analysis also confirms that each Fe atom transfers 0.87e electrons to the B framework.

Fig. 1 (a) Geometric structures, (b) ELF, (c) phonon spectrum and (d) AIMD simulations for the α-FeB₃ monolayer. The brown and green spheres represent Fe and B atoms, respectively. The top and side views of α-FeB₃ at the end of the AIMD simulation are shown in (d).

Next, we evaluate the stability of the newly predicted FeB₃ monolayer. The thermodynamic stability is examined by calculating the cohesive energies. The estimated energy is 5.93 eV per atom, which is larger than that of other stable monolayers, such as FeB₂ (4.87 eV per atom) and FeB₆ (5.56–5.79 eV per atom).^30,31 Such large cohesive energy suggests that the FeB₃ sheet is thermodynamically stable. Then, Fig. 1(c) shows that the phonon spectrum presents no imaginary frequency, meaning that the compound is also kinetically stable. In addition, we also evaluate the thermal stability of α-FeB₃ by an ab initio molecular dynamics (AIMD) simulation at 800 K for 10 ps. In Fig. 1(d), the energy of the α-FeB₃ monolayer fluctuates in a small range (∼0.1 eV per atom) during the entire simulation, and the final structure is well-preserved at the high temperature, indicating good thermal stability. To further investigate the mechanical stability, we calculate the elastic constants of the FeB₃ monolayer. These are computed as C₁₁ = 198.80, C₁₂ = 58.42, C₂₂ = 145.34 and C₆₆ = 22.02 N m⁻¹, namely they satisfy the Born criteria (C₁₁, C₂₂ and C₆₆ > 0, and C₁₁C₂₂ – C₁₂² > 0). This indicates that the FeB₃ monolayer is mechanically stable. Moreover, the calculated Young's modulus shows a large difference between the a and b directions (175.04 and 128.17 N m⁻¹), suggesting its strong structural anisotropy (see Fig. S3 in the ESI†).

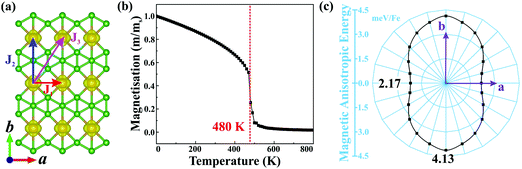
Planar α-FeB₃ with a highly stable structure is a promising candidate for 2D magnetism, given the presence of the partially occupied Fe 3d orbitals. Thus, to determine its magnetic ground state, we examine the 2 × 2 supercells having different magnetic configurations (see Fig. S4, ESI†). The calculated corresponding total energies are listed in Table S1 (ESI†). Accordingly, the magnetic ground state is found to be FM with the lowest energy among the examined configurations. As shown in Fig. 2(a), the spin density is localized around the Fe atoms, suggesting that the magnetism is mainly contributed by the Fe 3d electrons. The net magnetic moment of each Fe atom is 2.89 μ_B. We then calculate the magnetic coupling parameters of α-FeB₃ based on the Ising model. Herein, J₁, J₂ and J₃ describe the exchange interactions between nearest-neighbour (NN), second-NN and third-NN Fe atoms, respectively. The calculated parameters are J₁ = 10.51, J₂ = 58.03 and J₃ =18.30 meV; thus, the estimated Curie temperature from Monte Carlo simulations is about 480 K [Fig. 2(b)], much higher than room temperature (details are in the ESI†). Finally, we calculate the MAE with respect to the out-of-plane direction by the equation of MAE = E_x−y − E_z (a positive value represents perpendicular magnetism). Fig. 2(c) shows that the α-FeB₃ monolayer possesses perpendicular uniaxial anisotropy with a MAE reaching 4.13 meV per Fe, almost six times larger than that of the most-studied 2D magnets, such as CrI₃ (∼0.70 meV per Cr)³⁷ and Fe₃GeTe₂ (∼0.67 meV per Fe).³⁸ The orbital-resolved MAE (see Fig. S5, ESI†) shows that the significant magnetic anisotropy in α-FeB₃ is mainly contributed by the coupling between Fe d_yz and d_xz orbitals. The contribution of the coupling of d_xy–d_x²−y², d_yz–d_z² and d_xz–d_z² orbitals is only half of that of d_yz–d_xz coupling.

Fig. 2 (a) Spin-dependent charge density of the α-FeB₃ monolayer, (b) average magnetic moment as a function of temperature and (c) MAE in the x–y plane with respect to the out-of-plane direction. The isovalue of the spin charge density is set to be 0.01 e Å⁻³.

In order to understand the origin of such 2D magnetism, we analyse the exchange interactions between the magnetic atoms. In α-FeB₃, the distance between NN Fe atoms is 2.90 Å, suggesting weak Fe–Fe direct exchange.¹¹ Thus, the dominant magnetic coupling is likely to be the indirect RKKY interaction, due to the existence of electron deficient orbitals in boron, as found in other rare earth borides.^39,40 Importantly, the exchange parameters of the RKKY interaction decay in an oscillatory way with the distance between the magnetic atoms. To elucidate this point, we examine the relation between the exchange parameters and the Fe–Fe distance. Herein, biaxial strains from −5% to 5% per formula unit (f.u.) are adopted to change the distance between Fe atoms. The calculated total energies of α-FeB₃ in Table S2 (ESI†) indicate that the magnetic ground state of α-FeB₃ undergoes a FM to stripe antiferromagnetic (AFM-1 and AFM-2) transition under compressive and tensile strains of 4% per f.u., respectively. As shown in Fig. S6 (ESI†), the estimated magnetic exchange fluctuates between FM and AFM coupling with respect to the change in the Fe–Fe distance, consistent with an RKKY-type interaction.

Since magnetism controllable by an external stimulus may extend the range of application of a magnet, we explore two possible approaches, strain and charge-carrier doping, to externally modulate the magnetism. In brief, we find that the Fe magnetization increases under tensile strains, while it decreases upon compression [Fig. S7(a), ESI†]. Upon charge-carrier doping (≤0.5 e/h per f.u.), the Fe magnetization first slightly drops and then rises again with the hole concentration, whereas it remains monotonous for electron doping [Fig. S7(b), ESI†]. The transition temperatures of the FeB₃ monolayer are then estimated through Monte Carlo simulations (Fig. S8 and S9, ESI†), whose results are summarised in Fig. 3(a) and (b). Clearly, biaxial strains remarkably decrease the transition temperature of FeB₃ with the value dropping to 30 K (at 5% per f.u.), due to the large oscillations of the RKKY exchange. Interestingly, the Curie temperature of the α-FeB₃ monolayer drops to 160 K after peaking at 610 K (at 0.2 h per f.u.) for hole doping, whereas it decreases monotonically under electron doping. In addition, Fig. 3(c) and (d) summarise the changes of the MAE under the external stimulus. Herein, the α-FeB₃ monolayer keeps the perpendicular magnetic anisotropy under biaxial strains, whereas the MAE changes to in-plane (along the a and b directions) under electron and hole doping over 0.4 e/h per f.u, respectively. In Fig. 3(c), a decrease of the MAE is shown under biaxial strains. Besides, as shown in Fig. 3(d), the presence of additional electrons reduces the magnetic anisotropy, while a hole concentration of around 0.1 h per f.u. maximizes the MAE (4.55 meV per Fe). This then suggests that moderate hole-doping represents the ideal condition for magnetism by simultaneously promoting the magnetic exchange and the uniaxial MAE.

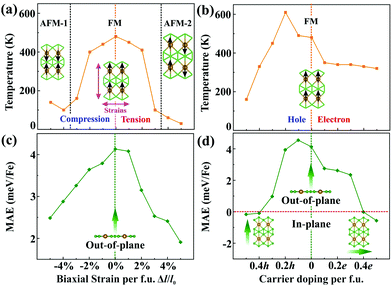Fig. 3 Transition temperature and magnetic anisotropy energy (MAE) of the FeB₃ monolayer as a function of (a and c) external strains and (b and d) charge-carrier doping, respectively.

Next, we turn our attention to the electronic properties of the planar α-FeB₃. As shown in Fig. 4, the α-FeB₃ monolayer is metallic with several Dirac points above and below the Fermi surface, having an n- and p-type dispersion, respectively. Due to the strong interaction between Fe and B, the contribution of these Dirac points involves orbitals from both atoms (Fig. S10, ESI†). For instance, the p-type Dirac point I in the spin-up channel is contributed by both B p_z, p_x + p_y and Fe d_yz, d_x²−y² orbitals [Fig. 4(c)], while the orbital components for the n-type one in the spin-down channel are the p_z orbital of B1 and B2 and the Fe d_yz, d_xz orbitals [Fig. 4(d)]. Besides, the Fermi velocities of Dirac point I and II are calculated to be 20.84 and 8.39 × 10⁵ m s⁻¹, which are comparable to the value of graphene and borophene (∼10⁶ m s⁻¹).^28,41 Since spin–orbit coupling (SOC) will affect the electronic properties, we then calculate the band structure of the α-FeB₃ monolayer by considering the SOC effect, as shown in Fig. S11 (ESI†). We can see that the p-type Dirac point I keeps the linear dispersion with the SOC effect, whereas the n-type Dirac point II shows a small gap of 0.18 eV. Thus, the SOC effect truly affects some of the Dirac-type dispersions; however, some Dirac dispersions are still retained in α-FeB₃ monolayers. The combination of the intriguing magnetic and electronic properties makes 2D FeB₃ a candidate for the exploration of diverse spintronic effects (such as the anomalous Hall effect).⁴²

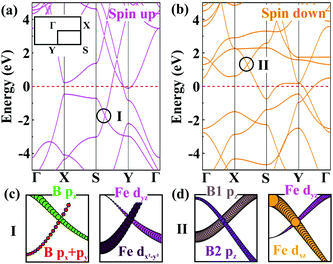Fig. 4 Band structures of the α-FeB₃ monolayer for the (a) spin up and (b) spin down channels. The orbital-resolved band structures of Dirac point (c) I and (d) II.

Finally, we investigate one possible route for experimental synthesis of the α-FeB₃ monolayer. As we all know, atomically thin boron allotropes have been synthesised for a long time.^43,44 Accordingly, the newly predicted α-FeB₃ monolayer is expected to be experimentally realized by adsorbing the Fe atoms onto the δ₄ boron nanosheet. Although a δ₄ boron layer has not been synthesised yet, its lower formation energy than some of the fabricated ones suggests feasibility in experimental synthesis.⁴⁵ The possible adsorption sites for Fe atoms on the δ₄ boron sheet are marked in Fig. S12(a) (ESI†). The Fe adsorption energy is calculated by E_ads = E_Fe–boron − E_boron − E_Fe, where E_Fe–boron, E_boron and E_Fe represent the total energies of the Fe adsorbed boron sheet, the pure boron sheet and a single Fe atom. Generally, the adsorption of Fe on the single-layer boron sheet is energetically favourable with negative E_ads for all sites [see Fig. S12(b), ESI†]. Notably, the adsorption energy at site I is remarkably lower than the other examined sites, indicating that the Fe atoms prefer to adsorb on that site. As shown in Fig. S12(c) (ESI†), the Fe adsorbed δ₄ boron sheet can change its phase to our predicted α-FeB₃ monolayer under uniaxial strains along the b direction with a very small barrier energy of around 16 meV. Therefore, the α-FeB₃ monolayer is likely to be realized in an experiment by adsorbing Fe atoms and then applying external strains on the δ₄ boron sheets.

Conclusions

In conclusion, based on PSO global minimization and ab initio calculations, we have discovered an iron triboride polymorph (α-FeB₃) with completely planar hypercoodination. This is also a member of a new family of magnetic MB allotropes with unusual B stoichiometry. The predicted α-FeB₃ monolayer exhibits ferromagnetism at a high temperature of 480 K. The origin of its magnetic coupling is ascribed to the B-mediated RKKY interactions. Intriguingly, α-FeB₃ possesses perpendicular magnetic anisotropy reaching a MAE value of 4.13 meV per Fe, which is several times larger than what is found in experimentally realized 2D magnets. Notably, both external strain and charge-carrier doping can be used to effectively tune its 2D magnetism. Finally, the α-FeB₃ monolayer is metallic with Dirac dispersions in both spin channels for n- and p-type doping. Our findings pave the way for the discovery of new hypercoodinate MB allotropes as a promising 2D material platform for high-performance spin-enabled applications.

Computational details

We have performed a swarm-intelligence structural search by mean of the CALYPSO code.^46,47 This is powered by DFT using the Vienna ab initio simulation package (VASP)^48,49 at the level of the Perdew–Burke–Erzenhof (PBE)⁵⁰ exchange–correlation functional within the projector-augmented wave (PAW) method.⁵¹ In order to describe the strong interaction of d electrons, a Hubbard on-site Coulomb potential was set for Fe to U − J = 4.0 eV.^52,53 This value is comparable to pioneering work.^11,54 The Heyd–Scuseria–Ernzerhof functional was adopted for electronic calculations.⁵⁵ The cut-off energy was set to 500 eV, and a 13 × 7 × 1 Monkhorst k-mesh was used to sample the first Brillouin zone. The interactions between neighbouring layers were shielded by a vacuum layer over 20 Å. Additionally, DFT-D3 corrections were included for interlayer van der Waals interactions.⁵⁶ The structures were optimized until the energy and forces on each atom converged to 10⁻⁶ eV and 0.001 eV Å⁻¹, respectively. Moreover, a 2 × 2 supercell of the α-FeB₃ monolayer was adopted when considering the different magnetic configurations (more details can be found in the ESI†).

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors acknowledge generous grants of high-performance computer resources provided by Queensland University of Technology, NCI National Facility, the Pawsey Supercomputing Centre through the National Computational Merit Allocation Scheme supported by the Australian Government, the Government of Western Australia. A. D. greatly appreciates the financial support from the Australian Research Council under Discovery Project (DP170103598). S. S. thanks the Irish Research Council Advanced Laureate Award (IRCLA/2019/127) for financial support.

References

1. C.-Z. Chang, J. Zhang, X. Feng, J. Shen, Z. Zhang, M. Guo, K. Li, Y. Ou, P. Wei and L.-L. Wang, Science, 2013, 340, 167–170.
2. W. Han, R. K. Kawakami, M. Gmitra and J. Fabian, Nat. Nanotechnol., 2014, 9, 794.
3. Z. Wang, C. Tang, R. Sachs, Y. Barlas and J. Shi, Phys. Rev. Lett., 2015, 114, 016603.
4. S. Jiang, J. Shan and K. F. Mak, Nat. Mater., 2018, 17, 406–410.
5. N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133.
6. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang and Y. Wang, Nature, 2017, 546, 265–269.
7. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire and D. H. Cobden, Nature, 2017, 546, 270–273.
8. M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289–293.
9. Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu and J. Zhu, Nature, 2018, 563, 94–99.
10. D. J. O’Hara, T. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta and D. W. McComb, Nano Lett., 2018, 18, 3125–3131.
11. A. Bandyopadhyay, N. C. Frey, D. Jariwala and V. B. Shenoy, Nano Lett., 2019, 19, 7793–7800.
12. M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289.
13. S.-J. Gong, C. Gong, Y.-Y. Sun, W.-Y. Tong, C.-G. Duan, J.-H. Chu and X. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8511–8516.
14. C. Zhang, Y. Nie, S. Sanvito and A. Du, Nano Lett., 2019, 19, 1366–1370.
15. B. Cui, X. Zheng, J. Wang, D. Liu, S. Xie and B. Huang, Nat. Commun., 2020, 11, 1–8.
16. M. Xu, C. Huang, Y. Li, S. Liu, X. Zhong, P. Jena, E. Kan and Y. Wang, Phys. Rev. Lett., 2020, 124, 067602.
17. X. Li and J. Yang, J. Am. Chem. Soc., 2018, 141, 109–112.
18. C. Huang, J. Feng, F. Wu, D. Ahmed, B. Huang, H. Xiang, K. Deng and E. Kan, J. Am. Chem. Soc., 2018, 140, 11519–11525.
19. Y. Sun, Z. Zhuo, X. Wu and J. Yang, Nano Lett., 2017, 17, 2771–2777.
20. Y. Ma, Y. Dai, M. Guo, C. Niu, Y. Zhu and B. Huang, ACS Nano, 2012, 6, 1695–1701.
21. X. Zhang, B. Wang, Y. Guo, Y. Zhang, Y. Chen and J. Wang, Nanoscale Horiz., 2019, 4, 859–866.
22. G. Akopov, M. T. Yeung and R. B. Kaner, Adv. Mater., 2017, 29, 1604506.
23. S. Carenco, D. Portehault, C. Boissiere, N. Mezailles and C. Sanchez, Chem. Rev., 2013, 113, 7981–8065.
24. X. Wu, J. Dai, Y. Zhao, Z. Zhuo, J. Yang and X. C. Zeng, ACS Nano, 2012, 6, 7443–7453.
25. B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563.
26. E. S. Penev, A. Kutana and B. I. Yakobson, Nano Lett., 2016, 16, 2522–2526.
27. D. Li, J. Gao, P. Cheng, J. He, Y. Yin, Y. Hu, L. Chen, Y. Cheng and J. Zhao, Adv. Funct. Mater., 2020, 30, 1904349.
28. F. Ma, Y. Jiao, G. Gao, Y. Gu, A. Bilic, Z. Chen and A. Du, Nano Lett., 2016, 16, 3022–3028.
29. W.-L. Li, X. Chen, T. Jian, T.-T. Chen, J. Li and L.-S. Wang, Nat. Rev. Chem., 2017, 1, 0071.
30. H. Zhang, Y. Li, J. Hou, A. Du and Z. Chen, Nano Lett., 2016, 16, 6124–6129.
31. H. Zhang, Y. Li, J. Hou, K. Tu and Z. Chen, J. Am. Chem. Soc., 2016, 138, 5644–5651.
32. X. Qu, J. Yang, Y. Wang, J. Lv, Z. Chen and Y. Ma, Nanoscale, 2017, 9, 17983–17990.
33. C. Zhang, T. He, S. K. Matta, T. Liao, L. Kou, Z. Chen and A. Du, J. Phys. Chem. Lett., 2019, 10, 2567–2573.
34. B. Song, Y. Zhou, H.-M. Yang, J.-H. Liao, L.-M. Yang, X.-B. Yang and E. Ganz, J. Am. Chem. Soc., 2019, 141, 3630–3640.
35. B. Wang, X. Zhang, Y. Zhang, S. Yuan, Y. Guo, S. Dong and J. Wang, Mater. Horiz., 2020, 7, 1623–1630.
36. H. Tang and S. Ismail-Beigi, Phys. Rev. Lett., 2007, 99, 115501.
37. J. L. Lado and J. Fernández-Rossier, 2D Mater., 2017, 4, 035002.
38. Y. J. Deng, Y. J. Yu, Y. C. Song, J. Z. Zhang, N. Z. Wang, Z. Y. Sun, Y. F. Yi, Y. Z. Wu, S. W. Wu, J. Y. Zhu, J. Wang, X. H. Chen and Y. B. Zhang, Nature, 2018, 563, 94.
39. S. Gabani, K. Flachbart, K. Siemensmeyer and T. Mori, J. Alloys Compd., 2020, 821, 153201.
40. T. Mori, T. Takimoto, A. Leithe-Jasper, R. Cardoso-Gil, W. Schnelle, G. Auffermann, H. Rosner and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104418.
41. J. Scott, Science, 2007, 315, 954–959.
42. Z. Liu, G. Zhao, B. Liu, Z. Wang, J. Yang and F. Liu, Phys. Rev. Lett., 2018, 121, 246401.
43. A. J. Mannix, X.-F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago and J. R. Guest, Science, 2015, 350, 1513–1516.
44. B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563–568.
45. W. Li, L. Kong, C. Chen, J. Gou, S. Sheng, W. Zhang, H. Li, L. Chen, P. Cheng and K. Wu, Sci. Bull., 2018, 63, 282–286.
46. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
47. Y. Wang, M. Miao, J. Lv, L. Zhu, K. Yin, H. Liu and Y. Ma, J. Chem. Phys., 2012, 137, 224108.
48. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
49. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
51. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
52. S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
53. L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
54. Z. Fang, K. Terakura, H. Sawada, T. Miyazaki and I. Solovyev, Phys. Rev. Lett., 1998, 81, 1027.
55. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
56. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nh00598c

---