Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
van der Waals solid solution crystals for highly efficient in-air photon upconversion under subsolar irradiance†
Riku
Enomoto
 a,
Megumi
Hoshi
a,
Hironaga
Oyama
b,
Hideki
Agata
c,
Shinichi
Kurokawa
d,
Hitoshi
Kuma
d,
Hidehiro
Uekusa
b and
Yoichi
Murakami
a,
Megumi
Hoshi
a,
Hironaga
Oyama
b,
Hideki
Agata
c,
Shinichi
Kurokawa
d,
Hitoshi
Kuma
d,
Hidehiro
Uekusa
b and
Yoichi
Murakami
 *ae
*ae
aSchool of Engineering, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8552, Japan. E-mail: murakami.y.af@m.titech.ac.jp
bDepartment of Chemistry, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8551, Japan
cNissan Motor Co., Ltd., 2 Takaracho, Kanagawa-ku, Yokohama, Kanagawa 220-8623, Japan
dIdemitsu Kosan Co., Ltd., 1-2-1 Otemachi, Chiyoda-ku, Tokyo 100-8321, Japan
ePRESTO, JST, 4-1-8 Honcho, Kawaguchi, Saitama 332-0012, Japan
First published on 28th October 2021
Abstract
Triplet-sensitized photon upconversion (UC) has been proposed for broad applications. However, the quest for superior solid materials has been challenged by the poor exciton transport often caused by low crystallinity, a small crystal domain, and aggregation of triplet sensitizers. Here, we demonstrate substantial advantages of the van der Waals solid solution concept to yield molecular crystals with extraordinary performance. A 0.001%-order porphyrin sensitizer is dissolved during recrystallization into the molecular crystals of a blue-fluorescent hydrocarbon annihilator, 9-(2-naphthyl)-10-[4-(1-naphthyl)phenyl]anthracene (ANNP), which contains bulky side groups. This attempt yields millimeter-sized, uniformly colored, transparent solid solution crystals, which resolves the long-standing problem of sensitizer aggregation. After annealing, the crystals exhibit unprecedented UC performance (UC quantum yield reaching 16% out of a maximum of 50% by definition; excitation intensity threshold of 0.175 sun; and high photostability of over 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s) in air, which proves that this concept is highly effective in the quest for superior UC solid materials.
000 s) in air, which proves that this concept is highly effective in the quest for superior UC solid materials.
New conceptsHerein, the concept of van der Waals solid solutions has been demonstrated to yield triplet-sensitized photon upconversion (UC) organic crystals with extraordinary performance. The use of a hydrocarbon annihilator with bulky side groups (ANNP), which we discovered to embody this concept, has been shown to dissolve triplet-sensitizing porphyrins into the crystals of ANNP during recrystallization and generate uniformly colored and transparent crystals, which are solid solutions we aimed towards. The large conformational freedom of the side group in the crystal is elucidated to be the key to generate solid solutions. Near-equilibrium formation of only the α-phase (ANNP crystal doped with sensitizer molecules) without generating the β-phase (sensitizer aggregates) differentiates this concept from the existing kinetically controlled concept that causes a small crystal domain size and a short exciton diffusion length. The present concept effectively enhances the lifetime and diffusion length of triplet excitons because of the high crystallinity. After annealing, the crystals exhibit outstanding UC performance in air, which demonstrates the effectiveness of this concept. Suppression of the detrimental back energy transfer from the annihilator to the sensitizer has been shown to be an additional advantage. Therefore, the proof-of-concept here opens a large domain of versatile dispersion-force-based organic systems in the quest for superior UC solids. |
Introduction
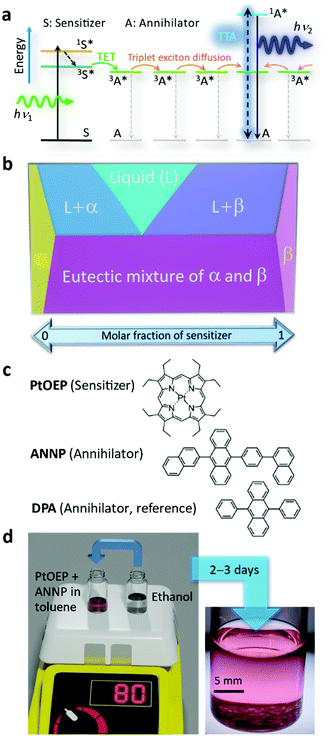
Photon upconversion (UC) creates high-energy photons that are useful for many purposes from less-useful, longer-wavelength photons. UC based on triplet–triplet annihilation (TTA) is an active area of research because of broad applicability spanning solar energy harvesting,1–3 optoelectronics,4,5 photochemistry,6–8 photoelectrochemistry,9–11 and bio-related applications.12,13To date, the majority of reports on TTA-UC have studied liquid samples.1–3 However, liquid samples have risks of freezing, evaporation, and ignition, although some samples have high stability even against a flame.14,15 Furthermore, the large gas diffusivity in liquids requires suppression of damaging singlet oxygen.12,16–18 To resolve these issues, a solid UC system is being quested19–22 where triplet energy transfer (TET) from the sensitizer to the annihilator and triplet exciton diffusion should be efficiently designed (Fig. 1a).
After some initial works,23–28 the major obstacle has been the segregation of the sensitizer from the condensed phase of the annihilator,29–38 which forms an aggregate of the sensitizer and greatly diminishes the UC quantum yield (ΦUC, defined as a maximum of 50% in this report), as typically reported for the combination of platinum octaethylporphyrin (PtOEP, Fig. 1b) and 9,10-diphenylanthracene (DPA, Fig. 1b).29–33
To avoid this segregation issue, previous studies used a kinetically controlled approach30–38 where organic solids were quickly formed. For example, Simon and coworkers30 reported the fabrication of molecular glasses by rapidly cooling a hot melt of a sensitizer–annihilator mixture, but suppression of the aggregate was incomplete. Other studies31–38 formed organic thin films by casting a solvent solution on a flat substrate, where researchers, to an effective extent, suppressed the segregation of the sensitizer from the annihilator chromophores.
Some mechanistic studies showed, however, that the grain boundary and thus the grain size were the limiting factors for triplet exciton diffusion.39,40 Mikhnenko et al.41 pointed out a significant degree of disorder in amorphous and polycrystalline organic thin films, in particular when the films were cast from solution.
Although the number of reports is limited, some studies used nonkinetic approaches.13,42–45 For example, Oldenburg et al.42 fabricated sensitizer–annihilator heterojunctions of thin metal–organic framework (MOF) layers and reported ΦUC < 0.1% and an excitation threshold intensity‡ (Ith) of ca. 1 mW cm−2. Ogawa et al.43 reported an aggregation-free dispersion of an anionic sensitizer in the crystal of an ionic annihilator utilizing ionic interactions between the chromophores (ΦUC = 3% and Ith = 49 mW cm−2 in Ar), in which the photographs of the crystals, photostability data, and information on whether or not the crystals included the solvent methanol were not presented. Recently, Roy et al.45 reported MOF crystals with ΦUC = 1.95% and Ith = 5.1 mW cm−2. However, these values were, as in other MOF-based reports,13,44 for a liquid suspension and no photostability data were shown, whereas ref. 13 (ΦUC = 0.64% and Ith = 2.5 mW cm−2) showed photodegradation data.
Surprisingly, van der Waals crystals formed by dispersion forces, representing the simplest class of organic crystals, have been nearly unexplored in the quest for high-performance UC solids. This lack of study may be because of the impact of the initial work29 that showed considerable segregation of PtOEP from the molecular crystal of DPA, which was also found in subsequent reports;30–33 the authors of ref. 43 described that dispersion-force based strategies sacrifice the advantages of crystalline systems.
The dispersion force approach has, however, many inherent advantages. First, by use of a weak dispersion force, the cost of the chromophores can be minimized because there is no need for elaborate moieties or ligands that cause specific interactions. Second, by use of a defined phase, samples can gain thermodynamic stability. This is in contrast with the previous strategy of using kinetically controlled methods because solids formed by such rapid methods rely on a nonequilibrium state.
Herein, we show, to our best knowledge, the first explicit exploitation of van der Waals forces to unequivocally resolve the long-standing sensitizer segregation problem by means of the classical but resurging concept of solid solutions.46 In solid solutions, represented by α and β phases in Fig. 1b, mixing entropy is the driving force that molecularly disperses one component into a solid of the other component.46,47 Thus, the strategy envisaged here is to selectively generate dispersion-force-based α crystals and avoid emergence of a β phase that is the sensitizer aggregate (Fig. 1b). We generated such solid solution crystals with an extremely low sensitizer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) annihilator mole ratio (ca. 1
annihilator mole ratio (ca. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). Note that the similar term mixed crystal can include heterogeneous systems, such as a mixture of α and β phases,47 which was not targeted here.
000). Note that the similar term mixed crystal can include heterogeneous systems, such as a mixture of α and β phases,47 which was not targeted here.
One of the key factors of the success here is attributable to our discovery of an excellent hydrocarbon annihilator, 9-(2-naphthyl)-10-[4-(1-naphthyl)phenyl]anthracene (ANNP, Fig. 1c), originally developed as a blue organic light-emitting diode (OLED) chromophore. Researchers often choose an asymmetric structure in OLED molecules.48,49 The key mechanism responsible for successful formation of α-phase crystals is attributable to the 4-(1-naphthyl)phenyl side group, which features two distinct conformations and provides an interstitial site in the crystal. The sample was generated by a recrystallization method (Fig. 1d and Experimental section, ESI†) over 2–3 days. We thereby generated crystals that display extraordinary performance in air, as shown below.
Results and discussion
The crystals were pinkish (color of PtOEP) and transparent (Fig. 2a), with a flat-plate shape and thickness between ca. 50 and 250 μm (Fig. 2b). Polarization microscopy indicated twin-like multiple single-crystalline domains (Fig. 2b). The results were highly reproducible and we found no polymorph.Optical absorption measurements of a crystal were straightforward because of the flat shape (Fig. S1, ESI†). The absorption spectrum of the single crystal (Fig. 2c) was identical to that of a dilute toluene solution of PtOEP, albeit with a 3.5 nm redshift of the peak. Fig. 2c also shows a spectrum of an over-saturated suspension of PtOEP in toluene, exhibiting an aggregation feature at 550 nm.50,51 The absence of the aggregation feature in the UC crystal indicates molecular dissolution of PtOEP in the crystal of ANNP and thus formation of a solid solution. Optical microscopic observations at a high magnification did not indicate aggregates (Fig. S2, ESI†). The spectrum did not depend on the light polarization (Fig. S3, ESI†) and thus PtOEP had no preferential orientation, at least for the direction normal to the largest crystal plane. From the absorption spectra, the concentration of PtOEP in the crystals was ca. 5 × 10−5 M (Table S1, ESI†). This corresponds to a significantly low sensitizer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) annihilator mole ratio of ca. 1
annihilator mole ratio of ca. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, which also supports that the crystals in Fig. 2 are a solid solution.
000, which also supports that the crystals in Fig. 2 are a solid solution.
Below, we conducted all of our experiments in air. We excited the samples with a laser at 542 nm, which was 3.5 nm away from the absorption peak at 538.5 nm (Fig. 2c), unless otherwise stated. In this report, an excitation of 1 mW cm−2 intensity at 542 nm corresponds to a sensitizer excitation density52,53 of ca. 4.8 × 10−5 M s−1. We used a microscope-based setup (Fig. S4, ESI†) to investigate the photoemission from a single crystal.
During excitation at 542 nm, we observed an UC emission peaked at 434 nm (Fig. 3a). Conversely, we observed no UC emission from a reference crystal prepared with DPA by the same method (Fig. 3a and S5, ESI†). This demonstrates that the side groups of ANNP (Fig. 1c) played a key role in accommodating PtOEP in the crystal, as discussed below. The quantum yield of the phosphorescence of PtOEP (inset of Fig. 3a) was ca. 1 × 10−5, indicating that the TET from PtOEP to ANNP was quantitative.
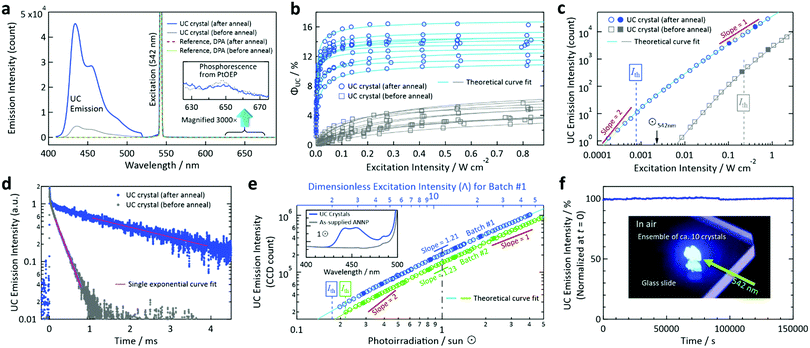 | ||
| Fig. 3 Photoemission properties measured in air. (a) Typical emission spectra acquired from a UC crystal before and after annealing. For comparison, we show the results of a reference crystal prepared with DPA (Fig. S5, ESI†), from which we observed no UC emission. The inset shows a 3000× magnification of the 625–675 nm range. (b) Dependence of ΦUC on the excitation intensity at 542 nm acquired from 10 crystals for the cases of before and after annealing. Refer to Table S1 (ESI†) for the entire dataset for the 20 crystals in total. (c) Dependence of the UC emission intensity on the excitation intensity at 542 nm acquired from samples #A7 and #B2 in Table S1 (ESI†) (refer also to Figs. S6 and S7, ESI†). We fit the curves by a theoretical function (ref. 53), from which we obtained Ith values. (d) Time-resolved UC emission intensity decay curves (excitation: 540 nm, monitor: 455 nm) acquired from an ensemble of ca. 10 UC crystals before and after annealing. Note that the triplet lifetime τT is twice the decay time-constant of the UC emission intensity. (e) Dependence of the UC emission intensity on the simulated sunlight irradiance in units of sun (⊙) to an ensemble (3.2 mg) of the UC crystals. Refer to the Experimental section for details. The inset shows the emission spectra acquired under 1⊙ irradiance after being passed through a 510 nm long-pass filter, where the results obtained with the as-supplied ANNP powder (3.2 mg) are also presented. (f) Photostability test under continuous irradiation of 542 nm laser light (intensity: 20 mW cm−2) to an ensemble of ca. 10 UC crystals on a glass slide, as shown by the inset photograph acquired through a notch filter. We corrected the fluctuation of the excitation laser power during the measurement (refer to Fig. S14, ESI†). In panels (c) and (e), we acquired the data represented by open marks first by increasing the excitation light power, and then we acquired the data represented by filled marks to check the quantitative reproducibility. | ||
Notably, we greatly enhanced the emission intensity (Fig. 3a), ΦUC (Fig. 3b), and Ith (Fig. 3c) of the as-generated crystals by annealing at 90 °C for 4 days to ΦUC = 16.4% and Ith = 0.77 mW cm−2 for the maximum and lowest values, respectively, for measurements of 10 samples. The average values were 13.4% and 2.1 mW cm−2, respectively; Table S1 and Fig. S6 and S7 (ESI†) present the entire data. This dramatic enhancement is attributable to the improved crystallinity, as supported by the selective increase of the intensities of higher-angle peaks in the powder X-ray diffraction patterns by annealing (Fig. S8, ESI†). This hypothesis is further supported by the drastic increase of the triplet lifetime τT from a value of 470 μs to a value of 5.1 ms (Fig. 3d). We also found a slight increase in the fluorescence quantum yield ΦFL (from a value of 38.7% to a value of 41.7%, Table S2, ESI†). Note that these values were lower than the ΦFL of ANNP in a toluene solution (3 × 10−6 M, deaerated by three freeze–pump–thaw cycles), which was measured to be 84.3%; refer to Fig. S9 in the ESI† for the fluorescence spectra of ANNP in the crystal and toluene solution. Therefore, ΦUC in the present materials system is largely limited by ΦFL in the crystalline state.
In Fig. 3c, we regarded 2.31 mW cm−2, obtained by integrating an AM1.5 solar spectrum54 over the range of 538.5 ± 7 nm, as an equivalent solar irradiance for monochromatic excitation at 542 nm (⊙![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542nm) based on eqn (1):
542nm) based on eqn (1):
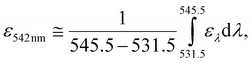 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542nm is that it cannot include ελ that is outside the integration range of eqn (1).
542nm is that it cannot include ελ that is outside the integration range of eqn (1).
We thus resort to direct evaluation using a solar simulator. We passed the simulated sunlight through a 510 nm long-pass filter and irradiated onto an ensemble (3.2 mg) of the crystals (batch #1) (Experimental section and Fig. S10, ESI†). We obtained the UC emission from the sample under one-sun (1⊙) irradiance, whereas we observed no emission when we replaced the crystals by the same quantity of ANNP (inset of Fig. 3e). This verified that the blue fluorescence exclusively originated from UC. From the dependence of the UC emission intensity on the irradiance (Fig. 3e), the slope in the double-logarithmic scale was 1.21 at 1⊙. Using this slope, we calculated the dimensionless excitation intensity53 (Λ) to be 11.1 at 1⊙. Because this is well above the value Λ = 2 that corresponds to Ith,53 we have confirmed the subsolar nature of the present UC. The theoretical curve fit53 to the data points yielded Ith = 0.175⊙, which matched Λ = 2 as shown by the top axis of Fig. 3e. This Ith value is unprecedentedly low. The reproducibility check carried out using another sample batch (batch #2, 3.2 mg) reproduced the results with a slightly different Ith = 0.216⊙.
There are two additional features of the crystals. First, the crystals exhibit high photostability under continuous photoirradiation in air (Fig. 3f, at 542 nm and 20 mW cm−2). Such photostability may come from the close-packed molecular arrangement that is attributable to the high crystallinity. Second, thermo-gravimetric analysis (TGA) showed that the crystals contained 2.1 wt% solvent, and this quantity did not change by annealing (Fig. S11, ESI†). This indicates stable accommodation of the solvent, which can escape at a temperature greater than 150 °C (Fig. S11, ESI†).
We analyzed single-crystal X-ray diffraction (sc-XRD) data for a single crystal of the as-received ANNP (Fig. 4a) and a single domain cut out of the UC crystal (Fig. 4b). For the latter, only the case after annealing is shown here because the change in the crystallographic parameters caused by annealing is too small to be clearly evident pictorially (see Table S3 for these crystallographic data, ESI†). In Fig. 4b, PtOEP is not seen because of its significantly low concentration.
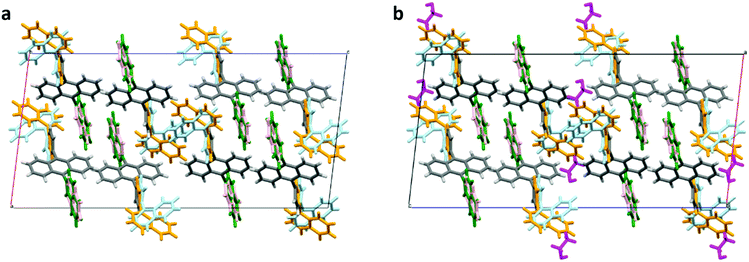 | ||
| Fig. 4 Crystal structures determined from the single crystal X-ray diffraction data. (a) As-supplied ANNP and (b) UC crystal after annealing. Here, the side groups of ANNP have two distinct conformations (4-(1-naphthyl)phenyl group in light blue and orange, and 2-naphthyl group in green and light pink) that coexist in both cases. In panel (b), ethanol molecules are shown in magenta. Refer to Table S3 (ESI†) for the crystallographic data for all the cases. CCDC deposition numbers 2109297 and 2109300 contain the supplementary crystallographic data for panels (a) and (b), respectively. | ||
These data indicate that the 2-naphthyl group had two slightly different conformations, displayed in green and light pink whose ratio was 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 for both Fig. 4a and b. Conversely, the 4-(1-naphthyl)phenyl group had two substantially different conformations, displayed in light blue and orange whose ratio was 51
28 for both Fig. 4a and b. Conversely, the 4-(1-naphthyl)phenyl group had two substantially different conformations, displayed in light blue and orange whose ratio was 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 for both Fig. 4a and b. As evident in the center of the graphics, simultaneously adopting light-blue configurations by two adjacent ANNP molecules is prohibited because of their spatial overlap. Only “light blue + orange” or “orange + orange” pairs are allowed. This large conformational freedom suggests the presence of an interstitial space near it.
49 for both Fig. 4a and b. As evident in the center of the graphics, simultaneously adopting light-blue configurations by two adjacent ANNP molecules is prohibited because of their spatial overlap. Only “light blue + orange” or “orange + orange” pairs are allowed. This large conformational freedom suggests the presence of an interstitial space near it.
We discuss two notable points. First, as shown in Fig. 4b, there are ethanol molecules, shown in magenta color, near this conformational freedom with a mole ratio of ANNP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol = 5
ethanol = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This ratio did not change by annealing, which agrees with the constant quantity of the included solvent (2.1 wt%) by annealing found by TGA. Here, 2.1 wt% ethanol corresponds to the mole ratio of ANNP
1. This ratio did not change by annealing, which agrees with the constant quantity of the included solvent (2.1 wt%) by annealing found by TGA. Here, 2.1 wt% ethanol corresponds to the mole ratio of ANNP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol ≅ 4
ethanol ≅ 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which roughly agrees with the ratio determined by the sc-XRD analysis. Second, the crystal structure of the UC crystal did not change from that of the as-supplied ANNP, except for slight changes in the crystallographic parameters (Table S3, ESI†). This implies the rigidity of the ANNP arrangement in the crystal. From the sc-XRD data, the density of ANNP was 2.44 × 103 mol m−3, which is much lower than those of anthracene (6.99 × 103 mol m−3)55 and DPA (3.72 × 103 mol m−3).56 We surmise that PtOEP molecules were also accommodated near that side group, although not directly evident by this analysis. Thus, the rigid and low-density network of ANNP and the movable 4-(1-naphthyl)phenyl side group are the key factors for realizing the concept we targeted. Notably, analysis of the sc-XRD data assuming toluene instead of ethanol was impossible. However, a trace quantity of toluene could have also been included. The inclusion of a much lesser quantity of toluene could be ascribed to the larger molecular volume of toluene in organic crystals (Voronoi–Dirichlet polyhedron volume, 157.5 Å3) than that of ethanol (86.4 Å3).57
1, which roughly agrees with the ratio determined by the sc-XRD analysis. Second, the crystal structure of the UC crystal did not change from that of the as-supplied ANNP, except for slight changes in the crystallographic parameters (Table S3, ESI†). This implies the rigidity of the ANNP arrangement in the crystal. From the sc-XRD data, the density of ANNP was 2.44 × 103 mol m−3, which is much lower than those of anthracene (6.99 × 103 mol m−3)55 and DPA (3.72 × 103 mol m−3).56 We surmise that PtOEP molecules were also accommodated near that side group, although not directly evident by this analysis. Thus, the rigid and low-density network of ANNP and the movable 4-(1-naphthyl)phenyl side group are the key factors for realizing the concept we targeted. Notably, analysis of the sc-XRD data assuming toluene instead of ethanol was impossible. However, a trace quantity of toluene could have also been included. The inclusion of a much lesser quantity of toluene could be ascribed to the larger molecular volume of toluene in organic crystals (Voronoi–Dirichlet polyhedron volume, 157.5 Å3) than that of ethanol (86.4 Å3).57
Triplet exciton diffusion characterizes the properties of a solid TTA-UC system.41,58 Monguzzi et al. derived59
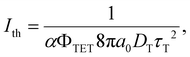 | (2) |
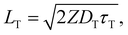 | (3) |
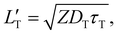 | (4) |
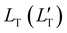 of 1.68 (1.19) μm. These values are approximately two orders of magnitude larger than the previously reported values for solid TTA-UCs,13,40,60,61 except LT ∼1.6 μm for water-suspended MOF nanoparticles of ca. 55 nm size.13 We compared these reported LT and D values in Table S4 (ESI†). Thus, within a sphere with radius
of 1.68 (1.19) μm. These values are approximately two orders of magnitude larger than the previously reported values for solid TTA-UCs,13,40,60,61 except LT ∼1.6 μm for water-suspended MOF nanoparticles of ca. 55 nm size.13 We compared these reported LT and D values in Table S4 (ESI†). Thus, within a sphere with radius 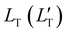 , there are approximately 1.25 × 106 (4.43 × 105) PtOEP molecules. Therefore, the significantly low concentration of PtOEP caused by our use of the α-phase (cf.Fig. 1b) was not problematic. These results reconfirm previous suggestions39,40,43 that high crystallinity and a large crystalline domain are important for efficient UC in solids.
, there are approximately 1.25 × 106 (4.43 × 105) PtOEP molecules. Therefore, the significantly low concentration of PtOEP caused by our use of the α-phase (cf.Fig. 1b) was not problematic. These results reconfirm previous suggestions39,40,43 that high crystallinity and a large crystalline domain are important for efficient UC in solids.
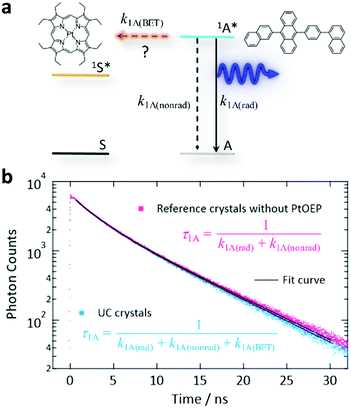
Finally, we discuss back-energy transfer (BET, Fig. 5a). BET was previously regarded as inevitable in a binary sensitizer–annihilator solid based on the estimated BET efficiency (ΦBET) as high as 40%.35 When Förster resonance energy transfer (FRET)62 is the dominant mechanism, ΦBET can be estimated by comparing the fluorescence decay time-constant (τ1A) from the UC crystals and τ1A from the crystals prepared without PtOEP (Fig. 5b). Note that this method cannot be used to evaluate the BET caused by simple reabsorption of UC photons by the sensitizer because this reabsorption does not change τ1A. Thus, here we assess the BET by FRET that actively quenches the 1A* state. Our double-exponential fits in Fig. 5b yielded fast and slow components, where the time-constants were 2.50 and 7.04 ns for the UC sample, and 2.45 and 7.18 ns for the reference, respectively. These small differences are considered to have mostly arisen from the uncertainty in the curve fitting. Thus, ΦBET in the present system is negligible because of the low concentration of PtOEP. We mention that the τ1A of ANNP in a toluene solution (3 × 10−6 M, deaerated by three freeze–pump–thaw cycles) was 3.78 ns (Fig. S13, ESI†), which was similar to τ1A for the crystals.
Conclusions
We demonstrated the concept of explicitly exploiting van der Waals solid solution crystals consisting of only an α-phase to resolve the long-standing problem of sensitizer segregation and realize materials with outstanding UC performance. Compared with the existing concept of using kinetically controlled fast-solidification conditions, the present approach has the advantages of (i) higher thermodynamic stability because of the reliance on (near-)equilibrium states and (ii) higher UC performance because of the simultaneous achievements of a long triplet exciton diffusion length and suppression of detrimental BET from the 1A* states. The factors in (ii) were caused, respectively, by the large single-crystal domain with high crystallinity and the significantly low concentration of the sensitizer. To form crystalline solid solutions, the interstitial site created by the bulky and movable side group of ANNP has been found to be the key factor, as supported by the comparison with a reference crystal prepared with DPA. The elucidated high ΦUC, low Ith, and high photostability in air are promising for applications. In particular, the extraordinarily low Ith demonstrated by using simulated sunlight indicates that solar concentration optics are no longer needed for efficient upconversion of terrestrial sunlight. Probably the most important advantage of this concept lies in its reliance on the versatile van der Waals force and hydrocarbon annihilators. Overall, the proof-of-concept here is a major technical leap forward in the quest for high-performance UC solids, which will open up diverse photonics technologies in the future.Author contributions
Y. M. conceived the idea and supervised the project. Y. M., H. A., S. K., and H. K. led the project. R. E. and M. H. performed the experiments and analyzed the data. H. K. and S. K. contributed to searching for and selecting the annihilator. R. E. conducted single-crystal X-ray diffraction measurements. H. U. and H. O. analyzed the diffraction data and determined the crystal structure. Y. M. and R. E. wrote the manuscript. All authors commented on the manuscript and agreed with the submission of this manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by JSPS KAKENHI Grant Numbers JP17H03183 and JP20H02082 (Y. M.) and JP18H04504 and JP20H04661 (H. U.). We cordially thank Prof. Masahiro Miyauchi at Tokyo Tech for valuable help and advice provided for the experiments using the solar simulator.Notes and references
- S. Baluschev, T. Miteva, V. Yakutkin, G. Nelles, A. Yasuda and G. Wegner, Phys. Rev. Lett., 2006, 97, 143903 CrossRef CAS PubMed.
- V. Gray, D. Dzebo, M. Abrahamsson, B. Albinsson and K. Moth-Poulsen, Phys. Chem. Chem. Phys., 2014, 16, 10345–10352 RSC.
- T. F. Schulze and T. W. Schmidt, Energy Environ. Sci., 2015, 8, 103–125 RSC.
- K. Börjesson, P. Rudquist, V. Gray and K. Moth-Poulsen, Nat. Commun., 2016, 7, 12689 CrossRef PubMed.
- R. Ieuji, K. Goushi and C. Adachi, Nat. Commun., 2019, 10, 5283 CrossRef PubMed.
- B. D. Ravetz, A. B. Pun, E. M. Churchill, D. N. Congreve, T. Rovis and L. M. Campos, Nature, 2019, 565, 343–346 CrossRef CAS PubMed.
- A. Tokunaga, L. M. Uriarte, K. Mutoh, E. Fron, J. Hofkens, M. Sliwa and J. Abe, J. Am. Chem. Soc., 2019, 141, 17744–17753 CrossRef CAS PubMed.
- B. Pfund, D. M. Steffen, M. R. Schreier, M. S. Bertrams, C. Ye, K. Börjesson, O. S. Wenger and C. Kerzig, J. Am. Chem. Soc., 2020, 142, 10468–10476 CrossRef CAS PubMed.
- R. S. Khnayzer, J. Blumhoff, J. A. Harrington, A. Haefele, F. Deng and F. N. Castellano, Chem. Commun., 2012, 48, 209–211 RSC.
- H. Kim, O. S. Kwon, S. Kim, W. Choi and J. H. Kim, Energy Environ. Sci., 2016, 9, 1063–1073 RSC.
- M. Barawi, F. Fresno, R. Pérez-Ruiz and V. A. de la Peña O’Shea, ACS Appl. Energy Mater., 2019, 2, 207–211 CrossRef CAS.
- Q. Liu, B. Yin, T. Yang, Y. Yang, Z. Shen, P. Yao and F. Li, J. Am. Chem. Soc., 2013, 135, 5029–5037 CrossRef CAS PubMed.
- J. Park, M. Xu, F. Li and H. C. Zhou, J. Am. Chem. Soc., 2018, 140, 5493–5499 CrossRef CAS PubMed.
- Y. Murakami, Y. Himuro, T. Ito, R. Morita, K. Niimi and N. Kiyoyanagi, J. Phys. Chem. B, 2016, 120, 748–755 CrossRef CAS PubMed.
- Y. Murakami, S. K. Das, Y. Himuro and S. Maeda, Phys. Chem. Chem. Phys., 2017, 19, 30603–30615 RSC.
- F. Marsico, A. Turshatov, R. Peköz, Y. Avlasevich, M. Wagner, K. Weber, D. Donadio, K. Landfester, S. Baluschev and F. R. Wurm, J. Am. Chem. Soc., 2014, 136, 11057–11064 CrossRef CAS PubMed.
- C. Mongin, J. H. Golden and F. N. Castellano, ACS Appl. Mater. Interfaces, 2016, 8, 24038–24048 CrossRef CAS PubMed.
- D. Dzebo, K. Moth-Poulsen and B. Albinsson, Photochem. Photobiol. Sci., 2017, 16, 1327–1334 CrossRef CAS PubMed.
- Y. C. Simon and C. Weder, J. Mater. Chem., 2012, 22, 20817–20830 RSC.
- V. Gray, K. Moth-Poulsen, B. Albinsson and M. Abrahamsson, Coord. Chem. Rev., 2018, 362, 54–71 CrossRef CAS.
- B. Joarder, N. Yanai and N. Kimizuka, J. Phys. Chem. Lett., 2018, 9, 4613–4624 CrossRef CAS PubMed.
- P. Bharmoria, H. Bildirir and K. Moth-Poulsen, Chem. Soc. Rev., 2020, 49, 6529–6554 RSC.
- P. E. Keivanidis, S. Baluschev, T. Miteva, G. Nelles, U. Scherf, A. Yasuda and G. Wegner, Adv. Mater., 2003, 15, 2095–2098 CrossRef CAS.
- S. Baluscheva, P. E. Keivanidis, G. Wegner, J. Jacob, A. C. Grimsdale, K. Müllen, T. Miteva, A. Yasuda and G. Nelles, Appl. Phys. Lett., 2005, 86, 061904 CrossRef.
- R. R. Islangulov, J. Lott, C. Weder and F. N. Castellano, J. Am. Chem. Soc., 2007, 129, 12652–12653 CrossRef CAS PubMed.
- P. B. Merkel and J. P. Dinnocenzo, J. Lumin., 2009, 129, 303–306 CrossRef CAS.
- A. Monguzzi, R. Tubino and F. Meinardi, J. Phys. Chem. A, 2009, 113, 1171–1174 CrossRef CAS PubMed.
- T. N. Singh-Rachford, J. Lott, C. Weder and F. N. Castellano, J. Am. Chem. Soc., 2009, 131, 12007–12014 CrossRef CAS PubMed.
- A. Monguzzi, R. Tubino, S. Hoseinkhani, M. Campione and F. Meinardi, Phys. Chem. Chem. Phys., 2012, 14, 4322–4332 RSC.
- R. Vadrucci, C. Weder and Y. C. Simon, J. Mater. Chem. C, 2014, 2, 2837–2841 RSC.
- R. Karpicz, S. Puzinas, V. Gulbinas, A. Vakhnin, A. Kadashchuk and B. P. Rand, Chem. Phys., 2014, 429, 57–62 CrossRef CAS.
- H. Goudarzi and P. E. Keivanidis, J. Phys. Chem. C, 2014, 118, 14256–14265 CrossRef CAS.
- H. Goudarzi and P. E. Keivanidis, ACS Appl. Mater. Interfaces, 2017, 9, 845–857 CrossRef CAS PubMed.
- M. Hosoyamada, N. Yanai, T. Ogawa and N. Kimizuka, Chem. – Eur. J., 2016, 22, 2060–2067 CrossRef CAS PubMed.
- T. Ogawa, M. Hosoyamada, B. Yurash, T. Q. Nguyen, N. Yanai and N. Kimizuka, J. Am. Chem. Soc., 2018, 140, 8788–8796 CrossRef CAS PubMed.
- T. Ogawa, N. Yanai, H. Kouno and N. Kimizuka, J. Photonics Energy, 2018, 8, 022003 Search PubMed.
- K. Kamada, Y. Sakagami, T. Mizokuro, Y. Fujiwara, K. Kobayashi, K. Narushima, S. Hirata and M. Vacha, Mater. Horiz., 2017, 4, 83–87 ( J. Int. Biomed. Inf. Data , 2018 , 5 , 1219 ) RSC.
- A. Abulikemu, Y. Sakagami, C. Heck, K. Kamada, H. Sotome, H. Miyasaka, D. Kuzuhara and H. Yamada, ACS Appl. Mater. Interfaces, 2019, 11, 20812–20819 CrossRef CAS PubMed.
- G. M. Akselrod, P. B. Deotare, N. J. Thompson, J. Lee, W. A. Tisdale, M. A. Baldo, V. M. Menon and V. Bulovic, Nat. Commun., 2014, 5, 3646 CrossRef CAS PubMed.
- K. Narushima, S. Hirata and M. Vacha, Nanoscale, 2017, 9, 10653–10661 RSC.
- O. V. Mikhnenko, P. W. M. Blom and T. Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888 RSC.
- M. Oldenburg, A. Turshatov, D. Busko, S. Wollgarte, M. Adams, N. Baroni, A. Welle, E. Redel, C. Wöll, B. S. Richards and I. A. Howard, Adv. Mater., 2016, 28, 8477–8482 CrossRef CAS PubMed.
- T. Ogawa, N. Yanai, S. Fujiwara, T. Q. Nguyen and N. Kimizuka, J. Mater. Chem. C, 2018, 6, 5609–5615 RSC.
- J. M. Rowe, J. Zhu, E. M. Soderstrom, W. Xu, A. Yakovenko and A. J. Morris, Chem. Commun., 2018, 54, 7798–7801 RSC.
- I. Roy, S. Goswami, R. M. Young, I. Schlesinger, M. R. Mian, A. E. Enciso, X. Zhang, J. E. Hornick, O. K. Farha, M. R. Wasielewski, J. T. Hupp and J. F. Stoddart, J. Am. Chem. Soc., 2021, 143, 5053–5059 CrossRef CAS PubMed.
- M. Lusi, CrystEngComm, 2018, 20, 7042–7052 RSC.
- A. I. Kitaigorodsky, Mixed Crystals, Springer-Verlag, Berlin, 1984. See, e.g., the Preface and Chapter 5 Search PubMed.
- X. Zeng, Y. H. Huang, S. Gong, P. Li, W. K. Lee, X. Xiao, Y. Zhang, C. Zhong, C. C. Wu and C. Yang, Mater. Horiz., 2021, 8, 2286–2292 RSC.
- M. Kubota, M. Funahashi and C. Hosokawa, European Patent EP1696015A1, 2006, URL: https://patents.google.com/patent/EP1696015A1.
- X. F. Zhang, Q. Xi and J. Zhao, J. Mater. Chem., 2010, 20, 6726–6733 RSC.
- J. Kalinowski, W. Stampor, J. Szmytkowski, M. Cocchi, D. Virgili, V. Fattori and P. D. Marco, J. Chem. Phys., 2005, 122, 154710 CrossRef CAS PubMed.
- Y. Zhou, F. N. Castellano, T. W. Schmidt and K. Hanson, ACS Energy Lett., 2020, 5, 2322–2326 CrossRef CAS.
- Y. Murakami and K. Kamada, Phys. Chem. Chem. Phys., 2021, 23, 18268–18282 RSC.
- Reference Air Mass 1.5 Spectra, ASTM G-173-03, https://www.nrel.gov/grid/solar-resource/spectra-am1.5.html.
- R. Mason, Acta Crystallogr., 1964, 17, 547–555 CrossRef CAS.
- J. M. Adams and S. Ramdas, Acta Crystallogr., 1979, B35, 679–683 CrossRef CAS.
- I. A. Baburin and V. A. Blatov, Acta Crystallogr., 2004, B60, 447–452 CAS.
- X. Li and M. L. Tang, Chem. Commun., 2017, 53, 4429–4440 RSC.
- A. Monguzzi, J. Mezyk, F. Scotognella, R. Tubino and F. Meinardi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 195112 CrossRef.
- S. Raišys, K. Kazlauskas, S. Juršėnas and Y. C. Simon, ACS Appl. Mater. Interfaces, 2016, 8, 15732–15740 CrossRef PubMed.
- S. Raišys, O. Adomėnien
![[i with combining dot above]](https://www.rsc.org/images/entities/char_0069_0307.gif) , P. Adomėnas, A. Rudnick, A. Köhler and K. Kazlauskas, J. Phys. Chem. C, 2021, 125, 3764–3775 CrossRef.
, P. Adomėnas, A. Rudnick, A. Köhler and K. Kazlauskas, J. Phys. Chem. C, 2021, 125, 3764–3775 CrossRef. - N. J. Turro, V. Ramamurthy and J. C. Scaiano, Principles of Molecular Photochemistry: An Introduction, University Science Books, Sausalito, CA, USA, 2009, pp. 396–413 Search PubMed.
- Section 17.1 of A. E. Siegman, Lasers, University Science Books, Sausalito, CA, USA, 1986 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2109297–2109300. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1mh01542g |
| ‡ When calculating Ith, the definition of the laser spot area is important. Some researchers used the 1/e2 diameter to calculate the spot area for Gaussian laser beams. However, as described in ref. 63, the laser spot area calculated by the 1/e2 diameter yields a 50% lower excitation intensity than the actual peak intensity in the laser spot. In all previous TTA-UC papers authored by Y. M., a FWHM diameter of the Gaussian profile was used to calculate the spot area, yielding a 1.44 times higher intensity than the actual peak intensity; i.e., conservative calculation of Ith. In the present article, however, all excitation beams had a top-hat intensity profile (cf. Fig. S4, ESI†), and therefore the intensity values for all laser-based experiments matched the actual excitation intensity on the sample. |
| This journal is © The Royal Society of Chemistry 2021 |