Open Access Article
Open Access ArticleArtificial intelligence and machine learning in design of mechanical materials
Kai
Guo
 a,
Zhenze
Yang
a,
Zhenze
Yang
 ab,
Chi-Hua
Yu
ab,
Chi-Hua
Yu
 ac and
Markus J.
Buehler
ac and
Markus J.
Buehler
 *ade
*ade
aLaboratory for Atomistic and Molecular Mechanics (LAMM), Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, 77 Massachusetts Ave. 1-290, Cambridge, Massachusetts 02139, USA. E-mail: mbuehler@MIT.EDU; Tel: +1 617 452 2750
bDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Ave., Cambridge, Massachusetts 02139, USA
cDepartment of Engineering Science, National Cheng Kung University, No. 1, University Road, Tainan City 701, Taiwan
dCenter for Computational Science and Engineering, Schwarzman College of Computing, Massachusetts Institute of Technology, 77 Massachusetts Ave, Cambridge, Massachusetts 02139, USA
eCenter for Materials Science and Engineering, 77 Massachusetts Ave, Cambridge, Massachusetts 02139, USA
First published on 17th December 2020
Abstract
Artificial intelligence, especially machine learning (ML) and deep learning (DL) algorithms, is becoming an important tool in the fields of materials and mechanical engineering, attributed to its power to predict materials properties, design de novo materials and discover new mechanisms beyond intuitions. As the structural complexity of novel materials soars, the material design problem to optimize mechanical behaviors can involve massive design spaces that are intractable for conventional methods. Addressing this challenge, ML models trained from large material datasets that relate structure, properties and function at multiple hierarchical levels have offered new avenues for fast exploration of the design spaces. The performance of a ML-based materials design approach relies on the collection or generation of a large dataset that is properly preprocessed using the domain knowledge of materials science underlying chemical and physical concepts, and a suitable selection of the applied ML model. Recent breakthroughs in ML techniques have created vast opportunities for not only overcoming long-standing mechanics problems but also for developing unprecedented materials design strategies. In this review, we first present a brief introduction of state-of-the-art ML models, algorithms and structures. Then, we discuss the importance of data collection, generation and preprocessing. The applications in mechanical property prediction, materials design and computational methods using ML-based approaches are summarized, followed by perspectives on opportunities and open challenges in this emerging and exciting field.
Introduction
Materials are of significant importance to us as they are the building blocks of the tools to develop our civilization. Numerous effective methods to find new materials have been invented owing to the discovery of the intimate connection between the structure of materials and their various properties, which can be tentatively classified into mechanical, thermal, optical, electrical, chemical, nuclear, and others.1 Among those properties, mechanical properties of materials are of particular interest owing to their intimate relationship with the integrity of structures, which ensures that the materials can consistently work as designed without mechanical failures like material degradation, cracking, buckling and delamination. Design of mechanical materials is the process of tailoring the composition and structure of materials to achieve desired or even unprecedented mechanical properties, which are of great importance to many families of advanced materials. For instance, synthetic composites can be engineered in terms of the composition of each constituent material and the structure of the composites.2 Bio-inspired materials mimic the excellent multifunctionality including mechanical and biological properties of natural biomaterials, while difficult to design due to the complexity of hierarchical and heterogeneous structures of the mimicked biomaterials.3–8 Another emerging category of composites that are rationally designed, called metamaterials, have attracted great interest due to their unprecedented properties compared to conventional materials, attributed to the breakthroughs in experimental techniques and computer-aided optimization tools to design complex material structures.9,10 Architected materials, as a class of new metamaterials, have demonstrated superior mechanical properties, such as high stiffness/strength-to-weight ratios, recoverability under suppression, and damage resistance.11–14 The complexity of compositional and topological structures of advanced materials, however, can easily lead to massive design spaces that exceed the computational limit of brute force approaches and other conventional design algorithms, implying the need for new design approaches.Over the past a few decades, it has been found that artificial intelligence (AI), a study of computations which perceive, reason, and act like human beings, has the potential to address these challenges.15 Specifically, the most promising one is an approach to AI called machine learning (ML), which can discover the mapping from high-throughput input data to output that is used to make decisions. In simple ML algorithms, the representation of input data is hand-designed by researchers, and each piece in the representation is referred to as a feature. Yet, it was extremely challenging to manually extract appropriate features from some sort of raw data that are easy to understand for human but difficult for machines, i.e., photographs of streets where cars are supposed to be recognized, until the emerge of deep learning (DL), a specific type of ML that can not only learn the representation of the input data but also parse the representation into multiple levels—from simple features to abstract ones—attributed to complex neural network structures.16 ML, especially DL, has achieved many exciting breakthroughs in algorithms and led to great success in computer vision, natural language processing and autonomous driving.17 Materials and mechanics communities are aware of the great opportunities of leveraging ML as a potential new paradigm. Several general reviews of materials design using ML have been published during the past few years.18–21 In the meantime, numerous research articles in this topic are coming out, and so do reviews of ML in specific materials or mechanics branches, involving energy materials,22,23 glasses,24 composites,25 polymers,26 bio-inspired materials,27 additive manufacturing,28,29 continuum materials mechanics,30 and so on.
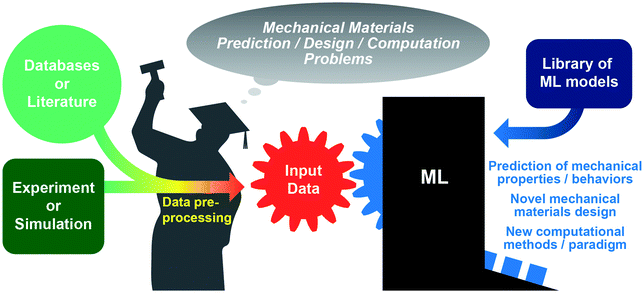
In this review, we focus on reviewing the growth and state of the art of research efforts on mechanical materials design using ML, and also attempt to depict a general methodology for performing ML-based mechanical materials researches. As schematically shown in Fig. 1, a typical workflow for combining ML and materials research consists of three key components: (i) a well-organized material dataset either collected from literature and existing databases or generated from experiments and simulations; (ii) a ML model that is capable to learn and parse the representation for certain tasks; and (iii) a well-defined research problem of mechanical materials that has not been addressed by conventional methods, or has been solved but can be outperformed by ML-based approaches. A ML-based material research needs to glue all of these three components together, and a crucial step is the preprocessing of the raw material database into an appropriate numerical representation, also referred to as a descriptor. The preprocessed data should match the input data structure required by the selected ML model, and consist of essential material features to ensure high accuracy and training efficiency. A high-quality preprocessing requires not only expertise in mechanics and materials science, but also domain knowledge in related ML models. The former tells how to identify a challenging mechanical materials problem, acquire a database, and devise data preprocessing. The latter helps to select a suitable ML model to leverage and maximize its strength in given tasks, from prediction of mechanical behaviors of target materials, design of de novo mechanical materials, to development of new computational approaches.
To further discuss the foregoing methodology with the aid of present works in the literature, the paper is organized as follows. We begin with a brief summary of state-of-the-art ML models, algorithms and architectures. Readers can skip the description of the methods if they have already been familiar with them. To learn more about the methods of interest, we refer to the research articles and reviews cited in this section in which more details about the algorithms and examples are presented. Then we move on to a discussion of approaches to collect or generate datasets that are amenable to the ML models, followed by a review of existing applications of ML methods to various mechanical materials design problems. In these sections, inspiring strategies for data preparation, preprocessing, materials problem and ML model selection are highlighted. The paper is concluded with a few perspectives on the new computational paradigm that integrates mechanics and materials science with ML techniques.
A Brief summary of ML models, algorithms and structures
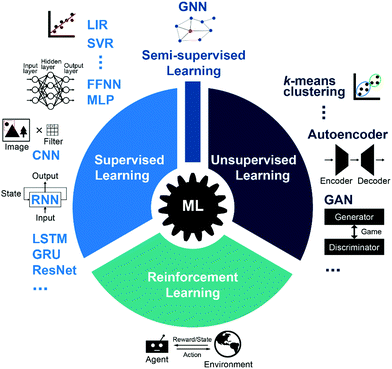
General ML approaches can be classified into three categories known as supervised learning, unsupervised learning and reinforcement learning (Fig. 2). Supervised learning is a task-driven approach to map inputs to outputs with data being labeled (known as the ground truth) during training, while unsupervised learning are data-driven methods trained with unlabeled data to search for undetected patterns of the given dataset. Reinforcement learning is fairly different compared to supervised learning and unsupervised learning which can be distinguished by the presence of labels. Reinforcement learning focuses on interaction between agents such as Go player with the environment such as chessboard. Both supervised learning and unsupervised learning evaluates the model's performance by minimizing a loss function or objective function. By contrast, the objective of reinforcement learning is to maximize the notion of cumulative reward. There is another category of ML approaches called semi-supervised learning. As the name implies, it lies between supervised and unsupervised learning due to the use of both labeled and unlabeled data (generally mostly unlabeled) during training. In the current field of mechanical materials designs, supervised learning approaches are most widely used as supervised tools are more accurate and mature to implement compared to the tools in other categories. Due to rapid and constant development of ML, the methods listed in the section, which cannot claim to be an exhaustive enumeration of existing ML approaches, briefly summarizes some of them that are feasible for designs of mechanical materials to the best of our knowledge.Within this context, the simplest forms of ML without complex multilayer structures are classical ML algorithms. Linear regression (LIR)31 is one of the simplest algorithms aimed to find a linear relation between the input features and continuous output. Least Absolute Shrinkage and Selection Operator (LASSO)32 is a modification of LIR with additional absolute value penalization added to the loss function. Another reasonable extension of LIR is polynomial regression (PR)31 which includes polynomial terms in finding linear solutions. To further support non linearity, regression algorithms such as support vector regression (SVR)33 and random forest (RF)34 are introduced. These nonlinear models usually handle outliers better and show higher accuracy than linear models. Apart from regression, the other major category of ML tasks is classification. Instead of predicting specific values such as housing prices, the classification algorithms classify input into predefined categories. An example of classification algorithms is logistic regression (LOR),35 which is a classification algorithm with a loss function in logistic form despite it is named with “regression”. There are many other classical ML algorithms which can handle both regression and classification problems such as decision tree (DT)36 and gradient boosting.37,38
Beyond classical ML techniques, scientists have developed artificial neural networks (ANNs), loosely inspired by the interconnected neurons in human brains, for deep data mining. The original idea is derived from perceptron, a simple precursor formulation dating back to 1958.39 By stacking multiple layers of neurons, a network structure is developed to learn nonlinear relation between input and output or delicate data distribution. As the depth of layer-by-layer networks increases, the resulting DL models offer tremendous impacts in computer science and various related interdisciplinary areas.
Feedforward neural networks (FFNNs) or multilayer perceptron (MLP)40,41 are probably the simplest and quintessential DL models. As the names indicate, the information passes through the network in a unidirectional manner for FFNNs. More specifically, each layer which consists of multiple neurons computes the output to the next layer based on the input from the previous layer. The weights or trainable parameters used for calculation for each neuron are optimized to minimize the loss function. In order to approach the minimum of the loss function during the training process, back propagation (BP), a widely used technique in ANNs training, is implemented together with gradient descent (GD) algorithm.42 BP functions as similar as calculating derivatives and GD algorithms determine the direction to jump down to the minimum. The process iterates until the loss function is close to its minimum.
Besides general FFNNs, two types of DL architectures are gaining vast attention due to their applications in computer vision and natural language processing (NLP), known as convolutional neural networks and recurrent neural networks.
Convolutional neural networks (CNNs) were first introduced in 1980,43 and reformulated in 1999.44 CNNs are image-based DL architecture by calculating mathematical operation “convolution” to extract features of images. Convolution preserves the spatial relationship between pixels and is calculated by multiplying the image matrix with the filter matrix. Filters contain trainable weights which are optimized during training for feature extraction. With different filters, separate operations such as edge detection can be performed to one image. By stacking the convolutional layers, simple features will be gradually assembled to intact and complicated ones.45 The CNNs are applied to and show exciting performances in face recognition, images classification and object detection.40 In materials design problems, with the capacity of capturing features at different hierarchical levels, CNNs are well suited to describe the properties of materials (which innately have hierarchical levels), especially biomaterials. These hierarchical features are not just found in materials, but in many other representations of matter, sound and language, and hence universal to the description of key societal systems.46,47
Recurrent neural networks (RNNs) also gain popularity due to their capability of dealing with sequential data. In CNNs, inputs and outputs are supposed to be independent of each other, which might not be suitable for some tasks that emphasize the sequence of the data. For instance, given an incomplete sentence, it would be difficult to predict the next word if the sequential structure of the sentence is omitted. Instead, RNNs act on the sequential data with the output being depended on the previous and later sequence and utilize “memories” in determining output of each layer or state. For RNNs with large depth, the gradient calculated by BP easily vanishes or explodes.48,49 To address this issue, plenty of mechanisms including Long short-term memory (LSTM),50 Gated recurrent unit (GRU),51 ResNet52 and Attention53,54 have been developed, increasing the impact of RNNs in NLP tasks such as language translation and speech processing. RNNs also shed light on scientific problems such as protein folding and de novo protein design.55–57
Generative models have been established to generate new data points based on the distribution of existing data. An intriguing and successful category of architectures among them are generative adversarial networks (GANs),58 which consist of two neural networks, the generator and the discriminator. The generator proposes new data instances and the discriminator compares the generated data with the real data. These two components contest with each other during the training as the generator aims to “fool” the discriminator by producing more genuine images while the discriminator attempts to distinguish real images from false images as accurately as possible. GANs reach convergence when the generator and the discriminator are at Nash equilibrium. The process of balancing the performances of the generator and the discriminator is somewhat similar to equilibrating a physical system with both attractive and repulsive forces which indicates that GANs can potentially shed light on describing physical phenomena. Furthermore, with the objective of generating fake data with restricted conditions or characteristics, a subtype of GANs named conditional GANs (cGANs)59 have been developed which include labels as a control variable. One of the applications of cGANs is image-to-image translation60,61 in which an image is used as the constrain of the generator. Unlike GANs, variational autoencoder (VAE)62 is another type of generative models that uses one neural network which first encodes the input data into an inexplainable code named as latent code and then decodes the latent code to reconstruct the output.
ML methods can also be used to evaluate and improve the performance of other applied ML models. Bayesian learning (BL)40 is an approach used for parameter estimation and probability comparison to evaluate a given algorithm. Gaussian process regression (GPR)63 is a nonparametric approach which can provide uncertainty measurements of predictions and build reduced-order models based on Bayesian learning. These approaches are potentially useful for mechanical materials designs problems as they are suitable for relatively small datasets and are working well without prior knowledge of model forms. Moreover, active learning is a learning algorithm that interactively inquires the user and selects data to be labeled.64 Training data would be augmented in an active learning loop with post-hoc experiments or simulations. For further discussion on the application of active learning in materials science, we refer to a recent review paper.65
Reinforcement learning (RL) is an area of ML in which the agent takes action based on the variation of the environment to maximum long-term gains.66 The training process is aiming at finding a balance between exploration (of uncharted territory) and exploitation (of current knowledge).66 From 2014 to 2017, the presence of AlphaGo,67 a RL-based AI was able to beat top-notch Go players, showing the power of RL and its potential applications to materials problems such as interactive materials design.
Graph neural networks (GNNs), unlike standard neural networks operating on Euclidean data, operate on graphs that have non-Euclidean data structures consisting of nodes connected by edges without natural orders.68 Recent breakthroughs in GNNs, such as graph convolutional networks (GCNs),69 have demonstrated the capability of GNNs to learn graph embeddings through message passing between the nodes and its outstanding performance on semi-supervised classification tasks, which are potentially applicable to many materials and mechanics problems that inherently consist of graph structures.
Popular ML models and algorithms used in the design of mechanical materials, along with example applications, are tabulated in Table 1.
| ML method | Characteristics | Example applications in mechanical materials design |
|---|---|---|
| Linear regression; polynomial regression | Model the linear or polynomial relationship between input and output variables | Modulus112 or strength123 prediction |
| Support vector machine; SVR | Separate high-dimensional data space with one or a set of hyperplanes | Strength123 or hardness125 prediction; structural topology optimization159 |
| Random forest | Construct multiple decision trees for classification or prediction | Modulus112 or toughness130 prediction |
| Feedforward neural network (FFNN); MLP | Connect nodes (neurons) with information flowing in one direction | Prediction of modulus,97,112 strength,93 toughness130 or hardness;97 prediction of hyperelastic or plastic behaviors;143,145 identification of collision load conditions;147 design of spinodoid metamaterials163 |
| CNNs | Capture features at different hierarchical levels by calculating convolutions; operate on pixel-based or voxel-based data | Prediction of strain fields104,105 or elastic properties102,103 of high-contrast composites, modulus of unidirectional composites,136 stress fields in cantilevered structures,137 or yield strength of additive-manufactured metals;121 prediction of fatigue crack propagation in polycrystalline alloys;140 prediction of crystal plasticity;120 design of tessellate composites;107–109 design of stretchable graphene kirigami;155 structural topology optimization156–158 |
| Recurrent neural network (RNN); LSTM; GRU | Connect nodes (neurons) forming a directed graph with history information stored in hidden states; operate on sequential data | Prediction of fracture patterns in crystalline solids;114 prediction of plastic behaviors in heterogeneous materials;142,144 multi-scale modeling of porous media173 |
| Generative adversarial networks (GANs) | Train two opponent neural networks to generate and discriminate separately until the two networks reach equilibrium; generate new data according to the distribution of training set | Prediction of modulus distribution by solving inverse elasticity problems;138 prediction of strain or stress fields in composites;139 composite design;164 structural topology optimization;165–167 architected materials design115 |
| Gaussian process regression (GPR); Bayesian learning | Treat parameters as random variables and calculate the probability distribution of these variables; quantify the uncertainty of model predictions | Modulus122 or strength123,124 prediction; design of supercompressible and recoverable metamaterials110 |
| Active learning | Interacts with a user on the fly for labeling new data; augment training data with post-hoc experiments or simulations | Strength prediction124 |
| Genetic or evolutionary algorithms | Mimic evolutionary rules for optimizing objective function | Hardness prediction;126 designs of active materials;160,161 design of modular metamaterials162 |
| Reinforcement learning | Maximize cumulative awards with agents reacting to the environments. | Deriving microstructure-based traction-separation laws174 |
| Graph neural networks (GNNs) | Operate on non-Euclidean data structures; applicable tasks include link prediction, node classification and graph classification | Hardness prediction;127 architected materials design168 |
Data collection, generation and preprocessing
If ML models are the engines to tackle various tasks, then data is the fuel to power the models. Sufficient amount of data is a prerequisite to make the models work, and high-quality data enable the models to run efficiently. Nevertheless, there arise several vital and difficult questions: how much data is sufficient? How to obtain those data? What is the quality of the input data? And how to improve it? These questions are crucial for the ML-based design of mechanical materials since the data relate the mechanics problems of interest to the applied ML models. Researchers can either collect data from the literature or existing databases, or generate their own databases via high-throughput experiments or simulations (Fig. 1). Feeding the raw data into the ML model is usually accompanied with the following issue: when the data is either too easy or too hard to be obtained, it would be unnecessary or difficult to implement ML-based methods for solving the problem. For instance, there is no need to use ML if the existing method can travel through the entire design space at an acceptable cost, and a more common scenario is that the obtained datasets only cover a small portion of the design space. It is also possible that the collected databases of images or texts are understandable for human but uninterpretable for machines. In those cases, the raw data are, in general, required to be preprocessed before fed into the ML model, emphasizing the importance of leveraging the domain knowledge of the researchers to obtain representative data and perform data preprocessing in a proper manner for better results from the ML model. In this section, we briefly review and discuss some methods for data collection, generation and preprocessing in the literature that might shed light on the study of mechanical materials design problems using ML, including several pioneering approaches developed for data-driven computational mechanics,70–73 and data-driven frameworks of materials analysis and design.74–81Data collection from existing databases or literature
The advent of high-throughput computational materials design leads to the construction of many materials databases,82 such as AFLOW,83 Materials Project (MP),84 MATDAT,85 MatWeb,86 MatMatch,87 MakeItForm,88 and MatNavi.89 These databases consist of enormous materials properties obtained from experimental measurements and first-principles calculations, including mechanical properties like elastic constants, tensile/flexural/shear/fatigue strengths, fracture toughness, hardness, and so on. Detailed mechanical features of these databases are listed in Table 2. According to the mechanical problems of interest, sub-datasets of specific properties or material classes can be filtered and collected effectively through the online platforms of those databases. For instance, mechanical properties of inorganic compounds from the MP database have been systematically explored.90 In a separate study, more than one hundred vanadium oxide materials along with various unique compositions have been found in the MP database.91 In order to train DL models, this dataset has been significantly enlarged via a virtual substitution of existing binary materials. As an inspiring example, Raccuglia et al. have leveraged the unreported entries about failed experiments from their archived laboratory notebooks to build a database for use in training and testing the applied ML model.92| Database name | Material categories | Mechanical features | URL |
|---|---|---|---|
| AFLOW83 | Alloys; inorganic compounds | Elastic properties | http://www.aflowlib.org/ |
| Materials Project (MP)84 | Inorganic compounds; nanoporous materials | Elastic properties | https://materialsproject.org/ |
| MATDAT85 | Steels; aluminum and titanium alloys; weld metals; etc. | Static properties; nonlinear stress-strain behaviors; cyclic stress–strain behaviors; fatigue behaviors | https://www.matdat.com |
| MatWeb86 | Polymers; metals; ceramics; semiconductors; fibers; etc. | Elastic properties; strength; toughness; hardness; etc. | http://www.matweb.com |
| MatMatch87 | Metals; composites; ceramics; polymers; glasses; etc. | Elastic properties; strength; toughness; hardness; etc. | https://matmatch.com |
| MakeItForm88 | Metals; polymers; ceramics | Elastic properties; strength; toughness; hardness; etc. | https://www.makeitfrom.com |
| NIMS materials database (MatNavi)89 | Polymers; inorganic materials; metals | Elastic properties; strength; hardness; etc. | https://mits.nims.go.jp/en/ |
Labeled datasets can be obtained from surveying the literature as well, such as datasets of copper alloys with different tensile strengths and electrical conductivities,93 ABO3 compounds,94 high-temperature ferroelectric perovskites,95 and single-molecule magnets.96 In addition, a glass dataset of experimental data was collected from both literature and existing databases.97 The size of the collected dataset relies heavily on the amount of accumulated literatures in the corresponding field. Relatively small datasets with tens to hundreds data points are acceptable for optimization approaches if equipped with an active learning loop.95,98
Furthermore, text processing techniques can be utilized to replace manual labor in the extraction of features from research articles. With NLP techniques adopted, an automated workflow of article retrieval, text extraction and database construction was developed. to build a dataset of synthesis parameters across 30 different oxide systems, which is autonomously compiled and tabulated by training the text processing approach using over 640![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials synthesis journal articles.99 The materials synthesis databases obtained from this approach enable a broader applications of ML methods than before, such as the prediction of materials synthesis conditions100 and candidate precursors for target materials.101
000 materials synthesis journal articles.99 The materials synthesis databases obtained from this approach enable a broader applications of ML methods than before, such as the prediction of materials synthesis conditions100 and candidate precursors for target materials.101
Data generation
When performing high-throughput experiments or simulations, researchers have more freedom to design the features and control the size and distribution of the datasets to be generated. Nevertheless, a major challenge is to balance the expense of data generation and the resulting performance of the applied ML model. Existing works in the literature have shown that leveraging domain knowledge in materials science, solid mechanics and other related fields results in datasets that are more representative of the design spaces and thus display better results from the applied models.Computational methods can be used to simulate materials of interest and relate the mechanical properties to the representative structures of the materials at different scales, from continuum to atomistic levels. For example, finite element method (FEM) was implemented to generate datasets of three-dimensional (3-D) microstructures of high-contrast composites,102–106 two-dimensional (2-D) tessellate composites,107–109 and metamaterials.110 Yang et al. created a dataset of synthetic microstructure images of materials with various compositional and dispersive patterns using Gaussian random field (GRF) method.111 High-throughput molecular dynamics (MD) can be utilized as a design space sampling method for the atomistic structures and behaviors of materials like silicate glasses,112 metal–organic frameworks (MOFs),113 as well as brittle materials with different crystal orientations.114
A framework for data-driven analysis of materials has been built to avoid unacceptable computational expense of data generation from high-fidelity analyses, such as FEM simulations involving plasticity and damage, and reduced order methods were utilized to generate large databases suitable for ML.77,78,81 It is also possible to reduce the scale of design spaces by considering the symmetries in the materials problems to be investigated. The design spaces of 2-D tessellate composites under symmetric loadings can be truncated by half,107–109 and the generated topologies of architected materials were classified into 17 datasets according to the crystallographic symmetry groups in 2-D space.115
Benchmark databases, such as MNIST,116 are particularly useful for comparing the accuracy and efficiency of various ML techniques on specific tasks. Recently, a benchmark dataset named Mechanical MNIST was constructed by converting the MNIST bitmap images into heterogeneous blocks of materials.117 This dataset, labeled by different forms of mechanical responses calculated from FEM simulations, can be used to evaluate the performance of metamodels of heterogeneous materials under large deformation.
Performing experiments to create sufficient large datasets for training DL models is currently difficult due to the extremely high cost. However, high-throughput experiments are applicable to the validation of trained ML models,118 and relatively small training sets can be augmented via post-hoc experiments in an active learning loop.95,98 Recently, an autonomous research system has been built to enable not only automated experimentation but also the selection of subsequent experiments under a framework of Bayesian optimization, which can be utilized to mechanical materials design problems such as optimization of additive manufacturing structures.119
Data preprocessing
ML models expect certain data structures (i.e., images, texts, graphs) as input and thus the datasets need to be preprocessed before fed into the applied model. During preprocessing, data augmentation techniques can be implemented to enlarge the datasets, and irrelevant data points that would deteriorate the performance of the model should be removed.In a recent work on the prediction of fracture patterns in brittle materials, the discrete atoms in a triangular lattice, which is adopted from the MD simulations to generate the datasets of crack patterns, were mapped into ordered pixels in an image that can not only be treated as input to the first convolutional layer of the applied LSTM model but also eliminate the irrelevant information in the atomic structure other than the spatial features of the crack.114 In another example, least angle regression (LARS) was utilized as a feature selection algorithm for a large glass dataset taken from the literature and online databases.97 Image processing techniques, such as rescaling and cropping, were utilized to augment the initial dataset that might be insufficiently large to train a DL model.120 It has been demonstrated that less efforts on preprocessing are required to design features for DL than conventional ML methods due to the ability of the DL models to parse the representation from simple to abstract features through the training process.121 The techniques used to develop data-driven solvers might also inspire efficient methods to process sparse and noisy data of materials responses.70,71
Applications
Prediction of mechanical behaviors
The ML models, trained on the datasets containing materials information, are supposed to give fast and accurate predictions of target mechanical properties or behaviors, or to discover compositions or structures that outperform the training data in the design space.Materials with complex and disordered microstructures, such as glasses and alloys, typically have large databases obtained from experiments or simulations focusing on composition-property relationships. Thus, the selected features like concentrations of components are usually arranged as feature vectors, and ML methods good at processing input vectors are particularly suitable for the property prediction tasks of these materials. For instance, different ML algorithms (PR, LASSO, RF and MLP) were adopted to predict the Young's modulus of silicate glasses.112 Among those methods, MLP gives the highest accuracy, and the LASSO algorithm offers a slightly lower accuracy but higher simplicity and interpretability of the model. It is subsequently shown that using GPR instead of neural networks can avoid overfitting for a sparse dataset.122 Recently, a large dataset obtained from the literature and glass datasets was preprocessed to train deep FFNNs that allow the design of eight essential properties of oxide glasses, including Young's modulus, shear modulus and hardness.97 Wang et al. developed a design system based on neural networks for copper alloys that can rapidly screen the composition design space and provide the compositional design of new copper alloys with a target ultimate tensile strength and electrical conductivity.93 To discover strong and conductive copper alloys, Zhao et al. recently reported a systematic study of the selection of ML models (LIR, SVR, regression tree and GPR), dimensionality reduction techniques (principal component analysis, correlation-based and genetic algorithm) and additional features.123 For gradient nanostructured metals, Gaussian process based active learning surrogate models were developed to study the structural gradient effects on strength and deformation mechanisms.124 Furthermore, new superhard materials were proposed with the aid of ML techniques such as SVR,125 evolutionary algorithms,126 and GNNs.127 In a study by Wen et al., high entropy alloys predicted by the applied ML models were synthesized, showing higher hardness values than any other sample in the training dataset.128 ML models can also be trained to capture the relationship between salient structural features and mechanical properties. For example, deep neural networks that were trained to learn the relationship between the geometric patterns and mechanical responses of non-uniform cellular materials are capable of solving both forward and inverse problems.129 Liu et al. have achieved the fracture toughness prediction of polycrystalline silicon specimens using two different ML algorithms, RFs and FFNNs.130 In a recent study, the strength and toughness of spider webs were predicted by using a neural network trained with fiber lengths and orientations, as well as web connectivity and density.131
ML-based prediction of mechanical properties can also be achieved using atomistic descriptors. For example, local properties (bond length, angle and dihedrals), global properties (density or ring sizes distribution) and porosity-related properties were fed as entries into a gradient boosting regressor to predict mechanical properties of zeolite frameworks.132,133 Given the system temperature, strain rate, vacancy defect and chirality, mechanical properties of single-layer graphene were predicted using different ML algorithms (stochastic gradient descent, k-nearest neighbors, SVR, DT, ANN).134 In a separate work by Moghadam et al., the relationship between the structure and mechanical stability of thousands of MOF materials has been established to predict the bulk modulus of MOF materials using an ANN that inputs structural or topological descriptors.113
For materials that can be represented as tessellated spatial grids of multi-phase voxels, CNNs are advantageous over conventional ML methods in learning embeddings at different length scales ranging from voxels to representative volume elements (RVEs). The elastic deformation fields and effective elastic properties of high-contrast two-phase composites were predicted using 3-D CNN and datasets of 3-D volume elements with different microstructures (Fig. 3).102–105 Convolutional networks with different architectures were used to predict the mechanical properties of polymer nanocomposites based on microstructure images,135 thermo and mechanical properties of unidirectional composites,136 and stress fields in cantilevered structures.137 In particular, Herriott and Spear implemented two conventional ML methods (Ridge regression and gradient boosting) and a CNN model to predict the effective yield strength of additive-manufactured metals.121 When 3D images of the microstructures represented by crystal orientation are input to the CNN model, it outperforms the other two methods fed with microstructural features, demonstrating the strengths of CNN in learning higher-level features directly from image data and reducing the efforts on preprocessing and feature extraction.
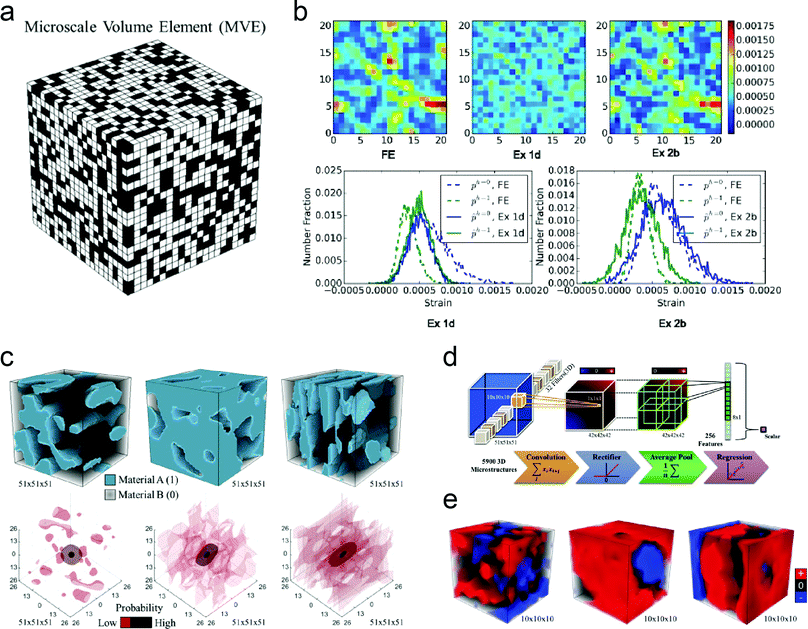 | ||
| Fig. 3 Predicting elastic behaviors of high-contrast composites using convolutional neural network (CNN). (a) An example microscale volume element, and (b) a comparison of strain field prediction from FEM and statistical models. (Licensed under CC-BY).104 (c) The compositional structures (top) and spatial statistics (bottom) of three example generated microstructure volume elements, (d) a schematic of the applied 3-D CNN architecture, and (e) a selection of three learned filters that help to distinguish microstructures similar to the three examples shown in (c), respectively (Reproduced with permission.103 Copyright 2017 Elsevier). | ||
The capability of generative models to deal with image-to-image translation tasks can be harnessed to achieve fast conversion between material distribution and mechanical fields. Ni and Gao developed a cGAN model to address the inverse elasticity problem of calculating elastic modulus distribution from observed displacement or strain fields in inclusion systems, mimicking an application scenario for real-time elastography and high-throughput non-destructive evaluation techniques.138 Recently, Yang et al. introduced a deep learning approach which predicts complex strain or stress fields of hierarchical composites directly from geometric information.139 Image-to-image translation using GANs has been implemented to investigate mechanical systems and exhibited astonishing performances in reproducing mechanical fields, extracting secondary information and extending to various loading conditions, component shapes and hierarchies. This framework could be further applicable to fast prediction of other physical fields with geometric information in image-based representation.
Mechanical problems involving nonlinearities such as plasticity, fracture and dynamic impact are known to be difficult and computationally expensive for conventional numerical simulation schemes. ML-based approaches have created new opportunities for addressing these long-standing problems.
For fracture problems, Pierson et al. developed a CNN-based methodology to predict the microstructure-sensitive propagation of a 3-D fatigue crack in a polycrystalline alloy based on the past crack surface.140 Guilleminot and Dolbow reported a data-driven framework that can generate new crack patterns in random heterogeneous microstructures through the combination of a manifold learning approach and a crack path reconstruction procedure.141 Moreover, Hsu et al. presented a ML-based approach combining convolutional layers and LSTM for predicting fracture patterns in crystalline solids based on atomistic molecular simulations (Fig. 4a).114 The proposed approach not only captures complex fracture processes but also shows good agreement regarding fracture toughness and crack length (Fig. 4b). The work further examined the crack propagation in more complicated crystal structures including bicrystalline materials and graded microstructures (Fig. 4c). The strong predictive power of their approach can be potentially applied to design materials with enhanced crack resistance.
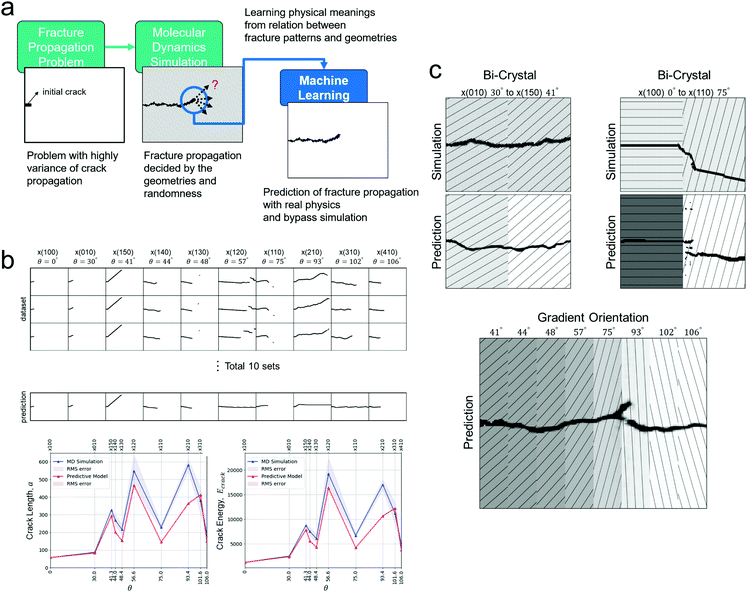 | ||
| Fig. 4 Predicting dynamical fracture using a deep learning approach, dependent on microstructural details. (a) Workflow of fracture patterns prediction. (b) Comparison of crack path, length and energy release between molecular simulations and the ML approach. (c) Prediction of crack patterns in bicrystalline and gradient materials (Reproduced with permission.114 Copyright 2020 Elsevier). | ||
For nonlinear deformation problems, Mozaffar et al. recently established a data-driven framework consisting of RNNs to learn history-dependent behaviors of heterogeneous RVEs loaded along different deformation paths, and it has enabled the prediction of plasticity-constitutive laws in an efficient and accurate manner without adopting the widely-used assumptions in existing plasticity theories (Fig. 5).142 Huang et al. developed a hyperelastic model using FFNNs and a plasticity framework via a combination of FFNNs and Proper Orthogonal Decomposition (POD).143 Yang et al. trained a deep residual network that can predict crystal plasticity using high-throughput discrete dislocation simulations.120 Wu et al. designed a RNN based on GRU to predict the stress–strain evolutions of elasto-plastic composite RVEs subjected to random loading paths.144 Yang et al. utilized ANNs to construct constitutive laws for isotropic hardening elastoplastic materials with complex microstructures.145 In a study by Zhou et al., a discrete dislocation dynamics model of straight dislocations on two parallel slip planes was self-consistently transformed into a continuum model via the integration of asymptotic analysis and ML methods.146 Chen et al. utilized DL models to find the inverse solution to collision load conditions with the post-collision plastic deformation of shell structures given.147 Stern et al. reported a framework for supervised learning in thin creased sheets which can not only accurately classify the patterns of training forces but also generalize to unseen test force patterns, demonstrating how learning can be achieved from plasticity and nonlinearities in materials.148 In order to solve both forward and inverse indentation problems, many efforts have been made using neural networks.149–153 Recently, Lu et al. demonstrated a general framework for extracting elastoplastic properties of materials from instrumented indentation results with significantly elevated accuracy and training efficiency, which have been furtherly improved by considering known physical and scaling laws and by utilizing transfer learning techniques when additional new experimental data are available.154
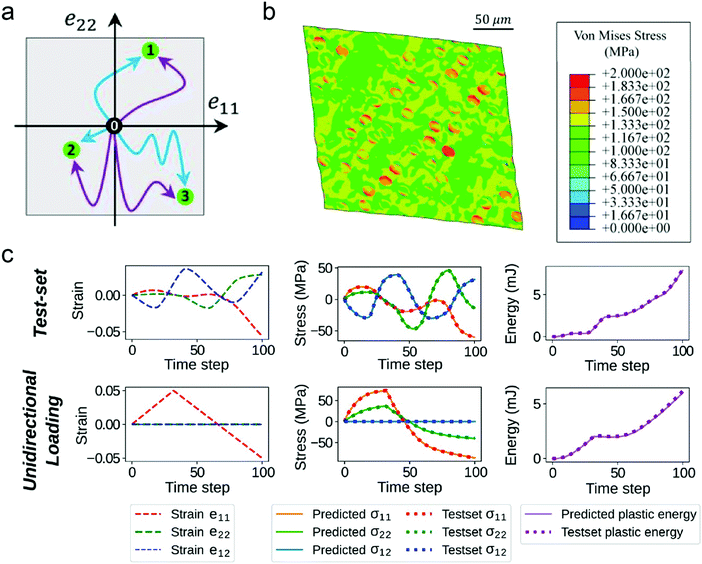 | ||
| Fig. 5 Learning history-dependent plasticity using recurrent neural networks. (a) Schematic of sampling temporally deformation paths. (b) A deformed heterogeneous representative volume element (RVE) with distributed circular fillers in the generated database. (c) Comparison of the results predicted by recurrent neural networks and calculated from FEM analyses for two different RVEs under different loading conditions (Licensed under CC-BY).142 | ||
Topological design
Designing topological structures of multi-phase materials such as composites or architected materials is intractable in some aspects for conventional optimization methods due to the dauntingly large design spaces, while ML-based models have the capability to explore the design spaces more efficiently and to find unprecedented designs with better performance than the structures in training sets.2-D structures of materials can be represented as pixel images, fed as input to image processing models like CNNs and GANs. These models can significantly enlarge the design spaces to be explored for the optimal design, and the design process can be furtherly accelerated through the integration of appropriate optimization algorithms in the workflow. For instance, Gu et al. used CNN to design tessellate composites with optimized strength and fracture toughness (Fig. 6a–d).107,108 CNN was applied to extract local patterns of the composite around the crack tip in the framework. In these problems, the scale of the design space increases exponentially with the number of grid elements in the composites, and finding the optimal design can be easily intractable for brute-force approaches by elevating the grid resolution. In order to address this issue, Yu et al. integrated the CNN model with a genetic algorithm to accelerate the search process using the ML prediction as the fitness function for the optimization algorithm (Fig. 6e and f).109 In a study by Hanakata et al., a CNN-based search algorithm was developed to find optimal arrangements of kirigami cuts in graphenes to maximize stretchability.155
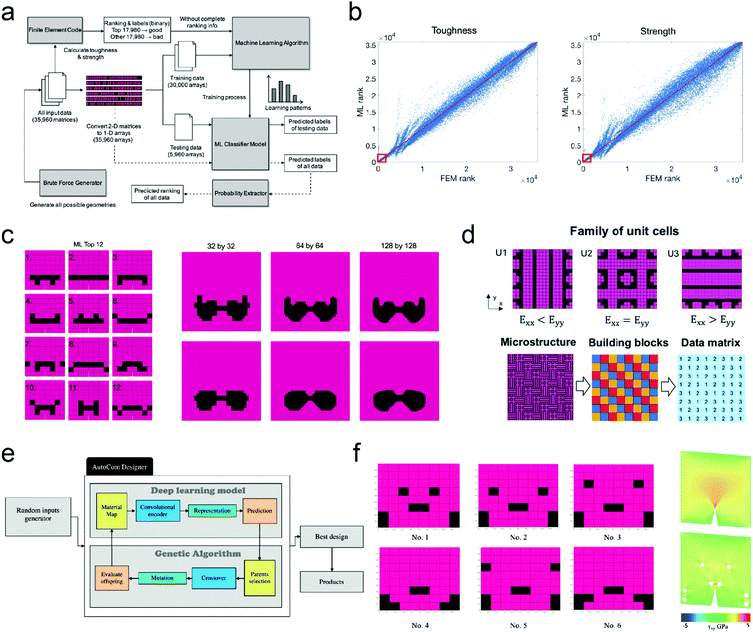 | ||
| Fig. 6 ML-based tessellate composites design for optimal strength and fracture toughness. (a) Workflow of the ML approach for the prediction of mechanical properties of composites. (b) Ranking comparison between the results from the ML approach and FEM simulations. (c) Optimal designs regarding strength and toughness in mode I test at various resolutions (Reproduced with permission.107 Copyright 2017 Elsevier). (d) Extended implementation to composites consisting of anisotropic building blocks (Licensed under CC-BY).108 (e) Framework embedded with genetic algorithm to accelerate the design process and (f) optimal designs in mode II test validated by MD simulations (Reproduced with permission.109 Copyright 2019 IOP Publishing Ltd). | ||
Encoder and decoder frameworks based on convolutional layers can be employed to accelerate the process of topology optimization of mechanical structures.156–158 Since the models were trained with the structures that have already been optimized by standard optimization methods, direct evaluation of mechanical properties (e.g., compliance) in loss functions can be avoided. As a trade-off, designs predicted by ML models may have mechanical incompatibility such as structural discontinuity, but these issues can be refined by connecting a cGAN model to the trained encoder and decoder network.156 Different from a pixel-based representation, a structural topology optimization method has been achieved through the movement of morphable components as basic building blocks, and both SVR and the k-nearest neighbors algorithm were adopted to extract the mapping between the external load and design parameters.159 Even though this approach shrinks the design space, it can avoid mesh dependency and model complexity issues induced by preprocessing structures into pixel images.
Topological design approaches using other ML techniques have also been widely reported in the literature. For example, structural designs of active composite beams and hard-magnetic soft active materials with target deflected shapes were obtained using evolutionary algorithms.160,161 Recently, Wu et al. reported an approach to design modular metamaterials using genetic algorithm and neural networks.162 They applied the method to the design problems of phononic metamaterials and optimization problems of interconnect for stretchable electronics. Kumar et al. built an inverse design framework of spinodoid metamaterials using deep neural networks that can provide optimal topologies for desired properties.163
Leveraging the strengths of advanced ML techniques usually offers new pathways for the design of mechanical materials. Bayesian machine learning is a powerful approach for handling noisy data and can quantify the uncertainty of model predictions, which are particularly useful for design of metamaterials that are often sensitive to manufacturing imperfections. Bessa et al. demonstrated that data-driven designs of supercompressible and recoverable metamaterials made of brittle polymeric base materials can be found with the aid of Bayesian machine learning methods (Fig. 7).110 Generative methods have the ability to create plenty of new designs with different structures and even better mechanical performance compared to those in the training set, suitable for not only composite design,164 but also topology optimization.165–167 Mao et al. harnessed GANs to acquire hundreds of designs of 2D periodic units in architected materials that approach the Hashin-Shtrikman upper bounds and at the same time attain desired crystallographic symmetries and porosities.115 Other work reported the development of a semi-supervised approach to design architected materials using GNNs and the analogy between architected materials and graphs, that is, truss elements to edges, and truss pin joints to nodes.168 Graph connectivity and the load levels of a small fraction of nodes are fed as input to the GNNs that can predict the distribution of the load levels of the remaining nodes, and then the GNN model is integrated with a design algorithm to engineer the topological structures of the architected materials.
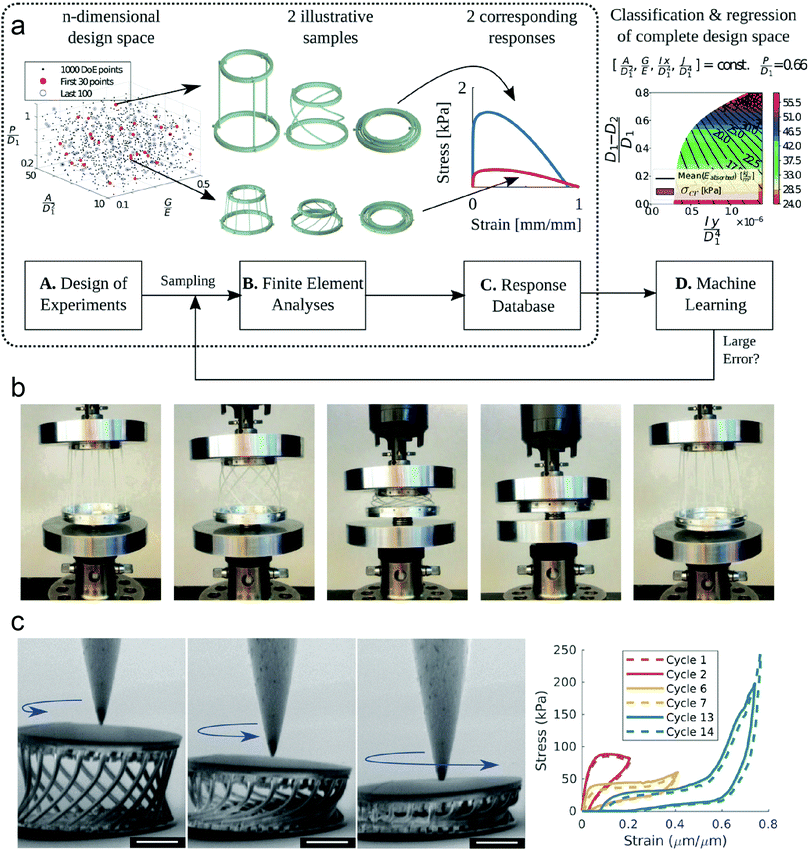 | ||
| Fig. 7 Data-driven design of supercompressible and recoverable metamaterials using Bayesian machine learning. (a) Workflow of the data-driven design approach of supercompressible metamaterials. (b and c) Mechanical testing of the obtained designs of (b) a recoverable and highly compressible metamaterial produced by fused filament fabrication using polylactic acid, and (c) a monolithic metamaterial manufactured by two-photon nanolithography (scale bars, 50 μm) (Licensed under CC-BY).110 | ||
Development of new computational methods
Data-driven approaches, developed for computational mechanics and materials analysis, are aimed to solve mechanics problems in which large datasets of material behaviors are available while governing equations or parameters for standard computational methods are elusive.70–73,77,78 Recently, the integration of data-driven frameworks with ML algorithms have offered new perspectives for computational approaches for modeling mechanical phenomena of materials at multi-level scales.For instance, in order to solve nonlinear heterogeneous structure problems, neural networks have been used in a decoupled computational homogenization method where the effective strain-energy density is first computed at discrete points in a macroscopic strain space and then interpolated on RVEs.76 Inspired by the previous method, a data-driven framework aiming to model and design new composite material systems and structures has been built, accompanied with a method called self-consistent clustering analysis that make the framework applicable to materials problems involving irreversible deformation.78 Moreover, Liu et al. reported a data-driven method called deep material network, which is developed for structure–property predictions of heterogeneous materials under the effects of nonlinear, failure and interfacial behaviors.169–172
Wang and Sun leveraged RNNs and the concept of directed graph to address the issues on the linkages between multi-scale models of porous media using a recursive data-driven approach, where the databases generated from smaller-scale simulations are used to train RNN models at larger scales (Fig. 8).173 They also implemented reinforcement learning to generate traction–separation laws for materials with heterogeneous microstructures.174 Capuano and Rimoli developed a new type of finite elements called “smart elements” in which ML models provide force predictions based on the elements’ states, circumventing the computation of internal displacement field and the need for numerical iterations.175 Chan et al. reported an unsupervised approach that combines techniques such as topology classification, image processing, and clustering algorithms to promptly identify and characterize microstructures, including grains in polycrystalline solids, voids in porous materials, and micellar distribution in complex solutions (Fig. 9).176 In a recent work by Samaniego et al., deep neural networks based on the variational form of the boundary value problems were implemented as solvers for partial differential equations (PDEs) in various solid mechanics problems, using a fundamental idea that the energy of the system to be minimized can be naturally treated as a loss function for the neural networks.177
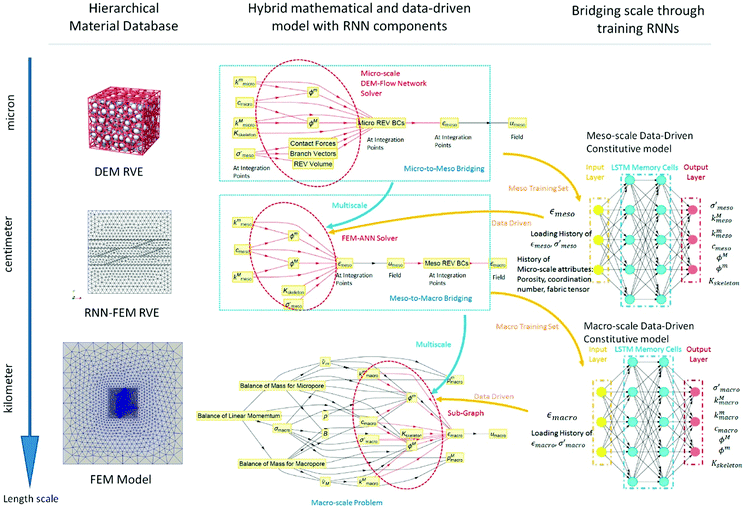 | ||
| Fig. 8 A multi-scale multi-physics framework for poromechanics problems driven by directed graph representation and recurrent neural networks (Reproduced with permission.173 Copyright 2018 Elsevier). | ||
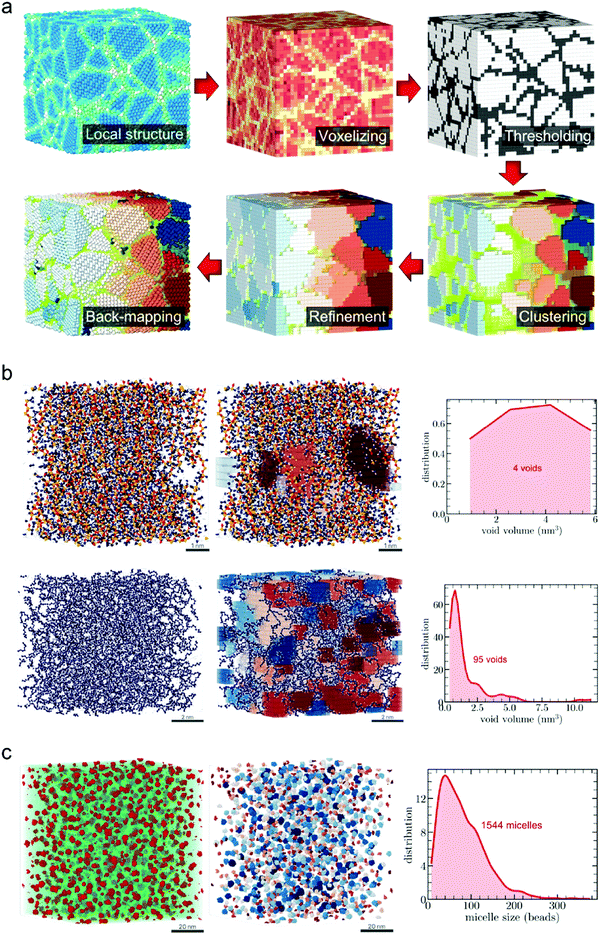 | ||
| Fig. 9 An unsupervised approach for the identification and characterization of microstructures in 3-D samples of various material systems. (a) A workflow for autonomous microstructural characterization of 3-D polycrystalline solids. (b and c) Results of the ML-based microstructural analysis method on the analysis of (b) voids in porous materials and (c) micellar distribution in complex solutions (Licensed under CC-BY).176 | ||
Perspectives
A straightforward benefit ML brings to materials and mechanics researches is promoting the efficiency of materials designs via experiments and simulations. Exploring a massive design space of novel materials is often intractable for brute force approaches and too complicated to achieve using physical intuition. Instead, ML-based design approaches can incorporate materials and mechanical features during the preprocessing of input data, learn the relationship between materials structures and mechanical behaviors during training, and provide targeted designs using the trained models. It should be pointed out that ML algorithms may not necessarily be beneficial when dealing with material problems in which the overall cost of training and design procedures is more expensive than standard approaches. A promising way to elevate the performance of ML-based methods in those problems is to encode scientific knowledge not only in data preprocessing but also in neural networks architectures. In this regard, recent development in physics-guided ML frameworks, such as physics-informed neural networks (PINNs) in which governing equations in the form of PDEs are incorporated into loss functions,178 offers new perspectives for the integration of ML and mechanical materials design.ML approaches that can discover new physics may have a broad application in materials and mechanics researches. It has shown that ML can be trained to learn symbolic expression of physical laws. Well-known physics concepts including Hamiltonian, Lagrangian are predicted by symbolic regression.179 Brunton et al. revealed governing equations underlying a dynamical system with ML algorithms.180 Recent ML work using GNN has shown that the algorithms are capable to discover new analytical solutions for dark matter mass distribution.181 These works derived governing equations in a unique way and may offer a potential new direction for understanding the mechanisms and mechanical behaviors of various materials.
As summarized in this review, most of current researches focus on applying ML algorithms to solve materials and mechanics problems. Yet, it is worth pointing out that mechanical insights also have the potential to facilitate the development of ML. Geiger et al. showed that loss landscape of deep neural networks can be interpreted with a paradigm based on jamming transition.182 Inspired by information process in natural neural networks, spike neural networks (SNNs) transmit sparse and asynchronous binary signals between neurons which incorporates time into deep learning networks. As a consequence, SNNs have exhibited favorable properties including low power consumption, fast inference, and event-driven information processing.183 Despite the popularity of ML systems, they are arguably treated as “black boxes” due to the difficulty of inspecting how and why those algorithms can make accomplishments. The known knowledge in mechanics and materials science may help us understand the mechanisms behind ML algorithms and develop new learning techniques that can tackle challenging problems in materials design, such as design of hierarchical structures or multifunctional materials with desired overall performance of a set of material properties.
So far, the potential of using ML in design of mechanical materials has not been fully exploited yet with opportunities and challenges lying ahead to be explored and overcome. It is promising that ML-based approaches will revolutionize the way we understand and design materials.
List of abbreviations
| ABBREVIATION | MEANING |
| 2-D | Two-dimensional |
| 3-D | Three-dimensional |
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| BL | Bayesian learning |
| BP | Back propagation |
| cGAN | conditional generative adversarial network |
| CNN | Convolutional neural network |
| DL | Deep learning |
| DT | Decision tree |
| FEM | Finite element method |
| FFNN | Feedforward neural network |
| GAN | Generative adversarial network |
| GCN | Graph convolutional network |
| GD | Gradient descent |
| GNN | Graph neural network |
| GPR | Gaussian process regression |
| GRF | Gaussian random field |
| GRU | Gated recurrent unit |
| LASSO | Least absolute shrinkage and selection operator |
| LIR | Linear regression |
| LOR | Logistic regression |
| LSTM | Long short-term memory |
| MD | Molecular dynamics |
| ML | Machine learning |
| MLP | Multilayer perceptron |
| MOF | Metal-organic framework |
| MP | Materials Project |
| NLP | Natural language processing |
| PDE | Partial differential equation |
| PINN | Physics-informed neural network |
| POD | Proper Orthogonal Decomposition |
| PR | Polynomial regression |
| RF | Random forest |
| RL | Reinforcement learning |
| RNN | Recurrent neural network |
| RVE | Representative volume element |
| SNN | Spike neural network |
| SVR | Support vector regression |
| VAE | Variational autoencoder |
Conflicts of interest
The authors declare no conflict of interests.Acknowledgements
We acknowledge support by the Office of Naval Research (N000141612333), AFOSR-MURI (FA9550-15-1-0514), the Army Research Office (W911NF1920098), NIH U01 EB014976 and Ministry of Science and Technology (MOST), Taiwan, (MOST 109-2222-E-006-005-MY2 and MOST 109-2224-E-007-003-). Further, support from the IBM-MIT AI lab, MIT Quest, and Google Cloud Computing, is acknowledged.References
- M. A. Meyers and K. K. Chawla, Mechanical Behavior of Materials, Cambridge University Press, 2nd edn, 2008 Search PubMed.
- E. J. Barbero, Introduction to Composite Materials Design, CRC Press, 3rd edn, 2017 Search PubMed.
- M. A. Meyers, P. Y. Chen, A. Y. M. Lin and Y. Seki, Prog. Mater. Sci., 2008, 53, 1–206 CrossRef CAS.
- P. Y. Chen, J. McKittrick and M. A. Meyers, Prog. Mater. Sci., 2012, 57, 1492–1704 CrossRef CAS.
- U. G. K. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Nat. Mater., 2015, 14, 23–36 CrossRef CAS.
- S. W. Cranford and M. J. Buehler, Biomateriomics, Springer, 2012 Search PubMed.
- G. X. Gu, I. Su, S. Sharma, J. L. Voros, Z. Qin, M. J. Buehler, S. Sharma, Z. Qin, I. Su, G. X. Gu, M. J. Buehler, I. Su, S. Sharma, J. L. Voros, Z. Qin and M. J. Buehler, J. Biomech. Eng, 2016, 138, 021006 CrossRef.
- I. Su, G. S. Jung, N. Narayanan and M. J. Buehler, Curr. Opin. Biomed. Eng., 2020, 15, 59–67 CrossRef.
- Y. Liu and X. Zhang, Chem. Soc. Rev., 2011, 40, 2494–2507 RSC.
- M. Kadic, G. W. Milton, M. van Hecke and M. Wegener, Nat. Rev. Phys., 2019, 1, 198–210 CrossRef.
- L. R. Meza, S. Das and J. R. Greer, Science, 2014, 345, 1322–1326 CrossRef CAS.
- L. R. Meza, A. J. Zelhofer, N. Clarke, A. J. Mateos, D. M. Kochmann and J. R. Greer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11502–11507 CrossRef CAS.
- M. S. Pham, C. Liu, I. Todd and J. Lertthanasarn, Nature, 2019, 565, 305–311 CrossRef CAS.
- X. Zhang, Y. Wang, B. Ding and X. Li, Small, 2020, 16, 1902842 CrossRef CAS.
- P. H. Winston, Artificial intelligence, Pearson, 3rd edn, 1992 Search PubMed.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, 2016 Search PubMed.
- Y. Lecun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444 CrossRef CAS.
- Y. Liu, T. Zhao, W. Ju, S. Shi, S. Shi and S. Shi, J. Mater, 2017, 3, 159–177 Search PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS.
- S. Ramakrishna, T. Y. Zhang, W. C. Lu, Q. Qian, J. S. C. Low, J. H. R. Yune, D. Z. L. Tan, S. Bressan, S. Sanvito and S. R. Kalidindi, J. Intell. Manuf., 2019, 30, 2307–2326 CrossRef.
- R. Batra, L. Song and R. Ramprasad, Nat. Rev. Mater., 2020 DOI:10.1038/s41578-020-00255-y.
- J. Wei, P. De Luna, Y. Bengio, A. Aspuru-Guzik and E. Sargent, Nature, 2017, 552, 23–25 CrossRef.
- G. H. Gu, J. Noh, I. Kim and Y. Jung, J. Mater. Chem. A, 2019, 7, 17096–17117 RSC.
- H. Liu, Z. Fu, K. Yang, X. Xu and M. Bauchy, J. Non. Cryst. Solids, 2019, 119419, DOI:10.1016/j.jnoncrysol.2019.04.039.
- C. T. Chen and G. X. Gu, MRS Commun., 2019, 9, 556–566 CrossRef CAS.
- G. Chen, Z. Shen, A. Iyer, U. F. Ghumman, S. Tang, J. Bi, W. Chen and Y. Li, Polymers, 2020, 12, 163 CrossRef CAS.
- C. Zhai, T. Li, H. Shi and J. Yeo, J. Mater. Chem. B, 2020, 8, 6562–6587 RSC.
- L. Meng, B. McWilliams, W. Jarosinski, H. Y. Park, Y. G. Jung, J. Lee and J. Zhang, JOM, 2020, 72, 2363–2377 CrossRef.
- G. D. Goh, S. L. Sing and W. Y. Yeong, Artif. Intell. Rev., 2020 DOI:10.1007/s10462-020-09876-9.
- F. E. Bock, R. C. Aydin, C. J. Cyron, N. Huber, S. R. Kalidindi and B. Klusemann, Front. Mater., 2019, 6, 110 CrossRef.
- D. C. Montgomery, E. A. Peck and G. G. Vining, Introduction to linear regression analysis, John Wiley & Sons, 2012, vol. 821 Search PubMed.
- R. Tibshirani, J. R. Statist. Soc. B, 1996, 58, 267–288 Search PubMed.
- C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–297 Search PubMed.
- L. Breiman, Mach. Learn, 2001, 45, 5–32 CrossRef.
- P. McCullagh and J. A. Nelder, Generalized Linear Models, Second eqn, Taylor & Francis, 1989 Search PubMed.
- J. R. Quinlan, Mach. Learn., 1986, 1, 81–106 Search PubMed.
- J. H. Friedman, Comput. Stat. Data Anal., 2002, 38, 367–378 CrossRef.
- J. H. Friedman, Ann. Stat., 2001, 29, 1189–1232 CrossRef.
- F. Rosenblatt, Psychol. Rev., 1958, 65, 386–408 CAS.
- S. Russell and P. Norvig, Artificial intelligence: a modern approach, 2nd edn, 2003 Search PubMed.
- S. Haykin and N. Network, Neural Networks, 2004, 2, 41 Search PubMed.
- J. Schmidhuber, Neural Networks, 2015, 61, 85–117 CrossRef.
- K. Fukushima and S. Miyake, Competition and cooperation in neural nets, Springer, 1982, pp. 267–285 Search PubMed.
- Y. LeCun, P. Haffner, L. Bottou and Y. Bengio, Shape, contour and grouping in computer vision, Springer, 1999, pp. 319–345 Search PubMed.
- Q. Zhang, M. Zhang, T. Chen, Z. Sun, Y. Ma and B. Yu, Neurocomputing, 2019, 323, 37–51 CrossRef.
- M. J. Buehler, Nano Futur., 2020, 4, 035004 CrossRef CAS.
- S. L. Franjou, M. Milazzo, C.-H. Yu and M. J. Buehler, Expert Rev. Proteomics, 2019, 16, 875–879 CrossRef CAS.
- R. Pascanu, T. Mikolov and Y. Bengio, On the difficulty of training recurrent neural networks, Proceedings of the 30th International Conference on International Conference on Machine Learning (ICML 2013), 2013.
- S. Hochreiter, Int. J. Uncertainty, Fuzziness Knowledge-Based Syst., 1998, 06, 107–116 CrossRef.
- S. Hochreiter and J. Schmidhuber, Neural Comput., 1997, 9, 1735–1780 CrossRef CAS.
- K. Cho, B. Van Merriënboer, C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk and Y. Bengio, Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation, Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), 2014, pp. 1724–1734.
- K. He, X. Zhang, S. Ren and J. Sun, Deep Residual Learning for Image Recognition, Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), 2016, pp. 770–778.
- D. Bahdanau, K. Cho and Y. Bengio, 2014, arXiv:1409.0473, arXiv preprint, https://arxiv.org/abs/1409.0473.
- V. Mnih, N. Heess, A. Graves and K. Kavukcuoglu, Adv. Neural Inf. Process. Syst., 2014, 3, 2204–2212 Search PubMed.
- A. W. Senior, R. Evans, J. Jumper, J. Kirkpatrick, L. Sifre, T. Green, C. Qin, A. Žídek, A. W. R. Nelson, A. Bridgland, H. Penedones, S. Petersen, K. Simonyan, S. Crossan, P. Kohli, D. T. Jones, D. Silver, K. Kavukcuoglu and D. Hassabis, Nature, 2020, 577, 706–710 CrossRef CAS.
- C.-H. Yu, Z. Qin, F. J. Martin-Martinez and M. J. Buehler, ACS Nano, 2019, 13, 7471–7482 CrossRef CAS.
- C.-H. Yu and M. J. Buehler, APL Bioeng., 2020, 4, 016108 CrossRef CAS.
- I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Generative Adversarial Nets, Advances in Neural Information Processing Systems 27 (NIPS 2014), 2014, pp. 2672–2680 Search PubMed.
- M. Mirza and S. Osindero, 2014, arXiv:1411.1784, arXiv preprint, https://arxiv.org/abs/1411.1784.
- J. Zhu, T. Park, P. Isola and A. A. Efros, Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks, 2017 IEEE International Conference on Computer Vision (ICCV), 2017, pp. 2242–2251.
- P. Isola, J. Y. Zhu, T. Zhou and A. A. Efros, Image-to-image translation with conditional adversarial networks, Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), 2017, pp. 5967–5976.
- D. P. Kingma and M. Welling, 2013, arXiv:1312.6114, arXiv preprint, https://arxiv.org/abs/1312.6114.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning), The MIT Press, 2005 Search PubMed.
- B. Settles, Active learning literature survey, Univeristy of Wiconsin Madison, 2009, vol. 52 Search PubMed.
- T. Lookman, P. V. Balachandran, D. Xue and R. Yuan, npj Comput. Mater., 2019, 5, 21 CrossRef.
- L. Pack Kaelbling, M. L. Littman, A. W. Moore and S. Hall, Reinforcement Learning: A Survey, 1996, vol. 4 Search PubMed.
- D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre, G. Van Den Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, S. Dieleman, D. Grewe, J. Nham, N. Kalchbrenner, I. Sutskever, T. Lillicrap, M. Leach, K. Kavukcuoglu, T. Graepel and D. Hassabis, Nature, 2016, 529, 484–489 CrossRef CAS.
- J. Zhou, G. Cui, Z. Zhang, C. Yang, Z. Liu, L. Wang, C. Li and M. Sun, 2018, arXiv:1812.08434, arXiv preprint, https://arxiv.org/abs/1812.08434.
- T. N. Kipf and M. Welling, Semi-Supervised Classification with Graph Convolutional Networks, 5th International Conference on Learning Representations (ICLR 2017), 2017.
- T. Kirchdoerfer and M. Ortiz, Comput. Methods Appl. Mech. Eng., 2016, 304, 81–101 CrossRef.
- T. Kirchdoerfer and M. Ortiz, Comput. Methods Appl. Mech. Eng., 2017, 326, 622–641 CrossRef.
- T. Kirchdoerfer and M. Ortiz, Int. J. Numer. Methods Eng., 2018, 113, 1697–1710 CrossRef.
- L. Stainier, A. Leygue and M. Ortiz, Comput. Mech., 2019, 64, 381–393 CrossRef.
- J. Yvonnet, D. Gonzalez and Q. C. He, Comput. Methods Appl. Mech. Eng., 2009, 198, 2723–2737 CrossRef.
- A. Clément, C. Soize and J. Yvonnet, Int. J. Numer. Methods Eng., 2012, 91, 799–824 CrossRef.
- B. A. Le, J. Yvonnet and Q.-C. He, Int. J. Numer. Methods Eng., 2015, 104, 1061–1084 CrossRef.
- Z. Liu, M. A. Bessa and W. K. Liu, Comput. Methods Appl. Mech. Eng., 2016, 306, 319–341 CrossRef.
- M. A. Bessa, R. Bostanabad, Z. Liu, A. Hu, D. W. Apley, C. Brinson, W. Chen and W. K. Liu, Comput. Methods Appl. Mech. Eng., 2017, 320, 633–667 CrossRef.
- W. Yan, S. Lin, O. L. Kafka, Y. Lian, C. Yu, Z. Liu, J. Yan, S. Wolff, H. Wu, E. Ndip-Agbor, M. Mozaffar, K. Ehmann, J. Cao, G. J. Wagner and W. K. Liu, Comput. Mech., 2018, 61, 521–541 CrossRef.
- Z. Liu, M. Fleming and W. K. Liu, Comput. Methods Appl. Mech. Eng., 2018, 330, 547–577 CrossRef.
- H. Li, O. L. Kafka, J. Gao, C. Yu, Y. Nie, L. Zhang, M. Tajdari, S. Tang, X. Guo, G. Li, S. Tang, G. Cheng and W. K. Liu, Comput. Mech., 2019, 64, 281–305 CrossRef.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS.
- S. Curtarolo, W. Setyawan, S. Wang, J. Xue, K. Yang, R. H. Taylor, L. J. Nelson, G. L. W. Hart, S. Sanvito, M. Buongiorno-Nardelli, N. Mingo and O. Levy, Comput. Mater. Sci., 2012, 58, 227–235 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- MATDAT, https://www.matdat.com, accessed 21 October 2020.
- MatWeb, http://www.matweb.com, accessed 21 October 2020.
- MatMatch, https://matmatch.com, accessed 21 October 2020.
- MakeItForm, https://www.makeitfrom.com, accessed 21 October 2020.
- MatNavi, https://mits.nims.go.jp/en/, accessed 21 October 2020.
- S. Chibani and F. X. Coudert, Chem. Sci., 2019, 10, 8589–8599 RSC.
- J. Noh, J. Kim, H. S. Stein, B. Sanchez-Lengeling, J. M. Gregoire, A. Aspuru-Guzik and Y. Jung, Matter, 2019, 1, 1370–1384 CrossRef.
- P. Raccuglia, K. C. Elbert, P. D. F. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73–76 CrossRef CAS.
- C. Wang, H. Fu, L. Jiang, D. Xue and J. Xie, npj Comput. Mater., 2019, 5, 87 CrossRef.
- P. V. Balachandran, A. A. Emery, J. E. Gubernatis, T. Lookman, C. Wolverton and A. Zunger, Phys. Rev. Mater., 2018, 2, 043802 CrossRef CAS.
- P. V. Balachandran, B. Kowalski, A. Sehirlioglu and T. Lookman, Nat. Commun., 2018, 9, 1668 CrossRef.
- L. Holleis, B. S. Shivaram and P. V. Balachandran, Appl. Phys. Lett., 2019, 114, 222404 CrossRef.
- R. Ravinder, K. H. Sridhara, S. Bishnoi, H. S. Grover, M. Bauchy, Jayadeva, H. Kodamana and N. M. A. Krishnan, Mater. Horiz., 2020, 7, 1819–1827 RSC.
- R. Yuan, Z. Liu, P. V. Balachandran, D. Xue, Y. Zhou, X. Ding, J. Sun, D. Xue and T. Lookman, Adv. Mater., 2018, 30, 1702884 CrossRef.
- E. Kim, K. Huang, A. Tomala, S. Matthews, E. Strubell, A. Saunders, A. McCallum and E. Olivetti, Sci. Data, 2017, 4, 170127 CrossRef CAS.
- E. Kim, K. Huang, A. Saunders, A. McCallum, G. Ceder and E. Olivetti, Chem. Mater., 2017, 29, 9436–9444 CrossRef CAS.
- E. Kim, Z. Jensen, A. van Grootel, K. Huang, M. Staib, S. Mysore, H. S. Chang, E. Strubell, A. McCallum, S. Jegelka and E. Olivetti, J. Chem. Inf. Model., 2020, 60, 1194–1201 CrossRef CAS.
- Z. Yang, Y. C. Yabansu, R. Al-Bahrani, W. Liao, A. N. Choudhary, S. R. Kalidindi and A. Agrawal, Comput. Mater. Sci., 2018, 151, 278–287 CrossRef CAS.
- A. Cecen, H. Dai, Y. C. Yabansu, S. R. Kalidindi and L. Song, Acta Mater., 2018, 146, 76–84 CrossRef CAS.
- R. Liu, Y. C. Yabansu, A. Agrawal, S. R. Kalidindi and A. N. Choudhary, Integr. Mater. Manuf. Innov., 2015, 4, 192–208 CrossRef.
- R. Liu, Y. C. Yabansu, Z. Yang, A. N. Choudhary, S. R. Kalidindi and A. Agrawal, Integr. Mater. Manuf. Innov., 2017, 6, 160–171 CrossRef.
- Z. Yang, Y. C. Yabansu, D. Jha, W. Liao, A. N. Choudhary, S. R. Kalidindi and A. Agrawal, Acta Mater., 2019, 166, 335–345 CrossRef CAS.
- G. X. Gu, C. T. Chen and M. J. Buehler, Extrem. Mech. Lett., 2018, 18, 19–28 CrossRef.
- G. X. Gu, C. T. Chen, D. J. Richmond and M. J. Buehler, Mater. Horiz., 2018, 5, 939–945 RSC.
- C.-H. Yu, Z. Qin and M. J. Buehler, Nano Futur., 2019, 3, 035001 CrossRef CAS.
- M. A. Bessa, P. Glowacki and M. Houlder, Adv. Mater., 2019, 31, 1904845 CrossRef CAS.
- Z. Yang, X. Li, L. C. Brinson, A. N. Choudhary, W. Chen and A. Agrawal, J. Mech. Des., 2018, 140, 111416 CrossRef.
- K. Yang, X. Xu, B. Yang, B. Cook, H. Ramos, N. M. A. Krishnan, M. M. Smedskjaer, C. Hoover and M. Bauchy, Sci. Rep., 2019, 9, 8739 CrossRef.
- P. Z. Moghadam, S. M. J. Rogge, A. Li, C.-M. Chow, J. Wieme, N. Moharrami, M. Aragones-Anglada, G. Conduit, D. A. Gomez-Gualdron, V. Van Speybroeck and D. Fairen-Jimenez, Matter, 2019, 1, 219–234 CrossRef.
- Y.-C. Hsu, C.-H. Yu and M. J. Buehler, Matter, 2020, 3, 197–211 CrossRef.
- Y. Mao, Q. He and X. Zhao, Sci. Adv., 2020, 6, eaaz4169 CrossRef.
- Y. Lecun and C. Cortes, The MNIST database of handwritten digits, http://yann.lecun.com/exdb/mnist/.
- E. Lejeune, Extrem. Mech. Lett., 2020, 36, 100659 CrossRef.
- F. Ren, L. Ward, T. Williams, K. J. Laws, C. Wolverton, J. Hattrick-Simpers and A. Mehta, Sci. Adv., 2018, 4, eaaq1566 CrossRef.
- A. E. Gongora, B. Xu, W. Perry, C. Okoye, P. Riley, K. G. Reyes, E. F. Morgan and K. A. Brown, Sci. Adv., 2020, 6, eaaz1708 CrossRef.
- Z. Yang, S. Papanikolaou, A. C. E. Reid, W. Liao, A. N. Choudhary, C. Campbell and A. Agrawal, Sci. Rep., 2020, 10, 8262 CrossRef CAS.
- C. Herriott and A. D. Spear, Comput. Mater. Sci., 2020, 175, 109599 CrossRef CAS.
- S. Bishnoi, S. Singh, R. Ravinder, M. Bauchy, N. N. Gosvami, H. Kodamana and N. M. A. Krishnan, J. Non. Cryst. Solids, 2019, 524, 119643 CrossRef CAS.
- Q. Zhao, H. Yang, J. Liu, H. Zhou, H. Wang and W. Yang, Mater. Des., 2021, 197, 109248 CrossRef CAS.
- X. Chen, H. Zhou and Y. Li, Mater. Des., 2019, 183, 108085 CrossRef.
- A. Mansouri Tehrani, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper, F. Lin, L. Miyagi, T. D. Sparks and J. Brgoch, J. Am. Chem. Soc., 2018, 140, 9844–9853 CrossRef CAS.
- P. Avery, X. Wang, C. Oses, E. Gossett, D. M. Proserpio, C. Toher, S. Curtarolo and E. Zurek, npj Comput. Mater., 2019, 5, 89 CrossRef.
- E. Mazhnik and A. R. Oganov, J. Appl. Phys., 2020, 128, 075102 CrossRef CAS.
- C. Wen, Y. Zhang, C. Wang, D. Xue, Y. Bai, S. Antonov, L. Dai, T. Lookman and Y. Su, Acta Mater., 2019, 170, 109–117 CrossRef CAS.
- C. Ma, Z. Zhang, B. Luce, S. Pusateri, B. Xie, M. H. Rafiei and N. Hu, npj Comput. Mater., 2020, 6, 40 CrossRef.
- X. Liu, C. E. Athanasiou, N. P. Padture, B. W. Sheldon and H. Gao, Acta Mater., 2020, 190, 105–112 CrossRef CAS.
- E. L. Buehler, I. Su and M. J. Buehler, Extrem. Mech. Lett., 2021, 42, 101034 CrossRef.
- J. D. Evans and F. O.-X. Coudert, Chem. Mater., 2017, 29, 7833–7839 CrossRef CAS.
- R. Gaillac, S. Chibani and F. X. Coudert, Chem. Mater., 2020, 32, 2653–2663 CrossRef CAS.
- Z. Zhang, Y. Hong, B. Hou, Z. Zhang, M. Negahban and J. Zhang, Carbon, 2019, 148, 115–123 CrossRef CAS.
- Y. Wang, M. Zhang, A. Lin, A. Iyer, A. S. Prasad, X. Li, Y. Zhang, L. S. Schadler, W. Chen and L. C. Brinson, Mol. Syst. Des. Eng., 2020, 5, 962–975 RSC.
- Q. Chen, W. Tu and M. Ma, J. Appl. Phys., 2020, 127, 175101 CrossRef.
- Z. Nie, H. Jiang and L. B. Kara, J. Comput. Inf. Sci. Eng., 2020, 20, 011002 CrossRef.
- B. Ni and H. Gao, MRS Bull., 2020 DOI:10.1557/mrs.2020.231.
- Z. Yang, C.-H. Yu and M. J. Buehler, Deep Learning Model to Predict Complex Stress and Strain Fields in Hierarchical Composites, Sci. Adv., in revision Search PubMed.
- K. Pierson, A. Rahman and A. D. Spear, JOM, 2019, 71, 2680–2694 CrossRef.
- J. Guilleminot and J. E. Dolbow, Mech. Res. Commun., 2020, 103, 103443 CrossRef.
- M. Mozaffar, R. Bostanabad, W. Chen, K. Ehmann, J. Cao and M. A. Bessa, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 26414–26420 CrossRef CAS.
- D. Huang, J. N. Fuhg, C. Weißenfels and P. Wriggers, Comput. Methods Appl. Mech. Eng., 2020, 365, 113008 CrossRef.
- L. Wu, V. D. Nguyen, N. G. Kilingar and L. Noels, Comput. Methods Appl. Mech. Eng., 2020, 369, 113234 CrossRef.
- H. Yang, H. Qiu, S. Tang, Q. Xiang and X. Guo, J. Appl. Mech, 2020, 87, 091005 CrossRef.
- Z. Zhou, Y. Zhu, J. Luo, X. Yang and X. Guo, Int. J. Solids Struct., 2020, 198, 57–71 CrossRef.
- G. Chen, T. Li, Q. Chen, S. Ren, C. Wang and S. Li, Comput. Mech., 2019, 64, 435–449 CrossRef.
- M. Stern, C. Arinze, L. Perez, S. E. Palmer and A. Murugan, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14843–14850 CrossRef CAS.
- N. Huber, A. Konstantinidis and C. Tsakmakis, J. Appl. Mech. Trans. ASME, 2001, 68, 218–223 CrossRef.
- N. Huber and C. Tsakmakis, J. Appl. Mech. Trans. ASME, 2001, 68, 224–229 CrossRef.
- E. Tyulyukovskiy and N. Huber, J. Mater. Res., 2006, 21, 664–676 CrossRef CAS.
- R. Haj-Ali, H. K. Kim, S. W. Koh, A. Saxena and R. Tummala, Int. J. Plast., 2008, 24, 371–396 CrossRef CAS.
- H. Li, L. Gutierrez, H. Toda, O. Kuwazuru, W. Liu, Y. Hangai, M. Kobayashi and R. Batres, Int. J. Solids Struct., 2016, 81, 151–159 CrossRef CAS.
- L. Lu, M. Dao, P. Kumar, U. Ramamurty, G. E. Karniadakis and S. Suresh, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 7052–7062 CrossRef CAS.
- P. Z. Hanakata, E. D. Cubuk, D. K. Campbell and H. S. Park, Phys. Rev. Lett., 2018, 121, 255304 CrossRef CAS.
- Y. Yu, T. Hur, J. Jung and I. G. Jang, Struct. Multidiscip. Optim., 2019, 59, 787–799 CrossRef.
- I. Sosnovik and I. Oseledets, Russ. J. Numer. Anal. Math. Model, 2019, 34, 215–223 Search PubMed.
- D. W. Abueidda, S. Koric and N. A. Sobh, Comput. Struct., 2020, 237, 106283 CrossRef.
- X. Lei, C. Liu, Z. Du, W. Zhang and X. Guo, J. Appl. Mech. Trans. ASME, 2019, 86, 011004 CrossRef.
- C. M. Hamel, D. J. Roach, K. N. Long, F. Demoly, M. L. Dunn and H. J. Qi, Smart Mater. Struct., 2019, 28, 065005 CrossRef.
- S. Wu, C. M. Hamel, Q. Ze, F. Yang, H. J. Qi and R. Zhao, Adv. Intell. Syst., 2020, 2, 2000060 CrossRef.
- L. Wu, L. Liu, Y. Wang, Z. Zhai, H. Zhuang, D. Krishnaraju, Q. Wang and H. Jiang, Extrem. Mech. Lett., 2020, 36, 100657 CrossRef.
- S. Kumar, S. Tan, L. Zheng and D. M. Kochmann, npj Comput. Mater., 2020, 6, 73 CrossRef.
- C. Chen and G. X. Gu, Adv. Sci., 2020, 7, 1902607 CrossRef CAS.
- S. Oh, Y. Jung, I. Lee and N. Kang, Design automation by integrating generative adversarial networks and topology optimization, Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC/CIE 2018), 2018.
- S. Oh, Y. Jung, S. Kim, I. Lee and N. Kang, J. Mech. Des. Trans. ASME, 2019, 141, 111405 CrossRef.
- C. Sharpe and C. C. Seepersad, Topology design with conditional generative adversarial networks, Proceedings of the ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC/CIE 2019), 2019.
- K. Guo and M. J. Buehler, Extrem. Mech. Lett., 2020, 41, 101029 CrossRef.
- Z. Liu and C. T. Wu, J. Mech. Phys. Solids, 2019, 127, 20–46 CrossRef CAS.
- Z. Liu, Comput. Methods Appl. Mech. Eng., 2020, 363, 112913 CrossRef.
- Z. Liu, C. T. Wu and M. Koishi, Comput. Methods Appl. Mech. Eng., 2019, 345, 1138–1168 CrossRef.
- Z. Liu, C. T. Wu and M. Koishi, Comput. Mech., 2019, 64, 451–465 CrossRef.
- K. Wang and W. C. Sun, Comput. Methods Appl. Mech. Eng., 2018, 334, 337–380 CrossRef.
- K. Wang and W. Sun, Comput. Methods Appl. Mech. Eng., 2019, 346, 216–241 CrossRef.
- G. Capuano and J. J. Rimoli, Comput. Methods Appl. Mech. Eng., 2019, 345, 363–381 CrossRef.
- H. Chan, M. Cherukara, T. D. Loeffler, B. Narayanan and S. K. R. S. Sankaranarayanan, npj Comput. Mater., 2020, 6, 1 CrossRef.
- E. Samaniego, C. Anitescu, S. Goswami, V. M. Nguyen-Thanh, H. Guo, K. Hamdia, X. Zhuang and T. Rabczuk, Comput. Methods Appl. Mech. Eng., 2020, 362, 112790 CrossRef.
- M. Raissi, P. Perdikaris and G. E. Karniadakis, J. Comput. Phys., 2019, 378, 686–707 CrossRef.
- M. Schmidt and H. Lipson, Science, 2009, 324, 81–85 CrossRef CAS.
- S. L. Brunton, J. L. Proctor and J. N. Kutz, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 3932–3937 CrossRef CAS.
- M. Cranmer, A. Sanchez-Gonzalez, P. Battaglia, R. Xu, K. Cranmer, D. Spergel and S. Ho, Discovering Symbolic Models from Deep Learning with Inductive Biases, Advances in Neural Information Processing Systems 33 pre-proceedings (NeurIPS 2020), 2020 Search PubMed.
- M. Geiger, S. Spigler, S. D’Ascoli, L. Sagun, M. Baity-Jesi, G. Biroli and M. Wyart, Phys. Rev. E, 2019, 100, 012115 CrossRef CAS.
- M. Pfeiffer and T. Pfeil, Front. Neurosci., 2018, 12, 774 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |