Open Access Article
Open Access ArticleBifurcations in flows of complex fluids around microfluidic cylinders
Simon J.
Haward
 *,
Cameron C.
Hopkins
*,
Cameron C.
Hopkins
 ,
Stylianos
Varchanis
,
Stylianos
Varchanis
 and
Amy Q.
Shen
and
Amy Q.
Shen

Micro/Bio/Nanofluidics Unit, Okinawa Institute of Science and Technology, Onna, Okinawa 904-0495, Japan. E-mail: simon.haward@oist.jp; Tel: +81(0)98 966 8289
First published on 14th October 2021
Abstract
Flow around a cylinder is a classical problem in fluid dynamics and also one of the benchmarks for testing viscoelastic flows. The problem is of wide relevance to understanding many microscale industrial and biological processes and applications, such as porous media and mucociliary flows. In recent years, we have developed model microfluidic geometries consisting of very slender cylinders fabricated in glass by selective laser-induced etching. The cylinder radius is small compared with the channel width, which allows the effects of the stagnation points in the flow to dominate over the effects of squeezing between the cylinder and the channel walls. Furthermore, the cylinders are contained in high aspect ratio microchannels that render the flow field approximately two-dimensional (2D) and therefore conveniently permit comparison between experiments and 2D numerical simulations. A number of different viscoelastic fluids including wormlike micellar and various polymer solutions have been tested in our devices. Of particular interest to us has been the occurrence of a striking, steady-in-time, flow asymmetry that occurs for certain non-Newtonian fluids when the dimensionless Weissenberg number (quantifying the importance of elastic over viscous forces in the flow) increases above a critical value. In this perspective review, we present a summary of our key findings related to this novel flow instability and present our current understanding of the mechanism for its onset and growth. We believe that the same fundamental mechanism may also underlie some important non-Newtonian phenomena observed in viscoelastic flows around particles, drops, and bubbles, or through geometries composed of multiple bifurcation points such as cylinder arrays and other porous media. Knowledge of the instability we discuss will be important to consider in the design of optimally functional lab-on-a-chip devices in which viscoelastic fluids are to be used.
1 Introduction
Viscoelastic fluids possess intermediate properties between viscous liquids and elastic solids and are found ubiquitously in biology (e.g., most bodily fluids), and engineering (e.g., foods, paints, cosmetics, detergents). The viscoelasticity arises due to the presence of mesoscopic structuring in the fluid (formed by e.g., suspended proteins, polysaccharides, synthetic polymers, or micellar aggregates), which resist deformation by an applied stress (i.e., under flow) due to entropic relaxation mechanisms.1 Since in general, stresses vary locally in a flow field, microstructural conformations also vary, leading to local modifications in the stress that feed back on the flow field. The microstructural conformations induced in regions of shearing flow typically cause a decrease in the resistance to flow due to “shear-thinning” of the viscosity. In contrast, strong stretching of the microstructure induced in regions of extensional flow can result in a large increase in the extensional viscosity known as “extension-thickening”.2 Consequently, the resulting flow dynamics of viscoelastic fluids can be startlingly different from those of constant viscosity Newtonian fluids (such as water). In particular, instabilities in flows of Newtonian fluids are typically driven by inertial forces, quantified by the Reynolds number, Re = U![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /ν, where U is the average flow velocity,
/ν, where U is the average flow velocity, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is a characteristic length scale and ν is the dynamic viscosity. However, for viscoelastic fluids, instabilities can arise due to purely elastic forces, even when inertia is negligible.3–10 Elastic forces in the flow can be quantified using the Weissenberg number Wi = λU/
is a characteristic length scale and ν is the dynamic viscosity. However, for viscoelastic fluids, instabilities can arise due to purely elastic forces, even when inertia is negligible.3–10 Elastic forces in the flow can be quantified using the Weissenberg number Wi = λU/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , where λ is a measure of the characteristic relaxation time of the fluid microstructure. Deformation of the microstructure, hence elastic effects, are expected to become dominant for Wi ≳ 0.5.11,12
, where λ is a measure of the characteristic relaxation time of the fluid microstructure. Deformation of the microstructure, hence elastic effects, are expected to become dominant for Wi ≳ 0.5.11,12
The flow around cylinders and spheres have been considered as benchmark systems for studying the dynamics of viscoelastic fluids.20–22 The flow field around a confined cylindrical or spherical object comprises a mix of shearing and extensional kinematics. At the leading axial stagnation point upstream of the object, the compression of fluid elements causes the divergence of streamlines around the sides of the object into regions of strong shear and transient elongational flow between the object and the confining walls. In the locality of the trailing axial stagnation point downstream of the object, fluid is subjected to high extensional rates and residence times.23–25 As demonstrated in Fig. 1, the mixture of stresses exerted on viscoelastic fluids resulting from this complex flow leads to a variety of phenomena of relevance to understanding various industrial and biological problems. The downstream stagnation point is particularly effective at restructuring a complex fluid, as illustrated by Fig. 1(a), which shows the flow-induced birefringence (FIB) in the wake of a sphere settling under gravity through a solution of high molecular weight linear polymers. The FIB arises due to the stretching and orientation of the polymer molecules in the high streamwise velocity gradients realized near the rear stagnation point of the sphere. The occurrence of FIB implies high elastic tensile stress (or extension-thickening) in the fluid induced by the resistance of the polymer to stretch. The decay of the FIB with downstream distance behind the sphere is due to the relaxation of the polymer molecules towards their equilibrium coiled conformation. The high elastic stress in the downstream wake of a sphere translating in a viscoelastic fluid gives rise to effects including so-called “negative wakes”,26–28 and oscillating settling velocities [illustrated by Fig. 1(b) for a wormlike micellar (WLM) fluid],13,29 and influences the pairwise interactions that occur between vertically and horizontally aligned spheres [illustrated by Fig. 1(c) for a high molecular weight polymer solution].14,30–33 A comprehensive review of phenomena involving bubbles, drops and particles in viscoelastic fluids is provided by Zenit and Feng.34
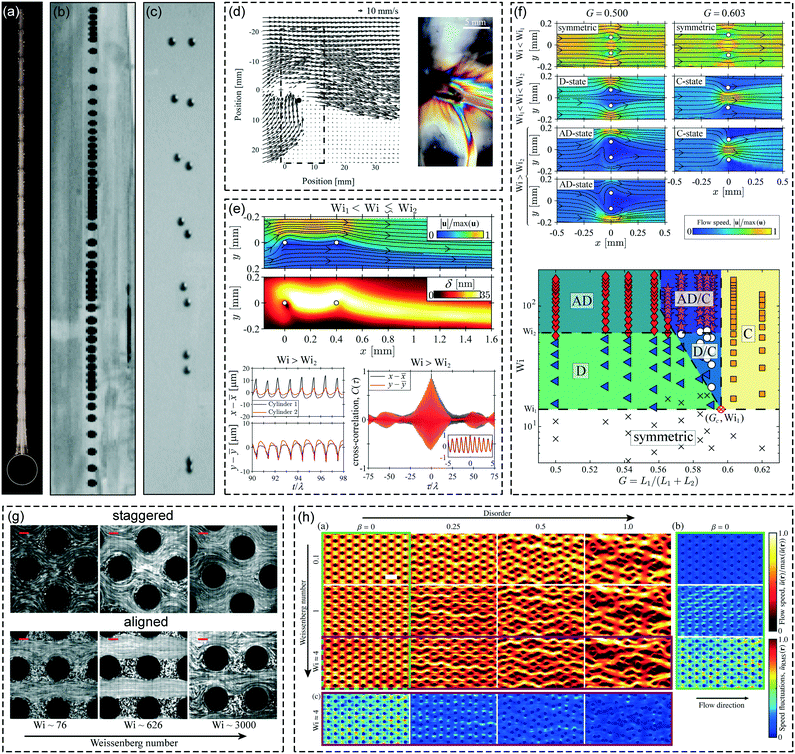 | ||
Fig. 1 Study of viscoelastic flow around a cylinder can lend insight into a variety of fundamental problems. (a)–(c) Spheres falling through viscoelastic fluids: (a) a 10 mm diameter stainless-steel sphere falling through a 3000 ppm 10.2 MDa poly(styrene) solution, showing an elastic birefringent wake, (b) collage of images of a 4.8 mm diameter Teflon sphere falling through a WLM solution, showing oscillations in the settling velocity. Reprinted with permission from A. Jayaraman and A. Belmonte, Phys. Rev. E 62, 065301 (2003).13 Copyright (2003) by the American Physical Society. (c) Collage of images of two initially horizontally-aligned stainless-steel spheres (separation 25 mm) in a 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm poly(acrylamide) solution, showing convergence and reorientation as they settle. Reprinted from ref. 14, with permission from Elsevier. (d) and (e) Viscoelastic fluid–structure interactions: (d) a flexible PDMS cylinder in a WLM solution is displaced from the channel centerline by a strongly asymmetric flow pattern (right) and the asymmetric distribution of extensional stress indicated by the FIB (left). Reprinted with permission from A. Dey, Y. Modarres-Sadeghi, and J. P. Rothstein, Phys. Rev. Fluid 3, 063301 (2018).15 Copyright (2018) by the American Physical Society, (e) asymmetric flow past two axially-aligned cantilevered glass cylinders, the x and y displacements of the cylinders vary in time and are highly correlated.16 (f) Flow of WLM fluid past side-by-side cylinders leads to a variety of bifurcation phenomena that depend on Wi and the dimensionless cylinder–cylinder separation number, G.17 (g) and (h) Viscoelastic flows of polymer solutions through porous media lead to different instabilities depending on the geometry: (g) staggered or aligned square arrays of cylinders. Reproduced from ref. 18 with permission from the Royal Society of Chemistry. (h) Introducing disorder to a staggered hexagonal array of cylinders suppresses chaotic fluctuations. Scale bar, 150 μm. Reprinted with permission from D. M. Walkama, N. Waisbord, and J. Guasto, Phys. Rev. Lett. 124, 164501 (2020).19 Copyright (2020) by the American Physical Society. 000 ppm poly(acrylamide) solution, showing convergence and reorientation as they settle. Reprinted from ref. 14, with permission from Elsevier. (d) and (e) Viscoelastic fluid–structure interactions: (d) a flexible PDMS cylinder in a WLM solution is displaced from the channel centerline by a strongly asymmetric flow pattern (right) and the asymmetric distribution of extensional stress indicated by the FIB (left). Reprinted with permission from A. Dey, Y. Modarres-Sadeghi, and J. P. Rothstein, Phys. Rev. Fluid 3, 063301 (2018).15 Copyright (2018) by the American Physical Society, (e) asymmetric flow past two axially-aligned cantilevered glass cylinders, the x and y displacements of the cylinders vary in time and are highly correlated.16 (f) Flow of WLM fluid past side-by-side cylinders leads to a variety of bifurcation phenomena that depend on Wi and the dimensionless cylinder–cylinder separation number, G.17 (g) and (h) Viscoelastic flows of polymer solutions through porous media lead to different instabilities depending on the geometry: (g) staggered or aligned square arrays of cylinders. Reproduced from ref. 18 with permission from the Royal Society of Chemistry. (h) Introducing disorder to a staggered hexagonal array of cylinders suppresses chaotic fluctuations. Scale bar, 150 μm. Reprinted with permission from D. M. Walkama, N. Waisbord, and J. Guasto, Phys. Rev. Lett. 124, 164501 (2020).19 Copyright (2020) by the American Physical Society. | ||
Quite recently there has been a growing interest in the area of viscoelastic fluid–structure interactions (or viscoelastic FSI), whereby viscoelastic flow instabilities cause the displacement of an object in the flow, which in turn affects the flow field.15,16,35–38 As in Newtonian FSI, where inertial vortex shedding downstream of an obstacle causes the obstacle to vibrate,39 flexible, cantilevered or flexibly-mounted circular cylinders provide good model systems for studying viscoelastic FSI [see Fig. 1(d) and (e)].15,16,37 The first such study by Dey et al. involved the flow of a WLM solution past a flexible rubbery cylinder pinned at both ends to the walls of a channel.15 As the flow rate was increased so that the Weissenberg number exceeded a critical value Wi1, the authors noted the onset of oscillations of the cylinder in the primary flow direction, which corresponded to oscillations in the FIB observed downstream of the cylinder. This behaviour is analogous to the oscillations in settling velocity of the sphere shown in Fig. 1(b). Above a second, higher critical Weissenberg number Wi2, Dey et al. reported the striking off-axis displacement and oscillations of the cylinder lateral to the flow direction. A strongly heterogeneous distribution of the flow occurred, with nearly all of the fluid passing the cylinder around one of the sides and a stagnant region developing on the opposite side [Fig. 1(d), left].15 Flow-induced birefringence imaging using crossed polarizers [Fig. 1(d), right] showed enhanced elastic stress along the divisions between fast flowing and stagnant regions, and the authors noted the possibility that the birefringent strand below the cylinder may represent an elastic wave. This off-axis displacement of the cylinder may also have bearing on the lateral motion of the falling spheres shown in Fig. 1(c).
A study of viscoelastic FSI by Hopkins et al. examined the flow of a WLM solution around two axially aligned cantilevered glass cylinders in a microchannel.16 In this study, at the first critical Weissenberg number Wi1, the flow field became laterally asymmetric around both cylinders while the cylinder deflection remained static [top image in Fig. 1(e)]. The two cylinders became linked by a strand of highly stressed fluid, as indicated by the FIB [quantified in terms of the retardation, δ shown in the middle image in Fig. 1(e)]. For Wi > Wi2 both cylinders began to oscillate periodically in both the x and the y directions [bottom-left of Fig. 1(e)]. The cross-correlation function of the displacement signals showed a peak of close to unity at a time lag too short for fluid advection between the objects, and likely explained by the propagation of an elastic wave along the strand of FIB.16 The authors speculate that elastic strands may form connections between cilia and flagella translating in viscoelastic biological fluids like mucous, thus playing a role in mediating their collective motion.
In a very recent paper, Hopkins et al. examined the flow of WLM and polymer solutions past two rigidly pinned microcylinders positioned side-by-side in a microchannel.17 They reported a range of behaviour that depended on the imposed Wi and the dimensionless intercylinder gap G = L1/(L1 + L2), where L1 and L2 are the cylinder–cylinder and cylinder-wall separations, respectively [Fig. 1(f), top]. For low Wi < Wi1, the flow remained symmetric regardless of G, but for Wi > Wi1 a bifurcation resulted in the flow either diverging around the two cylinders if G was small (D-state), or converging between the cylinders if G was large (C-state).17 For small G, and beyond a second critical Weissenberg number Wi2, the D-state itself underwent a second bifurcation to an asymmetric-diverging AD-state, where fluid randomly selected passage around just one side of the two cylinders. By examining a wide range of values of G and Wi, the authors constructed a phase diagram for the different possible flow states, exhibiting regions of bistability and even tristability [Fig. 1(f), bottom]. The implications are quite clear for understanding particle–particle interactions in viscoelastic fluids. For instance, if the D-state arose around mobile objects, then the two objects would converge. In contrast, the C-state would cause the two objects to diverge. Furthermore, these results have clear relevance to the path selection and switching observed in viscoelastic porous media flows.18,19,40–42
Porous media are frequently modelled in microfluidics experiments using many circular cylinders arranged in arrays [see examples shown in Fig. 1(g) and (h)].18,19,40–42,49–52 In a pertinent study, Kawale et al. showed how the nature of viscoelastic flow instabilities in a staggered square arrangement of cylinders is qualitatively changed by a simple 45-degree rotation of the array to make clear flow paths between the now aligned rows of cylinders [Fig. 1(g)].18 Several more recent studies have investigated the effect of introducing random disorder to arrays of posts [e.g., Fig. 1(h)].19,51,52 Depending on the orientation of the initially ordered geometry (staggered or aligned) it has been shown that disorder can either suppress or enhance the strength of temporal fluctuations that develop in the flow as Wi is increased. It appears that the occurrence of stagnation points exposed to the flow field is the controlling factor for the flow dynamics.51,52
Obstacles such as posts are frequently incorporated in lab-on-a-chip type devices in order to manipulate the flow dynamics and to perform complex functions (Fig. 2). Often the fluids of interest are complex and viscoelastic, for example blood, serum or other biofluids, which can show significant elastic effects at microfluidic length scales.53–59Fig. 2(a) illustrates the separation of cells in whole blood by the technique of deterministic lateral displacement by flow through an array of microposts aligned at an angle to the flow direction.43,60–68 Functionalized post structures [including nanoporous posts formed by carbon nanotube forests, Fig. 2(b)] are also used for the capture and detection of cells, bacteria and other biomolecules.44,69–72 Arrays of flexible post-like structures containing embedded magnetic nanoparticles are used as magnetically-actuated artificial cilia for fluid pumping in microchannels [Fig. 2(c)].45,73 Additionally, microposts can be used for performing droplet manipulations [Fig. 2(d)],46 generating lipid membrane nanotubes for the study of cellular processes [Fig. 2(e)],47 and forming functional nanogel materials based on viscoelastic micelle solutions [Fig. 2(f)].48,74
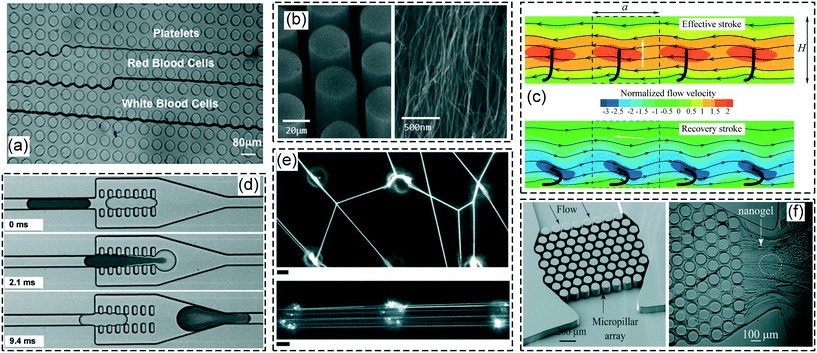 | ||
| Fig. 2 Flows around obstacles are employed in numerous lab-on-a-chip devices that can involve complex and viscoelastic fluids: (a) flow through an array of microposts is used for the separation of particles by deterministic lateral displacement, in this case to separate the cells in whole blood. Reproduced from ref. 43 with permission from the Royal Society of Chemistry. (b) Nano-porous objects can be used for the trapping and detection of circulating tumor cells, bacteria and other bioparticles: (left) an array of nanoporous microposts, (right) a zoomed image of the nanoporous structure. Reproduced from ref. 44 with permission from the Royal Society of Chemistry. (c) Arrays of magnetically-activated cilia-like objects are used to pump a fluid in a microchannel (channel height, H = a = 2 L = 140 μm, where a and L are the cilia spacing and length, respectively). The white arrows indicate the direction of the magnetic field used to activate the cilia motion. Reproduced from ref. 45 with permission from the Royal Society of Chemistry. (d) Carefully positioned microposts in a channel can be used for droplet manipulation – here to induce their rapid merging and mixing. Reproduced from ref. 46 with permission from the Royal Society of Chemistry. (e) Posts in a microchannnel are shown to produce lipid membrane nanotubes in the form of webs (top), and parallel assemblies (bottom). Scale bars: 4 μm. Reproduced from ref. 47 with permission from the Royal Society of Chemistry. (f) An array of micropillars is used to generate a nanogel from a viscoelastic wormlike micelle solution, which can be used as a scaffold for functional materials – here for glucose oxidase in order to form a glucose sensor. Reproduced from ref. 48 with permission from the Royal Society of Chemistry. | ||
A circular cylinder is perhaps the most fundamental model for a two-dimensional (2D) object or obstacle in a flow field, which can be rendered flexible for study of fluid–structure interactions, or used as a building block for models representing aspects of complex geometries such as porous media. Furthermore the 2D flow around a cylinder provides insight into the three-dimensional (3D) flows around particles, droplets or bubbles, while being significantly easier to study. Experimentally, a cylinder can be fixed in the laboratory frame by pinning the ends of the cylinder to the walls of a channel. This facilitates the imposition of a wider (and more continuous) range of flow rates than possible with particles, for instance, where the settling velocity in a given fluid is controlled only by varying the particle's density and size. Additionally, channels containing cylinders are relatively straightforward to fabricate and study at the microscale, where strong elastic effects (Wi ≫ 1) can arise for negligible inertia (Re ≪ 1),75,76 conditions characteristic of viscoelastic flows through micro-porous structures, around microscopic objects like cilia and flagella, and in lab-on-a-chip devices. Furthermore, at least over the range of Wi for which the flow remains steady, viscoelastic flow around a cylinder can be modelled in 2D, making the problem much more amenable to numerical simulation than the 3D flow around a sphere. For these reasons, viscoelastic flow around a circular cylinder confined in a channel is a widely studied problem both experimentally23,77–87 and numerically,24,82,88–92 and has become a common test for confirming the accuracy of viscoelastic flow simulations.22 A detailed recent review of the literature on viscoelastic flows around cylinders is contained in ref. 87.
From the discussion above, the importance of fully understanding the viscoelastic flow around a single rigid circular cylinder should be evident. Accordingly, in our research group we have invested significant effort in this direction using novel microfluidic geometries, a wide range of viscoelastic fluids with different rheological properties, and a combination of experiments and numerical simulations. In this perspective review, we provide a personal account of our recent research in this area, with a particular emphasis on characterizing and understanding the nature of an unusual steady flow asymmetry that we have observed. We draw together our results from a number of recent publications and summarize our overall conclusions as to the mechanism of this novel flow instability. We believe this instability underlies many of the phenomena presented in Fig. 1, and that it will be important to consider in the design and optimization of devices such as those illustrated in Fig. 2 when viscoelastic fluids are being employed.
2 Experimental methods
2.1 Microchannel design and fabrication
The microfluidic cylinder device used in all the studies presented in the remainder of this perspective review is depicted schematically in Fig. 3(a) and photographically in Fig. 3(b)–(d). The device was fabricated by selective laser-induced etching (SLE) in fused silica glass using a “LightFab” 3D printer (LightFab GmbH).94–96 The SLE fabrication is a two-step process: the shape of the channel is first written within a solid block of fused silica using a femtosecond laser, modifying the material locally, and next, the modified material is selectively removed by a wet chemical etchant (KOH). The volume occupied by the cylinder is left untouched during the laser writing step and is simply left behind within the channel following the chemical etching step, resulting in a monolithic construction with both ends of the cylinder fixed to the channel walls. The device fabrication is completed by bonding stainless steel tubing connectors to the inlet and outlet of the glass channel using a 2-part epoxy, see Fig. 3(d). The channel has inner dimensions of W = 400 μm and H = 2 mm, providing a relatively high aspect ratio AR = H/W = 5. The good approximation to uniform flow through the channel height was confirmed by some of our first experiments with Newtonian and viscoelastic fluids.93,97 The length of the channel from inlet to outlet is 25 mm and the cylinder is located half way along it. The cylinder radius is R = 20 μm, which provides a low blockage ratio BR = 2R/W = 0.1. The cylinder itself is very slender with an aspect ratio H/2R = 50, but due to the high modulus of fused silica (≈75 GPa), remains rigid and essentially undeflected under imposed flow.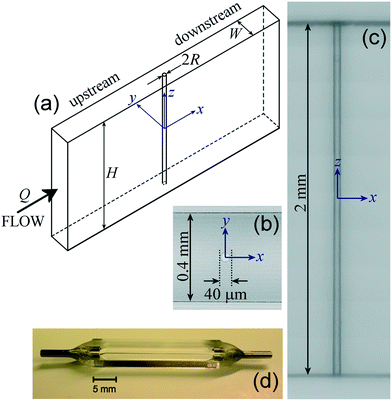 | ||
| Fig. 3 Graphical depiction of the high-aspect ratio microfluidic device used in the experiments: (a) schematic drawing of the flow geometry: a circular cylinder of radius R is located at the origin of coordinates inside a channel of width W and height H. Q represents the volumetric flow rate. (b) and (c) show micrographs of the flow geometry taken from top and side-on views, respectively. (d) Complete device in fused silica, assembled with stainless-steel inlet and outlet connectors. Haward et al. (2019)93 – published by the Royal Society of Chemistry. | ||
2.2 Flow control and dimensionless groups
The flow in the rectangular microchannel is driven at controlled volumetric flow rate Q using two Nemesys low-pressure syringe pumps (Cetoni GmbH), one infusing at the inlet and the second withdrawing at an equal and opposite rate from the outlet. The average flow velocity inside the channel is then U = Q/(WH). The dimensionless Reynolds number decribes the relative importance of inertial to viscous forces in a flow. For flow around the cylinder we define the Reynolds number as: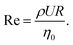 | (1) |
The dimensionless Weissenberg number for the flow, which describes the relative importance of elastic to viscous forces, is defined as:
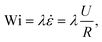 | (2) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ∼ U/R. Microstructural deformation and consequent extension-thickening is expected for Wi ≳ 0.5.11,12
∼ U/R. Microstructural deformation and consequent extension-thickening is expected for Wi ≳ 0.5.11,12
2.3 Test fluids
We present data obtained from a large number of diverse viscoelastic fluids including solutions of different kinds of polymers and also of wormlike micelles (WLMs). Details of the fluids and their rheological characterization will be given during the discussion of the respective results.2.4 Flow visualizations
For measurements using the Exicor Microimager, a light-emitting diode sends collimated monochromatic light (wavelength 535 nm) along an optical line consisting of (a) a linear polarizer at 0°, (b) a photoelastic modulator (PEM) at 45°, (c) the sample (i.e., the microfluidic device), (d) a PEM at 0° and (e) a linear polarizer at 45°. The transmitted light is focussed onto a 2048 × 2048 pixel, 12-bit CCD array. A stroboscopic illumination technique101,102 is used to determine the elements of the 4 × 4 Mueller matrix necessary to compute the pixelwise sample retardance δ and angle of the high refractive index (i.e., slow) optical axis θ over the full field of view.
The CRYSTA PI-1P system combines a “micropolarizer array” in front of a high-speed CMOS imaging sensor. The micropolarizer array consists of 1024 × 1024 linear polarizing elements, each the size of one pixel of the 1024 × 1024 CMOS sensor. The polarizing elements are arranged in sets of 2 × 2 with orientations of 0°, 45°, 90°, and 135°. White light is passed through a band-pass filter (wavelength 527 nm) and a circular polarizer, before passing through the sample and being focussed through the micropolarizer array and onto the imaging sensor of the camera. By analysing the light intensity received at the individual pixels in each 2 × 2 grouping, a spatially-resolved and quantitative measurement of the retardation, δ and orientation angle θ is obtained.93
The retardation is an extrinsic quantity that describes the total phase shift occurring as light polarized at θ and θ + 90° passes through the sample. The phase shift is due to the difference in the refractive indices (n1 and n2) along the two directions (i.e., due to the birefringence Δn = n1 − n2). The birefringence itself is an intrinsic quantity related to the retardation by Δn = δ/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , where
, where ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is the pathlength through the birefringent material.103,104 For imaging through the channel height (z-direction), an approximation can be made that
is the pathlength through the birefringent material.103,104 For imaging through the channel height (z-direction), an approximation can be made that ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ≈ H, however we prefer to report the measured values of δ without assuming a value for
≈ H, however we prefer to report the measured values of δ without assuming a value for ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) .
.
At this point it may be instructive to demonstrate the various flow visualization techniques described above. This also provides an opportunity to outline some common effects observed for viscoelastic flows around cylinders and to highlight some important features of our SLE-fabricated microfluidic device compared with more typical devices fabricated by soft lithography. Fig. 4(a)–(d) shows streak imaging carried out for flows in microchannels fabricated by soft lithography using poly(dimethyl siloxane) (PDMS), which has long since been the most common method of making microfluidic devices.105 Due to the low modulus of PDMS (≈750 kPa), cylinders fabricated in this material must have a low aspect ratio in order to avoid large deformations under imposed flows. The resulting channels therefore also typically have a low aspect ratio AR ≪ 1 (also limited by the thickness of photoresist that can be applied to make PDMS moulds) and are blocked significantly by the presence of the cylinder, BR ≳ 0.5.84,106–109 In such channels, the flow of a Newtonian fluid at low Reynolds number appears as expected, with good symmetry of the streamlines both laterally (side-to-side) and longitudinally (fore-aft), see Fig. 4(a) for the flow of an aqueous glycerol solution at Re ≈ 0.01 and BR = 0.5 visualized by streak photography. However, as shown in Fig. 4(b), when the fluid is viscoelastic (here a solution of poly(ethylene oxide), or PEO, in an aqueous solvent) and the Weissenberg number is sufficiently high, the development of recirculations upstream of the cylinder is observed. Fig. 4(c) and (d) show similar effects with the same PEO solution at higher blockage ratios of BR = 0.67 and BR = 0.83, respectively. Dominant effects upstream of the cylinder are typical in microscale viscoelastic flows with high BR ≳ 0.5 and generally attributed to the build up of elastic stress due to the transient extensional flow and high shear rates where fluid elements are squeezed between the cylinder and the channel walls.84,106–109
 | ||
Fig. 4 Geometry can have a profound effect on the dynamics of viscoelastic flows around cylinders. (a)–(d) Streak imaging with fluorescent tracer particles for flows through PDMS-fabricated microfluidic devices with W = 600 μm, H = 100 μm (AR = 0.167): (a) Newtonian flow at low Re and BR = 0.5; (b)–(d) flow of a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm PEO solution at the indicated Wi and BR = 0.5 (b), BR = 0.67 (c), and BR = 0.83 (d). Scale bar indicates 250 μm. (e)–(g) Flows through the microfluidic device shown in Fig. 3: (e) flow velocimetry with a Newtonian fluid at low Re; (f) and (g) flow velocimetry and flow-induced birefringence (respectively) for the flow of a 700 ppm 6.9 MDa poly(styrene) solution at Wi = 54.2. The colour scales in (e) and (f) indicate the normalized velocity magnitude in the range 0 < |u|/U < 1.8. The colour scale in (g) indicates the retardation in the range 0 < δ < 24 nm. Parts (e) to (g) are reprinted from S. J. Haward, K. Toda-Peters, and A. Q. Shen, J. Non-Newtonian Fluid Mech. 254, 23–35 (2018), with permission from Elsevier. In all images the flow is from left to right. 000 ppm PEO solution at the indicated Wi and BR = 0.5 (b), BR = 0.67 (c), and BR = 0.83 (d). Scale bar indicates 250 μm. (e)–(g) Flows through the microfluidic device shown in Fig. 3: (e) flow velocimetry with a Newtonian fluid at low Re; (f) and (g) flow velocimetry and flow-induced birefringence (respectively) for the flow of a 700 ppm 6.9 MDa poly(styrene) solution at Wi = 54.2. The colour scales in (e) and (f) indicate the normalized velocity magnitude in the range 0 < |u|/U < 1.8. The colour scale in (g) indicates the retardation in the range 0 < δ < 24 nm. Parts (e) to (g) are reprinted from S. J. Haward, K. Toda-Peters, and A. Q. Shen, J. Non-Newtonian Fluid Mech. 254, 23–35 (2018), with permission from Elsevier. In all images the flow is from left to right. | ||
Fig. 4(e) shows quantitative μ-PIV obtained for low-Re Newtonian flow through our SLE-fabricated high aspect ratio AR = 5 and low blockage ratio BR = 0.1 microfluidic device illustrated in Fig. 3. As expected, the flow appears highly symmetric both laterally and longitudinally about the cylinder. Data extracted from this measured flow field in fact shows that flow profiles across the channel width u(y) upstream and downstream of the cylinder agree well with the analytical prediction for fully-developed Poiseuille flow in a rectangular channel of AR = 5.97,110 Furthermore, the flow profile along the channel centreline passing through the cylinder u(x)|y=0 is in agreement with a full 3D numerical prediction.97Fig. 4(f) shows the flow of a solution of high molecular weight poly(styrene) flowing through the low-BR cylinder device at Wi = 54.2. In contrast to the behaviour seen at high BR [Fig. 4(b)–(d)], at low BR the dominant effect of elasticity on the flow field is seen downstream of the cylinder. Here, a long downstream wake of low flow velocity [blue region in Fig. 4(f)] is observed, which corresponds to a region of intense FIB, as shown by Fig. 4(g).97 The long downstream wake effects observed for low BR are associated with the strong stretching and alignment of polymers (and the consequent extension-thickening) due to the high velocity gradients and residence times experienced near the axial stagnation points.24,86,97,111
It is clear that, by causing a variation in the relative importance of the stagnation points and the squeezing and shearing flow around the sides of the cylinder, BR plays a fundamental role in determining the dynamics of viscoelastic flows around cylinders.
3 2D numerical simulations
In the numerical simulations, we consider the 2D creeping flow (i.e., Re → 0) of a non-Newtonian fluid in a planar channel (width W) that features a circular cylinder (radius R) located at the coordinate origin mid-way between the walls [see Fig. 5(a)]. The fluid is incompressible with constant density ρ, solvent viscosity ηs, zero shear rate viscosity η0 and characteristic relaxation time λ. The length of channel is L = 250R, and in all simulations the flow domain spans −125 ≤ x/R ≤ 125. The fluid is driven into the channel by the action of a pressure gradient generating a volumetric flow rate Q = UW per unit depth, where U is the average flow velocity of the fluid far from the cylinder. We scale all lengths with the cylinder radius R, velocities with the average flow velocity U and times with the characteristic flow time R/U. The dimensionless groups that arise are the blockage ratio, the Weissenberg number, and the Newtonian solvent-to-total viscosity ratio β = ηs/η0.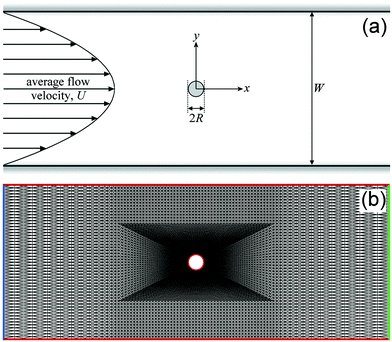 | ||
| Fig. 5 Illustrations of the two-dimensional problem set up in the numerical simulations. (a) A circular cylinder of radius R is located at the origin of coordinates inside a channel of width W and subjected to flow at an average velocity U. (b) A zoomed-in view of one of the numerical meshes employed. The boundary conditions are no slip and no penetration on the solid walls of the channel and the cylinder (marked red), fully-developed at the inlet upstream of the cylinder (blue), and open at the downstream outlet (green). Reprinted from S. Varchanis, C. C. Hopkins, A. Q. Shen, J. Tsamopoulos, and S. J. Haward, Phys. Fluids, 32, 053103 (2020),112 with the permission of AIP publishing. | ||
3.1 Governing equations
The non-Newtonian flow is described by the incompressible and isothermal Cauchy equations coupled with a constitutive equation, which accounts for the contribution of the non-Newtonian stresses. Neglecting inertia, the forms of the continuity, momentum and constitutive equation are expressed, respectively, as:| ∇·u = 0, | (3) |
∇·(−PI + τ + ηs![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a2.gif) ) = 0, ) = 0, | (4) |
g(τ,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a2.gif) ) = 0, ) = 0, | (5) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a2.gif) , is defined as:
, is defined as:![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_char_e0a2.gif) = ∇u + (∇u)T, = ∇u + (∇u)T, | (6) |
No-slip and no-penetration boundary conditions (i.e., u = 0) are imposed on the cylinder surface and channel walls [Fig. 5(b)]. Fully-developed velocity and stress fields are imposed at the inflow boundary (x = −125R), hence, one-dimensional (1D) equations for the velocities and the components of the stress tensor are solved together with the 2D equations for the rest of the domain. More specifically, in each time-step we solve the governing equations for 1D flow in the channel, under the constraint of a flow rate that is gradually increased from zero to Q:
| Q = ∫W/2−W/2u|x=−125R dy = UW(1 − e−tU/R), | (7) |
The form of the operator g (given as a function of τ and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a2.gif) in eqn (5)) depends on the choice of the constitutive model. We have considered the behaviour of various non-Newtonian models including the shear-thinning but inelastic Carreau–Yasuda (C–Y) generalized Newtonian fluid (GNF) model and the elastic but non-shear-thinning Chilcott–Rallison finitely extensible non linear elastic dumbbell (FENE-CR) model.112 However, in this perspective review we focus mainly on one particular model known as the linear Phan-Thien and Tanner (l-PTT) model, which allows us to vary the strength of both the shear-thinning and the elasticity of the fluid. The l-PTT constitutive equation is given in terms of the conformation tensor C as:
in eqn (5)) depends on the choice of the constitutive model. We have considered the behaviour of various non-Newtonian models including the shear-thinning but inelastic Carreau–Yasuda (C–Y) generalized Newtonian fluid (GNF) model and the elastic but non-shear-thinning Chilcott–Rallison finitely extensible non linear elastic dumbbell (FENE-CR) model.112 However, in this perspective review we focus mainly on one particular model known as the linear Phan-Thien and Tanner (l-PTT) model, which allows us to vary the strength of both the shear-thinning and the elasticity of the fluid. The l-PTT constitutive equation is given in terms of the conformation tensor C as:
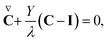 | (8) |
| Y = 1 + εtr(C). | (9) |
| τ = G(C − I), | (10) |
3.2 Numerical method
The Petrov–Galerkin stabilized finite element method for viscoelastic flows (PEGAFEM-V),90 is used to solve the governing equations. The aforementioned finite element (FE) method makes use of linear interpolants for all variables and combines classical finite element stabilization techniques115–117 with the log-conformation representation of the constitutive equation.118 The variational formulation along with a detailed explanation of the FE method is given by Varchanis et al.90The mesh is generated by the quasi-elliptic mesh generator introduced by Dimakopoulos and Tsamopoulos.119 In all simulations we use triangular elements. Fig. 5(b) shows the least refined of the three consecutively-doubled meshes used to confirm mesh convergence. Time integration is performed using a fully implicit 2nd order backward finite difference scheme preceded by a quadratic extrapolation step for the prediction of the solution at each new time instant. Consequently, the numerical method features 2nd order accuracy in space and time.
4 Experimental investigations
Our first experiments on the flow through the glass microfluidic cylinder geometry shown in Fig. 3 involved using μ-PIV to confirm the expected behaviour for a Newtonian fluid at low Re [see Fig. 4(e)], and using a combination of μ-PIV and FIB imaging to examine the steady viscoelastic flow of a dilute polymer solution [see Fig. 4(f) and (g)].97 The fluid used in those experiments was an elastic, but almost non-shear-thinning solution of a 6.9 MDa poly(styrene) dissolved in dioctyl phthalate. For this fluid, as Wi was increased the formation of a long, laterally symmetric downstream wake of low flow velocity and high birefringence was observed [see Fig. 4(f) and (g)]. However, the first experiments we wish to discuss in detail involve the flow of a particular wormlike micellar (WLM) solution.4.1 Flow of a WLM solution
WLMs are elongated semiflexible aggregates formed by the self-assembly of surfactant molecules in aqueous solution.120 WLM solutions have viscoelastic properties similar to polymer solutions, but possess additional relaxation mechanisms due to the ability of the aggregates to break and reassemble.121–124 As a result, WLMs impart unique rheological properties to fluids that make them useful in a wide range of industrial applications and consumer products.125–130 Understanding the behaviour of WLM systems in complex flows is therefore of considerable importance and interest.131,132The wormlike micellar test solution we employed in our flow experiments around microfluidic cylinders was composed of 100 mM cetylpyridinium chloride and 60 mM sodium salicylate (both supplied by Sigma Aldrich) dissolved in deionised (DI) water. This is a well-studied surfactant/counterion system known to form long and entangled wormlike micelles at the selected concentrations.123,133 The steady shear rheology of the test solution, measured at 24 °C (ambient laboratory temperature) using a combination of rotational rheometer (DHR3, TA Instruments Inc.) and m-VROC microfluidic slit rheometer (Rheosense Inc.)134 is presented in Fig. 6(a). The flow curve shows a constant viscosity region (where η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) ≈ η0 = 50 Pa s) at low shear rates followed by a stress-plateau region indicative of shear-banding,135,136 that spans ≈3 decades before the shear stress begins to increase again at higher shear rates. The steady shear rheology is well described by the C–Y GNF model,137 as shown by the solid lines in Fig. 6(a). The storage (G′) and loss (G′′) moduli measured by small angle oscillatory shear at 24 °C on the rotational rheometer are well-described over most of the frequency range using a single mode Maxwell model that provides a value for the relaxation time of λ = 1.8 s [see Fig. 6(b)]. The viscometric properties of the fluid are typical for this WLM formulation.138–140
) ≈ η0 = 50 Pa s) at low shear rates followed by a stress-plateau region indicative of shear-banding,135,136 that spans ≈3 decades before the shear stress begins to increase again at higher shear rates. The steady shear rheology is well described by the C–Y GNF model,137 as shown by the solid lines in Fig. 6(a). The storage (G′) and loss (G′′) moduli measured by small angle oscillatory shear at 24 °C on the rotational rheometer are well-described over most of the frequency range using a single mode Maxwell model that provides a value for the relaxation time of λ = 1.8 s [see Fig. 6(b)]. The viscometric properties of the fluid are typical for this WLM formulation.138–140
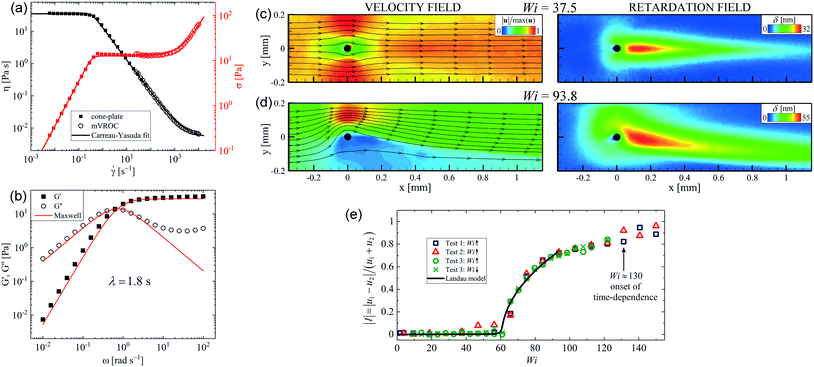 | ||
| Fig. 6 Flow of a WLM solution in the microfluidic cylinder device. (a) Steady shear rheology of the WLM solution fitted with the Carreau–Yasuda model. (b) Oscillatory shear rheology of the WLM solution fitted with a single-mode Maxwell model giving a relaxation time λ ≈ 1.8 s. (c) and (d) Velocity fields (left) and retardation fields (right) for the flow of the WLM solution past the microcylinder at two different Wi. (e) The absolute value of the asymmetry parameter |I| as a function of Wi. Haward et al. (2019)93 – published by the Royal Society of Chemistry. | ||
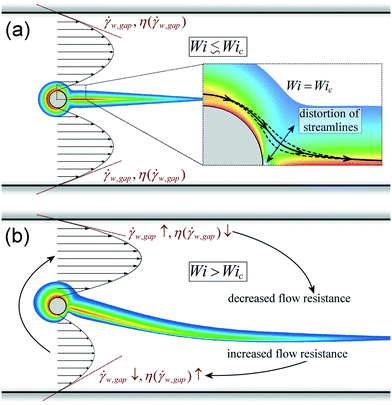
In examining the flow of the shear-banding WLM solution around the slender glass cylinder, a sequence of flow transitions was observed as the Weissenberg number was increased, starting with the onset of a laterally asymmetric flow regime for Wi > Wic.93 Examples of time averaged flow velocimetry and FIB imaging results for Wi < Wic and Wi > Wic are presented in Fig. 6(c) and (d), respectively. For Wi < Wic [e.g., Wi = 37.5, Fig. 6(c)], the flow field was steady and approximately symmetric both laterally and longitudinally. A birefringent strand developed downstream of the cylinder, centred along the x-axis, and which increased in size and intensity with increasing Wi. For Wi > Wic (see e.g., Fig. 6(d) for Wi = 93.8), the flow remained steady, but a clear lateral asymmetry became apparent in the flow field, with the fluid taking a preferential path around one side of the cylinder and an almost stagnant region developing on the opposite side. In the example shown the flow is faster for y > 0 than for y < 0, but it is important to note that the asymmetry could also develop in the opposite sense, with the direction being selected randomly. The asymmetry was also evident in the birefringent strand downstream of the cylinder, which followed the division between the almost stagnant and fast-flowing regions and became shifted towards the channel side wall at y = −0.2 mm.
At the time this work was carried out, the only similar-looking lateral flow asymmetry reported in the literature was for the flow of another WLM fluid around a flexible low modulus PDMS cylinder inside a macroscale channel [see Fig. 1(d)].15 The authors of that work attributed the asymmetry to the off-axis lateral displacement of the cylinder in the flow. However, in our experiment the high-modulus glass cylinder was effectively rigid. Based on the solution to the Euler–Bernoulli equation for a circular cylinder with two pinned ends and estimates of the force per unit length on the cylinder at the highest imposed flow rates, the maximum streamwise deflection of the cylinder at its midpoint, Δxmax ∼ O(1 μm), which is on the same order as the cylinder roughness. Therefore, the occurrence of the asymmetry required an explanation that did not depend on geometric modification caused by the flow.
The extent of the asymmetry was characterized by measuring the flow velocity on either side of the cylinder u1 = u|x=0,y=(0.5W+R)/2, u2 = u|x=0,y=−(0.5W+R)/2 and comparing them to provide an asymmetry, or bifurcation, parameter:
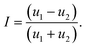 | (11) |
Based on our observations, we proposed (speculatively) that the asymmetry develops from an initially random sideways fluctuation of the highly-stressed downstream birefringent wake at Wi = Wic. We argued that such a fluctuation would cause an (initially small) imbalance between the flow resistance around either side of the cylinder, such that the fluid would preferentially select the least resistant path. This would cause a shear rate imbalance and hence, due to the strong shear-thinning of the fluid, a mismatch between the fluid viscosity on either side of the cylinder that would compound the imbalance in flow resistance and maintain the asymmetry. Further increases in Wi would then cause the instability to grow as the viscosity mismatch increased. However, since such asymmetries had until now only been observed in WLM solutions, several questions remained: (1) what is the importance of shear-banding? (2) what is the importance of relaxation mechanisms peculiar to self-assembled WLM systems (i.e., breakage and reformation)?121,122 In addition, if the hypothesized mechanism is correct, then what is the relative importance of extension-thickening in the downstream wake and shear-thinning at the sides of the cylinder, and how do they interact?
An obvious way to check the importance of the highly specific rheological properties of WLM solutions in the generation of this flow instability is to see whether or not the same situation arises in polymer solutions.
Assuming a polymer solution would show the same effect, then two strategies would allow for testing the hypothesized instability mechanism: (1) varying the geometry through BR, or (2) varying the rheology through degrees of shear-thinning and elasticity. In method (1), by keeping the cylinder radius constant, varying BR would provide different shear rates around the cylinder for a given Wi. However, we considered that spanning a sufficient range of shear rate between the low and high shear rate plateaus would be complicated. On the other hand, considering method (2), experimentally it is unfeasible to vary the shear-thinning and elasticity of a fluid independently. On balance of likely success, our first experimental approach to the problem was to test a range of polymer solutions in our existing microfluidic device, as we describe in the following section.
4.2 Flow of polymeric solutions
Our first effort to gain a deeper understanding of the cause of the lateral flow asymmetry observed for WLM flow around the microfluidic cylinder93 involved the study of a range of viscoelastic polymer solutions.141 The viscoelastic test fluids were composed of a high molecular weight (Mw = 18 MDa) sample of partially hydrolyzed poly(acrylamide) (HPAA, Polysciences Inc.) dissolved in DI water over a range of concentrations 50 ≤ c ≤ 3000 ppm (by weight). The viscosities of the fluids were measured at 25 °C in steady shear using an Anton-Paar MCR 502 stress-controlled rheometer fitted with a stainless steel double-gap geometry. The results are presented in terms of shear stress σ versus shear rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) [Fig. 7(a)]. The fluids are all shear-thinning with flow curves that are well-described by the C–Y GNF model (shown in the plots by the correspondingly-coloured solid lines).
[Fig. 7(a)]. The fluids are all shear-thinning with flow curves that are well-described by the C–Y GNF model (shown in the plots by the correspondingly-coloured solid lines).
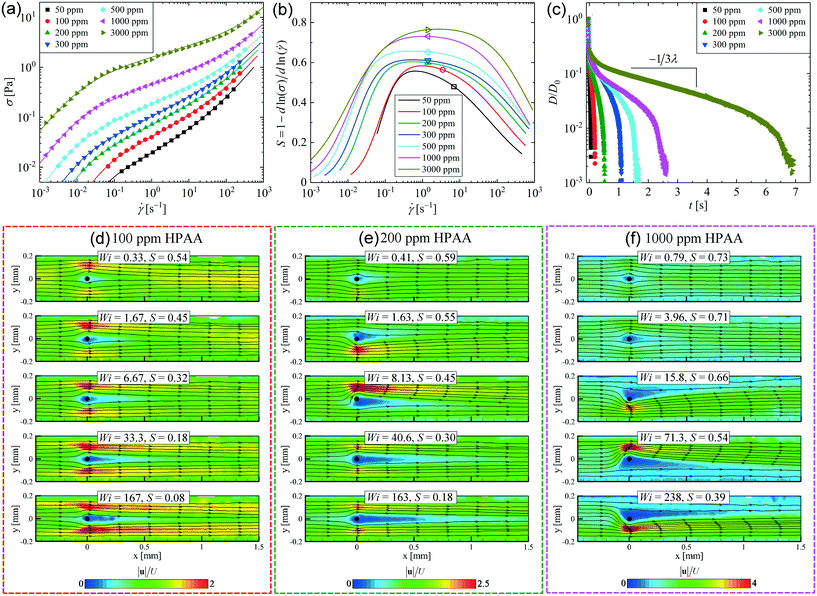 | ||
| Fig. 7 Flow of hydrolyzed poly(acrylamide) (HPAA) aqueous solutions through the microfluidic cylinder device. (a) Steady shear rheology of the polymer solutions over a range of concentrations, fitted with the C–Y model. (b) Shear-thinning parameter, S, derived from the C–Y model fits shown in part (a). The open symbols indicate the characteristic shear rate and value of S at the lowest Wi imposed in the cylinder flow experiments. (c) Capillary breakup measurements from which the fluid relaxation times λ are obtained. (d)–(f) Velocity fields for the flow of the HPAA solutions past the microcylinder at the indicated concentration for progressively increasing Wi. Adapted from Haward et al.141 | ||
To characterize the importance of shear-thinning at any given flow rate imposed in the microfluidic cylinder device, we employed the “shear-thinning parameter” S:142,143
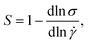 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ/dln
σ/dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1 and S = 0. For a general shear-thinning fluid, 0 < dln
= 1 and S = 0. For a general shear-thinning fluid, 0 < dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ/dln
σ/dln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) < 1 and S attains a positive value 0 < S < 1. For a shear-banding fluid such as a WLM solution exhibiting a stress plateau, S can reach its maximum value of unity.
< 1 and S attains a positive value 0 < S < 1. For a shear-banding fluid such as a WLM solution exhibiting a stress plateau, S can reach its maximum value of unity.
Fig. 7(b) shows S versus ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for the various polymeric test solutions. S is close to zero at low shear rates (i.e., the fluid is only weakly shear-thinning) and increases to a maximum at some intermediate shear rate as shear-thinning increases. At higher shear rates, S decreases again as the high shear rate plateau in viscosity is approached. In general, the curves are all of similar shape, but S becomes increasingly large over a wider range of shear rates as the HPAA concentration increases.
for the various polymeric test solutions. S is close to zero at low shear rates (i.e., the fluid is only weakly shear-thinning) and increases to a maximum at some intermediate shear rate as shear-thinning increases. At higher shear rates, S decreases again as the high shear rate plateau in viscosity is approached. In general, the curves are all of similar shape, but S becomes increasingly large over a wider range of shear rates as the HPAA concentration increases.
In the microfluidic cylinder geometry we evaluated eqn (12) at a nominal value of the wall shear rate in the gap between the cylinder and the channel side wall, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap ≈ 6 U/0.5W. Note that the open symbols marked on the plots of S versus
w,gap ≈ 6 U/0.5W. Note that the open symbols marked on the plots of S versus ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) shown in Fig. 7(b) indicate the minimum value of
shown in Fig. 7(b) indicate the minimum value of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap accessed for each fluid in the cylinder flow experiments.141
w,gap accessed for each fluid in the cylinder flow experiments.141
The characteristic relaxation times (λ) of the fluids at 25 °C were determined by measuring the diameter as a function of time of the liquid bridge generated in a capillary thinning extensional rheology device (Haake CaBER 1, Thermo Scientific) and finding the time constant of the exponential decay in the elasto-capillary thinning regime [see Fig. 7(c)].144,145
In the cylinder flow experiments with HPAA solutions, we assumed that the importance of elasticity (or extension-thickening) in the cylinder wake was quantified by the magnitude of the Weissenberg number (computed as before, Wi = λU/R).141 Note that both Wi and S depend on the applied flow rate so are not varied independently for a given fluid.
In flow around the cylinder, the behaviour of the polymeric test solutions depended on the polymer concentration.141 At lower concentrations [exemplified by the flow velocimetry shown in Fig. 7(d) for c = 100 ppm] the flow remained essentially laterally symmetric for all imposed Wi, although the development of an extended downstream wake of low flow velocity was observed as Wi was increased. HPAA is only very weakly birefringent, but the form of the wake is reminiscent of that previously observed in a birefringent poly(styrene) solution [cf., Fig. 4(f) and (g)] so it is reasonable to assume that the wake in the HPAA solution is also a result of polymer stretching, i.e., extension-thickening.
For intermediate HPAA concentrations [e.g., 200 ppm, Fig. 7(e)], the lateral flow asymmetry was observed as Wi was initially increased starting from a low value, but surprisingly, the symmetry was recovered at higher Wi.
At higher HPAA concentrations [e.g., 1000 ppm, Fig. 7(f)], the lateral asymmetry developed and became increasing intense with increasing Wi, with the flow adopting a very similar pattern to that observed previously with the WLM solution [see Fig. 6(d)].
The fact that the same asymmetric flow patterns are exhibited by polymer solutions obviously means that any peculiarities of the rheology of WLM fluids, such as shear-banding, are of no importance to the onset of the laterally asymmetric flow profiles. We evaluated the asymmetry parameter I (eqn (11)) as a function of the imposed flow rate for each of the HPAA test fluids and assembled the data as a function of Wi and S in a 3D plot, see Fig. 8. Here, the coloured lines mark the trajectories of the test solutions through the 3D space as the flow rate is varied, and the mesh surface is a fit through those trajectories using a combination of sigmoidal functions in S and Wi.141 Plotted in this way, it becomes clear that for lower polymer concentrations where flow stays symmetric (e.g., 50 ppm, black line), S is high only when Wi is low and S rapidly diminishes as Wi increases. The strongly asymmetric flows observed at higher polymer concentrations (e.g., 3000 ppm, dark yellow line) arise when there is a combination of high S and high Wi (i.e., strong shear-thinning and high elasticity, or extension-thickening). For intermediate polymer concentrations (e.g., 300 ppm, blue line), there is a limited region where shear-thinning and elasticity are sufficient to induce asymmetry, but with increasing flow rate the shear-thinning is lost and symmetry is recovered, even though elasticity (as quantified by Wi) continues to increase.
 | ||
| Fig. 8 Magnitude of the asymmetry parameter |I| as a function of S and the imposed Weissenberg number. The coloured lines represent the trajectories of the various test fluids through the 3D space. The continuous mesh surface is formed by fitting the trajectories of the fluids with the product of two sigmoidal functions.141 | ||
These results provided strong support to our original hypothesis regarding the roles of shear-thinning at the sides of the cylinder and of extension-thickening in the wake downstream of the cylinder. However, as discussed above, it would be more ideal if elasticity and shear-thinning could be varied independently. For this reason we pursued the possibility of simulating the flow numerically with the l-PTT viscoelastic constitutive model.
5 Numerical modelling
5.1 Rheological effects
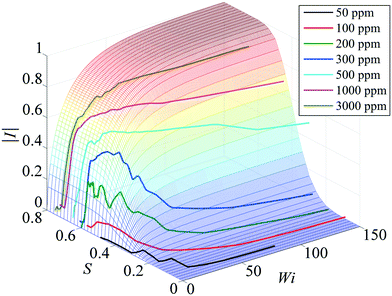
Our 2D numerical modelling of the flow around the cylinder was validated by comparison against three experimental polymer solutions with contrasting rheological characteristics. The first fluid was a strongly shear-thinning but nearly inelastic solution of xanthan gum (XG), which was modelled by the inelastic C–Y GNF model. The second fluid was a highly elastic but almost constant viscosity solution of 4 MDa PEO (PEO4) in a mixture of glycerol and water, which was modelled using the non-shear-thinning FENE-CR model. The third fluid was a both shear-thinning and elastic solution of 8 MDa PEO (PEO8) in water, which was modelled using the l-PTT model (see sec. 3.1). The steady shear rheology of the three experimental test fluids and the three corresponding models is shown in Fig. 9(a). Fig. 9(b) shows the extensional rheology given by the three models.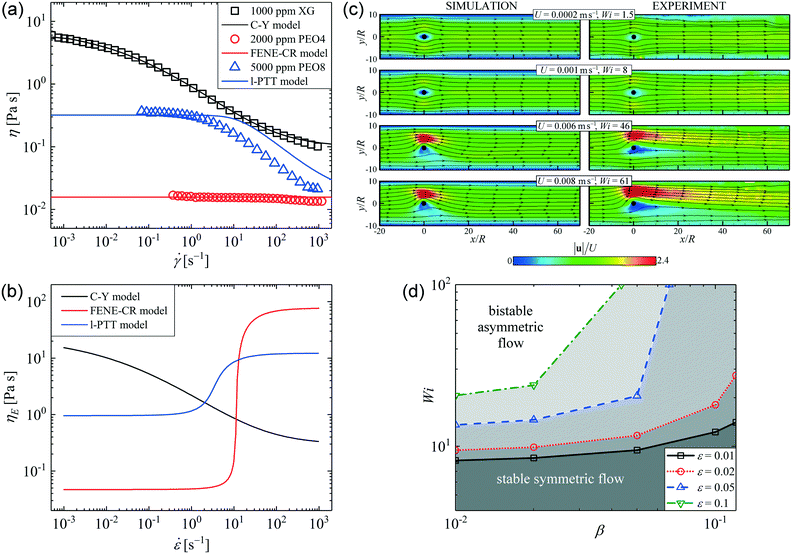 | ||
| Fig. 9 Numerical investigation of rheological effects on the steady flow asymmetry. (a) Numerical models are selected to represent the shear rheology of three contrasting experimental test fluids: a shear-thinning but inelastic 1000 ppm XG solution represented by the C–Y model, a non-shear-thinning but elastic 2000 ppm PEO4 solution represented by the FENE-CR model, and a both shear-thinning and elastic 5000 ppm PEO8 solution represented by the l-PTT model. (b) Extensional rheology of the fluids as indicated by the representative models. (c) Flow velocity fields obtained from numerical simulations with the l-PTT model (β = ε = 0.05) show the onset of asymmetric flow above a critical Wi, in good agreement with experiments carried out with the PEO8 solution. (d) Stability diagram in Wi–β parameter space obtained from simulations with the l-PTT model by varying β and ε, where the critical Wi for the onset of asymmetry lie along contours of constant ε (see text for the full description). Reprinted from S. Varchanis, C. C. Hopkins, A. Q. Shen, J. Tsamopoulos, and S. J. Haward, Phys. Fluids, 32, 053103 (2020),112 with the permission of AIP publishing. | ||
Despite the strong shear-thinning, the inelastic XG fluid and C–Y model fluid showed no signs of lateral flow asymmetry, and the flow remained qualitatively Newtonian-like [see Fig. 4(e)] even at the highest flow rates we could impose. Also, the flow of the strongly elastic but constant viscosity PEO4 fluid and FENE-CR model fluid remained laterally symmetric for all imposed Wi, although in both the real fluid and the model, the development of long elastic downstream wakes was observed at higher Wi, in qualitative similarity to Fig. 4(f). Contrastingly, the PEO8 fluid and the corresponding l-PTT model fluid, characterized by both shear-thinning and elastic effects, both showed the onset of the lateral flow asymmetry at comparable critical values of Wi [see Fig. 9(c)].112
Having validated the l-PTT model as being able to reproduce the instability around the cylinder, we proceeded to investigate the influence of the shear-thinning parameter β and the extension-thickening parameter ε in the response of the model. Recall (sec. 3.1) that lower β implies stronger shear-thinning and lower ε implies stronger extension-thickening with increasing Wi. The results of varying β and ε in the model are summarized concisely in the stability diagram in Wi–β parameter space shown in Fig. 9(d), where the boundaries between symmetric and asymmetric flow states are marked along lines of constant ε. Following lines of constant ε from high to low β, Wic decreases (i.e., shear-thinning is destabilizing). As ε is decreased for fixed β, Wic also decreases (i.e., extension-thickening is also destabilizing). However, for a given value of Wi, the flow destabilizes at lower β as ε is increased (or at lower ε as β is increased). Clearly there is an interplay between the shear-thinning and the extension-thickening. Low levels of shear-thinning can be compensated for by high levels of extension-thickening and vice versa. However, our results showed that as β → 1, then infinite extension-thickening is necessary to induce asymmetry. Conversely, if extension-thickening is weak, then asymmetry can only be induced if β → 0. Thus, simulations with the l-PTT model confirm that both shear-thinning and extension-thickening are required to induce the instability.112
5.2 Geometric effects
2D numerical simulations with the l-PTT model were also used to investigate the influence of the blockage ratio BR of the flow geometry for fixed conditions of shear-thinning β = 0.05 and extension-thickening ε = 0.05. BR was varied by keeping the cylinder radius R constant and adjusting the channel width W. Thus, for a given average flow rate U, the Weissenberg number remained constant but the nominal shear rate around the cylinder![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap increased with increasing BR.
w,gap increased with increasing BR.
First, we considered the magnitude of the asymmetry parameter, |I|, as a function of Wi at various values of BR, see Fig. 10(a). Clearly, geometry has a significant effect on the instability. With decreasing BR, Wic progressively increases. For a fixed value of Wi (say Wi = 25, dashed vertical gray line), the degree of asymmetry progressively decreases with decreasing BR [Fig. 10(b)]. Moving the channel walls further from the cylinder reduces ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap, with an apparent stabilizing effect on the flow.112
w,gap, with an apparent stabilizing effect on the flow.112
 | ||
| Fig. 10 Numerical investigation of geometrical effects on the steady flow asymmetry. (a) Asymmetry parameter I as a function of the Weissenberg number Wi for various values of the blockage ratio BR. (b) Normalized velocity fields at Wi = 25 for different blockage ratios. (c) I as a function of BR at various values of Wi. For increasing BR, stars mark the points where the flow loses symmetry and circles mark the points where symmetry is recovered. (d) Flow curve of the l-PTT fluid, with the critical shear rates for loss and recovery of symmetry marked by the stars and circles (respectively), coloured according to the imposed Wi in part (c). The inset plot in (d) shows the critical blockage ratio at the onset of asymmetry BR,c as a function of 1/Wi, demonstrating the scaling predicted by McKinley et al.4 Reprinted from S. Varchanis, C. C. Hopkins, A. Q. Shen, J. Tsamopoulos, and S. J. Haward, Phys. Fluids, 32, 053103 (2020),112 with the permission of AIP publishing. | ||
An alternative approach to the problem, which yielded further insight, was to vary BR for fixed Wi. Fig. 10(c) shows |I| as a function of BR at various values of Wi, revealing a “bubble” of asymmetry between two critical values of BR. As BR is increased for a given Wi, the flow destabilizes to the asymmetric state at a first critical value BR,c (marked by star symbols). However, the flow restabilizes and recovers symmetry at a second critical value BR,c2 (marked by circles). In the range of Wi covered, this instability “bubble” expands with increasing Wi. The recovery of symmetric flow for BR > BR,c2, is reminiscent of the recovery of symmetry seen in the experiments with polymer solutions at intermediate concentration (cf., Fig. 7(e) and 8). The difference is that in the experiments, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap was varied by controlling the flow velocity (which also varied Wi); here
w,gap was varied by controlling the flow velocity (which also varied Wi); here ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap is varied independently of Wi by controlling BR.112
w,gap is varied independently of Wi by controlling BR.112
For BR,c (stars) and BR,c2 (circles), we computed the corresponding nominal values of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap and placed them on the l-PTT model flow curve in Fig. 10(d). For all investigated values of Wi, the instability bubble occurs when the nominal shear rates lie on the most strongly shear-thinning region of the flow curve. As Wi is increased, BR,c2 progressively extends towards the high shear rate, pseudo-Newtonian plateau [i.e., instability is supported by weaker shear-thinning, as anticipated by Fig. 9(d)]. However, the value of
w,gap and placed them on the l-PTT model flow curve in Fig. 10(d). For all investigated values of Wi, the instability bubble occurs when the nominal shear rates lie on the most strongly shear-thinning region of the flow curve. As Wi is increased, BR,c2 progressively extends towards the high shear rate, pseudo-Newtonian plateau [i.e., instability is supported by weaker shear-thinning, as anticipated by Fig. 9(d)]. However, the value of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap at BR,c appears to be almost independent of Wi, hinting at some universality for the onset of asymmetry at this point.
w,gap at BR,c appears to be almost independent of Wi, hinting at some universality for the onset of asymmetry at this point.
McKinley and coworkers4,5,7 presented a well-known and well-established criterion for the onset of purely elastic instabilities based on the effects of elastic tensile stresses acting along curving streamlines. Using simple arguments based on experimental measurements, and linear stability analysis near the rear stagnation point of a cylinder, they provided a prediction for how the onset of instability in the downstream wake of a cylinder depends on BR, giving 1/Wic ∼ BR (or alternatively BR,c ∼ 1/Wi).4 As shown by the inset plot in Fig. 10(d), our simulation results gave an excellent agreement with this prediction.
6 Discussion and conclusions
We have carried out extensive experimental and numerical investigations of a novel viscoelastic flow instability observed around cylinders, whereby the flow field breaks symmetry but remains steady in time while the fluid passes the cylinder on a randomly-chosen preferential side. Our results indicate that extension-thickening in the wake downstream of the cylinder and shear-thinning in the fluid passing the sides of the cylinder are both required for the asymmetric flow state to develop. All of our results are, in fact, explained in the framework of our speculative mechanism outlined in sec. 4.1, which with greater confidence, we now summarize schematically in Fig. 11.When the flow is symmetric for Wi ≲ Wic [Fig. 11(a)], shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap, hence also the shear-rate-dependent fluid viscosity η(
w,gap, hence also the shear-rate-dependent fluid viscosity η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w,gap), are equal on both sides of the cylinder and the extensionally-thickened strand of fluid (indicated by the coloured region around the grey cylinder) lies symmetrically about the flow axis. At the onset of critical conditions [i.e., Wi = Wic, inset to Fig. 10(a)], the accumulation of elastic tensile stress along the streamlines curving near the rear stagnation point of the cylinder causes a disturbance that perturbs the elastic downstream wake randomly to one side or the other. As outlined in Fig. 11(b), the deflection of the elastic wake to one side causes an increased flow resistance around the same side of the cylinder. Consequently, the shear rate is reduced and the local viscosity is increased. To maintain a constant volumetric flow rate, the shear rate on the opposite side of the cylinder must increase, hence the local viscosity is decreased, acting to decrease the flow resistance around that side. Thus, for a shear-thinning viscoelastic fluid, an initial pertubation of the elastic downstream wake by a purely elastic mechanism can be fixed in place by the positive feedback resulting from the shear-thinning. If shear-thinning remains significant as Wi is increased beyond Wic, strongly asymmetric flow patterns like those in Fig. 6(d) and 7(f), can arise. We note the recent publication of numerical simulations of viscoelastic flow around cylinders using the two-species Vasquez–Cook–McKinley model for WLM solutions, in which long chains can break into two shorter chains, and two shorter chains can combine to form one longer chain.92,146 Those authors also found a general agreement with our basic outlined mechanism, although with additional complexity arising from varying the model parameter controlling the chain breakage and combination rates specific to WLM solutions. The onset of asymmetric flows around two aligned cylindrical posts has also been reported in recent simulations using the FENE-P constitutive model.147 In that study, varying the degree of shear-thinning, dumbbell extensibility, and channel blockage ratio all had effects consistent with the predictions of our proposed mechanism.
w,gap), are equal on both sides of the cylinder and the extensionally-thickened strand of fluid (indicated by the coloured region around the grey cylinder) lies symmetrically about the flow axis. At the onset of critical conditions [i.e., Wi = Wic, inset to Fig. 10(a)], the accumulation of elastic tensile stress along the streamlines curving near the rear stagnation point of the cylinder causes a disturbance that perturbs the elastic downstream wake randomly to one side or the other. As outlined in Fig. 11(b), the deflection of the elastic wake to one side causes an increased flow resistance around the same side of the cylinder. Consequently, the shear rate is reduced and the local viscosity is increased. To maintain a constant volumetric flow rate, the shear rate on the opposite side of the cylinder must increase, hence the local viscosity is decreased, acting to decrease the flow resistance around that side. Thus, for a shear-thinning viscoelastic fluid, an initial pertubation of the elastic downstream wake by a purely elastic mechanism can be fixed in place by the positive feedback resulting from the shear-thinning. If shear-thinning remains significant as Wi is increased beyond Wic, strongly asymmetric flow patterns like those in Fig. 6(d) and 7(f), can arise. We note the recent publication of numerical simulations of viscoelastic flow around cylinders using the two-species Vasquez–Cook–McKinley model for WLM solutions, in which long chains can break into two shorter chains, and two shorter chains can combine to form one longer chain.92,146 Those authors also found a general agreement with our basic outlined mechanism, although with additional complexity arising from varying the model parameter controlling the chain breakage and combination rates specific to WLM solutions. The onset of asymmetric flows around two aligned cylindrical posts has also been reported in recent simulations using the FENE-P constitutive model.147 In that study, varying the degree of shear-thinning, dumbbell extensibility, and channel blockage ratio all had effects consistent with the predictions of our proposed mechanism.
In conclusion, the onset of asymmetric flow of viscoelastic fluids around cylinders is a complex phenomenon that depends on a combination of fluid rheological properties and flow geometry. A given imposed flow rate must (1) cause the formation of an elastic wake downstream of the cylinder, and (2) provide shear rates at the sides of the cylinder that lie in the shear-thinning region of the flow curve. Although such conditions sound rather specific, they seem to be quite readily achieved in microscale channel flows, since the asymmetric flow state has been experimentally demonstrated for a wide variety of fluids, and numerically demonstrated for a range of blockage ratios. We believe this instability (in a benchmark flow configuration) may be fundamental to the understanding of non-Newtonian phenomena observed for sedimenting particles, rising bubbles and for flows through more complex geometries composed of e.g., flexible or cantilevered posts, arrays of cylinders, and porous media flows in general (cf., Fig. 1). The possibility of this effect arising in a given flow configuration should therefore be considered in the optimal design of many lab-on-a-chip type devices in which viscoelastic fluids are employed (cf., Fig. 2).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the support of the Okinawa Institute of Science and Technology Graduate University (OIST) with subsidy funding from the Cabinet Office, Government of Japan. SJH, CCH and AQS also acknowledge funding from the Japan Society for the Promotion of Science (JSPS, Grant No. 20K14656 and 21K03884) and the Joint Research Projects (JRPs) supported by the JSPS and the Swiss National Science Foundation. We thank Kazumi Toda-Peters of the Micro/Bio/Nanofluidics Unit at OIST for assistance with microdevice fabrication.References
- R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, New York, 1999 Search PubMed.
- C. W. Macosko, Rheology: Principles, Measurements and Applications, Wiley, New York, 1994 Search PubMed.
- R. G. Larson, Rheol. Acta, 1992, 31, 213–263 CrossRef CAS.
- G. H. McKinley, P. Pakdel and A. Öztekin, J. Non-Newtonian Fluid Mech., 1996, 67, 19–47 CrossRef CAS.
- P. Pakdel and G. H. McKinley, Phys. Rev. Lett., 1996, 77, 2459–2462 CrossRef CAS PubMed.
- E. S. G. Shaqfeh, Annu. Rev. Fluid Mech., 1996, 28, 129–185 CrossRef.
- A. Öztekin, B. Alakus and G. H. McKinley, J. Non-Newtonian Fluid Mech., 1997, 72, 1–29 CrossRef.
- S. J. Muller, Korea Aust. Rheol. J., 2008, 20, 117–125 Search PubMed.
- S. J. Haward, G. H. McKinley and A. Q. Shen, Sci. Rep., 2016, 6, 33029 CrossRef PubMed.
- S. S. Datta, A. M. Ardekani, P. E. Arratia, A. N. Beris, I. Bischofberger, G. H. McKinley, J. G. Eggers, J. E. López-Aguilar, S. M. Fielding, A. Frishman, M. D. Graham, J. S. Guasto, S. J. Haward, A. Q. Shen, S. Hormozi, R. J. Poole, A. Morozov, V. Shankar, E. S. G. Shaqfeh, H. Stark, V. Steinberg, G. Subramanian and H. A. Stone, arXiv, 2021, arXiv:2108.09841v1 [physics.flu–dyn] Search PubMed.
- P. G. De Gennes, J. Chem. Phys., 1974, 60, 5030–5042 CrossRef CAS.
- J. J. Magda and R. G. Larson, J. Non-Newtonian Fluid Mech., 1988, 30, 1–19 CrossRef CAS.
- A. Jayaraman and A. Belmonte, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 065301 CrossRef PubMed.
- M. M. Gumulya, R. R. Horsley, V. Pareek and D. D. Lichti, Chem. Eng. Sci., 2011, 66, 5822–5831 CrossRef CAS.
- A. A. Dey, Y. Modarres-Sadeghi and J. P. Rothstein, Phys. Rev. Fluids, 2018, 3, 063301 CrossRef.
- C. C. Hopkins, S. J. Haward and A. Q. Shen, Small, 2020, 16, 1903872 CrossRef CAS PubMed.
- C. C. Hopkins, S. J. Haward and A. Q. Shen, Phys. Rev. Lett., 2021, 126, 054501 CrossRef CAS PubMed.
- D. Kawale, E. Marques, P. L. J. Zitha, M. T. Kreutzer, W. R. Rossen and P. E. Boukany, Soft Matter, 2017, 13, 765–775 RSC.
- D. M. Walkama, N. Waisbord and J. S. Guasto, Phys. Rev. Lett., 2020, 124, 164501 CrossRef CAS PubMed.
- L. G. Leal, M. M. Denn and R. Keunings, J. Non-Newtonian Fluid Mech., 1988, 29, 1–8 CrossRef.
- R. A. Brown and G. H. McKinley, J. Non-Newtonian Fluid Mech., 1994, 52, 407–413 CrossRef.
- M. A. Alves, P. J. Oliveira and F. T. Pinho, Annu. Rev. Fluid Mech., 2021, 53, 509–541 CrossRef.
- R. Cressely and R. Hocquart, Opt. Acta, 1980, 27, 699–711 CrossRef CAS.
- M. D. Chilcott and J. M. Rallison, J. Non-Newtonian Fluid Mech., 1988, 29, 381–432 CrossRef CAS.
- O. G. Harlen, J. M. Rallison and M. D. Chilcott, J. Non-Newtonian Fluid Mech., 1990, 34, 319–349 CrossRef CAS.
- C. Bisgaard, J. Non-Newtonian Fluid Mech., 1983, 12, 283–302 CrossRef CAS.
- M. Arigo and G. H. McKinley, Rheol. Acta, 1998, 37, 307–327 CrossRef CAS.
- O. G. Harlen, J. Non-Newtonian Fluid Mech., 2002, 108, 411–430 CrossRef CAS.
- H. Mohammadigoushki and S. J. Muller, J. Rheol., 2016, 60, 587–601 CrossRef CAS.
- M. J. Riddle, C. Narvaez and R. B. Bird, J. Non-Newtonian Fluid Mech., 1977, 2, 23–35 CrossRef CAS.
- W. M. Jones, A. H. Price and K. Walters, J. Non-Newtonian Fluid Mech., 1994, 53, 175–196 CrossRef.
- D. D. Joseph, Y. J. Liu, M. Poletto and J. Feng, J. Non-Newtonian Fluid Mech., 1994, 54, 45–86 CrossRef CAS.
- S. J. Haward and J. A. Odell, Rheol. Acta, 2004, 43, 350–363 CrossRef CAS.
- R. Zenit and J. J. Feng, Annu. Rev. Fluid Mech., 2018, 50, 505–534 CrossRef.
- A. A. Dey, Y. Modarres-Sadeghi and J. P. Rothstein, J. Fluid Mech., 2017, 813, R5 CrossRef.
- A. A. Dey, Y. Modarres-Sadeghi and J. P. Rothstein, Soft Matter, 2020, 16, 1227–1235 RSC.
- A. A. Dey, Y. Modarres-Sadeghi and J. P. Rothstein, J. Fluids Struct., 2020, 96, 103025 CrossRef.
- A. A. Dey, Y. Modarres-Sadeghi and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2020, 286, 104433 CrossRef CAS.
- C. H. K. Williamson and R. Govardhan, Annu. Rev. Fluid Mech., 2004, 36, 413–455 CrossRef.
- M. Müller, J. Vorwerk and P. O. Brunn, Rheol. Acta, 1998, 37, 189–194 CrossRef.
- S. De, J. van der Schaaf, J. A. M. Deen, N. G. Kuipers, E. A. J. F. Peters and J. T. Padding, Phys. Fluids, 2017, 29, 113102 CrossRef.
- U. Eberhard, H. J. Seybold, E. Secchi, J. Jiménez-Martínez, P. A. Rühs, A. Ofner, J. S. Andrade Jr. and M. Holzne, Sci. Rep., 2020, 10, 11733 CrossRef CAS PubMed.
- J. McGrath, M. Jimenez and H. Bridle, Lab Chip, 2014, 14, 4139–4158 RSC.
- G. D. Chen, F. Fachin, E. Colombini, B. L. Wardle and M. Toner, Lab Chip, 2012, 12, 3159–3167 RSC.
- S. N. Khaderi, C. B. Craus, J. Hussong, N. Schorr, J. Belardi, J. Westerweel, O. Prucker, J. Rühe, J. M. J. den Toonder and P. R. Onck, Lab Chip, 2011, 11, 2002–2010 RSC.
- X. Niu, S. Gulati, J. B. Edel and A. J. deMello, Lab Chip, 2008, 8, 1837–1841 RSC.
- J. M. M. Galvez, M. Garcia-Hernando, F. Benito-Lopez, L. Basabe-Desmonts and A. V. Shnyrova, Lab Chip, 2020, 20, 2748–2755 RSC.
- J. J. Cardiel, Y. Zhao, L. Tonggu, L. Wang, J.-H. Chung and A. Q. Shen, Lab Chip, 2014, 14, 3912–3916 RSC.
- D. Kawale, G. Bouwman, S. Sachdev, P. L. J. Zitha, M. T. Kreutzer, W. R. Rossen and P. E. Boukany, Soft Matter, 2017, 13, 8745–8755 RSC.
- S. De, P. Krishnan, J. van der Schaaf, J. A. M. Kuipers, E. A. J. F. Peters and J. T. Padding, J. Colloid Interface Sci., 2018, 510, 262–271 CrossRef CAS PubMed.
- S. J. Haward, C. C. Hopkins and A. Q. Shen, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2111651118 CrossRef PubMed.
- A. Chauhan, S. Gupta and C. Sasmal, arXiv, 2021, arXiv:2107.10617v1 [physics.flu–dyn] Search PubMed.
- M. Brust, C. Shaefer, R. Doerr, L. Pan, M. Garcia, P. E. Arratia and C. Wagner, Phys. Rev. Lett., 2013, 110, 078305 CrossRef CAS PubMed.
- S. Varchanis, Y. Dimakopoulos, C. Wagner and J. Tsamopoulos, Soft Matter, 2018, 14, 4238–4251 RSC.
- S. J. Haward, V. Sharma and J. A. Odell, Soft Matter, 2011, 7, 9908–9921 RSC.
- S. J. Haward, Biopolymers, 2014, 101, 287–305 CrossRef CAS PubMed.
- P. C. Sousa, F. T. Pinho, M. S. N. Oliveira and M. A. Alves, Biomicrofluidics, 2011, 5, 014108 CrossRef CAS PubMed.
- S. Gulati, S. J. Muller and D. Liepmann, J. Non-Newtonian Fluid Mech., 2008, 155, 51–66 CrossRef CAS.
- R. Hidema, T. Oka, Y. Komoda and H. Suzuki, Phys. Fluids, 2019, 31, 072005 CrossRef.
- R. L. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Science, 2004, 304, 987–990 CrossRef PubMed.
- N. Li, D. T. Kamei and C.-M. Ho, 2007 2nd IEEE International Conference on Nano/Micro Engineered and Molecular Systems, 2007, pp. 932–936 Search PubMed.
- N. Pamme, Lab Chip, 2007, 7, 1644–1659 RSC.
- D. W. Inglis, Appl. Phys. Lett., 2009, 94, 013510 CrossRef.
- D. R. Gossett, W. M. Weaver, A. J. Mach, S. C. Hur, H. T. K. Tse, W. Lee, H. Amini and D. Di Carlo, Anal. Bioanal. Chem., 2010, 397, 3249–3267 CrossRef CAS PubMed.
- K. K. Zeming, N. V. Thakor, Y. Zhang and C.-H. Chen, Lab Chip, 2016, 16, 75–85 RSC.
- M. Anfolk and T. Laurell, Anal. Chim. Acta, 2017, 965, 9–35 CrossRef PubMed.
- X. Jiang, K. H. K. Wong, A. H. Khankhel, M. Zeinali, E. Reategui, M. J. Phillips, X. Luo, N. Aceto, F. Fachin, A. N. Hoang, W. Kim, A. E. Jensen, L. V. Sequist, S. Maheswaran, D. A. Haber, S. L. Stott and M. Toner, Lab Chip, 2017, 17, 3498–3503 RSC.
- S. Feng, A. M. Skelley, A. G. Anwer, G. Liu and D. W. Inglis, Biomicrofluidics, 2017, 11, 024121 CrossRef PubMed.
- S. Nagrath, L. Sequist, S. Maheswaran, D. W. Bell, D. Irimia, L. Ulkus, M. R. Smith, E. L. Kwak, S. Digumarthy, A. Muzikansky, P. Ryan, U. J. Balis, R. G. Thompkins, D. A. Haber and M. Toner, Nature, 2007, 450, 1235–1239 CrossRef CAS PubMed.
- G. D. Chen, F. Fachin, M. Fernandez-Suarez, B. L. Wardle and M. Toner, Small, 2011, 8, 1061–1067 CrossRef PubMed.
- F. Fachin, G. D. Chen, M. Toner and B. L. Wardle, J. Microelectromech. Syst., 2011, 20, 1428–1438 CAS.
- K. K. Zeming, T. Salafi, S. Shikha and Y. Zhang, Nat. Commun., 2018, 9, 1254 CrossRef PubMed.
- S. Hanasoge, P. J. Hesketh and A. Alexeev, Microsyst. Nanoeng., 2018, 4, 11 CrossRef PubMed.
- J. J. Cardiel, Y. Zhao, J.-H. Kim, J.-H. Chung and A. Q. Shen, Carbon, 2014, 80, 203–212 CrossRef CAS.
- H. A. Stone, A. D. Stroock and A. Ajdari, Annu. Rev. Fluid Mech., 2004, 36, 381–411 CrossRef.
- T. M. Squires and S. R. Quake, Rev. Mod. Phys., 2005, 77, 977–1026 CrossRef CAS.
- G. H. McKinley, R. C. Armstrong and R. A. Brown, Philos. Trans. R. Soc., A, 1993, 344, 265–304 CrossRef.
- A. H. Shiang, A. Öztekin, J. C. Lin and D. Rockwell, Exp. Fluids, 2000, 28, 128–142 CrossRef CAS.
- J. M. Verhelst and F. T. M. Nieuwstadt, J. Non-Newtonian Fluid Mech., 2004, 116, 301–328 CrossRef CAS.
- C. J. Pipe and P. A. Monkewtiz, J. Non-Newtonian Fluid Mech., 2006, 139, 54–67 CrossRef CAS.
- G. R. Moss and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2010, 165, 1505–1515 CrossRef CAS.
- V. M. Ribeiro, P. M. Coelho, F. T. Pinho and M. A. Alves, Chem. Eng. Sci., 2014, 111, 364–380 CrossRef CAS.
- D. F. James, T. Shiau and P. M. Aldridge, J. Rheol., 2016, 60, 1137–1149 CrossRef CAS.
- Y. Zhao, A. Q. Shen and S. J. Haward, Soft Matter, 2016, 12, 8666–8681 RSC.
- C.-L. Sun and H.-Y. Huang, Biomicrofluidics, 2016, 10, 011903 CrossRef PubMed.
- K. P. Nolan, A. Agarwal, S. Lei and R. Shields, Microfluid. Nanofluid., 2016, 20, 101 CrossRef.
- T. Rodrigues, F. J. Galindo-Rosales and L. Campo-Deaño, J. Non-Newtonian Fluid Mech., 2020, 286, 104406 CrossRef CAS.
- M. A. Alves, F. T. Pinho and P. J. Oliveira, J. Non-Newtonian Fluid Mech., 2001, 97, 207–232 CrossRef CAS.
- P. J. Oliveira and A. I. P. Miranda, J. Non-Newtonian Fluid Mech., 2005, 127, 51–66 CrossRef CAS.
- S. Varchanis, A. Syrakos, Y. Dimakopoulos and J. Tsamopoulos, J. Non-Newtonian Fluid Mech., 2019, 267, 78–97 CrossRef CAS.
- M. B. Khan and C. Sasmal, Soft Matter, 2020, 16, 5261–5272 RSC.
- M. B. Khan and C. Sasmal, arXiv, 2021, arXiv:2101.06367v1 [physics.flu–dyn] Search PubMed.
- S. J. Haward, N. Kitajima, K. Toda-Peters, T. Takahashi and A. Q. Shen, Soft Matter, 2019, 15, 1927–1941 RSC.
- J. Gottmann, M. Hermans and J. Ortmann, Phys. Procedia, 2012, 39, 534–541 CrossRef.
- G. Meineke, M. Hermans, J. Klos, A. Lenenbach and R. Noll, Lab Chip, 2016, 16, 820–828 RSC.
- N. Burshtein, S. T. Chan, K. Toda-Peters, A. Q. Shen and S. J. Haward, Curr. Opin. Colloid Interface Sci., 2019, 43, 1–14 CrossRef CAS.
- S. J. Haward, K. Toda-Peters and A. Q. Shen, J. Non-Newtonian Fluid Mech., 2018, 254, 23–35 CrossRef CAS.
- C. D. Meinhart, S. T. Wereley and M. H. B. Gray, Meas. Sci. Technol., 2000, 11, 809–814 CrossRef CAS.
- S. T. Wereley and C. D. Meinhart, Microscale Diagnostic Techniques, Springer-Verlag, Heidelberg, 2005, pp. 51–112 Search PubMed.
- S. T. Wereley and C. D. Meinhart, Annu. Rev. Fluid Mech., 2010, 42, 557–576 CrossRef.
- C.-Y. Han and Y.-F. Chao, Rev. Sci. Instrum., 2006, 77, 023107 CrossRef.
- S. Nichols, J. Freudenthal, O. Arteaga and B. Kahr, Polarization: Measurement, Analysis, and Remote Sensing XI, 2014, p. 909912 Search PubMed.
- G. G. Fuller, Optical Rheometry of Complex Fluids, Oxford University Press, New York, 1995 Search PubMed.
- J. A. Odell, Handbook of Experimental Fluid Mechanics, Springer-Verlag, Heidelberg, 2007, pp. 724–732 Search PubMed.
- J. C. McDonald and G. M. Whitesides, Acc. Chem. Res., 2002, 35, 491–499 CrossRef CAS PubMed.
- S. Kenney, K. Poper, G. Chapagain and G. Christopher, Rheol. Acta, 2013, 52, 485–497 CrossRef CAS.
- F. J. Galindo-Rosales, L. Campo-Deaño, P. C. Sousa, V. M. Ribeiro, M. S. N. Oliveira, M. A. Alves and F. T. Pinho, Exp. Therm. Fluid Sci., 2014, 59, 128–139 CrossRef.
- X. Shi, S. Kenney, G. Chapagain and G. F. Christopher, Rheol. Acta, 2015, 54, 805–815 CrossRef CAS.
- B. Qin, P. F. Salipante, S. D. Hudson and P. E. Arratia, J. Fluid Mech., 2019, 864, R2 CrossRef CAS PubMed.
- R. K. Shah and A. L. London, Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data, Academic Press, New York, 1978 Search PubMed.
- N. François, D. Lasne, Y. Amarouchene, B. Lounis and H. Kellay, Phys. Rev. Lett., 2008, 100, 018302 CrossRef PubMed.
- S. Varchanis, C. C. Hopkins, A. Q. Shen, J. Tsamopoulos and S. J. Haward, Phys. Fluids, 2020, 32, 053103 CrossRef CAS.
- T. C. Papanastasiou, N. Malamataris and K. Ellwood, Int. J. Numer. Methods Fluids, 1992, 14, 587–608 CrossRef CAS.
- S. Varchanis, Y. Dimakopoulos and J. Tsamopoulos, J. Rheol., 2018, 62, 25–47 CrossRef CAS.
- T. E. Tezduyar, Adv. Appl. Mech., 1991, 28, 1–44 Search PubMed.
- M. Pasquali and L. E. Scriven, J. Non-Newtonian Fluid Mech., 2002, 108, 363–409 CrossRef CAS.
- A. N. Brooks and T. J. R. Hughes, Comput. Methods Appl. Mech. Eng., 1982, 32, 199–259 CrossRef.
- M. A. Hulsen, R. Fattal and R. Kupferman, J. Non-Newtonian Fluid Mech., 2005, 127, 27–39 CrossRef CAS.
- Y. Dimakopoulos and J. Tsamopoulos, J. Comput. Phys., 2003, 192, 494–522 CrossRef.
- J. N. Israelachvili, Intermolecular and Surface Forces: With Applications to Colloidal and Biological Systems, Academic Press, London, 1985 Search PubMed.
- M. E. Cates, Macromolecules, 1987, 20, 2289–2296 CrossRef CAS.
- M. S. Turner and M. E. Cates, Langmuir, 1991, 7, 1590–1594 CrossRef CAS.
- H. Rehage and H. Hoffmann, Mol. Phys., 1991, 74, 933–973 CrossRef CAS.
- J. Appell, G. Porte, A. Khatory, F. Kern and S. J. Candau, J. Phys. II, 1992, 2, 1045–1052 CrossRef CAS.
- H. Hoffmann, H. Löbl, H. Rehage and I. Wunderlich, Tenside, Surfactants, Deterg., 1985, 22, 290–298 CrossRef CAS.
- H. Hoffmann, Structure and Flow in Surfactant Solutions, American Chemical Society, 1994, pp. 2–31 Search PubMed.
- J. P. Rothstein, Rheol. Rev., 2008, 6, 1–46 Search PubMed.
- J. Yang, Curr. Opin. Colloid Interface Sci., 2002, 7, 276–281 CrossRef CAS.
- S. Kefi, J. Lee, T. Pope, P. Sullivan, E. Nelson, A. Hernandez, T. Olsen, M. Parlar, B. Powers, A. Roy, A. Wilson and A. Twynam, Oilfield Rev., 2005, 16, 10–23 Search PubMed.
- S. Ezrahi, E. Tuval and A. Aserin, Adv. Colloid Interface Sci., 2006, 128, 77–102 CrossRef PubMed.
- Y. Zhao, P. Cheung and A. Q. Shen, Adv. Colloid Interface Sci., 2014, 211, 34–46 CrossRef CAS PubMed.
- J. P. Rothstein and H. Mohammadigoushki, J. Non-Newtonian Fluid Mech., 2020, 285, 104382 CrossRef CAS.
- H. Rehage and H. Hoffmann, J. Phys. Chem., 1988, 92, 4712–4719 CrossRef CAS.
- C. J. Pipe, T. S. Majmudar and G. H. McKinley, Rheol. Acta, 2008, 47, 621–642 CrossRef CAS.
- R. W. Mair and P. T. Callaghan, Europhys. Lett., 1996, 36, 719–724 CrossRef CAS.
- S. M. Fielding, J. Rheol., 2016, 60, 821–834 CrossRef CAS.
- R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, John Wiley and Sons, New York, 1987 Search PubMed.
- J. Y. Lee, G. G. Fuller, N. E. Hudson and X. F. Yuan, J. Rheol., 2005, 49, 537–550 CrossRef CAS.
- T. J. Ober, J. Soulages and G. H. McKinley, J. Rheol., 2011, 55, 1127–1159 CrossRef CAS.
- S. J. Haward, T. J. Ober, M. S. N. Oliveira, M. A. Alves and G. H. McKinley, Soft Matter, 2012, 8, 536–555 RSC.
- S. J. Haward, C. C. Hopkins and A. Q. Shen, J. Non-Newtonian Fluid Mech., 2020, 278, 104250 CrossRef CAS.
- V. Sharma and G. H. McKinley, Rheol. Acta, 2012, 51, 487–495 CrossRef CAS.
- S. J. Haward and G. H. McKinley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 031502 CrossRef PubMed.
- V. M. Entov and E. J. Hinch, J. Non-Newtonian Fluid Mech., 1997, 72, 31–54 CrossRef CAS.
- S. L. Anna and G. H. McKinley, J. Rheol., 2001, 45, 115–138 CrossRef CAS.
- P. A. Vasquez, G. H. McKinley and P. L. Cook, J. Non-Newtonian Fluid Mech., 2007, 144, 122–139 CrossRef CAS.
- M. Kumar and A. M. Ardekani, Phys. Fluids, 2021, 33, 074107 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |