Fast Na diffusion and anharmonic phonon dynamics in superionic Na3PS4†
Mayanak K.
Gupta‡
*a,
Jingxuan
Ding
a,
Naresh C.
Osti
 b,
Douglas L.
Abernathy
b,
Douglas L.
Abernathy
 b,
William
Arnold
c,
Hui
Wang
b,
William
Arnold
c,
Hui
Wang
 c,
Zachary
Hood
c,
Zachary
Hood
 d and
Olivier
Delaire
d and
Olivier
Delaire
 aef
aef
aMechanical Engineering and Materials Science, Duke University, Durham, NC 27708, USA. E-mail: mg422@duke.edu; olivier.delaire@duke.edu
bNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
cDepartment of Mechanical Engineering, University of Louisville, Louisville, KY 40292, USA
dApplied Materials Division, Argonne National Laboratory, Lemont, IL 60439, USA
eDepartment of Physics, Duke University, Durham, NC 27708, USA
fDepartment of Chemistry, Duke University, Durham, NC 27708, USA
First published on 10th November 2021
Abstract
The design of new solid electrolytes (SEs) hinges on identifying and tuning relevant descriptors. Phonons describe the atomic dynamics in crystalline materials and provide a basis to encode possible minimum energy pathways for ion migration, but anharmonic effects can be large in SEs. Identifying and controlling the pertinent phonon modes coupled most strongly with ionic conductivity, and assessing the role of anharmonicity, could therefore pave the way for discovering and designing new SEs via phonon engineering. Here, we investigate phonons in Na3PS4 and their coupling to fast Na diffusion, using a combination of neutron scattering, ab initio molecular dynamics (AIMD), and extended molecular dynamics based on machine-learned potentials. We identify that anharmonic soft-modes at the Brillouin zone boundary of the anharmonically stabilized cubic phase constitute key phonon modes that control the Na diffusion process in Na3PS4. We demonstrate how these strongly anharmonic phonon modes enable Na-ions to hop along the minimum energy pathways. Further, the quasi-elastic neutron scattering (QENS) measurements, supplemented with ab initio and machine-learned molecular dynamics simulations, probe the Na diffusivity and diffusion mechanism. These results offer detailed microscopic insights into the dynamic mechanism of fast Na diffusion and provide an avenue to search for further Na solid electrolytes.
Broader contextAs part of the growing interest in renewable energy, the push for vehicle electrification motivates developing battery technologies based on safer and more abundant materials. While the dominant battery technology is currently Li-based, Li is a relatively rare element, present in large quantities in only few geographical locations, potentially posing a challenge for future growth in demand. Na constitutes a promising alternative as it is a low-cost and abundant chemical element worldwide. However, few materials exhibit sufficient Na-ion conductivity for battery applications. Hence, it is important to accelerate the discovery of new Na solid electrolytes (SEs), which requires a better fundamental microscopic understanding and the identification of descriptors relevant for fast Na-ion diffusion. Our investigation of atomic dynamics in Na3PS4, combining neutron scattering experiments and first-principles modeling, considers both the effects of Na vacancies and of the phonon modes of the host crystal. We identified anharmonic soft-modes that greatly facilitate the Na diffusion process in Na3PS4. Such anharmonic soft-modes could constitute a useful descriptor for designing new SEs. These results provide a microscopic understanding of how atomic vibrations facilitate the diffusion of Na ions through the material. |
1 Introduction
The current push for safer rechargeable batteries with higher power densities is driving the search for solutions beyond the current Li-ion battery technology based on liquid or gel electrolytes, prompting investigations of all-solid designs leveraging solid-state electrolytes.1–7 Besides safety concerns and performance limitations of liquid electrolytes, the high cost and limited availability of lithium are motivating research into batteries based on more abundant sodium.8 However, traditional Na-based solid electrolytes (SEs), such as β-alumina and NASICON compounds have achieved only limited ionic conductivity at room temperature. More recently, the thiophosphate Na ion conductor Na3PS4 and related compounds reached promising ionic conductivities near room temperature.9–15 These Na superionic conductors (SICs) further offer promising tunability in their operating temperature by varying the host lattice composition. The atomistic mechanisms underlying fast ion conduction in solid electrolytes are currently the subject of intense scrutiny. In particular, a central question is how the vibrational properties of the crystal lattice, together with the presence of defects, may increase ionic diffusivity. The influence of the time-averaged structure and vacancies on the diffusion behavior has been studied in a range of SEs.5,14–23 Studies of lattice dynamics in Na3PS4−xSex, Li-argyrodites, and Li-ionic conductors from LISICON and olivines families investigated the correlation between average phonon frequencies of mobile species and the hopping activation energy as well as the attempt frequency, and proposed that such an average phonon frequency could be a useful descriptor in the search for new SEs.24–27 Yet, the characteristics of the host lattice that control Na or Li diffusion, in particular the influence of the flexibility of the lattice and of its large anharmonicity on the associated phonons, remain insufficiently understood to achieve predictive materials design.27–30Previous phonon studies in SEs drew useful correlations between lattice dynamics and diffusion, but remained largely limited to considerations of harmonic phonons, for example the average phonon frequency or density of states (DOS), thereby missing important considerations of mode-resolved dynamics and of the strong anharmonicity characterizing SICs.31–33 In the harmonic picture of phonon theory, a Taylor expansion of the free energy surface is truncated at the second-order (harmonic), which results in independent phonon quasiparticles with well-defined energies.34 However, this harmonic phonon picture is unable to account for properties such as diffusion, thermal expansion, thermal conductivity, or soft-mode phase transitions.35 Higher-order anharmonic terms in the free energy need to be considered, and result in energy shifts and linewidth broadening of phonon spectra.35 Because of their large-amplitude atomic motions and shallow potentials, superionic conductors tend to exhibit strong anharmonic effects.31–33 Strong anharmonicity, as for example in the case of double-well potentials, may result in imaginary (unphysical) phonon frequencies within the harmonic approximation. Properly including higher-order anharmonic terms and finite temperature effects renormalizes phonon spectra, which can then be compared with experiments.32,33,36,37
The relatively simple structure of Na3PS4 provides an opportunity to identify the structural and dynamical descriptors underlying its superionic behavior. The system crystallizes in a tetragonal phase (P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c, α-Na3PS4) at low temperature and transforms to a superionic cubic phase (I
21c, α-Na3PS4) at low temperature and transforms to a superionic cubic phase (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m, β-Na3PS4) at 530 K9,11 (Fig. 1).
3m, β-Na3PS4) at 530 K9,11 (Fig. 1).
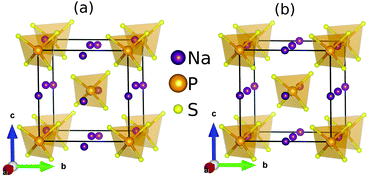 | ||
Fig. 1 The crystal structure of (a) low temperature tetragonal phase (P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c) and (b) high temperature superionic cubic (I 21c) and (b) high temperature superionic cubic (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m) phase of Na3PS4. 3m) phase of Na3PS4. | ||
Further, Na3PS4 exhibits a high-temperature polymorph (γ-Na3PS4) for T ≥ 800 K, with an order-of-magnitude jump in ionic conductivity across the transition.19 The closely related compound Na11Sn2PS12 (NSPS) also exhibits very high ionic conductivity.38,39 Combining diffraction, impedance spectroscopy, and ab initio or classical molecular dynamics simulations, previous studies suggested that the underlying host dynamics in these materials play an important role in enabling the high Na mobility.19,39,40 In γ-Na3PS4, the reorientational dynamics of PS4 units (rotational jumps between symmetrically allowed PS4 orientations) was proposed to be a key factor enabling high ionic conductivity.19 A classical MD study of Na3PS4 based on simple parameterized interatomic potentials also found a correlation between Na hopping and polyanion reorientations in the high-T γ phase, and a jump in Na-conductivity across the β–γ phase transition, but did not discuss phonons.40 AIMD simulations of NSPS also suggested that the large Na conductivity is facilitated by PS4 reorientation dynamics.39 Ref. 19, 39 and 40 all invoked a “paddle wheel” mechanism (involving reorientation dynamics of structural subunits favoring diffusion). Yet, a fundamental understanding of the diffusion mechanism in terms of the mode-resolved phonons of the parent structure (wave-vector and branch-resolved eigenvectors), and of the importance of lattice potential anharmonicity, remains elusive.
Both NSPS and γ-Na3PS4 possess an open framework structure with a large volume per atom, in comparison to conventional solid ionic conductors.19,39 However, few materials (such as Na11Sb2PS12 and Li6PS5I) with larger volumes still exhibit limited diffusion coefficients compared to other family members.39,41,42 Thus, an open-structure with large volume could be a necessary but non-sufficient condition to facilitate fast diffusion. Apart from the structure of the host lattice, its dynamics may also contribute to cation diffusion. In particular, the presence of low-energy modes (combining wiggling and librational motions of structural subunits) and their coupling with the diffusing ions may facilitate the diffusion process.19,39,40,43,44 Such low-energy phonons could be an important descriptor of ionic conductivity and need to be investigated thoroughly. Further, the traditional quasiharmonic phonon picture of conventional crystalline materials breaks down in superionic materials, owing to very strong anharmonic effects and dynamic disorder.31–33 Thus, temperature-dependent measurements and simulations investigating phonon anharmonicity in superionic conductors are critical, yet remain scarce.24,25,27
In this article, we report our investigations of atomic dynamics in Na3PS4 across a wide temperature range, considering on an equal footing the effect of Na vacancies and the phonons of the overall crystal structure, and their coupling, on the diffusive dynamics of Na ions. We use a combination of inelastic neutron scattering (INS) and quasi-elastic neutron scattering (QENS) experiments to obtain a full picture of the atomic dynamics. QENS probes the time and length scales characteristic of the diffusion process, while INS provides access to the phonon dynamics of the crystal lattice over a wide energy range and across the entire Brillouin zone (BZ). We performed temperature-dependent QENS and INS measurements of Na3PS4 across the phase transitions (100 K to 600 K) to probe the Na diffusion and the role of low-energy (E) phonons in the fast diffusion process. To rationalize our measurements and gain atomistic insights, we further performed ab initio molecular dynamics (AIMD) simulations, and extended these simulations to long time scales using machine-learned neural-network potentials. AIMD simulations are known for their high accuracy in predicting the thermodynamics properties but remain constrained by their high computational cost. Using machine-learning, we trained the surrogate potential against AIMD trajectories, which was then used to extend MD simulations to length and time scales several orders of magnitude larger than possible with AIMD while retaining high accuracy (“machine learned molecular dynamics”, MLMD).
Our experiments and simulations show that strongly anharmonic low-E phonon modes are already present in the normal phase and facilitate the Na-ion diffusion in the superionic phase. Specifically, facile Na jumps are enabled by the large amplitudes of low-E floppy dynamics of PS4 subunits coupled with Na translations in 1D channels. We trace the key dynamic mechanism to zone-boundary soft modes (anharmonic low-energy modes) in the anharmonically stabilized cubic phase, which enable the fast ion conduction. These insights provide a potential new type of dynamic descriptor in screening for future solid electrolyte candidates, and highlight the importance of anharmonic effects in the lattice dynamics.
2 Materials and methodology
2.1 Neutron scattering
We performed the INS measurements using the high-flux ARCS time-of-flight45 spectrometer at the Spallation Neutron Source (SNS) at Oak Ridge National Laboratory (ORNL). A polycrystalline sample of Na3PS4 (mass ∼ 6 grams) was encased in a 3/8′′ cylindrical aluminum sample holder and mounted in a high-temperature cryostat.The INS data were collected using three incident neutron energies, Ei = 20, 40, and 100 meV. The measurements with Ei = 20 meV provide high resolution to resolve low-E peaks and accurately determine their energy shift with temperature, while the higher Ei data enable a survey covering the whole phonon spectrum, extending up to about 70 meV. The background from the empty aluminum holder was measured with the same settings at each temperature and subtracted from the measurement of the sample. The Mantid software was used for data reduction.46
The dynamical structure factor, S(Q,E), contains comprehensive information on atomic dynamics. The neutron-weighted phonon DOS (g(n)(E)) in the incoherent approximation was obtained from measured S(Q,E) as described in ref. 47, after corrections for multiphonon and multiple scattering:
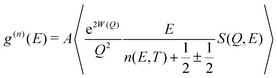 | (1) |
The calculated g(n)(E) was obtained from the partial DOS (gj(E)) as:
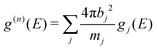 | (2) |
The weighting factors 4πbj2/mj (in units of barns per amu) are: 0.143, 0.107, and 0.032 for Na, P, and S, respectively, using neutron scattering lengths from ref. 48. The partial DOS, gj(E) were obtained from MLMD simulation using eqn (6) described in the next section.
The QENS measurements were performed on the same powder sample as the INS experiment, using the BASIS backscattering spectrometer49 at the SNS, ORNL. We used Si(111) analyzers with neutron wavelength of 6.4 Å and a chopper frequency of 60 Hz. In this configuration, the spectrometer provides an energy transfer range of −100 < E < 100 μeV with an energy resolution of 3.4 μeV, and momentum transfer coverage of 0.2 < Q < 2.0 Å−1. The data were normalized and corrected for detector efficiency using a vanadium standard. A top-loading closed-cycle refrigerator with hot stage was used to measure at temperature T = 100 K, 300 K, 400 K, 500 K, and 600 K. The 100 K data do not show any broadening beyond the instrumental intrinsic width, as the Na dynamics are slow enough to be considered frozen, which were thus used as a resolution function for the analysis of QENS spectra at higher temperatures. The data from various detectors were grouped into Q bins of width 0.2 Å−1. The data reduction and analysis were performed using the software packages Mantid46 and Dave.50 We fit the S(Q,E) from QENS using the following model:
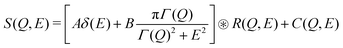 | (3) |
The Q dependence of Γ was analyzed using the Chudley–Elliot (CE) model for jump-diffusion:31
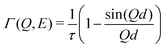 | (4) |
| D = d2/6τ | (5) |
2.2 Computational modeling
The partial (gj(E)) and total phonon DOS (g(E)) were obtained from MD simulations via the Fourier transform of the velocity auto-correlation function as:
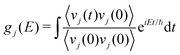 | (6) |
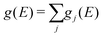 | (7) |
The MSD(〈uj2(t)〉) of element j at time t is given by:
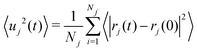 | (8) |
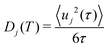 | (9) |
We also computed the angular autocorrelation function, ς(t) of PS4 tetrahedra, defined as:40
ς(t′) = 〈![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (t)· (t)·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (t + t′)〉 (t + t′)〉 | (10) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (t) is a unit vector connecting P and S within a tetrahedron at time t′, and 〈…〉 representing an average over multiple time origins.
(t) is a unit vector connecting P and S within a tetrahedron at time t′, and 〈…〉 representing an average over multiple time origins.
3 Results and discussion
3.1 Phonon DOS and low-energy modes
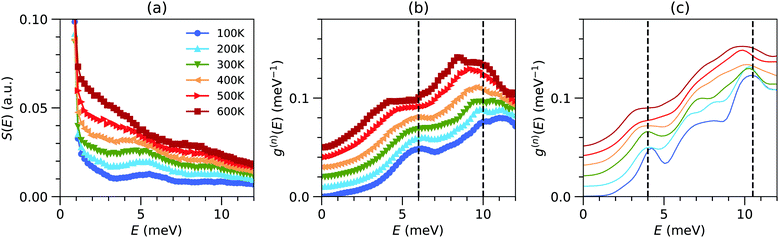
Fig. 2(b) shows the resulting g(n)(E) and its temperature evolution, focusing on the low-E range. The DOS measured over a wider E range is shown in Fig. S1 (ESI†). As can be seen in Fig. 2(b), g(n)(E) exhibits peaks at very low energies E ∼ 6 meV at 100 K, which is surprising considering the low mass of the atoms in the compound. From our MLMD simulations, we extracted the species-decomposed partial DOS (Fig. S2, ESI†). We can see that the Na dynamics dominate g(n)(E) contributions below 30 meV, while the P and S contribute to the entire spectral range. It is unusual for a very light atomic species to exhibit such low-frequency vibrations (ω = (K/M)1/2) with M the mass and K a characteristic force-constant), revealing the extremely soft bonding of the Na ions. The low-E peaks are also seen to soften (shift to lower energy) and broaden drastically on warming, revealing the strong anharmonicity of the interatomic potential, both in INS and MD simulations (Fig. 2(b and c)). We also observe some softening and more moderate broadening of other high energy peaks in the DOS on warming, indicating an overall softness and anharmonicity of the structure. The softening and broadening of low-E modes on warming is even clearer in the measured S(E) (Fig. 2(a)). We can also see that the low-E modes in Na3PS4 become strongly damped at high T, extending towards the elastic line in a quasielastic fashion (Lorentzian peak centered at E = 0). The large softening and broadening of these modes reflects that Na vibrations occur in strongly anharmonic potential wells and that the vibrational dynamics are strongly perturbed and overdamped when the rate of Na diffusion hops increases at higher temperatures, leading to a breakdown of phonon quasiparticles for Na-dominated modes, as detailed below.Recently, Famprikris et al. reported temperature-dependent inelastic neutron scattering (INS) spectra, Raman spectra, and diffraction measurements above room temperature in Na3PS4. Their study focused on the nature of phase transitions, the local structure in different Na3PS4 polymorphs, and thermal expansion.23 They suggested that low-energy modes below E ∼ 25 meV contribute to Na-hopping, but did not present spectra resolved to very low-energies. While our INS spectra agree well with INS measurements reported by Famprikris et al., our measurements with lower incident neutron energy (Ei = 20 meV) enabled us to critically resolve the key low-energy phonons below ∼7 meV that evolve into the quasielastic signal at high-T. Our QENS measurements of very low energy dynamics (E < 0.5 meV) further probe the Na hopping process. Combined with our anharmonic lattice dynamics simulations, the INS and QENS reveal the coupling of Na hoping with specific soft anharmonic phonons of the parent structure.
3.2 Diffusion pathway and phonon projection
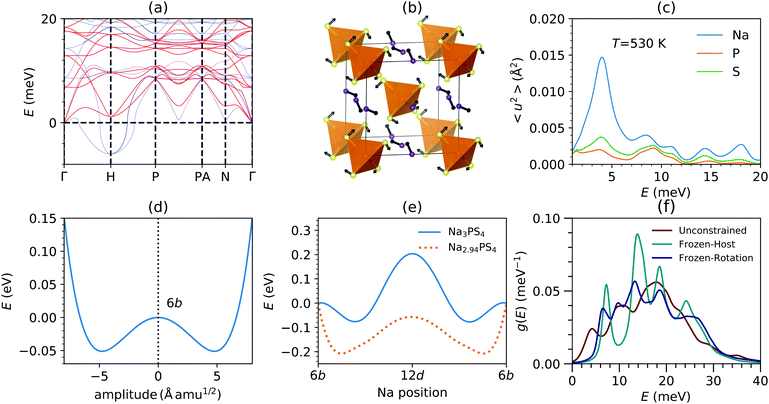
To further investigate the role of phonons in Na diffusion, we performed nudged elastic band (NEB) simulations and projected these onto phonon eigenvectors. We start by considering the phonon dispersions in both cubic and tetragonal phases of Na3PS4 computed within the quasi-harmonic approximation (QHA), see Fig. 3(a) and Fig. S5 (ESI†). We observe stable phonon modes in the tetragonal phase, while the cubic phase exhibits unstable phonons (imaginary frequencies represented as negative values) revealing that it is dynamically unstable at T = 0 K in the harmonic approximation.The maximum instability is observed at the H point, at (1/2, 1/2, 1/2) in reciprocal lattice units (rlu). The eigenvector of this mode, shown in Fig. 3(b), clearly exhibits librations of PS4 units combined with Na translation along 〈100〉 channels. From an amplitude mode analysis,59 we find that this H-point instability is the primary order parameter for the cubic–tetragonal phase transition. The unstable mode corresponds to a double-well potential for the potential energy along this eigenvector, characteristic of soft-mode instabilities (Fig. 3(d)). This indicates that symmetric PS4 libration dynamics in the cubic phase freeze in with a finite amplitude in the tetragonal phase below Tc. The energy required to unlock these libration dynamics corresponds to the energy barrier between minima of the double-well (50 meV ≃ 580 K), which is fairly close to the observed transition temperature in Na3PS4.11 On warming above Tc, anharmonic renormalization stabilizes phonons in the cubic phase, as shown in our finite-T phonon dispersion simulations (solid red lines in (Fig. 3(a)). The kinetic energy gain above Tc enables PS4 units to oscillate between double-well minima and stabilizes the symmetric H-point mode, but its energy remains low, just a few meV.
At high T, such low-energy modes lead to large vibrational amplitudes, particularly Na translations and PS4 librations and wiggling. This is shown by the decomposed MSD of individual elements as a function of phonon energy in Fig. 3(c). The MSD of atom j contributed by phonon of energy E was obtained as:
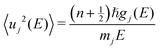 | (11) |
Importantly, the motions of PS4 units widen the gateway for Na hopping, as we now detail. We have identified the minimum (near 12d site) and maximum diameters (near 6b) along the Na diffusion channels and their dependence on PS4 motions (Table 1). We find that PS4 motions indeed increase the channel diameter thus facilitating Na migration. This effect is similar to prior findings in the related compound NSPS.38 Hence, cooperative effects between Na translation and PS4 dynamics, captured in the anharmonic low-E phonon modes at the H-point, are critical for the fast Na hopping.
| (Rmin)/(Rmax) (Å) | Channel volume (Å3) | |
|---|---|---|
| At equilibrium | 1.63/2.13 | 146.2 |
| At saddle point | 1.68/2.22 | 146.6 |
Our MD simulations further confirm that Na diffuses via jumps between 6b Wyckoff sites along the interconnected 1D channels. Hence, the most probable minimum energy pathway (MEP) is across 6b sites via the intermediate 12d sites (halfway between 6b sites along [100]). NEB calculations provide an estimated Eb ∼ 0.3 eV. In addition, we also find that the presence of Na-vacancies (∼2.0%) significantly lowers Eb, to ∼0.2 eV. By decomposing the NEB path onto the phonon eigenvector basis (ζNEB), we find that for small distortion amplitudes around 6b sites, the NEB profile and ζ6bNEB closely follow the H-point phonon potential and eigenvector (ζHphonon) (Fig. 3(d and e) and Table S1, ESI†). However, the NEB path near the 12d site (ζ12dNEB) deviates significantly from ζHphonon, indicating either that: (i) at higher distortion amplitude ζHphonon changes significantly, and/or (ii) ζ12dNEB (Na pathways) cannot be represented by ζHphonon. To understand this further, we performed calculations including the large distortion amplitude corresponding to the saddle-point configuration (moving 3 Na atoms from 6b site to 12d in a conventional unit cell). Strikingly, the phonon eigenvector with saddle-point configuration  follows the ζ12dNEB (Table S1, ESI†). This further confirms that these low-E phonons indeed constitute precursors of the Na-hopping motions.
follows the ζ12dNEB (Table S1, ESI†). This further confirms that these low-E phonons indeed constitute precursors of the Na-hopping motions.
3.3 Hopping dynamics and diffusion mechanism
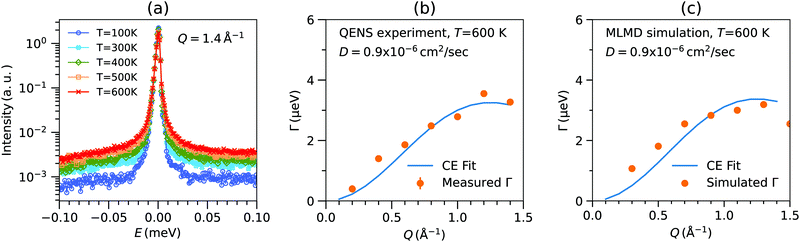
The temperature evolution of experimental QENS spectra at Q = 1.4 Å−1 is shown in Fig. 4(a). A characteristic broadening is seen upon warming, which can be attributed to Na diffusion, as supported by our simulations. In particular, we find a negligible contribution of PS4 dynamics to the QENS signal, see below. The Q dependence of QENS width contains rich information about the hopping process. The fits of QENS spectra are shown in Fig. S6 (ESI†). The fitting was performed over a Q range of 0.2 to 1.5 Å−1. The results for Γ vs. Q at 600 K is shown in Fig. 4(b). The Q dependence of Γ follows the CE model well, and the estimated jump length is 3.6 Å. The estimated diffusion coefficient D is on the order of ∼10−6 cm2 s−1 at 600 K, typical of superionic conductors (Table 2).| d (Å) | τ (ps) | D (×10−6 cm2 s−1) | |
|---|---|---|---|
| QENS | 3.6 | 246 | 0.9 |
| MLMD | 3.6 | 237 | 0.9 |
We performed the AIMD simulations at 100 K to 1000 K using an NVT ensemble. The calculated MSD for the stoichiometric compositions Na3PS4 did not show any signs of Na diffusion, as seen in Fig. S8 (ESI†), in agreement with previous investigations.14 Upon introducing Na vacancies in simulations, fast diffusion occurs in Na3−xPS4 (Fig. S8, ESI†). This result is intuitive, since fully filled 1D channels are expected to block the diffusion path. Hence, some vacant Na sites are needed to enable diffusion. To analyze the QENS spectra, we employed MLMD to reach sufficient long simulation times (see details in Materials and methodology section). This enables us to achieve the required energy and Q resolution to simulate the QENS spectra, which was impractical with AIMD simulations. We also note that AIMD trajectories of limited duration can result in significant errors in estimates of diffusion coefficients due to limited statistics of jump events, especially at low T.61
Further, we use MLMD simulations to assess the contributions to the QENS signal and resolve the element-specific coherent and incoherent contributions. While separating these components based on measurements alone is not practical. We identified that mobile Na atoms mainly contribute to the QENS spectra. The measured intensity in neutron scattering experiments is the sum of coherent and incoherent components:62
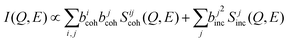 | (12) |
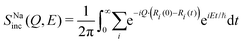 | (13) |
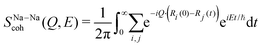 | (14) |
We computed SNainc(Q,E) and SNa−Nacoh(Q,E) in Na3PS4 with 0.6% Na-vacancy from our NVT-MLMD simulations (Fig. S7, ESI†). Our calculated SPinc(Q,E) and SSinc(Q,E) do not show any significant quasi-elastic contribution, confirming that Na dynamics dominate the QENS (Fig. S13, ESI†). This can be understood as follows. At elevated temperatures (∼600 K), the large vibrational amplitude of anharmonic low-energy modes (involving Na vibrations and PS4 librations) results in intermittent stochastic Na hopping along (100) channels, which generates the QENS signal. However, the PS4 units do not undergo stochastic reorientations at 600 K. Thus, they do not contribute to QENS (from low-frequency stochastic dynamics), but rather to the inelastic signal at higher frequency. To further establish this, we have also calculated an angular autocorrelation function, ς(t) of PS4 tetrahedra.40 This quantity remains very close to unity at all times at 600 K (see Fig. S14, ESI†), confirming the absence of stochastic reorientations of PS4. The calculated SNainc(Q,E) was fit with a single Lorentzian and the Q-dependence of Γ was satisfyingly described by a CE model. The simulated SNa–Nacoh(Q,E) has a much smaller intensity than SNainc(Q,E) (Fig. S7, ESI†), except near the Bragg peaks, indicating the dominance of incoherent diffusion. In Fig. 4(c), we show the simulated Γ(Q) from SNainc(Q,E), in excellent agreement with our QENS measurements. Further, we also computed the MSD of each species in Na3PS4 with 0.6% Na-vacancy at several temperatures from 100 K to 600 K (Fig. S4, ESI†). The estimated D from MSD is ∼10−6 cm2 s−1 at 600 K, in good agreement with our estimates from QENS. Higher Na-vacancy concentrations enhance Na diffusion in Na3PS4 (see Table 3 and Fig. S10, ESI†). A recent study on Na3−xPn1−xWxS4 (Pn = P, Sb) also showed that Na-vacancy significantly enhances the Na-conductivity,63 consistent with our finding.
| (a) Host-flexibility vs. D, with 2% Na-vacancy | |
|---|---|
| Degree of host-flexibility | D (×10−6 cm2 s−1) |
| Unconstrained | 2.4 |
| Frozen PS4 | 0.5 |
| Frozen PS4 rotation | 2.1 |
| (b) Na-vacancy vs. D | |
|---|---|
| % Na-Vacancy | D (×10−6 cm2 s−1) |
| 0.0 | 0.0 |
| 0.6 | 1.0 |
| 1.8 | 2.7 |
So far, we discussed the effect of vacancies and the possible role of low-E phonons on Na diffusion based on our lattice dynamics analysis. We now isolate the effect of host framework dynamics on Na diffusion via constrained MLMD simulations (see Materials and methodology section). We compare NVT-MLMD simulations performed with: (i) unconstrained host-lattice, (ii) frozen host-lattice and, (iii) frozen PS4 rotation (but ‘wiggling’ translations allowed). The resulting MSD for the three cases are shown in Fig. S11 (ESI†). Upon freezing the host dynamics, D decreases by about a factor of five, clearly demonstrating the importance of lattice flexibility (Table 3). We find that only freezing the PS4 rotations (case (iii)) also results in a suppression of Na MSD but to a lesser extent than the fully frozen lattice (case (ii)).
Further, we also compare the Na partial DOS in all three cases (Fig. 3(f)). We find that constraining the PS4 dynamics significantly reduces the soft phonon modes at E ∼ 5 meV. In addition, we find that, conversely, increased Na-vacancy concentrations enhance the phonon-DOS at E ∼ 3–5 meV (Fig. S3, ESI†), and thus the slow PS4 modes coupled with Na diffusion. Thus, all our simulations point to a significant role of low-energy PS4 dynamics coupled with Na translation in promoting the Na diffusion in Na3PS4. Thus, we have shown that some vacant Na sites are needed to enable diffusion in 1D channels in β-Na3PS4. Yet, even in the presence of Na vacancies, the host dynamics of PS4 units enable a significant increase in the Na diffusivity (see Table 3 and Fig. S11, ESI†). Hence, while a minimum Na-vacancies is required to enable the onset of diffusion, low-energy phonons of the host lattice play an important role of their own.
4 Conclusions
In the present study, we used high-resolution INS and QENS measurements combined with extensive simulations of atomic dynamics, to investigate the role of phonons in enabling fast Na diffusion in Na3PS4. We revealed the existence of prominent phonon modes with surprisingly low energy in such a light-atom compound (E < 7 meV), and showed that these modes drastically broaden and soften with increasing temperature, corresponding to a breakdown of harmonic phonon quasiparticles. We computationally established how these modes involve coupled motions of Na ions in 1D channels together with PS4 dynamics, and how the large population of these modes at elevated temperatures yields a large vibrational amplitude that helps Na to diffuse in 1D channels. Importantly, we show that the dynamics of low energy modes at the Brillouin zone boundary match the minimum energy pathways for Na hopping, and thereby link these anharmonic soft phonon modes with Na diffusion. Further, we investigated the coupled effects of both host dynamics and Na vacancies on diffusion and found that both contribute significantly toward increasing Na diffusivity. Our results emphasize the importance of anharmonic host dynamics for fast diffusion, in addition to the better known effect of vacancies. These results thus represent new insights into the role of phonon dynamics in solid electrolytes. Our QENS measurements and large-scale MLMD simulations both show the presence of long-range diffusion at 600 K and provide diffusion constants in remarkable agreement, D ∼ 10−6 cm2 s−1.These results establish the importance of anharmonic low-energy modes in a soft crystal structure near a structural phase transition as a means of facilitating fast ion conduction, which provides a new type of descriptor in screening for future solid electrolyte candidates. INS and Raman measurements of phonons as a function of temperature, as well as ultrasonic sound-velocity measurements, can detect soft anharmonic phonon modes and can be used to screen for such effects in candidate SEs.24–27 In addition, first-principles simulations can be used to reveal incipient lattice instabilities and potentially beneficial anharmonic soft modes.
Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
We thank Linda Nazar for interesting discussions. Neutron scattering measurements were supported by the USA Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, under Award No. DE-SC0019978. Simulations and data analysis were supported by Duke startup funds. HW acknowledges financial support from NSF EPSCOR RII Track 4 award (No. 2033397). The research at Oak Ridge National Laboratory's Spallation Neutron Source and High Flux Isotope Reactor was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, USA DOE. Theoretical calculations were performed using resources of the National Energy Research Scientific Computing Center, a U.S. DOE Office of Science User Facility supported by the Office of Science of the USA Department of Energy under Contract No. DE-AC02-05CH11231. Z. D. H. was supported by Laboratory Directed Research and Development (LDRD) funding from Argonne National Laboratory, provided by the Director, Office of Science, of the U.S. Department of Energy under Contract No. DE-AC02-06CH11357.Notes and references
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 1–4 CrossRef.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier and M. Armand, et al. , Energy Environ. Sci., 2018, 11, 1945–1976 RSC.
- X.-B. Cheng, R. Zhang, C.-Z. Zhao and Q. Zhang, Chem. Rev., 2017, 117, 10403–10473 CrossRef CAS PubMed.
- K. H. Park, Q. Bai, D. H. Kim, D. Y. Oh, Y. Zhu, Y. Mo and Y. S. Jung, Adv. Energy Mater., 2018, 8, 1800035 CrossRef.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 1–16 Search PubMed.
- J. B. Boyce and B. A. Huberman, Phys. Rep., 1979, 51, 189–265 CrossRef CAS.
- M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–958 CrossRef CAS.
- N. Tanibata, M. Deguchi, A. Hayashi and M. Tatsumisago, Chem. Mater., 2017, 29, 5232–5238 CrossRef CAS.
- L. Zhang, K. Yang, J. Mi, L. Lu, L. Zhao, L. Wang, Y. Li and H. Zeng, Adv. Energy Mater., 2015, 5, 1501294 CrossRef.
- A. Hayashi, K. Noi, N. Tanibata, M. Nagao and M. Tatsumisago, J. Power Sources, 2014, 258, 420–423 CrossRef CAS.
- A. Banerjee, K. H. Park, J. W. Heo, Y. J. Nam, C. K. Moon, S. M. Oh, S.-T. Hong and Y. S. Jung, Angew. Chem., 2016, 128, 9786–9790 CrossRef.
- S. Xiong, Z. Liu, H. Rong, H. Wang, M. McDaniel and H. Chen, Sci. Rep., 2018, 8, 1–7 CAS.
- Z. Zhu, I.-H. Chu, Z. Deng and S. P. Ong, Chem. Mater., 2015, 27, 8318–8325 CrossRef CAS.
- N. J. de Klerk and M. Wagemaker, Chem. Mater., 2016, 28, 3122–3130 CrossRef CAS.
- X. He, Y. Zhu and Y. Mo, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed.
- S.-H. Bo, Y. Wang, J. C. Kim, W. D. Richards and G. Ceder, Chem. Mater., 2016, 28, 252–258 CrossRef CAS.
- M. Duchardt, U. Ruschewitz, S. Adams, S. Dehnen and B. Roling, Angew. Chem., Int. Ed., 2018, 57, 1351–1355 CrossRef CAS PubMed.
- T. Famprikis, J. A. Dawson, F. Fauth, O. Clemens, E. Suard, B. Fleutot, M. Courty, J.-N. Chotard, M. S. Islam and C. Masquelier, ACS Mater. Lett., 2019, 1, 641–646 CrossRef CAS.
- T. Krauskopf, S. P. Culver and W. G. Zeier, Inorg. Chem., 2018, 57, 4739–4744 CrossRef CAS PubMed.
- C. K. Moon, H.-J. Lee, K. H. Park, H. Kwak, J. W. Heo, K. Choi, H. Yang, M.-S. Kim, S.-T. Hong and J. H. Lee, et al. , ACS Energy Lett., 2018, 3, 2504–2512 CrossRef CAS.
- Q. Zhang, C. Zhang, Z. D. Hood, M. Chi, C. Liang, N. H. Jalarvo, M. Yu and H. Wang, Chem. Mater., 2020, 32, 2264–2271 CrossRef CAS.
- T. Famprikis, H. Bouyanfif, P. Canepa, J. Dawson, M. Zbiri, E. Suard, F. Fauth, H. Y. Playford, D. Dambournet, O. Borkiewicz, M. Courty, J.-N. Chotard, S. Islam and C. Masquelier, Chem. Mater., 2021, 33(14), 5652–5667 CrossRef CAS PubMed.
- T. Krauskopf, S. Muy, S. P. Culver, S. Ohno, O. Delaire, Y. Shao-Horn and W. G. Zeier, J. Am. Chem. Soc., 2018, 140, 14464–14473 CrossRef CAS PubMed.
- T. Krauskopf, C. Pompe, M. A. Kraft and W. G. Zeier, Chem. Mater., 2017, 29, 8859–8869 CrossRef CAS.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef CAS PubMed.
- S. Muy, J. C. Bachman, L. Giordano, H.-H. Chang, D. L. Abernathy, D. Bansal, O. Delaire, S. Hori, R. Kanno and F. Maglia, et al. , Energy Environ. Sci., 2018, 11, 850–859 RSC.
- S. Muy, R. Schlem, Y. Shao-Horn and W. G. Zeier, Adv. Energy Mater., 2020, 2002787 Search PubMed.
- S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Prog. Energy, 2020, 2, 022001 CrossRef.
- K. Gordiz, S. Muy, W. G. Zeier, Y. Shao-Horn and A. Henry, Cell Rep. Phys. Sci., 2021, 2, 100431 CrossRef CAS.
- K. Wakamura, Solid State Ionics, 2004, 171, 229–235 CrossRef CAS.
- J. L. Niedziela, D. Bansal, A. F. May, J. Ding, T. Lanigan-Atkins, G. Ehlers, D. L. Abernathy, A. Said and O. Delaire, Nat. Phys., 2019, 15, 73–78 Search PubMed.
- J. Ding, J. L. Niedziela, D. Bansal, J. Wang, X. He, A. F. May, G. Ehlers, D. L. Abernathy, A. Said and A. Alatas, et al. , Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 3930–3937 CrossRef CAS PubMed.
- A. Maradudin, Theory of lattice dynamics in the harmonic approximation, Academic Press, New York, 1971 Search PubMed.
- P. Brüesch, Phonons: Theory and Experiments I - Lattice Dynamics and Models of Interatomic Forces, Springer Series in Solid-State Sciences, New York, 1982. vol. 34 Search PubMed.
- X. He, D. Bansal, B. Winn, S. Chi, L. Boatner and O. Delaire, Phys. Rev. Lett., 2020, 124, 145901 CrossRef CAS PubMed.
- T. Lanigan-Atkins, X. He, M. Krogstad, D. Pajerowski, D. Abernathy, G. N. Xu, Z. Xu, D.-Y. Chung, M. Kanatzidis and S. Rosenkranz, et al. , Nat. Mater., 2021, 1–7 Search PubMed.
- Z. Zhang, E. Ramos, F. Lalère, A. Assoud, K. Kaup, P. Hartman and L. F. Nazar, Energy Environ. Sci., 2018, 11, 87–93 RSC.
- Z. Zhang, P.-N. Roy, H. Li, M. Avdeev and L. F. Nazar, J. Am. Chem. Soc., 2019, 141, 19360–19372 CrossRef CAS PubMed.
- K. Sau and T. Ikeshoji, J. Phys. Chem. C, 2020, 124, 20671–20681 CrossRef CAS.
- E. P. Ramos, Z. Zhang, A. Assoud, K. Kaup, F. Lalere and L. F. Nazar, Chem. Mater., 2018, 30, 7413–7417 CrossRef CAS.
- I. Hanghofer, M. Brinek, S. Eisbacher, B. Bitschnau, M. Volck, V. Hennige, I. Hanzu, D. Rettenwander and H. Wilkening, Phys. Chem. Chem. Phys., 2019, 21, 8489–8507 RSC.
- K. E. Kweon, J. B. Varley, P. Shea, N. Adelstein, P. Mehta, T. W. Heo, T. J. Udovic, V. Stavila and B. C. Wood, Chem. Mater., 2017, 29, 9142–9153 CrossRef CAS.
- J. G. Smith and D. J. Siegel, Nat. Commun., 2020, 11, 1–11 Search PubMed.
- D. L. Abernathy, M. B. Stone, M. Loguillo, M. Lucas, O. Delaire, X. Tang, J. Lin and B. Fultz, Rev. Sci. Instrum., 2012, 83, 015114 CrossRef CAS PubMed.
- O. Arnold, J.-C. Bilheux, J. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal and M. Gigg, et al. , Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- O. Delaire and C. Stassis, Characterization of Materials, ch. Phonon Studies, Wiley, 2012, pp. 1–22 Search PubMed.
- V. F. Sears, Neutron News, 1992, 3, 26–37 CrossRef.
- E. Mamontov and K. W. Herwig, Rev. Sci. Instrum., 2011, 82, 085109 CrossRef CAS PubMed.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. Tregenna-Piggott, C. M. Brown, J. R. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- T. Tadano, Y. Gohda and S. Tsuneyuki, J. Phys.: Condens. Matter, 2014, 26, 225402 CrossRef CAS PubMed.
- H. Wang, L. Zhang, J. Han and E. Weinan, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- D. Orobengoa, C. Capillas, M. I. Aroyo and J. M. Perez-Mato, J. Appl. Crystallogr., 2009, 42, 820–833 CrossRef CAS.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149(1), 134–141 CrossRef CAS.
- X. He, Y. Zhu, A. Epstein and Y. Mo, npj Comput. Mater., 2018, 4, 1–9 CrossRef CAS.
- M. Bee, Biology and Materials Science, Adam Hilger, Bristol, 1988, p. 193 Search PubMed.
- T. Fuchs, S. P. Culver, P. Till and W. G. Zeier, ACS Energy Lett., 2019, 5, 146–151 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee01509e |
| ‡ Present address: Solid State Physics Division, Bhabha Atomic Research Centre, Mumbai 400085, India. |
| This journal is © The Royal Society of Chemistry 2021 |