Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Homogenous metallic deposition regulated by defect-rich skeletons for sodium metal batteries†
Zhen
Xu‡
 a,
Zhenyu
Guo‡
a,
Zhenyu
Guo‡
 a,
Rajesh
Madhu
a,
Rajesh
Madhu
 a,
Fei
Xie
b,
Ruixuan
Chen
a,
Jing
Wang
a,
Fei
Xie
b,
Ruixuan
Chen
a,
Jing
Wang
 c,
Mike
Tebyetekerwa
c,
Mike
Tebyetekerwa
 d,
Yong-Sheng
Hu
d,
Yong-Sheng
Hu
 b and
Maria-Magdalena
Titirici
b and
Maria-Magdalena
Titirici
 *a
*a
aDepartment of Chemical Engineering, Imperial College London, South Kensington Campus, London SW7 2AZ, UK. E-mail: m.titirici@imperial.ac.uk
bKey Laboratory for Renewable Energy, Beijing Key Laboratory for New Energy Materials and Devices, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
cBristol Composites Institute (ACCIS), School of Civil, Aerospace, and Mechanical Engineering, University of Bristol, University Walk, Bristol BS8 1TR, UK
dSchool of Engineering, College of Engineering and Computer Science, The Australian National University, Canberra, ACT 2601, Australia
First published on 12th August 2021
Abstract
Sodium metal batteries are attracting increasing attention on account of their high energy densities as well as the abundance of sodium-based resources. However, the uneven metallic deposition and dendrite formation during cycling hinder the application of sodium metal anodes. Carbon skeletons have been reported in the literature to mitigate the dendrite formation during the plating and stripping of metallic sodium. Still, the role played by different carbon structural features (i.e., pores vs. defects) and relative mechanisms are not well understood, preventing the controllable interface engineering at the anode side. Here, we have rationally designed the structural features of sustainable carbon skeletons from a renewable precursor to unveil the roles of defects and pores for metallic deposition. The obtained carbon skeleton with rich defects and negligible pores exhibits the best performance when applied to protect metal anodes. After long cycling (>1200 hours), the retained high Coulombic efficiency (∼99.9%) of the plating and stripping processes indicates the importance of defects for inducing uniform metallic deposition. Combined with different types of cathodes (e.g., Prussian blue and sulfur), “anode-less” sodium metal batteries with enhanced electrochemical performance are also demonstrated in terms of sustainability.
Broader contextSodium metal batteries with high energy densities are a cost-effective alternative to lithium-ion batteries for future energy storage systems. However, the practical applications of sodium metal batteries suffer from unstable metallic deposition processes at the anode side. The limited understanding of how the structural features of carbon materials induce the sodium plating and stripping processes fails the rational design and further development of functional carbon hosts for the protection of sodium metal anode from dendrites. In this work, sustainable carbon skeletons with rich defects and negligible pores have been engineered via electrospinning and used as hosts for the formation of stable sodium metal anodes. Advanced characterisation methods and multi-scale modelling were employed to elucidate the roles of defects versus pores towards dendrite-free interfaces, which can lay a solid foundation and provide universal guidance for the development of high-performance sodium metal batteries. |
1. Introduction
Owing to the scarcity and constrained geographical availability of lithium (Li) resources (0.0017 wt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) % in the earth's crust), sodium (Na) batteries based on the abundant sodium resources (2.3 wt
% in the earth's crust), sodium (Na) batteries based on the abundant sodium resources (2.3 wt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) % in the earth's crust) have gradually become a promising successor to lithium batteries.1,2 Among numerous anode materials, it is widely accepted that metallic sodium will be the ultimate anode choice for next-generation sodium batteries due to its ultra-high theoretical capacity of 1166 mA h g−1 and a low negative electrochemical potential of −2.714 V (Na+/Na vs. standard hydrogen electrode).3 However, because of the random process of metallic sodium deposition onto a current collector, the severe sodium dendrite formation during cycling can cause the short circuit and limit their electrochemical performance.4
% in the earth's crust) have gradually become a promising successor to lithium batteries.1,2 Among numerous anode materials, it is widely accepted that metallic sodium will be the ultimate anode choice for next-generation sodium batteries due to its ultra-high theoretical capacity of 1166 mA h g−1 and a low negative electrochemical potential of −2.714 V (Na+/Na vs. standard hydrogen electrode).3 However, because of the random process of metallic sodium deposition onto a current collector, the severe sodium dendrite formation during cycling can cause the short circuit and limit their electrochemical performance.4
Carbon mats, therefore, have been widely employed as a functional skeleton to guide the metallic deposition through uniform nucleation based on the interaction between sodium ions and specific carbon structures during the very first cycle.5 Most studies have attributed pore structures to be beneficial to the uniform sodium metallic deposition since pores in carbon materials can induce the initial nucleation by concentrating the ion flux.6–8 For example, a porous carbon nanotube felt was employed as the host for a sodium metal anode.6 The obtained carbon nanotube host can manipulate the ion flux, thus improving the electrochemical performance of sodium metal anodes with a dendrite-free surface. Furthermore, a nitrogen and sulfur co-doped carbon fibre mat with abundant pore structures was utilised as the substrate to boost the reversibility of a sodium metal anode by inducing homogenous nucleation,9 where the sodium/carbon composite anodes can display an average Coulombic efficiency of 99.52% after 600 cycles at 1.0 mA cm−2. So far, the individual role of defects in carbon structures has not been carefully considered. Currently, it is unknown that how defects versus pores are influencing the metallic sodium nucleation and consequently the entire electrochemical performance. Most porous carbon materials have rich defects at the same time, which makes it impossible to distinguish their individual roles in sodium deposition behaviour.10
Furthermore, most reported carbon fabrics are fabricated from fossil fuels rather than renewable biomass,5,11,12 which hinders the overall sustainability of sodium batteries.13 Differing from other renewable biomass, lignin, which is the only aromatic biopolymer in natural plants, can be extracted as a by-product from the paper industry at a rate of 70 million tons per year.14,15 Compared with the kraft lignin, organosolv lignin is prepared by a milder extraction process, which can be also used as the precursor for carbon skeletons because of its high carbon and low ash content.16 In addition, organosolv lignin can dissolve in water, which allows the formation of aqueous spinnable solutions with low-cost polymers (e.g. polyethylene oxide) and activation agents (e.g., NaOH) for electrospinning.17 Novel utilisation procedures of low-cost lignin into advanced carbon materials represent a promising method to valorise biomass precursors and to diversify the market for the current biomass-derived carbon materials dominated by cellulosic feedstocks.
Here, sustainable carbon skeletons with rich defects and negligible pores have been rationally synthesized by one-step annealing at a low temperature (only 700 °C) from electrospun lignin mats, and then were employed as three-dimensional (3D) hosts for metallic sodium anodes. Multiscale modelling from atoms to macroscale in concert with operando and ex situ characterisation have been conducted to deepen the fundamental understanding of metallic sodium deposition behaviour and electrochemical interfaces formed onto our carbon skeletons. We have successfully demonstrated for the first time in the literature that defects in carbon materials play a more important role in facilitating the nucleation and deposition of metallic sodium than pores. In addition, we have investigated different electrolytes and revealed that diglyme in combination with low-cost and stable NaCF3SO3 salt can regulate the ionic conductivity and increase the lowest unoccupied molecular orbital (LUMO) energy of the electrolyte,18–20 which additionally contributes to a uniform metallic sodium deposition. To authenticate the potential of our lignin-derived carbon mats in practical applications for the concept of “anode-less” sodium metal batteries, we have coupled them with various cathodes such as Prussian blue (PB) crystals or sulfur (S). Our lignin-derived carbon skeletons with a 3D structure play an important role in reducing electrochemical polarisation by improving the ion and mass diffusion in electrodes. In this work, we not only developed and studied novel carbon skeletons with rich defects for stable metallic sodium anodes, but also optimised the whole system from electrodes to electrolytes to help the development of sodium metal batteries with enhanced sustainability, thus paving the way for the future improvement of next-generation energy storage devices beyond lithium-ion battery technologies.
2. Results and discussion
2.1. Synthesis and structural characterisation of carbon skeletons
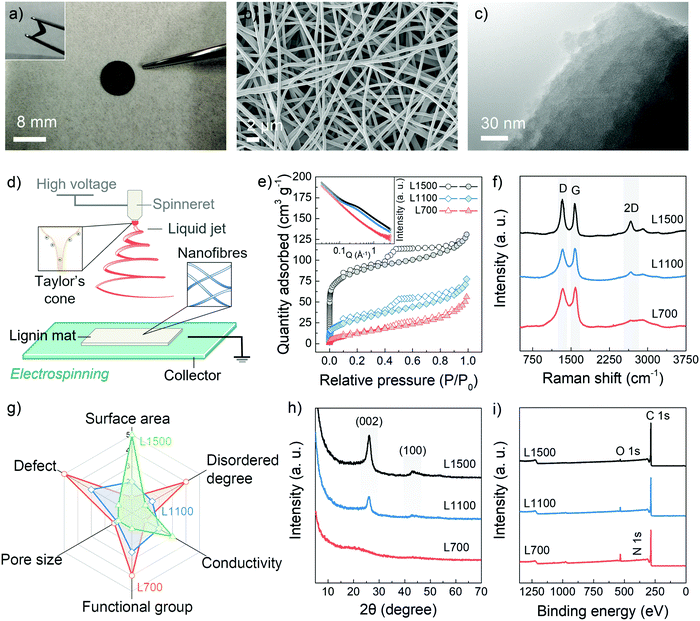
The carbon skeletons were synthesized via the aqueous electrospinning of lignin, followed by the low-temperature pyrolysis (700 °C) under a nitrogen gas atmosphere. To tune defect and pore structures of carbon skeletons, the pyrolysis temperatures were also increased to 1100 °C and 1500 °C. These samples are annotated as L700, L1100 and L1500 depending on their carbonisation temperatures of 700 °C, 1100 °C and 1500 °C, respectively. Fig. 1a and Fig. S1 (ESI†) show that obtained carbon skeletons can maintain a free-standing and flexible format, in which a non-woven fabric with a 3D structure formed by interconnected nanofibres can be observed according to the scanning electron microscopy (SEM) image in Fig. 1b. Such 3D morphology results from the inherent properties of the electrospinning method. After the Taylor cone is formed because of the polarisation of the spinning solution, the lignin nanofibres are pulled out from the prepared aqueous spinning solution under a high-voltage field (Fig. 1d). During the electrospinning process, the volatilised solvent randomly deposits on a collector as single nanofibres, forming a 3D skeleton.21,22 The inner structure of the carbon skeleton is identified with the help of the transmission electron microscopy (TEM) (Fig. 1c) from which the turbostratic nanostructure, a characteristic amorphous feature of biomass-derived hard carbons, can be observed.The pore structures of the carbon skeletons are investigated with the help of the N2 adsorption and desorption isotherms (Fig. 1e). From the isotherms, the obtained Brunauer–Emmett–Teller (BET) specific surface area (SBET) of L700 (50.4 m2 g−1) is lower than those of L1100 (103.6 m2 g−1) and L1500 (282.3 m2 g−1). The pore size distribution based on the non-local density functional theory (NLDFT) method is also shown in Fig. S2a (ESI†). The average diameter of pores decreases with the increase in carbonisation temperatures (Table 1), which means that higher carbonisation temperatures create more micropores (<2 nm, diameter). Small-angle X-ray scattering (SAXS) is utilised as a complementary technique to further probe the pore structure, which can corroborate the BET and NLDFT results. From the inserted image in Fig. 1e, a plateau region from 0.1 to 1 Å−1 in SAXS patterns become more obvious with the increase in carbonisation temperatures. Based on SAXS patterns fitted by Stevens and Dahn's Porod method,23,24 L700 depicts a lower surface area and negligible pore structures than L1500 (Fig. S2c–h and Table S1, ESI†).
| d 002 (nm) | FWHM002b (°) | I D/IGc | L a (nm) | S BET (m2 g−1) | V t (cm3 g−1) | D A (nm) | |
|---|---|---|---|---|---|---|---|
| a d 002: calculated average interlayer spacing of graphene layers from XRD patterns. b FWHM002: fitted full width at half maximum of (002) peaks from XRD patterns. c I D/IG: intensity ratio of D-peak to G-peak based on fitted Raman spectra. d L a: average in-plane distance of the graphene layer from Raman spectra. e S BET: specific surface areas calculated using the multipoint Brunauer–Emmett–Teller (BET) method. f V t: total pore volume from N2 adsorption and desorption isotherms. g D A: average pore diameter from N2 adsorption and desorption isotherms based on NLDFT method (out of brackets) and from SAXS patterns based on Porod method (within brackets). | |||||||
| L700 | 0.396 | 7.92 | 0.94 | 1.22 | 50.4 | 0.081 | 6.2 (2.34) |
| L1100 | 0.345 | 2.25 | 0.97 | 1.24 | 103.6 | 0.083 | 5.4 (2.09) |
| L1500 | 0.343 | 1.98 | 1.04 | 1.29 | 282.3 | 0.141 | 4.8 (1.79) |
To characterise the defects, Raman spectroscopy, X-ray diffraction (XRD) and X-ray photoelectron spectroscopy (XPS) are utilised. The Raman spectra of L700, L1100 and L1500 show broad characteristic D- and G-peaks (Fig. 1f), indicating they are all disordered hard carbons categorised as Stage II in a three-stage model proposed by Ferrari et al.,25–28 which is different from ordered graphitic carbons such as graphite, graphene and carbon nanotubes. In Stage II of this model, the intensity ratio of D- to G-peaks (ID/IG) of hard carbons increases when the defect concentration among graphene layers within hard carbons decreases. According to the calculated values of ID/IG from the fitted Raman spectra (Table 1 and Fig. S3, ESI†), the graphene planes of L700 are more defective than those of L1100 and L1500. Additionally, the 2D-peaks become broader with a decrease in the carbonisation temperatures, which also proves the stacks of graphene planes become more disordered. The uniformity of defect sites of L700 can be recognised based on the TEM image and multi-point Raman scanning of L700 in Fig. S3 (ESI†). The defect structures demonstrated in the Raman spectra can further be categorised into intrinsic defects and extrinsic defects.29,30 The trends of intrinsic defects derived from turbostratic nanostructures can be clarified by the XRD analysis (Fig. 1h),31 and the extrinsic defects caused by heteroatom doping on the surface of carbon skeletons can be further confirmed by XPS (Fig. 1i).32 From XRD patterns (Fig. 1h), two peaks attributed to the (002) and (100) planes of expanded inner structures can be observed at 2θ ≈ 24° and 44° in L1100 and L1500, while L700 shows two wider peaks whose full width at half maximum of (002) planes (FWHM002) can reach 7.92°. The calculated average interlayer spacing of graphene layers (d002) of hard carbons decreases when carbonisation temperatures increase (Table 1). L700, therefore, is more disordered than L1100 and L1500, suggesting more intrinsic defect sites. XPS survey (Fig. 1i) and the fitted C 1s, N 1s and O 1s core-level XPS spectra (Fig. S4, ESI†) show that the atomic amount of nitrogen- and oxygen-doping of L700 can reach 2.3 at% and 9.6 at%, respectively. As the carbonisation temperatures increases, the amount of doping in L1100 and L1500 decreases (Table S2, ESI†). In general, L700 has rich defects and negligible pores compared with L1500 possessing abundant pores and few defects.
It is worth noting that in this study, the pore and defect structures of lignin-derived carbon materials show reverse trends with the presence of the activation agents when the carbonisation temperatures increase. The reasons for this phenomenon are listed as follows: (1) differing from the linear molecular chain of cellulose consisting of repeated units of D-glucose, lignin belongs to phenolic polymers. The degree of order and defective structures of carbon skeletons from lignin are sensitive to temperatures because a large number of benzene rings exist, which has also been discussed in detail in our reported studies;16,17 (2) the electrospinning process under high-voltage can orient the inherently amorphous polymer chains of lignin, thus allowing the increase in the ordered degree of lignin materials; and (3) the amount of activation agents (NaOH) used in this study is one-tenth of that in traditional chemical activation of biomass to avoid the excessive oxidation and achieve the appropriate pore-forming at 1100 and 1500 °C rather than 700 °C. These rational experimental designs all contribute to the successful implementation of the reverse trend between defect structures and pore structures (Fig. 1g) with the change of carbonisation temperatures, enabling deep insights and a good platform for the current mechanism study.
2.2. Electrochemical performance in half cell configurations
To correlate the structure of the carbon skeletons and the sodium deposition behaviour, sodium plating and stripping experiments were carried out in a half cell in which the carbon skeletons were placed against a piece of metallic sodium with the same size (inserted image in Fig. 2a) using 1 M NaCF3SO3 in ethylene carbonate-propylene carbonate (EC-PC, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v%) mixed solvents, ethylene carbonate-diethyl carbonate (EC-DMC, 1
1 v%) mixed solvents, ethylene carbonate-diethyl carbonate (EC-DMC, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v%) mixed solvents or diethylene glycol dimethyl ether (diglyme) as electrolytes (Fig. S5, ESI†). We selected NaCF3SO3 because of its lower cost, lower fluorine content, high solubility (9.26 M in non-aqueous electrolytes)33 and good stability34 compared with traditional salts like NaPF6 and NaTFSI for sodium batteries. Commercial current collectors including aluminium (Al), nickel (Ni), tin (Sn) and copper (Cu) were also employed as substrates for comparison (Fig. S6, ESI†). The galvanostatic charge and discharge (GCD) of the cell was operated using a constant current density of 1.0 mA cm−2 with a fixed specific charge and discharge capacity of 2.0 mA h cm−2.
1 v%) mixed solvents or diethylene glycol dimethyl ether (diglyme) as electrolytes (Fig. S5, ESI†). We selected NaCF3SO3 because of its lower cost, lower fluorine content, high solubility (9.26 M in non-aqueous electrolytes)33 and good stability34 compared with traditional salts like NaPF6 and NaTFSI for sodium batteries. Commercial current collectors including aluminium (Al), nickel (Ni), tin (Sn) and copper (Cu) were also employed as substrates for comparison (Fig. S6, ESI†). The galvanostatic charge and discharge (GCD) of the cell was operated using a constant current density of 1.0 mA cm−2 with a fixed specific charge and discharge capacity of 2.0 mA h cm−2.
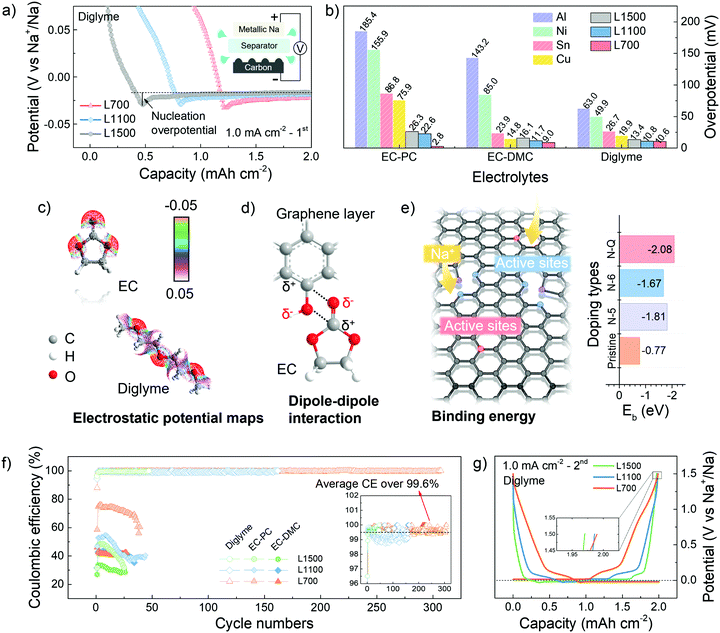
A potential dip (<0 V vs. Na+/Na) can be observed in the potential-capacity profiles, followed by a plateau region of potential representing the sodium deposition process (Fig. 2a). The sodium nucleation overpotentials are first determined by the difference between the bottom value of the potential dip and the value of the plateau region potential. A smaller initial nucleation overpotential represents a lower energy barrier of the nuclei formation needed to be overcome, thus helping identify the sodiophilic properties of a substrate.3,35 Compared with other commerical substrates, our carbon skeletons always show smaller initial nucleation overpotentials (Fig. 2b), which means the sodiophilic properties of carbon skeletons are much better than other substrates no matter in what electrolytes. Moreover, L700 always has the smallest initial nucleation overpotentials of 2.8 mV in EC-PC, 9.0 mV in EC-DMC and 10.6 mV in diglyme, indicating the best sodiophilic properties of L700. Actually, the initial nucleation overpotentials of the various commercial substrates shown in Fig. 2b are almost incomparable with the lignin-derived carbon skeletons because of the different surface situations even under the same constant current density of 1.0 mA cm−2 and with a fixed specific charge and discharge capacity of 2.0 mA h cm−2. Namely, the surface conditions of substrates can make a big difference on the initial nucleation overpotentials.
For the same substrate, the electrostatic interaction between solvent molecules and the heteroatom doping in carbon skeletons can be simulated to understand the influence of electrolytes on nucleation overpotentials.36 According to the electrostatic potential maps of solvent molecules (Fig. 2c), the negative charge region (red) are mostly localised on the oxygen atoms of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of EC, thus polarizing the solvent molecules into a local dipole. Meanwhile, in L700, the charges on the carbon atoms are delocalized by nitrogen and oxygen atoms in the functional groups of L700, and a positive charge region can be formed, which represents the formation of another local dipole. These local dipoles in L700 and ester solvent molecules can strongly interact with each other (Fig. 2d).37 However, based on the electrostatic potential maps of diglyme, the negative charge regions (red) are distributed more uniformly because of its molecular structure, which means no strong dipole–dipole interaction can exist between L700 and ether solvent molecules. Therefore, ester solvent molecules have stronger dipole–dipole interactions with the enriched functional groups on the L700 surface, so the initial nucleation overpotentials of L700 in ester-based electrolytes are smaller than those in ether-based electrolytes. Even so, L700 in diglyme still performs better for long cycling testing, which will be discussed and explained in the following parts.
O groups of EC, thus polarizing the solvent molecules into a local dipole. Meanwhile, in L700, the charges on the carbon atoms are delocalized by nitrogen and oxygen atoms in the functional groups of L700, and a positive charge region can be formed, which represents the formation of another local dipole. These local dipoles in L700 and ester solvent molecules can strongly interact with each other (Fig. 2d).37 However, based on the electrostatic potential maps of diglyme, the negative charge regions (red) are distributed more uniformly because of its molecular structure, which means no strong dipole–dipole interaction can exist between L700 and ether solvent molecules. Therefore, ester solvent molecules have stronger dipole–dipole interactions with the enriched functional groups on the L700 surface, so the initial nucleation overpotentials of L700 in ester-based electrolytes are smaller than those in ether-based electrolytes. Even so, L700 in diglyme still performs better for long cycling testing, which will be discussed and explained in the following parts.
In the same electrolytes, L700 shows better sodiophilic properties than L1500 since the initial nucleation overpotentials of L700 are smaller than those of L1500 (Fig. 2b). According to the literature, porous structures, especially micropores, are beneficial to the nucleation process,7 but the importance of defects in carbon materials cannot be distinguished from pores. In this study, the benefits of defects to the nucleation process can be independently recognised by comparing the discrepancy in structural features of L700 and L1500 with their nucleation overpotentials. Based on our reported studies on the sodium storage mechanism in hard carbons using 23Na nuclear magnetic resonance (NMR), X-ray and neutron scattering,38–40 we proved that defects within hard carbons formed by tortuous and imperfect graphene layers can lead to the sloping regions in the GCD curves, where defects serve as active sites to enhance the capacitive interaction with sodium ions. As observed from Fig. 2g and Fig. S8c (ESI†), the GCD curves of L700 always have higher sloping capacities, which can be correlated with rich defects in the L700.31 In this study, DFT calculations were further conducted to clarify the beneficial role of defects for nucleation. According to the XPS data displayed in Fig. S4 (ESI†), L1500 has no nitrogen content. Therefore, idealised models can be created to symbolise the most obvious difference in defect structure between L700 and L1500. The single pristine graphene layer represents L1500, while the single graphene layer with different types of nitrogen doping signifies L700 (Table S2, ESI†). Here, L700 with nitrogen-containing functional groups exhibit relatively higher binding energies with sodium atoms than L1500 (Fig. 2e), validating the stronger interaction between sodium atoms and defect sites. Among different types of nitrogen doping including pyridinic nitrogen (N-6), pyrrolic nitrogen (N-5) and quaternary nitrogen (N-Q), the quaternary nitrogen-doped L700 has the largest binding energy of −2.1 eV. Meanwhile, we can confirm that nitrogen-containing functional groups of L700 are dominated by quaternary nitrogen based on XPS fitting analysis (Table S3, ESI†). In comparison to L1500, the local charge densities between sodium atoms and quaternary nitrogen-doped L700 increase because of the stronger interaction between sodium atoms and defect sites (Fig. S9, ESI†). Combined with the binding energy simulations reported in the literature,40–45 we can attest that defects including extrinsic heteroatom-doped sites and intrinsic carbon defects can all offer binder sites for sodium nucleation by enhancing the binding energy of sodium ions and the defective carbon substrates.
The cycling performance of L700, L1100 and L1500 was tested in a half cell at a current density of 1.0 mA cm−2 with a specific charge and discharge capacity of 2.0 mA h cm−2 (Fig. S10, ESI†). Upon cycling, metallic sodium kept plating onto and stripping from carbon skeletons. The lower Coulombic efficiency means more irreversible capacity, which mostly results from the formation of so-called “dead sodium” including the sodium consumed in solid electrolyte interphase (SEI) and isolated metallic sodium.46 In the ether-based electrolyte, L700 exhibits the most stable plating and stripping process of over 1200 h (4 h per cycle, over 300 cycles) with the highest average Coulombic efficiency of over 99.6% and the highest last cycle Coulombic efficiency of over 99.9% at the same time (Fig. 2f), which is one of the best carbon substrates for metallic sodium deposition.11,47 The initial Coulombic efficiencies of L700, L1100 and L1500 for sodium plating and stripping are 87.9%, 94.4% and 96.2%, respectively. Differing from the traditional hard carbon anode for sodium-ion batteries with a low initial Coulombic efficiency (usually below 80%),39 our carbon mats have quite high initial Coulombic efficiencies during the first cycle of sodium plating and stripping because of fewer irreversible reactions like SEI formation. In ester-based electrolytes, although EC-PC and EC-DMC both deliver poor cycling performance (which will be explained in the following parts), L700 still shows the highest Coulombic efficiency and lowest IRdrop compared with L1100 and L1500 (Fig. S10, ESI†). These results all identify that the defective structures of L700 can significantly improve the reversibility of metallic sodium deposition rather than porous structures of L1500. In addition, combined with the comparison of our carbon mats to commercial defect-free carbon samples, we can further prove that defects play a beneficial role when metallic sodium deposits onto carbon materials (Fig. S11, ESI†).
2.3. Fundamental mechanism insights into interfacial phenomena and deposition behaviour
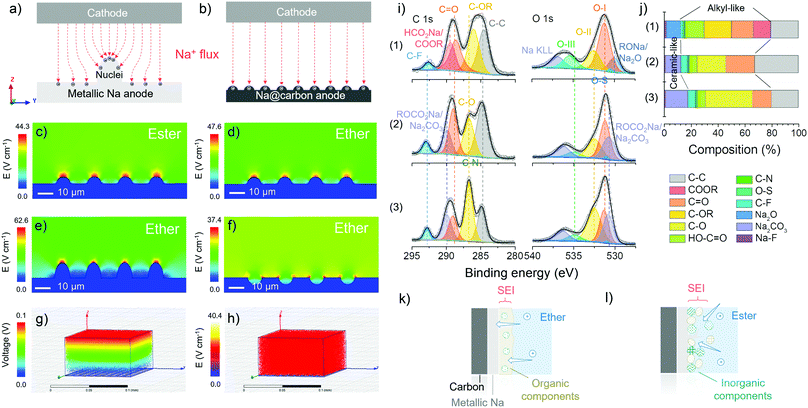
As mentioned before, with the same substrate, the difference in metallic deposition is caused by the properties of electrolytes used. Finite element simulation is employed to study the electric field distribution and corroborate the superior uniformity of ion flux when employing carbon skeletons in the ether-based electrolytes (Fig. 3a and b). First, in Fig. 3c–f, the substrate (blue) on the bottom is defined as metallic sodium with the same nuclei on the surface. The colours above the substrate represent the differences in the electric field distribution, which indicates the change rate of voltage and the density of ion flux. The tip induction of ion flux is observed both in Fig. 3c and d, but the density of ion flux in the ester-based electrolyte is more concentrated at the tip of nuclei than that in the ether-based electrolyte because the higher ionic conductivity of ester-based electrolyte facilitates the rapid metallic deposition to form sharper dendrites on the surface.48 The initial ionic conductivity of electrolytes can be confirmed by electrochemical impedance spectroscopy (EIS) of half cells before cycling (Fig. S12, ESI†), where the charge transfer resistance in ester-based electrolytes is smaller than that in the ether-based electrolyte at the beginning. Combined with the modelling of the other two surface scenarios in the ether-based electrolyte (Fig. 3e and f), we verify that the rough surface can strengthen the ion flux and then accelerate the dendrite formation, which causes a short lifetime and severe safety problems.49 In comparison to the bare metallic sodium, carbon mats are replaced as the substrate (grey) in the simulation, where the homogenous ion flux and uniform voltage change can be observed in Fig. 3g and h. The identical electric field distribution can validate the controlled nucleation and deposition dynamics of carbon skeletons at the macro-level in the ether-based electrolyte.50 Hence, the utilisation of carbon skeletons and ether-based electrolytes theoretically support the prevention of dendrite formation, providing the opportunity for stable sodium metal anode (Fig. S13, ESI†).
Ex situ XPS is used to analyse the interface of the cycled electrodes, in particular the differences in the solid electrolyte interphase (SEI) “composition” formed in various electrolytes. The XPS analysis was conducted after the initial deposition onto the carbon skeletons at 1.0 mA cm−2 with a specific discharge capacity of 2.0 mA h cm−2. During the transfer process from the glovebox to the XPS facility, a vacuum transfer capsule was used to load the samples, preventing surface contamination. According to the fitted C 1s, O 1s and Na 1s core-level XPS spectra of plated L700 (Fig. 3i and Fig. S14, ESI†), the percentage of composition of SEI layers in different electrolytes is revealed (Fig. 3j). First, the peaks of C–C (284.8 eV), C–OR (∼286 eV), C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (∼288.6 eV), O
O (∼288.6 eV), O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O (∼289 eV) and C–F (∼292 eV) can be observed in Fig. 3i(1). Differing from Fig. 3i(1), the peaks of C–O (∼287 eV) and CO3 (∼289.9 eV) can be seen in Fig. 3i(2) and (3). Secondly, the peaks of C
C–O (∼289 eV) and C–F (∼292 eV) can be observed in Fig. 3i(1). Differing from Fig. 3i(1), the peaks of C–O (∼287 eV) and CO3 (∼289.9 eV) can be seen in Fig. 3i(2) and (3). Secondly, the peaks of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O carbonyl groups (O–I, ∼531.5 eV), C–OH hydroxyl or C–O–C ether groups (O–II, ∼532.5 eV), and O
O carbonyl groups (O–I, ∼531.5 eV), C–OH hydroxyl or C–O–C ether groups (O–II, ∼532.5 eV), and O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–OH carboxyl groups (O–III, ∼535.5 eV) can be spotted in all three samples. Furthermore, the presence of Na2O can be stated when 1 M NaCF3SO3 in diglyme is used, while the Na2CO3 can be detected when 1 M NaCF3SO3 in EC-PC or EC-DMC is employed. For the ether-based electrolytes, the formed SEI is dominated by organic components (∼68 at%), leading to the establishment of a continuous phase with more flexibility.48 Besides, inorganic components (∼12 at%) are dispersed in the dominated continuous organic phase, which finally becomes a uniform and compact mixture of organics and inorganics on the surface of electrodes (Fig. 3k).18 Such an SEI layer is beneficial to enhanced stability during the repeated platting and stripping process, which has been demonstrated in our reported work.51 Meanwhile, the two ester-based electrolytes decompose to form a relatively higher proportion of inorganics (∼18 at%), thus forming more ceramic features, e.g., a fragile and brittle non-uniform mixture of inorganics and fewer organics (Fig. 3I).52
C–OH carboxyl groups (O–III, ∼535.5 eV) can be spotted in all three samples. Furthermore, the presence of Na2O can be stated when 1 M NaCF3SO3 in diglyme is used, while the Na2CO3 can be detected when 1 M NaCF3SO3 in EC-PC or EC-DMC is employed. For the ether-based electrolytes, the formed SEI is dominated by organic components (∼68 at%), leading to the establishment of a continuous phase with more flexibility.48 Besides, inorganic components (∼12 at%) are dispersed in the dominated continuous organic phase, which finally becomes a uniform and compact mixture of organics and inorganics on the surface of electrodes (Fig. 3k).18 Such an SEI layer is beneficial to enhanced stability during the repeated platting and stripping process, which has been demonstrated in our reported work.51 Meanwhile, the two ester-based electrolytes decompose to form a relatively higher proportion of inorganics (∼18 at%), thus forming more ceramic features, e.g., a fragile and brittle non-uniform mixture of inorganics and fewer organics (Fig. 3I).52
Combined with molecular modelling, the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO) levels of EC, DMC, PC and diglyme molecules are also compared since the LUMO and HOMO levels are related to the electrochemical redox potentials (Fig. S15, ESI†). Because the LUMO levels of solvent molecules are lower than the energy level of metallic sodium (Na+/Na), SEI layers confirmed by the XPS analysis can be attributed to the spontaneous decomposition of electrolytes. In addition, free ester molecules like EC, DMC and PC have much lower LUMO levels (average around −0.40 eV) than free diglyme molecules (around −0.03 eV).53 Hence, ester molecules can obtain electrons from the energy level of metallic sodium, which means ester-based electrolytes are more likely to be reduced by metallic sodium during the plating process. However, ether molecules have a less pronounced reduction tendency, resulting in a less pronounced electrolyte decomposition and a thinner SEI layer (Fig. 3k).54
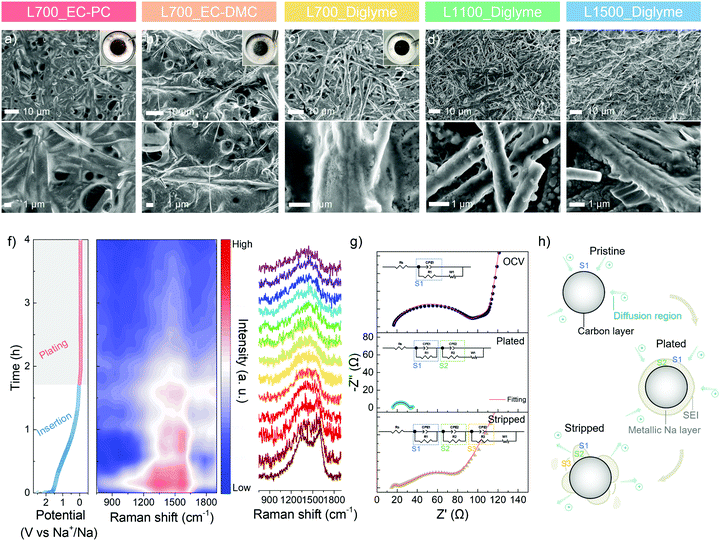
To visualise the metallic sodium deposition behaviour on the carbon skeletons, the morphology evolution is analysed via ex situ SEM. After 10 cycles of platting and stripping at 1.0 mA cm−2 with a specific discharge capacity of 2.0 mA h cm−2, the morphologies of a series of carbon skeletons in different electrolytes at a plated state are shown in Fig. 4a–e. An inhomogeneous surface and spherical nuclei can be directly observed on L700 in the ester-based electrolytes (Fig. 4a and b), with the random metallic sodium and exfoliated carbon dust in the cycled coin cells (Inserted photograph in Fig. 4a and b), which is consistent with our cycling performance and finite element simulation results. In comparison, all carbon skeletons show smoother surfaces in the ether-based electrolyte owing to the electrochemical stability of ether-based electrolytes explained above. However, in Fig. 4d and e, numerous small spherical nuclei can still be observed on both the plated L1100 and L1500. L700 exhibits the smoothest and most homogenous surface without any noticeable spherical nuclei in the ether-based electrolyte (Fig. 4c), with the “clean” separator and electrode surface after cycling (inserted photograph in Fig. 4c), which can additionally identify the more beneficial role of defects for uniform metallic deposition.
To further correlate defects and metallic sodium deposition, operando Raman spectroscopy is performed to analyse the electrochemical behaviour in the different regions of the GCD curve at 0.5 mA cm−2 with a specific discharge capacity of 2.0 mA h cm−2 (Fig. 4f). The set-up of the operando Raman spectroscopy is shown in Fig. S16 (ESI†). Raman beam (532 nm) was continuously focused on a fixed spot on the surface of L700 during testing. The first Raman spectrum of L700 before discharging has broad characteristic D- and G-peaks (Fig. 4f). Specifically, the G-peak (∼1580 cm−1) refers to the first-order Raman scattering from a phonon in the plane of crystalline graphene layers, while the D-peak (∼1350 cm−1) corresponds to the disordered scatting.25 During the whole sodiation (i.e., insertion) (>0 V vs. Na+/Na) process in the discharge curve, the insertion of Na+ ions into the carbon bulk phase happens, where the intensities of D- and G-peaks both slightly decrease. For the main sloping region of sodiation (>0.1 V vs. Na+/Na), both peaks are found to become broader, while the D-peak is gradually shifting to a higher wavenumber (blue shift), meaning that in this region, Na+ ions are forming chemical bonding with atoms at in-plane defect sites such as carbon vacancies, substitutional impurities, interstitial impurities.55,56 These findings can also support that the longest sloping region in the GCD curve of L700 results from the interaction of Na+ ions with defect sites. The position of the G-peak remains almost unchanged during the main sloping region of sodiation, suggesting no significant electrochemical interaction of Na+ ions with the graphitic bands since the G-peak position and width are highly sensitive to electron or ion doping.55 When the potential is close to 0 V vs. Na+/Na, the decrease of G-peak position can be measured concomitant with an increase in its width because Na+ ions are interacting with graphitic bands in this region. The transfer of charge from the sodium atoms to π* antibonding orbitals of carbons affects the length of the C–C bonds.55 Upon the first sodiation, the formation of SEI also contributes to the slight decrease in the intensities of both peaks.
From the perspective of reaction kinetics, the diffusion coefficient of Na+ ions (DNa+) can be calculated according to the galvanostatic intermittent titration technique (GITT) testing (Fig. S17, ESI†).57 During the main sloping region of sodiation (>0.1 V vs. Na+/Na), the interaction of Na+ ions with defect sites as a surface-controlled pseudocapacitance takes place first, showing a higher average DNa+ and faster kinetics. However, the interaction of Na+ ions with graphitic bands is hindered by the diffusion-controlled reaction including insertion into graphitic layers and pore filling with lower average DNa+ and slower kinetics, which happens at the left region of sodiation (0–0.1 V vs. Na+/Na). Compared with GITTs of L1100 and L1500 (Fig. S17, ESI†), the diffusion coefficients of L700 exhibits the lowest decrease rate because of the largest insertion capacity.
During the whole plating process in the discharge curve (<0 V vs. Na+/Na), D- and G-peaks finally merge into a single peak as the deposition of metallic sodium onto carbon surfaces starts to happen with the lowest DNa+ and slowest kinetics. In the meantime, a continuous decrease in the intensities of D- and G-peaks can be detected. After plating for 30 min, the intensity reduces to around half of the initial value because the surface of carbon skeletons has been partially covered by metallic sodium. When the discharge capacity reaches 2.0 mA h cm−2, the D- and G-peaks disappear as the carbon features on the surface are fully covered with metallic sodium. In this region, the steady decrease in the signal intensity reveals the uniform ion distribution at the interface and the even deposition of metallic sodium.50 Therefore, we can further confirm that the largest sloping capacity (i.e., insertion capacity) of L700 results from its abundant defects. Meanwhile, the sodiophilic properties and durability of L700 for sodium plating and stripping can be enhanced since the stronger interaction between Na+ ions and defect sites of L700 is beneficial to the uniform nucleation and deposition process,58,59 as mentioned above.
Besides operando Raman spectra, electrochemical impedance spectroscopy (EIS) from 100 kHz to 0.01 Hz of L700 at the initial open-circuit voltage (OCV), plated and stripped states of the first cycle are employed to understand the sodium plating and stripping behaviour. The specific parts of the obtained Nyquist plots are correlated to the resistor and capacitor elements in Randles equivalent circuits with different charge-transfer resistance parts, thus illustrating the interface condition between the electrolyte and electrode.60 In the Randles equivalent circuit (eqn (S7)–(S9), ESI†), Rs (Ω) is the inner resistance, Rct (Ω) is the charge-transfer resistance.61 First, the EIS tested at OCV is a typical Nyquist plot that shows a semicircle at the high-frequency region and a long sloping line at the low-frequency region (Fig. 4g). At the low-frequency region (close to 0.01 Hz), the decrease in the frequency is accompanied by an increase in capacitance.62 The long sloping line corresponds to the ion diffusion in liquid and capacitive accumulation at the opening surface of carbon skeletons, thus forming a diffusion layer on the surface (Fig. 4h).62 In the high-frequency region (close to 100 kHz), the semicircle represents the ion and charge transfer in the intermediate phase (S1), namely the diffusion layer (Fig. 4h).62 Based on this region, the charge-transfer resistance can be obtained (eqn (S7), ESI†). At the maximum frequency, the starting point of the semicircle refers to the inner resistance. Differing from the EIS at OCV, the EIS tested at the plated state shows a shorter sloping line and a smaller semicircle (Fig. 4g). As the carbon surface is fully covered by metallic sodium at the plated state, the diminished opening surface of carbon and negligible diffusion layers both contribute to the considerable reduction of the sloping line. Hence, the ion and charge need to transfer in two new intermediate phases before reaching the carbon (Fig. 4h). One is the SEI layer (S1), and the other is the metallic sodium layer (S2).60 Along with the decreased charge transfer resistance, the smaller semicircle composed of two individual semicircles suggests the increased charge transfer abilities in metallic sodium (S2) and SEI layer (S1), which can be perfectly fitted by eqn (S8) (ESI†) with two charge-transfer resistance sections. Finally, at the stripped state, a long sloping line appears again at the low-frequency region (Fig. 4g) since the stripping of metallic sodium exposes the opening surface of carbon skeletons. Because of the accumulated ions on the exposed opening surface of carbon, the diffusion layer is built up again. Also, a little metallic sodium is inactive and remains on the surface of carbon. Consequently, a small semicircle and a big semicircle consisting of two individual semicircles can be observed at the high-frequency region, which correspond to the ion and charge transfer in the SEI layer (S1), residual metallic sodium layer (S2) and diffusion layer (S3), respectively (Fig. 4h and eqn (S9) ESI†).60
2.4. Practical applications of sodium metal batteries
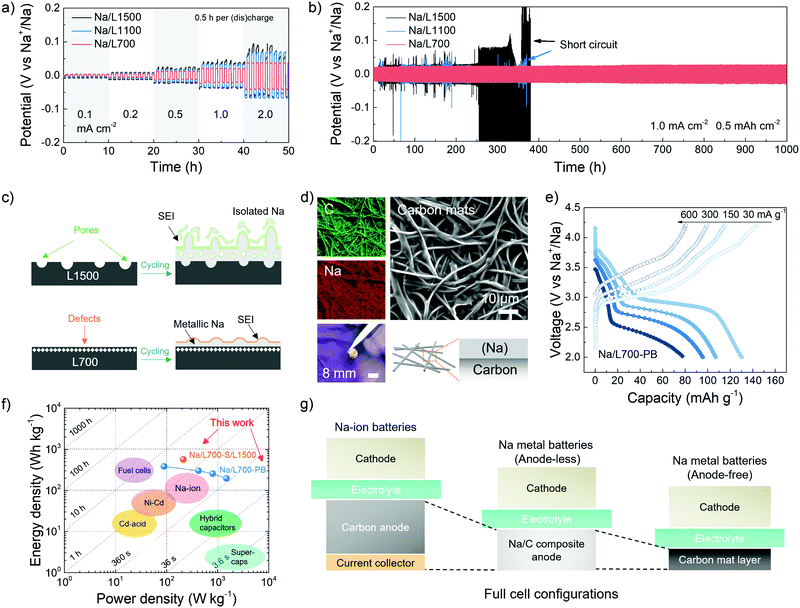
In addition to understanding the fundamentals governing the deposition behaviour of metallic sodium on carbon skeletons, the potential for practical application of the Na/C composite anode is also evaluated. The rate and cycling performance of the Na/C composite anodes in a symmetric cell with two identical electrodes is shown in Fig. 5a and b. Before assembling the symmetric cells using 1 M NaCF3SO3 in diglyme, a certain amount of metallic sodium (8.0 mA h cm−2) was initially pre-deposited on carbon skeletons at a fixed current density of 1.0 mA h cm−2 for 8 h in the same electrolyte to fabricate Na/C composite anodes including Na/L700, Na/L1100 and Na/L1500,63 followed by disassembly of the plated carbons from coin cells. For the rate performance, the composite electrodes in the symmetric cell were repeatedly stripped and plated between each other at 0.1, 0.2, 0.5, 1.0 and 2.0 mA cm−2 for 0.5 h per (dis-)charge process. As shown in Fig. 5a, when the current density increases to 2.0 mA cm−2, the potential hysteresis of Na/L1100 and Na/L1500 start to fluctuate, indicating uncontrolled sodium dendrite growth. However, Na/L700 exhibits the most stable potential hysteresis with the lowest overpotentials (<50 mV) at different current densities. For the cycling performance, the composite electrodes in the symmetric cell were tested at 1.0 mA cm−2 with a specific capacity of 0.5 mA h cm−2. The potential hysteresis of Na/L1100 and Na/L1500 obviously fluctuates after just around 350 h of cycling (Fig. 5b). Especially for Na/L1500 with few defects but abundant pores, its potential hysteresis varies a lot, and a significant increase in the plating/stripping overpotentials can be seen because of the formation of dendrite and isolated sodium after cycling (Fig. 5c). However, for the Na/L700 with rich defects but negligible pores, the plating and stripping overpotentials remain stable without any noticeable increase even after 1000 h of cycling, which can also prove the more important role played by defects for uniform metallic deposition. No obvious fluctuation of working potentials can be observed in the Na/L700 symmetric cells after over 100 cycles at the higher current densities (2 and 3 mA cm−2) (Fig. S18, ESI†), which can successfully prove the excellent stability of L700 for fast sodium plating and stripping. In addition, compared with the cycling performance of bare metallic sodium symmetric cells (Fig. S19, ESI†), the enhanced cycling stability due to the existence of carbon skeletons can be further verified. The SEM image, elemental mapping, photograph and schematic illustration of the Na/L700 composite anodes with a certain amount of plated metallic sodium (8.0 mA h cm−2) are respectively shown in Fig. 5d from which the uniform distribution of metallic sodium on the carbon skeletons can be recognised.Subsequently, the Na/L700 composite anodes can be applied in a full cell to fabricate sodium metal batteries, coupled with various cathodes including the Prussian blue cathode and sulfur cathode. In the Na/L700 composite anodes, the free-standing carbon skeletons can act as a protection matrix and current collector at the same time, eliminating a large amount of bulk metallic sodium and heavy aluminium or copper current collectors at the anode side compared with a bare sodium metal anode. Therefore, the so-called “anode-less” sodium metal batteries has the potential to decrease the cost of the whole battery and achieve a higher energy density.64 In the sodium metal batteries with the Prussian blue (PB) cathode (Fig. 5e), the full cell (Na/L700-PB) can deliver a reversible capacity of 130.3 mA h g−1 at 30 mA g−1 based on the active mass of the cathode. When the current densities increase to 150, 300 and 600 mA cm−2, the reversible capacities can maintain at 107.1, 95.7 and 77.5 mA h g−1, respectively (Fig. S20c, ESI†). After 50 cycles of the full cell at 30 mA g−1, a stable cycling performance with no obvious loss of reversible capacity can be achieved (Fig. S20d, ESI†). Prussian blue was prepared based on the reported method in literature (Fig. S20a and b, ESI†).65 In principle, the Prussian blue cathode provides the capacity through a two-electron redox reaction where the cubic FeIIIFeIII(CN)6 is converted into cubic NaFeIIIFeII(CN)6 and further into rhombohedral Na2FeIIFeII(CN)6 with the insertion of Na+ ions (Fig. S20e, ESI†).66 We note that, although the low-temperature synthesis methods of Prussian blue cathodes based on aqueous systems are energy-saving, the working potential and Coulombic efficiency of Prussian blue cathodes need to be further improved due to the possible existence of coordinated or interstitial water in Prussian blue cathodes.67
Moreover, proof-of-concept sodium metal batteries with sulfur cathodes are also studied. The full cell with the configuration of Na/L700 anode and sulfur/L1500 cathode (Na/L700–S/L1500) is compared with the full cell based on the bare metallic sodium anode and sulfur/carbon black cathode (bare Na–S) (Fig. S21a and b, ESI†). The sulfur cathode was prepared based on the reported method in the literature.68 In Fig. S21c (ESI†), the obtained full cell with the supporting of carbon skeletons can exhibit a discharge capacity of 447.3 mA h g−1 at 167.5 mA g−1, while the full cell without the carbon skeletons can only display a discharge capacity of 407.1 mA h g−1 at the same current density. Besides, the on-set potential of the full cell with the supporting of carbon skeletons (1.8 V vs. Na+/Na) is much lower and smoother than that of the full cell without carbon skeletons (2.2 V vs. Na+/Na), which refer to less polarisation of electrochemical reaction as a result of the utilisation of carbon skeletons. After 30 cycles of the full cells at 167.5 mA g−1, a more pronounced polarisation in the full cell without carbon skeletons can be observed, which further substantiates the importance of carbon skeletons to improve the electrochemical performance (Fig. S21c, ESI†).69 At the anode side, the defective structure of L700 facilitates the uniform platting and stripping of metallic sodium, while at the cathode side, the porous structure of L1500 allows the conversion reaction of insulative sulfur (Fig. S21d, ESI†).70,71 Both metallic sodium and sulfur are effectively confined in the 3D structure of carbon skeletons with enhanced conductivity of the whole electrode.
Finally, the calculated energy and power densities of Na/L700-PB and Na/L700–S/L1500 are displayed in Fig. 5f. For Na/L700-PB, the energy densities can reach 384.0, 300.9, 255.8 and 195.4 W h kg−1 at the power densities of 89.1, 423.0, 802.2 and 1490.3 W kg−1, respectively, while for Na/L700–S/L1500, the energy density is 567.2 W h kg−1 when the power density is 212.4 W kg−1. For comparison, the energy and power densities of the “anode-less” sodium metal batteries are superior to other kinds of energy devices (Table S5, ESI†).1,14,23,57 Moreover, our defect-rich carbon skeletons have a promising application potential for the next generation “anode-free” sodium metal batteries without using any metallic sodium or pre-deposition process during the cell assembly (Fig. 5g). A sodium-containing cathode is placed against a piece of the carbon protection layer for sodium deposition only. The stable metallic sodium deposited on the carbon protection layer all originates from the cathode at a suitable voltage.72,73 Hence, this “anode-free” design can accomplish the excellent volumetric and gravimetric cell energy density. Besides, Na+ ions from the cathode will not be wasted to form excessive SEI because of the high initial Coulombic efficiencies of our carbon mats, thus reducing the production costs of the “anode-free” cells. Overall, this work shown here successfully paves the way for the future preparation of “anode-free” sodium metal batteries. However, real devices using this concept will require further optimisation and demonstration in pouch cells which will be the focus of future studies in our research group.
3. Conclusions
In this work, we have presented the preparation and application of sustainable carbon nanofibre skeletons from the renewable precursor as a free-standing and flexible host for the protection of metallic sodium anodes. Specifically, the tunable microstructures of carbon skeletons are designed and compared to understand the role of various carbon structural features in the electrochemical processes. According to this study, defects in carbon skeletons play a more important role than porosity for inducing uniform metallic deposition. Using a combination of advanced characterisation and multi-scale modelling, we have obtained fundamental insights into interfacial phenomena, SEI composition and deposition behaviour in defect-rich carbon structures using different electrolytes. Defects in carbon structure can enhance sodiophilic properties of carbon skeletons by promoting the interaction with Na+ ions. The utilisation of diglyme with stable NaCF3SO3 salts can regulate the ionic conductivity and increase the lowest unoccupied molecular orbital (LUMO) energy level of the electrolyte system, which all contribute to suppressing the dendrite formation during cycling. The “anode-less” sodium metal batteries exhibited here represent an initial proof-of-concept towards circumventing the safety hazards while exhibiting high energy densities, demonstrating their potentials for flexible or structural energy storage systems in electric vehicles (EVs) and large-scale electrical grids.74 In addition to the excellent performance metrics, the sustainability of material synthesis and battery manufacturing should also be considered from the entire technological scale,75 where our approach utilises renewable and abundant resources, eco-friendly aqueous spinning method, relatively low carbonisation temperature (only 700 °C) and low-cost electrolytes. In conclusion, this work provides new insights into the fundamental understanding of defect-induced metallic deposition mechanism in sustainable carbon skeletons for high-performance sodium metal anodes, which are of great importance to assist with the rational design of cost-effective carbon protection layers for sodium metal batteries in the future.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work is supported by the grants from Engineering and Physical Sciences Research Council (EP/R021554/2, EP/S018204/2), a RAEng Chair in Emerging Technologies as well as Science and Technology Facilities Council (STFC) Batteries Network (ST/R006873/1). Z. X., Z. G., R. C., and J. W. acknowledge the China Scholarship Council for the PhD scholarships. R. M. thank the EU for the Marie Curie Research Fellowship (786952) through the project LIGNOCAP. M. T. acknowledges the Australian Government Research Training Program Scholarship.Notes and references
- B. Dunn, H. Kamath and J. M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- C. Zhao, Q. Wang, Z. Yao, J. Wang, B. Sánchez-Lengeling, F. Ding, X. Qi, Y. Lu, X. Bai, B. Li, H. Li, A. Aspuru-Guzik, X. Huang, C. Delmas, M. Wagemaker, L. Chen and Y.-S. Hu, Science, 2020, 370, 708 CrossRef CAS PubMed.
- M. Q. Zhu, S. M. Li, B. Li, Y. J. Gong, Z. G. Du and S. B. Yang, Sci. Adv., 2019, 5, eaau6264 CrossRef CAS PubMed.
- B. Lee, E. Paek, D. Mitlin and S. W. Lee, Chem. Rev., 2019, 119, 5416–5460 CrossRef CAS PubMed.
- R. Zhang, X. Chen, X. Shen, X. Q. Zhang, X. R. Chen, X. B. Cheng, C. Yan, C. Z. Zhao and Q. Zhang, Joule, 2018, 2, 764–777 CrossRef CAS.
- B. Sun, P. Li, J. Zhang, D. Wang, P. Munroe, C. Wang, P. H. L. Notten and G. Wang, Adv. Mater., 2018, 30, e1801334 CrossRef PubMed.
- G. Huang, J. Han, F. Zhang, Z. Wang, H. Kashani, K. Watanabe and M. Chen, Adv. Mater., 2019, 31, e1805334 CrossRef PubMed.
- X. Li, L. Zhao, P. Li, Q. Zhang and M.-S. Wang, Nano Energy, 2017, 42, 122–128 CrossRef CAS.
- X. Zheng, P. Li, Z. Cao, W. Luo, F. Sun, Z. Wang, B. Ding, G. Wang and Y. Huang, Small, 2019, 15, e1902688 CrossRef PubMed.
- W. Luo, Y. Zhang, S. Xu, J. Dai, E. Hitz, Y. Li, C. Yang, C. Chen, B. Liu and L. Hu, Nano Lett., 2017, 17, 3792–3797 CrossRef CAS PubMed.
- S. S. Chi, X. G. Qi, Y. S. Hu and L. Z. Fan, Adv. Energy Mater., 2018, 8, 1702764 CrossRef.
- K. Li, Z. Hu, J. Ma, S. Chen, D. Mu and J. Zhang, Adv. Mater., 2019, 31, e1902399 CrossRef PubMed.
- J. Peters, D. Buchholz, S. Passerini and M. Weil, Energy Environ. Sci., 2016, 9, 1744–1751 RSC.
- S. Herou, M. C. Ribadeneyra, R. Madhu, V. Araullo-Peters, A. Jensen, P. Schlee and M. Titirici, Green Chem., 2019, 21, 550–559 RSC.
- W. E. Tenhaeff, O. Rios, K. More and M. A. McGuire, Adv. Funct. Mater., 2014, 24, 86–94 CrossRef CAS.
- S. Hérou, M. Crespo Ribadeneyra, P. Schlee, H. Luo, L. Cristian Tanase, C. Roβberg and M. Titirici, J. Energy Chem., 2021, 53, 36–48 CrossRef.
- S. Hérou, M. Crespo and M. Titirici, CrystEngComm, 2020, 22, 1560–1567 RSC.
- Z. W. Seh, J. Sun, Y. Sun and Y. Cui, ACS Cent. Sci., 2015, 1, 449–455 CrossRef CAS PubMed.
- L. Jiang, L. Liu, J. Yue, Q. Zhang, A. Zhou, O. Borodin, L. Suo, H. Li, L. Chen, K. Xu and Y. S. Hu, Adv. Mater., 2020, 32, e1904427 CrossRef PubMed.
- L. Jiang, Y. Lu, C. Zhao, L. Liu, J. Zhang, Q. Zhang, X. Shen, J. Zhao, X. Yu, H. Li, X. Huang, L. Chen and Y.-S. Hu, Nat. Energy, 2019, 4, 495–503 CrossRef CAS.
- M. Tebyetekerwa, Z. Xu, W. Li, X. Wang, I. Marriam, S. Peng, S. Ramkrishna, S. Yang and M. Zhu, ACS Appl. Energy Mater., 2018, 1, 377–386 CrossRef CAS.
- M. Tebyetekerwa and S. Ramakrishna, Matter, 2020, 2, 279–283 CrossRef.
- F. Xie, Z. Xu, A. C. S. Jensen, F. Ding, H. Au, J. Feng, H. Luo, M. Qiao, Z. Guo, Y. Lu, A. J. Drew, Y.-S. Hu and M.-M. Titirici, J. Mater. Chem. A, 2019, 7, 27567–27575 RSC.
- D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 4428 CrossRef CAS.
- A. C. Ferrari and D. M. Basko, Nat. Nanotechnol., 2013, 8, 235–246 CrossRef CAS PubMed.
- C. Casiraghi, A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085401 CrossRef.
- A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14095–14107 CrossRef CAS.
- A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401 CrossRef CAS PubMed.
- Z. F. Li, Y. C. Chen, Z. L. Jian, H. Jiang, J. J. Razink, W. F. Stickle, J. C. Neuefeind and X. L. Ji, Chem. Mater., 2018, 30, 4536–4542 CrossRef CAS.
- E. Olsson, J. Cottom and Q. Cai, Small, 2021, 2007652, DOI:10.1002/smll.202007652.
- R. Guo, C. Lv, W. Xu, J. Sun, Y. Zhu, X. Yang, J. Li, J. Sun, L. Zhang and D. Yang, Adv. Energy Mater., 2020, 10, 1903652 CrossRef CAS.
- M. Titirici, Nat. Catal., 2019, 2, 642–643 CrossRef.
- M. H. Lee, S. J. Kim, D. Chang, J. Kim, S. Moon, K. Oh, K.-Y. Park, W. M. Seong, H. Park, G. Kwon, B. Lee and K. Kang, Mater. Today, 2019, 29, 26–36 CrossRef CAS.
- J. L. Ma, F. L. Meng, Y. Yu, D. P. Liu, J. M. Yan, Y. Zhang, X. B. Zhang and Q. Jiang, Nat. Chem., 2019, 11, 64–70 CrossRef CAS PubMed.
- J. Cui, S. Yao, M. Ihsan-Ul-Haq, J. Wu and J.-K. Kim, Adv. Energy Mater., 2019, 9, 1802777 CrossRef.
- J. Bae, Y. Qian, Y. Li, X. Zhou, J. B. Goodenough and G. Yu, Energy Environ. Sci., 2019, 12, 3319–3327 RSC.
- Y. Jie, X. Liu, Z. Lei, S. Wang, Y. Chen, F. Huang, R. Cao, G. Zhang and S. Jiao, Angew. Chem., Int. Ed., 2020, 59, 3505–3510 CrossRef CAS PubMed.
- Y. M. Li, Y. S. Hu, M. M. Titirici, L. Q. Chen and X. J. Huang, Adv. Energy Mater., 2016, 6, 1600659 CrossRef.
- F. Xie, Z. Xu, A. C. S. Jensen, H. Au, Y. Lu, V. Araullo-Peters, A. J. Drew, Y. S. Hu and M. M. Titirici, Adv. Funct. Mater., 2019, 29, 1901072 CrossRef.
- H. Au, H. Alptekin, A. C. S. Jensen, E. Olsson, C. A. O’Keefe, T. Smith, M. Crespo-Ribadeneyra, T. F. Headen, C. P. Grey, Q. Cai, A. J. Drew and M.-M. Titirici, Energy Environ. Sci., 2020, 13, 3469–3479 RSC.
- H. Li, D. Chao, B. Chen, X. Chen, C. Chuah, Y. Tang, Y. Jiao, M. Jaroniec and S.-Z. Qiao, J. Am. Chem. Soc., 2020, 142, 2012–2022 CrossRef CAS PubMed.
- E. Olsson, J. Cottom, H. Au, M.-M. Titirici and Q. Cai, Carbon, 2021, 177, 226–243 CrossRef CAS.
- L. Ye, M. Liao, T. Zhao, H. Sun, Y. Zhao, X. Sun, B. Wang and H. Peng, Angew. Chem., Int. Ed., 2019, 131, 17210–17216 CrossRef.
- X. Hu, P. H. Joo, H. Wang, E. Matios, C. Wang, J. Luo, X. Lu, K. Yang and W. Li, Adv. Funct. Mater., 2019, 29, 1807974 CrossRef.
- J. Liu, Y. Zhang, L. Zhang, F. Xie, A. Vasileff and S. Z. Qiao, Adv. Mater., 2019, 31, e1901261 CrossRef PubMed.
- C. Fang, J. Li, M. Zhang, Y. Zhang, F. Yang, J. Z. Lee, M. H. Lee, J. Alvarado, M. A. Schroeder, Y. Yang, B. Lu, N. Williams, M. Ceja, L. Yang, M. Cai, J. Gu, K. Xu, X. Wang and Y. S. Meng, Nature, 2019, 572, 511–515 CrossRef CAS PubMed.
- F. Wu, J. Zhou, R. Luo, Y. Huang, Y. Mei, M. Xie and R. Chen, Energy Storage Mater., 2019, 22, 376–383 CrossRef.
- K. Westman, R. Dugas, P. Jankowski, W. Wieczorek, G. Gachot, M. Morcrette, E. Irisarri, A. Ponrouch, M. R. Palacín, J. M. Tarascon and P. Johansson, ACS Appl. Energy Mater., 2018, 1, 2671–2680 CrossRef CAS.
- R. Zhang, X. Shen, X.-B. Cheng and Q. Zhang, Energy Storage Mater., 2019, 23, 556–565 CrossRef.
- W. Chen, Y. Hu, W. Lv, T. Lei, X. Wang, Z. Li, M. Zhang, J. Huang, X. Du, Y. Yan, W. He, C. Liu, M. Liao, W. Zhang, J. Xiong and C. Yan, Nat. Commun., 2019, 10, 4973 CrossRef PubMed.
- F. Xie, Z. Xu, Z. Guo and M.-M. Titirici, Prog. Energy, 2020, 2, 042002 CrossRef.
- X. Zheng, H. Fu, C. Hu, H. Xu, Y. Huang, J. Wen, H. Sun, W. Luo and Y. Huang, J. Phys. Chem. Lett., 2019, 10, 707–714 CrossRef CAS PubMed.
- Y. Lee, J. Lee, J. Lee, K. Kim, A. Cha, S. Kang, T. Wi, S. J. Kang, H. W. Lee and N. S. Choi, ACS Appl. Mater. Interfaces, 2018, 10, 15270–15280 CrossRef CAS PubMed.
- Z. Ye, S. Xie, Z. Cao, L. Wang, D. Xu, H. Zhang, J. Matz, P. Dong, H. Fang, J. Shen and M. Ye, Energy Storage Mater., 2021, 37, 378–386 CrossRef.
- J. S. Weaving, A. Lim, J. Millichamp, T. P. Neville, D. Ledwoch, E. Kendrick, P. F. McMillan, P. R. Shearing, C. A. Howard and D. J. L. Brett, ACS Appl. Energy Mater., 2020, 3, 7474–7484 CrossRef CAS.
- F. Xie, H. Li, X. Wang, X. Zhi, D. Chao, K. Davey and S.-Z. Qiao, Adv. Energy Mater., 2021, 11, 2003419 CrossRef CAS.
- Z. Xu, F. Xie, J. Wang, H. Au, M. Tebyetekerwa, Z. Guo, S. Yang, Y. S. Hu and M. M. Titirici, Adv. Funct. Mater., 2019, 29, 1903895 CrossRef.
- W. Liu, Y. Xia, W. Wang, Y. Wang, J. Jin, Y. Chen, E. Paek and D. Mitlin, Adv. Energy Mater., 2019, 9, 1802918 CrossRef.
- B. A. Zhang, C. M. Ghimbeu, C. Laberty, C. Vix-Guterl and J. M. Tarascon, Adv. Energy Mater., 2016, 6, 1501588 CrossRef.
- P. Ge, S. Li, L. Xu, K. Zou, X. Gao, X. Cao, G. Zou, H. Hou and X. Ji, Adv. Energy Mater., 2019, 9, 1803035 CrossRef.
- Y. Shao, M. F. El-Kady, J. Sun, Y. Li, Q. Zhang, M. Zhu, H. Wang, B. Dunn and R. B. Kaner, Chem. Rev., 2018, 118, 9233–9280 CrossRef CAS PubMed.
- U. Krewer, F. Röder, E. Harinath, R. D. Braatz, B. Bedürftig and R. Findeisen, J. Electrochem. Soc., 2018, 165, A3656–A3673 CrossRef CAS.
- X. Wang, G. Pawar, Y. Li, X. Ren, M. Zhang, B. Lu, A. Banerjee, P. Liu, E. J. Dufek, J.-G. Zhang, J. Xiao, J. Liu, Y. S. Meng and B. Liaw, Nat. Mater., 2020, 19, 1339–1345 CrossRef CAS PubMed.
- J. Xiang, L. Yang, L. Yuan, K. Yuan, Y. Zhang, Y. Huang, J. Lin, F. Pan and Y. Huang, Joule, 2019, 3, 2334–2363 CrossRef CAS.
- Y. You, X. L. Wu, Y. X. Yin and Y. G. Guo, Energy Environ. Sci., 2014, 7, 1643–1647 RSC.
- J. F. Qian, C. Wu, Y. L. Cao, Z. F. Ma, Y. H. Huang, X. P. Ai and H. X. Yang, Adv. Energy Mater., 2018, 8, 1702619 CrossRef.
- E. Goikolea, V. Palomares, S. Wang, I. R. Larramendi, X. Guo, G. Wang and T. Rojo, Adv. Energy Mater., 2020, 10, 2002055 CrossRef CAS.
- C. Zhou, J. Wang, X. Zhu, K. Chen, Y. Ouyang, Y. Wu, Y.-E. Miao and T. Liu, Nano Res., 2021, 14, 1541–1550 CrossRef CAS.
- M. Salama, Rosy, R. Attias, R. Yemini, Y. Gofer, D. Aurbach and M. Noked, ACS Energy Lett., 2019, 4, 436–446 CrossRef CAS.
- Y. Yao, H. Wang, H. Yang, S. Zeng, R. Xu, F. Liu, P. Shi, Y. Feng, K. Wang, W. Yang, X. Wu, W. Luo and Y. Yu, Adv. Mater., 2020, 32, e1905658 CrossRef PubMed.
- B. Chen, D. Chao, E. Liu, M. Jaroniec, N. Zhao and S.-Z. Qiao, Energy Environ. Sci., 2020, 13, 1096–1131 RSC.
- Y.-G. Lee, S. Fujiki, C. Jung, N. Suzuki, N. Yashiro, R. Omoda, D.-S. Ko, T. Shiratsuchi, T. Sugimoto, S. Ryu, J. H. Ku, T. Watanabe, Y. Park, Y. Aihara, D. Im and I. T. Han, Nat. Energy, 2020, 5, 99–308 Search PubMed.
- Y. Qiao, H. Yang, Z. Chang, H. Deng, X. Li and H. Zhou, Nat. Energy, 2021, 6, 653–662 CrossRef.
- Z. Zhu and Z. Xu, Renewable Sustainable Energy Rev., 2020, 134, 110308 CrossRef CAS.
- M.-M. Titirici, Adv. Energy Mater., 2021, 11, 2003700 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee01346g |
| ‡ These authors contributed equally towards this work. |
| This journal is © The Royal Society of Chemistry 2021 |