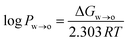Phenolic compounds alter the ion permeability of phospholipid bilayers via specific lipid interactions†
Sheikh I.
Hossain
 a,
Suvash C.
Saha
a,
Suvash C.
Saha
 b and
Evelyne
Deplazes
b and
Evelyne
Deplazes
 *ac
*ac
aSchool of Life Sciences, University of Technology Sydney, Ultimo, NSW 2007, Australia. E-mail: e.deplazes@uq.edu.au
bSchool of Mechanical and Mechatronic Engineering, University of Technology Sydney, Ultimo, NSW 2007, Australia
cSchool of Chemistry and Molecular Biosciences, University of Queensland, St Lucia, QLD 4072, Australia
First published on 27th September 2021
Abstract
This study aims to understand the role of specific phenolic–lipid interactions in the membrane-altering properties of phenolic compounds. We combine tethered lipid bilayer (tBLM) electrical impedance spectroscopy (EIS) with all-atom molecular dynamics (MD) simulations to study the membrane interactions of six phenolic compounds: caffeic acid methyl ester, caffeic acid, 3,4 dihydroxybenzoic acid, chlorogenic acid, syringic acid and p-coumaric acid. tBLM/EIS experiments showed that caffeic acid methyl ester, caffeic acid and 3,4 dihydroxybenzoic acid significantly increase the permeability of phospholipid bilayers to Na+ ions. In contrast, chlorogenic acid, syringic acid and p-coumaric acid showed no effect. Experiments with lipids lacking the phosphate group show a significant decrease in the membrane-altering effects indicating that specific phenolic–lipid interactions are critical in altering ion permeability. MD simulations confirm that compounds that alter ion permeability form stable interactions with the phosphate oxygen. In contrast, inactive phenolic compounds are superficially bound to the membrane surface and primarily interact with interfacial water. Our combined results show that compounds with similar structures can have very different effects on ion permeability in membranes. These effects are governed by specific interactions at the water–lipid interface and show no correlation with lipophilicity. Furthermore, none of the compounds alter the overall structure of the phospholipid bilayer as determined by area per lipid and order parameters. Based on data from this study and previous findings, we propose that phenolic compounds can alter membrane ion permeability by causing local changes in lipid packing that subsequently reduce the energy barrier for ion-induced pores.
1. Introduction
Characterising how small molecules interact with biological membranes is critical for understanding fundamental processes and is relevant to many applications in pharmacology, biotechnology, and biomedical sciences. Examples include the membrane permeability of pharmaceuticals or endogenous substances such as hormones or neurotransmitters,1–3 or the use of organic molecules in the cryopreservation of plant germplasm.4,5Studying small molecule–membrane interactions (SMMIs) is challenging for several reasons. Cellular membranes are complex, supra-molecular structures composed of a phospholipid bilayer with embedded membrane proteins. The phospholipid bilayer contains hundreds of different lipids that are laterally diffusing, meaning that membranes provide a heterogeneous and constantly changing binding surface. Small molecules bound to membranes often do not show a single binding mode but several binding modes of similar energies, resulting in a frequent interchange between them. The amphipathic structure of phospholipids also creates two distinctly different environments for small molecules to interact with; the hydrophobic core and the more hydrophilic lipid–water interface. Furthermore, SMMIs can range from simple surface binding or passive diffusion across the membranes to more complex mechanisms such as membrane destabilisation or pore formation. Finally, the structure of a phospholipid bilayer can change in response to environmental conditions such as temperature, pH, ionic strengths, or hydration levels. As a result of this complexity, characterising SMMIs requires complementary information from different methods.
A wide range of wet-lab and in silico methods have been used to study the structure of membranes and their interactions with small molecules.6–11 Molecular Dynamics (MD) simulations are routinely employed to provide atomistic-level insight into the structural, dynamical, and morphological properties of lipid membrane systems, including the effect of small molecules on these properties.10,12–14 MD simulations are particularly useful when the properties of interest are inaccessible or difficult to access by wet-lab techniques. A compelling approach is to combine MD simulations with wet-lab techniques that provide complementary information. Ideally, the systems used in the simulations and wet-lab experiments should match with respect to phospholipid bilayer composition, pH and concentration and type of ions present.
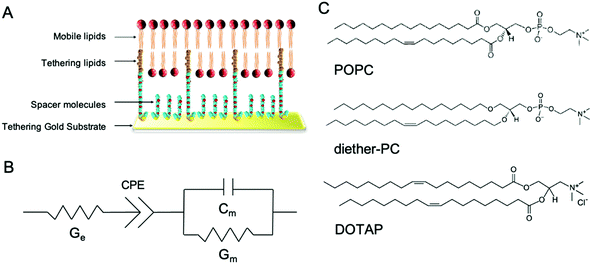
In this study, we demonstrate the use of tethered lipid bilayer (tBLM) electrical impedance spectroscopy (EIS) combined with MD simulations to study SMMIs. tBLM/EIS is a technique to monitor the ion permeability of phospholipid bilayers in real-time. A tBLM is formed by anchoring tether molecules to the surface of a pure gold substrate (Fig. 1A). The tethers are interspersed with spacer molecules. Onto this sparsely tethered monolayer, a mobile phospholipid bilayer is formed using a solvent exchange technique. The resulting bilayer consists of 90% freely mobile phospholipids in the inner leaflet and 100% mobile phospholipids in the outer leaflet and thus mimics the fluidity of cell membranes. If a potential gradient is applied, the bilayer acts as an impediment to the movement of ions in the buffer, which can be measured using swept frequency EIS. The resulting impedance and phase data are fitted to an equivalent circuit (Fig. 1B) to obtain a measure of membrane conductivity.15 An increase in conduction upon treating a membrane with a specific compound reflects an increase in ions moving across the membrane, i.e., an increase in the permeability of the lipid bilayer towards ions. The underlying assumption of our EIS experiments that increased ion permeability is the result of changes in lipid packing or other local changes in membrane structures, which make it easier for ions to move through the bilayer.16–18
In this study, tBLMs were composed of the neutral phospholipids POPC and dietherPC or the positively charged lipid DOTAP. Diether-PC and DOTAP are structurally similar to POPC but lack the ester (carbonyl) oxygens or the phosphate group, respectively (Fig. 1C). Comparing the conduction between membranes composed of POPC, diether-PC and DOTAP treated with the same compounds allows insight into how specific interactions at the water–lipid interface affect membrane disruption.
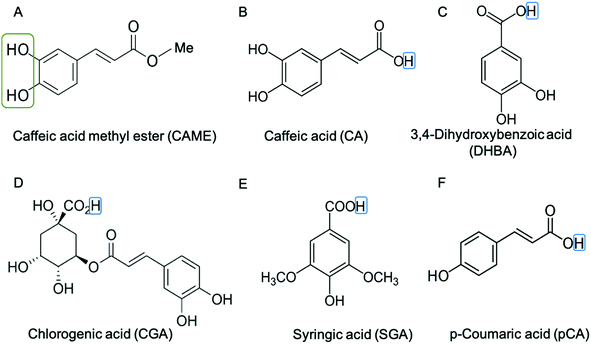
We instigated the membrane interactions of the following six phenolic compounds: caffeic acid methyl ester (CAME, also called methyl caffeate), caffeic acid (CA), 3,4 dihydroxybenzoic acid (DHBA), chlorogenic acid (CGA), syringic acid (SGA) and p-coumaric acid (pCA). The structures of these six compounds are shown in Fig. 2. We selected these six compounds based on our work studying the membrane-altering effects of honey.19 All these phenolic compounds are found in honey.20–23 Further, the six compounds are similar in structure and physico-chemical properties. Thus, understanding differences in their membrane-altering properties requires detailed structural information and makes these compounds an ideal set to study by combined tBLM/EIS and MD simulations.
Phenolic compounds are a diverse class of aromatic molecules found in plants that have been extensively investigated for their biological activity and potential applications in the pharmaceutical, cosmetics and food industries. For example, CA and CGA show antioxidant, anticancer and anti-inflammatory activities.24–27 CA also offers protective effects against oxidising agents in red blood cells by preventing morphological changes and lysis.28 Phenolic compounds also have metal-chelating properties where the complexation occurs by the metal interacting with the hydroxyl or catechol group.29–31 In many cases, the antioxidant activities of the phenolic compounds and metal chelation are related.32 For example, the catechol motif escalates the antioxidant activity compared to a single hydroxyl group.32
Some of the biological activities of phenolic compounds relate to their interactions with the phospholipid bilayer component of membranes.33–35 These membrane-related activities are associated with specific lipid–phenolic interactions (e.g. in preventing lipid peroxidation36) and with non-specific effects by altering the biophysical properties of the membrane.33,37 For example, a recent in vitro study reported that the hydration state of the lipid interface affects the antiradical activity of CAG.38 The biological activity of phenolic compounds is also affected by lipid composition33,35,39 and the location of the compound in the membrane.33,39 These studies highlight the complexity of phenolic–membrane interactions and demonstrate how characterising them can assist in understanding their biological activity and inform their use in various applications.
2. Methods and materials
2.1. tBLM/EIS experiments
After formation, the tBLM was washed at least three times with 200 μL tris buffer or until a stable baseline conductance was achieved where stable was considered at least five readings with no more than 10% variation in absolute conductance.
To measure the effect of phenolic compounds on conductance, an experiment consisted of the following addition-washout protocol. A single addition – washout cycle consisted of one addition, followed by two buffer washouts. For the addition, 200 μL of the 500 ppm phenolic compound solution was added to the wells, and the tBLM was left for at least 10 sweeps. For the washout, the 200 μL of tris buffer was added to wells, and the tBLM was left for at least 10 sweeps, followed by an identical second washout. This addition – washout cycle was repeated. For each phenolic compound, at least four independent experiments on separate membranes were conducted.
Unpaired t-tests were used to determine the difference in membrane conduction between experiments of a given phenolic compound on tBLMs composed of different lipids. All statistical analyses were carried out using Orange version 3.29.1.
2.2. MD simulations
where ΔGw→o is the Gibbs free energy of moving the compound from the water to the octanol phase, R = 8.314 J mol−1 K−1 is the universal gas constant, and T is the temperature in Kelvin (298 K).
ΔGw→o was obtained from the potential of mean force (PMF), which was calculated using umbrella sampling (US). The distance between the centre of mass (COM) of the phenolic compound and the COM of the octanol phase along the z-axis of the simulation system was used as a reaction coordinate. The simulation system consisted of a pre-equilibrated water–octanol system that contained 5417 water molecules and 310 octanol molecules in a rectangular box of dimension 5 nm × 5 nm × 10 nm. To this, one phenolic compound was added. To create a series of starting structures for the US simulations, a 2 ns pull simulation in the NPT ensemble was carried in which the phenolic compound was moved along the reaction coordinate with a force constant of 1000 kJ mol−1 nm−2 and a pull rate of 2 nm ns−1. From the resulting trajectory, 20 configurations with phenolic–octanol COM distances between 0 and 4.0 nm were extracted. For the US simulations, 20 windows were simulated for 100 ns, each using the same NPT settings as for the pull simulation. Windows were separated by 0.2 nm, and the position of the phenolic compound was restrained along the reaction coordinate with a force constant of 1000 kJ mol−1 nm−2. The PMF was reconstructed using the weighted histogram analysis method (WHAM),45 and the statistical error was estimated using bootstrapping analysis method.46,47 The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pw→o values obtained from the US simulations are listed in Table S1 in the ESI,† along with experimental values.
Pw→o values obtained from the US simulations are listed in Table S1 in the ESI,† along with experimental values.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 377 water molecules, 77 Na+ and 77 Cl− ions in a rectangular box with dimensions ∼13 nm × 13 nm × 11.5 nm. This corresponds to an ionic strength of 100 mM NaCl. The system was energy minimised using the steepest descent algorithm and equilibrated for 500 ns in an NPT ensemble. Equilibration was monitored using area per lipid (APL) vs. time. This POPC-only system later served as a reference system for analysis.
377 water molecules, 77 Na+ and 77 Cl− ions in a rectangular box with dimensions ∼13 nm × 13 nm × 11.5 nm. This corresponds to an ionic strength of 100 mM NaCl. The system was energy minimised using the steepest descent algorithm and equilibrated for 500 ns in an NPT ensemble. Equilibration was monitored using area per lipid (APL) vs. time. This POPC-only system later served as a reference system for analysis.
The last frame from the POPC-only simulation was used as the starting structure for all POPC-phenolic simulations. In total there were six simulation systems: one for each phenolic compound. For each system, 10 phenolic compounds were added by replacing randomly selected water molecules. In the case of CA, SYG, DHBA, p-CA and CGA, 10 additional Na+ ions were added to neutralise the system. Each system was again energy minimised, followed by a 500 ns NPT run.
All systems were simulated using GROMACS versions 2020.348 and GROMACS 2020.4.49 POPC, water and ions were described using Lipid14, TIP3P water50 and ions and the Amber force field.51 Periodic boundary conditions were applied in all directions of the simulation system. Non-bonded interactions were modelled by Lennard-Jones and Coulomb potentials with a cut-off of 1.0 nm and 0.12 nm grid spacing. The neighbour list was updated every 20 steps. Electrostatic interactions were calculated using the PME method.52 The equation of motion in all the simulations was integrated using the Verlet algorithm53 with 2 fs time step size. The system components POPC, water with ions and phenolic compounds were coupled independently to a Nose–Hoover thermostat54 with a bath temperature of 298 K and a time constant of 0.1 ps. The POPC and solute were coupled separately to the water and ions. A Parrinello–Rahman barostat55 with semi-isotropic pressure coupling was applied using a time constant of 2 ps and compressibility of 4.5 × 10−5 bar−1 in all directions of the simulation box.
Simulations were analysed using GROMACS tools, Visual Molecular Dynamics (VMD)56 and python scripts using the MDAnalysis package.57 Unless otherwise stated, all analyses were carried out using frames from the last 200 ns of the 500 ns simulation. The minimum distance between any atom in a phenolic compound and the POPC phosphate oxygen was calculated using gmx mindist. The orientation between the phenolic compound and the membrane surface was estimated by the angle formed between the bilayer normal that runs along the z-axis of the simulation system and a vector connecting two atoms in the phenolic compound. The atoms used to define these vectors are shown in Fig. S1 in the ESI.† As the compounds have free rotation in solution, the distributions of orientation angles were calculated using only compounds that are within 0.8 nm of the membrane surface (as defined by the phosphate oxygen in POPC). The insertion depth of each phenolic compound is defined by the distance between the z-component of the membrane COM and two atoms at opposing ends of the phenolic compound (referred to as the head and tail of the compound58). The atoms that define head and tail are shown in Fig. S2 in the ESI.†
3. Results
3.1. tBLM/EIS data
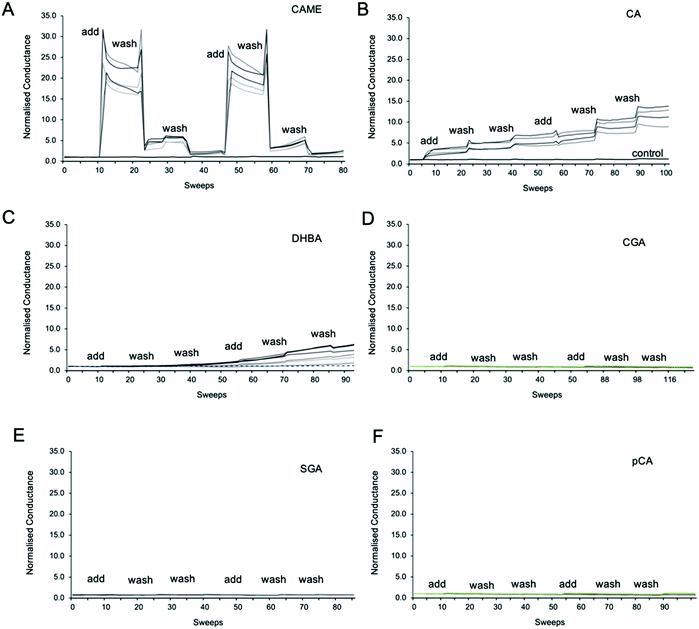
Fig. 3 shows representative traces of normalised conductance vs. time for tBLMs composed of POPC that were treated with 500 ppm solutions of CAME, CA, DBHA, CGA, SGA and pCA, respectively. The treatment consisted of adding the phenolic compound solution (add), followed by two washes with tris buffer (wash). For all experiments, the conductance of a control membrane treated with buffer only was recorded (indicated in Fig. 3B). Note that an increase in conductance reflects an increase in ions moving through the membrane. Conductance is thus not a measure of the permeability of the phenolic compound but of the permeability of the membrane towards ions.Comparison between the conductance traces shows substantial variations in how the six phenolic compounds affect the ion permeability of a POPC bilayer. CAME, CA and DBHA show an increase in conductance while CGA, SGA and pCA show no such effect. Further, a comparison of the conductance traces from CAME, CA and DBHA suggests that there are differences in the mechanism of how these compounds alter membrane ion permeability. Addition of CAME causes a significant and rapid increase in normalised conductance from a baseline of 1.0 ± 0.0 to 19.1 ± 0.3 (p < 0.001). After the first washout, conductance drops to 5.0 ± 0.2, and after the second washout, further drops to 2.4 ± 0.1. The same pattern is observed in the second treatment cycle. These results suggest that CAME significantly affects membrane permeation but the effect is reversible once the compound is washed out.
For CA, the first addition causes a sudden increase in normalised conductance to 3.0 ± 0.1. Each washout causes a further, small increase of conductance, which continues for the second treatment cycle. The final, normalised conductance after the two treatment cycles is 10.2 ± 0.3. This is significantly higher than baseline conductance (p < 0.001) but lower than the levels reached with CAME (p < 0.01). Thus, compared to CAME, CA has less effect on membrane ion permeation but changes to the membrane appear more permanent.
For DHBA the onset of the increase in conduction is even slower than for CAME and CA. After the first treatment cycle, the normalised conductance is 1.1 ± 0.1, which is the same as the normalised conductance for control experiments 0.97 ± 0.04. The conductance continues to increase with each addition of DHBA or buffer washout, reaching a final conductance of 2.7 ± 0.3. As for CA, the conductance data for DHBA suggests that the compound remains in the membrane even after buffer washout.
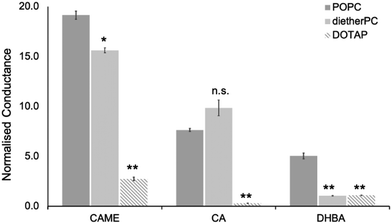
For the three phenolic compounds that caused membrane disruption, the tBLM/EIS experiments were repeated using bilayers composed of diether-PC or DOTAP. These two lipids lack the ester (carbonyl) oxygens or the phosphate group, respectively (Fig. 1C). Fig. 4 reports the normalised conductance reached after the second addition of the phenolic compound to bilayers composed of POPC, diether-PC or DOTAP. For CAME, replacing the POPC with dietherPC or DOTAP significantly reduces conductance from 19.1 ± 0.3 to 15.6 ± 0.2 and 2.7 ± 0.2, respectively. For CA, the conductance does not significantly differ between POPC and dietherPC (7.8 ± 0.2 compared to 9.9 ± 0.8). In contrast, the conductance for DOTAP is significantly reduced to 0.3 ± 0.8, which is even below baseline conductance. Finally, for DHBA, the conductance is significantly reduced for both dietherPC and DOTAP from 2.7 ± 0.8 and 1.1 ± 0.0, respectively.
3.2. Simulations
| Phenolic compound | Percentage of frames |
|---|---|
| CAME | 99.48 ± 1.37 |
| CA | 91.39 ± 11.28 |
| DHBA | 92.10 ± 4.95 |
| CGA | 74.81 ± 40 |
| SGA | 12.72 ± 3.44 |
| pCA | 39.69 ± 6.94 |
An interesting point can be made when considering the time spent in proximity of the membrane alongside the partition coefficients (log P). The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values predicted from the free energy calculations for DHBA, CA, SGA and pCA are, in increasing order, 0.5, 0.98, 1.05 and 1.1. This order does not agree with their order of time spent close to the membrane surface: SGA ≪ pCA ≪ DHBA ≈ CA. The discrepancies between log
P values predicted from the free energy calculations for DHBA, CA, SGA and pCA are, in increasing order, 0.5, 0.98, 1.05 and 1.1. This order does not agree with their order of time spent close to the membrane surface: SGA ≪ pCA ≪ DHBA ≈ CA. The discrepancies between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and membrane proximity are particularly strong when comparing CA, SG and pCA. Their log
P and membrane proximity are particularly strong when comparing CA, SG and pCA. Their log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values are very close, yet their time spent close to the membrane range from >90% for CA to 12% for SGA. These large differences are a first indication that log
P values are very close, yet their time spent close to the membrane range from >90% for CA to 12% for SGA. These large differences are a first indication that log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values are not a reliable indicator to predict surface interactions for these phenolic compounds, which will be outlined in more detail in the discussion.
P values are not a reliable indicator to predict surface interactions for these phenolic compounds, which will be outlined in more detail in the discussion.
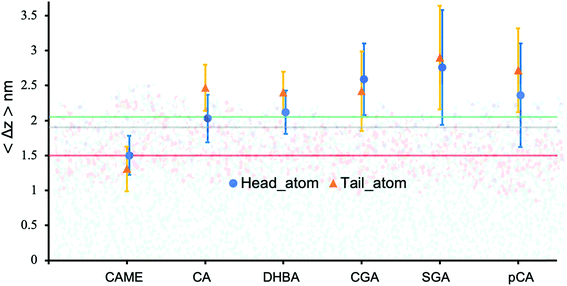 | ||
| Fig. 5 Insertion depth for phenolic compounds, estimated by the average distance 〈Δz〉 of the head and tail of phenolic compounds to the COM of the POPC bilayer. The atoms defining the head and tail of each phenolic are shown in Fig. S2 of the ESI.† The three horizontal lines represent the average position of the nitrogen (green), phosphate (grey) and carbonyl (orange) atoms in POPC. All values were calculated from the last 200 ns of the 500 ns production run and averaged over the 10 compounds. Error bars represent standard deviations. | ||
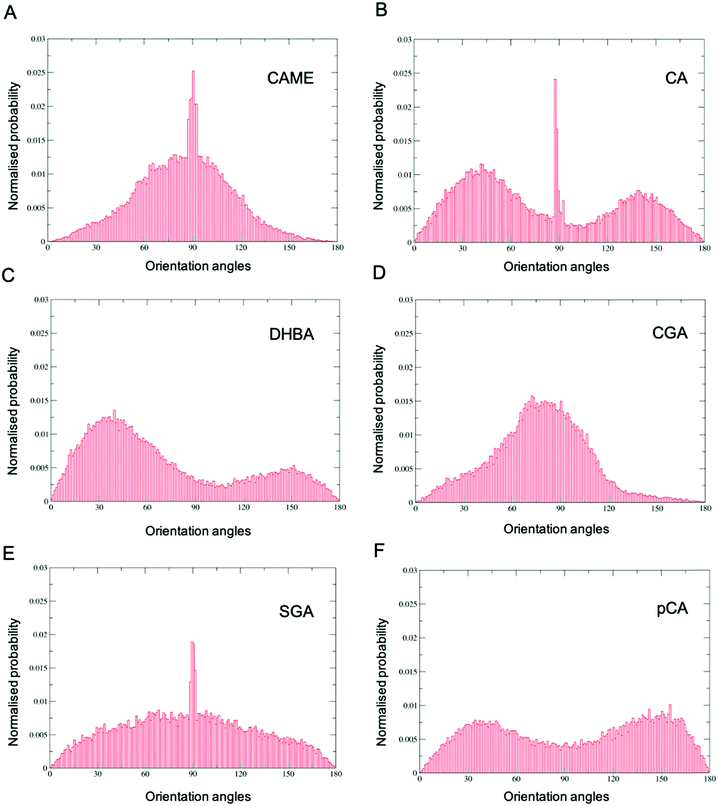
Comparison of the distributions shows that CAME and CGA have a unimodal distribution with a slight preference for orientations close between ∼60° to ∼120° with the most preferred orientation at α = 90°. In contrast, CA, pCA and DHBA show bimodal distributions with a maximum of around α = 40° and α = 140° to 150°. SGA shows the broadest distribution. Note that the spikes in CAME, CA and SGA are caused by two or three compounds that stay in specific orientations for long periods of time, biasing the distributions. Overall, the analysis shows that except for SGA, all phenolic compounds show a preferred orientation with respect to the membrane surface.
| Phenolic compound | % frames during which two, three or four molecules are found in a cluster | ||
|---|---|---|---|
| 2 molecules | 3 molecules | 4 molecules | |
| CAME | 32% | 4% | 0% |
| CA | 6% | 0% | 0% |
| DHBA | 0% | 0% | 0% |
| CGA | 0% | 1% | 98% |
| SGA | 4% | 0% | 0% |
| pCA | 3% | 0% | 0% |
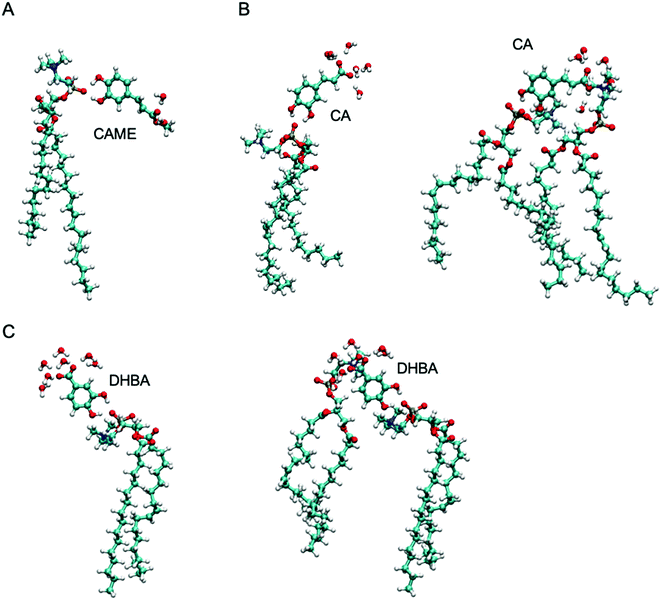 | ||
| Fig. 7 The most common interactions formed by (A) caffeic acid methyl ester (CAME), (B) caffeic acid (CA) and (C) 3,4-dihydroxy benzoic acid (DHBA) with lipids and interfacial water. | ||
The most common binding mode for CAME involves the catechol group interacting with the phosphate oxygen and the methyl ester surrounded by interfacial water. This mode accounts for 84% of binding events. A similar binding mode is observed for CA and DHBA. Like CAME, both compounds show a preference for the phosphate group, and the most common binding mode is the catechol interacting with the phosphate oxygen and the carboxylic acid interacting with water. This mode accounts for 66% and 70% of binding events in CA and DHBA, respectively. In addition, both CA and DHBA show a binding mode where the catechol group is bound to the phosphate oxygen, and the carboxylic acid moiety interacts with both water and hydrogens in the lipid headgroup. These account for approximately 15% of interactions. Note, this binding mode of bridging two lipids is not possible for CAME. For all three phenolic compounds, less than 1% of interactions involve the lipid carbonyl oxygen.
The other phenolic compounds do not show such strong preferences for a specific binding mode. Also, pCA, SGA and CGA show much less interaction with lipid oxygens and prefer interfacial water instead. The most common binding mode for pCA is similar to CA and DHBA, where the hydroxyl group interacts with the phosphate oxygen, and the carboxylic acid interacts with water. This mode, however, only accounts for 30% of binding events. All other times when pCA is close to the membrane surface, the compound interacts with interfacial water. SGA shows even lower levels of interactions with lipids. Only 15% of interactions involve phosphate oxygen, and there are no interactions with carbonyl oxygen or other parts of the lipid. For SGA, the carboxylic moiety interacts exclusively with interfacial water, and there is very little interaction with the lipid oxygens. The catechol group in CGA shows no interaction with lipid oxygens and exclusively interact with interfacial water. While the hydroxyl and carboxylic acid groups in the non-aromatic ring show some interactions with the lipid phosphate oxygen, most interactions are with interfacial water.
4. Discussion
In this study we aimed to investigate the interaction of six phenolic compounds with phospholipid bilayers with a particular focus on the role of specific phenolic–lipid interactions in the compounds’ ability to alter membrane ion permeability. For this, we used tBLM/EIS to compare the effect of six different phenolic compounds on the ion permeability of phospholipid bilayers composed of POPC. In addition, we used MD simulations of phenolic compounds in the presence of a POPC bilayer to provide information on the insertion depth, orientation, aggregation properties and phenolic–lipid interactions on each of the phenolic compounds.The tBLM/EIS experiments revealed that of the six compounds, CGA, SGA and pCA do no alter the conductance in phospholipid bilayers membrane while CAME, CA and DHBA significantly increase conductance. Further, the time-dependent conductance traces from CAME, CA and DHBA suggest major differences in the mechanism by which these three compounds alter membrane ion permeability. Potential reasons for these differences will be discussed later in the context of results from the MD simulations.
In the EIS experiments, a weak electric field of 25 mV (0.025 V) peak to peak and 0 mV bias is applied. If the electric field would cause large disruptions when adding charged compounds to the membrane, we would see this for SYG, CGA and pCA as well. Our EIS data indicates that the disruption only occurs with selected compounds.
As noted in the introduction, the underlying assumption of our tBLM/EIS experiments is that an increase in conductance reflects a change in ion permeability of the membrane, which is caused by the phenolic compound altering the packing of lipids in the bilayer. Under this assumption, an increase of conductance thus indicates a membrane disrupting effect. There are, however, other mechanisms that can cause an increase in conduction. For example, protonophores able to transport protons across membranes have been shown to increase conductance in phospholipid bilayers as measured by EIS.59 Protonophores operate via a mechanism that does not necessarily require disruption of lipid packing. The anionic form of the protonophore adsorbs to the membrane surface, where it associates with protons to form a neutral form of the compound. There is ample evidence that protons accumulate on and move along water–lipid interface.60–68 The protonated form is less polar and able to translocate across the hydrophobic core of the membrane. The compound dissociates again into the anionic protonophore, and protons are released on the other side of the membrane. In a tBLM/EIS experiment, this transport of protons across the membrane would cause an increase in conductance. While we cannot exclude that protonophore activity contributes to the increase in conductance, for the reasons outlined below, we think that the effect from the phenolic compounds is at least partially caused by disrupting the lipid packing and subsequent formation of water-filled pores rather than protonophore activity alone.
First, the only difference between CAME and CA is that in the former the carboxylic acid is replaced by a methyl ester (Fig. 2). If the increase in conduction by CAME and CA were caused predominantly by a protonophore activity, the anionic nature of CA would likely make it a better protonophore and thus cause a stronger effect than CAME. Our experiments show the opposite effect, i.e., CAME causes a much larger increase in conductance than CA (Fig. 3). Similarly, DHBA also contains a carboxylic acid group yet shows significantly less increase in conductance than CAME. The compounds CGA, SGA, and pCA show no increase in conductance compared to treatment with just buffer.
Second, the reduced conductance for CAME and DHBA with dietherPC further supports the presence of membrane disruption. Several landmark studies have shown that protons can migrate along the membrane surface.69–71 This lateral transfer of protons relies upon the presence of interfacial water and is facilitated by the more stable hydrogen bonds and reduced mobility of water molecules on the membrane surface compared to bulk water.67,72–78 Water reorientation is increased in bilayers composed of dietherPC compared to POPC79 likely due to the lack of hydrogen bonding with the carbonyl oxygen. We would thus expect proton transfer to be increased in the presence of dietherPC. In the case of protonophore activity, this should also cause an increase in conductance. However, our data shows that replacing POPC with dietherPC reduces conductance for CAME and DHBA and does not significantly differ for CA.
In addition to protonophore activity, there are other processes we need to consider in the interpretation of our results. Weak acids can cross the membrane in their protonated forms.80–83 The process is the same as described in the protonophore case where the compound is protonated at the water–lipid interface and permeates across the membrane in its uncharged form. Thus, at the water–lipid interface protonated and unprotonated states co-exist. Our analysis neither contradicts nor exclude this process and lipid disruption is still possible for the protonated compound. The analysis of CA and DHBA shows that the lipid–phenolic interactions are predominantly between the catechol group and the phosphate oxygen in the lipid. The carboxylic acid moiety interacts mostly with interfacial water, which is possible in the protonated or deprotonated form.
It is likely that compounds such as pCA, SGA and CGA that cannot cause disruption will move through the membrane in a protonated form. Again, our analysis does not exclude or contradict this. Our simulations suggest that these compounds mostly interact with interfacial water. Even in its protonated form, the carboxylic moiety is polar and capable of forming hydrogen bonds. Thus, as for the membrane-disrupting compounds, the interactions predicted by our simulations are still compatible with the model of these acids to move through the membrane in a protonated form. In fact, this is consistent with our EIS data that suggest these compounds do not induce pores, which would be the case for a compound that moves through the hydrophobic core without significantly disrupting lipid packing.
The tBLM/EIS experiments with dietherPC and DOTAP can also provide information on the role of specific phenolic–lipid interactions in altering ion membrane permeability. For all three compounds, the membrane ion permeability is significantly reduced with DOTAP compared to POPC. This suggests that the interaction with the phosphate oxygen is involved in the membrane-altering effects of CAME, CA and DHBA. The results from the MD simulations support this as they showed that all three compounds form stable interactions with the phosphate oxygen. The binding mode where the catechol group is bound to the phosphate oxygen accounts for most phenolic–lipid interactions in the simulation of CAME, CA and DHBA with POPC bilayers. Results from the tBLM/EIS experiments with dietherPC show varying effects depending on the compound. In the case of CAME, conductance is reduced by 20% with dietherPC compared to POPC. For DHBA, the reduction is 80%. In contrast, there is no significant difference in conductance between dietherPC and POPC for CA. This suggests that the carbonyl oxygen is involved in the lipid interactions of CAME and DHBA but not of CA. However, based on the simulations, none of the three compounds shows stable interactions with the carbonyl oxygen. In the case of CA, the simulation data could be a direct explanation of the lack of change in conductance between dietherPC and POPC. For CAME and DHBA, it is possible that the lack of carbonyl oxygen causes a change in how DBHA or CAME interact with the lipids, and this alternate binding mode is less effective at causing membrane disruption. As there are currently no parameters for dietherPC in the Amber force field, we cannot use simulations with this lipid to directly test these possibilities.
Table 3 provides an overview of the combined results from the tBLM/EIS experiments and the MD simulations. Despite the similarities in the structure and physico-chemical properties of the six compounds, particular the strong structural similarity of CAME, CA and pCA, the compounds show diverse interactions with the phospholipid bilayer. Neither the presence of the catechol group or the carboxylic group correlates with the ability to increase membrane ion permeability. The same can be said for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. Based on our study of these six phenolic compounds, lipophilicity on its own cannot be used to predict whether a compound alters membrane permeability. log
P. Based on our study of these six phenolic compounds, lipophilicity on its own cannot be used to predict whether a compound alters membrane permeability. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P has been found to relate to other membrane-altering activities of phenolic compounds, such as changes in the transition temperature or membrane-destabilising effects.84 However, these effects relate to the ability of the phenolic compound to insert into the hydrophobic core, a property that is captured by log
P has been found to relate to other membrane-altering activities of phenolic compounds, such as changes in the transition temperature or membrane-destabilising effects.84 However, these effects relate to the ability of the phenolic compound to insert into the hydrophobic core, a property that is captured by log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. Conversely, altering the packing of lipids relates to the interaction of the compounds with lipids at the water-phospholipid interface, which is poorly captured by log
P. Conversely, altering the packing of lipids relates to the interaction of the compounds with lipids at the water-phospholipid interface, which is poorly captured by log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P.
P.
| Phenolic compound | Calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
Membrane permeability | Membrane proximity | Insertion depth | Preferred orientation | Clustering | Binding mode |
|---|---|---|---|---|---|---|---|
| CAME | 2.35 ± 0.02 | Increase | ∼100% | Top of hydrophobic core | Parallel to membrane surface | Yes, clusters of two on the membrane surface | Strong preference for phosphate oxygen |
| CA | 0.98 ± 0.02 | Increase | >90% | Water–lipid interface, lipid headgroups | ∼45° to membrane surface | Very low tendency | Strong preference for phosphate oxygen, ‘bridging’ of lipids |
| DHBA | 1.10 ± 0.13 | Increase | >90% | Water–lipid interface, lipid headgroups | ∼45° to membrane surface | No | Strong preference for phosphate oxygen, ‘bridging’ of lipids |
| CGA | 0.30 ± 0.10 | No effect | 74% | Interfacial water | Parallel to membrane surface | Yes, clusters of four but only one on the membrane surface | Very few interactions with lipids |
| SGA | 1.05 ± 0.25 | No effect | 12% | Interfacial water | No preferred orientation | No | Very few interactions with lipids |
| pCA | 0.50 ± 0.13 | No effect | 30% | Interfacial water | ∼45° to membrane surface | No | Few interactions with lipids |
Note that simulations were carried out without an electric field. We know from test simulations carried out for previous work17 and published work that such a weak electric field is not sufficient to induce pores in simulations. To induce pores in membranes in the absence of an electrochemical gradient, an electric field strength of 0.3 V or higher is required.85–88 These fields are at least 10 times higher than the ones used in our experiments.
The three compounds that cause an increase in membrane permeability have the following in common: they spend most of the time in the proximity of the membrane, where they form strong interactions with the lipid head groups rather than interfacial water. Given the small sample size, these properties are unlikely enough to predict which types of compounds can cause membrane disruption or an increase in ion membrane permeability. Nevertheless, the molecular level detail gained from our analysis allows us to provide new insight into potential mechanisms of how specific interactions at the water–lipid interface relate to membrane permeability. In our recent work, we used tBLM/EIS experiments and MD simulations to demonstrate how the differences in membrane permeability of Na+ and K+ ions originate from distinction coordination by carbonyl oxygens at the phospholipid–water interface.17 Specifically, we proposed that the ability of Na+ to create a greater number of coordinating interactions with lipids compared to K+ causes a higher localised energy barrier for ion-induced pores, which then results in a higher membrane permeability observed in EIS experiments. We can use a similar argument to understand why CAME and CA cause an increase in membrane ion permeability while structurally similar pCA does not. The catechol group in CAME and CA form stable interactions with the phosphate oxygen while the methyl ester or carboxylic acid group interacts with either a second lipid or interfacial water. In both cases, the compound pushes lipids apart, causing local disruption of lipid packing and weakening the interactions between the lipids. This reduces the energy barrier for water-filed pores to be formed, thus increasing the permeability of membranes to ions. This not only increases the ion permeation, as is evident from the significant increase in conduction in our EIS experiments, but also allows the phenolic compound itself to move through the membrane in its unprotonated (charged) form. On the other hand, pCA does not form stable interactions with the lipid headgroup and is mostly bound to the membrane surface via interfacial water. This does not alter lipid packing, and hence pCA does not change the probability of pore formation, leaving ion membrane permeability unaltered.
The differences in binding mode between CAME compared to CA and DHBA might also explain why CAME appears to be able to wash out from the membrane easier than CA and DHBA, despite its higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value (and thus higher lipophilicity). CAME only forms interactions with a single lipid while CA and DHBA can bridge two lipids. It is possible that this makes it is easier for CAME to be washed out and for the membrane to restore its lipid packing, thus restoring membrane permeability close to baseline levels. In the case of CA and DHBA, the bridging of two lipids might make the washout and restoration of lipid packing less favorable.
P value (and thus higher lipophilicity). CAME only forms interactions with a single lipid while CA and DHBA can bridge two lipids. It is possible that this makes it is easier for CAME to be washed out and for the membrane to restore its lipid packing, thus restoring membrane permeability close to baseline levels. In the case of CA and DHBA, the bridging of two lipids might make the washout and restoration of lipid packing less favorable.
5. Conclusion
We have reported the combined use of tBLM/EIS and MD simulations to study the interactions of phenolic compounds with phospholipid bilayer. Results from tBLM/EIS experiments showed that CAME, CA and DHBA significantly increase phospholipid bilayer permeability while CGA, SGA and pCA have no effect. Despite the similarities in the structure and physico-chemical properties of the six phenolic compounds, they show diverse insertion depths, orientation, and lipid interactions. The ability to alter membrane permeability does not appear to correlate with the lipophilicity of a compound as indicated by its log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value. The combined results from tBLM/EIS experiments and MD simulations show that specific phenolic–lipid interactions are critical in the membrane-altering activity of CAME, CA and DHBA. Interestingly, none of the compounds that increase permeability cause a change in the structure of morphology of the phospholipid bilayer as assessed by APL or order parameters. This is consistent with our previous study of ion–lipid interactions and their role in membrane permeability. We propose that phenolic compounds can alter membrane permeability by causing local changes in lipid packing that subsequently reduce the energy barrier for ion-induced pores.
P value. The combined results from tBLM/EIS experiments and MD simulations show that specific phenolic–lipid interactions are critical in the membrane-altering activity of CAME, CA and DHBA. Interestingly, none of the compounds that increase permeability cause a change in the structure of morphology of the phospholipid bilayer as assessed by APL or order parameters. This is consistent with our previous study of ion–lipid interactions and their role in membrane permeability. We propose that phenolic compounds can alter membrane permeability by causing local changes in lipid packing that subsequently reduce the energy barrier for ion-induced pores.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. D. was funded by the UTS Chancellor's Postdoctoral Fellowship scheme. This work was supported by resources provided by the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia and computational resources provided by the UTS eResearch High Performance Computer Cluster. This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI Australia), an NCRIS enabled capability supported by the Australian Government.References
- S. Nagar and K. Korzekwa, Drug distribution. Part 1. Models to predict membrane partitioning, Pharm. Res., 2017, 34(3), 535–543 CrossRef PubMed.
- X. Liu, B. Testa and A. Fahr, Lipophilicity and its relationship with passive drug permeation, Pharm. Res., 2011, 28(5), 962–977 CrossRef PubMed.
- A. Dahan and J. M. Miller, The solubility–permeability interplay and its implications in formulation design and development for poorly soluble drugs, AAPS J., 2012, 14(2), 244–251 CrossRef PubMed.
- B. Funnekotter, R. L. Mancera and E. Bunn, Advances in understanding the fundamental aspects required for successful cryopreservation of Australian flora, In Vitro Cell. Dev. Biol.: Plant, 2017, 53(4), 289–298 CrossRef.
- A. Kaczmarczyk, et al., Current issues in plant cryopreservation, in Current frontiers in cryobiology, InTech, 2012, pp. 417–438 Search PubMed.
- Y. Bagheri, A. A. Ali and M. You, Current Methods for Detecting Cell Membrane Transient Interactions, Front. Chem., 2020, 8, 603259 CrossRef CAS PubMed.
- X. Chen, et al., Real-Time Structural Investigation of a Lipid Bilayer during Its Interaction with Melittin Using Sum Frequency Generation Vibrational Spectroscopy, Biophys. J., 2007, 93(3), 866–875 CrossRef CAS PubMed.
- I. M. Le-Deygen, A. A. Skuredina and E. V. Kudryashova, Experimental Methods to Study the Mechanisms of Interaction of Lipid Membranes with Low-Molecular-Weight Drugs, Russ. J. Bioorg. Chem., 2020, 46(4), 480–497 CrossRef CAS.
- H. Li, T. Zhao and Z. Sun, Analytical techniques and methods for study of drug–lipid membrane interactions, Rev. Anal. Chem., 2018, 37(1), 20170012 CAS.
- C. Martinotti, et al., Molecular dynamics simulation of the interaction of small molecules with biological membranes, ChemPhysChem, 2020, 21, 1486–1514 CrossRef CAS PubMed.
- C. Ohe, et al., Investigations of Polymyxin B–Phospholipid Interactions by Vibrational Sum Frequency Generation Spectroscopy, J. Phys. Chem. B, 2004, 108(46), 18081–18087 CrossRef CAS.
- O. S. Ollila and G. Pabst, Atomistic resolution structure and dynamics of lipid bilayers in simulations and experiments, Biochim. Biophys. Acta, Biomembr., 2016, 1858(10), 2512–2528 CrossRef CAS PubMed.
- C. Chan and X. Cheng, Molecular dynamics simulation studies of small molecules interacting with cell membranes, in Characterization of Biological Membranes, De Gruyter, 2019, pp. 603–630 Search PubMed.
- D. Jefferies and S. Khalid, Molecular Simulations of Complex Membrane Models, in Modeling of Microscale Transport in Biological Processes, Elsevier, 2017, pp. 1–18 Search PubMed.
- C. Cranfield, et al., The assembly and use of tethered bilayer lipid membranes (tBLMs), Methods Mol. Biol., 2015, 1232, 45–53 CrossRef CAS PubMed.
- A. Alghalayini, et al., The use of tethered bilayer lipid membranes to identify the mechanisms of antimicrobial peptide interactions with lipid bilayers, Antibiotics, 2019, 8(1), 12 CrossRef CAS PubMed.
- E. Deplazes, et al., Role of Ion–Phospholipid Interactions in Zwitterionic Phospholipid Bilayer Ion Permeation, J. Phys. Chem. Lett., 2020, 11(15), 6353–6358 CrossRef PubMed.
- A. Garcia, et al., Label-Free, Real-Time Phospholipase-A Isoform Assay, ACS Biomater. Sci. Eng., 2020, 6(8), 4714–4721 CrossRef PubMed.
- D. Bouzo, et al., Characterizing the Mechanism of Action of an Ancient Antimicrobial, Manuka Honey, against Pseudomonas aeruginosa Using Modern Transcriptomics, MSystems, 2020, 5(3), e00106 CrossRef PubMed.
- J. M. Alvarez-Suarez, et al., The Composition and Biological Activity of Honey: A Focus on Manuka Honey, Foods, 2014, 3(3), 420–432 CrossRef PubMed.
- F. C. Biluca, et al., Phenolic compounds, antioxidant capacity and bioaccessibility of minerals of stingless bee honey (Meliponinae), J. Food Compos. Anal., 2017, 63, 89–97 CrossRef CAS.
- S. Oelschlaegel, et al., Classification and characterization of manuka honeys based on phenolic compounds and methylglyoxal, J. Agric. Food Chem., 2012, 60(29), 7229–7237 CrossRef CAS PubMed.
- T. M. S. Silva, et al., Phenolic compounds, melissopalynological, physicochemical analysis and antioxidant activity of jandaíra (Melipona subnitida) honey, J. Food Compos. Anal., 2013, 29(1), 10–18 CrossRef CAS.
- G. Kanimozhi and N. Prasad, Anticancer effect of caffeic acid on human cervical cancer cells, in Coffee in health and disease prevention, Academic Press, 2015, pp. 655–661 Search PubMed.
- L. Toma, et al., Caffeic acid attenuates the inflammatory stress induced by glycated LDL in human endothelial cells by mechanisms involving inhibition of AGE-receptor, oxidative, and endoplasmic reticulum stress, BioFactors, 2017, 43(5), 685–697 CrossRef CAS PubMed.
- Z. Lou, et al., Assessment of antibacterial activity of fractions from burdock leaf against food-related bacteria, Food Control, 2010, 21(9), 1272–1278 CrossRef CAS.
- Y. Sato, et al., In vitro and in vivo antioxidant properties of chlorogenic acid and caffeic acid, Int. J. Pharm., 2011, 403(1–2), 136–138 CrossRef CAS PubMed.
- J. R. Colina, et al., An in vitro study of the protective effect of caffeic acid on human erythrocytes, Arch. Biochem. Biophys., 2019, 662, 75–82 CrossRef CAS PubMed.
- R. C. Hider, Z. D. Liu and H. H. J. M. i. e. Khodr, Metal chelation of polyphenols, Methods Enzymol., 2001, 335, 190–203 CAS.
- J.-P. Cornard, A. Caudron and J.-C. J. P. Merlin, UV-visible and synchronous fluorescence spectroscopic investigations of the complexation of Al (III) with caffeic acid, in aqueous low acidic medium, Polyhedron, 2006, 25(11), 2215–2222 CrossRef CAS.
- S. C. Živanović, et al., The study of the influence of Mg (II) and Ca (II) ions on caffeic acid autoxidation in weakly alkaline aqueous solution using MCR-ALS analysis of spectrophotometric data, New J. Chem., 2018, 42(8), 6256–6263 RSC.
- N. Razzaghi-Asl, et al., Antioxidant properties of hydroxycinnamic acids: a review of structure-activity relationships, Curr. Med. Chem., 2013, 20(36), 4436–4450 CrossRef CAS PubMed.
- H. A. Filipe, et al., Differential targeting of membrane lipid domains by caffeic acid and its ester derivatives, Free Radical Biol. Med., 2018, 115, 232–245 CrossRef CAS PubMed.
- N. P. Ulrih, A. Ota and V. J. I. J. o. F. S. Abram, Impact of selected polyphenolics on the structural properties of model lipid membranes—a review, Int. J. Food Stud., 2017, 6(2), 159–177 Search PubMed.
- N. P. Ulrih, Effects of caffeic, ferulic, and p-coumaric acids on lipid membranes, in Coffee in Health and Disease Prevention, Elsevier, 2015, pp. 813–821 Search PubMed.
- L. Prokai, N. M. Rivera-Portalatin and K. J. I. j. o. m. s. Prokai-tatrai, Quantitative structure-activity relationships predicting the antioxidant potency of 17β-estradiol-related polycyclic phenols to inhibit lipid peroxidation, Int. J. Mol. Sci., 2013, 14(1), 1443–1454 CrossRef CAS PubMed.
- M. H. Gordon, Dietary antioxidants in disease prevention, Nat. Prod. Rep., 1996, 13(4), 265–273 RSC.
- J. Cejas, et al., Interaction of chlorogenic acid with model lipid membranes and its influence on antiradical activity, Biochim. Biophys. Acta, Biomembr., 2021, 1863(1), 183484 CrossRef PubMed.
- S. Selvaraj, et al., Influence of membrane lipid composition on flavonoid–membrane interactions: implications on their biological activity, Prog. Lipid Res., 2015, 58, 1–13 CrossRef PubMed.
- D. A. Case, et al., AMBER 2020, University of California, San Francisco, 2020 Search PubMed.
- J. Wang, et al., Development and testing of a general amber force field, J. Comput. Chem., 2004, 25(9), 1157–1174 CrossRef PubMed.
- J. Wang, P. Cieplak and P. A. Kollman, How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules?, J. Comput. Chem., 2000, 21(12), 1049–1074 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. W. S. Da Silva and W. F. Vranken, ACPYPE-Antechamber python parser interface, BMC Res. Notes, 2012, 5(1), 1–8 CrossRef PubMed.
- S. Kumar, et al., The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13(8), 1011–1021 CrossRef CAS.
- J. S. Hub, B. L. De Groot and D. Van Der Spoel, g_wham. A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates, J. Chem. Theory Comput., 2010, 6(12), 3713–3720 CrossRef CAS.
- B. Efron, Bootstrap methods: another look at the jackknife, in Breakthroughs in statistics, Springer, 1992, pp. 569–593 Search PubMed.
- E. Lindahl, et al., GROMACS 2020.3, Source code, 2020.
- Lindahl, Abraham, Hess, & van der Spoel, (2020, October 6), GROMACS 2020.4 Manual (Version 2020.4), Zenodo, DOI: 10.5281/zenodo.4054996.
- P. Mark and L. J. T. J. o. P. C. A. Nilsson, Structure and dynamics of the TIP3P, SPC, and SPC/E water models at 298 K, J. Phys. Chem. A, 2001, 105(43), 9954–9960 CrossRef CAS.
- D. A. Case, et al., The Amber biomolecular simulation programs, J. Comput. Chem., 2005, 26(16), 1668–1688 CrossRef CAS PubMed.
- U. Essmann, et al., A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103(19), 8577–8593 CrossRef CAS.
- L. J. P. r. Verlet, Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules, Phys. Rev., 1967, 159(1), 98 CrossRef CAS.
- D. J. Evans and B. L. J. T. J. o. c. p. Holian, The nose–hoover thermostat, J. Chem. Phys., 1985, 83(8), 4069–4074 CrossRef CAS.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52(12), 7182–7190 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38 CrossRef CAS.
- N. Michaud-Agrawal, et al., MDAnalysis: a toolkit for the analysis of molecular dynamics simulations, J. Comput. Chem., 2011, 32(10), 2319–2327 CrossRef CAS PubMed.
- K. Atkovska, et al., Rationalizing steroid interactions with lipid membranes: Conformations, partitioning, and kinetics, ACS Cent. Sci., 2018, 4(9), 1155–1165 CrossRef CAS PubMed.
- T. Rawling, et al., Aryl urea substituted fatty acids: a new class of protonophoric mitochondrial uncoupler that utilises a synthetic anion transporter, Chem. Sci., 2020, 11(47), 12677–12685 RSC.
- N. Amdursky, et al., Exploring fast proton transfer events associated with lateral proton diffusion on the surface of membranes, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(7), 2443–2451 CrossRef CAS PubMed.
- Y. N. Antonenko and P. Pohl, Microinjection in combination with microfluorimetry to study proton diffusion along phospholipid membranes, Eur. Biophys. J., 2008, 37(6), 865–870 CrossRef CAS PubMed.
- M. Brändén, et al., Localized proton microcircuits at the biological membrane–water interface, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(52), 19766–19770 CrossRef PubMed.
- E. Deplazes, et al., Competing for the same space: protons and alkali ions at the interface of phospholipid bilayers, Biophys. Rev., 2019, 11(3), 483–490 CrossRef PubMed.
- B. Gabriel, M. Prats and J. Teissié, Proton lateral conduction along a lipid monolayer spread on a physiological subphase, Biochim. Biophys. Acta, 1994, 1186(3), 172–176 CrossRef.
- T. Sandén, et al., Surface-coupled proton exchange of a membrane-bound proton acceptor, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(9), 4129–4134 CrossRef PubMed.
- S. Serowy, et al., Structural proton diffusion along lipid bilayers, Biophys. J., 2003, 84(2 Pt 1), 1031–1037 CrossRef CAS.
- M. G. Wolf, H. Grubmüller and G. Groenhof, Anomalous surface diffusion of protons on lipid membranes, Biophys. J., 2014, 107(1), 76–87 CrossRef CAS PubMed.
- T. Yamashita and G. A. Voth, Properties of hydrated excess protons near phospholipid bilayers, J. Phys. Chem. B, 2010, 114(1), 592–603 CrossRef CAS PubMed.
- U. Alexiev, et al., Rapid long-range proton diffusion along the surface of the purple membrane and delayed proton transfer into the bulk, Proc. Natl. Acad. Sci. U. S. A., 1995, 92(2), 372 CrossRef CAS PubMed.
- J. Heberle, et al., Proton migration along the membrane surface and retarded surface to bulk transfer, Nature, 1994, 370(6488), 379–382 CrossRef CAS PubMed.
- A. Springer, et al., Protons migrate along interfacial water without significant contributions from jumps between ionizable groups on the membrane surface, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(35), 14461–14466 CrossRef CAS PubMed.
- M. L. Berkowitz and R. Vácha, Aqueous Solutions at the Interface with Phospholipid Bilayers, Acc. Chem. Res., 2012, 45(1), 74–82 CrossRef PubMed.
- S. Y. Bhide and M. L. Berkowitz, Structure and dynamics of water at the interface with phospholipid bilayers, J. Chem. Phys., 2005, 123(22), 224702 CrossRef PubMed.
- S. Y. Bhide and M. L. Berkowitz, The behavior of reorientational correlation functions of water at the water–lipid bilayer interface, J. Chem. Phys., 2006, 125(9), 094713 CrossRef PubMed.
- H. Binder, Water near lipid membranes as seen by infrared spectroscopy, Eur. Biophys. J., 2007, 36(4–5), 265–279 CrossRef CAS PubMed.
- E. Deplazes, F. Sarrami and D. J. T. J. O. P. C. B. Poger, Effect of H3O+ on the Structure and Dynamics of Water at the Interface with Phospholipid Bilayers, J. Phys. Chem. B, 2020, 124(8), 1361–1373 CrossRef CAS PubMed.
- E. A. Disalvo, et al., Structural and functional properties of hydration and confined water in membrane interfaces, Biochim. Biophys. Acta, Biomembr., 2008, 1778(12), 2655–2670 CrossRef CAS.
- C. Zhang, et al., Water at hydrophobic interfaces delays proton surface-to-bulk transfer and provides a pathway for lateral proton diffusion, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(25), 9744 CrossRef CAS PubMed.
- S. Mukherjee and A. Chattopadhyay, Influence of Ester and Ether Linkage in Phospholipids on the Environment and Dynamics of the Membrane Interface:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Wavelength-Selective Fluorescence Approach, Langmuir, 2005, 21(1), 287–293 CrossRef CAS PubMed.
A Wavelength-Selective Fluorescence Approach, Langmuir, 2005, 21(1), 287–293 CrossRef CAS PubMed. - M. Gabba, et al., Weak Acid Permeation in Synthetic Lipid Vesicles and Across the Yeast Plasma Membrane, Biophys. J., 2020, 118(2), 422–434 CrossRef CAS.
- C. Hannesschlaeger, et al., The Effect of Buffers on Weak Acid Uptake by Vesicles, Biomolecules, 2019, 9(2), 63 CrossRef PubMed.
- S. M. Saparov, Y. N. Antonenko and P. Pohl, A new model of weak acid permeation through membranes revisited: does Overton still rule?, Biophys. J., 2006, 90(11), L86–L88 CrossRef CAS PubMed.
- A. Walter and J. Gutknecht, Monocarboxylic acid permeation through lipid bilayer membranes, J. Membr. Biol., 1984, 77(3), 255–264 CrossRef CAS PubMed.
- A. Ota, et al., Interactions of p-coumaric, caffeic and ferulic acids and their styrenes with model lipid membranes, Food Chem., 2011, 125(4), 1256–1261 CrossRef CAS.
- R. A. Böckmann, et al., Kinetics, statistics, and energetics of lipid membrane electroporation studied by molecular dynamics simulations, Biophys. J., 2008, 95(4), 1837–1850 CrossRef PubMed.
- L. Delemotte, et al., Modeling Membranes under a Transmembrane Potential, J. Phys. Chem. B, 2008, 112(18), 5547–5550 CrossRef CAS PubMed.
- M. Tarek, Membrane electroporation: a molecular dynamics simulation, Biophys. J., 2005, 88(6), 4045–4053 CrossRef CAS PubMed.
- D. P. Tieleman, et al., Simulation of Pore Formation in Lipid Bilayers by Mechanical Stress and Electric Fields, J. Am. Chem. Soc., 2003, 125(21), 6382–6383 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03250j |
| This journal is © the Owner Societies 2021 |