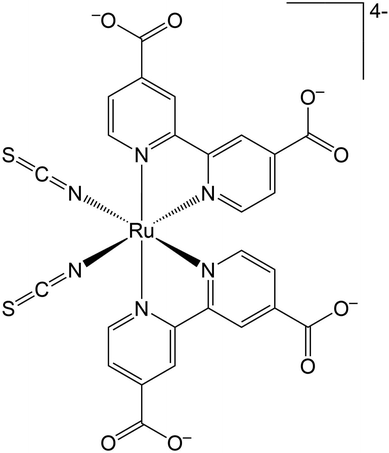
Direct observation of the solvent organization and nuclear vibrations of [Ru(dcbpy)2(NCS)2]4−, [dcbpy = (4,4′-dicarboxy-2,2′-bipyridine)], via ab initio molecular dynamics†
Fulvio
Perrella
 a,
Alessio
Petrone
a,
Alessio
Petrone
 *ab and
Nadia
Rega
*ab and
Nadia
Rega
 *abc
*abc
aDepartment of Chemical Sciences, University of Napoli Federico II, Complesso Universitario di M.S. Angelo, via Cintia 21, I-80126, Napoli, Italy. E-mail: alessio.petrone@unina.it; nadia.rega@unina.it
bScuola Superiore Meridionale, Largo San Marcellino 10, I-80138, Napoli, Italy
cCRIB, Centro Interdipartimentale di Ricerca sui Biomateriali, Piazzale Tecchio 80, I-80125, Napoli, Italy
First published on 11th August 2021
Abstract
Environmental effects can drastically influence the optical properties and photoreactivity of molecules, particularly in the presence of polar and/or protic solvents. In this work we investigate a negatively charged Ru(II) complex, [Ru(dcbpy)2(NCS)2]4− [dcbpy = (4,4′-dicarboxy-2,2′-bipyridine)], in water solution, since this system belongs to a broader class of transition-metal compounds undergoing upon photo-excitation rapid and complex charge transfer (CT) dynamics, which can be dictated by structural rearrangement and solvent environment. Ab initio molecular dynamics (AIMD) relying on a hybrid quantum/molecular mechanics scheme is used to probe the equilibrium microsolvation around the metal complex in terms of radial distribution functions of the main solvation sites and solvent effects on the overall equilibrium structure. Then, using our AIMD-based generalized normal mode approach, we investigate how the ligand vibrational spectroscopic features are affected by water solvation, also contributing to the interpretation of experimental Infra-Red spectra. Two solvation sites are found for the ligands: the sulfur and the oxygen sites can interact on average with ∼4 and ∼3 water molecules, respectively, where a stronger interaction of the oxygen sites is highlighted. On average an overall dynamic distortion of the C2 symmetric gas-phase structure was found to be induced by water solvation. Vibrational analysis reproduced experimental values for ligand symmetric and asymmetric stretchings, linking the observed shifts with respect to the gas-phase to a complex solvent distribution around the system. This is the groundwork for future excited-state nuclear and electronic dynamics to monitor non-equilibrium processes of CT excitation in complex environments, such as exciton migration in photovoltaic technologies.
1 Introduction
The Ru(II) complex [Ru(dcbpy)2(NCS)2]4−, [dcbpy = (4,4′-dicarboxy-2,2′-bipyridine)] (Fig. 1) or “N34−” is a popular and efficient dye, employed in solar cell and light harvesting applications.1–9 N3 and its charged variants belong to a broader class of transition-metal compounds undergoing rapid and complex photo-induced charge transfer (CT) dynamics, which can be dictated by structural and solvent rearrangements. Such CT dynamics can involve multiple electronic states from the singlet initial metal to ligand charge transfer 1MLCT photoinduced state(s). Then, an ultrafast inter-system crossing (ISC) leads to a long-lived final triplet 3MLCT, both in solution10–15 and on semiconductor substrates.16–23 New insights about the fast N3 ISC have been recently offered by 2D electronic-vibrational spectroscopy in water solution.241MLCT states that are vibronically coupled to 3MLCT vibrational modes and so likely involved in the ISC were in fact identified. Such states, called 1MLCTA and 1MLCTB, respectively located at 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400–24
400–24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 (410–405 nm) and 25
700 cm−1 (410–405 nm) and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–25
000–25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 (400–395 nm), are characterized by an important electronic density redistribution from the Ru(NCS)2 moiety towards the dcbpy rings, with a transition electric dipole moment predominantly located on the equatorial plane.25,26 Vibrational modes involving both the Ru(NCS)2 charge-donor and the dcbpy charge-acceptor segments on the N34− molecule are then probed with a mid-IR pulse to correlate as many 1MLCT states as possible with the final 3MLCT. The electron density on the dcbpy ligands should affect the carboxylate vibrations, because an increased electron density is expected to downshift the vibrational frequency.
300 cm−1 (400–395 nm), are characterized by an important electronic density redistribution from the Ru(NCS)2 moiety towards the dcbpy rings, with a transition electric dipole moment predominantly located on the equatorial plane.25,26 Vibrational modes involving both the Ru(NCS)2 charge-donor and the dcbpy charge-acceptor segments on the N34− molecule are then probed with a mid-IR pulse to correlate as many 1MLCT states as possible with the final 3MLCT. The electron density on the dcbpy ligands should affect the carboxylate vibrations, because an increased electron density is expected to downshift the vibrational frequency.
The carboxylate IR bands and their anisotropic transient absorption should therefore be good reporters on the localization of the MLCT excitation. Moreover, these carboxylate vibrational bands are quite sensitive to the adsorption modes of N34− onto TiO2, since the carboxylates act as anchoring groups on the semiconductor surface.8,27 In addition, time-resolved IR measurements on PbS colloidal quantum dots were used to distinguish intraband vs. trap-to-band transitions based on the presence of ligand carboxylate stretching vibrational signatures.28–30
Environmental effects can drastically influence the optical properties and photoreactivity of molecules, particularly in the presence of polar and/or protic solvents.31–40 Exactly knowing the equilibrium solvation of a CT system in solution, such as N34−, is crucial since, for example, the atomistic interpretation of time-resolved signals and non-equilibrium CT dynamics can be derived from photoinduced changes of hydrogen bonding between the solute and nearby water molecules.41,42 Discriminating the solvent effects from the charge recombination is the first step of our study of N34− system, because the metal–ligand complex wave function is influenced by ligand-solvent binding and the high-frequency vibrational modes of the ligands are also expected to play a role in the exciton dynamics.43
From a theoretical and computational perspective, accurately simulating and modeling the solute–solvent interactions is very challenging, but at same time mandatory to provide a molecular picture of the interplay between spectroscopic data and microsolvation. Once solvent effects and charge redistribution upon excitation combine together, theory is required to disentangle these effects on both the (non) equilibrium microsolvation and the vibration dynamics of photoactive molecules in solution. Routinely used computational spectroscopy relies on the study of solute–solvent clusters corresponding to energy minimum structures on the potential energy surface that are representative, on average, of the dye microsolvation. As a complementary approach, configurational sampling provided by ab initio molecular dynamics (AIMD) simulations may be a suitable choice to describe solvent effects on solute chemical-physical properties and spectroscopic features. Describing the solvent by a flexible model, as in this work, is also required for this aim to provide a more accurate description of solute–solvent dynamics, in particular those of possible hydrogen-bond networks, strongly impacting several system properties, that is, solvent viscosity, mobility of solvation shells, solute–solvent vibrational couplings.
Solute–solvent vibrations and electrostatic interactions with bulk solvent are indeed the main actors in predicting accurate Infrared and Raman vibrational spectra. Nowadays, different protocols exist to also enable the vibrational analysis using these AIMD-based methods, expressing the ab initio molecular dynamics in normal-like modes. These modes, hereafter called generalized modes, correspond to vibrational frequencies that are anharmonic and coupled in nature.44–46 In this work, we employed ab initio molecular dynamics relying on a hybrid quantum/molecular mechanic (QM/MM) scheme to probe the equilibrium microsolvation around N34− in terms of radial distribution functions of the main solvation sites along with monitoring the effects of solvent on the overall equilibrium structure. Then, using the AIMD-based generalized normal mode approach, we investigate how N34− vibrational spectroscopic features are affected by water solvation, also contributing to the interpretation of experimental Infra-Red(IR) spectra. Density functional theory (DFT) was employed for the ab initio treatment of the QM part, since it has an optimal balance between accuracy and computational cost and, in its hybrid version, it has been vastly used for the theoretical characterization of both vibrational/dynamical properties of molecules47–49 and the description of the electronic structure of both the ground and excited electronic states in macro-molecular systems of material50–62 or biological63–71 interest. Moreover, DFT and its time-dependent version have shown to be effective for theoretical characterization of many Ru complexes in different environments.72–89 This study represents an important starting point for future excited-state nuclear and electronic dynamics to gauge non-equilibrium processes of CT excitation in complex environments, such as exciton migration in photovoltaic technologies.
2 Methods
2.1 Computational details
A ground-state molecular dynamics trajectory of N34− compound in explicit water solution was collected. A spherical box (of 22 Å radius, Fig. S1, ESI†) including explicitly at least four solvation shells for each N34− site was carved out from a previously equilibrated larger cubic box (extracted from the AmberTools90 solvent box database) whose density resembled the experimental value at 298 K. The N34−, treated at DFT level, was then located at the center of the resulting sphere (eliminating the colliding water molecules in the same region), retaining a final number of 1462 water molecules, treated at MM level and described by the TIP3P force field.91 In particular, a flexible version of the TIP3P water model was employed, which includes the water bending contribution.92 A parametrization procedure gave as water bending force field parameters θ0 = 104.52°, kθ = 50 kJ mol−1 rad−2. A flexible MM solvent model has proven in fact useful to accurately describe coupled solute–solvent motions.92 The electronic structures of QM part were obtained by solving the Kohn–Sham equation using the global hybrid Becke, 3-parameter, Lee–Yang–Parr (B3LYP) density functional93–95 with the def2-SVP96 basis set and associated electronic core potential (ECP) for Ru.97 This level of theory was already validated in a previous study for the system under investigation.98 The QM and MM potentials were combined according to the ONIOM QM/MM scheme.99–102 The electrostatic interaction between QM and MM layers was treated including the MM charges in the QM Hamiltonian (i.e., an ‘electronic’ embedding). General AMBER Force Field103 atom types (and so van der Waals non-bonding parameters) were assigned to the N34− atoms.Non-periodic boundary conditions were introduced through a hybrid explicit/implicit solvent model.67,104–107 A solute–solvent explicit (i.e., atomistic) system is confined in a fixed-radius sphere and perturbed by the mean field of the surrounding bulk, implicit, solvent. The explicit part can be so considered as an NVT ensemble. The Helmholtz free energy (A) for a given nuclear configuration R and electronic density P of the explicit system can be derived as:
| A(R) = E(R,P) + W(R,P) | (1) |
| W(R) = Wdisp-rep(R) + Welec(R) + Wcav(R) | (2) |
A preliminary equilibration step of ∼2 ps was carried out on our system, then a ∼8.6 ps production run was collected. A T = 298 K temperature was kept during the production through velocity rescaling every 1 ps. The Atom-centered Density Matrix Propagation extended Lagrangian approach (ADMP) was employed:117–119 the density matrix in an orthonormal Gaussian atom-centered basis is propagated along with the nuclear degrees of freedom, avoiding a convergence procedure at each step. A mass-weighting scheme which attributes a higher mass to the core functions was chosen, together with a 0.2 amu bohr2 valence mass. This allowed to employ a 0.1 fs time step, obtaining a total energy conservation within 0.01 hartree.
Concerning static calculations, two representative N34− geometries were obtained via energy minimization procedure either in gas-phase or using a N34− plus explicit water molecules cluster model embedded in implicit solvent (in its conductor-like version). One solvent molecule was added for each solvation site (Fig. S2, ESI,† namely 10wat/CPCM). Geometries were considered fully optimized when both the forces (maximum and RMS force, 0.000450 and 0.000300 hartree bohr−1 thresholds, respectively) and displacement (maximum and RMS displacement, 0.0018 and 0.0012 bohr thresholds, respectively) values for all atoms were below the threshold criteria.
In all calculations the part treated at DFT level was assumed to have an overall 4− charge. We checked that in the ground state the entire negative charge was mostly located on the N34− by performing Mulliken population analysis on the 10wat/CPCM cluster, where in principle the 10 closest water molecules can partially accept the negative charge. In fact, a − 3.77 e− charge (94.32%) is actually located on the N34−, while only a − 0.23 e− charge (5.68%) is overall found on the first-shell solvent molecules, meaning that each water molecule presents a very small amount of charge on average (∼−0.02 e−, please refer to Table S1 in the ESI† for the atomic charges and the total charges on N34− and 10 water molecules).
All calculations were performed with a development version of the Gaussian software.120
2.2 Vibrational analysis
Besides routine normal mode vibrational analysis through diagonalization of the Hessian matrix evaluated at an energy minimum structure, generalized, anharmonic, modes at finite temperature can be extracted from a Molecular Dynamics phase-space sampling.44,45,121,122In the following discussion, the cartesian atomic coordinates and generalized normal modes coordinates are respectively called q(t) = {qi(t)} and Q(t) = {Qk(t)}. The generalized normal modes are defined such that the velocities ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) k are non-correlated:
k are non-correlated:
〈![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) k(t) k(t)![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) l(t)〉 ≈ δkl l(t)〉 ≈ δkl | (3) |
Generalized normal modes (GNMs) directions are obtained as the eigenvectors of the covariance matrix K of the atomic mass-weighted velocities:
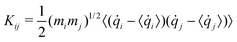 | (4) |
![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) i is qi velocity.
i is qi velocity.
Generalized modes velocities are calculated as the projections of atomic velocities along the generalized normal modes directions:
![[Q with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0051_0307.gif) (t) = L† (t) = L†![[q with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0071_0307.gif) (t) (t) | (5) |
![[q with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0071_0307.gif) is the atomic velocity vector.
is the atomic velocity vector.
The frequency associated with the k-th generalized mode can be then obtained by the Fourier Transform of the mode velocity ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) k autocorrelation (i.e.,
k autocorrelation (i.e., ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) k power spectrum):
k power spectrum):
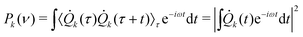 | (6) |
3 Results and discussion
3.1 N34− structure and solvation in water solution
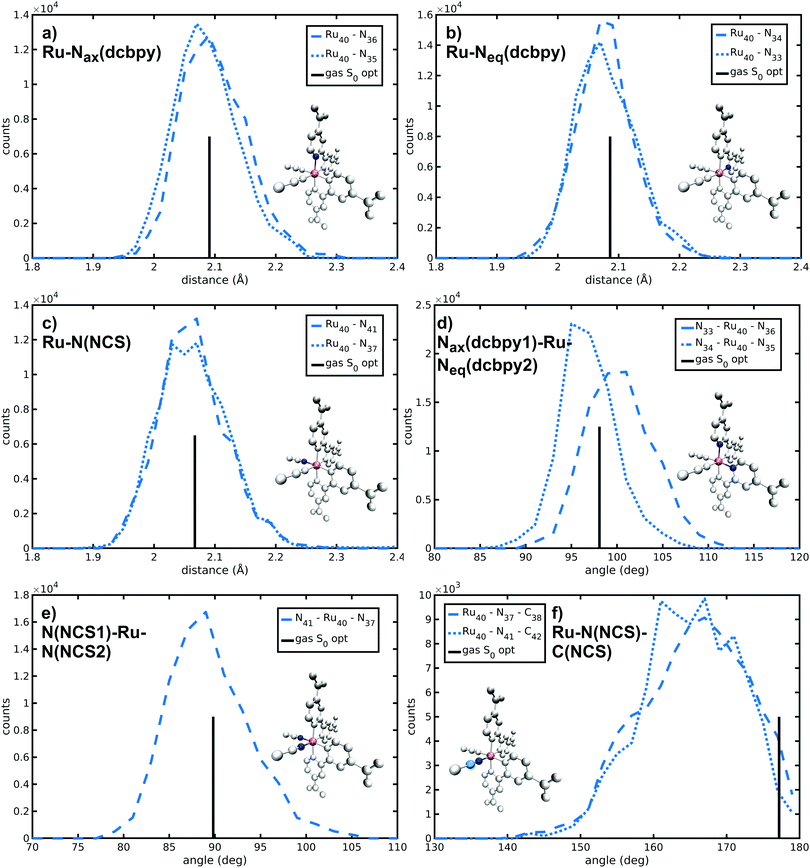
N34− main coordination structural parameters sampled by ab initio MD in explicit water solution have been compared to those of two representative structures obtained via energy minimization procedure by adopting the same level of theory (see Methods section). We wish to point out that AIMD provide not only average values, but also their equilibrium distributions. The Ru-ligand distances in water solution are totally comparable to those obtained from both optimized structures, differing at most for 0.01 Å (Table 1 and Fig. 2a–c). In particular, the Ru–N(dcbpy) bonds (2.08 Å for the equatorial bonds, 2.09–2.10 Å for the axial ones) are only 0.01–0.04 Å longer than the Ru–N(NCS) bonds. The two Nax–Ru–Neq angles involving different dcbpy ligands (so not being the dcbpy N–Ru–N bite angle and not being constrained by dcbpy chelation), as well as the NCS–Ru–NCS angle, seem not to be affected by water solvation (Fig. 2d and e). While the former assume a ≈100° value, the latter retains an almost ideal octahedral (89°) angle. A solvation-induced distortion can be observed instead in the Ru–N(NCS)-C(NCS) angles, describing isothiocyanate coordination linearity. While in both optimized (gas-phase and 10wat/CPCM) structures NCS− coordination is actually almost linear (≈177°), the AIMD trajectory in explicit water solution samples, on average, a slightly bent coordination (165°, Fig. 2f), showing moreover some conformational flexibility (≈7° standard deviation). A trajectory-averaged isodensity plot of the occupancy map of NCS moieties reveals in fact a conic-shaped region actually explored by NCS− ligands (Fig. 3).| AIMD | Gas-phase | 10wat/CPCM | |
|---|---|---|---|
| Ru–Nax(dcbpy) | 2.10 (0.05) | 2.091 | 2.085 |
| 2.09 (0.05) | |||
| Ru–Neq(dcbpy) | 2.08 (0.05) | 2.086 | 2.071 |
| 2.08 (0.05) | |||
| Ru–N(NCS) | 2.06 (0.06) | 2.067 | 2.054 |
| 2.07 (0.06) | |||
| Nax(dcbpy1)–Ru–Neq(dcbpy2) | 100 (4) | 98.08 | 97.25 |
| 97 (3) | |||
| N(NCS1)–Ru–N(NCS2) | 89 (4) | 89.82 | 90.40 |
| Ru–N(NCS)–C(NCS) | 165 (7) | 177.20 | 177.94 |
| 165 (7) |
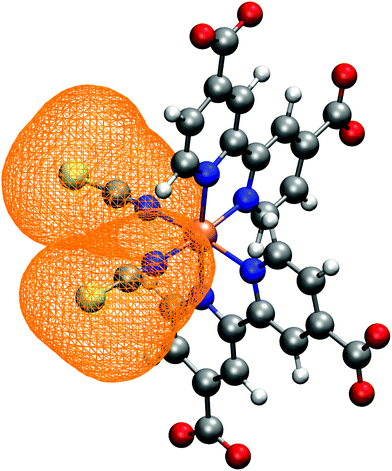 | ||
| Fig. 3 NCS− ligands spatial distribution, calculated as trajectory-averaged occupancy map with the volmap tool of VMD program.123 The map isosurface (0.2 isovalue) is depicted as orange wireframe around the ligands. | ||
N34− microsolvation in water solution has been investigated in detail next. The N34− complex has in fact several solvation sites on NCS− sulfur and dcbpy oxygen atoms (Fig. S3, ESI†), both able to interact with the surrounding solvent molecules. Because of N34− high negative charge, a strong solvation by polar solvents (such as water) is expected. Solute–solvent g(r) radial distribution functions reveal that the water molecules are mostly found at 3.10 and 2.70 Å from S(NCS−) and O(dcbpy), respectively (S(NCS)–O(wat) and O(dcbpy)–O(wat) g(r) peaks, Fig. 4 and Fig. S4 and Table 2 and Table S2, ESI†). The solvent molecules are therefore closer to the oxygen sites, likely because of the dcbpy oxygen atoms higher negative charge and smaller atomic radius. However, sulfur atoms can interact on average with a number (∼4) of water molecules higher than oxygen sites (∼3). Looking in detail at S–O(wat) and O–O(wat) g(r) features, actually the sulfur solvation peaks do not appear much less structured than the oxygen ones. Nevertheless, a second solvation shell at a 4.5–5 Å distance can be observed only for the oxygen sites.
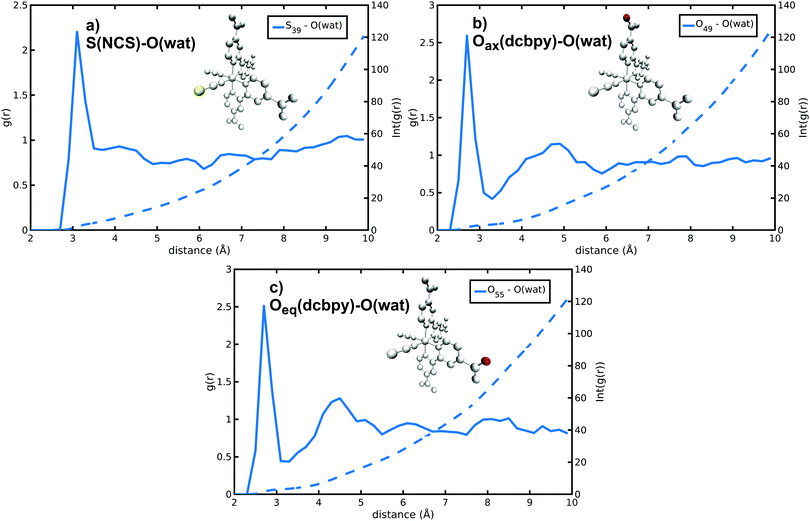 | ||
| Fig. 4 S(NCS)–O(wat) and O(dcbpy)–O(wat) radial distribution functions and integrated number of solvent molecules for selected S(NCS−) and O(dcbpy) N34− solvation sites. | ||
| r max (Å) | n wat | |
|---|---|---|
| S(NCS) | 3.10 | 4.44 |
| O(dcbpy) | 2.70 | 3.31 |
Finally we monitored the probability of finding water molecules around the solvation sites. For this purpose, isodensity plots of spatial distributions of water molecules around O(dcbpy) and S(NCS) are reported in Fig. 5. Comparing the two distributions at the same occupancy isovalue (0.3) and within the same distance (3.5 Å) from the O(dcbpy) and S(NCS) sites, some differences can be observed. In fact, while solvent occupancy is slightly higher and more uniform around dcbpy carboxylate groups (Fig. 5a), a more diffuse and less tight distribution around NCS− ligands can be instead observed (Fig. 5b).
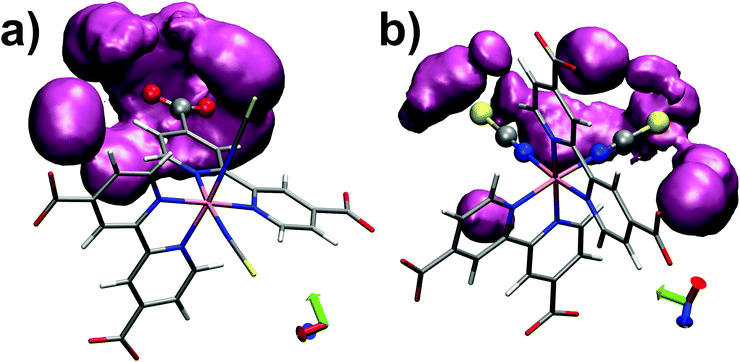 | ||
| Fig. 5 Isodensity plots (0.3 occupancy isovalue) of water molecules spatial distributions around O(dcbpy) (a) and S(NCS) (b) within 3.5 Å, calculated as trajectory-averaged O(wat) occupancy maps with the volmap tool of VMD program.123 | ||
Monitoring the ground-state finite temperature N34− microsolvation via the average number of water interactions, their distances and their spatial distribution around the solvation sites is a very important information, since the changes in these parameters are proxy of CT dynamics and can be probed by frequency shifts in time-resolved spectroscopic signals.
The dynamical perturbation of N34− structural symmetry in water solution is then explored. N34− “ideal” minimum energy geometry belongs in fact to the C2 symmetry group, with its C2 symmetry axis bisecting the NCS–Ru–NCS angle (please refer to Fig. 1). Nevertheless, vibration and environment effects are indeed able to instantaneously lower such symmetry to some degree. This dynamic deviation from a symmetric structure is relevant first from a spectroscopic point of view, since it provides a mechanism to overcome in part symmetry-based selection rules. The transition probability of dark electronic states, forbidden in an ideal, “frozen”, geometry, could therefore increase. Moreover, in the specific case of N3 and other Ru-polypyridyl complexes, the localized nature of MLCT excited states, with the photo-excited electron on only one bipyridine ligand, has been recognized as a result of symmetry-breaking vibrations and environment fluctuations.7,124–133 The localization of CT excitation is potentially relevant, since it enables intra-molecular, inter-ligand electron transfer processes among bpy acceptor ligands.131–133
A continuous symmetry measure (CSM) of N34− minimal deviation from C2 symmetry (i.e., the minimized root mean square (r.m.s.) deviation of the structure from its image generated through the C2 operation, normalized to the r.m.s. size of the structure)134–136 has been evaluated along the AIMD trajectory in water solution. To improve computational efficiency, a reduced N34− model (a smaller model able to retain a symmetry not higher than C2 as the full N34− structure, Fig. S5, ESI†) has been employed for C2-CSM calculations. Looking at the distribution from the N34− AIMD in water solution (Fig. 6), two small CSM values (∼0.1 and 0.2) appear as the most populated, although higher symmetry distortions (∼0.45) are occasionally also explored. Therefore, compared to the static minimum energy structure having an ideal C2 symmetry (zero CSM value), the dynamical picture offered by AIMD simulations reveals that N34− at room temperature in water solution actually slightly deviates, on average, from the C2 symmetry, due to its vibrational motions and solvent environment fluctuations (mean C2-CSM: 0.21 ± 0.12). Such N34− symmetry-lowering flexibility can potentially make dark excited states experimentally accessible and contributes to localize the photo-excited electron in MLCT states.
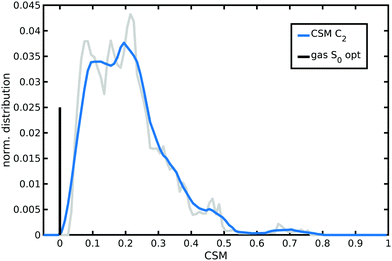 | ||
| Fig. 6 Normalized distribution of the continuous symmetry measure (CSM) with respect to C2 symmetry group sampled by N34− AIMD in water solution. CSM values have been calculated with the program provided in ref. 136. A lower value in the [0,1] range corresponds to a more symmetric structure. An averaged distribution function (the blue curve) is shown for better clarity. The zero value of the optimized gas-phase N34− symmetric structure is also reported as a vertical black bar with arbitrary height. | ||
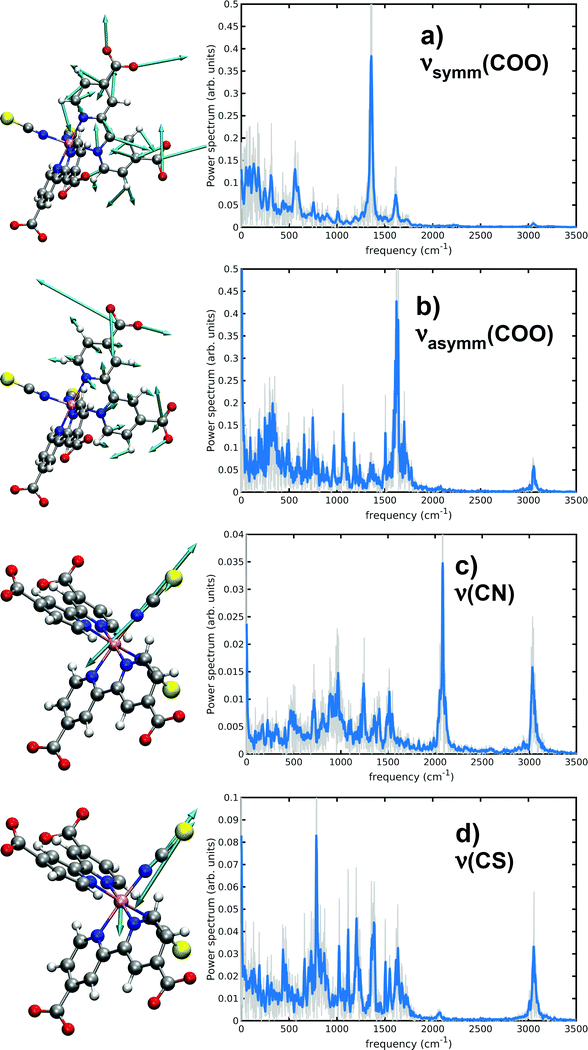
3.2 N34− vibrational signatures
Several works have experimentally characterized the N34− IR absorption, in solution,24,131 in the solid state and adsorbed onto TiO2 films.8,27 Experimental frequencies from ref. 24 are here provided for comparison, since they were measured in water solution as our calculated ones. As already discussed in Methods section, a vibrational analysis of the sampled N34− AIMD trajectory in water solution necessarily includes both anharmonicity and solvent effects, which cannot be completely captured instead by ‘static’ vibrational calculations (i.e., evaluating the Hessian matrix on a minimum energy structure). In particular, dcbpy carboxyl groups symmetric and asymmetric stretchings and thiocyanates C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and C
N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretching modes have been characterized through both approaches (Table 3 and Fig. 7). Two static vibrational calculations have been performed for comparison, one on the gas-phase optimized N34− structure and another on the optimized 10wat/CPCM cluster (Fig. S2, ESI†).
S stretching modes have been characterized through both approaches (Table 3 and Fig. 7). Two static vibrational calculations have been performed for comparison, one on the gas-phase optimized N34− structure and another on the optimized 10wat/CPCM cluster (Fig. S2, ESI†).
| Experimental | Static, harmonic | AIMD | ||
|---|---|---|---|---|
| Gas-phase | 10wat/CPCM | |||
| ν symm(COO) (cm−1) | 1375 | 1368 | 1409 | 1354 |
| ν asymm(COO) | 1596 | 1767 | 1700 | 1621 |
| ν(CN) | 2120 | 2210 | 2209 | 2080 |
| ν(CS) | 820 | 814 | 786 | |
From the displacement vectors of generalized modes it can be seen that ab initio MD-based vibrational analysis can be used to catch the nature of the system normal modes. Considering first the symmetric COO− stretching (experimentally found at 1375 cm−1), the inclusion of solvent effects through the two distinct approaches (explicitly adding some QM water molecules and introducing an implicit bulk solvent, or a dynamics in explicit MM water) leads to opposite deviations from the harmonic gas-phase value (10wat/CPCM: 41 cm−1, AIMD: −14 cm−1, respectively). The ‘dynamical’ approach results to be more accurate with a −21 cm−1 error, if both approaches are compared to the experiment. Both solvent methods predict instead a red-shift of the asymmetric COO− stretching (experimentally at 1596 cm−1) from the gas-phase harmonic value (10wat/CPCM: −67 cm−1, AIMD: −146 cm−1); the higher red-shift by the AIMD vibrational approach allows again a lower (25 cm−1) error vs. the experimental value. This important red shift has been previously noted to be typical of carbonyl moieties of amidic groups in aqueous solution as well.92 This is due to the weakening of the double bond nature of the CO bond because of the oxygen interaction with surrounding water molecules. Monitoring their dynamical evolution over time can be used to show the intrinsic dynamical nature of the system also under equilibrium conditions. As matter of fact, all AIMD spectra are enriched indeed with low frequency bands related to the coupling with water librations and collective hydrogen bond stretching and bending (region of 100–400 cm−1) modes.
While the inclusion of one explicit QM water molecule near each NCS− ligand does not significantly alter the gas-phase C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and C
N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretchings, the AIMD vibrational analysis reveals instead red-shifts of −130 and −34 cm−1, achieving a better accuracy in particular for the C
S stretchings, the AIMD vibrational analysis reveals instead red-shifts of −130 and −34 cm−1, achieving a better accuracy in particular for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretching (a −40 cm−1 error from the 2120 cm−1 experimental value).
N stretching (a −40 cm−1 error from the 2120 cm−1 experimental value).
4 Conclusions
Our work provides an investigation of equilibrium solvation of N34− in water, where the metal–ligand–water structuration and equilibrium fluctuations are investigated in details via ab initio molecular dynamics. Two solvation sites are found for the ligands: the sulfur and the oxygen sites can interact on average with ∼4 and ∼3 water molecules, respectively. A stronger interaction of the oxygen sites (RDF maximum at 2.70 Å) with respect to the sulfur ones (RDF maximum at 3.10 Å) is highlighted by this study. Additionally we find that a dynamic distortion of the C2 symmetric structure, revealed by a continuous symmetry measure, is induced by molecular internal motions and water solvation, mostly modifying the NCS− ligand coordination geometry, which is influenced by a precession motion, as clearly identified by isodensity maps.Analyzing solute–solvent hydrogen bonding network is very important for monitoring the CT dynamics of these systems since the strong modification of the solvent network induced by electronic excitation of the solute can provide useful molecular insights on how specific solute–solvent interactions respond to intramolecular electron transfer.42 Additionally, in this work a fine characterization of the charged ligand carboxyl symmetric and asymmetric stretchings has been made available via generalized normal mode analysis. By using an accurate description of the solute–solvent interactions along with the anharmonic nature of AIMD sampling, we were able to reproduce the experimental values and link the observed shifts with respect to the gas-phase to a complex solvent distribution around ligands, mostly spherically distributed around the oxygen atoms.
Knowing the exact solvent distribution around dcbpy groups and its effect on carboxyl stretching is very important, since shifts of the order of ∼10 cm−1 can be used to distinguish between different binding motifs and detect exciton migration.30 More broadly this work provides the grounds for future excited-state nuclear and electronic dynamics to monitor non-equilibrium processes of CT excitation in complex environments, such as exciton migration in photovoltaic applications.
Author contributions
FP, AP, and NR: project. FP: data collections. FP and AP: data analysis. All authors interpretation of data and writing.Conflicts of interest
The are no conflicts of interest to declare.Acknowledgements
FP and NR thanked Gaussian Inc. for financial support. Italian Ministry of Education, University and Research (MIUR) is also gratefully acknowledged for financial support (AP: Project AIM1829571-1 CUP E61G19000090002, NR: Project PRIN 2017YJMPZN001).Notes and references
- M. Grätzel, Inorg. Chem., 2005, 44, 6841–6851 CrossRef PubMed.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- B. Lee, J. He, R. P. Chang and M. G. Kanatzidis, Nature, 2012, 485, 486–489 CrossRef PubMed.
- M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145–153 CrossRef.
- M. Chergui, Acc. Chem. Res., 2015, 48, 801–808 CrossRef CAS PubMed.
- E. A. Juban, A. L. Smeigh, J. E. Monat and J. K. McCusker, Coord. Chem. Rev., 2006, 250, 1783–1791 CrossRef CAS.
- J. K. McCusker, Acc. Chem. Res., 2003, 36, 876–887 CrossRef CAS PubMed.
- M. K. Nazeeruddin, R. Humphry-Baker, P. Liska and M. Grätzel, J. Phys. Chem. B, 2003, 107, 8981–8987 CrossRef CAS.
- Q.-B. Meng, K. Takahashi, X.-T. Zhang, I. Sutanto, T. Rao, O. Sato, A. Fujishima, H. Watanabe, T. Nakamori and M. Uragami, Langmuir, 2003, 19, 3572–3574 CrossRef CAS.
- J. B. Asbury, R. J. Ellingson, H. N. Ghosh, S. Ferrere, A. J. Nozik and T. Lian, J. Phys. Chem. B, 1999, 103, 3110–3119 CrossRef CAS.
- M. R. Waterland and D. F. Kelley, J. Phys. Chem. A, 2001, 105, 4019–4028 CrossRef CAS.
- L. C. T. Shoute and G. R. Loppnow, J. Am. Chem. Soc., 2003, 125, 15636–15646 CrossRef CAS PubMed.
- B. E. Van Kuiken, N. Huse, H. Cho, M. L. Strader, M. S. Lynch, R. W. Schoenlein and M. Khalil, J. Phys. Chem. Lett., 2012, 3, 1695–1700 CrossRef CAS PubMed.
- O. Bräm, F. Messina, A. M. El-Zohry, A. Cannizzo and M. Chergui, Chem. Phys., 2012, 393, 51–57 CrossRef.
- R. Horvath, M. G. Fraser, C. A. Clark, X.-Z. Sun, M. W. George and K. C. Gordon, Inorg. Chem., 2015, 54, 11697–11708 CrossRef CAS PubMed.
- Y. Tachibana, J. E. Moser, M. Grätzel, D. R. Klug and J. R. Durrant, J. Phys. Chem., 1996, 100, 20056–20062 CrossRef CAS.
- T. Hannappel, B. Burfeindt, W. Storck and F. Willig, J. Phys. Chem. B, 1997, 101, 6799–6802 CrossRef CAS.
- J. R. Durrant, Y. Tachibana, I. Mercer, J. E. Moser, M. Grätzel and D. R. Klug, Z. Phys. Chem., 1999, 212, 93–98 CrossRef CAS.
- J. B. Asbury, E. Hao, Y. Wang, H. N. Ghosh and T. Lian, J. Phys. Chem. B, 2001, 105, 4545–4557 CrossRef CAS.
- J. Kallioinen, G. Benkö, V. Sundström, J. E. I. Korppi-Tommola and A. P. Yartsev, J. Phys. Chem. B, 2002, 106, 4396–4404 CrossRef CAS.
- J. B. Asbury, N. A. Anderson, E. Hao, X. Ai and T. Lian, J. Phys. Chem. B, 2003, 107, 7376–7386 CrossRef CAS.
- N. A. Anderson and T. Lian, Annu. Rev. Phys. Chem., 2005, 56, 491–519 CrossRef CAS PubMed.
- C. C. Rich, M. A. Mattson and A. T. Krummel, J. Phys. Chem. C, 2016, 120, 6601–6611 CrossRef CAS.
- J. D. Gaynor, A. Petrone, X. Li and M. Khalil, J. Phys. Chem. Lett., 2018, 9, 6289–6295 CrossRef CAS PubMed.
- J. D. Gaynor, J. Sandwisch and M. Khalil, Nat. Chem., 2019, 10, 1–9 Search PubMed.
- J. D. Gaynor, A. Petrone, X. Li and M. Khalil, J. Phys. Chem. Lett., 2018, 9, 6289–6295 CrossRef CAS PubMed.
- K. S. Finnie, J. R. Bartlett and J. L. Woolfrey, Langmuir, 1998, 14, 2744–2749 CrossRef CAS.
- J. Tang, K. W. Kemp, S. Hoogland, K. S. Jeong, H. Liu, L. Levina, M. Furukawa, X. Wang, R. Debnath and D. Cha, et al. , Nat. Mater., 2011, 10, 765–771 CrossRef CAS PubMed.
- K. S. Jeong, J. Tang, H. Liu, J. Kim, A. W. Schaefer, K. Kemp, L. Levina, X. Wang, S. Hoogland, R. Debnath, L. Brzozowski, E. H. Sargent and J. B. Asbury, ACS Nano, 2012, 6, 89–99 CrossRef CAS PubMed.
- J. D. Leger, M. R. Friedfeld, R. A. Beck, J. D. Gaynor, A. Petrone, X. Li, B. M. Cossairt and M. Khalil, J. Phys. Chem. Lett., 2019, 10, 1833–1839 CrossRef CAS PubMed.
- C. Adamo, M. Cossi, N. Rega and V. Barone, in Theoretical Biochemistry, ed. L. A. Eriksson, Theoretical and Computational Chemistry, Elsevier, Amsterdam, The Netherlands, 2001, vol. 9, pp. 467–538 Search PubMed.
- V. Barone, R. Improta and N. Rega, Acc. Chem. Res., 2008, 41, 605–616 CrossRef CAS PubMed.
- C. Reichardt, Chem. Rev., 1994, 94, 2319–2358 CrossRef CAS.
- E. Krystkowiak, K. Dobek and A. Maciejewski, J. Photochem. Photobiol., 2006, 184, 250–264 CrossRef CAS.
- K. M. Solntsev, D. Huppert and N. Agmon, J. Phys. Chem. A, 1999, 103, 6984–6997 CrossRef CAS.
- K. M. Solntsev, D. Huppert, L. M. Tolbert and N. Agmon, J. Am. Chem. Soc., 1998, 120, 7981–7982 CrossRef CAS.
- H. A. Frank, J. A. Bautista, J. Josue, Z. Pendon, R. G. Hiller, F. P. Sharples, D. Gosztola and M. R. Wasielewski, J. Phys. Chem. B, 2000, 104, 4569–4577 CrossRef CAS.
- V. Barone, N. Rega, T. Bally and G. N. Sastry, J. Phys. Chem. A, 1999, 103, 217–219 CrossRef CAS.
- R. Improta, N. Rega, C. Aleman and V. Barone, Macromolecules, 2001, 34, 7550–7557 CrossRef CAS.
- E. Langella, N. Rega, R. Improta, O. Crescenzi and V. Barone, J. Comput. Chem., 2002, 23, 650–661 CrossRef CAS PubMed.
- A. Petrone, G. Donati, P. Caruso and N. Rega, J. Am. Chem. Soc., 2014, 136, 14866–14874 CrossRef CAS PubMed.
- E. Biasin, Z. W. Fox, A. Andersen, K. Ledbetter, K. S. Kjær, R. Alonso-Mori, J. M. Carlstad, M. Chollet, J. D. Gaynor, J. M. Glownia, K. Hong, T. Kroll, H. J. Lee, C. Liekhus-Schmaltz, M. Reinhard, D. Sokaras, Y. Zhang, G. Doumy, A. M. March, S. H. Southworth, S. Mukamel, K. J. Gaffney, R. W. Schoenlein, N. Govind, A. A. Cordones and M. Khalil, Nat. Chem., 2021, 13, 343–349 CrossRef CAS PubMed.
- J. D. Leger, M. R. Friedfeld, R. A. Beck, J. D. Gaynor, A. Petrone, X. Li, B. M. Cossairt and M. Khalil, J. Phys. Chem. Lett., 2019, 10, 1833–1839 CrossRef CAS PubMed.
- N. Rega, Theor. Chem. Acc., 2006, 116, 347–354 Search PubMed.
- A. Strachan, J. Chem. Phys., 2004, 120, 1–4 CrossRef CAS PubMed.
- M.-P. Gaigeot, M. Martinez and R. Vuilleumier, Mol. Phys., 2007, 105, 2857–2878 CrossRef CAS.
- R. Beck, A. Petrone, J. M. Kasper, M. J. Crane, P. J. Pauzauskie and X. Li, J. Phys. Chem. C, 2018, 122, 8573–8580 CrossRef CAS.
- A. Petrone, D. B. Williams-Young, D. B. Lingerfelt and X. Li, J. Phys. Chem. A, 2017, 121, 3958–3965 CrossRef CAS PubMed.
- E. Q. Chong, D. B. Lingerfelt, A. Petrone and X. Li, J. Phys. Chem. C, 2016, 120, 19434–19441 CrossRef CAS.
- J. Hafner, C. Wolverton and G. Ceder, MRS Bull., 2006, 31, 659–668 CrossRef.
- R. Beaulac, Y. Feng, J. W. May, E. Badaeva, D. R. Gamelin and X. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195324 CrossRef.
- P. J. Lestrange, P. D. Nguyen and X. Li, J. Chem. Theory Comput., 2015, 11, 2994–2999 CrossRef CAS PubMed.
- J. Aarons, M. Sarwar, D. Thompsett and C.-K. Skylaris, J. Chem. Phys., 2016, 145, 220901 CrossRef PubMed.
- A. Petrone, J. J. Goings and X. Li, Phys. Rev. B, 2016, 94, 165402 CrossRef.
- G. Donati, D. B. Lingerfelt, A. Petrone, N. Rega and X. Li, J. Phys. Chem. A, 2016, 120, 7255–7261 CrossRef CAS PubMed.
- N. Li, Z. Zhu, C.-C. Chueh, H. Liu, B. Peng, A. Petrone, X. Li, L. Wang and A. K.-Y. Jen, Adv. Energy Mater., 2016, 7, 1601307 CrossRef.
- D. C. Gary, S. E. Flowers, W. Kaminsky, A. Petrone, X. Li and B. M. Cossairt, J. Am. Chem. Soc., 2016, 138, 1510–1513 CrossRef CAS PubMed.
- D. C. Gary, A. Petrone, X. Li and B. M. Cossairt, Chem. Commun., 2017, 53, 161–164 RSC.
- J. L. Stein, M. I. Steimle, M. W. Terban, A. Petrone, S. J. L. Billinge, X. Li and B. M. Cossairt, Chem. Mater., 2017, 29, 7984–7992 CrossRef CAS.
- G. Donati, D. B. Lingerfelt, C. M. Aikens and X. Li, J. Phys. Chem. C, 2017, 121, 15368–15374 CrossRef CAS.
- S. Xu, J. E. T. Smith, S. Gozem, A. I. Krylov and J. M. Weber, Inorg. Chem., 2017, 56, 7029–7037 CrossRef CAS PubMed.
- U. Raucci, M. G. Chiariello, F. Coppola, F. Perrella, M. Savarese, I. Ciofini and N. Rega, J. Comput. Chem., 2020, 41, 1835–1841 CrossRef CAS PubMed.
- E. Battista, P. L. Scognamiglio, N. Di Luise, U. Raucci, G. Donati, N. Rega, P. A. Netti and F. Causa, J. Mater. Chem. B, 2018, 6, 1207–1215 RSC.
- A. Wildman, G. Donati, F. Lipparini, B. Mennucci and X. Li, J. Chem. Theory Comput., 2018, 15, 43–51 CrossRef PubMed.
- F. Perrella, U. Raucci, M. G. Chiariello, M. Chino, O. Maglio, A. Lombardi and N. Rega, Biopolymers, 2018, 109, e23225 CrossRef PubMed.
- G. Donati, A. Petrone, P. Caruso and N. Rega, Chem. Sci., 2018, 9, 1126–1135 RSC.
- U. Raucci, F. Perrella, G. Donati, M. Zoppi, A. Petrone and N. Rega, J. Comput. Chem., 2020, 41, 2228–2239 CrossRef CAS PubMed.
- A. Petrone, D. B. Lingerfelt, N. Rega and X. Li, Phys. Chem. Chem. Phys., 2014, 16, 24457–24465 RSC.
- G. Lever, D. J. Cole, R. Lonsdale, K. E. Ranaghan, D. J. Wales, A. J. Mulholland, C.-K. Skylaris and M. C. Payne, J. Phys. Chem. Lett., 2014, 5, 3614–3619 CrossRef CAS PubMed.
- A. Petrone, D. B. Lingerfelt, D. B. Williams-Young and X. Li, J. Phys. Chem. Lett., 2016, 7, 4501–4508 CrossRef CAS PubMed.
- F. Coppola, F. Perrella, A. Petrone, G. Donati and N. Rega, Front. Mol. Biosci., 2020, 7, 283 Search PubMed.
- R. Horvath, M. G. Fraser, C. A. Clark, X.-Z. Sun, M. W. George and K. C. Gordon, Inorg. Chem., 2015, 54, 11697–11708 CrossRef CAS PubMed.
- A. Vlček Jr and S. Záliš, Coord. Chem. Rev., 2007, 251, 258–287 CrossRef.
- M. Jaeger, L. Freitag and L. Gonzalez, Coord. Chem. Rev., 2015, 304, 146–165 CrossRef.
- J. E. Monat, J. H. Rodriguez and J. K. McCusker, J. Phys. Chem. A, 2002, 106, 7399–7406 CrossRef CAS.
- F. De Angelis, S. Fantacci, A. Selloni, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. C, 2010, 114, 6054–6061 CrossRef CAS.
- F. De Angelis, S. Fantacci, E. Mosconi, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. C, 2011, 115, 8825–8831 CrossRef CAS.
- B. E. Van Kuiken, N. Huse, H. Cho, M. L. Strader, M. S. Lynch, R. W. Schoenlein and M. Khalil, J. Phys. Chem. Lett., 2012, 3, 1695–1700 CrossRef CAS PubMed.
- A. Y. Koposov, T. Cardolaccia, V. Albert, E. Badaeva, S. Kilina, T. J. Meyer, S. Tretiak and M. Sykora, Langmuir, 2011, 27, 8377–8383 CrossRef CAS PubMed.
- T. Véry, D. Ambrosek, M. Otsuka, C. Gourlaouen, X. Assfeld, A. Monari and C. Daniel, Chem. – Eur. J., 2014, 20, 12901–12909 CrossRef PubMed.
- C. Daniel, in Absorption Spectroscopy, Emissive Properties, and Ultrafast Intersystem Crossing Processes in Transition Metal Complexes: TD-DFT and Spin–Orbit Coupling, ed. N. Ferré, M. Filatov and M. Huix-Rotllant, Springer International Publishing, Cham, 2016, pp. 377–413 Search PubMed.
- T. Ono, N. Planas, P. Miró, M. Z. Ertem, E. C. Escudero-Adán, J. Benet-Buchholz, L. Gagliardi, C. J. Cramer and A. Llobet, ChemCatChem, 2013, 5, 3897–3903 CrossRef CAS.
- N. Planas, T. Ono, L. Vaquer, P. Miró, J. Benet-Buchholz, L. Gagliardi, C. J. Cramer and A. Llobet, Phys. Chem. Chem. Phys., 2011, 13, 19480–19484 RSC.
- M. Heindl, J. Hongyan, S.-A. Hua, M. Oelschlegel, F. Meyer, D. Schwarzer and L. González, Inorg. Chem., 2021, 60, 1672–1682 CrossRef CAS PubMed.
- S.-A. Hua, M. Cattaneo, M. Oelschlegel, M. Heindl, L. Schmid, S. Dechert, O. S. Wenger, I. Siewert, L. González and F. Meyer, Inorg. Chem., 2020, 59, 4972–4984 CrossRef CAS PubMed.
- M. Jäger, L. Freitag and L. González, Coord. Chem. Rev., 2015, 304–305, 146–165 CrossRef.
- F. Labat, I. Ciofini, H. P. Hratchian, M. J. Frisch, K. Raghavachari and C. Adamo, J. Phys. Chem. C, 2011, 115, 4297–4306 CrossRef CAS.
- I. Ciofini, C. A. Daul and C. Adamo, J. Phys. Chem. A, 2003, 107, 11182–11190 CrossRef CAS.
- I. Ciofini, P. P. Lainé, F. Bedioui and C. Adamo, J. Am. Chem. Soc., 2004, 126, 10763–10777 CrossRef CAS PubMed.
- D. Case, H. Aktulga, K. Belfon, I. Ben-Shalom, S. Brozell, D. Cerutti, T. Cheatham, III, V. Cruzeiro, T. Darden, R. Duke, G. Giambasu, M. Gilson, H. Gohlke, A. Goetz, R. Harris, S. Izadi, S. Izmailov, C. Jin, K. Kasavajhala, M. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. OHearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. Simmerling, N. Skrynnikov, J. Smith, J. Swails, R. Walker, J. Wang, H. Wei, R. Wolf, X. Wu, Y. Xue, D. York, S. Zhao and P. Kollman, Amber, 2021 Search PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- G. Donati, A. Petrone and N. Rega, Phys. Chem. Chem. Phys., 2020, 22, 22645–22661 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chem. Acc., 1990, 77, 123–141 Search PubMed.
- J. D. Gaynor, A. Petrone, X. Li and M. Khalil, J. Phys. Chem. Lett., 2018, 9, 6289–6295 Search PubMed.
- M. Svensson, S. Humbel, R. D. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357–19363 CrossRef CAS.
- K. Morokuma, Q. Wang and T. Vreven, J. Chem. Theory Comput., 2006, 2, 1317–1324 CrossRef CAS PubMed.
- T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery Jr, K. Morokuma and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 815–826 CrossRef CAS PubMed.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- G. Brancato, N. Rega and V. Barone, Chem. Phys. Lett., 2009, 483, 177–181 CrossRef CAS.
- N. Rega, G. Brancato and V. Barone, Chem. Phys. Lett., 2006, 422, 367–371 CrossRef CAS.
- G. Brancato, N. Rega and V. Barone, J. Chem. Phys., 2008, 128, 144501 CrossRef PubMed.
- G. Brancato, V. Barone and N. Rega, Theor. Chem. Acc., 2007, 117, 1001–1015 Search PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef CAS.
- B. Mennucci, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 386–404 CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- G. Brancato, N. Rega and V. Barone, J. Chem. Phys., 2008, 128, 04B607 CrossRef PubMed.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335 CrossRef CAS.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS.
- M. Cossi and V. Barone, J. Chem. Phys., 2000, 112, 2427–2435 CrossRef CAS.
- G. Brancato, A. Di Nola, V. Barone and A. Amadei, J. Chem. Phys., 2005, 122, 154109 CrossRef PubMed.
- H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758–9763 CrossRef CAS.
- S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291–10302 CrossRef CAS.
- N. Rega, S. S. Iyengar, G. A. Voth, H. B. Schlegel, T. Vreven and M. J. Frisch, J. Phys. Chem. B, 2004, 108, 4210–4220 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, P. V. Parandekar, N. J. Mayhall, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian Development Version Revision H.37+, 2014 Search PubMed.
- S. Thicoipe, P. Carbonniere and C. Pouchan, Chem. Phys. Lett., 2014, 591, 243–247 CrossRef CAS.
- P. Carbonniere, A. Dargelos, I. Ciofini, C. Adamo and C. Pouchan, Phys. Chem. Chem. Phys., 2009, 11, 4375–4384 RSC.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- N. H. Damrauer, G. Cerullo, A. Yeh, T. R. Boussie, C. V. Shank and J. K. McCusker, Science, 1997, 275, 54–57 CrossRef CAS PubMed.
- K. Kalyanasundaram, Coord. Chem. Rev., 1982, 46, 159–244 CrossRef CAS.
- A. Juris, V. Balzani, F. Barigelletti, S. Campagna, P. L. Belser and A. V. von Zelewsky, Coord. Chem. Rev., 1988, 84, 85–277 CrossRef CAS.
- E. M. Kober, B. P. Sullivan and T. J. Meyer, Inorg. Chem., 1984, 23, 2098–2104 CrossRef CAS.
- R. F. Dallinger and W. H. Woodruff, J. Am. Chem. Soc., 1979, 101, 4391–4393 CrossRef CAS.
- D. H. Oh and S. G. Boxer, J. Am. Chem. Soc., 1989, 111, 1130–1131 CrossRef CAS.
- M. Myrick, R. Blakley and M. DeArmond, J. Am. Chem. Soc., 1987, 109, 2841–2842 CrossRef CAS.
- B. P. Rimgard, J. Föhlinger, J. Petersson, M. Lundberg, B. Zietz, A. M. Woys, S. A. Miller, M. R. Wasielewski and L. Hammarström, Chem. Sci., 2018, 9, 7958–7967 RSC.
- M. Waterland and D. Kelley, J. Phys. Chem. A, 2001, 105, 4019–4028 CrossRef CAS.
- G. Benkö, J. Kallioinen, P. Myllyperkiö, F. Trif, J. E. Korppi-Tommola, A. P. Yartsev and V. Sundström, J. Phys. Chem. B, 2004, 108, 2862–2867 CrossRef.
- H. Zabrodsky, S. Peleg and D. Avnir, J. Am. Chem. Soc., 1992, 114, 7843–7851 CrossRef CAS.
- M. Pinsky, D. Casanova, P. Alemany, S. Alvarez, D. Avnir, C. Dryzun, Z. Kizner and A. Sterkin, J. Comput. Chem., 2008, 29, 190–197 CrossRef CAS PubMed.
- M. Pinsky, C. Dryzun, D. Casanova, P. Alemany and D. Avnir, J. Comput. Chem., 2008, 29, 2712–2721 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Graphical representation of the spherical water box, Mulliken population analysis on 10wat/CPCM cluster, the optimized 10wat/CPCM cluster and solvation sites for the N34− system, X–O(wat) RDF plot along with maxima rmax values and the corresponding integrated number of solvent molecules in the first shell for each N34− solvation site, reduced N34− model for C2 continuous symmetry measure (CSM) calculations. See DOI: 10.1039/d1cp03151a |
| This journal is © the Owner Societies 2021 |