DOI:
10.1039/D1CP02946K
(Perspective)
Phys. Chem. Chem. Phys., 2021,
23, 21419-21436
Solvate electrolytes for Li and Na batteries: structures, transport properties, and electrochemistry
Received
29th June 2021
, Accepted 15th September 2021
First published on 15th September 2021
Abstract
Polar solvents dissolve Li and Na salts at high concentrations and are used as electrolyte solutions for batteries. The solvents interact strongly with the alkali metal cations to form complexes in the solution. The activity (concentration) of the uncoordinated solvent decreases as the salt concentration is increased. At extremely high salt concentrations, all the solvent molecules are involved in the coordination of the ions and form the solvates of the salts. In this article, we review the structures, transport properties, and electrochemistry of Li/Na salt solvates. In molten solvates, the activity of the uncoordinated solvent is negligible; this is the main origin of their peculiar characteristics, such as high thermal stability, wide electrochemical window, and unique ion transport. In addition, the solvent activity greatly influences the electrochemical reactions in Li/Na batteries. We highlight the attractive features of molten solvates as promising electrolytes for next-generation batteries.

Yosuke Ugata
| Yosuke Ugata was born in Kanagawa, Japan in 1995. He received his Bachelor's (2018) and Master's (2020) degrees from Yokohama National University (YNU) under the supervision of Prof. Kaoru Dokko, Prof. Kazuhide Ueno, and Prof. Masayoshi Watanabe. He is a PhD candidate and studying the ion transport and electrochemical properties of liquid electrolytes for Li-based secondary batteries. |

Keisuke Shigenobu
| Keisuke Shigenobu recieved BS (2018) and MS (2020) degrees from Yokohama National University, where he is currently pursuing his PhD in the group of Prof. Kaoru Dokko and Prof. Kazuhide Ueno. His current research interests include studies of ion dynamics in the electrolyte solutions and the electrolyte design for the next generation batteries. |

Ryoichi Tatara
| Ryoichi Tatara is an Assistant Professor at the Tokyo University of Science. He received his PhD from Yokohama National University in 2017 under the supervision of Prof. Masayoshi Watanabe and Prof. Kaoru Dokko. He subsequently worked at Massachusetts Institute of Technology as a postdoctoral associate with Prof. Yang Shao-Horn. In 2020, he joined the Tokyo University of Science. His current research interests include the physicochemical properties of electrolyte solutions, interfacial chemistry at the electrode/electrolyte interface, and electrochemical reactions in Li/Na/K batteries. |

Kazuhide Ueno
| Kazuhide Ueno is an Associate Professor at Yokohama National University. He received his PhD degrees in 2009 with Prof. M. Watanabe from Yokohama National University. He was a postdoctoral fellow at Tohoku University working with Prof. K. Kurihara, at Arizona State University working with Prof. C. Austen Angell, and at Yokohama National University. In 2015, he was appointed as assistant professor at Yamaguchi University. His research interests include ionic liquid-based soft materials and battery electrolytes. |

Masayoshi Watanabe
| Masayoshi Watanabe is a Specially Appointed Professor at Yokohama National University since 2020. He received his BS, MS, and PhD degrees from Waseda University. After working with Prof. Royce W. Murray at Univerity of North Carolina (1988–1990), he moved to Yokohama National University in 1992 and was promoted to a full Professor in 1998. He received the Award of The Society of Polymer Science, Japan in 2006, the Award of The Electrochemical Society of Japan (Takei Award) and ECS Max Bredig Award in 2016, and The Chemical Society of Japan Award in 2021. His current research interests are the materials design of ionic liquids and polymers for electrochemical applications and phase-behaviour and self-assembly of polymers and colloids in ionic liquids. |

Kaoru Dokko
| Kaoru Dokko is a Professor at Yokohama National University. He received PhD from Tohoku University in 2001 under the supervision of Prof. Isamu Uchida. He was a postdoctoral researcher at Case Western Reserve University and Tokyo Metropolitan University. He joined Yokohama National University in 2008. His current research interests are the physicochemical properties of concentrated electrolytes, nanostructured materials for energy conversion and storage, and electrochemical reaction process in electrochemical devices. |
1. Introduction
The electrolyte salts for Li and Na batteries comprise alkali metal cations and counter anions. When dissolved in polar solvents, the electrolyte salts dissociate into cations and anions (Fig. 1). The hard cations such as Li+ and Na+ are Lewis acids that form complexes with solvent molecules to produce solvate cations [M(solvent)n]+ (M: Li or Na). The soft anions such as PF6−, BF4−, and bis(trifluoromethanesulfonyl)amide (TFSA−) are weak Lewis bases. They are commonly selected as counter anions because they interact weakly with the cations, and can provide a high degree of salt dissociation in the solution. Currently, the electrolytes used in lithium-ion batteries (LIBs) are Li salts dissolved in an aprotic solvent at a concentration of approximately 1 mol dm−3,1 and the electrolyte shows the maximum ionic conductivity at this concentration.2 The ionic conductivity (σ) can be written as3| | 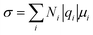 | (1) |
where N is the number of carriers per unit volume, q is the electric charge per carrier, and μ is the carrier mobility. The number of carriers increases with the increase in the concentration of the salt, whereas the mobility decreases as the viscosity of the solution increases with increasing salt concentration, i.e. there is a trade-off relationship between the number of carriers and carrier mobility. This trade-off relationship results in maximum ionic conductivity at a salt concentration of approximately 1 mol dm−3. Because electrolyte solutions with salt concentrations higher than 1 mol dm−3 have low ionic conductivities owing to high viscosities, it was believed that there is no advantage in adding large amounts of expensive Li salts to the electrolyte. However, nowadays, researchers are extensively investigating “super-concentrated” or “solvent-in-salt” electrolytes with Li salt dissolved at a concentration exceeding ∼3 mol dm−3 because certain super-concentrated electrolytes have been reported to improve the performance of lithium batteries.4–9 Increasing the salt concentration in a solution decreases its solvent/salt molar ratio. In aprotic electrolyte solutions, the coordination numbers of Li+ and Na+ are typically 4–6 and 5–7, respectively.10–14 In highly concentrated solutions with molar ratios of solvent/salt lower than the coordination number of the cations, almost all the solvent molecules are coordinated to M+ ions, and free (uncoordinated) solvent molecule hardly exists in the solution (Fig. 1). In addition, the anions also participate in the coordination of the M+ ions to satisfy the coordination number of M+ ion. These highly concentrated solutions without free solvent molecules are regarded as “molten solvates”.
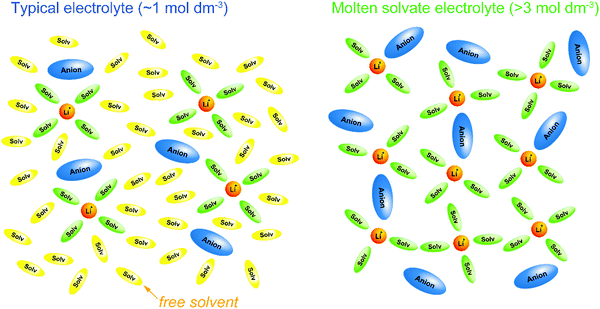 |
| | Fig. 1 Schematic illustrations of solvation structures in a typical Li salt electrolyte solution (∼1 mol dm−3) and a molten Li salt solvate electrolyte (>3 mol dm−3). In a typical electrolyte solution containing excess solvent, each Li+ ion forms a complex with 4 or 5 solvent molecules, and uncoordinated (free) solvent molecules exist abundantly. In a molten solvate electrolyte, Li+ ions form complexes with solvents and anions, and free solvent hardly exists. | |
Henderson et al. systematically investigated the crystal structures of glyme solvates of Li salts;15–18 moreover, we reported the physicochemical properties and battery applications of molten glyme solvates.19–23 Glyme molecules (CH3O(CH2CH2O)nCH3) serve as multidentate ligands and form long-lived complexes with alkali metal cations in the solution.24 The triglyme (G3) and tetraglyme (G4) molecules have 4 and 5 oxygen atoms, respectively, and the number of oxygen atoms matches the coordination number of Li+. The G3 and G4 coordinate to Li+ in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and form [Li(G3)]+ and [Li(G4)]+ in solutions, respectively. The 1
1, and form [Li(G3)]+ and [Li(G4)]+ in solutions, respectively. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of G3 (or G4) and certain Li salts, such as LiTFSA and LiBETA (BETA: bis(pentafluoroethanesulfonyl)amide), are regarded as ionic liquids composed of complex cations [Li(G3 or G4)]+ and the counter anions are regarded as “solvate ionic liquids”. Earlier, we have reviewed the physicochemical properties and electrochemistry of glyme-solvate ionic liquids.25–27 The present article reviews recent progress in the researches on molten solvates and highly concentrated electrolytes comprising various aprotic solvents and Li/Na salts (Fig. 2). The molten Li salt hydrate electrolytes, so called “water-in-salt” electrolytes, which enable the stable operation of 3 V-class aqueous LIBs have also been extensively studied;28–30 however, these aqueous electrolytes do not have sufficient reductive stability against Li metal. The molten solvate electrolytes with aprotic solvents possess high thermal stability and wide electrochemical window and are promising electrolytes for next-generation batteries, such as high voltage Li/Na batteries,31–37 Li–O2 batteries,38 and Li–S batteries.39 Li metal is one of the most attractive anode materials owing to its high theoretical capacity (3860 mA h g−1) and low electrode potential (–3.04 V vs. SHE).40–50 Highly concentrated aprotic electrolytes have been reported to be useful in achieving a high Coulombic efficiency of Li metal deposition/stripping and a long charge/discharge cycle life of Li metal batteries.33,51–56 In addition to these attractive features, we recently found that a unique transport process of Li/Na ions emerges in highly concentrated electrolytes.31 The Li/Na cations exchange ligands (solvent and anion) rapidly in certain concentrated electrolytes, which enables them to diffuse faster than the solvent molecules and anions in the solutions, resulting in the high transference numbers of Li/Na ions. The high transference numbers are effective in suppressing the concentration polarization of Li/Na batteries during discharging at high current densities and may be useful in improving the power densities of the batteries.
1 mixtures of G3 (or G4) and certain Li salts, such as LiTFSA and LiBETA (BETA: bis(pentafluoroethanesulfonyl)amide), are regarded as ionic liquids composed of complex cations [Li(G3 or G4)]+ and the counter anions are regarded as “solvate ionic liquids”. Earlier, we have reviewed the physicochemical properties and electrochemistry of glyme-solvate ionic liquids.25–27 The present article reviews recent progress in the researches on molten solvates and highly concentrated electrolytes comprising various aprotic solvents and Li/Na salts (Fig. 2). The molten Li salt hydrate electrolytes, so called “water-in-salt” electrolytes, which enable the stable operation of 3 V-class aqueous LIBs have also been extensively studied;28–30 however, these aqueous electrolytes do not have sufficient reductive stability against Li metal. The molten solvate electrolytes with aprotic solvents possess high thermal stability and wide electrochemical window and are promising electrolytes for next-generation batteries, such as high voltage Li/Na batteries,31–37 Li–O2 batteries,38 and Li–S batteries.39 Li metal is one of the most attractive anode materials owing to its high theoretical capacity (3860 mA h g−1) and low electrode potential (–3.04 V vs. SHE).40–50 Highly concentrated aprotic electrolytes have been reported to be useful in achieving a high Coulombic efficiency of Li metal deposition/stripping and a long charge/discharge cycle life of Li metal batteries.33,51–56 In addition to these attractive features, we recently found that a unique transport process of Li/Na ions emerges in highly concentrated electrolytes.31 The Li/Na cations exchange ligands (solvent and anion) rapidly in certain concentrated electrolytes, which enables them to diffuse faster than the solvent molecules and anions in the solutions, resulting in the high transference numbers of Li/Na ions. The high transference numbers are effective in suppressing the concentration polarization of Li/Na batteries during discharging at high current densities and may be useful in improving the power densities of the batteries.
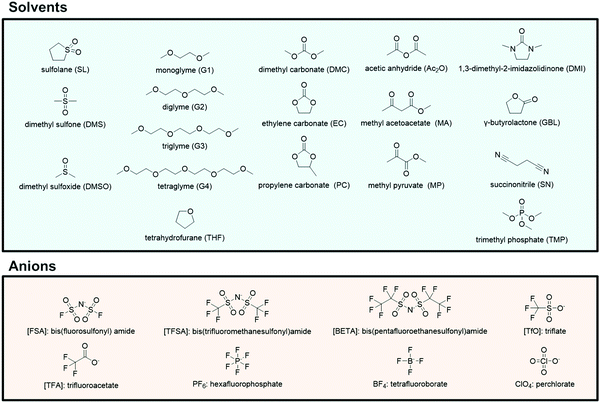 |
| | Fig. 2 Chemical structures and abbreviations of the various solvents and anions. | |
We highlight the unique features of molten solvates as promising electrolytes for next-generation batteries. With increasing the salt concentration in the electrolytes, the activity (concentration) of solvent decreases. So far, the effects of solvent activity on the physicochemical properties of the electrolytes and the electrochemical reaction processes in the electrolytes have often been overlooked. In molten solvates, the activity of the free solvent is negligible, which is the main origin of their unique physicochemical properties. In the following Section 2, the effects of activity of free solvent in electrolytes on the equilibrium of electrochemical reactions and the thermal stability of the electrolytes are discussed. The activity of free solvent is negligible in the molten solvate electrolytes, and this significantly affects the thermodynamic properties of the electrolytes. In Section 3, the crystal and liquid structures of solvate electrolytes are reviewed, and the correlation between liquid structures and ion transport properties of the molten solvate electrolytes is discussed in Section 4. Finally, the application of solvate electrolytes to next generation batteries is demonstrated in Section 5. The solvent activity and the ion transport properties of the molten solvate electrolytes greatly influence the charge–discharge performance of Li/Na batteries.
2. Effects of solvent activity and solvated ion activity
2.1. Electrode potential
In case of the Li deposition/stripping reactions, the solvated Li+, [Li(solvent)n]+, reacts at the electrode, and the desolvation/solvation of Li+ occur as shown in eqn (2). The equilibrium electrode potential, E, of the electrochemical reaction is described by the Nernst eqn (3) using the activity of the species in the system.57| | [Li(solvent)n]+ + e− ⇄ Li + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent solvent | (2) |
| | 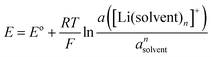 | (3) |
where E° is the standard electrode potential for eqn (2), R is the gas constant, T is the absolute temperature, F is the Faraday constant, a([Li(solvent)n]+) and asolvent are the activities of [Li(solvent)n]+ and the uncoordinated (free) solvent, respectively. Activity of an ionic species in an electrolyte solution is a measure of the effective concentration under non-ideal condition, defined as a = γ±c, where c and γ± are the concentration and the mean activity coefficient of the electrolyte salt, respectively. Conventionally, the activity of free solvent in an electrolyte solution has been assumed to be constant, i.e., asolvent = 1. This assumption is based on that the mole fraction of solvent (xsolvent) is nearly unity in a dilute electrolyte solution (a mixture of a large excess solvent and a small amount of salt), and asolvent = fxsolvent ≈ 1 where f is the activity coefficient of solvent. This is definitely valid for a dilute electrolyte containing abundant free solvent, and a linear relation between E and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cLi (where cLi is the concentration of Li salt) can be observed in the low concentration region as shown in Fig. 3. The electrode potential of Li metal is linear to log
cLi (where cLi is the concentration of Li salt) can be observed in the low concentration region as shown in Fig. 3. The electrode potential of Li metal is linear to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cLi at lower than 1 mol dm−3 (log
cLi at lower than 1 mol dm−3 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cLi = 0), however, the potential deviates from linearity and shifts significantly to a positive potential at concentrations above 1 mol dm−3.58,59 With increasing the Li salt concentration, the mole fraction of solvent xsolvent decreases, and the activity of free solvent is no longer assumed to be 1, i.e., asolvent becomes lower than 1. Actually, the mole fraction of free solvent in molten glyme solvates of Li salts was very low, which was revealed by Raman spectroscopy.59 In addition, Arai et al. measured the vapor–pressure of Li salt solutions and concluded that the activity coefficients of solvents in highly concentrated solutions were considerably lower than 1.60 Therefore, the nonlinear relationship between E and log
cLi = 0), however, the potential deviates from linearity and shifts significantly to a positive potential at concentrations above 1 mol dm−3.58,59 With increasing the Li salt concentration, the mole fraction of solvent xsolvent decreases, and the activity of free solvent is no longer assumed to be 1, i.e., asolvent becomes lower than 1. Actually, the mole fraction of free solvent in molten glyme solvates of Li salts was very low, which was revealed by Raman spectroscopy.59 In addition, Arai et al. measured the vapor–pressure of Li salt solutions and concluded that the activity coefficients of solvents in highly concentrated solutions were considerably lower than 1.60 Therefore, the nonlinear relationship between E and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cLi in the high concentration region >1 mol dm−3 (Fig. 3) is reasonably attributed to the decrease in free solvent activity. The effects of the considerably low activity of free solvent in the molten solvate electrolytes on the electrochemical reactions in batteries will be discussed later.
cLi in the high concentration region >1 mol dm−3 (Fig. 3) is reasonably attributed to the decrease in free solvent activity. The effects of the considerably low activity of free solvent in the molten solvate electrolytes on the electrochemical reactions in batteries will be discussed later.
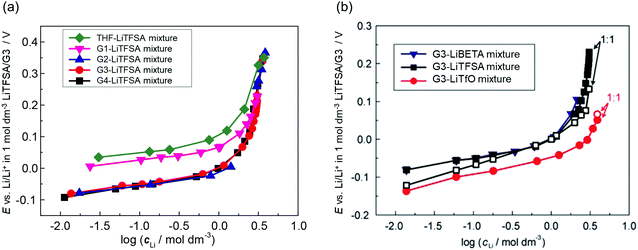 |
| | Fig. 3 Plots of the Li/Li+ electrode potential against a common logarithm of the Li salt concentration in (a) G4 (tetraglyme), G3 (triglyme), G2 (diglyme), G1 (monoglyme), and THF–LiTFSA mixtures; (b) G3–LiTfO, –LiTFSA, and –LiBETA mixtures at 30 °C. Reference electrode was Li/Li+ in 1 mol dm−3 LiTFSA/G3. (b) was reprinted with permission from ref. 59 Copyright 2015 PCCP Owner Societies. | |
2.2. Effects of solvent species
The standard electrode potential E° of the Li metal electrode (eqn (3)) can be described as follows:| | 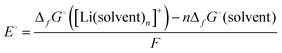 | (4) |
where ΔfG°([Li(solvent)n+]) and ΔfG°(solvent) are the standard Gibbs energies for the formation of solvated Li+ ions ([Li(solvent)n]+) and free solvent, respectively. Fig. 3a shows the order of the electrode potentials of Li metal electrode in different ether solvents at salt concentrations less than 1 mol dm−3: THF (tetrahydrofuran) > G1 (monoglyme) > G2 (diglyme) ∼ G3 (triglyme) ∼ G4 (tetraglyme). This suggests that the values of ΔfG°([Li(solvent)n+]) in the solvents serving as chelates decrease, and the bidentate ligand G1 and the multidentate ligands (G2, G3, and G4) further stabilise Li+ as compared with the monodentate THF.61 It is well known that multidentate ligands (solvents) can form more stable complex ions owing to the chelate effect.
Fig. 4 shows the electrode potentials of Li metal electrode in 1 mol dm−3 LiTFSA solutions with various solvents. Gutmann's donor number (DN) is a good metric to determine the electron donating ability or Lewis basicity of a solvent.62,63 It is defined as the molar enthalpy of the reaction with SbCl5 as the standard acceptor. The electrode potential decreases on increasing the DN of the solvent, suggesting that a solvent with a higher DN stabilises Li+ ions further decreasing the ΔfG°([Li(solvent)n+]).
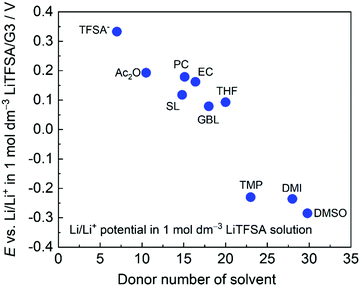 |
| | Fig. 4 Li/Li+ potential in 1 mol dm−3 LiTFSA in different solvents plotted against donor number of each solvent, measured at 30 °C. TFSA− indicates 1 mol dm−3 LiTFSA/[P13][TFSA]. [P13][TFSA]: N-Methy-N-propylpyrrolidinium bis(trifluoromethanesulfonyl)amide, Ac2O: acetic anhydride, TMP: trimethyl phosphate, and DMI: 1,3-dimethyl-2-imidazolidinone. Reference electrode: Li/Li+ in 1 mol dm−3 LiTFSA/G3. | |
2.3. Effects of anion species
Weak Lewis basic anions, such as BETA−, TFSA−, and PF6−, interact with Li+ ions weakly and dissociate easily. However, relatively strong Lewis basic anions, such as TfO− (trifluoromethanesulfonate), NO3−, and TFA− (trifluoroacetate), strongly interact with Li+ ions, forming ion pairs and ionic aggregates in the electrolytes. Because the solvent and anions competitively coordinate to the Li+ cations in the electrolyte solution, the strong Lewis basic anions remove the solvent molecules from the solvation shell of the Li+ ions (Fig. 5), resulting in an increased solvent activity even at high salt concentrations.24,64,65 Henderson et al. reported the order of Li salts association in a glyme solution: BPh4− < BETA− ∼ TFSA− ∼ SbF6− ∼ AsF6− < PF6− ∼ I− < SCN− < BF4− < TfO− < Br− < NO3− < TFA−.18 It can be observed that the Li electrode potential decreases with increasing strength of Lewis bases (TFSA− < TfO−) (Fig. 3b). Fig. 6 exhibits the Raman spectrum of [Li(G3)1][TfO], which indicates that most of the TfO− anions are coordinated to Li+ ions to form a contact ion pair (CIP) and ionic aggregates (AGG), whereas the spectrum of [Li(G3)1][TFSA] indicates that half of the TFSA− exists as free anion (or solvent-separated ion pair, SSIP) because of its relatively weak Lewis basicity.58 Raman spectroscopic studies indicate that the fraction of the free solvent molecules increases with increasing anion Lewis basicity,59 which proves that strong Lewis bases strongly coordinate to Li+. In addition, the anion coordination may further stabilise Li+ ions to form [Li(solvent)nX] (X: anion), resulting in a lower value of ΔfG°([Li(solvent)nX]) than ΔfG°([Li(solvent)n+]) and a decreased electrode potential.
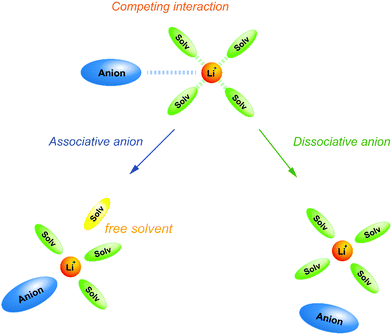 |
| | Fig. 5 Schematic illustration for the effect of Lewis basicity of anion on the solvation structure in highly concentrated electrolytes. | |
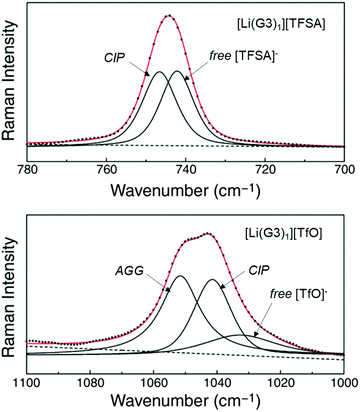 |
| | Fig. 6 Raman spectra of [Li(G3)1][TFSA] in the range 700–780 cm−1 (top, CF3 bending mode) and of [Li(G3)1][TfO] in the range 1000–1100 cm−1 (bottom, SO3 stretching mode) at 60 °C. Reprinted with permission from ref. 58 Copyright 2014 American Chemical Society. | |
2.4. Thermal stability
The decrease in the solvent activity also contributes to the thermal stability of the electrolytes. For example, Fig. 7 exhibits the thermogravimetric analysis (TGA) for electrolyte solutions of NaFSA (FSA: bis(fluorosulfonyl)amide) dissolved in sulfolane (SL).34 In case of pure SL, the weight loss starts at ∼100 °C because of evaporation. Similarly, in the solution with molar ratio of NaFSA/SL = 1/10, the weight loss starts at approximately 100 °C. Na+ ion is solvated with SL, and FSA anion is scarcely coordinated to Na+ in the NaFSA/SL = 1/10 solution. Since the coordination number of Na+ in organic solvents is generally 5–7,35,66,67 ∼50% of the SL molecules are free in the solution, and free SL can evaporate at lower temperature compared to coordinated SL. In contrast, the weight loss was not observed up to 250 °C at the molar ratio of NaFSA/SL = 1/1. The population of free SL decreases with increasing the salt concentration in the electrolyte,34 and the thermal stability can be improved.21
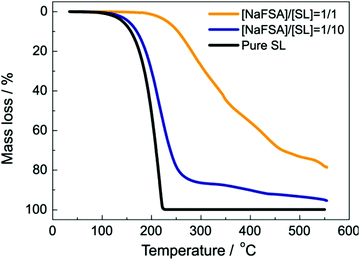 |
| | Fig. 7 Thermogravimetric curves of NaFSA/SL electrolytes at a heating rate of 10 °C min−1. Reprinted with permission from ref. 34 Copyright 2020 American Chemical Society. | |
3. Structure of solvates
3.1. Crystalline solvates
Binary mixtures of Li salts and solvents can form stable crystalline solvates in stoichiometric ratios. In the crystalline solvates, the anions and solvent molecules that enclose the Li+ ions are packed in long-range ordered crystalline lattices. Understanding the crystal structures of the solvates helps in estimating the Li+ coordination structures in the molten state. Henderson et al. investigated the structures of various crystalline solvates of Li salts.15,16,68–70 These solvates take a variety of forms such as solvent-separated ion pairs (SSIPs), contact ion pairs (CIPs), and aggregates (AGGs), where a single anion is coordinated to zero, one, and more than one Li+, respectively.
Earlier, we reported the crystal structures of sulfolane (SL) solvates of Li salts.31,39 Hereafter, the solvate composed of Li salt (LiX) and solvent with a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n is denoted as [Li(solvent)n][X]. Fig. 8a and b show the crystal structures of [Li(SL)1][BF4] and [Li(SL)2][ClO4] solvates analysed by single-crystal X-ray crystallography. The coordination number of Li+ ions is 4 or 5 in the crystals, as shown in Fig. 8. In the crystal of the [Li(SL)1][BF4] solvate, all SL molecules bridge different Li+ ions, forming a polymeric network structure. In addition, each BF4− anion coordinates to more than one Li+ ion (i.e. AGG coordination). In [Li(SL)2][ClO4] solvates, monodentate-type and bridging-type SL molecules coexist in a 1
n is denoted as [Li(solvent)n][X]. Fig. 8a and b show the crystal structures of [Li(SL)1][BF4] and [Li(SL)2][ClO4] solvates analysed by single-crystal X-ray crystallography. The coordination number of Li+ ions is 4 or 5 in the crystals, as shown in Fig. 8. In the crystal of the [Li(SL)1][BF4] solvate, all SL molecules bridge different Li+ ions, forming a polymeric network structure. In addition, each BF4− anion coordinates to more than one Li+ ion (i.e. AGG coordination). In [Li(SL)2][ClO4] solvates, monodentate-type and bridging-type SL molecules coexist in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (Fig. 8b). Each ClO4− anion coordinates to a Li+ ion in a monodentate form (i.e. CIP coordination). Furthermore, it is to be noted that the solvent-bridged structure (Li+–SL–Li+) is commonly formed in SL-based crystalline solvates. However, this unique structure is not a particular case for the solvates of cyclic SL. A similar bridging-type coordination is found in Li salt solvates of acyclic sulfones such as dimethyl sulfone.71 Similar solvent-bridged networks are also formed in crystalline solvates composed of Li salts and bridging ligands with multiple coordinating sites. In the single crystals of Li salt solvates of methyl pyruvate (MP) and methyl acetoacetate (MA), the ketone carbonyl oxygen and the ester carbonyl oxygen atoms bind to different Li+ ions forming a solvent-bridged structure (Fig. 8c).72 Crystalline solvates composed of LiFSA and dinitriles, such as succinonitrile (SN), glutaronitrile (GN), and adiponitrile (ADN), have unique mesh structures, in which all the dinitrile molecules link to different Li+ ions, whereas FSA− anions exist in the vacant sites and do not coordinate to Li+ ions (Fig. 8d).73 In addition to the Li-based systems, the crystalline solvates of Na salts have also been studied.34,35 The coordination number of Na+ in these crystalline solvates is 6, which is larger than that of Li+, because of its larger ionic radius.
1 ratio (Fig. 8b). Each ClO4− anion coordinates to a Li+ ion in a monodentate form (i.e. CIP coordination). Furthermore, it is to be noted that the solvent-bridged structure (Li+–SL–Li+) is commonly formed in SL-based crystalline solvates. However, this unique structure is not a particular case for the solvates of cyclic SL. A similar bridging-type coordination is found in Li salt solvates of acyclic sulfones such as dimethyl sulfone.71 Similar solvent-bridged networks are also formed in crystalline solvates composed of Li salts and bridging ligands with multiple coordinating sites. In the single crystals of Li salt solvates of methyl pyruvate (MP) and methyl acetoacetate (MA), the ketone carbonyl oxygen and the ester carbonyl oxygen atoms bind to different Li+ ions forming a solvent-bridged structure (Fig. 8c).72 Crystalline solvates composed of LiFSA and dinitriles, such as succinonitrile (SN), glutaronitrile (GN), and adiponitrile (ADN), have unique mesh structures, in which all the dinitrile molecules link to different Li+ ions, whereas FSA− anions exist in the vacant sites and do not coordinate to Li+ ions (Fig. 8d).73 In addition to the Li-based systems, the crystalline solvates of Na salts have also been studied.34,35 The coordination number of Na+ in these crystalline solvates is 6, which is larger than that of Li+, because of its larger ionic radius.
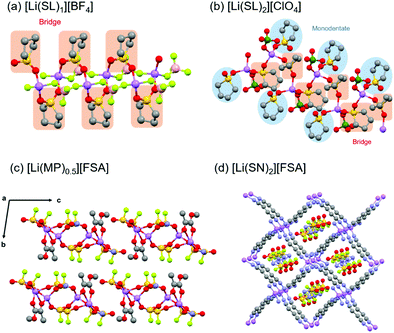 |
| | Fig. 8 Crystal structures of (a) [Li(SL)1][BF4] and (b) [Li(SL)2][ClO4] solvates. Reprinted with permission from ref. 31. Copyright 2018 American Chemical Society. (c) Crystal structure of [Li(MP)0.5][FSA]. Reprinted with permission from ref. 72. Copyright 2019 PCCP Owner Societies. (d) Crystal structure of [Li(SN)2][FSA] solvate. Hydrogen atoms are not shown. Purple, Li; red, O; grey, C; yellow, S; light green, F; pink, B; and green, Cl. | |
3.2. Liquid structure of molten solvates
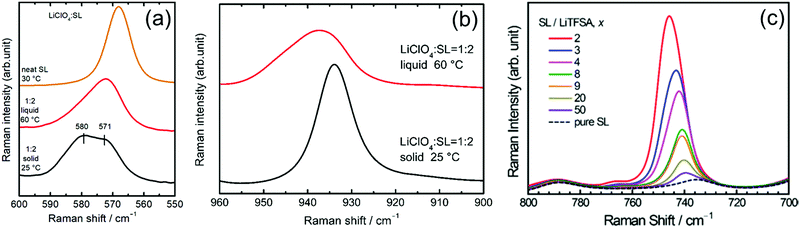
Raman spectroscopy was performed to study the coordination structures of the solvates in the molten/liquid state. The Raman spectra of the solvates in the liquid and solid states were compared. Fig. 9a shows the Raman spectra for pure SL and the solid and liquid states of [Li(SL)2][ClO4] solvate in the range 550–600 cm−1. The pure SL shows a peak at 568 cm−1 assigned to the scissoring vibration of SL;74 on complexation with Li+ ions, this peak shifts to a higher wavenumber. The solid state [Li(SL)2][ClO4] solvate exhibits two peaks centred at 571 and 580 cm−1. In the crystal structure of the [Li(SL)2][ClO4] solvate (Fig. 8b), half of the SL molecules act as monodentate ligands for the Li+ ion, and the remaining half act as bridging ligands. Therefore, the two peaks of SL at 571 and 580 cm−1 in the [Li(SL)2][ClO4] crystal can be assigned to monodentate and bridging types of SL molecules, respectively. Upon melting, the integral intensity of the lower wavenumber peak increases compared with that of the higher wavenumber peak, suggesting that a certain amount of the bridging type SL molecules changes to monodentate-type molecules with a solid-to-liquid phase transition. However, the broadened peak of the liquid state [Li(SL)2][ClO4] contains a higher wavenumber peak for the bridging type SL. This suggests that the solvent-bridged structures of Li+–SL–Li+ observed in the crystal (Fig. 8a and b) are partially maintained even in the liquid state.
 |
| | Fig. 9 Raman spectra of (a) scissoring mode of the SO2 group of SL and (b) Cl–O symmetric stretch vibration mode of ClO4− in the [Li(SL)2][ClO4] solvate. Reprinted with permission from ref. 31 Copyright 2018 American Chemical Society. (c) Raman spectra of the S–N stretching vibration mode of TFSA− anion in the LiTFSA/SL binary mixtures. Reprinted with permission from ref. 39 Copyright 2019 American Chemical Society. | |
Fig. 9b shows the Raman spectra for the Cl–O symmetric stretch vibration mode of ClO4− in the [Li(SL)2][ClO4] solvate. The crystal of [Li(SL)2][ClO4] shows a sharp Raman band at 934 cm−1, which is assigned to the CIP coordination where the ClO4− anion is coordinated to a single Li+ ion. Upon melting, the ClO4− peak shifts to a higher wavenumber, suggesting that a ClO4− anion is coordinated to multiple Li+ ions in the molten [Li(SL)2][ClO4] solvate.16 This is because the number of bridging type SL decreases with the melting of [Li(SL)2][ClO4] crystal (vide supra), and thus, ClO4− anions should be involved in the coordination of more than one Li+ ion (i.e. AGG coordination) to satisfy the preferred coordination number of Li+.
The salt concentration significantly affects the liquid structure of the electrolytes. Fig. 9c exhibits the Raman spectra in the wavenumber range 700–800 cm−1 for LiTFSA/SL binary mixtures with different solvent/Li salt molar ratios (x), corresponding to the S–N stretching vibration mode of TFSA anions.75,76 The peak in this region is sensitive to ion association and is often utilised to characterise different forms of Li+–TFSA− coordination.69,77,78 In the dilute region with x ≥ 20, the Raman bands of TFSA− appear at 740 cm−1, corresponding to SSIP in which TFSA− anions are uncoordinated.69,78 The peak gradually shifts to a higher wavenumber with decreasing x (i.e. increasing salt concentration), indicating the complexation of Li+ and TFSA− anions in the mixture. In the high salt concentration region with x < 4, the Raman peak position exceeds 744 cm−1, suggesting the formation of the CIP and AGG solvates in which the TFSA− anions are coordinated to one or more Li+ ions.69,78,79 These results indicate that when the x is lower than 4 (the preferred coordination number of Li+), anions participate in the coordination of Li+ ions to form CIPs and AGGs. Similar ion pairs and ionic aggregates are also formed in the solvent-deficient electrolyte solutions incorporating other anions and alkaline metal ions.78,80–84
4. Transport properties
4.1. Self-diffusion coefficients
The Li+ transport properties of liquid electrolytes are assumed to be one of the most significant parameters for improving the battery performance. In particular, the ionic conductivity of the electrolytes has been linked to the rapid charge and discharge ability. As we described in Section 1, the overall ionic conductivity (σion) depends on both the number of carriers and carrier mobility. Hence, the total ionic conductivity reaches a maximum value at a salt concentration of ∼1 mol dm−3 and drastically decreases upon further increase in the salt concentration to the concentrated region.31,61,72,73 The σion values of some molten solvate electrolytes at 30 °C are listed in Table 1. The molten solvate electrolytes exhibit approximately one or two orders of magnitude lower conductivity than that of a conventional organic electrolyte (1 mol dm−3 LiPF6 in EC/DMC (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt%)) due to significantly high viscosity of the molten solvate electrolytes.
50 wt%)) due to significantly high viscosity of the molten solvate electrolytes.
Table 1 Viscosity (η), ion conductivity (σion), transference numbers of Li ion evaluated by PFG – NMR method (tNMRLi) and potentiostatic polarisation method (tPPLi) for electrolytes at 30 °C
| Sample |
η/mPa s |
σ/mS cm−1 |
t
NMRLi
|
t
PPLi
|
|
Ref. 85 and 86.
Ref. 87.
Ref. 73.
Ref. 79.
|
1 mol dm−3 LiPF6 in EC/DMC (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt%)a 50 wt%)a |
3.77 |
13 |
0.41 |
0.07 |
| [Li(G1)2][TFSA]b |
33.9 |
3.7 |
0.54 |
0.35 |
| [Li(SL)2][TFSA]b |
622 |
0.42 |
0.61 |
0.68 |
| [Li(SL)2][BF4] |
743 |
0.61 |
0.61 |
0.82 |
| [Li(SN)0.8][FSA]c |
3140 |
0.26 |
0.62 |
0.74 |
| [Li(GN)1.5][TFSA]d |
1420 |
0.21 |
0.56 |
0.74 |
In addition to the ionic conductivity, the self-diffusion coefficients of Li cations (DLi), anions (Danion), and solvents (Dsol), which are obtained from pulse field gradient – nuclear magnetic resonance (PFG–NMR) spectroscopy, have been studied in liquid electrolytes.88 In the case of conventional electrolyte solutions containing ca. 1 mol dm−3 Li salt, the order of diffusion coefficients is as follows: DLi < Danion < Dsol.88 This is because Li+ ions are solvated in the solution. According to the Stokes–Einstein equation, the diffusion coefficient D is related to the viscosity (η) and the hydrodynamic radius (r) as follows: D = kBT/6πrη (for spherical particles) where kB is the Boltzmann constant. The hydrodynamic radius of solvated Li+ ion ([Li(solvent)n]+) is larger than that of anion and free solvent, and Li+ ion mainly diffuses in the form of solvated cation.
The diffusivity ratio of the solvent and Li (Dsol/DLi) is a particularly useful metric to evaluate the extent to which the self-diffusion of Li+ ion is decoupled from that of the solvent. Fig. 10a exhibits the plot of Dsol/DLiversus the Li salt concentration for ether-,61 sulfone-,31 keto ester-,72 and nitrile-73 based molten Li salt solvates. The electrolytes with concentrations below 3 mol dm−3 show Dsol/DLi > 1 indicating that, on average, Li ions diffuse slower than the solvent molecules, similar to the conventional liquid electrolytes with ∼1 mol dm−3 salt concentration (vide supra). By contrast, at concentrations above 3 mol dm−3, Dsol/DLi and Danion/DLi (Fig. 10b) are below unity, indicating that Li ions diffuse most rapidly among the components, except for the ether-based molten Li salt solvates. The main reason for the fastest diffusion of Li ions among the components at high concentrations >3 mol dm−3 can likely be attributed to the Li ion hopping/exchange mechanism (Fig. 11) through the unique Li ion coordination structures mentioned in the previous section. For instance, in [Li(SL)2][BF4], Li ions form ion aggregates such as [Li+x(SL)y[BF4]−z](x−z) and/or a solvent-bridged structure (–Li+–SL–Li+–SL–) in the liquid states.31 The keto ester- and nitrile-based molten Li salt solvates also have similar solvent-shared, polymeric Li ion coordination structures.72,73,79 A single SN molecule has two different coordination sites to which two different Li ions can coordinate resulting in the formation of solvent-bridged network structures (Li+–SN–Li+). In these cases, solvents and anions serve as a framework for Li-ion conduction paths, which regulate the diffusion of the solvent and anions. Therefore, Li ions are considered to be carried through percolating ion aggregates and solvent-bridged structures via unique Li ion hopping/exchange mechanism.
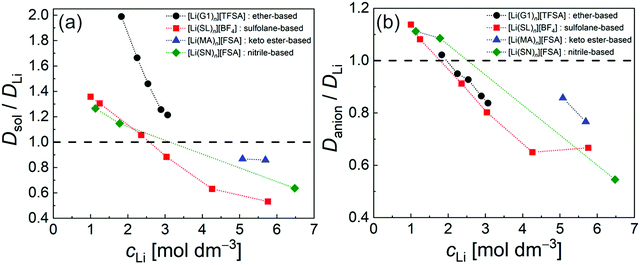 |
| | Fig. 10 Diffusivity ratio (a) Dsol/DLi and (b) Danion/DLi of ether-, sulfolane-, keto ester-, and nitrile-based electrolytes at 30 °C. ([Li(G1)n][TFSA]: n = 1.8, 2, 2.5, 3, and 4; [Li(SL)n][BF4]: n = 1.35, 2, 3, 4, 8, and 10; [Li(MA)n][FSA]: n = 0.8 and 1; and [Li(SN)n][FSA]: n = 0.8, 6 and 10). Data were collected from ref. 31, 61, 72 and 73 and replotted. | |
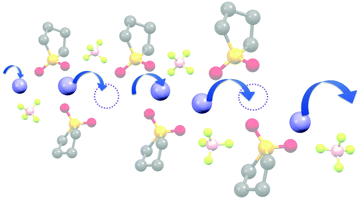 |
| | Fig. 11 Schematic image of the Li ion hopping/exchange conduction of molten SL solvates of Li salts. Reprinted with permission from ref. 31 Copyright 2018 American Chemical Society. | |
In the case of ether-based molten solvate [Li(G1)2][TFSA], G1 molecules are assumed to coordinate to Li ions in a bidentate manner along with the formation of AGGs and/or CIPs between Li+–[TFSA]−.17 However, Li ions solvated with G1 molecules exhibit relatively low stabilisation energy,89 which enables Li ions to exchange the G1 ligand with other solvated Li ions and/or to leave the ligand as “free” G1. Therefore, G1 molecules diffuse more rapidly than Li ions (resulting in Dsol/DLi > 1) even at high concentrations.
4.2. Transference number
In addition to ionic conductivity, the Li+ transference number has been considered as another significant parameter of electrolytes affecting the battery performance.90–92 Various methods have been proposed for the estimation of the transference number: electrophoretic NMR,93 PFG–NMR,24,88 Hittorf method,94 potentiostatic polarisation method95,96 and very-low-frequency electrochemical impedance spectroscopy (EIS).85 PFG–NMR method (tNMRLi), based on the Nernst–Einstein equation, has been extensively studied for Li ion conducting liquid electrolytestNMRLi. tNMRLi is evaluated as the ratio of the self-diffusion coefficients of ion species: tNMRLi = DLi/(DLi + Danion). However, tNMRLi does not reflect the true Li+ transference number for highly concentrated electrolytes with strong ion interactions and correlations because this method is based on ideal electrolyte solutions where ions are completely dissociated and move independently.
An electrochemical method using a Li metal symmetric cell has often been applied to estimate the transference number. This transference number (tPPLi) is obtained by combining the potentiostatic polarisation with EIS and is defined as follows:95,96
| | 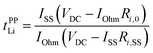 | (5) |
where
VDC is the constant applied voltage,
IOhm (=
VDC/(
Rbulk +
Ri,0)),
ISS are the initial and stationary state currents, and
Ri,0 and
Ri,SS are the initial and stationary state interfacial resistance values, respectively.
97 The
tPPLi shows the true transference number only when there are no ionic interactions in the electrolytes (
i.e. ideal electrolyte). Balsara
et al. suggested that
tPPLi simply shows the “current fraction” carried by Li ions in non-ideal electrolytes.
97 However,
tPPLi can be measured easily and is used to examine the actual Li-ion transport properties in electrochemical cells, such as Li-ion batteries, which include both migration and diffusion effects (under anion-blocking conditions). A high
tPPLi suggests that the concentration polarisation of electrolytes can be alleviated in the electrochemical cells.
The two experimental Li transference numbers (tNMRLi and tPPLi) of ether-, sulfolane-, and nitrile-based molten Li salt solvates are shown in Table 1. The values of those numbers for conventional organic electrolyte, 1 mol dm−3 LiPF6 in EC/DMC, are reported as 0.41 for tNMRLi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 86 and 0.07 for tPPLi.85 Apparently, the molten Li salt solvates are prone to exhibiting higher values compared with that of conventional organic electrolytes. The tPPLi values of the SL- and nitrile-based molten Li salt solvates with unique Li ion diffusion behaviour are much higher than those of the ether-based [Li(G1)2][TFSA]. It has been suggested that the solvent-bridged Li ion coordination structure exerts a strong impact on the enhancement of tPPLi and tNMRLi values. The SL- and GBL-based molten Na salt solvates also exhibit high tPPNa values of 0.81 for [Na(SL)1][FSA]34 and 0.84 for [Na(GBL)1][FSA].35 The two molten Na salt solvates have ligand-bridged structures (Na+–(solvent or FSA)–Na+) resembling the solvent-bridged structure confirmed in the molten Li salt solvates, which enables the dynamic ligand-exchange conduction of Na+. All these molten solvates maintain a unique solvent-bridged structure consisting of solvent and anions concurrently with the formation of CIPs and/or AGGs therein. Therefore, the motion of smaller Li (or Na) ions via dynamic ligand-exchange conduction is not relatively regulated compared with those of the solvent molecules and anions in the ion coordination, which results in the improvement of tPPLi (or tPPNa).
86 and 0.07 for tPPLi.85 Apparently, the molten Li salt solvates are prone to exhibiting higher values compared with that of conventional organic electrolytes. The tPPLi values of the SL- and nitrile-based molten Li salt solvates with unique Li ion diffusion behaviour are much higher than those of the ether-based [Li(G1)2][TFSA]. It has been suggested that the solvent-bridged Li ion coordination structure exerts a strong impact on the enhancement of tPPLi and tNMRLi values. The SL- and GBL-based molten Na salt solvates also exhibit high tPPNa values of 0.81 for [Na(SL)1][FSA]34 and 0.84 for [Na(GBL)1][FSA].35 The two molten Na salt solvates have ligand-bridged structures (Na+–(solvent or FSA)–Na+) resembling the solvent-bridged structure confirmed in the molten Li salt solvates, which enables the dynamic ligand-exchange conduction of Na+. All these molten solvates maintain a unique solvent-bridged structure consisting of solvent and anions concurrently with the formation of CIPs and/or AGGs therein. Therefore, the motion of smaller Li (or Na) ions via dynamic ligand-exchange conduction is not relatively regulated compared with those of the solvent molecules and anions in the ion coordination, which results in the improvement of tPPLi (or tPPNa).
The relationship between the Li ion-anion interactions and the tPPLi values for SL-based electrolytes was also studied. As shown in Table 1, [Li(SL)2][BF4] has a larger tPPLi value (0.82) than [Li(SL)2][TFSA] (0.68). [Li(SL)3][ClO4] shows a similar tPPLi value (0.65) to that of [Li(SL)2][TFSA]. The apparent dissociation degree of LiBF4 is known to be smaller than that of LiTFSA and LiClO4 in organic solvents.18 Therefore, AGGs are more prominent in [Li(SL)2][BF4] than in [Li(SL)2][TFSA] and [Li(SL)3][ClO4]. Similarly, it was found that tPPLi increases with more associative anions in glyme-based molten Li salt solvates.98 The stronger Li ion-anion interaction forming more-pronounced AGG networks in [Li(SL)2][BF4] will positively contribute to the enhancement of tPPLi in addition to the solvent-bridged structures.
4.3. Dynamic ion correlations
The Li-ion transport in the concentrated electrolytes has been studied in more detail in the light of the dynamic ion correlations. Woolf and Harris systematically evaluated the dynamic ion correlations in aqueous electrolyte solutions by introducing velocity cross-correlation functions.99,100 Regarding solid polymer electrolytes, Balsara and Newman introduced Stefan–Maxwell diffusion coefficients.97,101,102 For non-aqueous liquid electrolyte solutions, Roling and Bedrov's groups investigated the dynamic ion correlations based on Onsager's linear irreversible thermodynamics and evaluated the Onsager transport coefficients for the glyme-based molten solvates of LiTFSA.85,103
In the Onsager transport formalism, the ionic conductivity σion is written as follows:
| | | σion = σ++ + σ−− − 2σ+− | (6) |
where
σ++,
σ−−, and
σ+− are the Onsager transport coefficients. The Onsager coefficients
σ++ and
σ−− can be divided into self-terms and distinct terms, and
eqn (6) can then be written as follows:
| | | σion = σself+ + σdistinct++ + σself− + σdistinct−− − 2σ+− | (7) |
The self-terms, σself+ and σself−, are related to the self-diffusion coefficients of cation and anion, respectively, via the Nernst–Einstein equation. The distinct terms, σdistinct++, σdistinct−−, and σ+−, represent the dynamic cation–cation, anion–anion, and cation–anion ion correlations, respectively. The signs on these distinct terms indicate the dynamic ion motions; the correlated ion motion occurs when it is positive, whereas the anti-correlated motion is dominant when the sign is negative. The non-correlated ion motions expected in ideal electrolyte solutions are represented by the zero values of these coefficients. Based on eqn (7), the correlated motion of ions with the same sign positively contributes to the overall ionic conductivity, whereas that of the cation–anion correlation (σ+−) contributes negatively.
We evaluated the Onsager coefficients for molten Li salt solvates to elucidate the ion correlations.87,98 The values of σself+ and σself− were calculated from the self-diffusion coefficients of ions. The values of σ++, σ−−, and σ+− were estimated from the experimentally obtained quantities: ionic conductivity, transference number (tPPLi), salt diffusion coefficients, and the slope of the concentration dependence of the concentration cell potentials. The normalised Onsager transport coefficients for the molten solvate electrolytes are shown in Fig. 12.
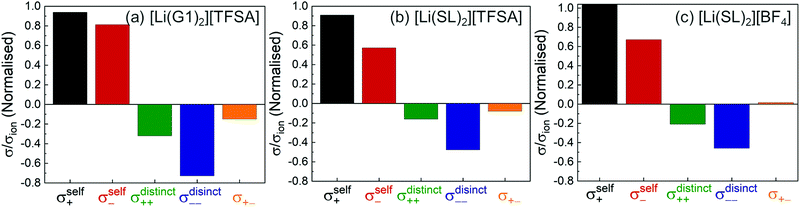 |
| | Fig. 12 Normalised Onsager transport coefficients (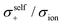 , , 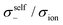 , , 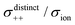 , , 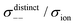 , and , and 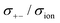 :left to right) of (a) [Li(G1)2][TFSA], (b) [Li(SL)2][TFSA], and (c) [Li(SL)2][BF4]. The graphs (a) and (b) are reprinted with permission from ref. 87. Copyright 2020 PCCP Owner Societies. :left to right) of (a) [Li(G1)2][TFSA], (b) [Li(SL)2][TFSA], and (c) [Li(SL)2][BF4]. The graphs (a) and (b) are reprinted with permission from ref. 87. Copyright 2020 PCCP Owner Societies. | |
As shown in Fig. 12a, the ether-based Li salt molten solvate, [Li(G1)2][TFSA], shows negative values for all cross-correlation coefficients (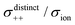 ,
, 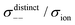 , and
, and 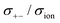 ), suggesting that the ion motions are anti-correlated. Interestingly, in [Li(SL)2][TFSA] and [Li(SL)2][BF4], the dynamic cation − cation (
), suggesting that the ion motions are anti-correlated. Interestingly, in [Li(SL)2][TFSA] and [Li(SL)2][BF4], the dynamic cation − cation (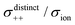 ) cross-correlations are less anti-correlated and the dynamic cation – anion (
) cross-correlations are less anti-correlated and the dynamic cation – anion (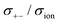 ) cross-correlations are nearly non-correlated (Fig. 12b and c) even at almost the same salt concentration as that of [Li(G1)2][TFSA]. It is likely that Li ion hopping/exchange conduction is reflected by the nearly non-correlated ion motions, which further contributes to the higher tPPLi for the SL-based electrolytes. The σ+−/σion exhibits a slightly negative value for [Li(SL)2][TFSA]; however, it shifts to nearly zero for [Li(SL)2][BF4]. This supports the more pronounced association of LiBF4 than that of LiTFSA in the SL-based molten solvates. Therefore, the developed AGG networks31 accompanied by the bridged structure are responsible for the considerably high tPPLi in [Li(SL)2][BF4].
) cross-correlations are nearly non-correlated (Fig. 12b and c) even at almost the same salt concentration as that of [Li(G1)2][TFSA]. It is likely that Li ion hopping/exchange conduction is reflected by the nearly non-correlated ion motions, which further contributes to the higher tPPLi for the SL-based electrolytes. The σ+−/σion exhibits a slightly negative value for [Li(SL)2][TFSA]; however, it shifts to nearly zero for [Li(SL)2][BF4]. This supports the more pronounced association of LiBF4 than that of LiTFSA in the SL-based molten solvates. Therefore, the developed AGG networks31 accompanied by the bridged structure are responsible for the considerably high tPPLi in [Li(SL)2][BF4].
Considering the aforementioned results, unique SL-bridged structures and continuous Li+ ordering structures in AGG offset the anti-correlations of cation–cation and cation–anion motions, resulting in the large contribution of Li ions to the overall ionic conductivity.
5. Electrochemistry
5.1. Li metal electrode
Highly concentrated electrolytes have various advantages in battery applications. These advantages are attributed to the peculiar liquid structures of the highly concentrated electrolytes. Here, we show how the activities of the solvated metal ions and free solvent molecules in the electrolyte affect the electrochemical properties of Li- and Na-based batteries. Li metal is an attractive anode material for high energy density rechargeable batteries, and extensive efforts have been devoted to developing Li metal batteries (LMBs). However, the practical application of Li metal anode is hindered by the unfavourable dendritic Li growth during repeated charge/discharge processes and the low Coulombic efficiency due to the side reactions of the electrolytes with Li metal.40,43–45,47,48 One of the effective approaches to address these issues is to develop the electrolyte that forms a stable and uniform solid–electrolyte interphase (SEI) on the Li metal surface.41,42,46,49,50 Aprotic electrolytes reductively decompose on the Li metal, and the decomposition products form an SEI layer on the Li metal electrode. SEI layer is considered to be an electronic insulator but a Li-ion conductor, and SEI can suppress the subsequent decomposition of electrolytes and enables the electrochemical Li metal deposition/dissolution. The stability of SEI layer gives the significant effects on the Coulombic efficiency of Li deposition/dissolution, and the distribution of SEI on Li metal affects the morphology of the deposited Li metal. The composition and properties of SEI are strongly affected by the electrolyte formulation such as solvents, anions, and salt concentration. Several research groups reported that highly concentrated LiFSA-based electrolytes are effective in suppressing the dendritic Li metal deposition and the reductive decomposition of the electrolyte at the Li metal electrode, resulting in the highly reversible Li metal deposition/dissolution. For example, Qian et al. reported that a Li/Cu cell with 4 mol dm−3 LiFSA/G1 electrolyte can be cycled for more than 1000 cycles without the dendrite growth of Li metal (Fig. 13) and a high average Coulombic efficiency of 98.4%.52 This excellent cycling performance of Li metal electrode can be attributed to the improved electrolyte reductive stability due to reduced availability of reactive solvent and the formation of FSA-derived SEI layer. In the highly concentrated electrolytes, most of the anions form complexes with Li+ ions due to the deficiency of solvent (vide supra). According to the computational studies reported by Yamada et al., the complexation of the anion with Li+ ion in the highly concentrated electrolytes leads to the lowering of the lowest unoccupied molecular orbital (LUMO) energy level of anion, and the FSA− anion reductively decomposes prior to the decomposition of the solvent.104,105 The decomposition products of the FSA− anion form the effective SEI layer mainly composed of inorganic species such as LiF on the Li metal surface, which may induce uniform Li deposition and effectively suppress the reductive decomposition of the electrolyte.33,53,56,106–108
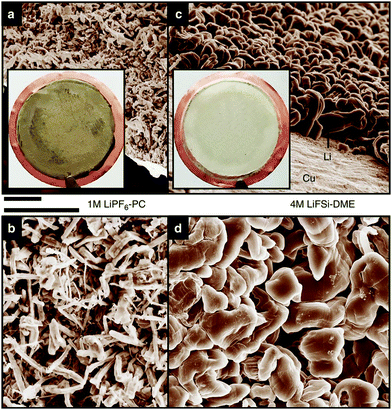 |
| | Fig. 13 Scanning electron microscope images of the morphologies of Li metal after plating on Cu substrates in different electrolytes. (a and b) 1 mol dm−3 LiPF6/PC. (c and d) 4 mol dm−3 LiFSA/DME (G1). The current density was 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mA mA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−2 and the deposition time was 1.5 cm−2 and the deposition time was 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h. The diameter of the Cu substrate shown in the inset of (a and c) was 2 h. The diameter of the Cu substrate shown in the inset of (a and c) was 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm. Scale bar, 10 cm. Scale bar, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μm. Reprinted with permission from ref. 52 Copyright 2015 Nature Publishing Group. μm. Reprinted with permission from ref. 52 Copyright 2015 Nature Publishing Group. | |
5.2. Li+ intercalation into graphite electrode
Electrochemical Li+ intercalation into graphite has been exploited as a negative electrode reaction in LIBs. Ethylene carbonate (EC) is known to be an essential electrolyte solvent because its reductive decomposition products form an effective passivation film on the graphite surface and suppress the further reductive decomposition of the electrolyte and co-intercalation of solvent into the interlayer of graphite during the Li+ intercalation process.109–111 However, several groups reported that the co-intercalation of the solvent can be suppressed and reversible Li+ intercalation into graphite electrode can occur in highly concentrated electrolytes without EC.4,104,112–115 We reported the effect of salt-concentration on the electrochemical reaction of the graphite electrode in LiTFSA/G3 mixtures.58 In electrolytes containing excess G3 (n > 1 in [Li(G3)n][TFSA]), irreversible co-intercalation of G3 and Li+, i.e. intercalation of solvated Li+ ([Li(G3)1]+), takes place. By contrast, a reversible Li+ intercalation reaction (desolvation of Li+) is observed in the molten [Li(G3)1][TFSA] complex. The electrode potential of the Li+ intercalation reaction changes significantly depending on not only the solvate [Li(G3)1]+ cation activity but also the free G3 activity in the electrolyte because of the desolvation of Li+ at the interface during Li+ intercalation, as well as in the case of Li metal deposition (eqn (3)). By contrast, the electrode potential for the intercalation of [Li(G3)1]+ depends solely on the activity of [Li(G3)1]+, irrespective of the free G3 activity. In the molten [Li(G3)1][TFSA] complex, the activity of free G3 is negligible, and the electrode potential of Li+ intercalation is anticipated to increase because of the significantly low activity of G3 and the high activity of [Li(G3)1]+. The increase in the chemical potential of [Li(G3)1]+, i.e. destabilisation of solvated Li+, may induce the desolvation of Li+ at the interface between the graphite electrode and the molten complex. In addition to the electrode potential shift, the SEI formed on the graphite electrode is also an important factor. Yamada et al. reported that the SEI derived from anions is formed on the graphite electrode and kinetically suppresses the solvent co-intercalation in highly concentrated LiTFSA solutions.104,105 Thus, both thermodynamic and kinetic effects may contribute to the reversible Li+ intercalation into a graphite electrode in highly concentrated electrolytes.
The anion species in highly concentrated electrolytes significantly influences the kinetics of the Li+ interaction reaction of graphite. Fig. 14 exhibits the charging (lithiation) curves of the graphite electrodes measured at various current densities in the SL-based electrolytes. On increasing the current density, the charging capacity of the graphite electrode decreases because the overvoltage for charging increases with the current density, and the voltage of the Li/graphite cell reaches the cut-off voltage (0 V) prior to achieving the full capacity of the graphite. As shown in Fig. 14, the rate capability of the cell greatly depends on the anionic species in the electrolyte. EIS was performed to investigate the kinetics of the electrochemical reactions in the Li/graphite cells. Fig. 15a shows the Nyquist plots for the cells acquired at a 67% state of charge (cell voltage ∼75 mV). A depressed semicircle is observed for each cell in the high-frequency region; the diameter of this semicircle is assigned to the interfacial resistance (Rint) of the electrochemical reactions in a cell. As shown in Fig. 15b, the interfacial resistance of the Li electrode in each electrolyte is smaller than that of the Li/graphite cell with each electrolyte. Therefore, the difference in Rint value of the Li/graphite cells with different electrolytes is mainly ascribed to the difference in the resistance of the graphite/electrolyte interface. The Rint value of the Li/graphite cell with [Li(SL)3][FSA] electrolyte is considerably smaller than that of ones with [Li(SL)2][BF4] and [Li(SL)2][TFSA] electrolytes, leading to the high rate capability of the cell with [Li(SL)3][FSA] (Fig. 14). The anion species in highly concentrated electrolytes may affect the composition and resistance of the SEI on the graphite electrode. Further investigations may be needed to fully understand the interfacial kinetics of Li+ intercalation at the graphite/highly concentrated electrolyte interface.
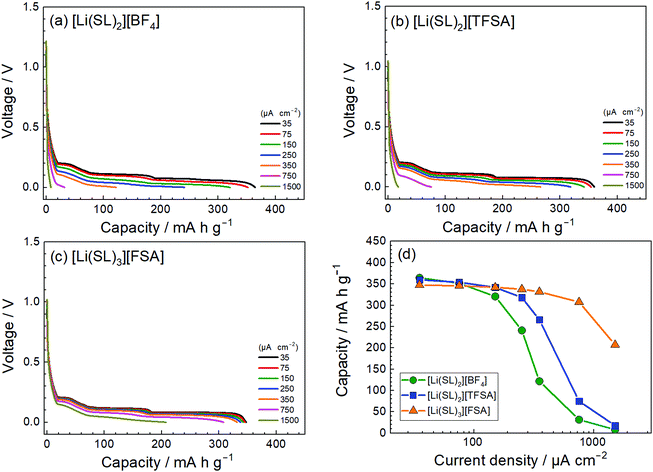 |
| | Fig. 14 Charge curves for the Li/graphite cells containing electrolytes of (a) [Li(SL)2][BF4], (b) [Li(SL)2][TFSA], and (c) [Li(SL)3][FSA] at various current densities at 30 °C. (d) Charge capacities of the cells as functions of current density. Following each charge measurement, the cell was fully discharged at the low current density of 35 μA cm−2. | |
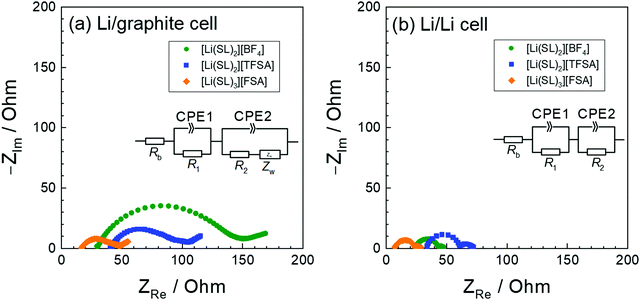 |
| | Fig. 15 Nyquist plots of (a) Li/graphite cells at a 67% state of charge in the 3rd cycle and (b) Li/Li symmetric cells containing electrolytes of [Li(SL)2][BF4], [Li(SL)2][TFSA], and [Li(SL)3][FSA] at 30 °C. The geometrical areas of the Li-metal and graphite electrodes were both 2.0 cm2. | |
5.3. Oxidative stability
Side reactions on the positive electrode side of LIBs can also be prevented by reducing the solvent activity in the electrolyte. Ethers have not been utilised as electrolyte solvents for 4 V class lithium batteries because they are oxidised at around 4 V vs. Li/Li+.116 However, 4 V class lithium batteries with glyme-LiTFSA molten solvates can be charged and discharged reversibly despite the use of ether-based electrolytes. The oxidative stability is enhanced by decreasing the activity of free glyme.20 Furthermore, according to ab initio molecular orbital calculations, the highest occupied molecular orbital (HOMO) energy level of the solvent is lowered by complexation with Li+ ions, leading to an enhanced oxidative stability. This should also be true for solvate electrolytes other than glyme solvates. The oxidative stability enhancement of the electrolytes is useful in suppressing the irreversible decomposition of the electrolytes on the positive electrode surface in LIBs, and may be instrumental in achieving the highly efficient charge–discharge and the long cycle performance of a high voltage LIB.117
5.4. Suppression of corrosion of Al current collectors
It is known that the corrosion of Al current collectors occurs at electrode potentials higher than 4 V vs. Li/Li+ in the electrolyte containing amide-type anions;118–120 therefore, the amide-based Li salts are not utilised as the main electrolyte salts in LIBs. However, Al corrosion can be suppressed by decreasing the solvent activity.77,121–123 In LiTFSA-based dilute electrolyte solutions, a large amount of the free solvent easily dissolves the Al–TFSA complexes produced by corrosion at the Al/electrolyte interface, resulting in severe Al corrosion.124,125 By contrast, in highly concentrated electrolytes, the scarcity of the free solvent leads to the extremely low solubility of the Al–TFSA complexes, and they act as a passivation layer on the Al surface.
5.5. Oxygen reduction reaction
The proportion of free solvent molecules in the electrolyte solution influences the oxygen reduction reaction (ORR) in Li–O2 batteries. The ORR in Li–O2 batteries utilising nonaqueous electrolyte solutions is known to proceed via one-electron reduction of O2 to produce soluble lithium superoxide (LiO2). Subsequently, LiO2 is electrochemically reduced and/or the chemical disproportionation reaction of LiO2 proceeds to produce solid lithium peroxide (Li2O2), as follows:126,127| | 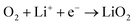 | (8) |
| | 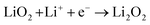 | (9) |
| | 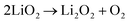 | (10) |
The parasitic reactions of the highly reactive LiO2 with the electrolyte components and/or carbon electrode hinder the long-term operation of Li–O2 batteries.128–131 In our previous study, we investigated the effects of the Li salt concentration on the reversibility of the ORR in LiTFSA/dimethyl sulfoxide (DMSO) solutions.38 The ORR in 1 and 3 mol dm−3 LiTFSA/DMSO solutions was assessed by rotating ring-disk electrode (RRDE) measurements (Fig. 16). In each electrolyte, the current for the ORR was observed during the cathodic scan of the disk electrode, and the current for the oxygen evolution reaction (OER) appeared during the anodic scan. The reversibility of OER/ORR is improved by increasing the LiTFSA concentration in the electrolyte. The Coulombic efficiencies for OER/ORR at the disk electrode are 32% and 58% in the 1 and 3 mol dm−3 LiTFSA/DMSO solutions, respectively. The difference in the Coulombic efficiencies was mainly due to the difference in the LiO2 solubility in the solution. In the 1 mol dm−3 solution, the anodic current was detected at the ring electrode, where the potential of the ring electrode was set at 3.3 V vs. Li, indicating that the LiO2 (generated at the disk electrode) partially dissolved into the solution and was oxidised at the ring electrode. By contrast, the ring current was negligible for the 3 mol dm−3 solution, suggesting that LiO2 hardly dissolves in the highly concentrated solution. Raman spectroscopy revealed that the fraction of DMSO bound to Li+ and free DMSO increases and decreases, respectively, with increasing LiTFSA concentration as shown in Fig. 17.38 Free DMSO was found to be 8.7% in the 2.3 mol dm−3 solution (Li[TFSA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO = 1
DMSO = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4), and only trace amounts of free DMSO were present in the high concentration LiTFSA/DMSO solutions above 2.3 mol dm−3. It is considered that LiO2 cannot be solvated in a highly concentrated electrolyte because of the absence of free solvent, resulting in very low solubility of LiO2. Therefore, LiO2 is converted to Li2O2 mainly on the disk electrode surface, resulting in an improved reversibility of the OER/ORR at the disk electrode.
4), and only trace amounts of free DMSO were present in the high concentration LiTFSA/DMSO solutions above 2.3 mol dm−3. It is considered that LiO2 cannot be solvated in a highly concentrated electrolyte because of the absence of free solvent, resulting in very low solubility of LiO2. Therefore, LiO2 is converted to Li2O2 mainly on the disk electrode surface, resulting in an improved reversibility of the OER/ORR at the disk electrode.
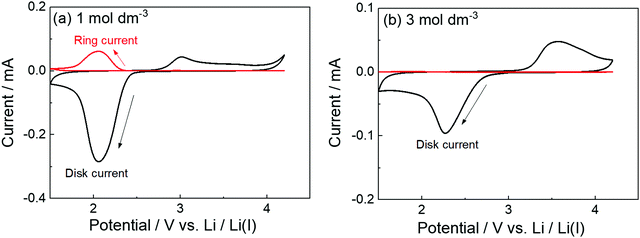 |
| | Fig. 16 RRDE responses on glassy carbon (GC) disk/GC ring electrode measured at 1000 rpm at 100 mV s−1 in O2 saturated (a) 1 mol dm−3 and (b) 3 mol dm−3 LiTFSA/DMSO at 30 °C. Reference electrode: Li metal in 1 mol dm−3 LiTFSA/G3. The potential of the GC disk electrode was swept from the open circuit potential (OCP) of ca. 3 V vs. Li/Li+ to the negative direction, and the sweep direction was reversed at 1.5 V vs. Li/Li+. The potential of the GC ring electrode was set at 3.3 V vs. Li/Li+. Reprinted and partially modified with permission from ref. 38. Copyright 2017 American Chemical Society. | |
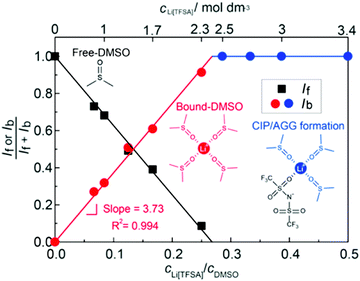 |
| | Fig. 17 Fraction of the integrated intensities of Raman peaks corresponding to free DMSO, If/(If + Ib) and bound DMSO, Ib/(If + Ib) in the Li[TFSA]/DMSO solutions. Reprinted with permission from ref. 38 Copyright 2017 American Chemical Society. | |
5.6. Li–S batteries
Elimination of the free solvent in the electrolyte solution is an effective strategy for highly reversible lithium–sulphur (Li–S) batteries. Li–S batteries have attracted considerable attention for their high theoretical energy density because of the high theoretical capacities of the S cathode (1672 mA h g−1) and Li metal anode (3860 mA h g−1) compared with the typical electrodes used in conventional LIBs such as LiNi1/3Mn1/3Co1/3O2 cathode (160 mA h g−1) and graphite anode (372 mA h g−1).126,132 One of the obstacles hindering the practical use of Li–S batteries is the dissolution of lithium polysulfides (LPS), which are the reaction intermediates of the S cathode. The dissolution of LPS causes a low Coulombic efficiency of discharge/charge and a loss of the active materials from the positive electrode.133–135 To solve these issues, for the first time, we proposed the glyme–Li salt molten complexes as sparingly solvating electrolytes for Li–S batteries.22 The solubility of LPS in molten complex electrolytes is very low, owing to the lack of free solvent molecules having high solute solvating abilities. Thus, the Li–S cells can be charged and discharged for more than 400 cycles with high Coulombic efficiencies of over 98%.
Highly concentrated SL-based electrolytes also function as sparingly solvating electrolytes in Li–S cells. SL-based electrolytes possessing high Li+ ion transference number via Li+ ion hopping conduction enabled a higher rate performance of the Li–S cell.39Fig. 18 exhibits the charge and discharge performances of Li–S cells with molten solvate electrolytes [Li(SL)2][TFSA] and [Li(G4)1][TFSA]. Both cells show high Coulombic efficiencies (>98%) owing to the limited solubility of LPS in the electrolytes. Interestingly, the cell with the SL-based solvate exhibited a higher rate capability than one with the G4-based solvate, regardless of the lower ionic conductivity of the former electrolyte (SL: 0.42 mS cm−1vs. G4: 1.6 mS cm−1). The difference in the rate capability can be attributed to the difference in the Li+ transference number (tPPLi) of the electrolytes. The tPPLi of the SL-based molten solvate is 0.68, which is much higher than that of the glyme-based solvate (tPPLi = 0.028).87 The higher tPPLi decelerates the growth of the Li salt concentration gradient in the vicinity of the sulphur cathode during the high-rate discharge, which mitigates the concentration polarisation, leading to a higher rate of capability of the cell.
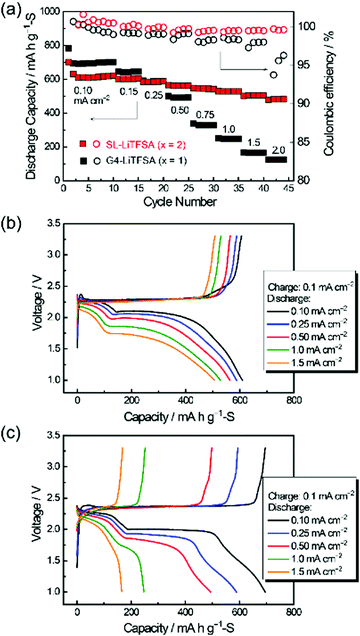 |
| | Fig. 18 (a) Discharge capacity and Coulombic efficiency at different discharge current densities, and charge and discharge curves of the cells using the concentrated electrolytes, (b) [Li(SL)2][TFSA] and (c) [Li(G4)1][TFSA]. Reprinted with permission from ref. 39 Copyright 2019 American Chemical Society. | |
6. Summary and outlook
In this article, the structures, physicochemical properties, and transport properties of molten solvate electrolytes were reviewed. In molten solvate, the activity of the free solvent is negligible. This is one of the main causes for the peculiar features of molten solvates, such as high thermal stability, wide electrochemical window, and unique ion transport. The liquid structures of the molten solvates significantly affect the transport properties. In molten solvates, the solvated cations and anions are adjacent to each other, resulting in hopping/ligand exchange conduction of alkali metal ions in certain molten solvate electrolytes. The Li ion hopping/ligand exchange conduction increases the transference number of Li ions in the electrolyte, and this is effective in enhancing the rate capability of lithium batteries. The solvent activity influences the electrochemical reaction processes in the electrolyte. The electrode potential changes significantly depending on the solvent activity. The solubility of the electrochemically generated products decreases with decreasing solvent activity in the electrolyte. This is effective in suppressing the corrosion of the Al current collector, achieving the high reversibility of the ORR/OER, and increasing the Coulombic efficiency of charge/discharge of a Li–S cell. In solvent-deficient Li salt solutions, the complex formation of Li+ and anions is induced, which affects the formation of SEI layers on Li metal and graphite electrodes. Electrochemistry in the molten solvates of Na salts are also significantly influenced by the solvent activity and anion species.34,35,136,137 The concept of solvate electrolytes can be expanded further; for example, the molten solvates of K, Mg, Ca, and Zn salts may be preparable and useful as battery electrolytes.
The drawbacks of molten solvate electrolytes are their high viscosity and relatively low ionic conductivity compared with that of the conventional electrolytes. The strong interactions of the cation with the solvent and anion cause the high viscosity and low mobility of the ions. The low viscosity and highly conductive molten solvates are favourable for use as battery electrolytes. To achieve this, the selection and design of solvents and anions are crucial. In addition, understanding the dynamics of ion conduction and interfacial charge transfer reactions is important for the development of new solvate electrolytes. For instance, the rotational motions and conformational changes of the solvent and anions may affect the ion conduction and electrochemical reaction mechanisms in the molten solvate electrolytes. Further experimental and computational studies on the dynamics are required to provide useful insights.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This study was partially supported by JSPS KAKENHI (Grant No. 18H03926, 19H05813, 20J20165, and 21H04697) from the Japan Society for the Promotion of Science (JSPS), ALCA-SPRING (Grant No. JPMJAL1301) from the Japan Science and Technology Agency (JST), and the Element Strategy Initiative of MEXT (Grant No. JPMXP0112101003) from the Ministry of Education, Culture, Sports, Science, and Technology, Japan. The authors thank Mr. Shohei Sasagawa (Yokohama National University) for performing the electrochemical measurements of the graphite electrodes.
References
- K. Xu, Chem. Rev., 2004, 104, 4303–4418 CrossRef CAS PubMed.
- D. Brouillette, G. Perron and J. E. Desnoyers, J. Solution Chem., 1998, 27, 151–182 CrossRef CAS.
-
K. Izutsu, Electrochemistry in Nonaqueous Solutions, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2nd edn, 2009 Search PubMed.
- S.-K. Jeong, M. Inaba, Y. Iriyama, T. Abe and Z. Ogumi, J. Power Sources, 2008, 175, 540–546 CrossRef CAS.
- Y. Yamada and A. Yamada, J. Electrochem. Soc., 2015, 162, A2406–A2423 CrossRef CAS.
- M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239 CrossRef CAS PubMed.
- Y. Yamada, J. Wang, S. Ko, E. Watanabe and A. Yamada, Nat. Energy, 2019, 4, 269–280 CrossRef CAS.
- O. Borodin, J. Self, K. A. Persson, C. Wang and K. Xu, Joule, 2020, 4, 69–100 CrossRef CAS.
- M. Li, C. Wang, Z. Chen, K. Xu and J. Lu, Chem. Rev., 2020, 120, 6783–6819 CrossRef CAS PubMed.
- S.-A. Hyodo and K. Okabayashi, Electrochim. Acta, 1989, 34, 1551–1556 CrossRef CAS.
- M. Morita, Y. Asai, N. Yoshimoto and M. Ishikawa, J. Chem. Soc., Faraday Trans., 1998, 94, 3451–3456 RSC.
- Y. Kameda, Y. Umebayashi, M. Takeuchi, M. A. Wahab, S. Fukuda, S. Ishiguro, M. Sasaki, Y. Amo and T. Usuki, J. Phys. Chem. B, 2007, 111, 6104–6109 CrossRef CAS PubMed.
- D. Monti, E. Jónsson, M. R. Palacín and P. Johansson, J. Power Sources, 2014, 245, 630–636 CrossRef CAS.
- R. Tatara, G. M. Leverick, S. Feng, S. Wan, S. Terada, K. Dokko, M. Watanabe and Y. Shao-Horn, J. Phys. Chem. C, 2018, 122, 18316–18328 CrossRef CAS.
- J. Grondin, D. Talaga, J.-C. Lassègues and W. A. Henderson, Phys. Chem. Chem. Phys., 2004, 6, 938–944 RSC.
- J. Grondin, J.-C. Lassègues, M. Chami, L. Servant, D. Talaga and W. A. Henderson, Phys. Chem. Chem. Phys., 2004, 6, 4260–4267 RSC.
- W. A. Henderson, F. McKenna, M. A. Khan, N. R. Brooks, V. G. Young and R. Frech, Chem. Mater., 2005, 17, 2284–2289 CrossRef CAS.
- W. A. Henderson, J. Phys. Chem. B, 2006, 110, 13177–13183 CrossRef CAS PubMed.
- T. Tamura, K. Yoshida, T. Hachida, M. Tsuchiya, M. Nakamura, Y. Kazue, N. Tachikawa, K. Dokko and M. Watanabe, Chem. Lett., 2010, 39, 753–755 CrossRef CAS.
- K. Yoshida, M. Nakamura, Y. Kazue, N. Tachikawa, S. Tsuzuki, S. Seki, K. Dokko and M. Watanabe, J. Am. Chem. Soc., 2011, 133, 13121–13129 CrossRef CAS PubMed.
- K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2011, 115, 18384–18394 CrossRef CAS.
- K. Dokko, N. Tachikawa, K. Yamauchi, M. Tsuchiya, A. Yamazaki, E. Takashima, J.-W. Park, K. Ueno, S. Seki, N. Serizawa and M. Watanabe, J. Electrochem. Soc., 2013, 160, A1304–A1310 CrossRef CAS.
- H. Moon, T. Mandai, R. Tatara, K. Ueno, A. Yamazaki, K. Yoshida, S. Seki, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2015, 119, 3957–3970 CrossRef CAS.
- K. Ueno, K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2012, 116, 11323–11331 CrossRef CAS PubMed.
- T. Mandai, K. Dokko and M. Watanabe, Chem. Rec., 2019, 19, 708–722 CrossRef CAS PubMed.
- T. Mandai, K. Yoshida, K. Ueno, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2014, 16, 8761–8772 RSC.
- M. Watanabe, K. Dokko, K. Ueno and M. L. Thomas, Bull. Chem. Soc. Jpn., 2018, 91, 1660–1682 CrossRef CAS.
- L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, Science, 2015, 350, 938–943 CrossRef CAS PubMed.
- L. Suo, O. Borodin, W. Sun, X. Fan, C. Yang, F. Wang, T. Gao, Z. Ma, M. Schroeder, A. von Cresce, S. M. Russell, M. Armand, A. Angell, K. Xu and C. Wang, Angew. Chem., Int. Ed., 2016, 55, 7136–7141 CrossRef CAS PubMed.
- Y. Yamada, K. Usui, K. Sodeyama, S. Ko, Y. Tateyama and A. Yamada, Nat. Energy, 2016, 1, 16129 CrossRef CAS.
- K. Dokko, D. Watanabe, Y. Ugata, M. L. Thomas, S. Tsuzuki, W. Shinoda, K. Hashimoto, K. Ueno, Y. Umebayashi and M. Watanabe, J. Phys. Chem. B, 2018, 122, 10736–10745 CrossRef CAS PubMed.
- J. Alvarado, M. A. Schroeder, M. Zhang, O. Borodin, E. Gobrogge, M. Olguin, M. S. Ding, M. Gobet, S. Greenbaum, Y. S. Meng and K. Xu, Mater. Today, 2018, 21, 341–353 CrossRef CAS.
- X. Ren, S. Chen, H. Lee, D. Mei, M. H. Engelhard, S. D. Burton, W. Zhao, J. Zheng, Q. Li, M. S. Ding, M. Schroeder, J. Alvarado, K. Xu, Y. S. Meng, J. Liu, J. G. Zhang and W. Xu, Chem, 2018, 4, 1877–1892 CAS.
- Y. Okamoto, S. Tsuzuki, R. Tatara, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2020, 124, 4459–4469 CrossRef CAS.
- R. Tatara, S. Nishimura, Y. Okamoto, K. Ueno, M. Watanabe and K. Dokko, J. Phys. Chem. C, 2020, 124, 15800–15811 CrossRef CAS.
- J. Wang, Y. Yamada, K. Sodeyama, C. H. Chiang, Y. Tateyama and A. Yamada, Nat. Commun., 2016, 7, 12032 CrossRef CAS PubMed.
- S. Ko, Y. Yamada and A. Yamada, Joule, 2021, 5, 998–1009 CrossRef CAS.
- R. Tatara, D. G. Kwabi, T. P. Batcho, M. Tulodziecki, K. Watanabe, H. M. Kwon, M. L. Thomas, K. Ueno, C. V. Thompson, K. Dokko, Y. Shao-Horn and M. Watanabe, J. Phys. Chem. C, 2017, 121, 9162–9172 CrossRef CAS.
- A. Nakanishi, K. Ueno, D. Watanabe, Y. Ugata, Y. Matsumae, J. Liu, M. L. Thomas, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2019, 123, 14229–14238 CrossRef CAS.
- W. Xu, J. Wang, F. Ding, X. Chen, E. Nasybulin, Y. Zhang and J.-G. Zhang, Energy Environ. Sci., 2014, 7, 513–537 RSC.
- X. B. Cheng, R. Zhang, C. Z. Zhao, F. Wei, J. G. Zhang and Q. Zhang, Adv. Sci., 2016, 3, 1500213 CrossRef PubMed.
- M. D. Tikekar, S. Choudhury, Z. Tu and L. A. Archer, Nat. Energy, 2016, 1, 16114 CrossRef CAS.
- D. Lin, Y. Liu and Y. Cui, Nat. Nanotechnol., 2017, 12, 194–206 CrossRef CAS PubMed.
- X. B. Cheng, R. Zhang, C. Z. Zhao and Q. Zhang, Chem. Rev., 2017, 117, 10403–10473 CrossRef CAS PubMed.
- J. Liu, Z. Bao, Y. Cui, E. J. Dufek, J. B. Goodenough, P. Khalifah, Q. Li, B. Y. Liaw, P. Liu, A. Manthiram, Y. S. Meng, V. R. Subramanian, M. F. Toney, V. V. Viswanathan, M. S. Whittingham, J. Xiao, W. Xu, J. Yang, X.-Q. Yang and J.-G. Zhang, Nat. Energy, 2019, 4, 180–186 CrossRef CAS.
- R. Weber, M. Genovese, A. J. Louli, S. Hames, C. Martin, I. G. Hill and J. R. Dahn, Nat. Energy, 2019, 4, 683–689 CrossRef CAS.
- C. Fang, X. Wang and Y. S. Meng, Trends Chem., 2019, 1, 152–158 CrossRef CAS.
- Y. Zhang, T.-T. Zuo, J. Popovic, K. Lim, Y.-X. Yin, J. Maier and Y.-G. Guo, Mater. Today, 2020, 33, 56–74 CrossRef CAS.
- J. G. Zhang, W. Xu, J. Xiao, X. Cao and J. Liu, Chem. Rev., 2020, 120, 13312–13348 CrossRef CAS PubMed.
- Z. Yu, H. Wang, X. Kong, W. Huang, Y. Tsao, D. G. Mackanic, K. Wang, X. Wang, W. Huang, S. Choudhury, Y. Zheng, C. V. Amanchukwu, S. T. Hung, Y. Ma, E. G. Lomeli, J. Qin, Y. Cui and Z. Bao, Nat. Energy, 2020, 5, 526–533 CrossRef CAS.
- L. Suo, Y. S. Hu, H. Li, M. Armand and L. Chen, Nat. Commun., 2013, 4, 1481 CrossRef PubMed.
- J. Qian, W. A. Henderson, W. Xu, P. Bhattacharya, M. Engelhard, O. Borodin and J. G. Zhang, Nat. Commun., 2015, 6, 6362 CrossRef CAS PubMed.
- X. Fan, L. Chen, X. Ji, T. Deng, S. Hou, J. Chen, J. Zheng, F. Wang, J. Jiang, K. Xu and C. Wang, Chem, 2017, 4, 174–185 Search PubMed.
- Z. Zeng, V. Murugesan, K. S. Han, X. Jiang, Y. Cao, L. Xiao, X. Ai, H. Yang, J.-G. Zhang, M. L. Sushko and J. Liu, Nat. Energy, 2018, 3, 674–681 CrossRef CAS.
- S. Jiao, X. Ren, R. Cao, M. H. Engelhard, Y. Liu, D. Hu, D. Mei, J. Zheng, W. Zhao, Q. Li, N. Liu, B. D. Adams, C. Ma, J. Liu, J.-G. Zhang and W. Xu, Nat. Energy, 2018, 3, 739–746 CrossRef CAS.
- Y. Maeyoshi, D. Ding, M. Kubota, H. Ueda, K. Abe, K. Kanamura and H. Abe, ACS Appl. Mater. Interfaces, 2019, 11, 25833–25843 CrossRef CAS PubMed.
-
J. O. M. Bockris and A. K. N. Reddy, Modern Electrochemistry, Springer, US, New York, 2nd edn, 1998 Search PubMed.
- H. Moon, R. Tatara, T. Mandai, K. Ueno, K. Yoshida, N. Tachikawa, T. Yasuda, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2014, 118, 20246–20256 CrossRef CAS.
- K. Ueno, R. Tatara, S. Tsuzuki, S. Saito, H. Doi, K. Yoshida, T. Mandai, M. Matsugami, Y. Umebayashi, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2015, 17, 8248–8257 RSC.
- N. Arai, H. Watanabe, E. Nozaki, S. Seki, S. Tsuzuki, K. Ueno, K. Dokko, M. Watanabe, Y. Kameda and Y. Umebayashi, J. Phys. Chem. Lett., 2020, 11, 4517–4523 CrossRef CAS PubMed.
- C. Zhang, K. Ueno, A. Yamazaki, K. Yoshida, H. Moon, T. Mandai, Y. Umebayashi, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2014, 118, 5144–5153 CrossRef CAS PubMed.
- V. Gutmann and E. Wychera, Inorg. Nucl. Chem. Lett., 1966, 2, 257–260 CrossRef CAS.
- U. Mayer, V. Gutmann and W. Gerger, Monatsh. Chem., 1975, 106, 1235–1257 CrossRef CAS.
- K. Ueno, J.-W. Park, A. Yamazaki, T. Mandai, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2013, 117, 20509–20516 CrossRef CAS.
- G. Leverick, R. Tatara, S. Feng, E. Crabb, A. France-Lanord, M. Tułodziecki, J. Lopez, R. M. Stephens, J. C. Grossman and Y. Shao-Horn, J. Phys. Chem. C, 2020, 124, 4953–4967 CrossRef CAS.
- T. Mandai, K. Yoshida, S. Tsuzuki, R. Nozawa, H. Masu, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2015, 119, 1523–1534 CrossRef CAS PubMed.
- S. Terada, T. Mandai, R. Nozawa, K. Yoshida, K. Ueno, S. Tsuzuki, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2014, 16, 11737–11746 RSC.
- S.-D. Han, J. L. Allen, E. Jónsson, P. Johansson, D. W. McOwen, P. D. Boyle and W. A. Henderson, J. Phys. Chem. C, 2013, 117, 5521–5531 CrossRef CAS.
- D. M. Seo, P. D. Boyle, R. D. Sommer, J. S. Daubert, O. Borodin and W. A. Henderson, J. Phys. Chem. B, 2014, 118, 13601–13608 CrossRef CAS PubMed.
- D. M. Seo, P. D. Boyle, J. L. Allen, S.-D. Han, E. Jónsson, P. Johansson and W. A. Henderson, J. Phys. Chem. C, 2014, 118, 18377–18386 CrossRef CAS.
- Y. Ugata, S. Sasagawa, R. Tatara, K. Ueno, M. Watanabe and K. Dokko, J. Phys. Chem. B, 2021, 125, 6600–6608 CrossRef CAS PubMed.
- S. Kondou, M. L. Thomas, T. Mandai, K. Ueno, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2019, 21, 5097–5105 RSC.
- Y. Ugata, M. L. Thomas, T. Mandai, K. Ueno, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2019, 21, 9759–9768 RSC.
- J. E. Katon and W. R. Feairheller, Spectrochim. Acta, 1965, 21, 199–201 CrossRef CAS.
- D. Brouillette, D. E. Irish, N. J. Taylor, G. Perron, M. Odziemkowski and J. E. Desnoyers, Phys. Chem. Chem. Phys., 2002, 4, 6063–6071 RSC.
- Y. Umebayashi, T. Mitsugi, S. Fukuda, T. Fujimori, K. Fujii, R. Kanzaki, M. Takeuchi and S. Ishiguro, J. Phys. Chem. B, 2007, 111, 13028–13032 CrossRef CAS PubMed.
- D. W. McOwen, D. M. Seo, O. Borodin, J. Vatamanu, P. D. Boyle and W. A. Henderson, Energy Environ. Sci., 2014, 7, 416–426 RSC.
- D. M. Seo, O. Borodin, S.-D. Han, P. D. Boyle and W. A. Henderson, J. Electrochem. Soc., 2012, 159, A1489–A1500 CrossRef CAS.
- Y. Ugata, R. Tatara, K. Ueno, K. Dokko and M. Watanabe, J. Chem. Phys., 2020, 152, 104502 CrossRef CAS PubMed.
- D. M. Seo, O. Borodin, S.-D. Han, Q. Ly, P. D. Boyle and W. A. Henderson, J. Electrochem. Soc., 2012, 159, A553–A565 CrossRef CAS.
- S.-D. Han, O. Borodin, J. L. Allen, D. M. Seo, D. W. McOwen, S.-H. Yun and W. A. Henderson, J. Electrochem. Soc., 2013, 160, A2100–A2110 CrossRef CAS.
- S.-D. Han, O. Borodin, D. M. Seo, Z.-B. Zhou and W. A. Henderson, J. Electrochem. Soc., 2014, 161, A2042–A2053 CrossRef CAS.
- J. Wang, Y. Yamada, K. Sodeyama, E. Watanabe, K. Takada, Y. Tateyama and A. Yamada, Nat. Energy, 2018, 3, 22–29 CrossRef CAS.
- N. Xiao, W. D. McCulloch and Y. Wu, J. Am. Chem. Soc., 2017, 139, 9475–9478 CrossRef CAS PubMed.
- F. Wohde, M. Balabajew and B. Roling, J. Electrochem. Soc., 2016, 163, A714–A721 CrossRef CAS.
- P. Porion, Y. R. Dougassa, C. Tessier, L. El Ouatani, J. Jacquemin and M. Anouti, Electrochim. Acta, 2013, 114, 95–104 CrossRef CAS.
- K. Shigenobu, K. Dokko, M. Watanabe and K. Ueno, Phys. Chem. Chem. Phys., 2020, 22, 15214–15221 RSC.
- K. Hayamizu, Y. Aihara, S. Arai and C. G. Martinez, J. Phys. Chem. B, 1999, 103, 519–524 CrossRef CAS PubMed.
- S. Tsuzuki, W. Shinoda, S. Seki, Y. Umebayashi, K. Yoshida, K. Dokko and M. Watanabe, ChemPhysChem, 2013, 14, 1993–2001 CrossRef CAS PubMed.
- M. Doyle, T. F. Fuller and J. Newman, Electrochim. Acta, 1994, 39, 2073–2081 CrossRef CAS.
- K. M. Diederichsen, E. J. McShane and B. D. McCloskey, ACS Energy Lett., 2017, 2, 2563–2575 CrossRef CAS.
- P. Barai, K. Higa and V. Srinivasan, J. Electrochem. Soc., 2018, 165, A2654–A2666 CrossRef CAS.
- M. Gouverneur, J. Kopp, L. van Wüllen and M. Schönhoff, Phys. Chem. Chem. Phys., 2015, 17, 30680–30686 RSC.
- P. G. Bruce, M. T. Hardgrave and C. A. Vincent, Solid State Ionics, 1992, 53-56, 1087–1094 CrossRef CAS.
- P. G. Bruce, J. Evans and C. A. Vincent, Solid State Ionics, 1988, 28-30, 918–922 CrossRef.
- M. Watanabe, S. Nagano, K. Sanui and N. Ogata, Solid State Ionics, 1988, 28-30, 911–917 CrossRef.
- M. D. Galluzzo, J. A. Maslyn, D. B. Shah and N. P. Balsara, J. Chem. Phys., 2019, 151, 020901 CrossRef PubMed.
- K. Shigenobu, M. Shibata, K. Dokko, M. Watanabe, K. Fujii and K. Ueno, Phys. Chem. Chem. Phys., 2021, 23, 2622–2629 RSC.
- L. A. Woolf, J. Phys. Chem., 1978, 82, 959–962 CrossRef CAS.
- L. A. Woolf and K. R. Harris, J. Chem. Soc., Faraday Trans. 1, 1978, 74, 933–947 RSC.
- D. M. Pesko, K. Timachova, R. Bhattacharya, M. C. Smith, I. Villaluenga, J. Newman and N. P. Balsara, J. Electrochem. Soc., 2017, 164, E3569–E3575 CrossRef CAS.
- I. Villaluenga, D. M. Pesko, K. Timachova, Z. Feng, J. Newman, V. Srinivasan and N. P. Balsara, J. Electrochem. Soc., 2018, 165, A2766–A2773 CrossRef CAS.
- D. Dong, F. Sälzer, B. Roling and D. Bedrov, Phys. Chem. Chem. Phys., 2018, 20, 29174–29183 RSC.
- Y. Yamada, K. Furukawa, K. Sodeyama, K. Kikuchi, M. Yaegashi, Y. Tateyama and A. Yamada, J. Am. Chem. Soc., 2014, 136, 5039–5046 CrossRef CAS PubMed.
- K. Sodeyama, Y. Yamada, K. Aikawa, A. Yamada and Y. Tateyama, J. Phys. Chem. C, 2014, 118, 14091–14097 CrossRef CAS.
- L. E. Camacho-Forero, T. W. Smith and P. B. Balbuena, J. Phys. Chem. C, 2016, 121, 182–194 CrossRef.
- K. Takada, Y. Yamada and A. Yamada, ACS Appl. Mater.
Interfaces, 2019, 11, 35770–35776 CrossRef CAS PubMed.
- Y. Ugata, R. Tatara, T. Mandai, K. Ueno, M. Watanabe and K. Dokko, ACS Appl. Energy Mater., 2021, 4, 1851–1859 CrossRef CAS.
- R. Fong, U. von Sacken and J. R. Dahn, J. Electrochem. Soc., 1990, 137, 2009–2013 CrossRef CAS.
- D. Aurbach, A. Zaban, Y. Ein-Eli, I. Weissman, O. Chusid, B. Markovsky, M. Levi, E. Levi, A. Schechter and E. Granot, J. Power Sources, 1997, 68, 91–98 CrossRef CAS.
- D. Aurbach, J. Power Sources, 2000, 89, 206–218 CrossRef CAS.
- S.-K. Jeong, M. Inaba, Y. Iriyama, T. Abe and Z. Ogumi, Electrochem. Solid-State Lett., 2003, 6, A13–A15 CrossRef CAS.
- M. Nie, D. P. Abraham, D. M. Seo, Y. Chen, A. Bose and B. L. Lucht, J. Phys. Chem. C, 2013, 117, 25381–25389 CrossRef CAS.
- Y. Yamada, M. Yaegashi, T. Abe and A. Yamada, Chem. Commun., 2013, 49, 11194–11196 RSC.
- Y. Yamada, K. Usui, C. H. Chiang, K. Kikuchi, K. Furukawa and A. Yamada, ACS Appl. Mater. Interfaces, 2014, 6, 10892–10899 CrossRef CAS PubMed.
- S. Seki, Y. Kobayashi, H. Miyashiro, A. Yamanaka, Y. Mita and T. Iwahori, J. Power Sources, 2005, 146, 741–744 CrossRef CAS.
- J. Ling, C. Karuppiah, S. G. Krishnan, M. V. Reddy, I. I. Misnon, M. H. Ab Rahim, C.-C. Yang and R. Jose, Energy Fuels, 2021, 35, 10428–10450 CrossRef CAS.
- L. J. Krause, W. Lamanna, J. Summerfield, M. Engle, G. Korba, R. Loch and R. Atanasoski, J. Power Sources, 1997, 68, 320–325 CrossRef CAS.
- M. Morita, T. Shibata, N. Yoshimoto and M. Ishikawa, J. Power Sources, 2003, 119-121, 784–788 CrossRef CAS.
- A. Abouimrane, J. Ding and I. J. Davidson, J. Power Sources, 2009, 189, 693–696 CrossRef CAS.
- K. Matsumoto, K. Inoue, K. Nakahara, R. Yuge, T. Noguchi and K. Utsugi, J. Power Sources, 2013, 231, 234–238 CrossRef CAS.
- C. Zhang, A. Yamazaki, J. Murai, J. W. Park, T. Mandai, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2014, 118, 17362–17373 CrossRef CAS.
- Y. Yamada, C. H. Chiang, K. Sodeyama, J. Wang, Y. Tateyama and A. Yamada, ChemElectroChem, 2015, 2, 1687–1694 CrossRef CAS.
- X. Wang, E. Yasukawa and S. Mori, Electrochim. Acta, 2000, 45, 2677–2684 CrossRef CAS.
- R.-S. Kühnel, M. Lübke, M. Winter, S. Passerini and A. Balducci, J. Power Sources, 2012, 214, 178–184 CrossRef.
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J. M. Tarascon, Nat. Mater., 2011, 11, 19–29 CrossRef PubMed.
- D. Aurbach, B. D. McCloskey, L. F. Nazar and P. G. Bruce, Nat. Energy, 2016, 1, 16128 CrossRef CAS.
- S. A. Freunberger, Y. Chen, Z. Peng, J. M. Griffin, L. J. Hardwick, F. Barde, P. Novak and P. G. Bruce, J. Am. Chem. Soc., 2011, 133, 8040–8047 CrossRef CAS PubMed.
- B. D. McCloskey, D. S. Bethune, R. M. Shelby, G. Girishkumar and A. C. Luntz, J. Phys. Chem. Lett., 2011, 2, 1161–1166 CrossRef CAS PubMed.
- M. M. Ottakam Thotiyl, S. A. Freunberger, Z. Peng and P. G. Bruce, J. Am. Chem. Soc., 2013, 135, 494–500 CrossRef CAS PubMed.
- D. M. Itkis, D. A. Semenenko, E. Y. Kataev, A. I. Belova, V. S. Neudachina, A. P. Sirotina, M. Havecker, D. Teschner, A. Knop-Gericke, P. Dudin, A. Barinov, E. A. Goodilin, Y. Shao-Horn and L. V. Yashina, Nano Lett., 2013, 13, 4697–4701 CrossRef CAS PubMed.
- B. L. Ellis, K. T. Lee and L. F. Nazar, Chem. Mater., 2010, 22, 691–714 CrossRef CAS.
- R. D. Rauh, K. M. Abraham, G. F. Pearson, J. K. Surprenant and S. B. Brummer, J. Electrochem. Soc., 1979, 126, 523–526 CrossRef CAS.
- H. Yamin and E. Peled, J. Power Sources, 1983, 9, 281–287 CrossRef CAS.
- Y. V. Mikhaylik and J. R. Akridge, J. Electrochem. Soc., 2004, 151, A1969–A1976 CrossRef CAS.
- R. Cao, K. Mishra, X. Li, J. Qian, M. H. Engelhard, M. E. Bowden, K. S. Han, K. T. Mueller, W. A. Henderson and J.-G. Zhang, Nano Energy, 2016, 30, 825–830 CrossRef CAS.
- K. Takada, Y. Yamada, E. Watanabe, J. Wang, K. Sodeyama, Y. Tateyama, K. Hirata, T. Kawase and A. Yamada, ACS Appl. Mater. Interfaces, 2017, 9, 33802–33809 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
|
| This journal is © the Owner Societies 2021 |
 Open Access Article
Open Access Article bc,
Kazuhide
Ueno
bc,
Kazuhide
Ueno
 ad,
Masayoshi
Watanabe
ad,
Masayoshi
Watanabe
 d and
Kaoru
Dokko
d and
Kaoru
Dokko
 *acd
*acd
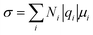
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and form [Li(G3)]+ and [Li(G4)]+ in solutions, respectively. The 1
1, and form [Li(G3)]+ and [Li(G4)]+ in solutions, respectively. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of G3 (or G4) and certain Li salts, such as LiTFSA and LiBETA (BETA: bis(pentafluoroethanesulfonyl)amide), are regarded as ionic liquids composed of complex cations [Li(G3 or G4)]+ and the counter anions are regarded as “solvate ionic liquids”. Earlier, we have reviewed the physicochemical properties and electrochemistry of glyme-solvate ionic liquids.25–27 The present article reviews recent progress in the researches on molten solvates and highly concentrated electrolytes comprising various aprotic solvents and Li/Na salts (Fig. 2). The molten Li salt hydrate electrolytes, so called “water-in-salt” electrolytes, which enable the stable operation of 3 V-class aqueous LIBs have also been extensively studied;28–30 however, these aqueous electrolytes do not have sufficient reductive stability against Li metal. The molten solvate electrolytes with aprotic solvents possess high thermal stability and wide electrochemical window and are promising electrolytes for next-generation batteries, such as high voltage Li/Na batteries,31–37 Li–O2 batteries,38 and Li–S batteries.39 Li metal is one of the most attractive anode materials owing to its high theoretical capacity (3860 mA h g−1) and low electrode potential (–3.04 V vs. SHE).40–50 Highly concentrated aprotic electrolytes have been reported to be useful in achieving a high Coulombic efficiency of Li metal deposition/stripping and a long charge/discharge cycle life of Li metal batteries.33,51–56 In addition to these attractive features, we recently found that a unique transport process of Li/Na ions emerges in highly concentrated electrolytes.31 The Li/Na cations exchange ligands (solvent and anion) rapidly in certain concentrated electrolytes, which enables them to diffuse faster than the solvent molecules and anions in the solutions, resulting in the high transference numbers of Li/Na ions. The high transference numbers are effective in suppressing the concentration polarization of Li/Na batteries during discharging at high current densities and may be useful in improving the power densities of the batteries.
1 mixtures of G3 (or G4) and certain Li salts, such as LiTFSA and LiBETA (BETA: bis(pentafluoroethanesulfonyl)amide), are regarded as ionic liquids composed of complex cations [Li(G3 or G4)]+ and the counter anions are regarded as “solvate ionic liquids”. Earlier, we have reviewed the physicochemical properties and electrochemistry of glyme-solvate ionic liquids.25–27 The present article reviews recent progress in the researches on molten solvates and highly concentrated electrolytes comprising various aprotic solvents and Li/Na salts (Fig. 2). The molten Li salt hydrate electrolytes, so called “water-in-salt” electrolytes, which enable the stable operation of 3 V-class aqueous LIBs have also been extensively studied;28–30 however, these aqueous electrolytes do not have sufficient reductive stability against Li metal. The molten solvate electrolytes with aprotic solvents possess high thermal stability and wide electrochemical window and are promising electrolytes for next-generation batteries, such as high voltage Li/Na batteries,31–37 Li–O2 batteries,38 and Li–S batteries.39 Li metal is one of the most attractive anode materials owing to its high theoretical capacity (3860 mA h g−1) and low electrode potential (–3.04 V vs. SHE).40–50 Highly concentrated aprotic electrolytes have been reported to be useful in achieving a high Coulombic efficiency of Li metal deposition/stripping and a long charge/discharge cycle life of Li metal batteries.33,51–56 In addition to these attractive features, we recently found that a unique transport process of Li/Na ions emerges in highly concentrated electrolytes.31 The Li/Na cations exchange ligands (solvent and anion) rapidly in certain concentrated electrolytes, which enables them to diffuse faster than the solvent molecules and anions in the solutions, resulting in the high transference numbers of Li/Na ions. The high transference numbers are effective in suppressing the concentration polarization of Li/Na batteries during discharging at high current densities and may be useful in improving the power densities of the batteries.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent
solvent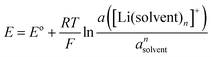
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cLi (where cLi is the concentration of Li salt) can be observed in the low concentration region as shown in Fig. 3. The electrode potential of Li metal is linear to log
cLi (where cLi is the concentration of Li salt) can be observed in the low concentration region as shown in Fig. 3. The electrode potential of Li metal is linear to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cLi at lower than 1 mol dm−3 (log
cLi at lower than 1 mol dm−3 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cLi = 0), however, the potential deviates from linearity and shifts significantly to a positive potential at concentrations above 1 mol dm−3.58,59 With increasing the Li salt concentration, the mole fraction of solvent xsolvent decreases, and the activity of free solvent is no longer assumed to be 1, i.e., asolvent becomes lower than 1. Actually, the mole fraction of free solvent in molten glyme solvates of Li salts was very low, which was revealed by Raman spectroscopy.59 In addition, Arai et al. measured the vapor–pressure of Li salt solutions and concluded that the activity coefficients of solvents in highly concentrated solutions were considerably lower than 1.60 Therefore, the nonlinear relationship between E and log
cLi = 0), however, the potential deviates from linearity and shifts significantly to a positive potential at concentrations above 1 mol dm−3.58,59 With increasing the Li salt concentration, the mole fraction of solvent xsolvent decreases, and the activity of free solvent is no longer assumed to be 1, i.e., asolvent becomes lower than 1. Actually, the mole fraction of free solvent in molten glyme solvates of Li salts was very low, which was revealed by Raman spectroscopy.59 In addition, Arai et al. measured the vapor–pressure of Li salt solutions and concluded that the activity coefficients of solvents in highly concentrated solutions were considerably lower than 1.60 Therefore, the nonlinear relationship between E and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cLi in the high concentration region >1 mol dm−3 (Fig. 3) is reasonably attributed to the decrease in free solvent activity. The effects of the considerably low activity of free solvent in the molten solvate electrolytes on the electrochemical reactions in batteries will be discussed later.
cLi in the high concentration region >1 mol dm−3 (Fig. 3) is reasonably attributed to the decrease in free solvent activity. The effects of the considerably low activity of free solvent in the molten solvate electrolytes on the electrochemical reactions in batteries will be discussed later.

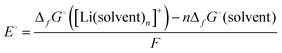



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n is denoted as [Li(solvent)n][X]. Fig. 8a and b show the crystal structures of [Li(SL)1][BF4] and [Li(SL)2][ClO4] solvates analysed by single-crystal X-ray crystallography. The coordination number of Li+ ions is 4 or 5 in the crystals, as shown in Fig. 8. In the crystal of the [Li(SL)1][BF4] solvate, all SL molecules bridge different Li+ ions, forming a polymeric network structure. In addition, each BF4− anion coordinates to more than one Li+ ion (i.e. AGG coordination). In [Li(SL)2][ClO4] solvates, monodentate-type and bridging-type SL molecules coexist in a 1
n is denoted as [Li(solvent)n][X]. Fig. 8a and b show the crystal structures of [Li(SL)1][BF4] and [Li(SL)2][ClO4] solvates analysed by single-crystal X-ray crystallography. The coordination number of Li+ ions is 4 or 5 in the crystals, as shown in Fig. 8. In the crystal of the [Li(SL)1][BF4] solvate, all SL molecules bridge different Li+ ions, forming a polymeric network structure. In addition, each BF4− anion coordinates to more than one Li+ ion (i.e. AGG coordination). In [Li(SL)2][ClO4] solvates, monodentate-type and bridging-type SL molecules coexist in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (Fig. 8b). Each ClO4− anion coordinates to a Li+ ion in a monodentate form (i.e. CIP coordination). Furthermore, it is to be noted that the solvent-bridged structure (Li+–SL–Li+) is commonly formed in SL-based crystalline solvates. However, this unique structure is not a particular case for the solvates of cyclic SL. A similar bridging-type coordination is found in Li salt solvates of acyclic sulfones such as dimethyl sulfone.71 Similar solvent-bridged networks are also formed in crystalline solvates composed of Li salts and bridging ligands with multiple coordinating sites. In the single crystals of Li salt solvates of methyl pyruvate (MP) and methyl acetoacetate (MA), the ketone carbonyl oxygen and the ester carbonyl oxygen atoms bind to different Li+ ions forming a solvent-bridged structure (Fig. 8c).72 Crystalline solvates composed of LiFSA and dinitriles, such as succinonitrile (SN), glutaronitrile (GN), and adiponitrile (ADN), have unique mesh structures, in which all the dinitrile molecules link to different Li+ ions, whereas FSA− anions exist in the vacant sites and do not coordinate to Li+ ions (Fig. 8d).73 In addition to the Li-based systems, the crystalline solvates of Na salts have also been studied.34,35 The coordination number of Na+ in these crystalline solvates is 6, which is larger than that of Li+, because of its larger ionic radius.
1 ratio (Fig. 8b). Each ClO4− anion coordinates to a Li+ ion in a monodentate form (i.e. CIP coordination). Furthermore, it is to be noted that the solvent-bridged structure (Li+–SL–Li+) is commonly formed in SL-based crystalline solvates. However, this unique structure is not a particular case for the solvates of cyclic SL. A similar bridging-type coordination is found in Li salt solvates of acyclic sulfones such as dimethyl sulfone.71 Similar solvent-bridged networks are also formed in crystalline solvates composed of Li salts and bridging ligands with multiple coordinating sites. In the single crystals of Li salt solvates of methyl pyruvate (MP) and methyl acetoacetate (MA), the ketone carbonyl oxygen and the ester carbonyl oxygen atoms bind to different Li+ ions forming a solvent-bridged structure (Fig. 8c).72 Crystalline solvates composed of LiFSA and dinitriles, such as succinonitrile (SN), glutaronitrile (GN), and adiponitrile (ADN), have unique mesh structures, in which all the dinitrile molecules link to different Li+ ions, whereas FSA− anions exist in the vacant sites and do not coordinate to Li+ ions (Fig. 8d).73 In addition to the Li-based systems, the crystalline solvates of Na salts have also been studied.34,35 The coordination number of Na+ in these crystalline solvates is 6, which is larger than that of Li+, because of its larger ionic radius.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt%)) due to significantly high viscosity of the molten solvate electrolytes.
50 wt%)) due to significantly high viscosity of the molten solvate electrolytes.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt%)a
50 wt%)a

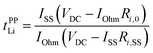
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 86 and 0.07 for tPPLi.85 Apparently, the molten Li salt solvates are prone to exhibiting higher values compared with that of conventional organic electrolytes. The tPPLi values of the SL- and nitrile-based molten Li salt solvates with unique Li ion diffusion behaviour are much higher than those of the ether-based [Li(G1)2][TFSA]. It has been suggested that the solvent-bridged Li ion coordination structure exerts a strong impact on the enhancement of tPPLi and tNMRLi values. The SL- and GBL-based molten Na salt solvates also exhibit high tPPNa values of 0.81 for [Na(SL)1][FSA]34 and 0.84 for [Na(GBL)1][FSA].35 The two molten Na salt solvates have ligand-bridged structures (Na+–(solvent or FSA)–Na+) resembling the solvent-bridged structure confirmed in the molten Li salt solvates, which enables the dynamic ligand-exchange conduction of Na+. All these molten solvates maintain a unique solvent-bridged structure consisting of solvent and anions concurrently with the formation of CIPs and/or AGGs therein. Therefore, the motion of smaller Li (or Na) ions via dynamic ligand-exchange conduction is not relatively regulated compared with those of the solvent molecules and anions in the ion coordination, which results in the improvement of tPPLi (or tPPNa).
86 and 0.07 for tPPLi.85 Apparently, the molten Li salt solvates are prone to exhibiting higher values compared with that of conventional organic electrolytes. The tPPLi values of the SL- and nitrile-based molten Li salt solvates with unique Li ion diffusion behaviour are much higher than those of the ether-based [Li(G1)2][TFSA]. It has been suggested that the solvent-bridged Li ion coordination structure exerts a strong impact on the enhancement of tPPLi and tNMRLi values. The SL- and GBL-based molten Na salt solvates also exhibit high tPPNa values of 0.81 for [Na(SL)1][FSA]34 and 0.84 for [Na(GBL)1][FSA].35 The two molten Na salt solvates have ligand-bridged structures (Na+–(solvent or FSA)–Na+) resembling the solvent-bridged structure confirmed in the molten Li salt solvates, which enables the dynamic ligand-exchange conduction of Na+. All these molten solvates maintain a unique solvent-bridged structure consisting of solvent and anions concurrently with the formation of CIPs and/or AGGs therein. Therefore, the motion of smaller Li (or Na) ions via dynamic ligand-exchange conduction is not relatively regulated compared with those of the solvent molecules and anions in the ion coordination, which results in the improvement of tPPLi (or tPPNa).
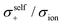 ,
, 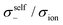 ,
, 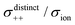 ,
, 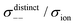 , and
, and 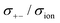 :left to right) of (a) [Li(G1)2][TFSA], (b) [Li(SL)2][TFSA], and (c) [Li(SL)2][BF4]. The graphs (a) and (b) are reprinted with permission from ref. 87. Copyright 2020 PCCP Owner Societies.
:left to right) of (a) [Li(G1)2][TFSA], (b) [Li(SL)2][TFSA], and (c) [Li(SL)2][BF4]. The graphs (a) and (b) are reprinted with permission from ref. 87. Copyright 2020 PCCP Owner Societies.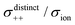 ,
, 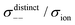 , and
, and 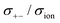 ), suggesting that the ion motions are anti-correlated. Interestingly, in [Li(SL)2][TFSA] and [Li(SL)2][BF4], the dynamic cation − cation (
), suggesting that the ion motions are anti-correlated. Interestingly, in [Li(SL)2][TFSA] and [Li(SL)2][BF4], the dynamic cation − cation (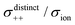 ) cross-correlations are less anti-correlated and the dynamic cation – anion (
) cross-correlations are less anti-correlated and the dynamic cation – anion (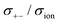 ) cross-correlations are nearly non-correlated (Fig. 12b and c) even at almost the same salt concentration as that of [Li(G1)2][TFSA]. It is likely that Li ion hopping/exchange conduction is reflected by the nearly non-correlated ion motions, which further contributes to the higher tPPLi for the SL-based electrolytes. The σ+−/σion exhibits a slightly negative value for [Li(SL)2][TFSA]; however, it shifts to nearly zero for [Li(SL)2][BF4]. This supports the more pronounced association of LiBF4 than that of LiTFSA in the SL-based molten solvates. Therefore, the developed AGG networks31 accompanied by the bridged structure are responsible for the considerably high tPPLi in [Li(SL)2][BF4].
) cross-correlations are nearly non-correlated (Fig. 12b and c) even at almost the same salt concentration as that of [Li(G1)2][TFSA]. It is likely that Li ion hopping/exchange conduction is reflected by the nearly non-correlated ion motions, which further contributes to the higher tPPLi for the SL-based electrolytes. The σ+−/σion exhibits a slightly negative value for [Li(SL)2][TFSA]; however, it shifts to nearly zero for [Li(SL)2][BF4]. This supports the more pronounced association of LiBF4 than that of LiTFSA in the SL-based molten solvates. Therefore, the developed AGG networks31 accompanied by the bridged structure are responsible for the considerably high tPPLi in [Li(SL)2][BF4].
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mA
mA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−2 and the deposition time was 1.5
cm−2 and the deposition time was 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h. The diameter of the Cu substrate shown in the inset of (a and c) was 2
h. The diameter of the Cu substrate shown in the inset of (a and c) was 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm. Scale bar, 10
cm. Scale bar, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μm. Reprinted with permission from ref. 52 Copyright 2015 Nature Publishing Group.
μm. Reprinted with permission from ref. 52 Copyright 2015 Nature Publishing Group.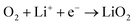
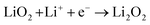
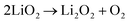
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO = 1
DMSO = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4), and only trace amounts of free DMSO were present in the high concentration LiTFSA/DMSO solutions above 2.3 mol dm−3. It is considered that LiO2 cannot be solvated in a highly concentrated electrolyte because of the absence of free solvent, resulting in very low solubility of LiO2. Therefore, LiO2 is converted to Li2O2 mainly on the disk electrode surface, resulting in an improved reversibility of the OER/ORR at the disk electrode.
4), and only trace amounts of free DMSO were present in the high concentration LiTFSA/DMSO solutions above 2.3 mol dm−3. It is considered that LiO2 cannot be solvated in a highly concentrated electrolyte because of the absence of free solvent, resulting in very low solubility of LiO2. Therefore, LiO2 is converted to Li2O2 mainly on the disk electrode surface, resulting in an improved reversibility of the OER/ORR at the disk electrode.













