Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Taming the dynamics in a pharmaceutical by cocrystallization: investigating the impact of the coformer by solid-state NMR†
Patrick M. J.
Szell
 a,
Józef R.
Lewandowski
a,
Józef R.
Lewandowski
 b,
Helen
Blade
b,
Helen
Blade
 c,
Leslie P.
Hughes
c,
Leslie P.
Hughes
 *c,
Sten O.
Nilsson Lill
*c,
Sten O.
Nilsson Lill
 d and
Steven P.
Brown
d and
Steven P.
Brown
 *a
*a
aDepartment of Physics, University of Warwick, Coventry, CV4 7AL, UK. E-mail: S.P.Brown@warwick.ac.uk
bDepartment of Chemistry, University of Warwick, Coventry, CV4 7AL, UK
cOral Product Development, Pharmaceutical Technology & Development, Operations, AstraZeneca, Macclesfield, UK. E-mail: Les.Hughes2@astrazeneca.com
dEarly Product Development and Manufacturing, Pharmaceutical Sciences, R&D, AstraZeneca, Gothenburg, Sweden
First published on 2nd September 2021
Abstract
Pharmaceuticals in their crystalline state may display a range of dynamics that can affect their physicochemical properties and chemical stability. With pharmaceutical cocrystals continuing to gain attention, there is an opportunity to investigate how the dynamics are changing in these new solid forms. Here, we investigate the dynamics in efavirenz, an anti-HIV drug, and a series of its cocrystals using a combination of DFT calculations and solid-state magic-angle spinning (MAS) NMR spectroscopy. We show that the crystalline form of efavirenz has a highly dynamic cyclopropyl group, and displays additional rocking motion. In contrast, the dynamics in the efavirenz cocrystals appear to be tamed, with the cyclopropyl group in the (efavirenz)(L-proline) cocrystal being the most constrained, and these constraints originating from a more favourable crystal packing in the cocrystals.
Pharmaceutical cocrystallization is a recent strategy where an active pharmaceutical ingredient (API) is crystallized with one or more coformers.1–3 This approach can provide control of the physicochemical properties, having been shown to be highly beneficial, for example, in improving dissolution rates and mechanical properties.4–7 Interestingly, cocrystals have also been shown to influence the chemical stability of an API,8,9 potentially extending their shelf-lives. In recent years, the field of pharmaceutical cocrystals has flourished, with several commercial products now being available or under development.10
Despite the general conception that solids are rigid and fixed in place, molecules in their crystalline state may display a range of motions. In the context of this study, we refer to these motions as dynamics. Dynamics have been shown to be important for the function of proteins,11–13 materials,14 and molecular machines,15,16 and can be modified by intermolecular interactions and the crystal packing.17,18 However, molecular motion may be undesirable in pharmaceuticals as this has been shown to influence their chemical and physical stabilities.19–21 In addition, dynamics can render an API difficult to crystallize, making the development of a commercially relevant process challenging, while also complicating the process of structural characterization due to the added uncertainty inherent with crystallographic disorder.22 As a result, the ability to control dynamics may lead to better quality drug products with a consistent performance and improved manufacturability. Recent work has shown that dynamics in crystalline solids can be influenced by manipulating the chemical environment,23,24 the crystallographic environment,22,25,26 or by introducing a dynamics catalyst.27 More specifically, the dynamics present in crystalline pharmaceuticals have previously been investigated,28–31 showing an impact on the dynamics for preparing new polymorphs,32 the salt form,33,34 or even pharmaceuticals supported in a matrix.35,36 However, to the best of our knowledge, there is no systematic investigation on how the dynamics change in pharmaceuticals as coformers are introduced into the structure. With the rise of pharmaceutical cocrystals, insights on how the dynamics are being modified in these new solid forms can provide crucial structural understandings on the next generation of medicines.
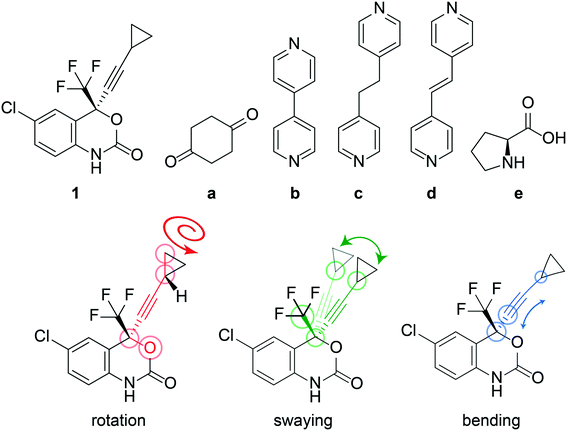
The anti-HIV pharmaceutical efavirenz (1) features a dynamic cyclopropyl group that adopts multiple crystallographic positions,37 and a trifluoromethyl group which is known to rotate (see Fig. 1). Having a dynamic moiety and several of its cocrystals reported in the Cambridge Structural Database (CSD),37–401 provides an ideal opportunity to investigate if the dynamics are changing in the cocrystals. Here, we investigate the dynamics of the cyclopropyl group in 1 and a series of its reported cocrystals,37–39 as shown in Fig. 1, using a combination of DFT calculations and solid-state NMR. Several polymorphs of 1 have previously been reported, however only form I is investigated here as it is the most stable of the polymorphs.37
In this work, information on the dynamics of 1 is obtained using 13C cross polarisation (CP) and 19F solid-state magic-angle spinning (MAS) NMR spectroscopy under the theme of NMR crystallography.41,42 Spin–lattice (T1) relaxation time measurements are applied to extract the thermodynamic parameters of the fast ps-ns motion of the cyclopropyl ring, and is interpreted using the Bloembergen–Purcell–Pound (BPP) relaxation theory.43,44 These data are summarized in terms of their correlation times (τ), which characterise the average rate of the dynamic events, and the activation energy (Ea), the average energy of a dynamic process occurring on the NMR timescale. The activation energies were further investigated using transition state (TS) calculations, potential energy surface calculations, and an analysis of the interaction energies in each crystal structure. Overall, the objective of this work is to investigate the dynamics present in 1 and whether cocrystallization may be a viable strategy to reduce undesired dynamics in a pharmaceutical.
Results
i) X-ray diffraction
The crystal structure of 1, reported by Mahapatra et al.,37 features three molecules in the asymmetric unit (Z′ = 3), with one of the cyclopropyl groups exhibiting crystallographic disorder over two positions. The nature of the disordered cyclopropyl group in 1 appears to be dynamic in origin, and consists of a rotation of 136 ± 35° along the ethynyl axis, with the error considering the sizes of the atomic displacement parameters (ADPs) as represented by thermal ellipsoids and shown in Fig. 2. This corresponds to a rotation whereby the torsion angle between the cyclopropyl group axis and the efavirenz axis (θO–C–C–C, see Fig. 1) range from −42 ± 26° to 94 ± 24° (see Table S37†). Further, as illustrated in Fig. 1, the experimental structure reveals a swaying of the entire cyclopropylethynyl group and a bending of the C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C axis from linearity, corresponding to a change in θsway and θbend of 17 ± 15° and 29 ± 30°, respectively (see Tables S38 and S39†). In addition, there is a rocking motion of the double ring backbone, which is manifested in the crystal structure as an elongation of the thermal ellipsoids for most non-cyclopropyl atoms in 1, as shown in Fig. 2. These dynamics are investigated further in the cocrystals.
C–C axis from linearity, corresponding to a change in θsway and θbend of 17 ± 15° and 29 ± 30°, respectively (see Tables S38 and S39†). In addition, there is a rocking motion of the double ring backbone, which is manifested in the crystal structure as an elongation of the thermal ellipsoids for most non-cyclopropyl atoms in 1, as shown in Fig. 2. These dynamics are investigated further in the cocrystals.
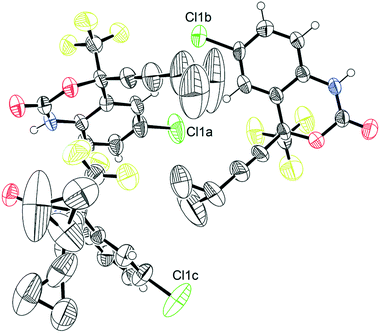 | ||
| Fig. 2 Thermal ellipsoid plot of pure 1.45 This figure was generated for the X-ray diffraction structure CSD# 767883 from Mahapatra et al.37 | ||
The crystal structures of cocrystals 1a and 1d, reported by Mahapatra et al.37 and de Melo et al.,38 respectively, do not have crystallographic disorder but the ADPs of the cyclopropyl group are distorted. The crystal structures of cocrystals 1b and 1c, reported by Mahapatra et al.37 and de Melo et al.,38 respectively, both have dynamic crystallographic disorder and some distortions in the ADPs of the cyclopropyl groups. Structure 1e is a cocrystal featuring the zwitterion form of L-proline, and was reported by Marques et al.39 Structure 1e is not disordered and has been solved from powder diffraction using isotropic displacement parameters and constraints on bond lengths and angles. All other structures apart from 1e have been solved by single crystal X-ray diffraction, and their ORTEP plots45 can be found in Fig. S37–S41 of the ESI.† The thermal ellipsoids of all atoms in the structure, which are a measure of the uncertainty on the atomic positions arising from the magnitude and direction of the thermal vibrations of atoms, are significantly larger for 1 than in the cocrystals. The average volume of the thermal ellipsoids of the CH2 carbon atoms of the cyclopropyl groups were calculated at a 50% ellipsoid probability and, as shown in Table 1, is largest in 1 and decreases in the cocrystals, suggesting the occurrence of reduced dynamics of the cyclopropyl group in the cocrystals. While there are additional cocrystals with 1 reported in the literature,46,47 we have restricted our investigations to the structures available in the CSD.40 Selected experimental X-ray parameters have been summarized in Table 2.
| Sample | X-ray | DFT | 13C NMR relaxation | Assignmentd | |
|---|---|---|---|---|---|
| Thermal ellipsoids volumea (Å3) | Interaction energyb (kJ mol−1) | E a (kJ mol−1) | τ 25°C/s | ||
| a Average volume of the thermal ellipsoids (calculated at a 50% ellipsoid probability) of the CH2 carbon atoms on the cyclopropyl group. b Breakdown given in Tables S13–S24.† c DFT-calculated Ea are given in brackets. d Crystallographic assignments are given in Table S37 of the ESI.† e Isotropic thermal ellipsoids. f Site is crystallographically disordered. g Obtained from three resolved features at δ(13C): 8.8 ppm, 8.0 ppm, and 7.4 ppm, respectively. | |||||
| 1 | 2.72 | −95.3 | 12 ± 2 [8.8] | (3.1 ± 1.0) × 10−11 | Site 1f,g |
| −142.3 | 10 ± 2 | (1.3 ± 0.5) × 10−11 | Site 2g | ||
| −99.4 | 11 ± 2 | (1.1 ± 0.3) × 10−12 | Site 3g | ||
| 1a | 1.80 | −163.9 | 8 ± 2 | (2.6 ± 0.9) × 10−12 | Site 1 |
| −120.4 | Site 2 | ||||
| 1b | 1.09 | −149.2 | 2 ± 1 [2.1] | (5.6 ± 1.1) × 10−13 | Site 1f |
| −142.5 | Site 2f | ||||
| 1c | 0.58 | −145.8 | 4 ± 2 [5.3] | (1.0 ± 0.4) × 10−12 | Site 1 |
| −142.5 | Site 2f | ||||
| 1d | 0.40 | −149.2 | 3 ± 1 | (6.4 ± 1.0) × 10−13 | Site 1 |
| −150.6 | Site 2 | ||||
| 1e | 0.25e | −218.3 | 1 ± 1 | (1 ± 2) × 10−13 | Site 1 |
| Sample | Acquisition temperature (K) | R-Factor (%) | Thermal ellipsoids volumea (Å3) | Diffraction technique | CSD # (REFCODE) | Ref. |
|---|---|---|---|---|---|---|
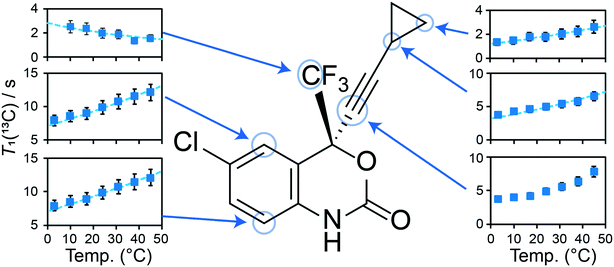
a Volume of the anisotropic displacement parameter (ADP) of the CH2 group of the cyclopropyl group on the efavirenz molecule at a 50% probability. The volume was calculated using the equation: 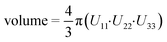 using Uij converted to units of Å.
b Isotropic thermal ellipsoids. using Uij converted to units of Å.
b Isotropic thermal ellipsoids.
|
||||||
| 1 | 250 | 6.56 | 2.72 | Crystal | 767883 (AJEYAQ02) | Mahapatra et al.37 |
| 1a | 293 | 9.43 | 1.80 | Crystal | 768815 (QUSREC) | Mahapatra et al.37 |
| 1b | 298 | 4.73 | 1.09 | Crystal | 767759 (QUSQOL) | Mahapatra et al.37 |
| 1c | 120 | 3.79 | 0.58 | Crystal | 909386 (XICRUY) | de Melo et al.38 |
| 1d | 120 | 7.80 | 0.40 | Crystal | 909385 (XICSAF) | de Melo et al.38 |
| 1e | 298 | 3.59 | 0.25b | Powder | 1847168 (HUDRAC) | Marques et al.39 |
ii) DFT calculations
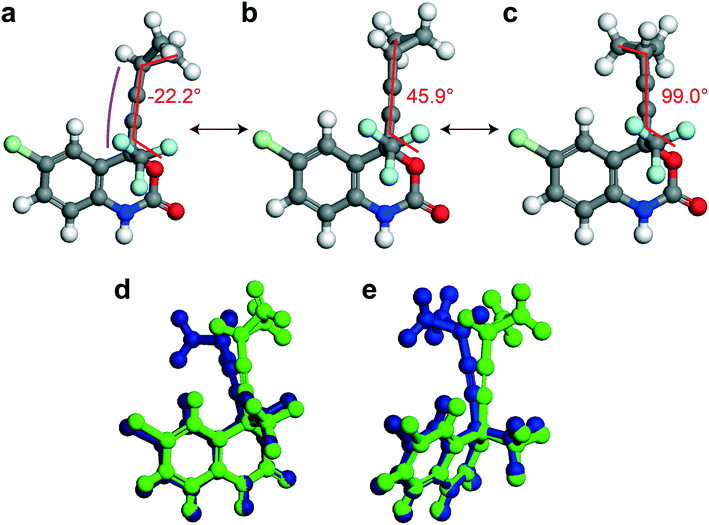
In this section, different types of DFT calculations are applied to probe and rationalise the observed dynamics. First, DFT calculations featuring the periodicity of the crystal lattice were performed to investigate the origins of the energy barriers of the cyclopropyl dynamics using CASTEP transition state calculations. All structures were initially optimized using CASTEP, giving rise to small differences in θO–C–C–C, θsway and θbend (see Tables S37–S39 of the ESI†). As structures 1a, 1d, and 1e did not have disordered cyclopropyl groups, the transition state calculations were limited to structures 1, 1b, and 1c, and were performed by specifying the disordered positions as the starting and end points to the calculations. In the case of 1, the calculated motion of the cyclopropyl group was a ΔθO–C–C–C = 121.2° rotation around the ethynyl axis, a swaying of the cyclopropyl group (Δθsway = 4.8°), a bending of the ethynyl group (Δθbend = 10.3°), and a rocking motion of the double ring backbone, as shown in Fig. 3, with a calculated energy barrier of 8.8 kJ mol−1. The calculated motion in 1b and 1c were rotations of ΔθO–C–C–C = 60.5° and 79.5° for the cyclopropyl group along the ethynyl axis, respectively, a small bending of the ethynyl group (Δθbend of 12.5° for 1b, 10.4° for 1c), some swaying (Δθsway = 2.9° for 1b, 7.9° for 1c), and a slight amount of rocking motion (see Fig. S33 and S34 of the ESI†). The calculated energy barriers for 1b and 1c were 2.1 kJ mol−1 and 5.3 kJ mol−1.Potential energy surfaces (PES) were calculated with DMol3 using DFT for the rotation of the cyclopropyl group of the efavirenz molecule, corresponding to systematically changing the θO–C–C–C torsion angle, and are in close agreement with the TS results obtained from CASTEP. In all cases, the calculations were performed using a periodic model of their respective crystal structure. Intriguingly, as shown in Fig. 4, the PES calculations reveal a broad energy well with two minima in 1, 1b, and 1c, supporting the dynamic crystallographic disorder observed in their X-ray structures. The barriers are small in samples 1, 1b, and 1c, and appear to be higher in 1. In the case of 1d, while there is only one position of the cyclopropyl group in the X-ray structure, the DFT-calculated energy well is also broad but in this case there is a single energy minimum with an elevated rotational energy barrier. The PES for both cyclopropyl sites in 1b, 1c, and 1d were similar. In contrast, the energy profiles of 1a and 1e are narrower with higher barriers resulting in crystal structures constrained in a single cyclopropyl orientation. As there are two unique cyclopropyl groups in the crystal structure of 1a (Z′ = 2), the PES has been computed for both groups. Cyclopropyl site 1 for 1a has a calculated energy barrier of 33 kJ mol−1 (see Fig. 4), whereas cyclopropyl site 2 for 1a has a calculated energy barrier of 14 kJ mol−1 (see Fig. S36 of the ESI†). In 1e, additional constraints on the cyclopropyl ring results in a narrow energy well with a barrier of 32 kJ mol−1 and 38 kJ mol−1 on the sides of the minimum. Consequently, a single preferred cyclopropyl position is observed in 1e, in agreement with the X-ray crystal structure.
 | ||
| Fig. 4 DFT-calculated potential energy surface for the rotation of a cyclopropyl group along the ethynyl axis in 1 (site 1), 1b (site 2), 1c (site 2), 1d (site 2), 1a (site 1), and 1e (site 1). The molecular structures above highlight the θO-C-C-C torsion angle and the cyclopropyl orientations. The Y-axis reports the relative energy. The torsion angles from the X-ray structure (exp.), DFT-optimized structure (calc.), and DFT-calculated transition state are indicated by the red, black, and blue arrows, respectively, and are tabulated in Table S37 of the ESI.† | ||
In order to provide greater context for the impact of the crystallographic environment on the energy barrier, the calculation was repeated on an isolated molecule of 1, with the PES shown in Fig. S35 of the ESI.† The calculated rotational barrier for the cyclopropyl group in an isolated molecule was 2.6 kJ mol−1, which is in excellent agreement with the 2.8 kJ mol−1 reported in a previous investigation.37 In the investigation reported here, the higher energy barriers observed computationally in 1, 1a–1e originate from constraints arising from through-space interactions involving neighbouring molecules in the crystal.
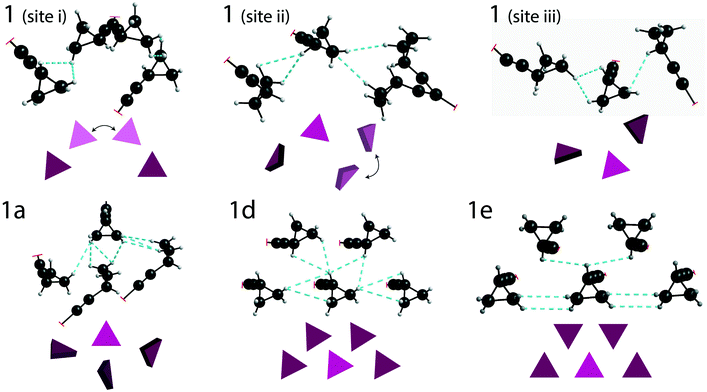
DFT calculations (with GAUSSIAN16) were used to estimate the total energy of the through-space interactions involving each cyclopropyl group, and is referred to here as the total interaction energy.48,49 Sample 1 has the least constraining environment of all samples and the cocrystals have a higher number of constraining interactions, as shown in Fig. 5, summarized in Table 1, and fully tabulated in Tables S13–S24 of the ESI.† For instance, the disordered cyclopropyl group in 1 (site 1) features five interactions from neighbouring molecules, with the sum of the interaction energies being −95.3 kJ mol−1. The sum of the interaction energies in the cocrystals are progressively higher at −120.4 kJ mol−1 in 1a (site 2), and −149.2 kJ mol−1 in 1d (site 1). In stark contrast, the cyclopropyl group in 1e interacts primarily with four adjacent cyclopropyl groups from neighbouring molecules, as shown in Fig. 5. The sum of all interactions involving the cyclopropyl group in 1e (site 1), which also includes two weaker interactions, has a total interaction energy of −218.3 kJ mol−1. Although 1e has a zwitterion L-proline molecule in the structure, there are no interactions involving the cyclopropyl group and the L-proline molecule. Interestingly, the cyclopropyl groups in all cases interact with other molecules of 1 rather than the coformer.
iii) Solid-state NMR
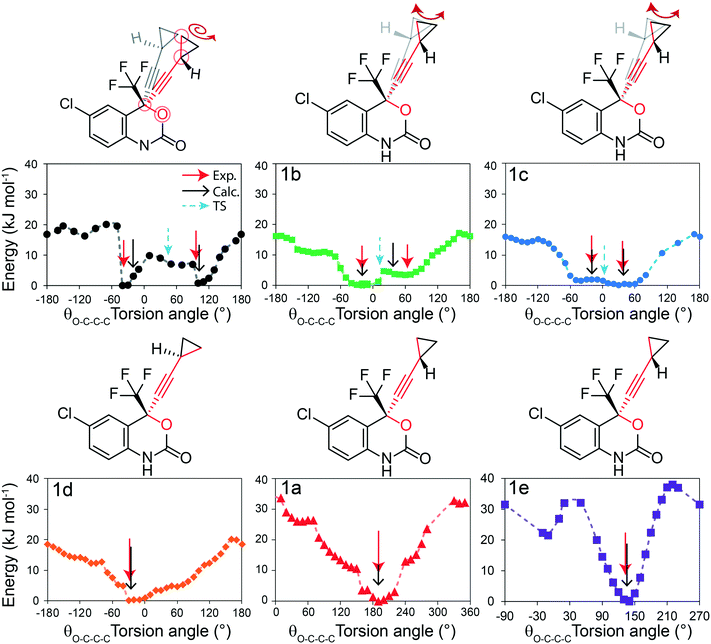
Solid-state NMR experiments observing both the 13C and 19F nucleus were applied to confirm the structural models and to observe changes in the 13C and 19F chemical shifts (δ(13C), δ(19F)). There have been previous reports of 13C solid-state NMR experiments to characterize 1, and the results presented here are in good agreement.50,51 As shown in Fig. 6i, the 13C solid-state NMR spectra show clear δ(13C) changes between 1 and cocrystals 1a–1e for the resonances assigned to the CH2 and CH carbons of the cyclopropyl group. For instance, a δ(13C) difference of 4.4 ppm is observed between structures 1 and 1e for the CH carbon of the cyclopropyl group. The full 13C NMR spectra are reported in Fig. S19–S24† together with assignments based on GIPAW DFT calculations and discussed further in the ESI.† The 19F solid-state NMR spectra provide a secondary indicator for the successful preparation of the cocrystals, observing δ(19F) changes of up to 3.6 ppm, for instance, between 1 and 1e. A small amount (∼5%, denoted by a dagger) of residual 1 has been identified from the 13C, 19F, and PXRD of 1a. Fortunately, the chemical shifts in 1a were sufficiently resolved from the starting material not to affect the T1 measurements.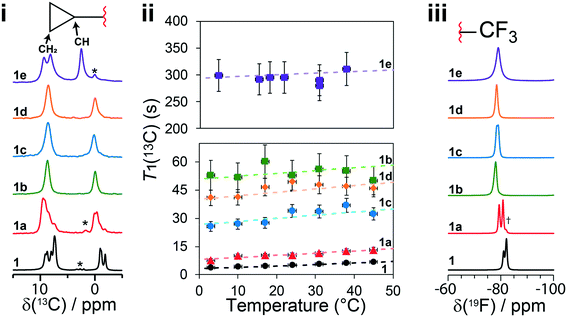 | ||
Fig. 6 (i) 13C CPMAS solid-state NMR spectra of 1 and cocrystals 1a to 1e, with a magnified view of the cyclopropyl resonances. (ii) T1(13C) relaxation times of the CH2 carbon atoms of the cyclopropyl ring at several temperatures. (iii) 19F one-pulse solid-state MAS NMR spectra of the CF3 group in 1 and cocrystals 1a to 1e. The dashed lines in (ii) denote the fits to eqn (S5),† and the Y-axis scale is different for the top (1e) and bottom (1 and 1a to 1d) parts. The asterisks denote spinning sidebands, and the dagger denotes a trace amount of starting material (νL(1H) = 500 MHz, νMAS = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 Hz). Errors on T1(13C) are estimated to be 10%. 750 Hz). Errors on T1(13C) are estimated to be 10%. | ||
The T1(13C) relaxation times provide direct insights into the dynamics occurring on the ps–ns timescales and have been measured at several temperatures from 3 °C to 45 °C. Upon the occurrence of motion with a given amplitude near the 13C Larmor frequency (ωL = 125.9 MHz in this case), the T1(13C) relaxation times are shorter (<30 s), such as in 1 and 1a, and are shortest when the rate of the dynamics (τ−1) is at the Larmor frequency (τ ≈ 1/νL). In this work, the longer T1(13C) relaxation times (>30 s), such as for 1b, 1c, 1d and 1e, are associated with dynamics occurring at a rate faster than the 13C Larmor frequency (τ ≪ 1/ωL). Being the inverse of the rate, we assume the correlation time at a given temperature (τx°C) follows the Arrhenius equation (see eqn (S2)†) and can be calculated from the preexponential factor, τ0, and the activation energy, Ea. The Ea is an Arrhenius parameter that describes the average energy of a dynamic process occurring in this timescale. Both Ea and τ0 are used to calculate (see eqn (S3)†) the spectral density function, J(ωL,τ), which is used to calculate T1(13C). As a result, fitting the T1(13C) relaxation time at several temperatures allows for both τ0 and Ea to be determined. For protonated carbons, including the CH2 and CH carbon atoms of the cyclopropyl group, the 13C–1H dipolar coupling relaxation mechanism dominates the T1(13C). Moreover, because samples contain 13C at natural abundance, averaging of the rates due to proton driven spin diffusion typically observed in the solid state for 13C labelled systems is not a concern.52
In the case of 1, the T1(13C) relaxation times of the CH2 atoms of the cyclopropyl group are the shortest of all samples investigated here, ranging between 0.2 s to 2.0 s. Furthermore, as shown in Fig. 7, the short T1(13C) relaxation times extend to carbon atoms well beyond the cyclopropyl group, with the ethynyl carbons and even all other protonated carbon atoms on 1 having T1(13C) values of less than 15 seconds, and are orders of magnitude shorter than in the cocrystals. Additional T1(13C) plots for the other resonances of 1 are shown in Fig. S31 and S32 of the ESI.† The T1(13C) relaxation times of the CH2 cyclopropyl atoms in 1a are slightly longer than for 1, with values of up to 12.7 seconds. As shown in Fig. 6ii, the T1(13C) relaxation times of the CH2 carbons are much longer in cocrystals 1b, 1c, and 1d, with T1(13C) values of up to 60 seconds. In stark contrast, the T1(13C) relaxation times of 1e are on the order of 300 seconds, supporting the occurrence of significant changes to the dynamics.
 | ||
| Fig. 7 T 1(13C) for selected carbon atoms in pure 1 as a function of the temperature. The dashed lines in the plots denote the fits for protonated carbons using eqn (S5)† (see Fig. 6ii and S31 and S32†). The T1(13C) of the cyclopropylethynyl group were measured from the resonances assigned to the disordered molecule of 1. The fitting parameters can be found in Table S10 of the ESI.† | ||
For each sample, the T1(13C) relaxation times of the CH2 carbon atoms of the cyclopropyl group have been fitted using eqn (S5) from the ESI† assuming the presence of a single dominant motional mode, with the resulting fits shown on Fig. 6ii. The fitting parameters have been tabulated in Table 1, summarizing the activation energy (Ea) and the correlation time at 25 °C (τ25°C). These parameters were verified by fitting the T1(13C) relaxation times of the CH carbon atom of the cyclopropyl group, with all parameters being in excellent agreement. Using the NMR assignments obtained from the GIPAW calculations, the thermodynamic parameters have been assigned to their crystallographic site. The activation energy is highest in 1 at 12 ± 2 kJ mol−1 and is in close agreement with the CASTEP transition state calculations. The slightly lower energy barrier (8.8 kJ mol−1) obtained from these calculations were likely due to being performed on a reduced model of 1 as a result of computational limitations. The dynamics in 1 are assigned to the total motion of the cyclopropyl group observed from the X-ray crystal structure and DFT calculations, that is, the rotation of the cyclopropyl group, the swaying of the cyclopropylethynyl moiety, and the bending of the ethynyl axis (see Fig. 1). The environment surrounding the disordered cyclopropyl ring in 1 appears to be loosely packed in the crystal structure (see Fig. 5), thus providing the required space for the group to rotate and sway. As shown in Fig. 7 and S31 and S32 of the ESI,† the T1(13C) for the other protonated carbon atoms in 1 appear to follow the same thermal activation parameters as the cyclopropyl group, supporting the occurrence of a rocking motion of the double ring backbone. The Ea's are progressively lower in the cocrystals, with 1a having an Ea of 8 ± 2 kJ mol−1 & 1e having an Ea of 1 ± 1 kJ mol−1, and 1b and 1c are in excellent agreement with the computational results. The low Ea measured in 1e suggests that due to the heightened rotational energy barrier originating from the crystal packing, the cyclopropyl group does not rotate on the time scales to which T1 measurements are sensitive to, with the experiment instead capturing local librations of the CH bonds in the cyclopropyl group. Interestingly, the two CH2 carbons of the cyclopropyl group in 1e are resolved in the 13C NMR spectrum, further supporting the absence of chemical exchange by rotational motion at this timescale. With a decrease in Ea observed in the cocrystals, the τ25°C of the dynamics in the cocrystals decreases, and T1(13C) increases significantly.
Discussion
The experimental X-ray crystal structure shows that the cyclopropyl groups are highly dynamic in pure 1, which is reflected by the occurrence of crystallographic disorder and distorted ADPs. Based on the crystal structure of 1, the dynamics of the disordered cyclopropyl group have been assigned to a rotation along the ethynyl axis, a swaying of the entire cyclopropylethynyl group, a bending of the C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C axis, and a rocking motion of the double ring backbone. The dynamics observed in the experimental crystal structure are also supported by DFT, calculating an energy barrier of 8.8 kJ mol−1 and reproducing the rocking motion. The DFT-calculated potential energy surface of 1, as shown in Fig. 4, shows a relatively low energy barrier between the two experimentally observed crystallographic positions of the disordered cyclopropyl group, allowing for the rotation of the cyclopropyl group to occur. The experimental T1(13C) relaxation data supports these observations, with a measured Ea of 12 ± 2 kJ mol−1 being in close agreement with the calculations. The short T1(13C) across the entire molecule of 1, as shown in Fig. 7, supports the occurrence of rocking motion, and appears to correlate with the dynamics of the cyclopropyl groups.
C–C axis, and a rocking motion of the double ring backbone. The dynamics observed in the experimental crystal structure are also supported by DFT, calculating an energy barrier of 8.8 kJ mol−1 and reproducing the rocking motion. The DFT-calculated potential energy surface of 1, as shown in Fig. 4, shows a relatively low energy barrier between the two experimentally observed crystallographic positions of the disordered cyclopropyl group, allowing for the rotation of the cyclopropyl group to occur. The experimental T1(13C) relaxation data supports these observations, with a measured Ea of 12 ± 2 kJ mol−1 being in close agreement with the calculations. The short T1(13C) across the entire molecule of 1, as shown in Fig. 7, supports the occurrence of rocking motion, and appears to correlate with the dynamics of the cyclopropyl groups.
In contrast to 1, there is a remarkable change in the dynamics occurring in the cocrystals. Given the reduction of these dynamics, we denote this effect as a taming of the dynamics. While there was no crystallographic disorder observed in the X-ray structures of 1a, 1d, and 1e, dynamic crystallographic disorder with two separated cyclopropyl positions was observed in the structures of 1b and 1c. The DFT calculations ascribe the motion in 1b and 1c to a 61° and 79° rotation of the cyclopropyl group along the ethynyl axis, respectively, with a smaller amount of rocking motion. Moreover, the average volumes of the ADPs of the cyclopropyl's CH2 atoms are significantly smaller in the cocrystals than in 1, further supporting the occurrence of tamed dynamics. In 1b and 1c, the PES calculations suggests the occurrence of a broad double well energy minimum and low rotational energy barriers, with the cyclopropyl groups rotating between two positions within this minimum. In 1d, while the energy minimum is also broad, there is only a single energy minimum. A significantly higher energy barrier is observed in 1e, reflecting the presence of additional interactions constraining the cyclopropyl group.
The taming of the dynamics in 1 is in direct contrast to a previous investigation showing the potential of catalysing or promoting dynamics through the introduction of a halogenated coformer,27,53,54 and can be rationalized by the crystal packing. As shown in Fig. 5, the crystallographic environment surrounding the disordered cyclopropyl group in 1 appears to be loosely packed, allowing the dynamics to occur with a total calculated interaction energy of −95.3 kJ mol−1. Of all the samples investigated here, 1e has the most tightly packed crystallographic environment, as shown in Fig. 5, and has a total calculated interaction energy of −218.3 kJ mol−1. The interaction energies correlate well with the experimental results, and are manifested in the PES of 1e as a narrow energy well with high barriers on both sides of the minimum, constraining the dynamics of the cyclopropyl group. Interestingly, the melting point of 1e was 164.1 °C, which is the highest of all compounds and is 25.2 °C above that of pure 1, supporting the occurrence of some stabilization in the cocrystal.
The ability to tame the dynamics in 1 through the introduction of a coformer, arises from a twofold effect: by reducing the rotational freedom to a single energy minimum on the PES, such as in 1a, 1d, and 1e, and by increasing the energy barrier surrounding this energy minimum, such as in 1e. In order to place these results in a wider context, a search of the CSD database40 for cyclopropyl groups was conducted (see section VI of the ESI†). Of the 166 structures that featured both a cyclopropyl group and disorder, in 37% of the cases, the disorder involved the cyclopropyl group. With pharmaceuticals featuring increasingly complex molecules, the strategy of cocrystallization may be helpful in taming troublesome dynamics that are known to complicate crystallization, structural characterization, physicochemical stability, and commercial manufacturing.
We recognise that the amorphous phase may offer advantages over the crystalline phase in terms of solubility, but from the perspective of pharmaceutical development, an amorphous form may present significant challenges in terms of physical and chemical stability. In addition, chemical mobility has been found to reduce chemical stability in amorphous pharmaceuticals,21 and 1 in particular has been shown to have multiple degradation pathways.55 As part of our investigation, we did attempt to prepare the pure amorphous form of 1, but it quickly converted to the crystalline form within hours, precluding our investigation. Polymer-stabilized amorphous solid dispersions is a potential route to amorphous pharmaceuticals, and we note that this approach has been investigated on 1.56–61 However, the cost of developing and commercialising a polymer-stabilised solid dispersion can be significant, and alternative strategies to develop commercially attractive medicines are always sought, such as cocrystallisation. Interestingly, new cocrystals featuring 1 have been recently reported, and have been shown to be stable for 6 months without chemical degradation.62
In conclusion, we report an instance of taming dynamics in a pharmaceutical using cocrystallization as a strategy. While the pure starting material 1 has a highly dynamic cyclopropyl group and displays an additional rocking motion of the double ring backbone, X-ray crystallography, DFT calculations, and solid-state NMR results support that the cocrystals have remarkably less dynamics. The most significant changes were observed in the L-proline cocrystal, 1e, where the cyclopropyl group is being constrained in its position by intermolecular interactions arising from the crystal packing. This study provides the first systematic evidence of the ability to tame the dynamics occurring in pharmaceuticals by cocrystallization, potentially leading towards more consistent performances and improved manufacturability.
Experimental and computational
Sample preparation
Efavirenz (1, >98%), 1,2-di(pyridin-4-yl)ethane (c, >98%), and L-proline (e, >99%) were purchased from Tokyo Chemical Industry. Cyclohexane-1,4-dione (a, 98%), 4,4′-bipyridine (b, 99%) and (E)-1,2-di(pyridin-4-yl)ethene (d, 97%) were purchased from Sigma Aldrich. HPLC grade acetonitrile was purchased from VWR. All cocrystals were prepared by solvent-assisted grinding for 30 minutes using a Retsch MM400 ball mill in a 5 mL stainless steel milling jar, a single 10 mm stainless steel milling ball, and a milling frequency of 30 Hz. Each cocrystal was prepared at a 300 mg scale with 30 μL of acetonitrile in either a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric ratio (1a, 1e) or 2
1 stoichiometric ratio (1a, 1e) or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric ratio (1b, 1c, 1d) and recovering 90% of the resulting powder.
1 stoichiometric ratio (1b, 1c, 1d) and recovering 90% of the resulting powder.
13C solid-state NMR
All samples were packed into 4 mm zirconium oxide MAS rotors, and experiments were performed on a Bruker Avance III spectrometer operating at a 1H Larmor frequency of 500 MHz using a 4 mm Bruker HFX probe. A magic angle spinning rate of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 Hz was used throughout all experiments. The 1D 13C CPMAS spectra were acquired using a ramped contact pulse on 1H (from 50% to 100% amplitude),63 a contact time of 2 ms, a 1H π/2 pulse duration of 2.5 μs, and co-adding 1024 transients. SPINAL64 proton decoupling64 was used with a 1H nutation frequency of 100 kHz and a 4.4 μs pulse length. The 13C spectrum was calibrated using glycine and referenced to 176.0 ppm relative to TMS at 0 ppm.65,66 The T1(13C) measurements were performed using the same cross-polarization parameters followed by an inversion recovery sequence, with a 13C π/2 pulse duration of 4 μs. A total of 8 delays were used for all inversion recovery experiments, with delays adjusted to appropriately sample the T1 curve. Temperatures were calibrated externally using the 207Pb resonance of lead nitrate.67,68 Additional 19F → 13C CPMAS experiments were used to measure the T1(13C) of the trifluoromethyl group. These experiments were performed using a 4 ms contact time with a ramped contact pulse,63 SPINAL-64 19F decoupling at a 19F nutation frequency of 62.5 kHz, and a 19F π/2 pulse duration of 4 μs.
750 Hz was used throughout all experiments. The 1D 13C CPMAS spectra were acquired using a ramped contact pulse on 1H (from 50% to 100% amplitude),63 a contact time of 2 ms, a 1H π/2 pulse duration of 2.5 μs, and co-adding 1024 transients. SPINAL64 proton decoupling64 was used with a 1H nutation frequency of 100 kHz and a 4.4 μs pulse length. The 13C spectrum was calibrated using glycine and referenced to 176.0 ppm relative to TMS at 0 ppm.65,66 The T1(13C) measurements were performed using the same cross-polarization parameters followed by an inversion recovery sequence, with a 13C π/2 pulse duration of 4 μs. A total of 8 delays were used for all inversion recovery experiments, with delays adjusted to appropriately sample the T1 curve. Temperatures were calibrated externally using the 207Pb resonance of lead nitrate.67,68 Additional 19F → 13C CPMAS experiments were used to measure the T1(13C) of the trifluoromethyl group. These experiments were performed using a 4 ms contact time with a ramped contact pulse,63 SPINAL-64 19F decoupling at a 19F nutation frequency of 62.5 kHz, and a 19F π/2 pulse duration of 4 μs.
19F solid-state NMR
All samples were packed into 4 mm zirconium oxide MAS rotors, and experiments were performed on a Bruker Avance III spectrometer operating at a 1H Larmor frequency of 500 MHz using a 4 mm Bruker HFX probe. A magic angle spinning rate of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 Hz was used throughout all experiments. The 1D 19F spectra were acquired using a π/2 pulse with SPINAL64 1H decoupling at a 1H nutation frequency of 100 kHz and a 4.8 μs pulse length, co-adding 32 transients. An inversion recovery sequence was used to measure the T1(19F) relaxation times with 8 variable delays, collecting 16 transients at each delay. These delays were manually adjusted to appropriately sample the T1(19F) curve of each sample. The 19F chemical shifts were referenced using PTFE to −122.0 ppm.69
750 Hz was used throughout all experiments. The 1D 19F spectra were acquired using a π/2 pulse with SPINAL64 1H decoupling at a 1H nutation frequency of 100 kHz and a 4.8 μs pulse length, co-adding 32 transients. An inversion recovery sequence was used to measure the T1(19F) relaxation times with 8 variable delays, collecting 16 transients at each delay. These delays were manually adjusted to appropriately sample the T1(19F) curve of each sample. The 19F chemical shifts were referenced using PTFE to −122.0 ppm.69
Powder X-ray diffraction
Powder X-ray diffraction experiments were performed on a Bruker D4 Endeavor diffractometer, scanning 2θ from 2° to 65° with steps of 0.02° at a rate of 5° per minute (Cu Kα1/2 = 1.5418 Å).Thermogravimetric analysis
Thermogravimetric analysis was performed on a TA Instrument Q2000, heating the sample in an Al pan from 25 °C to 300 °C at a constant heating rate of 10 °C min−1.NMR calculations
All DFT70–72 calculations were performed using the gauge-including projector augmented-wave (GIPAW)73 method as implemented in CASTEP74 as part of Materials Studio version 17.75 The structural model used in the calculations used the structures published on the CSD: 767883 (1),37 768815 (1a),37 767759 (1b),37 909386 (1c),38 909385 (1d),38 1847168 (1e).39 The GGA PBE functional76 was employed for all calculations, beginning with a geometry optimization routine with constrained unit cell parameters prior to calculating the NMR chemical shifts. The geometry optimization was performed with TS DFT-D correction,77 on the fly ultrasoft pseudopotentials, and Koelling–Harmon relativistic treatment. The cut-off energies and k-point separations can be found in Table S1 of the ESI.† NMR calculations were subsequently performed using the same parameters as the geometry optimization, apart from the cut-off energy. The calculated σcalc values were extracted using a script and converted into δcalc using a σref(13C) of 170 ppm and the equation δcalc = σref – σcalc. The σiso(19F) were averaged between the three fluorine atoms on the same CF3 group. The σref(19F) values are given in the figure captions.Transition state calculations
The transition state search calculations were performed using CASTEP, OFG ultrasoft pseudopotentials, TS DFT-D, and the linear synchronous transit method.78,79 A k-point separation of 0.05 Å−1 and a cut-off energy of 700 eV was used in the calculation, optimizing the transition state. The calculations were performed on 1, 1b, and 1c by specifying the disordered positions as the starting and end points, with the calculation finding the transition state between both conformations. The transition state calculation for the cyclopropyl rotation in pure 1 was performed by removing distant molecules from the unit cell in order to reduce computational costs.Potential energy surface calculations
Potential energy surface (PES) calculations were performed using DMol3 (ref. 80 and 81) as part of Materials Studio, using the crystal structures as models and featuring periodicity. The torsion angle between the cyclopropyl group and the main efavirenz molecular fragment (θO–C–C–C) was modified at steps of 10°, optimizing the structure at each step with a constraint on the torsion angles. The calculations were performed using the DNP basis set, the GGA PBE functional,76 TS DFT-D corrections,77 and a k-point separation of 0.05 Å−1.Crystal interactions analysis
Crystal Interaction (CrysIn), a tool developed in-house, was used to evaluate the static interactions between molecules present in a crystal based on DFT.48 The intermolecular interaction energies in the first coordination cell of each molecule in the asymmetric unit of the crystal were calculated using B3LYP-D3/6-31G(d,p) as reported in GAUSSIAN16.49 This is a comparable method to that employed in, for instance, the energy framework calculations in Crystal Explorer82 or PIXEL.83 This approach enables the quantification of the intermolecular interactions present in a crystal.84,85Author contributions
PMJS conceived and designed the experiments, prepared and analyzed the samples, performed the data analysis and computational work, and prepared the manuscript. JRL, HB, LPH, SONL, and SPB designed the experiments, performed the data analysis, prepared the manuscript, supervised the work, and provided guidance.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was funded by Innovate UK and AstraZeneca (grant number: KTP11570). The authors thank Lydia Coates from AstraZeneca for performing the thermogravimetric analysis. Data for this study are provided as a supporting data set from WRAP, the Warwick Research Archive Portal at https://wrap.warwick.ac.uk/157143/.References
- D. J. Berry and J. W. Steed, Adv. Drug Delivery Rev., 2017, 117, 3–24 CrossRef CAS PubMed.
- G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967 CrossRef CAS PubMed.
- P. Brázda, L. Palatinus and M. Babor, Science, 2019, 364, 667–669 CrossRef PubMed.
- O. Almarsson and M. J. Zaworotko, Chem. Commun., 2004, 1889–1896 RSC.
- N. K. Duggirala, M. L. Perry, O. Almarsson and M. J. Zaworotko, Chem. Commun., 2016, 52, 640–655 RSC.
- G. Bolla and A. Nangia, Chem. Commun., 2016, 52, 8342–8360 RSC.
- J. F. Remenar, S. L. Morissette, M. L. Peterson, B. Moulton, J. M. MacPhee, H. R. Guzmán and O. Almarsson, J. Am. Chem. Soc., 2003, 125, 8456–8457 CrossRef CAS PubMed.
- Y. Gao, J. Gao, Z. Liu, H. Kan, H. Zu, W. Sun, J. Zhang and S. Qian, Int. J. Pharm., 2012, 438, 327–335 CrossRef CAS PubMed.
- Y. Gao, H. Zu and J. Zhang, J. Pharm. Pharmacol., 2011, 63, 483–490 CrossRef CAS PubMed.
- R. Shaikh, R. Singh, G. M. Walker and D. M. Croker, Trends Pharmacol. Sci., 2018, 39, 1033–1048 CrossRef CAS PubMed.
- J. R. Lewandowski, M. E. Halse, M. Blackledge and L. Emsley, Science, 2015, 348, 578–581 CrossRef CAS PubMed.
- J. A. Davey, A. M. Damry, N. K. Goto and R. A. Chica, Nat. Chem. Biol., 2017, 13, 1280–1285 CrossRef CAS PubMed.
- S. Kosol, A. Gallo, D. Griffiths, T. R. Valentic, J. Masschelein, M. Jenner, E. L. C. de Los Santos, L. Manzi, P. K. Sydor, D. Rea, S. Zhou, V. Fülöp, N. J. Oldham, S. C. Tsai, G. L. Challis and J. R. Lewandowski, Nat. Chem., 2019, 11, 913–923 CrossRef CAS PubMed.
- P. K. Biswas, S. Saha, T. Paululat and M. Schmittel, J. Am. Chem. Soc., 2018, 140, 9038–9041 CrossRef CAS PubMed.
- S. Kassem, A. T. L. Lee, D. A. Leigh, V. Marcos, L. I. Palmer and S. Pisano, Nature, 2017, 549, 374–378 CrossRef CAS PubMed.
- G. De Bo, M. A. Y. Gall, S. Kuschel, J. De Winter, P. Gerbaux and D. A. Leigh, Nat. Nanotechnol., 2018, 13, 381–385 CrossRef CAS PubMed.
- J. M. Lamley, C. Öster, R. A. Stevens and J. R. Lewandowski, Angew. Chem., Int. Ed., 2015, 54, 15374–15378 CrossRef CAS PubMed.
- V. Kurauskas, S. A. Izmailov, O. N. Rogacheva, A. Hessel, I. Ayala, J. Woodhouse, A. Shilova, Y. Xue, T. Yuwen, N. Coquelle, J. P. Colletier, N. R. Skrynnikov and P. Schanda, Nat. Commun., 2017, 8, 145 CrossRef PubMed.
- K. Grzybowska, M. Paluch, A. Grzybowski, Z. Wojnarowska, L. Hawelek, K. Kolodziejczyk and K. L. Ngai, J. Phys. Chem. B, 2010, 114, 12792–12801 CrossRef CAS PubMed.
- E. Shalaev, K. Wu, S. Shamblin, J. F. Krzyzaniak and M. Descamps, Adv. Drug Delivery Rev., 2016, 100, 194–211 CrossRef CAS PubMed.
- S. Yoshioka and Y. Aso, J. Pharm. Sci., 2007, 96, 960–981 CrossRef CAS PubMed.
- P. M. J. Szell, S. P. Brown, L. P. Hughes, H. Blade and S. O. Nilsson Lill, Chem. Commun., 2020, 56, 14039–14042 RSC.
- J. Baudry, J. Am. Chem. Soc., 2006, 128, 11088–11093 CrossRef CAS PubMed.
- S. Khazaei and D. Sebastiani, J. Chem. Phys., 2016, 145, 234506 CrossRef PubMed.
- X. Wang, P. A. Beckmann, C. W. Mallory, A. L. Rheingold, A. G. DiPasquale, P. J. Carroll and F. B. Mallory, J. Org. Chem., 2011, 76, 5170–5176 CrossRef CAS PubMed.
- X. Wang, F. B. Mallory, C. W. Mallory, H. R. Odhner and P. A. Beckmann, J. Chem. Phys., 2014, 140, 194304 CrossRef PubMed.
- P. M. J. Szell, S. Zablotny and D. L. Bryce, Nat. Commun., 2019, 10, 916 CrossRef PubMed.
- H. E. Kerr, L. K. Softley, K. Suresh, A. Nangia, P. Hodgkinson and I. R. Evans, CrystEngComm, 2015, 17, 6707–6715 RSC.
- A. Pajzderska, K. Drużbicki, M. A. Gonzalez, J. Jenczyk, B. Peplińska, M. Jarek, J. Mielcarek and J. Wąsicki, J. Phys. Chem. B, 2014, 118, 6670–6679 CrossRef CAS PubMed.
- D. C. Apperley, A. F. Markwell, I. Frantsuzov, A. J. Ilott, R. K. Harris and P. Hodgkinson, Phys. Chem. Chem. Phys., 2013, 15, 6422–6430 RSC.
- X. Kong, L. A. O'Dell, V. Terskikh, E. Ye, R. Wang and G. Wu, J. Am. Chem. Soc., 2012, 134, 14609–14617 CrossRef CAS PubMed.
- R. K. Chandrappa, P. Ochsenbein, C. Martineau, M. Bonin, G. Althoff, F. Engelke, H. Malandrini, B. Castro, M. El Hajji and F. Taulelle, Cryst. Growth Des., 2013, 13, 4678–4687 CrossRef CAS.
- E. Carignani, S. Borsacchi and M. Geppi, J. Phys. Chem. A, 2011, 115, 8783–8790 CrossRef CAS PubMed.
- S. O. Nilsson Lill, C. M. Widdifield, A. Pettersen, A. Svensk Ankarberg, M. Lindkvist, P. Aldred, S. Gracin, N. Shankland, K. Shankland, S. Schantz and L. Emsley, Mol. Pharmaceutics, 2018, 15, 1476–1487 CrossRef CAS PubMed.
- E. Carignani, S. Borsacchi, P. Blasi, A. Schoubben and M. Geppi, Mol. Pharmaceutics, 2019, 16, 2569–2578 CrossRef CAS PubMed.
- A. Pajzderska, K. Drużbicki, P. Bilski, J. Jenczyk, M. Jarek, J. Mielcarek and J. Wąsicki, J. Phys. Chem. C, 2019, 123, 18364–18375 CrossRef CAS.
- S. Mahapatra, T. S. Thakur, S. Joseph, S. Varughese and G. R. Desiraju, Cryst. Growth Des., 2010, 10, 3191–3202 CrossRef CAS.
- A. C. C. de Melo, I. F. de Amorim, M. d. L. Cirqueira and F. T. Martins, Cryst. Growth Des., 2013, 13, 1558–1569 CrossRef CAS.
- M. Marques, W. Braga, J. S. Junior, L. Prado, H. Rocha, F. Ferreira, G. Ferreira and J. A. L. C. Resende, CSD Communication, 2019 Search PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- R. K. Harris, Solid State Sci., 2004, 6, 1025–1037 CrossRef CAS.
- B. Elena, G. Pintacuda, N. Mifsud and L. Emsley, J. Am. Chem. Soc., 2006, 128, 9555–9560 CrossRef CAS PubMed.
- D. A. Torchia and A. Szabo, J. Magn. Reson., 1982, 49, 107–121 CAS.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854 CrossRef CAS.
- R. Chadha, A. Saini, P. Arora, S. Chanda and Dharamvirsinghjain, Int. J. Pharm. Pharm. Sci., 2012, 4, 244–250 CAS.
- J. B. Ngilirabanga, P. P. Rosa, M. Aucamp, Y. Kippie and H. Samsodien, J. Drug Delivery Sci. Technol., 2020, 60, 101958 CrossRef CAS.
- A. Halme, M. J. Quayle, S. O. Nilsson Lill, A. Pettersen, M. Fransson and C. Boissier, Cryst. Growth Des., 2019, 19, 3670–3680 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Ding Williams, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- E. G. R. Sousa, E. M. de Carvalho, R. A. da Silva San Gil, T. C. D. Santos, L. B. Borré, O. A. Santos-Filho and J. Ellena, J. Pharm. Sci., 2016, 105, 2656–2664 CrossRef PubMed.
- C. Fandaruff, G. S. Rauber, A. M. Araya-Sibaja, R. N. Pereira, C. E. M. de Campos, H. V. A. Rocha, G. A. Monti, T. Malaspina, M. A. S. Silva and S. L. Cuffini, Cryst. Growth Des., 2014, 14, 4968–4975 CrossRef CAS.
- J. R. Lewandowski, J. Sein, H. J. Sass, S. Grzesiek, M. Blackledge and L. Emsley, J. Am. Chem. Soc., 2010, 132, 8252–8254 CrossRef CAS PubMed.
- L. Catalano, S. Pérez-Estrada, G. Terraneo, T. Pilati, G. Resnati, P. Metrangolo and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2015, 137, 15386–15389 CrossRef CAS PubMed.
- L. Catalano, S. Perez-Estrada, H. H. Wang, A. J.-L. Ayitou, S. I. Khan, G. Terraneo, P. Metrangolo, S. Brown and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2017, 139, 843–848 CrossRef CAS PubMed.
- M. Kurmi, A. Sahu, D. K. Singh, I. P. Singh and S. Singh, J. Pharm. Biomed. Anal., 2018, 148, 170–181 CrossRef CAS PubMed.
- S. Sarabu, V. R. Kallakunta, S. Bandari, A. Batra, V. Bi, T. Durig, F. Zhang and M. A. Repka, Carbohydr. Polym., 2020, 233, 115828 CrossRef CAS PubMed.
- A. Schittny, S. Philipp-Bauer, P. Detampel, J. Huwyler and M. Puchkov, J. Controlled Release, 2020, 320, 214–225 CrossRef CAS PubMed.
- H. C. Arca, L. I. Mosquera-Giraldo, D. Dahal, L. S. Taylor and K. J. Edgar, Mol. Pharmaceutics, 2017, 14, 3617–3627 CrossRef CAS PubMed.
- Z. M. M. Lavra, D. Pereira de Santana and M. I. Ré, Drug Dev. Ind. Pharm., 2017, 43, 42–54 CrossRef CAS PubMed.
- J. Pawar, A. Tayade, A. Gangurde, K. Moravkar and P. Amin, Eur. J. Pharm. Sci., 2016, 88, 37–49 CrossRef CAS PubMed.
- J. Yang, K. Grey and J. Doney, Int. J. Pharm., 2010, 384, 24–31 CrossRef CAS PubMed.
- B. H. Jaswanth Gowda, S. K. Nechipadappu, S. J. Shankar, M. Chavali, K. Paul, M. G. Ahmed, A. Sanjana and H. K. Shanthala, Mater. Today: Proc., 2021 DOI:10.1016/j.matpr.2021.05.535 , In press.
- G. Metz, X. L. Wu and S. O. Smith, J. Magn. Reson., Ser. A, 1994, 110, 219–227 CrossRef CAS.
- B. M. Fung, A. K. Khitrin and K. Ermolaev, J. Magn. Reson., 2000, 142, 97–101 CrossRef CAS PubMed.
- C. R. Morcombe and K. W. Zilm, J. Magn. Reson., 2003, 162, 479–486 CrossRef CAS PubMed.
- M. J. Potrzebowski, P. Tekely and Y. Dusausoy, Solid State Nucl. Magn. Reson., 1998, 11, 253–257 CrossRef CAS PubMed.
- A. Bielecki and D. P. Burum, J. Magn. Reson., 1995, 116, 215–220 CrossRef CAS.
- X. Guan and R. E. Stark, Solid State Nucl. Magn. Reson., 2010, 38, 74–76 CrossRef CAS PubMed.
- A. Vyalikh, P. Simon, E. Rosseeva, J. Buder, U. Scheler and R. Kniep, Sci. Rep., 2015, 5, 15797 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- Dassault Systèmes BIOVIA, Materials Studio, version 17, Dassault Systèmes, San Diego, 2017 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- N. Govind, M. Petersen, G. Fitzgerald, D. King-Smith and J. Andzelm, Comput. Mater. Sci., 2003, 28, 250–258 CrossRef CAS.
- T. A. Halgren and W. N. Lipscomb, Chem. Phys. Lett., 1977, 49, 225–232 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS.
- M. J. Turner, S. P. Thomas, M. W. Shi, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2015, 51, 3735–3738 RSC.
- A. Gavezzotti, Z. Kristallogr., 2005, 220, 499–510 CAS.
- H. Abouhakim, S. O. Nilsson Lill, M. J. Quayle, S. T. Norberg, A. Hassanpour and C. M. Pask, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 275–284 CrossRef CAS PubMed.
- O. D. Putra, A. Pettersen, S. O. Nilsson Lill, D. Umeda, E. Yonemochi, Y. P. Nugraha and H. Uekusa, CrystEngComm, 2019, 21, 2053–2057 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: The supplementary information contains additional experimental and computational details, powder X-ray diffraction data, spectral data, T1(13C) and T1(19F) relaxation times, thermogravimetric analysis, computational results, thermal ellipsoid plots, experimental X-ray details, crystal packing diagrams, and an analysis of the CSD. See DOI: 10.1039/d1ce01084k |
| This journal is © The Royal Society of Chemistry 2021 |