Open Access Article
Open Access ArticleSelf-division of giant vesicles driven by an internal enzymatic reaction†
Ylenia
Miele
 a,
Zsófia
Medveczky
b,
Gábor
Holló
c,
Borbála
Tegze
d,
Imre
Derényi
a,
Zsófia
Medveczky
b,
Gábor
Holló
c,
Borbála
Tegze
d,
Imre
Derényi
 ef,
Zoltán
Hórvölgyi
d,
Emiliano
Altamura
g,
István
Lagzi
ef,
Zoltán
Hórvölgyi
d,
Emiliano
Altamura
g,
István
Lagzi
 *bc and
Federico
Rossi
*bc and
Federico
Rossi
 *ah
*ah
aDepartment of Chemistry and Biology “A. Zambelli”, University of Salerno, Via Giovanni Paolo II 132, 84084 – Fisciano, SA, Italy. E-mail: federico.rossi2@unisi.it
bDepartment of Physics, Budapest University of Technology and Economics, H-1111, Budafoki ut 8, Budapest, Hungary. E-mail: istvanlagzi@gmail.com
cMTA-BME Condensed Matter Research Group, Budapest University of Technology and Economics, H-1111, Budafoki út 8, Budapest, Hungary
dDepartment of Physical Chemistry and Materials Science, Budapest University of Technology and Economics, H-1111 Budafoki ut 8, Budapest, Hungary
eDepartment of Biological Physics, Eötvös Loránd University, H-1117 Pázmány Péter sétány 1/A, Budapest, Hungary
fMTA-ELTE Statistical and Biological Physics Research Group, Eötvös Loránd University, H-1117 Pázmány Péter sétány 1/A, Budapest, Hungary
gDepartment of Chemistry, University of Bari, “Aldo Moro”, Via Orabona 4, I-70125 Bari, Italy
hDepartment of Earth, Environmental and Physical Sciences – DEEP Sciences, University of Siena, Pian dei Mantellini 44, 53100 – Siena, Italy
First published on 4th March 2020
Abstract
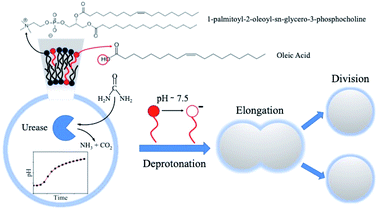
Self-division is one of the most common phenomena in living systems and one of the most important properties of life driven by internal mechanisms of cells. Design and engineering of synthetic cells from abiotic components can recreate a life-like function thus contributing to the understanding of the origin of life. Existing methods to induce the self-division of vesicles require external and non-autonomous triggers (temperature change and the addition of membrane precursors). Here we show that pH-responsive giant unilamellar vesicles on the micrometer scale can undergo self-division triggered by an internal autonomous chemical stimulus driven by an enzymatic (urea–urease) reaction coupled to a cross-membrane transport of the substrate, urea. The bilayer of the artificial cells is composed of a mixture of phospholipids (POPC, 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine) and oleic acid molecules. The enzymatic reaction increases the pH in the lumen of the vesicles, which concomitantly changes the protonation state of the oleic acid in the inner leaflet of the bilayer causing the removal of the membrane building blocks into the lumen of the vesicles thus decreasing the inner membrane area with respect to the outer one. This process coupled to the osmotic stress (responsible for the volume loss of the vesicles) leads to the division of a mother vesicle into two smaller daughter vesicles. These two processes must act in synergy; none of them alone can induce the division. Overall, our self-dividing system represents a step forward in the design and engineering of a complex autonomous model of synthetic cells.
Introduction
Synthetic cells (SCs) or minimal cells can be defined as artificial cell-like systems constructed in the laboratory by introducing biological or synthetic molecules inside and on the surface of lipid vesicles (liposomes).1–4 In a bottom-up approach to the construction of SCs, the emphasis is on mimicking the processes and the functions typical of living cells rather than reproducing their single biochemical components. In this context, the construction of entities with minimal complexity, yet being able to reproduce biological processes offers new perspectives and advantages in many fields, including medicine, materials science and the origin of life studies.Compartmentalization into separate domains is an essential characteristic of biological systems and this feature is universally recognized as the basis on which SCs can be constructed.1,5–8 Giant unilamellar vesicles (GUVs) are water-in-water compartments stabilized by amphiphilic molecules (phospholipids for example) that self-assemble into bilayers and create membranes. GUVs range from 1 μm to more than 100 μm in size depending on the preparation method employed, and their popularity as artificial cell chassis increased because of a few distinctive advantages:9 (i) they can be observed in real-time through optical microscopes; (ii) the membrane composition is tunable, which allows us to control various bilayer properties such as curvature, stiffness and permeability; (iii) they are suitable for hosting chemical9 and biochemical10 reactions and biomimetic processes.11
Synthetic GUVs are also very important in origin-of-life studies because they can be devised and constructed as models of primitive cells (protocells).12 Szostak et al., for example, recently proposed a fatty acid (oleic acid, HOA)–phospholipid (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine, POPC) mixture as plausible intermediates in protocellular evolution;13 these mixed GUVs, in fact, combine the stability typical of POPC bilayers (for example they do not precipitate in the presence of divalent cations) with the plasticity and permeability of HOA structures.14 Moreover, both components are present in living organisms (e.g., POPC is in the membrane of eukaryotic cells and HOA is a component of animal fats and vegetable oils).15
Among the various cellular functions, vesicle “self-replication” and “self-division” attract distinguished attention of many research groups, because these features are essential prerequisites for life. Since the pioneering work of Luisi in the 1990s, most experimental studies have focused on the division and replication of micelles, reverse micelles and vesicles made of fatty acids.16–21 Few experiments involving GUVs have also been reported,22–32 but in the origin-of-life perspective, they have been rarely considered, mainly because either (i) the scarce biomimetic character of the membranes and/or (ii) the strong external control exerted on the systems to induce divisions.12,33 It should also be pointed out that, in most of the systems explored, the trigger for the onset of the division process had a physical character (e.g., the addition of membrane precursors and temperature change) and acted externally on the outer surface of the protocell. In contrast, the cell division in living systems is a process governed by the biochemical reaction network of the cell, which is an internal and autonomous process, often induced by environmental inputs sensed by the cell through cross-membrane transport of chemical and biochemical information.34 One attempt has been made to internally drive GUV shape transformation. A protein system (Min) has been encapsulated into the GUVs and used to reversibly control the shape transformation of GUVs from pear shape to dumbbell shape and to drive periodic budding and subsequent merging of the buds with the mother vesicles.35
In this work, we propose a model for protocell division based on a chemical trigger, activated by the transmembrane transport of a substrate, acting inside the lumen of the artificial cells. In particular, we employed mixed POPC/HOA vesicles and we exploited the characteristic sensitivity of HOA (pKa ∼ 7.2–7.5 in a phospholipid bilayer) to pH stimuli15,36 and the osmotic concentration gradient to induce the protocell division. As an internal chemical trigger, we used the urea–urease enzymatic reaction, i.e. the enzymatic hydrolysis of the urea catalyzed by the Ni-protein urease. This reaction produces ammonia and carbonic acid that, in unbuffered media, shift the pH towards the alkaline range.37 The reaction rate, as a function of pH, has a bell shape of the Michaelis–Menten type (see the ESI, Fig. S1a†) that, in time, generates a pH profile typical of an autocatalytic process (Fig. S1b†).38 In fact, when the initial pH is set to low values, the reaction products contribute to the increase of the pH, which leads to a rapid acceleration of the hydrolysis. After reaching a maximum in the proximity of neutrality (pH = 7.4), the reaction rate decreases with pH to finally attain a plateau generating a characteristic sigmoidal kinetic curve for the pH change.
Results and discussion
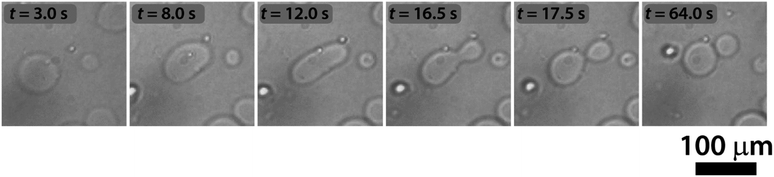
The sketch in Fig. 1 summarizes the basic features of our experiments. A population of about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 units of GUVs was prepared with a size between 5 and 50 μm, by using a phase transfer method.39,40 Following our previous studies,41,42 we encapsulated the enzyme urease (0.5 U mL−1) together with a pH-sensitive fluorescent dye (pyranine) (50 μM) into the lumen of the vesicles. Both the enzyme and the fluorescent dye are firmly confined into the GUVs;41 however, the mixed bilayer allows the passage of small nonpolar molecules,43 such as urea, which is dispersed in the outer medium and can enter the lumen of the vesicles to trigger the reaction. Fig. 2 shows a typical division process, taking place in about 1 minute after a solution containing urea (180 mM) is added to a dispersion of GUVs (t = 0, [urea]0 = 60 mM): starting from a spherical shape, the GUV elongates in a prolate form (t ∼ 12 s), assumes a pear shape (t ∼ 16 s) and eventually divides into two daughter vesicles (t ∼ 60 s) (Video S1†).
000 units of GUVs was prepared with a size between 5 and 50 μm, by using a phase transfer method.39,40 Following our previous studies,41,42 we encapsulated the enzyme urease (0.5 U mL−1) together with a pH-sensitive fluorescent dye (pyranine) (50 μM) into the lumen of the vesicles. Both the enzyme and the fluorescent dye are firmly confined into the GUVs;41 however, the mixed bilayer allows the passage of small nonpolar molecules,43 such as urea, which is dispersed in the outer medium and can enter the lumen of the vesicles to trigger the reaction. Fig. 2 shows a typical division process, taking place in about 1 minute after a solution containing urea (180 mM) is added to a dispersion of GUVs (t = 0, [urea]0 = 60 mM): starting from a spherical shape, the GUV elongates in a prolate form (t ∼ 12 s), assumes a pear shape (t ∼ 16 s) and eventually divides into two daughter vesicles (t ∼ 60 s) (Video S1†).
We explored several membrane compositions by changing the ratio of concentrations α = [POPC]/[HOA] and keeping the total amount of amphiphiles constant s = [POPC] + [HOA] = 5 mM. The ideal ratio to obtain the highest proportion of divisions in the population of vesicles was found to be α ∼ 1 (2.6 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
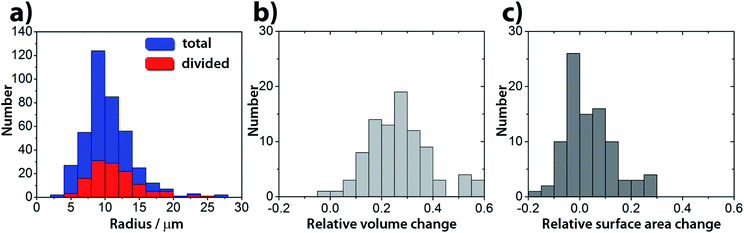
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.4 mM). Under these conditions in a population of GUVs, the pH triggered self-division process is a frequent event with a success rate of 25% irrespective of their size (400 GUVs analyzed in 3 experiments, Fig. 3 and S2†). The rest of the GUVs elongated and changed shape, but did not complete the division process. Greater α provided stable, but non-pH responsive GUVs, while a lower α generated less stable GUVs in the course of the increase of the pH.
2.4 mM). Under these conditions in a population of GUVs, the pH triggered self-division process is a frequent event with a success rate of 25% irrespective of their size (400 GUVs analyzed in 3 experiments, Fig. 3 and S2†). The rest of the GUVs elongated and changed shape, but did not complete the division process. Greater α provided stable, but non-pH responsive GUVs, while a lower α generated less stable GUVs in the course of the increase of the pH.
Complete separation of the daughter vesicles has not been observed. The vesicles always stay in close proximity and, therefore, most probably remain connected by a narrow neck. This is in agreement with the widely accepted hypothesis that fission and fusion are activated processes with an energy barrier of at least 20 kBT.44,45 In biology, these processes rarely occur spontaneously and are mediated by proteins.44 To check whether the lumens of the two daughter vesicles are contiguous, we carried out FRAP (fluorescence recovery after photobleaching) experiments. The fluorescence of one of the two daughter vesicles was bleached after the division process with a laser beam. This perturbation, however, resulted in a complete separation of the daughter vesicles, which then diffused away from each other, also preventing the fluorescence recovery of the bleached vesicle (Fig. S3†). This behavior is reminiscent of what was found by Zhu and Szostak in experiments with fatty-acid vesicles, where the kinetic energy of mildly agitated liquid water triggered the division and breaking up of thread-like aggregates.26 In our case, the energy of the laser beam provides the trigger to complete the separation process. Based on our FRAP experiments, it can be concluded that after division the daughter vesicles remain connected by a common membrane neck, which can be broken by additional environmental triggers.
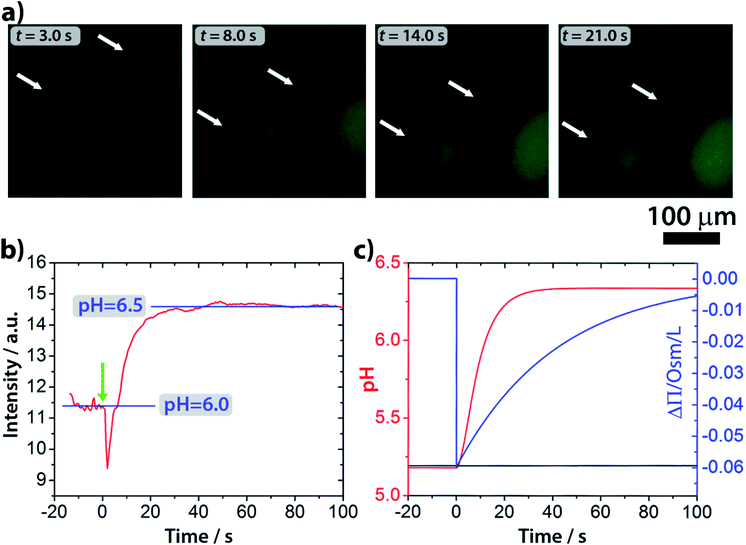
Epifluorescence imaging of the system confirmed that the stages of the division process correlate with the increase of the pH inside the vesicles (Fig. 4a and Video S2†). Based on these measurements, the pH inside the GUVs changes from pH ∼ 6 to ∼6.5 (Fig. 4b and S4†), which, under our experimental conditions, can cause a change of up to 20% (considering pKa = 7.2) in the protonation rate of the HOA molecules.
Interestingly, in almost all successful divisions, the mother vesicles divided into two daughter vesicles. Sometimes, especially when bigger GUVs divided (R > 15 μm), the GUVs budded off several smaller ones. During the transition from a sphere to a prolate spheroid, both the surface area and the volume decreased after the addition of the substrate (area and volume were estimated from the optical micrographs) and at the end of the division process, the volume of the vesicles was found to be decreased by about 25% on average (Fig. 3b), while the average total surface area remained within the 10% of the mother vesicle (Fig. 3c).
We carried out control experiments in a buffered medium (inside and outside of the GUVs) at pH = 6.4 adjusted by a phosphate buffer (0.14 M, K2HPO4/KH2PO4) to check whether the pH change is indeed responsible for the self-division. In the case of buffered media, we did not observe any vesicle divisions, but only the elongation of a few GUVs (Video S3†). This observation shows that pH change is an important ingredient of the division process. Additionally, we investigated the influence of an osmotic shock in the absence of a pH change by two types of control experiments. In the first approach, NaCl (0.1–0.3 M) was added to the external solution in the absence of the substrate urea; the ionic couple Na+Cl− cannot cross the bilayer and creates an outer hypertonic solution. As expected, a few vesicles deflated in time and some of them underwent small deformations, but divisions were never detected. A second check was performed by adding urea in the outer solution, but without encapsulating the enzyme into the lumen of the GUVs; in principle, urea is permeable towards the bilayer, and it should not cause a long term osmotic stress to the membrane. However, the permeability of urea is several orders of magnitude smaller than that of water and a temporary osmotic stress is present until the urea gradient is smoothed out. As in the NaCl case, vesicles became smaller and a few of them underwent deformation, but again, no division was observed. This finding indicates that the osmotic concentration gradient itself is not enough to cause division.
To explain the pH change (induction time and magnitude) and the osmotic concentration gradient inside and outside the GUVs driven by the urea–urease enzymatic reaction, we constructed a simple kinetic model that qualitatively describes the behavior observed in the experiments using the pH-sensitive fluorescent dye. The sketch in Fig. S5† shows all chemical species responsible for the pH changes inside the vesicles and in the outer environment. The enzyme (E) and the fluorescent dye (pyrOH) are confined into the lumen of the vesicles and cannot cross the membranes. The HOA molecules, which participate in the acid–base equilibrium, are considered homogeneously partitioned into the membranes, and both flip-flop movement from one leaflet to the other and the exchange of monomers with the water solution are neglected because of the short timescales of these processes.46 The substrate, urea (S), delivered into the outer solution at time t = 0 in the kinetic simulations, the reaction products, CO2 and NH3, produced inside the vesicles and the acetic acid (HA), added inside and outside the vesicle to lower the initial pH, are free to cross the membrane by passive diffusion. The concentration of each chemical species inside a vesicle changes due to chemical reaction and transport. The corresponding differential equation is as follows (details in the ESI†):
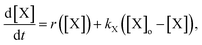 | (1) |
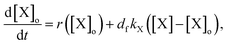 | (2) |
The osmotic concentrations (Π) inside and outside the vesicles were calculated as the sums of the concentrations of the ionic species that cannot cross the membrane due to electro-neutrality constrains (CH3COO−, NH4+, CO32−, and HCO3−), the concentrations of bulky molecules initially encapsulated into the GUVs (urease and pyranine), and the concentration of urea. Here, we considered N identical vesicles having an average radius calculated from the size distribution in Fig. 3a. The results of the numerical simulations (Fig. 4c) are in accordance with the pH dynamics reconstructed from fluorescence time series in Fig. 4b. In fact, the pH jump is about one unit, similar to the experiments, and both the induction (inflection) time (i.e., when the pH increase rate reaches its maximum) and the plateau time are also consistent with the experiments (Fig. 4b and c). We performed simulations by varying those few parameters for which we had only rough estimates, namely the total number of vesicles in the sample (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 < N < 50
000 < N < 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and the average radius of vesicles (5 μm < R < 15 μm), without revealing any significant deviation from what is reported in Fig. 4c. Fig. 4c also shows the simulated osmotic concentration difference (ΔΠ) between the vesicle lumen and the outer solution (volumes are assumed to be constant in the simulations) that explains the volume loss (∼25%) observed during the division process. In fact, such a volume change is enough to smooth out the calculated osmotic concentration gradient, mostly due to the addition of urea (ΔΠ ≃ 60 mM). Fig. 4c also shows that, in the first 20 s, pH increases faster than urea permeates the membrane by passive diffusion; therefore, the deprotonation of the OA must act in synergy with the osmotic stress.
000) and the average radius of vesicles (5 μm < R < 15 μm), without revealing any significant deviation from what is reported in Fig. 4c. Fig. 4c also shows the simulated osmotic concentration difference (ΔΠ) between the vesicle lumen and the outer solution (volumes are assumed to be constant in the simulations) that explains the volume loss (∼25%) observed during the division process. In fact, such a volume change is enough to smooth out the calculated osmotic concentration gradient, mostly due to the addition of urea (ΔΠ ≃ 60 mM). Fig. 4c also shows that, in the first 20 s, pH increases faster than urea permeates the membrane by passive diffusion; therefore, the deprotonation of the OA must act in synergy with the osmotic stress.
To get some insight into how the change in the protonation rate of the HOA molecules at one side of the bilayer affects the inner leaflet of the GUVs, we performed molecular dynamics (MD) simulations (NPT – isothermal–isobaric ensemble – simulations with a semi-isotropic pressure coupling). One of the two leaflets of the POPC/HOA bilayer was deprotonated step by step: in each step 10% of the HOA molecules were deprotonated, then the system was equilibrated for 10 ns, and the process was repeated until all HOA molecules became deprotonated. Fig. S6 and S7† show the results of the MD simulations. Due to the electrostatic repulsion between the negatively charged head groups of the leaflet being deprotonated, the average molecular surface area of this leaflet increased monotonically with the deprotonation ratio, resulting in both an increase in the total surface area of the bilayer and buckling of the membrane towards the deprotonated leaflet (Fig. S6 and S7†). A similar effect due to a pH change was previously observed in a mixed bilayer of lysophosphatidylcholine and free fatty acids.47 The expansion of a POPC/HOA leaflet due to the electrostatic repulsion between the deprotonated HOA molecules was also confirmed by the Wilhelmy film balance experiments at different pHs in buffered media (Fig. S8†).
To understand the division mechanism, we have to bear in mind that both the bilayer-couple (BC)48–51 and the area-difference-elasticity (ADE)51,52 models of membranes predict that any shape transformation of an initially spherical vesicle into a pear-shaped vesicle and, eventually, to two separate vesicles must be driven by two parallel processes: (i) the volume loss of vesicles and (ii) the decrease of the surface area of the inner leaflet relative to the outer one. The volume decrease can be explained by the transport of the water molecules through the bilayer from the vesicles induced by the initial osmotic concentration gradient. The decrease of the surface area is in an apparent contradiction with the results observed in both Wilhelmy film balance experiments and MD simulations. A possible mechanism behind this phenomenon is the formation of protrusions and micro aggregates (possibly vesicles) inside the lumen of the mother protocell (due to the preference of the deprotonated HOA molecules for curved and expanded surfaces) and the dissolution of deprotonated HOA molecules (prompted by their higher water solubility). Such a possibility is in line with both the surface area shrink measured during the division process and the ADE theory. The evidence for the formation of invaginated aggregates inside the lumen of vesicles can be seen in the confocal micrographs reported in Fig. 5.
 | ||
| Fig. 5 Self-division process in a GUV and the formation of protrusions inside the vesicles (indicated by the white arrows) observed by using confocal microscopy. | ||
Note that the relative area difference between the inner and the outer leaflets of a spherical vesicle is 2w/R, where w (a few nm) is the distance between the leaflets, and R is the radius of the vesicle. For our GUVs (5 μm < R < 15 μm) this relative area difference is very small, of the order of 10−3. The shape transformation of a single sphere into two spheres requires only a similarly small amount of relative decrease of the inner leaflet.
Thus, in our interpretation, the initially added urea solution generates osmotic stress, and urea penetrates into GUVs; however, concurrently, some water leaves vesicles to equilibrate the osmotic concentration difference. Since the permeability of water is several orders of magnitude greater than that of urea, the volume of the vesicles decreases. Parallel with this process, the urease–urea reaction starts in the GUVs and the pH of the inner compartment increases due to ammonia production. Any increase in pH (close to the pKa of HOA) inside the vesicles involves an increase in the deprotonation rate of HOA, thus introducing negative charges in the inner leaflets of the GUVs. This charge accumulation affects the membrane stability and induces the formation of oleate aggregates inside the GUV lumen, thereby decreasing the surface area of the inner leaflet with respect to that of the outer one. Both the volume loss and the surface area change between the inner and outer leaflets drives the shape transformation of the GUVs and leads to their self-division.
To highlight the synergy between the action of the osmotic concentration gradient (inducing volume loss) and the pH change inside the vesicles (inducing the decrease of the inner surface area), we carried out two additional sets of experiments. In the first set, we avoided the initial osmotic gradient due to the urea by adjusting the sugar concentration (required by the phase transfer method) in the outer solution. In this case, we observed no division, which means that pH change itself cannot produce a division of GUVs. Similarly, we observed no division if the induction time (clock time) of the enzymatic reaction was set to ∼4 min by increasing the concentration of the acetic acid (1 mM) (reducing the initial pH) inside the vesicles even if the initial osmotic concentration gradient was present. From these observations, we can draw the conclusion that neither the osmotic concentration gradient (responsible for the volume loss) nor the pH change (responsible for the decrease of the inner surface area) alone can induce division. They must act in synergy, approximately on the same time scale.
Conclusions
We presented a simple autonomous internally triggered self-dividing system based on the fission of mixed giant unilamellar vesicles. Unlike previous approaches, the stimulus driving the division process is generated inside the lumen of the vesicles and triggered by cross-membrane transport. Also, the basic chemistry involved in our experiments and the type of membrane-forming amphiphile render this system a plausible model for studying the self-division process of protocells under prebiotic conditions.Experimental
Materials
For the enzymatic reaction, stock solutions were prepared using acetic acid (Carlo Erba), urea (Sigma), and urease (Sigma, Type III, from Jack Beans, typically 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 units per g solid). Glucose and sucrose (Sigma) were used to adjust the density of the solutions for the vesicle preparation; pyranine was chosen for monitoring the pH changes. POPC (Lipoid) and oleic acid (HOA, Sigma-Aldrich) stock solutions were prepared in mineral oil (Sigma-Aldrich M5904). All the reactants were used as received without any further purification. The solutions of urease, sucrose, glucose and oleic acid were freshly prepared daily.
310 units per g solid). Glucose and sucrose (Sigma) were used to adjust the density of the solutions for the vesicle preparation; pyranine was chosen for monitoring the pH changes. POPC (Lipoid) and oleic acid (HOA, Sigma-Aldrich) stock solutions were prepared in mineral oil (Sigma-Aldrich M5904). All the reactants were used as received without any further purification. The solutions of urease, sucrose, glucose and oleic acid were freshly prepared daily.
Preparation of the vesicles
Giant vesicles made of POPC and HOA were prepared using the “droplet (phase) transfer” method.39–41 An Eppendorf tube was filled with 500 μL of an aqueous phase, the so-called outer solution (O-solution) containing 200 mM glucose and 10−3 mM acetic acid and 300 μL of an interfacial phase ([POPC] = 2.6 mM and [HOA] = 2.4 mM in mineral oil). The interface was settled for 10–15 minutes.A second Eppendorf tube was used to prepare a water/oil microemulsion. 20 μL of an aqueous solution, the so-called inner solution (I-solution): 200 mM sucrose, urease 0.5 U mL−1, 1 × 10−3 mM acetic acid and 50 μM pyranine solutions were mixed by pipetting up and down with 600 μL of an oil phase ([POPC] = 2.6 mM and [HOA] = 2.4 mM in mineral oil). This microemulsion was poured over the first Eppendorf tube. The formation of vesicles was facilitated by centrifuging the tube at 6000 rpm for 10 minutes at room temperature (∼22 °C).
After the centrifugation step, a white pellet was visible at the bottom of the Eppendorf tube. The oil phase and the aqueous phase were carefully removed with a micropipette. The pellet was gently washed with 100 μL of O-solution to remove free solutes. 30 μL of pellet were finally resuspended in 60 μL of O-solution.
Observation of the vesicles and their self-division
20 μL of the final diluted solution were placed into a well of a multiwell plate letting the vesicles deposit on the support for few minutes. 10 μL of a solution containing 180 mM urea ([urea]0 = 60 mM), 200 mM glucose and 1 × 10−3 mM acetic acid were added to trigger the division. The urea permeates through the lipid bilayer and it is converted into ammonia. After this addition we covered the multiwell plate with a lid in order to avoid the evaporation of the sample.The number and the size of the vesicles were investigated with an epifluorescence microscope (ORMATEK TL-INV 100). Images were taken every 0.5 s with a CMOS camera (PIXELINK PL-D755CU) both in visible and in fluorescence (λex = 450 nm and λem = 510 nm) mode. Fluorescence intensity was used to characterize the pH change inside the vesicles. Recorded images were analyzed by means of ImageJ software.53
Calibration of the pH was based on the fluorescence intensity. A calibration procedure was performed to relate the fluorescence intensity of pyranine, calculated as the grey-scale level of the images, with the pH-values of the system. The calibration was performed by preparing a series of vesicles containing different buffers (using sodium phosphate monobasic dihydrate (Sigma-Aldrich) and sodium phosphate dibasic heptahydrate (Sigma-Aldrich)) in the pH range of 5.5 and 7.5 (Fig. S4†).
FRAP experiments
In FRAP experiments, the same experimental protocol was applied except that the pyranine was replaced with fluorescein because the latter fluorescent dye is more sensitive to photobleaching. The samples were characterized by confocal laser scanning microscopy with a Leica SP8 X. Images were recorded with an HC PL APO CS2 40×/1.30 OIL objective. Line 488 of an argon laser was used as the excitation source while green fluorescence emission was recorded in the range 500–600 nm. Internal GUV photobleaching was obtained zooming in the target vesicle lumen and harvesting the sample until the fluorescence disappeared. Then, images were recorded every 30 seconds with xyt scan mode.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by National Research, Development and Innovation Office of Hungary (NN125752, K128266 and K131425) and the BME-Nanotechnology FIKP grant of EMMI (BME FIKP-NAT). FR gratefully acknowledges the University of Salerno for supporting this work through the projects ORSA174250 and ORSA167988. FR and ZM gratefully acknowledge the COST action CM1304 “Emergence and Evolution of Complex Chemical Systems” for funding a Short Term Scientific Mission. Prof. Pasquale Stano is gratefully acknowledged for fruitful discussions. Francesca Rossi and dunque studio are gratefully acknowledged for graphical support.Notes and references
- P. L. Luisi, The Emergence of Life: From Chemical Origins to Synthetic Biology, Cambridge University Press, Cambridge, U.K., 2006 Search PubMed.
- P. Luisi, F. Ferri and P. Stano, Naturwissenschaften, 2006, 93, 1–13 CrossRef CAS.
- P. Stano and P. L. Luisi, Chem. Commun., 2010, 46, 3639–3653 RSC.
- P. Stano, G. Rampioni, F. D'Angelo, E. Altamura, F. Mavelli, R. Marangoni, F. Rossi and L. Damiano, in Advances in Bionanomaterials, Springer, Cham, 2018, pp. 141–154 Search PubMed.
- J. W. Szostak, D. P. Bartel and P. L. Luisi, Nature, 2001, 409, 387–390 CrossRef CAS.
- D. Segre, D. Ben-Eli, D. W. Deamer and D. Lancet, Origins Life Evol. Biospheres, 2001, 31, 119–145 CrossRef CAS.
- P. L. Urban, New J. Chem., 2014, 38, 5135–5141 RSC.
- K. Kurihara, Y. Okura, M. Matsuo, T. Toyota, K. Suzuki and T. Sugawara, Nat. Commun., 2015, 6, 8352 CrossRef CAS.
- P. Walde, K. Cosentino, H. Engel and P. Stano, ChemBioChem, 2010, 11, 848–865 CrossRef CAS PubMed.
- A. Küchler, M. Yoshimoto, S. Luginbühl, F. Mavelli and P. Walde, Nat. Nanotechnol., 2016, 11, 409–420 CrossRef PubMed.
- E. Altamura, F. Milano, R. R. Tangorra, M. Trotta, O. H. Omar, P. Stano and F. Mavelli, PNAS, 2017, 114, 3837–3842 CrossRef CAS PubMed.
- K. Ruiz-Mirazo, C. Briones and A. de la Escosura, Chem. Rev., 2014, 114, 285–366 CrossRef CAS PubMed.
- L. Jin, N. P. Kamat, S. Jena and J. W. Szostak, Small, 2018, 14, 1704077 CrossRef PubMed.
- K. Morigaki and P. Walde, Curr. Opin. Colloid Interface Sci., 2007, 12, 75–80 CrossRef CAS.
- P. L. Luisi and P. Walde, Giant Vesicles, Wiley-Interscience, Chichester, UK, 2000 Search PubMed.
- P. L. Luisi and F. J. Varela, Origins Life Evol. Biospheres, 1989, 19, 633–643 CrossRef CAS.
- P. A. Bachmann, P. Walde, P. L. Luisi and J. Lang, J. Am. Chem. Soc., 1990, 112, 8200–8201 CrossRef CAS.
- P. A. Bachmann, P. L. Luisi and J. Lang, Nature, 1992, 357, 57–59 CrossRef CAS.
- P. Walde, R. Wick, M. Fresta, A. Mangone and P. L. Luisi, J. Am. Chem. Soc., 1994, 116, 11649–11654 CrossRef CAS.
- N. Berclaz, M. Müller, P. Walde and P. L. Luisi, J. Phys. Chem. B, 2001, 105, 1056–1064 CrossRef CAS.
- P. Stano, E. Wehrli and P. L. Luisi, J. Phys.: Condens. Matter, 2006, 18, S2231–S2238 CrossRef CAS.
- J. Käs and E. Sackmann, Biophys. J., 1991, 60, 825–844 CrossRef.
- K. Takakura, T. Toyota and T. Sugawara, J. Am. Chem. Soc., 2003, 125, 8134–8140 CrossRef CAS.
- T. Baumgart, S. T. Hess and W. W. Webb, Nature, 2003, 425, 821–824 CrossRef CAS.
- T. Toyota, K. Takakura, Y. Kageyama, K. Kurihara, N. Maru, K. Ohnuma, K. Kaneko and T. Sugawara, Langmuir, 2008, 24, 3037–3044 CrossRef CAS.
- T. F. Zhu and J. W. Szostak, J. Am. Chem. Soc., 2009, 131, 5705–5713 CrossRef CAS.
- P. Peterlin, V. Arrigler, K. Kogej, S. Svetina and P. Walde, Chem. Phys. Lipids, 2009, 159, 67–76 CrossRef CAS.
- K. Kurihara, M. Tamura, K.-I. Shohda, T. Toyota, K. Suzuki and T. Sugawara, Nat. Chem., 2011, 3, 775–781 CrossRef CAS.
- Y. Sakuma and M. Imai, Phys. Rev. Lett., 2011, 107, 198101 CrossRef.
- J. Dervaux, V. Noireaux and A. J. Libchaber, Eur. Phys. J. Plus, 2017, 132, 284 CrossRef.
- M. Fiore, O. Maniti, A. Girard-Egrot, P.-A. Monnard and P. Strazewski, Angew. Chem., Int. Ed., 2018, 57, 282–286 CrossRef CAS PubMed.
- M. Kurisu, H. Aoki, T. Jimbo, Y. Sakuma, M. Imai, S. Serrano-Luginbühl and P. Walde, Commun. Chem., 2019, 2(117), 1–10 CAS.
- J. M. Castro, H. Sugiyama and T. Toyota, Sci. Rep., 2019, 9, 165 CrossRef PubMed.
- B. Novák and J. J. Tyson, Nat. Rev. Mol. Cell Biol., 2008, 9, 981–991 CrossRef.
- T. Litschel, B. Ramm, R. Maas, M. Heymann and P. Schwille, Angew. Chem., Int. Ed., 2018, 57, 16286–16290 CrossRef CAS.
- K. Ikari, Y. Sakuma, T. Jimbo, A. Kodama, M. Imai, P.-A. Monnard and S. Rasmussen, Soft Matter, 2015, 11, 6327–6334 RSC.
- B. Krajewska, J. Mol. Catal. B: Enzym., 2009, 59, 9–21 CrossRef CAS.
- G. Hu, J. A. Pojman, S. K. Scott, M. M. Wrobel and A. F. Taylor, J. Phys. Chem. B, 2010, 114, 14059–14063 CrossRef CAS.
- S. Pautot, B. J. Frisken and D. A. Weitz, Langmuir, 2003, 19, 2870–2879 CrossRef CAS.
- P. Stano, T. P. de Souza, P. Carrara, E. Altamura, E. D'Aguanno, M. Caputo, P. L. Luisi and F. Mavelli, Mech. Adv. Mater. Struct., 2015, 22, 748–759 CrossRef.
- Y. Miele, T. B. Jr, A. F. Taylor, P. Stano and F. Rossi, in Advances in Artificial Life, Evolutionary Computation and Systems Chemistry, ed. F. Rossi, F. Mavelli, P. Stano and D. Caivano, Springer International Publishing, 2016, pp. 197–208 Search PubMed.
- Y. Miele, T. Bánsági, A. F. Taylor and F. Rossi, in Advances in Bionanomaterials, ed. S. Piotto, F. Rossi, S. Concilio, E. Reverchon and G. Cattaneo, Springer International Publishing, Cham, 2018, pp. 63–74 Search PubMed.
- A. Walter and J. Gutknecht, J. Membr. Biol., 1986, 90, 207–217 CrossRef CAS PubMed.
- S. Morlot, V. Galli, M. Klein, N. Chiaruttini, J. Manzi, F. Humbert, L. Dinis, M. Lenz, G. Cappello and A. Roux, Cell, 2012, 151, 619–629 CrossRef CAS PubMed.
- C. François-Martin, J. E. Rothman and F. Pincet, PNAS, 2017, 114, 1238–1241 CrossRef PubMed.
- F. Kamp and J. A. Hamilton, PNAS, 1992, 89, 11367–11370 CrossRef CAS PubMed.
- K. Lähdesmäki, O. H. S. Ollila, A. Koivuniemi, P. T. Kovanen and M. T. Hyvönen, BBA, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 938–946 CrossRef PubMed.
- M. P. Sheetz and S. J. Singer, PNAS, 1974, 71, 4457–4461 CrossRef CAS PubMed.
- S. Svetina and B. Žekš, Eur. Biophys. J., 1989, 17, 101–111 CrossRef CAS.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A, 1991, 44, 1182–1202 CrossRef CAS PubMed.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- L. Miao, U. Seifert, M. Wortis and H.-G. Döbereiner, Phys. Rev. E, 1994, 49, 5389–5407 CrossRef CAS.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Description of the chemical model for the confined urea–urease enzymatic reaction. Descriptions of molecular dynamics simulations and film balance experiments. Description of videos (Videos S1–S3). Supporting Tables S1, S2 and Fig. S1–S8. See DOI: 10.1039/c9sc05195c |
| This journal is © The Royal Society of Chemistry 2020 |