A perfect triangular dysprosium single-molecule magnet with virtually antiparallel Ising-like anisotropy†
Guang
Lu‡
a,
Yang
Liu‡
a,
Wei
Deng
a,
Guo-Zhang
Huang
a,
Yan-Cong
Chen
 a,
Jun-Liang
Liu
a,
Jun-Liang
Liu
 *a,
Zhao-Ping
Ni
*a,
Zhao-Ping
Ni
 *a,
Marcus
Giansiracusa
*a,
Marcus
Giansiracusa
 *b,
Nicholas F.
Chilton
*b,
Nicholas F.
Chilton
 *b and
Ming-Liang
Tong
*b and
Ming-Liang
Tong
 a
a
aKey Lab of Bioinorganic and Synthetic Chemistry of Ministry of Education, School of Chemistry, Sun Yat-Sen University, Guangzhou 510275, P. R. China. E-mail: liujliang5@mail.sysu.edu.cn; nizhp@mail.sysu.edu.cn
bDepartment of Chemistry, School of Natural Sciences, The University of Manchester, Oxford Road, Manchester M13 9PL, UK. E-mail: nicholas.chilton@manchester.ac.uk
First published on 6th July 2020
Abstract
We report a trinuclear dysprosium single-molecule magnet, [Dy3(μ3-CO3)(Clbbpen)3](CF3SO3)·6MeCN, which has a perfectly equilateral triangular structure. The Ising-like anisotropy of each Dy(III) site is oriented almost normal to the triangular plane, and magnetic dipole interactions between the spins cause an antiparallel Ising ground state. Crossing of the antiferromagnetic states by the ferromagnetic state occurs at ca. 0.2 T and gives rise to a characteristic step in magnetic hysteresis loops. This molecule thus serves as a perfectly triangular model system to explore frustrated Ising anisotropy.
Introduction
Trinuclear complexes with a triangular arrangement of spins are of great interest in molecular magnetism, since their geometry is prototypical to realize toroidal magnetism1–6 and spin frustration,7–10 but they can also function as single-molecule magnets (SMMs).11–16 Competing antiferromagnetic interactions can cause spin frustration, which in extended lattices gives rise to exotic quantum states, where the trigonal Kagomé lattice is one of the most famous examples.17–26 In zero-dimensional systems, such as molecular magnets, frustration leads to degenerate spin ground states.7 Indeed, triangular trimetallic complexes are the simplest model of this phenomenon, and are small enough to obtain precise information on the quantum states,27–34 and thus explain the observed magnetic phenomena.Antisymmetric and anisotropic exchange interactions can remove the degeneracy of the frustrated ground state,10 and thus magnetically isotropic ions are most common for the observation of frustration in C3-symmetric molecules.35–40 While not impossible, designing spin frustration on the basis of strongly anisotropic ions (e.g. Ising spins) is non-trivial, since it is difficult to control the orientations of each principal magnetic axis in a molecule. The ideal frustrated Ising triangle would consist of a perfect equilateral triangle of spins whose principal magnetic axes are all perpendicular to the plane of the triangle, so that the dipolar magnetic coupling leads to a frustrated ground state.
While there have been some examples of trigonal Dy3 complexes previously, these compounds either are not C3 symmetric,13 have in-plane principal magnetic axes,14,15 or show large tilt angles away from the normal direction.11 Inspired by our recent work on highly-anisotropic Dy(III) ions in pentagonal bipyramidal geometries, e.g. the high-performance [Dy(bbpen)Br]41a and the para-/diamagnetic cyanometallate-bridged [Dy2(bbpen)2{M(CN)6}]− (M = Fe, Co) via building block approaches,41b herein we have replaced the terminal anion with a C3-symmetric μ3-η2:η2:η2 bridging CO32− ligand, yielding [Dy3(μ3-CO3)(Clbbpen)3](CF3SO3)·6MeCN (1, H2Clbbpen = N,N‘-bis(5-chloro-2-hydroxybenzyl)-N,N‘-bis(2-picolyl)ethylenediamine). This new trinuclear molecular magnet has a crystallographically-enforced equilateral triangular geometry, and herein we investigate its magnetic properties such as the multi-step hysteresis loops related to the Ising-like ground states, combining experimental measurements and electronic structure calculations.
Results and discussion
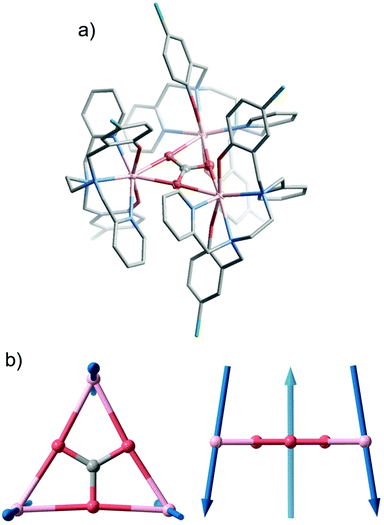
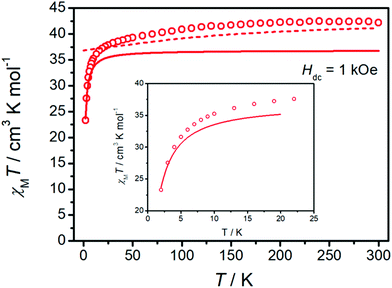
The crystal structure of 1 was determined by single-crystal X-ray diffraction (Fig. 1a and Table S1†). Compound 1 crystallizes in trigonal space group R32, and the asymmetric unit contains only one half of Dy(III) ion, one half of Clbbpen2− ligand, one third of CO32− and one sixth of CF3SO3−. As illustrated in Fig. 1a, each Dy(III) is supported by the hexadentate Clbbpen2− ligand, connecting with four N atoms from amines/pyridines and two O atoms from phenols. The three Dy(III) are bridged by a central CO32− in the μ3-η2:η2:η2 coordination mode (Fig. 1a), forming an equilateral triangle. Due to the trigonal symmetry, all the intramolecular Dy⋯Dy distances are perfectly identical (4.828 Å). For compound 1, the axial and the equatorial Dy–O distances are 2.211 and 2.417 Å, respectively, and the equatorial Dy–N distances are 2.504 and 2.655 Å. The axial O–Dy–O angle is nearly linear at 161.1°. The short axial Dy–O bonds, near linear axial O–Dy–O angle, and longer equatorial bonds should generate large magnetic anisotropy at each Dy site, as observed for [Dy(bbpen)Br] and its anologues.41The variable temperature magnetic susceptibility of a polycrystalline sample of 1 was measured under a 1 kOe direct current (dc) field (Fig. 2). The χMT value at room temperature is 42.19 cm3 K mol−1, in good agreement with three non-interacting Dy(III) ions (6H15/2, 42.51 cm3 K mol−1), and that calculated ab initio (41.14 cm3 K mol−1). We note that the 2.5% discrepancy between experimental and calculated data at high temperatures is likely due a combination of uncertainties in sample mass and diamagnetic corrections, as well as the approximations introduced in the ab initio calculations. Upon cooling, the value gradually decreases to 23.31 cm3 K mol−1 at 2 K, which is generally due to the depopulation of crystal field states of the J = 15/2 manifold, though might also indicate magnetic interactions or slow magnetic dynamics at low temperatures. The magnetization saturates at 15 NμB at 5 K and 7 T (Fig. S4†), indicating that each Dy(III) ion has a mJ = ±15/2 ground state.42 Zero-field-cooled and field-cooled (ZFC-FC) magnetizations (Fig. S6†) diverge below 4.2 K, suggesting slow magnetic dynamics at low temperatures.
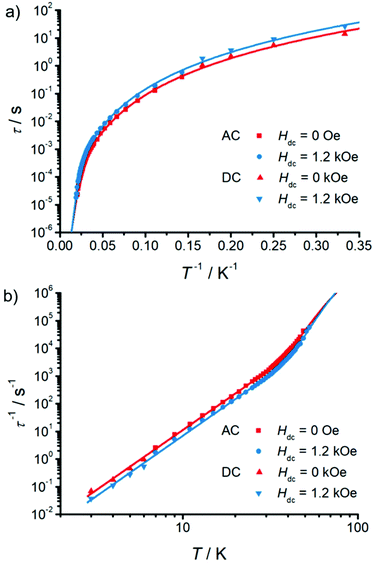
Investigating the magnetic dynamics of 1 with temperature- and frequency-dependent alternating current (ac) magnetic susceptibility, reveals the typical patterns of SMM behaviour (Fig. 3 and S7–S9†). Two peaks are observed in the out-of-phase (χM′′) signal below 21 K (Fig. S9a†), while only one peak is observed above 21 K (Fig. S9b†). The presence of two peaks indicates the existence of two relaxation times (a fast relaxation, FR, and a slow relaxation, SR, component); such behaviour has been reported previously that could involve the high-density exchange spectrum.11,15,16,43–49 Fitting the low temperature data with the sum of two generalized Debye functions gives αFR = 0.34–0.49 and αSR = 0.003–0.023 (Fig. S9a and Table S4†), while the high-temperature data are well modelled with a single generalized Debye function, giving α = 0.027–0.076 (Fig. S9b and Table S5†). The αFR values are very large, indicating a large distribution of relaxation times, while those for αSR and those at high temperatures are very small, indicating a narrow distribution for relaxation times.50 Application of a magnetic field has a very small effect on the relaxation times (Fig. 4, S11, S12 and Table S8†), where the most obvious change is suppression of the FR process (Fig. S8b†); a generalized Debye fit of ac data in an optimum field of 1.2 kOe also show a reasonably narrow distribution of relaxation times with α = 0.006–0.10 (7–53 K, Fig. S10 and Table S6†). We also examine the relaxation time at lower temperatures (3–6 K) using dc magnetization decay experiments (Fig. S13 and Table S7†), both in zero and 1.2 kOe fields; the β values are 0.89–0.99 (0 kOe) and 0.80–0.85 (1.2 kOe) and thus suggest a narrow-to-moderate distribution of relaxation times, consistent with the ac data.51
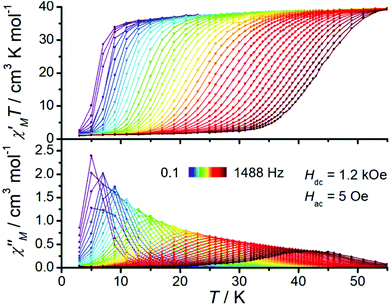 | ||
| Fig. 3 Variable-frequency temperature-dependent ac magnetic susceptibilities for 1 under 1.2 kOe dc field. The solid lines are guided for the eyes. | ||
Examination of the temperature dependence of the relaxation times (we only discuss the SR process in zero field, due to the large distribution in the FR relaxation times and limited data) shows a strongly-temperature-dependent regime at high temperatures, and a power-law temperature dependence at lower temperatures, suggesting exponential (Orbach-like) and Raman relaxation mechanisms, respectively (Fig. 4). These data can be modelled with τ−1 = τ0−1exp(−Ueff/kBT) + CTn, with best-fit parameters Ueff/kB = 504(25) K, τ0 = 1.3(7)×10−9 s, C = 4.5(3)×10−4 s−1 K−n and n = 4.39(2) for the zero-field data, and Ueff/kB = 577(26) K, τ0 = 4.5(24)×10−10 s, C = 2.6(2)×10−4 s−1 K−n and n = 4.42(2) for the 1.2 kOe data.
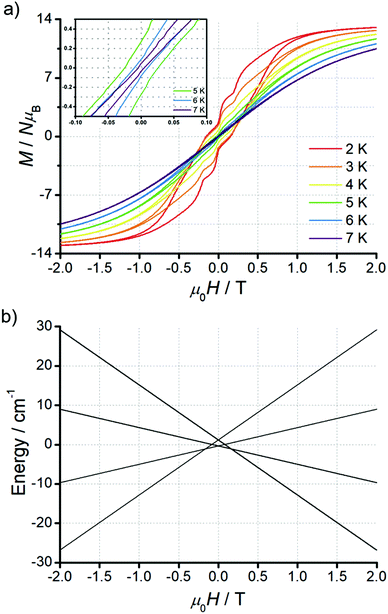
Magnetic hysteresis loops can be observed for 1 up to 6 K (0.02 T s−1, Fig. 5a), where loops at the lowest temperatures show clear steps at ca. 0.2 and 0 T. Indeed, we also observe a slight drop in the relaxation time in field-dependent ac susceptibility measurements at 0.2 T at a higher temperature of 12 K (Fig. S12†), supporting the field position of this fast-relaxation event. Both experimental results suggest the existence of level (anti-)crossings between ground and excited states that are polarized by the applied magnetic fields, which may be related to the frustrated Ising ground states (see theoretical analysis and discussions below).
To examine the electronic structure of the Dy(III) ions, we have performed complete active space self-consistent field spin–orbit (CASSCF-SO) calculations on the single unique Dy site in 1 (see ESI† for details). We find that the ground state is mJ = ±15/2, with a first excited mJ = ±13/2 state at 439 K. The second excited state is reasonably well-described as 86% mJ = ±11/2 (825 K), but the third excited state (992 K) is strongly mixed (Table S9†). Most importantly, however, we find that the principal magnetic axis for each Ising-like Dy(III) site in 1 is almost perpendicular to the plane of the triangle (Fig. 1b); suggesting that 1 may possess near-ideal geometry to exhibit frustrated Ising behaviour. This is in contrast to most other Dy3 triangles that have been studied with a focus on their toroidal magnetic ground states.1,2,4–6 In those cases, the Ising-like magnetic anisotropy of the Dy(III) sites is oriented in the plane of the triangle at tangents to the vertices, and because the local magnetic anisotropy is far stronger than the magnetic interactions between the ions, the ground state is a pair of chiral non-magnetic states (Scheme 1).1c
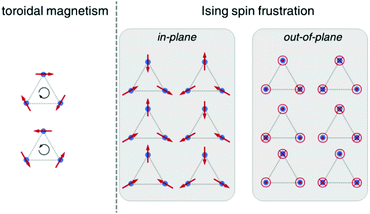 | ||
| Scheme 1 Representations of toroidal magnetism and Ising spin frustration as in-plane type and out-of-plane type (this work). | ||
To start understanding the magnetic properties of 1, we first consider a perfect equilateral Ising triangle (principal magnetic axes perpendicular to the triangular plane). The Dy(III) ions are described as perfect mJ = ±15/2 states by Seff = 1/2 with axial gz = 20 (gxy = 0), where z is the normal of the triangle. Assuming negligible superexchange and dominant dipolar interactions (eqn (1)), the coupling between these spins yields only Jzz non-zero, corresponding to a perfect frustrated Ising system.7
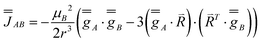 | (1) |
For this example, we use Dy–Dy distance from 1 (4.828 Å) to obtain Jzz = −0.770 cm−1 (as the only non-zero entry of 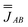 ), where the z axis is defined by the C3 axis of the ideal triangular system. The negative value for Jzz is due to the dipolar magnetic field of each spin and leads to a frustrated ground state. The magnetic properties of such a triangle can be modelled by diagonalization of Hamiltonian eqn (2) using PHI.52
), where the z axis is defined by the C3 axis of the ideal triangular system. The negative value for Jzz is due to the dipolar magnetic field of each spin and leads to a frustrated ground state. The magnetic properties of such a triangle can be modelled by diagonalization of Hamiltonian eqn (2) using PHI.52
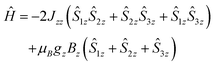 | (2) |
The frustrated ground state is six-fold degenerate and arises from two aligned spins and one inverted spin (↑↑↓, ↑↓↑, ↓↑↑, ↓↓↑, ↓↑↓ and ↑↓↓), while the first excited state at 1.54 cm−1 is doubly degenerate from the ferromagnetic alignment of the spins (↑↑↑ and ↓↓↓). Due to the pure Ising doublets of each site, all states are non-magnetic in the plane of the triangle, however both states are magnetic with a field perpendicular to the plane of the triangle (Fig. 5b); n.b. this is the opposite to toroidal magnetic states. The excited ferromagnetic state shows a crossing with the ground frustrated states in a field of ca. 0.17 T (Fig. 5b), which would be directly observable in mK single-crystal/powder magnetization experiments (Fig. S14†), and indirectly in powder magnetic susceptibility measurements (Fig. S15†). Again, this idealised model can already explain the experimentally observed steps at ca. 0.2 and 0 T in the hysteresis loop of 1 (Fig. 5a): these steps are characteristic of quantum tunnelling of magnetization (QTM), which arises from enhanced relaxation where there is a (anti-)crossing between states.
Moving to the specific case of 1, we now implement a model based on the CASSCF-SO-calculated properties of the ground Kramers doublets for the Dy sites (they are all the same due to three-fold crystallographic symmetry, Tables S9 and S10†): the g-values are not perfectly Ising (gx = 0, gy = 0.0005, gz = 19.82) and the orientation of gz is not perpendicular to the triangular plane but slightly tilted away by ca. 10° (Fig. 1b and Table S10†). Using this model (Table S10,† where z remains defined by the C3 axis, y is parallel to the Dy1–Dy3 vector, and x is their cross product), the dipolar interaction matrices between the ions (in cm−1) are given in eqn (3)–(5), which can be incorporated in the full Hamiltonian eqn (7) and solved with PHI.52 Note that eqn (3)–(5) are related by a 2π/3 rotation around z, such that 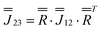 and
and 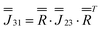 , where
, where 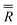 is given in eqn (6).
is given in eqn (6).
 | (3) |
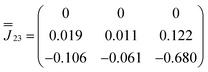 | (4) |
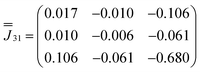 | (5) |
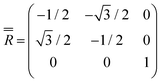 | (6) |
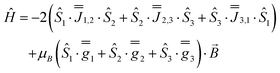 | (7) |
This purely dipolar interaction agrees well with the experimental magnetic data for this compound at low temperatures (Fig. 2 and S4†), and predicts an anti-crossing between the ferro- and antiferromagnetic states at ca. 0.15 T (Fig. S16†) in good agreement with the hysteresis data, suggesting that the superexchange contribution is minimal here, similarly as found directly for a Dy2 species.53 Compared to our model of the perfect frustrated Ising triangle, the six-fold degenerate frustrated ground state in 1 is split into three doublets at 0, 0.10 and 0.18 cm−1 respectively (which represent mixed wavefunction composed of the various antiferromagnetic combinations), while the excited ferromagnetic state lies at 1.47 cm−1. The lower symmetry at the Dy(III) sites and the misalignment of the magnetic axes means that some states are now weakly magnetic in the plane of the triangle (Fig. S17†) and the crossing of the ground state by the excited ferromagnetic states is smeared out over a wider field range (Fig. S16†). However, the degeneracy breaking is small (0.18 vs. 1.47 cm−1), and thus, much as [Dy3(μ3-OH)2(o-vanillin)3Cl(H2O)5]Cl3·4H2O is regarded as the archetypal molecular toroic,1,21 can be regarded as the archetypal molecular frustrated Ising magnet.
Conclusions
By utilizing a strongly anisotropic Dy(III) building unit and a C3-symmetric CO32− ligand, we have prepared a trinuclear dysprosium triangle with a crystallographically-enforced equilateral form. The molecule shows SMM properties with hysteresis loops visible up to 6 K, but most interestingly exhibits a clear step at ca. 0.2 T in low-temperature hysteresis data. A simple dipolar model suggests that this step arises from crossings between the ferromagnetic and near-degenerate frustrated Ising ground states. We anticipate that this molecule will be a useful model to probe Ising frustration in further detailed experimental efforts.Experimental section
Materials and methods
All reactions and manipulations were carried out under aerobic conditions. The ligand N,N′-bis(5-chloro-2-hydroxybenzyl)-N,N′-bis(2-picolyl)ethylenediamine (H2Clbbpen) was prepared in good yield according to the reported methods.54 All other starting reagents were commercially available and used without further purification. The C, H, and N microanalyses were performed with an Elementar Vario-EL CHNS elemental analyzer. The FT-IR spectra were recorded from KBr pellets in the range 4000–400 cm−1 on an EQUINOX 55 spectrometer. Thermogravimetric analysis was carried out on a NETZSCH TG209F3 thermogravimetric analyzer. Ac magnetic measurements were performed with a 5 Oe oscillating field. Magnetic susceptibility measurements were performed with a Quantum Design PPMS VSM and MPMS XL-7 SQUID. Data were corrected for the diamagnetic contribution calculated from Pascal constants. X-ray powder diffraction intensities for polycrystalline samples were measured on Bruker D8 Advance Diffractometer (Cu-Kα, λ = 1.54056 Å). Single-crystal diffraction data were collected on a Bruker D8 QUEST diffractometer with Mo-Kα radiation (λ = 0.71073 Å) for complex 1. The structures were solved based on SHELXS methods by using OLEX2 program,55,56 and all non-hydrogen atoms were refined anisotropically by least-squares on F2 using the SHELXL.57Computational details
We have performed complete active space self-consistent field spin–orbit (CASSCF-SO) calculations on the X-ray structure of 1 with no optimisation using MOLCAS 8.0.58 The DyIII ion was described using the ANO-RCC-VTZP basis, the first coordination sphere atoms with the ANO-RCC-VDZP basis and all other atoms described with the ANO-RCC-VDZ basis.59,60 The metal centres not in focus of the calculation were substituted for diamagnetic LuIII ions with the ANO-RCC-VDZ basis. We employed Cholesky decomposition of the two electron integrals with a threshold of 10−8. The active space incorporated the 9 4f electrons of Dy(III) in seven 4f orbitals. State-averaged CASSCF calculations were performed for 21 sextet, 224 quartet and 490 doublet spin states, and then 21 sextets, 128 quartets and 130 doublets were mixed by SO coupling in the RASSI routine. The wavefunctions were extracted using SINGLE_ANISO where the quantisation axis was the principal gz-value of the ground Kramers doublet.61 As 1 is symmetric, only one calculation was performed owing to the crystallographic symmetry.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Research and Development Program of China (2018YFA0306001), the NSFC (Grant No., 21620102002, 21771200, 21822508, 21821003), and the Pearl River Talent Plan of Guangdong (2017BT01C161). NFC thanks The Royal Society for a University Research Fellowship and MJG thanks The University of Manchester for a President's Doctoral Scholarship award.Notes and references
- (a) L. Ungur, S.-Y. Lin, J. Tang and L. F. Chibotaru, Single-molecule toroics in Ising-type lanthanide molecular clusters, Chem. Soc. Rev., 2014, 43, 6894–6905 RSC; (b) L. Ungur, W. Van den Heuvel and L. F. Chibotaru, Ab initio investigation of the non-collinear magnetic structure and the lowest magnetic excitations in dysprosium triangles, New J. Chem., 2009, 33, 1224–1230 RSC; (c) L. F. Chibotaru, L. Ungur and A. Soncini, The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment, Angew. Chem., Int. Ed., 2008, 47, 4126–4129 CrossRef CAS PubMed.
- J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Dysprosium Triangles Showing Single-Molecule Magnet Behavior of Thermally Excited Spin States, Angew. Chem., Int. Ed., 2006, 45, 1729–1733 CrossRef CAS PubMed.
- S.-Y. Lin, W. Wernsdorfer, L. Ungur, A. K. Powell, Y.-N. Guo, J. Tang, L. Zhao, L. F. Chibotaru and H.-J. Zhang, Coupling Dy3 Triangles to Maximize the Toroidal Moment, Angew. Chem., Int. Ed., 2012, 51, 12767–12771 CrossRef CAS PubMed.
- J. Luzon, K. Bernot, I. J. Hewitt, C. E. Anson, A. K. Powell and R. Sessoli, Spin Chirality in a Molecular Dysprosium Triangle: The Archetype of the Noncollinear Ising Model, Phys. Rev. Lett., 2008, 100, 247205 CrossRef PubMed.
- S. K. Langley, K. R. Vignesh, T. Gupta, C. J. Gartshore, G. Rajaraman, C. M. Forsyth and K. S. Murray, New examples of triangular terbium(III) and holmium(III) and hexagonal dysprosium(III) single molecule toroics, Dalton Trans., 2019, 48, 15657–15667 RSC.
- Y.-X. Wang, W. Shi, H. Li, Y. Song, L. Fang, Y. Lan, A. K. Powell, W. Wernsdorfer, L. Ungur, L. F. Chibotaru, M. Shen and P. Cheng, A single-molecule magnet assembly exhibiting a dielectric transition at 470 K, Chem. Sci., 2012, 3, 3366–3370 RSC.
- O. Kahn, Competing spin interactions and degenerate frustration for discrete molecular species, Chem. Phys. Lett., 1997, 265, 109–114 CrossRef CAS.
- J. Schnack, Effects of frustration on magnetic molecules: a survey from Olivier Kahn until today, Dalton Trans., 2010, 39, 4677–4686 RSC.
- M. L. Baker, G. A. Timco, S. Piligkos, J. S. Mathieson, H. Mutka, F. Tuna, P. Kozłowski, M. Antkowiak, T. Guidi, T. Gupta, H. Rath, R. J. Woolfson, G. Kamieniarz, R. G. Pritchard, H. Weihe, L. Cronin, G. Rajaraman, D. Collison, E. J. L. McInnes and R. E. P. Winpenny, A classification of spin frustration in molecular magnets from a physical study of large odd-numbered-metal, odd electron rings, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19113–19118 CrossRef CAS PubMed.
- J. Yoon and E. I. Solomon, Electronic structures of exchange coupled trigonal trimeric Cu(II) complexes: Spin frustration, antisymmetric exchange, pseudo-A terms, and their relation to O2 activation in the multicopper oxidases, Coord. Chem. Rev., 2007, 251, 379–400 CrossRef CAS.
- M. M. Hänninen, A. J. Mota, D. Aravena, E. Ruiz, R. Sillanpää, A. Camón, M. Evangelisti and E. Colacio, Two C3-Symmetric Dy3III Complexes with Triple Di-μ-methoxo-μ-phenoxo Bridges, Magnetic Ground State, and Single-Molecule Magnetic Behavior, Chem. – Eur. J., 2014, 20, 8410–8420 CrossRef PubMed.
- K. R. Vignesh, A. Soncini, S. K. Langley, W. Wernsdorfer, K. S. Murray and G. Rajaraman, Ferrotoroidic ground state in a heterometallic {CrIIIDyIII6} complex displaying slow magnetic relaxation, Nat. Commun., 2017, 8, 1023 CrossRef PubMed.
- Y.-S. Meng, Y.-S. Qiao, M.-W. Yang, J. Xiong, T. Liu, Y.-Q. Zhang, S.-D. Jiang, B.-W. Wang and S. Gao, Weak exchange coupling effects leading to fast magnetic relaxations in a trinuclear dysprosium single-molecule magnet, Inorg. Chem. Front., 2020, 7, 447–454 RSC.
- (a) R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, K. Krämer, S.-X. Liu, S. Decurtins, A. Popov, S. Yang, L. Dunsch and T. Greber, Tunneling, remanence, and frustration in dysprosium-based endohedral single-molecule magnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 060406 CrossRef; (b) V. Vieru, L. Ungur and L. F. Chibotaru, Key Role of Frustration in Suppression of Magnetization Blocking in Single-Molecule Magnets, J. Phys. Chem. Lett., 2013, 4, 3565–3569 CrossRef CAS.
- S.-G. Wu, C.-Y. Zhan, G.-Z. Huang, Z.-Y. Ruan, J.-L. Liu and M.-L. Tong, Slow magnetic dynamics in centrosymmetric didysprosium and equilateral triangular tridysprosium molecules, Dalton Trans., 2020, 49, 4164–4171 RSC.
- S.-Y. Lin, Y.-N. Guo, Y. Guo, L. Zhao, P. Zhang, H. Ke and J. Tang, Macrocyclic ligand encapsulating dysprosium triangles: axial ligands perturbed magnetic dynamics, Chem. Commun., 2012, 48, 6924–6926 RSC.
- P. W. Anderson, Resonating valence bonds: A new kind of insulator?, Mater. Res. Bull., 1973, 8, 153–160 CrossRef CAS.
- P. W. Anderson, The Resonating Valence Bond State in La2CuO4 and Superconductivity, Science, 1987, 235, 1196–1198 CrossRef CAS PubMed.
- S. Yan, D. A. Huse and S. R. White, Spin-Liquid Ground State of the S=1/2 Kagome Heisenberg Antiferromagnet, Science, 2011, 332, 1173–1176 CrossRef CAS PubMed.
- M. R. Norman, Colloquium: Herbertsmithite and the search for the quantum spin liquid, Rev. Mod. Phys., 2016, 88, 041002 CrossRef.
- M. P. Shores, E. A. Nytko, B. M. Bartlett and D. G. Nocera, A Structurally Perfect S=1/2 Kagomé Antiferromagnet, J. Am. Chem. Soc., 2005, 127, 13462–13463 CrossRef CAS PubMed.
- X.-Y. Wang, L. Wang, Z.-M. Wang and S. Gao, Solvent-Tuned Azido-Bridged Co2+ Layers: Square, Honeycomb, and Kagomé, J. Am. Chem. Soc., 2006, 128, 674–675 CrossRef CAS PubMed.
- J. N. Behera and C. N. R. Rao, A Ni2+ (S=1) Kagome Compound Templated by 1,8-Diazacubane, J. Am. Chem. Soc., 2006, 128, 9334–9335 CrossRef CAS PubMed.
- S. K. Pati and C. N. R. Rao, Role of the spin magnitude of the magnetic ion in determining the frustration and low-temperature properties of kagome lattices, J. Chem. Phys., 2005, 123, 234703 CrossRef PubMed.
- L.-F. Wang, C.-J. Li, Y.-C. Chen, Z.-M. Zhang, J. Liu, W.-Q. Lin, Y. Meng, Q.-W. Li and M.-L. Tong, Spin Frustration in a Family of Pillared Kagomé Layers of High-Spin Cobalt(II) Ions, Chem. – Eur. J., 2015, 21, 2560–2567 CrossRef CAS PubMed.
- H. Xue, Y. Yang, F. Gao, Y. Chong and B. Zhang, Acoustic higher-order topological insulator on a kagome lattice, Nat. Mater., 2019, 18, 108–112 CrossRef CAS PubMed.
- M. I. Belinsky, Spin-frustrated V3 and Cu3 nanomagnets with Dzialoshinsky–Moriya exchange. 1. Inelastic neutron scattering and EPR in scalene, isosceles and equilateral trimers, Chem. Phys., 2009, 361, 137–151 CrossRef CAS.
- B. Cage, F. A. Cotton, N. S. Dalal, E. A. Hillard, B. Rakvin and C. M. Ramsey, Observation of Symmetry Lowering and Electron Localization in the Doublet-States of a Spin-Frustrated Equilateral Triangular Lattice: Cu3(O2C16H23)·1.2C6H12, J. Am. Chem. Soc., 2003, 125, 5270–5271 CrossRef CAS PubMed.
- M. I. Belinsky, Field-dependent spin chirality and frustration in V3 and Cu3 nanomagnets in transverse magnetic field. 1. Correlations between variable planar spin configurations, vector and scalar chiralities and magnetization, Chem. Phys., 2014, 435, 62–94 CrossRef CAS.
- H. Wei, B. Wang and Z. Chen, Magnetic exchange of trinuclear spin frustration system: CASPT2 and density functional theory study on hydroxo-bridged chromium complex [Cr3(NH3)10(OH)4]·Br5, Chem. Phys. Lett., 2005, 407, 147–152 CrossRef CAS.
- C. P. Raptopoulou, V. Tangoulis and V. Psycharis, Synthesis and Structural, Spectroscopic, and Magnetic Characterization of (NH4)[Fe3(μ3-OH)(H2L)3(HL)3] (H3L=Orotic Acid) Presenting Two Novel Metal-Binding Modes of the Orotate Ligand: The Case of a Spin-Frustrated System, Inorg. Chem., 2000, 39, 4452–4459 CrossRef CAS.
- Y. Yu, C. Li, B. Yin, J.-L. Li, Y.-H. Huang, Z.-Y. Wen and Z.-Y. Jiang, Are trinuclear superhalogens promising candidates for building blocks of novel magnetic materials? A theoretical prospect from combined broken-symmetry density functional theory and ab initio study, J. Chem. Phys., 2013, 139, 054305 CrossRef PubMed.
- L.-L. Wang, Y.-M. Sun, Z.-Y. Yu, Z.-N. Qi and C.-B. Liu, Theoretical Investigation on Triagonal Symmetry Copper Trimers: Magneto-Structural Correlation and Spin Frustration, J. Phys. Chem. A, 2009, 113, 10534–10539 CrossRef CAS PubMed.
- B. Sarkar, M. S. Ray, M. G. B. Drew, A. Figuerola, C. Diaz and A. Ghosh, Trinuclear Cu(II) complexes containing peripheral ketonic oxygen bridges and a μ3-OH core: Steric influence on their structures and existence, Polyhedron, 2006, 25, 3084–3094 CrossRef CAS.
- B. Kintzel, M. Böhme, J. Liu, A. Burkhardt, J. Mrozek, A. Buchholz, A. Ardavan and W. Plass, Molecular electronic spin qubits from a spin-frustrated trinuclear copper complex, Chem. Commun., 2018, 54, 12934–12937 RSC.
- O. Schiemann, J. Plackmeyer, J. Fritscher, J. Pebler and C. Elschenbroich, Trovacenyl-based organometallic triradicals: Spin frustration, competing interactions and redox splitting, Appl. Magn. Reson., 2004, 26, 171–182 CrossRef CAS.
- H.-Z. Kou, B. C. Zhou and R.-J. Wang, Heterotrimetallic 4f–3d Coordination Polymers: Synthesis, Crystal Structure, and Magnetic Properties, Inorg. Chem., 2003, 42, 7658–7665 CrossRef CAS PubMed.
- J. A. Hatnean, R. Raturi, J. Lefebvre, D. B. Leznoff, G. Lawes and S. A. Johnson, Assembly of Triangular Trimetallic Complexes by Triamidophosphine Ligands: Spin-Frustrated Mn2+ Plaquettes and Diamagnetic Mg2+ Analogues with a Combined Through-Space, Through-Bond Pathway for 31P-31P Spin–Spin Coupling, J. Am. Chem. Soc., 2006, 128, 14992–14999 CrossRef CAS PubMed.
- M. U. Anwar, L. K. Thompson and L. N. Dawe, Spin frustration in a Cu(II)3 triangle frustrated?, Dalton Trans., 2011, 40, 1437–1440 RSC.
- B. Le Guennic, S. Petit, G. Chastanet, G. Pilet, N. B. Amor and V. Robert, Antiferromagnetic Behavior Based on Quasi-Orthogonal MOs: Synthesis and Characterization of a Cu3 Oxidase Model, Inorg. Chem., 2008, 47, 572–577 CrossRef CAS PubMed.
- (a) J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, A Stable Pentagonal Bipyramidal Dy(III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed; (b) Y. Liu, Y.-C. Chen, J. Liu, W.-B. Chen, G.-Z. Huang, S.-G. Wu, J. Wang, J.-L. Liu and M.-L. Tong, Cyanometallate-Bridged Didysprosium Single-Molecule Magnets Constructed with Single-Ion Magnet Building Block, Inorg. Chem., 2020, 59, 687–694 CrossRef CAS PubMed.
- J.-L. Liu, Y.-C. Chen and M.-L. Tong, Symmetry strategies for high performance lanthanide-based single-molecule magnets, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- Y.-N. Guo, G.-F. Xu, P. Gamez, L. Zhao, S.-Y. Lin, R. Deng, J. Tang and H.-J. Zhang, Two-Step Relaxation in a Linear Tetranuclear Dysprosium(III) Aggregate Showing Single-Molecule Magnet Behavior, J. Am. Chem. Soc., 2010, 132, 8538–8539 CrossRef CAS PubMed.
- Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, Strong Axiality and Ising Exchange Interaction Suppress Zero-Field Tunneling of Magnetization of an Asymmetric Dy2 Single-Molecule Magnet, J. Am. Chem. Soc., 2011, 133, 11948–11951 CrossRef CAS PubMed.
- I. J. Hewitt, Y. Lan, C. E. Anson, J. Luzon, R. Sessoli and A. K. Powell, Opening up a dysprosium triangle by ligand oximation, Chem. Commun., 2009, 6765–6767 RSC.
- S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, An Organometallic Single-Ion Magnet, J. Am. Chem. Soc., 2011, 133, 4730–4733 CrossRef CAS PubMed.
- P.-H. Lin, T. J. Burchell, L. Ungur, L. F. Chibotaru, W. Wernsdorfer and M. Murugesu, A Polynuclear Lanthanide Single-Molecule Magnet with a Record Anisotropic Barrier, Angew. Chem., Int. Ed., 2009, 48, 9489–9492 CrossRef CAS PubMed.
- W.-M. Wang, X.-M. Kang, H.-Y. Shen, Z.-L. Wu, H.-L. Gao and J.-Z. Cui, Modulating single-molecule magnet behavior towards multiple magnetic relaxation processes through structural variation in Dy4 clusters, Inorg. Chem. Front., 2018, 5, 1876–1885 RSC.
- L. Zhang, J. Jung, P. Zhang, M. Guo, L. Zhao, J. Tang and B. Le Guennic, Site-Resolved Two-Step Relaxation Process in an Asymmetric Dy2 Single-Molecule Magnet, Chem. – Eur. J., 2016, 22, 1392–1398 CrossRef CAS PubMed.
- D. Reta and N. F. Chilton, Uncertainty estimates for magnetic relaxation times and magnetic relaxation parameters, Phys. Chem. Chem. Phys., 2019, 21, 23567–23575 RSC.
- P. Evans, D. Reta, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, Bis-Monophospholyl Dysprosium Cation Showing Magnetic Hysteresis at 48 K, J. Am. Chem. Soc., 2019, 141, 19935–19940 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- E. M. Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Direct measurement of dysprosium(III)˙˙˙dysprosium(III) interactions in a single-molecule magnet, Nat. Commun., 2014, 5, 5243 CrossRef PubMed.
- E. Wong, S. Liu, S. Rettig and C. Orvig, Gallium and Indium Complexes of Hexadentate Ligands Containing Pendant Pyridyl and Phenolate Groups, Inorg. Chem., 1995, 34, 3057–3064 CrossRef CAS.
- G. Sheldrick, SHELXT - Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, Molcas 8: New capabilities for multiconfigurational quantum chemical calculations across the periodic table, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, New Relativistic ANO Basis Sets for Transition Metal Atoms, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Ab Initio Crystal Field for Lanthanides, Chem. – Eur. J., 2017, 23, 3708–3718 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis, additional characterization, crystal structure data, ab initio calculations of 1. CCDC 1983277. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0qi00655f |
| ‡ These authors contributed equally to this work. |
| This journal is © the Partner Organisations 2020 |