Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Improving the exchange and correlation potential in density-functional approximations through constraints
Timothy J.
Callow
ab,
Benjamin J.
Pearce
a,
Tom
Pitts
a,
Nektarios N.
Lathiotakis
 c,
Matthew J. P.
Hodgson
c,
Matthew J. P.
Hodgson
 a and
Nikitas I.
Gidopoulos
a and
Nikitas I.
Gidopoulos
 *a
*a
aDepartment of Physics, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: timothy.callow@durham.ac.uk; b.j.pearce@durham.ac.uk; tom.pitts@durham.ac.uk; matthew.j.hodgson@durham.ac.uk; nikitas.gidopoulos@durham.ac.uk
bMax-Planck-Institut für Mikrostrukturphysik, Weinberg 2, D-06120 Halle, Germany
cTheoretical and Physical Chemistry Institute, National Hellenic Research Foundation, Vass. Constantinou 48, 116 35 Athens, Greece. E-mail: lathiot@eie.gr
First published on 6th July 2020
Abstract
We review and expand on our work to impose constraints on the effective Kohn–Sham (KS) potential of local and semi-local density-functional approximations. Constraining the minimisation of the approximate total energy density-functional invariably leads to an optimised effective potential (OEP) equation, the solution of which yields the KS potential. We review briefly our previous work on this and demonstrate with numerous examples that despite the well-known mathematical issues of the OEP with finite basis sets, our OEP equations are numerically robust. We demonstrate that appropriately constraining the ‘screening charge’ which corresponds to the Hartree, exchange and correlation potential not only corrects its asymptotic behaviour but also allows the exchange and correlation potential to exhibit a non-zero derivative discontinuity, a feature of the exact KS potential that is necessary for the accurate prediction of band-gaps in solids but very hard to capture with semi-local approximations.
I. Introduction
A challenge with common density-functional approximations is the accuracy imbalance between the energy functionals and the corresponding Kohn–Sham (KS) potentials, i.e. the functional derivatives of the energy density-functionals. Although the accuracy and quality of an energy density-functional are often quite good, the resulting KS potential is inferior.1–3 The quest to derive ever more accurate energy density-functionals to obtain moderate improvements of the KS potential may not be the best strategy (it is vulnerable to diminishing returns in the accuracy of the KS potential). We explore different routes to improved accuracy for these calculations.Previously, we explored the minimisation of potential functionals defined by an energy difference, instead of density-functionals of the total energy, as a means of improving the quality of the KS potential.4–7 The advantage of this approach is that the energy difference is bound from below, even in approximations from finite-order (second) perturbation theory; the latter can then be employed directly to derive accurate exchange–correlation (xc) potentials without the risk of variational collapse.4,6
In this paper, we review briefly and expand on our work8–10 to improve the performance of local and semi-local density-functional approximations (DFAs), by imposing physical constraints on the single-particle, local, effective (KS) potential, whose orbitals minimise the total energy functional. In ref. 8–10 we argued that these constraints improve the asymptotic behaviour and overall quality of the KS potential by removing the erroneous effects of self-interactions (SIs). As evidence, we demonstrated that, compared with the results from the unconstrained minimisation, the ionisation potentials (IPs)51 of a large number of atoms, molecules and even anions obtained from our constrained minimisation improved significantly, while the calculated total energies increased only minimally.
In this work, we further show that with a judicious choice, the constraints imposed on the KS potential of local and semi-local DFAs enable their (constrained) exchange and correlation potential to exhibit exotic, non-analytic behaviour, expected only in more elaborate and computationally costly levels of theory, or from higher rungs on Jacob’s ladder of DFAs, as envisaged by John Perdew and co-workers.11
II. Constrained minimisation of density-functional approximations
In the constrained minimisation method,8–10 we employ the standard total energy expression in DFT, using a density-functional approximation for the xc energy density-functional, EDFAxc[ρ],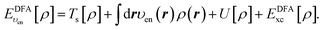 | (1) |
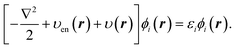 | (2) |
In the constrained method, we treat the Hxc screening density, or electron repulsion density, ρscr(r),52 as the fundamental quantity. It is defined via Poisson’s equation from the Laplacian of the (exact or approximate) KS potential minus the external potential, ∇2[υs(r) − υen(r)]; for example, the Hxc screening density of the exact KS potential is given by
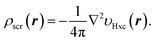 | (3) |
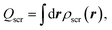 | (4) |
The Hxc screening charge of the exact KS potential satisfies the intuitive sum rule,14–16
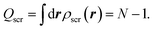 | (5) |
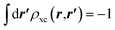 , which is satisfied by LDA and common GGAs. The quantities ρxcscr(r) and ρxc(r,r′) are not directly related.
, which is satisfied by LDA and common GGAs. The quantities ρxcscr(r) and ρxc(r,r′) are not directly related.
Accordingly, in the constrained minimisation of DFAs8–10 (which we henceforth refer to as the CDFA method), our strategy to mitigate the effects of SIs on the effective potential is to ensure that the KS orbitals satisfy eqn (2) with the effective potential υ(r) represented by the effective screening density
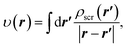 | (6) |
| Qscr = N − 1, | (7) |
| ρscr(r) ≥ 0. | (8) |
Nonetheless, the positivity constraint (8) has a double role in the constrained minimisation method. As explained in ref. 8–10, the CDFA minimization procedure must be solved within the optimized effective potential (OEP) framework.12,13 Primarily, the positivity constraint allows the mathematical problem of constrained minimisation to remain well posed in the limit of complete orbital and auxiliary basis sets;8,9 without the positivity constraint, there is nothing to prevent the screening density from separating into a component in the energetically important spatial region near the molecule, with charge Qascr = N, and a separate component with charge Qbscr = −1 pushed out to infinity (within the basis set limits). Secondly, the solution of the OEP equation in Gaussian basis set codes is a longstanding problem in DFT, which has hindered the widespread adoption of OEP-based methods in practical calculations. Various methods have been developed to overcome these numerical difficulties which typically manifest themselves as spurious oscillations in the effective potential.17,18,22 With finite orbital and auxiliary basis sets, the positivity constraint (8) offers a simple way to reduce drastically the variational flexibility of ρscr(r) and of υ(r) and thereby helps to overcome mathematical pathologies in the solution of the OEP equation.
In the previous implementation of the CDFA method, the positivity constraint was used in combination with a singular value decomposition (SVD) of the density–density response matrix to ensure the solution of the OEP equation was well-behaved. Instead, here we apply the method of ref. 23 to solve the OEP equation with the CDFA method. We review the main ideas below; see ref. 23 and the subsequent discussion in ref. 24 and 25 for details.
The OEP equation (Fredholm integral equation of the first kind) is obtained by taking the functional derivative of an energy term with respect to the density (e.g. Ts[ρ], Ex[ρ], Exc[ρ]) when this energy term is written as an implicit functional of the density. Alternatively, it can be obtained by minimising the DFT total energy expression (eqn (1)) indirectly by searching for the effective potential υ(r) in eqn (2) whose KS orbitals minimise the total energy.26,27 Either way, we obtain the integral OEP equation,
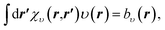 | (9) |
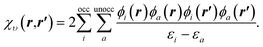 | (10) |
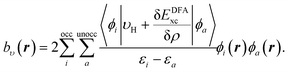 | (11) |
To understand the effect of finite orbital basis sets on the solution of the OEP equation, we focus on the density–density response function; the analysis below also applies to the RHS, bυ(r). We split χυ into two terms, the first of which can be represented exactly in the orbital basis, and the second of which must be approximated. χυ is given, for λ = 1, by
χλυ(r,r′) = χ0υ(r,r′) + λ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) υ(r,r′), υ(r,r′), | (12) |
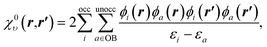 | (13) |
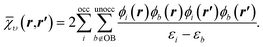 | (14) |
![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) υ of the response function, which we denote the ‘complement’ of the response function, was typically omitted.
υ of the response function, which we denote the ‘complement’ of the response function, was typically omitted.
By definition, the complement ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) υ cannot be represented exactly so we must approximate it. We use the Ünsold approximation28 together with the completeness relation for the KS orbitals (in much the same manner as the well-known Krieger–Li–Iafrate (KLI) approximation29,30 and common energy denominator approximation (CEDA)31,32 methods), in which case
υ cannot be represented exactly so we must approximate it. We use the Ünsold approximation28 together with the completeness relation for the KS orbitals (in much the same manner as the well-known Krieger–Li–Iafrate (KLI) approximation29,30 and common energy denominator approximation (CEDA)31,32 methods), in which case ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) υ reduces to
υ reduces to
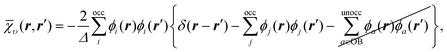 | (15) |
We observe that, as long as Δ > 0, the value of Δ does not play a role in the results, since Δ always appears together with λ in the ratio λ/Δ, and we investigate the limit λ → 0. We shall also consider the limit λ → ∞, for which the value of positive Δ does not matter either. It is straightforward to confirm that ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) υ is negative semi-definite, like χ0υ, and that the only null eigenfunction of
υ is negative semi-definite, like χ0υ, and that the only null eigenfunction of ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) υ is the constant function.
υ is the constant function.
The same procedure is applied for the RHS, bυ(r), of eqn (10), which yields the following expressions for the terms b0υ(r) and its complement ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) υ(r),
υ(r),
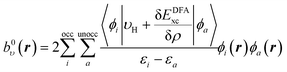 | (16) |
 | (17) |
 | (18) |
Prior to ref. 23, the finite orbital basis OEP was given by the solution of eqn (18) at λ = 0. However, this solution leaves the effective potential υ0(r) indeterminate in the null space of χ0υ, which is infinite-dimensional. In order to obtain a smooth potential υ0(r), one must restrict the freedom of υ0(r), which has spawned a variety of approaches in the literature. These include, for example, schemes to balance the relative sizes of the orbital and auxiliary basis sets;18,19 regularization techniques to smooth the effective potential;33,34 and removing the additional freedom of an auxiliary basis set.35 In our method, rather than restricting the freedom of υ0(r), we instead solve the OEP equation to find the potential υλ(r) which is defined mathematically to be unique for finite λ.
The main point of ref. 23 is the observation that the solution of eqn (18) for any finite λ > 0, even for λ tending to zero, determines the effective potential fully, up to a constant. The extension of the response function with ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) υ amounts to using an effectively complete orbital basis. Numerically, we find that the solution of eqn (18) is smooth for almost any λ > 0,53 including the limits for small and for large λ, which correspond respectively to the OEP potential in a finite orbital basis, υλ→0(r), and to its (Unsöld) approximation with a common energy denominator, υ∞(r). It turns out that for the effective xc potentials in the constrained minimisation method, the two solutions are close to each other.
υ amounts to using an effectively complete orbital basis. Numerically, we find that the solution of eqn (18) is smooth for almost any λ > 0,53 including the limits for small and for large λ, which correspond respectively to the OEP potential in a finite orbital basis, υλ→0(r), and to its (Unsöld) approximation with a common energy denominator, υ∞(r). It turns out that for the effective xc potentials in the constrained minimisation method, the two solutions are close to each other.
(A) Relaxing the positivity constraint
In ref. 8–10 we solved the OEP equation for the CDFA method, using finite orbital and auxiliary basis sets, with λ = 0. The indeterminacy of the effective potential was restricted by expressing υ(r) in terms of the screening density ρscr(r) in eqn (6) and then constraining the screening charge Qscr(7) as well as the sign of ρscr(r) (8).However, the positivity constraint, implemented with a penalty function,10 is a computational bottleneck for the calculation. In a forthcoming paper, we implement the positivity constraint more efficiently, by writing ρscr(r) = |fscr(r)|2, and solving for the screening amplitude fscr(r),36 which ensures the constrained minimization is mathematically well posed regardless of basis set size.
In the next part, we investigate the effects of relaxing the positivity constraint on the convergence of the screening potential and screening density. A weak effect, for sufficiently flexible auxiliary basis sets, will justify the relaxation of the positivity constraint and reduce the computational effort. The auxiliary basis sets we use are uncontracted cc-pVXZ,37,38 with X = D, T, Q.
In the rest of this section, we show indicative results for the CDFA method applied to the LDA functional, henceforth denoted by CLDA, where the minimisation was performed under just the constraint for the screening charge, Qscr = N − 1 (7). In order to determine υ(r) and ρscr(r), we employ the extended response function χλυ(r,r′), in the limit of small λ. We use λ/Δ = 0.01, but the results seem to converge and do not change if we reduce λ/Δ by an order of magnitude. The positivity constraint enabled the constrained minimisation problem to remain well posed in the limit of large (complete) orbital and auxiliary basis sets. Consequently, we expect the screening charge to change gradually as we increase the size of the auxiliary basis. This effect will be stronger for systems with fewer electrons, since then, the difference between N − 1 and N is largest.
Calculations were performed in the Gaussian basis set code HIPPO,54 with one- and two-electron integrals for the Cartesian Gaussian basis elements calculated using the GAMESS code.39,40 Basis set data was obtained from the Basis Set Exchange database.41
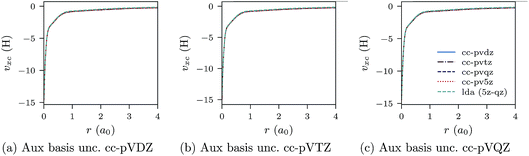
In Fig. 1a–c, the CLDA xc potential is shown for the Ne atom and three auxiliary basis sets: un-contracted cc-pVXZ, with X = D, T, Q. In each sub-figure, υCLDAxc(r) is shown for fixed auxiliary basis and various orbital basis sets: cc-pVXZ, with X = D, T, Q, 5. For comparison, the LDA potential υLDAxc(r) is also shown with a green dashed line.
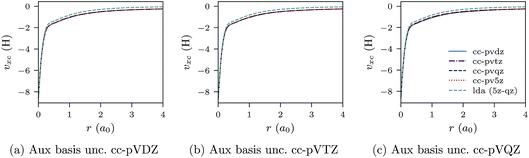 | ||
| Fig. 1 CLDA xc potentials υxc(r) for the Ne atom obtained using fixed auxiliary basis sets with various orbital basis sets. The green dashed line represents LDA. | ||
In Fig. 2a–c, r2ρscr(r) (CLDA screening density multiplied by r2) is shown for the Ne atom and three auxiliary basis sets: un-contracted cc-pVXZ, with X = D, T, Q. In each sub-figure, r2ρscr(r) is shown for fixed auxiliary basis and various orbital basis sets: cc-pVXZ, with X = D, T, Q, 5. The overall convergence of the xc potential is excellent. The convergence of ρscr(r) for fixed auxiliary basis and increasing size of orbital basis is also very good. Before proceeding, it is worth noting that despite not deploying the positivity constraint (8) that would restrict the flexibility of the screening density and the xc potential, the latter (solutions of CLDA-OEP eqn (12) and (15) in ref. 10) turn out to be smooth functions, not showing any wild oscillations characteristic of OEP-finite-basis pathologies for any combination of orbital and auxiliary basis sets. This confirms our claim that on extending the domain of the density–density response function (eqn (12) and (18)), the solution of the finite-basis-OEP equations is well behaved.
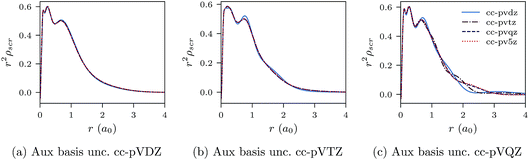 | ||
| Fig. 2 CLDA results for r2ρscr(r) for the Ne atom. Each sub-figure shows the expansion of ρscr(r) for fixed auxiliary basis set and various orbital basis sets. | ||
Fig. 3a–c and 4a–c show similar results to Fig. 1a–c and 2a–c, but for the Be atom.
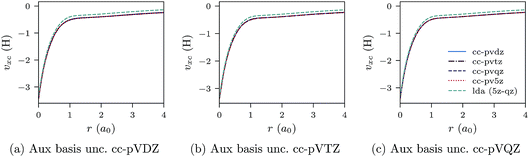 | ||
| Fig. 3 CLDA xc potentials υxc(r) for the Be atom obtained using fixed auxiliary basis sets with various orbital basis sets. The green dashed line represents LDA. | ||
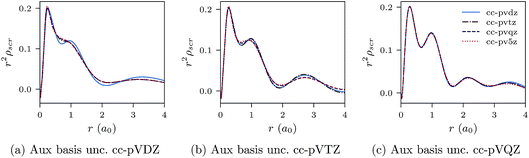 | ||
| Fig. 4 CLDA results for r2ρscr(r) for the Be atom. Each sub-figure shows the expansion of ρscr(r) for fixed auxiliary basis set and various orbital basis sets. | ||
We proceed to discuss Fig. 5a–c and 6a–c, which show similar results to Fig. 1a–c, 2a–c, 3a–c and 4a–c, but for the He atom. The convergence of the xc potential for fixed auxiliary basis and increasing orbital basis size is good. Note that for any combination of orbital and auxiliary basis, the xc potential is smooth. The convergence of the screening density for fixed auxiliary basis and increasing size of orbital basis is slower than for the other systems. In addition, as the size of the auxiliary basis increases, as shown in Fig. 6a–c, the screening density changes considerably. Note specifically the negative part of the screening density in Fig. 6a–c. In Fig. 6a the negative hump is centred around 2.5a0 away from the origin, in Fig. 6b it is centred around 3.0a0 away from the origin, and in Fig. 6c it has moved to 3.5a0. This is the effect we discussed in Section II. The positivity constraint enables the constrained minimisation problem to remain well posed for large basis sets (here large auxiliary bases). With only the constraint on Qscr enabled and without the positivity constraint, during the total energy minimisation, it becomes energetically preferable to converge to a screening density with the screening charge locally equal to N (=QLDAscr), and to shift negative charge density away from the system. This effect is already evident for the moderately large auxiliary bases used in our study, because the difference between N − 1 and N is relatively large for N = 2.
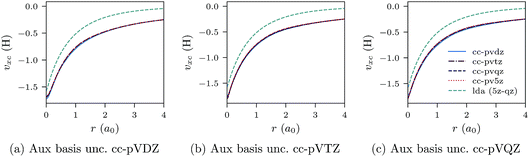 | ||
| Fig. 5 CLDA xc potentials υxc(r) for the He atom obtained using fixed auxiliary basis sets with various orbital basis sets. The green dashed line represents LDA. | ||
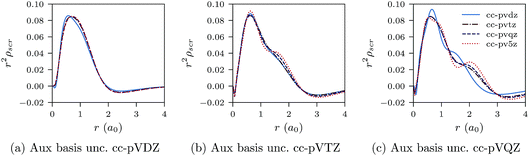 | ||
| Fig. 6 CLDA screening densities ρscr(r) for the He atom expanded in fixed auxiliary basis sets with various orbital basis sets. | ||
Negatively charged ions are another class of difficult systems where LDA fails qualitatively. In Fig. 7a–c and 8a–c we plot the CLDA xc potential and screening density of the chloride anion Cl−. The orbital basis sets are augmented cc-pVXZ, with X = D, T, Q, 5. It is evident that both the CLDA xc potential and the CLDA screening density are well converged and these systems do not present a challenge to the constrained minimisation, at least regarding convergence.
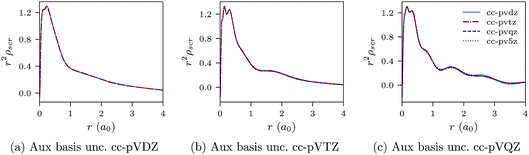 | ||
| Fig. 8 CLDA screening densities ρscr(r) for the Cl− anion expanded in fixed auxiliary basis sets with various orbital basis sets. | ||
In Table 1 we show the IPs of several systems, including anions, obtained as the negative of the HOMO eigenvalue. For comparison with our previous CLDA method, in which we imposed the positivity constraint, we show the CLDA IPs with (fourth column) and without positivity (fifth column). The results with positivity are from ref. 8. The resulting IPs do not depend strongly on the positivity constraint, except in helium, where we see a larger difference. We still see the familiar improvement of CLDA over the LDA results.
| Basis | LDA | CLDA pos. | CLDA no pos. | Exp. | |
|---|---|---|---|---|---|
| a For the negative ions, the orbital basis was aug-cc-pVTZ. | |||||
| He | T–Q | 15.46 | 23.14 | 21.57 | 24.6 |
| Be | T–T | 5.59 | 8.62 | 8.11 | 9.32 |
| Ne | T–T | 13.16 | 18.94 | 18.94 | 21.6 |
| H2O | T–T | 6.96 | 11.24 | 11.34 | 12.8 |
| NH3 | T–T | 6.00 | 9.81 | 9.77 | 10.8 |
| CH4 | D–D | 9.28 | 12.52 | 10.51 | 14.4 |
| C2H2 | D–D | 7.02 | 10.63 | 10.31 | 11.5 |
| C2H4 | D–D | 6.67 | 9.57 | 9.35 | 10.7 |
| CO | D–D | 8.75 | 12.73 | 12.11 | 14.1 |
| NaCl | D–D | 5.13 | 7.87 | 7.82 | 8.93 |
| F− | Ta–T | ε H > 0 | 2.23 | 2.16 | 3.34 |
| Cl− | Ta–T | ε H > 0 | 2.61 | 2.59 | 3.61 |
| OH− | Ta–T | ε H > 0 | 0.99 | 0.93 | 1.83 |
| CN− | Ta–T | 0.13 | 2.87 | 2.86 | 3.77 |
In concluding this section, we first recall the reasons why our CDFA method was implemented with the positivity constraint (8). This constraint is intuitive if one considers each electron to experience a repulsive electronic density from the other N − 1 electrons, but it also serves two computational purposes: (i) to avoid shifting negative screening density to infinity as the size of the orbital and auxiliary basis sets increase and (ii) as a regularization technique to avoid pathological behaviour of the OEP solution. As we have seen from the good convergence of the screening densities and potentials, the latter reason is no longer necessary with the introduction of the complement terms in the OEP (eqn (18)).
Regarding the first reason (i), we note that for the moderately large auxiliary basis sets we tested, it is safe to carry out constrained minimisations of the DFA total energy under the constraint of the screening charge only, Qscr = N − 1, except for systems with few electrons; for these systems the omission of the positivity constraint manifests itself by shifting negative screening density away from the origin. As such, the benefits of removing the positivity condition, which is a computational bottleneck, usually outweigh the disadvantages. For the benefit of readers less familiar with OEP calculations, we outline the full simplified procedure for solving the CDFA equations in Appendix A.
In the next section, we shall argue that the screening charge constraint endows the xc potential of local and semi-local DFAs with exotic qualities, such a finite derivative discontinuity Δxc. Although crucial for the accurate prediction of band gaps, Δxc is notoriously hard to capture in approximations. Advanced approximations have been proposed which capture this discontinuous behaviour, e.g., ref. 42–46, however, further development is required for these methods to yield reliable band gaps for all materials.
III. Derivative discontinuity of the CDFA xc potential
The discontinuity of the xc potential is defined by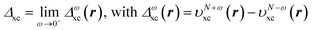 | (19) |
The ensemble KS densities with N ± ω electrons are given by
| ρυenN−ω(r) = ωρυenN−1(r) + (1 − ω)ρυenN(r), | (20) |
| ρυenN+ω(r) = (1 − ω)ρυenN(r) + ωρυenN+1(r), | (21) |
We seek the derivative discontinuity Δxc of the CLDA xc potential from eqn (19) for reference. In order to obtain Δωxc(r) and then Δxc, one must first find the ensemble KS xc potentials with densities ρυenN±ω(r) and subtract them. Work is in progress in our group to obtain directly these ensemble KS xc potentials. Here, we use the method of ref. 47 and 48 to obtain the ensemble KS xc potential by constructing the ensemble density ρυenN±ω from separate KS calculations for N, and N ± 1 particles and then inverting ρυenN±ω(r) to obtain υN±ωxc(r).
Let us follow this construction in detail. The two KS ground state densities that build the ensemble density ρυenN+ω(r) can be written:
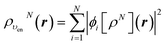 | (22) |
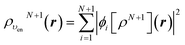 | (23) |
In terms of the ensemble KS orbitals {ϕi[ρN+ω](r)}, the ensemble density is given by
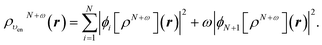 | (24) |
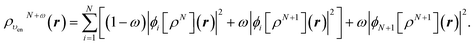 | (25) |
We conclude that when the number of electrons increases past an integer value, the value of the screening charge QN+ωscr increases stepwise,
| QM+ωscr = M, with M = N, N ± 1, … and 0 < ω ≤ 1. | (26) |
| QNscr = N − 1, QN+scr = N, | (27) |
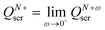 .
.
This stepwise increase in screening charge obviously causes a discontinuous jump in the constrained xc potential υN+ωxc(r). In the limit ω → 0+, the jump in the xc potential is υN+xc(r) − υNxc(r), where 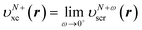 . From eqn (19), the jump in the xc potential due to the stepwise increase in the screening charge gives the derivative discontinuity in the CDFA method,
. From eqn (19), the jump in the xc potential due to the stepwise increase in the screening charge gives the derivative discontinuity in the CDFA method,
| ΔCDFAxc(r) = υN+xc(r) − υNxc(r). | (28) |
In the last part of the paper, we shall compare Δxc from the constrained minimisation method (eqn (28)) with the result for Δxc from eqn (19). We shall calculate the differences
| Δωxc(r) ≃ υN+ωxc(r) − υNxc(r) | (29) |
Before we continue, we note that in the simple model we have constructed to predict the derivative discontinuity, using the inversion of the ensemble density (eqn (19)) and the CDFA method (eqn (28)), we have restricted the freedom of the Hxc potentials by the ansatz in eqn (6); the restriction is that υN+ωxc(∞) = 0. Consequently, the derivative discontinuities we obtain with eqn (19) and (28) cannot be perfect constant functions but have to vanish at r → ∞. We aim to investigate whether the resulting approximate derivative discontinuity, Δxc(r), as a function of r remains flat and almost equal to a constant over the region of the atom or the molecule. Finally, we want to obtain the converged value of the constant in the limit of an infinite basis set.
In order to proceed and construct the ensemble density ρυenN+ω(r), we need the densities from two KS calculations for N and N + 1 particles, allowing us to then find the corresponding ensemble xc potential against which ΔCDFAxc can be compared. We use our CLDA method to obtain the densities ρυenN(r) and ρυenN+1(r), in order to control the screening densities of the constituent xc potentials. One of the integers N or N + 1 is an odd number, corresponding to an open shell system. The LDA exchange energy for open shells contains an error (“ghost-exchange error”49) in modelling exchange with half the electrons spin-up and half spin-down. In a forthcoming publication,49 we propose a way to correct this error, still within LDA (not local spin density approximation). Hence, in the KS calculation for an odd number of electrons (either for N or for N + 1), we employ our method to correct for the ghost-exchange error, in order to improve the accuracy of the resulting CLDA xc potential and density. Details will be published in ref. 49.
Once we construct the ensemble density, we invert it to obtain the ensemble KS potential, υN+ωxc(r). For the inversion, we apply the method in ref. 5 and 50. The inversion method50 requires the a priori selection of a value for the screening charge of the xc potential. According to eqn (26), for υN+ωxc(r) we set QN+ωscr = N.
In Fig. 9a and b, the ensemble xc potentials υN+ωxc(r) and screening densities are shown for various values of ω, obtained by inverting the ensemble densities (eqn (25)). The screening charge for the ensemble densities is set as QN+ωscr = N. The xc potentials and screening densities are very close, as expected, which is an indication of the quality of convergence and the inversion method.
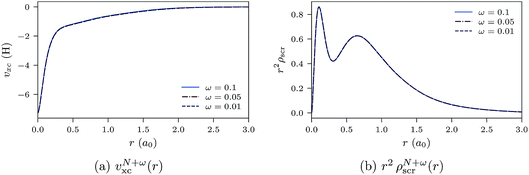 | ||
| Fig. 9 Ensemble xc potentials and screening densities for various values of ω for the Ne atom. The orbital and auxiliary basis sets are uncontracted cc-pVTZ. | ||
In Fig. 10a, the ensemble xc potential, υN+ωxc(r), for ω = 0.1 (with QN+ωscr = N) is shown together with υNxc(r) and υN+xc(r), which have screening charges QNscr = N − 1 and QN+scr = N. In Fig. 10b, the ω-dependent derivative discontinuity (eqn (29)), Δωxc(r) = υN+ωxc(r) − υNxc(r), is shown for various values of ω. In the limit of small ω, Δωxc(r) yields the derivative discontinuity using ensembles, Δω→0xc(r) = Δxc(r).
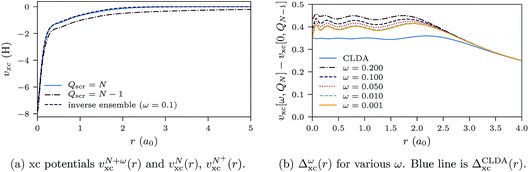 | ||
| Fig. 10 xc potentials and differences in xc potentials for the Ne atom. The orbital and auxiliary basis sets are uncontracted cc-pVTZ. | ||
The inversion method has some numerical instabilities which are exaggerated when the difference of two potentials is taken. This explains why Δxc(r) is not flat for small r. The distance r after which Δxc(r) tends to zero depends on the basis set. However, we do not propose this method as a means of computing the derivative discontinuity in practice, but rather to compare with the results of the CDFA method.
The blue line in Fig. 10b shows the CLDA prediction for the derivative discontinuity, ΔCLDAxc(r), without an ensemble calculation. ΔCLDAxc(r) remains almost constant up to a distance of about 2.5a0, beyond which it tends to zero. The differences Δωxc(r) for decreasing ω approach the line for ΔCLDAxc, both in height and in the spatial extent over which ΔCLDAxc and Δωxc stay almost constant. The value of the constant can be obtained by inspection of Fig. 10b and is approximately 0.35 hartrees, or about 9.5 eV. We can obtain the constant more accurately from the shift of the occupied single-particle energy levels between the two xc potentials υNxc(r) and υN+xc(r). For the uncontracted cc-pVTZ basis used for the results in Fig. 10b, we find ΔCLDAxc = 9.48 eV (see Table 2).
| cc-pVDZ | cc-pVTZ | cc-pVQZ | cc-pV5Z | |
|---|---|---|---|---|
| ε N 1s | −830.10 | −829.96 | −830.60 | −829.63 |
| ε N+1s | −817.86 | −820.48 | −822.86 | −823.02 |
| Δ 1s | 12.24 | 9.48 | 7.74 | 6.61 |
| ε N 2s | −40.68 | −41.14 | −41.91 | −40.97 |
| ε N+2s | −28.45 | −31.66 | −34.17 | −34.35 |
| Δ 2s | 12.23 | 9.48 | 7.74 | 6.62 |
| ε N 2p | −18.07 | −18.65 | −19.44 | −18.52 |
| ε N+2p | −5.86 | −9.17 | −11.71 | −11.9 |
| Δ 2p | 12.21 | 9.48 | 7.73 | 6.62 |
| Δ CLDAxc | 12.22 | 9.48 | 7.73 | 6.62 |
We conclude this section by investigating the influence of basis set size on (a) the height of ΔCDFAxc(r) in the region where it is almost flat and (b) the spatial extent of the region over which ΔCDFAxc(r) remains flat.
We calculated the xc derivative discontinuity ΔCDFAxc(r) with our model (eqn (28)), using as orbital and auxiliary basis sets the uncontracted cc-pVXZ sets, with X = D, T, Q, 5. The last row of Table 2 shows the value of the derivative discontinuity, ΔCDFAxc, for each basis set.
Each column in Table 2 shows the eigenvalues of the occupied orbitals in the Ne atom, with the two constrained xc potentials υNxc(r) and υN+xc(r), for a specific choice of orbital and auxiliary basis sets. Each column also shows the shift of each eigenvalue Δi = εN+i − εNi. The average value of these shifts gives ΔCLDAxc in the specific basis. Using the uncontracted cc-pVDZ orbital and auxiliary basis, the shifts of the orbital eigenvalues are almost the same within 0.03 eV. In the uncontracted cc-pVTZ orbital and auxiliary basis, the differences between the shifts in each energy level are smaller than 0.01 eV. In the two larger basis sets, the differences between the almost constant shifts of each energy level are within 0.01 eV. These results are consistent with an almost perfectly constant ΔCLDAxc over the whole spatial region where the electronic density of the Ne atom is appreciable.
For the uncontracted cc-pVTZ basis, we performed another check to confirm that the difference between the two xc potentials υN+xc(r) and υNxc(r) is almost constant over a large region of space. We evaluated the overlaps of the occupied orbitals in the two potentials, 〈ϕN+i∣ϕNi〉, i = 1s, 2s, 2p (triply degenerate). We found that the numerical values of all overlaps were indeed very close to one, with the overlap in the worst case differing from one by ∼10−7.
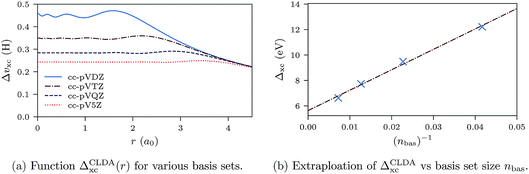
In Fig. 11a we show the derivative discontinuity ΔCLDAxc(r) as a function of r (eqn (28)) for uncontracted cc-pVXZ (X = D, T, Q, 5) orbital and auxiliary basis sets. These functions have a plateau at the origin where the atom lies. The extent of the plateau increases with basis set size, and the height decreases and seems to converge. To establish that the discontinuity ΔCLDAxc (height of the plateau) indeed converges and does not vanish in the limit of infinite basis set, we plot ΔCLDAxc against the inverse of the number of basis set elements, nbas. The behaviour is fitted well by a straight line with equation ΔCLDAxc(nbas) = 5.6 + 160 × (nbas)−1. The extrapolation gives a non-zero derivative discontinuity of 5.6 eV for the infinite basis limit.
IV. Conclusions
A common theme of popular local and semi-local density-functional approximations is the accuracy imbalance between energy density-functionals, which can be quite accurate, and the corresponding effective KS potentials, with inferior accuracy.1–3 We have approached this problem from several directions.4–6 In this paper, we review and expand our work on imposing physical constraints during the energy minimisation in order to yield a more accurate corresponding xc potential.8–10 Specifically, we investigate the relaxation of a constraint that is computationally expensive and find that its omission leads to well behaved results, except for very small systems with only a few electrons. The constraints we impose raise the total energy minimally8,10 but have a dramatic impact on the quality of the effective KS potential, giving it the correct asymptotic behaviour and enabling it to exhibit important non-analytic behaviour (derivative discontinuity) shared by the exact KS potential but elusive for the lower rungs of Jacob’s ladder of DFAs where semi-local DFAs reside.Appendix A
Below we summarize the full computational procedure for the constrained DFA method described in Section II(A).(1) Make an initial guess for the KS orbitals and the screening density, which is expanded in the auxiliary basis set,
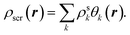 | (A1) |
(2) Construct the matrices
Akl = 〈![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) k|χ0| k|χ0|![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) l〉 + λ〈 l〉 + λ〈![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) k| k|![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) | |![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) l〉, l〉, | (A2) |
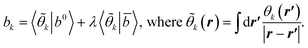 | (A3) |
(3) Solve the OEP matrix equation,
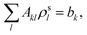 | (A4) |
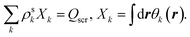 | (A5) |
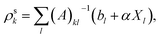 | (A6) |
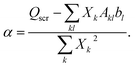 | (A7) |
(4) With the new Hxc potential constructed via the screening density from the previous step, diagonalize the KS Fock matrix to update the KS orbitals.
(5) Repeat steps 2–4 until the energy and density matrices are converged.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
N. I. G. and T. P. acknowledge financial support from The Leverhulme Trust, through a Research Project Grant with number RPG-2016-005. N. I. G. thanks Prof. Rod Bartlett for helpful discussions during his visit to Durham University in early 2019 and acknowledges the Institute of Advanced Study at Durham University for hosting this visit. N. I. G. and T. J. C. thank Prof. E. K. U. Gross for helpful discussions. M. J. P. H. gratefully acknowledges support from Prof. E. K. U. Gross.References
- R. J. Bartlett, J. Chem. Phys., 2019, 151, 160901, DOI:10.1063/1.5116338.
- A. Wasserman, J. Nafziger, K. Jiang, M.-C. Kim, E. Sim and K. Burke, Annu. Rev. Phys. Chem., 2017, 68, 555, DOI:10.1146/annurev-physchem-052516-044957 , pMID: 28463652.
- E. Sim, S. Song and K. Burke, J. Phys. Chem. Lett., 2018, 9, 6385 CrossRef CAS.
- N. I. Gidopoulos, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 040502, DOI:10.1103/PhysRevA.83.040502.
- T. Hollins, S. Clark, K. Refson and N. Gidopoulos, J. Phys.: Condens. Matter, 2016, 29, 04LT01 CrossRef , http://stacks.iop.org/0953-8984/29/i=4/a=04LT01.
- T. J. Callow and N. I. Gidopoulos, Eur. Phys. J. B, 2018, 91, 209 CrossRef CAS.
- T. J. Irons, J. W. Furness, M. S. Ryley, J. Zemen, T. Helgaker and A. M. Teale, J. Chem. Phys., 2017, 147, 134107 CrossRef.
- N. Gidopoulos and N. Lathiotakis, J. Chem. Phys., 2012, 136, 224109, DOI:10.1063/1.4728156.
- N. Gidopoulos and N. N. Lathiotakis, in Advances In Atomic, Molecular, and Optical Physics, ed. E. Arimondo, C. C. Lin, and S. F. Yelin, Academic Press, 2015, vol. 64, pp. 129–142, http://www.sciencedirect.com/science/article/pii/S1049250X15000063 Search PubMed.
- T. Pitts, N. I. Gidopoulos and N. N. Lathiotakis, Eur. Phys. J. B, 2018, 91, 130, DOI:10.1140/epjb/e2018-90123-8.
- J. Perdew and K. Schmidt, Density Functional Theory and its Applications to Materials, American Institute of Physics, Melville, New York, 2001, vol. 577 of API Conference Proceedings, pp. 1–20 Search PubMed.
- R. T. Sharp and G. K. Horton, Phys. Rev., 1953, 90, 317, DOI:10.1103/PhysRev.90.317.
- J. D. Talman and W. F. Shadwick, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 14, 36, DOI:10.1103/PhysRevA.14.36.
- A. Görling, Phys. Rev. Lett., 1999, 83, 5459, DOI:10.1103/PhysRevLett.83.5459.
- S. Liu, P. W. Ayers and R. G. Parr, J. Chem. Phys., 1999, 111, 6197, DOI:10.1063/1.479924.
- P. W. Ayers and M. Levy, J. Chem. Phys., 2001, 115, 4438, DOI:10.1063/1.1379333.
- S. Hirata, S. Ivanov, I. Grabowski, R. J. Bartlett, K. Burke and J. D. Talman, J. Chem. Phys., 2001, 115, 1635, DOI:10.1063/1.1381013.
- A. Heßelmann, A. W. Götz, F. Della Sala and A. Görling, J. Chem. Phys., 2007, 127, 054102, DOI:10.1063/1.2751159.
- A. Görling, A. Heßelmann, M. Jones and M. Levy, J. Chem. Phys., 2008, 128, 104104, DOI:10.1063/1.2826366.
- D. R. Rohr, O. V. Gritsenko and E. J. Baerends, J. Mol. Struct.: THEOCHEM, 2006, 762, 193 CrossRef CAS , ISSN 0166-1280, http://www.sciencedirect.com/science/article/pii/S0166128005007785.
- R. Dreizler and E. Gross, Density Functional Theory: An Approach to the Quantum Many-Body Problem, 1990 Search PubMed.
- V. N. Staroverov, G. E. Scuseria and E. R. Davidson, J. Chem. Phys., 2006, 124, 141103, DOI:10.1063/1.2194546.
- N. I. Gidopoulos and N. N. Lathiotakis, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 052508, DOI:10.1103/PhysRevA.85.052508.
- C. Friedrich, M. Betzinger and S. Blügel, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 046501, DOI:10.1103/PhysRevA.88.046501.
- N. I. Gidopoulos and N. N. Lathiotakis, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 046502, DOI:10.1103/PhysRevA.88.046502.
- T. Grabo, T. Kreibich and E. K. U. Gross, Mol. Eng., 1997, 7, 27 CrossRef CAS.
- E. Engel, in A Primer in Density Functional Theory, Springer, 2003, pp. 56–122 Search PubMed.
- A. Unsöld, Z. Phys., 1927, 43, 563 CrossRef.
- J. Krieger, Y. Li and G. Iafrate, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 101, DOI:10.1103/PhysRevA.45.101.
- J. Krieger, Y. Li and G. Iafrate, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 5453, DOI:10.1103/PhysRevA.46.5453.
- O. V. Gritsenko and E. J. Baerends, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 042506, DOI:10.1103/PhysRevA.64.042506.
- F. Della Sala and A. Görling, J. Chem. Phys., 2001, 115, 5718 CrossRef CAS.
- Q. Wu and W. Yang, J. Theor. Comput. Chem., 2003, 02, 627, DOI:10.1142/S0219633603000690.
- T. Heaton-Burgess, F. A. Bulat and W. Yang, Phys. Rev. Lett., 2007, 98, 256401, DOI:10.1103/PhysRevLett.98.256401.
- C. Kollmar and M. Filatov, J. Chem. Phys., 2008, 128, 064101, DOI:10.1063/1.2834214.
- T. Pitts, S. Bousiadi, N. I. Gidopoulos and N. N. Lathiotakis, not published yet.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007, DOI:10.1063/1.456153.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358, DOI:10.1063/1.464303.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. a. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen and S. Su, et al. , J. Comput. Chem., 1993, 14, 1347, DOI:10.1002/jcc.540141112.
- M. S. Gordon and M. W. Schmidt, in Theory and Applications of Computational Chemistry, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 1167–1189, ISBN 978-0-444-51719-7, http://www.sciencedirect.com/science/article/pii/B9780444517197500846 Search PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814, DOI:10.1021/acs.jcim.9b00725 , pMID: 31600445.
- X. Andrade and A. Aspuru-Guzik, Phys. Rev. Lett., 2011, 107, 183002, DOI:10.1103/PhysRevLett.107.183002.
- E. Kraisler and L. Kronik, J. Chem. Phys., 2014, 140, 18A540 CrossRef.
- B. Senjean and E. Fromager, Phys. Rev. A, 2018, 98, 022513, DOI:10.1103/PhysRevA.98.022513.
- B. Senjean and E. Fromager, Int. J. Quantum Chem., 2020, e26190 Search PubMed.
- A. Guandalini, C. A. Rozzi, E. Räsänen and S. Pittalis, Phys. Rev. B, 2019, 99, 125140, DOI:10.1103/PhysRevB.99.125140.
- M. J. P. Hodgson, E. Kraisler, A. Schild and E. K. U. Gross, J. Phys. Chem. Lett., 2017, 8, 5974, DOI:10.1021/acs.jpclett.7b02615 , pMID: 29179553.
- E. Kraisler, M. J. P. Hodgson, E. K. U. Gross, 2020, arXiv:2008.12029.
- T. J. Callow, B. J. Pearce and N. I. Gidopoulos, not published yet.
- T. J. Callow, N. N. Lathiotakis and N. I. Gidopoulos, J. Chem. Phys., 2020, 152, 164114, DOI:10.1063/5.0005781.
- Calculated as the negative of the HOMO eigenvalue.
- For brevity we often use the term ‘screening density’. It should not be confused with the similar term used by Baerends et al..
- There are some restrictions for this to always hold: (i) the auxiliary basis cannot be significantly larger than the orbital basis and (ii) the value of λ cannot be arbitrarily small in numerical applications.
- Contact N. N. L. at E-mail: lathiot@eie.gr for information.
| This journal is © The Royal Society of Chemistry 2020 |