Highly selective chromoionophores for ratiometric Na+ sensing based on an oligoethyleneglycol bridged bithiophene detection unit†
Maximilian
Moser
 *a,
Karl J.
Thorley
*a,
Karl J.
Thorley
 a,
Floriana
Moruzzi
a,
James F.
Ponder
Jr.
a,
Floriana
Moruzzi
a,
James F.
Ponder
Jr.
 a,
Iuliana P.
Maria
a,
Alexander
Giovannitti
a,
Iuliana P.
Maria
a,
Alexander
Giovannitti
 b,
Sahika
Inal
b,
Sahika
Inal
 c and
Iain
McCulloch
c and
Iain
McCulloch
 ad
ad
aDepartment of Chemistry and Centre for Plastic Electronics, Imperial College London, London, SW7 2AZ, UK. E-mail: maximilian.moser13@imperial.ac.uk
bDepartment of Physics and Centre for Plastic Electronics, Imperial College London, London, SW7 2AZ, UK
cBiological and Environmental Sciences and Engineering Division, King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Kingdom of Saudi Arabia
dKing Abdullah University of Science and Technology (KAUST), Physical Sciences and Engineering Division, KAUST Solar Center (KSC), Thuwal 23955-6900, Saudi Arabia
First published on 16th April 2019
Abstract
Rapid and efficient measurement of sodium ion concentrations will benefit future studies and healthcare due to the importance of sodium to many biological processes. Ratiometric optical probes, where light absorption wavelengths shift according to ion concentration, can be used as a quick measurement method. In contrast to the currently available UV absorbing probes, we have synthesised a series of sensors which absorb in different regions of the visible spectrum. In addition to measurement by conventional UV-Vis spectroscopy, this also enables analysis of sodium ion concentration from colorimetry, opening the door to faster and cheaper analysis. Finally, the optical properties of the dyes were well reproduced by computational methods, with and without the presence of sodium, enabling acceleration of design of future materials.
Sodium is the sixth most abundant element in the earth's crust and plays several important roles in both animal and plant biology by enabling neural signalling, muscle contraction, metabolism in C4 plants, amongst others.1–8 Characteristic Na+ concentrations in organisms range between 1–200 mM, thereby defining the region of interest for Na+ measurements in living systems.9–11 Currently, the two primary methods for quantifying Na+ ion concentrations are based on either electrochemical or optical means. In this context, optical probes have shown several attractive features such as their (i) high sensitivity, (ii) ease of operation, (iii) fast data readout and (iv) comparatively low-cost experimental set-up.12,13 The general structure of Na+ selective optical probes consists of a unit capable of absorbing light (chromophore), that is covalently linked to an ion-binding unit (ionophore). To fully function as a sensor, the optical properties of the probe must be modulated upon analyte binding. In this regard, optical chemosensors can be categorised into two classes. In ‘on–off’ probes, the absorption or emission wavelength remains unchanged yet the optical transition intensity increases or decreases upon Na+ chelation. The main drawback of this class of dyes is the variability of their absorption or emission intensity from analyte-independent factors, such as sample background signal and instrumental noise.14,15 Conversely, in ratiometric probes, both the absorption or emission wavelength and transition intensity change upon Na+ binding. This unique property of ratiometric dyes effectively permits for facile Na+ concentration quantification by probing the optical properties of the dye at two wavelengths. Despite the numerous Na+ optical probes that have been developed over the past decades, only a handful of these display ratiometric sensing behaviour.16–19 One frequently encountered drawback of the currently available ratiometric Na+ colorimetric sensors is their absorption predominantly in the UV-region, leading to low tissue penetration and phototoxic damage in biological specimens. Another disadvantage of their absorption profiles in the short wavelength region is the requirement to evaluate their optical and ion-binding properties employing spectrophotometers. The deployment of such instruments is however not always feasible in field or point-of-care settings due to their highly sophisticated, bulky and relatively expensive nature.20–22 These limitations have motivated us to develop a novel series of ratiometric Na+ selective chromoionophores, in which we were able to progressively shift the maximum absorption wavelength (λmax) of the dyes across the entire visible region. Consequently, this has enabled us to accurately discriminate between Na+ concentrations in the biologically relevant mM range not only by conventional UV-Vis absorption spectroscopy but also by low-cost colorimetry.
Central to our molecular design, was the use of a 2,2′-bithiophene core functionalised at the 3 and 3′ positions with an oligoether chain, yielding a 15-crown-5 derivative ((17-crown-5)T2). This unit has already been demonstrated in previous literature to feature excellent Na+versus K+ selectivity and give rise to a ratiometric optical response upon metal chelation due to a conformational twist in the bithiophene backbone.23,24 The chromaticity of our probes was tuned by the introduction of flanking auxophores with different degrees of electron donating or electron-withdrawing abilities. These were in turn coupled to the central ionophore through direct C–H heteroarylation, thereby avoiding the use of any organotin intermediates, which are known to be highly toxic to biological systems, and reducing the synthetic complexity. A notable selectivity towards Na+ over other alkali and alkali earth metal ions was observed for each sensor in both organic and mixed aqueous-organic media, whereby the sensitivity, maximum absorption wavelength and colorimetric response could be tuned judiciously by the introduction of various flanking units.
As the synthesis of our sensors nonetheless incurred a relatively high cost and time-commitment, we have also developed a reliable computational protocol for accurately predicting the optical properties of our sensors, thereby simplifying the synthesis of the next generation of sensor materials. Time-dependent density functional theory (TD-DFT) calculations provide a good balance between computational cost and accuracy for evaluation of excited state properties, particularly in larger molecules of interest with extended conjugated π-systems. Further improvement in excitation energy prediction was achieved through the use of range separated functionals, where the range separation was optimised for each system. While this optimisation increases the overall time of each calculation, it provides a more theoretically correct approach than using functionals optimised against sets of test molecules. The excellent agreement between theoretical and experimental results obtained here justify the extra time cost, and provides a universal platform for prediction of optical properties.
The synthesis of the various Na+ selective colorimetric sensors, S1–S9, is displayed in Scheme 1. The ionophore (17-crown-5)T2 was prepared according to literature procedures by Ullmann coupling of 3-bromothiophene with tetraethylene glycol, followed by subsequent cuprate formation and oxidation (see Section S2 of the ESI†).23,24(17-crown-5)T2 was obtained in improved yields compared to those reported in the literature (13.6% over two steps compared to 6.2–7.5% lit.).23,24(17-crown-5)T2 was then subjected to direct C–H heteroarylation with the various aryl-bromide coupling partners employing a set of general reaction conditions to give the final phenyl-(S1–S3), thienyl-(S4–S6) and benzothiadiazole-based sensors (S7–S9). Overall, the direct C–H heteroarylation step afforded the sensor molecules (S1–S9) in high yields (67–97%), comparable to those obtained in literature for the direct C–H heteroarylation of other substituted thiophene units (59–95%).25,26 Moreover, by foregoing the use of any organotin coupling partners that have been employed so far for the cross-couplings of (17-crown-5)T2, two synthetic steps are avoided, whilst also significantly benefiting atom economy by ∼25% and reaction safety (see Table S1 in the ESI† for atom economy calculations).23,24
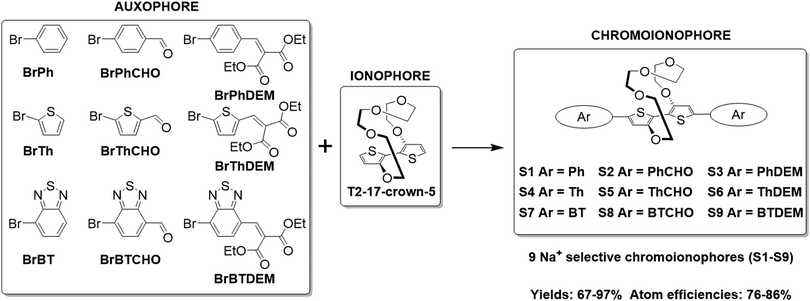 | ||
| Scheme 1 Synthetic scheme illustrating the direct C–H heteroarylation of (17-crown-5)T2 with the various auxophores. | ||
The optical properties of the chemosensors S1–S9 were first evaluated by conducting UV-Vis absorption spectroscopy titrations in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v solutions of tetrahydrofuran
1 v/v solutions of tetrahydrofuran![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
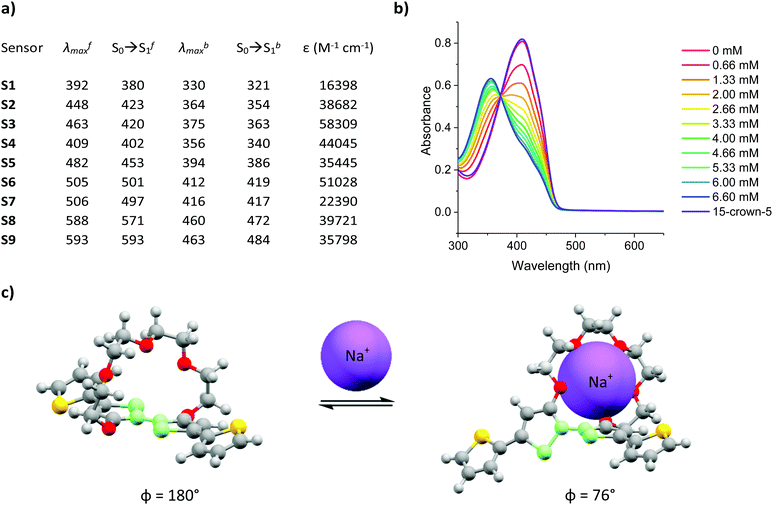
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetonitrile and varying the concentration of added Na+ between 0–6.66 mM, in increments of 0.66 mM. The experimentally recorded maximum absorption wavelength (λmax), computationally simulated S0 → S1 of the Na+ free (λfmax and S0 → Sf1) and Na+ bound (λbmax and S0 → Sb1) forms of sensors S1–S9 as well as their corresponding molar extinction coefficients (ε) are summarised in Fig. 1a and the corresponding absorption spectra can be found in Fig. S28–S36 the ESI.† A more detailed explanation for the sample preparation procedure can be found in Table S2 in the ESI.†
acetonitrile and varying the concentration of added Na+ between 0–6.66 mM, in increments of 0.66 mM. The experimentally recorded maximum absorption wavelength (λmax), computationally simulated S0 → S1 of the Na+ free (λfmax and S0 → Sf1) and Na+ bound (λbmax and S0 → Sb1) forms of sensors S1–S9 as well as their corresponding molar extinction coefficients (ε) are summarised in Fig. 1a and the corresponding absorption spectra can be found in Fig. S28–S36 the ESI.† A more detailed explanation for the sample preparation procedure can be found in Table S2 in the ESI.†
Upon Na+ binding, the absorption maxima of each dye was blue-shifted towards a shorter wavelength, thus agreeing with previous findings in the literature.23,24,27 A concomitant increase and decrease in the absorbance at the shorter and longer wavelength absorption bands was also noted, thus highlighting the ratiometric nature of the sensor, see Fig. 1b (see Fig. S28–S36 in ESI† for absorption spectra of remaining sensors). The origin of this behaviour was rationalised in terms of a conformational twist in the bithiophene backbone of the central ionophore. Specifically, previous X-ray crystallographic findings of the (17-crown-5)T2 unit have suggested that the S–C–C–S dihedral angle measured across the central thiophene–thiophene bond, highlighted in light green in Fig. 1c, is altered from near 180° to 76° upon Na+ chelation, thereby decreasing the conjugation length which in turn increases the bandgap of the system.24 To test the reversibility of this host–guest equilibrium, 50 μL of a known Na+ chelator, with a higher binding constant than our sensor molecules (15-crown-5), was added to the samples containing the highest Na+ concentration (6.66 mM). For each sensor, this restored the optical signature of the corresponding Na+ free form, thus confirming the reversibility of this equilibrium.
Fig. 1a also shows that modulation of the electron-donating or -withdrawing character of the auxophores, i.e. replacing the phenyl end caps with either thiophene or benzothiadiazole ones (e.g. when going from S2 to S5 to S8), progressively shifted the absorption maxima of the dyes towards longer wavelengths as a result of either the added electron-richness and planarity of the thiophene unit or the increased push–pull character conferred by the benzothiadiazole one. The absorption maxima were further extended into the red region by the introduction of additional electron withdrawing moieties, specifically aldehyde and arylidene malonate groups (e.g. when going from S1 to S2 to S3), ultimately yielding a series of colorimetric Na+ sensors with λfmax ranging from 392–593 nm. Comparing the experimentally recorded absorption maxima of both the Na+ free and Na+ bound sensors with those obtained by computational simulations indicated a strong agreement between the two data sets. In fact in eight out of nine cases for the Na+ free form of the sensors, the computationally simulated S0 → Sf1 transitions lied within 25 nm of the experimentally obtained λfmax. Although computational simulations with similar accuracies have been reported in the literature, these have been conducted for a well-known class of highly rigid dyes with similar molecular structures and absorption maxima lying within a wavelength range of less than 100 nm.28 Moreover, these calculations also required the use of a mixed functional protocol to achieve such accuracy. To further highlight the potential of our computational model, we also predicted the S0 → Sb1 transition of the bound sensor. To the best of our knowledge this report is the first to predict the optical properties of ion-bound chromoionophores. Ultimately, our model was able to correctly predict the absorption maxima for the Na+ bound forms of each sensor within our 25 nm accuracy cut-off. The encouraging agreement between theoretical and experimental results obtained in this work can ultimately serve as a powerful platform to not only predict the optical properties of chromoionophores in their unbound state, but also when interacting with the analyte, thereby acting as a good screening tool for the development of sensors with a particular set of desired properties.
The selectivity of S1–S9 was evaluated by performing UV-Vis absorption titrations of each chromoionophore against Li+, K+ and Ca2+, whilst employing the same protocol as for the optical titrations against Na+. Li+, K+ and Ca2+ were deemed most relevant as competing ions, since their ionic and hydrodynamic radii are the most similar of both group I and II elements compared to Na+.29,30 As indicated by the absorption spectra of S1–S9 (see Fig. S37–S45 in the ESI†) neither addition of Li+, K+ or Ca2+ resulted in the same ratiometric response as observed for Na+, in fact only a slight depression of the absorption intensity was noted upon the addition of K+. To quantify the selectivity of S1–S9 for Na+ over Li+, K+ and Ca2+, the percentage change in the absorbance (Δ%A), i.e. contrast, at the maximum absorption wavelength for the various concentrations was measured, see Fig. 2a. On average, sensors S1–S9 displayed a 68-fold, 13-fold and 21-fold stronger response towards Na+ compared to Li+, K+ and Ca2+ respectively, indicating excellent analyte selectivity and comparable to those of other Na+ ion selective ratiometric optical probes.16–19 The varying degrees of contrast between sensors S1–S9 in their Na+ free and bound form (20–70%) can be attributed to their different dissociation constants (Kd). These in turn were obtained from the Benesi–Hildebrand plot of each sensor (see Fig. S55–S63 in the ESI†).
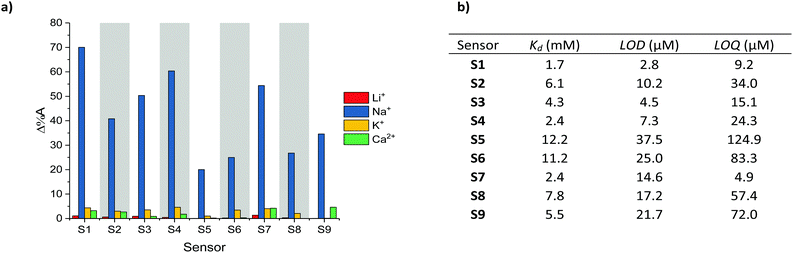 | ||
| Fig. 2 (a) Maximum contrast obtained during the titration of S1–S9 against Li+, Na+, K+ and Ca2+, (b) Kd, LOD and LOQ with respect to Na+ obtained for S1–S9. | ||
The sensitivity of sensors S1–S9, including their Kd, limit of detection (LOD) and limit of quantification (LOQ) relative to Na+ are summarised in Fig. 2b (see Section 12 in the ESI† for LOD and LOQ calculations). As expected, the sensors with the Kds closest to the midpoint of the chosen 0–6.66 mM concentration range, (Kd of S1 = 2.4 mM, Kd of S4 = 1.7 mM and Kd of S7 = 2.4 mM) evoked the strongest changes in their absorbance (Δ%A = 60%, 70% and 54% between 0–6.66 mM Na+ for S1, S4 and S7 respectively). From a molecular design point of view the lower Kds of the H-end capped S1, S4 and S7 sensors suggest that both aldehyde and arylidene malonate groups can inhibit the host–guest interaction of the (17-crown-5)T2 ionophore with Na+. This behaviour was attributed to the presence of two lone pairs of electrons on the carbonyl moieties, which are known to interact with metal ions. The on average inferior Kd of the thiophene containing sensors (S4–S6) compared to those containing phenyl (S1–S3) and benzothiadiazole (S7–S9) on the other hand was rationalised due to the smaller steric requirement imposed by the thienyl groups, thereby facilitating efficient host–guest binding. Moreover, the more electron-rich character of the thienyl group relative to both the phenyl and benzothiadiazole ones should also enhance the electron density on the central (17-crown-5)T2 unit, thereby further promoting chelation to the electron deficient Na+ centre. Ultimately, by varying the chemical design of the various Na+ chromoionophores the sensors’ Kds could be modulated over one order of magnitude.
To confirm the ability of chromoionophores S1–S9 to be able to selectively bind Na+ over Li+, K+ and Ca2+ even in the presence of water, sensors S1–S9 were dissolved in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 v/v solutions of water
3 v/v solutions of water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
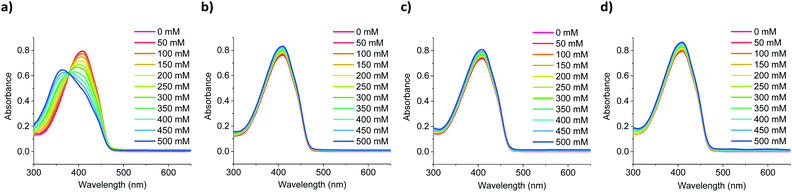
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tetrahydrofuran, while varying the concentration of added salt between 0–500 mM in increments of 50 mM. As the sensors’ solubility was negligible in water, high tetrahydrofuran ratios had to be employed, to achieve full dissolution. As shown in Fig. 3, switching from an all-organic to a mixed aqueous-organic medium still allowed for the selective detection of Na+ over Li+, K+ and Ca2+, again leading to a ratiometric response. The absorption spectra of the remaining sensors showed similar responses and can be found in Fig. S46–S54 in the ESI.† Compared to the measurements performed in all organic media, the measurements in mixed aqueous-organic media required higher Na+ concentrations to evoke the same spectral changes, thus agreeing with previous literature findings.31,32
tetrahydrofuran, while varying the concentration of added salt between 0–500 mM in increments of 50 mM. As the sensors’ solubility was negligible in water, high tetrahydrofuran ratios had to be employed, to achieve full dissolution. As shown in Fig. 3, switching from an all-organic to a mixed aqueous-organic medium still allowed for the selective detection of Na+ over Li+, K+ and Ca2+, again leading to a ratiometric response. The absorption spectra of the remaining sensors showed similar responses and can be found in Fig. S46–S54 in the ESI.† Compared to the measurements performed in all organic media, the measurements in mixed aqueous-organic media required higher Na+ concentrations to evoke the same spectral changes, thus agreeing with previous literature findings.31,32
The stability of the sensors was also evaluated by comparing their optical response towards Na+ after storing sample solutions under ambient conditions for two and seven days. No discernible difference was noted in the absorption profiles of the samples at either titration end point (see Fig. S73–S81 in the ESI†), thus highlighting the excellent stability of our sensors in solution.
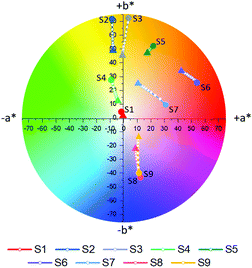
Following complete evaluation of the optical properties by spectroscopic means, colorimetric analysis of S1–S9 was performed, employing the CIE 1976 CIEL*a*b* color space. In this color space, L* can vary between 0–100 and represents the lightness of a color, whereby L* = 0 corresponds to black and L* = 100 to white. The color channels a* and b* on the other hand define the hue of a given color by describing the red (+a* value)-green (−a* value) and yellow (+b* value)-blue (−b* value) components respectively. The a*b* color tracks of probes S1–S9 upon the addition of different concentrations of Na+ (0–6.66 mM) are illustrated in Fig. 4a, while the exact color values at 0 mM and 6.66 mM Na+ can be found in Table 1. It should be noted that color coordinates are typically compared with solutions or films with the same absorbance, however as these sensors were compared at a fixed concentration during spectroscopic measurements, the sensors were also compared at a fixed concentration during their colorimetric analysis. As the various sensors have different molar extinction coefficients, listed in Fig. 1a, the resulting absorbances of the solutions vary.
Based on their colorimetric properties, sensors S1–S9 can broadly be divided into four groups, those with a colorless (S1), yellow-orange (S2–S5), red (S6 and S7) and blue (S8 and S9) appearance. Besides for S1, all sensors display a discernible variation in their color upon incrementing Na+ concentration, thus highlighting the adequate nature of colorimetry for the evaluation of the sensor's optical properties. The lacking response in S1 can be understood due to its absorption almost entirely <380 nm, thus lying outside of the human visual perception range (380–700 nm). For sensors S2–S5 addition of Na+ resulted in a decrease in both a* and b*, effectively decoloring the sensors. Similarly, increasing Na+ concentrations also resulted in the fainter appearance of sensors S8 and S9. These findings were reflected in the progressively lowering color saturations (Sab) of the various probes upon increasing Na+ concentrations (see eqn (S8) in the ESI† for the calculation of Sab).33 For sensors S6 and S7 addition of Na+ resulted mainly in a decrease in a*, hence reducing the contribution of their red component, but also a concomitant increase in b*, thereby increasing the yellow component in their appearance. As a result of these opposing factors, the average change in the color saturation of S6 and S7 when going from their Na+ free to Na+ bound form was smaller compared to the average of the other sensors.
To accurately quantify the difference in color between samples upon Na+ additions, eqn (1) was employed.33,34
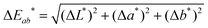 | (1) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (λ) and ȳ(λ) color matching functions that were employed to calculate the L*a*b* coordinates of each sensor. The superior colorimetric performance of S9 is further highlighted by the fact that each 0.66 mM increment in Na+ concentration resulted in a ΔEab* greater than 2.2. As a ΔEab* in excess of 2.2 signifies that a standard observer can distinguish between colors, these results suggest that Na+ concentration determination when employing S9 could theoretically also be performed by naked-eye. Based on this discussion, it is important to note that in colorimetric measurements the Kd of chromoionophores is not the only factor in determining the contrast that can be achieved with a specific dye. Consequently, this redefines the parameters affecting dye performance, which in turn can lead to spectroscopically inferior sensors outperforming their competitors in colorimetric measurements.
(λ) and ȳ(λ) color matching functions that were employed to calculate the L*a*b* coordinates of each sensor. The superior colorimetric performance of S9 is further highlighted by the fact that each 0.66 mM increment in Na+ concentration resulted in a ΔEab* greater than 2.2. As a ΔEab* in excess of 2.2 signifies that a standard observer can distinguish between colors, these results suggest that Na+ concentration determination when employing S9 could theoretically also be performed by naked-eye. Based on this discussion, it is important to note that in colorimetric measurements the Kd of chromoionophores is not the only factor in determining the contrast that can be achieved with a specific dye. Consequently, this redefines the parameters affecting dye performance, which in turn can lead to spectroscopically inferior sensors outperforming their competitors in colorimetric measurements.
Comparison between the optical properties of sensors S1 and S4, S6 and S7 and S8 and S9 obtained by conventional spectroscopy and colorimetry highlights another benefit of the latter analytical technique. According to their λfmax and λbmax, the appearance of S1 and S4, S6 and S7, S8 and S9 is expected to be virtually indistinguishable. Quantitative comparison of the L*a*b* color values however illustrates that the ΔEab* obtained between each sensor pair in both forms is greater than 2.2, thereby meaning that the two colors are easily distinguishable from each other by colorimetry and visual inspection alone.
It was also possible to monitor Na+ selectivity over Li+, K+ and Ca2+ by colorimetry. Here, the color tracks obtained when titrating each sensor against Na+, Li+, K+ and Ca2+ were superimposed (shown in Fig. S82–S84 in the ESI†). Compared to the color tracks obtained when titrating against Na+ addition of neither Li+, K+ or Ca2+ evoked a strong change in color, in fact in no circumstance did the ΔEab* obtained for the two titration end points exceed a value of 2.2. By employing ΔEab* as a figure of merit, similar to Δ%A when employing spectroscopy, the average response of sensors S1–S9 with respect to Na+ was 42-fold, 21-fold and 23-fold larger than for Li+, K+ and Ca2+ respectively, thus comparing well with the results obtained by UV-Vis spectroscopy (see Table S3 in the ESI†).
In summary, nine novel ratiometric Na+ optical probes (S1–S9) based on a bithiophene-crown ether sensing unit have been synthesised and their absorption maxima progressively shifted across the entire visible range. A computational model for accurately predicting the absorption maxima of the sensors in both their Na+ bound and Na+ free forms has also been developed, whereby an excellent agreement between theoretical and experimental results was obtained, thus suggesting its use as a good prediction tool for the optical properties of future sensors. The optical and binding properties of S1–S9 were assessed by conventional UV-Vis absorption spectroscopy in both organic media and subsequently in mixed aqueous-organic solutions, whereby excellent Na+ selectivity over other alkali and alkali earth metals was retained in both cases. One limitation of the developed sensor series is their limited water solubility, thus preventing their use in purely aqueous solutions. To overcome this limitation, current research efforts are being dedicated towards the immobilisation of ionophores S1–S9 into an inert polymer matrix, as well as the development of fully water soluble sensors. Evaluation of the probes by colorimetry was also performed, affording comparable results to UV-Vis spectroscopy, hence highlighting the appropriate nature of colorimetry as a low-cost alternative analytical tool to study the optical properties of chromoionophores.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We gratefully thank Dr Lisa Haigh, for performing mass spectrometry and Augustus Lang for colorimetric support. We acknowledge funding from KAUST, as well as EPSRC Project EP/G037515/1, EP/M005143/1, ECFP7 Project SC2 (610115), EP/N509486/1, for the financial support. M. M. gratefully thanks the Imperial College Schrödinger Scholarship for financial support.Notes and references
- R. C. Thomas, Physiol. Rev., 1971, 52, 563 CrossRef PubMed.
- A. L. Hodgkim and A. F. Huxley, J. Physiol., 1952, 117, 500 CrossRef.
- M. P. Blaustein, W. F. Goldman, G. Fontana, B. K. Krueger, E. M. Santiago, T. D. Steele, D. N. Weiss and P. J. Yarowsky, Ann. N. Y. Acad. Sci., 1991, 639, 254 CrossRef CAS.
- M. P. Blaustein, Am. J. Physiol., 1977, 232, C165 CrossRef CAS.
- A. Horowitz, C. B. Menice, R. Laporte and K. G. Morgan, Physiol. Rev., 1996, 76, 967 CrossRef CAS PubMed.
- T. Furumoto, T. Yamaguchi, Y. Ohshima-Ichie, M. Nakamura, Y. Tsuchida-Iwata, M. Shimamura, J. Ohnishi, S. Hata, U. Gowik, P. Westhoff, A. Bräutigam, A. P. M. Weber and K. Izui, Nature, 2011, 476, 472 CrossRef CAS PubMed.
- F. J. M. Maathuis, J. Exp. Bot., 2014, 65, 849 CrossRef CAS PubMed.
- G. V. Subbarao, O. Ito, W. L. Berry and R. M. Wheeler, CRC Crit. Rev. Plant. Sci., 2003, 22, 391 Search PubMed.
- R. Munns and M. Tester, Annu. Rev. Plant Biol., 2008, 59, 651 CrossRef CAS.
- D. E. Carden, D. J. Walker, T. J. Flowers and A. J. Miller, Plant Physiol., 2003, 131, 676 CrossRef CAS.
- D. M. Bers, W. H. Barry and S. Despa, Cardiovasc. Res., 2003, 57, 897 CrossRef CAS.
- Y. Liu, G. Yu, M. Tian and H. Zhang, Contrast Media Mol. Imaging, 2011, 6, 169 CAS.
- T. Terai and T. Nagano, Curr. Opin. Chem. Biol., 2008, 12, 515 CrossRef CAS PubMed.
- S. G. Liu, N. Li, L. Han, L. J. Li, N. Bing Li and H. Q. Luo, Mater. Horiz., 2018, 5, 454 RSC.
- G. Grynkiewicz, M. Poenie and R. Y. Tsien, J. Biol. Chem., 1985, 260, 3440 CAS.
- A. T. Harootunian, J. P. Y. Kao, B. K. Eckert and R. Y. Tsien, J. Biol. Chem., 1989, 264, 19458 CAS.
- V. V. Martin, A. Rother, Z. Diwu and K. R. Gee, Bioorg. Med. Chem. Lett., 2004, 14, 5313 CrossRef CAS PubMed.
- M. Taki, H. Ogasawara, H. Osaki, A. Fuazawa, Y. Sato, K. Ogasawara, T. Higashiyama and S. Yamaguchi, Chem. Commun., 2015, 51, 11880 RSC.
- N. B. Sankaran, S. Nishizawa, M. Watanabe, T. Uchida and N. Teramae, J. Mater. Chem., 2005, 15, 2755 RSC.
- B. C. Thompson, P. Schottland, K. Zong and J. R. Reynolds, Chem. Mater., 2000, 12, 1563 CrossRef CAS.
- D. A. C. Czegan and D. K. Hoover, J. Chem. Educ., 2012, 89, 304 CrossRef CAS.
- D. R. Albert, M. A. Todt and H. Floyd Davis, J. Chem. Educ., 2012, 89, 1432 CrossRef CAS.
- M. J. Marsella and T. M. Swager, J. Am. Chem. Soc., 1993, 115, 12214 CrossRef CAS.
- A. Giovannitti, C. B. Nielsen, J. Rivnay, M. Kirkus, D. J. Harkin, A. J. P. White, H. Sirringhaus, G. G. Malliaras and I. McCulloch, Adv. Funct. Mater., 2016, 26, 514 CrossRef CAS.
- C.-Y. Liu, H. Zhao and H.-H. Yu, Org. Lett., 2011, 13, 4068 CrossRef CAS PubMed.
- S.-Y. Chang, P.-H. Lin and C.-Y. Liu, RSC Adv., 2014, 4, 35868 RSC.
- T. Oike, T. Kurata, K. Takimiya, T. Otsubo, Y. Aso, H. Zhang, Y. Araki and O. Ito, J. Am. Chem. Soc., 2005, 127, 15372 CrossRef CAS PubMed.
- S. Di Tommaso, D. Bousquet, D. Moulin, F. Baltenneck, P. Riva, H. David, A. Fadli, J. Gomar, I. Ciofini and C. Adamo, J. Comput. Chem., 2017, 38, 998 CrossRef CAS PubMed.
- A. G. Volkov, S. Paula and D. W. Deamer, Bioelectrochem. Bioenerg., 1997, 42, 153 CrossRef CAS.
- G. Gao, Y. Cao, W. Liu, D. Li, W. Zhou and J. Liu, Anal. Methods, 2017, 9, 5570 RSC.
- T. Schwarze, H. Müller, D. Schmidt, J. Riemer and H.-J. Holdt, Chem. – Eur. J., 2017, 23, 7255 CrossRef CAS PubMed.
- H. He, M. A. Mortellaro, M. J. P. Leiner, S. T. Young, R. J. Fraatz and J. K. Tusa, Anal. Chem., 2003, 75, 549 CrossRef CAS PubMed.
- G. Wyszecki and W. S. Stiles, Color Science: Concepts and Methods, Quantitative Data and Formulae, Wiley, Hoboken (NJ), 2000 Search PubMed.
- J. F. Ponder, Jr., A. M. Österholm and J. R. Reynolds, Macromolecules, 2016, 49, 2106 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8tc06000b |
| This journal is © The Royal Society of Chemistry 2019 |