Room temperature demonstration of a sodium superionic conductor with grain conductivity in excess of 0.01 S cm−1 and its primary applications in symmetric battery cells†
Qianli
Ma
 *ab,
Chih-Long
Tsai
*ab,
Chih-Long
Tsai
 ab,
Xian-Kui
Wei
ab,
Xian-Kui
Wei
 c,
Marc
Heggen
c,
Frank
Tietz
c,
Marc
Heggen
c,
Frank
Tietz
 ab and
John T. S.
Irvine
ab and
John T. S.
Irvine
 *d
*d
aForschungszentrum Jülich GmbH, Institute of Energy and Climate Research, Materials Synthesis and Processing (IEK-1), 52425 Jülich, Germany. E-mail: q.ma@fz-juelich.de
bHelmholtz-Institute Münster, c/o Forschungszentrum Jülich GmbH, 52425 Jülich, Germany
cErnst Ruska-Centre for Microscopy and Spectroscopy with Electrons, Peter Grünberg Institute, Forschungszentrum Jülich GmbH, 52425 Jülich, Germany
dSchool of Chemistry, University of St Andrews, St Andrews, Fife KY16 9ST, UK. E-mail: jtsi@st-andrews.ac.uk
First published on 25th February 2019
Abstract
The lack of suitable candidate electrolyte materials for practical application limits the development of all-solid-state Na-ion batteries. Na3+xZr2Si2+xP1−xO12 was the very first series of NASICONs discovered some 40 years ago; however, separation of bulk conductivity from total conductivity at room temperature is still problematic. It has been suggested that the effective Na-ion conductivity is ∼10−4 S cm−1 at room temperature for Na3+xZr2Si2+xP1−xO12 ceramics; however using a solution-assisted solid-state reaction for preparation of Na3+xZr2Si2+xP1−xO12, a total conductivity of 5 × 10−3 S cm−1 was achieved for Na3.4Zr2Si2.4P0.6O12 at 25 °C, higher than the values previously reported for polycrystalline Na-ion conductors. A bulk conductivity of 1.5 × 10−2 S cm−1 was revealed by high frequency impedance spectroscopy (up to 3 GHz) and verified by low temperature impedance spectroscopy (down to −100 °C) for Na3.4Zr2Si2.4P0.6O12 at 25 °C, indicating further the potential of increasing the related total conductivity. A Na/Na3.4Zr2Si2.4P0.6O12/Na symmetric cell showed low interface resistance and high cycling stability at room temperature. A full-ceramic cell was fabricated and tested at 28 °C with good cycling performance.
Introduction
Although Li-ion batteries (LIBs) still dominate the global market of energy storage devices today, the application of Na-ion batteries (NIBs) has been extensively explored and discussed.1–6 Since the Na ion is heavier (23.0 g mol−1versus 6.9 g mol−1), and has a lower ionization potential (−2.7 V versus −3.06 V) than the Li ion, NIBs are slightly inferior to LIBs both in terms of energy density and power density; however, sodium possesses the advantage of higher elemental abundance (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm versus 20 ppm in the Earth's crust) and lower costs for raw materials and resulting compounds. Therefore in stationary applications such as storage of renewable energy, NIBs have the potential to outperform LIBs as energy production costs along with battery life are more important than energy and power density.1–6
000 ppm versus 20 ppm in the Earth's crust) and lower costs for raw materials and resulting compounds. Therefore in stationary applications such as storage of renewable energy, NIBs have the potential to outperform LIBs as energy production costs along with battery life are more important than energy and power density.1–6
Since LIBs with liquid or polymer electrolytes have intrinsic problems due to flammability, complex reactions at the solid/liquid or solid/polymer interface, thermal instability, etc., LIBs in the all-solid-state (non-liquid/polymer-contained) design are becoming increasingly significant today.7–11 Theoretically, an LIB with a solid-state electrolyte is not only able to overcome the disadvantages mentioned above, but also achieve both higher energy and power densities.10,11 The above concept also applies to NIBs because of the high similarities between NIBs and LIBs.
Na3+xZr2Si2+xP1−xO12 (NZSPx) was discovered some 40 years ago to be a Na-ion conductor.12,13 Its structure exhibits high tolerance and flexibility for cation-substitution, leading to the foundation of the whole NASICON (Na Super-Ionic CONductors).14,15 Together with β/β′′-aluminas,16,17 they were regarded as the most promising candidates for possible solid electrolytes of NIBs because of their relatively high total ionic conductivities (σtotal, including bulk (σb) and grain-boundary (σgb) conductivity). Comparatively, β/β′′-aluminas are superior in σtotal (1–2 × 10−3 S cm−1versus ∼10−4 S cm−1 at room temperature,14–16 as a standard, liquid electrolytes normally have conductivities of 5–10 × 10−3 S cm−1 at room temperature18), while NASICONs show benefits of processing temperatures (∼1200 °C versus ∼1600 °C).14,15,17 More than 400 publications have discussed NASICONs as Na-ion conductors (ESI Fig. S1†). However, until now even the separation of σb from σtotal of NASICONs at room temperature was problematic. In the published literature, only σtotal has generally been reported largely due to difficulty in observing the high frequency response in available instruments. The possible reasons for the inadequate understanding of NASICONs are: (1) in the past, NASICONs were mainly considered as electrolyte materials for high-temperature sodium batteries. Thus, the performance of NASICONs at temperatures of 200–300 °C was mainly targeted (ESI Fig. S1†). The literature discussing the properties of the NASICONs at room temperature is quite limited. (2) When Hong et al. discovered NZSPx 40 years ago,12,13 they believed that the highest σtotal of the series occurs at −0.2 ≤ x ≤ 0.2 (i.e. Na content range from 2.8 to 3.2 mol per formula unit of the NASICONs). In the following 40 years, most research studies concentrated on a similar composition range and achieved similar values of σtotal.14,15 The range of composition studied still seems deficient.
In the present study, the detailed investigation of NZSPx (with 0 ≤ x ≤ 0.6) using a more systematic substitution strategy and a more advanced processing method reveals that the σtotal of NZSPx, or even of NASICONs is largely underestimated. The σb of the samples is clearly distinguished from the σtotal. In particular, Na3.4Zr2Si2.4P0.6O12 (NZSP0.4) is found to exhibit the highest σtotal among all polycrystalline Na-ion conductors. Together with sodium metal as electrodes, symmetric cells show high cycling stability at room temperature. Together with Na3V2P3O12 (NVP, which also has a NASICON structure) as an electrode material (both as positive and negative electrodes), full-NASICON-ceramic NIBs based on this superior NZSP0.4 electrolyte were developed. An all-solid-state NIB was successfully operated at room temperature.
Results
Properties of powders
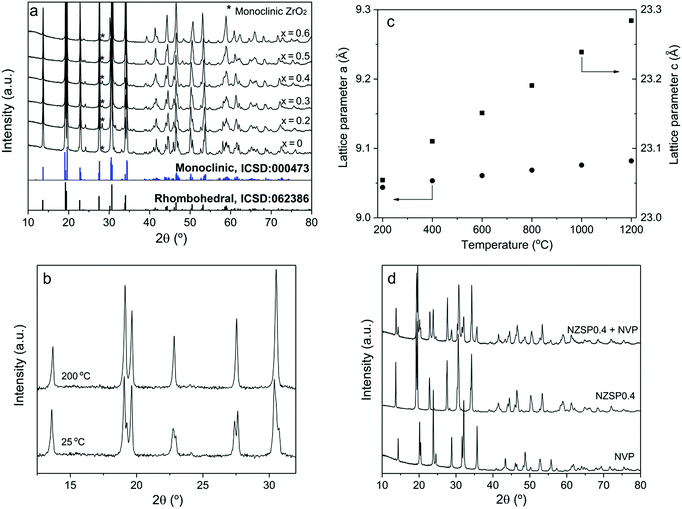
The NZSPx powders were prepared using a solution-assisted solid-state reaction method (SA-SSR),19–21 which is adaptable to large-scale preparation and guarantees low costs of the product. A relative density of >95% can be easily obtained for all the samples from NZSP0 to NZSP0.6 by conventional uniaxial pressing and conventional sintering at 1250–1300 °C for 5 h.At room temperature, the NZSPx samples exhibit the NASICON structure, as a monoclinic phase (NZSP0 and 0.2), as a rhombohedral phase (NZSP0.6), or as a mixture of both (NZSP0.3–NZSP0.5). Evidently, from NZSP0 to NZSP0.6, the crystal structure of the samples at room temperature gradually changes from monoclinic to rhombohedral (Fig. 1a). Rietveld analysis yields that NZSP0.3, NZSP0.4 and NZSP0.5 are mixed by two phases with quantitative weight ratios of rhombohedral over monoclinic at 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63, 48
63, 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 and 66
52 and 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34, respectively (ESI Fig. S2†). A slight secondary phase of monoclinic ZrO2 is observed in all compositions.20,21 Fortunately, their concentration is so small and has no apparent influence on σtotal of the samples.
34, respectively (ESI Fig. S2†). A slight secondary phase of monoclinic ZrO2 is observed in all compositions.20,21 Fortunately, their concentration is so small and has no apparent influence on σtotal of the samples.
All compositions exhibit the rhombohedral phase at >200 °C.22 A phase transformation from the rhombohedral to monoclinic structure occurs for samples of NZSP0–NZSP0.5 when the temperature decreases from 200 °C to 100 °C. An example of NSZP0 is shown in Fig. 1b (other compositions are shown in the ESI Fig. S3†). The XRD pattern of the monoclinic structure is quite similar to that of the rhombohedral structure, because it is merely a slightly twisted rhombohedral structure. Nevertheless, they can be easily distinguished by splitting the diffraction peaks of the monoclinic phase. The lattice parameters a and c of the rhombohedral NZSPx change differently when the temperature increases from 200 to 1200 °C. Compared to a, parameter c expands more on heating the samples, as shown in Fig. 1c (NZSP0 is shown as an example, the rest of the compositions are shown in the ESI Fig. S4†) resulting in the differences in thermal expansion coefficient (TEC) values, shown in Table 1. The TEC value of the a-axis is obviously much smaller than that of the c-axis. Similar results were reported for other NASICONs and defined as thermal-expansion anisotropy (TEA).23 In the present study, the TEC of a decreases with the x value in NZSPx, while that of c increases, thus indicating that the anisotropy continuously increases with the x value.
| NZSP0 | NZSP0.2 | NZSP0.3 | NZSP0.4 | NZSP0.5 | NZSP0.6 | |
|---|---|---|---|---|---|---|
| TEC a (10−6 K−1) | 4.2 | 3.6 | 3.5 | 3.5 | 3.2 | 3.2 |
| TEC c (10−6 K−1) | 9.8 | 9.7 | 10.4 | 10.7 | 11.5 | 12.7 |
The primary particles of the NZSPx powder exhibit a favorable morphology. They are small (<100 nm), homogeneous, and almost spherical in shape (ESI Fig. S5†). They are important prerequisites for the further processing of the final ceramic product.
The NVP samples reveal a pure rhombohedral phase when sintered at 750 °C in Ar containing 2% H2 (Fig. 1d), in agreement with previous results.24 In addition, according to XRD patterns, NVP and NZSP0.4 do not exhibit detectable reactions after co-sintering up to 900 °C in Ar containing 2% H2 (Fig. 1d). The chemical compatibility of NVP and NZSP0.4 is a necessary requirement for fabricating a full ceramic cell.
Properties of the sintered samples
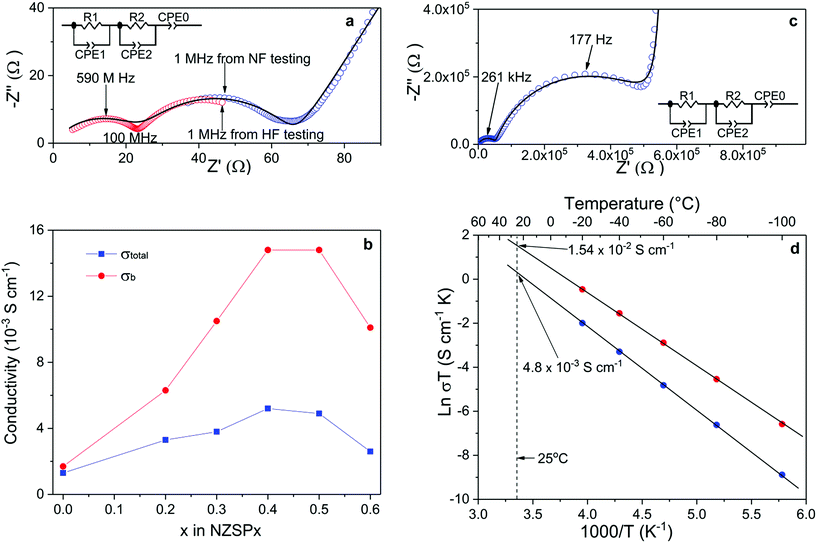
The σtotal and σb of the sintered samples are determined by fitting Nyquist plots of the impedance spectra, as shown in Fig. 2a. The equivalent circuit is shown as an inset of Fig. 2a, where R and CPE indicate the resistance and constant phase element (CPE), respectively. A number of key parameters of the equivalent circuit are shown in Table 2. Since the capacitance values of CPE1, CPE2 and CPE0 fit well to the characteristic capacitance25 from the contribution of the bulk (high-frequency semi-cycle), the grain-boundary (middle-frequency semi-cycle) and the interface between electrolyte and electrodes (low-frequency line), respectively, R1 and R2 are attributed to the bulk and grain-boundary resistances (Rb and Rgb), respectively. It is quite common to discuss the conductivity of NASICON materials using Nyquist plots.20,21,26–32 However, limited by the frequency range of common impedance spectroscopy systems (up to 20 MHz), they usually show only one (or even half of one) semi-circle in the plots at room temperature. Therefore, it is difficult to separate Rb and Rgb contributions. Only the total resistance (Rtotal, which equals to Rb + Rgb) can be determined from such plots. In the present study, two impedance spectroscopy systems were used in combination to solve this problem, with frequency ranges from 3 GHz to 1 MHz and from 3 MHz to 0.01 Hz. As shown in Fig. 2a, the Nyquist plot of NSZP0.4 shows almost two complete semi-circles, starting very close from the origin of both the x and y axis. Nyquist plots of other samples are shown in the ESI Fig. S6.†Fig. 2b shows the conductivity data of the σtotal and σb of NZSPx measured at 25 °C, derived from the same method as in Fig. 2a. With increasing amounts of the x value, the σtotal of the NZSPx samples increases until x = 0.4, reaching a peak value of 5.2 × 10−3 S cm−1. σb exhibits a similar dependence on the x value, reaching 1.49 × 10−2 S cm−1. When x ≥ 0.5, both σtotal and σb decrease with increasing x value. Experimental σb data of NASICONs at room temperature were never reported before, and such a value is unexpectedly high, even significantly higher than that of liquid-based Na-ion conductors.18 Moreover, it is also observed that Rb shows less contribution to Rtotal with increasing amounts of the x value, i.e. Rgb becomes more and more significant in Rtotal.
The σb of NZSPx can also be determined by normal-frequency impedance spectroscopy at low temperatures, since the time constant (τ) of the parallel RC element (R1 and CPE1) representing the bulk component is shifted to the normal-frequency range because of the increased resistance of the samples at low temperatures.25 An example is shown in Fig. 2c. At −100 °C, two complete semi-circles are observed for a sintered NZSP0.4 sample by impedance spectroscopy with a maximum frequency of 10 MHz. The capacitance values of CPE1, CPE2 and CPE0 in Fig. 2c also fit well to the characteristic capacitance25 from the contribution of bulk, grain-boundary and the interface between electrolyte and electrodes (Table 2), indicating that R1 and R2 are attributed to Rb and Rgb, respectively. Nyquist plots of the sample tested at other temperatures are shown in the ESI Fig. S7.† Until −20 °C, at least part of the semi-circle representing the bulk component can be recognized using the Nyquist plot. σb and σtotal at these temperatures are then determined and the Arrhenius plots which are shown in Fig. 2d. Both plots of σb and σtotal show ideally linear behavior, with the activation energy of 0.28 and 0.32 eV, respectively. The fitted Arrhenius plot lines can be extended to the room-temperature range, where the σb and σtotal are determined indirectly to be 1.54 × 10−2 and 4.8 × 10−3 S cm−1 at 25 °C, respectively, which fit well with the results tested directly at 25 °C by the combination of the high and normal-frequency impedance spectroscopy systems (Fig. 1a). Since σb is the intrinsic property of the composition and is the upper limit that σtotal can reach (in an ideal situation when Rgb could be reduced to 0), the superior σb reported in the present work indicates further potential of increasing the related σtotal when the microstructure of the samples is further optimized in the future.
Based on the above analysis, with respect to the influences of the parameters on the σtotal of NZSPx samples, the following explanations are given: firstly, theoretically σb is directly proportional to the amount of charge carriers,33 indicating that the increasing Na-ion occupancy in the structure also causes σb to increase, which may be the reason for the increasing σb in NZSPx up to x = 0.4 or 0.5. However, at the same time, it is important that some Na-ion vacancies are present in the structure to allow the motion of Na-ions. Otherwise, when all possible Na ion positions are occupied, it is not possible for Na-ions to hop from one site to another due to the lack of vacancies. The maximum Na ion occupation in one unit cell of NZSPx is 4,20 which means that the best ratio between occupied and vacant Na-ion sites is about 3.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6 or 3.5
0.6 or 3.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5. It should be emphasized that this ratio mainly influences σb and does not necessarily relate to σgb.
0.5. It should be emphasized that this ratio mainly influences σb and does not necessarily relate to σgb.
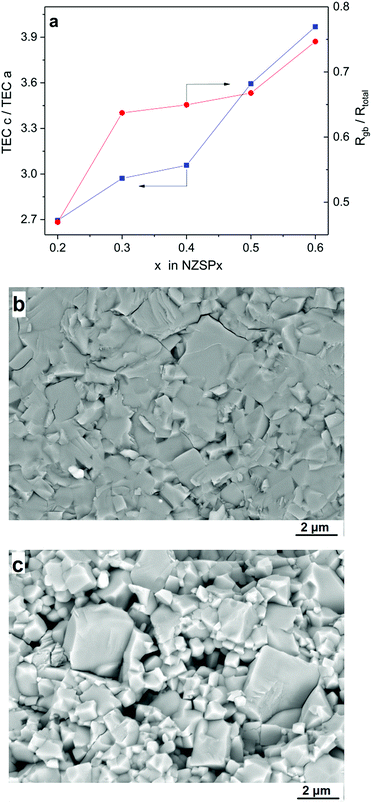
Secondly, the TEA (see Table 1) leads to differential contraction during cooling after sintering and the contact between the grains may be degraded, and Rgb is thusly increased. Fig. 3a compares the TEA, i.e. the ratio of TECs along lattice parameters c and a (derived from Table 1) and the ratio of Rgb divided by Rtotal (derived from Fig. S6†), both as a function of the x value in NZSPx. They both increase with the x value and also show a similar slope, indicating the influence of TEA on σgb and accordingly on σtotal. When the TEA increases, more contact losses occur and even micro-cracking along grain boundaries may be induced, leading to an apparent higher contribution of Rgb in Rtotal. The influence of TEA on σgb is further proved by the microstructure of the samples. Fig. 3b and c compare the microstructure of sintered NZSP0.4 and NZSP0.6 samples, with a relative density of 97% and 95%, respectively. Clearly, the contact of the grains of NZSP0.4 is tight, with only a few micro-cracks along the grain boundaries, while the contact of the grains of NZSP0.6 shows less adhesive bonding with much more micro-cracks because of the higher TEA (see Table 1 and Fig. 3a).
In comparison, other reported NASICONs have been extensively investigated by means of scanning electron-microscopy (SEM).29,34–38 They typically exhibit more severe cracks, poor contact between grains, and lower relative density due to the inappropriate processing technology. This explains why NASICONs have previously exhibited inferior σtotal and the value of σtotal scattered greatly even for the same composition at room temperature.14,15 The Rgb was significantly higher and more uncontrollable. Moreover, this also explains why despite most subsequent research studies14,15 having accepted the composition range from Hong et al. (−0.2 ≤ x ≤ 0.2, i.e. Na content range from 2.8 mol to 3.2 mol per formula unit of the NASICONs)12,13 as the best composition for σtotal, several research studies in the last two years reported that the highest σtotal at room temperature appears at a Na content near 3.4 mol per formula unit of the NASICONs.20,24,32,39 The enhanced processing technology decreases the Rgb and the σtotal is then significantly influenced by the σb of the sample, as shown in the present study.
Thirdly, a phase transition from a rhombohedral structure to a monoclinic structure exists for the samples of NZSP0–NZSP0.5 when the temperature decreases from 200 °C to 100 °C (Fig. 1b and ESI Fig. S3†). The transition should be accompanied by both a pathway change of Na-ion conduction in the lattice and a dimensional change of the grains in different directions, influencing both the Rb and Rgb of the samples accordingly. Other parameters like secondary phases existing in the grain boundaries, their conductivity, the volume ratio and distribution of grain-boundaries in the sintered sample etc. also influence the conductivity of NZSPx. Further experiments are needed to analyze these dependencies in detail.
The σtotal of a typical NZSP0.4 is compared with other NASICON materials, as shown in Fig. 4a.13,20,24,26,34,37,40 In general, early studies paid more attention to Na content range from 2.8 mol to 3.2 mol per formula unit of the NASICONs, and normally exhibited σtotal under 1 × 10−3 S cm−1 at room temperature.14,15 In the last two years, NASICON materials attracted great interest with Na3.4Sc0.4Zr2Si2PO12 (ref. 20) and Na3.3La0.3Zr1.7Si2PO12 (ref. 24) showing reasonably good σtotal of 2–4 × 10−3 S cm−1 at 25 °C. In the present study, 5.2 × 10−3 S cm−1 was obtained at 25 °C for a rare-earth free composition, which permits high performance and low cost simultaneously.
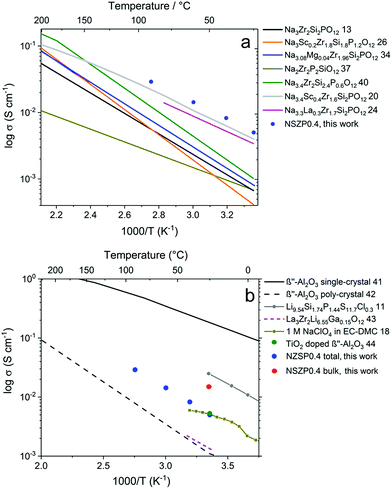 | ||
| Fig. 4 Temperature dependence of σtotal for NZSP0.4 and comparison with (a) other NASICON materials and (b) other Na and Li conductors. | ||
The conductivity of NZSP0.4 is also compared with other Na and Li-ion conductors (Fig. 4b).11,18,41–44 Single-crystalline β′′-alumina exhibits the highest conductivity of all Na-ion conducting solid electrolytes, which reaches 0.16 S cm−1 at 25 °C.41 However, since β′′-alumina exhibits two-dimensional Na-ion migration,16,17 the σtotal for polycrystalline β′′-alumina is only 1–2 × 10−3 S cm−1 at room temperature due to the unavoidably high Rgb caused by a mismatch in the conducting direction of different grains.42 The σtotal of NZSP0.4 is even comparable with common liquid electrolytes of NIBs, e.g. 1 M NaClO4 in the mixture of ethylene carbonate and dimethyl carbonate (EC–DMC).18 Moreover, a wide window for electrochemical stability (from 0 up to 9 V versus Na/Na+) of the NASICON materials was also proven,20,39 which is much higher than the liquid based electrolyte (lower than 5 V). The only comparable poly-crystalline Na-ion conductor is TiO2 doped β′′-alumina reported in 2018, which has a room-temperature conductivity of 5.4 × 10−3 S cm−1.44 When compared to the best solid-state Li-ion conductors, NZSP0.4 shows a lower σtotal than that of Li9.54Si1.74P1.44S11.7Cl0.3 (2.5 × 10−2 S cm−1 at 25 °C).11 However, the application of sulfide is problematic because this material is very air-sensitive and unstable,45 while NZSPx can be processed directly in ambient air. In addition to the sulfides, the most favored solid-state electrolyte for LIBs is La3Zr2Li7O12-based materials, of which La3Zr2Li6.55Ga0.15O12 exhibits the best reported σtotal (1.3 × 10−3 S cm−1 at 24 °C).43 The higher σtotal of NZSP0.4 compared to Li7La3Zr2O12-based materials could play an important role in the further development of NIBs and LIBs in all-solid-state designs.
Na/NZSP0.4/Na symmetric cells
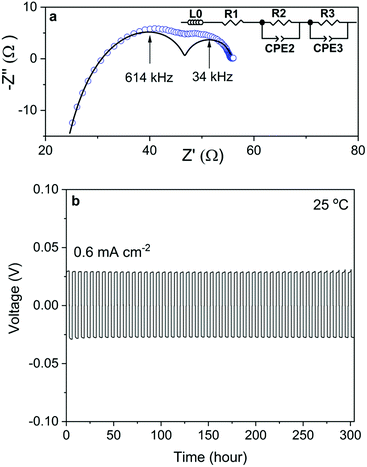
The Nyquist plot of the impedance spectra of a Na/NZSP0.4/Na symmetric cell is shown in Fig. 5a, which is also fitted by the equivalent circuit shown as an inset of the figure, where L0 indicates the inductance induced by conductive parts in the measurement setup, R and CPE indicate the resistance and constant phase element, respectively. The sum of R1 and R2 is attributed to Rtotal of NZSP0.4 because their relative conductivity is calculated to be 4.8 × 10−2 S cm−1 at 25 °C, which fits well to the σtotal of NZSP0.4 itself. Then R3 and CPE3 are reasonably attributed to the contribution of interface resistance (Rint) between Na and NZSP0.4. The calculated Rint (per interface) is 4.1 Ω cm2 at 25 °C. As reference, Ma et al.20 got >100 Ω cm2 for Sc substituted NASICON at 25 °C, while the current best Rint between Li metal and Li-conducting ceramic is 2 Ω cm2 at room temperature.46 The cycling behavior of the Na/NZSP0.4/Na symmetric cell is shown in Fig. 5b. The cell was cycled for 300 h at ±0.6 mA−2 cm at 25 °C, with 3 h per charge or discharge process, i.e. 1.8 mA h cm−2 per charge or discharge. No apparent polarization was observed during the operation, and so was the dendrite formation. In comparison, Zhou et al.47 reported a Na/NASICON/Na symmetric cell that only a reached current density of 0.25 mA cm−2 and areal charge density of 0.25 mA h cm−2, at 65 °C. Another example for Li/Li-ceramic conductor/Li symmetric cell46 shows a current density of 0.2 mA cm−2 and areal charge density of 0.2 mA h cm−2, at 25 °C. The above cited references are both among the current best level of interfaces between Na (Li) and a ceramic electrolyte. The results in this work are a step forward. The parameters influence the Rint and the cycle-performance of the symmetric cells need more intensive investigations. However, a high σtotal of NZSP0.4 is definitely one of the most important reasons for the low Rint and high cycle stability of the symmetric cells.All ceramic sodium-ion batteries
All-NASICON-ceramic cells with sintered NZSP0.4 as the electrolyte and a mixture of NVP–NZSP0.4–carbon (54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 in weight ratio) as both positive and negative electrodes were fabricated by sintering electrodes on the electrolyte at 750 °C in Ar containing 2% H2. NVP and their fluorine-containing variant Na3V2P2O8F3 have been extensively investigated and considered as promising candidates for NIBs. Conventional NIBs based on them and liquid electrolytes have already delivered impressive performances,.48–52 It is known that the electrochemical extraction of Na+ from NVP to NaV2P3O12 occurs after a two-phase reaction at 3.4 V versus Na/Na+, and the V3+ ions in NVP can also be reduced to V2+ through the insertion of one Na-ion towards Na4V2P3O12 at 1.6 V versus Na/Na+. Therefore NVP can be used as a positive as well as a negative electrode in a Na-ion battery and offers the possibility of assembling symmetrical cells (NVP/electrolyte/NVP) capable of delivering 1.8 V.31,49,50,53 The microstructure of a typical prepared cell is shown in Fig. 6a and b. NZSP0.4 and NVP both form their network for Na-ion conduction and exchange, guaranteeing the processes of electrochemical reactions in the electrodes. Since NVP powder was prepared by Pechini's method,54 which means NVP particles are first coated with organics and then sintered in Ar containing 2% H2, each NVP particle in the electrodes is covered by a carbon “shell”. Under the observation of SEM, only carbon with certain agglomeration can be seen (Fig. 6a). While under the examination of a scanning transmission electron microscope (STEM) with an energy-dispersive X-ray spectroscope (EDS), the carbon “shell” can be observed for all NVP particles (a typical image is shown in the ESI Fig. S8†), thus ensuring electronic conduction within the electrodes. The interface between the grains of NZSP0.4 and NVP of a prepared electrode is sharp and neat (Fig. 6c–f), indicating that the co-sintering (750 °C) of the two materials did not induce any obvious solid-state reactions or diffusions between NZSP0.4 and NVP, in accord with XRD patterns (Fig. 1d). In addition, the presence of carbon “shell” on NVP particles is proved again (Fig. 6f). While the signal of carbon on NZSP0.4 is weak and can almost be regarded as background noise. This fits well with the expectation because NZSP0.4 is first sintered at 1260 °C and then mixed with NVP prepared by Pechini's method. No carbon "shell" is supposed to cover NZSP0.4 particle.
6 in weight ratio) as both positive and negative electrodes were fabricated by sintering electrodes on the electrolyte at 750 °C in Ar containing 2% H2. NVP and their fluorine-containing variant Na3V2P2O8F3 have been extensively investigated and considered as promising candidates for NIBs. Conventional NIBs based on them and liquid electrolytes have already delivered impressive performances,.48–52 It is known that the electrochemical extraction of Na+ from NVP to NaV2P3O12 occurs after a two-phase reaction at 3.4 V versus Na/Na+, and the V3+ ions in NVP can also be reduced to V2+ through the insertion of one Na-ion towards Na4V2P3O12 at 1.6 V versus Na/Na+. Therefore NVP can be used as a positive as well as a negative electrode in a Na-ion battery and offers the possibility of assembling symmetrical cells (NVP/electrolyte/NVP) capable of delivering 1.8 V.31,49,50,53 The microstructure of a typical prepared cell is shown in Fig. 6a and b. NZSP0.4 and NVP both form their network for Na-ion conduction and exchange, guaranteeing the processes of electrochemical reactions in the electrodes. Since NVP powder was prepared by Pechini's method,54 which means NVP particles are first coated with organics and then sintered in Ar containing 2% H2, each NVP particle in the electrodes is covered by a carbon “shell”. Under the observation of SEM, only carbon with certain agglomeration can be seen (Fig. 6a). While under the examination of a scanning transmission electron microscope (STEM) with an energy-dispersive X-ray spectroscope (EDS), the carbon “shell” can be observed for all NVP particles (a typical image is shown in the ESI Fig. S8†), thus ensuring electronic conduction within the electrodes. The interface between the grains of NZSP0.4 and NVP of a prepared electrode is sharp and neat (Fig. 6c–f), indicating that the co-sintering (750 °C) of the two materials did not induce any obvious solid-state reactions or diffusions between NZSP0.4 and NVP, in accord with XRD patterns (Fig. 1d). In addition, the presence of carbon “shell” on NVP particles is proved again (Fig. 6f). While the signal of carbon on NZSP0.4 is weak and can almost be regarded as background noise. This fits well with the expectation because NZSP0.4 is first sintered at 1260 °C and then mixed with NVP prepared by Pechini's method. No carbon "shell" is supposed to cover NZSP0.4 particle.
 | ||
| Fig. 6 The microstructure of NVP and NZSP0.4 grains in the electrode. (a and b) Cross sectional view by SEM. (c–f) STEM observation and the elemental distribution maps acquired by EDS. | ||
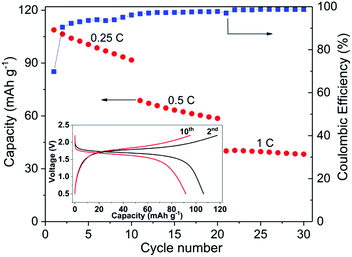
Fig. 7 shows the cycling performance of a typical all-NASICON-ceramic battery operating at 28 °C. The battery was running at 0.25C, 0.5C and 1C for 10 cycles each, respectively. During the first charge up to 2.2 V at 0.25C, an extra capacity (about 30% higher than the theoretical capacity) is observed and disappears upon further cycling, which may be the result of side-reactions of the electrodes, and also observed and discussed in previous reports on all-solid-state NIBs and LIBs.53,55,56 A discharge capacity of 108.8 mA h g−1 is obtained for the first cycle, which reaches 92.5% of the theoretical capacity of the battery. Degradation in the capacity and increase in polarization occur during each cycle in which the fixed C-rate is observed, especially for the low C-rate. At 0.25C, the discharge capacity decreases for 16% after 10 cycles. It is possible that the fading of the capacity comes from the dimensional change of NVP during charging and discharging.24 The corresponding impedance spectrum supports this explanation (ESI Fig. S9†). However, further experiments are needed to better understand this process in detail. The coulombic efficiency of the cell starts at 70% for the first cycle due to the side-reactions, increases with the cycle number and C-rate, and reaches 99% after 30 cycles. According to the analysis of STEM-EDS (ESI Fig. S10†), the cell-operating processes also induce no obvious solid-state reactions or diffusions between NZSP0.4 and NVP, which further proves the electrochemical compatibility of the two materials.
Compared to conventional NIBs with a liquid electrolyte, the above performance is rather moderate. As an example, batteries in similar configuration, i.e. NVP/liquid electrolyte/NVP can cycle up to 100C and have a cycle life of 2000 (at 10C), both at room temperature.49,50 Because NVP and liquid electrolyte have full and “soft” contact, interface problems can be neglected. In comparison, NVP and NZSP0.4 have insufficient and rigid contact, which is problematic when Na-ions have to cross the interface of NVP and NZSP0.4. However, the performance of the present study is acceptable for such a new concept as a rechargeable battery. In this battery, all the interfaces are between rigid ceramics. No liquid or polymer components are used at all. In comparison, Lalère et al.53 reported a similar full-ceramic NIB composed of NVP–NZSP0–carbon/NZSP0/NVP–NZSP0–carbon. The cell was tested at 200 °C, but the degradation is much faster than the cell reported in the present study. Zhang et al.24 also reported a ceramic half-cell with sodium metal as the negative electrode, which was based on Na3.57Zr1.72La0.21Si2.08P0.92O12 as an electrolyte material and ran at 80 °C. The charge–discharge performance is comparable to the performance in Fig. 7. Inoishi et al.57 also announced full-ceramic NIBs operating at room temperature. Their batteries only contain one single material of Na2.6V1.6Zr0.4P3O12, which serves as the material for Na-ion storage, Na-ion conduction and electric conduction at the same time. In that case, although the material has a much smaller conductivity (∼1 × 10−4 S cm−1 at room temperature), the battery has no interface problems because it contains only one material. In the case of this work, although NSZP0.4 has a much higher conductivity, the interface between NZSP0.4 and NVP is a potential transport barrier because of the much lower Na-ion conductivity of NVP (<10−7 S cm−1 at room temperature57) and the rigid contact with NSZP0.4. The advanced fabrication method can bring better performances. Kehne et al.58 applied the pulsed laser deposition method to deposit the NaxCoO2 cathode onto Na3.4Sc0.4Zr1.6Si2PO12 ceramic electrolyte. With sodium metal as the anode material, the assembled thin-film NIB had only 25% performance degradation after 100 cycles under 0.15C and at room temperature. Some oxide-ceramic LIBs with lithium metal as the negative electrode were also reported in recent years.56,59,60 However, their operating temperature was even higher than the NIBs mentioned above,24 and cell performance was even worse. As mentioned above, the better performance of NIBs is due to the better electrolyte material with its higher conductivity at room temperature. In the present study, the high σtotal of the electrolyte, high chemical stability between the electrolyte and electrode, and favorable microstructure of both electrolyte and electrode lead to the desired performance of the full-ceramic battery operated at room temperature, thus indicating a promising future for full-ceramic NIBs.
Conclusions
NZSPx (x = 0–0.6) were prepared by means of SA-SSR synthesis. The synthesis method has the potential for use in industrial mass production. Benefiting from the optimized primary powders, NZSPx ceramics exhibit an optimized microstructure after sintering and result in high σtotal. The σtotal of NZSPx increases from x = 0 to x = 0.4, and decreases from x = 0.4 to x = 0.6, which may result from the combined influences of the ratio between the occupied and vacant Na ion sites, TEA between lattice parameters a and c, and the phase transition between the rhombohedral and monoclinic phase at 200 °C–100 °C. The σb and σtotal of the samples can be separated at 25 °C by combining two impedance spectroscopy systems with different frequency ranges. At 25 °C, NZSP0.4 exhibits a σb of 1.5 × 10−2 S cm−1 and a σtotal of 5 × 10−3 S cm−1, which is the best value of all reported polycrystalline Na-ion conductors, and are comparable to common liquid electrolytes of NIBs. A Na/NZSP0.4/Na symmetric cell showed a low interface resistance of 4.1 Ω cm2 and a high cycling performance of 1.8 mA h cm−2 per charge or discharge process, both at 25 °C. The superior σtotal of NZSP0.4, high chemical stability between the NZSP0.4 electrolyte and NVP electrode, and favorable microstructure of both electrolyte and electrode lead to a full-ceramic cell of NVP–NZSP0.4–carbon/NZSP0.4/NVP–NZSP0.4–carbon which was successfully tested at 28 °C with reasonable cycling performances.Experimental
Preparation of NZSPx and NVP powders
NZSPx (x = 0–0.6) powders can be prepared on a laboratory scale (10 g–1 kg) using a solution-assisted solid-state reaction method (SA-SSR).19–21 NaNO3 (VWR, 99.7%), ZrO(NO3)2 (Aldrich, 99%), Si(OCH2CH3)4 (Merck, 99%) and NH4H2PO4 (Merck, 99%) were used as starting materials. Corresponding amounts of NaNO3, and ZrO(NO3)2 were dissolved into deionized water. A stoichiometric amount of Si(OCH2CH3)4 was also added to the solution while stirring. When Si(OCH2CH3)4 was hydrolyzed, the corresponding amount of NH4H2PO4 was added to the system while also stirring. The homogeneous aqueous system then changed to a mixture of a colloidal sol and precipitates of complex zirconium oxyphosphate compounds.The whole mixture was dried at 85 °C. The dried powder was calcined at 800 °C for 3 h. After calcination, a white powder was obtained. The calcined powder was then milled in ethanol with zirconia balls on a milling bench for 48 h, and dried at 70 °C for 12 h.
NVP powders were prepared by using the Pechini's method.47 NaH2PO4 (Sigma-Aldrich, 99%) and NH4VO3 (Merck, 99%) were applied as starting materials. Corresponding amounts of NaH2PO4 and NH4VO3 were dissolved into deionized water. Double the amount of moles (sum of NaH2PO4 and NH4VO3) of citric acid was also dissolved into the same solution, before subsequently adding the same amount of ethylene glycol. The solution was dried at 200 °C while stirring, and calcined at 400 °C for 5 h. The calcined powder was then milled in ethanol with zirconia balls on a milling bench for 24 h, and dried at 70 °C for 12 h. The NVP powder has a rhombohedral structure after reduction at 750 °C for 8 h in Ar containing 2% H2, with 10 wt% of carbon remaining in the powder, which comes from the incomplete combustion of citric acid and ethylene glycol. The carbon content was determined by heating the powder at 650 °C in air, where carbon was burnt out, while NVP was also decomposed because of its instability in air at high temperature. The decomposed NVP was then heated up at 750 °C in Ar containing 2% H2 again. Pure phase NVP was obtained again. The weight difference of the final achieved powder and the original powder is regarded as the carbon content.
Fabrication of specimens and single cells
For conductivity testing, the milled NZSPx powders were put into a cylindrical pressing mold with a diameter of 8–13 mm and pressed with a uniaxial pressure of 100 MPa at room temperature. The pressed pellets were then sintered at 1250 °C–1300 °C for 5 h. The pellets had obtained a diameter of 6.5–10.5 mm and thickness of about 1 mm. For the preparation of electrolytes of the single cells, the procedure is just like above, but specifically only with NZSP0.4 powder, using a cylindrical pressing mold with a diameter of 13 mm and sintered at 1260 °C for 5 h. The pellets obtained had a diameter of about 10 mm and thickness of about 1 mm.Some of the milled NZSP0.4 powder was sintered at 1260 °C for 5 h, then ground and ball-milled again on a milling bench for 48 h. The sintered NZSP0.4 powder obtained was mixed with the milled NVP powder with a NZSP0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NVP (with carbon) = 40
NVP (with carbon) = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, i.e. NZSP0.4
60, i.e. NZSP0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NVP
NVP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C weight ratio of 40
C weight ratio of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. The mixed powder was then screen-printed on both sides of the sintered NZSP0.4 pellets as negative and positive electrodes, followed by co-sintering at 750 °C for 8 h in Ar containing 2% H2. The single cells subsequently had a positive electrode weight of 0.1–1 mg. The weight of the negative electrode was adjusted to reach about 210% of the positive electrodes. The prepared single cells were then sealed inside aluminum pouch-bags, with Ni-metal pellets 12 mm in diameter as the current-collector for both anode and cathode sides.
6. The mixed powder was then screen-printed on both sides of the sintered NZSP0.4 pellets as negative and positive electrodes, followed by co-sintering at 750 °C for 8 h in Ar containing 2% H2. The single cells subsequently had a positive electrode weight of 0.1–1 mg. The weight of the negative electrode was adjusted to reach about 210% of the positive electrodes. The prepared single cells were then sealed inside aluminum pouch-bags, with Ni-metal pellets 12 mm in diameter as the current-collector for both anode and cathode sides.
Characterization
The XRD patterns of the sintered samples of NZSPx and/or NVP were recorded using a Bruker D4 ENDEAVOR diffractometer with Cu Kα radiation in the temperature range of 25–1200 °C. The lattice parameters and the quantitative phase analysis of the samples were determined by the Pawley and Rietveld refinement method using the TOPAS program (Bruker AXS GmbH). The microstructure of the powders or sintered samples was analyzed using a scanning electron microscope Zeiss Ultra55.The prepared dense pellets of NSZSPx (x = 0–0.6) were sputtered with gold on both sides. The impedance spectra of the samples were measured at 25 °C using two commercial electrochemical systems (Keysight E4991B and Biologic VMP-300), with an AC frequency range from 3 GHz to 1 MHz and from 3 MHz to 1 Hz, respectively. The results were adjusted according to the dimension of the samples by multiplying with the conducting area and dividing with the thickness of the samples and fitted using software “Z-view” (Scribner Associates Inc.). The temperature was controlled using a climate chamber (Vötsch, VT4002). The temperature-dependent impedance of the NZSPx sample was measured between −100 °C and 90 °C using another commercial electrochemical system (Novocontrol Alpha-A, with normal frequency range of 10 MHz–0.01 Hz) including a temperature-controlling system, a liquid-nitrogen contained cooling system and a furnace.
The charge–discharge behavior of the all ceramic single cells was tested using an electrochemical system (Biologic VMP-300) with controlled temperature in a climate chamber (Vötsch, VT4002). A uniaxial pressure of about 100 MPa was applied during testing, while the samples were sealed in the pouch-bags and clipped between the two Ni-metal current collectors. The microstructure of the cells was analyzed by SEM (ZEISS Merlin) together with an Ar-cross-section polisher (JEOL, SM-09010). The scanning transmission electron microscopy (STEM) experiments were performed on an FEI Titan 80–200 Chemi-STEM equipped with a Super-X energy-dispersive X-ray spectroscopy (EDS) detector system.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr D. Grüner (IEK-2) and Dr D. Sebold (IEK-1) for SEM investigations, and also Dr Y. J. Sohn (IEK-1) for XRD investigations. Partial financial support from the German Federal Ministry of Education and Research (BMBF) in the frame of the BenchBatt project (reference number 03XP0047B) is gratefully acknowledged.Notes and references
- H. Pan, Y.-S. Hu and L. Chen, Energy Environ. Sci., 2013, 6, 2338–2360 RSC.
- V. Palomares, M. Casas-Cabanas, E. Castillo-Martínez, M. H. Han and T. Rojo, Energy Environ. Sci., 2013, 6, 2312–2337 RSC.
- M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–958 CrossRef CAS.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed.
- M. Sawicki and L. L. Shaw, RSC Adv., 2015, 5, 53129–53154 RSC.
- D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- A. Aboulaich, R. Bouchet, G. Delaizir, V. Seznec, L. Tortet, M. Morcrette, P. Rozier, J.-M. Tarascon, V. Viallet and M. Dollé, Adv. Energy Mater., 2011, 1, 179–183 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- K. Takada, Acta Mater., 2013, 61, 759–770 CrossRef CAS.
- A. L. Robinson and J. Janek, MRS Bull., 2014, 39, 1046–1047 CrossRef.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- H. Y. P. Hong, Mater. Res. Bull., 1976, 11, 173–182 CrossRef CAS.
- J. B. Goodenough, H. Y. P. Hong and J. A. Kafalas, Mater. Res. Bull., 1976, 11, 203–220 CrossRef CAS.
- K.-D. Kreuer, H. Kohler and J. Maier, High conductivity ionic conductors: Recent trends and application, ed. T. Takahashi, 1986, pp. 242–279 Search PubMed.
- M. Guin and F. Tietz, J. Power Sources, 2015, 273, 1056–1064 CrossRef CAS.
- J. W. Fergus, Solid State Ionics, 2012, 227, 102–112 CrossRef CAS.
- X. Lu, G. Xia, J. P. Lemmon and Z. Yang, J. Power Sources, 2010, 195, 2431–2442 CrossRef CAS.
- A. Bhide, J. Hofmann, A. K. Dürr, J. Janek and P. Adelhelm, Phys. Chem. Chem. Phys., 2014, 16, 1987–1998 RSC.
- Q. Ma, F. Tietz, S. Naqash and O. Guillon, Ger. Pat., DE102015013155, 2015.
- Q. Ma, M. Guin, S. Naqash, C.-L. Tsai, F. Tietz and O. Guillon, Chem. Mater., 2016, 28, 4821–4827 CrossRef CAS.
- S. Naqash, Q. Ma, F. Tietz and O. Guillon, Solid State Ionics, 2017, 302, 83–91 CrossRef CAS.
- U. von Alpen, M. F. Bell and W. Wichelhaus, Mater. Res. Bull., 1979, 14, 1317–1322 CrossRef CAS.
- T. Oota and I. Yamai, J. Am. Ceram. Soc., 1986, 69, 1–6 CrossRef CAS.
- Z. Zhang, Q. Zhang, J. Shi, Y. S. Chu, X. Yu, K. Xu, M. Ge, H. Yan, W. Li, L. Gu, Y. S. Hu, H. Li, X. Q. Yang, L. Chen and X. Huang, Adv. Energy Mater., 2106, 6, 1601196 Search PubMed.
- J. T. S. Irvine and D. C. Sinclair, Adv. Mater., 1990, 2, 132–138 CrossRef CAS.
- M. A. Subramanian, P. R. Rudolf and A. Clearfield, J. Solid State Chem., 1985, 60, 172–181 CrossRef CAS.
- R. O. Fuentes, F. M. Figueiredo, M. R. Soares and F. M. B. Marques, J. Eur. Ceram. Soc., 2005, 25, 455–462 CrossRef CAS.
- J. S. Lee, C. M. Chang, Y. Lee, J. H. Lee and S. H. Hong, J. Am. Ceram. Soc., 2004, 87, 305–307 CrossRef CAS.
- A. Ahmad, T. A. Wheat, A. K. Kuriakose, J. D. Canaday and A. G. Mcdonald, Solid State Ionics, 1987, 24, 89–97 CrossRef CAS.
- J. Gulens, B. W. Hildebrandt, J. D. Canaday, A. K. Kuriakose, T. A. Wheat and A. Ahmad, Solid State Ionics, 1989, 35, 45–49 CrossRef.
- Y. Noguchi, E. Kobayashi, L. S. Plashnitsa, S. Okada and J.-I. Yamaki, Electrochim. Acta, 2013, 101, 59–65 CrossRef CAS.
- M. Guin, F. Tietz and O. Guillon, Solid State Ionics, 2016, 293, 18–26 CrossRef CAS.
- A. R. West, Solid state chemistry and its applications, Wiley, 1987 Search PubMed.
- T. Takahashi, K. Kuwabara and M. Shibata, Solid State Ionics, 1980, 1, 163–175 CrossRef CAS.
- H. Perthuis and P. Colomban, Ceram. Int., 1986, 12, 39–52 CrossRef CAS.
- J. H. Kim, T. S. Oh, M. S. Lee, J. G. Park and Y. H. Kim, J. Mater. Sci., 1993, 28, 1573–1577 CrossRef CAS.
- N. Gasmi, N. Gharbi and H. Zarrouk, J. Sol-Gel Sci. Technol., 1995, 4, 231–237 CrossRef CAS.
- A. Ignaszak, P. Pasierb, R. Gajerski and S. Komornicki, Thermochim. Acta, 2005, 426, 7–14 CrossRef CAS.
- S. Song, H. M. Duong, A. M. Korsunsky, N. Hu and L. Lu, Sci. Rep., 2016, 6, 32330 CrossRef CAS PubMed.
- J. A. Kafalas and R. J. Cava, Fast ion transport in solids, ed. P. Vashishta, J. N. Mundy and G. K. Shenoy, North-Holland, Amsterdam, 1979 Search PubMed.
- J. L. Briant and G. C. Farrington, J. Solid State Chem., 1980, 33, 385–390 CrossRef CAS.
- W. I. Archer, R. D. Armstrong, D. P. Sellick, W. G. Burden and J. H. Duncan, J. Mater. Sci., 1980, 15, 2066–2072 CrossRef CAS.
- C. Bernuy-Lopez, W. Manalastas Jr, J. M. Lopez del Amo, A. Aguadero, F. Aguesse and J. A. Kilner, Chem. Mater., 2014, 26, 3610–3617 CrossRef CAS.
- E. Yi, E. Temeche and R. M. Laine, J. Mater. Chem. A, 2018, 6, 12411–12419 RSC.
- Y. Wang and W.-H. Zhong, ChemElectroChem, 2015, 2, 22–36 CrossRef CAS.
- A. Sharafi, E. Kazyak, A. L. Davis, S. Yu, T. Thompson, D. J. Siegel, N. P. Dasgupta and J. Sakamoto, Chem. Mater., 2017, 29, 7961–7968 CrossRef CAS.
- W. Zhou, Y. Li, S. Xin and J. B. Goodenough, ACS Cent. Sci., 2017, 3, 52–57 CrossRef CAS PubMed.
- Q. Liu, D. Wang, X. Yang, N. Chen, C. Wang, X. Bie, Y. Wei, G. Chen and F. Du, J. Mater. Chem. A, 2015, 3, 21478–21485 RSC.
- Y. Zhang, H. Zhao and Y. Du, J. Mater. Chem. A, 2016, 4, 7155–7159 RSC.
- C. Zhu, P. Kopold, P. A. van Aken, J. Maier and Y. Yu, Adv. Mater., 2016, 28, 2409–2416 CrossRef CAS PubMed.
- E. Gu, S. Liu, Z. Zhang, Y. Fang, X. Zhou and J. Bao, J. Alloys Compd., 2018, 767, 131–140 CrossRef CAS.
- Y. Fang, X. Xu, Y. Du, X. Zhu, X. Zhou and J. Bao, J. Mater. Chem. A, 2018, 6, 11244–11251 RSC.
- F. Lalère, J. B. Leriche, M. Courty, S. Boulineau, V. Viallet, C. Masquelier and V. Seznec, J. Power Sources, 2014, 247, 975–980 CrossRef.
- M. P. Pechini, US Pat., 3330697, 1967.
- G. Oh, M. Hirayama, O. Kwon, K. Suzuki and R. Kanno, Chem. Mater., 2016, 28, 2634–2640 CrossRef CAS.
- K. Park, B.-C. Yu, J.-W. Jung, Y. Li, W. Zhou, H. Gao, S. Son and J. B. Goodenough, Chem. Mater., 2016, 28, 8051–8059 CrossRef CAS.
- A. Inoishi, T. Omuta, E. Kobayashi, A. Kitajou and S. Okada, Adv. Mater. Interfaces, 2017, 6, 1600942 CrossRef.
- P. Kehne, C. Guhl, Q. Ma, F. Tietz, L. Alff, R. Hausbrand and P. Komissinskiy, J. Power Sources, 2019, 409, 86–93 CrossRef CAS.
- T. Kato, S. Iwasaki, Y. Ishii, M. Motoyama, W. C. West, Y. Yamamoto and Y. Iriyama, J. Power Sources, 2016, 303, 65–72 CrossRef CAS.
- J. van den Broek, S. Afyon and J. L. M. Rupp, Adv. Energy Mater., 2016, 6, 1600736 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta00048h |
| This journal is © The Royal Society of Chemistry 2019 |