Photocatalytic activity of exfoliated graphite–TiO2 nanoparticle composites
Gloria
Guidetti
a,
Eva A. A.
Pogna
bc,
Lucia
Lombardi
d,
Flavia
Tomarchio
d,
Iryna
Polishchuk
 e,
Rick R. M.
Joosten
f,
Alessandro
Ianiro
e,
Rick R. M.
Joosten
f,
Alessandro
Ianiro
 f,
Giancarlo
Soavi
dg,
Nico A. J. M.
Sommerdijk
f,
Giancarlo
Soavi
dg,
Nico A. J. M.
Sommerdijk
 f,
Heiner
Friedrich
f,
Heiner
Friedrich
 f,
Boaz
Pokroy
f,
Boaz
Pokroy
 e,
Anna K.
Ott
d,
Marco
Goisis
h,
Francesco
Zerbetto
e,
Anna K.
Ott
d,
Marco
Goisis
h,
Francesco
Zerbetto
 a,
Giuseppe
Falini
a,
Giuseppe
Falini
 a,
Matteo
Calvaresi
a,
Matteo
Calvaresi
 a,
Andrea C.
Ferrari
a,
Andrea C.
Ferrari
 *d,
Giulio
Cerullo
*d,
Giulio
Cerullo
 *b and
Marco
Montalti
*b and
Marco
Montalti
 *a
*a
aDepartment of Chemistry G. Ciamician, Universitá di Bologna, Bologna, 40126, Italy. E-mail: marco.montalti2@unibo.it
bDepartment of Physics, Politecnico di Milano, Milano, 20133, Italy
cNEST, Istituto Nanoscienze-CNR and Scuola Normale Superiore, P. zza S. Silvestro 12, Pisa, 56127, Italy
dCambridge Graphene Centre, University of Cambridge, Cambridge CB3 0FA, UK
eDepartment of Materials Science and Engineering, Technion Israel Institute of Technology, Haifa, 3200003, Israel
fDepartment of Chemical Engineering and Chemistry, Eindhoven University of Technology, Eindhoven, 5612 AZ, Netherlands
gInstitut für Festkörperphysik, Friedrich Schiller Universität Jena, Jena, 07743, Germany
hGlobal Product Innovation Department, Italcementi Heidelberg Cement Group, Bergamo, 24126, Italy
First published on 18th October 2019
Abstract
We investigate the photocatalytic performance of composites prepared in a one-step process by liquid-phase exfoliation of graphite in the presence of TiO2 nanoparticles (NPs) at atmospheric pressure and in water, without heating or adding any surfactant, and starting from low-cost commercial reagents. These show enhanced photocatalytic activity, degrading up to 40% more pollutants with respect to the starting TiO2-NPs, in the case of a model dye target, and up to 70% more pollutants in the case of nitrogen oxides. In order to understand the photo-physical mechanisms underlying this enhancement, we investigate the photo-generation of reactive species (trapped holes and electrons) by ultrafast transient absorption spectroscopy. We observe an electron transfer process from TiO2 to the graphite flakes within the first picoseconds of the relaxation dynamics, which causes the decrease of the charge recombination rate, and increases the efficiency of the reactive species photo-production.
1. Introduction
Air and water pollution are major environmental risks to human health.1 According to the World Health Organization (WHO),1 in the last decade one out of every nine deaths was related to air pollution,2 while at least 1.8 bn people used a contaminated drinking-water source.3 For air pollution remediation, environmental contaminants4 (e.g. NO, NO2, SO2, suspended organic particulate, volatile organic compounds, aromatic hydrocarbons, etc.) must be turned into harmless compounds. This can be achieved exploiting photocatalysts to absorb light and produce reactive holes (h) and electrons (e) that degrade the pollutants via redox processes.5 The photocatalytic quantum efficiency (PQE) is defined as the ratio between the rate at which the target molecules undergo photo-degradation (moles of molecules per unit time) [mol s−1], and the rate of photon absorption (moles of absorbed photons per unit time) [mol s−1].6,7 Since photocatalytic degradation relies on the Sun and on the photocatalyst, not consumed during the process,4,8 this is a potentially low-cost and environment friendly approach for pollution abatement.4Amongst oxide semiconductor photocatalysts4 (such as ZnO, FeO3, WO3), titanium dioxide nanoparticles (TiO2-NPs) have a wide range of applications, including self-cleaning,9 sterilization of surfaces,10 air11 and water12 purification. TiO2-NPs have the advantages of stability in water,4 biocompatibility13 and low cost (∼1900 USD per ton at 2016 prices![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14). Due to its wide band gap (3.25 eV (ref. 4)), TiO2 absorbs only the UV part of the solar spectrum.15 TiO2-NPs with diameter >10 nm (ref. 7) do not display quantum confinement effects, which would result in a blue shift of the absorption spectra.6 Hence, TiO2-NPs exploit just the UV part (∼4%
14). Due to its wide band gap (3.25 eV (ref. 4)), TiO2 absorbs only the UV part of the solar spectrum.15 TiO2-NPs with diameter >10 nm (ref. 7) do not display quantum confinement effects, which would result in a blue shift of the absorption spectra.6 Hence, TiO2-NPs exploit just the UV part (∼4%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16) of the solar radiation to perform photodegradation,4,15,17,18 wasting ∼96% of the usable spectrum. Even considering only the UV component, TiO2-NPs have a modest PQE ∼ 10%,7 limited by the recombination of the photo-generated e–h pairs that occurs with 90% quantum efficiency.19 The PQE increases with the number of generated e–h pairs per absorbed photon, i.e. the photo-generation yield,19 and with the carriers’ lifetime.7 Integration with materials able to accept e or h may slow down charge recombination, leading to a PQE increase.
16) of the solar radiation to perform photodegradation,4,15,17,18 wasting ∼96% of the usable spectrum. Even considering only the UV component, TiO2-NPs have a modest PQE ∼ 10%,7 limited by the recombination of the photo-generated e–h pairs that occurs with 90% quantum efficiency.19 The PQE increases with the number of generated e–h pairs per absorbed photon, i.e. the photo-generation yield,19 and with the carriers’ lifetime.7 Integration with materials able to accept e or h may slow down charge recombination, leading to a PQE increase.
The integration of TiO2 with carbon materials, such as nanotubes,20 dots,21 graphene oxide (GO)22 and reduced graphene oxide (RGO),23 was pursued to enhance PQE.22–61 The e–h pair generation and evolution in TiO2/carbon composites, such as TiO2/RGO62,63,61 and TiO2/graphene quantum dots (GQD),64 was investigated by transient absorption (TA) spectroscopy.65 In TiO2/GQD,64 TiO2/RGO62 and Ti0.91O2/RGO,63 TiO2 acts as e acceptor when excited with visible light below the TiO2 optical gap. In TiO2/GQD, the e-injection occurs with a time constant <15 fs.62 In Ti0.91O2/RGO with 0.1 wt% RGO, RGO was found to act as e acceptor, decreasing the recombination rate in TiO2.61 Thus, when excited with UV photons above the TiO2 gap, RGO acts as e-acceptor causing the decrease of the charge carriers’ recombination rate, resulting in PQE enhancement. However, ref. 61 did not quantify the lifetime of the photo-generated carriers, because of the limited time resolution used (∼μs). Ref. 66 theoretically investigated the charge transfer processes, predicting that charge and energy transfer in TiO2/single layer graphene (SLG) would proceed in both directions, depending on the energy of the excited charges. Here, we apply ultrafast transient absorption spectroscopy to investigate charge separation in exfoliated graphite/TiO2. Our results explain the mechanism responsible for the increased PQE in TiO2/carbon composites.
Our TiO2/exfoliated graphite (TiO2/Gr) photocatalyst is prepared by sonication-assisted exfoliation of graphite in presence of TiO2-NPs, using commercial starting materials suitable for large scale production. Liquid-phase exfoliation (LPE) of graphite typically exploits surfactants,67,68 such as sodium deoxycholate69 and pluronics.70 Here we use the TiO2-NPs themselves to exfoliate graphite in water and produce the photocatalytic composite. The exfoliation process is investigated varying both sonication time and concentration of TiO2-NPs and comparing the chemical composition and crystal structure by high-resolution powder X-ray diffraction (HR-PXRD). The photocatalytic activity is evaluated by measuring the rate of degradation of a model organic compound (Rhodamine B) in water under UV irradiation. An increase up to ∼40% of the degradation rate, with respect to the TiO2-NPs used as starting material, is observed.
We also study photodegradation of nitrogen oxides, NOx. These pollutants are extremely relevant to society since NOx produced by anthropogenic emissions, in large part by on-road diesel vehicles, are key precursors of fine particulate matter (particle pollution smaller than 2.5 μm) and tropospheric ozone air pollution, that affect human health, crop yields and climate worldwide.71,72 We find a 70% increase in the photocatalytic activity with respect to TiO2. The photophysical mechanism underlying this enhanced photocatalytic activity is investigated by ultrafast TA spectroscopy with sub-200 fs time resolution and broad spectral coverage (430–1400 nm). We compare the decays of photo-generated e–h pairs in the composite with those in pristine TiO2 and we observe that TiO2-NPs inject e into the graphite flakes. The increased photo-production of reactive species explains the photocatalytic activity improvement, with exfoliated graphite acting as e-acceptor.
2. Results and discussion
The preparation of the photo-catalysts for environmental remediation needs to be as simple as possible, low-cost and easily scalable (e.g. photocatalyst in concrete is used up to 3% w/w, hence 70 kg m−3, see ref. 81). As discussed in ref. 82, processes based on hydrothermal synthesis and the use of autoclaves (as, e.g., in ref. 83 and 84) are expensive (because of the cost of the equipment), difficult to control (the morphology and activity of the final product is affected by minimal changes in the process) and hazardous, because of the use of high pressures (>2 atm) and high temperatures (>120 °C). Since these risks are proportional to the scale of production, these methods are not suitable for production of tons of photocatalyst, as required considering that in 2018, 30k tons of TiO2 NPs were used for photocatalytic applications.85 More generally, since the photocatalytic process is needed to clean the environment, the production of the catalyst itself has to be environmentally friendly and hazardous reagents and high temperatures or pressures should be avoided. State-of-the-art carbon/TiO2 photocatalytic materials do not meet these requirements, since: (i) they are prepared in multi-step processes (ref. 83); (ii) at high temperatures (>120 °C) and high pressures (>2 atm), such as in ref. 73, 83 and 84; (iii) with toxic reagents, such as in ref. 73; (iv) they cannot be prepared on the multi-ton scale, such as in ref. 73, 83 and 84.Here we use a one-pot process exploiting sono-chemical reactions at room temperature and atmospheric pressure. This is not disturbed by oxygen and can be scaled up. The process starts from low-cost (∼1900 USD per ton at 2016 prices for TiO2 NPs14 and ∼1000 USD per ton for graphite platelets at 2018 prices86) safe reactants, such as graphite and pre-formed TiO2 NPs, combining all the characteristics required for environmental remediation.
The composites are prepared by ultra sonication of graphite in a 2 mg ml−1 aqueous dispersion of TiO2-NPs for 4 hours (ELMATransonicT460/H-35 kHz) at 40 °C. The exfoliation is performed in Millipore ultrapure water (resistivity 18.2 MΩ cm at 25 °C). We use flakes from Sigma-Aldrich with size ∼150 μm and TiO2-NPs in the anatase form from HOMBIKAT AHP 200, Sachtleben Chemie GmbH (purity of the crystalline phase ≥94% w/w, average surface area ∼193 m2 g−1). Two sets of samples are prepared starting from a different mass ratio of TiO2 NPs and graphite. Samples having a mass ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of TiO2 with respect to graphite are labelled TiO2-Gr1:1. Those with a mass ratio 10
1 of TiO2 with respect to graphite are labelled TiO2-Gr1:1. Those with a mass ratio 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are labelled TiO2-Gr10:1. TiO2 NPs are labelled TiO2.
1 are labelled TiO2-Gr10:1. TiO2 NPs are labelled TiO2.
In order to study the effect of TiO2-NPs during liquid-phase sonication, we perform HR-PXRD measurements as a function of sonication time. Samples are loaded into 1 mm borosilicate glass capillaries and diffraction patterns collected at ambient temperature with an incident X-ray wavelength of 0.319902 Å. The full width at half maximum (FWHM) of the (002) graphite diffraction peak is deduced by the Rietveld refinement method,87 using the General Structure Analysis System (GSAS) program and EXPGUI interface.88,89
Diffraction patterns collected after 30 min sonication are shown in Fig. 1. For longer time, up to 4 h, further structural changes are not observed. Thus samples sonicated for 30 min can be considered as the final products. Fig. 1 confirms the presence of TiO2 anatase (as for The Joint Committee on Powder Diffraction Standards, JCPDS 21-127290) and graphite (JCPDS 75-2078).91 Moreover, the basal reflection shifts towards higher d-spacings (d002 = 3.357 Å) with respect to graphite (JCPDS 75-2078, d002 = 3.347 Å (ref. 91)). This suggests that TiO2-NPs assisted exfoliation increases the interplanar spacing of the resulting flakes. The (002) diffraction peak of TiO2-Gr10:1 has lower intensity than in TiO2-Gr1:1. This indicates that an increase in TiO2-NPs concentration leads to a decrease in the number of planes oriented along (002).91 As the concentration of TiO2-NPs increases, the 002 reflection broadens and the corresponding FWHM increases. The broadened FWHM is due to a smaller crystallite size91,92 (∼195 nm, ∼241 nm and ∼255 nm for TiO2-Gr10:1, TiO2-Gr1:1 and graphite, respectively) as determined by the Rietveld method87 using the software GSAS-II of ref. 93.
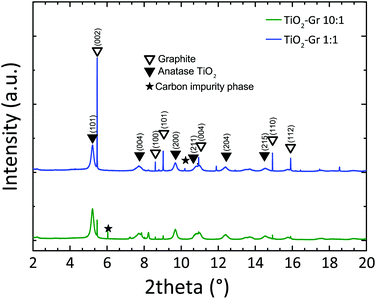 | ||
| Fig. 1 HR-PXRD diffraction profiles of TiO2-Gr1:1 and TiO2-Gr10:1 sonicated for 30 min, with peak assignment. | ||
We then investigate the photo-physical properties of the samples by UV-visible (UV-Vis) diffuse reflectance spectrometry with a PerkinElmer Lambda45 UV-Vis spectrophotometer with Harricks praying mantis diffuse reflectance. For each sample, 10 mg is mixed with a 500 mg NaCl matrix. We use a quartz cuvette with 0.5 cm optical path. The reflectance background of NaCl (reference) is taken as baseline for each measurement. The diffuse reflectance can be linked to the absorption coefficient through the Kubelka–Munk (KM) function94F(R). For a sample thickness >3 mm,95,96 with no light transmission, F(R) can be written as:97
| F(R) = (1 − R)2/2R = K/s = 2.303ε·c/s | (1) |
| Khν = A(hν − ET)n | (2) |
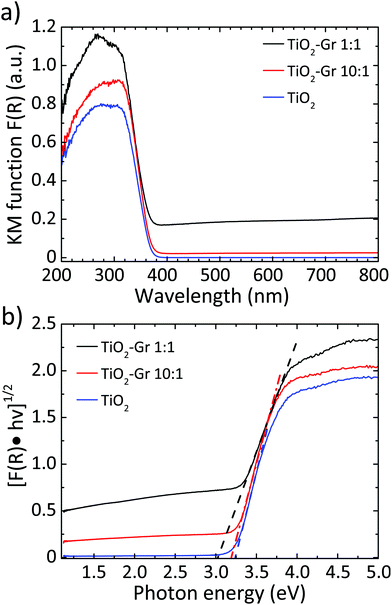 | ||
| Fig. 2 (a) F(R) elaborated and normalized with KM;94 (b) Tauc plot of the modified KM function. Dotted lines show the linear extrapolation of the Tauc gap. | ||
The photocatalytic activity is investigated by measuring the photo-degradation of a molecular non-azo-dye (rhodamineB; RhB). This compound is taken as model for organic volatile pollutants, since its molecular structure is close to that of the environmental contaminants used in industry and agriculture.103 This test follows the same procedures used to characterize other TiO2–carbon composites.28,37 TiO2, TiO2-Gr10:1 and TiO2-Gr1:1 are dispersed in an aqueous solution and sonicated for 4 h. In order to understand the effect of the graphite flakes on PQE, the amount of TiO2-Gr10:1 and TiO2-Gr1:1 is chosen to guarantee the same concentration of TiO2 (2 mg ml−1) inside each suspension. We test 10 ml mixtures comprising 2.86%ml of an aqueous solution of RhB (0.05 mg ml−1, 1 × 10−4 M), 2.14% ml H2O and 50% suspension of TiO2-Gr10:1 or TiO2-Gr1:1. Considering the affinity of graphitic flakes, due to the π–π stacking of their aromatic systems, for polycyclic aromatic and cationic compounds like RhB,104 the suspensions are magnetically stirred for 40 min in the dark, in order to attain adsorption–desorption equilibrium between composite and dye. Ref. 104 reported that, when RhB is adsorbed onto 2–3 layers graphene flakes, there is a ground state interaction that leads to a decrement in the intensity of UV/Vis absorption and photoluminescence (PL) of the dye independent of photodegradation. It is thus necessary to determine the fraction of RhB that remains free inside the solution, since this is required to discriminate whether the change in the dye concentration under irradiation is due to a photoreaction or to adsorption. To obtain the adsorption, after stirring in the dark, 0.75 ml of the RhB-composite suspension is taken and centrifuged at 9000 rpm for 10 min at T = 25 °C in order to separate the sample from the RhB solution. The upper 0.5 ml is collected and diluted with water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 ratio) to reach the 3 ml volume of analysis of a standard cuvette for a UV/Vis spectrophotometer. The concentration CD (mol L−1) of free RhB after incubation in the dark is derived from UV/Vis absorption spectra (λmax = 554 nm) recorded at 25° with a Cary300 UV-Vis spectrophotometer and a 180 μm path-length cuvette. The percentage of RhB adsorbed, Ads, is calculated starting from the initial concentration C0 (mol L−1) of the used dye, as:105
6 ratio) to reach the 3 ml volume of analysis of a standard cuvette for a UV/Vis spectrophotometer. The concentration CD (mol L−1) of free RhB after incubation in the dark is derived from UV/Vis absorption spectra (λmax = 554 nm) recorded at 25° with a Cary300 UV-Vis spectrophotometer and a 180 μm path-length cuvette. The percentage of RhB adsorbed, Ads, is calculated starting from the initial concentration C0 (mol L−1) of the used dye, as:105
| Ads = [(C0 − CD)/C0] × 100 | (3) |
The photoreactivity after photoexcitation of TiO2 is investigated by exposing each sample to a lamp emitting in the UVA/UVB range (280–400 nm), matching the absorption spectra of the composites, Fig. 2. The lamp has irradiance, i.e. emitted power per unit area, I ∼ 3 W m−2 in the UVA (280–315 nm) and ∼13.6 W m−2 in UVB (315 nm–400 nm), at 0.5 m from the source. The samples are placed 35 cm from the lamp. We use 1 mW UVA/UVB for 60 min, sampling 0.75 ml every time interval t of 10 min. The collected volumes are centrifuged, diluted and analyzed with the same procedure used for the determination of CD, detecting the concentration C(t) of RhB not degraded after t from the beginning of the irradiation. The percentage of RhB photodegraded, P(t), is:106
| P(t) = [(CD − C(t))/C0] × 100 | (4) |
Using this approach, the photocatalytic activity is assessed independently of the possible adsorption of the dye onto the surface of the photoactive material, since the concentration of the dye after pre-equilibration is taken as a reference. For TiO2-Gr10:1, Table 1 shows an increment of P(t) with respect to TiO2 of ∼16% after 20 min and ∼21% after 40 min. For TiO2-Gr1:1, the increment is ∼7% after 20 min while a decrement ∼2% occurs after 40 min. The adsorption of RhB increases from ∼5% in TiO2-Gr10:1 to ∼35% in TiO2-Gr1:1. These results indicate that TiO2-Gr1:1 does not show improvement in photocatalytic activity with respect to TiO2. The reason for this is the presence of a residual of graphite that is not electronically interacting with TiO2 in TiO2-Gr1:1. The excess of graphite is demonstrated by the broad absorption in the 400–800 nm region in Fig. 2. Graphite adsorbs RhB as demonstrated by the increase of the adsorbed fraction from 5% to 35%, but it is not photocatalyically active. As a result, the fraction of light absorbed by this non-photochemically active component is dissipated without giving photodegradation of RhB, causing a decrease of P. We thus identify TiO2-Gr10:1 as a promising photocatalytic compound since it gives an enhanced P(t) with respect to TiO2, for a similar RhB adsorption. The observed lack of improvement in photocathalytic activity of TiO2-Gr1:1 with respect to TiO2 is in agreement with ref. 28, 48, 51 and 107, where the adsorption and photocatalytic activity of TiO2 composites with GO and RGO was reported: a GO/TiO2 or RGO/TiO2 weight ratio >10% was associated with a decrease of photocatalytic activity. Hence, we focus on TiO2-Gr10:1 hereafter.
| TiO2 | TiO2-Gr10:1 | TiO2-Gr1:1 | |
|---|---|---|---|
| P(20 min) | 38% | 54% | 45% |
| P(40 min) | 66% | 87% | 64% |
| Ads | 5% | 5% | 35% |
Fig. 3 compares the concentration of RhB during photodegradation upon UV irradiation for: (i) TiO2-Gr10:1, (ii) reference TiO2, (iii) graphite, (iv) no photocatalyst, (v) TiO2-Gr10:1R which is not ultrasonicated. The trends indicate that the dye's degradation temporal profile is a combination of a zero-order and a first-order kinetics. In zero-order kinetics, the rate is independent of reactant concentration and the RhB concentration decreases linearly with time,108 while in first order, the rate is proportional to the dye concentration.
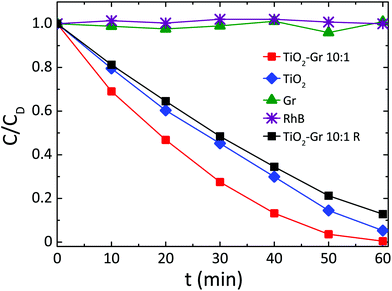 | ||
| Fig. 3 Photocatalytic degradation of RhB under UV light irradiation in the presence of TiO2-Gr10:1 ultra-sonicated and not ultra-sonicated (TiO2-Gr10:1R), TiO2 and Gr. | ||
Since neither zero-order nor first order models fit the data of Fig. 3, we use a pseudo-zero-order kinetic model commonly adopted in the case of organic dye photodegradation in heterogeneous systems:109
| 1 − C(t)/CD = kt | (5) |
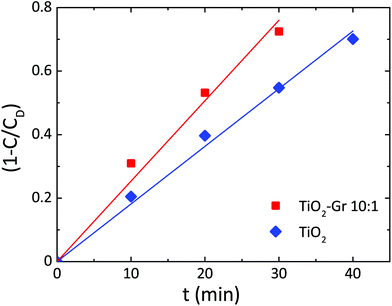 | ||
| Fig. 4 Photodegradation kinetics of RhB for TiO2, TiO2-Gr10:1. Lines are fits to the data with eqn (5). | ||
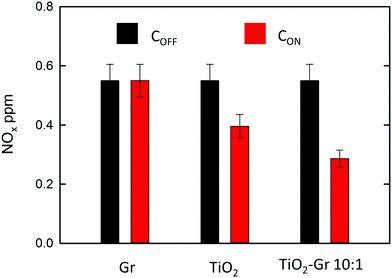
NOx abatement tests are performed according to the UNI 11247 standard for determination of the degradation of NOx in air by inorganic photocatalytic materials.110 (1) An artificial atmosphere generator system with a NOx source, to provide a continuous flow with a constant NOx concentration. (2) A reaction chamber containing the sample with a UV lamp (irradiance between 300 and 400 nm, 300 Watt power at 365 nm) providing an accurate light intensity (20 W m−2) on the sample surface. The chamber (3 liters) is sized in order to test samples with a defined exposed surface area (65 cm2). (3) The NOx concentration at the outlet is measured with a chemiluminescence NOx meter, as follows: (1) The sample is placed inside the reaction chamber with the polluted air flow (3 l min−1) and the UV lamp switched off. This phase lasts ∼ one hour and is necessary to equalize the adsorption processes and assure a constant NOx concentration (i.e. gas flow stabilization) in the air supply flow. This initial value is noted as COFF. (2) The UV lamp is switched on and the system is allowed to equalize for a certain time (normally ∼ one hour). The irradiated equilibrium concentration is noted as CON. (3) The UV lamp is switched off and the NOx concentration is checked to its initial value. The samples are prepared as follows: (i) mixing the composite with 2-propanol, (ii) bath sonication of the mixture for 10 min, (iii) drying at room temperature in a Petri glass to make a thin (1 mm) deposit of the photocatalyst on the bottom of a Petri glass. A fixed incoming flow of air ∼1.5 l min−1 is used, with a 0.55 ppm concentration of NOx, including 0.15 ppm NO2 and 0.4 ppm NO, corresponding to atmospheric pollution as for ref. 111. The NOx concentrations at the outlet of the reaction chamber measured in stationary flow conditions, either under UV illumination, CON, or without illumination, COFF, are shown in Fig. 5 for Gr, TiO2 and TiO2-Gr10:1. The NOx photocatalytic decomposition percentage under UV radiation is calculated as Q = 100(COFF − CON)/COFF. Fig. 5 indicates no NOx photodegradation for Gr, 28% for TiO2 and 48% for Gr-TiO2 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, with an increase 70% of photodegradation yield of NOx with respect to TiO2.
1, with an increase 70% of photodegradation yield of NOx with respect to TiO2.
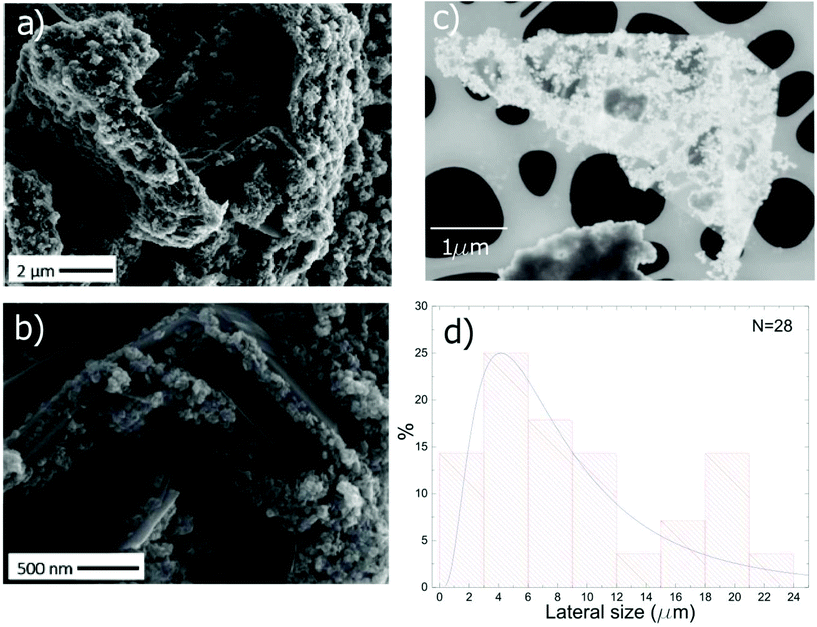
The morphology of TiO2-Gr10:1 is investigated by scanning electron microscopy (SEM, Quanta3D, FEI Company). Fig. 6a shows graphitic flakes covered by TiO2-NPs. The higher magnification image Fig. 6b indicates that the flakes edges are decorated by NP agglomerates. The lateral size of the flakes is evaluated by Scanning Transmission Electron Microscopy (STEM, Magellan 400L FEI) depositing ∼20 μl TiO2-Gr10:1 on a holey carbon Cu grid (300 mesh). From a statistical analysis of isolated flakes similar to that in Fig. 6c, an average lateral size ∼5 μm is estimated, Fig. 6d.
To exclude that the TiO2-NPs adhesion to the flakes is due to the drying of the TiO2-Gr10:1 suspension, we perform Cryo-TEM (CRyoTitan FEI) experiments. 20 μl TiO2-Gr10:1 is deposited on a holey carbon grid (Quantifoil R2/2 200 mesh), then loaded into the chamber of a FEI Vitrobot™ Mark III, that maintains 100% humidity at 4 °C. Inside the chamber there are two blotting papers on either side of the sample, which close on the grid and leave a layer of suspension ∼ hundreds nm thick.112 The sample is then plunged into liquid ethane at −183.3 °C, which avoids the formation of ice crystals,113 creating a vitreous ice (amorphous solid form of water).113 This allows us to investigate themorphology of TiO2-Gr10:1 in the liquid phase, confirming that TiO2-NPs adhere to the flakes, both on the surface (red rectangle) and at the edges (blue rectangle), Fig. 7.
 | ||
| Fig. 7 Cryo-TEM of TiO2-Gr10:1 in suspension with TiO2-NPs decorating the flake surface (red rectangle) and the edges (blue rectangle). | ||
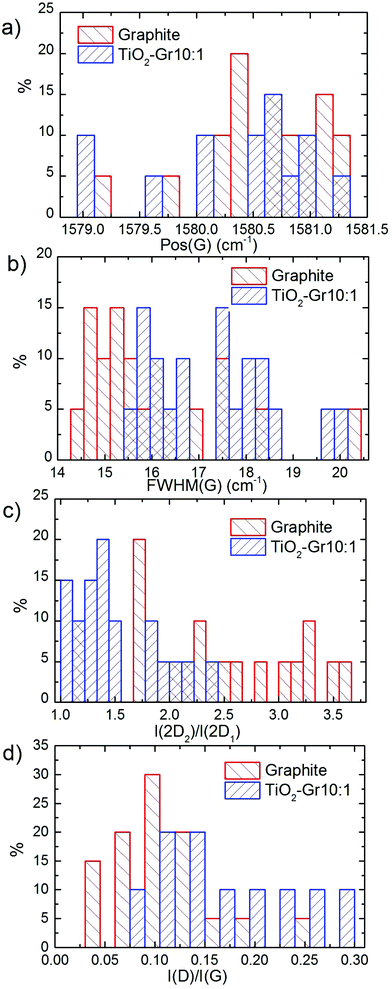
TiO2-Gr10:1 and the starting graphite are also characterized by Raman spectroscopy. 60 μl is drop cast onto a Si/SiO2 substrate, then heated at 100 °C for 20 min, to ensure water evaporation. Raman spectra are acquired at 514.5 nm using a Renishaw InVia spectrometer with a Leica DM LM microscope and a 50× objective. The power is kept below 1 mW to avoid any possible damage and heating. The spectral resolution is ∼1 cm−1. A statistical analysis is performed as follows: the substrate is divided into 4 regions ∼500 × 500 μm2 and in each 5 points are acquired. Fig. 8 plots representative Raman spectra of the starting graphite (black line) and of TiO2-Gr10:1 (blue line) both on Si/SiO2. The peaks at 144, 397, 518 and 639 cm−1 are the Eg, B1g, A1g and Eg modes of anatase TiO2.114 The TiO2 peak at 518 cm−1 is very close to the first order peak of silicon ∼521 cm−1 (ref. 115) and they are partially overlapping. The crystallite size of TiO2-NPs can be estimated from the position Pos(Eg@144 cm−1) and FWHM(Eg@144 cm−1).116 In our case Pos(Eg@144 cm−1) ∼ 147 cm−1 and FWHM ∼ 20 cm−1 correspond to a NPs size ∼7 nm,116 in agreement with an estimate from TEM images, as in Fig. 7, of ∼5–10 nm. Fig. 9a and b show no significant difference between Pos(G) and FWHM(G) of graphite and TiO2-Gr10:1. The 2D peak shape for TiO2-Gr10:1 still resembles that of graphite117 with two components (2D1, 2D2), but their intensity ratio I(2D2)/I(2D1) is reduced from 2.4 to ∼1.4, Fig. 9c. This indicates that the bulk flakes have undergone exfoliation.118
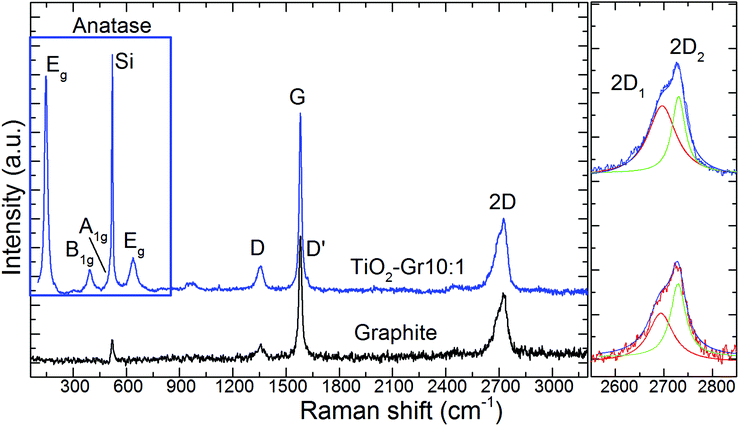 | ||
| Fig. 8 Representative Raman spectra at 514.5 nm for graphite (black curve) and TiO2-Gr10:1 (blue curve) both recorded on a Si/SiO2 substrate. | ||
When compared to the initial graphite, TiO2-Gr10:1 has a higher I(D)/I(G) and FWHM(G). I(D)/I(G) varies inversely with the crystal size, La, according to the Tuinstra and Koenig (TK) relation:118,119I(D)/I(G) ∼ 4.4 nm/La. Alternatively, this can be seen as proportional to the average interdefect distance,121LD: I(D)/I(G) ∼ 130 nm/LD2. I(D)/I(G) can also be affected by doping.120 The lack of up shift of Pos(G) and of FWHM(G) narrowing in TiO2-Gr10:1 when compared to graphite suggests a level of doping similar to the starting graphite, with a negligible effect on I(D)/I(G). We thus derive LD ∼ 31 nm and La ∼ 33 nm for TiO2-Gr10:1, and for the starting graphite we get LD ∼ 43 nm and La ∼ 63 nm. Given the average flakes lateral size in Fig. 7, these numbers reflect the defective nature of the starting graphite, and show that defects increase after sonication. La determined by Raman is consistent with that derived from HR-PXRD, although lower. Hence, the Raman spectra in Fig. 8 and their fitting parameters in Fig. 9 indicate that our material has changed with respect to the starting flakes, thus graphite itself is not involved in the photo-catalytic activity.
Fig. 10a plots the UV-Vis absorbance, −log10(T), with T the transmittance of TiO2 and TiO2-Gr10:1. These have two bands in the UV region at 270 and 306 nm, characteristic of TiO2-NPs,122 assigned to the first allowed vertical transitions that occur at the center of the Brillouin zone of TiO2-NPs.7 The PL spectra of TiO2 and TiO2-Gr10:1 in the liquid phase, following excitation at 266 nm, are reported in Fig. 10b. While the shape of the spectra is similar, the PL intensity quenching in TiO2-Gr10:1 points to an interaction between the excited TiO2 and the exfoliated graphite, which prevents radiative recombination of the photogenerated e–h pairs.
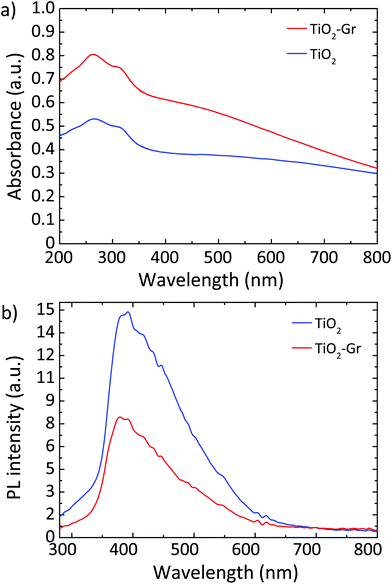 | ||
| Fig. 10 (a) UV-Vis absorbance of TiO2 and TiO2-Gr10:1. (b) PL spectra for 266 nm excitation of TiO2 and TiO2-Gr10:1. | ||
In order to investigate the photodegradation mechanism, we perform singlet oxygen detection experiments by monitoring the NIR luminescence with an Edinburgh FLS 980 Spectrofluorimeter equipped with a InGaAs detector and a 450 W xenon excitation lamp. Excitation is performed at 350 nm, above the bandgap of TiO2.4 No luminescence, hence no singlet oxygen formation, is detected. We thus rule out formation of singlet oxygen during rhodamine photo-degradation, in contrast to ref. 123, and suggest that degradation occurs via photogeneration of hydroxyl radicals, as for ref. 84.
The generation of reactive oxygen species5 (ROS) was identified as the photodegradation mechanism of organic pollutants55 and RhB.31 The presence of exfoliated graphite in TiO2-Gr10:1 may result in a higher ROS generation, due to e-transfer from TiO2 to graphite, allowing a more stable charge separation in TiO2. The first step of the photocatalytic degradation reaction is the photo-excitation of e–h pairs in TiO2-NPs by absorption of UV photons with energy exceeding the TiO2 gap. The ROS generation depends on the competition between charge recombination, either radiative or non-radiative, and the separation of the photo-excited charges required to initiate the oxidative (reductive) pathways.5 Accordingly, the enhancement of photocatalytic activity may be traced back to modifications of the relaxation channels of photoexcited e–h in TiO2, induced by graphite flakes.
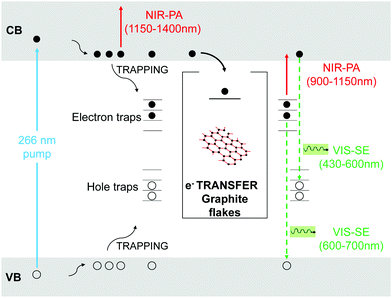
In order to identify these channels, we perform a comparative study of charge-carriers dynamics in pristine TiO2 and TiO2-Gr10:1 using broadband TA spectroscopy with sub-200 fs time-resolution. We use an amplified Ti:sapphire laser (Coherent, Libra) with 100 fs, 500 μJ pulses at 800 nm and 1 kHz. The 266 nm-pump pulse is generated by frequency tripling the laser output and it is modulated with a chopper at 500 Hz. The broadband probe pulse is obtained by white light continuum generation in a plate of sapphire, for the visible, or yttrium aluminium garnet (YAG), for the near-infrared (NIR). The probe spectrum is detected by an optical multichannel analyzer with a wavelength resolution ∼1 nm. The parallel linearly polarized pump and probe pulses are focused on the sample in a non-collinear geometry with spot sizes ∼180 and ∼80 μm, in order to guarantee homogeneous excitation of the detected sample region. The pump power is 1.6 mW, corresponding to an incident fluence ∼3 mJ cm−2 (∼1016 photons per cm2). The measured signal is the delay-dependent differential transmission spectrum,65 defined as ΔT/T(λ,τ) = Ton(λ,τ)/Toff(λ) − 1, where Ton and Toff are the probe spectra transmitted through the excited and the unexcited sample, respectively, λ is the probe wavelength and τ the pump–probe delay, controlled with a motorized translation stage. The temporal resolution is ∼180 fs. We excite with UV pulses at 266 nm, well above the band gap of TiO2,4 and measure ΔT/T from 430 to 1400 nm.
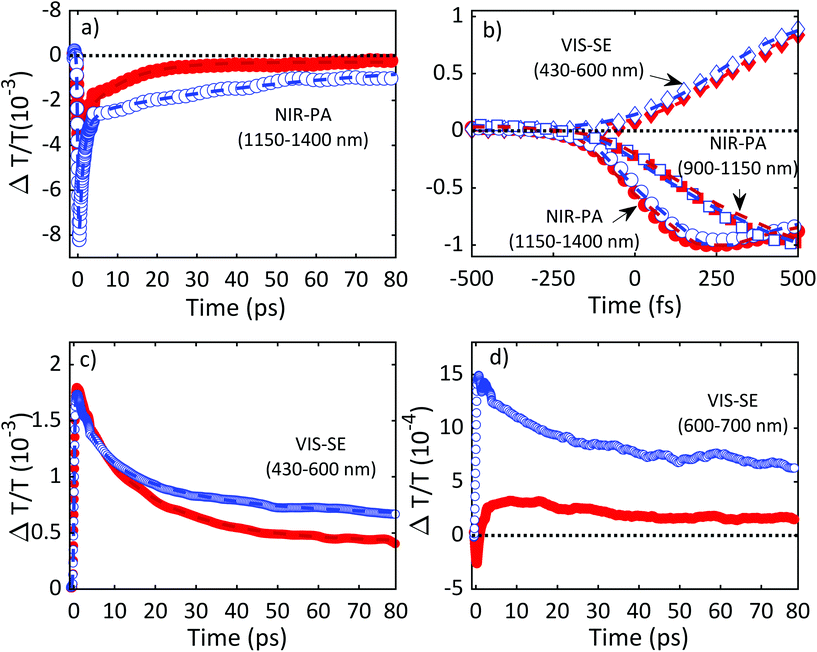
Fig. 11 plots ΔT/T (λ,τ) maps as a function of λ and τ. In the NIR, Fig. 11a and b, both TiO2 and TiO2-Gr10:1 exhibit broad photo-induced absorption (PA, ΔT/T < 0) from 900 to 1400 nm. We assign it to intraband transitions of the photo-excited free e from the conduction band (CB) edge, as reported for anatase TiO2-NPs.124–127 An additional source of PA in the NIR comes from the transition of trapped e to the CB.128 A large variety of trapping states is expected in TiO2, with energy distribution dependent on sample preparation.129 According to ref. 125 and 130 the contribution of trapped e to the PA signal should dominate in the range 900–1150 nm, while the free e absorption, which scales as λn with n = 1.7,125 dominates at longer wavelengths. In the NIR, both SLG131 and multilayer graphene132 show a positive ΔT/T, corresponding to photo-bleaching (PB) due to Pauli blocking131,132 from the hot e distribution in the CB.133,134 Since the TA spectrum of TiO2-Gr10:1 in the NIR consists of a PA band, we conclude that its optical response is dominated by TiO2, due both to the higher intensity of the transient signal from TiO2 and higher concentration of TiO2 with respect to graphite flakes.
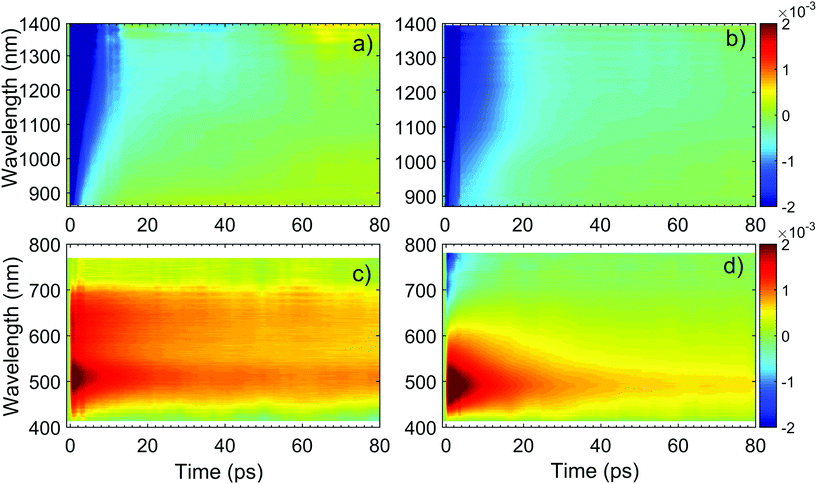 | ||
| Fig. 11 ΔT/T maps as a function of probe wavelength and pump–probe delay of TiO2 in (a) NIR (c) visible. ΔT/T maps of TiO2-Gr10:1 in (b) NIR and (d) visible. | ||
The TA maps of TiO2-Gr10:1 and TiO2 in the NIR differ for their time decay, as shown in Fig. 12a. The portion of the PA band in the range 1150–1400 nm can be attributed to free e, as confirmed by the resolution limited formation of the signal in Fig. 12b, and by the monotonic increase of the signal with probe wavelength. For TiO2, this PA relaxes following a bi-exponential decay with time constants τ1TiO2/PA = 500 fs, τ2TiO2/PA = 45 ps. In the presence of exfoliated graphite, the relaxation dynamics is best fit by a three-exponential decay with time constants τ1G/PA = 500 fs, τ2G/PA = 4 ps, τ3G/PA = 20 ps. In both TiO2 and TiO2-Gr10:1, the first sub-ps decay component is associated to the trapping of free e.130,135,136 The appearance of an additional decay channel, and the overall shortening of the PA bands lifetime observed in the composite with respect to the pristine TiO2-NPs can be explained by ultrafast charge transfer from TiO2 to the graphite flakes, which act as e scavengers. The PA dynamics in the range 900–1150 nm, mainly related to absorption from trapped e,125,130 appears almost unperturbed by the presence of exfoliated graphite, suggesting that e transfer mostly involves free e. In both samples, this PA band shows a build-up with a 400–500 fs time constant (Fig. 12b), related to e trapping. This rise time, consistent with the ∼200 fs time constant measured in Pt-loaded TiO2 particles,137 matches the sub-ps decay component (indicated as τ1TiO2/PA, τ1G/PA) of PA in the range 1150–1400 nm, observed in both TiO2 and TiO2-Gr10:1, which we attribute to free e trapping. Further evidence of e transfer from TiO2 to flakes can be found in the out-of-equilibrium optical response in the visible range, Fig. 11c and d. In the TiO2 sample we observe an increase in transmission (ΔT/T > 0) in the visible which, considering the vanishing ground state absorption in this spectral range, can be assigned to stimulated emission (SE), i.e. amplification of the probe beam due to optical gain.65 We identify two overlapping SE bands: the first, in the range 430–600 nm, due to the recombination of free e with trapped h. The second, in the range 600–700 nm, due to recombination of trapped e with free h. In TiO2-Gr10:1 the second, red shifted SE band is strongly quenched and a residual component appears few ps after excitation, Fig. 12d. The SE band in the range 430–600 nm, related to trapped h recombination can be observed in both samples, but in TiO2-Gr10:1 it decreases faster to equilibrium, see Fig. 12c. This band has a single exponential build up with 400–500 fs time constant, possibly due to h trapping, Fig. 12b. The SE relaxation dynamics can be fit by a bi-exponential decay on top of a long-lasting component related to the emission on the ns timescale.127 In TiO2, we get τ1TiO2/SE = 5 ps, τ2TiO2/SE = 45 ps, while in TiO2-Gr10:1 we have τ1G/SE = 4 ps, τ2G/SE = 20 ps (Fig. 12c). While τ1TiO2/SE could depend on the lifetime of the trapped h, the other three relaxation components τ2TiO2/SE, τ1G/SE and τ2G/SE, match those observed for the PA decay in the NIR (equal to τ2TiO2/PA, τ2G/PA, τ3G/PA) indicating that the SE band at 430–600 nm and the PA band at 1150–1400 nm decay with similar dynamics. These components can be associated to the population dynamics of free e, whose lifetime in TiO2-Gr10:1 is limited by the charge transfer to graphitic flakes, which occurs on a time-scale ∼4–20 ps. Previous ultrafast spectroscopy studies136,137 on Pt loaded TiO2-NPs suggested a similar e transfer time of several ps. In our case, e transfer to the graphitic flakes increases the trapped h lifetime, because it inhibits one of their recombination channels, enhancing the oxidative photocatalytic reactivity of the composite.
Fig. 13 summarizes the photoexcitation and relaxation pathways of TiO2 and TiO2-Gr10:1 derived from our ultrafast TA experiments. In pristine TiO2, the free e and h photo-excited into CB and VB by the UV-pump pulse (blue arrow), can either be excited by the probe pulse into higher energy states via intraband transitions responsible for the instantaneous PA band in the range 1100–1500 nm, or they can relax into intragap trapped states. The trapped charge carriers can radiatively recombine with free charges giving rise to the SE bands in the range 430–600 nm and 600–700 nm. Trapped e can also be photo-excited into CB as indicated by the PA bands in the range 900–1150 nm. All the bands related to the relaxation of trapped charge carriers share the same build-up dynamics due to the trapping. The interaction with graphitic flakes influences the optical properties of TiO2-Gr, when compared to TiO2, by opening an additional relaxation channel for the free e, which can efficiently transfer to the graphite flakes, thus slowing down e–h recombination, enhancing the photocatalytic activity.
3. Conclusions
We reported TiO2/Gr composites with enhanced photocatalytic activity with respect to pristine TiO2-NPs. These are produced via liquid phase exfoliation of graphite in presence of TiO2-NPs, without surfactants which could prevent the energy or charge transfer between TiO2 and graphite flakes. The observed photo-degradation kinetics consists of a combination of zero-order and first-order processes. We assigned the increase in photocatalytic activity to electron transfer from TiO2 to the graphite flakes, which occurs within the first ps of the relaxation dynamics.Our 40% improvement of photocatalytic performance with respect to TiO2 NPs is almost 400% larger that reported for state of the art RGO-TiO2.73 A similar result was achieved in ref. 74, but using carbon nanotubes in combination to RGO. This approach is not suitable for environmental remediation since, due to concerns on toxicity,75 the dispersion of carbon nanotubes in the environment as a result, e.g., of progressive release from the photocatalytic surfaces, should be avoided. Ref. 76 and 77 showed that water phase exfoliated graphite does not produce environmental concerns. Thus, our composite is designed to fit the requirements for environmental remediation: to treat water (or air) containing pollutants at low concentration (<ppm). Thus, material costs and environmental impact are the main issues. Materials used for environmental remediation, if not properly designed, may become themselves pollutants if dispersed in the environment.78 It is hence fundamental they are biocompatible. The environmental impact of photocatalyst production also needs to be considered in the assessment of the environmental sustainability of photocatalytic processes for air and water remediation.79 For different applications, such as fuel photo-production, see e.g.ref. 80, different features are required, in particular the value of the photo-product justifies the use of expensive elements such as Pt, Au or Ag.
Due to the simplicity and cost effectiveness of the preparation procedure of our samples, and the enhanced photocatalytic activity in the photodegradation of relevant environmental contaminants such as NOx, with respect to pristine TiO2-NPs, we anticipate applications to smart photoactive surfaces for environmental remediation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank G. Grancini for useful discussions. We acknowledge funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No. 785219 (GrapheneCore2), EU Neurofibres, ERC Minegrace and Hetero2D, EPSRC Grants EP/509K01711X/1, EP/K017144/1, EP/N010345/1, EP/M507799/5101, and EP/L016087/1.References
- http://www.who.int/topics/en .
- http://www.who.int/mediacentre/news/releases/2016/air-pollution-estimates/en .
- https://www.unicef.org/publications/files/Progress_on_Drinking_Water_Sanitation_and_Hygiene_2017.pdf .
- M. R. Hoffmann, S. T. Martin, W. Y. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69 CrossRef CAS.
- T. Hirakawa and Y. Nosaka, Langmuir, 2002, 18, 3247 CrossRef CAS.
- N. Serpone, D. Lawless, R. Khairutdinov and E. Pelizzetti, J. Phys. Chem., 1995, 99, 16655 CrossRef CAS.
- N. Serpone, D. Lawless and R. Khairutdinov, J. Phys. Chem., 1995, 99, 16646 CrossRef CAS.
- Q. Zhang, Q. An, X. Luan, H. Huang, X. Li, Z. Meng, W. Tong, X. Chen, P. K. Chu and Y. Zhang, Nanoscale, 2015, 7, 14002 RSC.
- Y. Lai, J. Huang, Z. Cui, M. Ge, K. Zhang, Z. Chen and L. Chi, Small, 2016, 12, 2203 CrossRef CAS PubMed.
- S. Nishimoto and B. Bhushan, RSC Adv., 2013, 3, 671 RSC.
- A. Mamaghani, F. Haghighat and C. S. Lee, Appl. Catal., B, 2017, 203, 247 CrossRef CAS.
- C. Yu, W. Zhou, H. Liu, Y. Liu and D. D. Dionysiou, Chem. Eng. J., 2016, 287, 117 CrossRef CAS.
- T. Xia, M. Kovochich, J. Brant, M. Hotze, J. Sempf, T. Oberley, C. Sioutas, J. I. Yeh, M. R. Wiesner and A. E. Nel, Nano Lett., 2006, 6, 1794 CrossRef CAS PubMed.
- http://www.cnchemicals.com/Press/88893-CCM .
- A. L. Linsebigler, G. Q. Lu and J. T. Yates, Chem. Rev., 1995, 95, 735 CrossRef CAS.
- I. Foyo-Moreno, I. Alados, F. J. Olmo and L. Alados-Arboledas, Agric. For. Meteorol., 2003, 120, 101 CrossRef.
- X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891 CrossRef CAS PubMed.
- A. Fujishima, X. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515 CrossRef CAS.
- N. Serpone, J. Photochem. Photobiol., A, 1997, 104, 1 CrossRef CAS.
- K. Dai, T. Peng, D. Ke and B. Wei, Nanotechnology, 2009, 20, 125603 CrossRef PubMed.
- M. Sun, X. Ma, X. Chen, Y. Sun, X. Cui and Y. Lin, RSC Adv., 2014, 4, 1120 RSC.
- K. R. Reddy, M. Hassan and V. G. Gomes, Appl. Catal., A, 2015, 489, 1 CrossRef CAS.
- L. Han, P. Wang and S. Dong, Nanoscale, 2012, 4, 5814 RSC.
- R. Leary and A. Westwood, Carbon, 2011, 49, 741 CrossRef CAS.
- W. Tu, Y. Zhou and Z. Zou, Adv. Funct. Mater., 2013, 23, 4996 CrossRef CAS.
- H. X. Wang, Q. Wang, K. G. Zhou and H. L. Zhang, Small, 2013, 9, 1266 CrossRef CAS PubMed.
- N. Zhang, M. Q. Yang, S. Liu, Y. Sun and Y. J. Xu, Chem. Rev., 2015, 115, 10307 CrossRef CAS PubMed.
- N. Zhang, Y. Zhang and Y. J. Xu, Nanoscale, 2012, 4, 5792 RSC.
- C. Chen, W. Cai, M. Long, B. Zhou, Y. Wu, D. Wu and Y. Feng, ACS Nano, 2010, 4, 6425 CrossRef CAS PubMed.
- J. Du, X. Lai, N. Yang, J. Zhai, D. Kisailus, F. Su, D. Wang and L. Jiang, ACS Nano, 2011, 5, 590 CrossRef CAS PubMed.
- Y. Gao, X. Pu, D. Zhang, G. Ding, X. Shao and J. Ma, Carbon, 2012, 50, 4093 CrossRef CAS.
- J. Guo, S. Zhu, Z. Chen, Y. Li, Z. Yu, Q. Liu, J. Li, C. Feng and D. Zhang, Ultrason. Sonochem., 2011, 18, 1082 CrossRef CAS PubMed.
- B. Jiang, C. Tian, Q. Pan, Z. Jiang, J. Q. Wang, W. Yan and H. Fu, J. Phys. Chem. C, 2011, 115, 23718 CrossRef CAS.
- C. H. Kim, B. H. Kim and K. S. Yang, Carbon, 2012, 50, 2472 CrossRef CAS.
- I. Y. Kim, J. M. Lee, T. W. Kim, H. N. Kim, H. I. Kim, W. Choi and S. J. Hwang, Small, 2012, 8, 1038 CrossRef CAS PubMed.
- N. Li, G. Liu, C. Zhen, F. Li, L. Zhang and H. M. Cheng, Adv. Funct. Mater., 2011, 21, 1717 CrossRef CAS.
- Y. Liang, H. Wang, H. S. Casalongue, Z. Chen and H. Dai, Nano Res., 2010, 3, 701 CrossRef CAS.
- Y. T. Liang, B. K. Vijayan, K. A. Gray and M. C. Hersam, Nano Lett., 2011, 11, 2865 CrossRef CAS PubMed.
- Y. T. Liang, B. K. Vijayan, O. Lyandres, K. A. Gray and M. C. Hersam, J. Phys. Chem. Lett., 2012, 3, 1760 CrossRef CAS PubMed.
- J. Liu, Z. Wang, L. Liu and W. Chen, Phys. Chem. Chem. Phys., 2011, 13, 13216 RSC.
- S. Liu, H. Sun, S. Liu and S. Wang, Chem. Eng. J., 2013, 214, 298 CrossRef CAS.
- X. Pan, Y. Zhao, S. Liu, C. L. Korzeniewski, S. Wang and Z. Fan, ACS Appl. Mater. Interfaces, 2012, 4, 3944 CrossRef CAS PubMed.
- L. M. Pastrana-Martinez, S. Morales-Torres, V. Likodimos, J. L. Figueiredo, J. L. Faria, P. Falaras and A. M. T. Silva, Appl. Catal., B, 2012, 123, 241 CrossRef.
- M. S. A. S. Shah, A. R. Park, K. Zhang, J. H. Park and P. J. Yoo, ACS Appl. Mater. Interfaces, 2012, 4, 3893 CrossRef PubMed.
- J. Shen, M. Shi, B. Yan, H. Ma, N. Li and M. Ye, Nano Res., 2011, 4, 795 CrossRef CAS.
- N. P. Thuy-Duong, P. Viet Hung, E. W. Shin, P. Hai-Dinh, S. Kim, J. S. Chung, E. J. Kim and S. H. Hur, Chem. Eng. J., 2011, 170, 226 CrossRef.
- P. Wang, J. Wang, T. Ming, X. Wang, H. Yu, J. Yu, Y. Wang and M. Lei, ACS Appl. Mater. Interfaces, 2013, 5, 2924 CrossRef CAS PubMed.
- Y. Wang, R. Shi, J. Lin and Y. Zhu, Appl. Catal., B, 2010, 100, 179 CrossRef CAS.
- G. Williams, B. Seger and P. V. Kamat, ACS Nano, 2008, 2, 1487 CrossRef CAS PubMed.
- N. Yang, Y. Liu, H. Wen, Z. Tang, H. Zhao, Y. Li and D. Wang, ACS Nano, 2013, 7, 1504 CrossRef CAS PubMed.
- H. Zhang, X. Lv, Y. Li, Y. Wang and J. Li, ACS Nano, 2010, 4, 380 CrossRef CAS PubMed.
- J. Zhang, Z. Xiong and X. S. Zhao, J. Mater. Chem., 2011, 21, 3634 RSC.
- L. W. Zhang, H. B. Fu and Y. F. Zhu, Adv. Funct. Mater., 2008, 18, 2180 CrossRef CAS.
- P. Zhang, C. Shao, Z. Zhang, M. Zhang, J. Mu, Z. Guo and Y. Liu, Nanoscale, 2011, 3, 2943 RSC.
- Y. Zhang, Z. R. Tang, X. Fu and Y. J. Xu, ACS Nano, 2010, 4, 7303 CrossRef CAS PubMed.
- Y. Zhang, Z. R. Tang, X. Fu and Y. J. Xu, ACS Nano, 2011, 5, 7426 CrossRef CAS PubMed.
- Y. Zhang, N. Zhang, Z. R. Tang and Y. J. Xu, Phys. Chem. Chem. Phys., 2012, 14, 9167 RSC.
- D. Zhao, G. Sheng, C. Chen and X. Wang, Appl. Catal., B, 2012, 111, 303 CrossRef.
- N. Yang, J. Zhai, D. Wang, Y. Chen and L. Jiang, ACS Nano, 2010, 4, 887 CrossRef CAS PubMed.
- T. F. Yeh, J. Cihlaář, C. Y. Chang, C. Cheng and H. Teng, Mater. Today, 2013, 16, 78 CrossRef CAS.
- A. Morais, C. Longo, J. R. Araujo, M. Barroso, J. R. Durrant and A. F. Nogueira, Phys. Chem. Chem. Phys., 2016, 18, 2608 RSC.
- P. Wang, N. M. Dimitrijevic, A. Y. Chang, R. D. Schaller, Y. Liu, T. Rajh and E. A. Rozhkova, ACS Nano, 2014, 8, 7995 CrossRef CAS PubMed.
- K. K. Manga, Y. Zhou, Y. Yan and K. P. Loh, Adv. Funct. Mater., 2009, 19, 3638 CrossRef CAS.
- K. J. Williams, C. A. Nelson, X. Yan, L. S. Li and X. Zhu, ACS Nano, 2013, 7, 1388 CrossRef CAS PubMed.
- S. De Silvestri, C. Manzoni, R. Borrego-Varillas, A. Oriana and G. Cerullo, Riv. Nuovo Cimento, 2017, 41, 1 Search PubMed.
- R. Long, N. J. English and O. V. Prezhdo, J. Am. Chem. Soc., 2012, 134, 14238 CrossRef CAS PubMed.
- Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. McGovern, B. Holland, M. Byrne and Y. K. Gun'Ko, et al. , Nat. Nanotechnol., 2008, 3, 563 CrossRef CAS PubMed.
- F. Bonaccorso, A. Lombardo, T. Hasan, Z. Sun, L. Colombo and A. C. Ferrari, Mater. Today, 2012, 15, 564 CrossRef CAS.
- M. Lotya, P. J. King, U. Khan, S. De and J. N. Coleman, ACS Nano, 2010, 4, 3155 CrossRef CAS PubMed.
- A. C. Ferrari, F. Bonaccorso, V. Fal'ko, K. S. Novoselov, S. Roche, P. Boggild, S. Borini, F. H. L. Koppens, V. Palermo and N. Pugno, et al. , Nanoscale, 2015, 7, 4598 RSC.
- S. C. Anenberg, J. Miller, R. Minjares, L. Du, D. K. Henze, F. Lacey, C. S. Malley, L. Emberson, V. Franco, Z. Klimont and C. Heyes, Nature, 2017, 545, 467 CrossRef CAS PubMed.
- J. Lelieveld, J. S. Evans, M. Fnais, D. Giannadaki and A. Pozzer, Nature, 2015, 525, 367 CrossRef CAS PubMed.
- Á. Tolosana-Moranchel, A. Manassero, M. L. Satuf, O. M. Alfano, J. A. Casas and A. Bahamonde, Appl. Catal., B, 2019, 246, 1 CrossRef.
- Y. Huang, D. Chen, X. Hu, Y. Qian and D. Li, Nanomaterials, 2018, 8, 431 CrossRef.
- N. Kobayashi, H. Izumi and Y. Morimoto, J. Occup. Health, 2017, 59, 394 CrossRef CAS.
- C. Martín, K. Kostarelos, M. Prato and A. Bianco, Chem. Commun., 2019, 55, 5540 RSC.
- S. Gurunathan and J.-H. Kim, Int. J. Nanomed., 2016, 11, 1927 CrossRef CAS PubMed.
- D. M. Mitrano, S. Motellier, S. Clavaguera and B. Nowack, Environ Int, 2015, 77, 132 CrossRef CAS PubMed.
- J. Luo, S. Zhang, M. Sun, L. Yang, S. Luo and J. C. Crittenden, ACS Nano, 2019, 13, 9811–9840 CrossRef CAS PubMed.
- K. Wenderich and G. Mul, Chem. Rev., 2016, 116, 14587 CrossRef CAS PubMed.
- J. Jiang, X. He, J. Du, X. Pang, H. Yang and Z. Wei, Mater. Lett., 2019, 244, 178 CrossRef.
- A. Tayel, R. A. Ramadan and A. O. El Seoud, Catalysts, 2018, 8, 491 CrossRef.
- Á. Tolosana-Moranchel, A. Casasa, A. Bahamonde, L. Pascual, L. I. Granone, J. Schneider, R. Dillert and D. W. Bahnemann, Appl. Catal., B, 2019, 241, 375 CrossRef.
- G. Luna-Sanguino, Á. Tolosana-Moranchel, C. Duran-Valle, M. Faraldos and A. Bahamonde, Catal. Today, 2019, 328, 172 CrossRef CAS.
- http://www.42teknanomaterials.com/ .
- http://www.northerngraphite.com/ .
- R. A. Young, The Rietveld method, International union of crystallography, 1993 Search PubMed.
- O. Tanaike and M. Inagaki, Carbon, 1997, 35, 831 CrossRef CAS.
- A. N. Fitch, J. Res. Natl. Inst. Stand. Technol., 2004, 109, 133 CrossRef CAS.
- W. Li, R. Liang, A. Hu, Z. Huang and Y. N. Zhou, RSC Adv., 2014, 4, 36959 RSC.
- B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210 CrossRef CAS.
- C. E. Holcombe, Report Y 1887, USAEC Oak Ridge Y 12 Plant, 1973 Search PubMed.
- B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544 CrossRef CAS.
- P. Kubelka and F. Munk, Z. Tech. Phys., 1931, 12, 593 Search PubMed.
- G. Kortüm, Reflectance spectroscopy: principles, methods, applications, Springer Science & Business Media, 2012 Search PubMed.
- J. Workman Jr. and A. Springsteen, Applied spectroscopy: a compact reference for practitioners, Academic Press, 1998 Search PubMed.
- A. A. Christy, O. M. Kvalheim and R. A. Velapoldi, Vib. Spectrosc., 1995, 9, 19 CrossRef CAS.
- S. D. Jackson and J. S. J. Hargreaves, Metal Oxide Catalysis, John Wiley & Sons, 2009 Search PubMed.
- K. M. Reddy, S. V. Manorama and A. R. Reddy, Mater. Chem. Phys., 2003, 78, 239 CrossRef.
- A. Murphy, Sol. Energy Mater. Sol. Cells, 2007, 91, 1326 CrossRef CAS.
- T. Smausz, B. Kondász, T. Gera, T. Ajtai, N. Utry, M. D. Pintér, G. Kiss-Albert, J. Budai, Z. Bozóki and G. Szabo, et al. , Appl. Phys. A, 2017, 123, 633 CrossRef.
- S. Ngamta, N. Boonprakob, N. Wetchakun, K. Ounnunkad, S. Phanichphant and B. Inceesungvorn, Mater. Lett., 2013, 105, 76 CrossRef CAS.
- R. Jain, M. Mathur, S. Sikarwar and A. Mittal, J. Environ. Manage., 2007, 85, 956 CrossRef CAS PubMed.
- G. Guidetti, A. Cantelli, R. Mazzaro, L. Ortolani, V. Morandi and M. Montalti, Nanoscale, 2016, 8, 8505 RSC.
- S. P. Patil, B. Bethi, G. H. Sonawane, V. S. Shrivastava and S. Sonawane, J. Ind. Eng. Chem., 2016, 34, 356 CrossRef CAS.
- T. S. Natarajan, M. Thomas, K. Natarajan, H. C. Bajaj and R. J. Tayade, Chem. Eng. J., 2011, 169, 126 CrossRef CAS.
- P. Zhu, A. S. Nair, S. Peng, S. Yang and S. Ramakrishna, ACS Appl. Mater. Interfaces, 2012, 4, 581 CrossRef CAS PubMed.
- F. Zhou, C. Yan, T. Liang, Q. Sun and H. Wang, Chem. Eng. Sci., 2018, 183, 231 CrossRef CAS.
- K. Rajeshwar, M. Osugi, W. Chanmanee, C. Chenthamarakshan, M. Zanoni, P. Kajitvichyanukul and R. Krishnan-Ayer, J. Photochem. Photobiol., C, 2008, 9, 171 CrossRef CAS.
- http://www.fotocatalisis.org/assets/doc497.pdf .
- R. Zouzelka and J. Rathousky, Appl. Catal., B, 2017, 217, 466 CrossRef CAS.
- http://www.fei.com/products/vitrobot .
- H. Friedrich, P. M. Frederik, G. de With and N. A. Sommerdijk, Angew. Chem., Int. Ed., 2010, 49, 7850 CrossRef CAS PubMed.
- T. Ohsaka, F. Izumi and Y. Fujiki, J. Raman Spectrosc., 1978, 7, 321 CrossRef.
- P. A. Temple and C. E. Hathaway, Phys. Rev. B, 1973, 7, 3685 CrossRef CAS.
- V. Swamy, A. Kuznetsov, L. S. Dubrovinsky, R. A. Caruso, D. G. Shchukin and B. C. Muddle, Phys. Rev. B, 2005, 71, 184302 CrossRef.
- A. C. Ferrari, et al. , Phys. Rev. Lett., 2006, 97, 187401 CrossRef CAS PubMed.
- A. C. Ferrari and J. Robertson, Phys. Rev. B, 2000, 61, 14095 CrossRef CAS.
- F. Tuinstra and J. L. Koenig, J. Chem. Phys., 1970, 53, 1126 CrossRef CAS.
- M. Bruna, A. K. Ott, M. Ijaes, D. Yoon, U. Sassi and A. C. Ferrari, ACS Nano, 2014, 8, 74327441 CrossRef PubMed.
- L. G. Cancado, A. Jorio, E. H. Martins Ferreira, F. Stavale, C. A. Achete, R. B. Capaz, M. V. O. Moutinho, A. Lombardo, T. S. Kulmala and A. C. Ferrari, Nano Lett., 2011, 11, 3190 CrossRef CAS PubMed.
- D. E. Gu, Y. Lu and B. C. Yang, Chem. Commun., 2008, 21, 2453 RSC.
- T. Takizawa, T. Watanabe and K. Honda, J. Phys. Chem., 1978, 82, 1391 CrossRef CAS.
- S. H. Szczepankiewicz, J. A. Moss and M. R. Hoffmann, J. Phys. Chem. B, 2002, 106, 2922 CrossRef CAS.
- T. Yoshihara, R. Katoh, A. Furube, Y. Tamaki, M. Murai, K. Hara, S. Murata, H. Arakawa and M. Tachiya, J. Phys. Chem. B, 2004, 108, 3817 CrossRef CAS.
- A. Yamakata, T. A. Ishibashi and H. Onishi, Chem. Phys. Lett., 2001, 333, 271 CrossRef CAS.
- A. Yamakata, T. A. Ishibashi and H. Onishi, J. Phys. Chem. B, 2001, 105, 7258 CrossRef CAS.
- F. J. Knorr, C. C. Mercado and J. L. McHale, J. Phys. Chem. C, 2008, 112, 12786 CrossRef CAS.
- J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919 CrossRef CAS PubMed.
- Y. Tamaki, A. Furube, R. Katoh, M. Murai, K. Hara, H. Arakawa and M. Tachiya, C. R. Chim., 2006, 9, 268 CrossRef CAS.
- M. Breusing, S. Kuehn, T. Winzer, E. Malic, F. Milde, N. Severin, J. P. Rabe, C. Ropers, A. Knorr and T. Elsaesser, Phys. Rev. B, 2011, 83, 153410 CrossRef.
- D. Sun, Z. K. Wu, C. Divin, X. Li, C. Berger, W. A. de Heer, P. N. First and T. B. Norris, Phys. Rev. Lett., 2008, 101, 157402 CrossRef PubMed.
- D. Brida, A. Tomadin, C. Manzoni, Y. J. Kim, A. Lombardo, S. Milana, R. R. Nair, K. S. Novoselov, A. C. Ferrari, G. Cerullo and M. Polini, Nat. Commun., 2013, 4, 1987 CrossRef CAS PubMed.
- A. Tomadin, D. Brida, G. Cerullo, A. C. Ferrari and M. Polini, Phys. Rev. B, 2013, 88, 035430 CrossRef.
- K. Iwata, T. Takaya, H. O. Hamaguchi, A. Yamakata, T. A. Ishibashi, H. Onishi and H. Kuroda, J. Phys. Chem. B, 2004, 108, 20233 CrossRef CAS.
- Y. Tamaki, A. Furube, M. Murai, K. Hara, R. Katoh and M. Tachiya, Phys. Chem. Chem. Phys., 2007, 9, 1453 RSC.
- A. Furube, T. Asahi, H. Masuhara, H. Yamashita and M. Anpo, Chem. Phys. Lett., 2001, 336, 424 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |