Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Metal alkyls programmed to generate metal alkylidenes by α-H abstraction: prognosis from NMR chemical shift†
Christopher P.
Gordon‡
 a,
Keishi
Yamamoto‡
a,
Keishi
Yamamoto‡
 a,
Keith
Searles
a,
Keith
Searles
 a,
Satoru
Shirase
a,
Satoru
Shirase
 ab,
Richard A.
Andersen
ab,
Richard A.
Andersen
 *c,
Odile
Eisenstein
*c,
Odile
Eisenstein
 *de and
Christophe
Copéret
*de and
Christophe
Copéret
 *a
*a
aDepartment of Chemistry and Applied Biosciences, ETH Zürich, Vladimir Prelog Weg 1-5, 8093, Zürich, Switzerland. E-mail: ccoperet@ethz.ch
bDepartment of Chemistry, Graduate School of Engineering Science, Osaka University, Toyonaka, Osaka 560-8531, Japan
cDepartment of Chemistry, University of California, Berkeley, California 94720, USA. E-mail: raandersen@lbl.gov
dInstitut Charles Gerhardt, UMR 5253 CNRS-UM-ENSCM, Université de Montpellier, 34095 Montpellier, France. E-mail: odile.eisenstein@univ-montp2.fr
eHylleraas Centre for Quantum Molecular Sciences, Department of Chemistry, University of Oslo, P.O. Box 1033, Blindern, 0315 Oslo, Norway
First published on 5th January 2018
Abstract
Metal alkylidenes, which are key organometallic intermediates in reactions such as olefination or alkene and alkane metathesis, are typically generated from metal dialkyl compounds [M](CH2R)2 that show distinctively deshielded chemical shifts for their α-carbons. Experimental solid-state NMR measurements combined with DFT/ZORA calculations and a chemical shift tensor analysis reveal that this remarkable deshielding originates from an empty metal d-orbital oriented in the M–Cα–Cα′ plane, interacting with the Cα p-orbital lying in the same plane. This π-type interaction inscribes some alkylidene character into Cα that favors alkylidene generation via α-H abstraction. The extent of the deshielding and the anisotropy of the alkyl chemical shift tensors distinguishes [M](CH2R)2 compounds that form alkylidenes from those that do not, relating the reactivity to molecular orbitals of the respective molecules. The α-carbon chemical shifts and tensor orientations thus predict the reactivity of metal alkyl compounds towards alkylidene generation.
Introduction
Metal alkylidenes are key intermediates in many prominent chemical reactions, such as C–H activation, olefination reactions,1 and catalytic alkene and alkane metathesis.2–4 These compounds are commonly generated by deprotonation of a metal alkyl,5 carbene transfer or α-H abstraction from [M](CH2R)2 species.2,6–12 The latter process is particularly favoured for neopentyl (R = tBu) and related ligands, that were originally used to avoid the decomposition of these alkyl compounds via β-H transfer.13,14 These dialkyl compounds can however decompose via α-H abstraction, an intramolecular deprotonation process between two cis-bound alkyl ligands on a metal centre, typically with d0 configuration, related to σ-bond metathesis (Scheme 1a). While ubiquitous and used for the synthesis of numerous alkylidenes, no physical properties are currently available to guide the chemist in deciding which [M](CH2R)2 fragment will easily generate a [M](![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHR) species via α-H abstraction and in understanding why this process occurs.
CHR) species via α-H abstraction and in understanding why this process occurs.
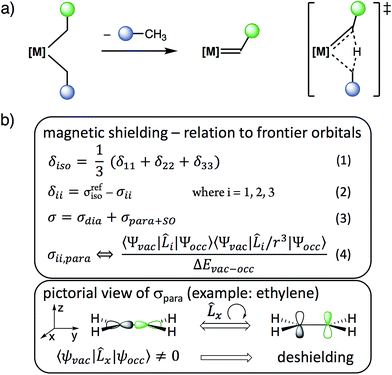 | ||
| Scheme 1 (a) Alkylidene formation from [M](CH2R)2via α-H abstraction and (b) relation between chemical shielding, chemical shift and frontier molecular orbitals. | ||
We reasoned that solid state NMR spectroscopy could be an ideal tool to probe this type of reactivity, since chemical shielding and associated 13C chemical shifts (δiso and the principal tensor components δ11 ≥ δ22 ≥ δ33) are directly linked to frontier molecular orbitals that control reactivity (Scheme 1b).15 This article reports the experimental measurement, calculation, and orbital analysis of the chemical shift tensor (CST) of the deshielded α-carbons in [M](CH2R)2 compounds that are prone to yield alkylidenes.
In short, we show that the occurrence of α-H abstraction from metal dialkyl compounds requires the presence of a low-lying empty metal d-orbital that points into the M–Cα–Cα′ plane. The signature of this orbital is the distinctively deshielded 13C chemical shift of the α-carbons and a specific orientation of the CST, arising from the alkylidene character on the α-carbon and polarization of the C−δ–H+δ bond. This situation is particularly pronounced for neopentyl ligands, explaining their propensity to generate alkylidenes via α-H abstraction.
Results and discussion
From the broad range of metal alkyl compounds that undergo α-H abstraction to yield well-defined alkylidenes or putative alkylidene species, a set of Ti and Ta compounds is selected as representative examples, chosen for historical reasons and their well-established reactivity patterns (Fig. 1). We focus on the Petasis reagent, Cp2Ti(CH3)2, a well-known olefination agent16 involving the putative methylidene intermediate Cp2Ti(CH2), which is trapped as Cp2Ti(CH2)(PMe3) in the presence of PMe3.17 We also include the related compound Cp*2Ti(CH3)2,18 Cp2Ti(CH2tBu)2,17 Ti(CH2tBu)4,19 and the cationic alkyl compound [nacnacTi(CH2tBu)2]+ (nacnac = [Ar]NC(CH3)CHC(CH3)N[Ar], Ar = 2,6-(CH(CH3)2)2C6H3), which generate the corresponding neopentylidenes.20 We also prepare the d0 tantalum compound, TaCl(CH2tBu)4,6 an isolable intermediate in the synthesis of the first well-defined metal alkylidene, Ta(CH2tBu)3(CHtBu), which cleanly transforms into the corresponding alkylidene TaCl(CH2tBu)2(CHtBu); analogous to the decomposition of Ta(CH2tBu)5 into Ta(CH2tBu)3(CHtBu).21,22 We also study TaCl2(CH2tBu)3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23,24 and Cp2Ta(CH3)3, which do not generate the corresponding alkylidenes (see Fig. 1b, red box), and the related cationic compound [Cp2Ta(CH3)2][BF4].25 These organometallic compounds provide an experimental test to distinguish between those metal dialkyl compounds that do and those that do not form alkylidenes.
23,24 and Cp2Ta(CH3)3, which do not generate the corresponding alkylidenes (see Fig. 1b, red box), and the related cationic compound [Cp2Ta(CH3)2][BF4].25 These organometallic compounds provide an experimental test to distinguish between those metal dialkyl compounds that do and those that do not form alkylidenes.
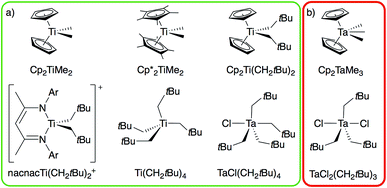 | ||
| Fig. 1 Ti and Ta alkyl compounds that (a) readily form alkylidenes via α-H abstraction (green box) or that (b) do not undergo α-H abstraction (red box). | ||
The structures of the studied metal alkyl compounds are shown in Fig. 1 and the measured and calculated chemical shift tensors are reported in Table 1. The isotropic chemical shift δiso, observed in solution NMR, is the average value of the three principal tensor components (δ11 ≥ δ22 ≥ δ33) obtained by solid-state NMR (Scheme 1b, eqn (1)).
| Compound | δ iso | δ 11 | δ 22 | δ 33 |
|---|---|---|---|---|
| a Axial, b Equatorial, c External and d Internal carbons. e Not measured. | ||||
| Cp2Ti(CH3)2 | 52 (52) | 121 (118) | 31 (35) | 3 (2) |
| Cp*2Ti(CH3)2 | 50 (51) | 100 (114) | 30 (26) | 22 (12) |
| Cp2Ti(CH2tBu)2 | 98 (86) | 193 (158) | 70 (60) | 31 (39) |
| Cp2Ti(CH2)-PMe3 | 286 (309) | 714 (754) | 82 (155) | 70 (17) |
| nacnacTi(CH2tBu)2+ | 143 (139) | 217 (212) | 184 (175) | 28 (30) |
| nacnacTi(CHtBu)(OTf) | 271 (277) | 569 (613) | 271 (265) | −28 (−47) |
| Ti(CH2tBu)4 | 119 (118) | 165 (158) | 137 (148) | 55 (49) |
| TaCl(CH2tBu)4a | 135 (142) | 214 (214) | 149 (147) | 43 (64) |
| TaCl(CH2tBu)4b | 113 (126) | 154 (159) | 146 (162) | 40 (58) |
| TaCl(CH2tBu)2(CHtBu) | 251 (264) | —e (484) | —e (310) | —e (−2) |
| TaCl2(CH2tBu)3 | 115 (130) | 156 (171) | 141 (152) | 48 (65) |
| Cp2Ta(CH3)3c | 25 (22) | 43 (37) | 28 (33) | 4 (−4) |
| Cp2Ta(CH3)3d | 22 (23) | 48 (49) | 19 (15) | −1 (7) |
| [Cp2Ta(CH3)2][BF4] | 57 (62) | 172 (164) | 24 (42) | −27 (−20) |
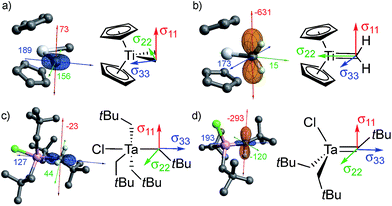
All of the metal alkyl compounds, with the exception of Cp2Ta(CH3)3, display unusually large spans (Ω = δ11 − δ33) for the α-alkyl-carbons with deshielded δiso. The low-field value of δiso is mostly due to the strongly deshielded δ11 component. The experimental values are compared to those obtained by DFT/ZORA calculations (see ESI† for Computational Details), which also provide the tensor orientation. The obtained shieldings and associated chemical shifts reproduce well the experimental isotropic values and show good agreements with the individual tensor components (Table 1). The calculated shielding tensors are shown for specific examples in Fig. 2 (the tensors of the other compounds are shown in Fig. S14†).
For Cp2Ti(CH3)2, the most deshielded component (δ11) is oriented perpendicular to the plane that contains the two M–Cα bonds (Fig. 2a). This orientation is the same as in the associated alkylidene, Cp2Ti(CH2) (Fig. 2b), and the isolated adduct Cp2Ti(CH2)(PMe3), for which the most deshielded component is oriented perpendicular to the σ(M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) and the π(M
C) and the π(M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) bonds.26 These similarities implicate alkylidene character in the carbon atoms of the methyl groups in Cp2Ti(CH3)2.
C) bonds.26 These similarities implicate alkylidene character in the carbon atoms of the methyl groups in Cp2Ti(CH3)2.
The axial carbon in the trigonal bipyramidal (TBP) molecule TaCl(CH2tBu)4 (Fig. 2c) has the two most deshielded tensor components δ11 and δ22 oriented perpendicular to the M–C axis, again with δ11 being perpendicular to the plane containing two M–Cα bonds, while the most shielded component δ33 is along the M–C axis. The orientation of the tensor in this compound is similar to that of the associated alkylidene (Fig. 2d). It should be noted that TaCl(CH2tBu)4 shows two distinct signals in the solution NMR at 144 and 116 ppm in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio, corresponding to axial and equatorial CH2tBu ligands of the trigonal bipyramidal structure, respectively. In solid-state NMR, the situation is complicated by the presence of several sites in the powdered sample. At 100 K, six distinct sites are observed in a chemical shift range of 113 to 135 ppm (the extreme values are reported in Table 1, for other values see Table S1†). The most deshielded site (135 ppm) stands out by a notably large span (Ω = 171 ppm) and is tentatively assigned to the axial carbon, while the other sites show spans (Ω) that vary between 102 and 143 ppm and presumably correspond to equatorial α-carbons in different environments. DFT calculations also show that the axial α-carbon is strongly deshielded (δiso/δ11 = 142/214 ppm), while the equatorial carbons are more shielded (δiso = 126–129 ppm, δ11 = 159–189 ppm). The calculations show the presence of several local minima upon rotation of the axial CH2tBu ligand in TaCl(CH2tBu)4, giving rise to an ensemble of conformations as a possible explanation for the observation of several peaks.
3 ratio, corresponding to axial and equatorial CH2tBu ligands of the trigonal bipyramidal structure, respectively. In solid-state NMR, the situation is complicated by the presence of several sites in the powdered sample. At 100 K, six distinct sites are observed in a chemical shift range of 113 to 135 ppm (the extreme values are reported in Table 1, for other values see Table S1†). The most deshielded site (135 ppm) stands out by a notably large span (Ω = 171 ppm) and is tentatively assigned to the axial carbon, while the other sites show spans (Ω) that vary between 102 and 143 ppm and presumably correspond to equatorial α-carbons in different environments. DFT calculations also show that the axial α-carbon is strongly deshielded (δiso/δ11 = 142/214 ppm), while the equatorial carbons are more shielded (δiso = 126–129 ppm, δ11 = 159–189 ppm). The calculations show the presence of several local minima upon rotation of the axial CH2tBu ligand in TaCl(CH2tBu)4, giving rise to an ensemble of conformations as a possible explanation for the observation of several peaks.
The origin of the deshielded chemical shift values is investigated by an orbital analysis of the corresponding shielding tensor (σ, eqn (2)).15 Decomposition of the shielding into diamagnetic (σdia) and paramagnetic contributions, which also include contributions from spin–orbit coupling (σpara+SO, eqn (3)), reveals that the variation in the shielding values is mostly associated with σpara+SO. For the compounds investigated here, spin–orbit coupling is relatively small (Table S7†), allowing for interpreting σpara+SO based solely on the paramagnetic contributions. These originate from the magnetically induced coupling of excited electronic states with the ground state, by action of the angular momentum operator ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) i (eqn (4)). Hence, the chemical shift is sensitive to the relative energy and orientation of the frontier orbitals, establishing a link to reactivity. For carbon p-orbitals, deshielding along direction i occurs when the vacant and occupied orbitals are oriented perpendicular to each other and to the i-axis.
i (eqn (4)). Hence, the chemical shift is sensitive to the relative energy and orientation of the frontier orbitals, establishing a link to reactivity. For carbon p-orbitals, deshielding along direction i occurs when the vacant and occupied orbitals are oriented perpendicular to each other and to the i-axis.
The individual orbital contributions to the most deshielded component of the CST (δ11/σ11), obtained through a Natural Chemical Shift (NCS) analysis26–56 of the representative examples, Cp2Ti(CH3)2 and TaCl(CH2tBu)4, and the associated alkylidenes are plotted in Fig. 3 (values given in Table S4†). Notably, the largest contribution to deshielding in the δ11/σ11 component of the metal alkyl compounds is always associated with the σ(M–Cα) bond, as found for the corresponding metal alkylidenes.
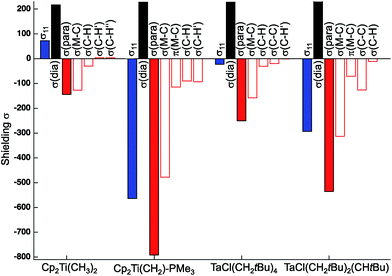 | ||
| Fig. 3 Orbital contributions to σ11 in Cp2Ti(CH3)2, TaCl(CH2tBu)4 (axial carbon atom), and associated alkylidenes. | ||
The large deshielding of the α-carbons, originating from the σ(M–Cα) bond, indicates the presence of a low-lying vacant orbital that is oriented perpendicular to the M–C axis and the direction of the deshielding. The emergence of this low-lying empty orbital is due to the weak π-donating ability of alkyl groups that, by interaction with an empty dπ metal orbital, develop a π-interaction by which the M–CH2R bond acquires alkylidene character, as shown for Cp2Ti(CH3)2 in Fig. 4c; this orbital is labelled as π(M–C). The associated π*(M–C) orbital, which is the LUMO of the compound (Fig. 4c right and S15†), is responsible for the observed deshielding by coupling with the occupied σ(M–C) orbital (Fig. 4a). In the corresponding alkylidene Cp2Ti(CH2), there is a smaller energy gap between the σ(M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) and π*(M
C) and π*(M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) orbitals, hence a significantly larger deshielding (Fig. 4b). Similarly, in TaCl(CH2tBu)4 the largest part of the deshielding on the axial α-carbon originates from the occupied σ(M–C) orbital (Fig. 4d left), which is coupled to the vacant π*(M–C) orbital (Fig. 4d right), again evidencing a π-type interaction of the metal atom with the alkyl ligand. The larger deshielding of the axial carbon atom as compared to the equatorial carbon atoms indicates larger π-character in the former M–C bond.
C) orbitals, hence a significantly larger deshielding (Fig. 4b). Similarly, in TaCl(CH2tBu)4 the largest part of the deshielding on the axial α-carbon originates from the occupied σ(M–C) orbital (Fig. 4d left), which is coupled to the vacant π*(M–C) orbital (Fig. 4d right), again evidencing a π-type interaction of the metal atom with the alkyl ligand. The larger deshielding of the axial carbon atom as compared to the equatorial carbon atoms indicates larger π-character in the former M–C bond.
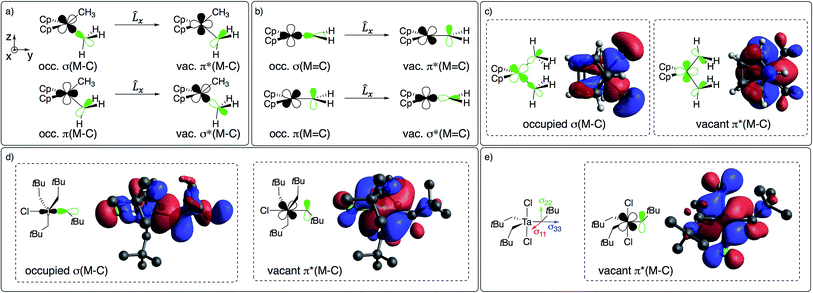 | ||
| Fig. 4 (a) Main orbital contributions to the paramagnetic term for δ11 in Cp2M(CH3)2 and (b) in Cp2Ti(CH2). Frontier molecular orbitals leading to deshielding in (c) Cp2M(CH3)2 (M = Ti or Ta+) and (d) TaCl(CH2tBu)4 (see Fig. 2 for orientation of CST). (e) CST orientation and LUMO of TaCl2(CH2tBu)3. | ||
A similar pattern and analysis applies to Cp*2Ti(CH3)2, Cp2Ti(CH2tBu)2, nacnacTi(CH2tBu)2+, and Ti(CH2tBu)4, where deshielding of the α-carbon mostly arises from the σ(M–C) bond, indicating a low-lying orbital of π*(M–C) character, oriented perpendicular to the σ(M–C) bond (Table S4 and Fig. S11†). The emergence of this orbital requires an empty metal d-orbital in the M–Cα–Cα′ plane of the correct symmetry to interact with the pπ-orbital of the alkyl ligand. Such an orbital is indeed present in all the aforementioned bis-alkyl compounds that generate alkylidenes via α-H abstraction (Fig. S15†). Thus, the deshielding is a signature of alkylidenic character in the metal–carbon bond.
The metal neopentyl compounds show particularly low 1JC–H coupling constants (e.g. 116 Hz for Cp2Ti(CH2tBu)2, 105 Hz and 110 Hz for the two α-carbons in nacnacTi(CH2tBu)2+, 110 Hz in Ti(CH2tBu)4, and 96 Hz for the axial carbon in TaCl(CH2tBu)4). This effect is slightly less pronounced in Cp*2TiMe2 (122 Hz average coupling constant). These lowered coupling constants indicate more p-orbital character in the C–H bonds, an additional signature of a π(M–C) type interaction. Notably, the equatorial carbons in TaCl(CH2tBu)4 show a larger 1JC–H coupling constant (115 Hz) than the axial carbon (96 Hz), indicating a less developed π-interaction in the former, in line with the less deshielded carbon atoms.
The formation of alkylidenes from bis-alkyl complexes via α-H abstraction requires the presence of a low-lying empty orbital in the plane of the M–Cα and M–Cα′ bonds. While the deshielded chemical shift value and large anisotropy of the CST indicate the presence of such an orbital, the CST orientation probes the location of this empty orbital. For example, TaCl2(CH2tBu)3 features a trigonal-bipyramidal geometry with two Cl-ligands in axial positions. The rather large deshielding on the α-carbon (115 ppm) indicates a low-lying empty orbital, but the most deshielded component (δ11) of the CST is not perpendicular to a plane containing two equatorial Ta–Cα bonds but rather perpendicular to the plane containing an equatorial Ta–Cα and an axial Ta–Cl bond, which is also the plane containing the LUMO (Fig. 4e). Accordingly, the alkylidenic character is not developed in the direction needed for α-H abstraction. This compound is therefore stable, even when heated to 100 °C in the presence of PMe3 for 4 h, in contrast to TaCl(CH2tBu)4. In other words, in a trigonal-bipyramidal structure, α-H abstraction is favoured between an axial and an equatorial alkyl ligand and is not readily accessible in TaCl2(CH2tBu)3, where both axial positions are occupied by Cl-ligands.
The importance of the presence of a vacant metal d-orbital with the appropriate orientation for the observed deshielding is further demonstrated by comparing Cp2Ti(CH3)2, Cp2Ta(CH3)3, and Cp2Ta(CH3)2+. While Cp2Ti(CH3)2 and Cp2Ta(CH3)2+ both show rather deshielded and anisotropic α-carbons, the NMR signatures of Cp2Ta(CH3)3 are markedly different (Fig. 5). The chemical shift drops from 52 ppm in Cp2Ti(CH3)2 to 22 and 25 ppm in Cp2Ta(CH3)3 (external and internal carbons, respectively), mostly originating from a large decrease of the δ11 component (121 ppm in Cp2Ti(CH3)2 as compared to <50 ppm for Cp2Ta(CH3)3). The third methyl-substituent in Cp2Ta(CH3)3 interacts with the empty metal orbital that is required for developing the alkylidene character (the remaining empty orbitals on the metal, which are involved in bonding with the Cp rings, are too high in energy for such an interaction). However, abstraction of a methyl-ligand generates Cp2Ta(CH3)2+, isoelectronic to Cp2Ti(CH3)2, and restores the highly anisotropic CST and deshielded chemical shift values (Fig. 5 and Table 1).
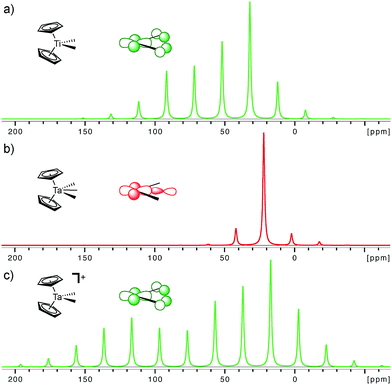 | ||
| Fig. 5 Simulated solid state NMR spectra for the α-carbons in Cp2Ti(CH3)2, Cp2Ta(CH3)3 (external carbon atom) and [Cp2Ta(CH3)2]+ at a magic angle spinning frequency of 2 kHz. The inserted molecular orbitals show the presence (a and c) and the absence (b) of the key empty orbital that leads to alkylidene character. The experimental solid state NMR spectra are available in the ESI.† | ||
The nature of the alkyl ligands also plays an important role in manipulating the alkylidene character on the α-carbon. This is illustrated by comparing the bis-neopentyl metallocene, Cp2Ti(CH2tBu)2 with the bis-methyl metallocenes, Cp2Ti(CH3)2 and Cp*2Ti(CH3)2, since detailed kinetic data on the decomposition via α-H abstraction is available for the latter metallocene.57 Cp2Ti(CH2tBu)2 displays a much more deshielded and anisotropic α-carbon, due to the coupling of σ(M–C) with π*(M–C), in addition to a significant contribution of the coupling of σ(Cα–Cβ) and π*(M–Cα) (Table S4 and Fig. S11†). The contribution of σ(Cα–Cβ) is associated with the wide calculated α(M–Cα–Cβ) angle of 136°, signalling the increased alkylidene character in the Ti–C bond. The NMR data thus suggest a lower activation energy for α-H abstraction in Cp2Ti(CH2tBu)2, which is confirmed by the calculated energy profiles. The calculated Gibbs activation (and associated reaction) energies at 298 K are +27.1 (−3.3) kcal mol−1 for Cp2Ti(CH2tBu)2vs. +30.8 (+8.2) kcal mol−1 and +32.1 (+5.3) kcal mol−1 for Cp2Ti(CH3)2 and Cp*2Ti(CH3)2, respectively. The lower calculated Gibbs activation energy for the α-H abstraction in the neopentyl derivative is consistent with the experimentally determined values found for Cp2Ti(CH2tBu)2 (+22.8 kcal mol−1)58 and Cp*2Ti(CH3)2 (+28.3 kcal mol−1 with kα(H)/kα(D) = 2.92 ± 0.10).57 The Gibbs activation energies correlate with the deshielded α-carbon chemical shift and the lower value of the 1JC–H coupling constant, consistent with more alkylidene character in the Ti–C bond and consequently a lower transition state energy for the α-H abstraction step (Fig. 6). Detailed kinetic studies have also been reported on the elimination of CH3tBu from Ti(CH2tBu)4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 and Ta(CH2tBu)5.21,22 Both compounds follow first order kinetics for α-H abstraction. For Ti(CH2tBu)4, values of ΔG‡ = 26.4 kcal mol−1 and kα(H)/kα(D) = 5.2 ± 0.4 were found. For Ta(CH2tBu)5 the values were ΔG‡ = 22.3 kcal mol−1 and kα(H)/kα(D) = 14.1 ± 0.8 (note that ΔG‡ was determined for the deuterated compound).
19 and Ta(CH2tBu)5.21,22 Both compounds follow first order kinetics for α-H abstraction. For Ti(CH2tBu)4, values of ΔG‡ = 26.4 kcal mol−1 and kα(H)/kα(D) = 5.2 ± 0.4 were found. For Ta(CH2tBu)5 the values were ΔG‡ = 22.3 kcal mol−1 and kα(H)/kα(D) = 14.1 ± 0.8 (note that ΔG‡ was determined for the deuterated compound).
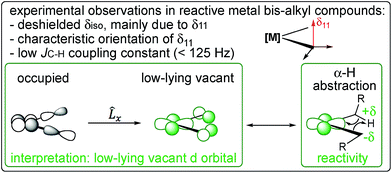 | ||
| Fig. 6 NMR chemical shift and 1JC–H coupling constant are signatures of a low-lying empty metal d-orbital that leads to a partial π(M–C) interaction and favours α-H abstraction. | ||
It is important to note the close analogy between alkylidenic character of the M–C bond and the occurrence of what is referred to as α-H agostic interactions.59,60 α-H Agostic interactions are evidenced by acute M–C–H angles (<109.47°) and are generally associated with low 1JC–H coupling constants for the carbon bound to the metal (<125 Hz). The presence of an α-H agostic interaction is associated with a π-type interaction of a p-orbital on the α-carbon with a vacant metal d-orbital, resulting in the observed geometrical features and lower 1JC–H coupling constants.61,62 Thus, an α-H agostic interaction is also an indirect reporter of an alkylidenic character in a M–C bond. However, the CST values that signal alkylidenic character can be present in the absence of geometrical features or lowered 1JC–H coupling constants associated with α-H agostic interactions. For example, in TaCl(CH2tBu)4, one M–C–H bond angle at the axial carbon is calculated to be 95° (which can be considered agostic), whereas, in Cp2Ti(CH3)2, the M–C–H angles are calculated to be 112.7° (the H atom in the σh plane) and 109.7° (the H atom out of σh plane). While both TaCl(CH2tBu)4 and Cp2Ti(CH3)2 have alkylidenic character, as evidenced by their CSTs, only the former is considered to be α-C–H agostic based on its calculated structure. Our view is that an α-C–H agostic interaction is better described as a π-donation from the carbon p-orbital, rather than as a 3-center-2-electron bond. The philosophical question remains: is the M⋯H–Cα interaction due to the alkylidenic character of the carbon atom bound to the metal, or does the alkylidenic character arise from the M⋯H–Cα interaction? Perhaps a distinction without a difference.
Conclusions
In summary, strongly deshielded chemical shift values of the α-carbons in [M](CH2R)2 compounds in combination with a large anisotropy and specific orientation of the chemical shift tensor reveal the presence and location of low-lying empty metal d-orbitals. The alkylidenic character in the M–CH2R bond activates the α-C–H bond towards α-H abstraction when the low-lying empty orbital is appropriately oriented. While this orbital arrangement can lead to the development of an α-C–H “agostic” interaction, the magnitude and orientation of the CST is a much more unequivocal signature of the alkylidenic character of the M–C bond. The CST shows that the parent alkyl compounds already contain inscribed information about the reaction products and are programmed to evolve into metal alkylidenes, a situation particularly favoured for neopentyl-type ligands. While this study has focused on Ti and Ta d0 compounds, the associated principle is likely applicable to a wide range of metal alkyls with low d-electron counts. The theme of this article is that NMR chemical shift values of atoms directly bonded to a metal centre provide information about the electronic structure and are powerful reporters of the location, orientation, and relative energy of the frontier molecular orbitals. This study shows that chemical shifts can be of predictive value of a compound's reactivity, making their physical interpretation an invaluable tool for the development and the understanding of mechanisms and reactivity. We are currently further exploring this connection.Conflicts of interest
There are no conflicts to declare.Acknowledgements
CPG and KS are supported by SNF grant number 2000201_169134 and 200020_149704. CPG is a recipient of the Scholarship Fund of the Swiss Chemical Industry. KY thanks the Canon foundation for a post-doctoral fellowship and the Murata Overseas Scholarship for Overseas Research Activities 2017. SS thanks the Osaka University Scholarship for Overseas Research Activities 2017. OE was partially supported by the Research Council of Norway through its Centres of Excellence scheme, project number 262695.Notes and references
- J. F. Payack, M. A. Huffman, D. Cai, D. L. Hughes, P. C. Collins, B. K. Johnson, I. F. Cottrell and L. D. Tuma, Org. Process Res. Dev., 2004, 8, 256–259 CrossRef CAS.
- R. R. Schrock, Chem. Rev., 2009, 109, 3211–3226 CrossRef CAS PubMed.
- J.-M. Basset, C. Copéret, D. Soulivong, M. Taoufik and J. T. Cazat, Acc. Chem. Res., 2010, 43, 323–334 CrossRef CAS PubMed.
- C. Copéret, Chem. Rev., 2010, 110, 656–680 CrossRef PubMed.
- R. R. Schrock, J. Am. Chem. Soc., 1975, 97, 6577–6578 CrossRef CAS.
- R. R. Schrock, J. Am. Chem. Soc., 1974, 96, 6796–6797 CrossRef CAS.
- R. R. Schrock, Acc. Chem. Res., 1979, 12, 98–104 CrossRef CAS.
- R. R. Schrock, Chem. Commun., 2005, 2773–2777 RSC.
- D. J. Mindiola, Acc. Chem. Res., 2006, 39, 813–821 CrossRef CAS PubMed.
- Z.-L. Xue and L. A. Morton, J. Organomet. Chem., 2011, 696, 3924–3934 CrossRef CAS.
- F. Rascón and C. Copéret, J. Organomet. Chem., 2011, 696, 4121–4131 CrossRef.
- R. R. Schrock and C. Copéret, Organometallics, 2017, 36, 1884–1892 CrossRef CAS.
- G. Wilkinson, Science, 1974, 185, 109–112 CAS.
- R. R. Schrock and G. W. Parshall, Chem. Rev., 1976, 76, 243–268 CrossRef CAS.
- C. M. Widdifield and R. W. Schurko, Concepts Magn. Reson., Part A, 2009, 34, 91–123 CrossRef.
- N. A. Petasis and E. I. Bzowej, J. Am. Chem. Soc., 1990, 112, 6392–6394 CrossRef CAS.
- J. D. Meinhart, E. V. Anslyn and R. H. Grubbs, Organometallics, 1989, 8, 583–589 CrossRef CAS.
- H. Brintzinger and J. E. Bercaw, J. Am. Chem. Soc., 1971, 93, 2045–2046 CrossRef CAS.
- J. Cheon, D. M. Rogers and G. S. Girolami, J. Am. Chem. Soc., 1997, 119, 6804–6813 CrossRef CAS.
- F. Basuli, B. C. Bailey, L. A. Watson, J. Tomaszewski, J. C. Huffman and D. J. Mindiola, Organometallics, 2005, 24, 1886–1906 CrossRef CAS.
- L. Li, M. Hung and Z. Xue, J. Am. Chem. Soc., 1995, 117, 12746–12750 CrossRef CAS.
- J. K. C. Abbott, L. Li and Z.-L. Xue, J. Am. Chem. Soc., 2009, 131, 8246–8251 CrossRef CAS PubMed.
- W. Mowat and G. Wilkinson, J. Organomet. Chem., 1972, 38, C35–C36 CrossRef CAS.
- R. R. Schrock and J. D. Fellmann, J. Am. Chem. Soc., 1978, 100, 3359–3370 CrossRef CAS.
- R. R. Schrock and P. R. Sharp, J. Am. Chem. Soc., 1978, 100, 2389–2399 CrossRef CAS.
- C. P. Gordon, K. Yamamoto, W.-C. Liao, F. Allouche, R. A. Andersen, C. Copéret, C. Raynaud and O. Eisenstein, ACS Cent. Sci., 2017, 3, 759–768 CrossRef CAS PubMed.
- Y. Ruiz-Morales, G. Schreckenbach and T. Ziegler, J. Phys. Chem., 1996, 100, 3359–3367 CrossRef CAS.
- J. A. Bohmann, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1997, 107, 1173–1184 CrossRef CAS.
- R. Salzmann, M. Kaupp, M. T. McMahon and E. Oldfield, J. Am. Chem. Soc., 1998, 120, 4771–4783 CrossRef CAS.
- J. Autschbach, J. Chem. Phys., 2008, 128, 164112 CrossRef PubMed.
- S. V. C. Vummaleti, D. J. Nelson, A. Poater, A. Gomez-Suarez, D. B. Cordes, A. M. Z. Slawin, S. P. Nolan and L. Cavallo, Chem. Sci., 2015, 6, 1895–1904 RSC.
- S. Halbert, C. Copéret, C. Raynaud and O. Eisenstein, J. Am. Chem. Soc., 2016, 138, 2261–2272 CrossRef CAS PubMed.
- K. Yamamoto, C. P. Gordon, W.-C. Liao, C. Copéret, C. Raynaud and O. Eisenstein, Angew. Chem., Int. Ed., 2017, 56, 10127–10131 CrossRef CAS PubMed.
- F. Aquino, B. Pritchard and J. Autschbach, J. Chem. Theory Comput., 2012, 8, 598–609 CrossRef CAS PubMed.
- G. Wu, D. Rovnyak, M. J. A. Johnson, N. C. Zanetti, D. G. Musaev, K. Morokuma, R. R. Schrock, R. G. Griffin and C. C. Cummins, J. Am. Chem. Soc., 1996, 118, 10654–10655 CrossRef CAS.
- E. L. Sceats, J. S. Figueroa, C. C. Cummins, N. M. Loening, P. Van der Wel and R. G. Griffin, Polyhedron, 2004, 23, 2751–2768 CrossRef CAS.
- J. B. Greco, J. C. Peters, T. A. Baker, W. M. Davis, C. C. Cummins and G. Wu, J. Am. Chem. Soc., 2001, 123, 5003–5013 CrossRef CAS PubMed.
- K. B. Wiberg, J. D. Hammer, K. W. Zilm, J. R. Cheeseman and T. A. Keith, J. Phys. Chem. A, 1998, 102, 8766–8773 CrossRef CAS.
- K. B. Wiberg, J. D. Hammer, K. W. Zilm and J. R. Cheeseman, J. Org. Chem., 1999, 64, 6394–6400 CrossRef CAS.
- D. Auer, C. Strohmann, A. V. Arbuznikov and M. Kaupp, Organometallics, 2003, 22, 2442–2449 CrossRef CAS.
- D. Auer, M. Kaupp and C. Strohmann, Organometallics, 2004, 23, 3647–3655 CrossRef CAS.
- D. Auer, M. Kaupp and C. Strohmann, Organometallics, 2005, 24, 6331–6337 CrossRef CAS.
- V. H. Gessner, F. Meier, D. Uhrich and M. Kaupp, Chem.–Eur. J., 2013, 19, 16729–16739 CrossRef CAS PubMed.
- A. H. Greif, P. Hrobarik and M. Kaupp, Chem.–Eur. J., 2017, 23, 9790–9803 CrossRef CAS PubMed.
- M. Karni, Y. Apeloig, N. Takagi and S. Nagase, Organometallics, 2005, 24, 6319–6330 CrossRef CAS.
- V. Kravchenko, R. Kinjo, A. Sekiguchi, M. Ichinohe, R. West, Y. S. Balazs, A. Schmidt, M. Karni and Y. Apeloig, J. Am. Chem. Soc., 2006, 128, 14472–14473 CrossRef CAS PubMed.
- A. J. Rossini, R. W. Mills, G. A. Briscoe, E. L. Norton, S. J. Geier, I. Hung, S. Zheng, J. Autschbach and R. W. Schurko, J. Am. Chem. Soc., 2009, 131, 3317–3330 CrossRef CAS PubMed.
- J. D. Epping, S. Yao, M. Karni, Y. Apeloig and M. Driess, J. Am. Chem. Soc., 2010, 132, 5443–5455 CrossRef CAS PubMed.
- S. Standara, K. Bouzkova, M. Straka, Z. Zacharova, M. Hocek, J. Marek and R. Marek, Phys. Chem. Chem. Phys., 2011, 13, 15854–15864 RSC.
- J. Toušek, M. Straka, V. Sklenář and R. Marek, J. Phys. Chem. A, 2013, 117, 661–669 CrossRef PubMed.
- J. Novotný, J. Vicha, P. L. Bora, M. Repisky, M. Straka, S. Komorovsky and R. Marek, J. Chem. Theory Comput., 2017, 13, 3586–3601 CrossRef PubMed.
- J. Zhu, T. Kurahashi, H. Fujii and G. Wu, Chem. Sci., 2012, 3, 391–397 RSC.
- M. Pascual-Borras, X. Lopez, A. Rodriguez-Fortea, R. J. Errington and J. M. Poblet, Chem. Sci., 2014, 5, 2031–2042 RSC.
- D. Marchione, M. A. Izquierdo, G. Bistoni, R. W. A. Havenith, A. Macchioni, D. Zuccaccia, F. Tarantelli and L. Belpassi, Chem.–Eur. J., 2017, 23, 2722–2728 CrossRef CAS PubMed.
- E. Lam, A. Comas-Vives and C. Copéret, J. Phys. Chem. C, 2017, 121, 19946–19957 CAS.
- D. P. Estes, C. P. Gordon, A. Fedorov, W. C. Liao, H. Ehrhorn, C. Bittner, M. L. Zier, D. Bockfeld, K. W. Chan, O. Eisenstein, C. Raynaud, M. Tamm and C. Copéret, J. Am. Chem. Soc., 2017, 139, 17597–17607 CrossRef CAS PubMed.
- C. McDade, J. C. Green and J. E. Bercaw, Organometallics, 1982, 1, 1629–1634 CrossRef CAS.
- H. van der Heijden and B. Hessen, J. Chem. Soc., Chem. Commun., 1995, 145–146 RSC.
- R. H. Grubbs and G. W. Coates, Acc. Chem. Res., 1996, 29, 85–93 CrossRef CAS.
- M. Brookhart, M. L. H. Green and G. Parkin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914 CrossRef CAS PubMed.
- O. Eisenstein and Y. Jean, J. Am. Chem. Soc., 1985, 107, 1177–1186 CrossRef CAS.
- T. A. Albright, J. K. Burdett and M.-H. Whangbo, Orbital Interactions in Chemistry, Wiley VCH, Weinheim, 2nd edn, 2013 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental and computational details, NMR spectra, results of NMR calculations and NCS analysis, graphical representation of shielding tensors, molecular orbital diagrams of selected compounds, optimized structures for all calculated species. See DOI: 10.1039/c7sc05039a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |