Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Internal standards in inductively coupled plasma mass spectrometry using kinetic energy discrimination and dynamic reaction cells†
Marcus
Korvela
,
Marit
Andersson
and
Jean
Pettersson

Department of Chemistry-BMC, Analytical Chemistry, Uppsala University, Box 599, 751 24 Uppsala, Sweden. E-mail: jean.pettersson@kemi.uu.se; Tel: +46-708351608
First published on 28th August 2018
Abstract
ICP-MS is a sensitive element analysis technique used for analyzing several different sample types. This can result in difficult matrixes which can affect both physical parameters and create overlaps of analyte elements. Some of the possible overlaps can be reduced by the use of reaction and/or collision cells, while the use of internal standards can help with reducing the physical interferences caused by a matrix. While both internal standardization and the use of cells have been studied separately, their effects on each other have not been investigated earlier. In this study ICP-MS was used to analyze 24Mg, 27Al, 47Ti, 49Ti, 51V, 52Cr, 53Cr, 55Mn, 57Fe, 59Co, 60Ni, 61Ni, 62Ni, 63Cu, 65Cu, 66Zn, 67Zn, 75As, 78Se, 82Se, 111Cd, and 208Pb with 9Be, 89Y, 69Ga, 103Rh, 115In, 193Ir, and 205Tl as internal standards with high concentrations of either HNO3, PBS-buffer, or Triton X-100 as the matrix, in reaction-, collision- and standard-cell modes. This was done to investigate which internal standards would compensate matrix effects in different cell modes. All internal standards, except Be, compensated fairly well (relative sensitivity RSD < 10%) even for severe matrix effects for most elements regardless of similarity in mass in the different cell modes. For Zn, As and Se no proper internal standard could be found, of the ones investigated.
Introduction
With the advent of the Inductively Coupled Plasma Atomic Emission Spectroscopy (ICP-AES) there was a hope that the high temperature of the plasma would make it less susceptible to the interferences that limited other elemental determination methods such as Graphite Furnace Atomic Absorption Spectroscopy and Flame Atomic Absorption Spectroscopy. While some of the interferences were removed, it still suffered from other ICP-specific interferences. Later Inductively Coupled Plasma Mass Spectrometry (ICP-MS) was developed to get better sensitivity1 and yet again there was a hope for reduction of interferences due to less complicated spectra. Once again, some improvements were made, but ICP-MS still had its fair share of interferences and matrix problems.2,3 This has been an area of interest due to the ICP-MS commonly being used to determine trace elements in several different samples with complicated matrixes like environmental, biological, industrial, and medical samples.4 To handle the many different matrixes, the analytical methods used with ICP-MS should ideally be flexible and robust while still preserving sensitivity.There are in essence two types of interferences to overcome: physical and spectral.2 The physical interferences are changes in signal intensity caused by changes in spray formation, volatilization, ionization, ion transport, etc. and spectral interferences are overlaps by isotopes of other elements, polyatomic interferences, and doubly charged ions. To get around some of the physical interferences methods such as isotope dilution, standard addition and internal standardization have been used.2 The spectral interferences have been dealt with using mathematical corrections, aerosol dilution,5,6 and different approaches where gas is added to the ion beam in a cell prior to the mass analyzer. The addition of gas follows two main approaches7 kinetic energy discrimination mode (KED) or ion–molecule reactions, in this paper referred to as dynamic reaction cell mode (DRC). With KED8 an inert collision gas, e.g. He, is used to collide with the analytes and polyatomic interferences in the ion beam, reducing the kinetic energy of all ions. This in combination with a kinetic energy threshold will generally reduce the polyatomic interferences more as they tend to have a lager cross-sectional area in comparison with the analytes, leading to a reduction or almost complete removal of some of the interferences. In DRC,9 a reactive gas like for example NH3 is used to, by charge transfers neutralize interferences or by ion/atom transfer to form new molecular ions which shift the m/z ratio of the interferences away from the m/z ratio of the analytes. Another possibility is to form polyatomic adducts with the analyte which shifts the m/z so it does not coincide with the common interferences.
Because the use of a collision or reaction cell is a rather severe change of the analyte environment, it is conceivable that it could also influence the choice of an appropriate internal standard. While several different parameters that affects the choice of internal standards in ICP-MS analysis have been investigated in several papers,10–15 to the knowledge of the authors, no systematic study has been published on how the use of DRC and/or KED affects the choice of internal standards. The reason is most likely that most authors have focused only on one or a few elements of interest and validating them together with commonly used internal standards, assuming that KED and DRC will marginally affect the choice of internal standard and that it would be detected if it was not so. While this assumption is probably true in most cases, the question if and to what extent KED and DRC generally affects the choice of internal standards remains.
Therefore this study aims to give a general overview which internal standards might be best suited for correction of the elements Mg, Al, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, As, Se, Cd, and Pb in three different types of matrixes using DRC and KED, as well as standard mode, with ICP-MS, to simulate the conditions of an unknown sample matrix. The analytes chosen were based on elements where the use of DRC and/or KED could be beneficial, with exception of Pb which was chosen as a control element due to its large mass and medium ionization energy as well as few known spectral interferences. Be, Ga, Y, Rh, In, Ir, and Tl were selected as internal standards to cover a range of different intrinsic properties such as mass and ionization energy, as well as how frequently they are used in the literature. The matrixes HNO3, PBS-buffer and Triton X-100 were selected to represent some of the different types of sample matrixes that can be commonly encountered, such as matrixes with high amounts of acid, inorganic salts and organic content respectively. The concentration range of the matrixes was chosen to be well over what is normally recommended. This was done to investigate whether internal standardization can be used to compensate for matrix effects when dilution is not an option due to low concentration of analyte in the sample.
Chemicals and solutions
All chemicals were of analytical or supra pure grade and solutions diluted with Milli-Q purified water (Millipore, Billerica, MA, USA), referred to henceforth as MQ. The nitric acid (65%, p.a, Merck) used was purified by a sub-boil distillation system (Heraeus Wittman, Heidelberg, Germany). A PBS-buffer stock solution prepared from a tablet (Sigma) diluted in 200 ml MQ was used for preparation of the PBS-buffer standard solutions. The Triton X-100 solutions were prepared by dilution from a 100% solution (Sigma). A multi element stock solution was prepared by dilution of appropriate single element stock solutions (Teknolab A/S, Drobak, Norway; Referensmaterial AB, Ulricehamn, Sweden and BDH Chemicals Ltd, Pool, England) in 5% (v/v) HNO3 and all the other standard solutions were prepared from the stock solution. An in-house prepared optimization solution containing 1 μg L−1 Be, Ce, Fe, In, Li, Mg, Pb, and U in 1% (v/v) HNO3, was used for the daily optimization procedures of the ICP-MS.Instrumental
A NexION 300D ICP-MS (Perkin Elmer, USA), using Syngistix™ 1.0 software and equipped with nickel cones, cyclonic spray chamber, ES-2040 PFA-ST MicroFlow nebulizer and standard factory tubing was used for analysis of 9Be, 24Mg, 27Al, 47Ti, 49Ti, 51V, 52Cr, 53Cr, 55Mn, 57Fe, 59Co, 60Ni, 61Ni, 62Ni, 63Cu, 65Cu, 66Zn, 67Zn, 69Ga, 75As, 78Se, 82Se, 89Y, 103Rh, 111Cd, 115In, 193Ir, 205Tl, 208Pb in each cell mode. The instrument was stabilized for at least 45 min before optimization of the system using the SmartTune™ function in the control software and the optimization solution. This procedure optimized the Ar gas flow to the nebulizer, aiming to keep doubly charged ions and oxide species (represented by Ce2+ and CeO) intensities below 0.025 of the Ce+ intensity while maintaining maximum signal intensity for In. The quadrupole ion deflector voltages were also optimized by using Be, Mg, In, Pb, and U to stepwise find the settings that maximize signal intensity over the mass range, as well as mass calibration of Li, Mg, In, and U.The MS-method used 3 replicate readings of 30 sweeps over the analyte mass-range with an integration time of 50 ms for each mass per sweep. The sample aspiration rate was 0.3 mL min−1 with a sample pre-flush of 65 s before analysis of each sample and a washing procedure after each sample with 1% HNO3 being flushed through the system for 45 s. When running the instrument in KED-mode, 4.2 ml min−1 of He gas was used and 0.9 ml min−1 of NH3 gas with a RpQ value of 0.55 when running the instrument in DRC-mode. The DRC settings were a compromise between the optimum for 57Fe and 75As, found using the instrument DRC-method development software. The measuring order for each cell was KED, DRC, and standard mode with a resting time between each mode resulting in a total measurement time of 13 min for each sample including rinsing.
Experimental
All sample preparations were done in Falcon BD polyethylene tubes and a laminar air flow bench was used to prevent contamination from airborne particles.Solutions containing Mg, Al, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, As, Se, Cd, and Pb (at concentrations of 0, 1, 5, and 10 μg L−1) were prepared for each matrix type and at three different matrix concentrations 1% (v/w), 5% (v/w), 10% (v/w) for HNO3 and PBS and 0.1% (v/w), 0.5% (v/w), 1.0% (v/w) for Triton X-100. Each solution contained at least 1% (v/w) HNO3 and 5 μg L−1 of Be, Ga, Y, Rh, In, Ir, and Tl as internal standards. Finally, solutions containing only matrix corresponding to each matrix composition were made, i.e. matrix concentration matched blanks.
All solutions were measured twice but in two separate series, with measurement order randomized within each series. The only exceptions were the samples containing only matrix and matrix with internal standard which were always measured after each other for each matrix concentration, to ensure that any background signal observed were not due to time dependent or sample order effects.
The optimization of the instrument was done to give robust16 measurement conditions (except for nebulizer gas flow) to replicate conditions present during normal usage of the instrument.
Data evaluation
Analyte elements for which the signal was not 3 times higher in the 5 ppb solutions compared to the signal of appropriate matrix concentration matched blanks and/or if intensities were below 10 cps, were not evaluated, in order to avoid interference from spectral overlaps. The internal standard elements were not evaluated if the signal intensity was less than 1% of the signal in standard mode. ANOVA calculations were done in Microsoft Excel 2012 comparing the sensitivity of each internal standard separately in the different matrixes and individually for each cell-mode, to see if the matrixes affected signal intensity. A principal component analysis (PCA), using Unscrambler 7.5 software, was done on centered ln(x)-transformed data to compare the behavior of the elements in different matrixes for each cell-mode to get a visual overview of which internal standards that could be used. The relative sensitivity (eqn (1)) was calculated for each element and internal standard combination using the average of the 5 ppb and 10 ppb solutions and then the relative standard deviation (RSD) of the relative sensitivity was calculated for all the matrix compositions in each cell-mode separately, to find out which internal standard gave the lowest RSD. A low RSD-value would indicate that the relative sensitivity was fairly consistent over matrixes, which is necessary for an internal standard to give a correct result.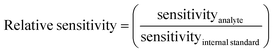 | (1) |
The concentration of the 5 ppb solution for each matrix composition and cell mode combination were calculated, using the 1% HNO3 matrix solutions as a calibration curve, with and without internal standard compensation, excluding analytes which had a squared correlation coefficient below 0.99. This was done to assess to what extent each internal standard would compensate for the different matrixes in each cell-mode when using a common calibration matrix.
Results
ANOVA
The results showed that there were significant differences (p < 0.0001) in sensitivity between matrix compositions in each cell-mode for all internal standard elements.Effects of matrix on sensitivity and evaluated results for each cell mode
The RSD-values for the relative sensitivity for the different isotopes in KED-mode (Table 1), indicated that for Fe, As, and Se there are no good internal standards (RSD-values > 10%). For the rest of the isotopes there were at least some internal standards that gave RSD-values less than 10% and for several isotopes even less than 5%.
| Isotope | <5% | <10% |
|---|---|---|
| 24Mg | Ga, Y, In | Ga, Y, Rh, In, Ir, Tl |
| 27Al | Ga, Y, Rh, In | |
| 49Ti | Y, In, Ir | |
| 51V | Ir | Ga, Y, Rh, In, Ir, Tl |
| 53Cr | Ga, Y, Rh, In, Ir, Tl | |
| 55Mn | Ga, Y, Rh, In, Ir, Tl | Ga, Y, Rh, In, Ir, Tl |
| 57Fe | ||
| 59Co | Ga, Y, Rh, In, Ir, Tl | Ga, Y, Rh, In, Ir, Tl |
| 61Ni | Rh, In, Tl | Ga, Y, Rh, In, Ir, Tl |
| 65Cu | Ga, Rh, Tl | Ga, Y, Rh, In, Ir, Tl |
| 67Zn | Be | |
| 75As | ||
| 82Se | ||
| 111Cd | Rh, In, Ir, Tl, Be | |
| 208Pb | Ga, Y, Rh, In, Tl | Ga, Y, Rh, In, Ir, Tl |
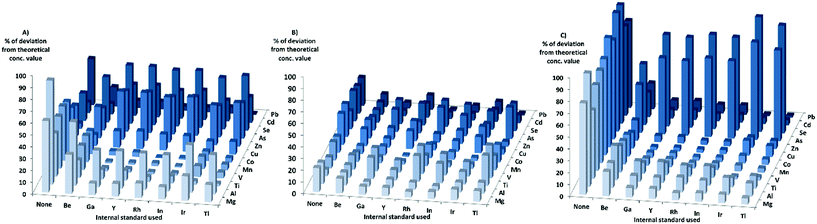
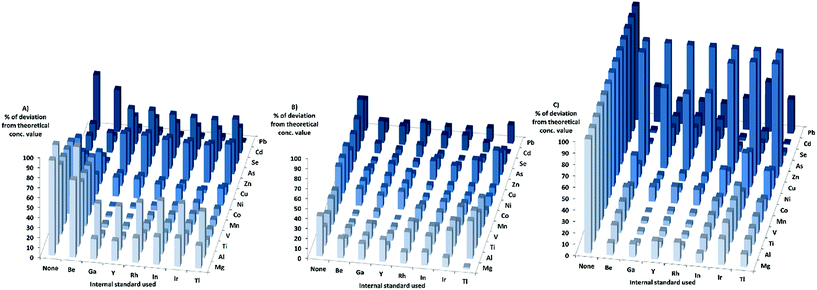
When looking at the matrixes separately with KED, for the HNO3-matrix, the sensitivity increased for most elements and internal standards with increasing matrix concentration. For Cr, Ni, and Cd the sensitivity increase was not as high compared to the other elements, while the sensitivity of Zn, Se, and As decreased when the matrix concentration was increased. When using the HNO3-matrix calibration to calculate the concentrations and comparing the absolute deviation from the theoretical values in KED-mode and HNO3-matrix (Fig. 2) Mg, Al, Ti, V, Mn, Co, Cu, and Pb showed an improvement with the internal standards. For Zn, As, Se and Cd no improvement could be observed, but rather there were increases in absolute deviation from the theoretical values when internal standards were used. It could also be seen that Ga, Y, Rh, and In gave lower absolute errors for most elements compared to Tl, Ir, and Be (which gave the least beneficial effect).
In the PBS-matrix with KED, the sensitivity decreased for all elements with increasing concentration of PBS. For the PBS-matrix (Fig. 2) there was an improvement when internal standards were used for all elements except Ti, V, and As, probably due to the lesser decrease in sensitivity. While the absolute errors were lower in comparison with the HNO3-matrix, the variation in absolute error was somewhat higher between different internal standards for a single element.
In the Triton-matrix in KED mode, all elements gained in sensitivity with increasing Triton concentration. The absolute deviations from theoretical concentration in the Triton-matrix in KED mode (Fig. 2) were lower for all elements when internal standards were used. The internal standards gave similar absolute error values for most elements, except for Be which gave the higher absolute errors for the analyte elements with the exception of As and Se, for which it gave the lowest absolute errors most likely due to higher increase in sensitivity.
The RSD-values for the relative sensitivity for the different isotopes in DRC-mode (Table 2) resulted in only Cu and Pb having RSD-values lower than 5% with some internal standards. In total only roughly, half of the isotopes had RSD-values less than 10% for at least two internal standards, while for Al, V, Cr, Fe, Zn, and Se there was no good internal standard.
| Isotope | <5% | <10% |
|---|---|---|
| 24Mg | Ga, Rh, In, Tl | |
| 27Al | ||
| 51V | ||
| 53Cr | ||
| 55Mn | Ga, In | |
| 57Fe | ||
| 59Co | Ga, In | |
| 61Ni | Ga, In | |
| 65Cu | Rh, Tl | Ga, Rh, In, Tl |
| 67Zn | ||
| 75As | Ga, In, Tl | |
| 82Se | ||
| 111Cd | In, Tl | |
| 208Pb | Ga, Rh, In, Tl | Ga, Rh, In, Tl |
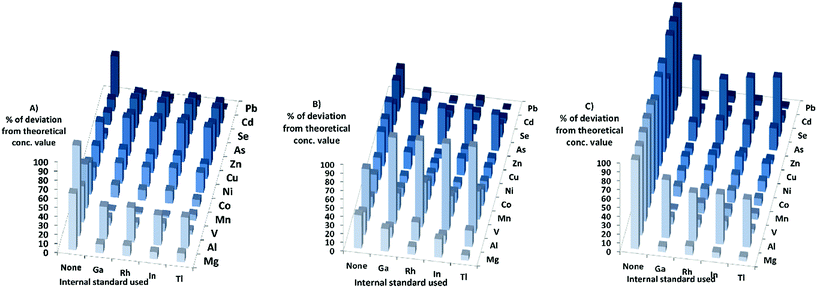
When it comes to the different matrixes in DRC-mode, for the HNO3-matrix the sensitivity increased for all elements, except Zn, As, and Se. The calculated concentrations in DRC-mode with HNO3-matrix calibration (Fig. 4) were closer to the theoretical values when internal standards were used for most elements except Ni, Zn, As, Se and Cd. The effects of using internal standards were roughly the same regardless of internal standard chosen.
When the PBS-matrix concentration was increased, in DRC-mode, V gained in sensitivity, while both Cr and Co were barely affected, and all other elements lost sensitivity. For the absolute errors in the PBS-matrix (Fig. 4) there was an improvement when using internal standards compared to not using them, for all elements except V, Cr, and Mn and all internal standards gave roughly the same absolute error.
For the Triton-matrix in DRC-mode an increase in matrix concentration led to an increase in sensitivity for all elements. The absolute errors (Fig. 4) for all elements were lower when internal standards were used, and the effects of the internal standards were similar regardless of internal standard used.
In standard-mode the RSD-values for the relative sensitivity (Table 3) were lower than 10% for most isotopes with several internal standards, except for Zn, As, and Se. For roughly half of the isotopes at least one internal standard could be found where the RSD-values were lower than 5%.
| Isotope | <5% | <10% |
|---|---|---|
| 24Mg | Ga, Y, Rh, In, Ir, Tl | |
| 27Al | Ga, Y, Rh, In, Ir, Tl | |
| 49Ti | Y | Ga, Y, Rh, In, Ir |
| 51V | Y, In | Ga, Y, Rh, In, Ir, Tl |
| 53Cr | Ga, Y, Rh, In, Ir, Tl | |
| 55Mn | Ga, Y, Rh, In | Ga, Y, Rh, In, Ir, Tl |
| 59Co | Ga, Y, Rh, In | Ga, Y, Rh, In, Ir, Tl |
| 61Ni | Ga, Rh | Ga, Y, Rh, In, Tl |
| 65Cu | Rh | Ga, Y, Rh, Ir, Tl |
| 67Zn | ||
| 75As | ||
| 82Se | ||
| 111Cd | Be | In, Ir, Be |
| 208Pb | Tl | Ga, Y, Rh, In, Ir, Tl |
The HNO3-matrix in standard-mode had an increase in sensitivity for most elements with increasing matrix concentration. The increase in sensitivity for As and Cd was minor, while Zn and Se lost sensitivity when the matrix concentration was increased. The calculated concentrations for the HNO3-matrix (Fig. 6) were closer to the theoretical concentration values for most elements when internal standards were used. Though for Zn, As, Se, and Cd the effects of the internal standards were the opposite, except for As and Cd, when Be was used as an internal standard. The effects of using internal standards were roughly the same regardless of internal standard chosen, except for Be which gave the highest absolute error for most elements.
An increase in matrix concentration of PBS in standard mode resulted in loss of sensitivity for all elements. The absolute deviation (Fig. 6) was lower when Be, Ga, Y, Rh, or In were used as internal standards for all elements. While the use of Ir and Tl as internal standards improved the absolute values for some elements, it resulted in higher absolute deviations for others.
For the Triton-matrix in standard-mode, the sensitivity of all elements increased with increasing matrix concentration. The absolute deviation for all elements were lower when internal standards were used, but for As, and Se absolute deviations were still close to 100% of the theoretical concentration. Ga, Y, and Rh gave better results for lower mass elements while Be, In, Ir, and Tl gave better results for higher mass elements.
Discussion
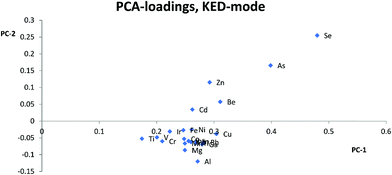
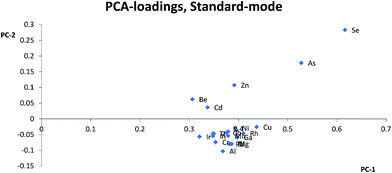
Most studies10,12,15,17 have suggested that similarities in mass is the most important parameter for selection of internal standards, while others suggest that both mass and ionization energy11 are important for the choice of internal standards. In this study, Zn, As, Se, and Cd were separated from the other elements and internal standards clustered together in the PCA loadings for KED- and standard-mode. In DRC-mode the same pattern was only observed for Zn and Se. This indicates that none of the internal standards investigated are ideally suited to compensate for matrix effects for these elements. The problems with Zn, As, and Se also suggests that mass similarity is not always a robust factor for prediction of the effectiveness of an internal standard, as well as the fact that mass did not seem a critical factor for any other element. When comparing the PCA loading plots with the RSD-values for the relative sensitivity, there was a good agreement between them, but one cannot always use the clusters from the PCA to predict to which extent and whether an element will benefit from the use of a specific internal standard. For example in KED-mode, comparing the position of Al, Mg, and Cu it is hard to say which element would benefit from one of the internal standards and to what extent. Similarly, from the same PCA there seems to be many internal standards that could be used for Fe, but according to Table 1 no internal standard is suitable. This is most likely due to low intensities combined with the ln-transformation. While RSD-values of 10% might seem a bit high, it is worth considering that they are the result of using very high matrix concentration far outside what is normally recommended for analysis. As such the results point to several internal standards can be used to compensate for rough matrixes, at an acceptable level, with little regard to the actual m/z difference between internal standard and analyte element. While this goes against earlier convention of choice in internal standardization it does agree with studies using more modern equipment.18One could have suspected that the KED-mode should have been more affected by m/z differences between internal standard and analyte elements due to the effects of the initial kinetic energy and collision rate of ions and the He-gas. The difference in the collision rate could lead to a less efficient compensation effect of the internal standard with an increase in m/z difference. While there were clear differences in signal loss ratio, between KED- and standard-mode, depending on size and m/z for each element the ratios were consistent enough so that there were little to no effect on which internal standard would be preferable to use.
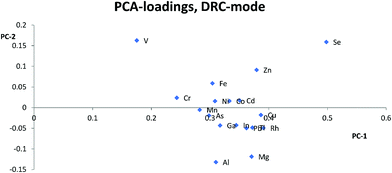
For the DRC-mode it was problematic to find good internal standards for most elements, compared to the KED-mode. Aside from the fact that Y and Ir were theoretically not likely to work,19 this most likely stems from the fact that you have reactions taking place in the cell with different kinetics and possible cluster formation involved, resulting in even more parameters for an internal standard to compensate for, in comparison to other cell modes. To minimize these problems each matrix blank, with and without, internal standard was checked so that there was no overlap of the used internal standards from matrix elements. Each internal standard was also checked for a linear increase in signal for the analyte containing solutions within the same matrix concentration. As the internal standard had a constant concentration a linear intensity gain correlating with analyte concentration would indicate of cluster formation with at least one analyte leading to an overlap and such an internal standard could not be used. This means that it becomes even harder to, without prior knowledge of the sample composition, to designate what would work as a good internal standard when using the DRC-mode, compared to KED-mode.
Usually Zn, As, and Se clustered together away from the other elements in the PCA loadings and since the trend is seen across all cell modes used it is not only due to the application of collision or reaction gas. The most likely reason for this difference is that Zn, As, and Se have higher ionization energies, between 9.39 eV and 9.79 eV, compared to the other analyte elements which have ionization energies between 5.99 eV(Al) and 8.99 eV(Cd). The higher ionization energy makes elements like Zn, As, and Se more susceptible to both suppressing and enhancing effects that a matrix can have on the ionization properties of a plasma. Therefore, elements with high ionization energies could behave quite differently to elements with lower ionization energies especially if a matrix suppresses ionization, but increases the signal through other effects, or vice versa. An example of this can be seen with Zn, As and Se in HNO3-matrix compared to other elements with lower ionization energies. While Zn, As, and Se almost always lose sensitivity, all the other elements gain in sensitivity with increasing HNO3-matrix concentration. And as seen in the calculated absolute errors there is an increase in deviation from the theoretical value for Zn, As, and Se if any of the internal standards is used, while for the other elements the use of internal standards leads to an improvement.
As discussed by Grindlay et al. different carbon species have different capabilities to improve the ionization of high ionization energy elements such as Zn, As, and Se,20 which adds another level of complexity to the choice of internal standards for such elements, i.e. it is not absolutely certain when or if elements will be affected by ionization changes in the plasma caused by the matrix. This is most likely the reason why Zn, As, and Se don't behave in a similar manner to either Be or Ir, both which are relatively hard to ionize at 9.23 eV and 8.97 eV respectively. While this could possibly have been explained by the high difference in mass between the elements, it is not likely because such a dependence on mass is not seen for Cd with the HNO3-matrix, in both KED- and standard-mode, where Be is superior to the other internal standards that are closer to Cd in mass. While it has been shown before that finding an internal standard can be problematic for As and Se,21 the results in this study indicate that it is hard to pin down exactly when the ionization energy is important or how large difference will lead to different behavior in a certain matrix, as seen for the behavior of Zn. Therefore, it is unwise to try to simply categorize elements into high and low ionization energy elements, but rather one should be extra careful when analyzing such elements in unknown or complicated matrixes.
Conclusion
As Finley-Jones et al. previously have pointed out,10 it's hard to give recommendations on which internal standards to use, based only on intrinsic properties such as mass and ionization energy. In this study, similar results could be obtained for most elements even under conditions with high matrix concentration regardless of whether Ga, Y, Rh, In, Ir or Tl is chosen as an internal standard. This indicates that mass is not a critical parameter, regardless of cell-mode used. The only cell specific problems are for DRC though, as the choice of internal standard is affected by possible heavy signal loss or overlap from cluster formation. Ionization energy on the other hand was shown to be an important parameter for hard to ionize elements such as Zn, As and Se, but only as a possible indicator that no good internal standard could be found among the ones used in this study.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to greatly acknowledge Rolf Danielsson for valuable data evaluation discussions, especially principal component analysis.References
- R. S. Houk, V. A. Fassel, G. D. Flesch, H. J. Svec, A. L. Gray and C. E. Taylor, Anal. Chem., 1980, 52, 2283–2289 CrossRef.
- C. Agatemor and D. Beauchemin, Anal. Chim. Acta, 2011, 706, 66–83 CrossRef PubMed.
- S. H. Tan and G. Horlick, J. Anal. At. Spectrom., 1987, 2, 745–763 RSC.
- D. Pröfrock and A. Prange, Appl. Spectrosc., 2012, 66, 843–868 CrossRef PubMed.
- A. I. Barros, F. C. Pinheiro, C. D. B. Amaral, R. Lorençatto and J. A. Nóbrega, Talanta, 2018, 178, 805–810 CrossRef PubMed.
- F. C. Pinheiro, R. Lorençatto, A. I. Barros, C. D. B. Amaral and J. A. Nóbrega, J. Braz. Chem. Soc., 2018, 29, 1570–1578 Search PubMed.
- S. D. Tanner, V. I. Baranov and D. R. Bandura, Spectrochim. Acta, Part B, 2002, 57, 1361–1452 CrossRef.
- N. Yamada, Spectrochim. Acta, Part B, 2015, 110, 31–44 CrossRef.
- D. R. Bandura, V. I. Baranov and S. D. Tanner, Fresenius. J. Anal. Chem., 2001, 370, 454–470 CrossRef PubMed.
- H. J. Finley-Jones, J. L. Molloy and J. A. Holcombe, J. Anal. At. Spectrom., 2008, 23, 1214–1222 RSC.
- J. J. Thompson and R. S. Houk, Appl. Spectrosc., 1987, 41, 801–806 CrossRef.
- F. Vanhaecke, H. Vanhoe, R. Dams and C. Vandecasteele, Talanta, 1992, 39, 737–742 CrossRef PubMed.
- C. Sartoros and E. D. Salin, Spectrochim. Acta, Part B, 1999, 54, 1557–1571 CrossRef.
- Y.-S. Kim, H. kawaguchi, T. Tanaka and A. Mizuike, Spectrochim. Acta, Part B, 1990, 45, 333–339 CrossRef.
- W. Doherty, Spectrochim. Acta, Part B, 1989, 44, 263–280 CrossRef.
- J. W. Tromp, M. Pomares, M. Alvarez-Prieto, A. Cole, H. Ying and E. D. Salin, Spectrochim. Acta, Part B, 2003, 58, 1927–1944 CrossRef.
- H. J. Finley-Jones and J. A. Holcombe, J. Anal. At. Spectrom., 2009, 24, 837–841 RSC.
- J. W. Olesik and S. Jiao, J. Anal. At. Spectrom., 2017, 32, 951–966 RSC.
- D. K. Bohme, http://www.chem.yorku.ca/profs/bohme/research/molecule/NH3.html, accessed 27/07, 2018.
- G. Grindlay, J. Mora, M. de Loos-Vollebregt and F. Vanhaecke, Spectrochim. Acta, Part B, 2013, 86, 42–49 CrossRef.
- J. Goossens, F. Vanhaecke, L. Moens and R. Dams, Anal. Chim. Acta, 1993, 280, 137–143 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ja00171e |
| This journal is © The Royal Society of Chemistry 2018 |