Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bioconcentration, bioaccumulation, biomagnification and trophic magnification: a modelling perspective
Donald
Mackay
a,
Alena K. D.
Celsie
 *ab,
David E.
Powell
c and
J. Mark
Parnis
*ab,
David E.
Powell
c and
J. Mark
Parnis
 ab
ab
aChemical Properties Research Group, Department of Chemistry, Trent University, Peterborough, ON K9L OG2, Canada. E-mail: alenacelsie@trentu.ca
bChemistry Department, Queens University, Kingston, ON K7L 3N6, Canada
cPER Consulting, Midland, MI 48642, USA
First published on 8th December 2017
Abstract
We present a modelling perspective on quantifying metrics of bio-uptake of organic chemicals in fish. The models can be in concentration, partition ratio, rate constant (CKk) format or fugacity, Z and D value (fZD) format that are shown to be exactly equivalent, each having it merits. For most purposes a simple, parameter-parsimonious one compartment steady-state model containing some 13 parameters is adequate for obtaining an appreciation of the uptake equilibria and kinetics for scientific and regulatory purposes. Such a model is first applied to the bioaccumulation of a series of hypothetical, non-biotransforming chemicals with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW (octanol–water partition ratio) values of 4 to 8 in 10 g fish ranging in lipid contents to deduce wet-weight and lipid normalized concentrations, bioaccumulation and biomagnification factors. The sensitivity of biomagnification factors to relative lipid contents is discussed. Second, a hypothetical 5 species linear food chain is simulated to evaluate trophic magnification factors (TMFs) showing the critical roles of KOW and biotransformation rate. It is shown that lipid normalization of concentrations is most insightful for less hydrophobic chemicals (log
KOW (octanol–water partition ratio) values of 4 to 8 in 10 g fish ranging in lipid contents to deduce wet-weight and lipid normalized concentrations, bioaccumulation and biomagnification factors. The sensitivity of biomagnification factors to relative lipid contents is discussed. Second, a hypothetical 5 species linear food chain is simulated to evaluate trophic magnification factors (TMFs) showing the critical roles of KOW and biotransformation rate. It is shown that lipid normalization of concentrations is most insightful for less hydrophobic chemicals (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW < 5) when bio-uptake is largely controlled by respiratory intake and equilibrium (equi-fugacity) is approached. For more hydrophobic chemicals when dietary uptake kinetics dominate, wet weight concentrations and BMFs are more insightful. Finally, a preferred strategy is proposed to advance the science of bioaccumulation using a combination of well-designed ecosystem monitoring, laboratory determinations and modelling to confirm that the perceived state of the science contained in the models is consistent with observations.
KOW < 5) when bio-uptake is largely controlled by respiratory intake and equilibrium (equi-fugacity) is approached. For more hydrophobic chemicals when dietary uptake kinetics dominate, wet weight concentrations and BMFs are more insightful. Finally, a preferred strategy is proposed to advance the science of bioaccumulation using a combination of well-designed ecosystem monitoring, laboratory determinations and modelling to confirm that the perceived state of the science contained in the models is consistent with observations.
Environmental significanceIt is internationally accepted that the three principal criteria for evaluating the adverse environmental effects of chemicals are: P persistence, B bioaccumulation and T toxicity. Here we address B and show that the use of simple and commonly accepted criteria for B can be flawed, especially for hydrophobic substances. We argue that mass balance models can contribute significantly to B assessments, especially when combined with laboratory tests under controlled conditions and well-designed monitoring programs. As specific examples, we present a modeling perspective on bioaccumulation factors of hypothetical relatively hydrophobic chemicals in a series of small fish ranging in lipid contents. We deduce wet-weight and lipid-normalized concentrations, bioaccumulation factors and biomagnification factors. We discuss the implications of lipid contents, which have unappreciated effects on both wet-weight and lipid-weight concentrations and their ratios. It is shown that lipid normalization of concentrations is more insightful for less hydrophobic chemicals (i.e. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW < 5) because bio-uptake is largely controlled by respiratory intake and equilibrium is approached, implying that lipid normalized concentration ratios are more insightful and less variable. On the contrary, for very hydrophobic chemicals dietary uptake kinetics dominate, and wet weight concentrations are more insightful, especially when estimating trophic magnification factors that are increasingly applied for regulatory purposes, often without a full appreciation of their inherent variability and uncertainties. We suggest strategies to advance the science of bioaccumulation, including more data on partitioning ratios for key biological tissues and the acquisition of more data on sediment/water concentration and fugacity ratios, spatial and temporal variabilities, reproductive losses and changing diets as a function of growth. KOW < 5) because bio-uptake is largely controlled by respiratory intake and equilibrium is approached, implying that lipid normalized concentration ratios are more insightful and less variable. On the contrary, for very hydrophobic chemicals dietary uptake kinetics dominate, and wet weight concentrations are more insightful, especially when estimating trophic magnification factors that are increasingly applied for regulatory purposes, often without a full appreciation of their inherent variability and uncertainties. We suggest strategies to advance the science of bioaccumulation, including more data on partitioning ratios for key biological tissues and the acquisition of more data on sediment/water concentration and fugacity ratios, spatial and temporal variabilities, reproductive losses and changing diets as a function of growth.
|
1 Introduction
Bioaccumulation of organic substances is an important component of chemical risk assessment for both scientific and regulatory purposes. Chemical concentrations in biota that are orders of magnitude larger than those in water and air are important for several reasons. Such large concentrations may adversely affect organisms across food webs, especially if internal concentrations reach toxic levels. Rather than measure the usually low concentrations in water or air it may be preferable to measure the relatively higher concentrations in biota resulting from bioaccumulation, but this requires information on the magnitude and determinants of these relative concentrations. Studies of bioaccumulation fall generally into one of the following categories: ecosystem monitoring, laboratory tests under controlled conditions, mass balance modelling, and in vivo and in vitro ADME studies. In this contribution we address insights that can be gained from modelling focusing primarily on aquatic organisms that respire in water and sediments but recognizing that similar principles apply to air-breathing mammals, birds, and reptiles. In Table 1 we define the bio-uptake factors and terminology employed herein and widely used in modelling and monitoring studies.1–5 The bioconcentration factor (BCF) expresses the increase in concentration, but with little or no increase in fugacity as measured in tests such as OECD 305.6 The bioaccumulation factor (BAF) includes a further concentration increase as well as a fugacity increase. It can be viewed as the product of the BCF and a ‘multiplier’ dependent on the BAF of the diet and the ratio of the rates of dietary uptake and respiratory uptake.7 The biomagnification factor BMF is essentially the ratio of the BAFs of the predator and the prey and may involve an increase in both concentration and fugacity. The TMF as the slope of the log concentration vs. trophic position is related to the mean BMF of the species comprising the food web. Considerable literature exists on these factors and especially BMFs and TMFs that may yield the highest concentrations and exposures.8–12 In the terminology of MacDonald et al.,13 a BCF represents solvent switching from water to lipid at a constant fugacity, while BAF, BMF and TMF represent additional solvent depletion as the ingested lipid solvent is hydrolysed causing an increase in fugacity.| Bio-uptake factors | Definition |
|---|---|
| Bioconcentration factor (BCF) | Ratio of fish to water concentrations with no dietary intake |
| Bioaccumulation factor (BAF) | Ratio of fish to water concentrations with dietary intake |
| Biomagnification factor (BMF) | Ratio of fish to diet concentrations |
| Trophic magnification factor (TMF) | Averaged BMF over a food web of several trophic levels |
In Table 1 the water concentration may be of whole water or (as in this study) only truly dissolved chemical. Biotic concentrations may be expressed as wet weight or lipid normalized quantities or they may be specific to defined tissues. Trophic magnification factors are generally obtained from the slope of a plot of log lipid normalised concentrations vs. trophic position or level, the latter being deduced from 15N measurements.8,14,15
It is obviously critical to define the concentration units derived from the mass balance equations for comparison with monitoring data. The most commonly used units are whole body (wet weight) CFW and lipid-normalized CFL concentrations where CFL equals CFW/L, and L is the lipid content. Here, subscript F refers to the organism (fish), W to wet weight and L to lipid normalised.
Homogenizing the whole fish, and using a standard method of lipid extraction may be used to determine these concentrations. It can be experimentally demanding to homogenize large fish, thus it may be convenient to analyse only part of the carcass; for example, a fillet that is largely muscle and is preferred for human consumption. The concentration in a fillet can be significantly different from that of the whole fish and this difference also applies to lipid-normalized concentrations because the lipid content of the fillet is usually much lower than that of the whole fish. For example, Niimi and Oliver16 obtained such data for PCBs in rainbow trout and showed that for the more recalcitrant congeners (penta- to deca-chloro) the muscle concentrations CFM (ng g−1 ww) averaged a factor of 3.84 lower than that of the whole fish concentrations CFW (ng g−1 ww). This is largely attributable to differences in the reported lipid content of 9.8% in the whole fish and 1.7% in muscle, a factor of 5.76. For example, if CFW is 100 ng g−1 ww then CFM may be approximately 100/3.84 or 26 ng g−1 ww. The corresponding lipid-normalized wet-weight and muscle concentration will be respectively 26/0.098 or 1020 ng g−1 lw and 26/0.017 or 1532 ng g−1 lw, a factor of 5.76/3.84 or 1.5 difference. Lipid-normalized muscle or fillet concentrations are thus likely to be significantly larger than lipid-normalized wet-weight concentrations for substances such as PCBs.
Another complication is the simplifying assumption that hydrophobic chemicals partition only to lipids. It is generally accepted that there is appreciable partitioning into other non-lipid phases such as protein. For example, the ratio of protein to lipid partition coefficients with respect to water being of the order of 0.03![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 implying that less chemical partitions into protein tissue compared with lipid. It follows that if the fillet protein content is much higher than that of the lipid, much of the solute will reside in the protein phase. The lipid-normalized concentration would then be over-estimated. Finally, there can be concerns about the accuracy of lipid content measurements, especially at low lipid levels as may occur in planktonic organisms of low lipid content for which the lipid-normalized concentrations are much larger than wet weight concentrations and are very sensitive to errors in lipid measurement. Endo, Goss and Brown17–19 have demonstrated that partitioning to different biotic phases is more accurately evaluated using Abraham or poly-parameter LFER methods rather than simple octanol–water partitioning (KOW). We assume, however, that for the present screening-level purposes, the lipid–water partition coefficient is approximately equal to the octanol–water partition coefficient KOW, recognizing that this is a significant simplification and does not apply to all chemicals, nor to all lipids.
1 implying that less chemical partitions into protein tissue compared with lipid. It follows that if the fillet protein content is much higher than that of the lipid, much of the solute will reside in the protein phase. The lipid-normalized concentration would then be over-estimated. Finally, there can be concerns about the accuracy of lipid content measurements, especially at low lipid levels as may occur in planktonic organisms of low lipid content for which the lipid-normalized concentrations are much larger than wet weight concentrations and are very sensitive to errors in lipid measurement. Endo, Goss and Brown17–19 have demonstrated that partitioning to different biotic phases is more accurately evaluated using Abraham or poly-parameter LFER methods rather than simple octanol–water partitioning (KOW). We assume, however, that for the present screening-level purposes, the lipid–water partition coefficient is approximately equal to the octanol–water partition coefficient KOW, recognizing that this is a significant simplification and does not apply to all chemicals, nor to all lipids.
Lipid-normalized concentrations prove to be very convenient when comparing concentrations between species in food webs, in part because they are proportional to fugacities, thus the equilibrium status of a chemical between water, sediment and organisms comprising food webs can be revealed by comparing lipid normalized or organic carbon normalized concentrations. Obviously, CFW for one fish should not be compared with CFL for another. This issue can become critical when calculating BMFs and TMFs that necessarily involve comparison of concentrations between prey and predator fish. Common practice is to measure and report both wet-weight and lipid-normalized concentrations along with the identity of the tissues analysed and the measured lipid contents.
2 Background
2.1 Evolution of bio-uptake models
Models of bioaccumulation have evolved considerably from the early bioconcentration work of Neely et al.20 More comprehensive dietary and respiratory uptake models such as that of Thomann21 address biomagnification in which the predators achieve higher concentrations than their prey.1,2 An issue common to all environmental models is the optimal number of compartments. To achieve greater fidelity to reality the number of compartments may be increased, but this is at the expense of requiring additional parameters and their associated uncertainties, especially those controlling inter-compartment transport and partitioning. A balance is needed between complexity and parsimony as dictated by the nature of the application as discussed by several authors.22,23 The currently preferred strategy is to use as parsimonious a model as possible consistent with satisfying the modelling objective.It is common to refer to one-compartment models in which there is no attempt to describe differences in internal distributions. Rates of input by respiration and dietary uptake are defined using a gross input rate and uptake efficiencies. This implies the existence of an external compartment in which there is a split between absorbed and non-absorbed chemical. It can be argued that the simple one-compartment model actually contains three compartments in which only the splitting performance of the two external compartments is defined, thus simplifying the model. If the chemical is subject to biotransformation in the gut as described by Lo and Gobas10 or the chemical properties change in response to pH variation during respiration as described by Erikson et al.,24–26 then it is essential to define the mass balances in these ‘external’ compartments.
For toxicokinetic and toxicodynamic or PBPK models in which uptake or effects in a target organ are evaluated it is essential to include that compartment explicitly.17,27 An extreme example is the recent model by Larisch et al.28 that treats 10 internal organs and 3 external organs.
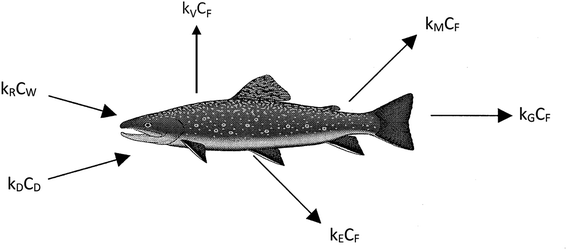
We believe a consensus has emerged that for many practical purposes a simple and parameter-parsimonious one compartment steady-state model with chemical uptake efficiencies is adequate to obtain an inherent appreciation of the dynamic uptake and loss processes as shown in Fig. 1. Exceptions to these processes are likely to occur when fish forage in regions that have particularly high or low contaminant concentrations, when spawning, or when losing large amounts of body mass in the winter.
The primary compartment of concern is the body, the organs, and the tissues, but it is essential to address chemical transport ‘splitting’ in the gut and the gill cavity as separate absorption efficiencies. The processes corresponding to the arrows in Fig. 1 can be expressed in conventional concentration-partition ratio, rate constant (CKk) or in fugacity-Z value, D value (fZD) format, but they are, or should be, algebraically equivalent.
The conventional differential and steady-state equations for uptake in CKk format are given in eqn (1)–(4), the various parameters being defined in Table 2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 6.0. Abbreviation for wet weight is ww and abbreviation for lipid weight is lw
KOW of 6.0. Abbreviation for wet weight is ww and abbreviation for lipid weight is lw
| Quantity | CKk format (units) | Value | fDZ format | Value |
|---|---|---|---|---|
| Chem. molar mass | MW (kg mol−1) | 0.1 | MW (kg mol−1) | 0.1 |
| Oct–water partition ratio | K OW | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
K OW = ZO/ZW | 1 × 106 |
| Fish size | M F (kg) | 0.01 | V F (m3) | 0.00001 |
| Lipid content of diet | L D | 0.05 | L D | 0.05 |
| Lipid content of fish | L F | 0.10 | L F | 0.10 |
| Z W = 1/H | 0.1 | |||
| Z O = ZW·KOW | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||
| Z D = LD·ZO | 5000 | |||
| Z f = LF·ZO | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||
| Equilibrium BCF | K OW·LF | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Z F/ZW | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Net respiration rate | G V (L per day) | 5 | G V (m3 per day) | 0.005 |
| Net feeding rate | G f (kg per day) | 0.0006 | G f (m3 per day) | 0.6 × 10−6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Transport parameters | ||||
| Q values diet/egestion | Q C = kD/kE | 6 | Q f = DD/DE = QC·ZD/ZF | 3 |
| Respiratory intake | k R (L/kg per day) | 500 | D R = GV·ZW | 0.0005 |
| Dietary intake | k D (L/kg per day) | 0.06 | D D = GF·ZD | 0.003 |
| Respiratory loss | k V = kR/BCF (days) | 0.005 | D V = DR | 0.0005 |
| Egestion | k E ∼ kD/QC (days) | 0.01 | D E = VF·ZF·kE | 0.001 |
| Biotransformation | k M, (days) | 0.01 | D M = VF·ZF·kM | 0.001 |
| Growth dilution | k G, (days) | 0.0025 | D G = VF·ZF·kG | 0.00025 |
| Total loss rate | kT = kV + kE + kM + kG | 0.0275 | D T = DV + DE + DM + DG | 0.00275 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Exposure quantities | ||||
| Water concentration | C W (mg L−1 or g m−3) | 0.001 | C W (mol m−3) | 0.00001 |
| Diet/water fugcity ratio | f D/fW | 1.5 | ||
| Diet concentration ww | C DW (mg kg−1, g m−3) | 75 | C DW (mol m−3) | 1.125 |
| Diet concentration lw | C DL (mg kg−1) | 1500 | C DL (mol m−3) | 22.5 |
| Water fugacity | f W (Pa) | f W = CW/ZW | 0.0001 | |
| Diet fugacity | f D (Pa) | f D = CDW/ZD | 0.00015 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Calculated quantities | Eqn (1)–(4) | Eqn (5)–(8) | ||
| Fish fugacity | f F (Pa) | 0.00018 | f F = CFW/ZF | 0.000182 |
| Fish lipid fugacity | f L (Pa) | f L = CFL/ZL | 0.000182 | |
| Fish concentration ww | C FW (mg kg−1, eqn (3)) | 181.82 | C FW = fF·ZF (mol m−3) | 1.8182 |
| Fish concentration lw | C FL = CFW/LF (mg kg−1) | 1818.2 | C FL = fF·ZO (mol m−3) | 18.182 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Bio-uptake factors | ||||
| Bioacc. factor ww BAFW | BAFW = CFW/CW | 181![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818.2 818.2 |
||
| Bioacc. factor lw BAFL | BAFL = CFL/CW | 181![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8182 8182 |
||
| Biomag. fact. ww BMFW | BMFW = CFW/CDW | 2.4242 | ||
| Biomag. fact. lw BMFL | BMFL = CFL/CDL | 1.2121 | ||
| Chem. quantity in fish | C FW × MF (mg) | 1.81 | V·ZF·fF mol | 1.82 × 10−5 |
| Total uptake rate | (mg per day) | 0.05 | mol per day | 5 × 10−7 |
| Half-time |
τ = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/kT, (days) 2/kT, (days) |
25.2 |
τ = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2·VF·ZF/DT 2·VF·ZF/DT |
25.2 |
Mass balance uptake differential equation in CKk format is:
| ΔCFW/Δt = (kRCw + kDCD) − CFW(kV + kE + kM + kG) | (1) |
| CFW = [(kRCW + kDCD)/kT] × [1 − ekTt] | (2) |
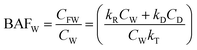 | (3) |
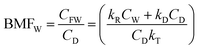 | (4) |
For hydrophobic chemicals when CD is large and kD ≫ kRCW/CD, BMFW approaches kD/kT.
Further, for a slowly metabolized, hydrophobic chemical in a slow-growing fish kE ≫ (kV + kM + kG), BMFW approaches kD/kE defined here as QC the ratio of dietary uptake and egestion rate constants.
The analogous uptake equations in fZD format are as follows, where DT is the sum of the loss D values.
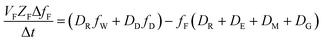 | (5) |
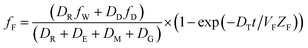 | (6) |
When DTt/VFZF ≫ 1 and steady state is approached, yielding eqn (7):
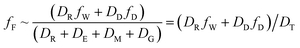 | (7) |
For less hydrophobic chemicals when DR ≫ DD, fF approaches fW, equilibrium applies, BCFW and BAFW approach ZF/ZW and are approximately equal to L·KOW where L is the fish lipid content. BMFW becomes less relevant because dietary uptake is unimportant.
On the contrary, for a persistent, hydrophobic chemical in a slow-growing fish with dietary uptake, DE ≫ (DV + DM + DG), fF approaches fD·DD/DE or fD·τ where Qf is defined as the ratio of dietary uptake and egestion D values. BAFW, CW and fW become less relevant because respiratory uptake is relatively unimportant. The lipid normalized uptake metric BMFL approaches Qf and is the ratio of the fish and diet fugacities. As before, the wet weight BMFW approaches QC and Qf·(ZF/ZD) or approximately Qf·(LF/LD). The two Q values are thus not equal and depend on the relative lipid contents of the fish (LF) and diet (LD). Qf directly expresses the increase in fugacity corresponding to biomagnification, while QC expresses the corresponding increase in concentration.
Substitution of the various rate constants and D values in Table 2 into eqn (3) and (7) demonstrates the exact equivalence of the two formats for a chemical of moderate hydrophobicity. The steady-state eqn (3) and (7) are most readily interpreted, and are of most interest for both scientific and regulatory purposes. It is relatively straightforward to apply the basic equations to multiple organisms in food webs with defined dietary preferences and to organisms that respire in sediments and the water column. The principal challenge is to obtain accurate values for the various equilibrium and rate parameters and dietary preferences.
For hydrophobic substances, the egestion loss rate constant and D value are particularly important, since as discussed later egestion along with biotransformation play a critical role in determining the extent of biomagnification. The most rigorous approach is to define the input diet and output feces compositions and rates and as relative quantities of materials such as lipids and non-lipids including protein, carbohydrate, inert fibrous material, and water and assign partition ratios relative to water for each material. An example is the Arnot and Gobas1 model that treats three materials, lipids, non-lipid organic matter (NLOM) and water in both diet and feces. Larisch et al.28 treat five materials. The capacity of the feces to absorb and transport the chemical is inevitably lower than that of the ingested diet by a factor typically ranging from 3 to 10. This factor is primarily determined by the quantities of lipid transported in food and feces, thus a simple and very approximate approach is to suggest, as in Table 2, a multiple Q in the range 3 to 10 by which the egestion rate constant kE or D value DE is less than that for the food. Inspection of the steady-state equation shows that for a persistent hydrophobic chemical in a fish that is not growing, the BMF will approach Q. It is noteworthy that QC in the CKk format is generally not equal to Qf in the fZD format, thus the BMF expressed as a whole body or wet weight concentration ratio is generally unequal to the fugacity ratio. In principle, it is possible and potentially attractive to define a Q for each material and calculate a lumped QC or Qf to deduce the egestion rate.
If there is no dietary uptake and the principal loss is by ventilation, a bioconcentration factor (BCF) can be calculated as kR/kV and equilibrium (equi-fugacity) is approached. If the very simplistic assumption is made that octanol and lipids have similar solvent properties for the chemical and lipids are the only absorbing phase, this BCF can also be estimated as the product of the fish lipid content and the octanol–water partition coefficient, namely LF·KOW. If kR is known, kV can then be estimated as approximately kR/BCF or kR/(LF·KOW). This BCF is effectively a thermodynamic partition ratio, however, it may be affected by weight gain (growth) or loss. For screening level purposes a lipid content L of 5% is often used thus a BCF of 5000 corresponds to a KOW of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 or log
000 or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 5. We accept the simplistic nature of this approach in that it applies only to a subset of chemicals. Other chemicals partition to other phases by electrostatic interactions, protein binding, and covalent bonding.
KOW of 5. We accept the simplistic nature of this approach in that it applies only to a subset of chemicals. Other chemicals partition to other phases by electrostatic interactions, protein binding, and covalent bonding.
2.2 Relationships between the CKk and fDZ mass balance equation formats
To illustrate the equivalence and relative merits of the two formats a simple spreadsheet was compiled to calculate the bio-uptake quantities from selected input parameters for a specimen chemical of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 6.0, Henry's constant 10 Pa m3 mol−1 and molar mass 100 g mol−1 in a 10 g fish of lipid content 10% with a growth rate constant of 0.0025 days. The fish is exposed to water at a concentration of 0.001 g m−3 and a diet of lipid content 0.05 g g−1 with a fugacity 1.5 times that of the water. The chemical is subject to biotransformation with a rate constant of 0.01 days−1. Respiratory and dietary uptake parameters were taken from allometric relationships used by Arnot and Gobas1 but quantities were rounded off to facilitate interpretation.
KOW of 6.0, Henry's constant 10 Pa m3 mol−1 and molar mass 100 g mol−1 in a 10 g fish of lipid content 10% with a growth rate constant of 0.0025 days. The fish is exposed to water at a concentration of 0.001 g m−3 and a diet of lipid content 0.05 g g−1 with a fugacity 1.5 times that of the water. The chemical is subject to biotransformation with a rate constant of 0.01 days−1. Respiratory and dietary uptake parameters were taken from allometric relationships used by Arnot and Gobas1 but quantities were rounded off to facilitate interpretation.
Calculations were done in both CKk and fZD formats independently and yield identical results as shown in Table 2, namely a fish wet weight concentration CFW of 182 g m−3 or 1.82 mol m−3. The corresponding lipid normalized concentrations are a factor of 10 greater. The equilibrium BCF of the fish is 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, the BAfW is 181
000, the BAfW is 181![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800, and the BAFL is 1
800, and the BAFL is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818
818![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The calculated BMFW is 2.42 and BMFL is 1.21. The fugacity of the chemical in water is 0.1 mPa, the diet is 0.15 mPa and the fish is 0.18 mPa, thus the fish to diet fugacity ratio is 1.2, equal to the BMFL, showing modest biomagnification.
000. The calculated BMFW is 2.42 and BMFL is 1.21. The fugacity of the chemical in water is 0.1 mPa, the diet is 0.15 mPa and the fish is 0.18 mPa, thus the fish to diet fugacity ratio is 1.2, equal to the BMFL, showing modest biomagnification.
The uptake processes are: respiration 10% and diet 90% with a total rate of 0.05 mg per day i.e. 0.5 μmol per day. Loss processes are: respiration 17%, egestion 41%, biotransformation 35% and growth dilution 8%. At steady state the body burden is 1.81 mg or 18.1 μmol. The half-lives for uptake and loss are both 25.2 days. The total input and loss rates are 0.05 mg per day, thus the residence time of the chemical in the fish is 36 days.
It is notable that the assumed ratio of dietary uptake to egestion rate parameters QC for the CKk format is 6 while Qf for the fZD format is 3. This difference is attributable to the different lipid contents of the diet and fish since Qf is QC·(LD/LF). QC and Qf represent limiting maximum BMFs on a concentration and fugacity or lipid normalized basis respectively as is apparent from eqn (4) and (7). For example, increasing log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW to 8 and setting biotransformation and growth rates to zero result in a BMFW of 5.98, approaching QC of 6 and a BMFL of 2.99, approaching Qf of 3. These Q values are critical determinants of BMFs for very hydrophobic chemicals. As KOW increases, dietary uptake becomes the dominant input process and respiration becomes negligible. The fish is then unaffected by the concentration in water except that this water concentration controls concentrations at lower trophic levels.
KOW to 8 and setting biotransformation and growth rates to zero result in a BMFW of 5.98, approaching QC of 6 and a BMFL of 2.99, approaching Qf of 3. These Q values are critical determinants of BMFs for very hydrophobic chemicals. As KOW increases, dietary uptake becomes the dominant input process and respiration becomes negligible. The fish is then unaffected by the concentration in water except that this water concentration controls concentrations at lower trophic levels.
Inspection of these results suggests that the CKk format is easier to understand and apply. Concentration ratios can, however, become very large and difficult to interpret and relative concentrations between fish and diet items can be misleading since both wet weight and lipid normalized concentrations can be used. This format proves to be most preferred for conditions under kinetic control as applies to hydrophobic chemicals.
The fZD format may be initially more difficult to apply, but it can provide additional insights into the bio-uptake process by revealing the relative equilibrium status between water, sediment and various aquatic species. Bio-uptake metrics expressed as fugacity ratios generally lie in the range 1 to 10 and are more easily interpreted. This format is most relevant when conditions are largely controlled by equilibrium processes as applies to less hydrophobic chemicals. Since BMFL factors and fugacity ratios are equivalent, either can be used to characterize trophic magnification in food webs, however this implies that all partitioning is into lipids and in this simple case that lipids are equivalent to octanol.
Connolly and Pederson29 first demonstrated this fugacity increase in monitoring data. This was followed by Gobas and colleagues30,31 who demonstrated experimentally that lipid digestion causes a fugacity increase in the digestive system and this elevated fugacity is transmitted into the body, causing biomagnification. As noted earlier, this process of fugacity increase can be viewed as being caused by ‘solvent depletion’.13 The fugacity format thus captures the fundamental cause of bioconcentration as being driven by differences in Z values (i.e. the capacity to absorb the chemical, dependent on solubility) between water and the fish, the ratio of which is a partition ratio. It also addresses the fundamental cause of biomagnification reflecting a reduction in Z value in ingested food during lipid digestion and corresponding increase in fugacity.
Ultimately, since both formats yield identical results either or both can be used.
3 Results
3.1 Mass-balance equations applied to bioaccumulation in a simple predator–prey system
We now discuss several implications of the models comprising these equations, especially the sensitivity of desired outcomes to the parameter values of the selected chemical. A significant advantage of having available a simple and robust validated model is that the implications of changes in parameters can be explored mathematically rather than by actual, demanding, and expensive testing. To illustrate these implications we compile simple bioaccumulation models employing realistic ranges of properties of typical organisms and chemical parameters. The models are outlined in a recent study of TMFs to predict TMFs and BMFs.9 We suggest typical values for rate constants as a function of fish species and the chemical. Uptake and loss parameters are given in Table 3 for five species using allometric correlations suggested by Arnot and Gobas1 as a function of fish mass and temperature. These rate constants (days−1) are defined in Table 2. Typical numerical values are included and applied initially to a 10 g fish i.e. smelt, namely kR (respiratory uptake) 470, kD (dietary uptake) 0.063, kG (growth dilution) 0.0025, and kE (egestion) 0.0105, conveniently estimated for screening level purposes as a factor Q of 6 less than kD. Dietary and respiratory assimilation efficiencies and the respiratory loss rate constant kV are KOW dependent and are estimated using parameters from the Arnot–Gobas model.1 Values of kM are later selected arbitrarily.| Species | Phytoplankton | Zooplankton | Mysis | Smelt | Trout |
| Mass (g) | Not required | 0.0001 | 0.1 | 10 | 100 |
| Lipid content, L (g g−1) | 0.05 | 0.03 | 0.2 | 0.1 | 0.25 |
| Q C = kD/kE | 6 | 6 | 6 | 6 | |
| Respiratory flow, GW (L per day) | 0.0049 | 0.44 | 8.77 | 39.2 | |
| Dietary uptake (kg per day) | 8.2 × 10−8 | 2.9 × 10−5 | 0.0015 | 0.010 | |
| k R (days−1) | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 660 |
2376 | 474 | 212 | |
| k D (days−1) | 0.348 | 0.124 | 0.062 | 0.044 | |
| k G (days−1) | 0.025 | 0.0063 | 0.0025 | 0.0005 | |
| k E (days−1) | 0.0581 | 0.0206 | 0.0103 | 0.0073 |
We first model the simple bioaccumulation of a series of hypothetical, non-biotransforming chemicals with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW values of 4, 5, 6, and 8 in three smelt of different lipid contents exposed to contaminant in the same diet and the same respired water. These predator smelt occupy a functional trophic level (TL) of 2.0 and are designated either as lean (L) with a lipid content of 2%, mean (M) with 10%, and fat (F) with 20%. These rather extreme lipid contents are selected to facilitate interpretation of results. The water concentration is 1 mg m−3, the diet has a lipid content of 10% and occupies a functional TL of 1.0 and is thus in equilibrium with the water as controlled by the lipid–water partition coefficient that is assumed to equal the octanol–water partition coefficient KOW. These dietary concentrations are designated CDW and CDL on a wet-weight and lipid-weight basis respectively. An arbitrary fugacity Z-value ZW of 0.01 mol m−3 Pa−1 in water is assumed corresponding to a Henry's law constant of 100 Pa m3 mol−1 to enable fugacities to be calculated and compared for the water and fish. In each case the wet-weight fish concentrations CFW and the lipid-normalized concentrations CFLi.e. CFW/L are deduced and compared. The bioaccumulation factors on a wet weight basis (BAFW) and on a lipid-weight basis (BAFL) are calculated as CFW/CW and CFL/CW respectively. The biomagnification factors on a wet-weight basis (BMFW) and on a lipid-weight basis (BMFL) are calculated as CFW/CDW and CFL/CDL respectively.
KOW values of 4, 5, 6, and 8 in three smelt of different lipid contents exposed to contaminant in the same diet and the same respired water. These predator smelt occupy a functional trophic level (TL) of 2.0 and are designated either as lean (L) with a lipid content of 2%, mean (M) with 10%, and fat (F) with 20%. These rather extreme lipid contents are selected to facilitate interpretation of results. The water concentration is 1 mg m−3, the diet has a lipid content of 10% and occupies a functional TL of 1.0 and is thus in equilibrium with the water as controlled by the lipid–water partition coefficient that is assumed to equal the octanol–water partition coefficient KOW. These dietary concentrations are designated CDW and CDL on a wet-weight and lipid-weight basis respectively. An arbitrary fugacity Z-value ZW of 0.01 mol m−3 Pa−1 in water is assumed corresponding to a Henry's law constant of 100 Pa m3 mol−1 to enable fugacities to be calculated and compared for the water and fish. In each case the wet-weight fish concentrations CFW and the lipid-normalized concentrations CFLi.e. CFW/L are deduced and compared. The bioaccumulation factors on a wet weight basis (BAFW) and on a lipid-weight basis (BAFL) are calculated as CFW/CW and CFL/CW respectively. The biomagnification factors on a wet-weight basis (BMFW) and on a lipid-weight basis (BMFL) are calculated as CFW/CDW and CFL/CDL respectively.
Also calculated are the percentages of uptake by diet and respiration and the percentages that each loss rate constant contributes to the total loss rate constant, thus identifying the dominant rate constant(s) and the half-times for uptake and clearance.
A selection of the results is given in Table 4 that gives calculated values of CFW and CFL for values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 4, 5, 6, and 8. In these simulations zero biotransformation is assumed i.e., kM is zero, but is varied later.
KOW of 4, 5, 6, and 8. In these simulations zero biotransformation is assumed i.e., kM is zero, but is varied later.
| Predator | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW = 4.0, CDW = 1.0, CDL = 10.0 KOW = 4.0, CDW = 1.0, CDL = 10.0 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW = 5.0, CDW = 10.0, CDL = 100.0 KOW = 5.0, CDW = 10.0, CDL = 100.0 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW = 6.0, CDW = 100.0, CDL = 1000.0 KOW = 6.0, CDW = 100.0, CDL = 1000.0 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW = 8.0, CDW = 10 KOW = 8.0, CDW = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, CDL = 100 000, CDL = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lean | Mean | Fat | Lean | Mean | Fat | Lean | Mean | Fat | Lean | Mean | Fat | |
| C FW | 0.23 | 1.10 | 2.15 | 4.43 | 18.31 | 30.12 | 182.5 | 379.6 | 438.9 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 471 471 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 609 609 |
| C FL | 11.3 | 11.0 | 10.8 | 221 | 183 | 151 | 9127 | 3796 | 2194 | 1.62 × 106 | 3.35 × 105 | 1.68 × 105 |
| Diet% | 11.9 | 11.87 | 11.87 | 57.17 | 57.17 | 57.17 | 92.89 | 92.89 | 92.89 | 99.75 | 99.75 | 99.75 |
| k T | 2.36 | 0.48 | 0.25 | 0.25 | 0.06 | 0.04 | 0.036 | 0.018 | 0.015 | 0.0059 | 0.0057 | 0.0057 |
| k V% | 99.5 | 97.30 | 94.74 | 94.78 | 78.42 | 64.50 | 64.89 | 26.99 | 15.60 | 4.00 | 0.83 | 0.41 |
| k E% | 0.45 | 2.19 | 4.26 | 4.22 | 17.44 | 28.69 | 28.26 | 58.77 | 67.94 | 53.87 | 55.65 | 55.88 |
| k M% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| k G% | 0.11 | 0.52 | 1.01 | 1.00 | 4.14 | 6.81 | 6.84 | 14.23 | 16.45 | 42.14 | 43.53 | 43.71 |
| BAFW | 226 | 1104 | 2150 | 4426 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307 307 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 116 116 |
1.83 × 105 | 3.80 × 105 | 4.39 × 105 | 3.24 × 107 | 3.35 × 107 | 3.36 × 107 |
| BAFL, fF/fW | 1.13 × 104 | 1.10 × 104 | 1.08 × 104 | 2.21 × 105 | 1.83 × 105 | 1.51 × 105 | 9.13 × 106 | 3.80 × 106 | 2.19 × 106 | 1.62 × 109 | 3.35 × 108 | 1.68 × 108 |
| BMFW | 0.23 | 1.10 | 2.15 | 0.44 | 1.83 | 3.01 | 1.83 | 3.80 | 4.39 | 3.24 | 3.35 | 3.36 |
| BMFL, fF/fD | 1.13 | 1.10 | 1.08 | 2.21 | 1.83 | 1.51 | 9.13 | 3.80 | 2.19 | 16.20 | 3.35 | 1.68 |
| τ, days | 0.3 | 1.4 | 2.8 | 2.8 | 11.5 | 18.9 | 19.0 | 39.5 | 45.6 | 116.8 | 120.7 | 121.2 |
The columns on the left (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 4.0) show that the lipid normalized concentration CFL is fairly constant (10.8 to 11.3) as are values of BAFL because the lipid is close to equilibrium with the water, but the wet weight concentrations CFW vary considerably (0.23 to 2.15) depending on the lipid content of the fish. The fish fugacities are directly proportional to values of BAFL. This proportionality applies only if lipid is the only sorbing phase. The ratio of fish to diet fugacity equals BMFL and varies from 1.08 to 1.13 indicating near-equilibrium and negligible biomagnification. The percentage chemical input from the diet is minimal (11.9%) because of the low concentration in the diet. The primary loss process is by ventilation, kV, (95 to 99%) which depends inversely on lipid content, thus the rate constant for total loss is smallest for the fat fish, but the absolute rates of input and loss are equal in all three cases. Bioaccumulation factors on a wet-weight basis (BAFW) range from 226 to 2150 reflecting the high variability in CFW. Wet-weight biomagnification factors (BMFW) vary similarly from 0.23 to 2.15. The total rate constant for loss ranges from 2.4 to 0.25 days−1 corresponding to short uptake and loss times of 0.3 to 2.8 days. The fat fish is slower to approach steady state because of its greater capacity for chemical. In this case it is clearly preferable to interpret the bioaccumulation phenomena on an equilibrium basis using CFL or fugacity, as is normal practice recommended by Borga et al.8 and Burkhart et al.4 Use of wet-weight parameters can obscure the interpretation.
KOW of 4.0) show that the lipid normalized concentration CFL is fairly constant (10.8 to 11.3) as are values of BAFL because the lipid is close to equilibrium with the water, but the wet weight concentrations CFW vary considerably (0.23 to 2.15) depending on the lipid content of the fish. The fish fugacities are directly proportional to values of BAFL. This proportionality applies only if lipid is the only sorbing phase. The ratio of fish to diet fugacity equals BMFL and varies from 1.08 to 1.13 indicating near-equilibrium and negligible biomagnification. The percentage chemical input from the diet is minimal (11.9%) because of the low concentration in the diet. The primary loss process is by ventilation, kV, (95 to 99%) which depends inversely on lipid content, thus the rate constant for total loss is smallest for the fat fish, but the absolute rates of input and loss are equal in all three cases. Bioaccumulation factors on a wet-weight basis (BAFW) range from 226 to 2150 reflecting the high variability in CFW. Wet-weight biomagnification factors (BMFW) vary similarly from 0.23 to 2.15. The total rate constant for loss ranges from 2.4 to 0.25 days−1 corresponding to short uptake and loss times of 0.3 to 2.8 days. The fat fish is slower to approach steady state because of its greater capacity for chemical. In this case it is clearly preferable to interpret the bioaccumulation phenomena on an equilibrium basis using CFL or fugacity, as is normal practice recommended by Borga et al.8 and Burkhart et al.4 Use of wet-weight parameters can obscure the interpretation.
The columns in the centre-left with a higher value of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 5.0 show that CFL and CFW now both vary considerably. Input is mainly or primarily from diet (57%) and remaining input is from respiration, reflecting the higher concentration in the diet. The primary loss processes are by ventilation (kV) which depends inversely on lipid content, and egestion (kE) which is independent of lipid content because the absolute rate is CFW·kE. The rate constant for total loss is now less sensitive to fish lipid content and corresponds to uptake and loss half-times from 2.8 to 19 days. The ratio of fish to diet fugacities (BMFL) now ranges from 2.21 to 1.51 indicating a higher fugacity in the fish than that in the water in all cases and greater biomagnification. In this case either CFW or CFL, or both, can be employed to interpret the bioaccumulation and trophic magnification.
KOW of 5.0 show that CFL and CFW now both vary considerably. Input is mainly or primarily from diet (57%) and remaining input is from respiration, reflecting the higher concentration in the diet. The primary loss processes are by ventilation (kV) which depends inversely on lipid content, and egestion (kE) which is independent of lipid content because the absolute rate is CFW·kE. The rate constant for total loss is now less sensitive to fish lipid content and corresponds to uptake and loss half-times from 2.8 to 19 days. The ratio of fish to diet fugacities (BMFL) now ranges from 2.21 to 1.51 indicating a higher fugacity in the fish than that in the water in all cases and greater biomagnification. In this case either CFW or CFL, or both, can be employed to interpret the bioaccumulation and trophic magnification.
The columns on the centre right (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 6.0) show that CFW now becomes more constant (182 to 440) and CFL is now more variable (9127 to 2194). Diet is now responsible for 93% of the input because of its high concentration. There is appreciable biomagnification with BMFW ranging from 1.8 to 4.4 while BMFL ranges from 9.1 to 2.2 i.e. the effect of lipid content reverses the BMF trend. The primary loss processes are by ventilation and egestion. The uptake and loss half-times range from 19 to 46 days.
KOW of 6.0) show that CFW now becomes more constant (182 to 440) and CFL is now more variable (9127 to 2194). Diet is now responsible for 93% of the input because of its high concentration. There is appreciable biomagnification with BMFW ranging from 1.8 to 4.4 while BMFL ranges from 9.1 to 2.2 i.e. the effect of lipid content reverses the BMF trend. The primary loss processes are by ventilation and egestion. The uptake and loss half-times range from 19 to 46 days.
The columns on the right with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 8 represent an extreme condition of super-hydrophobicity15,32 in which the diet is responsible for 99.8% of the inputs. The wet-weight concentrations are now nearly constant and the lipid-weight concentrations are highly variable. The primary loss processes are now by egestion (kE) and growth (kG) which are independent of lipid content, thus the rate constant for total loss (∼0.006 days−1) is also independent of lipid content and corresponds to a long half-time of 117 days. In this case it is clearly preferable to interpret the bioaccumulation phenomena using CFW rather than CFL because lipid normalization introduces an unnecessary variability. BMFW ranges narrowly from 3.24 to 3.35 to 3.36 but the trend reverses for BMFL with values of 16.2 to 3.35 to 1.68. CFL is now highly variable while CFW is fairly constant. For these conditions, it can be argued that it is preferable to use wet-weight concentrations and ratios.
KOW of 8 represent an extreme condition of super-hydrophobicity15,32 in which the diet is responsible for 99.8% of the inputs. The wet-weight concentrations are now nearly constant and the lipid-weight concentrations are highly variable. The primary loss processes are now by egestion (kE) and growth (kG) which are independent of lipid content, thus the rate constant for total loss (∼0.006 days−1) is also independent of lipid content and corresponds to a long half-time of 117 days. In this case it is clearly preferable to interpret the bioaccumulation phenomena using CFW rather than CFL because lipid normalization introduces an unnecessary variability. BMFW ranges narrowly from 3.24 to 3.35 to 3.36 but the trend reverses for BMFL with values of 16.2 to 3.35 to 1.68. CFL is now highly variable while CFW is fairly constant. For these conditions, it can be argued that it is preferable to use wet-weight concentrations and ratios.
These calculations illustrate several important features of BMFs and thus of TMFs. First, the wet-weight BMFW is CFW/CDW, while the lipid-weight BMFL is CFL/CDL, thus BMFW is BMFL(LF/LD) where LD and LF are the lipid contents of the diet and fish respectively. When a fish consumes a lean diet and LF/LD is <1.0 then BMFL will exceed the BMFW. On the contrary, when the fish is fattier than its diet the opposite occurs. Only when LF and LD are equal are the two BMFs equal as is apparent for the ‘mean lipid’ content fish. A BMFL exceeding 1.0 in a predator may be attributable, not to biomagnification, but to a lean diet. At high values of KOW lipid normalisation distorts the predator prey relationships if lipid contents are variable. These results suggest that when interpreting biomagnification data, both BMFW and BMFL should be inspected with the expectation that BMFL will be more useful for less hydrophobic chemicals under equilibrium control and BMFW more useful for highly hydrophobic chemicals under kinetic control.
Second, it may seem counter-intuitive that for highly hydrophobic substances lipid content is inconsequential because most of the chemical probably resides in the lipid phases. This insensitivity to lipid content arises because the fish concentration is controlled by the rate constant for loss kT, and the principal contributing rate constants are independent of lipid content. Only kV depends directly on lipid content, but it is small and insignificant, contributing less than 5% to the losses when log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW is 8.
KOW is 8.
Third, a common and correct justification for lipid normalization is that it reflects the fugacity of the fish relative to the fugacity of the water and the diet. For the data in Table 2 BMFL equals the ratio of the fish fugacity to that of the water and food. This ratio is close to 1.0 for the left-hand columns, but there is an increase in fugacity for the middle columns reflecting the expected biomagnification. For the columns on the right the fugacities in the fish are highly variable, specifically 16.2 to 1.68 times that of the water and food. Fugacities thus vary greatly depending on lipid levels of the predator. The biomagnification is not a result of thermodynamic partitioning, it is caused by the kinetic effect of a low and fairly constant value of kT and the high and constant diet concentration that yield constant values of CFW but highly variable values of CFL. Fugacities then become less relevant indicators of bioaccumulation and biomagnification. In addition, varied lipid contents of the diet may impact various rate processes of the predator fish, including the diet ingestion rate, the growth rate, and ultimately the BMF. These types of impacts should be considered by modelers, however further discussion of this topic is beyond the scope of this study.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW values in the same 3 fish and again with the same water and diets, but biotransformation is introduced as an arbitrarily selected rate constant kM of 0.01 days−1 corresponding to a half-life of approximately 70 days. The importance of this half-life has been reviewed by Arnot et al.33,34 and Goss et al.19 have suggested it as a direct metric of bioaccumulation potential.
KOW values in the same 3 fish and again with the same water and diets, but biotransformation is introduced as an arbitrarily selected rate constant kM of 0.01 days−1 corresponding to a half-life of approximately 70 days. The importance of this half-life has been reviewed by Arnot et al.33,34 and Goss et al.19 have suggested it as a direct metric of bioaccumulation potential.
The results in Table 5 are similar to those in Table 4 but biotransformation causes a reduction in all concentrations. The effect is greatest for the hydrophobic chemicals that have relatively slower non-biotransformation loss processes. Specifically, for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 4 the fish concentrations are similar to those in Table 1. For log
KOW of 4 the fish concentrations are similar to those in Table 1. For log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 5 and 6 the concentrations in the fat fish are lower by a factor of up to 2 because kM contributes up to 40% of the losses. For log
KOW of 5 and 6 the concentrations in the fat fish are lower by a factor of up to 2 because kM contributes up to 40% of the losses. For log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 8, kM becomes the dominant (63%) loss rate constant and concentrations fall by nearly a factor of 3. These reductions in concentration are the direct result of kM causing an increase in kT.
KOW of 8, kM becomes the dominant (63%) loss rate constant and concentrations fall by nearly a factor of 3. These reductions in concentration are the direct result of kM causing an increase in kT.
| Predator | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW = 4.0, CDW = 1.0, CDL = 10.0 KOW = 4.0, CDW = 1.0, CDL = 10.0 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW = 5.0, CDW = 10.0, CDL = 100.0 KOW = 5.0, CDW = 10.0, CDL = 100.0 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW = 6.0, CDW = 100.0, CDL = 1000.0 KOW = 6.0, CDW = 100.0, CDL = 1000.0 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW = 8.0, CDW = 10 KOW = 8.0, CDW = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.0, CDL = 100 000.0, CDL = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.0 000.0 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lean | Mean | Fat | Lean | Mean | Fat | Lean | Mean | Fat | Lean | Mean | Fat | |
| C W | 0.22 | 1.08 | 2.07 | 4.26 | 15.71 | 23.67 | 143.31 | 241.91 | 264.67 | 1.2 × 104 | 1.2 × 104 | 1.2 × 104 |
| C L | 11.24 | 10.82 | 10.33 | 212.76 | 157.07 | 118.35 | 7166 | 2419 | 1323 | 6.0 × 105 | 1.2 × 105 | 6.1 × 104 |
| Diet% | 11.87 | 11.87 | 11.87 | 57.17 | 57.17 | 57.17 | 92.89 | 92.89 | 92.89 | 99.75 | 99.75 | 99.75 |
| kT | 2.37 | 0.49 | 0.26 | 0.26 | 0.07 | 0.05 | 0.05 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 |
| k V% | 99.03 | 95.32 | 91.07 | 91.14 | 67.28 | 50.69 | 50.95 | 17.20 | 9.41 | 1.49 | 0.30 | 0.15 |
| k E% | 0.44 | 2.14 | 4.09 | 4.05 | 14.97 | 22.55 | 22.19 | 37.45 | 40.98 | 20.06 | 20.30 | 20.33 |
| k M% | 0.42 | 2.03 | 3.87 | 3.85 | 14.20 | 21.40 | 21.49 | 36.28 | 39.69 | 62.76 | 63.52 | 63.61 |
| k G% | 0.11 | 0.51 | 0.97 | 0.96 | 3.55 | 5.35 | 5.37 | 9.07 | 9.92 | 15.69 | 15.88 | 15.90 |
| BAFW | 2.2 × 102 | 1.1 × 103 | 2.1 × 103 | 4.3 × 103 | 1.6 × 104 | 2.4 × 104 | 1.4 × 105 | 2.4 × 105 | 2.6 × 105 | 1.2 × 107 | 1.2 × 107 | 1.2 × 107 |
| BAFL, fF/fW | 1.1 × 104 | 1.1 × 104 | 1.0 × 104 | 2.1 × 105 | 1.6 × 105 | 1.2 × 105 | 7.2 × 106 | 2.4 × 106 | 1.3 × 106 | 6.0 × 108 | 1.2 × 108 | 6.1 × 107 |
| BMFW | 0.22 | 1.08 | 2.07 | 0.43 | 1.57 | 2.37 | 1.43 | 2.42 | 2.65 | 1.21 | 1.22 | 1.22 |
| BMFL, fF/fD | 1.12 | 1.08 | 1.03 | 2.13 | 1.57 | 1.18 | 7.17 | 2.42 | 1.32 | 6.03 | 1.22 | 0.61 |
| τ, days | 0.3 | 1.4 | 2.7 | 2.7 | 9.8 | 14.8 | 14.9 | 25.1 | 27.5 | 43.5 | 44.0 | 44.1 |
For log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 8 the BMFW values are all approximately 1.2 but the BMFL values vary from 6.0 to 1.22 to 0.61 and are clearly being distorted by the varying lipid contents. The introduction of biotransformation as a significant loss process provides an additional incentive to avoid lipid normalization for very hydrophobic substances because the variation in CFW values is considerably less than those of CFL. Variation in lipid content for highly hydrophobic chemicals is inconsequential for steady state bioaccumulation and biomagnification, but it does affect the time required to reach steady state and this may be reflected in concentrations in ecosystems. It is thus interesting to explore how these assertions are reflected in food web simulations.
KOW of 8 the BMFW values are all approximately 1.2 but the BMFL values vary from 6.0 to 1.22 to 0.61 and are clearly being distorted by the varying lipid contents. The introduction of biotransformation as a significant loss process provides an additional incentive to avoid lipid normalization for very hydrophobic substances because the variation in CFW values is considerably less than those of CFL. Variation in lipid content for highly hydrophobic chemicals is inconsequential for steady state bioaccumulation and biomagnification, but it does affect the time required to reach steady state and this may be reflected in concentrations in ecosystems. It is thus interesting to explore how these assertions are reflected in food web simulations.
3.2 Linear food chain model to determine the TMF with and without biotransformation
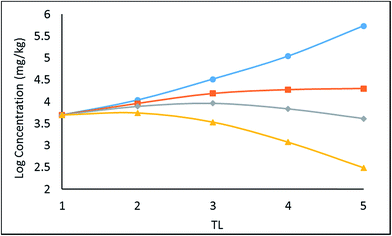
A simple 5 species, 5 trophic level obligate food chain is defined in which the phytoplankton are assigned a TL of 1 while other species 2 to 5 have an exclusive diet of the species below. The fish properties listed in Table 3 are deduced from Arnot–Gobas1 correlations and are regarded as typical values for the masses of the specific species with a QC value i.e. kD/kE ratio of 6. The model was run as before for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 4, 5, 6, and 8 and the concentrations CFW and CFL were calculated. Logarithmic values of both concentrations were plotted and regressed against trophic level to obtain a slope (β). The TMF is then calculated using the conventional method, namely the TMF is the antilog of the regression slope, β, of log
KOW of 4, 5, 6, and 8 and the concentrations CFW and CFL were calculated. Logarithmic values of both concentrations were plotted and regressed against trophic level to obtain a slope (β). The TMF is then calculated using the conventional method, namely the TMF is the antilog of the regression slope, β, of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C on TL.8,35,36 The results are presented in Fig. 2 as a series of TMF plots using both log
C on TL.8,35,36 The results are presented in Fig. 2 as a series of TMF plots using both log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CFW and log
CFW and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CFL as a function of TL (lower and upper plots respectively) from which TMFW and TMFL can be obtained, expecting that since TMF is essentially an average BMF, the same general conclusions will apply as discussed earlier for the lean, mean, and fat fish.
CFL as a function of TL (lower and upper plots respectively) from which TMFW and TMFL can be obtained, expecting that since TMF is essentially an average BMF, the same general conclusions will apply as discussed earlier for the lean, mean, and fat fish.
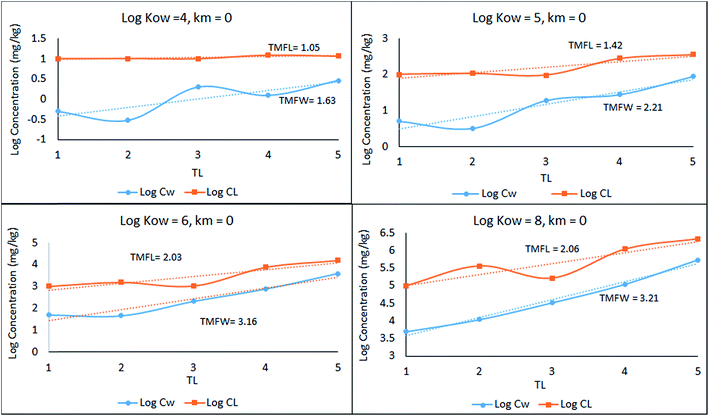 | ||
| Fig. 2 Regression of log chemical concentrations (wet-weight and lipid-normalized) across a 5-species obligate food chain, where the species have various lipid contents. | ||
There is a significant difference between wet-weight (CFW and TMFW) and lipid-normalized (CFL and TMFL) values. For less hydrophobic substances lipid normalization is clearly desirable because of the greater constancy of the CFL values. As KOW increases, the lipid-normalized lines have increased slopes and become more variable. In contrast, the wet-weight lines become less variable and approach straight lines indicating constancy in BMFW values. In contrast, for the more hydrophobic chemicals an improved regression is obtainable using TMFW. In general, the two TMF values are unequal.
Part of the differences between the two TMFs arises because of systematic changes in lipid content (L) with TL. Generally, if L increases with TL the CFW and CFL lines tend to converge. Only if the lipid contents of all species are equal will the lines be parallel and TMFW and TMFL are equal. A simple numerical example illustrates this dependence of TMF on lipid variations.
For a 4-species linear food chain with a constant BMFW of 3.0, the CFW values for a hypothetical example could be 1, 3, 9 and 27. If the lipid contents are equal, both TMFW and TMFL will be 3.0. If the lipid contents increase from 0.05 at TL of 1 by multiples of 1.2 to 0.06, 0.072 and 0.0864, the TMFW is unchanged at 3.0 but the TMFL decreases to 2.5 which is 3.0/1.2. Similarly, if the lipid contents decrease by a factor of 1.2, TMFL increases to 3.6. These results suggest that lipid normalization is desirable for species that are approaching equilibrium with water with relatively insignificant dietary uptake, with fast respiratory exchange dominating. The opposite applies to hydrophobic chemicals that biomagnify appreciably. Lipid normalization can change the slope of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CF on TL regression line, causing TMFW and TMFL to diverge. This effect is most important for substances that biomagnify and are likely subjects of regulatory TMF evaluations.
CF on TL regression line, causing TMFW and TMFL to diverge. This effect is most important for substances that biomagnify and are likely subjects of regulatory TMF evaluations.
We again suggest that both TMFW and TMFL be calculated from monitoring data. Their ratio is an indication of a systematic variation of L with TL. This ratio can be regarded as a trophic dependence on lipid content (TDL). If the ratio TMFL/TMFW and TDL is 1.0 there is no systematic dependence of TMF on L. A TDL < 1.0 indicates an increase in L with TL and a TDL > 1.0 indicates a decrease in L with increasing TL. An important implication is that if TMFs are to be used in a regulatory context it must be appreciated that TMFL is a function of both biomagnification and systematic changes in species lipid contents. In practice, large values of both TMFs indicate appreciable biomagnification and either or both can be used.
In Fig. 2 above, TMFW exceeds TMFL by a factor of approximately 1.6 indicating an increase in L with TL as is apparent from the lipid contents in Table 3.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CFW as a function of TL for kM values ranging from 0 to 0.05 days−1. The corresponding TMFs are given. As expected, an increase in kM reduces concentrations, BMFs and TMFs, especially at higher trophic levels.
CFW as a function of TL for kM values ranging from 0 to 0.05 days−1. The corresponding TMFs are given. As expected, an increase in kM reduces concentrations, BMFs and TMFs, especially at higher trophic levels.
It is notable that the slopes of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CFWvs. TL lines are most variable at high trophic levels. This is because the rate constants for other losses are slower for large fish thus the introduction of a specific kM has a greater effect on kT and thus on the BMFW. This raises an interesting possibility that if validated model is available then TMFW data could be used to deduce biotransformation rate constants.
CFWvs. TL lines are most variable at high trophic levels. This is because the rate constants for other losses are slower for large fish thus the introduction of a specific kM has a greater effect on kT and thus on the BMFW. This raises an interesting possibility that if validated model is available then TMFW data could be used to deduce biotransformation rate constants.
3.3 The key role of dietary and respiratory uptake rates
This analysis suggests that a major factor influencing bioaccumulation and biomagnification is the relative quantities of chemical taken up from water by respiration and from diet. Estimates of these rates require data on the volumetric or mass flows of water and food and the assimilation efficiencies in the gills and GI tract. Correlations and data37 are available for these processes but improved estimates would be invaluable. A related issue is the location of biotransformation as being either somatic or intestinal as discussed by Gobas and Lo.10,31 In a simple one compartment model this may be of little importance but for more detailed multi-compartment models this can be critical, especially if QSARs are used to estimate biotransformation rate constants that differ in location and thus reactive environments within the fish. This can cause variations in predicted BCF and BMF values.We believe that the three superhydrophobic permethylcyclosiloxanes D4, D5 and D6 serve as good examples because they cover a range in hydrophobicity from log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of 6.98 for D4 to 8.09 for D5 and 8.87 for D6. These chemicals have been extensively studied in recent years. For D4, D5 and D6 respiratory uptake and loss are negligible thus it can be argued that the chemical observed in high trophic level species such as trout reached their destination entirely by dietary uptake from lower trophic level (planktonic) species, with water playing a negligible role as a source. Greater respiratory uptake is expected for D4, relative to D5 and D6, because of greater water solubility and lower to organic carbon partitioning coefficient (KOC). This was tested using the model by setting the concentration in the plankton, then setting the water concentration as zero for all other species. As expected, this resulted in a negligible change in concentrations, BMFs and TMFs. A possible implication is that the source of these chemicals in lakes such as Lake Mjosa15 and marine ecosystems such as Tokyo Bay36 is not the dissolved chemical in water, it is the contaminated suspended biomass discharged from waste water treatment plants. Clearly more efficient contaminant removal is desirable because the discharged biomass is a direct source of diet to the resident biota. In the case of D5 this explains why contamination in fish is apparently not fully mitigated by the expected fast volatilization from the surfaces of these water bodies. Improved parameters for uptake from planktonic and other small organisms would be desirable because they play a critical role as the source of contamination.
KOW of 6.98 for D4 to 8.09 for D5 and 8.87 for D6. These chemicals have been extensively studied in recent years. For D4, D5 and D6 respiratory uptake and loss are negligible thus it can be argued that the chemical observed in high trophic level species such as trout reached their destination entirely by dietary uptake from lower trophic level (planktonic) species, with water playing a negligible role as a source. Greater respiratory uptake is expected for D4, relative to D5 and D6, because of greater water solubility and lower to organic carbon partitioning coefficient (KOC). This was tested using the model by setting the concentration in the plankton, then setting the water concentration as zero for all other species. As expected, this resulted in a negligible change in concentrations, BMFs and TMFs. A possible implication is that the source of these chemicals in lakes such as Lake Mjosa15 and marine ecosystems such as Tokyo Bay36 is not the dissolved chemical in water, it is the contaminated suspended biomass discharged from waste water treatment plants. Clearly more efficient contaminant removal is desirable because the discharged biomass is a direct source of diet to the resident biota. In the case of D5 this explains why contamination in fish is apparently not fully mitigated by the expected fast volatilization from the surfaces of these water bodies. Improved parameters for uptake from planktonic and other small organisms would be desirable because they play a critical role as the source of contamination.
4 Discussion
We first discuss the issue of whether or not to lipid normalize. In 1995 Hebert and Keenleyside38 published a paper aptly titled “To normalize or not to normalize? Fat is the question.” The authors acknowledged the value of lipid normalization when interpreting concentrations of hydrophobic contaminants in biota, but they pointed out that lipid normalization can lead to erroneous conclusions and direct interpretation of whole-body or wet-weight concentrations may be preferable. They cited three examples: concentrations of polychlorinated biphenyls (PCB) in herring gull (Larus argentatus) eggs in the Great Lakes, concentrations of hexachlorobenzene (HCB) in forage fish in the St. Clair and Detroit Rivers, and a hypothetical example of a hydrophobic contaminant in two species of fish. They concluded that both whole-body and lipid-normalized data should be examined and interpreted, as well as an alternative analysis of covariance (ANCOVA) approach. The paper has been cited over 100 times since 1995 testifying to its general acceptance. However, lipid normalization remains widely recommended and practiced, especially when assessing biomagnification and trophic magnification.8,39 The results from the present simulations support their assertion that both wet weight and lipid normalised concentrations should be used.Second, the results presented here suggest that BMFs and TMFs of very hydrophobic chemicals subject to biotransformation are primarily dependent on KOW and biotransformation half-lives. This is entirely consistent with the findings by Walters et al.40 in their ‘global synthesis’ of over 1500 TMF measurements, most of which used lipid-normalized data. We suggest, however, that TMFs may be best determined using both lipid normalized concentrations and whole fish (wet-weight) concentrations. A benefit of the latter approach is that it avoids problems of lipid determination, especially when the organism has a very low lipid content or when fillets or muscle are the sampled media. It also avoids the dependence of BMFs on relative lipid contents of the predator and prey. Regressions of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CFWvs. TL may be more robust than those using CFL. An uncontentious conclusion is that it is desirable when processing monitoring data to obtain and evaluate both wet-weight and lipid normalised concentrations, and since there is no added cost, costs for lipid determination could be reduced.
CFWvs. TL may be more robust than those using CFL. An uncontentious conclusion is that it is desirable when processing monitoring data to obtain and evaluate both wet-weight and lipid normalised concentrations, and since there is no added cost, costs for lipid determination could be reduced.
Inclusion of benthic organisms in food webs is often essential because the subject chemicals may have partitioned into sediments and persisted there for a prolonged period of time. Estimation of pore water concentrations and hence sediment and pore water fugacities is fraught with uncertainties. It is likely that in many cases the prevailing sediment fugacity exceeds the water column fugacity because of organic carbon mineralization, thus fugacities at low trophic levels may be uncertain.41 Models can be useful for exploring the effect of sediment/water fugacity ratios as discussed by Mackay et al.9 and Kim et al.35
The deductions presented above assume that the basic uptake eqn (1) is correct and no other factors substantially influence the uptake. The assumption that KOW equals the lipid–water partition coefficient is questionable but this should not affect the general conclusions concerning trends in hydrophobicity. Of course, real food webs are more complex and variable than those discussed here but we believe that the same principles may apply.
It must be appreciated that TMFs will differ when using wet-weight and lipid-normalised concentrations, especially if lipid contents vary throughout the food web. The differences in TMFs can be significant and in extreme cases one TMF may indicate trophic magnification whereas another TMF derived from the same data may indicate trophic dilution. This is most likely for hydrophobic chemicals that are appreciably biotransformed. In most cases, the two methods should yield similar, but unequal TMFs characterizing the extent of trophic magnification. For highly hydrophobic substances the calculation and evaluation of fugacities can be fraught with difficulties because concentrations are not influenced by lipid content. It is believed that these principles may apply to numerous hydrophobic substances including permethylcyclosiloxanes, phthalate esters, and halogenated hydrocarbons. Obviously when using BMFs and TMFs for regulatory purposes it is essential to appreciate the uncertainties introduced by these issues.
Finally, we comment on a semantic issue that it may be asserted that some chemicals biomagnify whereas others do not. Inspection of the uptake equation suggests that ALL chemicals biomagnify because kD inevitably exceeds kE and their ratio approaches Q. The reason that relatively hydrophilic chemicals do not apparently biomagnify is that the increase in fugacity caused by lipid digestion is mitigated by the relatively fast losses by ventilation or biotransformation. The experimental determinations of increases in fugacity in the GIT resulting from ‘solvent depletion’ by Gobas and colleagues42 present a compelling case for the fugacity increase in the GIT that is inevitably transmitted into the body of the fish, however, that increase may be subsequently dissipated by loss processes from the body that restore the body fugacity to a lower value similar to that of the food or water.
5 Conclusions: the continued evolution of bioaccumulation models; needs and priorities
In conclusion, we suggest that improvements in the science and modelling of bioaccumulation would benefit from advances in several subject areas.Since bioconcentration is basically a partitioning phenomenon, there is a need for more data on partition ratios to all relevant tissues by experimental determinations, QSAR development and fundamental computational methods, including the influences of temperature and ionization especially for cations that can be highly toxic. Such developments would enhance the use of tissue-specific parameters in PBPK models. Partitioning from sediment solids and pore water into benthic organisms can have a high degree of uncertainty, especially when water column concentrations are responding to changes in chemical emission rates. It would be useful to document passive sampling and other methods of determining sediment/water fugacity ratios.41
Chemical biotransformation or metabolism rates play a critical role in determining bioaccumulation, thus measurements and correlations need further improvement, including the differences between somatic (body) and gastrointestinal rates10 that occur in very different milieu.
Determination of trophic magnification in ecosystems must consider the effects of spatial and temporal variability, sediment-water fugacity ratios, reproductive losses and changing diets with growth.
There should be continuing consideration of the number and nature of fish compartments required for scientific and regulatory purposes, including consideration of the required accuracy and the degree of parsimony justified. The full implications of using steady state models as distinct from dynamic models also requires evaluation.
The various uptake and loss parameters are fundamentally linked to the organism's bioenergetics, thus consistency between these variables should be sought. There is a need for improvements in estimation methods for processes such as dietary and respiratory assimilation efficiencies and extents of digestion of various food items. The use of different Q values for each digested material should be explored.
As described here the model gives only point estimates of output quantities. Although incorporation of methods to evaluate probability and uncertainty would be useful it would be impractical for this paper because of the complexity and food web specificity. The probability and uncertainty associated with the model is a function of numerous variables that are dependent upon the sampled or defined food web under consideration. There is thus an obligation for the modeler to quantify the perceived accuracy of the results of each specific food web, especially as being best qualified to identify important parameters and covariances. There is increasing emphasis on presenting probabilistic estimates of model output using Monte Carlo and Bayesian approaches. A discussion of these methods, while beyond our scope here, deserves increased attention, especially when models are used for regulatory purposes. Nonetheless, Bayesian methods may readily be applied to a sampled food web using methods provided elsewhere (Powell et al.36,43).
Overall, it seems likely that a preferred strategy to advance the science of bioaccumulation is to continue ecosystem monitoring, laboratory determinations of the bio-uptake processes and model development, preferably in concert and supported by regulatory incentives. It is obvious that quantitative estimations of bioconcentration, bioaccumulation, biomagnification and trophic magnification as used in regulatory programs are essential for exposure and risk assessment, especially for hydrophobic substances. Ultimately, regulatory decisions are best justified using data from well-designed and carefully interpreted monitoring programs, preferably using benchmark chemicals. Models can play an invaluable complementary role to monitoring by confirming that the perceived state of the science contained in the models is consistent with the ecosystem observations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Centre Européen des Silicones (CES, division of CEFIC) for providing open access of this publication.References
- J. A. Arnot and F. A. P. C. Gobas, A food web bioaccumulation model for organic chemicals in aquatic ecosystems, Environ. Toxicol. Chem., 2004, 23, 2343–2355 CrossRef CAS PubMed.
- D. Mackay and A. Fraser, Bioaccumulation of persistent organic chemicals: mechanisms and models, Environ. Pollut., 2000, 110, 375–381 CrossRef CAS PubMed.
- F. A. Gobas, W. de Wolf, L. P. Burkhard, E. Verbruggen and K. Plotzke, Revisiting bioaccumulation criteria for POPs and PBT assessments, Integr. Environ. Assess. Manage., 2009, 5, 624–637 CrossRef CAS PubMed.
- L. P. Burkhard, K. Borga, D. E. Powell, P. Leonards, D. C. Muir, T. F. Parkerton and K. B. Woodburn, Improving the quality and scientific understanding of trophic magnification factors (TMFs), Environ. Sci. Technol., 2013, 47(3), 1186–1187 CrossRef CAS PubMed.
- European Chemicals Agency (ECHA), Guidance on Information Requirements and Chemical Safety Assessment, ch. R.11: PBT/vPvB assessment, Helsinki, Finland, 2014 Search PubMed.
- OECD, Test No. 305: Bioaccumulation in Fish: Aqueous and Dietary Exposure, OECD Publishing, 2012.
- D. Mackay, J. A. Arnot, F. A. Gobas and D. E. Powell, Mathematical relationships between metrics of chemical bioaccumulation in fish, Environ. Toxicol. Chem., 2013, 32(7), 1459–1466 CAS.
- K. Borga, K. A. Kidd, D. C. G. Muir, O. Berglund, J. Conder, F. A. P. C. Gobas, J. R. Kucklick, O. Malm and D. E. Powell, Trophic magnification factors: consideration of ecology, ecosystems, and study design, Integr. Environ. Assess. Manage., 2012, 8, 64–84 CrossRef CAS PubMed.
- D. Mackay, A. K. D. Celsie, J. A. Arnot and D. E. Powell, Processes influencing chemical biomagnification and trophic magnification factors in aquatic ecosystems: implications for chemical hazard and risk assessment, Chemosphere, 2016, 154, 99–108 CrossRef CAS PubMed.
- F. A. Gobas and J. C. Lo, Deriving bioconcentration factors and somatic biotransformation rates from dietary bioaccumulation and depuration tests, Environ. Toxicol. Chem., 2016, 32(12), 2968–2976 CrossRef PubMed.
- L. P. Burkhard, J. A. Arnot, M. R. Embry, K. J. Farley, R. A. Hoke, M. Kitano, H. A. Leslie, G. R. Lotufo, T. F. Parkerton, K. G. Sappington, G. T. Tomy and K. B. Woodburn, Comparing laboratory and field measured bioaccumulation endpoints, Integr. Environ. Assess. Manage., 2012, 8(1), 17–31 CrossRef CAS PubMed.
- L. P. Burkhard, C. Cowan-Ellsberry, M. R. Embry, R. A. Hoke and K. A. Kidd, Bioaccumulation data from laboratory and field studies: are they comparable?, Integr. Environ. Assess. Manage., 2012, 8(1), 13–16 CrossRef PubMed.
- R. Macdonald, D. Mackay and B. Hickie, Contaminant amplification in the environment, Environ. Sci. Technol., 2002, 36, 458A–462A CrossRef.
- D. E. Powell, Trophic magnification factors (TMF): mathematical relationships with other measures used to interpret bioaccumulation in aquatic environments, European Chemicals Agency (ECHA), Workshop on Scientific Advancements in Bioaccumulation Assessment, Helsinki, Finland, 2013 Search PubMed.
- K. Borga, E. Fjeld, A. Kierkegaard and M. S. McLachlan, Consistency in Trophic Magnification Factors of Cyclic Methyl Siloxanes in Pelagic Freshwater Food Webs Leading to Brown Trout, Environ. Sci. Technol., 2013, 47(24), 14394–14402 CrossRef PubMed.
- A. J. Niimi and B. G. Oliver, Biological half-lives of polychlorinated biphenyl (PCB) congeners in whole-fish and muscle of rainbow trout (Salmo gairdneri), J. Fish. Aquat. Sci., 1983, 40, 1388–1394 CrossRef CAS.
- S. Endo, T. N. Brown and K. U. Goss, General model for estimating partition coefficients to organisms and their tissues using the biological compositions and polyparameter linear free energy relationships, Environ. Sci. Technol., 2013, 47(12), 6630–6639 CrossRef CAS PubMed.
- K. U. Goss, Predicting the equilibrium partitioning of organic compounds using just one linear solvation energy relationship (LSER), Fluid Phase Equilib., 2005, 233(1), 19–22 CrossRef CAS.
- K. U. Goss, T. N. Brown and S. Endo, Elimination half-life as a metric for the bioaccumulation potential of chemicals in aquatic and terrestrial food chains, Environ. Toxicol. Chem., 2013, 32(7), 1663–1671 CAS.
- W. B. Neely, Estimating rate constants for the uptake and clearance of chemicals by fish, Environ. Sci. Technol., 1979, 13, 1506–1510 CrossRef CAS.
- R. V. Thomann, Bioaccumulation model of organic chemical distribution in aquatic food chains, Environ. Sci. Technol., 1989, 23, 699–707 CrossRef CAS.
- National Research Council (NRC), Models in environmental regulatory decision making, Committee on models in the regulatory decision process, Board on Environmental Studies and Toxicology, Washington, DC, 2007 Search PubMed.
- M. Z. Hauschild, M. A. Huijbregts, O. Jolliet, M. Macleod, M. Margni, D. Van de Meent, R. K. Rosenbaum and T. E. McKone, Building a model based on scientific consensus for life cycle impact assessment of chemicals: the search for harmony and parsimony, Environ. Sci. Technol., 2008, 42, 7032–7037 CrossRef CAS PubMed.
- R. J. Erickson, J. M. McKim, G. J. Lien, A. D. Hoffman and S. L. Batterman, Uptake and elimination of ionisable organic chemicals at fish gills: I. Model formulation, parameterization, and behaviour, Environ. Toxicol. Chem., 2006, 25, 1512–1521 CrossRef CAS PubMed.
- R. J. Erickson, J. M. McKim, G. J. Lien, A. D. Hoffman and S. L. Batterman, Uptake and elimination of ionisable chemicals at fish gills: II. Observed and predicted effects of pH, alkalinity, and chemical properties, Environ. Toxicol. Chem., 2006, 25, 1522–1532 CrossRef CAS PubMed.
- J. M. Armitage, J. A. Arnot, F. Wania and D. Mackay, Development and evaluation of a mechanistic bioconcentration model for ionogenic organic chemicals in fish, Environ. Toxicol. Chem., 2013, 32(1), 115–128 CrossRef CAS PubMed.
- A. Celsie, D. Mackay, J. M. Parnis and J. A. Arnot, A fugacity-based toxicokinetic model for narcotic organic chemicals in fish, Environ. Toxicol. Chem., 2016, 35(5), 1257–1267 CrossRef CAS PubMed.
- W. Larisch, T. N. Brown and K. U. Goss, A toxicokinetic model for fish including multiphase sorption features, Environ. Toxicol. Chem., 2017, 36(6), 1538–1546 CrossRef CAS PubMed.
- J. P. Connolly and C. J. Pedersen, A thermodynamic-based evaluation of organic chemical accumulation in aquatic organisms, Environ. Sci. Technol., 1988, 22(1), 99–103 CrossRef CAS PubMed.
- F. A. P. C. Gobas, J. B. Wilcockson, R. W. Russel and G. D. Haffner, Mechanism of biomagnification in fish under laboratory and field conditions, Environ. Sci. Technol., 1999, 33, 133–141 CrossRef CAS.
- F. A. P. C. Gobas, X. Zhang and R. Wells, Gastrointestinal magnification: the mechanism of biomagnification and food chain accumulation of organic chemicals, Environ. Sci. Technol., 1993, 27, 2855–2863 CrossRef CAS.
- D. Mackay, D. E. Powell and K. B. Woodburn, Bioconcentration and Aquatic Toxicity of Superhydrophobic Chemicals: A Modeling Case Study of Cyclic Volatile Methyl Siloxanes, Environ. Sci. Technol., 2015, 49(19), 11913–11922 CrossRef CAS PubMed.
- J. A. Arnot, D. Mackay and M. Bonnell, Estimating metabolic biotransformation rates in fish from laboratory data, Environ. Toxicol. Chem., 2008, 27, 341–351 CAS.
- J. A. Arnot, D. MacKay, T. F. Parkerton and M. Bonnell, A database of fish biotransformation rates for organic chemicals, Environ. Toxicol. Chem., 2008, 27, 2263–2270 CAS.
- J. Kim, F. A. P. C. Gobas, J. A. Arnot, D. E. Powell, R. M. Seston and K. B. Woodburn, Evaluating roles of biotransformation, spatial concentration differences, organism home range, and field sampling design on trophic magnification factors, Sci. Total Environ., 2016, 551–552, 438–451 CrossRef CAS PubMed.
- D. E. Powell, N. Suganuma, K. Kobayashi, T. Nakamura, K. Ninomiya, K. Matsumura, N. Omura and S. Ushioka, Trophic dilution of cyclic volatile methylsiloxanes (cVMS) in the pelagic marine food web of Tokyo Bay, Japan, Sci. Total Environ., 2017, 578, 366–382 CrossRef CAS PubMed.
- R. Froese and D. Pauly, FishBase: A global information system on fishes, http://www.fishbase.ca/home.htm, 2015 Search PubMed.
- C. E. Hebert and K. A. Keenleyside, To normalize or not to normalize? Fat is the question, Environ. Toxicol. Chem., 1995, 14(5), 801–807 CrossRef CAS.
- L. P. Burkhard, K. Borga, D. E. Powell, P. Leonards, D. C. G. Muir, T. F. Parkerton and K. B. Woodburn, Improving the quality and scientific understanding of Trophic Magnification Factors (TMFs), Environ. Sci. Technol., 2013, 47, 1186–1187 CrossRef CAS PubMed.
- D. M. Walters, T. D. Jardine, B. S. Cade, K. A. Kidd, D. C. Muir and P. Leipzig-Scott, Trophic Magnification of Organic Chemicals: A Global Synthesis, Environ. Sci. Technol., 2016, 50(9), 4650 CrossRef CAS PubMed.
- F. A. Gobas and L. G. Maclean, Sediment-water distribution of organic contaminants in aquatic ecosystems: the role of organic carbon mineralization, Environ. Sci. Technol., 2003, 37, 735–741 CrossRef CAS PubMed.
- F. A. P. C. Gobas, J. B. Wilcockson, R. W. Russell and G. D. Haffner, Mechanism of biomagnification in fish under laboratory and field conditions, Environ. Sci. Technol., 1999, 33(1), 133–141 CrossRef CAS.
- D. E. Powell, M. Schøyen, S. Øxnevad, R. Gerhards, T. Böhmer, M. Koerner, J. Durham and D. W. Huff, Bioaccumulation and trophic transfer of cyclic volatile methylsiloxanes (cVMS) in the aquatic marine food webs of the Oslofjord, Norway, Sci. Total Environ., 2017, 622–623, 127–139 Search PubMed.
| This journal is © The Royal Society of Chemistry 2018 |