Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Detection of Posner's clusters during calcium phosphate nucleation: a molecular dynamics study†
Giulia
Mancardi
 a,
Carlos Ernesto
Hernandez Tamargo
a,
Carlos Ernesto
Hernandez Tamargo
 a,
Devis
Di Tommaso
a,
Devis
Di Tommaso
 b and
Nora H.
de Leeuw
b and
Nora H.
de Leeuw
 *ac
*ac
aDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: giulia.mancardi.14@ucl.ac.uk
bSchool of Biological and Chemical Sciences, Queen Mary University of London, Mile End Road, London E1 4NS, UK
cSchool of Chemistry, Cardiff University, Main Building, Park Place, Cardiff, CF10 3XQ, UK. E-mail: deleeuwn@cardiff.ac.uk
First published on 21st July 2017
Abstract
Hydroxyapatite (HA), the main mineral phase of mammalian tooth enamel and bone, originates in body fluids from amorphous calcium phosphate (ACP). ACP presents short-range order in the form of small domains with size of 0.9 nm and chemical formula Ca9(PO4)6, known as Posner's clusters. In this study, the aggregation and clustering of calcium and phosphate ions in water has been investigated by means of shell-model molecular dynamics simulations. Calcium phosphate aggregates form in solution with compositions and Ca coordination that are similar to those found in Posner's cluster, but the stoichiometry of these species is dependent on the ionic composition of the solution: calcium-deficient clusters in solutions with low Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio; cluster containing protonated phosphate groups in neutral solutions; sodium ions partially substituting calcium in solutions containing a mixture of sodium and calcium ions. These Posner-like clusters can be connected by phosphate groups, which act as a bridge between their central calcium ions. The simulations of the aggregation in solution of calcium phosphate clusters are an unbiased and unequivocal validation of Posner's model, and reveal for the first time the structure and composition of the species that form during the early stages of ACP nucleation at a scale still inaccessible to experiment.
P ratio; cluster containing protonated phosphate groups in neutral solutions; sodium ions partially substituting calcium in solutions containing a mixture of sodium and calcium ions. These Posner-like clusters can be connected by phosphate groups, which act as a bridge between their central calcium ions. The simulations of the aggregation in solution of calcium phosphate clusters are an unbiased and unequivocal validation of Posner's model, and reveal for the first time the structure and composition of the species that form during the early stages of ACP nucleation at a scale still inaccessible to experiment.
1 Introduction
Calcium phosphates are the main inorganic components of bone tissue, where they are mainly present as crystalline hydroxyapatite (HA). Under conditions of normal temperature and pressure, HA is the thermodynamically most stable phase of calcium phosphate,1 but despite its supersaturation in body fluids, the direct nucleation of this important biomineral is inhibited in vivo, where other calcium phosphate phases precipitate before HA.2 In particular, amorphous calcium phosphate (ACP) has been proposed as the first phase to nucleate from aqueous solution.3Owing to the importance of calcium phosphate as a biomaterial, several experimental4–6 and theoretical7 studies have focussed on its nucleation and growth. In particular, using X-ray experiments, Betts and Posner discovered in the 1970s that, despite its lack of long-range order, ACP is characterised by spherical domains of approximately 1 nm in size, with a Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P molar ratio of 1.5 and chemical formula Ca9(PO4)6. These clusters, which were later named Posner's clusters, aggregate randomly in solution and form spherical particles, with water molecules filling the intercluster space.8
P molar ratio of 1.5 and chemical formula Ca9(PO4)6. These clusters, which were later named Posner's clusters, aggregate randomly in solution and form spherical particles, with water molecules filling the intercluster space.8
The formation of ACP from the aggregation of Posner's clusters was investigated using several experimental techniques. Onuma and Ito used in situ atomic force microscopy (AFM) to probe the crystal growth of HA in supersaturated body fluid solutions, and found the presence of calcium phosphate clusters with sizes in the range of 0.7 to 1.0 nm.9 They proposed that suitably oriented Posner's clusters are the building units of HA.9,10 Pure HA crystallises in the monoclinic space group P21/b at temperature below 250 °C and in the hexagonal group P63/m above 250 °C.11 However, naturally occurring impurities stabilise bone HA in the hexagonal crystalline form, where the OH− groups are positioned in a statistically disordered fashion along the z-axis.12 The presence of Posner's clusters can be identified clearly in the crystal structure of HA, where they have trigonal symmetry (C3 in the Schoenflies notation) and are stacked along the z direction, sharing half of their volume.13 In 2010, using high-resolution cryo-TEM, Dey et al. proved the existence of nanometric clusters in simulated body fluids, and found that the formation of apatite on an arachidic acid monolayer involves the aggregation of calcium phosphate clusters of size 0.87 ± 0.2 nm that densify in proximity of the monolayer.14 In 2012, using in situ AFM to follow the nucleation of ACP on a calcium carbonate surface, Wang et al. detected nanometric calcium phosphate aggregates that were linked to the presence of Posner's clusters.15 More recently, calcium K-Edge XANES experiments further supported Posner's hypothesis by proposing a hydrated form Ca9(PO4)6(H2O)30 as the structural building unit of ACP. Based on their interpretation of the XANES spectra during the early stages of calcium phosphate nucleation, the authors also considered deviations from the idealised cluster, and proposed the existence of protonated and Ca-deficient Posner-like clusters, as well as clusters containing monovalent counterions (e.g.: Na+, Cl−) to compensate for their negative or positive charges. The authors also observed that phosphate groups can bridge two central calcium ions, thus connecting different clusters.5,6
So far few computational studies have investigated the structure of the Posner's cluster. Yin and Stott performed ab initio Density Functional Theory (DFT) calculations to study the structure and the stability of a Posner's cluster in vacuum and in the presence of some ions normally contained in body fluids (H+, OH−, Na+ and Cl−). Relaxing the structure of a cluster taken from crystalline HA (i.e. having C3 symmetry) the authors found that the cluster loses its symmetry. Moreover, the cluster contracts due to the rearrangement of the ions and the number of Ca–O bonds increases. When the studied cluster binds six protons, it regains the C3 symmetry with an increase in stability; the further addition of six OH− brings about the formation of three water molecules, conserving the C3 symmetry; one or two sodium ions can also bind to the cluster, but without providing the same effect on the stability observed in the case of proton addition. The addition of six chlorine ions to the six protonated cluster leads to an energy decrease and retention of the C3 symmetry, but the authors report that the Cl− are weakly bound to the cluster.16 Treboux et al.17 used ab initio methods (Hartree–Fock level of theory) to compute the stability of [Ca3(PO4)2], its dimer and trimer form, and of the Posner's cluster. They found that in vacuum the most stable cluster is the Posner's, with a S6 symmetry, although there are several isomers within an energy range of a few kcal mol−1. However, these calculations were conducted in vacuum, using pre-assumed structures for the calcium phosphate clusters. Simulations of the behaviour of Posner's clusters in explicit water are thus required in order to obtain a better understanding of the early stages of ACP formation.
This study reports a molecular dynamics (MD) investigation of the aggregation and clustering of calcium and phosphate ions from aqueous solution using a force field model, developed in our group,18 to describe interatomic interactions in calcium phosphate materials, where polarisation effects are included through a shell-model. The aim is to obtain unbiased structural information concerning Posner's cluster that could support the interpretation of experimental data on the processes surrounding the early stages of ACP nucleation and growth.
2 Methods
2.1 Simulation details
MD simulations were performed using version 4.07 of the DL_POLY computational package.19 Our MD protocol consisted in an initial 25 ps equilibration in an NVE ensemble (constant number of particles, constant volume and constant energy), followed by a second 25 ps equilibration in an NVT ensemble (constant number of particles, constant volume and constant temperature). The Ca, Na and P atoms were kept frozen to prevent aggregation in a system not yet in equilibrium. Finally all the ions were let free to diffuse for 5 ns in an NPT ensemble (constant number of particles, constant pressure and constant temperature). This protocol is similar to previous procedures adopted to simulate processes of nucleation and growth.7,20,21 The simulation temperature was set at 310 K (body temperature) and the pressure at 1 bar. The timestep was set to 0.05 fs, which is compatible with the frequency of vibration of the core–shell units. The system cutoff was 8 Å, the Nosé–Hoover algorithm,22,23 with a relaxation time of 0.1 ps, was employed in both NVT and NPT ensembles to ensure consistency between the equilibration and the production runs. Analysis of the temporal behaviour of the total energy, cell volume and temperature shows that all systems considered in the present study have reached equilibrium within the first 200 ps of the production run (Fig. S8–S13 in the ESI†).2.2 Interatomic potential model
The interatomic potential model developed by Ainsworth et al.18 was used to describe the intramolecular and interatomic interactions of calcium–sodium–phosphate species. In this force field, phosphate is described as the sum of a Morse and a Coulombic potential, phosphate bond angles by a harmonic potential, and non-bonded interactions by Buckingham potentials. This force field makes use of a shell model in order to model the atom's electronic polarisability, in which each oxygen anion in the phosphate and hydroxyl groups consists of both a core and a massless shell connected by a spring. The parameters of this force field are listed in the ESI,† Table S5.The water molecules were described using two models: TIP3P,24 and the core–shell potential originally developed by De Leeuw and Parker20 with the modification introduced by Kerisit and Parker.25 The radial distribution functions (RDFs) of both types of water are reported in the ESI,† Fig. S2–S5. No significant differences in terms of either aggregation or shape of the calcium phosphate species were observed when comparing the results obtained using the TIP3P and core–shell water models. The results reported in the manuscript have been obtained using the water shell model,25 as the polarisability of the oxygen ions is explicitly included,26 and it allows better compatibility with the force field for the phosphate ions, which are also described using a core–shell potential.
The structure of a single Posner's cluster in 101 water molecules was also investigated using ab initio MD simulations using the computational details adopted in our previous study of calcium phosphate prenucleation complexes.27 The Cac–Ca, Cac–O, Cac–P, P–P, P–O and O–O pair distribution functions (where Cac is the central calcium of the Posner's cluster) obtained from classical and ab initio methods compare very well (see Fig. S6 and Table S6 in ESI†) and justify the use of the force field employed in this study.
2.3 Computational protocol
Supersaturation is the thermodynamic driving force for the crystal nucleation of a solid phase from a solution28 and body fluids are supersaturated with respect to HA. However, a simulation box truly representative of the concentrations of calcium and phosphate ions found in physiological solutions (2.5 mmol l−1) is computationally unfeasible as the number of particles would be too large and the timescale required to observe spontaneous aggregation of calcium phosphate particles too long. As such, artificially high supersaturation conditions were applied to induce the nucleation process.29Table 1 summarises the characteristics of the simulated solutions considered in the present study. Solution I corresponds to a calcium concentration, [Ca2+], equal to 0.65 mol l−1 generated by adding 44 Ca2+ ions in a cubic box dimension 50 × 50 × 50 Å, together with a mixture of H2PO4− and HPO42− with ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, both normally present at pH 7.4 (i.e. body fluid condition).30 Lower Ca2+ concentrations of 0.1 mol l−1 (8 Ca2+) and 0.3 mol l−1 (20 Ca2+) were also tested but after 5 ns of MD simulations statistically relevant populations of clusters were not observed. Solution II only contains Ca2+ and PO43− ions in order to be consistent with the composition of ACP. Solution III contained higher [Ca2+] and [PO43−] in order to induce the formation of larger calcium phosphate clusters. In body fluids and plasma, Na+ ions are far more concentrated than Ca2+.31 Consequently, we considered the effect of sodium ions on the aggregation of phosphate species in solution by replacing half Ca2+ in solutions I, II and III with Na+. In Table 1, these solutions are named Ia, IIa and IIIa, respectively.
3, both normally present at pH 7.4 (i.e. body fluid condition).30 Lower Ca2+ concentrations of 0.1 mol l−1 (8 Ca2+) and 0.3 mol l−1 (20 Ca2+) were also tested but after 5 ns of MD simulations statistically relevant populations of clusters were not observed. Solution II only contains Ca2+ and PO43− ions in order to be consistent with the composition of ACP. Solution III contained higher [Ca2+] and [PO43−] in order to induce the formation of larger calcium phosphate clusters. In body fluids and plasma, Na+ ions are far more concentrated than Ca2+.31 Consequently, we considered the effect of sodium ions on the aggregation of phosphate species in solution by replacing half Ca2+ in solutions I, II and III with Na+. In Table 1, these solutions are named Ia, IIa and IIIa, respectively.
| Ca2+ | [Ca2+] (mol l−1) | Na+ | [Na+] (mol l−1) | H2PO4− | HPO42− | PO43− | H2O | |
|---|---|---|---|---|---|---|---|---|
| Solution I | 44 | 0.65 | 0 | 0.00 | 22 | 33 | 0 | 4497 |
| Solution II | 45 | 0.66 | 0 | 0.00 | 0 | 0 | 30 | 4679 |
| Solution III | 150 | 2.32 | 0 | 0.00 | 0 | 0 | 100 | 4136 |
| Solution Ia | 22 | 0.33 | 44 | 0.66 | 22 | 33 | 0 | 4477 |
| Solution IIa | 22 | 0.32 | 46 | 0.67 | 0 | 0 | 30 | 4652 |
| Solution IIIa | 75 | 1.17 | 150 | 2.34 | 0 | 0 | 100 | 4044 |
2.4 Structural criteria for the detection of Posner's clusters
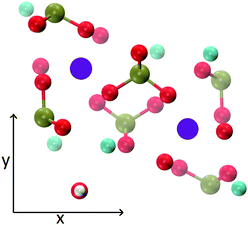
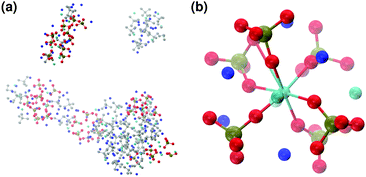
The MD trajectories of the solutions considered in the present study were analysed in order to identify the portions of the calcium–phosphate aggregates forming during the simulations which resemble the Posner's cluster in Fig. 1. In our simulations in water, however, many factors can alter the structure of the highly symmetric cluster identifiable in the crystal: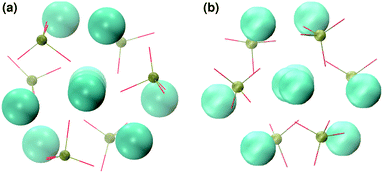 | ||
| Fig. 1 Projection on the xy plane of (a) Posner's cluster in hydroxyapatite, C3 symmetry; (b) Posner's cluster in water, simulated with the force field of Ainsworth et al.18 Colour key Ca: light blue, P: green, O: red. | ||
• Isolated the cluster loses its symmetry;13 our Classical MD and ab initio MD of a single Posner's cluster in water confirmed this finding;
• At pH 7.4, the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio is 0.8, and therefore only Ca-deficient clusters are observed during the simulations;
P ratio is 0.8, and therefore only Ca-deficient clusters are observed during the simulations;
• Other ions present in solution (in our case Na+) may substitute calcium.
In particular, a group of ions were defined as a Posner's cluster when 6 to 8 peripheral (Ca + Na) ions and 6 phosphate groups surrounded a central calcium ion (Cac). Cation-deficient clusters (i.e. 6 or 7 out of 8 cations) were also considered, because these calculations focus on the early stages of aggregation and further Ca binding occurs at a second stage.4 A calcium (or a sodium) ion or a phosphate group was considered to be part of a Posner's cluster when the Cac–Ca, Cac–Na and Cac–P distances were shorter than 5.0 Å. This value is larger than the position of the first minimum of the RDFs of the Cac–Ca (4.35 Å) and Cac–P (4.15 Å) pairs obtained from MD simulations of a single Posner's cluster in water. This allowed to consider slightly distorted Posner-like clusters during the analysis.
Phosphate groups can bridge different Cac, thus contributing to the formation of more than one Posner-like cluster. The P–Cac coordination number (CN) during the simulations was computed using the formula:
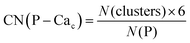 | (1) |
Crystalline HA is made up of superimposed Posner's clusters with opposite chirality. Each phosphate group bridges two Cac in the xy plane, as shown in Fig. 2. Along the z direction, Posner's clusters are stacked, i.e. when considering a cluster centred at the Cac site at level z = 0, its neighbours are centred respectively at level z = +1/2 and level z = −1/2 and share three phosphate groups with the one centred at level z = 0; meaning that in the z direction each phosphate bridges two additional Cac.13 Given that in a single unit cell of HA there are six phosphorous atoms and four Cac sites, which are at the centre of different Posner's clusters, then in the crystal structure the CN(P–Cac) is equal to:
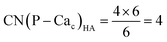 | (2) |
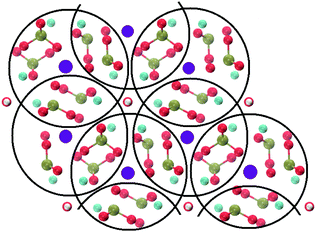 | ||
| Fig. 2 Projection on the xy plane of crystalline HA, with Posner's clusters circled in black. Colour key Ca1: purple, Ca2: light blue, P: green, O: red, H: white. | ||
3 Results
3.1 Symmetry of the Posner's cluster
The unit cell of HA, Ca10(PO4)6(OH)2, contains 10 Ca atoms, four of which can be named, according to their coordination environment, Ca1 and the remaining six Ca2 (see Fig. 3).32 Ca1 form columns that are perpendicular to the xy plane, whereas Ca2 are arranged in triangles around the hydroxyl groups, which form hexagonal channels along the z-direction. Each Ca1 is surrounded by 9 oxygen atoms belonging to six phosphate groups, whereas the Ca2 coordinate to six oxygen atoms from phosphates and one hydroxyl group.Fig. 1(a) shows the structure of a Posner's cluster within the crystalline structure of HA. The cluster consists of three calcium ions of type Ca1 stacked in the centre, with the middle one (Cac) coordinating six phosphate groups. The negative charge is then compensated by further coordination of six calcium ions of type Ca2 in HA; the symmetry of the cluster is C3. Because of the superimposition of the Posner clusters, in crystalline HA each Ca1 is also a Cac. The SymmetryTool plugin33 of the Visual Molecular Dynamics (VMD) software was used to analyse the symmetry of the Posner's cluster in Fig. 1(a), with coordinates taken from the Crystallographic Information File of HA.34 The Ca atoms alone, or the combination Ca + P, gives C2 symmetry, whereas a C3 symmetry is obtained when considering only P atoms, only O atoms, Ca + O atoms, P + O atoms or the entire cluster (see ESI,† Fig. S7). MD simulations of a single Posner's cluster in a 50 Å water box were then conducted using the force field of Ainsworth et al.18 where a loss of symmetry occurs as a result of the bonding of water to the outer layer atoms of the cluster (see Fig. 1(b)). According to Yin et al.,16 in vacuum the relaxation of the Posner's cluster causes a loss of the C3 symmetry, a contraction of the cluster radius to 4.35 Å, and an increase of the Ca–O coordination number. Conversely, the cluster radius increases to ≈5.25 Å during the simulation in water, which is due to the decrease of the Ca–O intracluster coordination as the outer layer of Ca ions interacts with water molecules (see ESI:† Tables S6–S8). Integration of the Cac–Owt radial distribution function (Cac is the central calcium of the Posner's cluster and Owt is the oxygen of water) gives an average of 25 water molecules in the first solvation sphere of the Posner's cluster. A recent Ca K-edge XANES study on wet-ACP redefined the idealised cluster model for the structural unit of ACP originally postulated by Du et al.5 as a cluster composed by a central Ca2+ and eight peripheral Ca2+ ions, each of which is coordinated to three to four water molecules.6 This leads to a total number of water molecules in the range 24–32, in agreement with the results obtained from our classical MD simulation.
3.2 Aggregation of Ca2+, H2PO4− and HPO42− ions in solution
In this section, the aggregation of calcium and phosphate ions in solution at neutral pH, which is close to physiological conditions, is reported (solution I in Table 1).In this solution the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ration is equal to 0.8. Experimental studies have shown that the aggregation of calcium and phosphate ions results in the formation of Ca-deficient clusters, which then incorporate other calcium ions from the solution, thereby increasing the Ca
P ration is equal to 0.8. Experimental studies have shown that the aggregation of calcium and phosphate ions results in the formation of Ca-deficient clusters, which then incorporate other calcium ions from the solution, thereby increasing the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio, releasing protons, and consequently lowering the pH of the solution.4,35 Xie and co-workers have also suggested that Ca-deficient clusters form because of the lower dehydration energy of the hydrogen phosphate (+299 kcal mol−1) and dihydrogen phosphate (+68 kcal mol−1) ions compared with Ca2+ (+381 kcal mol−1).35 In the original Posner's cluster, the Ca
P ratio, releasing protons, and consequently lowering the pH of the solution.4,35 Xie and co-workers have also suggested that Ca-deficient clusters form because of the lower dehydration energy of the hydrogen phosphate (+299 kcal mol−1) and dihydrogen phosphate (+68 kcal mol−1) ions compared with Ca2+ (+381 kcal mol−1).35 In the original Posner's cluster, the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio is 1.5 but such a large amount of calcium is not available in the solutions I and Ia, and Posner-like clusters made of six phosphate and nine cations were therefore not observed during the simulations. Thus, the minimum amount of calcium ions in a calcium–phosphate aggregate to be considered a Posner-like cluster was set to seven (Cac + 6Ca). This criterion is based on the symmetry considerations mentioned above, namely six phosphate groups are enough to provide Posner's C3 symmetry, and on the fact that Ca-deficient clusters have been detected experimentally during the early stages of CaP nucleation.35 For consistency, the same thresholds for Ca–Ca and Ca–P coordination numbers were used to analyse the other solutions considered in this study.
P ratio is 1.5 but such a large amount of calcium is not available in the solutions I and Ia, and Posner-like clusters made of six phosphate and nine cations were therefore not observed during the simulations. Thus, the minimum amount of calcium ions in a calcium–phosphate aggregate to be considered a Posner-like cluster was set to seven (Cac + 6Ca). This criterion is based on the symmetry considerations mentioned above, namely six phosphate groups are enough to provide Posner's C3 symmetry, and on the fact that Ca-deficient clusters have been detected experimentally during the early stages of CaP nucleation.35 For consistency, the same thresholds for Ca–Ca and Ca–P coordination numbers were used to analyse the other solutions considered in this study.
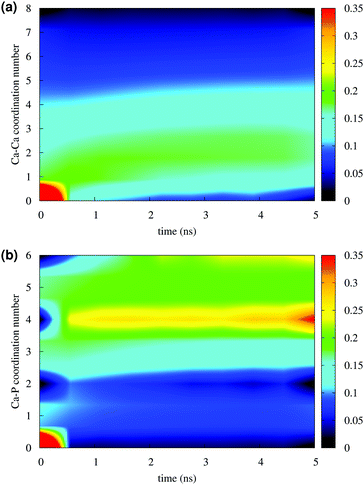
Fig. 4 reports the variation of the Ca–Ca and Ca–P coordination numbers during the simulation of solution I. The colour scale corresponds to the fraction of the total Ca having the coordination number specified on the y axis. An increase in coordination number is due to the loss of water molecules coordinated to Ca2+ ions and the aggregation process. Note that this process takes place during the first 0.5 ns. Throughout the simulation, the Ca–Ca coordination remains low, as more than 50% of Ca ions have other four or less Ca ions in close proximity (Fig. 4(a)), 35% or more Ca ions are coordinated to four phosphate groups and about 25% were surrounded by six phosphates (Fig. 4(b)), as in the Posner's cluster (Fig. 1(a)). Analysis of the simulation of solution I detects an average of fewer than two clusters, probably because of the low Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio (0.8) in the solution.
P ratio (0.8) in the solution.
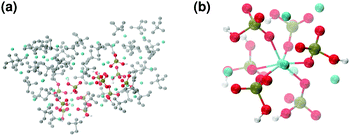
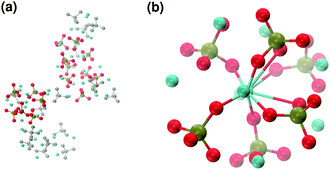
These clusters have symmetry C1 and are characterised by only 6–7 calcium ions, rather than 8 as in the Posner's model,8 and they are mainly formed of HPO42− rather than H2PO4− ions. This is probably due to the larger population at neutral pH of the hydrogen phosphate anions, but it could also be explained in terms of the preference of Ca2+ to coordinate to the double negatively charged monohydrogenphosphate ion (see ESI,† Fig. S14–S16). Fig. 5(a) displays the structure of the calcium phosphate aggregate at 5 ns, with the atoms forming Posner-like clusters in colour, and the atoms not participating in the clusters in grey. In Fig. 5(b) it is possible to discern a single Posner-like cluster with formula [Ca7(H2PO4)(HPO4)5]3+, where the central Ca coordinates six phosphate groups. The phosphates are arranged in a pseudo-octahedral geometry, whereas the outer layer is composed of six calcium ions which do not show any particular order. The three Ca ions in the centre of the cluster are not properly aligned as in the HA crystal (see Fig. 1), but the effect of the solvating water needs to be taken into account, which displaces the ions causing the cluster to lose the C3 symmetry, as observed during the MD simulation of a single Posner's cluster in water (Fig. 1(b)).
Bone HA is a highly substituted material. The amounts of CO32−, F−, Na+ and Mg+ depend on the bone site and the age of the subject.36 Half of the sodium present in a human body is stored in the bones, where it preferentially substitutes Ca2 in the HA lattice and is mainly located at the bone surface.37
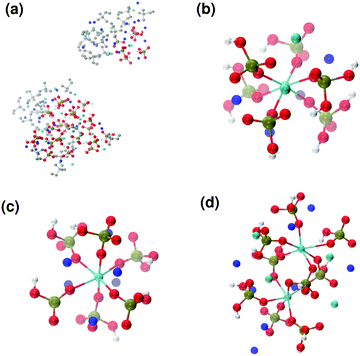
Fig. 6 reports clusters obtained from the simulation of Solution Ia (see Table 1), where half of Ca2+ are substituted by Na+. The presence of Na+ ions in solution inhibits the formation of large aggregates and only two medium size aggregates (≈15 Å and 24 Å in their longest direction) grow during the simulation (Fig. 6(a)). Posner-like clusters contain up to three Ca ions around the central one, and Na ions occupy some of the positions vacated by Ca. In Fig. 6(b) a cluster with formula [Ca3Na4(H2PO4)3(HPO4)3]+ is shown, where only one of the Ca2+ forming the outer layer of the cluster is aligned with the Cac and the other cations are packed in a disorderly fashion around the phosphate groups. Another example of a cluster obtained during the simulation is shown in Fig. 6(c), [CaNa6(HPO4)6]4−, where the central calcium ion is surrounded by six phosphate groups with six sodium ions partially counterbalancing the negative charge. Lastly, in Fig. 6(d) two clusters that have three phosphate groups bridging the two Cac are presented. In this structure, the average CN(P–Cac) is equal to 1.33 according to eqn (1).
The formation of positively and negatively charged clusters should not come as a surprise, as they are part of a larger aggregate that is not classified as a Posner-like structure, according to the criteria discussed in Section 2.4. Moreover, charged entities in solution have been detected experimentally during the early stages of calcium phosphate formation.4
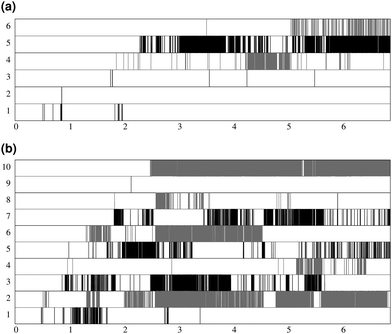
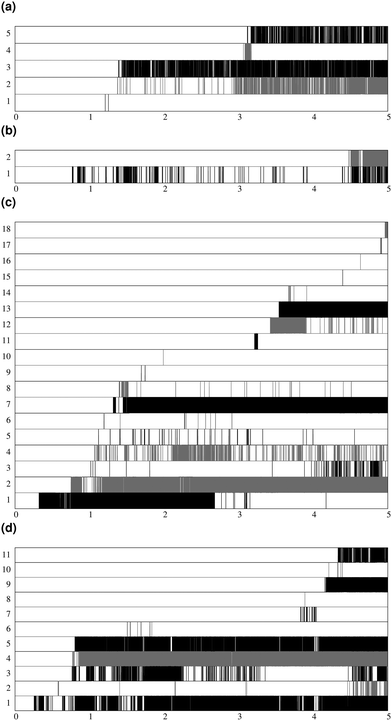
Fig. 7 shows the lifespan of the Posner-like clusters during 6.5 ns of trajectory. Each stripe refers to a Posner-like cluster centered on a different calcium ion. A stripe is shadowed when the Posner-like cluster is satisfying the criteria for Ca–P and Ca–Ca distances and coordination numbers, discussed in Section 2.4, whereas it is white for frames where the Posner-like cluster is not satisfying any of the criteria (i.e. it is not yet formed or it suffers structural distortions). In a solution of Ca2+, H2PO4− and HPO42−, a total of six different clusters appears (six horizontal stripes in the plot), whereas after introducing Na+ ten clusters are formed. As such, the plots in Fig. 7 suggest that sodium not only favours the formation of Posner-like clusters in a solution containing protonated phosphate species, but it also increases the structural stability of the clusters, evidenced by stripes with more regions coloured in grey or black. We reason that sodium ions are able to effectively counter-balance the low negative charges of the protonated phosphates, and are a valid substitute to calcium.
3.3 Aggregation of Ca2+ and PO43−
Our simulations of the aggregation of Ca2+ and PO43− mimic the subsequent stages of the aggregation process, after the release of the protons bound to the phosphate species. No OH− ions were added to the solution, as the first complexes originating from solution are calcium phosphate ion associations, and the OH− incorporates in a further stage of HA crystallisation.7Solution II only contains Ca2+ and PO43− ions and the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio corresponds to that in the original Posner's cluster and in ACP (Ca
P ratio corresponds to that in the original Posner's cluster and in ACP (Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 1.5). After 5 ns of simulation, five different Posner-like clusters form in solution: neutral ones with the same stoichiometry as Posner's cluster (see Fig. 8(b)) and Ca-deficient complexes, [Ca8(PO4)6]2−, occurring when adjacent clusters share phosphate groups.
P = 1.5). After 5 ns of simulation, five different Posner-like clusters form in solution: neutral ones with the same stoichiometry as Posner's cluster (see Fig. 8(b)) and Ca-deficient complexes, [Ca8(PO4)6]2−, occurring when adjacent clusters share phosphate groups.
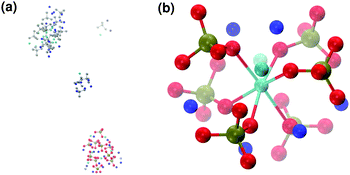
When substituting half of the calcium ions by sodium (solution IIa), a Posner-like cluster with formula [Ca3Na6(PO4)6]6− forms during the first 4.5 ns of the trajectory (Fig. 9(b)). This cluster is formed by six phosphate groups and only three Ca ions aligned in the centre of the cluster, whereas six sodium ions complete the clusters occupying the outer cationic positions. A second cluster, sharing part of the phosphate ions with the first one, appears after 4.5 ns, giving a final chemical formula Ca7Na16(PO4)10 and a CN(P–Cac) of 1.20.
Calcium and sodium have similar ionic radii, and thus Na could potentially occupy any cationic position in the Posner-like clusters. Nevertheless, analysis of the MD simulations shows a preference by Na to position itself in the outer cationic positions, i.e. the HA Ca2 sites, confirming the findings of El Feki et al. who experimentally studied substitutions of sodium and carbonate in HA.38 This also agrees with the preference of other impurity cations such as Mg2+ and Zn2+ for the Ca2 sites.32,39
Contrary to the case discussed in Section 3.2, sodium disfavours clustering upon complete deprotonation of the phosphate groups. This opposite tendency can be explained in terms of the higher negative charge of PO43−, compared to HPO42− and H2PO4−, which require doubly charged cations to counterbalance the charge. Consequently, substitution of Ca2+ by Na+ provokes a reduction in the clustering process.
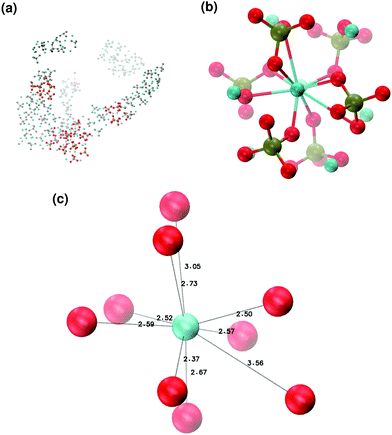
In order to promote the formation of larger clusters, the concentration of calcium ions in solution was increased to approximately [Ca2+] = 2.3 mol l−1. The formation of several Posner-like clusters takes place already during the first ns of simulation. These clusters are stable throughout the simulation, although their structure distorts during the dynamics and does not therefore satisfy the criteria previously imposed for them to be classified as Posner's cluster. Fig. 10(a) shows the structure of the aggregates after 5 ns, whose shape is needle-like instead of spherical as in the solution containing Ca2+, HPO4− and H2PO42− (Fig. 5(a)) and in the solution containing Ca2+, Na+, HPO4− and H2PO42− (Fig. 6(a)). Fig. 10(b) shows an example of the cluster with formula Ca9(PO4)6 obtained during the simulation, where three Ca1 are properly aligned, and the central calcium ion is coordinated to nine oxygens as in HA. Comparison of the distances with those reported by Laurencin et al. for HA32 indicates that the Ca1–O distances, shown in Fig. 10(c), are slightly longer. In particular we have only three oxygens at less than 2.55 Å and two at distances larger than 3.0 Å from the calcium, whereas these authors have reported six out of nine oxygens below 2.55 Å and three oxygens at 2.77 Å. The symmetry analysis with the VMD Symmetry tool gives an Oh point group when considering the phosphorous atoms or the calcium ions, with a tolerance of 0.23; taking into account both Ca and P at the same time, we obtained the Oh point group with a tolerance of 0.28.
In the presence of sodium with a Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca ratio of 2
Ca ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the aggregates are similar in shape to those obtained without sodium (see Fig. 11(a)) but a smaller number of different Posner-like clusters forms (see Fig. 12). The clusters have a lower level of symmetry when compared to those obtained without sodium, where C2 is the point group with highest symmetry obtained considering Ca and P sites; the C2 cluster is shown in Fig. 11(b). Other clusters obtained in the same trajectory, however, belong to the point group Cs, or they present no elements of symmetry at all. In general, the calcium ions have to be aligned with the central one (i.e. Ca1 in HA) in order to confer some sort of symmetry.
1, the aggregates are similar in shape to those obtained without sodium (see Fig. 11(a)) but a smaller number of different Posner-like clusters forms (see Fig. 12). The clusters have a lower level of symmetry when compared to those obtained without sodium, where C2 is the point group with highest symmetry obtained considering Ca and P sites; the C2 cluster is shown in Fig. 11(b). Other clusters obtained in the same trajectory, however, belong to the point group Cs, or they present no elements of symmetry at all. In general, the calcium ions have to be aligned with the central one (i.e. Ca1 in HA) in order to confer some sort of symmetry.
During the aggregation of Ca2+ and PO43−, the effect of sodium is opposite to what we observe in solutions I and Ia: there are more different Posner-like clusters without sodium. Furthermore under these conditions sodium shows itself to be a valid substitute for calcium in the external layer of the Posner-like clusters, as we experience various degrees of Na/Ca substitutions. We observe sharing of some of the phosphate ions among the clusters, as also found in the solution Ia.
4 Discussion
Under the solution conditions considered in the present study, the aggregation of calcium phosphate species takes place spontaneously during the first ns of the simulations and the coordination environment around the calcium ions does not show significant variations thereafter (see Fig. 4 and ESI,† 2D plots in Fig. S14–S17). The aggregates are spherical in the presence of protonated phosphate species, whereas they tend to be more fragmented and needle-like when constituted by PO43− ions. In general, they are flexible and may resemble the liquid-like ionic polymers observed for homogeneous nucleation of calcium carbonate by Demichelis et al.40The position of the first peaks in the Cac–Ca, Cac–P, Cac–Oph and Cac–Na RDFs of the Posner-like clusters detected during the simulations are in very good agreement with the RDF of the single Posner cluster in water (see ESI,† Fig. S18–S23). The Cac–P first peak positions also match in the presence of protonated phosphates (solution I, Fig. S18, ESI†), and the introduction of Na+ does not influence the Cac–Ca, Cac–P or Cac–Oph distances in the Posner-like clusters (solution Ia, Fig. S21, solution IIa, Fig. S22 and solution IIIa, Fig. S23, ESI†).
To form HA, each phosphate group needs to bridge four Ca1, resulting in a CN(P–Cac) equal to 4, where Cac is equivalent to Ca1 in the crystal structure of HA (all the Ca1 atoms are the centres of Posner clusters in a stoichiometric crystal) and represents the centre of a Posner cluster. The CN(P–Cac) is therefore an important measure of the progression from the early aggregates of calcium phosphate in solution to the formation of the solid phase. Table 2 reports the average CN(P–Cac) for each simulated solution considered in the present study, which have been calculated applying eqn (1) to the frames containing two or more clusters and some degree of phosphate bridging (i.e. CN(P–Cac) > 1). The CN(P–Cac) do not present significant differences between solutions I and Ia. Considering solutions II and IIa, the CN(P–Cac) is higher in the absence of sodium. Comparing the highly concentrated solutions III and IIIa, the CN(P–Cac) is larger in the presence of sodium, which is probably due to the inability of sodium to efficiently compensate the highly negative charges of the orthophosphate anions; here the clusters need to share part of the phosphate groups in order to maximise the interaction with the fewer Ca2+ ions. Contrary to what one might expect, the CN(P–Cac) decreases in more concentrated solutions (CN(P–Cac) in solution II and IIa is larger than in solutions III and IIIa) because a higher concentration leads to the formation of more clusters, which are not necessarily bridged, as they are diluted in a larger aggregate.
In the neutral solutions I and Ia, which simulate the process taking place in the early stages of calcium phosphate aggregation in body fluids, sodium can efficiently substitute calcium to generate a larger number of Posner-like clusters. Interestingly, the Ca-deficient clusters and the spherical aggregates obtained from the simulations fit into the post-nucleation stage discussed by Habraken et al., who described spherical aggregates with a Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio equal to 0.67 and post-nucleation clusters with formula [Ca2(HPO4)3]2−.4 Analysis of the simulations indeed reveals that (1) the central calcium may coordinate fewer than 8 outer calcium ions, (2) the Ca
P ratio equal to 0.67 and post-nucleation clusters with formula [Ca2(HPO4)3]2−.4 Analysis of the simulations indeed reveals that (1) the central calcium may coordinate fewer than 8 outer calcium ions, (2) the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio during the nucleation stage can be lower than 1.5 (typical of ACP), (3) other ions normally present in body fluids can substitute calcium and phosphates (in particular we verified the ability of sodium to replace calcium), and (4) some phosphate ions act as bridging ligands connecting different Posner-like clusters. In fact, the Posner-like clusters obtained in our simulations validate the assumptions of Du et al. that non-idealised clusters exist in solution.5 Lastly, the formation of clusters containing both H2PO4− and HPO42− is in agreement with experiment, because NMR studies show that HPO4− ions are present at the bone surface,41 and a certain degree of phosphate protonation (5–15%) is typical of ACP originating from a neutral solution.42
P ratio during the nucleation stage can be lower than 1.5 (typical of ACP), (3) other ions normally present in body fluids can substitute calcium and phosphates (in particular we verified the ability of sodium to replace calcium), and (4) some phosphate ions act as bridging ligands connecting different Posner-like clusters. In fact, the Posner-like clusters obtained in our simulations validate the assumptions of Du et al. that non-idealised clusters exist in solution.5 Lastly, the formation of clusters containing both H2PO4− and HPO42− is in agreement with experiment, because NMR studies show that HPO4− ions are present at the bone surface,41 and a certain degree of phosphate protonation (5–15%) is typical of ACP originating from a neutral solution.42
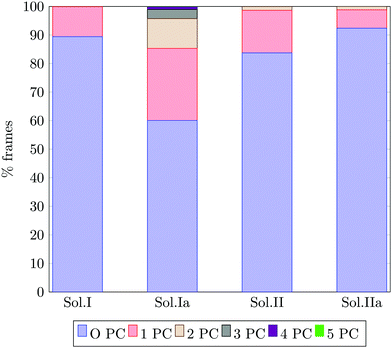
Fig. 13 reports the percentage of trajectory frames with zero, one or more Posner-like clusters. This graph suggests that the increase of the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio from 0.8 (solution I) to 1.5 (solution II) leads to the formation of more Posner-like clusters. This is evidenced by the increase in the number of MD frames with one or more clusters from 10.6% to 16.3%.
P ratio from 0.8 (solution I) to 1.5 (solution II) leads to the formation of more Posner-like clusters. This is evidenced by the increase in the number of MD frames with one or more clusters from 10.6% to 16.3%.
The aggregates originated in solutions I and Ia resemble the apatite-like structure of superficial bone tissue in contact with body fluids, where some of the phosphate ions are protonated and the sodium ions occupy a number of Ca2 sites.36 We observed that upon addition of Na ions, the proportion of frames with one or more Posner-like clusters significantly increases from 10.6% to 40%, and up to five clusters form simultaneously in solution Ia, with Na effectively occupying Ca2 positions. At the same time, the aggregates from solution II resemble the deep bone mineral phase, which is poor in hydrogen phosphate and sodium. The analysis of solutions II and IIa shows a clear decrease in the formation of Posner-like clusters in the presence of sodium ions: the percentage of frames with one or more Posner-like clusters decreases from 16.3% (solution II) to 7.4% (solution IIa). Our data suggest that the effect of sodium on the formation of the mineral phase depends on the counter ions present in solution: sodium is enhancing the clustering in the presence of HPO42− and H2PO4−, while it is inhibiting clustering in presence of PO43−. This trend is supported by experimental findings,36 which show the presence of Ca, Na and protonated phosphates at the surface of bones, and of Ca and PO43− in the deep tissue. We explained this phenomenon considering the charges of the ions: the 3-negative charge of PO43− is more efficiently counterbalanced by Ca2+ than Na+. Therefore, the Na+ ions, which help to form Posner-like clusters during the early stage of nucleation, should be replaced by Ca2+ in order to promote the formation of Posner-like clusters as the hydrogenated phosphates start to release the protons, explaining why sodium is found only in traces in bone tissue.43 The expulsion of a proton from a H2PO4− or a HPO42− leads to a more negatively charged phosphate ion, which is able to coordinate Ca2+ in solution, raising the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio of the ion association. Provided that the newly incorporated Ca2+ was already part of a calcium phosphate aggregate, the phosphate acts as a bridging ligand between two calciums, increasing its P–Ca coordination towards the value of 4 as found in HA.
P ratio of the ion association. Provided that the newly incorporated Ca2+ was already part of a calcium phosphate aggregate, the phosphate acts as a bridging ligand between two calciums, increasing its P–Ca coordination towards the value of 4 as found in HA.
5 Conclusions
In the present work, the aggregation of calcium and phosphate ions in water at body temperature and physiological pH was studied by means of classical Molecular Dynamics simulations. The aggregation of Ca2+ and PO43− in solution was also considered, in order to reproduce the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio and composition found in solid amorphous calcium phosphate. Under neutral pH conditions, Posner-like clusters deficient in calcium ions and composed of protonated phosphate groups form spontaneously during the simulation after a few ns. Sodium ions in solution, which are normally present in body fluids, were also considered and it was found that they can replace calcium in the outer layer of the Posner's cluster. The symmetry of the clusters originated at neutral pH is C1 (as it is in vacuum16), although the alignment of two calcium ions with the central one and the presence of deprotonated phosphate groups confers a higher symmetry to the cluster. Two or more clusters can share part of their ions, since one or more of their phosphate groups bridge two central calciums, as already observed in experiment5 and during MD simulations of Ca2+, PO43− and OH− clustering at a collagen template.7
P ratio and composition found in solid amorphous calcium phosphate. Under neutral pH conditions, Posner-like clusters deficient in calcium ions and composed of protonated phosphate groups form spontaneously during the simulation after a few ns. Sodium ions in solution, which are normally present in body fluids, were also considered and it was found that they can replace calcium in the outer layer of the Posner's cluster. The symmetry of the clusters originated at neutral pH is C1 (as it is in vacuum16), although the alignment of two calcium ions with the central one and the presence of deprotonated phosphate groups confers a higher symmetry to the cluster. Two or more clusters can share part of their ions, since one or more of their phosphate groups bridge two central calciums, as already observed in experiment5 and during MD simulations of Ca2+, PO43− and OH− clustering at a collagen template.7
The simulations reported in this study represent the first theoretical investigation of the structure of the Posner's cluster in solution, and confirm the formation of these species in the early stages of calcium phosphate crystallisation from solution, supporting previous experimental findings.
Future investigations on calcium phosphate aggregation in the presence of other cations (e.g.: K+, Mg2+) and anions (e.g.: Cl−, HCO3−, SO42−), also normally present in body fluids, will provide further understanding of such important processes.
Acknowledgements
We thank EPSRC for funding of a studentship. This work has used the computational facilities of the Advanced Research Computing @ Cardiff (ARCCA) Division, Cardiff University, Wales' national supercomputing service HPC Wales, and ARCHER UK National Supercomputing Service (http://www.archer.ac.uk) via our membership with the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202).References
- W. A. House, Environ. Technol., 1999, 20, 727–733 CrossRef CAS
.
- S. Jiang, H. Pan, Y. Chen, X. Xu and R. Tang, Faraday Discuss., 2015, 179, 451–461 RSC
.
- M. J. J. M. van Kemenade and P. L. de Bruyn, J. Colloid Interface Sci., 1987, 118, 564–585 CrossRef CAS
.
- W. J. E. M. Habraken, J. Tao, L. J. Brylka, H. Friedrich, L. Bertinetti, A. S. Schenk, A. Verch, V. Dmitrovic, P. H. H. Bomans, P. M. Frederik, J. Laven, P. van der Schoot, B. Aichmayer, G. de With, J. J. DeYoreo and N. a. J. M. Sommerdijk, Nat. Commun., 2013, 4, 1507 CrossRef PubMed
.
- L.-W. Du, S. Bian, B.-D. Gou, Y. Jiang, J. Huang, Y.-X. Gao, Y.-D. Zhao, W. Wen, T.-L. Zhang and K. Wang, Cryst. Growth Des., 2013, 13, 3103–3109 CAS
.
- Q. Zhang, Y. Jiang, B. D. Gou, J. Huang, Y. X. Gao, J. T. Zhao, L. Zheng, Y. D. Zhao, T. L. Zhang and K. Wang, Cryst. Growth Des., 2015, 15, 2204–2210 CAS
.
- N. Almora-Barrios and N. H. de Leeuw, Cryst. Growth Des., 2012, 12, 756–763 CAS
.
- F. Betts and A. Posner, Mater. Res. Bull., 1974, 9, 353–360 CrossRef CAS
.
- K. Onuma and A. Ito, Chem. Mater., 1998, 10, 3346–3351 CrossRef CAS
.
- A. Oyane, K. Onuma, T. Kokubo and A. Ito, J. Phys. Chem. B, 1999, 103, 8230–8235 CrossRef CAS
.
- S. V. Dorozhkin and M. Epple, Angew. Chem., Int. Ed., 2002, 41, 3130–3146 CrossRef CAS PubMed
.
- M. Corno, A. Rimola, V. Bolis and P. Ugliengo, Phys. Chem. Chem. Phys., 2010, 12, 6309–6329 RSC
.
- G. Treboux, P. Layrolle, N. Kanzaki, K. Onuma and A. Ito, J. Am. Chem. Soc., 2000, 122, 8323–8324 CrossRef CAS
.
- A. Dey, P. H. H. Bomans, Müller F. a., J. Will, P. M. Frederik, G. de With and N. a. J. M. Sommerdijk, Nat. Mater., 2010, 9, 1010–1014 CrossRef CAS PubMed
.
- L. Wang, S. Li, E. Ruiz-Agudo, C. V. Putnis and A. Putnis, CrystEngComm, 2012, 14, 6252 RSC
.
- X. Yin and M. J. Stott, J. Chem. Phys., 2003, 118, 3717–3723 CrossRef CAS
.
- G. Treboux, P. Layrolle, N. Kanzaki, K. Onuma and A. Ito, J. Phys. Chem. A, 2000, 104, 5111–5114 CrossRef CAS
.
- R. I. Ainsworth, D. Di Tommaso, J. K. Christie and N. H. de Leeuw, J. Chem. Phys., 2012, 137, 234502 CrossRef PubMed
.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911 RSC
.
- N. H. de Leeuw and S. C. Parker, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 13901–13908 CrossRef CAS
.
- J. Ma, J. Mater. Sci., 2014, 49, 3099–3106 CrossRef CAS
.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef
.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef
.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS
.
- S. Kerisit and S. C. Parker, J. Am. Chem. Soc., 2004, 126, 10152–10161 CrossRef CAS PubMed
.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90–103 CrossRef
.
- G. Mancardi, U. Terranova and N. H. de Leeuw, Cryst. Growth Des., 2016, 16, 3353–3358 CAS
.
- D. Kashchiev and G. M. van Rosmalen, Cryst. Res. Technol., 2003, 38, 555–574 CrossRef CAS
.
- J. Anwar and D. Zahn, Angew. Chem., Int. Ed., 2011, 50, 1996–2013 CrossRef CAS PubMed
.
-
J. H. Weaver and P. R. Frederikse, CRC Handbook of Chemistry and Physics (Internet Version), CRC Press, 2016, pp. 592–593 Search PubMed
.
- A. Oyane, H.-M. Kim, T. Furuya, T. Kokubo, T. Miyazaki and T. Nakamura, J. Biomed. Mater. Res., 2003, 65, 188–195 CrossRef PubMed
.
- D. Laurencin, N. Almora-Barrios, N. H. de Leeuw, C. Gervais, C. Bonhomme, F. Mauri, W. Chrzanowski, J. C. Knowles, R. J. Newport, A. Wong, Z. Gan and M. E. Smith, Biomaterials, 2011, 32, 1826–1837 CrossRef CAS PubMed
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed
.
- L. Veselinović, L. Karanović, Z. Stojanović, I. Bračko, S. Marković, N. Ignjatović and D. Uskoković, J. Appl. Crystallogr., 2010, 43, 320–327 Search PubMed
.
- B. Xie, T. J. Halter, B. M. Borah and G. H. Nancollas, Cryst. Growth Des., 2014, 14, 1659–1665 CAS
.
- D. Laurencin, A. Wong, W. Chrzanowski, J. C. Knowles, D. Qiu, D. M. Pickup, R. J. Newport, Z. Gan, M. J. Duer and M. E. Smith, Phys. Chem. Chem. Phys., 2010, 12, 1081–1091 RSC
.
- R. P. Heaney, J. Am. Coll. Nutr., 2006, 25, 271S–276S CrossRef CAS PubMed
.
- H. El Feki, J. Michel Savariault, A. Ben Salah and M. Jemal, Solid State Sci., 2000, 2, 577–586 CrossRef CAS
.
- Y. Tang, H. F. Chappell, M. T. Dove, R. J. Reeder and Y. J. Lee, Biomaterials, 2009, 30, 2864–2872 CrossRef CAS PubMed
.
- R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Nat. Commun., 2011, 2, 590–598 CrossRef PubMed
.
- S. Maltsev, M. J. Duer, R. C. Murray and C. Jaeger, J. Mater. Sci., 2007, 42, 8804–8810 CrossRef CAS
.
-
E. D. Eanes, in Amorphous Calcium Phosphate: Thermodynamic and Kinetic Considerations, ed. Z. Amjad, Springer US, Boston, MA, 1998, pp. 21–39 Search PubMed
.
- K. Matsunaga, J. Am. Ceram. Soc., 2010, 93, 1–14 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Choice of the water model, building of the solutions, validation of the force field, analysis of the symmetry of Posner's cluster in HA, proof that the collected data refer to an equilibrated system, analysis of Ca coordination, comparison of radial distribution functions of Posner-like clusters and single Posner cluster in water. See DOI: 10.1039/c7tb01199g |
| This journal is © The Royal Society of Chemistry 2017 |