Open Access Article
Open Access ArticleNegative ion photoelectron spectroscopy of P2N3−: electron affinity and electronic structures of P2N3˙†
Gao-Lei
Hou
a,
Bo
Chen
 *b,
Wesley J.
Transue
d,
David A.
Hrovat
*b,
Wesley J.
Transue
d,
David A.
Hrovat
 c,
Christopher C.
Cummins
c,
Christopher C.
Cummins
 *d,
Weston Thatcher
Borden
*c and
Xue-Bin
Wang
*d,
Weston Thatcher
Borden
*c and
Xue-Bin
Wang
 *a
*a
aPhysical Sciences Division, Pacific Northwest National Laboratory, P. O. Box 999, MS K8-88, Richland, WA 99352, USA. E-mail: xuebin.wang@pnnl.gov
bDepartment of Chemistry and Chemical Biology, Cornell University, Ithaca, NY 14853, USA. E-mail: cberic@hotmail.com
cDepartment of Chemistry and the Center for Advanced Scientific Computing and Modeling, University of North Texas, 1155 Union Circle, #305070, Denton, Texas 76203-5017, USA. E-mail: borden@unt.edu
dDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: ccummins@mit.edu
First published on 19th April 2016
Abstract
We report here a negative ion photoelectron spectroscopy (NIPES) and ab initio study of the recently synthesized planar aromatic inorganic ion P2N3−, to investigate the electronic structures of P2N3− and its neutral P2N3˙ radical. The adiabatic detachment energy of P2N3− (electron affinity of P2N3˙) was determined to be 3.765 ± 0.010 eV, indicating high stability for the P2N3− anion. Ab initio electronic structure calculations reveal the existence of five, low-lying, electronic states in the neutral P2N3˙ radical. Calculation of the Franck–Condon factors (FCFs) for each anion-to-neutral electronic transition and comparison of the resulting simulated NIPE spectrum with the vibrational structure in the observed spectrum allows the first four excited states of P2N3˙ to be determined to lie 6.2, 6.7, 11.5, and 22.8 kcal mol−1 above the ground state of the radical, which is found to be a 6π-electron, 2A1, σ state.
1. Introduction
Inspired by the unusual stability of the aromatic benzene molecule,1–3 chemists have long sought other aromatic compounds. In the 1950s, cyclopentadienide (C5H5−, Cp−) was first synthesized.4 This anion has a planar five-membered ring, containing 6π electrons; so Cp− fulfills the 4n + 2 Hückel rule for aromaticity.5 Indeed, Cp− is the prototype of an aromatic, organic, anionic species, and it has become the primary building block of metallocenes.6–10It took about 30 years until, in the 1980s, cyclo-pentaphosphorus cyclo-P5−, the all-phosphorus analog of C5H5−, was first prepared in alkali metal salts, MP5 (M = Li, Na).11–13 The cyclo-P5− ion also is found in the carbon-free metallocene complex (P5TiP5)2−,14 and in mixed-metallocene complexes Cp*MP5 (Cp* = C5Me5; M = Fe, Ru),12,13,15 as well as in nano-sized inorganic fullerene-like molecules.16–19 Thus, the discovery of cyclo-P5− has greatly enriched metallocene chemistry and impacted supramolecular and capsule chemistry.
During the past three decades, researchers have sought other, all-inorganic, aromatic species. For example, N2S32+,20 N3S2+,21 and SN2P2,22 which are isolobal to cyclo-P5−, have been identified; but N2S32+ is not stable in solutions (N2S32+), SN2P2 is only stable when isolated in an Ar matrix, and only N3S2+ has proven to be stable enough for isolation. Cyclo-N5−, the first-row congener of cyclo-P5−, has only been observed in the gas phase, where it can be formed via collision induced dissociation (CID) of a compound containing the N5 unit23,24 or its presence inferred via labeling studies of azide ion produced in the decomposition.25,26
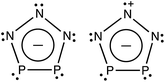
A recent report by Velian et al. of the successful synthesis of large amounts of a salt containing diphosphatriazolate (P2N3−, see Scheme 1) anion marks a breakthrough in synthetic phosphorus–nitrogen chemistry.27,28 As a 6π-electron aromatic species with a planar five-membered ring, P2N3− belongs to the set of (PnN5−n)− (n = 0–5) anions, which, except for the n = 5 member of this series, have until now remained elusive. Considering the substantial enrichment of inorganic and organometallic chemistry made possible by the discovery of cyclo-P5−, one may anticipate that the synthesis of bottleable P2N3− will impact chemistry in a similar way. Thus, this all-inorganic, aromatic species may serve as an important link in inorganic chemistry that is missing no longer.
Understanding the electronic structure of P2N3− is a prerequisite to fully understanding its relationship to related compounds, such as C5H5− and P5−. One of the most fundamental aspects of these anions is, of course, their aromaticity;29–31 and, as the prototypical aromatic anion, the electronic structure of C5H5− has been relatively well studied. For example, the electron affinity (EA), Jahn–Teller coupling, and vibronic energies of C5H5− and its neutral C5H5˙ radical have been investigated by negative ion photoelectron spectroscopy (NIPES),32,33 electronic spectroscopy,34 and ab initio calculations.35,36 The cyclo-P5− ion and its heavier analogs, composed of As, Sb, and Bi, also have been studied by NIPES with the aid of electronic structure calculations.37–39 All of these anions were found to have aromatic D5h ring structures in their electronic ground states and to have π-MOs similar to those in C5H5−.
In light of the potential importance of P2N3−, we wanted to obtain detailed information about the electronic structure of this ion and of the neutral radical, formed by loss of an electron from the anion. Therefore, we produced the P2N3− anion in the gas phase by electrospray ionization of an acetonitrile solution of a [Na-kryptofix-221] salt; and we characterized the electronic structures of P2N3− and P2N3˙ by NIPES, with the help of high level ab initio calculations. We have shown previously that electrospray ionization has the ability to retain the solid-state structure of the molecules in the gas phase40 and that NIPES is an excellent technique for investigating the electronic structures of cyclic organic molecules, such as (CO)n,41–43 (CS)4,44meta-benzoquinone (MBQ),45 and 1,2,4,5-tetraoxatetramethylenebenzene (TOTMB).46 In this paper we describe and analyze the NIPE spectra of P2N3−.
During the preparation of this manuscript, a paper by Jin et al. appeared, reporting calculations on the spectroscopy of P2N3−.47 Of particular interest to us, their IP-EOM-CCSD calculations predicted that the vertical ionization energy (IE) of P2N3− would be found to be 4.22 eV. We are thus able to compare this predicted value against the adiabatic value that we have measured and also against the vertical and adiabatic CCSD(T) values that we have computed.
2. Experimental methods
The NIPES experiments were performed with an apparatus48 consisting of an electrospray ionization source, a cryogenic ion trap, and a magnetic-bottle time-of-flight (TOF) photoelectron spectrometer. A pure acetonitrile solution of [Na-kryptofix-221][P2N3]27 was prepared in the glove box under a N2 atmosphere and was transferred immediately into the electrospray ionization source, which was purged with N2 to minimize the content of O2 and moisture. The electrospray ionization conditions were optimized to make sure there was only one dominant mass peak at m/z = 104, i.e., P2N3−, in the mass spectrum. The anions generated were guided by quadrupole ion guides into an ion trap, where they were accumulated and cooled by collisions with cold buffer gas for 20–100 ms, before being transferred into the extraction zone of a TOF mass spectrometer. In the current study, the ion trap temperature was set to 20 K. The cooling of the anions to 20 K eliminated the possibility of the appearance of extra spectral peaks in the NIPE spectra, due to hot bands.48The P2N3− anions were then mass selected, and decelerated before being photodetached. In the current study the wavelengths of the photodetachment lasers were 266 nm (4.661 eV) from a Nd:YAG laser, 193 nm (6.424 eV) from an ArF laser, and 157 nm (7.867 eV) from a F2 excimer laser. The lasers were all operated at a 20 Hz repetition rate, with the ion beam off in alternating laser shots, thus allowing shot-to-shot background subtraction to be carried out. Photoelectrons were collected at ∼100% efficiency with the magnetic bottle and analyzed in a 5.2 m long electron flight tube.
The TOF photoelectron spectra were converted into electron kinetic energy spectra by calibration with the known NIPE spectra of I−, OsCl2−, and/or Cu(CN)2−.48 The electron binding energies (EBE) were obtained by subtracting the electron kinetic energies from the photon energies of the detaching lasers. The energy resolution was about 2%, i.e., ∼20 meV for 1 eV kinetic energy electrons.
3. Computational methodology
In order to help analyze the NIPE spectra of P2N3−, two different types of electronic structure calculations were performed. B3LYP49 density functional theory (DFT) calculations and CCSD(T)50 coupled-cluster ab initio calculations were both carried out. The aug-cc-pVTZ basis set51 was used for both types of calculations. The B3LYP geometry optimizations (including time-dependent52 B3LYP calculations on the 22A1 state of P2N3˙) and vibrational analyses were performed using the Gaussian09 suite of programs.53 The CCSD(T) geometry optimizations and vibrational analyses were performed using the Molpro 10 program.54The program ezSpectrum55 was used to compute the Franck–Condon factors (FCFs)56 that were necessary, in order to simulate the vibrational progressions in the NIPE spectra of P2N3−. The NIPE spectra at 20 K were simulated, and no vibrational hot bands were seen in the simulations. In computing the FCFs for the simulations, the imaginary frequencies in the excited states of the neutral radical were treated as real frequencies; but the FCFs that were computed for these vibrational modes were zero; and, had they not been zero, we would have discarded them.
4. Results and discussion
4.1 The NIPE spectra of P2N3−
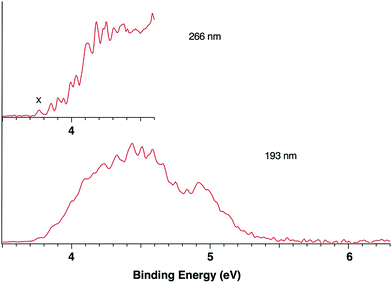
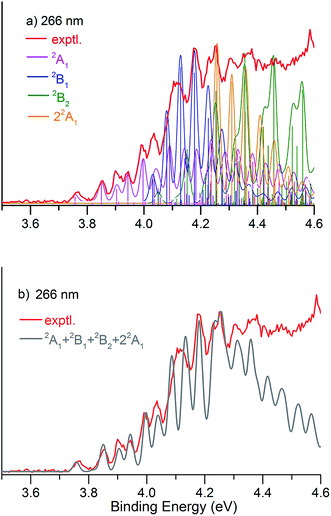
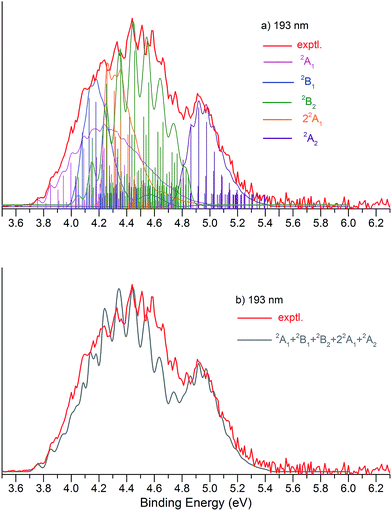
Fig. 1 presents the 20 K NIPE spectra of P2N3− at 266 and 193 nm, respectively. The 157 nm NIPE spectrum shows almost the same spectral features in the electron binding energy (EBE) range of 3.7–5.5 eV as in the 193 nm spectrum, and is provided in Fig. S1 of the ESI.† However, much higher EBE features at around 7.0 and 7.6 eV can be seen in the 157 nm spectrum.Partially resolved spectral features are seen at 266 nm in Fig. 1. The NIPE spectrum shows many rather closely-spaced peaks, suggesting that the spectrum probably contains multiple electronic state transitions and associated vibrational progressions. The adiabatic detachment energy (ADE) of P2N3− (i.e., the EA of P2N3˙) is determined from the 0–0 transition (X) in the 266 nm NIPE spectrum in Fig. 1 to be 3.765 ± 0.010 eV.
The EA value of P2N3˙ is only slightly smaller than that of P5˙, which was previously measured to have EA = 3.88 ± 0.03 eV,39 but the EA value of P2N3˙ is much larger than that of C5H5˙, which has EA = 1.786 ± 0.020 eV.32 Significantly, the measured value of EA(P2N3˙) = 3.765 ± 0.010 eV, which is the adiabatic IE of the P2N3− anion, is 0.45 eV lower than the predicted vertical IE of the anion, computed at the IP-EOM-CCSD level of theory.47
4.2 The electronic structures of P2N3− and P2N3˙
In order to help interpret the NIPE spectra of P2N3−, we carried out electronic structure calculations on both the P2N3− anion and the neutral P2N3˙ radical. Fig. 2 shows the calculated geometry of P2N3− at B3LYP/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ levels of theory. The calculated N–N bond lengths are in good agreement with those determined by X-ray diffraction in the solid salts;27 but the calculated N–P and P–P bond lengths are both a little longer than those found in the salt. It should be noted that the two N–N and also the two P–N bond distances in the X-ray structure of P2N3− are not the same, probably due to the packing effects in the crystal environment. However, the calculations predict a symmetric C2v geometry to be an energy minimum for the gas-phase anion. The CCSD(T)/aug-cc-pVTZ geometries are also very close to those calculated by Jin et al.47 at the same level of theory.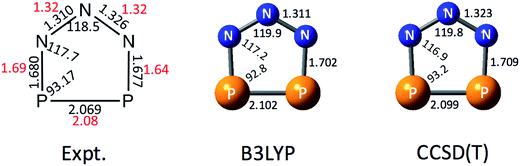 | ||
| Fig. 2 Comparison of the X-ray structure of P2N3− in [Na-kryptofix-221][P2N3] salt (major component in black, minor component in red)27 with the calculated structures at B3LYP/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ levels of theory. Bond distances are in angstroms (Å) and bond angles are in degrees (°). | ||
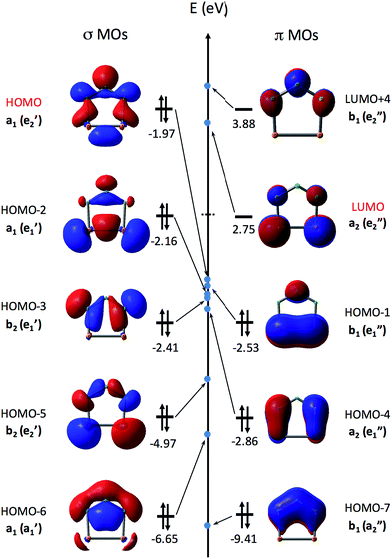
Fig. 3 shows the eight highest occupied molecular orbitals (HOMOs) and two virtual MOs of the ground state of P2N3−. These ten MOs, five π MOs and five σ MOs, are similar to those in P5−.39 Of course, substitution of three nitrogens for three phosphorus atoms in D5h P5− reduces the symmetry to C2v in P2N3−. Consequently, the degeneracy of four pairs of MOs in D5h P5− (e′′2, e′′1, e′2, and e′1) is lifted. Nonetheless, occupation of the three low-lying valence π MOs – HOMO−1, HOMO−4, and HOMO−7 – by 6 electrons indicates that P2N3− is aromatic, as was confirmed previously by NICS (Nucleus-Independent Chemical Shift) and QTAIM (Quantum Theory of Atoms in Molecules) calculations.27
Unlike the case of C5H5−, in which the five C–H σ MOs are all lower in energy than the three π MOs, the σ MOs in P5− (ref. 39) and in P2N3− (Fig. 3) are comparable to the π MOs in energy. In fact, as shown in Fig. 3, the HOMO of P2N3− is an a1 σ MO, with considerable lone-pair character on the central nitrogen.
As shown in Table 1, the B3LYP and CCSD(T) calculations each find five low-lying electronic states of P2N3˙, three different σ states (12A1, 2B2, and 22A1) and two different π states (2A2 and 2B1). In D5h P5˙ the 22A1 and 2B2 σ states of P2N3˙ would be a degenerate pair of 2E′1 states, and the π states of P2N3˙ would be a degenerate pair of 2E′′1 states. Substitution of nitrogen for three phosphorus atoms of P5˙ lifts the degeneracy of these states at the C2v equilibrium geometry of P2N3˙, so that the two degenerate 2E′1 σ states of P5˙ differ in energy by ca. 7 kcal mol−1 in P2N3˙, and the two degenerate 2E′′1 π states of P5˙ differ in energy by ca. 12 kcal mol−1 in P2N3˙. The states nearest in energy to each other in P2N3˙, are 2B1, a π state, and 2B2, a σ state.
| Molecule | Electronic state | Singly occupied MO | UB3LYP/aug-cc-pVTZ energies | UCCSD(T)/aug-cc-pVTZ energies | ||
|---|---|---|---|---|---|---|
| in kcal mol−1 | in eV | in kcal mol−1 | in eV | |||
| a Energy minimum. b This state has an imaginary, out-of plane, b1 vibrational mode, because a b1 geometry distortion gives the 2B1 excited state the same symmetry as the 2A1 ground state. c This state has an imaginary, in-plane, b2 vibrational mode with both methods and an additional imaginary, out-of-plane, b1 mode with UCCSD(T). A b2 geometry distortion gives the 2B2 excited state the same symmetry as the 2A1 ground state. d This state has an imaginary, in-plane, b2 vibrational mode, because a b2 geometry distortion gives 2A2 the same symmetry as 2B1, the π state of lower energy. e The ZPE correction is not available, due to unsuccessful UCCSD(T) frequency analysis. f The excited 2A1 state in which the unpaired electron occupies HOMO−2 in Fig. 3. UB3LYP vibrational analysis predicts an imaginary, in-plane b2 vibrational mode, because a b2 geometry distortion gives 22A1 the same symmetry as 2B2, the σ excited state of lower energy. g The energy of this state, computed using time-dependent DFT at the TD-UB3LYP/aug-cc-pVTZ//TD-UB3LYP/aug-cc-pVTZ level of theory, is 101.5 kcal mol−1 = 4.40 eV without ZPE correction. This energy is only 0.4 kcal mol−1 lower than the value computed by a ground state UB3LYP calculation, in which the unpaired electron remained in the HOMO−2 σ MO during the geometry optimization. h UCCSD(T) geometry optimization leads to the 12A1 ground state. Therefore, a single point UCCSD(T) calculation at the UB3LYP/aug-cc-pVTZ optimized geometry was carried out, in order to obtain the UCCSD(T)/aug-cc-pVTZ energy of the 22A1 state. | ||||||
| P2N3− | 1A1a | None | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| P2N3˙ | 12A1a | HOMO | 82.9 (82.7) | 3.59 (3.58) | 86.4 (86.2) | 3.75 (3.74) |
| 2B1b | HOMO−1 | 93.4 (91.4) | 4.05 (3.96) | 94.5 (93.3) | 4.10 (4.05) | |
| 2B2c | HOMO−3 | 94.8 (92.8) | 4.11 (4.02) | 96.4 (94.0) | 4.18 (4.08) | |
| 2A2d | HOMO−4 | 105.8 (104.9) | 4.59 (4.55) | 106.5 (e) | 4.62 (e) | |
| 22A1f | HOMO−2 | 101.9 (101.5)g | 4.42 (4.40)g | 100.4h | 4.36h | |
As shown in Table 1, both UB3LYP and UCCSD(T) methods predict that the ground state of neutral P2N3˙ is the 2A1 state. It can be generated by removing one electron from the a1 σ MO of P2N3−, which is the HOMO of the anion. The 2A1 state retains 6π electrons, and is a σ radical.
The EA of the 2A1 state of P2N3˙ is computed to be 3.74 eV at the UCCSD(T)/aug-cc-pVTZ level of theory, a value almost exactly the same as the EBE of the first resolved peak (3.765 ± 0.010 eV) in the 266 nm NIPE spectrum in Fig. 1. The excellent agreement between both the B3LYP and CCSD(T) calculations and the experimental value of the EA of P2N3˙ strongly suggests that the ground state of P2N3˙ is, indeed, the 2A1 state, in which the unpaired electron occupies the a1 σ MO.
As mentioned in the introduction, IP-EOM-CCSD/aug-cc-pVTZ calculations predict the vertical IE of P2N3− to be 4.22 eV.47 This value is 0.45 eV larger than the adiabatic IE of P2N3− (which is, of course, the same as the adiabatic EA of P2N3˙) from the NIPE spectrum in Fig. 1. The reason for the large difference between the calculated and measured IEs could be due to the fact that 4.22 eV was computed to be the vertical IE of P2N3−; whereas the observed value of 3.765 eV is the adiabatic IE.
Since our calculated adiabatic IE of 3.74 eV is in excellent agreement with the measured value of 3.765 eV, we could test accurately whether or not there is, in fact, a large difference between the vertical and adiabatic IEs of P2N3− by carrying out (U)CCSD(T)/aug-cc-pVTZ calculations of the vertical IE. The vertical IE that we obtained is 4.27 eV, which is 0.52 eV higher than our (U)CCSD(T)/aug-cc-pVTZ adiabatic value of 3.75 eV (without vibrational corrections) but only 0.05 eV higher than the IP-EOM-CCSD/aug-cc-pVTZ vertical IE that was computed by Jin et al.47 The 0.52 eV difference between the vertical and adiabatic (U)CCSD(T)/aug-cc-pVTZ IEs and the small difference between the (U)CCSD(T)/aug-cc-pVTZ and IP-EOM-CCSD/aug-cc-pVTZ vertical IEs shows that almost all of the difference between the IP-EOM-CCSD/aug-cc-pVTZ vertical IE of 4.22 eV, calculated by Jin et al.,47 and the experimental adiabatic IE of 3.765 eV, measured by us, is due to the large difference between the vertical and adiabatic IEs of P2N3−. The large geometry relaxation energy of ca. 0.5 eV on ionization is, presumably due to the fact that the electron lost occupies a σ bonding MO.
The three low-lying electronic states of C2v P2N3˙ – 2B1, 2B2, and 2A2 – that correspond to the three irreducible symmetry representations of the C2v point group, other than A1, can be generated by removing one electron from, respectively, the b1 HOMO−1, b2 HOMO−3, and a2 HOMO−4 in P2N3−. Since these MOs are lower in energy than the HOMO in P2N3−, it would be expected that more energy is needed to detach an electron from these three MOs than from the a1 HOMO in P2N3−. Therefore, the resulting three electronic states of P2N3˙, each of which places the unpaired electron in one of these three MOs, are expected to be higher in energy than the 2A1 state. As shown in Table 1, calculations show that the 2B1, 2B2, and 2A2 are, respectively, 7–11, 8–12, and 20–23 kcal mol−1 higher in energy than the 2A1 ground state of P2N3˙.
Removal of an electron from the HOMO−2 of P2N3− generates a 2A1 state, which has the same symmetry as the 12A1 ground state of the radical. Consequently, a time-dependent (TD)DFT calculation was necessary, in order to obtain the energy of the 22A1 state. Table 1 shows that a TD-UB3LYP/aug-cc-pVTZ//TD-UB3LYP/aug-cc-pVTZ calculation places the energy of the 22A1 state 18.6 kcal mol−1 above the 12A1 ground state of the radical and 4.3 kcal mol−1 below the 2A2 state.
Starting from the TD-UB3LYP optimized geometry for the 22A1 state, we were able to do ground-state UB3LYP/aug-cc-pVTZ geometry optimization and frequency analysis on this state, using a wavefunction in which the unpaired electron was forced to occupy the HOMO−2 of Fig. 3. The ground-state UB3LYP calculation predicts an energy for the 22A1 state that is within 0.4 kcal mol−1 of the energy obtained from the TD-UB3LYP calculation.
We also carried out UCCSD(T)/aug-cc-pVTZ//UB3LYP/aug-cc-pVTZ calculations on 22A1 that give a similar result. They predict that the 22A1 state is 14.0 kcal mol−1 above the 12A1 ground state and 6.1 kcal mol−1 below the 2A2 state. Therefore, at both levels of theory, the 22A1 state is predicted to be the second highest energy state among the five lowest-lying states of P2N3˙ in Table 1.
The UCCSD(T) predicted EA values of the five lowest-lying states of P2N3˙ (3.74–4.62 eV) are all lower than the 193 nm photon energy (6.424 eV). Therefore, these five states are all potentially accessible by photodetachment of P2N3−, and they are very likely to be responsible for at least the first half of the spectral features in the range of 3.7–4.6 eV in the 193 nm spectrum of Fig. 1. The second half of the spectral features in the 4.6 – 5.5 eV range of the 193 nm spectrum could be due to still higher energy excited states of P2N3˙, or they could also be due to vibrational progressions belonging to the five lowest energy electronic states of P2N3˙.
4.3 Simulation of the vibrational progressions in the NIPE spectra
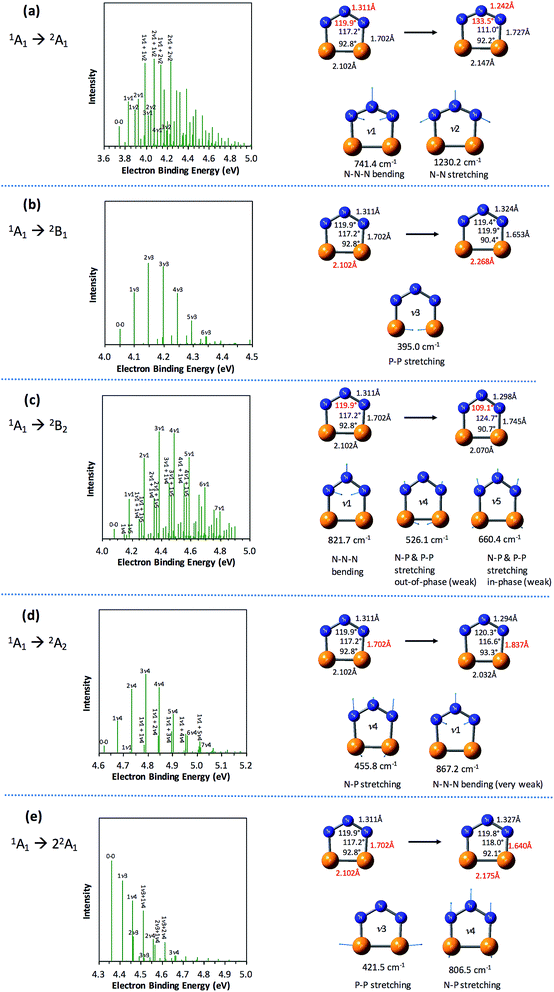
The partially resolved spectral features at 266 nm in Fig. 1 correspond to the transitions from the ground state of P2N3− to the ground and excited states of P2N3˙, along with the vibrational excitations associated with the formation of each electronic state. Therefore, in order to assign all of the peaks in the 266 nm NIPE spectrum, we calculated the Franck–Condon factors (FCFs)56 of transitions from the 1A1 ground state of P2N3− to each of the five, lowest-lying electronic states of P2N3˙ (2A1, 2B1, 2B2, 2A2, and 22A1).Fig. 4 shows the vibrational progressions, simulated using the UB3LYP geometries, frequencies and FCFs. The geometry changes and the active vibrational modes that yield the vibrational progressions for each transition are also shown in Fig. 4. Simulations using UCCSD(T) geometries, frequencies and FCFs gave very similar vibrational progression patterns as UB3LYP; and the UCCSD(T) stick spectra are provided in the ESI† of this manuscript.
As shown in Fig. 4, the electronic transitions from the 1A1 ground state of P2N3− to the five low-lying states of P2N3˙ all feature weak 0–0 peaks, except for the transition to the 22A1 state, in which the 0–0 peak is the most intense. Nevertheless, all five transitions show long vibrational progressions. The reason is that, as shown in Fig. 4, the calculations reveal significant geometry changes for each of these electronic transitions in the NIPE spectrum of P2N3−.
For example, in the 1A1 → 2A1 transition (Fig. 4a), one electron is removed from the a1 HOMO of P2N3− in Fig. 3. The HOMO contains N–N antibonding interactions, N–P and P–P bonding interactions, and a bonding interaction between non-nearest neighbor nitrogens. Removing one electron from this orbital leads to exactly the calculated geometrical changes that one would expect — shortening of the N–N bond lengths, lengthening of the N–P and P–P bonds, and expansion of the N–N–N bond angle.
Calculations show that the two most significant geometrical changes are shortening of the N–N bond length, from 1.311 to 1.242 Å, and expansion of the N–N–N bond angle from 119.9 to 133.5°. These large changes on going from the equilibrium geometry of P2N3− to that of P2N3˙ are responsible for the calculated difference of 0.52 eV between the vertical and adiabatic IEs of the anion.
N–N–N bending (ν1 = 741.4 cm−1) and N–N stretching (ν2 = 1230.2 cm−1) are the two vibrational modes that create the most significant changes in, respectively, the N–N–N bond angle and the N–N bond length. These a1 vibrational modes are active in the transition from the 1A1 ground state of the anion to the 2A1 ground state of the neutral. The four most intense peaks in the long vibrational progression that is associated with the 1A1 → 2A1 transition are due to coupled a1 vibrational modes, involving both N–N–N bending and N–N stretching.
Analysis of the other four electronic transitions in Fig. 4b–e in a similar fashion shows that the most active a1 vibrational modes in each of these transitions are P–P stretching (ν3 = 395.0 cm−1) in 1A1 → 2B1, N–N–N bending (ν1 = 821.7 cm−1) in 1A1 → 2B2, N–P stretching (ν4 = 455.8 cm−1) in 1A1 → 2A2, and P–P stretching (ν3 = 421.5 cm−1) and N–P stretching (ν3 = 806.5 cm−1) in 1A1 → 22A1.
4.4 Simulation of the NIPE spectra of P2N3−
We simulated the experimental 266 and 193 nm NIPE spectra of P2N3− by convoluting the UB3LYP calculated stick spectrum with Gaussian functions having full widths of 25 meV (for the 266 nm NIPE spectrum) and 55 meV (for the 193 nm spectrum) at half maxima for each stick. As shown in Figs. 5 and 6, after small adjustments of the UCCSD(T) calculated energies of the 0–0 bands for the five electronic states of P2N3˙, (+0.02 eV for 2A1, −0.02 eV for 2B1, −0.03 eV for 2B2, −0.10 eV for 22A1, and +0.13 eV for 2A2), the simulated NIPE spectra of P2N3− match the experimental 266 and 193 nm spectra quite well.It should be noted that, starting near EBE > 4.3 eV, the 266 nm experimental spectral bands seem to sit on top of a background, which makes the spectral features in this region appear more intense than they would be if only direct detachment processes were involved. Resonant photodetachment57 may give rise to an underlying band in this region, thus accounting for the differences between the experimental and simulated NIPE spectra in Fig. 5. Resonant photodetachment was previously used to explain the difference between the experimental and simulated NIPE spectra in our previous NIPES study of the TOTMB radical anion.46
These small adjustments of the calculated 0–0 bands for formation of the five lowest electronic states of P2N3˙ give the EAs of these states of P2N3˙ as 3.76, 4.03, 4.05, 4.26, and 4.75 eV, respectively. We have also simulated the NIPE spectra by slightly different adjustments of the calculated 0–0 energies of the four excited states, and these simulations are presented in the ESI† of this manuscript. These simulated spectra all agree reasonably well with the experimental spectra, but the simulations shown in Figs. 5 and 6 give the best agreement.
Our confidence in the absolute energies assigned to the 0–0 bands of the excited states is about 0.05 eV (1 kcal mol−1). Simulations using UCCSD(T) geometries, frequencies and FCFs gave similar vibrational patterns to the B3LYP simulations in Figs. 5 and 6. The UCCSD(T) stick spectra are provided in the ESI† of this manuscript.
In order to account for the variation of energy resolution of our TOF type photoelectron spectrometer in the photoelectron energy range of EBE = 3.8–4.4 eV, we also simulated the 266 nm NIPE spectrum, by convoluting the UB3LYP calculated stick spectrum with Gaussian functions having full widths of 20 and 30 meV at half maxima for each stick. These two simulated NIPE spectra, which are presented in the ESI† for this manuscript, gave fits to the experimental NIPE spectrum of the same quality as that in Fig. 5, which assumed a 25 meV energy resolution.
5. Conclusions
We report the NIPE spectra of P2N3−, an all-inorganic, aromatic species, which was recently isolated in bulk quantities as a salt. The NIPE spectra provide the measurement of the electron affinity (EA = 3.765 ± 0.010 eV) for the ground state of neutral P2N3˙. The NIPE spectra also indicate that other electronic states of P2N3˙ are quite close in energy to the ground state of this radical.Ab initio electronic structure calculations and simulations, based on computed Franck–Condon factors (FCFs), reveal that the ground state of P2N3˙ is 2A1, in which the unpaired electron occupies an a1 σ MO. The first four excited states of P2N3˙ are 2B1, 2B2, 22A1, and 2A2 with their energies calculated at the CCSD(T)/aug-cc-pVTZ level of theory to be 8.1, 10.0, 14.0, and 20.1 kcal mol−1 above the 2A1 ground state. Simulations of the NIPE spectrum of P2N3˙, based on the FCFs computed for formation of these five electronic states from the 1A1 ground state of the P2N3− anion provide a reasonable fit to the peaks in the NIPE spectrum of the anion.
The results in this paper, obtained from a combination of experiments and calculations, contribute fundamental information about the electronic structures of P2N3− and the P2N3˙ radical formed from it by photochemical electron detachment. This information is likely to prove useful in future investigations of P2N3−, P2N3˙, and their chemistry.
Conflict of interest
The authors declare no competing financial interest.Acknowledgements
The NIPES research done at PNNL was supported by U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, the Division of Chemical Sciences, Geosciences, and Biosciences, and performed using EMSL, a national scientific user facility sponsored by DOE's Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory, which is operated by Battelle Memorial Institute for the DOE. The theoretical calculations at UNT were supported by Grant B0027 from the Robert A. Welch Foundation. The synthesis work of [Na-kryptofix-221][P2N3] was supported by the National Science Foundation under grant no. CHE-1362118. G.-L. Hou thanks Dr Shaoguang Zhang from PNNL for providing the dry and degassed acetonitrile.References and notes
- M. Faraday, Philos. Trans. R. Soc. London, 1825, 115, 440 CrossRef.
- A. Kekuié, Justus Liebigs Ann. Chem., 1866, 137, 129 CrossRef.
- I. I. Naumov and R. J. Hemley, Acc. Chem. Res., 2014, 47, 3551 CrossRef CAS PubMed.
- K. Ziegler, H. Froitzheim-Kuhlhorn and K. Hafner, Chem. Ber., 1956, 89, 434 CrossRef CAS.
- (a) E. Hückel, Z. Phys., 1931, 70, 204 CrossRef; (b) E. Hückel, Z. Phys., 1931, 72, 310 CrossRef; (c) E. Hückel, Z. Phys., 1932, 76, 628 CrossRef.
- T. J. Kealy and P. L. Pauson, Nature, 1951, 168, 1039 CrossRef CAS.
- G. Wilkinson, M. Rosenblum, M. C. Whiting and R. B. Woodward, J. Am. Chem. Soc., 1952, 74, 2125 CrossRef CAS.
- E. O. Fischer and W. Pfab, Z. Naturforsch., B: J. Chem. Sci., 1952, 7, 377 Search PubMed.
- 1973 Nobel Prize in Chemistry, see http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1973/.
- H. Werner, Angew. Chem., Int. Ed., 2012, 51, 6052 CrossRef CAS PubMed.
- M. Baudler, D. Düster and D. Ouzounis, Z. Anorg. Allg. Chem., 1987, 544, 87 CrossRef CAS.
- M. Baudler, S. Akpapoglou, D. Ouzounis, F. Wasgestian, B. Meinigke, H. Budzikiewicz and H. Münster, Angew. Chem., Int. Ed., 1988, 27, 280 CrossRef.
- H. Grützmacher, Z. Anorg. Allg. Chem., 2012, 638, 1877 CrossRef.
- E. Urnėžius, W. W. Brennessel, C. J. Cramer, J. E. Ellis and P. V. R. Schleyer, Science, 2002, 295, 832 CrossRef PubMed.
- O. J. Scherer, Angew. Chem., Int. Ed. Engl., 1990, 29, 1104 CrossRef.
- J. Bai, A. V. Virovets and M. Scheer, Science, 2003, 300, 781 CrossRef CAS PubMed.
- M. Scheer, A. Schindler, R. Merkle, B. P. Johnson, M. Linseis, R. Winter, C. E. Anson and A. V. Virovets, J. Am. Chem. Soc., 2007, 129, 13386 CrossRef CAS PubMed.
- M. Fleischmann, J. S. Jones, F. P. Gabbai and M. Scheer, Chem. Sci., 2015, 6, 132 RSC.
- S. Heinl, E. Peresypkina, J. Sutter and M. Scheer, Angew. Chem., Int. Ed., 2015, 54, 13431 CrossRef CAS PubMed.
- W. V. F. Brooks, T. S. Cameron, S. Parsons, J. Passmore and M. J. Schriver, Inorg. Chem., 1994, 33, 6230 CrossRef CAS.
- S. Herler, P. Mayer, H. Nöth, A. Schulz, M. Suter and M. Vogt, Angew. Chem., Int. Ed., 2001, 40, 3173 CrossRef CAS.
- X. Zeng, H. Li, H. Sun, H. Beckers, H. Willner and H. F. Schaefer III, Angew. Chem., Int. Ed., 2015, 54, 1327 CrossRef CAS PubMed.
- A. Vij, J. G. Pavlovich, W. W. Wilson, V. Vij and K. O. Christe, Angew. Chem., 2002, 114, 3177 CrossRef.
- T. Schroer, R. Haiges, S. Schneider and K. O. Christe, Chem. Commun., 2005, 1607 RSC.
- R. N. Butler, J. M. Hanniffy, J. C. Stephens and L. A. Burke, J. Org. Chem., 2008, 73, 1354 CrossRef CAS PubMed.
- S. A. Perera, A. Gregušová and R. J. Bartlett, J. Phys. Chem. A, 2009, 113, 3197 CrossRef CAS PubMed.
- A. Velian and C. C. Cummins, Science, 2015, 348, 1001 CrossRef CAS PubMed.
- C. Hering-Junghans and E. Rivard, Angew. Chem., Int. Ed., 2015, 54, 10077 CrossRef CAS PubMed.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Chem. Rev., 2005, 105, 3842 CrossRef CAS PubMed.
- A. I. Boldyrev and L.-S. Wang, Chem. Rev., 2005, 105, 3716 CrossRef CAS PubMed.
- R. Hoffmann, Am. Sci., 2015, 103, 18 CrossRef.
- P. C. Engelking and W. C. Lineberger, J. Chem. Phys., 1977, 67, 1412 CrossRef CAS.
- T. Ichino, S. W. Wren, K. M. Vogelhuber, A. J. Gianola, W. C. Lineberger and J. F. Stanton, J. Chem. Phys., 2008, 129, 084310 CrossRef PubMed.
- B. E. Applegate, T. A. Miller and T. A. Barckholtz, J. Chem. Phys., 2001, 114, 4855 CrossRef CAS.
- W. T. Borden and E. R. Davidson, J. Am. Chem. Soc., 1979, 101, 3771 CrossRef CAS.
- X. Zhou, D. A. Hrovat and W. T. Borden, J. Am. Chem. Soc., 2007, 129, 10785 CrossRef CAS PubMed.
- R. O. Jones, G. Ganteför, S. Hunsicker and P. Pieperhoff, J. Chem. Phys., 1995, 103, 9549 CrossRef CAS.
- T. P. Lippa, S.-J. Xu, S. A. Lyapustina, J. M. Nilles and K. H. Bowen, J. Chem. Phys., 1998, 109, 10727 CrossRef CAS.
- H.-J. Zhai, L.-S. Wang, A. E. Kuznetsov and A. I. Boldyrev, J. Phys. Chem. A, 2002, 106, 5600 CrossRef CAS.
- G.-L. Hou, H. Wen, K. Lopata, W.-J. Zheng, K. Kowalski, N. Govind, X.-B. Wang and S. S. Xantheas, Angew. Chem., Int. Ed., 2012, 51, 6356 CrossRef CAS PubMed.
- J.-C. Guo, G.-L. Hou, S.-D. Li and X.-B. Wang, J. Phys. Chem. Lett., 2012, 3, 304 CrossRef CAS PubMed.
- X. Bao, D. A. Hrovat, W. T. Borden and X.-B. Wang, J. Am. Chem. Soc., 2013, 135, 4291 CrossRef CAS PubMed.
- B. Chen, D. A. Hrovat, R. West, S. H. M. Deng, X.-B. Wang and W. T. Borden, J. Am. Chem. Soc., 2014, 136, 12345 CrossRef CAS PubMed.
- J. Zhang, D. A. Hrovat, Z. Sun, X. Bao, W. T. Borden and X.-B. Wang, J. Phys. Chem. A, 2013, 117, 7841 CrossRef CAS PubMed.
- B. Chen, D. A. Hrovat, S. H. M. Deng, J. Zhang, X.-B. Wang and W. T. Borden, J. Am. Chem. Soc., 2014, 136, 3589 CrossRef CAS PubMed.
- D. A. Hrovat, G.-L. Hou, X.-B. Wang and W. T. Borden, J. Am. Chem. Soc., 2015, 137, 9094 CrossRef CAS PubMed.
- Y. Jin, A. Perera and R. J. Bartlett, Chem. Phys. Lett., 2015, 640, 68 CrossRef CAS.
- X.-B. Wang and L.-S. Wang, Rev. Sci. Instrum., 2008, 79, 073108 CrossRef PubMed.
- B3LYP is a combination of Becke’s 3-parameter hybrid exchange functional ( A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS ) with the electron correlation functional of Lee, Yang, and Parr ( C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef ).
- (a) G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910 CrossRef CAS; (b) K. Raghavachari, G. W. Trucks, J. A. Pople and M. H. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- (a) T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007 CrossRef; (b) R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, and M. Wang, MOLPRO, version 2010.1, a package of ab initio programs, see http://www.molpro.net Search PubMed.
- V. A. Mozhayskiy and A. I. Krylov, ezSpectrum, version 3.0, see http://iopenshell.usc.edu/downloads Search PubMed.
- (a) J. Franck, Trans. Faraday Soc., 1926, 21, 536 RSC; (b) E. Condon, Phys. Rev., 1926, 28, 1182 CrossRef CAS.
- J. Schiedt and R. Weinkauf, J. Chem. Phys., 1999, 110, 304 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The 20 K NIPE spectra of P2N3− at 266, 193, and 157 nm (Fig. S1); simulations of vibrational progressions (stick spectra), using UCCSD(T) geometries, frequencies and FCFs (Fig. S2); the simulation of the NIPE spectra by adjusting the calculated 0–0 band positions for each electronic state, relative to the experiments (Figs. S3 and S4); the simulated 266 nm spectra with Gaussian functions of 20 and 30 meV full widths at half maxima (Figs. S5 and S6); coordinates and energies of calculated structures (Table S1); computed Franck–Condon factors (Table S2). See DOI: 10.1039/c5sc04667j |
| This journal is © The Royal Society of Chemistry 2016 |