The use of the Rx spin label in orientation measurement on proteins, by EPR

Abstract

The bipedal spin label Rx is more restricted in its conformation and dynamics than its monopodal counterpart R1. To systematically investigate the utility of the Rx label, we have attempted to comprehensively survey the attachment of Rx to protein secondary structures. We have examined the formation, structure and dynamics of the spin label in relation to the underlying protein in order to determine feasibility and optimum conditions for distance and orientation measurement by pulsed EPR. The labeled proteins have been studied using molecular dynamics, CW EPR, pulsed EPR distance measurement at X-band and orientation measurement at W-band. The utility of different modes and positions of attachment have been compared and contrasted.

---

1 Introduction

Pulsed electron double resonance (PELDOR),^1,2 electron paramagnetic resonance (EPR) spectroscopy combined with site directed spin labelling (SDSL) is a powerful tool for deriving distance constraints in structural biology.³ PELDOR measures the dipolar coupling between two unpaired electrons, which are often introduced into the structure by site directed labelling. The vast majority of protein spin-labelling studies have used the MTSSL (R1) spin-label^4–6 (Fig. S1A, ESI†). This label has proven to be an excellent choice for the measurement of label–label distances. Because the conformational distribution of a surface exposed R1 label can often be predicted^7,8 so the distance measurement can be applied to the underlying protein in the refinement of macromolecular structures.⁹ Recently there have been a number of studies in which the utility of a bipedal spin label (Rx) (Fig. S1B, ESI†) has been described^10–13 Having two attachment points to the underlying protein, the Rx spin label is intrinsically more restricted in relation to the underlying protein structure. The Rx label has been used to exploit the increased spatial definition relative to the R1 label such that it might provide more accurate distance measurement on difficult targets such as membrane proteins.¹⁴ It has been demonstrated that at high frequencies PELDOR could be used to measure not only distances but also label orientation.¹⁵ Several studies have investigated the measurement of spin–spin orientation and addressed some of the difficulties inherent in the measurement, both in proteins and DNA.^16–21 Because the solvent exposed R1 spin label is normally highly dynamic it is infrequently a good subject for orientation measurements and its use in this way has been restricted to cases in which the spin-label is severely restrained by specific interactions.²² Because of its more restricted mobility, the Rx label is a candidate for orientation measurements. Although restricted conformation would make orientation measurement potentially viable even in fully solvent exposed positions, in order to use label–label orientations to define the underlying protein structure one must understand the conformation of the label in relation to the protein structure to which it is attached. A number of positions for attachment of Rx to proteins have been previously described. We have identified six generic positions, on protein secondary structure, that cover all available attachment types, that are restricted to defined secondary structure regions. Defined secondary structures have several advantages as attachment points for spin labels in that they (β-sheets and α-helices) are relatively stable, providing a direct link between the spin-label and the body of the underlying protein. These regions are also predictable from amino-acid sequence data.²³ Finally secondary structures in proteins maintain a reasonably constant distance relationship between side chains allowing the prediction of suitable attachment sites for Rx. The protein chosen for these studies was the histone chaperone Vps75. This protein is dimeric (at high salt concentration)²⁴ and contains suitable regions of α-helix and β-sheet. A number of crystal structures for Vps75 have previously been solved and the work reported here utilized the structure with protein data bank code 2ZD7.²⁵

We have used a combination of approaches to study attachment sites including, continuous wave (CW) EPR, computational molecular dynamics (MD) and X-band PELDOR distance distribution measurement. For those sites that appear most favourable we have made sequence mutations to explore the effect of neighbouring amino acids on the rigidity and conformational predictability and have used W-band PELDOR to determine viability of spin–spin orientation measurement.

Orientation specific, PELDOR measurements were first demonstrated, at high fields by the Frankfurt,²⁶ Mulheim¹⁶ and Zurich²⁷ groups. The Oxford²¹ Frankfurt^18–20 and Zurich¹⁷ groups subsequently demonstrated that it was also possible to extract useful orientation information at X-band using rigid spin labels. However, at X-band the g-tensor is not fully resolved and measurements are primarily sensitive to only three of the five angles that characterize the angular distributions.^17,18 The nitroxide g-tensor only becomes fully resolved at W-band or higher frequencies, allowing more general analyses for rigid spin labels. Orientation specific measurements on the Rx constructs at the i–i + 1 helical positions (19–20 and 26–27) were studied at W-band using the HIPER spectrometer,²⁸ which features a non-resonant sample holder and consequently large bandwidth as described in ESI† (S1). The large instantaneous band-width, allows full control over pump and observe frequencies, permitting the gathering of PELDOR data, specific to a choice of relative spin label orientations Fig. S2 (ESI†).

2 Results

2.1 Spin-labelling

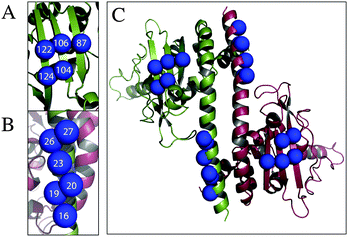
The criteria for cysteine pair positions, that could be labelled using Rx, have been previously explored by molecular modelling and defined as the i–i + 3 or i–i + 4 positions of an α-helix, at the i–i + 2 position of a β-strand, or at two cysteine residues perpendicular to each other across a β-sheet.¹⁰ We have identified by visual inspection and subsequent molecular modelling two further secondary structure positions, which we believed would be viable labelling sites, i–i + 1 in the α-helix and two positions situated diagonally across a β-sheet. Cysteine pair mutations of Vps75 were produced at the positions indicated (Table 1 and Fig. 1A–C) and labelled using Rx.

Table 1 Rx attachment sites and underlying structure

Rx attachment sites	Type of attachment
19–20	α-Helix i–i + 1
26–27	α-Helix i–i + 1
16–19	α-Helix i–i + 3
16–20	α-Helix i–i + 4
19–23	α-Helix i–i + 4
122–124	β-Strand i–i + 2
87–104	β-Sheet diagonal
104–122	β-Sheet diagonal
106–122	β-Sheet perpendicular
104–124	β-Sheet perpendicular

---

Fig. 1 Label attachment sites on the protein Vps75. Ribbon diagram with separate monomers coloured red or green and attachment sites for spin labels indicated by blue Cα spheres, with residue numbers in white (C), β-sheet attachment sites (A), helical attachment sites (B).

Labelling efficiencies were good, however complete removal of free Rx label, was considerably more difficult than for the R1 label. Although the levels of free Rx after standard dialysis and solvent exchange were acceptable for non-orientation PELDOR experiments they interfered significantly with CW spectra. Extensive dialysis at room temperature was used to remove all trace of free Rx. See additional information in S1 (ESI†) materials and Methods.

2.2 CW spectra

CW EPR spectra, recorded at room temperature on samples in 30 w/v% sucrose, indicated strongly immobilized nitroxides, with spectra being similar to the immobilized, Rx labelled spectra previously published.¹⁰ Initial examination revealed some small variation between labelling sites (Fig. S3, ESI†). Measurement of the large effective hyperfine splitting, 2A_zz′, also showed some small variation between labelling sites, probably arising from differences in nitroxide mobility (30) or possibly from strain-induced change to the electronic structure. Individual values of 2A_zz′ are given in Table S1 (ESI†).

2.3 Molecular dynamics simulation

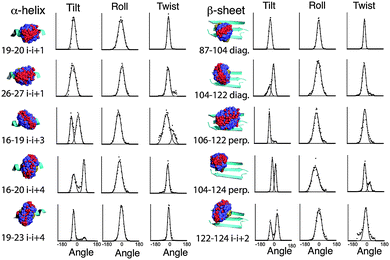
MD simulations of the spin label positions were carried out using parameters based on the CHARMM²⁹ force field, using the program Xplor-NIH.³⁰ The simulations were designed to reveal the sterically allowed conformations of the label, with the backbone of the Vps75 protein structure harmonically restrained and the side chain atoms allowed to move freely. No electrostatic potential was used and no water was included. Parameters for the Rx spin-label were adapted from those describing the R1 label.³¹ Trajectories were analysed in several ways. Fig. 2 shows overlaid frames for each unique labelling site. Visual inspection of the overlaid frames indicated that the tilt (S1 and Fig. S4, ESI† for definitions) motion predominates at all sites, however they also showed significant differences in the range of tilt angles. Measurement of the three angles defining the orientation of the nitroxides was made and graphs showing binned angle distributions for tilt, twist and roll are shown alongside the molecular graphics in Fig. 2.

Fig. 2 Combined frames taken from molecular dynamics on spin labelled Vps75. Underlying secondary structures shown as cyan coloured ribbons, oxygen of the nitroxide shown as red spheres, carbon atoms of the spin labels shown as blue spheres and sulphur atoms yellow spheres. The associated graphs show the extracted angle distributions for the spin labels in the order tilt, roll and twist. Binned values are shown as dots and fitted Gaussian curves are shown as continuous lines. Angle distributions are shown from −180 to +180.

The intrinsic rigidity of the Rx label offered by the two-point attachment is strongly reflected in the small distributions measured for twist and roll and the much larger ranges of tilt. An unexpected result of this analysis was that the tilt angle was in most cases distributed between two ranges (bimodal), which could be fitted reasonably well by Gaussian curves (Fig. 2). The exceptions to the bimodal distribution of tilt angles were the two α-helical i–i + 1 positions (19–20 & 26–27) and one of the diagonal β-sheet positions (87–104).

Examination of the steric environment of each of the label sites in the α-helix, indicated that a possible factor in determining the range and multiplicity of the tilt angle distributions was the position of flanking residues. The angle of tilt is perpendicular to the Rx attachment points on the cysteine side chains so the i–i + 1 position has flanking residues situated at i − 3 and i + 4 that directly block tilt movement. For attachment positions i–i + 3 and i–i + 4 no such flanking residues exist. It is interesting to note that the line-width of the fitted Gaussian curve for the α-helical i–i + 1 tilt, is somewhat broader than the individual distributions measured for the other positions on the helix, so although the i–i + 1 attachment site provides an essentially monotypic conformation, this distribution is slightly larger than the components of the bimodal distributions seen at alternative sites. The same analysis for the β-sheet attachment sites shows a similar buttressing effect by side-chains of residues in diagonal attachment sites and a lack of buttressing effect in both the i–i + 2 and the perpendicular attachment sites.

Although measurement of tilt, roll and twist are useful ways of looking at the conformational heterogeneity of the Rx label in isolation, another way is to look at the relative orientation of the N–O nitroxide vector between the two spin labels present in each snapshot structure along the dynamic trajectory. The tilt, roll and twist directly relate to the conformation of the spin label to the protein backbone and the N–O vector orientation is related directly to the spin–spin orientation which pertains directly to the orientation measurements made by EPR. The N–O polar-angle distributions derived from the MD of all Rx constructs studied are shown in ESI,† Fig. S5. The specific relationship between MD and experimentally determined orientation for two i–i + 1 examples (19–20, 26–27) is described and discussed later in the Results section.

2.4 The effect of alternative attachment sites

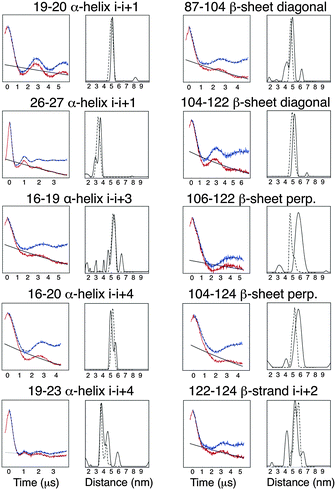
It has been previously reported that the Rx label gives rise to more restricted distance distributions than the R1 label.¹⁰ The label sites used in this study gave rise to spin-pairs due to the dimeric nature of Vps75 with spin–spin distances of between 30 and 60 Å. The X-band PELDOR data had strong and persistent echo oscillations (Fig. 3). Apart from for the shortest distance the oscillations continued to be significant up to the maximum time measurable. The quality of the Tikhonov derived distance distributions was generally good (Fig. 3) but varied somewhat, possibly due to the truncated oscillations (experiments with varied pump pulse position did not show significant change in the distributions). L-curves indicating the choice of broadening factor used in the processing are shown in ESI,† Fig. S6. Because the conformational dynamics of the spin label is extremely directional, the effect on experimentally measured distance distributions will vary, depending on the relative directions of tilt. MD trajectories were used to simulate distance distributions to compare with the X-band PELDOR derived distributions. The α-helical sites showed good agreement between simulation and experimental distance distributions (Fig. 3), with the i–i + 1 sites being best with regard to both distance and distribution width. In the cases where the Rx was attached to the β-sheet, the diagonal attachment shows good agreement with the experimental distribution but the rest show much poorer agreement, with the perpendicular attachment being most seriously different. Examination of the Rx attachment points on the crystal structure of Vps75 does show quite clearly that the β-sheet is significantly more irregular than the α-helix and that the external surface of the sheet is closely impinged on by a loop consisting of residues 91–98 and indeed by part of the long helix of the dimer interface. It is possible that some of the anomaly in the predicted distance distributions is due to deviations from the crystal structure.

Fig. 3 Diagram showing plots of X-band PELDOR data, uncorrected (red) and background corrected (blue) next to distance distributions calculated by Tikhonov regularization (solid black line) and predicted distributions from dynamic simulations (dashed line).

The sharp distance distributions measured from X-band PELDOR experiments and the largely monotypic tilt distribution seen in the case of Rx attachment to the helical i–i + 1 sites and possibly also at the diagonal attachment sites on the β-sheet make these types of attachment the most promising for accurate and precise distance and orientation measurement.

2.5 The effect of flanking residues on helix i–i + 1 attachment

To test the buttressing effect predicted for α-helical i–i + 1 sites, residues L16 and E23 (the i − 3 and i + 4 sites relative to the 19–20 label) were mutated, singly and together, to alanine. These mutations produced small but significant changes in the measured X-band PELDOR derived distance distributions as shown in Fig. 4. The distance distributions derived by Tikhonov regularization using L-curve derived broadening factors (Fig. S7, ESI†) clearly showed that mutation L16A, to the N-terminal side of the label had only a small effect on the distance distribution, giving a slight shift to longer distance. Mutation E23A had a more pronounced effect, both shifting the distance distribution to shorter values and broadening the distribution (Fig. 4).

Fig. 4 PELDOR derived distance distributions for mutations of residues surrounding Rx19–20. Diagram showing plots of distance distributions calculated by Tikhonov regularization for construct with surrounding mutations. Wild type L16–E23 (black), E23A (green), L16A (blue) and L16A–E23A (red).

A double mutation L16A/E23A produced a result that showed a median distance shifted a little back from that of the E23A single mutant but still to the longer side of the L16A and wild type constructs. The width of the distribution was also significantly the largest of all these constructs. Molecular dynamics analysis (data shown in ESI,† Fig. S8) supported the PELDOR results. The tilt angles indicated not only a greater range of tilt in the mutated samples but also a directionality of effect, which reflects the experimental results. The distance changes were small with a total spread of modal distance being only 3 Å. These observations support the proposition that although the Rx label is quite rigid, it does exhibit dynamic movement in the direction described by the tilt angle and because the changes appear to be predictable they could be factored into any prediction of underlying protein structure from PELDOR derived distances.

2.6 Orientation measurements

Orientation measurements were restricted to the two helical i–i + 1 label sites (19–20 and 26–27) due to these sites being judged as having the most suitable mono-modal conformation distributions and the most generally predictable secondary structure attachment positions. Orientation measurements are enabled by, measuring PELDOR at high frequencies where the g-anisotropy of nitroxide spin labels becomes fully resolved, and having large instantaneous bandwidth to cover the whole nitroxide spin label spectrum (400–500 MHz at W-band). The basic PELDOR measurement scheme used at W-band, has been described before³² but the analysis of the data has since been refined, optimized and automated and will be the subject of a subsequent paper. In its basic form the position of the pump and observe pulses are varied to measure different orientation correlations of the nitroxide spin label. By this means it is possible to calculate, or at least strongly constrain, the three Euler angles associated with the relative orientations of the spin pair, the two angles associated with the dipolar orientation and the distance distribution between the spins. Sensitivity and bandwidth are important as the most selective positions for pump and observe are at the edges of the spectrum (g_xx and g_zz orientations) where the relative numbers of spins excited is low. For g_xx–g_xx and g_yy–g_yy correlations, it is necessary to substantially reduce the excitation bandwidth of both pump and observe pulses to prevent overlap of pulses, and reduce effects related to (both inter and intra-molecular) instantaneous diffusion.³³ However this smaller bandwidth also sometimes requires a larger number of experiments.

2.7 Orientation analysis by fitting

A library of PELDOR modulation depths was simulated for a uniformly distributed array of rigid spin–spin orientations.³⁴ The modulation depth of a PELDOR signal is the value around which the dipolar modulation is oscillating.³ As long as the probe pulse is suitably selective, such that it can be assumed to excite on average only one spin, the modulation depth should depend only on the correlated excitation of pairs of spins, which can be expressed as a three dimensional rotation angle set (Euler angles are commonly used to describe this rotation). In this work the ZYZ Euler convention is used.³⁵ A root mean square deviation (RMSD) comparison between the libraries and the experimental measurement was first conducted to gain an insight into the relative angles between the spin label pairs and each of these relative angles was used as the starting value for global minimization routines.

The global minimization fitting routine was used to provide a best fit value for the relative angular distribution between the spin labels. Due to experimental symmetries there are 16 possible, symmetry-related, relative angle solutions.^36–38 The symmetry is due to the fact that the experiment is insensitive to the orientation of the axes of the magnetic tensors relative to the magnetic field. For example it is not possible to distinguish between g_xx and −g_xx or between spin label A or B. The one that is chosen by the optimizer depends on the starting value in the global minimization routine from which it is relatively easy to derive the equivalent solutions. It should be emphasized that each solution is consistent with the PELDOR data, although in practice many solutions can be eliminated by other known structural constraints. Symmetry related angular solutions for the systems measured here are shown in the ESI† in Table S2.

The distance distribution was included into the model as a Gaussian distribution where the initial mean and width values were chosen from the Tikhonov regularized distance solution to the weighted average (according to the pump pulse excitation fraction) of the experimental W-band PELDOR signals.³⁹ The fitting model distance distribution width and mean value was allowed to vary from the initial values within a range of initial value ±10 Å. The fitting model rotation angle values were allowed to vary within the full range of valid rotation angles. The algorithm used performs an iterated simulation and fitting to the experimental trace values, generating penalty values (RMSD) that were then fed back into the refinement. The global minimization used a genetic algorithm, with a population size of between 100 and 200 steps, to reduce the chance of settling in local minima. The algorithm was run independently 3 times for each of the 16 symmetric starting points, with different initial values, to ensure that a common minimum was found. It should be emphasized that each symmetry solution is consistent with the PELDOR data, although in practice many solutions can be eliminated by other known structural constraints.

To make a comparison between the angular components of the models obtained by the fitting algorithm and the MD simulations it was necessary to make a translation of the MD simulation model. This is a result of the way the PELDOR experiment is sensitive to the orientation angles between spin labels that we measure. In the PELDOR experiment we detect the relative angles between the spin labels in a frame defined by one of the pair. The angular relationship between the spin-pairs is illustrated in ESI,† Fig. S9.

A description of the comparison of experimental data, fitted results and PELDOR simulations of MD and random orientation is shown in S2 and Fig. S10 (ESI†).

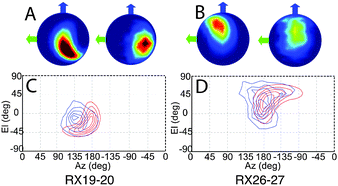
Refined relative orientation angles and distributions are shown in Table 2. Spherical density plot of relative spin–spin N–O vector directions for the fitted distribution is shown in Fig. 5 along with the equivalent distribution obtained from the MD frames. It is noted that the contours are equally spaced normalized to the maximum of the distribution. For both mutants there is a reasonable overlap between the contours derived from the MD frames and the contours derived from the fitting routine.

Table 2 Euler angles, mean values, derived from the fitting analysis results. Numbers in brackets are the standard deviations of a normal distribution around the mean values

	Alpha (Z)	Beta (Y)	Gamma (Z)
Rx19–20	135.0 (8.6)	139.0 (42.8)	135.0 (8.0)
Rx26–27	33.7 (13.5)	129.0 (40.4)	33.7 (1.1)

---

Fig. 5 The result derived from the fitting analysis and the MD are shown as spherical plots where the colour-scale shows the density of relative NO bond directions for (A) Rx19–20 and (B) Rx26–27, for each pair the left image represents the fitting analysis results and the MD results on right. Blue and green arrows indicate the g_yy and g_xx axes respectively. The same data is presented as 2D contour plots with the fitting analysis is shown in red and the MD results in blue for (C) Rx19–20 on the left and (D) Rx26–27.

Using the distribution found by fitting, the MD frames or a randomly sampled uniform distribution, we have generated PELDOR signals and compared them to the experimentally measured PELDOR signals. These are plotted for each case in Fig. 6.

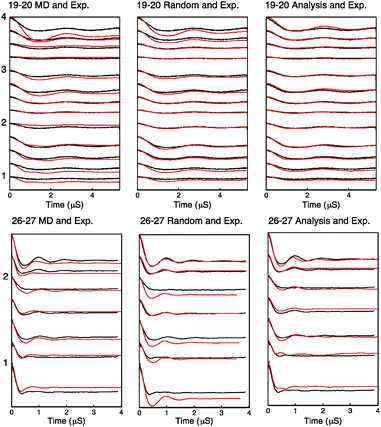Fig. 6 Simulated PELDOR signals for Rx26–27 and Rx19–20 are shown in red for the cases of left: simulated PELDOR signals for the MD predicted relative label distribution center: simulated PELDOR signals for a uniform distribution with no defined relative label orientation and right: the PELDOR signal result of the fitting analysis. The experimental PELDOR signal is shown in black. The experiment parameters used for sample RX19–20 and RX26–27 are shown in the order described in Table S5 and S6 (ESI†) respectively. Excitation profiles and FFT of traces for each experiment is shown in Fig. S11 and S12 (ESI†).

The modulation depth derived RMSD results (Fig. S10, ESI†) indicate a reasonable overlap between the RMSD minimum and the distribution predicted by MD despite using only the modulation depths from the PELDOR signals and none of the frequency components of the signals. It is noted that the lowest RMSD values show an expected set of 16 symmetric solutions (Table S2, ESI†). Using these angles as initial parameters for the fitting algorithm as described, the resulting PELDOR signal fits show good agreement with the experimental measured PELDOR signal. For Rx19–20 the MD does not predict the larger spread in the orientations that is experimentally observed. It is noted that the simulated PELDOR signals from the MD fit has a worse fit to the experimental data than the random orientation case. It can be seen in Fig. 5C that the distribution of the relative NO vector angles is smaller for the MD simulations compared to the fitting result. It is also noted from Fig. 5C and D that the MD distribution predicted for Rx19–20 is smaller than that predicted for the Rx26–27 case. For Rx26–27 the simulation of the MD derived PELDOR signal has, by contrast, a better fit to the experiment PELDOR signal than the random orientation, and the distribution of NO vector angles shown in Fig. 5D shows similarity between the MD and fitted results. In all cases the fitting results give the best fit to the experimental signal.

Although no method presently exists to directly refine a structure within MD, using the measured orientations as restraints. We were able to use the XANG restraint within XPLOR-NIH³⁰ to refine the positions of each nitroxide spin-pair. A set of polar angle restraints were calculated for each of the spin-pairs and the relative orientations could be refined for individual pairs. Combined refinement of both i–i + 1 spin-pairs was only possible by extrapolation of spin-orientation within each monomer using standard helical geometries. Global refinement of dimeric interactions using orientation measurements will be the subject of a subsequent publication.

3 Experimental

3.1 Construction, purification, and labelling of cysteine mutants

Vps75 mutants were expressed, purified and labelled as described in the ESI† (S1). Briefly, mutations were introduced into a pET30a vector containing a cysteine free version of Vps75 using QuickChange site directed mutagenesis (Agilent Technologies). Primers were designed and reactions carried out according to the recommended protocol, with mutations verified using DNA sequencing. Spin labelling was performed at room temperature by adding 4 × 0.5 molar equivalents of 3,4 bis-MTSSL to the sample at 5 minute intervals. The final reaction mixture was incubated at room temperature for 1 hour, after which excess 3,4 bis-MTSSL was removed by dialysis.

3.2 EPR spectroscopy

PELDOR samples were made by buffer exchanging the protein into a doubly concentrated D₂O buffer followed by mixing in a 1 : 1 ratio with D₈-glycerol. CW samples were run in a 30% sucrose solution. Details of EPR spectroscopy are described in ESI,† S1.

3.3 Molecular dynamics

Simulations were performed using Xplor-NIH³⁰ with the protein backbone fixed using harmonic restraints and side chain motion only restricted by their van der Waals radius. The Rx side chain was built onto a Vps75 crystal structure (PDB ID: 2ZD7) and simulations were performed in a vacuum with coordinates written out at 2 ns intervals with the simulation running over 4 μs. Distances were measured between the nitrogen of the nitroxide and orientations were measured using the nitroxide nitrogen to the midpoint of the two binding Cα bonds.

3.4 Orientation measurement analysis

Orientation selective PELDOR were performed at W-band with the 4-pulse refocused echo variant of the PELDOR pulse sequence,² where the microwave frequencies of the different pulse channels were adjusted to excited selections of the Rx label spectrum. The W-band PELDOR signal analysis was performed using home-written simulation scripts using the MATLAB 2013b package. Full details are included in ESI† (S1).

4 Conclusions

Using molecular dynamics and EPR measurement, of both distance and orientation, we have been able to explore alternative attachment sites on protein secondary structures and assess the utility of the Rx spin label. Six unique secondary structure associated sites were examined, three being on an α-helix (i–i + 1, i–i + 3 and i–i + 4) and three being on a β-sheet (i–i + 2, perpendicular across β-strands, and diagonal across β-strands). Simulations indicated that there were generally two conformations present for all sites except for the helical i–i + 1 and the diagonal sheet arrangements. The multiple conformations arose, largely, out of variations in the tilt angle (a motion perpendicular to the two amino-acid attachment points), with the other two available motions (twist and roll) being tightly restricted. PELDOR experiments were used to measure distance distributions between the dimer related spin-labels, showing that the distance distributions were generally better for the helical attachment points and best for the helical i–i + 1 and diagonal sheet attachment sites.

CW spectra showed all attachment positions to be close to the rigid limit. Analysis of the 2A_zz′ values, which has previously been correlated with the local spin-label dynamics, gave a rather surprising result in that on the helix the i–i + 1 positions gave values that were smaller, thus indicating more dynamic conformation, than the equivalent values for the i–i + 3 or i–i + 4 positions. The β-sheet positions showed no obvious correlation between the 2A_zz′ measurement and the conformational distributions from MD. Examination of the MD for the helical positions showed that while the i–i + 1 positions exhibited largely single conformations with the other helical sites having two conformations each, the variation within each conformation was larger for the i–i + 1 sites. Our interpretation of these results pointed towards a steric effect from neighbouring side chains. Only the i–i + 1 helical sites and the diagonal sheet attachment sites have side chains that are situated in the path of the tilt motion, all other sites do not. The i–i + 1 and diagonal positions are therefore buttressed in the direction of tilt and so occupy a conformation which places the spin label in a distribution essentially pointing straight upwards, from the underlying secondary structure, with the other sites tending to have conformations split between two extremes of tilt. We had previously observed this split conformational in a construct in which the Rx was situated on the dyad axis of the Vps75 dimer, crosslinking the two monomers.⁴⁰ A split conformation is also apparent in the crystallographically determined structure of Rx labelled lysozyme¹⁰ (PDB id 3L2X). Conformational distributions could be fitted with Gaussian peaks and the line-widths of these fitted peaks correlated well with the 2A_zz′ data. Overall the helical sites gave the most restrained labels but within the split conformations the peak widths were narrower and the 2A_zz′ values larger than the values observed for the single conformer i–i + 1 sites. The MD derived N–O vector orientation distributions (Fig. S5, ESI†) showed correlation to the local conformational distributions but was complicated by the direction of tilt with respect to the symmetrically related label position.

Having established that the i–i + 1 helical situation gives single and predictable conformational ranges, we made high field, orientation measurements. The orientations and distributions calculated from the analysis of the orientation selective PELDOR measurements on the i–i + 1 constructs showed good agreement with the MD predicted distributions but with a small shift of the modal points, particularly for position 19–20. A larger sample of experimentally and theoretically determined positions will be needed to refine the utility of this approach.

One of the major aims of this work was to show that it was possible to pre-calculate the expected narrow Euler angle distribution function of the Rx spin label for specific attachment points. The goal being building a library of “point spread functions” for the Rx spin label for different attachments and demonstrating that it could be used in situations where the underlying structure is not necessarily known a priori, but where changes in the protein structure can be accurately characterized. In principle it can also be used to improve the accuracy of distance distributions as if the relative orientations of the spin labels are known, their contribution to the distance and distance distribution can be eliminated.

The orientation fit made for selected label positions, to the measured W-band PELDOR data have been shown to be good, given that they do not take into account correlations between the distance and angular distributions and do not contain any additional correction or fitting terms beyond those calculated from first principles. In general the use of six or seven well chosen correlations are found to give a unique data set that puts strong constraints on the allowed angular distributions (allowing for symmetrical solutions).

The non-resonant sample holder enables one to address a broad spectral width, allowing the selection of all required orientation combinations. By using a pre-computed library approach we were able to extract the orientation parameters and an estimate of distribution. The orientations, which can be extracted from this data, are subject to experimental symmetries and so robust methods of incorporating such restraints into molecular refinement must still be developed. The force-field described as XANGLE in XPLOR-NIH³⁰ is able to partially utilize such restraints.

This work demonstrates a feasible, general strategy for the measurement of spin-label orientation in proteins. Furthermore because this approach uses labelling positions defined mainly by secondary structure, the approach may be of significant use even in a situation in which one or both partners of a protein–protein interaction have no previously determined tertiary structure.

Acknowledgements

M.A.S. & J.E.M. would like to acknowledge funding from the EPSRC as part of the iMR-CDT. The Authors would like to acknowledge funding from The http://MRC UK, Grant G1100021, EPSRC Basic Technology EP/F039034/1, and from the Wellcome Trust 099149/Z/12/Z.

References

1. A. D. Milov, K. M. Salikohov and M. D. Shirov, Fiz. Tverd. Tela, 1981, 23, 975–982.
2. M. Pannier, S. Veit, A. Godt, G. Jeschke and H. W. Spiess, J. Magn. Reson., 2000, 142, 331–340.
3. G. Jeschke, Annu. Rev. Phys. Chem., 2012, 63, 419–446.
4. H. Huang and D. S. Cafiso, Biochemistry, 2008, 47, 12380–12388.
5. C. Antoniou and L. W. M. Fung, Anal. Biochem., 2008, 376, 160–162.
6. P. V. L. Padmavathi and H. J. Steinhoff, J. Mol. Biol., 2008, 378, 204–214.
7. Y. Polyhach and G. Jeschke, Spectrosc. Int. J., 2010, 24, 651–659.
8. G. Hagelueken, D. Abdullin, R. Ward and O. Schiemann, Mol. Phys., 2013, 111, 2757–2766.
9. R. Ward, M. Zoltner, L. Beer, H. El Mkami, I. Henderson, T. Palmer and D. Norman, Structure, 2009, 17, 1187–1194.
10. M. R. Fleissner, M. D. Bridges, E. K. Brooks, D. Cascio, T. Kalai, K. Hideg and W. L. Hubbell, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16241–16246.
11. I. D. Sahu, R. M. McCarrick, K. R. Troxel, R. F. Zhang, H. J. Smith, M. M. Dunagan, M. S. Swartz, P. V. Rajan, B. M. Kroncke, C. R. Sanders and G. A. Lorigan, Biochemistry, 2013, 52, 6627–6632.
12. R. F. Rayes, T. Kálai, K. Hideg, M. A. Geeves and P. G. Fajer, PLoS One, 2011, 6, e21277.
13. A. R. Thompson, N. Naber, C. Wilson, R. Cooke and D. D. Thomas, Biophys. J., 2008, 95, 5238–5246.
14. H. S. McHaourab, P. R. Steed and K. Kazmier, Structure, 2011, 19, 1549–1561.
15. A. A. Dubinskii, Y. A. Grishin, A. N. Savitsky and K. Mobius, Appl. Magn. Reson., 2002, 22, 369–386.
16. A. Savitsky, A. A. Dubinskii, M. Flores, W. Lubitz and K. Mobius, J. Phys. Chem. B, 2007, 111, 6245–6262.
17. C. Abe, D. Klose, F. Dietrich, W. H. Ziegler, Y. Polyhach, G. Jeschke and H. J. Steinhoff, J. Magn. Reson., 2012, 216, 53–61.
18. A. Marko, D. Margraf, P. Cekan, S. T. Sigurdsson, O. Schiemann and T. F. Prisner, Phys. Rev. E, 2010, 81, 021911.
19. O. Schiemann, P. Cekan, D. Margraf, T. F. Prisner and S. T. Sigurdsson, Angew. Chem., Int. Ed., 2009, 48, 3292–3295.
20. A. Marko, D. Margraf, H. Yu, Y. Mu, G. Stock and T. Prisner, J. Chem. Phys., 2009, 130, 064102.
21. J. E. Lovett, A. M. Bowen, C. R. Timmel, M. W. Jones, J. R. Dilworth, D. Caprotti, S. G. Bell, L. L. Wong and J. Harmer, Phys. Chem. Chem. Phys., 2009, 11, 6840–6848.
22. J. E. D. Lillington, J. E. Lovett, S. Johnson, P. Roversi, C. R. Timmel and S. M. Lea, J. Mol. Biol., 2011, 405, 427–435.
23. J. Moult, K. Fidelis, A. Kryshtafovych, T. Schwede and A. Tramontano, Proteins, 2014, 82, 1–6.
24. A. Bowman, C. M. Hammond, A. Stirling, R. Ward, W. F. Shang, H. El-Mkami, D. A. Robinson, D. I. Svergun, D. G. Norman and T. Owen-Hughes, Nucleic Acids Res., 2014, 42, 6038–6051.
25. Y. J. Park, K. B. Sudhoff, A. J. Andrews, L. A. Stargell and K. Luger, Nat. Struct. Mol. Biol., 2008, 15, 957–964.
26. V. P. Denysenkov, T. F. Prisner, J. Stubbe and M. Bennati, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13386–13390.
27. Y. Polyhach, A. Godt, C. Bauer and G. Jeschke, J. Magn. Reson., 2007, 185, 118–129.
28. P. A. S. Cruickshank, D. R. Bolton, D. A. Robertson, R. I. Hunter, R. J. Wylde and G. M. Smith, Rev. Sci. Instrum., 2009, 80, 103102.
29. A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616.
30. C. D. Schwieters, J. J. Kuszewski, N. Tjandra and G. M. Clore, J. Magn. Reson., 2003, 160, 65–73.
31. R. A. Engh and R. Huber, Acta Crystallogr., Sect. A: Found. Crystallogr., 1991, 47, 392–400.
32. G. W. Reginsson, R. I. Hunter, P. A. S. Cruickshank, D. R. Bolton, S. T. Sigurdsson, G. M. Smith and O. Schiemann, J. Magn. Reson., 2012, 216, 175–182.
33. K. M. Salikhov and I. T. Khairuzhdinov, Appl. Magn. Reson., 2015, 46, 67–83.
34. H. Conroy, J. Chem. Phys., 1967, 47, 5307–5318.
35. A. Schweiger and G. Jeschke, Principles of pulse electron paramagnetic resonance, Oxford University Press, Oxford, UK, New York, 2001.
36. I. Tkach, S. Pornsuwan, C. Hobartner, F. Wachowius, S. T. Sigurdsson, T. Y. Baranova, U. Diederichsen, G. Sicoli and M. Bennati, Phys. Chem. Chem. Phys., 2013, 15, 3433–3437.
37. K. Mobius and A. Savitsky, High-Field EPR Spectroscopy on Proteins and their Model Systems: Characterization of Transient Paramagnetic States, The Royal Society of Chemistry, 2009, pp. 206–350, 10.1039/9781847559272-00206.
38. A. Marko and T. F. Prisner, Phys. Chem. Chem. Phys., 2013, 15, 619–627.
39. A. Godt, M. Schulte, H. Zimmermann and G. Jeschke, Angew. Chem., Int. Ed., 2006, 45, 7560–7564.
40. A. Bowman, R. Ward, N. Wiechens, V. Singh, H. El-Mkami, D. G. Norman and T. Owen-Hughes, Mol. Cell, 2011, 41, 398–408.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp04753f

‡ M.A.S. and J.E.M contributed equally to this work.

---