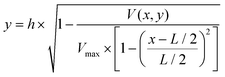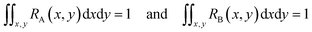Computational cell analysis for label-free detection of cell properties in a microfluidic laminar flow
Alex Ce
Zhang†
a,
Yi
Gu†
 a,
Yuanyuan
Han
a,
Zhe
Mei
b,
Yu-Jui
Chiu
c,
Lina
Geng
d,
Sung Hwan
Cho
b and
Yu-Hwa
Lo
*ac
a,
Yuanyuan
Han
a,
Zhe
Mei
b,
Yu-Jui
Chiu
c,
Lina
Geng
d,
Sung Hwan
Cho
b and
Yu-Hwa
Lo
*ac
aDepartment of Electrical and Computer Engineering, University of California at San Diego, La Jolla, California 92093-0407, USA. E-mail: ylo@ucsd.edu
bNanocellect Biomedical, Inc., San Diego, CA 92121, USA
cMaterials Science and Engineering Program, University of California, San Diego, 9500 Gilman Drive, La Jolla, California 92093-0418, USA
dSchool of Life Sciences, Beijing Institute of Technology, Beijing 100081, China
First published on 10th May 2016
Abstract
Although a flow cytometer, being one of the most popular research and clinical tools for biomedicine, can analyze cells based on the cell size, internal structures such as granularity, and molecular markers, it provides little information about the physical properties of cells such as cell stiffness and physical interactions between the cell membrane and fluid. In this paper, we propose a computational cell analysis technique using cells’ different equilibrium positions in a laminar flow. This method utilizes a spatial coding technique to acquire the spatial position of the cell in a microfluidic channel and then uses mathematical algorithms to calculate the ratio of cell mixtures. Most uniquely, the invented computational cell analysis technique can unequivocally detect the subpopulation of each cell type without labeling even when the cell type shows a substantial overlap in the distribution plot with other cell types, a scenario limiting the use of conventional flow cytometers and machine learning techniques. To prove this concept, we have applied the computation method to distinguish live and fixed cancer cells without labeling, count neutrophils from human blood, and distinguish drug treated cells from untreated cells. Our work paves the way for using computation algorithms and fluidic dynamic properties for cell classification, a label-free method that can potentially classify over 200 types of human cells. Being a highly cost-effective cell analysis method complementary to flow cytometers, our method can offer orthogonal tests in companion with flow cytometers to provide crucial information for biomedical samples.
Introduction
For decades, flow cytometers have been used to measure the physical properties of cells such as their size and granularity.1–7 Although labelling allows further differentiation of cells from fluorescent signals,7–13 cell labelling could unintentionally modify the properties of cells8 and in some cases affect cell viability14,15 in addition to adding cost and process complexity. Therefore, significant efforts have been devoted to attaining as much cell information as possible without labelling.16–21 In this paper we demonstrated enhanced abilities of label-free detection and analysis of cells in a laminar flow by employing innovative computation algorithms. Indeed, there have been numerous successful examples22,23 for applications of computation algorithms to obtain extra cellular information from biological samples, as demonstrated by super-resolution microscopy24–28 and imaging flow cytometry.29Realizing that cells of different physical properties find different equilibrium positions in a microfluidic laminar flow,30–39 we can acquire valuable cellular information from cell positions in principle. However, up to now such information has not become much useful because different types of cells or the same types of cells under different conditions (e.g. drug treatments or infections) often produce very small positional differences in a fluidic channel. To overcome this problem, at first we have to find a scheme to detect very small (a fraction of cell size) positional changes. A few years ago, we invented a space–time coding method to detect the cell position with better than one micrometer resolution.40–45 However, we still face another challenging problem resulted from the intrinsic inhomogeneity of biological cells. In other words, the property variations within the same cell group can be comparable to or even greater than the variations between two different cell groups. As a result, the distribution plots of two different cell groups may seriously overlap that no machine learning methods such as support vector machine (SVM) algorithms are able to separate the two groups.41 The key contribution of this paper is to devise an entirely new concept to address this critical issue. Instead of trying to classify each individual cell, we detect cells and their properties by groups. For two or more groups of cells with slightly different properties, our computation algorithms can (a) determine the cell population of each group, and (b) determine the spread and inhomogeneity of the properties within each cell group. Using the proposed computation method, we have demonstrated that even though two cell groups have their distribution plots overlapped by 80% or more, one can still accurately measure the population of each group of cells in samples of cell mixtures. To showcase potential applications of the computational cell analysis method, we demonstrate such unique capabilities in two examples. For point of care, we count neutrophils in whole blood for neutropenia detection, a critical and frequent test for chemotherapy patients.46–51 For drug testing based on phenotypical properties, we detect cellular response to drugs for target proteins (e.g. G-protein-coupled receptors).52,53
Experimental method
Computational cell analysis technique
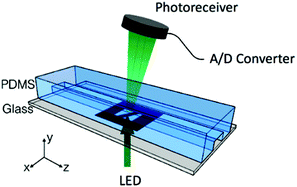
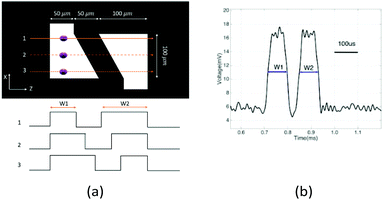
To determine the equilibrium position of a particular cell in the microfluidic channel, a spatial coding method was used to obtain the horizontal position and the velocity of the cell. The design and configuration of the system is illustrated in Fig. 1. The spatial mask has two oppositely oriented trapezoidal slits with the base lengths being 100 μm and 50 μm (Fig. 2(a)). An LED source was used to illuminate from the bottom of the microfluidic channel. The transmitted signal was detected by using a variable gain photoreceiver made of a Si photodiode and a transimpedance amplifier (Thorlab). All light blocking areas on the spatial mask were coated with a layer of Ti/Au on a glass slide. When cells flew through the spatial mask area, their forward scattering signal gave rise to a characteristic waveform encoded by the mask. The microfluidic channel is 5 cm long and has its inlet and outlet at the ends. The rectangular cross section of the channel is 100 μm wide and 50 μm high. The mask is located at 4.5 cm from the inlet. In the following discussion, we represent the channel width direction as the x-axis and channel height direction as the y-axis. The intensity modulated FS signal by the trapezoidal slits displays 2 peaks, as shown in Fig. 2(b). The ratio between the width of the first peak and the second peak provides information of the cell position in the x-axis, and the absolute value of the signal width gives information about cell velocity. Knowing the position along the x-axis and the cell velocity, the cell position along the y-axis can be obtained using the properties of a laminar flow that gives rise to a parabolic velocity profile represented by the following relation:39–44
In the above equation, y is the cell position in the channel height direction (y-axis), and h is the half channel height, 25 μm in this work. x is the horizontal position. V(x,y) is the velocity at a specific position. L is the channel width in the horizontal direction, in our case 100 μm. Vmax is the maximum velocity occurring at the center of the channel (i.e. x = L/2, y = 0, in our case, x = 50 μm, y = 0 μm). The target cells are suspended in PSB buffer solution (ρ = 103 kg m−3, μ = 1.05 × 10−3 Pa s). The flow rate used in the experiment is 180μL min−1. The microchannel hydraulic diameter, Dh = (2W × h)/(W + H), is 66.7 μm, where W and H are the width and height of the channel. The Reynolds number is calculated to be 38.1.
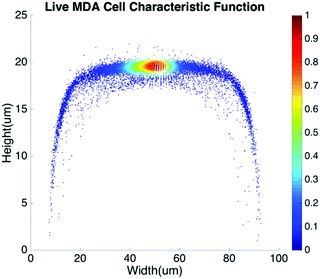
Basic algorithms. For given types of cells in a channel, their equilibrium positions can be represented by a characteristic distribution R(x,y). The characteristic distribution can be obtained in a diluted sample to avoid any effects caused by cell–cell interactions in the flow. Fig. 3 shows the characteristic distribution of live MDA-MB-231 cells. Without cell–cell interactions in the fluid, the spatial distribution of a sample containing multiple cell groups is the linear combination of the characteristic functions of each cell type.
If RA(x,y) and RB(x,y) are the characteristic functions of cell type A and cell type B, the spatial distribution, S(x,y), for a mixture of cell A and cell B can be described by eqn (1) where the coefficient, C, is the fraction of cell A in the sample:
| S(x,y) = C × RA(x,y) + (1 − C) × RB(x,y) | (1) |
Since both RA(x,y) and RB(x,y) are normalized over the entire cross section of the fluidic channel,
The distribution function S(x,y) for the sample is also normalized as in (2):
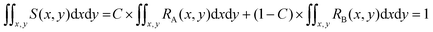 | (2) |
If we already know RA(x,y), RB(x,y) from the training data and measure S(x,y) from the sample, we can find from eqn (1) the only unknown, C, being the population of cell A, which is the information of interest.
In practice, the values of RA(x,y), RB(x,y) and S(x,y) at each specific position (x,y) are random variables. We divide the whole area of the channel cross section into meshes, so that the sets of random variables RA(x,y), RB(x,y) and S(x,y) follow the relations:
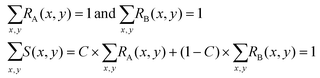 | (3) |
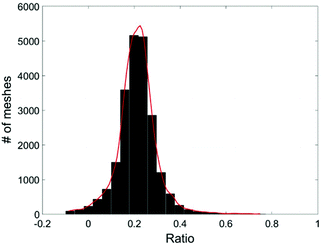
Due to the statistical nature of the problem, the resulting value of C, calculated at each position (x,y), is also a random variable. Thus we can plot the distribution of C, the percentage of cell A in the sample, in a histogram. The mean value of the histogram produces the most likely percentage for cell A in the sample and the spread of the histogram provides a good indication of the quality of the measurement. Fig. 5 shows an example of the histogram for C (Fig. 4).
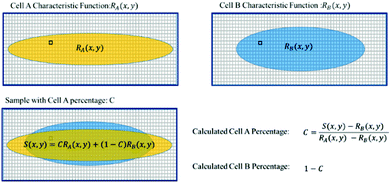 | ||
| Fig. 4 Illustration of the steps to calculate the cell ratio in a sample of a cell mixture. The yellow and blue patterns represent the characteristic distributions for cell A and cell B. | ||
Therefore, for any cell type possessing even a slightly different physical property than the rest of the cells in the sample, manifested by its largely overlapped spatial distribution with the rest of the samples, our method is still able to find the relative population of such a specific cell type in a cell mixture. This is a unique capability of the proposed method.
Obtaining characteristic functions from practical, non-purified, samples
In some practical cases, pure samples of a single cell type are not always available to allow us to obtain the characteristic functions (e.g. RA(x,y), RB(x,y), etc.). Even in the cases where one can use cultured cells to produce samples of pure cells, the distributions obtained from the cultured cells may be different from the real cells of the same type under physiological conditions.In the following we describe how one can obtain the characteristic functions (i.e. RA(x,y), RB(x,y), etc.) from cell mixtures directly without pure samples. These cell mixtures can be obtained directly from patient samples. To elucidate this method, let us start with two (or more) samples with different ratios (i.e. C1 and C2) of mixtures between cell A and cell B. We obtain the following relations:
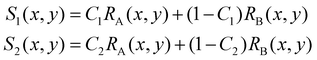 | (4) |
For training samples, we can label cells A and B so that one can use a conventional flow cytometer to find the cell ratios, C1 and C2 of the two training samples. The left hand side (LHS) of eqn (4) shows the measured distribution functions for the two mixtures. Then at each position (x,y), we can use eqn (4) to find the characteristic functions RA(x,y) and RB(x,y) for cells A and B since C1 and C2 are already known. Note that we only need to perform the above experiment once to establish the “library” of the characteristic functions for all cells of interest, and then these characteristic functions can be used for all future analyses of samples consisting of various cell mixtures. This process is further illustrated in Fig. 6.
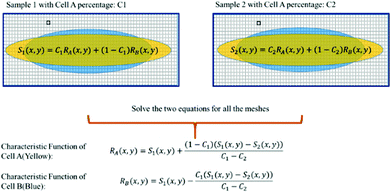 | ||
| Fig. 6 Use of cell mixtures as training samples to obtain the characteristic function of a specific cell type. | ||
For a mixture of two cell types with an unknown mixing ratio (C3), we can find its value using the same method described above (Fig. 7).
Note that the distribution function R(x,y) for each sample represents a set of position dependent random variables, so the reliability of its value at each position depends on the size of the ensemble within each mesh. To assure a good ensemble size at each position and to obtain the highest possible spatial resolution for R(x,y), we design meshes using the quad-tree algorithm that balances the weight of each mesh and the spatial resolution to yield the most distinctive and statistically sound results for cell detection.
Mesh definition for distribution functions: the quad-tree algorithm
Since the spatial distribution of the cell is not uniform across the channel, the weight of each mesh will be inevitably biased if the channel is divided into meshes of uniform size. In such a case, the information contained in those meshes with few cells flowing through (i.e. fewer data points) is less reliable. Those meshes, which may represent the majority of meshes for a distribution function concentrated to a relatively small area, can produce large noise and degrade the accuracy and confidence level of the result. On the other hand, for those meshes where there are too many cells flowing through, we do not take full advantage of the spatial resolution the data offer. To address these issues, we adopt meshes with non-uniform size based on the quad-tree algorithm.54 The quad-tree algorithm chooses mesh sizes dynamically based on the density of recorded cell positions. The channel is first divided into 4 meshes, each of which is further divided into another 4 meshes. Such a process continues to form a quad tree. Then the number of cells travelling through each mesh in each generation of quad in the tree is counted. If the number of cells within an older generation of quad (i.e. larger sized quad) is greater than the threshold for a statistically reliable ensemble, the next generation of quad will be used to gain a higher spatial resolution with a reduced ensemble size. The process continues until the smallest quads with slightly above threshold cell counts are reached. Fig. 8 shows how meshes are determined for a spatial distribution using the quad-tree algorithm. In this example, the distribution function was obtained by flowing 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells through a 100 μm × 50 μm channel.
000 cells through a 100 μm × 50 μm channel.
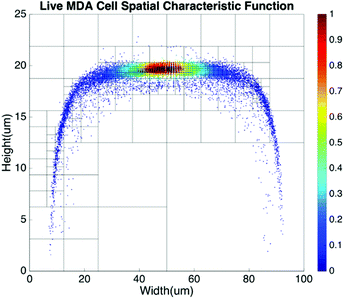 | ||
| Fig. 8 Spatial distribution of live MDA-MB-231 cells using meshes created by the quad-tree algorithm. | ||
Experimental results
Detection of the population of live and fixed cells
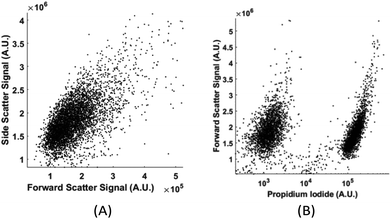
Without labelling, today's flow cytometers cannot find the percentage of live and dead cells in a culture because the scattering signals (forward, side, and back scattering) between live and dead cells overlap significantly in the distribution plot. We demonstrate that in spite of the high similarity in their physical properties of live and dead cells, the computation cell analysis technique enables us to give an unequivocal answer to the subpopulation of live cells from dead cells.We used live and fixed MDA-MB-231 cells to demonstrate the concept. MDA-MB-231 is a cell line for human breast cancer. In the experiment, we fixed one group of cultured MDA-MB-231 cells and labelled them fluorescently (propidium iodide), and then mixed these fixed cells with live cells in different ratios. Each sample with a specific ratio of live and fixed cells was divided into two parts, one running through our device and the other running through a commercial flow cytometer. Fig. 9(a) shows the distribution plot for forward and side scattering signals from a flow cytometer. It was impossible to determine the ratio between live and fixed MDA-MB-231 cells from the scattering signals by any gating or machine learning algorithms due to the significant overlap of the signals from live and dead cells. The only reliable method for a flow cytometer to detect the relative population of live cells from dead cells is by fluorescent labelling as shown in Fig. 9(b). Next we demonstrate how the computation cell analysis method can solve this problem.
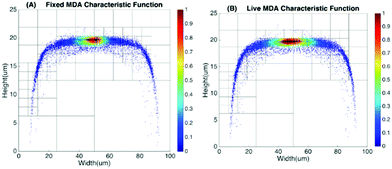
To produce characteristic functions for live and dead MDA-MB-231 cells, we ran through our system with two samples with 100% live MDA-MB-231 and 100% fixed MDA-MB-231. Fig. 10 shows the characteristic functions of live MDA-MB-231 cells and fixed MDA-MB-231 cells over the proposed quad-tree meshes. Fig. 11 shows the characteristic functions in a way that each mesh was assigned an index according to the ascending value of the characteristic function. Fig. 11 clearly reveals the differences in the characteristic function between live and fixed MDA-MB-231 cells. Then we ran multiple test samples with different ratios of live and fixed MDA-MB-231 cells. For each test sample, we ran the experiment 10 times, taking 3 minutes for each run, to test the reproducibility and reliability of the results. Fig. 12 shows comparisons between our method and the flow cytometer results by detecting the fluorescent signals of fluorescently labelled fixed cells. The excellent agreement and similar repeatability (10 repeats) of the results from both methods demonstrate the accuracy and reliability of our label-free computation cell analysis method.
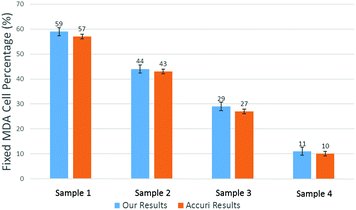 | ||
| Fig. 12 Measured mean value of live cell percentage in 4 samples. The error bars show the variations for 10 repeats for a cytometer (Accuri C6). | ||
Neutrophil counter for point-of-care applications
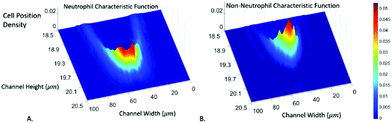
There are three major types of white blood cells, neutrophil, lymphocyte, and monocyte. Neutrophil count is an indicator of patient's immunity to infections and is particularly important for cancer patients undergoing chemotherapy since the treatment can lower the neutrophil count. Neutropenia develops when the neutrophil count falls below certain levels, substantially increasing the risk of infections.46,47 Therefore, the neutrophil count of chemotherapy patients has to be closely monitored, presenting the need for a point-of-care neutrophil counter without fluorescent labelling. In the following, we demonstrate how the computation cell analysis technique can count neutrophils in a point-of-care setting.We performed the experiment using blood purchased from San Diego blood bank. After red blood cell lysing, the blood was diluted with 1× PBS solution. Since we were interested in neutrophil count, we treated neutrophil as cell A and all non-neutrophil WBCs as cell B. Then we represent the characteristic function for neutrophil as RA(x,y) and all non-neutrophil white blood cells (WBCs) as RB(x,y). To obtain RA(x,y) and RB(x,y), we did not use blood samples with 100% pure neutrophils since complete removal of neutrophils from the samples can be practically difficult. Instead, we chose two blood samples with different neutrophil to non-neutrophil ratios. We used superparamagnetic beads (Dynabeads from ThermoFisher) to remove some neutrophils from the blood to produce samples with lower than normal amounts of neutrophils, which also simulated neutropenia patients. Using the aforementioned protocol, the superparamagnetic beads – Dynabeads CD15 – that were covalently coupled with an anti-human CD15 antibody were used to deplete human CD15+ myeloid cells, predominantly neutrophils, directly from whole blood. Different concentrations of Dynabeads CD15 were used to create blood samples having various percentages of neutrophils.55
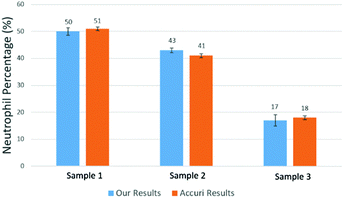
Using the above mentioned algorithm (see Fig. 6), we obtained the neutrophil and non-neutrophil characteristic functions as shown in Fig. 13. From these characteristic functions, one could apply eqn (4) to find the neutrophil ratio from samples of an unknown neutrophil population. Again, we have divided each test sample into two parts, one going through our device and another going through a commercial flow cytometer (Accuri C6). For each sample the test was repeated 10 times. Fig. 14 shows the comparison of results from both methods. The experiment was designed to cover the whole range of neutrophil ratios to simulate healthy samples and samples with different degrees of neutropenia.
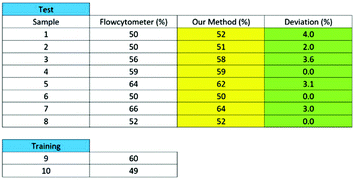
Table 1 summarizes results from another set of experiments out of 8 purchased blood samples from San Diego blood bank. The excellent agreement between the proposed method and the commercial flow cytometer shows that the computational cell analysis device, being a highly flexible and versatile technique, can operate as a cost effective, point-of-care neutrophil counter.
Drug response test from cell's phenotypical characteristics
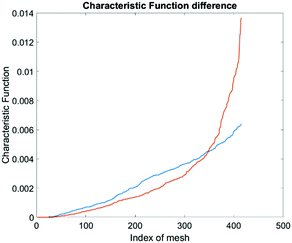
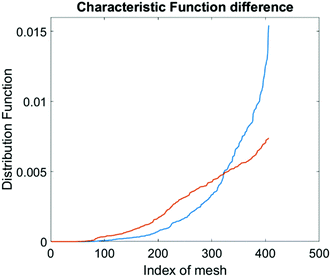
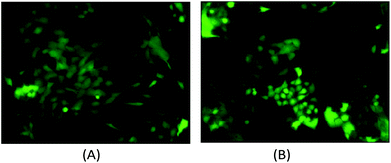
The computational cell analysis technique is capable of capturing minor changes in cell properties (e.g. cell size, shape, granularity, stiffness, surface properties, etc.) that are often hard to detect under conventional histology analysis. The unique ability of detecting such otherwise hard-to-detect cell property changes provides valuable insight and complements the existing methods in drug discovery. Drug responses of cells, especially the early stage response or responses under low drug dosages, may not be obvious and can skip people's attention.9 We have performed preliminary studies to investigate our method's capability of detecting subtle changes of cell properties under drug treatments.We divided breast cancer cells (MDA-MB-231) into two groups. For the first group, 15 nM of Paclitaxel was introduced into around one million cells for 48 hours. As a cytoskeletal drug, Paclitaxel stabilizes the microtubule cytoskeleton against depolymerization,56 and is reported to affect the cell surface roughness and stiffness57 due to increase in microtubule rigidity.56 As a control group, we introduced no drug into the second group of cells that were also cultured for 48 hours. Then the two groups of cells were run through our computation cell analysis system, yielding two characteristic functions corresponding to the drug treated and untreated cells. In Fig. 15, the x-axis is the index of the meshes following the quad-tree algorithm (see Fig. 8), and the y-axis is the value of characteristic functions. The difference of the characteristic function between the drug treated and untreated cells was presented in Fig. 15 where each mesh was assigned an index according to the ascending value of the characteristic function. Such representation helps us to visualize and quantify the differences of characteristic functions between cells. From Fig. 15 we observed clear differences between MDA-MB-231 cells with and without Paclitaxel treatment, suggesting that the fluid mechanic properties of the cells have been affected by the drug although the alterations of cell's phenotypical features were not apparent under a fluorescent microscope (Fig. 16).
Conclusions
In this paper, we report the invention of computational cell analysis as an entirely new method of detecting and analyzing cells from their spatial distribution in the microfluidic channel. A spatially coded mask was used to obtain the position of each cell by its optical scattering center. A mathematical algorithm was developed to calculate the composition of the cell mixture in the sample. This method is inherently label free and provides unique cellular information complementary to existing flow cytometers. Because the information is extracted from computation algorithms, the hardware of the apparatus is simple and inexpensive, making it suitable for point-of-care applications and amendable to many biomedical applications. To show the versatility of the technique, in this paper we demonstrate the functions of counting the population of live and dead cells, counting neutrophils from whole blood for neutropenia detection, and detecting cell property changes under drug treatments. These are a few examples from a large number of possible applications of the technique. We believe that the method of computational cell analysis opens a new avenue for cell analysis and offers a myriad of opportunities and capabilities complementary to the existing methods.Acknowledgements
The authors acknowledge the technical support of the staff of the San Diego Nanotechnology Infrastructure (SDNI), which is part of the National Nanotechnology Coordinated Infrastructure (NNCI). Research reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R43GM109241. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.References
- J. Godin, et al., Microfluidics and photonics for Bio-System-on-a-Chip: A review of advancements in technology towards a microfluidic flow cytometry chip, J. Biophotonics, 2008, 1(5), 355 CrossRef CAS PubMed.
- L. Pang, et al., Optofluidic devices and applications in photonics, sensing and imaging, Lab Chip, 2012, 12(19), 3543–3551 RSC.
- B. D. Piorek, et al., Free-surface microfluidic control of surface-enhanced Raman spectroscopy for the optimized detection of airborne molecules, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(48), 18898–18901 CrossRef CAS PubMed.
- J. Wu, G. Zheng and L. M. Lee, Optical imaging techniques in microfluidics and their applications, Lab Chip, 2012, 12(19), 3566–3575 RSC.
- C. Monat, P. Domachuk and B. J. Eggleton, Integrated optofluidics: A new river of light, Nat. Photonics, 2007, 1(2), 106–114 CrossRef CAS.
- J. Godin, et al., Microfluidics and photonics for Bio-System-on-a-Chip: A review of advancements in technology towards a microfluidic flow cytometry chip, J. Biophotonics, 2008, 1(5), 355 CrossRef CAS PubMed.
- D. V. Vezenov, et al., Integrated fluorescent light source for optofluidic applications, Appl. Phys. Lett., 2005, 86(4), 41104–41104 CrossRef.
- M. Brown and W. Carl, Flow cytometry: principles and clinical applications in hematology, Clin. Chem., 2000, 46(8), 1221–1229 CAS.
- B. Xi, et al., The application of cell-based label-free technology in drug discovery, Biotechnol. J., 2008, 3.(4), 484–495 CrossRef PubMed.
- C. D. Chin, V. Linder and S. K. Sia, Lab-on-a-chip devices for global health: Past studies and future opportunities, Lab Chip, 2007, 7(1), 41–57 RSC.
- G. M. Whitesides, The origins and the future of microfluidics, Nature, 2006, 442(7101), 368–373 CrossRef CAS PubMed.
- S. H. Cho, et al., Review article: recent advancements in optofluidic flow cytometer, Biomicrofluidics, 2010, 4(4), 043001 CrossRef PubMed.
- C. D. Chin, et al., Microfluidics-based diagnostics of infectious diseases in the developing world, Nat. Med., 2011, 17(8), 1015–1019 CrossRef CAS PubMed.
- Y. Fu and D. L. Kraitchman, Stem cell labeling for noninvasive delivery and tracking in cardiovascular regenerative therapy, Expert Rev. Cardiovasc. Ther., 2010, 8(8), 1149–1160 CrossRef PubMed.
- A. Gholamrezanezhad, et al., Cytotoxicity of 111In-oxine on mesenchymal stem cells: a time-dependent adverse effect, Nucl. Med. Commun., 2009, 30(3), 210–216 CrossRef CAS PubMed.
- D. R. Gossett, et al., Label-free cell separation and sorting in microfluidic systems, Anal. Bioanal. Chem., 2010, 397(8), 3249–3267 CrossRef CAS PubMed.
- X. Cheng, et al., A microfluidic device for practical label-free CD4+ T cell counting of HIV-infected subjects, Lab Chip, 2007, 7(2), 170–178 RSC.
- T. Blasi, et al., Label-free cell cycle analysis for high-throughput imaging flow cytometry, Nat. Commun., 2016, 7, 10256 CrossRef CAS PubMed.
- X. Shan, K. J. Foley and N. Tao, A label-free optical detection method for biosensors and microfluidics, Appl. Phys. Lett., 2008, 92(13), 133901 CrossRef.
- F. Vollmer and A. Stephen, Whispering-gallery-mode biosensing: label-free detection down to single molecules, Nat. Methods, 2008, 5(7), 591–596 CrossRef CAS PubMed.
- K. Cheung, G. Shady and R. Philippe, Impedance spectroscopy flow cytometry: on-chip label-free cell differentiation, Cytometry, Part A, 2005, 65(2), 124–132 CrossRef PubMed.
- G. A. Morrill, A. B. Kostellow and R. K. Gupta, Computational analysis of the extracellular domain of the Ca 2+-sensing receptor: An alternate model for the Ca 2+ sensing region, Biochem. Biophys. Res. Commun., 2015, 459(1), 36–41 CrossRef CAS PubMed.
- K. E. Rooney, Computational modeling of extracellular dopamine kinetics suggests low probability of neurotransmitter release, Synapse, 2015, 69(11), 515–525 CrossRef CAS PubMed.
- G. Shtengel, et al., Interferometric fluorescent super-resolution microscopy resolves 3D cellular ultrastructure, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(9), 3125–3130 CrossRef CAS PubMed.
- K. I. Mortensen, et al., Optimized localization analysis for single-molecule tracking and super-resolution microscopy, Nat. Methods, 2010, 7(5), 377–381 CrossRef CAS PubMed.
- S. J. Holden, U. Stephan and A. N. Kapanidis, DAOSTORM: an algorithm for high-density super-resolution microscopy, Nat. Methods, 2011, 8(4), 279–280 CrossRef CAS PubMed.
- B. Huang, et al., Three-dimensional super-resolution imaging by stochastic optical reconstruction microscopy, Science, 2008, 319(5864), 810–813 CrossRef CAS PubMed.
- B. Huang, M. Bates and X. Zhuang, Super resolution fluorescence microscopy, Annu. Rev. Biochem., 2009, 78, 993 CrossRef CAS PubMed.
- Y. Han and Yu.-H. Lo, Imaging Cells in Flow Cytometer Using Spatial-Temporal Transformation, Sci. Rep., 2015, 5, 13267 CrossRef CAS PubMed.
- C. D. Di, et al., Continuous inertial focusing, ordering, and separation of particles in microchannels, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(48), 18892–18897 CrossRef PubMed.
- C. D. Di, et al., Equilibrium separation and filtration of particles using differential inertial focusing, Anal. Chem., 2008, 80(6), 2204–2211 CrossRef PubMed.
- J. Oakey, et al. Particle focusing in staged inertial microfluidic devices for flow cytometry, Anal. Chem., 2010, 82(9), 3862–3867 CrossRef CAS PubMed.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli and P. Ian, Enhanced particle filtration in straight microchannels using shear-modulated inertial migration, Phys. Fluids, 2008, 20(10), 101702 CrossRef.
- H. Yun, et al., Simultaneous counting of two subsets of leukocytes using fluorescent silica nanoparticles in a sheathless microchip flow cytometer, Lab Chip, 2010, 10(23), 3243–3254 RSC.
- S. C. Hur, H. T. K. Tse and D. Di Carlo, Sheathless inertial cell ordering for extreme throughput flow cytometry, Lab Chip, 2010, 10(3), 274–280 RSC.
- S. C. Hur, et al., Deformability-based cell classification and enrichment using inertial microfluidics, Lab Chip, 2011, 11(5), 912–920 RSC.
- S. Mortazavi and G. Tryggvason, A numerical study of the motion of drops in Poiseuille flow. Part 1. Lateral migration of one drop, J. Fluid Mech., 2000, 411, 325–350 CrossRef.
- N. Pamme, Continuous flow separations in microfluidic devices, Lab Chip, 2007, 7(12), 1644–1659 RSC.
- J. Godin, L. Victor and Y. H. Lo, Demonstration of two-dimensional fluidic lens for integration into microfluidic flow cytometers, Appl. Phys. Lett., 2006, 89(6), 061106 CrossRef.
- T.-F. Wu, M. Zhe and Y. H. Lo, Optofluidic device for label-free cell classification from whole blood, Lab Chip, 2012, 12(19), 3791–3797 RSC.
- T.-F. Wu, M. Zhe and Y. H. Lo, Label-free optofluidic cell classifier utilizing support vector machines, Sens. Actuators, B, 2013, 186, 327–332 Search PubMed.
- T.-F. Wu, et al., Rapid white blood cell detection for peritonitis diagnosis, SPIE MOEMS-MEMS. International Society for Optics and Photonics, 2013 Search PubMed.
- T.-F. Wu, et al., Lab-on-a-Chip Device and System for Point-of-Care Applications, in Handbook of Photonics for Biomedical Engineering, Springer, Netherlands, 2013, pp. 1–30 Search PubMed.
- T.-F. Wu, et al., An optical-coding method to measure particle distribution in microfluidic devices, AIP Adv., 2011, 1(2), 022155 CrossRef PubMed.
- Z. Mei, et al., Applying an optical space-time coding method to enhance light scattering signals in microfluidic devices, Biomicrofluidics, 2011, 5(3), 034116 CrossRef PubMed.
- A. S. Deinard, et al., Studies on the neutropenia of cancer chemotherapy, Cancer, 1974, 33(5), 1210–1218 CrossRef CAS PubMed.
- J. Crawford, et al., Reduction by granulocyte colony-stimulating factor of fever and neutropenia induced by chemotherapy in patients with small-cell lung cancer, N. Engl. J. Med., 1991, 325(3), 164–170 CrossRef CAS PubMed.
- A. W. Martinez, et al., Diagnostics for the developing world: microfluidic paper-based analytical devices, Anal. Chem., 2009, 82(1), 3–10 CrossRef PubMed.
- X. Mao and T. J. Huang, Microfluidic diagnostics for the developing world, Lab Chip, 2012, 12(8), 1412–1416 RSC.
- A. W. Martinez, et al., Diagnostics for the developing world: microfluidic paper-based analytical devices, Anal. Chem., 2009, 82(1), 3–10 CrossRef PubMed.
- P. Yager, et al., Microfluidic diagnostic technologies for global public health, Nature, 2006, 442(7101), 412–418 CrossRef CAS PubMed.
- T. Klabunde and G. Hessler, Drug design strategies for targeting G-protein-coupled receptors, ChemBioChem, 2002, 3(10), 928–944 CrossRef CAS PubMed.
- R. Fredriksson, et al., The G-protein-coupled receptors in the human genome form five main families. Phylogenetic analysis, paralogon groups, and fingerprints, Mol. Pharmacol., 2003, 63(6), 1256–1272 CrossRef CAS PubMed.
- G. J. Sullivan and R. L. Baker, Efficient quadtree coding of images and video, IEEE Trans. Image Process., 1994, 3(3), 327–331 CrossRef CAS PubMed.
- I. Dransfield, S. Craig Stocks and C. Haslett, Regulation of cell adhesion molecule expression and function associated with neutrophil apoptosis, Blood, 1995, 85(11), 3264–3273 CAS.
- I. Arnal and R. H. Wade, How does taxol stabilize microtubules?, Curr. Biol., 1995, 5(8), 900–908 CrossRef CAS PubMed.
- K. S. Kim, et al., AFM-detected apoptotic changes in morphology and biophysical property caused by paclitaxel in Ishikawa and HeLa cells, PLoS One, 2012, 7(1), e30066 CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2016 |