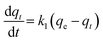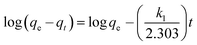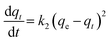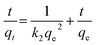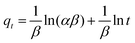DOI:
10.1039/C4RA15637D
(Paper)
RSC Adv., 2015,
5, 18438-18450
Removal of basic dye Auramine-O by ZnS:Cu nanoparticles loaded on activated carbon: optimization of parameters using response surface methodology with central composite design
Received
2nd December 2014
, Accepted 4th February 2015
First published on 4th February 2015
Abstract
This research is focused on the ultrasound-assisted removal of Auramine-O (AO) dye from aqueous solutions using ZnS:Cu nanoparticles loaded on activated carbon (ZnS:Cu-NP-AC) as an adsorbent. ZnS:Cu nanoparticles were synthesized and characterized using FESEM (Field-Emission Scanning Electron Microscopy) and XRD (X-Ray Diffraction) analysis. The experiments were designed by response surface methodology. A quadratic model was used to predict the variables. Analysis of variance was used for investigation of variables and interaction between them. High F-value (48.91), very low P-value (<0.00001), non-significant lack of fit, and the determination coefficient (R2 = 0.977) demonstrate good correlation between experimental and predicted values of the response. The highest removal percent attained was 99.76%, and the optimum parameters achieved are: adsorbent amount (0.02 g), initial dye concentration (20 mg L−1), sonication time (3 min) and pH = 7. Adsorption processes of AO by ZnS:Cu-NP-AC could be well described by a Langmuir isotherm and a pseudo-second-order kinetic model. The maximum adsorption capacity of AO by ZnS:Cu-NP-AC was determined as 183.15 mg g−1, suggesting a highly promising potential for ZnS:Cu-NP-AC to be used as a new adsorbent.
1. Introduction
The discharge of dyes into the biological ecosystem is worrying for both toxicological and esthetical aspects.1 Almost 45% of textile dyes produced worldwide belong to the reactive class.2 Reactive dyes are common dyes used for dying cellulosic fibres due to their favorable characteristics of bright color, water-fastness, simple application techniques and low energy consumption.3 Auramine-O (AO) and its hydrochloride salts are used as coloring agent in paper, textiles and leather industries.4 International agency for research on cancer (IARC) included AO among chemicals for which there is sufficient evidence of carcinogenicity due to its bio-transformation to reactive species in target organs of both rats and humans.5,6 Auramine-O (AO) is yellow in color and is frequently used in paper mills, textile mills, leather and carpet industry. Presence of these dyes is highly persistent and the manufacturers always go for the most stable dye. For the efficient removal of hazardous impurities, several physical and chemical methods such as coagulation,7 reverse osmosis,8 photo degradation,9 electrochemical oxidation,10 ozonation,11 biosorption12 and adsorption are used. Among all, adsorption as a popular alternative procedure, especially based on low cost adsorbent benefit from remarks such as, simple design, easy operation and the possibility of using green and non-toxic adsorbent. Many adsorbent were tested on the possibility of the hazardous dye removal such as carbon nanotube,13–21 MWCNTs22,23 activated carbon,24,25 fly ash,26 chitin,27 zeolite,28 polymer,29 low cost adsorbents,30–40 lignin,41,42 barley straw,43 nanocomposites44–47 and graphene oxide.48 Design and application of non-toxic adsorbent that was able to remove a huge amount of hazardous dyes molecule in short time are crucial requirements for the wastewater treatment. Nanoparticles exhibit intrinsic surface activity, high surface areas and reactive atom or functional group strongly chemisorbed many hazardous chemical compounds. The size, surface structure and interparticle interaction of nanomaterials determine their unique properties which proved nanoparticle an efficient adsorbent as well as several other potential applications in many relevant research areas. The key objective of the present work is the synthesis of ZnS:Cu nanoparticle loaded on AC, which is followed by a characterization via different analytical techniques such as UV-vis, SEM and XRD. The potential feasibility of ZnS:Cu-NP-AC for the adsorption process of AO was investigated and the influence of certain variables was studied and optimized by central composite design (CCD) combined with response surface methodology (RSM) using the desirability function (DF) as maximize criterion of the response. The results obtained from the presented models were compared with the experimental values. The adsorption kinetics and isotherms of dye removal on this adsorbent was also investigated. The adsorption rates were evaluated by fitting the experimental data to traditional kinetic models such as pseudo first-order, second-order and intraparticle diffusion models. The proposed sorbent will be useful for quantitative adsorption of the dye with high sorption capacities in short time.
2. Materials and methods
2.1. Materials and instruments
Auramine-O (4,4-dimethylaminobenzophenonimide) (AO) were considered as azo dye. Detailed description of this dye is shown in Table 1. The stock solution (200 mg L−1) of dye was prepared by dissolving 200 mg of solid dye in 1000 mL of double distilled water and the working concentrations were prepared daily by suitable dilution. The ZnS:Cu-NP-AC nanoparticles were prepared and characterized by using BET and SEM. The BET (Brunauer, Emmett, and Teller) surface area of the adsorbent material was measured using TriStar II 3020 (Micrometrics Instrument Corporation) surface area analyzer where N2 gas was used as adsorbate. The nitrogen sorption analysis was accomplished using a Belsorp-BEL, Inc. analyzer at 77 K. Prior to measurement, the materials was degassed at 373 K for 12 h. The surface area of the ZnS:Cu-NP-AC was calculated by BET method and the pore size distribution was calculated from the adsorption branch of the isotherm using BJH method. NaOH and HCl with the highest purity were purchased from Merck (Darmstadt, Germany). The pH measurements were carried out using pH/Ion meter model-686 (Metrohm, Switzerland, Swiss) and the AO concentrations were determined using Jusco UV-vis spectrophotometer model V-530 (Jasco, Japan) at wavelength of 434 nm, respectively. An ultrasonic bath with heating system (Tecno-GAZ SPA Ultra Sonic System) at 40 kHz of frequency and 130 W of power was used for the ultrasound-assisted adsorption procedure.
Table 1 Properties of the Auramine-O
| Color index number |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| CAS number |
2465-27-2 |
| Chemical formula |
C17H21N3·HCl |
| Molecular weight (g mol−1) |
303.83 |
| Maximum wavelength (λmax), nm |
434 |
| Molecular structure |
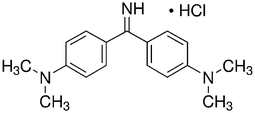 |
| Absorption spectrum |
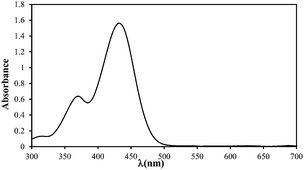 |
| Type of dye |
Basic yellow (cationic) |
| Use |
Paper mills, textile mills, leather and carpet industry |
2.2. Ultrasound-assisted adsorption method
A batch method was used to appraise the adsorption performance of AO dye from aqueous solutions onto ZnS:Cu-NP-AC in presence of ultrasonic wave. Adsorption experiments were performed in a cylindrical glass vessel by addition of adsorbent (0.02 g) into 50 mL of AO solutions at known concentration (5 and 30 mg L−1) and pH 7. The vessel was immersed in an ultrasonic bath for 3.0 min sonication time at the room temperature. After this time, solutions were analyzed for the final concentration of dyes by using a UV-vis spectrophotometer set at a wavelength of 434 nm for AO, respectively.
2.3. Measurements of dye uptake
The dye concentrations were determined according to calibration curve obtained at maximum wavelength over functioning concentration range. The efficiency of dye removal was determined at different experimental conditions and optimized according to the CCD method discussed in subsequent section. The dye removal percentage was calculated using the following equation:| |
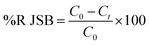 | (1) |
where C0 (mg L−1) and Ct (mg L−1) is the concentration of dye at initial and after time t, respectively.49
2.4. Kinetic experiments
Kinetic adsorption is performed to investigate the mechanism of adsorption and to determine the equilibrium time.50 For this purpose 0.01 and 0.02 g of adsorbent was contacted with 50 mL of AO solution with an initial concentration of AO, 10, 20 and 30 mg L−1, in ultrasonic at temperature for different time intervals at the optimum pH 7. The samples were filtered and determined using Jusco UV-vis spectrophotometer model V-530 (Jasco, Japan) at wavelength of 434 nm, respectively.51
2.5. Adsorption isotherms
Adsorption isotherms are used to describe the equilibrium behaviors of adsorbate uptake.52 For isotherms experiments, various amounts of adsorbents (0.01, 0.015 and 0.02 g) were contacted with 50 mL of solution AO with an initial concentration of (5–30 mg L−1), in 6 flasks at the optimum pH 7. The containers were mechanically agitated in a shaker at ultrasonic in room temperature for 3 min. The samples were filtered and determined using Jusco UV-vis spectrophotometer model V-530 (Jasco, Japan) at wavelength of 434 nm, respectively. The adsorbed dye amount (qe (mg g−1)) was calculated by the following mass balance relationship:| |
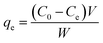 | (2) |
where qe is the amount of adsorbed manganese per gram adsorbent at equilibrium (mg g−1) and C0 and Ce are the concentrations of the metal ions before and after adsorption (mg L−1), V the volume of the aqueous phase (L) and m the mass of the adsorbent (g).53
2.6. Preparation of ZnS:Cu-NP-AC
Analytical reagent grade zinc sulfate (ZnSO4·2H2O), cupper(II) acetate (Cu(CH3COO)2) and thiourea (SC(NH2)2) were purchased from Merck company and used without further purification. The preparation of ZnS:Cu-NPs were carried out at two steps. In the first step, ZnS nanoparticles (ZnS-NPs) were synthesized. The precursor solution for synthesis of ZnS-NPs was prepared as follows: 0.6 mmol of zinc sulfate solution was mixed with 30 mL of 0.5 M thiourea solution at pH = 5.5 and deionized water was added to the mixed solutions to make a total volume of 250 mL. Then, 250 mL of the precursor solution in a baker was transferred to an autoclave at pressure of 1.25 bar for 3 h. The temperature of the autoclave was 125 °C. After 3 hours, the baker containing the reaction solution containing white colored ZnS-NPs in bottom of the baker was removed from autoclave. The obtained ZnS-NPs were filtered and washed several times by deionized water. In the second step, ZnS:Cu-NPs-AC was prepared. 250 mL of deionized water was added to the ZnS-NPs prepared from step 1 to form an insoluble suspension. 1 mL 0.2 M (Cu(CH3COO)2) solution was added to the ZnS-NPs suspension along with vigorous stirring for 5 min. After adding Cu2+ solution to ZnS-NPs suspension, its color slightly changes from milky white to light green because of the diffusion of Cu2+ ions to ZnS-NPs and formation of ZnS:Cu-NPs suspension. Finally, the homogenous deposition of ZnS:Cu-NPs on activated carbon (AC) was carried out by adding 10 g of AC to the obtained ZnS:Cu-NPs suspension and strong stirring for 20 h at room temperature. The prepared ZnS:Cu-NPs-AC were then filtered, washed several times by deionized water, dried at 60 °C for 3 h and used as an absorbent for adsorption experiments, the major impurities that may be present during the synthesis of ZnS:Cu nanoparticles are ZnO and Zn(OH)2, but the XRD pattern confirm high purity of ZnS:Cu-NP and its agreement with reference material without any further impurity.
2.7. Role of ZnS:Cu nanoparticles
ZnS:Cu nanoparticle posses a crucial role on the adsorption phenomenon, it lead to the enhancement of the surface area and number of active sites, hence it is an efficient adsorbent, when loaded on AC, it causes very rapid adsorption of hazardous materials i.e. dyes, even by using a very low amount of adsorbent dose i.e. 0.02, maximum 99.76% of the adsorption takes place. Hence to carry out at an efficient and maximum adsorption it is needed to coat ZnS:Cu nanoparticles on to the activated carbon because several parameters are effected like sonication time, pH, and adsorbent dose, a major change is reported in the sonication time parameter from 120 and 300 minutes it reduces to only 3 minutes to achieve the maximum adsorption.
2.8. Reusable capacity of ZnS:Cu nanoparticles
Like the other nanoparticles adsorbent i.e. Fe2O3, MnO etc, they can be reused as adsorbent after magnetic separation for removing the noxious toxic contaminants, it is seen that it can be used maximum four times without any change and modification in the developed adsorbent.54,55
2.9. Central composite design (CCD)
A central composite design (CCD) was used to determine the optimal conditions for the critical factors. For the adsorption process, significant variables, such as pH, AO concentration, adsorbent and sonication time, were chosen as the independent variables and designated as X1–X4, respectively. The pH (X1) ranged from 5 to 9, adsorbent (X2) ranged from 0.005 to 0.025 g, sonication time (X3) ranged from 1 to 5 min and the AO concentration (X4) ranged from 10 to 30 mg L−1, as shown in Table 2. The real values of the independent variables (Xi) were coded to zi according to eqn (3) by setting the lowest values as −2 and the highest values as +2:| |
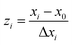 | (3) |
where zi is the dimensionless value of an independent variable, xi represents the real value of the independent variable, x0 is the real value of the independent variable at the center point, and ΔXi is the step change.56,57 The number of experiments was equal to eqn (4), where k and n are the number of factors and center runs, respectively (k = 4, n = 7), plus two additional points. A total of 31 experiments were performed.where k is the number of variables and nc is the number of central points. A four-factor five-level CCD was used to fit the general model of eqn (5) and to obtain optimal conditions for dependent variables (Y).| |
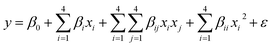 | (5) |
where y is the response, β0, βi, βii are the regression coefficients of variables for intercept, linear, quadratic and interaction terms, respectively. Xi and Xj are the independent variables and ε is the residual term. The STATISTICA software (Version 10.0) was used for data processing. Experimental data were fitted to a second-order polynomial equation, and regression coefficients were obtained. The analysis of variance (ANOVA) was performed to justify the significance and adequacy of the developed regression model. The adequacy of the response surface models were evaluated by calculation of the determination coefficient (R2) and also by testing it for the lack of fit.
Table 2 Design matrix for the central composite designs
| Factors |
Levels |
| Low (−1) |
Central (0) |
High (+1) |
−α |
+α |
| X1: pH |
6 |
7 |
8 |
5 |
9 |
| X2: adsorbent (g) |
0.01 |
0.015 |
0.02 |
0.005 |
0.025 |
| X3: time (min) |
2 |
3 |
4 |
1 |
5 |
| X4: AO concentration (mg L−1) |
15 |
20 |
25 |
10 |
30 |
3. Results and discussion
3.1. Characterization of adsorbent
The optical absorbance spectrum of the prepared ZnS:Cu-NP-AC has a steep absorption edge, indicating good homogeneity in the shape and size of the particles as well as low defect density near the band edge,64 it is well elucidated from Fig. 1. From the absorption data, the band gap energy of ZnS:Cu-NP-AC was estimated using the well-known relation for semiconductors:58,59| |
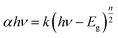 | (6) |
where, Eg is the band gap energy, k is a constant, and n is a constant equal to 1 or 4 for direct and indirect band gap materials, respectively. A plot of (αhν)2 versus hν (inset of Fig. 1) is linear at the absorption edge, which means that the mode of transition in these films has a direct nature. The band gap energy, Eg, was calculated about 3.97 eV from an extrapolation of the straight-line portion of the (αhν)2 vs. hν plot to zero absorption coefficient value. The obtained band gap energy for the prepared ZnS:Cu-NP is larger than that of the bulk ZnS (3.60 eV) which could be assigned to quantum confinement effects in nanosized material.
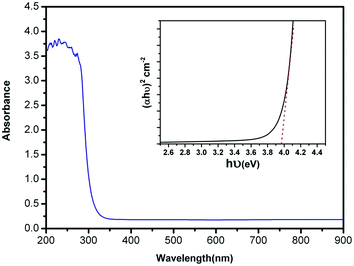 |
| | Fig. 1 UV-vis absorbance spectrum of the prepared ZnS:Cu-NP-AC (inset: plot of (αhν)2 vs. (hν) for the prepared ZnS:Cu-NP-AC). | |
The morphology and particle size of the prepared ZnS:Cu-NP were studied by FESEM (FE-SEM; Hitachi S-4160, Japan) under an acceleration voltage of 200 kV. The FESEM images of the prepared ZnS:Cu-NP at different magnifications were shown in Fig. 2a–c. The surface textural and morphology reveals the porous nature and rough surface of the developed adsorbent, it seems that the porous structure was due to the ZnS:Cu nanoparticles loaded on the AC, which should increase the effective surface for adsorption. The XRD patterns of ZnS:Cu nanoparticles prepared at 75 °C has good agreement with standard JCPDS (Joint Committee for Powder Diffraction Standards, JCPDS card no. 05-0566) pattern of ZnS (Fig. 3). The three broad peaks observed in the diffractogram at around 28.56°, 47.93° and 57.12° reveal a cubic lattice structure of (β-ZnS phase) planes (111), (220) and (311), respectively. The broad nature of XRD peaks confirms nanosized particles. According to full width at half-maximum (FWHM) of (110) peak and based on the Debye–Scherrer equation. The average crystalline sizes calculated from the full width at half-maximum (FWHM) of these peaks were about 22 and 21 nm for cubic and hexagonal ZnS:Cu nanoparticles, respectively.
 |
| | Fig. 2 FESEM images of the prepared ZnS:Cu-NPs-AC. | |
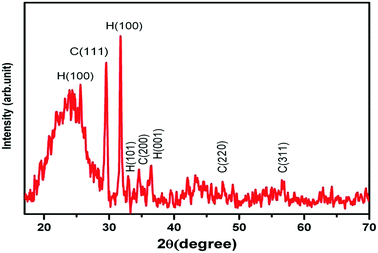 |
| | Fig. 3 XRD pattern for prepared ZnS:Cu-AC-NP. (H: hexagonal and C: cubic). | |
3.2. Central composite design (CCD)
3.2.1. Model fitting and statistical analysis. In the CCD step as presented in Table 2, four independent variables (pH (X1), adsorbent dosage (X2), sonication time (X3) and AO concentration (X4)) were prescribed into three levels (low, basal and high) with coded value (−1, 0, +1) and the star points of +2 and −2 for +α and −α respectively, were selected for each set of experiments. 31 experiments and their responses are presented in Table 3. In order to optimize AO adsorption, central composite design (CCD) with a total number of 31 experiments was used for the response surface modeling. Step-wise model fitting by STATISTICA 10.0 software was used to get the best fitted model. The software suggested quadratic model by supporting lack of fit and model summary statistics (Table 4). The model adequacy was further checked using ANOVA (Table 4).
Table 3 Design matrix for the CCDa
| Run |
X1 |
X2 |
X3 |
X4 |
% Removal Auramine-O |
| Observedb |
Predictedc |
| C: center point. Experimental values of response. Predicted values of response by RSM proposed model. |
| 1 |
7 |
0.015 |
3 |
10 |
94.98000 |
94.5652 |
| 2 |
6 |
0.020 |
2 |
15 |
96.78000 |
97.5729 |
| 3 |
7 |
0.005 |
3 |
20 |
60.78000 |
61.5518 |
| 4 |
7 |
0.025 |
3 |
20 |
96.78000 |
93.3768 |
| 5 |
8 |
0.010 |
2 |
25 |
73.97000 |
73.4753 |
| 6 |
6 |
0.010 |
4 |
25 |
81.56000 |
82.5158 |
| 7 |
9 |
0.015 |
3 |
20 |
81.89000 |
81.0778 |
| 8 |
6 |
0.020 |
4 |
25 |
95.80000 |
96.9945 |
| 9(C) |
7 |
0.015 |
3 |
20 |
98.50000 |
97.7686 |
| 10(C) |
7 |
0.015 |
3 |
20 |
98.67000 |
97.7686 |
| 11 |
6 |
0.020 |
4 |
15 |
99.76000 |
102.584 |
| 12 |
8 |
0.020 |
2 |
25 |
85.36000 |
87.6090 |
| 13 |
8 |
0.010 |
4 |
15 |
75.93000 |
77.8486 |
| 14 |
8 |
0.020 |
4 |
25 |
94.56000 |
96.3253 |
| 15 |
5 |
0.015 |
3 |
20 |
92.42300 |
90.6038 |
| 16(C) |
7 |
0.015 |
3 |
20 |
98.10000 |
97.7686 |
| 17 |
8 |
0.010 |
2 |
15 |
73.35000 |
72.4574 |
| 18(C) |
7 |
0.015 |
3 |
20 |
97.60000 |
97.7686 |
| 19 |
6 |
0.010 |
2 |
15 |
80.75000 |
81.3141 |
| 20 |
6 |
0.020 |
2 |
25 |
89.68000 |
90.0908 |
| 21(C) |
7 |
0.015 |
3 |
20 |
97.98000 |
97.7686 |
| 22(C) |
7 |
0.015 |
1 |
20 |
86.67000 |
85.2468 |
| 23 |
8 |
0.020 |
2 |
15 |
88.43000 |
89.8036 |
| 24(C) |
7 |
0.015 |
3 |
20 |
95.08000 |
97.7686 |
| 25 |
7 |
0.015 |
3 |
30 |
92.21000 |
89.9935 |
| 26 |
7 |
0.015 |
3 |
20 |
98.45000 |
97.7686 |
| 27 |
6 |
0.010 |
4 |
15 |
86.84000 |
84.8929 |
| 28 |
8 |
0.020 |
4 |
15 |
97.80000 |
96.6274 |
| 29 |
8 |
0.010 |
4 |
25 |
81.25000 |
80.7590 |
| 30 |
7 |
0.015 |
5 |
20 |
98.75000 |
97.5418 |
| 31 |
6 |
0.010 |
2 |
25 |
75.57000 |
77.0445 |
Table 4 Analysis of variance (ANOVA) for CCD (AO)b,c
| Source of variation |
Sum of square |
Dfa |
Mean square |
F-value |
P-value |
| Degree of freedom. * significant. ** not significant. |
| X1 |
136.117 |
1 |
136.117 |
88.5478 |
0.000082 |
* |
| X12 |
254.271 |
1 |
254.271 |
165.4105 |
0.000014 |
* |
| X2 |
1519.246 |
1 |
1519.246 |
988.3111 |
0.000000 |
* |
| X22 |
736.809 |
1 |
736.809 |
479.3143 |
0.000001 |
* |
| X3 |
226.751 |
1 |
226.751 |
147.5074 |
0.000019 |
* |
| X32 |
72.617 |
1 |
72.617 |
47.2393 |
0.000468 |
* |
| X4 |
31.350 |
1 |
31.350 |
20.3942 |
0.004035 |
* |
| X42 |
53.852 |
1 |
53.852 |
35.0325 |
0.001036 |
* |
| X1X2 |
1.183 |
1 |
1.183 |
0.7694 |
0.414155 |
** |
| X1X3 |
3.285 |
1 |
3.285 |
2.1371 |
0.194089 |
** |
| X1X4 |
27.958 |
1 |
27.958 |
18.1872 |
0.005294 |
* |
| X2X3 |
2.052 |
1 |
2.052 |
1.3349 |
0.291861 |
** |
| X2X4 |
10.320 |
1 |
10.320 |
6.7135 |
0.041154 |
* |
| X3X4 |
3.582 |
1 |
3.582 |
2.3299 |
0.177762 |
** |
| Lack-of-fit |
58.514 |
10 |
5.851 |
3.8065 |
0.057729 |
** |
| Pure error |
9.223 |
6 |
1.537 |
|
|
|
| Total |
2966.557 |
30 |
136.117 |
|
|
|
The ANOVA indicates that the model is highly significant through the F value of 48.91. There is only a 0.01% chance that a “model F value” could occur due to noise. Meanwhile, the p value of the model which is at p < 0.0001 also implies that the model is highly significant. The lack of fit value of 3.8065 confirms that the lack of fit is not significant relative to the pure error when p = 0.057729, which is >0.05. The insignificant lack of fit indicates good predictability. The “R-squared” of 0.97717 is in reasonable agreement with the “Adj R-squared” of 0.95719 which also indicates good predictability. Based on data analysis (Table 5), an empirical second order polynomial equation was obtained, which in terms of actual factors is as follows:
| |
yAO = −91 + 32X1 − 3X12 + 7730X2 − 203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 042X22 − 2X32 −0.0549X42 + 0.264X1X4 − 32X2X4 042X22 − 2X32 −0.0549X42 + 0.264X1X4 − 32X2X4
| (7) |
where,
y is the percentage removal of AO (%),
X1,
X2,
X3 and
X4 are terms for the coded values of pH, adsorbent, sonication time and concentration dye, respectively. (
Table 4) according to there should
P value of 0.05, it was revealed that pH (
X1), adsorbent dosage (
X2), sonication time (
X3) and concentration dye (
X4), quadratic pH (
X12), adsorbent dosage (
X22), sonication time (
X32) and concentration dye (
X42) and pH × initial AO concentration (
X1X4) and adsorbent × initial AO concentration (
X2X4) are significant model terms. The plot of experimental
versus calculated values of removal (%) indicate a good fit (as
Fig. 4) and presence of linear relationship between them with high correlation coefficient that indicates normal distribution of error around the mean and good applicability of model for explanation of experimental data. These plots are required to check the normality assumption in fitted model.
Table 5 Regression coefficients (AO)
| Factor |
Regression |
Std. Err. |
T |
P |
| Mean/interc. |
−91 |
19.151 |
−4.7349 |
0.003208 |
| X1 |
32 |
3.724 |
8.5673 |
0.000139 |
| X12 |
−3 |
0.232 |
−12.8612 |
0.000014 |
| X2 |
7730 |
603.619 |
12.8053 |
0.000014 |
| X22 |
−203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 042 042 |
9274.201 |
−21.8932 |
0.000001 |
| X3 |
6 |
3.018 |
2.1525 |
0.074851 |
| X32 |
−2 |
0.232 |
−6.8731 |
0.000468 |
| X4 |
0 |
0.631 |
0.4987 |
0.635739 |
| X42 |
−0 |
0.009 |
−5.9188 |
0.001036 |
| X1X2 |
54 |
61.992 |
0.8771 |
0.414155 |
| X1X3 |
0 |
0.310 |
1.4619 |
0.194089 |
| X1X4 |
0 |
0.062 |
4.2646 |
0.005294 |
| X2X3 |
72 |
61.992 |
1.1554 |
0.291861 |
| X2X4 |
−32 |
12.398 |
−2.5911 |
0.041154 |
| X3X4 |
0 |
0.062 |
1.5264 |
0.177762 |
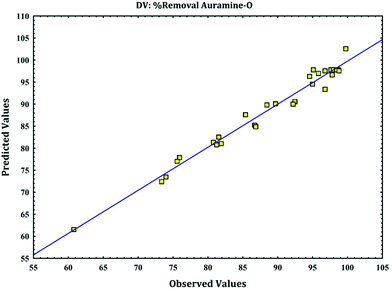 |
| | Fig. 4 The experimental data versus predicted data for removal of AO. | |
3.2.2. Three-dimensional response surface plots. The RSM correspond to CCD model was depicted and considered to optimize the critical factors and describe the nature of the response surface in the experiment. The curvature natures of Fig. 5 show the response surface plots of removal (%) confirm strong interaction between the variables.
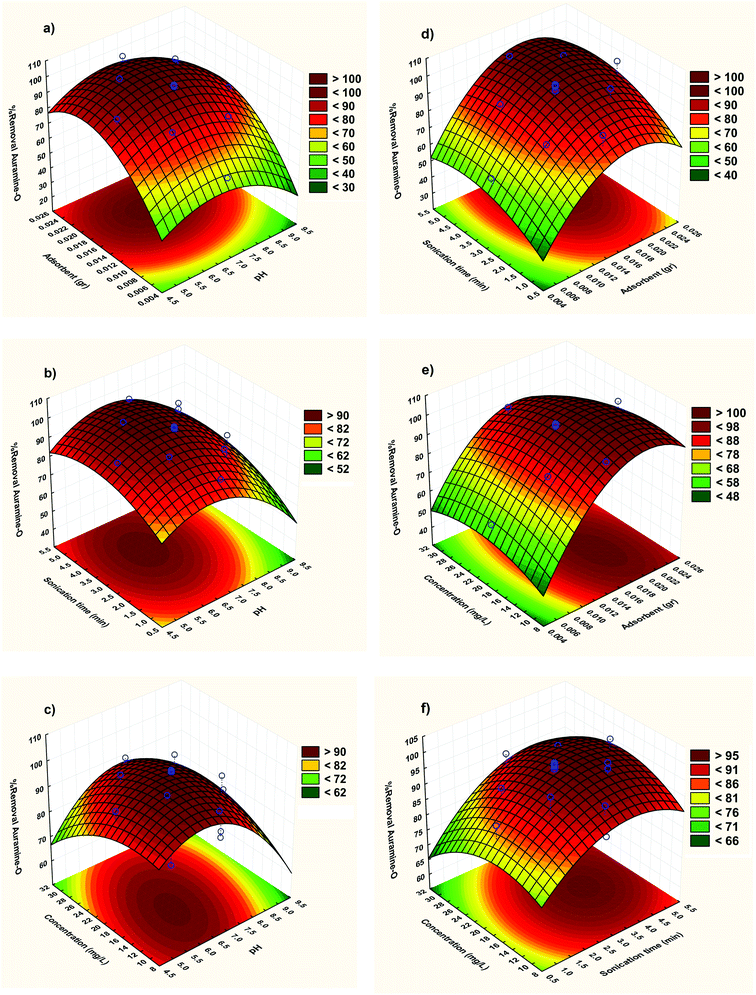 |
| | Fig. 5 Response surfaces for the AO removal: (a) X1–X2; (b) X1–X3 (c) X1–X4 (d) X2–X3; (e) X2–X4 and (f) X3–X4. | |
The three-dimensional response surface plots were used to assigning the interaction between the four variables. The relative impresses of two tested variables on the adsorption efficiency, while maintaining all other variables at fixed levels were illustrated in Fig. 5. Based on the quadratic model, the three-dimensional response surface plots were organized. The optimum situations of the relative variables will resemble with the coordinates of the central point in the upmost level in each of these figures.
Fig. 5a shows the combined effect of adsorbent and pH on adsorption of AO on ZnS:Cu-NP-AC at constant initial concentration of AO (20 mg L−1). It is evident from the figure that pH has a profound effect on removal of AO. With increase in pH, removal of AO decreases at lower amount of ZnS:Cu-NP-AC but at higher amount of ZnS:Cu-NP-AC, removal is almost constant with pH. At constant pH, removal increases with increase in amount of ZnS:Cu-NP-AC. It is quite obvious that when amount of adsorbent is high then removal is also high because available surface area for adsorption is much more.
Fig. 5b shows response surface plot of the adsorption efficiency as dependent on pH and the sonication time. It seems necessary to mention the surface charge of ZnS:Cu-NP-AC in the pH area under pHZPC is positive, because of the more H+ in the solution, and it helps the removal of anionic compounds, but in the pH area over pHZPC, the ZnS:Cu-NP-AC surface charge is negative due to the presence of OH− in the solution, and it helps in the removal of cationic compounds (pH area is considered as pHZPC in spaces, where the catalyst surface charge is zero.). In a low pH, ZnS:Cu-NP-AC has the positive surface charge and adsorbs the compounds with the negative charges like anionic dyes, but when the solution pH is over pHZPC, the oxide surface gets the negative charge and can make a complex with cationic compounds. So, according to these considerations, the basic conditions are more ideal for AO dye adsorption because AO dye is a cationic and cationic dye. In basic pH, adsorption happens along with the reduction of dye molecules by ZnS:Cu-NP-AC and in basic pH, adsorption may happen through adsorbing the dye molecules on the ZnS:Cu-NP-AC form.
Fig. 5c shows the three dimensional response surfaces of the combined effect of initial concentration and pH on percentage removal of dye at constant weight of ZnS:Cu-NP-AC (0.02 g). It is evident from the figure that removal of AO decreases when initial concentration increases. Removal attains its maximum value when pH is low and initial concentration is also low.
Fig. 5d clearly states that as the adsorbent amount and sonication time increases, the adsorption efficiency improves. It could be explained by the fact that the more amounts of ZnS:Cu-NP-AC cause an increase in the adsorbent surface and the active surfaces prepare some spaces for capturing AO dye molecules and increasing these spaces makes the dye get out faster.
To study the impact of the dye initial concentration on the adsorption efficiency, some experiments with concentrations (5–25 mg L−1) of AO dye and fixed sonication time (2 min) and pH (7) were designed and results displayed in Fig. 5e. The observed decreases in removal percentage at higher initial arrived from lower ratio of vacant sites to candidate dyes molecular that compete for binding to the surface. However at such situation there are not enough spaces for all molecules in high concentration of dye.
The effect of initial AO concentration on its removal percentage and its influence on their factors were shown Fig. 5f. It was seen that in despite of the increase in the amount of dye uptake, its removal efficiency was decreased. At lower dye concentrations, the ratio of solute concentrations to vacant reactive adsorbent sites is lower and accelerates dye adsorption which causes an increase in dye removal. At higher concentrations, lower adsorption yield is due to the saturation of adsorption sites. On the other hand, the percentage removal of dye was higher at lower initial dye concentrations and smaller at higher initial concentrations, which clearly indicate that the adsorption of AO from aqueous solution depend on its initial concentration.
3.3. Optimization of CCD by DF for extraction procedure
The profile for desirable option with predicted values in the STATISTICA 10.0 software was used for the optimization of the process (Fig. 6). The profile for desirable responses was chosen after specifying the DF for each dependent variable (removal percentage) by assigning predicted values. The scale in the range of 0.0 (undesirable) to 1.0 (very desirable) was used to obtain a global function (D) that its maximum (99.764%) and minimum (60.781%) value concern to JSB adsorption was achieved in this research.
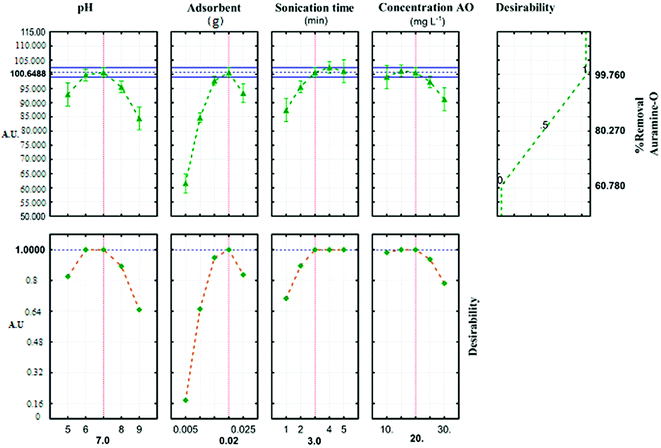 |
| | Fig. 6 Profiles for predicated values and desirability function for removal percentage of AO. Dashed line indicated current values after optimization. | |
Three solutions with different amounts of ideal conditions were used to predict the optimum conditions for AO dye adsorption onto ZnS:Cu-NP-AC (Table 6). The highest removal percent (99.8) achieved in the experiment number 5, compared to the other two experiments. Optimum parameters of the reaction are achieved at pH (7), (0.02 g) of ZnS:Cu-NP-AC, 3 min sonication time and initial concentration (20 mg L−l). The relative deviation coefficient 0.322% concern to RSM experimental design show good agreement and high correlation between actual and predicted amounts and reveal the suitability of empirical model resulted from the design could be used for well describing the relation between factors and the AO dye removal percentage.
Table 6 Optimum conditions derived by RSM design for dye removal
| Exp. |
Optimal conditions |
Removal (%) |
| pH |
Adsorbent (g) |
Sonication time (min) |
AO Concentration (mg L−1) |
Predicted value |
Predicted value |
RSE (%) |
| 1 |
7.0 |
0.02 |
3.0 |
20 |
99.671 |
100 |
0.329 |
| 2 |
7.0 |
0.02 |
3.0 |
20 |
99.542 |
100 |
0.458 |
| 3 |
7.0 |
0.02 |
3.0 |
20 |
98.877 |
100 |
1.123 |
| 4 |
7.0 |
0.02 |
3.0 |
20 |
99.678 |
100 |
0.322 |
| 5 |
7.0 |
0.02 |
3.0 |
20 |
98.321 |
100 |
1.679 |
3.4. Adsorption equilibrium study
Adsorption properties and equilibrium parameters of each isotherm model indicate the interaction of adsorbent–adsorbate and give comprehensive information about the nature of interaction.60–65 The widely used isotherm models such as Langmuir, Freundlich, Dubinin and Radushkevich (D–R) and Temkin were used to analyze the experimental equilibrium data obtained from the sorption process at room temperature over the concentration range of 5–30 mg L−1.
In the Langmuir isotherm,66 the intermolecular forces decrease rapidly with distance and the predicted monolayer coverage of the adsorbate on the outer surface of the adsorbent is represented in linear form as follows:
| |
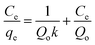 | (8) |
A plot 1/qe versus 1/Ce should represent a line with slope of 1/KaQm and 1/Qm intercept of 1/Qm and respective data are presented in Table 7. The high correlation (R2 > 0.999) coefficient shows that Langmuir isotherms are applicable for the interpretation of AO adsorption onto ZnS:Cu-NP-AC over the whole concentration range studies and maximum adsorption capacity of 92.26–183.15 mg g−1.
Table 7 Various isotherm constants and correlation coefficients calculated for the adsorption of Auramine-O onto ZnS:Cu-NP-AC
| Isotherm |
Parameters |
Value of parameters |
| 0.01 g |
0.015 g |
0.02 g |
| Langmuir |
Qm (mg g−1) |
183.15 |
122.54 |
94.26 |
| Ka (L mg−1) |
0.402 |
0.8111 |
1.102 |
| R2 |
0.990 |
0.994 |
0.998 |
| Freundlich |
1/n |
0.4544 |
0.4121 |
0.382 |
| KF (L mg−1) |
5.559 |
5.318 |
4.982 |
| R2 |
0.864 |
0.787 |
0.910 |
| Temkin |
B1 |
59.697 |
23.884 |
16.69 |
| KT (L mg−1) |
5.0964 |
10.665 |
18.56 |
| R2 |
0.984 |
0.925 |
0.986 |
| Dubinin–Radushkevich |
Qs (mg g−1) |
138.29 |
103.99 |
71.95 |
| B × 10−7 |
2.23 |
1.4 |
1.00 |
| E |
1497 |
1889 |
2236 |
| R2 |
0.960 |
0.984 |
0.913 |
The data was analyzed by the linearized form of Freundlich isotherm model:
| |
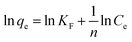 | (9) |
where
qe is the amount of adsorption,
KF is the Freundlich constant related to sorption capacity and 1/
n is a constant related to energy or intensity of adsorption. This gives an expression encompassing the surface heterogeneity and the exponential distribution of activated sites and their energies. This isotherm dose not predicts any saturation of the adsorbent surface. The Freundlich exponent's
kf and 1/
n can be determined from the linear plot of log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs.
qe vs. log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce
Ce. The values of the Freundlich constants
KF and 1/
n are 4.982–5.559 and 0.4544–1.130 respectively shown in
Table 7. The slope 1/
n ranging between 0 and 1 is a measure of adsorption intensity or surface heterogeneous, becoming more heterogeneous as its value gets closer to zero.
67
Table 7 shows that Langmuir model fits for AO dye (correlation coefficient 0.990–0.998) adsorption process. Heat of adsorption and the adsorbent–adsorbate interaction on adsorption isotherms were studied by Temkin,68 its equation is given as:
where
BT =
RT/
b,
T is the absolute temperature in K,
R the universal gas constant, 8.314 J mol
−1 K
−1,
KT the equilibrium binding constant (L mg
−1) and
B is related to the heat of adsorption. The constants obtained for Temkin isotherm are shown in
Table 7.
The linear form of Dubinin–Radushkevich isotherm equation can be expressed as.69
| |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qs − Bε2 Qs − Bε2
| (11) |
The plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. ε2 at different temperatures for AO is presented. The constant obtained for D–R isotherms are shown in Table 7. The mean adsorption energy (E) gives information about chemical and physical nature of adsorption.70
qe vs. ε2 at different temperatures for AO is presented. The constant obtained for D–R isotherms are shown in Table 7. The mean adsorption energy (E) gives information about chemical and physical nature of adsorption.70
The values of the parameters of the three isotherms and their related correlation coefficients are shown in Table 7, the Langmuir model yields a somewhat better fit (R2 = 0.990–0.998), Temkin isotherm (R2 = 0.925–0.986) than the Freundlich model (R2 = 0.787–0.910) and Dubinin–Radushkevich model (R2 = 0.913–0.984). Equilibrium data fitted well with the Langmuir model.
3.5. Kinetic study
Adsorption of a solute by a solid in aqueous solution usually occurs with a complex kinetics.71 The adsorption rate is strongly influenced by several parameters related to the state of the solid (generally with very heterogeneous reactive surface) and to physico-chemical conditions under which the adsorption is occurred. To investigate the adsorption processes of AO on the adsorbent, pseudo-first-order and pseudo-second-order adsorption were studied. The Lagergren pseudo-first-order model described the adsorption kinetic data.72 The Lagergren equation is commonly expressed as follows:| |
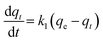 | (12) |
where qe and qt (mg g−1) are the adsorption capacities, at equilibrium and at time t respectively. k1 is the rate constant of the pseudo-first-order adsorption (L min−1). From the following model, plot of log(qe − qt) versus t was made and the values of k1 and qe were determined by using the slope and intercept of the plot, respectively.| |
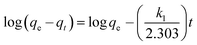 | (13) |
The fact that the intercept is not equal to qe, means that the reaction unlikely follows the first-order, regardless of the value of correlation coefficient.73 The variation in rate should be proportional to first power of concentration for strict surface adsorption. However, the relationship between initial solute concentration and rate of adsorption is linear when pore diffusion limits the adsorption process. Furthermore, the correlation coefficient, R2 is relatively low for most adsorption data (see Table 8). This indicates that the adsorption of AO onto ZnS:Cu-NP-AC was not a first-order reaction. Therefore, it is necessary to fit experimental data to another model. The adsorption kinetic may be described by the pseudo-second order model,74 which is generally given by the following equation:
| |
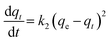 | (14) |
Table 8 Kinetic parameters for the adsorption of Auramine-O onto ZnS:Cu-NP-AC adsorbents
| Model |
Parameters |
Value of parameters |
| 0.01 (g) |
0.02 (g) |
| 10 (mg L−1) |
20 (mg L−1) |
30 (mg L−1) |
10 (mg L−1) |
20 (mg L−1) |
30 (mg L−1) |
| First-order kinetic |
k1 (min−1) |
0.0145 |
0.0131 |
0.0175 |
0.016 |
0.0135 |
0.024 |
| qe(calc) (mg g−1) |
3.907 |
5.844 |
8.385 |
7.23 |
11.716 |
25.14 |
| R2 |
0.969 |
0.983 |
0.922 |
0.972 |
0.863 |
0.965 |
| Pseudo-second-order kinetic |
k2 (min−1) |
0.001 |
0.0003 |
0.00018 |
0.004 |
0.0021 |
0.002 |
| qe(calc) (mg g−1) |
49.75 |
102.04 |
147.06 |
25.12 |
48.309 |
65.56 |
| R2 |
0.999 |
0.998 |
0.997 |
0.999 |
0.999 |
0.999 |
| Intraparticle diffusion |
Kdiff (mg g−1 min−1/2) |
1.363 |
2.958 |
4.822 |
0.372 |
0.758 |
0.484 |
| C (mg g−1) |
28.883 |
44.77 |
52.579 |
18.62 |
34.935 |
59.12 |
| R2 |
0.904 |
0.960 |
0.936 |
0.817 |
0.730 |
0.832 |
| Elovich |
β (g mg−1) |
0.159 |
0.0804 |
0.0545 |
0.475 |
0.544 |
0.382 |
| α (mg g−1 min−1) |
42.42 |
84.93 |
85.77 |
95.6 |
2899 |
28976 |
| R2 |
0.976 |
0.976 |
0.957 |
0.923 |
0.940 |
0.930 |
| qe(exp) (mg g−1) |
46.978 |
92.64 |
129.53 |
24.39 |
46.597 |
66.14 |
Eqn (13) is integrated over the interval 0 to t for t and 0 to qt for qt, to give
| |
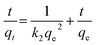 | (15) |
As mentioned above, the plot of log(qe − qt) versus t does not show good results for entire sorption period, while the plot of t/qt versus t shows a straight line. The values of k2 and equilibrium adsorption capacity (qe) were calculated from the intercept and slope of the plot of t/qt versus t (Table 8). For all concentrations and sorbent doses, the calculated qe values were mainly close to the experimental data and R2 values for the pseudo-second-order kinetic model were found to be larger than that for the pseudo-first-order kinetic. This indicates that the pseudo-second-order kinetic model applies better for the adsorption of AO dye for the entire sorption period. The intraparticle diffusion equation is given as:75
where
Kdif is the intraparticle diffusion rate constant (mg (g min
1/2)
−1) and
C shows the boundary layer thickness. The linear form of Elovich model equation is generally expressed as:
76| |
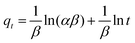 | (17) |
The kinetic data from pseudo-first and pseudo-second-order adsorption kinetic models and the intraparticle diffusion and Elovich model are given in Table 8. The linear plots of t/qt versus t indicated a good agreement between the experimental and calculated qe values for different initial dye concentrations. Furthermore, the correlation coefficients of the pseudo-second-order kinetic model (R2 ≥ 0.999) were greater than that of the pseudo-first-order model (R2 ≤ 0.983). As a result, it can be said that the adsorption fits to the pseudo-second-order better than the pseudo-first-order kinetic model.
3.6. Comparison with other methods
The ZnS:Cu-NP-AC prepared in this work had a relatively large adsorption capacity on AO compared to some other adsorbents reported in the literature, primarily when ZnS:Cu loaded on AC, it lead to rapid decrease in contact time parameter, it is reported that time taken by activated carbon is about 120 minutes,77 time taken by graphite loaded with titania is about 300 minutes,78 but when AC loaded with ZnS:Cu nanoparticle time taken by the adsorbent rapidly decrease and it takes nearly 3 minutes to adsorb the maximum amount of Auramine-O. Secondly the maximum amount of the adsorbate adsorbed on the adsorbent also increases form 1.509 mg g−1 (for AC) it becomes 94.26 mg g−1 (for ZnS:Cu nanoparticles loaded on AC).
Table 9 lists the comparison of maximum monolayer adsorption capacity of AO on various adsorbents. The adsorption capacity and contact time for proposed method in comparison with all of the adsorbents are preferable and superior to the literature which shows satisfactory removal performance for AO as compared to other reported adsorbents.77–80 The results indicated that the ultrasound assisted removal method has a remarkable ability to improve the removal efficiency of dyes. The ultrasonic-assisted enhancement of removal could be attributed to the high-pressure shock waves and high-speed microjets during the violent collapse of cavitation bubbles.81,82
Table 9 Comparison for the removal of Auramine-O by different methods and adsorbents
| Adsorbent |
Adsorbent dosage (g) |
Dye |
Concentration (mg L−1) |
Contact time (min) |
References |
| Bagasse fly ash (BFA) |
0.001 |
AO |
10 |
30–240 |
77 |
| Activated carbon-commercial grade (ACC) |
0.020 |
AO |
10 |
120–240 |
77 |
| Activated carbon-laboratory grade (ACL) |
0.002 |
AO |
10 |
120–240 |
77 |
| Graphite loaded with titania |
0.050 |
AO |
50 |
300 |
78 |
| Ag-NPs-AC |
8 |
MB |
2 |
16 |
79 |
| Ag-NPs-AC |
8 |
CR |
2 |
6 |
80 |
| Au-NPs-AC |
10 |
CR |
2 |
5 |
80 |
| ZnS:Cu-NP-AC |
0.020 |
AO |
20 |
3 |
Proposed method |
4. Conclusion
The results of the present studies showed that ZnS:Cu-NP-AC prepared by synthesis method was an efficient adsorbent for the Auramine-O removal. The use of response surface methodology involving central composite design for optimization of process parameters was studied. Experiments were performed as a function of initial pH, dye concentration, sonication time and absorbent dosage, these factors are well studied and optimized. The optimized values, at which the highest removal percent (99.76%) was attained, are achieved: pH = 7, initial concentration dye (20 mg L−1), sonication time (3 min) and adsorbent amount (0.02 g). In the present study, the analytical utility of experimental design for evaluation of optimum condition for the removal of AO in aqueous solution by ZnS:Cu-NP-AC coupled with ultrasound assisted adsorption method has been investigated. The equilibrium and kinetic studies were investigated for the adsorption process. The isotherm models such as Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich were evaluated and the equilibrium data were best described by the Langmuir model. The high correlation (R2 > 0.999) coefficient shows that Langmuir isotherms are applicable for the interpretation of AO adsorption onto ZnS:Cu-NP-AC over the whole concentration range studies and maximum adsorption capacity of 92.26–183.15 mg g−1. The process kinetics can be successfully fitted to the pseudo-second-order kinetic model.
Acknowledgements
The authors express their appreciation to the Graduate School and Research Council of the University of Yasouj for financial support of this work.
References
- H. M. Pignon, C. F. Brasquet and P. L. Cloirec, Sep. Purif. Technol., 2003, 31, 3–11 CrossRef.
- O. Tunc, H. Tanac and Z. Aksu, J. Hazard. Mater., 2009, 163, 187–198 CrossRef CAS PubMed.
- S. Dutta, A. Bhattacharyya, A. Ganguly, S. Gupta and S. Basu, Desalination, 2011, 275, 26–36 CrossRef CAS PubMed.
- A. Martelli, G. B. Campart, R. Canonero, R. Carrozzino, F. Mattioli, L. Robbiano and M. Cavanna, Mutat. Res., 1998, 414, 37–47 CAS.
- ARC, Monographs on the Evaluation of Carcinogenic Risk to Humans, Supplement 7: Overall Evaluations of Carcinogenicity: an Updating of IARC Monographs, International Agency for Research on Cancer, Lyon, France, 1987, vol. 1–42, pp. 118–119 Search PubMed.
- A. Dabrowski, Adv. Colloid Interface Sci., 2001, 93, 135–224 CrossRef CAS.
- O. Tunay, I. Kabdasli, G. Eremektar and D. Orhon, Water Sci. Technol., 1996, 34, 9–16 CrossRef CAS.
- E. Forgacs, T. Cserhat and G. Oros, Environ. Int., 2004, 30, 953–971 CrossRef CAS PubMed.
- K. Wu, Y. X. J. Zhao and H. Hidaka, J. Mol. Catal. A: Chem., 1999, 144, 77–86 CrossRef CAS.
- E. Kusvuran, O. Gulnaz, S. Irmak, O. M. Atanur, H. I. Yavuz and O. Erbatur, J. Hazard. Mater., 2004, 109, 85–93 CrossRef CAS PubMed.
- T. Robinson, G. McMullan, R. Marchant and P. Nigam, Bioresour. Technol., 2001, 77, 247–255 CrossRef CAS.
- M. Ghaedi, A. G. Nasab, S. Khodadoust, M. Rajabi and S. Azizian, J. Ind. Eng. Chem., 2014, 20, 2317–2324 CrossRef CAS PubMed.
- H. Mahmoodian, O. Moradi, B. Shariatzadeha, T. A. Saleh, I. Tyagi, A. Maity, M. Asif and V. K. Gupta, J. Mol. Liq., 2014, 202, 189–198 CrossRef PubMed.
- B. J. Sanghavi, S. Sitaula, M. H. Griep, S. P. Karna, M. F. Ali and N. S. Swami, Anal. Chem., 2013, 85, 8158–8165 CrossRef CAS PubMed.
- V. K. Gupta, R. Prasad, R. Mangla and P. Kumar, Anal. Chim. Acta, 2009, 420, 19–27 CrossRef.
- B. J. Sanghavi, W. Varhue, J. L. Chávez, C. F. Chou and N. S. Swami, Anal. Chem., 2014, 86, 4120–4125 CrossRef CAS PubMed.
- R. N. Goal, V. K. Gupta and S. Chatterjee, Talanta, 2008, 76, 662–668 CrossRef PubMed.
- B. J. Sanghavi, O. S. Wolfbeis, T. Hirsch and N. S. Swami, Microchim. Acta, 2015, 182, 1–41 CrossRef CAS PubMed.
- S. Wang, C. W. Ng, W. Wang, Q. Li and L. Li, J. Chem. Eng. Data, 2012, 57, 1563–1569 CrossRef CAS.
- T. A. Saleh and V. K. Gupta, Environ. Sci. Pollut. Res., 2012, 19, 1224–1228 CrossRef CAS PubMed.
- V. K. Gupta, S. Agarwal and T. A. Saleh, J. Hazard. Mater., 2011, 185, 17–23 CrossRef CAS PubMed.
- H. Khani, M. K. Rofouei, P. Arab, V. K. Gupta and Z. Vafaei, J. Hazard. Mater., 2010, 183, 402–409 CrossRef CAS PubMed.
- T. A. Saleh and V. K. Gupta, J. Colloid Interface Sci., 2012, 371, 101–106 CrossRef CAS PubMed.
- A. R. Dinçer, Y. Güneş, N. Karakaya and E. Güneş, Bioresour. Technol., 2007, 98, 834–839 CrossRef PubMed.
- T. E. Köse, H. Demiral and N. Öztürk, Desalin. Water Treat., 2011, 29, 110–118 CrossRef.
- P. Janoš, H. Buchtová and M. Rýznarová, Water Res., 2003, 37, 4938–4944 CrossRef PubMed.
- G. McKay, H. S. Blair and J. R. Gardner, J. Appl. Polym. Sci., 1982, 27, 3043–3057 CrossRef CAS.
- S. K. Alpat, Ö. Özbayrak, Ş. Alpat and H. Akçay, J. Hazard. Mater., 2008, 151, 213–220 CrossRef CAS PubMed.
- G. Crini, Dyes Pigm., 2008, 77, 415–426 CrossRef CAS PubMed.
- I. Ali and V. K. Gupta, Advance in water treatment by adsorption technology, Nat. Protoc., 2006, 1, 2661–2667 CrossRef CAS PubMed.
- V. K. Gupta, A. K. Singh, M. Al Khayat and B. Gupta, Anal. Chim. Acta, 2007, 590, 81–90 CrossRef CAS PubMed.
- I. Ali, Chem. Rev., 2012, 112, 5073–5091 CrossRef CAS PubMed.
- R. Jain, V. K. Gupta, N. Jadon and K. Radhapyari, Anal. Biochem., 2010, 407, 79–88 CrossRef CAS PubMed.
- I. Ali, Sep. Purif. Rev., 2014, 43, 175–2015 CrossRef CAS.
- V. K. Gupta, A. Mittal and J. Mittal, J. Colloid Interface Sci., 2010, 344, 497–507 CrossRef PubMed.
- V. K. Gupta, S. K. Srivastava, D. Mohan and S. Sharma, Waste Manage., 1998, 17, 517–522 CrossRef.
- V. K. Gupta, A. Mittal and J. Mittal, J. Colloid Interface Sci., 2010, 342, 518–527 CrossRef PubMed.
- V. K. Gupta, A. Mittal, D. Kaur, A. Malviya and J. Mittal, J. Colloid Interface Sci., 2009, 337, 345–354 CrossRef PubMed.
- V. K. Gupta, I. Ali, T. A. Saleh, A. Nayak and S. Agarwal, RSC Adv., 2012, 2, 6380–6388 RSC.
- A. Mittal, A. Malviya, J. Mittal and V. K. Gupta, J. Colloid Interface Sci., 2009, 340, 16–26 CrossRef CAS PubMed.
- P. J. M. Carrott, Suhas, M. M. L. Ribeiro Carrott, C. I. Guerrero and L. A. Delgado, J. Anal. Appl. Pyrolysis, 2008, 82, 264–271 CrossRef CAS PubMed.
- Suhas, P. J. M. Carrott and M. M. L. Ribeiro Carrott, Carbon, 2009, 47, 1012–1017 CrossRef CAS PubMed.
- B. C. Oei, S. Ibrahim, S. Wang and H. M. Ang, Bioresour. Technol., 2009, 100, 4292–4295 CrossRef CAS PubMed.
- Y. Yao, S. Miao, S. Liu, L. P. Ma, H. Sun and S. Wang, Chem. Eng. J., 2012, 184, 326–332 CrossRef CAS PubMed.
- V. K. Gupta, R. Jain, A. Mittal, S. Agarwal and S. Sikarwar, Mater. Sci. Eng C., 2012, 32, 12–17 CrossRef CAS PubMed.
- V. K. Gupta and A. Nayak, Chem. Eng. J., 2012, 180, 81–90 CrossRef CAS PubMed.
- V. K. Gupta, R. Jain, S. Agarwal and M. Shrivastava, Mater. Sci. Eng C., 2011, 31, 1062–1067 CrossRef CAS PubMed.
- P. Bradder, S. K. Ling, S. Wang, S. Liu and J. Chem, Eng. Data, 2011, 56, 138–141 CrossRef CAS.
- A. Shamsizadeh, M. Ghaedi, A. Ansari, S. Azizian and M. K. Purkait, J. Mol. Liq., 2014, 195, 212–218 CrossRef CAS PubMed.
- Y. Liu, Colloids Surf., A, 2006, 274, 34–36 CrossRef CAS PubMed.
- M. Ravanan, M. Ghaedi, A. Ansari, F. Taghizadeh and D. Elhamifar, Spectrochim. Acta, Part A, 2014, 123, 467–472 CrossRef CAS PubMed.
- J. R. Utrilla, I. B. Toledo, M. A. F. Garcy and C. Moreno, J. Chem. Technol. Biotechnol., 2001, 76, 1209–1215 CrossRef.
- A. Omri and M. Benzina, Alexandria Eng. J., 2012, 51, 343–350 CrossRef CAS PubMed.
- Y. G. Zhao, H. Y. Shen, S. D. Pan, M. Q. Hu and Q. H. Xia, J. Mater. Sci., 2010, 45(19), 5291–5301 CrossRef CAS.
- L. Wang, J. Li, Q. Jiang and L. Zhao, Dalton Trans., 2012, 41(15), 4544–4551 RSC.
- V. Gunaraj and N. Murugan, J. Mater. Process. Technol., 1999, 88, 266–275 CrossRef.
- A. R. Khataee, M. Zarei, M. Fathinia and M. Khobnasab Jafari, Desalination, 2011, 268, 126–133 CrossRef CAS PubMed.
- A. Goudarzi, G. Motedayen Aval, R. Sahraei and H. Ahmadpoor, Thin Solid Films, 2008, 516, 4953–4957 CrossRef CAS PubMed.
- S. D. Sartale, B. R. Sankapal, M. L. Steiner and A. Ennaui, Thin Solid Films, 2005, 480, 168–172 CrossRef PubMed.
- R. Liu, B. Zhang, D. Mei, H. Zhang and J. Liu, Desalination, 2011, 268, 111–116 CrossRef CAS PubMed.
- N. Kannan and M. M. Sundaram, Dyes Pigm., 2001, 51, 25–40 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1916, 38, 2221–2295 CrossRef CAS.
- A. Asfaram, M. R. Fathi, S. Khodadoust and M. Naraki, Spectrochim. Acta, Part A, 2014, 127, 415–421 CrossRef CAS PubMed.
- M. Ghaedi, M. Pakniat, Z. Mahmoudi, S. Hajati, R. Sahraei and A. Daneshfar, Spectrochim. Acta, Part A, 2014, 123, 402–409 CrossRef CAS PubMed.
- A. Mittal, D. Kaur and J. Mittal, J. Colloid Interface Sci., 2008, 326, 8–17 CrossRef CAS PubMed.
- M. Ghaedi, H. Tavallali, M. Sharifi, S. Nasiri Kokhdan and A. Asghari, Spectrochim. Acta, Part A, 2011, 86, 107–114 CrossRef PubMed.
- F. Haghseresht and G. Lu, Energy Fuels, 1998, 12, 1100–1107 CrossRef CAS.
- M. J. Temkin and V. Pyzhev, Acta Physicochim. URSS, 1940, 12, 217–222 Search PubMed.
- M. M. Dubinin and L. V. Radushkevich, Chem. Zentralbl., 1947, 1, 875–889 Search PubMed.
- G. Renmin, S. Yingzhi, C. Jian, L. Huijun and y. Chao, Dyes Pigm., 2005, 67, 175–181 CrossRef PubMed.
- M. J. Culzoni, A. V. Schenone, N. E. Llamas and M. Garrido, et al., J. Chromatogr. A, 2009, 1216, 7063–7070 CrossRef CAS PubMed.
- R. S. Juang, F. C. Wu and R. L. Tseng, Environ. Technol., 1997, 18, 525–531 CrossRef CAS.
- T. Robinson, G. McMullan, R. Marchant and P. Nigam, Bioresour. Technol., 2001, 77, 247–255 CrossRef CAS.
- M. R. Fathi, A. Asfaram and A. Farhangi, Spectrochim. Acta, Part A, 2015, 135, 364–372 CrossRef CAS PubMed.
- W. J. Weber Jr and J. C. Morris, J. Sanit. Eng. Div., Am. Soc. Civ. Eng., 1963, 89, 31–59 Search PubMed.
- Y. S. Ho and G. McKay, Biochemistry, 1999, 34, 451–465 CrossRef CAS.
- I. D. Mall, V. C. Srivastava and N. K. Agarwal, J. Hazard. Mater., 2007, 143, 386–395 CrossRef CAS PubMed.
- X.-Y. Pang, Eur. J. Chem., 2011, 8(4), 1644–1653 CAS.
- J. Pal and M. K. Deb, Appl. Nanosci., 2014, 4, 967–978 CrossRef CAS.
- J. Pal, M. K. Deb, D. K. Deshmukh and D. Verma, Appl. Water Sci., 2013, 3, 367–374 CrossRef CAS PubMed.
- S. R. Shirsath, D. V. Pinjari, P. R. Gogate, S. H. Sonawane and A. B. Pandit, Ultrason. Sonochem., 2013, 20, 277–286 CrossRef CAS PubMed.
- P. R. Gogate, V. S. Sutkar and A. B. Pandit, Chem. Eng. J., 2011, 166, 1066–1082 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2015 |
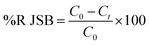
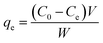
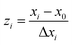
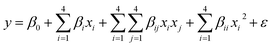
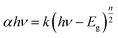

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 042X22 − 2X32 −0.0549X42 + 0.264X1X4 − 32X2X4
042X22 − 2X32 −0.0549X42 + 0.264X1X4 − 32X2X4
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 042
042

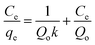
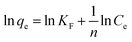
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. log
qe vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce. The values of the Freundlich constants KF and 1/n are 4.982–5.559 and 0.4544–1.130 respectively shown in Table 7. The slope 1/n ranging between 0 and 1 is a measure of adsorption intensity or surface heterogeneous, becoming more heterogeneous as its value gets closer to zero.67
Ce. The values of the Freundlich constants KF and 1/n are 4.982–5.559 and 0.4544–1.130 respectively shown in Table 7. The slope 1/n ranging between 0 and 1 is a measure of adsorption intensity or surface heterogeneous, becoming more heterogeneous as its value gets closer to zero.67
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KT + B
KT + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce
Ce
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln
qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qs − Bε2
Qs − Bε2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. ε2 at different temperatures for AO is presented. The constant obtained for D–R isotherms are shown in Table 7. The mean adsorption energy (E) gives information about chemical and physical nature of adsorption.70
qe vs. ε2 at different temperatures for AO is presented. The constant obtained for D–R isotherms are shown in Table 7. The mean adsorption energy (E) gives information about chemical and physical nature of adsorption.70