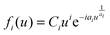Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Growth dynamics in supersonic molecular beam deposition of pentacene sub-monolayers on SiO2
Stefano
Gottardi
ab,
Tullio
Toccoli
a,
Yu
Wu
b,
Salvatore
Iannotta
a and
Petra
Rudolf
*b
aIMEM-CNR, Istituto Materiali per Elettronica e Magnetismo, Via alla Cascata 56/C, Povo Trento, Italy
bZernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747AG Groningen, The Netherlands. E-mail: p.rudolf@rug.nl
First published on 16th May 2014
Abstract
Studying highly energetic pentacene impinging on a surface, we demonstrated that the perpendicular component of the momentum drives the dynamics of molecule–molecule interactions and hence the island nucleation process, while the parallel component governs the dynamics of the interactions between the surface and the molecule and therefore determines the sticking coefficient and the island fractality.
Pentacene is widely studied as a prototype molecule to understand the processes involved in charge and energy transport in molecular solids.1 To this end high quality films starting from the first layer formation are required. The first layer plays a crucial role not only as a template for the growth of the subsequent layers but also for charge transport; hence several reports focused on the study of the early growth stages in the sub-monolayer regime.2,3 Recently a new deposition technique based on supersonic molecular beams (SuMBD)4 has been developed, which allows for improved control of the early stages of growth. With this technique the kinetic energy of impinging molecules can be easily tuned from thermal energy up to several eV by means of changing the degree of seeding in a lighter carrier gas (He, Ar, etc.).4,5 Several reports appeared on the comparison between pentacene submonolayer morphologies for layers grown by SuMBD and by thermal sublimation6 as well as on the carrier transport in field effect transistors based on SuMBD grown pentacene films.7 They show that the critical nucleus size, the crystallinity of the first monolayer and the structure of the molecular islands in the first pentacene layer are strongly correlated with the kinetic energy, Ek, at which the molecules impinge on the substrate surface. However the mechanisms are not completely understood. A fundamental study of the interaction between energetic pentacene molecules and a SiOx surface by A. S. Killampalli et al.8 proposed that the decrease of pentacene adsorption probability with increasing Ek is dominated by a trapping mediated process.9 The influence of parallel and normal momentum components of the impinging molecules was found to be equally important for adsorption under these conditions, as demonstrated by applying the energy scaling process in a regime between normal energy scaling10,11 and total energy scaling.12,13 However, so far no detailed study of the critical nucleus size, the variation of molecular island size and the evolution of sub-monolayer coverage for SuMBD growth at different Ek and momentum has been carried out. Here these relationships are revealed. We find that both the perpendicular and parallel momentum components of the molecules in the beam strongly influence the molecular sticking coefficient, the molecular island density, shape and size distribution as well as the critical nucleus size.
Pentacene was deposited under ultrahigh vacuum on a 500 nm thick SiOx/silicon wafer (purchased from Silicon Quest International, USA) with a low root mean square surface roughness (∼5–6 Å) as determined by atomic force microscopy in tapping mode (AFM). All substrates were moderately hydrophobic, with water contact angles of 55 ± 2° determined by the sessile drop method. Pentacene (Sigma-Aldrich, 99.98%) was purified before use by gradient vacuum sublimation. The SuMBD system was described previously.5 Samples were prepared by exposure to the supersonic beam (∼10 mm diameter) at different incident angles, θ: 0° (normal) incidence, 25°, 45° and 75° (see the inset of Fig. 2), at room temperature. The molecular beam was characterized on-line in terms of chemical purity, flux, and energy distribution by combining time of flight (TOF) mass spectrometry and multiphoton ionization spectroscopy. We chose an operation regime where no clustering effects and contaminants were detectable. The typical flux was 6 × 1011 molecules per (s cm2), estimated by cross correlating the TOF spectra at different Ek of the beam with that of a pentacene Knudsen source used as standard. The different Ek explored here were achieved by varying the degree of seeding by changing the He carrier gas pressure. Ex situ AFM was systematically carried out by scanning over multiple 10 × 10 μm2 areas at the sample centre (using Tap 300 probes, Budget sensor, on a Nanoscope IV multimode scanning probe microscope, Digital Instruments, Veeco Metrology Group, U.S.A.). The analysis of these AFM images (with the help of the WSxM software, Nanotec electronics S.L.) provided the information on the influence of the momentum components of the impinging molecules on the growth processes such as the island size distribution, the critical nucleus size, the island shape and the sticking coefficient.
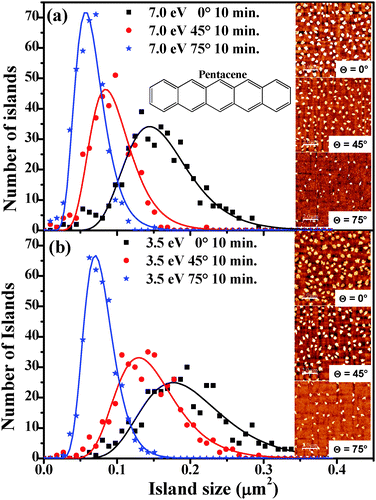
To gain insight into the growth dynamics, we considered samples obtained after 10 min exposure to the pentacene flux where the onset of island coalescence is not yet reached. The island size distribution and the average island size (Aav) for two different kinetic energies of the molecules (7.0 eV and 3.5 eV) impinging at three different incidence angles (0°, 45° and 75°) were extracted from the AFM images. AFM micrographs of the typical morphologies observed are shown in the inset of Fig. 1(a) and (b). At these early growth stages, the dependence of the morphology on the incident angle θ of the beam appears to be quite evident: both coverage and molecular island size decrease with increasing θ, while the distance between islands increases. We observe also that the coverage decrease and the increase of the inter-island distance are much more evident for the higher kinetic energy. Practically the role of the momentum component parallel to the surface associated with Ek, M∥, becomes evident. The higher the M∥, the larger is the probability for the molecules to be scattered out from the surface plane, so that not only the overall amount of deposited molecules reduces (reduced sticking) but also the density and size of islands decrease. These can be quantified in the island size distribution shown in Fig. 1(a) and (b) where the histograms of the island size (Aav) under different growth conditions as obtained from AFM images collected over 5 scanning areas of 10 × 10 μm2 for each case are reported. The histograms were fitted using a log normal function6,18 with a single peak to determine the average island size. The obtained average island sizes were found to be 0.15 ± 0.02, 0.09 ± 0.01 and 0.06 ± 0.01 μm2 for samples grown at Ek = 7.0 eV, at normal incidence, θ = 45° and 75°; the corresponding values for Ek = 3.5 eV amounted to 0.19 ± 0.03, 0.14 ± 0.02 and 0.07 ± 0.01 μm2 for normal incidence, θ = 45° and 75°. We observe that the average island size decreases with increasing θ and for each incidence angle, while the average island size for samples grown with Ek = 3.5 eV is always larger than the corresponding one for samples grown with Ek = 7.0 eV. This suggests that molecules which impinge with smaller Ek experience less molecule–surface scattering and lower surface diffusion, which in turn favours the lateral expansion of the islands via trapping of more molecules on the surface. With increasing θ, the distribution of island sizes obtained for the growth becomes narrower for both the kinetic energies used. The full width at half maximum of the peak drops from 0.10 μm2 (0.12 μm2) at normal incidence to 0.06 μm2 (0.10 μm2) at θ = 45° and to 0.05 μm2 (0.05 μm2) at θ = 75° for samples grown with Ek = 7.0 eV (3.5 eV). This indicates that the island size is more uniform when the molecules impinge at a larger incidence angle.
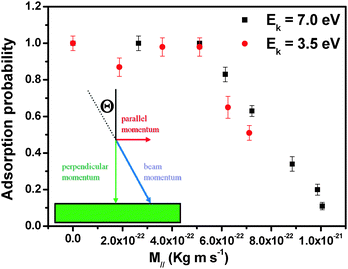
To quantify this effect we investigated the adsorption probability under different growth conditions. To compare the results obtained using different growth parameters, a surface coverage of 20% of a monolayer was chosen since at this stage of the growth the islands are big enough to show characteristic features but far away from coalescence. The flux of impinging molecules was adjusted to be constant at all angles of incidence. Moreover, we assumed a constant growth rate during the growth, which is a good assumption under our operation conditions. By comparing the deposition times that are needed to reach 20% coverage, one can obtain the adsorption probability which has been normalized to 1 for the reference samples grown with molecules impinging at normal incidence.
Fig. 2 shows the adsorption probability, as a function of the parallel momentum (M‖) of the incident molecules. Two different adsorption regimes are clearly distinguished: for low values of M∥ the adsorption probability is constant, while when the parallel momentum increases beyond a certain critical value (M∥ ∼ 5 × 10−22 kg m s−1) the adsorption probability decreases linearly with M∥. This is due to the difficulty in dissipating parallel momentum at the surface. The constant adsorption probability at lower M∥ is likely due to the fact that when a strong adsorption site becomes available, the influence of the parallel momentum on the adsorption probability is suppressed. In other words, desorption of the molecules can be activated only for sufficiently large values of M∥. The barrier height cannot be deduced directly in our experiments; a comparison of these data with simulations would be interesting.
The observed dependence of the adsorption probability on M∥ is an indication of trapping processes involving possibly not only one step, as in direct trapping. Such a decrease of adsorption probability with increasing θ has been observed in very few cases, mostly when trapping occurs via dissipation of Ek associated with the normal component of momentum (normal energy scaling), M⊥, as often true for simple (diatomic) molecules on surfaces of transition metals.14 Most of the cases where normal energy scaling is not observed have been interpreted in terms of (i) strong corrugation effects either of the potential energy surface or of the physical substrate surface, (ii) the role of internal degrees of freedom and/or (iii) inefficient accommodation of parallel momentum.9
A simple experimental way to quantify the relative role played by the perpendicular and parallel components of momentum linked to a specific kinetic energy of the impinging molecules is to introduce the empirical scaling function of the form EKf(θ) = EK(A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + B
θ + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) where A + B = 1 and the energy associated with the perpendicular (parallel) momentum scales with coefficient A (B).15 Following this procedure for our data, we find values for A and B which, within the error bars, are identical to those found by A. S. Killampalli et al.8 However, we do not arrive at their conclusion that the dissipation of the parallel and the perpendicular momentum component is roughly equally important.
θ) where A + B = 1 and the energy associated with the perpendicular (parallel) momentum scales with coefficient A (B).15 Following this procedure for our data, we find values for A and B which, within the error bars, are identical to those found by A. S. Killampalli et al.8 However, we do not arrive at their conclusion that the dissipation of the parallel and the perpendicular momentum component is roughly equally important.
In fact, an understanding of these trends may be achieved by comparing with classical molecular dynamics simulations for SuMBD of ethane on Si(100),13 a system where a similar sticking behaviour was observed experimentally. These simulations show that the energy exchanged upon the first impact on the surface largely dictates whether the incident molecule will stay on the surface or not. During this first collision the energy associated with the normal momentum component is dissipated very effectively, whereas that associated with the parallel momentum component is not. This process leaves the molecule in a vibrationally and rotationally excited state which allows it to make subsequent impacts on the surface and undergo further energy dissipation processes. However, molecules with a large parallel momentum component were found to retain it in large part after the initial impact on the surface.9 Parallel momentum, as well as any energy stored in rotations, can be converted into normal momentum during subsequent impacts, causing the molecules to scatter back into the vacuum. Therefore, molecules with high kinetic energy impinging at glancing angles have a much larger probability of being scattered from the surface before the parallel momentum can be dissipated. Our data on pentacene where the sticking coefficient becomes smaller with larger incident angle and Ek strongly support this mechanism.
The critical nucleus i (i + 1 = number of molecules forming a stable nucleus) determined under the different growth conditions is an important criterion to gather information on the effect of momentum and kinetic energy on the molecular assembly processes. i is determined from the general scaling function
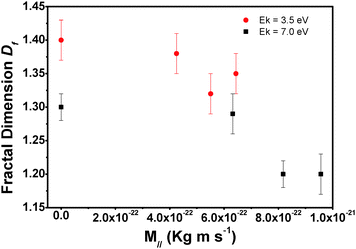
We also investigated how kinetic energy and incidence angle of the impinging molecules influence the island shape. To this end we determined the fractal dimension under different growth conditions from the AFM micrographs. The island fractal dimension (Df), calculated using the area–perimeter relationship, as proposed in ref. 21
| P = kADf/2 |
In conclusion, we analysed the surface morphology of pentacene submonolayers grown by supersonic molecular beam deposition on SiOx/Si kept at room temperature. In particular, we focused on the influence of the kinetic energy of the impinging molecules and of the incidence angle. The observations can be rationalized in the following way: when pentacene collides with the SiOx surface, it loses energy through different mechanisms which depend on its momentum and kinetic energy. In particular, M⊥ is primarily linked to the formation of the initial nuclei: increasing this component we observed that fewer molecules were needed for the formation of stable nuclei. Higher M⊥ also favours a higher number of islands and a decrease of inter-island distance. M∥ influences the interaction between the surface and molecules. Its dissipation modifies the sticking coefficient of the molecules and their relaxation processes, increasing their surface mobility. High values of M∥ decrease the number of molecules on the surface but favour the formation of more compact (less fractal) islands, hence leading to better ordered films. M∥ influences the dynamics of molecule–molecule interactions on the surface while M⊥ seems to be related to the dynamics of the coupling between molecules and surface phonons. To optimize the growth processes of organic molecules such as pentacene the right balance of both components is needed.
The authors would like to thank L. Venema, C. Corradi and M. Pola for technical assistance. We also thank Norbert Koch and Roberto Verucchi for precious discussions. This work was financially supported by the Dutch Foundation for Fundamental Research on Matter (FOM), and by the Breedtestrategie program of the University of Groningen.
Notes and references
- R. Ruiz, D. Choudhary, B. Nickel, T. Toccoli, K. C. Chang, A. C. Mayer, P. Clancy, J. M. Blakely, R. L. Headrick, S. Iannotta and G. G. Malliaras, Chem. Mater., 2004, 16, 4497 CrossRef CAS.
- D. Choudhary, P. Clancy, R. Shetty and F. Escobedo, Adv. Funct. Mater., 2006, 16, 1768 CrossRef CAS.
- S. Pratontep, M. Brinkmann, F. Nuesch and L. Zuppiroli, Phys. Rev. B, 2004, 69, 165201 CrossRef.
- Y. Wu, T. Toccoli, N. Koch, E. Iacob, A. Pallaoro, P. Rudolf and S. Iannotta, Phys. Rev. Lett., 2007, 98, 076601 CrossRef.
- S. Iannotta and T. Toccoli, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 2501 CrossRef CAS.
- Y. Wu, T. Toccoli, J. Zhang, N. Koch, E. Iacob, A. Pallaoro, S. Iannotta and P. Rudolf, Appl. Phys. A: Mater. Sci. Process., 2009, 95, 21 CrossRef CAS.
- T. Toccoli, A. Pallaoro, N. Coppedè, S. Iannotta, F. D. Angelis, L. Mariucci and G. Fortunato, Appl. Phys. Lett., 2006, 88, 132106 CrossRef PubMed.
- A. S. Killampalli, T. W. Schroeder and J. R. Engstrom, Appl. Phys. Lett., 2005, 87, 033110 CrossRef PubMed.
- C. T. Reeves, B. A. Ferguson, C. B. Mullins, G. O. Sitz, B. A. Helmer and D. B. Graves, J. Chem. Phys., 1999, 111, 7567 CrossRef CAS PubMed.
- F. O. Goodman and H. Y. Wachman, Dynamics of Gas – Surface Scattering, Academic Press, New York, 1976 Search PubMed.
- J. A. Barker and D. J. Auerbach, Surf. Sci. Rep., 1984, 4, 1 CrossRef.
- S. Andersson, L. Wilzen and J. Harris, Phys. Rev. Lett., 1986, 57, 1603 CrossRef CAS.
- C. T. Rettner, H. Stein and E. K. Schweizer, J. Chem. Phys., 1988, 89, 3337 CrossRef CAS PubMed.
- C. T. Rettner, D. J. Auerbach, J. C. Tully and A. W. Kleyn, J. Phys. Chem., 1996, 100, 13021 CrossRef CAS.
- M. C. McMaster, S. Schroeder and R. J. Madix, Surf. Sci., 1993, 297, 253 CrossRef CAS.
- J. G. Amar and F. Family, Phys. Rev. Lett., 1995, 74, 2066 CrossRef CAS.
- R. Ruiz, B. Nickel, N. Koch, L. C. Feldman, R. F. Haglund Jr., A. Kahn, F. Family and G. Scoles, Phys. Rev. Lett., 2003, 91, 136102 CrossRef.
- M. Tejima, K. Kita, K. Kyuno and A. Toriumi, Appl. Phys. Lett., 2004, 85, 3746 CrossRef CAS PubMed.
- B. Stadlober, U. Haas, H. Maresch and A. Haase, Phys. Rev. B, 2006, 74, 165302 CrossRef.
- A. C. Mayer, R. Ruiz, R. L. Headrick, A. Kazimirovc and G. G. Malliaras, Org. Electron., 2004, 5, 257 CrossRef CAS PubMed.
- P. A. Burrough, Principles of Geographical Systems for Land Resources Assessment, Clarendon, Oxford, 1986 Search PubMed.
| This journal is © The Royal Society of Chemistry 2014 |