Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantifying electrokinetics of NaCa0.6V6O16·3H2O cathode in aqueous zinc-ion batteries with ZnSO4 electrolyte†
Shichen Sun,
Boyu Wang and
Kevin Huang *
*
Department of Mechanical Engineering, University of South Carolina, SC29201, USA. E-mail: huang46@cec.sc.edu
First published on 21st July 2025
Abstract
Aqueous zinc-ion batteries (AZIBs) have been actively studied in recent years as a promising solution for next-generation stationary energy storage due to their inherent safety, low cost, and high energy density. However, their practical deployment remains hindered by the limited cycling stability of cathode materials. Overcoming this challenge requires a detailed understanding of cathodic electrokinetics and degradation mechanisms. In this study, we investigate the electrokinetic behavior of a NaCa0.6V6O16·3H2O (NaCaVO) cathode in ZnSO4 electrolyte through a combined application of the galvanostatic intermittent titration technique (GITT) and electrochemical impedance spectroscopy (EIS). For the first time, we quantify the exchange current density (i0) and interfacial charge-transfer resistance (RCT) of NaCaVO as a function of states of charge (SOCs). The results reveal that the V4+ ⇌ V3+ redox reaction exhibits significantly slower kinetics than the V5+ ⇌ V4+ counterpart. Further GITT-EIS studies using D2O–ZnSO4 electrolyte, complemented by X-ray diffraction (XRD) and X-ray photoelectron spectroscopy (XPS), indicate that the sluggish V4+ ⇌ V3+ process is predominantly associated with proton insertion. Distribution of Relaxation Time (DRT) analysis correlates the increased interfacial resistance with the intermediate phase formation induced by this proton insertion. The electrokinetic insights obtained in this work fill critical knowledge gaps in AZIB research and provide a foundation for designing more durable and efficient cathode materials in the future.
1. Introduction
Rechargeable aqueous zinc-ion batteries (AZIBs) are an emerging class of electrochemical energy storage devices well-suited for stationary energy storage where cost-effectiveness, safety, and environmental sustainability are important considerations.1–5 A typical AZIB consists of a high-energy-density zinc-metal anode, a layered or open-framework cathode, and a zinc-ion-conducting aqueous electrolyte – commonly a zinc salt solution.6–9 With Zn2+ and/or H+ serving as the working ions, the electrochemical reactions at both cathode/electrolyte and anode/electrolyte interfaces are generally reversible, enabling rechargeable operation – a key advantage over conventional non-rechargeable alkaline Zn/MnO2 batteries.10–14Despite their promise, the commercial development of AZIBs faces serious challenges, particularly due to degradations associated with the cathode and its interfacial interactions with the electrolyte.15–17 Therefore, the advancement of AZIB technology critically hinges on the development of high-capacity, durable cathode materials, which in turn requires a thorough understanding of cathodic degradation mechanisms.1,18–21 Additionally, there remains a substantial knowledge gap in the understanding of cathodic kinetics – especially those that govern the ion storage processes at various states of charge (SOCs).
To date, a major effort in aqueous zinc-ion battery (AZIB) research has been focused on engineering a stable zinc-anode/electrolyte interface to suppress the hydrogen evolution reaction (HER) at the zinc anode and mitigate zinc corrosion. Strategies such as surface coatings and electrolyte additives have been widely explored for this purpose. However, many of these additives inadvertently hinder cathodic kinetics, ultimately compromising overall battery performance despite effectively suppressing HER and reducing corrosion.22,23
In comparison, cathode-focused research has primarily centered on compositional modifications of MnO2− and V2O5− based materials to enhance capacity and cycling stability. A notable example is the pre-insertion of alkaline and alkaline-earth metal cations into V2O5-based structures.8,24–29 In these studies, a variety of in situ and ex situ surface and bulk characterization techniques – such as X-ray diffraction (XRD), X-ray photoelectron spectroscopy (XPS), Electron Microscopy, Fourier Transform Infrared Spectroscopy (FTIR), and X-ray absorption spectroscopy (XAS) – are routinely employed to probe material properties and elucidate underlying reaction mechanisms. In parallel, conventional electrochemical techniques30 such as Galvanostatic/Potentiostatic Intermittent Titration (GITT/PITT),31,32 electrochemical impedance spectroscopy (EIS),33 and cyclic voltammetry (CV)34,35 are used to study electrochemical behaviors. Despite these efforts, rigorous investigation of cathodic electrokinetics during actual charge and discharge processes remains rare. Furthermore, many early studies only evaluated charge-transfer resistance (RCT) under open-circuit conditions, which do not accurately represent real operating states of AZIBs, thereby limiting their value for mechanistic understanding and battery performance modeling.
In this study, we present a combined GITT and EIS approach to probe cathodic electrokinetics under actual operating conditions. The cathode material of choice is NaCa0.6V6O16·3H2O (NaCaVO), previously identified in our work as a stable and promising candidate for AZIB applications with outstanding cyclability (e.g., 94% capacity retention after 2000 cycles at 2 A g−1 and 83% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles at 5 A g−1).36 Electrokinetic measurements were conducted using a three-electrode configuration, with NaCaVO as the working electrode (WE), zinc metal as the counter electrode (CE), Ag/AgCl as the reference electrode (RE), and 2 M ZnSO4 as the electrolyte – an industry-relevant formulation. To deconvolute overlapping electrochemical processes and better interpret cathodic behavior, we also apply Distribution of Relaxation Times (DRT) analysis to EIS spectra, correlating observed features with the formation of interfacial secondary phases. Additionally, to investigate the co-intercalation mechanisms of Zn2+ and H+ into the NaCaVO structure, we employ water isotope solvent D2O in the ZnSO4 electrolyte system to distinguish the contributions of zinc ions from those of protons.
000 cycles at 5 A g−1).36 Electrokinetic measurements were conducted using a three-electrode configuration, with NaCaVO as the working electrode (WE), zinc metal as the counter electrode (CE), Ag/AgCl as the reference electrode (RE), and 2 M ZnSO4 as the electrolyte – an industry-relevant formulation. To deconvolute overlapping electrochemical processes and better interpret cathodic behavior, we also apply Distribution of Relaxation Times (DRT) analysis to EIS spectra, correlating observed features with the formation of interfacial secondary phases. Additionally, to investigate the co-intercalation mechanisms of Zn2+ and H+ into the NaCaVO structure, we employ water isotope solvent D2O in the ZnSO4 electrolyte system to distinguish the contributions of zinc ions from those of protons.
2. Results and discussion
2.1 Electrokinetics quantification using combined GITT-EIS method
The cyclic voltammetry (CV) profiles of the NaCaVO cathode in 2 M H2O–ZnSO4 electrolyte at scan rates ranging from 0.1 to 1.0 mV s−1 are shown in Fig. 1(a). Two distinct pairs of redox peaks, corresponding to the redox transitions of V-oxidation state, are consistently observed across all scan rates. The high-potential redox couple (D1 at ∼0.81–0.82 V and C1 at ∼0.91–0.93 V vs. Zn/Zn2+) is assigned to the V5+ ⇌ V4+ redox reaction, while the lower-potential couple (D2 at ∼0.56 V and C2 at ∼0.70 V) is related to the V4+ ⇌ V3+ reaction.37–41 With increasing scan rate, both anodic and cathodic peak currents rise systematically, indicating charge-transfer-controlled behavior. However, the lower-potential peaks (D2/C2) are consistently broader and exhibit smaller peak currents relative to D1/C1, suggesting that the V4+ ⇌ V3+ reaction proceeds with slower kinetics and greater polarization than the V5+ ⇌ V4+ reaction. Moreover, the potential separation between cathodic and anodic peaks slightly widens with scan rate, particularly for the V3+/V4+ redox couple, further indicating that kinetic limitations and sluggish charge transfer dominate at low potentials. Overall, there is no significant change in redox peak position at different scan rates, justifying our use of potential to characterize electrokinetic behaviors of the V5+ ⇌ V4+ and V4+ ⇌ V3+ redox reactions during the charge and discharge cycles. | ||
| Fig. 1 H2O–ZnSO4 system: (a) CV and (b) Ip vs. v1/2 of NaCaVO|2 M ZnSO4|Zn cell scanned at different rates. RE: Ag/AgCl; CE: Zn; WE: NaCaVO. | ||
Moreover, to investigate the ion diffusion characteristics in the NaCaVO cathode in H2O–ZnSO4 system, cyclic voltammetry (CV) conducted at varying scan rates (0.1–1.0 mV s−1) was further analyzed by plotting the peak currents corresponding to distinct redox reactions vs. square root of scanning rate to determine diffusion coefficient of the electroactive species of a diffusion-controlled redox process using Randles–Ševčík equation:42,43
| Ip = (2.69 × 105) × n3/2 × A × D1/2 × C × v1/2 | (1) |
Fig. 1(b) shows that a plot of Ip versus v1/2 of the four redox peaks follow a linear relationship, indicating semi-infinite diffusion as the rate-limiting process. The calculated diffusion coefficients related to the four redox peaks are 4.74 × 10−10 and 1.37 × 10−10 cm2 s−1 for C1 and D1, respectively, located at the high-potential region and 1.14 × 10−11 and 3.11 × 10−11 cm2 s−1 for C2 and D2, respectively, located at the low-potential peaks. The higher D values for the high-potential V4+/V5+ redox couple than the V3+/V4+ counterpart suggests a facile kinetics for the former, which will be further discussed in the following sections.
The potential (E) profiles collected by GITT during charge and discharge cycle are shown in Fig. 2(a). As potential E increases and decreases with time during charge and discharge cycle, respectively, pseudo-plateaus regions (quasi-flat regions) show good alignment with the two redox peaks identified in the CV (see Fig. 1(a)). During the charge cycle, the profile exhibits a mid-E pseudo-plateau around 0.85–0.95 V (corresponding to V4+ → V5+ oxidation peak) and a lower pseudo-plateau near 0.60–0.70 V (corresponding to V3+ → V4+ oxidation peak). Similar pseudo-plateaus are also observed during the discharge cycle, corresponding to V5+ → V4+ and V4+ → V3+ reduction peaks, respectively. The greater E changes in lower E region than in higher E region imply higher polarization and sluggish kinetics in the region.
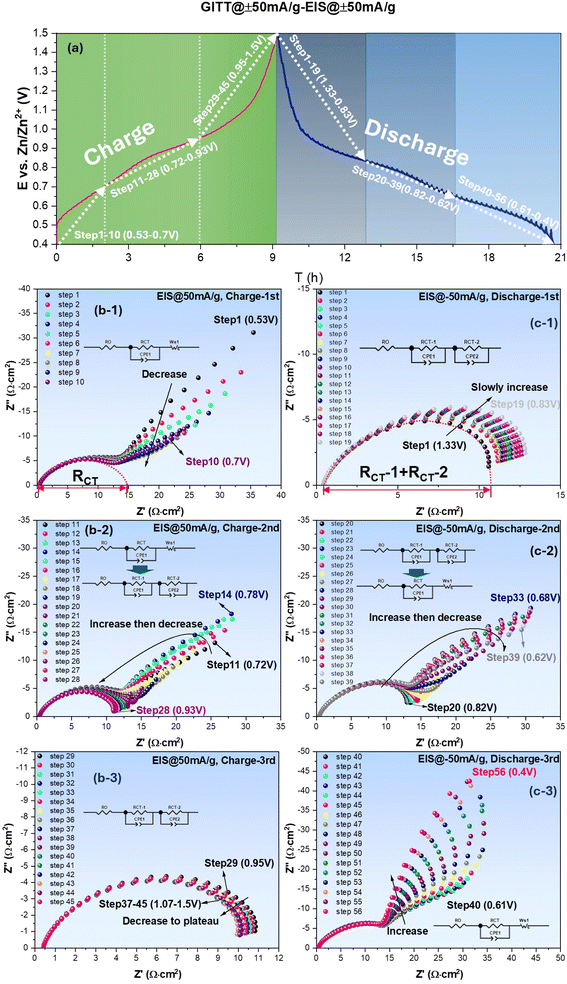 | ||
| Fig. 2 ZnSO4–H2O system: (a) E vs. time profile collected under ±50 mA g−1; EIS spectra measured with ±50 mA g−1 bias during charge (b) and discharge (c) cycles. | ||
The EIS spectra collected at each GITT step during charge and discharge cycled at ±50 mA g−1 (equivalent to ±0.024 mA cm−2) are shown in Fig. 2(b) and (c), respectively, as an example. Each spectrum is measured under different bias currents to obtain RCT= RCT(i) at a specific E (or SOC) created by the preceding galvanic polarization. From Fig. 2(b) collected during the charging cycle, it is evident that EIS spectra feature a charge transfer impedance at high frequencies, followed by low-frequency Warburg impedance (related to semi-infinitive surface diffusion of the active species) over low E range (step 1–10, 0.53–0.70 V). As E increases, the spectra gradually transit to a mixed Warburg (step 11–14, 0.72–0.78 V) and charge-transfer only feature (step 15–28, 0.80–0.93 V) over intermediate E range, and finally to charge-transfer only feature over high E range (step 29–45, 0.95–1.50 V). During the discharging cycle, the above trend remains, i.e., Warburg impedance appears at low E, whereas charge-transfer-only feature appears at high E. Note that the appearance of Warburg impedance at low E range implies diffusion limitation to the active species; we will further correlate it with the formation of an intermediate phase in the following section. The original E vs. time profiles and corresponding EIS spectra collected under OCV and other current densities such as 75–125 mA g−1 can be found in Fig. S1.† By comparing Fig. 2 and .S1,† it is concluded that the shape of all profiles (two distinct pseudo-plateau regions) remains the same, suggesting that the electrochemical reaction mechanisms remain unchanged by the applied current.
With the equivalent circuit model shown in Fig. 2(b-1), RCT under low E is extracted from the interception length on Z′-axis of the fitted curve (dotted), and for the high E cases, RCT (sum of RCT1 and RCT2) is similarly taken using the equivalent circuit model in Fig. 2(c-1). The obtained RCT is then plotted against E and shown in Fig. 3 for both charge and discharge cycle in a current range of 0–125 mA g−1. A clear dependence of RCT on E is observed. In both charge and discharge cycles, the RCT–E profiles can be divided into three stages. Stage-1, the lowest E range (0.40–0.60 V for both charge and discharge), RCT is generally the highest but decreases with E. Stage-2, the intermediate E range (0.68–0.91 V for charge and 0.60–0.83 V for discharge), a maximum is observed. Stage-3, the high E range (>0.91 V for charge and >0.83 V for discharge), a plateau is observed. The minimal RCT appears to occur at a high E close to the V5+ ⇌ V4+ as indicated in CV, see Fig. 1(a). In contrast, high RCT appears at lower E range close to the V4+ ⇌ V3+. Therefore, we can conclude from Fig. 3 that the V4+ ⇌ V3+ redox reaction is more sluggish than the V5+ ⇌ V4+ counterpart. This finding could be explained by a greater difficulty in inserting/extracting ions into/from NaCaVO at a deeper SOC. Another reason could be related to the formation of intermediate phase on the surface of NaCaVO cathode due to proton insertion; we will show evidence to support this assertion in a later section. On the other hand, in the higher E and shallow SOC regime, the charge transfer kinetics is facile with low RCT, suggesting a lower presence of the intermediate phase. In addition, the ohmic resistance RO of all cells studied was roughly ∼0.45 Ω cm2 (see Fig. 2 and S1†), independent of DC bias applied.
 | ||
| Fig. 3 H2O–ZnSO4 system: RCT vs. E during (a) charge and (b) discharge cycle under different current densities. | ||
The trend of enhanced charge transfer kinetics by the applied current agrees with Butler–Volmer law that predicts higher overpotential drives a lower RCT. The agreement also suggests that the charge transfer kinetics is a rate limiting step of the ion insertion process into NaCaVO. Although the shapes of two RCT–E profiles between charge and discharge cycle are close to a mirror image, the discharge cycle does exhibit a slightly higher RCT than the charge cycle at the same E, indirectly reflecting influence of the intermediate phase formation on charge transfer process.
2.2 Exchange current density (i0)
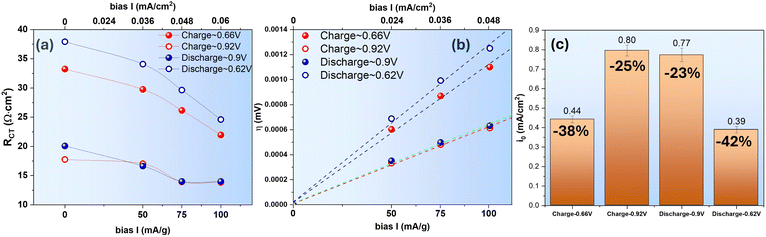
With the obtained RCT vs. i, we apply the “low-field” approximation of Butler–Volmer equation to extract exchange current density (i0), a key parameter of electrokinetics, as the current density range applied in this study generally falls into “weak polarization” regime:44| η = (RT/nF) × i/i0) | (2) |
 | ||
| Fig. 4 H2O–ZnSO4 system. (a) RCT vs. i, (b) η vs. i and (c) i0 comparison at 0.68 V and 0.91 V during charge and 0.83 V and 0.6 V during discharge. | ||
A comparison of i0 at different E of the charge and discharge cycle is given in Fig. 4(c); it informs that i0 is higher at higher E than at lower E. Between the charge and discharge cycle for the same pair of redox reaction, i0 is higher for the charge cycle than the discharge cycle. Again, these comparisons suggest that the V5+ ⇌ V4+ is a more facile redox reaction than the V4+ ⇌ V3+ counterpart. We hypothesize that the sluggish V4+ ⇌ V3+ redox reaction could be attributed to the intermediate phase formation induced by the H+ insertion at a deeper SOC. To verify this, we performed a further analysis on EIS spectra with DRT method and replacing of H2O with D2O as a solvent for the ZnSO4 electrolyte.
2.3 Analysis of EIS spectra with DRT method
Even though our GITT-EIS method provides E-dependent RCT data under different i, we still do not fully understand the reasons why the kinetics of V5+ ⇌ V4+ is faster than V4+ ⇌ V3+. We here apply DRT method to facilitate the understanding.45 Fig. 5 shows an exemplary contour plot of γ-function of DRT analysis over a time domain (τ, relaxation time constant, unit in s) superposed with E (SOC) during a constant polarization at 50 mA g−1, where τ is related to the frequency (f, in Hz) in EIS by:
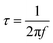 | (3) |
2.4 Evidence of intermediate phase formation
To identify the composition of the secondary phase, we performed ex situ XRD and XPS. Fig. 6 shows XRD patterns of NaCaVO cathode after being cycled under different SOCs. From the main peak of NaCaVO in Fig. 6(a), it is evident that the ion (de)insertion processes are generally reversible during the charge/discharge cycle, exhibiting lattice contraction during the discharge due to strong Zn2+-O2- interactions after Zn2+ are inserted and lattice expansion during the charge after Zn2+ are extracted. More importantly, Fig. 6(b) indicates that an intermediate phase with a composition of Zn4SO4(OH)6·xH2O (herein denoted as Zn-LDH) is detected in NaCaVO only after being cycled at low E between 0.40 and 0.80 V (related to V3+ ⇌ V4+). The finding of Zn-LDH at low-E-cycled NaCaVO provide chemical reason for the slow electrokinetics of V3+ ⇌ V4+ and aggravated diffusion impedance. Since it is well known to the AZIB community that Zn-LDH is a product of H+ insertion into the cathode, it further suggests that H+ insertion might take place at lower E.46,47 This contrasts with some theoretical calculations suggesting that H+ insertion takes place mainly at higher E.48–50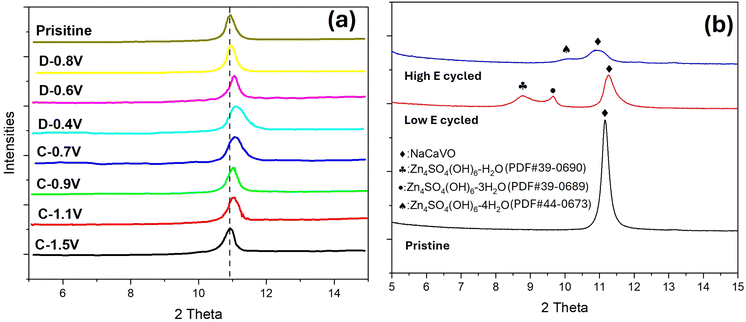 | ||
| Fig. 6 H2O–ZnSO4 system. Ex situ XRD patterns of NaCaVO cathode after (a) charge and discharge at different SOCs and (b) cycled at low and high E compared with the pristine. | ||
The XPS spectra shown in Fig. S4† indicate a weaker V-2p signal in NaCaVO after cycling at low E than those of the pristine and cycled at high E, suggesting possible blocking effect by the Zn-LDH formed. Furthermore, the ratio of V3+/V4+ in NaCaVO becomes significantly higher after cycling at low E compared to the pristine (with V5+ and trace V4+) and the high-E-cycled one (with much lower V3+/V4+ ratio), which is consistent with our previous results.36 These XPS results further suggest that the low-E redox reaction is associated with V3+ ⇌ V4+ and high-E redox reaction is related to V5+ ⇌ V4+.
2.5 Effect of D2O on electrokinetics
To further verify if the H2O-derived H+ insertion into NaCaVO is responsible for the redox reaction of V3+ ⇌ V4+, we performed the same GITT-EIS experiment using the same ZnSO4 electrolyte but isotope D2O as the solvent. Fig. S2† shows the original CV curves of NaCaVO in D2O–ZnSO4, which is notably different from the H2O–ZnSO4 case, especially in the low E range (0.5–0.7 V). In particular, the redox peaks associated with the V3+ ⇌ V4+ become less pronounced and shifted toward lower E, reflecting the impact of heavier D+ ions on this redox reaction. The more pronounced broadening and reduced peak current density suggests a retarded reaction kinetics. These observations support the hypothesis that H+/D+ impacts on the V3+ ⇌ V4+ redox reaction at lower E.The E-profiles collected from the D2O–ZnSO4 system under 50 mA g−1 by GITT during charge and discharge cycle are shown in Fig. 7 as an example; similar plots at other current densities can be found in Fig. S3.† The two-step pseudo-plateau feature remains, suggesting two active charge transfer processes: V3+ ⇌ V4+ and V4+ ⇌ V5+. However, a quick glance of EIS spectra indicate that RCT at low E is appreciably higher than the H2O–ZnSO4 counterpart, inferring that the V3+ ⇌ V4+ kinetics has become more sluggish by the slower D+ (de)insertion process.
A noticeable difference of EIS spectra of the D2O–ZnSO4 system from H2O–ZnSO4 system, see Fig. 7(b), is the appearance of a high-frequency semicircle (highlighted by red dotted circles) during the charge cycle. The magnitude of this small semicircle does not seem to change appreciably with SOC. Since D+ extraction from NaCaVO occurs during the charge cycle, the appeared semicircle (an extra charge transfer process) implies a reduced D+ extraction kinetics, which leads to a more sluggish V3+ ⇌ V4+ redox reaction and increased relaxation time constant. Another notable observation is that the Warburg impedance becomes less pronounced as E increases, the same trend as the H2O–ZnSO4 system.
For the subsequent discharge cycle, see Fig. 7(c), the EIS collected under high E (Fig. 7(c-1), step 1–19, 1.5–0.83 V) show a much less pronounced, small high-frequency semicircle than that observed during the charge cycle. As E decreases, see Fig. 7(c-2) (steps 20–39, 0.82–0.66 V) and (c-3) (steps 40–56, 0.65–0.4 V), this small high-frequency semicircle appears to increase slightly, while the Warburg impedance becomes more pronounced, like the H2O–ZnSO4 system. A comparison of EIS spectra vs. SOC between the H2O–ZnSO4 and D2O–ZnSO4 systems suggests similar charge transfer mechanisms, but the heavier D+ is more difficult to extract from the cathode, thus increasing the relaxation time constant of the process and depicting itself on the EIS spectrum within the frequency range studied. Since D2O has the most pronounced impact on RCT at low E, it is reasonable to speculate that H+/D+ (de)insertion into the cathode leads to the V3+ ⇌ V4+ redox reaction.
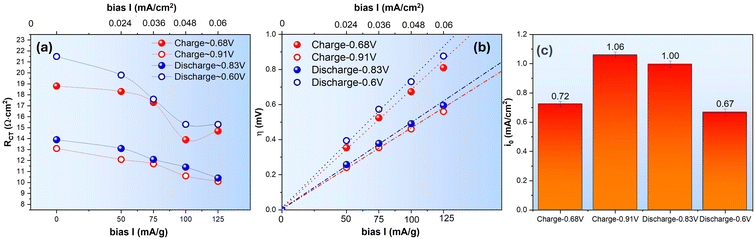
To better illustrate how RCT vary with SOC, we plot RCT vs. E under different current densities in Fig. 8. In general, the overall trend of each curve resembles Fig. 3 of the H2O–ZnSO4 system, i.e., they can be divided into three stages, featuring monotonically decreasing, peaking and flattening of RCT with SOC. However, the magnitude of RCT for the V3+ ⇌ V4+ is significantly higher (by nearly 2×) in the D2O–ZnSO4 system than the H2O–ZnSO4 counterpart, whereas RCT of the V4+ ⇌ V5+ is close for the two electrolyte systems. This observation further supports the assertion that it is H+/D+ that are mainly responsible for the V3+ ⇌ V4+ redox reaction.
 | ||
| Fig. 8 D2O–ZnSO4 system: RCT vs. E during (a) charge and (b) discharge cycle under different current densities. | ||
The dependence of RCT and η on the applied current density for the D2O–ZnSO4 system is plotted in Fig. 9(a) and (b), where RCT for the charge and discharge cycle at high E is seen to remain close but notably different at lower E, i.e. RCT during the charge is lower than the discharge at a given SOC, which is like the H2O–ZnSO4 system.
Using the “low-field” approximation, the obtained i0 of the D2O–ZnSO4 system is shown in Fig. 9(c). The results indicate a greater decrease in i0 than the H2O–ZnSO4 system, i.e., it is −38% and −42% for the charge and discharge cycle, respectively, for the V3+ ⇌ V4+ occurring at low E and it is −25% and −23% for the charge and discharge cycle, respectively, for the V4+ ⇌ V5+ occurring at high E. Such an increased difference could be attributed to the slower D+ (de)insertion kinetics than H+.
3. Conclusions
By applying a combined GITT-EIS approach, we quantitatively characterized the electrokinetics of NaCaVO cathode in AZIBs for the first time. Analysis of the charge transfer resistance (RCT) and exchange current density (i0) reveals that the V3+ ⇌ V4+ redox reaction, which occurs at lower potentials during cycling, is intrinsically more sluggish than the V4+ ⇌ V5+ counterpart at higher potentials. This difference is likely attributed to two possible factors: (1) a higher energy barrier for charge transfer at a deeper SOC, and/or (2) the formation of an intermediate Zn-LDH phase induced by the H+ insertion. The possibility of H+ insertion into the NaCaVO structure is further supported by XRD and XPS analyses, as well as by the observed increase in RCT upon replacing solvent H2O with D2O in the electrolyte. Since H+ insertion into oxide-based cathodes is inevitable, the resultant Zn-LDH formation can also be viewed as an alternative way of Zn-ion storage. Overall, this study provides important fundamental insights into ion storage mechanisms in V2O5-based cathodes and offers electrokinetic parameters for future computational modeling of AZIB systems.4. Experimental methods
4.1 Cathode synthesis and ink preparation
The NaCaVO cathode is synthesized using a hydrothermal method we developed previously.36 Briefly, VCl3 and Ca(NO3)2·6H2O are mixed in deionized water with the pH adjusted to 7. The solution is then thermally treated at 190 °C for 24 hours in an autoclave, followed by washing and drying the solid precipitates at 60 °C for 12 hours. The synthesized material is characterized using X-ray diffraction (XRD) to confirm phase purity.NaCaVO cathode ink is prepared by thoroughly mixing 66 wt% NaCaVO with 20 wt% Super-P and 14 wt% polyvinylidene fluoride (PVDF) in N-methyl pyrrolidone (NMP) solvent. The resultant slurry is then coated uniformly onto ϕ10 mm stainless steel meshes with ∼0.6 mg cm−2 active mass loading, followed by vacuum drying at 120 °C for about 12 h and compression under 10 MPa. The aqueous H2O–ZnSO4 and D2O–ZnSO4 electrolytes are prepared by dissolving 2 M ZnSO4–7H2O (Sigma-Aldrich, ACS reagent, 99%) in DI water and D2O (Sigma-Aldrich, 99.9 atom% D), respectively.
4.2 Electrochemical measurements
In this study, a 3-electrode electrochemical cell is constructed to characterize electrochemical behaviors of the NaCaVO cathode,51 in which NaCaVO is used as the WE, a zinc metal as CE, an Ag/AgCl as RE, and 2 M ZnSO4 as the electrolyte. During the measurement, Cyclic Voltammetry (CV) is first performed at different scanning rates (mV s−1) to determine the number of redox reactions and their respective potentials. Once the redox potential is determined, we then cycle the NaCaVO–Zn 3-electrode cell 5 times from 1.5 V to 0.4 V vs. Zn/Zn2+ at 0.2A g−1 to fully activate the cathode. We then perform stepwise GITT-EIS measurements within a voltage window of 1.5 V and 0.4 V vs. Zn/Zn2+ to simulate charge and discharge cycles. Each GITT-EIS run consists of three phases. Phase-1: a ten-minute constant current polarization at 50 mA g−1, either positive (charge) or negative (discharge), is applied to mockup galvanic charge/discharge operation in a battery; this operation creates many potential intervals representing different SOCs (see later Fig. 2(a)). Phase-2: EIS measurements are carried out right after the galvanic interruption under OCV as well as DC bias current in the range of ±50 to ±125 mA g−1 in step of ±25 mA g−1 within a frequency range of 1 M Hz to 1 Hz with a base AC amplitude of 1 mA. The DC bias current is superimposed on the AC signal. Phase-3: there is a 1-minute resting period under OCV between each bias current. From the measured EIS spectra, RCT under different bias are obtained using equivalent circuits. The obtained RCT–i relationship is then used to attain overpotential (η)–i through integration, from which i0 of NaCaVO at a specific potential can be obtained from the “low-field” approximation of Butler–Volmer equation given the low current density range used in this study. In addition, we also use DRT method to help analyze EIS data and facilitate the identification of elementary steps.To illustrate the phase compositions and the variations of V-oxidation state with SOCs, we employe XRD and XPS, respectively, to examine NaCaVO cycled at high voltage range (1.5–0.75 V at 0.2 A g−1 for 50 cycles) and low voltage range (0.75–0.4 V at 0.2 A g−1 for 50 cycles). The cycled samples are thoroughly rinsed with DI water before examinations to avoid interference from the electrolyte.
4.3 Materials characterization
The XRD is performed on fresh and post-tested NaCaVO samples using a Rigaku D/MAX-2100 with Cu Kα radiation (λ = 1.5418 Å). The data are recorded from 5 to 80° with an interval of 0.02° and a scan speed of 2° min−1.The surface oxidation states of the sample are investigated with AXIS Ultra DLD XPS (Kratos Analytical) instrument. The XPS system is equipped with a non-monochromatic Al Kα source (1486.8 eV) operated at 150 W X-ray gun power, a hemispherical analyzer and a load lock chamber for rapid introduction of samples without breaking vacuum. The X-rays were incident at an angle of 45°, with respect to the surface normal. Analysis was performed at a pressure of ∼1 × 10−9 Torr and high-resolution core level spectra were acquired in the constant analyzer energy mode using a pass energy of 10 eV and a 0.07 eV step size (for survey scans 80 eV pass energy is used with 0.08 eV step size). The XPS experiments were performed by using a low energy electron beam, directed at the sample, for charge neutralization. The Binding energies (BE) of all peaks are corrected in reference to the C ls peak at 285 eV and given with an accuracy of ±0.2 eV. The curve fitting procedure was carried out using the Avantage software.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was sponsored by the U.S. Army Research Office (ARO) and was accomplished under Grant Number W911NF-21-1-0308 and the U.S. Air Force Office of Scientific Research under Grant Number FA9550-23-1-0505. The views and conclusions in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of ARO or AFOSR or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes, notwithstanding any copyright notation herein. The XPS facility receives financial support from the Office of the Vice President for Research, University of South Carolina.References
- G. Li, L. Sun, S. Zhang, C. Zhang, H. Jin, K. Davey, G. Liang, S. Liu, J. Mao and Z. Guo, Adv. Funct. Mater., 2024, 34, 2301291 CrossRef CAS.
- S. W. Gourley, R. Brown, B. D. Adams and D. Higgins, Joule, 2023, 7, 1415–1436 CrossRef CAS.
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS.
- Z. Yang, J. Zhang, M. C. Kintner-Meyer, X. Lu, D. Choi, J. P. Lemmon and J. Liu, Chem. Rev., 2011, 111, 3577–3613 CrossRef CAS.
- C. Xia, J. Guo, P. Li, X. Zhang and H. N. Alshareef, Angew. Chem., 2018, 130, 4007–4012 CrossRef.
- K. Zhu, T. Wu, S. Sun, Y. Wen and K. Huang, ChemElectroChem, 2020, 7, 2714–2734 CrossRef CAS.
- K. Zhu, T. Wu, W. van den Bergh, M. Stefik and K. Huang, ACS Nano, 2021, 15, 10678–10688 CrossRef CAS PubMed.
- Y. Lu, T. Zhu, W. van den Bergh, M. Stefik and K. Huang, Angew. Chem., Int. Ed., 2020, 59, 17004–17011 CrossRef CAS.
- K. Zhu, T. Wu, S. Sun, W. van den Bergh, M. Stefik and K. Huang, Energy Storage Mater., 2020, 29, 60–70 CrossRef.
- J. J. Ye, P. H. Li, Z. Hou, W. Zhang, W. Zhu, S. Jin and H. Ji, Angew. Chem., 2024, 136, e202410900 CrossRef.
- C. Geng, P. Zhang, J.-M. Wu, J. Qin and W. Wen, ACS Nano, 2024, 18, 33119–33130 CrossRef CAS.
- W. Sun, F. Wang, S. Hou, C. Yang, X. Fan, Z. Ma, T. Gao, F. Han, R. Hu and M. Zhu, J. Am. Chem. Soc., 2017, 139, 9775–9778 CrossRef CAS.
- X. Gao, H. Wu, W. Li, Y. Tian, Y. Zhang, H. Wu, L. Yang, G. Zou, H. Hou and X. Ji, Small, 2020, 16, 1905842 CrossRef CAS.
- B. Zhang, P. Dong, S. Yuan, Y. Zhang, Y. Zhang and Y. Wang, Chem Bio Eng., 2024, 1, 113–132 CrossRef CAS PubMed.
- D. S. Liu, Z. Zhang, Y. Zhang, M. Ye, S. Huang, S. You, Z. Du, J. He, Z. Wen and Y. Tang, Angew. Chem., Int. Ed., 2023, 62, e202215385 CrossRef CAS PubMed.
- B. Tang, L. Shan, S. Liang and J. Zhou, Energy Environ. Sci., 2019, 12, 3288–3304 RSC.
- S. Zuo, X. Xu, S. Ji, Z. Wang, Z. Liu and J. Liu, Chem.–Eur. J., 2021, 27, 830–860 CrossRef CAS PubMed.
- B. Yong, D. Ma, Y. Wang, H. Mi, C. He and P. Zhang, Adv. Energy Mater., 2020, 10, 2002354 CrossRef CAS.
- Y. Lu, T. Zhu, W. van den Bergh, M. Stefik and K. Huang, Angew. Chem., 2020, 132, 17152–17159 CrossRef.
- V. Mathew, B. Sambandam, S. Kim, S. Kim, S. Park, S. Lee, M. H. Alfaruqi, V. Soundharrajan, S. Islam and D. Y. Putro, ACS Energy Lett., 2020, 5, 2376–2400 CrossRef CAS.
- X. Gao, H. Dong, C. Su, Y. Dai, Y. Liu, I. P. Parkin, C. J. Carmalt and G. J. E. He, Energy Environ. Sci., 2025, 18, 13–18 RSC.
- X. Li, J. Xiang, L. Qiu, X. Chen, Y. Zhao, Y. Wang, Q. Yue, T. Gao, W. Liu and D. Xiao, J. Energy Chem., 2025, 100, 770–778 CrossRef CAS.
- P. He, G. Zhang, X. Liao, M. Yan, X. Xu, Q. An, J. Liu and L. Mai, Adv. Energy Mater., 2018, 8, 1702463 CrossRef.
- Y. Yang, Y. Tang, G. Fang, L. Shan, J. Guo, W. Zhang, C. Wang, L. Wang, J. Zhou and S. Liang, Energy Environ. Sci., 2018, 11, 3157–3162 RSC.
- C. Liu, Z. Neale, J. Zheng, X. Jia, J. Huang, M. Yan, M. Tian, M. Wang, J. Yang and G. Cao, Energy Environ. Sci., 2019, 12, 2273–2285 RSC.
- C. Xia, J. Guo, P. Li, X. Zhang and H. N. Alshareef, Angew. Chem., Int. Ed., 2018, 130, 4007–4012 CrossRef.
- F. Ming, H. Liang, Y. Lei, S. Kandambeth, M. Eddaoudi and H. N. Alshareef, ACS Energy Lett., 2018, 3, 2602–2609 CrossRef CAS.
- T. Lv, G. Zhu, S. Dong, Q. Kong, Y. Peng, S. Jiang, G. Zhang, Z. Yang, S. Yang and X. Dong, Angew. Chem., Int. Ed., 2023, 135, e202216089 CrossRef.
- Y. Tan, F. An, Y. Liu, S. Li, P. He, N. Zhang, P. Li and X. Qu, J. Power Sources, 2021, 492, 229655 CrossRef CAS.
- W. Weppner and R. A. J. Huggins, J. Electrochem. Soc., 1977, 124, 1569 CrossRef CAS.
- E. Deiss, Electrochim. Acta, 2002, 47, 4027–4034 CrossRef CAS.
- S.-I. Pyun and J.-S. Bae, Electrochim. Acta, 1996, 41, 919–925 CrossRef CAS.
- X. Chen, L. Wang, H. Li, F. Cheng and J. Chen, J. Energy Chem., 2019, 38, 20–25 CrossRef.
- B. E. J. Conway, J. Electrochem. Soc., 1991, 138, 1539 CrossRef CAS.
- K. Zhu, T. Wu and K. Huang, Adv. Energy Mater., 2019, 9, 1901968 CrossRef CAS.
- N. Zhang, Y. Dong, M. Jia, X. Bian, Y. Wang, M. Qiu, J. Xu, Y. Liu, L. Jiao and F. Cheng, ACS Energy Lett., 2018, 3, 1366–1372 CrossRef CAS.
- M. Yan, P. He, Y. Chen, S. Wang, Q. Wei, K. Zhao, X. Xu, Q. An, Y. Shuang and Y. Shao, Adv. Mater., 2018, 30, 1703725 CrossRef.
- S. Deng, Z. Yuan, Z. Tie, C. Wang, L. Song and Z. Niu, Angew. Chem., Int. Ed., 2020, 59, 22002–22006 CrossRef CAS.
- J. Kim, S. H. Lee, C. Park, H. S. Kim, J. H. Park, K. Y. Chung and H. Ahn, Adv. Funct. Mater., 2021, 31, 2100005 CrossRef CAS.
- J. Ding, Z. Du, B. Li, L. Wang, S. Wang, Y. Gong and S. Yang, Adv. Mater., 2019, 31, 1904369 CrossRef CAS.
- A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical Methods: Fundamentals and Applications, John Wiley & Sons, 2022 Search PubMed.
- B. He, Y. Ling, Z. Wang, W. Gong, Z. Wang, Y. Liu, T. Zhou, T. Xiong, S. Wang and Y. Wang, eScience, 2024, 4, 100293 CrossRef.
- T. F. Fuller and J. N. Harb, Electrochemical Engineering, John Wiley & Sons, 2018 Search PubMed.
- T. H. Wan, M. Saccoccio, C. Chen and F. Ciucci, Electrochim. Acta, 2015, 184, 483–499 CrossRef CAS.
- Z. Li, S. Ganapathy, Y. Xu, Z. Zhou, M. Sarilar and M. Wagemaker, Adv. Energy Mater., 2019, 9, 1900237 CrossRef.
- A. Macrelli, M. Olivieri, A. Lamperti, V. Russo, B. Bozzini, M. Menegazzo, G. Bussetti, C. S. Casari and A. L. Bassi, Electrochim. Acta, 2023, 442, 141909 CrossRef CAS.
- M. Liu, Z. Li and Y. Zhang, J. Electroanal. Chem., 2023, 942, 117539 CrossRef CAS.
- F. Gong, Y. Feng, Y.-H. Fang, Y.-K. Hsu and Y.-C. Chen, ACS Appl. Mater. Interfaces, 2023, 15, 18808–18818 CrossRef CAS.
- D. Zhang, J. Cao, Y. Yue, T. Pakornchote, T. Bovornratanaraks, J. Han, X. Zhang, J. Qin and Y. Huang, ACS Appl. Mater. Interfaces, 2021, 13, 38416–38424 CrossRef CAS PubMed.
- S. Sun, A. Billings, B. Wang and K. Huang, ACS Electrochem., 2024, 1, 195–204 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta04992j |
| This journal is © The Royal Society of Chemistry 2025 |