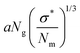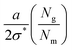Harnessing interfacial entropic effects in polymer grafted nanoparticle composites for tailoring their thermo-mechanical and separation properties
Aparna
Swain†
a,
Nimmi
Das Anthuparambil
bc,
Nafisa
Begam
d,
Sivasurender
Chandran
 *e and
J. K.
Basu
*e and
J. K.
Basu
 *a
*a
aDepartment of Physics, Indian Institute of Science Bangalore, 560012, India. E-mail: basu@iisc.ac.in
bDepartment of Physics, Universität Siegen, Walter-Flex-Str. 3, 57072 Siegen, Germany
cDeutsches Elektronen-Synchrotron DESY, Notkestr. 85, 22607 Hamburg, Germany
dDepartment of Physics, Institute of Science, Banaras Hindu University, Varanasi, Uttar Pradesh 221005, India
eSoft and Biological Matter Laboratory, Department of Physics, Indian Institute of Technology, Kanpur-208016, India. E-mail: schandran@iitk.ac.in
First published on 1st April 2025
Abstract
Nanocomposites based on polymeric materials have been extensively studied to understand and control the thermodynamics, flow, and mechanical properties of the underlying matrix as well to create new materials with diverse optical, electrical, magnetic, separation, catalytic, and biomedical properties. In the form of thin films or membranes, such materials can impart remarkable improvements in various properties of the underlying substrates. Using nanoparticles with grafted polymer chains usually overcomes a major hurdle in achieving enhancements in various properties by enabling better dispersion in the matrix while at the same time introducing a new parameter – interfacial entropy – leading to the emergence of new parameter space for tuning dispersion, flow and thermal properties. In this article, we highlight how this interfacial entropic effect can be harnessed to control various properties in thin films and membranes of grafted nanoparticle composites, in particular their thermo-mechanical properties, viscosity, fragility, glass transition temperature (Tg), and dynamic heterogeneity as well as their ability to act as highly selective gas separation and water desalination membranes. We discuss the application of a range of experimental techniques as well as molecular dynamics simulation to extract these properties and obtain microscopic insight into how the interplay of various surface and interfacial effects lies at the centre of these significant property improvements and enhanced functionality. Finally, we provide an outlook on future opportunities for designing sustainable PNCs, emphasizing their potential in environmental, energy, and biomedical applications, with advanced experiments and modelling driving further innovations.
1 Introduction
Polymer nanocomposites (PNCs) are multifunctional materials that have been extensively investigated in the last few decades due to their novel thermal, mechanical, electrical, optical and magnetic properties.1–18 Apart from the various applications in which PNCs have already been found to be useful, from a fundamental science perspective they have provided a platform for exploring rich emergent phenomena in soft matter and materials physics.19–27 The original motivation for incorporation of nanoparticles in a polymer matrix was to increase the effective interface area between the nanoparticles and the matrix to enhance the desired properties. Here, the assumption was that the nanoparticles are a passive additive and that the total area would simply scale with the particle volume fraction. However, as in other areas of condensed matter physics, the interface turned out to be an independent entity and phase by itself.28–32 This not only led to unexpected variations in physical properties like giant changes in the viscosity and thermo-mechanical properties4,33–35 of nanoparticle embedded polymers, but also led to the emergence of a complete phase diagram for the hierarchical self-organization of nanoparticles within polymer matrices.2,21,36,37In PNCs, both entropic and enthalpic effects contribute to their thermomechanical properties and overall performance. While minimizing enthalpic interactions is often desirable for achieving stable dispersion, it is important to recognize that enthalpic effects cannot be entirely disregarded in practical applications.38–41 Numerous studies and reviews have extensively explored the role of enthalpic interactions in PNCs, including polymer–nanoparticle interactions involving van der Waals forces, hydrogen bonding, and chemical compatibility, which significantly influence their dispersion and phase behaviours.4,13,42 Given the rich physics and literature on PNCs, covering all the aspects controlling their behavior is beyond the scope of a single review. Thus, to be concise and instructive, in this review, we limit our focus to enthalpically neutral mixtures of polymers and polymer grafted nanoparticles (PGNPs). The phase and dynamic behaviors of such systems are driven by the entropic interactions at the interface of polymers and PGNPs. We highlight how the entropic effects at the polymer–PGNP interface could be harnessed to achieve precise control of the dispersion of particles, and hence, gain a deeper understanding of the underlying mechanisms governing the behavior of PNCs. To this end, we describe how engineering the conformation of the grafted polymers by varying the graft chain length, grafting density or the nanoparticle core size can lead to dramatic changes in various properties of either PGNP assemblies or membranes and in PNCs made of polymers embedded with such grafted nanoparticles. In addition to the usual parameters mentioned above, an additional parameter has been introduced, which we use as an effective representation of the entropic interaction effect, f, between the grafted and matrix chains. We will delineate the role of f in controlling the dispersion of PGNPs in polymer matrices, thereby controlling the thermomechanical properties of PNCs and their performance in membrane technologies, such as water desalination and gas separation.
To establish a clear understanding of the entropic effects in polymer–PGNP systems, we begin by highlighting what we mean by interfacial entropy and how f allows controlling it. Upon mixing chemically identical matrices and graft polymers, deviations in the conformational entropy at the particle–polymer interface due to the stretching of graft/matrix polymers facilitate phase separation/homogeneous mixing. This conformational entropy of polymer chains at the particle–polymer interface is what we refer to as interfacial entropy. Grafting the nanoparticles with polymers allows harnessing the interfacial entropy via the particle size, grafting density, the molecular weight of matrix and grafting chains.43–48 In particular, the ratio of grafting molecular weight to the matrix molecular weight, defined as f, plays an important role. At a given grafting density, for systems with f > 1, the short matrix chains could mix without significant stretching of grafting polymers. This interpenetration between the grafted and matrix polymers results in a broad particle–polymer interface for f > 1, and hence, displays a homogeneous dispersion of particles.43 On the other hand, for systems with f < 1, the entropic penalty to accommodate long chains will be significantly larger, which, in turn, results in a sharp interface with reduced monomer density at the particle–polymer interface.43 This manifests into local or macroscopic phase separation. Naturally, interfacial entropy plays a crucial role in determining not only the dispersion behavior, but also the physical characteristics and hence the functionality of the PNCs.44,49
We organize this review as follows: we begin with a brief discussion of the technical aspects of the experimental methods and molecular dynamic simulations discussed in this article. Subsequently, we delineate the role of conformation of grafted chains in controlling the interfacial entropic effects and, hence, in tuning the dispersion of PGNPs in polymer matrices. Afterwards, we will highlight how interfacial entropic effects can be utilized to tune various thermo-mechanical properties such as the glass transition temperature, viscosity and fragility of PGNP based PNCs (bulk and thin films) and membranes. In particular, when PNCs are confined such as in thin films or thin coatings, we will emphasize the interplay of two interfaces: (i) the PGNP–matrix polymer interface, characterized by the thickness of the graft–matrix chain inter-mixed region ξ, and (ii) the substrate–film interface, defined by the thickness of the adsorbed layer hint. Furthermore, we discuss in detail how entropic coupling between graft and matrix chains can be tuned to create dispersed PNCs with high NP loading and membranes for gas and water separation. We conclude by outlining the prospects for creating sustainable PNCs, highlighting their potential for use in energy, biomedicine, and environmental applications.
2 Methodologies: experimental and computational approaches
2.1 Preparation of PGNPs
Polymer grafted nanoparticles, nanoparticles (often inorganic) grafted with long polymer chains, are a class of soft nanocolloidal systems with versatile properties. Grafting inorganic nanoparticles (NPs) with polymers, in addition to providing stabilization against aggregation, provides new levers to control the dispersion of the nanoparticles in polymer matrices. In this section, we briefly review the two methods – grafting-from50–52 and grafting-to53–61 – that are predominantly used for the synthesis of PGNPs. The grafting-from method involves growing polymer chains directly from nanoparticles by attaching initiators to their surface and polymerizing monomers.62 This approach allows for high grafting density and precise control of chain lengths but often results in higher polydispersity compared to the grafting-to method. Techniques like atom transfer radical polymerization (ATRP), reversible addition–fragmentation chain transfer polymerization (RAFT),20 or ring-opening polymerization (ROP) are commonly used for controlled polymerization. While the process can be complex, it ensures strong polymer–nanoparticle bonding and is ideal for applications requiring dense, stable polymer coatings.63,64 In contrast, the grafting-to approach involves attaching pre-synthesized polymer chains to the surface of nanoparticles. Thus, the grafting-to method typically results in a lower polydispersity of grafted chains compared to the grafting-from method. In this report, we focus broadly on studies investigating PGNPs synthesized using the grafting-to method. However, the physics underlying their phase and dynamic behaviors do not depend on their method of preparation.2.2 Advanced scattering techniques
Following Fresnel's theory of reflection, the reflected intensity of X-rays from a surface follows
 | (1) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) z =
z = ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) f −
f − ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i (
i (![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i and
i and ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) f being the incoming and outgoing wavevectors, respectively) is along the surface normal (z coordinate) and qc is the critical wave vector. Rephrasing Bragg's law of diffraction, qz follows
f being the incoming and outgoing wavevectors, respectively) is along the surface normal (z coordinate) and qc is the critical wave vector. Rephrasing Bragg's law of diffraction, qz follows | (2) |
 | (3) |
In summary, any representative reflectivity profile will exhibit (a) a plateau, due to total external reflection, at qz < qc, (b) a steep decrease for qz > qc, and (c) an asymptotic decay ∝qc−4 at large qz. In addition, the reflected intensity of a rough surface, with roughness δh, falls off exponentially following,
 | (4) |
On shining X-rays on a film (containing one or more layers) coated on a substrate or floating on a water surface, beyond a critical wave vector qc, rays get reflected from the top and the bottom surface resulting in periodic oscillations called the Kiessig fringes. At qz > qc, such oscillations ride on the decrease of R with qz following eqn (3). The amplitude of these oscillations scales with the electron density contrast of the layer and the interfaces (air–surface and substrate). In addition, the amplitude of such oscillations also decreases with the roughness of the surface following eqn (4).
Paratt's recursion formalism is used to model the reflection and transmission from all j interfaces. This relates the reflected amplitude Rj and transmitted amplitudes Tj at all j interfaces via
 | (5) |
 | (6) |
Using Born approximation, we could relate the reflectivity profile with the thickness dependent electron density ρe(z) as
 | (7) |
2.2.2.1 X-ray photon correlation spectroscopy. X-ray photon correlation spectroscopy (XPCS) is broadly being used to study dynamics in various hard and soft matter systems by utilizing coherent X-rays from third-generation synchrotron sources65,67,68 and X-ray free electron laser facilities.69 Coherent X-ray scattering experiments can explore a variety of phenomena at longer time scales, which is beyond the scope of neutron scattering experiments, and shorter time scales, which are not reached by normal light scattering experiments. The poor spatiotemporal coherence in lab X-ray sources is a limiting challenge. However, the emergence of powerful X-rays from third-generation synchrotron sources provides great opportunities to perform coherent X-ray scattering experiments. XPCS is an X-ray equivalent of dynamic light scattering (DLS). In XPCS, speckle patterns originating from the disorder in the systems are collected at intervals of δt. The time correlation of these speckles provides information about the dynamics of scatters in the system.70–73 Time correlation of intensity at (qx, 0) to a later time (qx, δt) follows,
 | (8) |
| g2(qx, δt) = 1 + b|Fs(qx, δt)|2 | (9) |
| Fs(qx, δt) = exp[−(δt/τ)β], | (10) |
2.2.2.2 Quasi-elastic neutron scattering. Quasi-elastic neutron scattering (QENS) is a versatile technique used to probe atomic and molecular dynamics in various systems like liquids, polymers, and biological macromolecules.74–78 In comparison to other scattering techniques, QENS requires fine energy resolution in the milli-electron volt range. By detecting small energy changes through neutron sources (reactors or spallation sources) and instruments like time-of-flight or backscattering spectrometers, QENS provides insights into microscopic motion over a broad momentum transfer range.79
The differential scattering cross-section is expressed as:
 | (11) |
 | (12) |
| Γ(q) = Dq2 + τ−1(1 − e−q2l2/6). | (13) |
The intermediate scattering function Fis(q, t), derived from the Fourier transform of S(q, ω), describes time-dependent molecular displacements:81
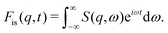 | (14) |
| Fis(q, t) = A(q)e−Γ(q)t, | (15) |
| Fis(q, t) = A(q)e−(t/τ(q))β, | (16) |
QENS uniquely reveals time and spatial scales of segmental motion, making it indispensable for studying diffusion in polymers, glass transition, and constrained dynamics in complex systems.61,79,81 Through Γ(q) and Fis(q, t), parameters like diffusion coefficients, relaxation times, and motion length scales are obtained, providing critical insights into materials' properties and molecular interactions.
2.3 AFM for probing viscoelastic properties
Atomic force microscopy (AFM) is a powerful technique, not only for imaging at the nanoscale, but also for probing the viscoelastic properties of materials at the nanoscale.82,83 AFM uses a sharp tip on a cantilever to interact with a sample surface, allowing to measure properties like stiffness and elasticity with high spatial resolution.84,85 This is especially useful for heterogeneous materials, such as polymers, biological tissues, and soft matter, where these properties can vary significantly over small length scales.86 Since conventional rheological techniques will not be reliable for measuring nanoscopic thin films, in Swain et al.,87 we extend the ability of this technique to estimate thin film viscosity using standard force–distance spectroscopy.88,89 Here, we provide a brief on the physics underlying the method.Typically, a force–distance curve characterizes the deflection of an AFM tip as it interacts with a sample during the approach (trace) and withdrawal (retrace) phases.88,89 In the non-contact regime, where the tip is far from the surface, no interaction forces are observed. As the tip approaches the sample, long-range attractive forces, predominantly van der Waals interactions, induce a sudden deflection toward the surface, a phenomenon termed jump-to-contact. Upon further indentation, short-range repulsive forces dominate, leading to cantilever bending, indicative of contact mode AFM imaging. During the retrace phase, the tip is withdrawn from the sample, experiencing adhesive, capillary and viscous forces. The tip detaches from the surface only when the elastic restoring force of the cantilever surpasses these attractive interactions, resulting in a sudden release known as jump-off-contact. Quantitative parameters such as tip-sample adhesion force, total contact force, and pull-off force can be directly extracted from force–distance spectroscopy measurements. The force experienced by the cantilever, when retracted from a viscous surface, is mainly a combination of viscous, Fvis, and capillary forces, Fcap.90 Thus, the pull-off force profile of force–distance retrace curves is modeled using the equation
| FAFM(L) = F0 + Fcap(L) + Fvis(L) | (17) |
 | (18) |
 is the retracting rate of the tip from the sample. On the other hand, Fcap is given by
is the retracting rate of the tip from the sample. On the other hand, Fcap is given by | (19) |
In fitting the obtained force–distance curves with eqn (17) the value of dL/dt was kept fixed, as was used in experiments, while all the remaining parameters were varied during the fitting of the data. To eliminate the possible uncertainties resulting from the mutual dependency of Rtip and η (refer to eqn (19)), we estimated the temperature-dependent Rtip values using reported η values of bulk PS of molecular weight 19 kDa.92–94 We fitted the force–distance curves obtained for the bare PS films. However, constrained fitting, where both Rtip and η are varied, also led to similar results. We have used two offset parameters named x0 and b0. Therefore, the force–distance curves are modeled using the equation given as:
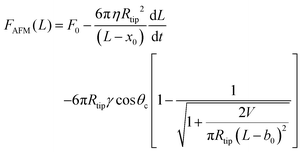 | (20) |
For comprehensive information regarding the fitting of the retrace curve within the force–distance data and the extraction of viscosity, please refer the work of Swain et al.87
2.4 Coarse grained molecular dynamics simulations
Computer simulations are beneficial for validating the experimental findings and providing more insights into a parameter space that is challenging to access experimentally. The coarse-grained molecular dynamics (CGMD) simulations have been widely used to model polymers and polymer-grafted nanoparticles. Several tools like LAMMPS (large-scale atomic/molecular massively parallel simulator), GROMACS, NAMD, HOOMD-blue, and dissipative particle dynamics (DPD) can be used to perform CGMD simulations. However, the LAMMPS package is often used to perform CGMD simulations due to superior scalability, customizability, and support for polymeric and reactive CG models. In this review, we discuss CGMD simulations on PNCs and membranes performed using the LAMMPS package.58,60,70,95 A pure polymer system is modeled using linear chains created using a bead-spring model with a hybrid potential of finite extensible nonlinear elastic (FENE) potential and harmonic potential with standard values of the parameters. The linear-chain-grafted nanoparticles were used as a model for PGNPs. All the species of the system interact through the shifted Lennard-Jones potential with the following form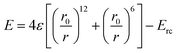 | (21) |
To model a PGNP membrane on the polymer substrate film, we use a bilayer system consisting of a single-layer of grafted nanoparticles atop bulk-free linear chains inside a rectangular box.58,60 The non-bonded graft–graft monomer interactions were modeled using eqn (21) with ε = 1.0kT, where k is the Boltzmann constant and T the temperature. To model the PGNP/PS system, non-bonded matrix–matrix and graft–matrix interactions were set as the Lennard-Jones potential with ε = 1.0kT and ε = 1.03kT, respectively.
2.5 Transport through desalination membranes
The solution–diffusion model explains membrane separation as a three-stage process.96–99 Molecules absorb into the membrane on the feed side, driven by chemical potential gradients and governed by solubility. They then diffuse through the membrane, where their rate depends on the molecular size and compatibility with the polymer, favoring smaller or more soluble molecules. Finally, molecules desorb on the permeate side, completing the transport. This process enables selective separation by leveraging differences in diffusion and solubility, making the model effective for gas separation, reverse osmosis, and pervaporation. However, it assumes ideal transport and may require adjustments for complex mixtures or swelling effects.The transmembrane flux J, representing either water flux (Jw) or salt flux (Js), is determined by the following equation:
 | (22) |
Here, Vs is determined using the following equation:
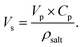 | (23) |
The salt rejection Rs is determined using
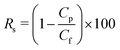 | (24) |
The water permeance A (in units of [L m2 h−1 bar−1]) and the salt permeability B (in units of [L m2 h−1]) are both determined from the relations between flux and permeance as
 | (25) |
 | (26) |
Here, ΔP is the applied pressure on the membrane during the flux experiment, ΔC is the difference between Cf and Cp, and Δπ is the osmotic pressure difference where the osmotic pressure π is defined as π = iMRT. Here, i is the van't Hoff factor, M is the molarity of solution, R is the ideal gas constant and T is the absolute temperature. Finally, we determine the water perm selectivity of the membrane as A/B.
To summarize, thus far, we have highlighted a palette of experimental and simulation methods allowing access to the structural information, microscopic (length-scale dependent) dynamics and macroscopic properties of PNCs. Building on this understanding, in the next section, we describe how the interfacial entropy at the polymer particle interface plays a crucial role in describing the structure and dynamical aspects of PGNPs and their mixtures with polymers.
3 Conformation of grafted chains in PGNPs
Grafting chains on inorganic nanoparticles (see Fig. 1a) provides two important advantages: the presence of an inorganic core provides an avenue to harness several physical properties, and the polymers grafted to the core nanoparticles allow controlling the interactions between them.1,100,101 As discussed in Section 2.1, several methods were developed to synthesize them either via grafted to or grafting from approaches.3,50–52,54–61,102 The morphology and interactions between PGNPs manifest several parameters including van der Waals interaction between the neighbouring nanoparticles, the enthalpic interaction between the core and the grafted polymers, the molecular weight of the grafting polymers, the grafting density and the quality of the solvent in which the particles are dispersed.52,103–106 Often, the core size of PGNPs is much smaller than the overall size of the particles. Thus, the contribution of the inorganic core nanoparticles to the interparticle interactions could be neglected. In such a limit, the radial monomer density profile, and hence, the interactions of PGNPs can be approximated with the star polymers.6,103 In an attempt to build an intuitive background, we begin with a brief discussion on their structural analogues called star polymers, which lack the inorganic core (Fig. 1b).107–109 We guide curious readers to the focused reviews of star polymers.107,109–114 Here, we provide a brief discussion of highlighting the parallels between star polymers and PGNPs.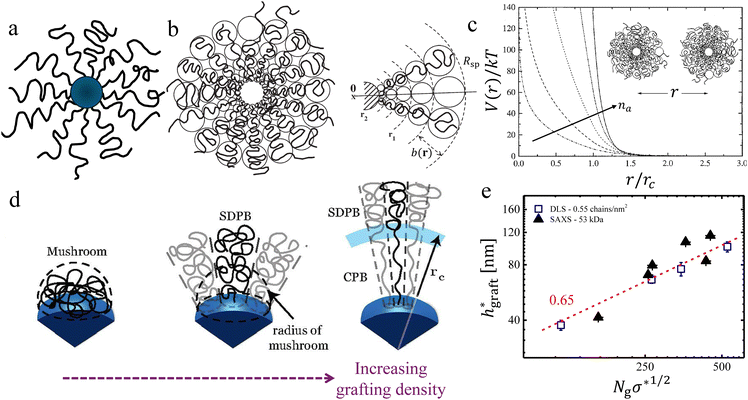 | ||
Fig. 1 Conformational transitions – equivalence between PGNPs and star polymers: (a) schematic of a polymer grafted nanoparticle, where the grafted polymers are shown in black lines and the inorganic core nanoparticles are shown as blue spheres. (b) Schematic of a star polymer, shown with blobs for highlighting the conformational transitions radially outward. (c) Effective interaction V(r), normalized with the thermal energy kT, is shown for star polymers with a different number of arms, denoted by na. Similar conformational transitions in PGNPs, dictated by the grafting density σ, are shown schematically in (d). The rescaled thickness of the grafted layer  of the melt graft layer thicknesses, obtained via SAXS measurements, and of the thickness in solutions, obtained via DLS measurements, are shown. Please refer to the text for discussion on rescaling. The schematic shown in (b) and the plots shown in (c) are adapted from Likos and co-workers,107,108 and the schematic in (d) is adapted from Dukes et al.48 Data in (e) are extracted from ref. 48 and 115. of the melt graft layer thicknesses, obtained via SAXS measurements, and of the thickness in solutions, obtained via DLS measurements, are shown. Please refer to the text for discussion on rescaling. The schematic shown in (b) and the plots shown in (c) are adapted from Likos and co-workers,107,108 and the schematic in (d) is adapted from Dukes et al.48 Data in (e) are extracted from ref. 48 and 115. | ||
A star polymer contains many polymer arms connected to its microscopic core. It is now well known that the physical behaviour and the interactions between the star polymers reflect the number of arms na connected to the core.113,114,116 Star polymers with low na have a uniform distribution of monomers from the surface. On the other hand, star polymers with large na possess a close packing of polymers on the surface, resulting in strong steric repulsion between the polymers, which, in turn, leads to a strong stretching of polymers near the core. It is easy to conceive that the volume available per chains increases as we go radially outward. As a result, the extent of stretching of chains decreases with an increase in the radial distance from the core surface. Reflecting such transitions in polymer conformation along the radius, it is convenient to separate a star polymer into three regions: the core, the stretched region near the surface, and the unswollen region at the edge. The effective size, quantified by radius Rsp, is effectively the sum of three contributions: the radius of the core Rcore, the length lswollen of the swollen/stretched region, and the length lunswollen of the unswollen region at the edge. The na dependence of Rsp is nicely captured by the blob model of Daoud and Cotton.117 In this model, a star polymer is regarded as a succession of concentric shells of blobs, each blob in the shell having size b(r). The radial variation in monomer concentration c(r) and the overall size of the star polymer depends on (a) the solvent quality, which determines the excluded volume parameter v of the chain, (b) the degree of polymerization N and (c) the number of polymers connected to the core also known as the functionality na. Using a simplifying assumption that the concentration c(r) of monomers vanishes beyond the radius Rsp of the star polymer, the conservation of the number of monomers yields109
 | (27) |
Using this conservation form and accounting for the different extents of stretching along the radial direction, the radius Rsp follows109
 | (28) |
This form of the radius manifests the radial distance-dependent concentration c(r), shown in Fig. 1b. The c(r) and Rsp provide an interesting form of the potential,109
 | (29) |
Qualitatively, the conformations of grafted polymers vary with grafting density σ in a manner similar to the na dependence in star polymers (see Fig. 1d). Let us define a reduced grafting density σ* = σ·a2, with a being the monomer size. When the grafting density satisfies σ* < Rg−3, where Rg is the radius of gyration, the grafted polymers display a swollen behavior and this type of conformation is called mushroom conformation. With further increase in σ*, grafted polymers reveal various conformations from mushroom-like to semi-dilute polymer brush (SDPB) and subsequently to concentrated polymer brush (CPB). Especially, at large σ*, grafted polymers stretch progressively as we go towards the center of the particle revealing transitions from SDPB to CPB. Extending the ideas of the Daoud–Cotton model, Dukes et al. showed that the thickness of the graft layer follows48
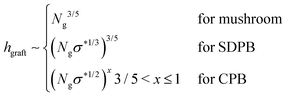 | (30) |
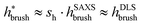 . Here, DLS experiments were performed on PGNPs with σ = 0.55 chains per nm2 but with different molecular weights Mg of grafted chains, while SAXS experiments were performed on PGNP melts with Mg = 53 kDa but with different σ values. Inspired by the work of Dukes et al.,48,119 we scaled σ* with the number of grafted monomers Ng of the grafted chains. We observe that
. Here, DLS experiments were performed on PGNPs with σ = 0.55 chains per nm2 but with different molecular weights Mg of grafted chains, while SAXS experiments were performed on PGNP melts with Mg = 53 kDa but with different σ values. Inspired by the work of Dukes et al.,48,119 we scaled σ* with the number of grafted monomers Ng of the grafted chains. We observe that  . Following eqn (30), this dependence reveals that the grafted chains are in the CPB regime. The conformation of grafted chains plays a crucial role in deciding the dispersion behavior of PGNPs in polymer matrices. We will focus on this aspect in the next section.
. Following eqn (30), this dependence reveals that the grafted chains are in the CPB regime. The conformation of grafted chains plays a crucial role in deciding the dispersion behavior of PGNPs in polymer matrices. We will focus on this aspect in the next section.
4 Dispersion of nanoparticles in polymer matrices
A major challenge in achieving the desired properties of polymer nanoparticle blends is in controlling the state of dispersion of the particles. As a result, extensive research2,16,56,120,121 is devoted over the last two decades to understand and develop the strategies for controlling the dispersion of PGNPs. In this section, we briefly describe the thermodynamical arguments allowing us to understand the dispersion of nanoparticles in polymer matrices.4.1 Dispersion of bare nanoparticles
We begin our discussion with the dispersion of spherical bare nanoparticles, i.e. without any grafting agents, in polymer matrices. For simplicity, we assume that the enthalpic interactions between the particle and the polymer are neutral (achieved by considering similar chemical nature for both the nanoparticles and polymers). In this case, the dispersion of particles simply depends on the balance of entropic forces acting in the system. There will be two components of entropy: (a) the mixing entropy and (b) the stretching entropy associated with the matrix chains. Given the neutral interactions between the particles and polymers, dispersion increases the entropy and decreases the free energy of the system. This free energy Fmix directly scales with the volume fraction of the particle ϕp and inversely scales with the volume (∼Rnp3).2,42 | (31) |
On the other hand, the host chains have to stretch in order to accommodate the particles. This, in turn, evokes an entropic penalty as stretching would limit the number of accessible conformations of the matrix polymers. The free energy Fstretch associated with stretching increases with increase in the particle size, with respect to the radius of gyration Rg of the polymer.2,42
 | (32) |
The balance of Fmix and Fstretch controls the dispersion of bare particles in polymer matrices. For all Rnp < Rg, the entropic gain Fmix due to mixing will be larger than the stretching penalty Fstretch of the chains. Thus, we expect the particles to disperse for Rnp < Rg, and not dispersed otherwise. Using polyethylene (PE) nanoparticles in polystyrene (PS) matrices, Mackay et al.22 demonstrated the possibility of dispersing particles by harnessing the relative size ratio of particles and polymer chains (see Fig. 2a). Despite the enthalpic unfavourability of PE in PS, small nanoparticles of PE displayed good miscibility in PS matrices due to the gain in translational entropy. Building on this understanding, we will now move towards the dispersion of PGNPs and how entropy allows harnessing dispersion of particles in polymer matrices.
 | ||
| Fig. 2 Dispersion of nanoparticles in polymer matrices: (a) phase diagram, polymer radius of gyration vs. nanoparticle radius, differentiating the miscible (dispersed nanoparticles) and immiscible states of polymer + nanoparticle mixtures. (b) TEM images capturing the dispersion of particles with different grafting densities σ and grafting molecular weight Mg. Each micrograph is defined by values corresponding to σ (in the units of chains per nm2), Mg (in the units of kg mol−1) at the top right corner. The matrix molecular weight is kept constant at Mm = 120 kg mol−1. (c) Phase diagram capturing the dispersion states of PGNPs in bulk. Here, f is the ratio of the graft to the matrix length. Panel (a) is adapted from ref. 22 and panels (b) and (c) are adapted from ref. 33. | ||
4.2 Dispersion of polymer grafted nanoparticles
The grafted polymers in PGNPs provide additional avenues to control the dispersion of PGNPs in polymer matrices. As discussed in Section 3, the conformations of grafted chains depend on various factors including grafting density σ and the molecular weight of the grafted polymer Mg. In Fig. 2(b), we display transmission electron micrographs of PS grafted silica nanoparticles mixed with linear PS of molecular weight Mm = 142 kDa (data adopted from ref. 33). Since the grafted and matrix polymers are of same chemical nature, the enthalpic interactions are neutral, i.e. the Flory Huggins parameter χ = 0. Thus, the dispersion will be dictated by the entropic interactions (to be discussed below) at the particle–polymer interface. A control over σ and Mg yields a rich control over the dispersion morphology of PGNPs varying from spherical clusters to strings, sheets, and complete dispersion. In a recent review, as shown in Fig. 2(c), Kumar et al. summarized the control over dispersion of PGNPs by controlling the σ, Mg and its ratio with the molecular weight Mm matrix polymer, f = Mg/Mm. In what follows, we provide thermodynamic arguments for understanding the dispersion of PGNPs in polymer matrices.Here, we will begin with the well-developed theories on the mixture between polymers and flat brushes to discuss the associated free energies.122,123 We consider no enthalpic interactions between the grafted and matrix polymers, i.e. we limit our discussion to systems with χ = 0. Upon mixing linear polymers with grafted brushes, the free energy will have contribution from the elastic energy required to stretch the grafted chains Fg and from the excluded volume interaction induced entropic repulsion from the matrix polymers Fm. At low grafting densities, the effective free energy could be approximated to ref. 122
 | (33) |
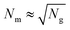 , the entropic repulsion due to excluded volume is of the order of kT and can be neglected. Thus, minimizing F = Fg yields hg ∼ aNg1/2, which matches with the radius of gyration of the polymer in melt conditions. With an increase in grafting density, the grafted chains begin to swell and beyond σ*/a2 ≡ 1/hg2, the swollen chains overlap. This leads to a grafting density dependent entropic repulsion Fm. Thus, the effective free energy takes the form122
, the entropic repulsion due to excluded volume is of the order of kT and can be neglected. Thus, minimizing F = Fg yields hg ∼ aNg1/2, which matches with the radius of gyration of the polymer in melt conditions. With an increase in grafting density, the grafted chains begin to swell and beyond σ*/a2 ≡ 1/hg2, the swollen chains overlap. This leads to a grafting density dependent entropic repulsion Fm. Thus, the effective free energy takes the form122 | (34) |
 | (35) |
The first term on the right corresponds to the additional elastic energy for stretching the chains by ξ and the second term corresponds to the entropic gain allowing for the diffusion of matrix polymers into the graft layer. The grafted and matrix polymers tend to disperse if the elastic stretching energy is larger than the entropic gain. The brush in this regime is denoted as the dry-brush. Upon minimizing eqn (35), we obtain ξ = (aNg)/(2σ*Nm). Using the packing constraints, we could show hg ≈ aNgσ*. When the penetration length ξ is of the order of hg, the dry-brush becomes the wet-brush. For large matrix chains, Nm > Ng, it could be visualized that the energy cost for diffusing into the grafted layer would be significantly higher. Thus, we may expect a dewetting zone at the particle–polymer interface. Such large grafting densities have been utilized in the literature to achieve autophobic dewetting.55,124,125 We summarize the dimensions (hg, ξ) corresponding to the different conformations in Table 1.
Now, let us focus on grafted chains on curved surfaces, as will be the case of polymer grafted to nanoparticles. As discussed in Section 4, the number density of grafted chains decreases as we progress from the center to the edge of a polymer grafted nanoparticle in the CPB regime.48 Thus, the grafting density σ and the interpenetration width ξ discussed in eqn (35) and (34) should be rescaled with the radius Rcore of the core of PGNPs. Trombly and Ganesan126 showed that the effective grafting density and the thickness of the graft layer of the curved surface takes the form
 | (36) |
 | (37) |
 | (38) |
For large particles Rcore ≫ hg, since the curvature effects would be minimal, the flat brush behaviour would be restored.
To summarize, entropic constraints due to the brush/host chain interactions are significant and can favour the mixing of the nanoparticles with the host chains or contribute toward phase separation between particles and host chains. The host/brush interactions are determined by the parameters Ng, Nm and σ. When the grafted chains are sufficiently long (Ng ≫ Nm) and σ is sufficiently low, that is, σ*·Ng1/2 < (Ng/Nm)1/2, then the host chains can interpenetrate or wet the brush layer, thereby forming a so-called wet brush.2,33,127 This would promote miscibility between the particles and the host chains. On the other hand, when the grafting density is very high and Ng ≪ Nm, specifically, when σ*·Ng1/2 < (Ng/Nm)1/2, the host chains are partially excluded from the grafted layer, thus forming a dewetting interface between the polymer and the particle.
4.3 Physical confinement allows harnessing dispersion
In various applications, PNCs are used in the form of films, often with thicknesses that are of the order of the unperturbed size of the matrix polymer. In such confined geometries, several studies reveal that the polymers are strongly deformed resulting in restrictions in their conformational degrees of freedom. Will such confinement-induced molecular deformations and therefore the resulting reduction in the conformational entropy of the chain affect the dispersion of nanoparticles?To address this aspect, we54 reported experiments on PS grafted gold nanoparticles dispersed in PS thin films with different thicknesses. For a systematic control over the entropy at the particle–polymer interface, Mg and Mm are varied in a way that f = Mg/Mm varies from 0.033 to 2.5. As described in Section 4.2, PGNPs in composites with f ≪ 1 is expected to phase segregate and the PGNPs in systems with f > 1 will stay dispersed. Scanning electron micrographs capturing the dispersion behaviour of PGNPs in composites with f = 0.033 ≪ 1 are summarized in Fig. 3(a) and (b). Expectedly, PGNPs mixed with polymer films of thickness h = 65 nm exhibit cluster formation at the air surface with no evidence of dispersion (see Fig. 3(a)). On the other hand, for thinner films shown in Fig. 3(b), we witness apparently well-dispersed PGNPs (small bright dots) in the background of small clusters (brighter and relatively larger dots) at the surface. This suggests an improved dispersion of PGNPs in thinner films.
 | ||
| Fig. 3 Confinement enhances the dispersion of PGNPs in polymer films: scanning electron micrographs of composite films with f = 0.033 for (a) h = 65 nm and (b) h = 20 nm. Scale bars in (a) and (b) correspond to 200 nm and 100 nm, respectively. (c) Fresnel normalized reflectivity R/RF is shown as a function of normal wave vector qz for composite films of three different thicknesses as defined in the panel. The electron density profiles obtained from the modelling of reflectivity curves are provided in the inset of (c). (d) Fraction ϕseg of segregated particles as a function of film thickness. (e) Dispersity G = ϕbulk/ϕseg is shown as a function of f for films of two different thicknesses. (f) Bond orientational order parameter sB along the film thickness z/d is shown for simulation boxes of three different thicknesses. (g) The excess surface absorption (normalized with appropriate volumes) of nanoparticles (Γn) and polymers (Γp) is shown as a function of the thickness Lz of the simulation boxes. All data are adapted from ref. 54. | ||
X-ray reflectivity measurements on composite films of different thickness provide further support to this observation.54 Apart from probing the film thickness (via Kiessig fringes), XR also allows probing the differences in the electron density contrasts along the film thickness (refer to Section 2.2). Thus, any preferential segregation of particles to the air surface or to the substrate interface, creating electron density modulation, could be captured from the raw data (without detailed modelling). In Fig. 3(c), Fresnel normalized XR profiles are shown for composite films of three different thicknesses, h = 20, 45, and 65 nm. The Fresnel part gives the wave-vector dependence of reflectivity i.e. RF ∼ qz−4 (see eqn (3)). For an ideal film with homogeneous density along the film thickness, the Fresnel normalized reflectivity should be oscillating, reflecting the thickness of the film, but flat without any additional qz-dependence. Clearly, as shown in Fig. 3(c), thicker films reveal a strong additional modulation, whose amplitude indicates the strength of the gradient in electron density, and the peak position indicates the thickness of such electron density modulation. This modulation reflects the segregation of PGNPs at the substrate interface. Interestingly, the amplitude of this additional modulation also decreases with the decrease in the film thickness. This suggests a decrease in the extent of interface segregation with h.
To extract quantitative information on dispersion and the preferential segregation to the surfaces, we54 performed detailed modelling of XR data (refer to eqn (5) and (6)) using an effective three-layer description of the film: a layer at the air surface, followed by bulk, and then a layer at the substrate interface. The thickness dependence of electron density extracted from such modelling is shown in the inset of Fig. 3(c). Supporting the Fresnel normalized reflectivity, the thickness dependence of electron density profiles reveals a strong segregation of particles at the substrate interface. There is an apparent decrease in the density of particles at the substrate interface with a decrease in film thickness. This aspect is quantified by discretizing the electron density into three effective layers and the fraction of PGNPs residing at the respective layers are defined as ϕsur, ϕblk, and ϕint with a restriction such that the total fraction ϕp = ϕsur + ϕblk + ϕint. For a given bulk fraction of ϕp = 1.2 wt%, a systematic decrease in the segregated fraction ϕseg = ϕsur + ϕint of PGNPs can be witnessed with decrease in film thickness (see Fig. 3(d)). This is interesting, as the entropy at the particle–polymer interface enables complete phase separation. To visualize this more clearly, Fig. 3(e) shows the extent of dispersion by plotting G = ϕblk/ϕseg as a function of f. As expected, G increases with increase in f. For all f, G values corresponding to thinner films are larger than those of the thicker films. Clearly, thickness serves as an additional parameter contributing to the dispersion of PGNPs in polymer films.
CGMD simulations using bead spring chains with FENE reveal further microscopic insights into the enhanced dispersion of PGNPs with the decrease in film thickness. To reflect the thickness-induced confinement, periodic boundary conditions were used in x and y, while z is confined between two parallel surfaces. The distance Lz between the parallel surfaces will act as a proxy to the film thickness h. Simulation parameters were carefully chosen to match the experimental parameters like σ, f and the size ratio of nanoparticles with the grafted and matrix polymers. Please refer to Chandran et al.54 for further details. Simulations corroborate the enhanced dispersion of PGNPs with confinement.54 To quantify the potential changes in the chain structure of the matrix polymers, we deduced the bond orientational order parameter sB = 0.5[3〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj,z〉i − 1], where θj,z is the angle between the bond (formed between j and j − 1 monomers) and z-axis (axis along the film thickness). As shown in Fig. 3(f), sB of chains in the bulk is negative for thinner films, while for thicker films, sB = 0. This suggests that the chains residing in thinner films are ordered, indicating a reduced conformational entropy. Such reduced conformational entropy is manifested in the excess surface adsorption of particles (and polymers), defined as
θj,z〉i − 1], where θj,z is the angle between the bond (formed between j and j − 1 monomers) and z-axis (axis along the film thickness). As shown in Fig. 3(f), sB of chains in the bulk is negative for thinner films, while for thicker films, sB = 0. This suggests that the chains residing in thinner films are ordered, indicating a reduced conformational entropy. Such reduced conformational entropy is manifested in the excess surface adsorption of particles (and polymers), defined as  where i corresponds to polymers or nanoparticles. As shown in Fig. 3(g), the surface excess of nanoparticles Γn decreased with decrease in Lz, while Γp increased with decrease in Lz. This suggests that the thinner films minimize density gradients, likely due to energetic penalty as the interfaces in thinner films are not decoupled as in thicker films. Similar observations were also reported for polymer blend films.128 Our results clearly demonstrate that physical confinement allows controlling the dispersion of particles that are otherwise expected to be phase-separated. Thus, confinement provides a new lever to control the dispersion and hence a whole spectrum of physical properties that depend on the state of dispersion of particles.
where i corresponds to polymers or nanoparticles. As shown in Fig. 3(g), the surface excess of nanoparticles Γn decreased with decrease in Lz, while Γp increased with decrease in Lz. This suggests that the thinner films minimize density gradients, likely due to energetic penalty as the interfaces in thinner films are not decoupled as in thicker films. Similar observations were also reported for polymer blend films.128 Our results clearly demonstrate that physical confinement allows controlling the dispersion of particles that are otherwise expected to be phase-separated. Thus, confinement provides a new lever to control the dispersion and hence a whole spectrum of physical properties that depend on the state of dispersion of particles.
Having understood the processes controlling the dispersion of particles in polymer matrices, in the next sections, we reveal the manifestations of the dispersed states in controlling the physical characteristics of PNC films. The interfacial entropic interactions between grafted and matrix polymers impose constraints on molecular mobility, leading to notable variations in viscosity and glass transition behaviour. These effects are particularly pronounced in thin films, where confinement amplifies interfacial entropy-driven phenomena, as discussed in the following sections.
4.4 Particle–polymer interface controls glassy behavior
Glass transition temperature and glassy dynamics are important parameters allowing the control of the processing of various polymeric structures. Accordingly, intensive efforts were devoted to understanding the glass transition behaviour of PNCs.129–131 Driven by the enormous data on the thickness dependence of glass transition temperature (Tg) of thin polymer films, initial efforts were devoted to understanding the Tg of PNC films in the same framework.125 Here, the interparticle distance hp acts as a proxy for the thickness of polymer films. Conceivably, control over the fraction ϕp of particles allows controlling hp. Assuming a random dispersion of particles allows a simple relation between hp and ϕp as where ϕrcp = 0.638 is the random close packing fraction.54,125 Bansal et al.125 performed pioneering experiments with different fractions of bare silica nanoparticles dispersed in polystyrene matrices. Fig. 4(a) displays the equivalence between pristine PS thin films and PS composites in bulk (adapted from Bansal et al.125). Qualitatively, the hp dependence of Tg for composites followed a dependence similar to that of the dependence of thickness dependent the Tg of pristine polystyrene films coated on neutral surfaces (refer to Bansal et al.125 for other equivalent definitions
where ϕrcp = 0.638 is the random close packing fraction.54,125 Bansal et al.125 performed pioneering experiments with different fractions of bare silica nanoparticles dispersed in polystyrene matrices. Fig. 4(a) displays the equivalence between pristine PS thin films and PS composites in bulk (adapted from Bansal et al.125). Qualitatively, the hp dependence of Tg for composites followed a dependence similar to that of the dependence of thickness dependent the Tg of pristine polystyrene films coated on neutral surfaces (refer to Bansal et al.125 for other equivalent definitions  ,
,  , and
, and  of the interparticle spacing). Here, we note that for wetting surfaces, polymer films and polymer nanocomposites exhibit an increase in Tg with decreasing hp.132 Given this background, it is natural to ask if the dependence of Tg will be the same for PGNPs with different f or σ. To shine light on this aspect, we discuss our experiments54,55,58 on PS grafted gold nanoparticles dispersed in PS films. For this purpose, in Fig. 4(b), we summarize the Tg as a function of ϕp for composite systems with different f values. For f = 0.033 ≪ 1, we observe a systematic decrease in Tg with ϕp. This is in accordance with the summary plot shown in Fig. 4(a). However, for the same ϕp, the extent of decrease in Tg is smaller for f = 0.15 in comparison with f = 0.033. More interestingly, composites with f > 1 display enhancement in Tg with ϕp. Using coarse-grained molecular dynamic simulations, we revealed95 that systems with f ≪ 1 have decreased monomer density at the particle–polymer interface. The presence of such dewetting regions around the polymer–particle interface creates additional free volume, which might explain the decrease in Tg for composites with f < 1. On the other hand, for composites with f > 1, the grafted chains and the matrix chains interpenetrate nicely, thereby imposing additional restrictions on the mobility of the monomers. This might underlie the observed enhancement in Tg. Recent theory and simulations on freestanding polymer films highlight that the deviations in the chain dynamics at substrate interfaces may underlie modifications in caging constraints at the surface and its manifestations to the local elastic barrier for the relaxation.133 We anticipate that similar mechanisms might underlie the enhanced (or suppressed) dynamics at the particle–polymer interface of f < 1 (or f > 1) systems.43,54,55,87,132,134 In addition, as discussed in the last section, we revealed that mere physical confinement increases the extent of dispersion of particles that are otherwise phase segregated. Such increased dispersion, in turn, manifests into a larger number of dewetting interfaces within the polymer film. Thus, as shown in Fig. 4(c), thinner films exhibit larger deviations in Tg for any given ϕp. To summarize, these results demonstrate that harnessing entropy at the polymer–particle interface, quantified via f, allows a systematic control over the glass transition behavior of PGNP-based polymer composites.
of the interparticle spacing). Here, we note that for wetting surfaces, polymer films and polymer nanocomposites exhibit an increase in Tg with decreasing hp.132 Given this background, it is natural to ask if the dependence of Tg will be the same for PGNPs with different f or σ. To shine light on this aspect, we discuss our experiments54,55,58 on PS grafted gold nanoparticles dispersed in PS films. For this purpose, in Fig. 4(b), we summarize the Tg as a function of ϕp for composite systems with different f values. For f = 0.033 ≪ 1, we observe a systematic decrease in Tg with ϕp. This is in accordance with the summary plot shown in Fig. 4(a). However, for the same ϕp, the extent of decrease in Tg is smaller for f = 0.15 in comparison with f = 0.033. More interestingly, composites with f > 1 display enhancement in Tg with ϕp. Using coarse-grained molecular dynamic simulations, we revealed95 that systems with f ≪ 1 have decreased monomer density at the particle–polymer interface. The presence of such dewetting regions around the polymer–particle interface creates additional free volume, which might explain the decrease in Tg for composites with f < 1. On the other hand, for composites with f > 1, the grafted chains and the matrix chains interpenetrate nicely, thereby imposing additional restrictions on the mobility of the monomers. This might underlie the observed enhancement in Tg. Recent theory and simulations on freestanding polymer films highlight that the deviations in the chain dynamics at substrate interfaces may underlie modifications in caging constraints at the surface and its manifestations to the local elastic barrier for the relaxation.133 We anticipate that similar mechanisms might underlie the enhanced (or suppressed) dynamics at the particle–polymer interface of f < 1 (or f > 1) systems.43,54,55,87,132,134 In addition, as discussed in the last section, we revealed that mere physical confinement increases the extent of dispersion of particles that are otherwise phase segregated. Such increased dispersion, in turn, manifests into a larger number of dewetting interfaces within the polymer film. Thus, as shown in Fig. 4(c), thinner films exhibit larger deviations in Tg for any given ϕp. To summarize, these results demonstrate that harnessing entropy at the polymer–particle interface, quantified via f, allows a systematic control over the glass transition behavior of PGNP-based polymer composites.
 | ||
| Fig. 4 Dispersion state allows controlling glass transition temperature: (a) deviations in glass transition temperature Tg is shown as a function of interparticle spacing. Also shown are the deviations in Tg for pristine polystyrene films of different thicknesses. (b) Deviations in Tgi.e. ΔTg is shown as a function of the fraction ϕp of particles mixed with polymer films of thickness 65 nm. Data corresponding to composites with three different f values, as defined in the panel, are shown. Horizontal dashed lines in (a) and (b) correspond to the bulk Tg of polystyrene. (c) ΔTgvs. ϕp for films of two different thicknesses as defined in the panel. Data shown in (a) are reproduced from ref. 125. Data shown in (b) and (c) are replotted from ref. 54, 55 and 58. | ||
4.5 Controlling interfacial entropy yields giant changes in viscosity
Viscosity is a crucial parameter, in addition to designing processing conditions, allowing the interpretation of the molecular characteristics of polymers, free volume content, and the dispersion states of nanoparticles in polymer matrices. PGNPs provide novel pathways to control the viscosity of polymers via the interfacial layer (IL) between the matrix and the grafted polymer.45,58,60,61,70,87,135,136 As discussed in Section 4.2, the width ξ of the interfacial layer can be experimentally controlled by tuning the size of the particle, f, and σ. Thus, extensive work has been devoted to developing an understanding of how the viscosity of PNCs depends on these experimental parameters controlling the dispersion states and the nature of IL in PNCs.58,61,70,87,135 Due to interfacial effects of PGNPs, research has indicated both an increase and a decrease in viscosity upon the introduction of particles. The increase in viscosity is well-documented and can be characterized by the Batchelor and Einstein relation.137 Conversely, certain investigations have reported a reduction in viscosity associated with particle incorporation.138–141 A variety of models have been proposed to elucidate this phenomenon.139,142 Here, we will provide a brief of these models.The Einstein-Batchelor relation provides a relation between the effective viscosity and the concentration of the inclusions in a dilute suspension of spherical particles.137 This relation, which builds on earlier work conducted by Albert Einstein,143 is particularly useful in colloid science and rheology for understanding how suspended particles increase a fluid's viscosity.144,145
| ηeff = η0(1 + 2.5ϕ), | (39) |
| ηeff = η0(1 + 2.5ϕ + 6.2ϕ2), | (40) |
In contrast, several reports reveal that the PNCs may exhibit a decrease in the viscosity, in comparison with the pristine polymers. Addressing this aspect, here we highlight the Wang–Hill (WH) model140 describing the intrinsic viscosity [η] of polymer solutions, incorporating polymer–solvent interactions, molecular weight, and chain conformation. This model describes a negative intrinsic viscosity in the framework of the presence of an interfacial layer at the NP–matrix interface with a viscosity and density different from that of the bulk. The WH model for intrinsic viscosity [η] is often expressed as:
 | (41) |
Both models are essential in rheology for predicting fluid viscosity. The Wang–Hill model applies to polymeric solutions, while the Batchelor equation describes particle laden fluids. Understanding them aids in optimizing industrial processes involving polymers and suspensions. These are the classical models used to describe viscosity changes in polymers. However, when PGNPs are introduced into the polymer matrix, forming PNCs, numerous additional parameters come into play, influencing the flow behaviour. In PNCs, the presence of PGNPs and the interfacial layer significantly impacts the system's rheology, which can be better understood through modelling approaches that incorporate entropic contributions. In the following section, we explore how these interfacial effects influence the overall transport properties, providing deeper insights into the role of entropic parameters in governing the behaviour of PNCs.
Various studies have been conducted to understand the rheological behaviour of polymer nanocomposites (PNCs) through both experimental and computational approaches. In particular, the work of Kalathi et al.,135 including experiments and simulations, highlighted how the viscosity of PNCs changes in miscible (athermal) and immiscible (thermal) blends of polymers with PGNPs. As shown in Fig. 5, Kalathi et al. summarized the role of the diameter of the nanoparticles in controlling the viscosity η of PNCs in comparison with the viscosity ηp of the neat polymers. They investigated how nanoparticle (NP) incorporation affects polymer melt viscosity, focusing on polymer–NP interactions, NP size, and polymer chain length. A “viscosity crossover” criterion is introduced to predict the impact of NPs on viscosity based on the properties of both the polymer and the nanoparticles. Fig. 5(a) highlights systems with chemically similar polymers and NPs, showing a transitional point where the viscosity of nanocomposites either exceeds or falls below that of the pure polymer melt, influenced by the NP size and polymer chain characteristics. Fig. 5(b) addresses chemically dissimilar systems, where immiscibility often leads to increased viscosity due to poor dispersion and NP aggregation. In cases of moderate attraction between polymers and NPs, viscosity trends resemble those in miscible systems. These insights are crucial for designing nanocomposites with tailored flow properties.
 | ||
| Fig. 5 Polymer radius of gyration vs. nanoparticle (NP) diameter and viscosity ratio of nanoparticle blends: (a) experimental data for athermal systems, adapted from ref. 139 and 146. Systems above the solid orange line are predicted to be miscible. The black “viscosity” line represents extrapolated results from simulations. (b) Corresponding data for “thermal” NP–polymer systems. Experimental data points are represented as follows: (□) for η/ηp < 1, (◊) for η/ηp > 1, (○) for η/ηp ≈ 1 at low NP loading, and (Δ) for cases where viscosity (η) initially increases with NP loading and subsequently decreases. Only the viscosity line is displayed, with data from ref. 5, 142 and 147, adapted from ref. 135. | ||
Most studies on PNCs have focused on their bulk properties;148 however, numerous applications utilize them as coatings and thin films.26,125 In such confined systems, the strong confinement effects and the presence of a substrate interface can introduce new aspects that influence viscosity.149–155 Therefore, it is crucial to measure the viscosity of thin films and understand interfacial dynamics to enhance processability and optimize their applications. In bulk systems, oscillating rheometry is the standard technique for viscosity measurements, but for nanoscopic thin films, viscosity measurements are more challenging. X-ray scattering techniques have been employed to determine thin film viscosity; however, these methods face limitations, particularly when dealing with highly loaded particle systems. To address these challenges, Swain et al.87 utilized the AFM-based force–distance technique (discussed in Section 2.3) to extract viscosity and analyze interfacial effects, including segmental changes.
The force–distance curves obtained for PNC films at various temperatures are illustrated in Fig. 6(a) and (b) for both PNC types, with a fixed PGNP volume fraction. Clearly, the reduction in viscosity with increasing temperature affects the force–distance curves, as evidenced by the decrease in both the pull-off force and the curvature of the liquid bridge. The adhesion force and force–distance profile during tip retraction vary with temperature for both f contents, highlighting the influence of f on the shape of the force–distance curves, as seen in Fig. 6(c). To investigate this phenomenon, we modelled the force–distance curves using eqn (17)–(20) and extracted the viscosity of the films. Viscosities for all samples are presented in Fig. 6(d) and (e) as a function of temperature for all volume fractions. As expected, a decrease in viscosity with temperature is observed. PNCs with f = 1 exhibit a significantly higher viscosity than bulk polystyrene (PS), with this difference becoming more pronounced as the volume fraction of PGNPs increases. Conversely, PNCs with f = 0.15 show a viscosity reduction compared to PS. Fig. 6(f) illustrates normalized viscosity as a function of volume fraction at different temperatures. The data reveal distinct pathways of viscosity change, with an increasing ratio for PNCs with f = 1 and a decreasing ratio for those with f = 0.15. The giant increase in the viscosity increase for systems with f = 1 surpasses predictions by the Batchelor–Einstein model.156,157
 | ||
| Fig. 6 Harnessing entropy for controlling the viscosity of PNCs: force–distance curves shift with temperature, showing distinct behavior for samples with (a) f = 0.15 and (b) f = 1; (c) pure PS and high-f PNC samples reveal the impact of filler content on F–D curves at 423 K. Temperature dependent viscosity of (d) f = 1 and (e) f = 0.15 samples at different volume fractions of particles. The open black squares represent the η of bulk PS of molecular weight 19 kDa. In (d), red, green, blue and cyan symbols correspond to ϕp = 0.21, 0.59, 0.77, and 0.90, respectively. In (e), red, green and cyan symbols correspond to ϕp = 0.20, 0.34, and 0.83, respectively. (f) Normalized η for all the PNC samples with respect to the bare PS films, ηPS, as a function of ϕp is shown for both f = 1 (open symbols) and f = 0.15 (closed symbols). Also shown are the predictions of Bactchelor-Einstein equation (continuous black line), WH predictions with χ = 4 (dashed blue lines) and χ = 0.0001 (green dashed lines). (g) η/ηPS as a function of Tg/Tg-PS. The figure is adapted from Swain et al.87 | ||
Our study highlights substantial viscosity enhancements for PNCs with f = 1, supported by enthalpically matched and unentangled chain structures that mitigate the effects of filler attraction and entanglement interactions. Furthermore, our findings align with recent reports on f, attributing anomalous viscosity reduction to an interfacial viscosity lower than the bulk viscosity for lower filler contents.87 The results emphasize the significant impact of f on viscosity due to interfacial entropic interactions between the polymer matrix and grafted chains. The effects are amplified at high ϕp.
As previously discussed, different models, including the Batchelor–Einstein (BE) and Wang–Hill (WH) models, describe viscosity changes in the polymer. The WH model, in particular, predicts a negative intrinsic viscosity due to the presence of an interfacial layer at the nanoparticle (NP)–matrix interface, which exhibits distinct viscosity and density compared to the bulk material. In Fig. 6(f), the blue and dark green dashed lines correspond to the WH model for different interfacial parameter χ12 values, showing both increase and decrease in viscosity. Although varying χ aligns with our findings, the observed viscosity variations are significantly greater. Previous studies141,146,158 have linked viscosity increases to dynamics at reptation length scales, while decreases relate to shorter length scales or segmental-level dynamics influenced by the interface. Our observations indicate both increases and decreases for systems with identical particle–polymer interfaces, prompting us to propose a single mechanism for these viscosity (η) changes. We found that interfacial chain penetration ξ increases with volume fraction (ϕ), indicating a stronger interaction between grafted and matrix monomers at higher f. This emphasizes the need to explore additional experimental parameters sensitive to segmental-level changes. Recognizing that glass transition processes occur at the segmental level, we measured glass transition temperature (Tg).
We correlated changes in Tg with η to illustrate overall behavior, plotting η/ηPS against normalized Tg (=Tg/Tg-PS) in Fig. 6(g). The entire sample set aligns along one master curve, suggesting that segmental dynamics predominantly influence viscosity changes. Lower normalized Tg values indicate reduction in both Tg and η, while higher values correspond to increases in both metrics. Thus, interfacial entropic interactions between PGNPs and matrix polymer chains alter interfacial segmental dynamics, leading to the observed viscosity changes in PNCs.
4.6 Hydrodynamic interactions between the particles in the polymer matrix
Dynamics at the nanoparticle–matrix interfaces often deviate from the bulk. As discussed in the previous sections, our group and others have established the relationship between the control over the interfacial layer (as e.g. via f, σ, and particle size) and deviations in physical properties including glass transition temperature and viscosity.1,136,159,160 Here, we highlight our work quantifying the nature of dynamics and the boundary conditions (quantified via interfacial slip) at the PGNP–polymer interface.43,136 Addressing this aspect, we probed temperature-dependent and confinement-dependent microscopic dynamics by employing CGMD simulations43 and XPCS measurements136 on PNC films made of PGNPs with controlled f and σ.CGMD simulations allowed us to probe the role of interfacial entropy, tuned via f and σ, in the boundary conditions between PGNPs and polymer interfaces.43 The results are summarized in Fig. 7(a) and (b) by plotting the interfacial slip length δ as a function of f and σ. The dewetting interfaces, with small f, result in a large slip, while the wetting interfaces (large f) display a smaller interfacial slip. Clearly, the width of the interfacial layer i.e. extent of matrix chain penetration into the grafted chains controls the slip length. At smaller f, the smaller penetration leads to a larger slip and a larger f results in a larger penetration and consequently smaller slip length as shown in Fig. 7(a). On the other hand, keeping f fixed while increasing the grafting density σ, the δ decreases (Fig. 7(b)), which contradicts the conventional understanding, i.e. a higher grafting density is predicted to exhibit dry brush (due to a lower degree of mixing between graft and matrix chains) and hence a larger slip effect. However, the present behaviour reveals the opposite, meaning larger σ results in smaller δ. This behaviour is due to the effect of the nanoparticle curvature.43 Due to the large curvature (small core radius), we may expect that the grafted chains will experience a progressive decrease in crowding with an increase in the radial distance from the core. Consequently, grafted chains could interpenetrate with the matrix chains for PGNPs with higher σ. Such increased interpenetration might underlie the decrease in δ with increase in σ.
 | ||
Fig. 7 Hydrodynamic interactions at particle–polymer interface: (a) slip length experienced by the particle at the particle–matrix interface as a function of entropic compatibility parameter f; (b) slip length as a function of grafting density. (a) and (b) are extracted from molecular dynamic simulations. (c) Comparison of the renormalized relaxation times for films of thicknesses 65 and 39 nm is shown with respect to the expected scaling of renormalized bulk matrix viscosity. (d) Evolution of  as a function of temperature is shown for a composite film of thicknesses 65 nm (open squares) and 39 nm (open circles). The horizontal dashed-dotted line indicates the expected behavior, in the absence of interfacial effects on the dynamics of nanoparticles. Panels (a) and (b) are adapted from Ibrahim et al.95 Panels (c) and (d) are adapted from Begam et al.136 as a function of temperature is shown for a composite film of thicknesses 65 nm (open squares) and 39 nm (open circles). The horizontal dashed-dotted line indicates the expected behavior, in the absence of interfacial effects on the dynamics of nanoparticles. Panels (a) and (b) are adapted from Ibrahim et al.95 Panels (c) and (d) are adapted from Begam et al.136 | ||
XPCS measurements allowed us to probe the correlations between such interfacial slip and macroscopic viscosity.136 Especially, the temperature dependence of the relaxation time τ, reflecting the microscopic dynamics of PGNPs in polymer thin films of different thicknesses, is probed and compared with the expected temperature dependence of viscosity. Fig. 7(c) summarizes the results of systems with f (=0.033) ≪ 1. Interestingly, compared to the viscosity ratio ηi/η473, the renormalized relaxation time differs significantly while these parameters are expected to be proportional in the absence of the reduced effective interface viscosity. The deviation is clearly visible using the anomaly parameter ζ, defined as the ratio of the normalized τ to normalized η, as shown in Fig. 7(d) (defined in the caption). Clearly, the deviation increases under confinement as well as with decreasing temperature approaching the glass transition of the matrix. These results suggest that the viscosity at the particle polymer interface, i.e. the interfacial viscosity, is significantly different from bulk viscosity. The presence of such interfacial layers with different viscosities is in line with the theoretical model of Servantine and Mueller.138 In addition, the relaxation time had anomalous wavevector q dependence.136 For instance, the relaxation times measured for films of thickness 39 nm revealed q independence, though the Brownian motion of nanoparticles is expected to result in τ ∼ q−2. This suggests that these systems display strong length scale-dependent hydrodynamic interactions due to the presence of an interfacial layer with an interfacial slip. This is interesting as hydrodynamic interactions in polymer melts are expected to be screened within the size of a monomer.
4.7 Fragility of PNCs
The behaviour of glasses near Tg is still a mystery. The relationship between fast-increasing relaxation times and heterogeneous dynamics near Tg is not fully understood. There are various contradicting results in this field. Fragility is a key dynamical parameter used to understand the glass-forming ability of such materials.19,161,162 The notion of fragility was proposed by Angell in 1980s,163 to categorize glass formers into strong and fragile based on the variation of α relaxation time (τα) or viscosity η near Tg. Fragility measures how fast the variation in viscosity changes or alpha relaxation dynamics slows down near Tg when approached from T > Tgi.e.,70,164 | (42) |
For polymer glasses, fragility depends on the strength of inter-particle interactions. A sharp slowing down of dynamics near glass transition temperature for PNCs with small nanoparticles (diameter ≈ 1.8 nm) as compared to conventional nanocomposites with particles of diameters 10–50 nm is reported by Cheng et al.165 The study of the influence of C60 fullerenes on the fragility of PS161 shows that the dynamic fragility of PS increases with C60 content in fresh samples and decreases in annealed PNCs due to agglomeration of fullerenes. Reduction in fragility by reducing the molecular weight of tethered chains is reported in PS-grafted silica nanoparticles.166 The effect of polymer–nanoparticle interactions on the fragility of PNCs is investigated using equilibrium CGMD simulations by Starr and Douglas.19 Simulations suggest that PNCs with non-attractive polymer–nanoparticle interactions are less fragile and those with attractive interactions are more fragile. However, the reduction in fragility with nanoparticle concentration for both attractive and nonattractive nanoparticle interactions is also reported.167 Given this background, in the next section, we discuss work from our group, revealing how an interplay of the film–substrate interface and the PGNP–particle interface controls the viscosity and fragility of PNC thin films.70
As depicted in Fig. 8a and b, in line with the discussions in Section 4.3, CGMD simulations reveal that the NP segregation in the interface layer decreases by increasing entropic compatibility between graft and matrix chains defined by the f parameter. The NP density profile extracted from the simulation studies shows a peak at the interface and the peak height decreases with increasing f (refer to Fig. 8c). XR experiments reveal that the thickness of this adsorbed layer hint decreased with increasing film thickness h (Fig. 8d). Overall, in line with the literature on polymer films,32 the viscosity of the PNC films increased systematically with increasing polymer–substrate interfacial layer thickness, hint. Interestingly, for films with similar hint, the particle–polymer IL played a decisive role in determining the absolute viscosity of the film (Fig. 8e). Upon comparing PNC films with similar hint, films with higher f values (correspondingly larger ξ) displayed higher viscosity. This observation reveals the effect of the subtle interplay of two interfacial layer thicknesses (ξ and hint) on the viscosity of PNC thin films. Similarly, interfacial entropic interactions are found to affect the fragility of polymer films under confinement. The PNC with a smaller ξ (smaller-f) exhibits an increase in fragility with increasing confinement (Fig. 8f). In contrast, both pristine PS and PNCs with a greater ζ (higher-f) become stronger glasses with confinement as measured by their fragility.
 | ||
| Fig. 8 Changes in substrate–polymer interfacial thickness, viscosity and fragility with confinement: snapshots of coarse-grained MD simulations, generated using visual molecular dynamics (VMD), of the PNC systems for (a) small-f (=0.075) and (b) high-f (=0.375). The system consists of PGNPs embedded in a matrix of pure PS chains confined between two walls (green and rose in colour). For clarity in display, matrix polymers are removed from the simulation system. (c) Normalized nanoparticle density profile (with respect to bulk density ρbulk) along the confinement direction xsim estimated from the simulation. (d) Normalized adsorbed layer thickness hint with respect to total thickness h for PS and PNC films with various thicknesses. Schematic of the film structure is shown in the inset. (e) Viscosity, η, at T = 423 K as a function of film-substrate IL, hint, for all the PS and PNC films of various film thicknesses, h, from the experiment. The pink shaded regions indicate the scaling of η with f for approximately similar values of hint. (f) Absolute values of fragility, m, as a function of thickness for pure PS and PNC films with different f values. All the plots are adapted from ref. 70. | ||
5 Interfacial entropic effect on temperature-dependent microscopic structural dynamics
Polymer and PNC melts are known to exhibit a hierarchy of length and time scales, especially showing a variety of relaxation spectra at different length scales. Polymer relaxation processes are typically categorized into three types: alpha-relaxation, beta-relaxation, and gamma-relaxation.170 However, several studies61,171 reveal an intermittent relaxation process that could not be classified into any of the above-mentioned relaxation categories. Upon comparing the measured relation spectra of polystyrene with alpha- and beta-relaxation spectra, Kanaya et al.171 used the terminology fast and slow processes for the experimentally observed relaxation processes. The fast process is associated with the librational motion of phenyl rings of polystyrene, which is coupled with main chain motion near the glass transition temperature. Although the origin of the slow process is not clear, Kanaya et al.171 hypothesised that the slow process is an elementary step of the conformational transition of the main chain.While information on such processes for pure polymers is well established, our knowledge of equivalent features for PNCs remains incomplete. The enthalpic and entropic interactions between embedded nanoparticles (NPs) and polymer matrix chains may yield interesting deviations in the length and time scales corresponding to these ranges of microscopic dynamics. Based on this aspect, here we discuss the length-scale dependent dynamics observed in PNC melts utilizing quasi-elastic neutron scattering.61
For diffusive processes, the microscopic relaxation times τ are expected to follow q−2 scaling with the wave vector. For polymeric systems, the sub-diffusive motion of the segments results in τ ∼ q−2/β, where β is the KWW exponent. This stronger dependence of τ is universal and observed for various polymers and glassformers.172–174 Furthermore, a dynamical crossover from a scaling of q−2/β at low q to q−2 is observed at a critical wave vector qc,172,175 revealing the existence of a cut-off in length scales. Such crossover in q dependence also followed a transition from Gaussian to non-Gaussian dynamics (see ref. 176 and 177 for experiments and simulations on polyisoprene melts). As summarized in Fig. 9, Jhalaria et al.175 reported the presence of similar behaviour in poly(methylacrylate) (PMA) grafted silica nanoparticles. Fig. 9a reveals that the τ of grafted polymers is less than the τ corresponding to ungrafted polymers. This indicates that a grafted chain experiences fewer local constraints than the corresponding pure polymer. Interestingly, qc revealed a non-monotonic dependence with the molecular weight Mg of the grafted polymer (see Fig. 9(b)). In addition, the normalised segmental diffusivity shows a peak value around 61 kDa and these trends are similar to the nonmonotonic behaviour of the diffusion coefficient of CO2 as depicted in Fig. 9(c). This nonmonotonic transport behaviour is explained as a thermodynamic consequence of the CPB-SDPB transition.175
 | ||
| Fig. 9 Local dynamics and nonmonotonic behaviour as a function of graft molecular weight (Mg): (a) comparison of relaxation time for a composite with Mg ≈ 88 kDa (black squares) and a bulk polymer with Mg ≈ 96 kDa (green circles). (b) Crossover wave vectors (qc) for grafted samples and the bulk polymer (gray band). (c) Normalized segmental diffusivity (black circles) and CO2 diffusivity in PGNPs (red symbols) as functions of Mg, showing similar nonmonotonic trends with quantitative differences. The plots are adapted from ref. 175. | ||
Using QENS, we probed the effect of interfacial entropy, characterized by two different f values, on the microscopic dynamics of PS-grafted Au nanoparticle based bulk PNCs.61 The results are summarized in Fig. 10. As depicted in Fig. 10(a), the τ of PNCs with larger f is smaller than that of the pure polymer. In contrast, τ of PNCs with smaller f is found to be larger than that of the neat polymer (Fig. 10(b)). Upon comparing our work with the literature171,178,179 in Fig. 10(c), we find that the relaxation time extracted for PS and PNCs using QENS is probing complex fast dynamics (compared to alpha- and beta-relaxation). Similar to pure polymers176,177 and pure PGNPs,175 a length scale cut off qc, which characterizes the cross-over from Gaussian to non-Gaussian behaviour, is observed in PNC systems as well (small vertical lines in Fig. 10(a) and (b)). Furthermore, the absolute value of qc depends on the temperature and f parameter.
 | ||
| Fig. 10 Length-scale dependent microscopic dynamics of PS and PNCs: comparison of wavevector-dependent relaxation time (τ) for (a) L-PNCs (f = 0.225) and (b) S-PNCs (f = 0.03) with a pristine polymer at T = 410 K. (c) Comparison of temperature-dependent characteristic relaxation times in our work61 with other dynamic processes in PS (measured using different techniques) extracted from the literature.171,178,179 (d) Dynamical crossover wave vector (qc) from Gaussian to non-Gaussian behavior as a function of temperature. Diffusion coefficient (D) as a function of temperature for (e) high-f and (f) low-f compared with the respective pure pristine systems. The plots are adapted from ref. 61. | ||
A comparison of the cross-over wave vector qc between PS and PNC systems reveals the intriguing entropic effect as depicted in Fig. 10(d). Clearly, the qc of high-f samples is higher than that of all other samples, including their pure counterparts, at all temperatures. On the other hand, for low-f cases, qc stays almost the same (until T = 410 K) or lower (T > 410 K) than that of the pure polymer. This reveals an intricate effect of entropic compatibility on the key dynamical features of PNCs. The qc values of pure PGNPs are reported to be lower relative to neat polymers (Fig. 9(b)), indicating that locally diffusive dynamics are apparently persistent to larger length scales in the PGNPs.175 To account for the cross-over of τ from q−2/β to q−2, τ is modelled using a jump-diffusion model (JDM),175,177,180,181 which considers the existence of an underlying distribution of jumps that give rise to the sub-diffusive regime at long times. The variation of τ with q is modeled using,
 | (43) |
 | (44) |
The estimated values of τ0 for PNCs were found to follow the same trend as that of τ, meaning that larger-f (smaller-f) samples have a smaller (larger) relaxation time compared to neat polymers. Furthermore, the normalized scaled diffusion of PMA-grafted nanoparticles showed a non-monotonic trend as a function of Mg as depicted in Fig. 9(c).175 However, in PNCs, the scaled diffusion coefficient D of a lower f sample is higher than that of the neat polymer, whereas that of a higher f sample shows the opposite trend (Fig. 10(e) and (f)). These results indicate the intriguing effect of entropic compatibility on the length scale-dependent dynamics of PNCs.
6 Interfacial entropic effects on the properties of blends
Polymer blends combined with nanoparticles (NPs) are a new class of hybrid functional materials capable of exhibiting tunable novel physical properties.182–184 However, the ability to control the dispersion state of NPs has been a challenge in the development of such materials for their wide range of applications.Given this background, here we discuss our approach182 harnessing the interfacial entropy at a particle–polymer interface in the thermodynamically demixing mixture of polymers – PS and PVME (poly(vinyl methyl ether)). As shown in Fig. 11, the PS and PVME mixture reveals a lower critical solution temperature (LCST) transition. We made films of 60/40 (w/w) ratio of PS and PVME containing PS-grafted gold nanoparticles. The mixture is coated on a silicon substrate. Due to low interfacial tension and preferential affinity, PVME wets both air–polymer and silicon–polymer interfaces and hence enriches the surface. Temperature modulated differential scanning calorimetry reveals variation in both Tg and its breadth in the presence of PS grafted gold nanoparticles (PS-g-nAu). High-magnification AFM images reveal the localization of PS-g-nAu on the PVME phase in the blend. The nanoparticle localization is shown in the phase diagram of the blend in Fig. 11. The expulsion of PS-g-nAu from PS is driven purely by entropic interaction. Despite the PS coating over the gold core, the screening of the core with a short polymer chain is negligible. As a result, enthalpic interaction between PVME and the gold core leads to the localization of nanoparticles in the PVME phase. When the grafted chains are long, PS and nanoparticles experience an entropically favorable interaction producing well-dispersed nanoparticle states in the PS matrix. This result demonstrates that controlling the Mg allows the localization of particles in different domains in polymer blends.
 | ||
| Fig. 11 Interfacial entropy allows controlling phase behavior of blends: phase diagram temperature T vs. weight fraction of PS, capturing the phase separation of PS-PVME. Also shown are schematics for demonstrating the localization of PGNPs in PS or PVME-rich regions controlled via Mg. The figure is adapted from Kar et al.182 | ||
So far we have demonstrated how harnessing the interfacial entropy allows us to control the dispersion of PGNPs, which, in turn, resulted in significant variations in the microscopic dynamics and in various properties and processing parameters including glass transition temperature, fragility and viscosity. In the next section, we highlight how such PGNPs allow accessing new parameter space in applications. While there are various application aspects, we do this by discussing the ability of PGNP membranes to enable efficient gas separation and water desalination.
7 Formation and understanding of PGNP membranes
Ultra-thin functional membranes made using nanoparticles show promise for a variety of uses, including gas and water filtration and flexible electronics and sensors.185–191 These membranes are frequently composed of core–shell nanoparticles, and the degree of nanoparticle ordering and the softness and penetrability of the shell control the mechanical characteristics of these membranes. In this section, we discuss the formation of the PGNP membranes, and the effect of entropic compatibility on their thermal stability.7.1 Preparation of PGNP membranes
PGNP membranes were prepared at the air/water interface in a Langmuir–Blodgett (LB) trough using the following steps.59,60,192 Step 1: a homogeneous solution of PGNPs in chloroform was spread on the water surface using a Hamilton syringe. Due to unfavourable hydrophobic interactions between graft-polymer and water, the thin liquid film decomposes and forms a network of PGNP grains.58,59,192 Step 2: using the Teflon barriers of the LB trough, the monolayer was compressed to obtain a thin dense membrane with a thickness below 10 nm. The typical surface pressure used is 35 mN m−1. Step 3: this PGNP layer was transferred onto different hydrophobic substrates through the horizontal dipping (Langmuir–Schaefer) method. The AFM image of a transferred membrane is given in Fig. 12a. Step 4: these membranes were dried under vacuum for the complete removal of water. | ||
| Fig. 12 Stability of the PGNP membrane: (a)–(c) AFM surface topography of the PGNP membrane on a PS substrate at different temperatures as mentioned in the legends (scale bar: 400 nm). (d) Schematic illustrating PGNP penetration into the PS bottom layer during heating. (e) The penetration depth of PGNPs into PS melts with varying f. The plots are adopted from ref. 58. | ||
7.2 Thermal stability of PGNP membranes
According to recent reports, under ambient circumstances, ultra-thin, freestanding membranes are found to have remarkable mechanical capabilities.193 Nonetheless, in the majority of real-world uses, the membranes are supported by stable substrates and necessitate non-ambient functioning.194 Therefore, it is important to investigate the function of contacts with the underlying substrates and the thermal stability of these ultra-thin nanoparticle-based membranes to fully realize their potential in a variety of applications and enhance their characteristics. Given this background, here we discuss how the thermal stability of PGNP membranes depends on the entropic interactions, defined by f, between the membrane and substrates.59 We made PS grafted gold nanoparticle membranes on PS thin films of thickness h ≈ 80 nm. We probed the temperature-dependent structure of the PGNP membranes in real space using AFM measurements and the penetration of the PGNPs into the films via in situ XR measurements.59 The temperature-induced disordering of PGNP membranes on the PS thin film is summarized Fig. 12a–c. When heated above the Tg of both graft and matrix polymers, membranes lose their granular structure as individual PGNPs penetrate into the underlying polymer substrate as depicted in the schematic in Fig. 12d. Utilizing in situ XR, we show that during heating, penetration of PGNPs from the membrane layer to the substrate polymer layer is f-dependent, indicating the effect of entropic compatibility on facilitating fast PGNP penetration.58 When the PGNP membrane is placed on chemically identical polymer substrates with different levels of entropic compatibility (defined by f), higher PGNP penetration (during heating) is observed at large f (Fig. 12e). As summarized in Fig. 12e, the temperature stability of the membranes increased monotonously with a decrease in f, specifically by changing the molecular weight of the polymers comprising the substrate.58,597.3 Creation of high-density PNCs from PGNP membranes
The penetration of PGNPs, at high temperatures, into the polymer substrates provides a new lever to increase the loading fraction of PGNPs into polymer films. It is conceivable that the subsequent transfer and penetration of the membranes into the polymer substrates would yield an increase in the fraction of dispersed particles in the polymer matrices. This technique could be utilized as an effective tool to create PNCs with a high volume fraction of PGNPs. To utilize this approach, we need to understand the penetration kinetics of PGNPs into the substrates during heating and the interplay of different parameters such as particle size, softness, graft length, etc. Furthermore, nanoparticle penetration is important in various fields starting from targeted nanoparticle-based drug delivery to generating hybrid PNC materials.195–197 By exploring the penetration of PS-grafted Au nanoparticles (PGNPs) into PS films, we show the formation of PNC layers close to the membrane–substrate film interface.58,60 We followed the kinetics of penetration at different temperatures using in situ AFM.60 The penetration of the PGNPs into polymer substrates results in a progressive decrease in the thickness of the membrane, as quantified in Fig. 13(a) and (b). By modelling the time-dependent decrease in the membrane height as an exponential with single relaxation time τp, we quantified the penetration time scales. Fig. 13c summarizes the temperature dependence of τp for systems with two different f values. Clearly, systems with higher entropic compatibility penetrate into the films at a rapid rate. Complementary CGMD simulations support the results as summarized in Fig. 12(d) and (e). These results highlight that f provides a new lever to control the stability of the membranes and the penetration kinetics. We believe these findings could be leveraged to create high-density PNCs that have potential in various membrane-related applications. | ||
| Fig. 13 Penetration kinetics of PGNPs into the substrate film at elevated temperatures: (a) decay of normalized height (h/h0) as a function of waiting time (t/t0) at temperatures near the respective (Tg) for f = 0.06 and f = 1.06. Data (symbols) are fitted with an exponential decay (solid lines). (b) Penetration time τpvs. (T/Tg) for PGNP–PS systems, highlighting differences between f = 0.06 and f = 1.06, controlled by entropic barriers. (c) MD simulations capture the entropic barrier effects. Representative snapshots of simulation boxes are shown for (d) f = 1.06 at (t = 2 × 104τsim) and (e) f = 1.06 at t = 2 × 105τsim. (f) Temporal evolution of the normalized surface density of PGNPs for the PGNP–PS system, adapted from ref. 60. | ||
8 Applications: PGNP membranes for gas separation and water desalination
By harnessing interfacial entropy, we can design PNCs with tailored properties, making them highly effective for applications such as selective membranes for water desalination, and high-performance coatings. The ability to control interfacial entropy provides a powerful tool for engineering next-generation functional materials. Polymer membrane desalination technologies, like reverse osmosis (RO) and nanofiltration (NF), have advanced since the 1960s.198 Membrane performance, often inversely correlated between water permeance and salt rejection, shows a tradeoff and possible upper bound.191,199 Using water permeability and water/salt permeability selectivity for analysis reveals clearer trends. Selectivity is largely driven by diffusivity rather than solubility.Water and salt transport in dense polymeric membranes follows the solution–diffusion mechanism, where small molecules first partition into the polymer matrix and then diffuse across it under a chemical potential gradient.200,201 This process occurs within the free volume of amorphous regions, characterized by high chain mobility.202,203 Studies have shown that modifying free volume properties, through changes in chain mobility or arrangement, influences the permselectivity of gas separation and ion-exchange membranes, which also operate via the solution–diffusion mechanism.204,205 However, the impact of polymer structure on water and salt transport in desalination membranes remains insufficiently explored.191
Understanding this relationship is vital for designing membranes with enhanced selectivity, lower energy costs, and greater longevity. PGNPs have been extensively studied for gas separation, showing improvements that approach the upper bound curve. High-density ultrathin PGNP layers also demonstrate superior thermal and mechanical strength compared to conventional polymer membranes. These enhancements are attributed to the free volume effects and molecular variations in grafted chains175,206–209 shown in Fig. 14. Bilchak et al.206 reported that the free volume distribution of PGNPs can be tuned by adding free polymer chains. Adding short free chains, evenly distributed within the PGNP polymer layer, uniformly reduces gas permeability without significantly enhancing selectivity. In contrast, free chains of similar length to the grafts, which occupy interstitial spaces between PGNPs, selectively hinder larger gas molecules, boosting selectivity by up to two orders of magnitude with only moderate permeability loss for smaller gases. This finding highlights the potential to optimize GNP membranes for selective gas transport by leveraging entropic effects through tailored free polymer addition.206 This work highlights the gas transport behaviour in polymer-grafted nanoparticle (PGNP) membranes, emphasizing the role of the interfacial layer in controlling permeability and selectivity. Fig. 14(A) presents a Robeson plot of CO2/CH4 separation, showing how GNP membranes surpass conventional polymers by manipulating free volume and interfacial interactions. The interfacial layer, formed by grafted polymer chains surrounding nanoparticles, creates a heterogeneous transport medium that enhances gas diffusion. Fig. 14(B) shows the effect of Mg on CO2 permeability, where increased Mg initially enhances free volume and permeability but later leads to chain interpenetration and densification of the interfacial layer, reducing transport efficiency. Fig. 14(C) highlights the reduced aging effects in PMMA GNP membranes, attributed to the constrained motion of polymer chains in the interfacial region, which limits relaxation and densification over time. Fig. 14(D) presents CO2 permeance and CO2/CH4 selectivity as a function of film thickness, showing that thin-film PGNP membranes maintain high performance due to the stabilizing effects of the interfacial layer. Finally, Fig. 14(E) provides a schematic of GNP membranes, where the interfacial layer creates free volume, particularly in the distal regions between nanoparticles, facilitating selective gas transport. Altogether, these figures provide a comprehensive understanding of how polymer grafting, interfacial layers, and nanoparticle structuring influence membrane performance, underpinned by fundamental polymer physics and free volume theory.
 | ||
| Fig. 14 Pure gas transport in PGNP/free chain mixtures: (A) CO2/CH4 Robeson plot of PMA- and PMMA-grafted nanoparticle (NP) membranes under similar conditions. PMA systems include Mg ≈ 100 kDa with “short” (Mfree ≈ 6 kDa) and “long” (Mfree ≈ 96 kDa) free chains. PMMA systems include Mg ≈ 100 kDa with “short” (Mfree ≈ 3 kDa) and “long” (Mfree ≈ 90 kDa) chains. PAn-based composites (Mg ≈ 30 kDa, Mfree ≈ 30 kDa) are also shown. The solid black line represents the 2008 Robeson upper bound. (B) CO2/CH4 selectivity enhancements in PMA–GNP composites (Mg ≈ 100 kDa) with varying Mfree and weight fractions. The neat PMA–GNP (open black square) shows maximum selectivity enhancement at Mfree ≈ 96 kDa. (C) CH4 permeability enhancement in PMA–GNP composites with Mfree ≈ 6 kDa and Mfree ≈ 96 kDa at different ωfree values. Inset: CO2 permeability enhancement. Solid lines represent model fits. (D) Critical ω values (ω*) as a function of gas kinetic diameter (dgas2) in PMA-based composites for two Mfree values. (E) Schematic illustration of gas transport in composite systems: longer free chains (Mfree) segregate to distal regions, hindering larger gas molecules' transport while facilitating smaller molecule diffusion. The figure is adapted from ref. 206. | ||
Inspired by the success of PGNP membranes in gas separation, we explored the applicability of membranes obtained via layer-by-layer assembly, using the Langmuir–Blodgett technique, in water desalination.99 This would be beneficial as such frugal methods could effectively reduce the overall cost of clean water production. We modified polyamide (PA) membranes by coating multilayers of PGNP membranes as captured in the schematic shown in Fig. 15(a). Unlike most current studies focused on conventional surface treatments of PA membranes, this LB approach ensures complete surface coverage, thus paving new pathways for material development. We utilize the equations derived in the section on water desalination membranes to calculate key parameters such as Jw, A, Rs, and the A/B ratio from eqn (22)–(27), enabling a detailed analysis of membrane performance. We observed that the water permeance of these membranes scales inversely with their thickness when comprised of at least three nanoparticle (NP) layers (Fig. 15(b)). Notably, permeability exhibits a maximum performance for an intermediate Mg (refer Fig. 15(c) and (d)). Through osmotic compressibility measurements, we establish that these effects are driven by the non-monotonic relationship between membrane-free volume and Mg, consistent with findings based on gas permeability.206 Given that solvent and solute transport mechanisms differ, our constructs provide independent parameters to control solvent permeance and permselectivity. This offers an alternative route for developing low-cost, energy-efficient water desalination membrane technologies. Additionally, our methodology can be extended to other membrane separation applications, including gas separation, due to the versatility of the LB approach used in fabricating these PGNP multilayers.
 | ||
| Fig. 15 Comparison and innovation in RO membranes: (a) schematic of membrane preparation-pristine PA-TFC to processed membranes with PGNP layers added via the Langmuir–Blodgett (LB) method. (b) Water perm-selectivity (A/B) vs. water permeance (A) for input pressures of 60 psi (closed symbols) and 75 psi (half-open symbols). Membranes with N ≥ 5 and N = 4 at 75 psi exceed the empirical upper bound for RO membranes (dashed line). Tests were conducted with 2000 ppm NaCl at 25 °C and 60 psi. Higher transfer pressure (Π) improves A/B, indicating it as a key parameter alongside Mg, N, and input pressure. (c) Histogram of salt rejection (RS) and water flux (Jw) for M-PA membranes with varying layer numbers (N). (d) Comparison plot of water perm-selectivity (A/B) versus water permeance (A) for various membrane types, highlighting the enhanced performance and novelty of the modified PA membrane with PGNP layers. (e) Dependence of κf on Π for Langmuir monolayers of all PGNPs. (f) Water permeance (A) of the PNC-modified PA membrane Mg, for N = 5 layers of PGNPs, adapted from ref. 99. | ||
As illustrated in Fig. 15(c), membranes with one NP layer exhibit water permeance comparable to that of the PA layer, likely due to layer imperfections (“pin holes”). In contrast, membranes exceeding three NP layers demonstrate a permeance that decreases inversely with PGNP membrane thickness, aligning with expectations from the solution diffusion model.97,210 Furthermore, for membranes with five NP layers, permeance reaches a maximum near an average molecular weight (Mg) of approximately 88 kDa, echoing trends observed in gas permeability for similar materials Fig. 15(e). To understand the non-monotonicity, we probed the membrane compressibility characteristics, defined by κf (summarized in Fig. 15(e)). Careful examination of the curves for the three grafting molecular weights reveals that at Π = 35 mN m−1, the compressibility factor (κf) is minimized for the M-PGNP configuration (Fig. 15(c)–(d)). From standard thermodynamic principles, κf is an inverse measure of density fluctuations and thus relates to available free volume. This indicates that among equally compact PGNP layers, as captured in Fig. 15(f), for a fixed number of layers, the permeance A exhibits a non-monotonic dependence on the graft molecular weight, peaking around a specific molecular weight. This behavior is ascribed to variations in free volume within the interfacial layer, as indicated by the osmotic compressibility modulus (κf). The lowest κf, which suggests maximal free volume and consequently higher water flux (Jw), is observed for the intermediate graft molecular weight. The lowest κf, indicating maximal free volume and thus higher water flux, is observed for the intermediate graft molecular weight. This finding aligns with previous studies on gas transport,206,208 confirming that enhanced free volume facilitates solvent transport. This work summarizes that by tuning the Mg and layer thickness, membrane performance can be optimized, offering a strategy for improving water permeance while maintaining high selectivity in desalination applications.99 The interplay between free volume and the emergent properties of membranes highlights their transformative potential as a design principle. This intrinsic property links the microscopic dynamics of glass-forming systems with macroscopic functionalities, enabling the rational tuning of membrane selectivity, permeability, and stability. By leveraging the principles of free volume, researchers can navigate the intricate physics of polymer dynamics to develop next-generation membranes for critical applications in gas separation, water purification, and beyond, underscoring the profound synergy between condensed matter physics and materials engineering.
9 Perspectives
In this review, we emphasize the pivotal role of the nanoparticle–polymer interface in defining the flow, thermal, mechanical, optical, and electrical properties of polymer PNCs. The interplay between enthalpic and entropic interactions at this interface fundamentally differentiates the behaviour of PNCs, particularly when comparing conventional composites to those based on PGNPs. The structure and properties of the interfacial layer (IL) in enthalpic PNCs are influenced primarily by NP–polymer interactions and the molecular weight of the matrix polymer. Conversely, in PGNP-based entropic PNCs, parameters such as the molecular weight ratio f, grafting density, and NP size dictate the IL properties, entropic interactions, and ultimately, the dispersion and performance of the composite material. A key insight is the ability to control the microscopic parameter ξ, representing matrix chain penetration depth, through variations in f. This parameter not only modulates the entropic interactions but also governs the dispersion state of PNCs, enabling tailored material properties. For entropic PNCs, the well-dispersed and stable composites achievable even at high particle fractions offer unique opportunities to enhance physical properties, such as glass transition temperature, viscosity, and dynamic heterogeneity. The versatility of the f-parameter, which can control chain penetration, underscores its central role in designing advanced PNC materials.When applied to confined systems, such as thin films or coatings, the dynamics become more complex due to the presence of a second interface between the film and substrate. Notably, the dynamical properties of PNC thin films are influenced by the interplay between two critical interfaces: (a) the PGNP–polymer interface, characterized by ξ, and (b) the substrate–polymer interface, defined by the thickness of the adsorbed layer (hint). These two parameters can be independently tuned through variations in grafted chain size and film processing conditions, offering a pathway to systematically modulate viscosity, fragility, and other dynamical properties under confinement.
In the domain of polymeric membranes for gas separation and water desalination, the chain penetration between the grafted polymer layers on adjacent PGNPs emerges as a decisive factor in controlling parameters like porosity and free volume, which plays a very important role in improving separation efficiency. The non-monotonic behaviour of gas separation efficiency observed in these systems highlights the intricate relationship between graft molecular weight and membrane free volume. Specifically, the inverse dependence of density fluctuations (κf) on free volume aligns with enhanced water flux (Jw) and selective gas permeability, providing novel insights into the design of energy-efficient separation technologies. By decoupling the transport mechanisms for solvents and solutes, PGNP membranes offer independent control over solvent permeance and permselectivity, paving the way for innovative, low-cost solutions in membrane applications.
Overall, this review illustrates how precise manipulation of NP–polymer interfaces, grafting parameters, and interfacial dynamics can enable transformative advances in PNC applications. The modular nature of these systems holds immense potential for breakthroughs in sustainability-focused technologies, including high-performance gas separation and water desalination membranes. Future investigations into the effects of graft chemistry, hydrophobicity, and density could further deepen our understanding and drive the next generation of tailored nanocomposite materials.
Looking ahead, a key challenge is leveraging entropic effects at PGNPs interfaces to design materials with tailored properties. The discussions in this review focused on the equilibrium phase behaviour of polymer nanoparticle mixtures. However, polymers and polymer nanocomposites are often processed at rapid rates and elevated temperatures. Several experiments suggest that the subsequent quenching to lower temperatures may freeze polymers in non-equilibrium conditions.211–213 Such nonequilibrated polymers display a rich range of structure formation processes and properties beyond the predictions of the equilibrium framework.211–213 Furthermore, external fields like temperature (heating and cooling of composites) could introduce additional contributions to the free energy, thereby allowing the control of the dispersion of PGNPs. For instance, we revealed57 that elevated temperatures enhance the dispersion of PGNPs in otherwise immiscible systems. Similarly, any dynamic changes invoking new contributions to free energy could allow the harnessing of the dispersion behaviour of PGNPs. Thus, efforts focusing on understanding the phase behaviour of nanoparticles in nonequilibrium conditions, involving processing and external fields, could provide new avenues to control the dispersion of particles in polymer matrices. This, in turn, could allow tuning the desired properties of PNCs in a controlled manner. On the other hand, phase separation phenomena, such as those in bicontinuous interfacially jammed emulsions (Bijels), offer opportunities to create interconnected networks with tunable mechanical and transport properties. The interplay between grafted polymer chains and the matrix introduces entropic constraints that influence phase behaviour and stability. By exploring how grafting density, molecular weight ratio, and nanoparticle size affect interfacial entropic interactions, researchers can develop PGNP-based materials with enhanced phase stability, hierarchical structures, and adaptive properties. Such advances could enable breakthroughs in energy storage, filtration, catalysis, and responsive coatings, while also deepening our understanding of polymer dynamics in confined environments.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Venkat Padmanabhan (Materials Design and Discovery, Avery Dennison, 8080 Norton Parkway Mentor, Ohio 44060, USA) and Mohd Ibrahim (Technical University of Munich, Germany) for their contributions to molecular dynamics (MD) simulations. We also extend our gratitude to Suryasarathi Bose (Department of Materials Engineering, Indian Institute of Science, Bangalore, India), Sanat K. Kumar (Department of Chemical Engineering, Columbia University, New York, USA), Brian C. Benicewicz (Department of Chemistry and Biochemistry, University of South Carolina, Columbia, SC, USA), Michael Sprung (Deutsches Elektronen-Synchrotron, Hamburg, Germany) and Victoria García Sakai (ISIS Neutron and Muon Source, Rutherford Appleton Laboratory, Chilton, Oxfordshire OX11 0QX, UK) for their valuable suggestions, experimental data collection and analysis guidance, and insightful discussions. S. C. acknowledges funding from the Kotak School of Sustainability (KSS), IIT Kanpur via DORA/2023508C.Notes and references
- S. K. Kumar, B. C. Benicewicz, R. A. Vaia and K. I. Winey, Macromolecules, 2017, 50, 714–731 CrossRef CAS.
- P. F. Green, Soft Matter, 2011, 7, 7914–7926 RSC.
- Z. Zhang, N. Marioni, H. S. Sachar and V. Ganesan, ACS Macro Lett., 2023, 12, 1351–1357 CrossRef CAS PubMed.
- P. Akcora, S. K. Kumar, J. Moll, S. Lewis, L. S. Schadler, Y. Li, B. C. Benicewicz, A. Sandy, S. Narayanan and J. Ilavsky, et al. , Macromolecules, 2010, 43, 1003–1010 CrossRef CAS.
- S. Y. Kim and C. F. Zukoski, Soft Matter, 2012, 8, 1801–1810 RSC.
- A. Milchev, S. A. Egorov, D. A. Vega, K. Binder and A. Nikoubashman, Macromolecules, 2018, 51, 2002–2016 CrossRef CAS.
- B. Cappella and D. Silbernagl, Thin Solid Films, 2008, 516, 1952–1960 CrossRef CAS.
- M. R. Bockstaller and E. L. Thomas, J. Phys. Chem. B, 2003, 107, 10017–10024 CrossRef CAS.
- A. P. Holt, V. Bocharova, S. Cheng, A. M. Kisliuk, B. T. White, T. Saito, D. Uhrig, J. P. Mahalik, R. Kumar and A. E. Imel, et al. , ACS Nano, 2016, 10, 6843–6852 CrossRef CAS PubMed.
- C.-C. Lin, P. J. Griffin, H. Chao, M. J. Hore, K. Ohno, N. Clarke, R. A. Riggleman, K. I. Winey and R. J. Composto, J. Chem. Phys., 2017, 146, 203332 CrossRef PubMed.
- P. Choudhury, S. Dinda and P. K. Das, Soft Matter, 2020, 16, 27–53 RSC.
- M. Zafar, S. M. Imran, I. Iqbal, M. Azeem, S. Chaudhary, S. Ahmad and W. Y. Kim, Results Phys., 2024, 107655 CrossRef.
- J. Jancar, J. F. Douglas, F. W. Starr, S. Kumar, P. Cassagnau, A. Lesser, S. S. Sternstein and M. Buehler, Polymer, 2010, 51, 3321–3343 CrossRef CAS.
- A. C. Balazs, T. Emrick and T. P. Russell, Science, 2006, 314, 1107–1110 CrossRef CAS PubMed.
- L. M. Hall, B. J. Anderson, C. F. Zukoski and K. S. Schweizer, Macromolecules, 2009, 42, 8435–8442 CrossRef CAS.
- T. B. Martin, P. M. Dodd and A. Jayaraman, Phys. Rev. Lett., 2013, 110, 018301 CrossRef PubMed.
- S. T. Gobena and A. D. Woldeyonnes, Discover Mater., 2024, 4, 52 CrossRef CAS.
- H. Jamil, M. Faizan, M. Adeel, T. Jesionowski, G. Boczkaj and A. Balčiūnaitė, Molecules, 2024, 29, 1267 CrossRef CAS PubMed.
- F. W. Starr and J. F. Douglas, Phys. Rev. Lett., 2011, 106, 115702 CrossRef PubMed.
- A. Bansal, H. Yang, C. Li, B. C. Benicewicz, S. K. Kumar and L. S. Schadler, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2944–2950 CrossRef CAS.
- S. K. Kumar and R. Krishnamoorti, Ann. Rev. Chem. Biomol. Eng., 2010, 1, 37–58 CrossRef CAS PubMed.
- M. E. Mackay, A. Tuteja, P. M. Duxbury, C. J. Hawker, B. Van Horn, Z. Guan, G. Chen and R. Krishnan, Science, 2006, 311, 1740–1743 CrossRef CAS PubMed.
- R. Teijido, L. Ruiz-Rubio, A. G. Echaide, J. L. Vilas-Vilela, S. Lanceros-Mendez and Q. Zhang, Prog. Org. Coat., 2022, 163, 106684 CrossRef CAS.
- H. D. Wagner and R. A. Vaia, Mater. Today, 2004, 7, 38–42 CrossRef CAS.
- S. C. Tjong, Mater. Sci. Eng., R, 2006, 53, 73–197 CrossRef.
- S. Sharma, P. Sudhakara, A. A. B. Omran, J. Singh and R. Ilyas, Polymers, 2021, 13, 2898 CrossRef CAS PubMed.
- S. Ghosh and J. F. Douglas, J. Chem. Phys., 2024, 160, 104903 CrossRef CAS PubMed.
- R. A. Riggleman, G. Toepperwein, G. J. Papakonstantopoulos, J.-L. Barrat and J. J. de Pablo, J. Chem. Phys., 2009, 130, 244903 CrossRef PubMed.
- M. Z. Rong, M. Q. Zhang and W. H. Ruan, Mater. Sci. Technol., 2006, 22, 787–796 CrossRef CAS.
- M. A. Ashraf, W. Peng, Y. Zare and K. Y. Rhee, Nanoscale Res. Lett., 2018, 13, 1–7 CrossRef CAS PubMed.
- Y. Yang, H. Tian, S. Napolitano and B. Zuo, Prog. Polym. Sci., 2023, 144, 101725 CrossRef CAS.
- S. Napolitano, Soft Matter, 2020, 16, 5348–5365 RSC.
- S. K. Kumar, N. Jouault, B. Benicewicz and T. Neely, Macromolecules, 2013, 46, 3199–3214 CrossRef CAS.
- J. Liu, L. Zhang, D. Cao and W. Wang, Phys. Chem. Chem. Phys., 2009, 11, 11365–11384 RSC.
- X. Zhang, X. Yan, Q. He, H. Wei, J. Long, J. Guo, H. Gu, J. Yu, J. Liu and D. Ding, et al. , ACS Appl. Mater. Interfaces, 2015, 7, 6125–6138 CrossRef CAS PubMed.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos and V. Pryamitsyn, et al. , Nat. Mater., 2009, 8, 354–359 CrossRef CAS PubMed.
- M. Willinger and E. Reimhult, J. Phys. Chem. B, 2021, 125, 7009–7023 CrossRef CAS PubMed.
- M. A. Sattar, ChemistrySelect, 2021, 6, 5068–5096 CrossRef CAS.
- S. Bhadauriya, X. Wang, A. Nallapaneni, A. Masud, Z. Wang, J. Lee, M. R. Bockstaller, A. M. Al-Enizi, C. H. Camp Jr and C. M. Stafford, et al. , Nano Lett., 2021, 21, 1274–1281 CrossRef CAS PubMed.
- Y. Sui, Y. Cui, X. Meng and Q. Zhou, J. Appl. Polym. Sci., 2022, 139, 52096 CrossRef CAS.
- A. Swain, N. Das A, N. Begam, A. Bhattacharyya, J. Basu, S. Chandran and M. Sprung, APS March Meeting Abstracts, 2021, pp. Y63–008.
- S. Chandran, N. Begam and J. K. Basu, J. Appl. Phys., 2014, 116, 222203 CrossRef.
- M. Ibrahim, N. Begam, V. Padmanabhan and J. Basu, Soft Matter, 2018, 14, 6076–6082 RSC.
- X. Dai, C. Hou, Z. Xu, Y. Yang, G. Zhu, P. Chen, Z. Huang and L.-T. Yan, Entropy, 2019, 21, 186 CrossRef CAS PubMed.
- G. G. Vogiatzis and D. N. Theodorou, Arch. Comput. Methods Eng., 2018, 25, 591–645 CrossRef PubMed.
- T. V. Ndoro, E. Voyiatzis, A. Ghanbari, D. N. Theodorou, M. C. Böhm and F. Müller-Plathe, Macromolecules, 2011, 44, 2316–2327 CrossRef CAS.
- A. Tuteja, P. M. Duxbury and M. E. Mackay, Phys. Rev. Lett., 2008, 100, 077801 CrossRef PubMed.
- D. Dukes, Y. Li, S. Lewis, B. Benicewicz, L. Schadler and S. K. Kumar, Macromolecules, 2010, 43, 1564–1570 CrossRef CAS.
- R. Zhang, B. Lee, C. M. Stafford, J. F. Douglas, A. V. Dobrynin, M. R. Bockstaller and A. Karim, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2462–2467 CrossRef CAS PubMed.
- A. J. Chancellor, B. T. Seymour and B. Zhao, Anal. Chem., 2019, 91, 6391–6402 CrossRef CAS PubMed.
- N. Tsubokawa, Polym. J., 2007, 39, 983–1000 CrossRef CAS.
- B. V. Tawade, M. Singh, I. E. Apata, J. Veerasamy, N. Pradhan, A. Karim, J. F. Douglas and D. Raghavan, JACS Au, 2023, 3, 1365–1375 CrossRef CAS PubMed.
- C. K. Yee, R. Jordan, A. Ulman, H. White, A. King, M. Rafailovich and J. Sokolov, Langmuir, 1999, 15, 3486–3491 CrossRef CAS.
- S. Chandran, N. Begam, V. Padmanabhan and J. K. Basu, Nat. Commun., 2014, 5, 3697 CrossRef PubMed.
- S. Chandran, J. K. Basu and M. K. Mukhopadhyay, J. Chem. Phys., 2013, 138, 014902 CrossRef PubMed.
- S. Chandran and J. K. Basu, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 1–5 CrossRef PubMed.
- N. Begam, S. Chandran, N. Biswas and J. K. Basu, Soft Matter, 2015, 11, 1165–1173 RSC.
- N. A. Das, A. Swain, N. Begam, A. Bhattacharyya and J. K. Basu, Macromolecules, 2020, 53, 8674–8682 CrossRef.
- N. Das, N. Begam, S. Chandran, A. Swain, M. Sprung and J. K. Basu, Soft Matter, 2020, 16, 1117–1124 RSC.
- A. Swain, N. A. Das, S. Chandran and J. K. Basu, Soft Matter, 2022, 18, 1005–1012 RSC.
- A. Swain, N. Das, V. G. Sakai and J. K. Basu, Soft Matter, 2023, 19, 5396–5404 RSC.
- S. Minko, Polymer Surfaces and Interfaces, Springer, 2008, pp. 215–234 Search PubMed.
- J. Wong, C. J. Barrett and L. Reven, Langmuir, 2025, 41, 5782–5793 CrossRef CAS PubMed.
- A. L. Mohamed, M. E. El-Naggar and A. G. Hassabo, J. Mater. Res. Technol., 2021, 12, 542–554 CrossRef CAS.
- M. Tolan and M. Tolan, X-ray scattering from soft-matter thin films: materials science and basic research, Springer, 1999, vol. 148 Search PubMed.
- J. Daillant and A. Gibaud, X-ray and neutron reflectivity: principles and applications, Springer, 2008, vol. 770 Search PubMed.
- S. K. Sinha, Z. Jiang and L. B. Lurio, Adv. Mater., 2014, 26, 7764–7785 CrossRef CAS PubMed.
- G. Grübel and F. Zontone, J. Alloys Compd., 2004, 362, 3–11 CrossRef.
- F. Lehmkühler, W. Roseker and G. Grübel, Appl. Sci., 2021, 11, 6179 CrossRef.
- N. Das, N. Begam, M. Ibrahim, S. Chandran, V. Padmanabhan, M. Sprung and J. K. Basu, Nanoscale, 2019, 11, 8546–8553 RSC.
- A. Madsen, R. L. Leheny, H. Guo, M. Sprung and O. Czakkel, New J. Phys., 2010, 12, 055001 CrossRef.
- L. B. Lurio, G. M. Thurston, Q. Zhang, S. Narayanan and E. M. Dufresne, Synchrotron Radiat., 2021, 28, 490–498 CrossRef CAS PubMed.
- J. Song, Q. Zhang, F. de Quesada, M. H. Rizvi, J. B. Tracy, J. Ilavsky, S. Narayanan, E. Del Gado, R. L. Leheny and N. Holten-Andersen, et al. , Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2201566119 CrossRef CAS PubMed.
- Q. Berrod, K. Lagrené, J. Ollivier and J.-M. Zanotti, Z. Phys. Chem., 2010, 224, 5–32 CrossRef.
- J. P. Embs, F. Juranyi and R. Hempelmann, Z. Phys. Chem., 2010, 224, 5–32 CrossRef CAS.
- K. Aomura, Y. Yasuda, T. Yamada, T. Sakai and K. Mayumi, Soft Matter, 2023, 19, 147–152 RSC.
- J. Colmenero and A. Arbe, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 87–113 CrossRef CAS.
- E. J. Bailey and K. I. Winey, Prog. Polym. Sci., 2020, 105, 101242 CrossRef CAS.
- N. C. Osti, N. H. Jalarvo and E. Mamontov, Mater. Horiz., 2024, 11, 4535–4572 RSC.
- J. R. D. Copley and T. J. Udovic, J. Res. Natl. Inst. Stand. Technol., 1993, 98, 71 CrossRef CAS PubMed.
- M. Bée, Chem. Phys., 2003, 292, 121–141 CrossRef.
- D. Tranchida, Z. Kiflie, S. Acierno and S. Piccarolo, Meas. Sci. Technol., 2009, 20, 095702 CrossRef.
- G. Stan and S. W. King, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2020, 38, 060801 CAS.
- J. R. Withers and D. E. Aston, Adv. Colloid Interface Sci., 2006, 120, 57–67 CrossRef CAS PubMed.
- E. Finot, A. Passian and T. Thundat, Sensors, 2008, 8, 3497–3541 CrossRef PubMed.
- Y. M. Efremov, T. Okajima and A. Raman, Soft Matter, 2020, 16, 64–81 RSC.
- A. Swain, N. Begam, S. Chandran, M. Bobji and J. K. Basu, Soft Matter, 2020, 16, 4065–4073 RSC.
- B. Capella, P. Baschieri, C. Frediani, P. Miccoli and C. Ascoli, IEEE Eng. Med. Biol. Mag., 1997, 16, 58–65 CrossRef PubMed.
- H.-J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152 CrossRef CAS.
- O. Pitois, P. Moucheront and X. Chateau, J. Colloid Interface Sci., 2000, 231, 26–31 CrossRef CAS PubMed.
- S. Cai and B. Bhushan, Nanotechnology, 2007, 18, 465704 CrossRef PubMed.
- H. Kim, A. Rühm, L. B. Lurio, J. K. Basu, J. Lal, D. Lumma, S. G. J. Mochrie and S. K. Sinha, Phys. Rev. Lett., 2003, 90, 068302 CrossRef PubMed.
- D. J. Plazek and V. M. O'Rourke, J. Polym. Sci., Part A-2, 1971, 9, 209–243 CrossRef CAS.
- C. Li, T. Koga, C. Li, J. Jiang, S. Sharma, S. Narayanan, L. B. Lurio, X. Hu, X. Jiao, S. K. Sinha, S. Billet, D. Sosnowik, H. Kim, J. C. Sokolov and M. H. Rafailovich, Macromolecules, 2005, 38, 5144–5151 CrossRef CAS.
- M. Ibrahim, N. Begam, V. Padmanabhan and J. K. Basu, Soft Matter, 2018, 14, 6076–6082 RSC.
- L. Wang, T. Cao, J. E. Dykstra, S. Porada, P. Biesheuvel and M. Elimelech, Environ. Sci. Technol., 2021, 55, 16665–16675 CrossRef CAS PubMed.
- J. G. Wijmans and R. W. Baker, J. Membr. Sci., 1995, 107, 1–21 CrossRef CAS.
- J. G. Wijmans and R. W. Baker, Mater. Sci. Membr. Gas Vap. Sep., 2006, 1, 159–189 Search PubMed.
- A. Swain, S. Adarsh, A. Biswas, S. Bose, B. C. Benicewicz, S. K. Kumar and J. K. Basu, Nanoscale, 2023, 15, 11935–11944 RSC.
- M. R. Begley, D. S. Gianola and T. R. Ray, Science, 2019, 364, eaav4299 CrossRef CAS PubMed.
- A. Jayaraman, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 524–534 CrossRef CAS.
- J. C. Foster, S. C. Radzinski and J. B. Matson, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 2865–2876 CrossRef CAS.
- F. L. Verso, L. Yelash, S. A. Egorov and K. Binder, J. Chem. Phys., 2011, 135, 244701 CrossRef PubMed.
- M. J. A. Hore, L. T. J. Korley and S. K. Kumar, J. Appl. Phys., 2020, 128, 030401 CrossRef CAS.
- H. He, X. Shen and Z. Nie, Prog. Polym. Sci., 2023, 101710 CrossRef CAS.
- W. Wu, M. Singh, A. Masud, X. Wang, A. Nallapaneni, Z. Xiao, Y. Zhai, Z. Wang, T. Terlier and M. Bleuel, et al. , ACS Nano, 2021, 15, 12042–12056 CrossRef CAS PubMed.
- C. N. Likos, Soft Matter, 2006, 2, 478–498 RSC.
- C. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450 CrossRef CAS.
- C. N. Likos, Phys. Rep., 2001, 348, 267–439 CrossRef CAS.
- Ł. Baran and S. Sokołowski, J. Chem. Phys., 2017, 147, 044903 CrossRef PubMed.
- W. Wu, W. Wang and J. Li, Prog. Polym. Sci., 2015, 46, 55–85 CrossRef CAS.
- P. A. Tikhonov, N. G. Vasilenko and A. M. Muzafarov, Dokl. Chem., 2021, 1–17 CrossRef CAS.
- D. Vlassopoulos, G. Fytas, T. Pakula and J. Roovers, J. Phys.: Condens. Matter, 2001, 13, R855 CrossRef CAS.
- J. M. Ren, T. G. McKenzie, Q. Fu, E. H. Wong, J. Xu, Z. An, S. Shanmugam, T. P. Davis, C. Boyer and G. G. Qiao, Chem. Rev., 2016, 116, 6743–6836 CrossRef CAS PubMed.
- S. Srivastava, S. Chandran, A. K. Kandar, C. K. Sarika, J. K. Basu, S. Narayanan and A. Sandy, J. Chem. Phys., 2010, 133, 151105 CrossRef CAS PubMed.
- L. R. Hutchings and R. W. Richards, Macromolecules, 1999, 32, 880–891 CrossRef CAS.
- M. Daoud and J. P. Cotton, J. Phys., 1982, 43, 531–538 CrossRef CAS.
- J. K. Basu, J. C. Boulliard, B. Capelle, J. Daillant, P. Guenoun, J. W. Mays and J. Yang, Macromolecules, 2007, 40, 6333–6339 CrossRef CAS.
- J. D. Thomin, P. Keblinski and S. K. Kumar, Macromolecules, 2008, 41, 5988–5991 CrossRef CAS.
- D. Sunday, J. Ilavsky and D. L. Green, Macromolecules, 2012, 45, 4007–4011 CrossRef CAS.
- Y. Wang, J. Chen, C. Zhu, B. Zhu, S. Jeong, Y. Yi, Y. Liu, J. Fiadorwu, P. He and X. Ye, Nano Lett., 2021, 21, 5053–5059 CrossRef CAS PubMed.
- I. Borukhov and L. Leibler, Macromolecules, 2002, 35, 5171–5182 CrossRef CAS.
- P. G. Ferreira, A. Ajdari and L. Leibler, Macromolecules, 1998, 31, 3994–4003 CrossRef CAS.
- A. Arceo, L. Meli and P. F. Green, Nano Lett., 2008, 8, 2271–2276 CrossRef CAS PubMed.
- A. Bansal, H. Yang, C. Li, K. Cho, B. C. Benicewicz, S. K. Kumar and L. S. Schadler, Nat. Mater., 2005, 4, 693–698 CrossRef CAS PubMed.
- D. M. Trombly and V. Ganesan, J. Chem. Phys., 2010, 133, 154904 CrossRef PubMed.
- B. Natarajan, T. Neely, A. Rungta, B. C. Benicewicz and L. S. Schadler, Macromolecules, 2013, 46, 4909–4918 CrossRef CAS.
- A. Hariharan, S. K. Kumar, M. H. Rafailovich, J. Sokolov, X. Zheng, D. Duong, S. A. Schwarz and T. P. Russell, J. Chem. Phys., 1993, 99, 656–663 CrossRef CAS.
- D. Cangialosi, A. Alegria and J. Colmenero, Prog. Polym. Sci., 2016, 54, 128–147 CrossRef.
- L. Berthier and G. Biroli, Rev. Mod. Phys., 2011, 83, 587–645 CrossRef CAS.
- G. B. McKenna and S. L. Simon, Macromolecules, 2017, 50, 6333–6361 CrossRef CAS.
- F. Ondreas, P. Lepcio, M. Zboncak, K. Zarybnicka, L. E. Govaert and J. Jancar, Macromolecules, 2019, 52, 6250–6259 CrossRef CAS.
- A. Ghanekarade, A. D. Phan, K. S. Schweizer and D. S. Simmons, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104398118 CrossRef CAS PubMed.
- S. Y. Kim, H. W. Meyer, K. Saalwaächter and C. F. Zukoski, Macromolecules, 2012, 45, 4225–4237 CrossRef CAS.
- J. T. Kalathi, G. S. Grest and S. K. Kumar, Phys. Rev. Lett., 2012, 109, 198301 CrossRef PubMed.
- N. Begam, S. Chandran, M. Sprung and J. K. Basu, Macromolecules, 2015, 48, 6646–6651 CrossRef CAS.
- G. Batchelor, J. Fluid Mech., 1976, 74, 1–29 CrossRef.
- J. Servantie and M. Müller, Phys. Rev. Lett., 2008, 101, 026101 CrossRef CAS PubMed.
- M. E. Mackay, T. T. Dao, A. Tuteja, D. L. Ho, B. Van Horn, H.-C. Kim and C. J. Hawker, Nat. Mater., 2003, 2, 762–766 CrossRef CAS PubMed.
- M. Wang and R. J. Hill, Soft Matter, 2009, 5, 3940–3953 RSC.
- E. Senses, C. L. Kitchens and A. Faraone, J. Polym. Sci., 2022, 60, 1130–1150 CrossRef CAS.
- K. Nusser, G. J. Schneider, W. Pyckhout-Hintzen and D. Richter, Macromolecules, 2011, 44, 7820–7830 CrossRef CAS.
- G. K. Batchelor, J. Fluid Mech., 1970, 44, 419–440 CrossRef.
- A. L. Kholodenko and J. F. Douglas, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 1081 CrossRef CAS PubMed.
- J. T. Edward, J. Chem. Educ., 1970, 47, 261 CrossRef CAS.
- A. Tuteja, M. E. Mackay, C. J. Hawker and B. Van Horn, Macromolecules, 2005, 38, 8000–8011 CrossRef CAS.
- S. Jain, J. G. P. Goossens, G. W. Peters, M. van Duin and P. J. Lemstra, Soft Matter, 2008, 4, 1848–1854 RSC.
- J. Midya, M. Rubinstein, S. K. Kumar and A. Nikoubashman, ACS Nano, 2020, 14, 15505–15516 CrossRef CAS PubMed.
- J. F. Pressly, R. A. Riggleman and K. I. Winey, Macromolecules, 2019, 52, 6116–6125 CrossRef CAS.
- A. C. Zhang, K. Ohno and R. J. Composto, Macromolecules, 2024, 57, 6634–6645 CrossRef CAS.
- Z. Yang, X. Xu, J. F. Douglas and W.-S. Xu, J. Chem. Phys., 2024, 160, 044503 CrossRef CAS PubMed.
- A. Nikoubashman, J. Chem. Phys., 2021, 154(9), 090901 CrossRef CAS PubMed.
- G. Catalini, N. A. Garca, D. A. Vega and A. Nikoubashman, Macromolecules, 2024, 57, 2530–2538 CrossRef CAS.
- N. H. Nemati, K. R. Moghadam and N. Afra, Polymer Nanocomposite Films and Coatings, Elsevier, 2024, pp. 71–101 Search PubMed.
- S. Devasahayam and C. M. Hussain, Sustainable Mater. Technol., 2020, 26, e00233 CrossRef CAS.
- L.-H. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2011, 44, 7853–7863 CrossRef CAS PubMed.
- T. Kataoka, T. Kitano, M. Sasahara and K. Nishijima, Rheol. Acta, 1978, 17, 149–155 CrossRef CAS.
- C. Ye, C. G. Wiener, M. Tyagi, D. Uhrig, S. V. Orski, C. L. Soles, B. D. Vogt and D. S. Simmons, Macromolecules, 2015, 48, 801–808 CrossRef CAS.
- N. Begam, N. Das, S. Chandran, M. Ibrahim, V. Padmanabhan, M. Sprung and J. K. Basu, Soft Matter, 2018, 14, 8853–8859 RSC.
- S. Srivastava and J. K. Basu, Phys. Rev. Lett., 2007, 98, 165701 CrossRef CAS PubMed.
- A. Sanz, H. C. Wong, A. J. Nedoma, J. F. Douglas and J. T. Cabral, Polymer, 2015, 68, 47–56 CrossRef CAS.
- Z. Ma, H. Nie, J. Yan and O. K. Tsui, J. Chem. Phys., 2023, 159, 224905 CrossRef CAS PubMed.
- C. A. Angell, J. Non-Cryst. Solids, 1985, 73, 1–17 CrossRef CAS.
- R. Böhmer, K. L. Ngai, C. A. Angell and D. J. Plazek, J. Chem. Phys., 1993, 99, 4201–4209 CrossRef.
- S. Cheng, S.-J. Xie, J.-M. Y. Carrillo, B. Carroll, H. Martin, P.-F. Cao, M. D. Dadmun, B. G. Sumpter, V. N. Novikov and K. S. Schweizer, et al. , ACS Nano, 2017, 11, 752–759 CrossRef CAS PubMed.
- S. Askar, L. Li and J. M. Torkelson, Macromolecules, 2017, 50, 1589–1598 CrossRef CAS.
- B. A. P. Betancourt, J. F. Douglas and F. W. Starr, Soft Matter, 2013, 9, 241–254 RSC.
- M. J. Burroughs, S. Napolitano, D. Cangialosi and R. D. Priestley, Macromolecules, 2016, 49, 4647–4655 CrossRef CAS.
- N. G. Perez-de Eulate, M. Sferrazza, D. Cangialosi and S. Napolitano, ACS Macro Lett., 2017, 6, 354–358 CrossRef CAS PubMed.
- N. McCrum, Dale J. Meier, Gorden and Bread Sci, Publisher, New York, 1978 Search PubMed.
- T. Kanaya, T. Kawaguchi and K. Kaji, J. Chem. Phys., 1996, 104, 3841–3850 CrossRef CAS.
- J. Colmenero, A. Arbe, A. Alegria, M. Monkenbusch and D. Richter, J. Phys.: Condens. Matter, 1999, 11, A363 CrossRef CAS.
- A. Arbe, J. Colmenero, M. Monkenbusch and D. Richter, Phys. Rev. Lett., 1998, 81, 590 CrossRef CAS.
- E. Fischer, E. Donth and W. Steffen, Phys. Rev. Lett., 1992, 68, 2344 CrossRef CAS PubMed.
- M. Jhalaria, E. Buenning, Y. Huang, M. Tyagi, R. Zorn, M. Zamponi, V. Garca-Sakai, J. Jestin, B. C. Benicewicz and S. K. Kumar, Phys. Rev. Lett., 2019, 123, 158003 CrossRef CAS PubMed.
- J. Colmenero, F. Alvarez and A. Arbe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 041804 CrossRef CAS PubMed.
- A. Arbe, J. Colmenero, F. Alvarez, M. Monkenbusch, D. Richter, B. Farago and B. Frick, Phys. Rev. Lett., 2002, 89, 245701 CrossRef CAS PubMed.
- J. Zhao, Y. H. Chin, Y. Liu, A. A. Jones, P. T. Inglefield, R. P. Kambour and D. M. White, Macromolecules, 1995, 28, 3881–3889 CrossRef CAS.
- C. M. Roland and R. Casalini, J. Chem. Phys., 2003, 119, 1838–1842 CrossRef CAS.
- A. Narros, A. Arbe, F. Alvarez, J. Colmenero and D. Richter, J. Chem. Phys., 2008, 128, 224905 CrossRef CAS PubMed.
- A.-C. Genix, A. Arbe, F. Alvarez, J. Colmenero, B. Farago, A. Wischnewski and D. Richter, Macromolecules, 2006, 39, 6260–6272 CrossRef CAS.
- G. P. Kar, N. Begam, J. K. Basu and S. Bose, Macromolecules, 2014, 47, 7525–7532 CrossRef CAS.
- S. Srivastava, J. L. Schaefer, Z. Yang, Z. Tu and L. A. Archer, Adv. Mater., 2014, 26, 201–234 CrossRef CAS PubMed.
- H. Chao, B. A. Hagberg and R. A. Riggleman, Soft Matter, 2014, 10, 8083–8094 RSC.
- M. Segev-Bar and H. Haick, ACS Nano, 2013, 7, 8366–8378 CrossRef CAS PubMed.
- P. Kanjanaboos, X.-M. Lin, J. E. Sader, S. M. Rupich, H. M. Jaeger and J. R. Guest, Nano Lett., 2013, 13, 2158–2162 CrossRef CAS PubMed.
- J. A. Rogers, T. Someya and Y. Huang, Science, 2010, 327, 1603–1607 CrossRef CAS PubMed.
- K. E. Mueggenburg, X.-M. Lin, R. H. Goldsmith and H. M. Jaeger, Nat. Mater., 2007, 6, 656–660 CrossRef CAS PubMed.
- C. R. Bilchak, E. Buenning, M. Asai, K. Zhang, C. J. Durning, S. K. Kumar, Y. Huang, B. C. Benicewicz, D. W. Gidley and S. Cheng, et al. , Macromolecules, 2017, 50, 7111–7120 CrossRef CAS.
- J. He, X.-M. Lin, H. Chan, L. Vukovic, P. Král and H. M. Jaeger, Nano Lett., 2011, 11, 2430–2435 CrossRef CAS PubMed.
- H. B. Park, J. Kamcev, L. M. Robeson, M. Elimelech and B. D. Freeman, Science, 2017, 356, eaab0530 CrossRef PubMed.
- C. K. Sarika, G. Tomar, J. K. Basu and U. Thiele, Soft Matter, 2015, 11, 8975–8980 RSC.
- S. Markutsya, C. Jiang, Y. Pikus and V. V. Tsukruk, Adv. Funct. Mater., 2005, 15, 771–780 CrossRef CAS.
- R. Hou, C. Fong, B. D. Freeman, M. R. Hill and Z. Xie, Sep. Purif. Technol., 2022, 300, 121863 CrossRef CAS.
- X. Lu, W. Zhang, C. Wang, T.-C. Wen and Y. Wei, Prog. Polym. Sci., 2011, 36, 671–712 CrossRef CAS.
- S. Shen, Y.-C. Dong, W. K. Ng, L. Chia and R. Tan, Nanotechnologies for the life sciences, 2010 Search PubMed.
- R. De, M. K. Mahata and K.-T. Kim, Adv. Sci., 2022, 9, 2105373 CrossRef CAS PubMed.
- L. F. Greenlee, D. F. Lawler, B. D. Freeman, B. Marrot and P. Moulin, Water Res., 2009, 43, 2317–2348 CrossRef CAS PubMed.
- G. M. Geise, H. B. Park, A. C. Sagle, B. D. Freeman and J. E. McGrath, J. Membr. Sci., 2011, 369, 130–138 CrossRef CAS.
- R. W. Baker, Membrane technology and applications, John Wiley & Sons, 2023 Search PubMed.
- M. Mulder, Basic principles of membrane technology, Springer science & business media, 2012 Search PubMed.
- C. Nagel, K. Günther-Schade, D. Fritsch, T. Strunskus and F. Faupel, Macromolecules, 2002, 35, 2071–2077 CrossRef CAS.
- S. C. George and S. Thomas, Prog. Polym. Sci., 2001, 26, 985–1017 CrossRef CAS.
- H. Lin, E. Van Wagner, B. D. Freeman, L. G. Toy and R. P. Gupta, Science, 2006, 311, 639–642 CrossRef CAS PubMed.
- H. B. Park, C. H. Jung, Y. M. Lee, A. J. Hill, S. J. Pas, S. T. Mudie, E. Van Wagner, B. D. Freeman and D. J. Cookson, Science, 2007, 318, 254–258 CrossRef CAS PubMed.
- C. R. Bilchak, M. Jhalaria, Y. Huang, Z. Abbas, J. Midya, F. M. Benedetti, D. Parisi, W. Egger, M. Dickmann and M. Minelli, et al. , ACS Nano, 2020, 14, 17174–17183 CrossRef CAS PubMed.
- J. W. Barnett and S. K. Kumar, Soft Matter, 2019, 15, 424–432 RSC.
- M. Jhalaria, Y. Huang, E. Ruzicka, M. Tyagi, R. Zorn, M. Zamponi, V. Garca Sakai, B. Benicewicz and S. Kumar, Macromolecules, 2021, 54, 6968–6974 CrossRef CAS.
- C. R. Bilchak, M. Jhalaria, S. Adhikari, J. Midya, Y. Huang, Z. Abbas, A. Nikoubashman, B. C. Benicewicz, M. Rubinstein and S. K. Kumar, Macromolecules, 2022, 55, 3011–3019 CrossRef CAS PubMed.
- L. M. Robeson, J. Membr. Sci., 1991, 62, 165–185 CrossRef CAS.
- S. Chandran, J. Baschnagel, D. Cangialosi, K. Fukao, E. Glynos, L. M. Janssen, M. Müller, M. Muthukumar, U. Steiner and J. Xu, et al. , Macromolecules, 2019, 52, 7146–7156 CrossRef CAS.
- S. Chandran and G. Reiter, Macromolecular Engineering: From Precise Synthesis to Macroscopic Materials and Applications, 2022, pp. 1–30 Search PubMed.
- M. Müller, Prog. Polym. Sci., 2020, 101, 101198 CrossRef.
Footnote |
| † Current address: Department of Molecular and Cellular Biology, Harvard University, Cambridge, 02138, Massachusetts, USA. |
| This journal is © The Royal Society of Chemistry 2025 |