Open Access Article
Open Access ArticleMechanistic and thermodynamic insights into binding and activation of small molecules on metallozeolites – relevance for adsorption and catalysis
Filip Zasada
 ,
Piotr Pietrzyk
,
Piotr Pietrzyk
 ,
Mariusz Radoń
,
Mariusz Radoń
 and
Zbigniew Sojka
and
Zbigniew Sojka
 *
*
Faculty of Chemistry Jagiellonian University, ul. Gronostajowa 2, 30-387 Krakow, Poland. E-mail: sojka@chemia.uj.edu.pl
First published on 7th November 2025
Abstract
Metallozeolites exchanged with 3d transition metal ions (TMI) are versatile catalytic materials due to their well-defined framework structures, redox flexibility, and remarkable adsorption and catalytic properties. These features make them invaluable for both fundamental and applied research, underpinning numerous catalytic technologies. The binding and activation of small reactant molecules is governed by the complex mechanistic interplay of involved intrazeolite reactions, whose course is influenced by the flexible valence, spin, and coordination states of the encaged metal ions and the metal–oxo entities. Despite significant advances, the nature of active sites, confinement effects, and the complex activation mechanisms of reactant molecules, which act as both innocent and non-innocent ligands, remain subjects of ongoing debate. This has driven extensive research into the thermodynamic constraints and molecular-level insights into activation processes with orbital and spin resolution. This review critically examines the thermodynamic and molecular aspects of intrazeolite speciation of transition-metal ions and metal–oxo active sites, their structural dynamics, and reactivity toward catalytically relevant small molecules, including NH3, H2O, CO, N2, O2, NO, N2O. Particular emphasis is placed on ligand coordination, redox activation, and the role of electronic and spin states in dictating the catalytic behaviour of metallozeolites. The discussion integrates insights from site-selective spectroscopies and computational methods to elucidate the structural, thermodynamic, and molecular aspects of metal–ligand interactions and activation pathways, with an emphasis on the role of spin states in binding and reactivity. We hope that this review can serve as a relevant and valuable reference for researchers working with zeolite catalysts, providing new insights and inspiration.
1. Introduction – context, theoretical and experimental background
Shortly after the development of synthetic zeolite materials, they were ion-exchanged with various transition-metal ions (TMI)1,2 to acquire new, and often unique functionalities and reactivities, providing a solid foundation for their widespread applications in adsorption and redox catalysis.3–6 In this context, the numerous zeolite frameworks7 have provided a large variety of molecular architectures with the degree of perfection required for sensible molecular-level studies of the fundamental events in chemisorption and catalytic chemistry.8 Due to their unique structural features, metallozeolite catalysts provide an opportunity to investigate the transition from simple (molecular ligation via lone pair donation with spin conservation) to complex (dissociative redox processes with a change in spin state) adsorption events, as well as from single-site to multiple-site chemistry. They also made it possible to explore the intermediate reaction steps both stoichiometrically and structurally, using spectroscopic methods in combination with theoretical modelling at various levels of sophistication.1,2,8–11As a result, a large variety of promising research areas has emerged over the past few decades, including specific issues related to the substitution of TMI for the framework Al3+ or Si4+ ions, extra-framework accommodation of TMI, as well as capture, redox activation, and catalytic transformations of reactant molecules into desired products.6,8,12–14 The coupled redox and acid–base chemistries, as well as space-confined effects, significantly impact the latter processes. In this context, the unique properties of the encaged bare transition-metal ions and the metal–oxo active centres result from their flexible valence, spin, and coordination states, which, in conjunction with the space confinement effects, lead to specific catalytic performance not encountered in the counterpart homogeneous catalysis.12,13 Among the catalytic processes involving small-molecule gas-phase reactants, NH3-SCR,14,15 HC-SCR,16,17 CH4 oxidation,18,19 and N2O decomposition20,21 are the most notable.
The zeolite framework type, the Si/Al ratio, and the distribution of Al atoms within the cavities and channels (constrained by the Löwenstein rule22), essentially govern the intrazeolite speciation of TMI. It is manifested in the simultaneous presence of exchanged cations in various valence and coordination states. The mutually related intrazeolite hydrolysis, olation, and oxolation processes lead to the formation of oligomeric metal–oxo entities, particularly for the high valent cations. Besides the framework and extra-framework oxygen ligands (oxo-centers), reactant molecules (such as NO, NO2, O2, H2O, and NH3) can also be captured in the coordination sphere of encaged transition-metal ions in various modes of hapticity and stoichiometries. Therefore, the successful delineation of TMI speciation in metallozeolite catalysts requires the application of a broad suite of spectroscopic techniques. Nevertheless, due to common speciation effects, single spectroscopic techniques rarely provide a thorough insight into the complex structure of the intrazeolite TMI species in their particular framework locus, including valence and oxidation states. Thus, a combination of dedicated techniques is typically required for the successful resolution of the geometric, electronic, and magnetic structures of the active sites.17–20
The chemical states of transition-metal ions and their agglomeration can be monitored with several conventional and commonly available spectroscopic techniques such as UV-vis/UV-vis-NIR,23,29,30 EPR,1,3,17 MAS-NMR,24 IR,25,26 Raman (RS) and resonance Raman (rR),27 and luminescence (PL),28 applied directly or with using suitable probe molecules.31,32 More advanced methods include correlation 2D IR,33 pulse EPR (HYSCORE,34 ESEEM,35 ENDOR36), and high-field EPR,37 as well as a toolbox of powerful synchrotron X-ray absorption techniques (XAFS, XANES, EXAFS38), which have been of growing importance, recently.39 In addition to the wide-ranging applications of these methods, various techniques have been developed to study zeolites in operando/in situ modes, providing valuable insights into intrazeolite coordination chemistry and elucidating the catalytic reaction mechanisms based on the establishment of functional structure–property–performance relationships. Operando characterization techniques enable monitoring of the adsorption and desorption of reactants, as well as the identification of surface intermediates and their dynamics. Additionally, they aid in understanding how and why zeolite catalysts behave differently under working conditions in real-life applications in comparison to static experiments.18–20 However, the actual capacity of operando techniques to deliver definitive mechanistic insights is often limited by a compromise between the optimal circumstances for recording the high-quality spectra and the reaction conditions. The imposed constraints are particularly due to the temperature dependence of peak positions, line broadening effects, loss of the signal-to-noise ratio, and accumulation of spectator species. As a result, static and often low-temperature spectroscopic techniques still play a crucial role in providing high-quality reference spectra and reliable spectroscopic fingerprints, which can be used not only to guide the interpretation of operando results but also as crucial experimental constraints for ab initio molecular modelling.
Experimental studies on metallozeolites and their adsorption properties, as well as their catalytic chemistry, are consistently corroborated by theoretical modelling for the advanced interpretation of their intrinsic catalytic performance at both molecular (DFT, post-HF calculations) and phenomenological (ab initio thermodynamics) levels. Various quantum-chemical methods have been productively applied to characterise catalytically-relevant TMI systems, starting from commonly used and well-grounded density functional theory, progressing to more involved post-Hartree–Fock (post HF) methods, such as complete active space (CAS)40 or coupled cluster (CC)41,42 for proper treatment of correlated electron systems. Due to its overall good compromise between accuracy and computational cost, DFT remains the method of choice in computational catalysis. However, one should be aware of the limitations in currently available density functionals, which are approximated in their accuracy.43–45 Examples of particularly challenging problems in computational catalysis, where DFT methods may not be sufficiently precise, include the prediction of chemically accurate adsorption energies and barrier heights in extended systems,46–48 binding of noninnocent ligands to TMI,49–51 and the spin-state splittings in mononuclear52,53 and polynuclear complexes.54,55 In such cases, a critical evaluation of the DFT results may be necessary, including cross-checking with the results of post-HF wave function calculations and comparing them with experimental spectroscopic or thermodynamic quantities, wherever available. When properly used, quantum-chemical calculations have been of crucial importance in developing a comprehensive molecular description of the coordination chemistry of TMI in zeolites, explaining their structure, dynamics, reactivity, and spectroscopic features, which are not directly accessible by experimental techniques. Supplemented by molecular simulation methods including molecular dynamics (MD) at various sophistication levels,56–59 first-principles thermodynamics (FPT),60,61 advanced methods of electronic structure analysis, including natural orbitals for chemical valence combined with extended-transition-state method (ETS-NOCV),62–64 crystal orbital Hamiltonian population COHP,65,66 and machine learning (ML) approaches,67,68 they define a robust panoply of modern computational chemistry of zeolites.
In this review, we focus on the interfacial coordination chemistry of 3d transition-metal cations encaged in zeolites and its relevance for adsorption and catalysis, with the following topics that are covered: (1) accommodation and spectroscopic characterization of intrazeolite transition metal (TMI) centres (bare single, dual, and polynuclear metal–oxo), (2) survey of their structure and spectroscopic fingerprints, (3) first principles thermodynamic account of TMI speciation and stability at various pO2 and pH2O conditions, (4) coordination of extra-framework non-redox (H2O, NH3, N2, CO) and redox (NO, O2, N2O) molecules and their activation with the specific accent on the role of electronic and spin state of the active sites and (5) thermodynamic and molecular orbital interpretation of the binding and activation processes. The emphasis is placed on the utility and diagnostic capacity of selected molecular spectroscopies, particularly CW-EPR and related pulsed variants, UV-vis, Raman/resonance Raman, and IR techniques commonly applied in such investigations, and on ab initio thermodynamic and molecular modelling, supplemented by spin-resolved analysis of the nature of metal–ligand bonds using natural orbitals for chemical valence (NOCV).
The examples discussed herein demonstrate the capacity of these spectroscopies to probe the interaction of the reactant molecules with intrazeolite first-row 3d transition metal ions, and unravel various ways of their activation, particularly when the spin of TMI plays a crucial role. In selected cases of special relevance, this review is expanded to include non-transition metal ions (such as Zn) dispersed in zeolites. However, the framework cations obtained by isomorphous substitution, which form corner-sharing MO4 tetrahedra fully integrated with the zeolite structure through covalent framework M–O–Si bonds, are only scarcely considered. Lastly, we do not aim to provide a comprehensive review herein, but rather present illustrative examples that demonstrate the value of advanced concepts in establishing the rational basis of redox catalysis on metallozeolites, which complements the previous notable reviews devoted essentially to copper and iron.5,14,29,69–73
2. Localisation, structure, and speciation of cationic metallic active sites
The unique structural and topological features of zeolites, such as 3D and 2D channel networks, accessible void space, space confinement, the presence of ion-exchange sites, and Brønsted acidity, make them versatile catalysts of enormous importance for both fundamental investigations and wide-ranging practical applications, particularly when functionalized with transition metal ions.13,74–76The introduction of transition-metal ions to zeolite matrices gives rise to four broad types of accommodation scenarios: (1) substitution of alien cations for the framework Al or Si ions, (2) formation of charge balancing ionic pairs with the framework O–Al−–O centres, (3) encapsulation of metal species and entities within the channels and cages, (4) support of nanoparticles on the external zeolite surface. Depending on the Si/Al and M/Al ratio, zeolite topology, Al distribution, and the preparation method used, a variety of confined species of various site topologies, structures, and nuclearity, such as single and dual bare cations, and a diversity of polynuclear metal–oxo species, can appear (Fig. 1).
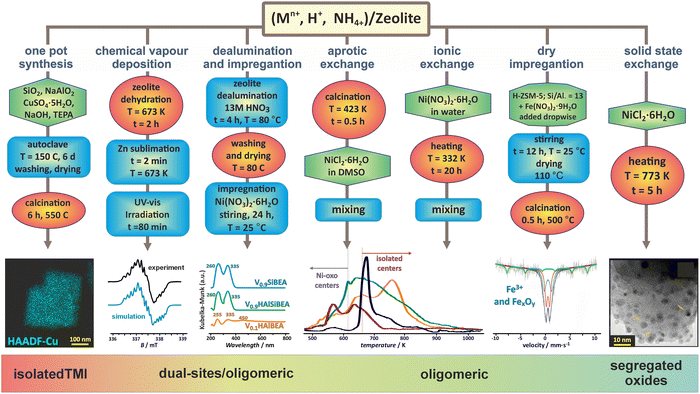 | ||
| Fig. 1 Selected preparation methods applied for synthesizing the metallozeolites, including one-pot synthesis (illustrated with TEM/EDX imaging of Cu in SSZ-13),33,77 chemical vapour deposition (with EPR spectrum of Zn+ cations dispersed in ZSM-5),78 dealumination and impregnation (with UV-vis of VO2+ species incorporated in Si-BEA),79 aprotic and ionic exchange (with H2-TPR profiles of Ni/BEA),80 dry impregnation (with Mössbauer spectra of iron in ZSM-5),81 and solid state exchange33 (with TEM image of segregated oxide nanocrystals). The figure was drawn based on data published in the quoted references. The microscopic images were adapted from ref. 33 with permission from Elsevier, Copyrights 2023. | ||
2.1. Isolated TMI centres
Hydrated metallozeolites are usually catalytically inert, but elevated temperature (prevailing during catalyst pretreatment and reaction conditions) drives off the labile ligands and generates coordinatively unsaturated active 3d metal (and/or metal-hydroxo and -oxo) centres. The resultant charge-balancing extra-framework cations hosted in the zeolites exhibit diverse low coordination states depending on their electronic configuration, charge, and spin (Fig. 2a). The topology of the sitting sites, size of the rings (Fig. 2b1), Si/Al ratio, and Al spatial distribution (Fig. 2b2 and b3) play a decisive role in the accommodation mode of these cations.82 This issue is illustrated by various coordination patterns of the bare 3dn cations in the MFI matrix, as well as for selected single and dimeric Cu and Fe cations hosted in the CHA and FER frameworks, which are derived from DFT structure optimization (Fig. 2b–d).83 Generally, ligation to more basic Al–O–Si oxygen atoms is preferred over Si–O–Si.5 Furthermore, the Al pairs (i.e., Al atoms arranged in the Al–O–(Si–O)2–Al sequences) are capable of stabilising M2+ cations, whereas the single Al atoms (present in the Al–O–(Si–O)n sequence, n > 2) can charge-balance only the monovalent ions or hydroxylated divalent cations, M2+–OH−, and any other oxo species of an effective charge q = 1.84 As a result, zeolite hosts with abundant Al–O–(Si–O)2–Al sequences are needed to obtain catalysts with an enhanced content of the divalent redox sites. Accommodation of TMI cations leads to significant deformation of the rings where the alien cations are sited, and the associated lowering of the local site symmetry. In this way, the flexible zeolite framework acting as a polydentate ligand tends to maximize the coordination number (Mnc, n = 1, 2, 3 …) of TMI, yet at the expense of forming appreciably strained bonds.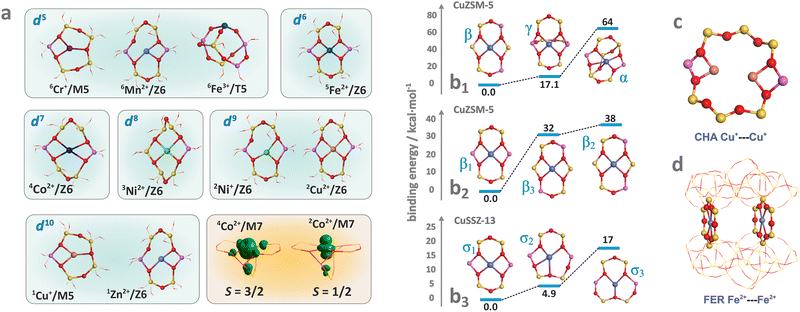 | ||
| Fig. 2 Exemplary (DFT optimized) coordination patterns of selected isolated TMI hosted in MFI frameworks with the illustrative spin density distribution for Co2+ cation in the high (S = 3/2) and low (S = 1/2) spin states (a). Coordination environments of single Cu2+ cations showing the effect of site topology (b1), and Al distribution (b2) and (b3) on the TMI relative stability (based on data published in the ref. 82). Dimer Cu–Cu sites in CHA (c) and Fe–Fe sites in FER (d). | ||
The resultant structural deformations are well reflected in the IR spectra of the T–O–T asymmetric skeletal vibrations (T = Si or Al).85 The extent of this perturbation and the ensuing shift of the perturbed asymmetric T–O–T vibration varies with the valence state, size, particular exchangeable position the hosted ion occupies in the zeolite framework, and the presence of co-ligands as well.86 The corresponding IR bands appear between two strong bands of antisymmetric and symmetric T–O–T vibrations, and are shifted from 1020–1100 cm−1 to about 800–1000 cm−1 upon accommodation of the alien cations. This effect can be exemplified by the Cu2+, Ni2+, and Mn2+ hosted in the FER matrix (Fig. 3a), and Cu2+, Cu2+–OH− and Cu+ in ZSM-5 (Fig. 3b) and SSZ-13 (Fig. 3c).86–88 In the case of small charge cations (Cu+, Cu2+–OH− or Zn+), these deformations and the associated T–O–T frequency shifts are less pronounced (Table 1). The perturbed T–O–T vibrations can be used, for instance, to differentiate between the single Cu2+ species located in 6MR (900 cm−1) and the Cu2+–OH− centres in 8MR (∼950 cm−1) rings present in the CHA zeolite.88
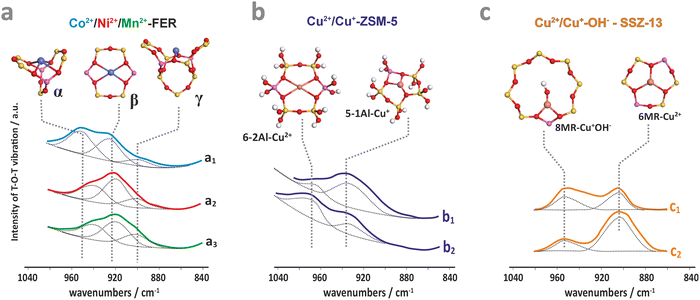 | ||
| Fig. 3 IR spectra of the perturbed T–O–T antisymmetric mode for dehydrated ferrierite substituted with Co (a1), Ni (a2), and Mn (a3),87 for ZSM-5 zeolite loaded with Cu2+ (b1) and Cu2+/Cu+ (b2),86 and for Cu-SSZ-13 with the Si/Al ratio of 6 (c1) and 30 (c2).88 The figure was drawn based on data published in the quoted references. | ||
| Zeolite framework | FER | MFI | CHA | Ref. | |||
|---|---|---|---|---|---|---|---|
| Cation | α-site | β-site | α-site | β-site | σ-site | τ-site | |
| Fe2+ | 935–940 | 913–915 | 927 | 89 and 90 | |||
| Co2+ | 942–945 | 918–920 | 970 | 931–935 | 895 | 924, 948(τ3Si) | 23, 87 and 89 |
| Mn2+ | 953 | 928 | 89 | ||||
| Ni2+ | 940 | 918 | 930 | 89 | |||
| Zn2+ | 935 | 915–917 | 84 | ||||
| Cu+ | 977 | 86 and 89 | |||||
| Cu2+ | 937 | 900–892 | 86 and 89 | ||||
| Cu2+–OH− | 950 | 88 | |||||
Direct insight into the ligation of TMI in zeolites can be derived using classic continuous wave CW-EPR91–94 or advanced pulse and high-field techniques (HYSCORE, ESEEM, ENDOR).95,96 For the series of Ti3+ (3d1), V3+ (3d2), Cr3+ (3d3), Cr2+ (3d4), Mn2+, Fe3+ (3d5), Fe2+ (3d6), Co2+ (3d7), Ni2+ (3d8) Cu2+, Ni+ (3d9) and Zn+ (3d104s1) ions of the first row, which can be hosted in zeolites, all tend to assume the high-spin configuration, noting the position of the zeolite oxygen (Oz) ligands in the spectrochemical series (AlO) < (Oz) < (SiO) ∼ (H2O) proposed by elswhere.97 Among them, those with S = 1/2 are amenable to straightforward investigations using the commonly available X-band CW-EPR technique.
The hyperfine coupling A- and the g-tensor values obtained from the EPR spectra are strongly affected by the local environment of the encaged TMI. Apart from the 3dn configuration, the g- and A-tensor anisotropies are sensitive to the local symmetry and the covalency of the M–Oz bonds with the zeolite framework oxygens. Simple perturbation theory treatment within the crystal field approximation allows for a straightforward (yet coarse) molecular interpretation of the g-tensor (gij) values of the S = 1/2 TMI hosted in zeolites, based on eqn (1):98
 | (1) |
For further discussion, upon a rudimentary account for the M–Oz bond covalency, gauged succinctly by the α coefficient (it accounts for the extent of delocalisation of the unpaired electron from the metal core into the ligands (Fig. 4d), for more details see ref. 99), this equation may be reframed in a simplified handy form as; g = ge ± mλα2/(ESOMO − En), where m = 2, 6, 8 (depending on the 3d orbital involved in SOMO – singly-occupied molecular orbital), ge = 2.0023, λ is the one-electron spin–orbit coupling constant, and Li, Lj are the orbital angular momentum operators that couple SOMO ≈ α|3d〉, with the |n〉 states of En energy. The requisite energy differences (ESOMO − En) can be derived from the d–d transitions observed in the complementary UV-vis spectra, as illustrated in Fig. 4a and b. Their relation with the corresponding EPR spectrum is shown in Fig. 4c.
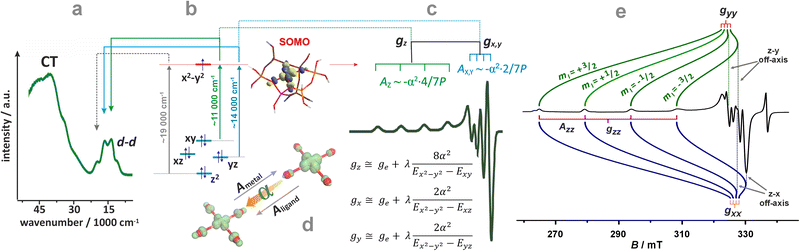 | ||
| Fig. 4 UV-Vis-NIR spectrum of dehydrated Cu-SSZ-13 (a), together with the 3d energy levels (b) and the corresponding simulated EPR spectrum (c) (panels a, b, and c inspired by ref. 100). Structural model showing influence of a shift of spin density between Cu- and ligand-based states on the magnitude of hyperfine coupling gauged by α coefficient (d). The road map showing the origin of the off-axis features in the EPR spectrum of Cu2+ hosted in the CHA matrix (e), based on ref. 83. | ||
The ligand field symmetry around the intrazeolite TMI in the hosting site imposes distinct constraints on the g-values. Axial signals with g‖ = gzz ≠ g⊥ = gx = gy are expected for the local D4h, C4v, D3h, C3v, D2d symmetries, whereas for lower symmetries (D2h, C2v, C2h, Cs) orthorhombic (or monoclinic) signals with gzz ≠ gxx ≠ gyy are anticipated. As a result, for a 3d1 (Ti3+) cation with the dxy SOMO in an exemplary tetragonal C4v environment, g⊥ < g‖ < ge is expected, and indeed experimentally observed, whereas for a 3d9 cation (Ni+), g‖ > g⊥ > ge for dx2−y2 SOMO (Fig. 5a and b) and g⊥ > g‖ ∼ ge for dz2 SOMO are typical. The hyperfine (hf) coupling constants for the unhybridized dx2−y2 SOMO can be expressed as Azz = As + P[−4/7α2 + Δgzz] and Ayy = As + P[−4/7α2 + Δgyy], Axx = As + P[−4/7α2 + Δgxx], where the α coefficient accounts again for the M–Oz bond covalency, P = gegNμBμN/〈r3〉, neglecting smaller terms.101 Thus, the value of the α coefficient can be assessed from the analysis of the A-tensor, using the calculated atomic values of the P parameters, which are tabulated for a given TMI elsewhere.99
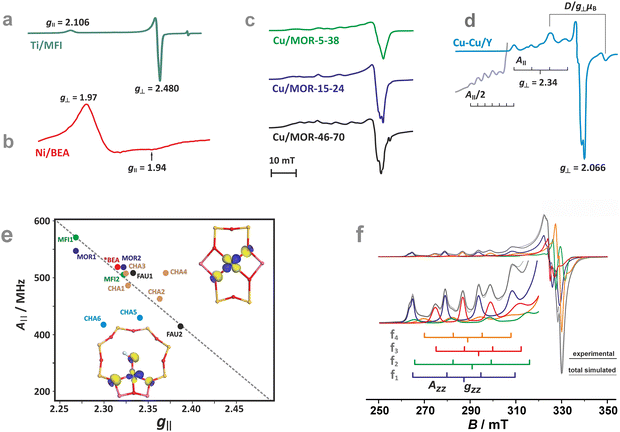 | ||
| Fig. 5 EPR spectra of Ti/MFI (a) Ni/BEA (b). EPR spectra of the dehydrated Cu-mordenite samples of various Si/Al ratios (Si/Al = 5, 15, 46) and Cu exchange levels (2Cu/Al = 38, 24, 70) (c). Room temperature EPR spectra of Cu⋯Cu pairs in CuCe/Y zeolite oxidized at 450 °C and evacuated at 600 °C (d). Blumberg–Peisach-type (P–B) plot for the EPR active Cu2+ species stabilized within different zeolite environments (e), (colours indicate various bare Cu2+ species hosted in different zeolite matrices. In the case of CHA, yellow and blue colours correspond to various Cu2+ and Cu2+–OH− species). The corresponding spin density contours are provided for exemplary Cu2+/6MR and Cu2+–OH−/8MR structures. EPR spectrum of Cu-SSZ-13 zeolite activated at 250 °C in vacuo (f), resolved into the contributing signals. The A‖ and g‖ values for the species identified in (f), labelled as (f1–4), are shown in the P–B plot as CHA1–4. The figure was drawn based on data from ref. 80, 83, 91, 92, 104 and 105 respectively. | ||
More ionic bonds of the encaged TMI with the framework Oz (small spin density delocalisation) increase the hyperfine AMetal values on the metal core and decrease the superhyperfine splitting on the ligands with magnetic nuclei (ALigand), such as 17O (I = 5/2) labelled Oz framework oxygen atoms, and vice versa (see Fig. 4d). In the latter case, the superhyperfine patter due to 17Oz can be used to ascertain the coordination environment of intrazeolite TMI (see below, Fig. 6).
 | ||
| Fig. 6 Experimental (black) and simulated (red) Q-band 17O ENDOR spectra, recorded at different magnetic field settings, of 17O isotopically enriched and fully dehydrated Cu-CHA (a1), together with the schematic representation of the isotopic enrichment of the zeolite framework (a2). Comparison of experimental (grey) and computed (red) maximum hyperfine coupling values (Amax) for 17O and 27Al nuclei for the three different Al distributions: 2Al-3NN, 2Al-3NN, and 1Al (b) (the black dashed lines represent the experimental range of Amax for 17O nuclei). Adapted from ref. 95 under the terms of the CC-BY 4.0 license, copyright 2021, published by Springer Nature. | ||
A comprehensive listing of the equations that can be used for molecular interpretation of the g and A tensors of TMI in ligand fields of various symmetries can be found elsewhere.102 It should be noted, however, that except for the regular features along the z and x, y directions, shown in Fig. 4c, additional off-axis lines may appear in the powder EPR spectra when
| 2Ai2 − hvAi/mI < (gi2Ai2 − gj2Aj2)/(gi2 − gj2) < 2Aj2 − hvAj/mI | (2) |
The M–Oz covalency depends primarily on the presence of Al in the coordination environment of the encaged TMI. The framework oxygen atoms in the Si–Oz–Al entities are more negatively charged than those in the Si–Oz–Si motives. These factors make g and A values structure sensitive, which can be illustrated concisely in the form of Blumberg–Peisach-type diagrams106 for Cu2+ in various zeolite frameworks and different Si/Al ratios.92,107 Although the application of such a diagram to zeolites, due to the absence of suitable model compounds, requires some caution, it demonstrates its usefulness for the preliminary sorting of the intrazeolite copper species based on their EPR fingerprints.
Overall, copper ions in the more positively charged environments are found in the lower right part (smaller A‖ and bigger g‖), whereas Cu2+ species in the more negative coordination environments are located in the upper left end (bigger A‖ and smaller g‖) of the trend line in the Blumberg–Peisach-type diagram (Fig. 5e). This is well exemplified by the different positions in the plot of two types of the Cu-MFI zeolites, with two Al atoms in a MR6 ring generating a higher charge (MFI2) and with only one Al atom in the MR6 ring with the resultant lower charge (MFI1).92 For the particular case of Cu-CHA, the EPR parameters for the MR6 ring (σ-site) fall in the middle of the trend line. The scattering of the positions in the plot reflects the sensitivity to the local symmetry of copper ligation (A‖(C2v) > A‖(C1)), yet the position of the Al atoms within the 6MR appears to be of less importance. The presence of a hydroxy OH− co-ligand in the coordination sphere of Cu2+ located in the MR8 (τ-sites, see CHA5 in Fig. 5e) considerably lowers the value of the hyperfine structure, providing a straightforward means for the distinction between the bare Cu2+ and hydroxylated Cu2+–OH− species.
As a result, the structural sensitivity of the g and A values can not only reveal the speciation of the TMI hosted in zeolites, but also provide a rational basis for unambiguous site-specific assignment, particularly using the benchmarking parameters calculated by DFT or post-HF methods. This is well illustrated for the most extensively investigated Cu2+ hosted in CHA, MFI, and BEA zeolites, as shown in Table 2.
| TMI–zeolite | Notesa | g tensor | A tensor/MHz | Ref. |
|---|---|---|---|---|
| a Calculated when the quantum chemical method is provided; otherwise, the g and A tensors are the experimental values.b Cluster models with different arrangements of Al sites.c Only one value (gzz, Azz) reported.d gx,y (g⊥) and Ax,y (A⊥) are not reported (for zeolites typical values of g⊥ ∼ 2.07 and A⊥ ∼ 30–40 MHz are structurally less informative than the g‖, A‖ values). | ||||
| Ti3+(3d1)/TS-1 | Experimental | 1.922; 1.939; 1.9897 | 108 | |
| 1.981; 1.960; 1.91 | ||||
| Ti+/(3d1)/ZSM-5 | Experimental | 1.94; 1.97 | 109 | |
| VO2+(3d1)/ZSM-5 | Experimental | 1.9843; 1.9843; 1.931 | 214; 214; 542 | 37 |
| VO2+(3d1)/BEA | Experimental | 1.987; 1.983; 1.927 | 234; 214; 558 | 110 |
| B3LYP calculated, 6MR | 1.987; 1.984; 1.952 | 156; 139; 440 | ||
| VO2(3d1)/SiBEA | Experimental | 1.803; 1.942; 1.968 | 676; 892; 876 | 110 |
| B3LYP calculated, 6MR | 1.853; 1.992; 1.998 | 838; 1124; 1043 | ||
| Cr5+(3d1)/Na-Y | Experimental, supercage site II | 1.98; 1.98; 1.92 | 111 | |
| Small cage site I or II | 1.98; 1.98; 1.92 | |||
| Cr5+(3d1)/Na-MOR | Experimental | 1.99; 1.98; 1.93 | 111 | |
| Fe3+(3d5)/ZSM-5 (Fe3+OH/ZSM-5) | Experimental | geff = 4.3 | 112 | |
| geff = 6.3; 5.7 | ||||
| Fe3+(3d5)/BEA (Fe3+OH/BEA) | Experimental | geff = 4.3 | 112 | |
| geff = 6.1 | ||||
| Co2+(3d7)/MFI | Experimental, S = 3/2 | geff = 5.1 | 113 | |
| Co2+(3d7)/AlPO | geff = 5.80–5.44; 2.0 | 119 and 120 | ||
| Ni+/(3d9)/ZSM-5 | Experimental | 2.49; 2.072; 2.072 | 64 | |
| Ni+(d9)/ZSM-5 | B3LYP calculated, 6MR | 2.337; 2.112; 2.159 | 114 | |
| Cu2+(3d9)/ZSM-5 | Experimental | 2.323d | 471d | 115 |
| Cu2+(3d9)/ZSM-5 | Experimental | 2.276d | 545d | 115 |
| Calculated, 6MR (α site) | 2.230d | 479d | ||
| 6MR (β site) | 2.192d | 497d | ||
| 6MR (γ site) | 2.206d | 531d | ||
| Cu2+(3d9)/CHA | Experimental | 2.352; 2.075; 2.075 | 470; 35; 35 | 116 |
| Experimental | 2.347d | 493d | 115 | |
| Cu2+(3d9)/CHA | Experimental | 2.325; 2.072; 2.072 | 490; 35; 35 | 116 |
| B2PLYP calculated, 6MR | 2.282c | 455c | ||
| Cu2+OH(3d9)/CHA | Experimental | 2.290; 2.072; 2.072 | 410; 45; 45 | 116 |
| B2PLYP calculated, 8MRb | 2.275, 2.135, 2029 | 388c | ||
| Cu2+OH− (3d9)/CHA | Calculated, 8MRb, B3LYP | 2.194d | 203d | 115 |
| 6MRb, B3LYP | 2.200d | 401d | ||
| 6MRb, B3LYP | 2.242d | 492d | ||
| D6R, B3LYP | 2.243d | 368d | ||
| Zn+/(3d104s1)ZSM-5 | Experimental | 1.9951; 1.9984; 2.0015 | 1520, 1520, 1535 | 78 |
| B3LYP calculated for: | ||||
| T7 site | 1.992, 1.9963, 2.0023 | 1321, 1325, 1347 | ||
| T8 site | 1.9946, 1.9975, 2.0023 | 1458, 1460, 1480 | ||
| T10 site | 1.9921, 1.9965, 2.0023 | 1331, 1335, 1357 | ||
As an example, the diagnostic A‖ region of the EPR spectra of CuSSZ-13 shows pronounced speciation of copper (Fig. 5f)83, which has been resolved into two tetracoordinate Cu2+ cations of the local C1 and C2v symmetry in the σ-rings (marked as CHA-3 and CHA-4 in Fig. 5e, respectively), and two types of the Cu2+OH− species hosted in the τ-sites of the CHA matrix (CHA-5 and CHA-6 in (Fig. 5e).
The local structure of single-site TMI cations hosted in zeolitic structures, and quantification of the covalency of the Cu–Oz bonds with an accuracy unattainable for other site-sensitive methods, can be ascertained using advanced EPR techniques combined with the 17O isotopic labelling of the zeolite framework.95 Of particular note here is the study of the CuSSZ-13 zeolite using 17O, 27Al ENDOR spectroscopy (Fig. 6a1), supported by DFT modelling.95,117 The requisite 17-O labelling of the zeolite framework can be achieved quite readily using isotopic exchange with H217O (Fig. 6a2).
In contrast to the metal A values, the 17O superhyperfine couplings depend significantly on the Al distribution in the 6MR ring, allowing for unambiguous discrimination between various Al tetrahedra locations. Their presence and number can be directly probed by 27Al HYSCORE or ENDOR spectroscopies. In particular, the σ-rings characterized by 2 Al atoms separated by two Si (2Al-3NN) or one Si atom (2Al-2NN), as well as the rings with one Al atom only, exhibit characteristic patterns of the 17O and 27Al superhyperfine coupling constants (Fig. 6b), providing the basis for the Al-resolved identification of hosting sites. The exquisite sensitivity of such couplings enables, therefore, the univocal identification of the Cu2+ coordination environments. This approach has also been used to examine the location of VO2+ (ref. 95) and Zn+ in ZSM-5,117 demonstrating that it is possible to ascertain the specific location of paramagnetic TMI active centres in zeolite matrices with the level of detail needed for the rational establishment of structure–reactivity relationships. It is worth mentioning here that anomalous X-ray powder diffraction at the K-edge, which probes the long-range order of aluminium atoms within the zeolite frameworks, can also be used to determine isolated Al atoms and pairs (i.e., the Al(–O–Si–O–)xAl sequences). Using this approach in combination with 27Al and 29Si MAS-NMR, the spatial distribution of Al atoms in ZSM-5 has recently been resolved.118
The TMI species with S > 1/2 (with more than one unpaired electron) exhibit zero-field splitting of the ground state gauged by the axial D and rhombic E parameters. The high-spin TMI can be divided into Kramers ions of half-integer spin numbers (S = 3/2, Co2+ and S = 5/2, Fe3+) and non-Kramers ions with integer spins (S = 1, Ni2+ and S = 2, Fe2+, Mn3+). The zero-field splitting can make the intrazeolite non-Kramers TMI “EPR-silent” using conventional X-band (∼0.3 cm−1) or Q-band (∼1.2 cm−1) EPR, or detectable, particularly for the Kramers ions, when the ZFS leads to a well-separated Ms = ±1/2 state as the lowest one (Fig. 7a and b1).119,120 Such systems can be treated simply as exhibiting effective S′ = 1/2 states, but due to closely lying energy states that promote fast relaxation, registration of the EPR spectra usually requires liquid helium temperatures.120,121 The zero-field splitting depends on the anisotropy of the local ligand field and is mediated by spin–orbit coupling (SOC). The magnitude of the latter increases as one passes from early to late 3d TMI across the periodic table. As a result, ZFS may vary from small values (of the order of 10−2 cm−1) for Mn(II) in symmetric environments to large values of the order of even 102 cm−1 for Co(II).119 Notable examples can be provided by liquid helium X/Q-band EPR studies of CoZSM-5 (Fig. 7b2)121 or CoAPO zeotypes with the Kramers Ms = ±1/2 ground state, which exhibit effective g-values of g⊥,eff ≈ 5.80–5.44 and g‖,eff ≈ 2.00, and the zero-field splitting of 7 cm−1. Another example of a Kramers high-spin system is provided by FeZSM-5 zeolites.122 The EPR signal at g‖,eff ≈ 2 with small ZFS has been associated with the highly symmetric α sites. In contrast, the signal at g⊥,eff = g⊥(S + 1/2) ≈ 6 and g‖,eff ≈ 2 to β sites of local axial symmetry (D ≫ hν, E ≈ 0), whereas the geff ≈ 4.3 signal to γ sites with rhombic ZFS (D ≫ hν, and D/E ≈ 1/3) (Fig. 7c1 and c2). It is more likely, however, that the trivalent ions are actually encaged in the ZSM-5 host in the form of hydroxo or oxo species, which can be more readily charge balanced by 2 Al and 1 Al atoms, respectively, since the configurations of 3 Al atoms per ring/cage are available in zeolites of low Si/Al ratio, such as X faujasite, only. A broad signal appearing at geff ≈ 2.3 corresponds, in turn, to small FexOy clusters. The extension of the low-field signal to geff ≈ 9.6 can mainly be attributed to the rhombicity D/E parameter, which characterizes the Fe3+ cations in highly anisotropic (low-symmetry) environments. A signal at g ∼ 3.3 may also appear for Fe3+ in the sites of trigonal symmetry, but some spectral features can be smeared out due to the strong dependence of their resonance magnetic fields on the spatial orientation of the paramagnets, or distribution of the ZFS values caused by local strain.
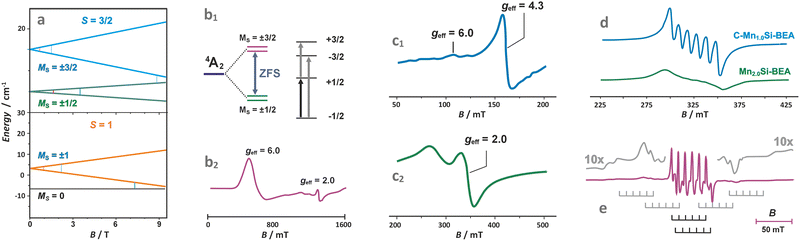 | ||
| Fig. 7 Splitting of the energy levels in the magnetic field for exemplary S = 3/2 and S = 1 states of TMI (a), zero-field splitting (ZFS) for the 4A2 state of Co2+ (d7) with D > 0 (b1), with the corresponding Q-band EPR spectrum of Co/AlPO (b2).119,120 X-band spectra of Fe/ZSM-5 (c1 – low field, c2 – high field component),122 Mn/BEA of different loading (d),123 and Q-band spectrum of Mn2+ in A zeolite matrix (e).124 The figure was drawn based on data published in the quoted references. | ||
In the case of Mn2+ ions exchanged into zeolite hosts, the EPR spectra show gradual smearing of the 6-line hyperfine structure due to I = 5/2 with an increasing Mn content due to dipolar broadening effects caused by the adjacent Mn2+ ions (Fig. 7d).123 The observed spectrum results from transitions within the Ms = ±1/2 doublet produced by the combined action of the ligand field and the spin–orbit coupling.
In fact, in powder spectra only the central line due to the Ms = −1/2 ↔ +1/2 transitions of the least angular dependence on the magnetic field is strong, whereas the other allowed inter-doublet transitions (such as Ms = −±3/2 ↔ ±1/2 or −±3/2 ↔ ±5/2, marked with the grey stick diagrams in Fig. 7e) are smeared to large extent, and barely observed as mere wings flanking the central hyperfine sexted. A relevant example is provided by Mn2+ exchanged in A zeolites.124
2.2. Terminal and bridging metal oxo centres
Besides the bare state (Co2+, Ni2+/Ni+, Cu2+/Cu+), extraframework cations, particularly those of z ≥ 3 (V5+, Ti4+ or Fe3+) hosted in zeolites of moderate Si/Al ratio, can be stabilised in the form of hydroxo and terminal or bridging oxo TMI centres of various nuclearity. Their appearance results from hydrolysis when the local pH during the catalysts preparation is too high ([M(H2O)n]z+(cage) + hH2O(cage) → [M(OH)h(H2O)n−h](z−h)+(cage) + hH3O+/Z), launching the intrazeolite olation/oxolation reactions that lead to the formation of M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O or O
O or O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) M
M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O oxo-species (for instance, [V(H2O)6]5+ → [V(OH)4(H2O)2]+ → [VO2(H2O)4]+ + 4H3O+ (ref. 125)). The relevant thermodynamic background of these processes is provided in Chapter 3. Notable examples of the intrazeolite terminal oxo-systems of high valent metals include mono-oxo ([V
O oxo-species (for instance, [V(H2O)6]5+ → [V(OH)4(H2O)2]+ → [VO2(H2O)4]+ + 4H3O+ (ref. 125)). The relevant thermodynamic background of these processes is provided in Chapter 3. Notable examples of the intrazeolite terminal oxo-systems of high valent metals include mono-oxo ([V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+/BEA, [W
O]2+/BEA, [W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]3+/ZSM-5126 or [Fe
O]3+/ZSM-5126 or [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+/MOR,26 [Fe
O]2+/MOR,26 [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+/CHA, [Fe
O]2+/CHA, [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+/BEA,19 and di-oxo species ([MoO2]2+/ZSM-5-127 and VO2/BEA zeolites110). Alternatively, metal–oxo species can also be formed during the redox-type interactions of bare (single and adjacent) TMI cations with O2 or N2O, and this chemistry is described in detail in Chapters 4.3.1 and 4.3.3.
O]2+/BEA,19 and di-oxo species ([MoO2]2+/ZSM-5-127 and VO2/BEA zeolites110). Alternatively, metal–oxo species can also be formed during the redox-type interactions of bare (single and adjacent) TMI cations with O2 or N2O, and this chemistry is described in detail in Chapters 4.3.1 and 4.3.3.
Generally, the metal–oxo bonding of TMI can be described in terms of σ- and π-type overlap between the 2p orbitals of the Ot moiety with the corresponding 3d orbitals of the Mz+ core. A tetragonal environment (for clarity, with enhanced C4v symmetry) with the M–Ot bond placed along the z-axis can be used as a basic, semiquantitative model for the TMI situated in the 6MR rings. In such case, the dz2 orbital is involved in the σ-overlap with the 2pz(O) in the M–Ot bond, the dzx, dzy orbitals participate in the π-overlap, whereas the dx2−y2 orbital is primarily engaged in the σ-bonding to the framework Oz ligands (assuming the x- and y-axes intersecting Oz ligand positions), and in a considerably weaker δ-type interaction with the terminal oxygen, as well. The dxy orbital remains essentially nonbonding. The resultant general scheme of the energy levels is shown in Fig. 8 (note, it may be altered by changes in the local site symmetry and oxidation state of the cations). All bonding oxo orbitals are occupied by the 6 electrons provided by the terminal Ot moiety. In contrast, the nonbonding dxy and the antibonding  , δ* and σ* orbitals are occupied by the electrons derived from the metal dn centres. Thus, for the d0–d1 TMI (exemplified by [VO2]+ and [VO]2+ hosted in BEA24 VO2+/MCM-22128 or [VO]2+ in ZSM-537), the M–Ot bonds acquire a distinct triple bond character (1σ and 2π), and are the strongest among the 3d series. For [VO]+/ZSM-5,129 the bond order decreases to 2.5, as in the high-spin d2 configuration, the antibonding
, δ* and σ* orbitals are occupied by the electrons derived from the metal dn centres. Thus, for the d0–d1 TMI (exemplified by [VO2]+ and [VO]2+ hosted in BEA24 VO2+/MCM-22128 or [VO]2+ in ZSM-537), the M–Ot bonds acquire a distinct triple bond character (1σ and 2π), and are the strongest among the 3d series. For [VO]+/ZSM-5,129 the bond order decreases to 2.5, as in the high-spin d2 configuration, the antibonding  becomes occupied.
becomes occupied.
Distinction between the diamagnetic [VO2]+ (3d0) and paramagnetic VO2 and VO2+ (3d1) cations, accommodated, e.g., in the BEA zeolite, can be performed by MAS-NMR (Fig. 9a) in combination with photoluminescence techniques (Fig. 9b1 and b2),130 and EPR spectroscopy (Fig. 9c1–c3),24,110 respectively. The resolved fine structure in the PL spectra of [VO2]+/BEA reveals directly not only the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds, but also speciation of the vanadium(V)-oxo species (Fig. 9b2).
O bonds, but also speciation of the vanadium(V)-oxo species (Fig. 9b2).
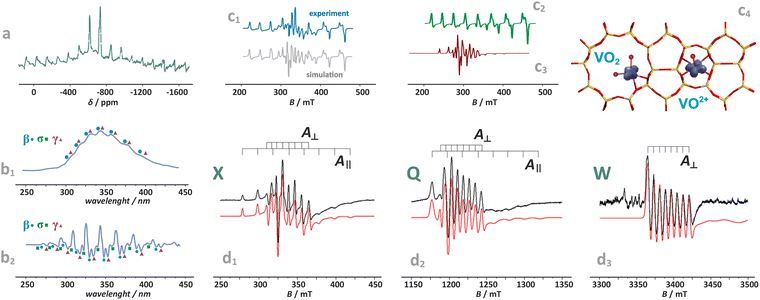 | ||
| Fig. 9 Exemplary NMR (a) and photoluminescence spectra of vanadium(V)-oxo species in BEA zeolite (b1) and (b2), (β, σ, γ indicate three vanadium species of various structures), based on data published in the ref. 130 redrawn and modified for clarity. Simulated and experimental EPR spectra of vanadium in the dealuminated BEA zeolite (c1) and the component signals of VO2+ (c2) and VO2 (c3) species, together with spin density contours calculated for the VO2 and VO2+ species (c4), adapted from ref. 110 with permission from American Chemical Society, Copyright 2007. Experimental (black) and simulated (red) EPR spectra of the VO2+/ZSM-5 sample registered at (d1) X-band, (d2) Q-band, and (d3) W-band, adapted from ref. 37 with permission from Elsevier Inc., Copyright 2020. | ||
The superimposed EPR spectra of the paramagnetic VO2+ and VO2 species observed in the dealuminated BEA zeolite are shown in Fig. 9c1 and the component signals in Fig. 9c2 and c3, whereas the associated structures with spin density contours are shown in Fig. 9c4.24 Different SOMO nature of both species (dx2−y2 for VO2+ and 3dz2/4s hybrid for VO2) is well reflected in the dramatically different EPR parameters: gxx = 1.987, gyy = 1.983, gzz = 1.927, |Axx| = 8.4, |Ayy| = 7.7, and |Azz| = 20.7 mT for VO2+, and VO2: gxx = 1.803, gyy = 1.942, gzz = 1.968, |Axx| = 26.8, |Ayy| = 32.8, and |Azz| = 31.8 mT. The isotropic hyperfine constant is extremely sensitive to the number of oxo-ligands, and therefore, can be used as a simple diagnostic for resolving the oxo vs. dioxo dichotomy of the vanadium(IV) species. Application of multifrequency EPR illustrates, in turn, a possibility of separation of the spectral A‖(Azz) and Ax,y(A⊥) features of the VO2+ entities exchanged in the ZSM-5 zeolites, and may be helpful to reveal their possible speciation (Fig. 9d1–d3).37
With an increasing electron count, the antibonding  orbitals become progressively populated (Fig. 8), decreasing the M–O bond order and weakening its strength. In the particular case of 3d4 cations, the bond order drops to 2. The resultant double bond in the M
orbitals become progressively populated (Fig. 8), decreasing the M–O bond order and weakening its strength. In the particular case of 3d4 cations, the bond order drops to 2. The resultant double bond in the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ot unit can be represented by a quintet [Fe
Ot unit can be represented by a quintet [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ ferryl species (dxy1dxz1dyz1(dz2−y2)1 σ2, S = 2, Fig. 8) stabilized in various zeolite matrices,90,131,132 which is featured by the presence of a low-lying ferric-oxyl septet (dxy1dxz1dyz1(dz2−y2)1(dz2)1, σ1, S = 3),20 or by isoelectronic [MnO]+ units hosted in ZSM-5 and SSZ-39 (AEI) modelled by DFT.133 Yet, both [Fe
O]2+ ferryl species (dxy1dxz1dyz1(dz2−y2)1 σ2, S = 2, Fig. 8) stabilized in various zeolite matrices,90,131,132 which is featured by the presence of a low-lying ferric-oxyl septet (dxy1dxz1dyz1(dz2−y2)1(dz2)1, σ1, S = 3),20 or by isoelectronic [MnO]+ units hosted in ZSM-5 and SSZ-39 (AEI) modelled by DFT.133 Yet, both [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ and [MnO]+ species hosted in the MFI and AEI topologies exhibit different sitting locus, the structure and stability of which depends considerably on the distribution of Al atoms within the rings. The most stable [Fe
O]2+ and [MnO]+ species hosted in the MFI and AEI topologies exhibit different sitting locus, the structure and stability of which depends considerably on the distribution of Al atoms within the rings. The most stable [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ species in ZSM-5 exhibit a square pyramidal (coordination number CN = 5) structure located in δ-sites of the 6MR(T11/T11) rings with the Al atoms in the para-position, whereas [MnO]+ species are most stable in the 10MR (T12) rings, assuming a trigonal structure of CN = 3,134 characteristic for intrazeolite monovalent species such as [CuO]+ or [ZnO]+.
O]2+ species in ZSM-5 exhibit a square pyramidal (coordination number CN = 5) structure located in δ-sites of the 6MR(T11/T11) rings with the Al atoms in the para-position, whereas [MnO]+ species are most stable in the 10MR (T12) rings, assuming a trigonal structure of CN = 3,134 characteristic for intrazeolite monovalent species such as [CuO]+ or [ZnO]+.
The [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ entity is known as α-oxygen and exhibits unique reactivity toward C–H bond cleavage, which is addressed in Section 4.3.3. Particularly, for the BEA topology, the spin Hamiltonian parameters (S = 2 and the sign and magnitude of D = 13 ± 1 cm−1) confirm the [5Fe(IV)
O]2+ entity is known as α-oxygen and exhibits unique reactivity toward C–H bond cleavage, which is addressed in Section 4.3.3. Particularly, for the BEA topology, the spin Hamiltonian parameters (S = 2 and the sign and magnitude of D = 13 ± 1 cm−1) confirm the [5Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ formulation of this species, definitely.135
O]2+ formulation of this species, definitely.135
In the case of the late intrazeolite transition metal cations (Co, Ni, Cu), the high-valent states (z ≥ 3) become more hardly accessible. With an increasing electron number, the corresponding M–Ot bonds gradually lose their oxo character. For the transition [Fe–O]+ (dxy1dxz1dyz1(dz2−y2)1(dz2)1 σ2, S = 5/2) and [Co–O]+ (dxy2dxz1dyz1(dz2−y2)1(dz2)1 σ2, S = 2) species, the bond order (bo) drops to 1.5, decreasing further upon passing to Ni2+–O (bo = 1) and Cu2+–O (bo = 1/2). Since the π(3dzx,yz–2px,y) overlap is significantly decreased, such entities acquire a distinct metal–oxyl (M–O˙) character with the high-spin metal core magnetically coupled to the oxyl-moiety.136 Elongation of the M–Ot bond, e.g., in the transition state while interacting with reactants, weakens the 3dπ–2pπ overlap, favouring the highly reactive oxyl state.137 Finally, in the case of the closed 3d10 shell the 3d–2p bond order ceases entirely, and, e.g., a [ZnII–O]+ bonding is realized essentially via the 4s–2p overlap,134 exhibiting a distinct zinc–oxyl nature ((3d)10(σ)2(O2px)2(O2py)1(σ*)0), with the nearly degenerate non-bonding 2px (HOMO) and 2py orbitals (SOMO), see Fig. 8.
Summarizing, vanadium, chromium, or molybdenum terminal oxo-species are relatively rigid and disposed to protonation138 or an electro-protic activity (Mz+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + HR → M(z−1)+–OH + R), which is mainly observed in the photocatalytic reactions, where the reactive excited oxyl state, Mz+
O + HR → M(z−1)+–OH + R), which is mainly observed in the photocatalytic reactions, where the reactive excited oxyl state, Mz+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → M(z−1)+–O˙−, becomes accessible by photon (hν) absorption139–141 or at elevated temperatures (typically 400–500 °C) for thermal catalytic processes.142,143 In the case of Fe, Co, Ni, and Cu, the terminal oxygen functionalities are more chemically labile (unstable), and featured by the co-existence (or close lying and thermally available) electromeric Mz+–O2− ↔ M(z−1)+–O˙− forms.137 They may appear as important intermediates, particularly involved in low-temperature catalytic redox reactions (150–350 °C), entailing hydrogen or oxygen atom transfer processes, exemplified by CH4 hydroxylation135,144 or appear during N2O decomposition that requires somewhat higher temperatures,145 see Chapter 4.3.3 for more details.
O → M(z−1)+–O˙−, becomes accessible by photon (hν) absorption139–141 or at elevated temperatures (typically 400–500 °C) for thermal catalytic processes.142,143 In the case of Fe, Co, Ni, and Cu, the terminal oxygen functionalities are more chemically labile (unstable), and featured by the co-existence (or close lying and thermally available) electromeric Mz+–O2− ↔ M(z−1)+–O˙− forms.137 They may appear as important intermediates, particularly involved in low-temperature catalytic redox reactions (150–350 °C), entailing hydrogen or oxygen atom transfer processes, exemplified by CH4 hydroxylation135,144 or appear during N2O decomposition that requires somewhat higher temperatures,145 see Chapter 4.3.3 for more details.
A brief survey of typical spectroscopic Raman, IR, PL, and UV-vis techniques used for the characterization of terminal Cr-, Mn-, Fe-, Co-, Ni-, Cu–oxo, and Zn–oxyl species encaged in various zeolitic matrices is shown in Fig. 10a–g.
 | ||
| Fig. 10 Survey of spectroscopic techniques used for probing the intrazeolite metal–oxo species. Raman spectra for the Cr/ZSM-5 (Si/Al = 15) catalyst (a).146 UV-Vis spectra of iron in CHA and BEA (b),147 FTIR spectra of Ni-, Mn-, and Co-ferrierite samples showing perturbation of the region of T–O–T vibrations by the corresponding oxo-species (α-oxygen), illustrated here by distant binuclear centers (c),148 UV-vis-NIR vibronic absorption spectra of the isotopically labelled ZnII–O˙− complex formed in the MFI-type zeolite framework (d).137 In situ UV resonance Raman spectra of the high-temperature-treated Fe/ZSM-35 samples with different Si/Fe ratios (e).149 In situ steady-state Raman spectra of Cu/CHA-I (top) and Cu/CHA-M (bottom) after activation with 16O2 and 18O2 and the corresponding structures along with the simulated Raman spectra (f).150 In situ UV-vis spectra of Cu/MOR during activation in O2 at 200 °C and the corresponding difference spectra (blue) obtained by subtracting the initial spectrum (g).151 The figure was based on data from the quoted references. | ||
Apart from providing the spectroscopic fingerprints for identification and monitoring of the investigated species during catalytic reactions, these examples also illustrate the structure sensitivity of the particular signals associated with the mono-oxo and di-oxo states (Fig. 10a–f). It includes the effect related with the Al content in the rings (Fig. 10a), local symmetry distortion of the 6MR rings in the CHA vs. BEA topologies (Fig. 10b), perturbation of T–O–T vibrations by various mono-oxo Mn, Fe, Ni species (Fig. 10c), and the unique structure features of the Zn–oxo entities (Fig. 10d). In the case of bridging-oxo species (vide infra) the effect of the Si/Fe (Fig. 10e), and influence of the Al atoms distribution within the 6MR rings of the CHA framework on the Raman features are shown in Fig. 10f. Formation of the trinuclear coper-oxo clusters, [μ-CuO]32+ accommodated in mordenite can be monitored, in turn, by UV-vis spectroscopy (Fig. 10g). However, it is important to critically evaluate many of the structural assignments of such species reported in the literature.
As already mentioned above, a nucleophilic character (negative partial charge) of the TMI–OH ligands triggers interazeolite olation and oxolation processes, which lead to the appearance of various di- and tri- and even tetranuclear species containing the bridging oxygen moieties (see Chapter 3). The structures of homo-metallic bridging μ-oxo, and bis(μ-oxo) species of various nuclearity for selected cations (Fe, Ni, Co, Cu, Zn) are shown in Fig. 11a–c. Examples of heterometallic M1–(μ-O)–M2 analogues (predicted by DFT) include [Cu(μ-O)Zn]2+ in MFI and FAU zeolites152 or [Cu(μ-O)Ag]2+ entities hosted in ZSM-5.153 The nearest environment (sitting topology) exhibits a noticeable effect on their stability, as illustrated by the μ-oxo [Fe(μ-O)Fe]2+ species, and even more markedly by the bis(μ-oxo) [Fe(μ-O)2Fe]2+ species accommodated in the α, β, γ, δ positions of the ZSM-5 zeolite (Fig. 11d1 and d2).154
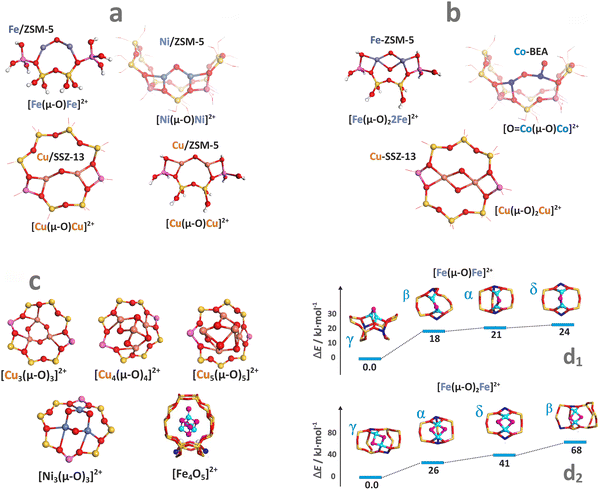 | ||
| Fig. 11 Structure of selected oligomeric oxo-species (derived from DFT optimisation). Mono-oxo species (a), dual oxygen species (b), and oligomeric MxOy species with x ≥ 3 (c).18,149,155–159 Relative stability of the μ-oxo [Fe(μ-O)Fe]4+ (d1), and the bis(μ-oxo) [Fe(μ-O)2Fe]2+ (d2) entities accommodated at the α, β, γ, δ positions of ZSM-5 zeolite.154 The figure was based on data from the quoted references. | ||
It should be emphasized that univocal spectroscopic identification of the particular oxo-entities in the presence of speciation, which is a typical case, is a challenging endeavour. Overlapping of signals, insufficient structure sensitivity, and poor resolution are typical impediments. These can be exemplified by Fe/ZSM-5 zeolites, which may exhibit UV-vis bands virtually identical to those of isolated and dimeric oxo iron sites when the antiferromagnetic coupling is weak.160 Therefore, the application of site-selective spectroscopies such as variable-temperature and variable-field magnetic circular dichroism (VTVH-MCD), resonance Raman, EXAFS, or advanced multifrequency EPR techniques, especially when combined with isotopic labelling, provides the most reliable information on metallozeolites regarding the actual nature of the active sites.5
Apart from the electronic structure, magnetic interactions may also exert an appreciable influence on the catalytic activity of the oxo-species. Therefore, their spin state and the structural and orbital factors that determine the magnetic exchange coupling between the TMI should also be examined for a thorough understanding of the structure–reactivity relationship. This issue has been recently addressed in the case of bridging [Cu(μ-O)Cu]2+ cores hosted in CHA and MFI zeolites.161 The dissimilar spin states, antiferromagnetic in MFI and ferromagnetic in CHA, revealed by variable-temperature/variable-field magnetic circular dichroism spectroscopy, exhibit different reactivities in CH4 hydroxylation. Coupling between both Cu2+ (S = 1/2) cations of the intrazeolite [Cu(μ-O)Cu]2+ species leads to an antiferromagnetic (S = 0) state in Cu-MFI (Fig. 12a) and ferromagnetic (S = 1) ground state in Cu-CHA (Fig. 12b). Surprisingly, it does not dependent on the Cu–O–Cu angle (as it usually is observed in homogeneous complexes), but is governed by the mutual arrangement of the bidentate (π-type ligation) moieties linked to the two copper cations (AlO–Cu–OAl). Therefore, the zeolite framework topology imposes unique spin patterns in the [Cu(μ-O)Cu]2+ cores, resulting in a distinctly different magnetic structure and reactivity through the rigid, stereo-specific bidentate ligation effect.161
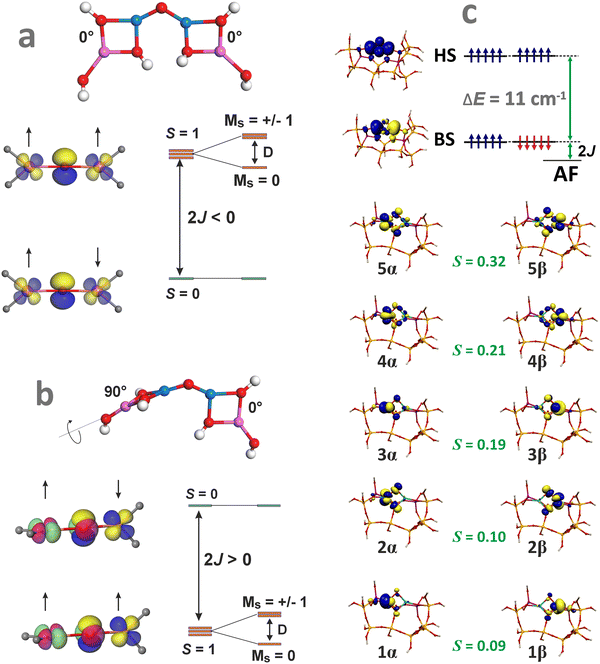 | ||
| Fig. 12 Structural features of the Cu–O–Cu entities that lead to an antiferromagnetic coupling in MFI (a) and a ferromagnetic coupling in CHA (b), based on data from ref. 161. Broken symmetry picture (UKS B3LYP/SOMF TZV/CP(PPP) calculations) of the magnetic structure of the [Fe(μ-O)2Fe]2+ species hosted in ZSM-5 zeolite matrix (c). | ||
Molecular orbital interpretation of the magnetic structure of the exchange-coupled oxygen-bridging cores can be analysed with the DFT broken symmetry (BS) calculations, taking as an example the [Fe(μ-O)2Fe]2+ species hosted in ZSM-5 zeolite.162 The relevant magnetic orbitals are visualized in Fig. 12c. The α/β pairs of magnetic orbitals shown in Fig. 12c constitute symmetric magnetic exchange pathways between the 3d Fe states via the in-plane σ–π overlap (orbitals 1, 2, 4), and the out-of-plane π–π overlap (orbitals 3 and 5) mediated by the 2p oxo orbitals. Such pathways indicate that the antiferromagnetic coupling is realized by the superexchange interactions via both μ-oxo bridges.163 The spin coupling parameter J can be calculated within the broken-symmetry approach using, for example, the EHS − EBS = −(2S1S2 + S2)J equation, which has been demonstrated to provide more accurate coupling constants for DFT calculations.164 The J values for several dinuclear oxo and hydroxo species hosted in the 6MR and 8MR rings of SSZ-13 and in ZSM-5 zeolites can be found elsewhere, along with the impact of the magnetic interactions on N2O decomposition.164,165 These points are discussed in Chapter 4.3.3.
3. Thermodynamic factors influencing the speciation of metal centres in zeolites
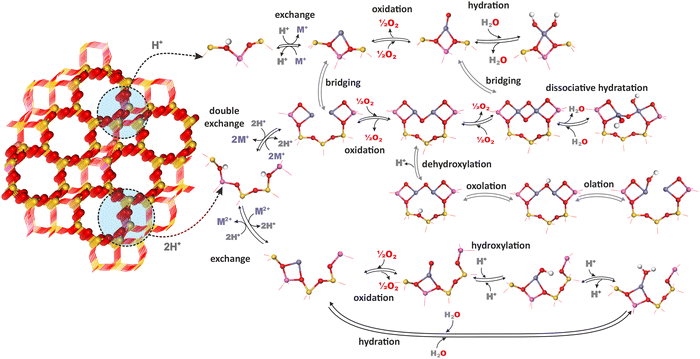
The chemistry of TMI in zeolites is complex because of speciation into isolated bare cations (of different valence state Mn+), isolated oxygen-containing species (metal–oxo and metal–oxyl complexes), dinuclear oxo-cations, larger oligomeric metal–oxo species, and segregated MxOy oxide particles that often coexist within the same zeolite catalyst. They may undergo distinct transformations evolving significantly under different conditions, ranging from catalyst pretreatment and activation to actual reaction conditions.71,166The most important chemical processes during activation of metallozeolites include hydration, hydroxylation, olation, oxolation, auto-reduction (in vacuo) or oxidation in the presence of O2.33,167,168 The interrelation of these processes for zeolite TMI centers (Mn+) associated with single (z1) and double (z2) aluminum sites (isolated and dual exchange centers, respectively), which bear a formal negative charge of −1 and −2, is schematically illustrated in Fig. 13, and the corresponding reactions are summarized in Table 3. The possibility of further transformations of dual metallic centers into polynuclear metal–oxo species is discussed below (Fig. 16). First-principles thermodynamic modelling is often used to provide a clear background for relating the feasibility of these processes to their energetics and various T,p conditions.
| Autoreduction of oxo-species | |
| 2[Mn+–O2−](z) ⇌ 2M(n−2)+(z) + O2 | |
| Direct oxidation to metal–oxo species | |
| Mn+(z) + 1/2O2(g) ⇌ [M–O]n+(z) | |
| Intrazeolite hydrolysis | |
| Associative hydration | Mn+(z) + mH2O(g) ⇌ (z)Mn+–(H2O)m |
| Dissociative hydration (hydroxylation) | Mn+(z) + H2O(g) ⇌ M(OH)(n−1)+(z) + H+ |
| Agglomeration into oligomeric metal–oxo entities | |
| Olation | M(OH)(n−1)+(z) + Mn+(z) → (M–OH–M)(2n−1)+(z2) |
| Oxolation | (M–OH–M)(2n−1)+(z2) → (M–O–M)(2n−2)+(z) + H+(z) |
| Oxidative oxolation | 3[(z)M2+–OH−)] + 1/2O2 → (z2)[M3(μ-O)3]2+ + H2O + H+(z) |
| Merging of metal–oxo species | 2[MO]n+(z) → [M(μ-O)2M]2n+(z2) |
3.1. First-principles thermodynamics of metallozeolites
One of the most useful computational techniques applied for the modelling of metallozeolite catalysts beyond the basic “0 K/UHV model”169 is the first principles thermodynamics (FPT). It integrates density functional theory (DFT) with statistical physics to describe the stability, possible transformations, and reactivity of the investigated system at the atomic level, as a function of the temperature and pressure of reactants.170,171 After appropriate adaptation, FPT is now routinely applied in modelling of the zeolite catalytic materials and their adsorption properties.15,165,172 Typically, (i) a parent zeolite network distinct by the amount and distribution of Al atoms, where formal negative charge generated by z AlOH4 units is counterballanced by z protons (zeolite (zH)), (ii) a bulk metal (M(bulk) – serving as the source of the metallic centers), and (iii) relevant gaseous reagents that may interact with the zeolite centers (e.g., H2O(gas) and O2(gas) in case of catalyst pretreatment) are used as convenient reservoirs of the involved species. Such an assembly is shown in Fig. 16a1, where gas phase, bulk metal, and zeolite parts (b1, b2, and b3, respectively) are used to build a specific model of metal-exchanged zeolite interacting with exemplary O2(g) and H2O(g) molecules. In this case, general equilibrium reaction (eqn (3)) of the zeolitic system (MxHnOm) formation may be formulated as:154
 | (3) |
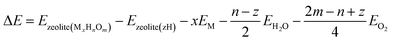 | (4) |
The change in the free energy ΔG due to intrazeolite chemical processes is given by:
 | (5) |
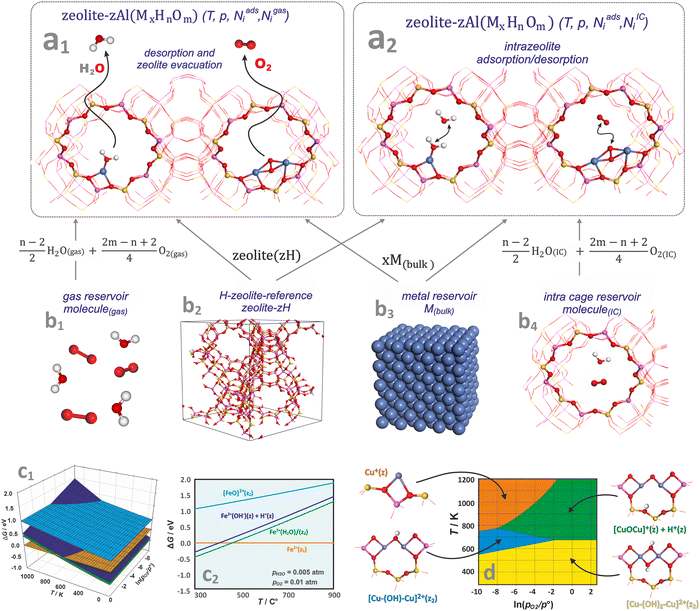 | ||
| Fig. 14 A molecular model of zeolite in equilibrium with free-standing molecules (a1), and molecules trapped inside zeolite cages (a2) together with molecular and bulk-phase reservoirs used in FTP modelling to assemble the zeolite catalyst in equilibrium with the reactants (b1)–(b4). The 3D (c1) and 2D (c2) representations of the thermodynamic diagrams representing the stability of iron species in the Fe/SSZ-13 zeolite as a function of (T,pO2) and (T), respectively. Bottom envelope of 3D FPT diagram representing stability regions (T,pO2) of dual copper sites in the Cu/CHA zeolite (d), based on ref. 181. | ||
Thermodynamic phase diagrams, constructed using first-principles data, provide insight into the various aspects of metal–zeolite chemistry within the widespread operational limits of pressure, temperature, and composition. They are typically presented in the form of 3D (see Fig. 14c1) and 2D (Fig. 14c2) plots, where the Gibbs energy is plotted as a function of temperature and the pressures (or chemical potentials) of the reactants. Due to the constraints imposed by the 2D/3D representation, thermodynamic properties are often presented assuming variable temperature and the partial pressure of one gas reactant, with the other variables fixed or constrained by the reaction stoichiometry (e.g., NO/NH3 = 1 in SCR reaction).
As an example, the stabilities of different iron species present in the Fe/SSZ-13 zeolite are compared in Fig. 14c2 as a function of temperature, with the oxygen and water partial pressures fixed at pO2 = 0.01 atm, and pH2O = 0.005 atm. At low temperatures, the most stable form is the hydrated Fe2+(H2O)(z2) center, which releases a water molecule at around 250 °C. The hydroxylated forms, Fe2+(OH)(z) + H+(z), are slightly less stable than the hydrated Fe cations across the entire temperature range (thus, both forms may coexist). In contrast, the terminal iron-oxo species, [FeO]2+(z2), of the highest free energy, are not expected to appear in the whole temperature range.
To present the results more explicitly, often only the lower envelope of the FPT diagrams (defining the most stable species) is shown (Fig. 14d). Such a 2D diagram, for instance, reveals the thermodynamic conditions of copper auto-reduction in the Cu/SSZ-13 zeolite.181 For low water vapor pressure (pH2O = 10−6), three stable dual-, and one mono-copper sites are expected depending on the (T,p) conditions. At lower temperatures (T < ∼500 K), regardless of the oxygen pressure, the Cu–(OH)2–Cu(z2) dimer dominates, whereas at higher temperatures it transforms into an oxygen-bridged entities, Cu–O–Cu(z) + H(z), with desorption of a water molecule, or into a Cu–(OH)–Cu(z2) dimer upon losing the OH group. These transformations are controlled by the oxygen pressure with a threshold value of ∼0.01 atm. Under the most reducing conditions (highest T and lowest pO2, orange area), copper bridges are expected to decompose, leading to the formation of two adjacent highly reactive monomeric copper(I) centres (Cu(z)) (Chapters 4.3.1 and 4.3.3).
FPT modeling is also a convenient tool that enables comparison of the stability and evolution of intrazeolite active sites such as (z)FeOH, (z2)FeOH, (z)FeO, (z2)[FeO]2+, (z)Fe-OH2 in the six- or eight-membered rings (6MR or 8MR) of Fe/SSZ-13.187 The corresponding phase diagram (Fig. 15a1) implies that H2O prefers to adsorb on a Fe+ cation in a wide range of temperatures. However, the hydrated sites are much less stable than the hydroxylated (z)FeOH and (z)FeO species, which dominate at low and high temperatures, respectively. The most energetically favourable sites for iron accommodation are 6MR rings (Fe in 8MR are less stable by 0.5 eV). Still, upon ligation of water, hydroxyl, and oxygen species, the energy gap between Fe located in the 8MR and 6MR sites becomes negligible. The K-edge of XANES spectra (see the simulated spectra in Fig. 15a2) is diagnostic for the presence of those ligands in the coordination sphere of the Fe cations.187
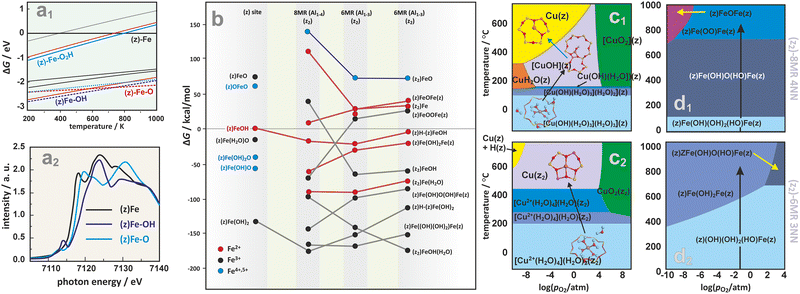 | ||
| Fig. 15 2D thermodynamic diagram representing stability of iron active centers formed within the six- or eight-membered rings (6MR or 8MR) of Fe/SSZ-13 (a1), together with the associated XANES spectra simulated for the most important species (a2).187 The expanded diagram (b) comparing the stability of Fe species on isolated (z1) and dual (z2) exchange centers positioned in 8MR and 6MR rings of CHA zeolite with different Al distribution (Al1–3 vs. Al1–4).165 Calculated (HSE06-TSvdw) copper speciation phase diagrams for 1Al (c1) and 2Al (c2) exchange sites of Cu/SSZ-13.188 Phase diagrams for iron speciation in Fe/SSZ-13 zeolite as a function of relative O2 pressure and temperature with p(H2O) set at 0.02 atm, constructed for sites stabilized within the z2-8MR (d1) and z2-6MR (d2) rings.165 The figure was based on data from the quoted references. | ||
A more advanced analysis of the stability of different iron forms in the isolated (z) and dual (z2) exchange centers in the chabazite-type zeolite is ilustrated in Fig. 15b, where ring multiplicity (8MR vs. 6MR), internal aluminum distribution (Al1–3 vs. Al1–4), formation of bridged species and the possibility of iron existing in higher oxidation states are taken into account as well.165 This diagram can be used to track the evolution of Fe sites under various pretreatment conditions, showing that autoreduction temperatures and water desorption conditions are highly dependent on the proximity of aluminum atoms and the nuclearity of iron.
In the case of Cu/SSZ-13 zeolite, the akin phase diagrams representing evolution of CuOH(z) and Cu(Z2) as a function of temperature and O2 pressure at fixed H2O pressure,188 are shown in Fig. 15c1 and c2, respectively. Both Cu sites are hydrated under ambient conditions (where solvated Cu2+–H2O and [CuOH]+ dominate), and become dehydrated at elevated temperatures in an O2 environment. However, only CuOH(z) species undergo autoreduction to monovalent copper (Cu(z)) in the inert environment (Fig. 15c1). The preference of populating the Cu(z2) sites over CuOH(z) sites is independent of the extent of hydration.15
A comparison of the Fe ions' stability in the 8MR (Fig. 15d1) and 6MR (Fig. 15d2) rings of the Fe/SSZ-13 zeolite as a function of T, pO2, and pH2O165 revealed a dramatic impact of the ring multiplicity on the distribution of dimeric iron centers. At room temperature, the most stable species are the iron-dimers ligated by water (without their detachment from the framework). They are initially in the most stable trivalent state, and as the temperature rises, all sites transform into partially dehydrated entities at T = 100 °C and 450 °C for 8MR and 6MR, respectively. An additional difference of even greater significance for the catalytic activity arises from the fact that the dimers in the 8MR ring transform into (z)Fe–(μ-O)2–Fe(z) bridging species, while the 6MR dimers are stabilized as (z)Fe–(OH)2–Fe(z). The latter sites contain divalent iron and may be treated as “autoreduced” (similarly to the monocopper sites in Cu-/SSZ-1361,188). The autor-eduction temperatures vary widely from site to site, and the high-temperature activated zeolites are expected to contain a mixture of Fe2+ and Fe3+. The validity of such prediction has been proven for Fe/ZSM-5 and Fe/Y zeolites heated in helium (or in vacuum) using the X-ray absorption and Mössbauer spectroscopies.189,190
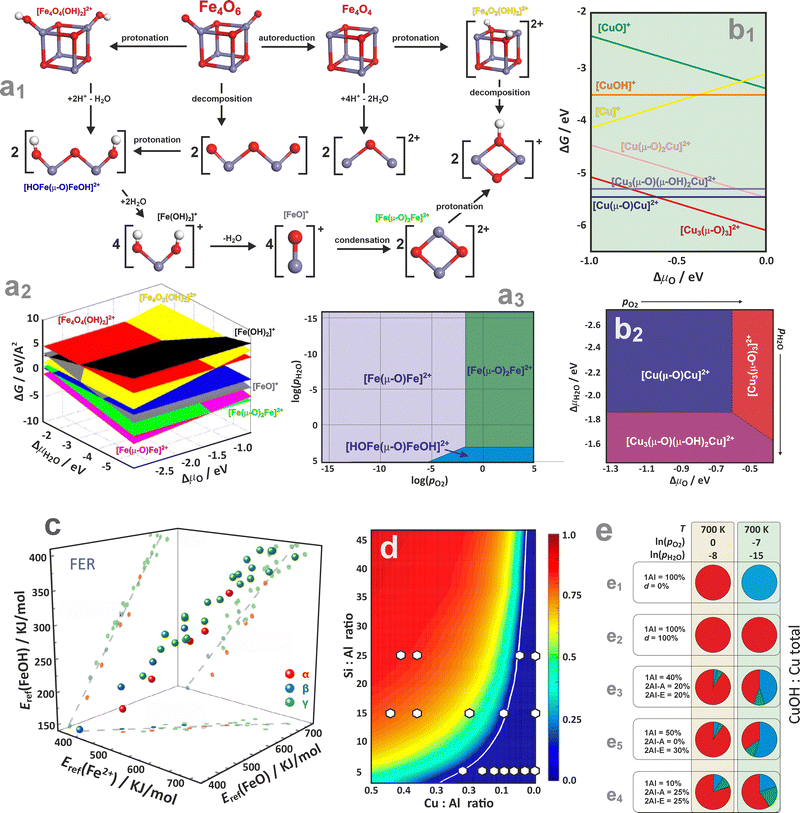 | ||
Fig. 16 Possible transformations of a cubic Fe4O6 cluster (a1), together with the FPT diagram representing the stability of the most important iron forms in the 3D (a2) and 2D (a3) representation, based on data from ref. 154. The relative stabilities of multi-nuclear copper species hosted in the ZSM-5 zeolite, as a function of ΔμO (b1) and (T,pO2) (b2), based on data from ref. 191. The stability correlations of the Fe2+, [FeO]2+, and [FeO]2+ species accommodated in the ferrierite α, β, and γ sites (c), adapted from ref. 195 with permission from Wiley, Copyright 2025. The CuOH/Cu fraction plotted as a function of the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al and Cu Al and Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al, revealing regions representing a composition space where Cu2+ species dominate (below white line), and a space where gradual increase in the [ZCuOH]+ fraction is expected (above the white line), white circles denotes experimental results (d), adapted from ref. 188 with permission from American Chemical Society, Copyright 2016. Distribution of Cu2+, Cu+, [Cu2OH]2+ species (coded with blue, red, and green, respectively), presented as pie charts for Cu/SSZ-13 zeolite hypothetical samples (e) based on data from ref. 61. Samples (e1)–(e5) differ in the distribution of the monomeric and dimeric exchangeable 1Al and 2Al centres, in Al pair arrangements, and in defect concentrations (d) and are studied under different conditions (top and bottom row). Al, revealing regions representing a composition space where Cu2+ species dominate (below white line), and a space where gradual increase in the [ZCuOH]+ fraction is expected (above the white line), white circles denotes experimental results (d), adapted from ref. 188 with permission from American Chemical Society, Copyright 2016. Distribution of Cu2+, Cu+, [Cu2OH]2+ species (coded with blue, red, and green, respectively), presented as pie charts for Cu/SSZ-13 zeolite hypothetical samples (e) based on data from ref. 61. Samples (e1)–(e5) differ in the distribution of the monomeric and dimeric exchangeable 1Al and 2Al centres, in Al pair arrangements, and in defect concentrations (d) and are studied under different conditions (top and bottom row). | ||
Going beyond the charged mono- and dimeric centres requires a sensible postulation of proper chemical processes interconnecting the dispersed and oligomeric metal species in the presence of H2O, O2, and the zeolitic protons as well. An exemplary diagram representing possible transformations of a bulky Fe4O6 cluster hosted in the Fe/ZSM-5 zeolite is shown in Fig. 16a1.154 Its decomposition into binuclear species (via protonation at Brønsted acid sites) proceeds either through hydrolysis, leading to isolated oxygenated or hydroxylated mononuclear species, or through dehydration, forming oxo-bridged [Fe(μ-O)Fe]2+ species. Thermodynamic diagrams confirm that the intrazeolite [Fe(μ-O)Fe]2+ and [Fe(μ-O)2Fe]2+ binuclear complexes represent the most stable species under typical reaction conditions (Fig. 16a2–a3). They preferentially occupy the γ site (8MR), but other iron varieties of comparable stability can also lodge at the α, δ, and β sites (6MR). Oxygen pressure controls the thermodynamically preferred mixing between the [Fe(μ-O)Fe]2+ and [Fe(μ-O)2Fe]2+ binuclear clusters. The formation of Fe2+ ions and binuclear complexes occurs only at high temperatures, aligning well with experimental observations.154
Comprehension of thermodynamic conditions is crucial when analysing multinuclear copper species in ZSM-5 zeolites, as the stability of the extra-framework complexes involved is strongly influenced by temperature and the composition of the gas phase (Fig. 16b1 and b2).191 The binuclear Cu sites correspond to the lowest-energy structures, yet under the O2-rich conditions, typically employed for the activation of Cu/ZSM-5 catalysts, when T- and p-related effects are taken into account, the [Cu3(μ-O)3]2+ trinuclear complex turns out to be more stable than the mono- and binuclear species. The intrazeolite mononuclear oxo- and hydroxo-complexes are generally less stable than the oligonuclear species.192–194
The thermodynamic analysis can also be used to draw more general conclusions than the relative stability of TMI within the given zeolite network structure. For example, a noteworthy analysis of the FTP data on iron species stabilized in the 6MR, 8MR sites of chabazite, and α, β and γ sites of ferrierite zeolites (Fig. 16c), allowed for the demonstration that there is a distinct linear correlation (R2 ∼ 0.9) between the stabilities of the Fe2+, [FeO], and [FeOH]+ species.195 This implies that the stability trends of the related Fe2+, [FeO], and [FeOH]+ species with the varying framework type and the Al distribution remain consistent, regardless of thermodynamic conditions, and are, therefore, of a more general character.
The impact of Al arrangements on the monomer and dimer configuration of Cu cations and their oxidation state, concerning the auto-reduction of Cu in SSZ-13,188 is illustrated in Fig. 16d. Within the assumption that the exchanged copper ions initially populate all available dual sites as Cu2+/z2, before occupying 1Al sites in the form of Cu2+OH/z, the CuOH/Cu fraction can be assessed as a function of the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al and Cu
Al and Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratios.196,197 Two distinct regions, where Cu2+ species associated with 2Al are expected to dominate (below the white line), and where a gradual increase in the Cu2+OH/z fraction is predicted (above the white line), can be distinguished. This diagram helps to rationalize the speciation of copper in real catalysts (white circles) depending on the Al/Si and Cu/Al ratios. Furthermore, the pie charts can be used for concise illustration of the relative contributions of key copper species in CHA61 (Cu+ – blue, Cu2+ – red, [Cu2OH]2+ – green), depending on the zeolite composition (Si/Al, Al pair arrangements, defect concentrations) and thermodynamic (oxidizing or reducing) conditions (Fig. 16e).
Al ratios.196,197 Two distinct regions, where Cu2+ species associated with 2Al are expected to dominate (below the white line), and where a gradual increase in the Cu2+OH/z fraction is predicted (above the white line), can be distinguished. This diagram helps to rationalize the speciation of copper in real catalysts (white circles) depending on the Al/Si and Cu/Al ratios. Furthermore, the pie charts can be used for concise illustration of the relative contributions of key copper species in CHA61 (Cu+ – blue, Cu2+ – red, [Cu2OH]2+ – green), depending on the zeolite composition (Si/Al, Al pair arrangements, defect concentrations) and thermodynamic (oxidizing or reducing) conditions (Fig. 16e).
4. Interfacial coordination chemistry – principal pathways of ligation
4.1. Molecular picture of ligation
Most simply, the binding of reactants to encaged metal centres can be rationalized in terms of the molecular orbital diagrams, which can be categorized into normal (NEL), mixed (MEL), and inverted (IEL) energy level schemes (Fig. 17a1, a2, and a3, respectively).198 In the case of open-shell cations such as Fe2+ (S = 2), Co2+ (S = 3/2) Ni2+ (S = 1) or Cu2+ (S = 1/2), typically involved in important catalytic reactions with zeolite materials,13,18,199 for sensible interpretation the corresponding energy level diagrams should be constructed for the α and β channels separately, including the exchange splitting (see Fig. 8). In the normal scheme (Fig. 17a1), the 3d levels of the metal centre lie above the occupied levels of the ligands. Since the filled 3s2p6 sub-shell shields the inner 3d orbitals, the resultant Pauli repulsion leads to ‘stretched’ M–L bonds, which secures the integrity of the 3dn configuration upon ligation.198 This classic Werner-type scheme is characteristic of the intrazeolite 3d cations, typically in the 2+ oxidation states interacting with the innocent σ-donor ligands such as NH3 or H2O (see Chapter 4.2). Intrazeolite adducts with more extensive metal–ligand covalency may lead to the mixed (MEL) pattern (Fig. 17a2). In the most extreme situations, when 3d levels are situated below those of the ligand, which may be caused by enhanced oxidation state and/or exchange interactions (in the case of open-shell systems), an inverted scheme (IEL) shown in (Fig. 17a3) is appropriate. Two mechanisms can be distinguished by which the Pauli shield (Fig. 17b) can be breached, and the 3dn integrity of the metal core perturbed. When the cation oxidation state becomes too positive, the 3d orbitals are shifted down in energy so far that the Pauli shield can be broken (from ‘outside’) by the redox ligands. Analogically, when the 3d orbitals become sufficiently electron-rich, they may overcome the Pauli shield from ‘inside’ and transfer electron density onto ligands (such as O2), altering the 3dn configuration of the metal core.198 These binding modes are discussed in detail in Chapter 4.3. | ||
| Fig. 17 Schematic representation of the metal–ligand energy levels (a1)–(a3), epitomic representation of the Pauli shield (b),198 and principal types of the molecular orbital overlap sorted by symmetry (c). Five categories of the spin density distributions defining a magnetophore of the open-shell intrazeolite adducts (d), and an exemplary illustration of a zeolite nano-cage reactor with the associated signifiers (e). | ||
Attachment of molecules to the caged transition-metal cations via σ, π, and δ type overlap (Fig. 17c) may occur in an isodesmic (with conservation of the number of bonds) or an alterdesmic (with a change in the total number of bonds) way. In the former case, new covalent bonds with the coordinated reactants are formed at the expense of the strained bonds between the metal center and the zeolite Oz ligands. The simplest behaviour of intrazeolite transition metal complexes of NEL character in the catalytic redox process consists of oxidation or reduction of the metal centre only, leaving the redox state of the ligands unaffected. Yet, the ligands control indirectly the redox properties of the metal core by modifying the energy levels of the 3d orbitals (see Chapter 4.2.4). In some cases, however, ligands can also participate in the redox process. Then, such ligands are referred to as non-innocent or redox ligands (see Chapters 4.3.1 and 4.3.2).
As a result, the four leading roles the ligated molecules can play in the catalytic reactions are as follows. (i) Tuning of the metal catalytic properties through reduction/oxidation, which strongly influences the affinity to capture reactants, and the mechanistic course of ensuing follow-up reactions. (ii) Acting as an “electron-reservoir” in the case of redox active ligand, which allows the metal to store and release electrons on the ligand moiety (anionic redox) in the elementary steps unavailable on the metal core only. (iii) The formation of reactive ligand-radicals that actively participate in the making and breaking of chemical bonds during catalysis. (iv) The modification of the substrate reactivity in cases where the substrate itself acts as a redox non-innocent ligand.200
The redox reactivity of the open-shell species, in particular, is governed by the spin density distribution between the metal core and the ligated molecule that both constitute a common magnetophore. The latter notion, analogous to the chromophore in optical spectroscopy, refers to the molecular fragment of a paramagnetic adduct where the bulk of the spin density is confined, thereby determining the magnetic properties of the entire system essentially. Three main magnetophore patterns are categorized as ligand-centred, mixed, and metal-centred (Fig. 17d). The locus of the highest spin density defines the centre of the preferential attack of paramagnetic reactants such as NO, O2, or NO2 (see Chapter 4.3.2). The zeolite aperture controls, in turn, the accessibility of these centres to the reactant molecules. In contrast, the speciation and reactivity of the active sites are significantly influenced by the framework topology and the associated confinement effects, as well as the Si/Al and M/Al ratios, and the spatial distribution of the Al atoms. Those aspects are epitomized in the form of a zeolite nanoreactor in Fig. 17e.
 | (6) |
The νk stands for the NOCV eigenvalues, and M for the number of basis functions. The eigenvalue expresses a fractional electron population transfer in each electron flow channel. For open-shell systems, the decomposition is carried out separately for the α and β electron densities (spin-resolved NOCV). Afterwards, the contributions of similar orbital character appearing in both spin densities can be treated jointly. The NOCV analysis, combined with the Ziegler–Rauk extended transition state energy decomposition scheme (ETS-NOCV),202 allows for the partitioning of the total orbital interaction energy into particular NOCV channels (k,−k):
 | (7) |
The integrals FTSij = 〈i|∇2/2 + Vne + VC[ρTS] + Vxc[ρTS]|j〉 are matrix elements of the Kohn–Sham operator evaluated for the electron density at the “TS” state, which is given by ρTS = 1/2ρ + 1/2ρ0 (ρ and ρ0 represents the electron density of interacting and non-interacting fragments, respectively).202 The NOCV method has enabled a deeper understanding of the origin of the IR red shift of the stretching C–C frequencies due to metal–ligand bonding on the Cu and Ni centres of ZSM-5 zeolite,203 and it has also provided a reliable description of various non-covalent interactions.204,205 The ETS-NOCV analysis has also been used to unravel the binding mechanism of dinitrogen, carbonyl (Chapters 4.2.3 and 4.2.4), superoxide (Chapter 4.3.1), and nitrosyl adducts (Chapter 4.3.2) of nickel, copper, and cobalt ions in the exchangeable positions of various zeolites.
4.2. Ligation of innocent molecules
Innocent molecules such as H2O, NH3 are the non-redox ligands that interact with metal centres in metallozeolites primarily through sigma-donation (Fig. 17a1). The strength and nature of sigma-donation depend on several factors, among them, the most important are electronegativity and hardness/softness of the metal centres (according to the HSAB principle, where Cu2+, Ni2+, Fe3+, etc., exhibit different affinities towards innocent ligands), availability of coordination sites on the metal ion within the zeolite framework, and the intracage solvation effects that may modulate metal–ligand interactions.206–208 Moreover, the ability of innocent molecules to form multiple coordination σ-bonds (poly-molecular adsorption) with metal ions is controlled by the oxidation state and the electronic structure of metal ions, and the cage size of the zeolite framework.209,210 It is well established that the interaction of H2O and NH3 with metallozeolites can also lead to partial or complete detachment of the metal ion from the zeolite framework.211 This occurs through ligand-induced solvation, where strong coordination of ligands stabilizes the metal ion inside the cage. This effect plays a vital role in modulating the catalytic activity within the zeolite pores. In light of these facts, although such reagents are considered innocent, their impact on the catalytic and adsorption properties of metallozeolites is significant. Other innocent ligands, often used to probe the valence and coordination states of the intrazeolite TMI by IR, are CO and N2 molecules. Although their adsorption energy has a pronounced dispersion component, a minute electron exchange between the ligated N2 or CO and the metal is responsible for the observed site sensitivity (see Chapters 4.2.3 and 4.2.4).While water is often considered a co-reagent in catalytic processes and implicated in specific reaction steps,152,213,214 more general studies aiming to identify general trends in its interaction with metal centres are relatively scarce. In this context, B3LYP-DFT cluster calculations of water adsorption on various divalent metal centres (Zn2+, Cu2+, Ni2+) stabilized at exchange positions I and II in zeolite Y (Fig. 18a) can be invoked as a suitable example.215 The oxidation state and type of the cation have a greater impact on the adsorption than the specific exchange position. An ALMO (absolutely localized molecular orbitals) analysis,216,217 allowed for the decomposition of the adsorption energy into none-CT (non-charge transfer), ligand to metal charge transfer (CT(X → MY)), metal to ligand charge transfer (CT(MY → X)), and CT(HO) terms. This reveals that the electronic H2O-TMI interactions are primarily governed by the non-CT and CT(X → MY) contributions, in contrast to those previously studied for alkali metal sites.
 | ||
| Fig. 18 Adsorption of water on divalent metal centres (Zn2+, Cu2+, Ni2+) located at the exchange positions I and II in zeolite Y, together with ALMO EDA analysis for Zn2+ in II site of Y zeolite (a), based on data from ref. 215. Cluster models (b1) and (b2) and water adsorption energies on Cu2+, Zn2+, and Fe2+ incorporated in FAU (b3), together with the iso-surface electron density contour for Fe2+–H2O (b3, insert), adapted from ref. 218 with permission from Royal Society of Chemistry, copyright 2022. Adsorption energy of water on various TMI centres incorporated in MOR framework in the high (HC) and low coverage (LC) limits (c), based on data from ref. 219. Optimised geometries of the copper poly-aqua complexes (d1)–(d5), together with the corresponding 2D thermodynamic stability diagrams constructed for the 8MR (e1) and 6MR (e2) exchangeable sites of CHA. The panels (a)–(d) were based on data from the respective references. Panels (e1) and (e2) were based on data from ref. 83. | ||
Comparison of water adsorption on divalent cations (Cu2+, Zn2+, Fe2+) incorporated in FAU zeolite (see Fig. 18b1–b3) shows that Zn2+ and Cu2+ exhibit the strongest interactions with water, with the adsorption energies of −105.3 kJ mol−1 and −81.6 kJ mol−1, respectively.218 These values, comparable to those of alkaline earth metal cations, may be attributed to their significant HSAB hardness. This is further supported by the iso-surface electron density contours (Fig. 18b3, insert), which agree well with theoretical studies on mordenite, where the influence of high (HC) and low (LC) coverage is illustrated (Fig. 18c).219
A more thorough approach to studying water ligation involves a set of copper multi-aqua complexes in different configurations (Fig. 18d1–d5)83 to construct 2D thermodynamic stability diagrams for the 8MR (Fig. 18e1) and 6MR (Fig. 18e2) exchangeable sites of CHA zeolite. This analysis reveals the level of ligation at which a copper cation is pulled out from the zeolite rings, gradually acquiring considerable mobility within the cages. Regardless of the site, this occurs when four H2O ligands are bound to a Cu cation. When the charge of the cation is reduced, a smaller number of solvent molecules is needed for the detachment, as illustrated by Cu+(H2O)2 species entrapped in mordenite.161 Then, the polyaqua-complexes exhibit sufficient mobility to migrate between the zeolite channels. For selected H2O pressure of 10−4 (typical for the NH3-SCR reaction, marked with a dashed line), this condition is met below 125 °C (8MR) and below 75 °C (6MR).
 | ||
| Fig. 19 Optimized geometries of the Cu2+–(NH3)n adducts located in the 6MR site of CHA (a). The 3-dimensional diagrams of ΔG vs. T, pNH3 (b1) and ΘNH3 vs. T, pNH3 (b2), together with the corresponding cross-sections for pNH3 set to 10−4 atm (b3) and (b4). The overall calculated TPD profile with all component bands (c1). The experimental NH3-TPD profile obtained for samples differing in Si/Al ratio (c2). Adapted from ref. 227 with permission from John Wiley and Sons, Copyright 2021. | ||
At lower temperatures, when higher coordination numbers of TMI to ammonia are expected (n > 2), detachment and mobilisation of the metal cations from the zeolite framework is typically observed (analogous to the water ligation case). This phenomenon has been extensively investigated due to its crucial role in the low-temperature NH3-SCR process.179,229 A combination of computational (DFT-HSE06) and experimental (XANES, XAS) studies has been applied to thoroughly examine different Cu–(NH3)n complexes under in situ, ex situ, and operando SCR conditions, considering variations in the catalyst composition.228 The copper speciation, mobility, and its actual siting are primarily dictated by environmental factors, rather than the initial location of the Cu cations or the type of zeolite framework. As an example, the mobility of [Cu(NH3)2]+ within the CHA framework, as revealed by ab initio meta-dynamic simulations, is shown in Fig. 20a1. The Cu ion migration through the 8-MR rings between two cages requires an activation energy ∼55 kJ mol−1, confirming that the CHA framework provides sufficiently large windows for efficient intrazeolite diffusion of the [Cu(NH3)2]+ species, triggering the oxidation half cycle (OHC) of the SCR reaction.15,179,229
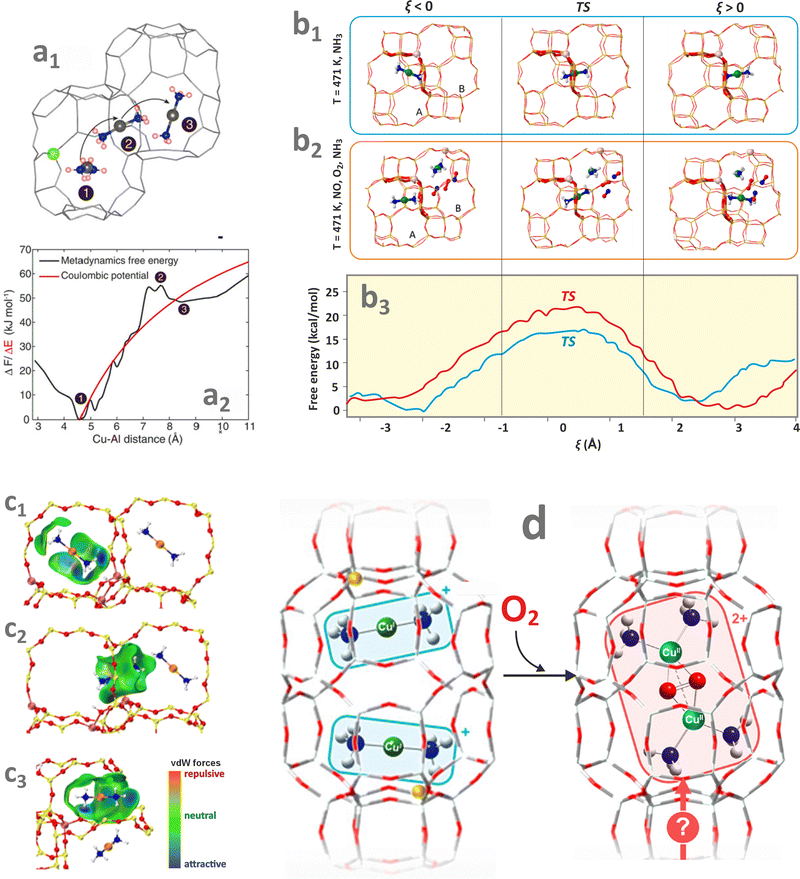 | ||
| Fig. 20 The migration pathway of [Cu(NH3)2]+ species presented inside the channels of CHA zeolite (a1), together with the corresponding free energy profile plotted against Cu–Al distance (a2), adapted from ref. 228 with permission from the American Association for the Advancement of Science, Copyright 2017. Representative configurations of [Cu(NH3)2]+ in the initial state (ξ < 0), transition state (TS, ξ = 0), and final state (ξ > 0) during the diffusion through the 8-membered ring windows of Cu-CHA without co-adsorbed molecules (b1) and in the presence of O2 and NO (b2), together with the corresponding free energy profiles as a function of the reaction progress ξ (b3) at 423 K, adapted from ref. 229 with permissions from American Chemical Society and The Authors, Copyright 2021. The initial (c1), transition (c2), and final state (c3) structures of the [Cu(NH3)2]+ complex migrating from 6MR rings with a single Al to 6MR with a pair of Al, adapted from ref. 231 with permission from American Chemical Society, Copyright 2024. Postulated route of formation of mobile μ-η2,η2-peroxo diamino dicopper(II) complexes upon oxidation of the [Cu(NH3)2]+ species (c), adapted from ref. 232 under the terms of the CC BY 4.0 license, Copyright 2022, published by American Chemical Society. | ||
The role of Cu ion mobility in Cu/SSZ-13 has also been explored using large-scale simulations, employing an interatomic potential obtained from machine learning that accurately replicates the ab initio results.229,230 A combination of biased and unbiased simulations enabled an in-depth analysis of the [Cu(NH3)2]+ mobility in Cu-CHA catalysts, revealing that the Al pairing within the 8-MR rings facilitates local hopping, whereas higher NH3 concentrations enhance long-range diffusion. The [Cu(NH3)2]+ migration under NH3–SCR–NOx conditions obtained from AIMD simulations is illustrated in Fig. 20b1–b3. The diffusion is hindered when additional NO/O2 molecules are present in the zeolite cavity (Fig. 20b2). Furthermore, a decrease in the number of BAS sites leads to an increase in the diffusion barrier of [Cu(NH3)2]+. The van der Waals interactions between [Cu(NH3)2]+ and the zeolite framework (Fig. 20c1–c3) are significantly influenced by the BAS distribution, inhibiting the low-temperature NH3-SCR activity.231 For zeolites of uneven Al distribution, variations in the interaction energy between [Cu(NH3)2]+ and the zeolite framework are mainly responsible for the inter-cage diffusion. The migration of [Cu(NH3)2]+ from an Al-poor cage to an Al-rich cage exhibits a lower diffusion barrier, favouring the formation of active dimer-Cu species and enhancing the SCR reaction.
The oxidation of mobile diamino copper complexes (Fig. 20d) monitored by XANES and EXAFS techniques shows consistently that the Si/Al ratio of the zeolite hosts influences the structure of the mobile μ-η2,η2-peroxo diamino dicopper(II) adducts, which are formed during the oxidation of [Cu(NH3)2]+ complexes by O2 (OHC).232
The interest in dinitrogen coordination chemistry is mainly associated with gas separation, such as N2/O2, CO2/N2, or CH4/N2233 and the challenging activation of the highly inert N2 molecule. Catalytic nitrogen fixation, as well as air separation, begins with the coordination of N2 to the transition metal centres. As a ligand, N2 exhibits certain similarity to the isoelectronic CO, since both molecules are diatomic, having a strong triple bond (σ,2π) and empty antibonding 2π* orbitals. Dinitrogen usually coordinates to metal cations in an end-on (η1) mode. In contrast to CO, which often forms polycarbonyl complexes (see Chapter 4.2.4), both experimental and theoretical results show that the dinitrogen complexes with the intrazeolite TMI ions usually contain one or two (at low temperatures) N2 ligands only.80,234 Typical examples include Cu+ and Cu2+ centers in ZSM-5235,236 MOR,237 and BEA,238 as well as Ni+ and Ni2+ hosted in ZSM-580,239 or Fe2+, Cu2+, Zn2+ in CHA.233 Apart from the most common η1-attachment, stable trans and cis μ-η1:η1 and μ-1,2 adducts of N2 with Cu+ in ZSM-5 (computationally optimized) have also been reported, see Fig. 21a.240 Dinitrogen interacts relatively strongly with the intrazeolite TMI with energies varying from −100 to −20 kcal mol−1, depending on the framework type and accommodation site (see Fig. 21b).234,240
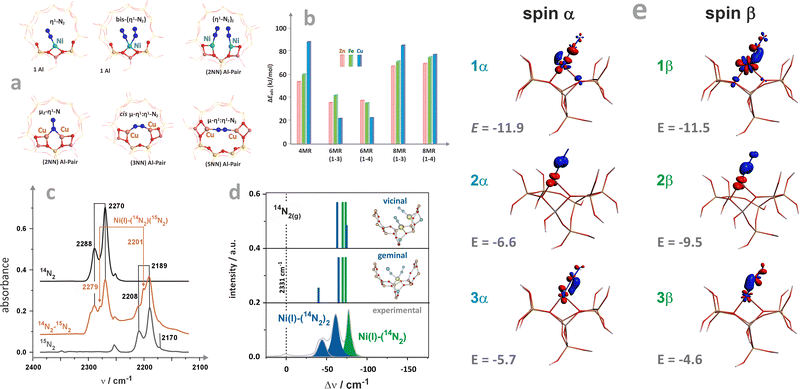 | ||
| Fig. 21 Stable binding modes of N2 to Ni+ and Cu+ in ZSM-5 (a). Adsorption energies of N2 on selected metallozeolites (b). IR spectrum of 14N2 and 15N2 adsorption on Ni+/ZSM-5 zeolite (c), together with the calculated IR bands for two possible conformations of di-N2 adducts (d). The NOCV analysis of the σ- and π-type bonds in {(η1-N2)2Ni+}/ZSM-5 complex (e). Panels a, b, and c were based on the data from ref. 234 and 240. Panels d and e adapted from ref. 80 with permission from Elsevier, Copyright 2020. | ||
While forming intrazeolite adducts, N2 is coordinated by σ- and π-type bonds. The TMI–N2 bonding depends on the overlap between the available 3d-orbital with the σ (HOMO) and 2π* (LUMO) orbitals of the dinitrogen molecule. Such an overlap pattern implies a synergy of the σ-donation and π-backdonation interactions.236 Therefore, the resultant electron density redistribution between the metal and N2 ligand leads to a decrease in the N–N bond order. As a result, the N–N stretching frequency is lower than the corresponding frequency of a gas-phase molecule (2331 cm−1), see, e.g., IR spectra of N2 with NiI/ZSM-5 in Fig. 21c. Apart from orbital contributions, the N–N vibration frequencies also have an electrostatic component, Δνtot = Δν(σ+π) + Δνel, which makes them particularly sensitive to the oxidation state of the metal centre.236 These features make the N2/IR method a convenient spectroscopic probe for measuring the electron donor/acceptor properties of the intrazeolite TMI. The N–N stretching frequency of the CuI–14N2 species is observed in the region of 2300–2285 cm−1,236 for NiI–N2 at 2254–2252 cm−1.80 In contrast, for NiII–N2 it increases to 2324 cm−1,239 revealing the different extent of back π-donation and the diverse oxidation states of the TMI centres as well.
The Ni+ ions hosted in Ni–ZSM-5, in contrast to Cu+/ZSM-5,241 can coordinate two N2 molecules simultaneously, and the ensuing {(η1-N2)2Ni+}9 adducts are characterized by νs at 2288 cm−1 and νas at 2270 cm−1.234 The coupling between the two N2 ligands is usually confirmed by co-adsorption of 14N2 and 15N2 isotopic mixtures. Because of the presence of mixed ligands (14N2 15N2), the resultant structural dichotomy of possible formation of the geminal (η1-N2)2Ni+/ZSM-5 and two coupled vicinal (η1-N2)Ni+⋯(η1-N2)Ni+ adducts can be resolved by complementary DFT modelling, see Fig. 21a.80 The calculated spectroscopic IR signatures of both types of dinitrogen adducts, shown in Fig. 21d, allow for a straightforward distinction between the types of complexes. In particular, the coupling through bonds in the geminal adducts is stronger (25 cm−1) than the coupling through space in the vicinal ones (12 cm−1).
The intimate mechanism of N2 bonding and the delicate balance between the σ-donation and the back-donation effects, which are responsible for the IR shifts, can be unravelled and quantified by NOCV analysis. The main orbital contributions to the α and β electron density flows are shown in Fig. 21e, together with the corresponding energy values. The α-polarized σ-donation from the N2 ligand (1α) is accompanied by electron relaxation of the β-3d manifold of the NiI centre, consisting of depopulation of 3dx2−z2 and population of 3dxz (1β), and both flow channels exhibit similar energy contribution to the binding. Such deep electronic relaxation is typical of the TMI that undergoes anisodesmic changes in its structure upon binding (CN = 4 for bare Ni+/ZSM-5 centre changes into CN = 3 in the case of dinitrogen adduct), see also Chapters 4.2.4, 4.3.1, and 4.3.2. The π channel of the back-donation is constituted by the 2α + 2β spinorbitals, and involves the out-of-plane  orbitals of N2 and 3dyz of Ni. The resultant electron density flow is primarily responsible for the lessening of the N–N stretching frequency. The second (3α + 3β) channel of the π-symmetry is formed by the overlap between
orbitals of N2 and 3dyz of Ni. The resultant electron density flow is primarily responsible for the lessening of the N–N stretching frequency. The second (3α + 3β) channel of the π-symmetry is formed by the overlap between  and 3dxz orbitals. The resultant flow of electron density along this channel leads to the accumulation of the electron density within the Ni–N bond at the expense of the π and 3d states. Therefore, it can be designated as a dative coordinative contribution. Overall, the π donation/back-donation effects account for 53% of the orbital interactions, whereas the σ channel is in charge of 24% of the binding strength. This allows for unravelling the intimate nature of the Ni+–N2 bonding and the observed bathochromic shift of the stretching vibrations.80
and 3dxz orbitals. The resultant flow of electron density along this channel leads to the accumulation of the electron density within the Ni–N bond at the expense of the π and 3d states. Therefore, it can be designated as a dative coordinative contribution. Overall, the π donation/back-donation effects account for 53% of the orbital interactions, whereas the σ channel is in charge of 24% of the binding strength. This allows for unravelling the intimate nature of the Ni+–N2 bonding and the observed bathochromic shift of the stretching vibrations.80
Structure of carbonyls and formation of TMI–CO bond. Transition-metal cations hosted in zeolites upon contact with CO form carbonyl adducts rapidly. The CO molecule prefers to bind via a metal–carbon bond, despite carbon being less electronegative than the oxygen atom. The HOMO of CO exhibits an essentially non-bonding character, and this orbital is primarily localized at the carbon moiety. Since the π and π* orbitals are relatively close in energy to the HOMO, they can also be involved in the bonding of carbonyls.
Bonding of CO to TMI in zeolites can be described by the classical synergistic effect of σ-donor and π-acceptor interactions (Fig. 22a), commonly referred to in textbooks as the Dewar–Chatt–Duncanson model. It serves as the basis for more advanced analysis based on quantum chemical calculations.242 Briefly, the σ-donor interaction relies on donating the electron density from the lone pair at the carbon into the empty metal 3d-orbitals, and in this way, a dative bond is formed. The donated electron density raises the energy levels of the 3d electrons due to an increased electron–electron repulsion. As a result, the 3d electrons are more easily accepted by the CO ligand through the π-acceptor interaction. The two lobes of the π* orbitals overlap with the lobes of a metal 3d orbitals of proper symmetry. This type of binding is highly efficient for low-valent metal centers, as the energy of the 3d electron manifold approaches the π* level. The efficiency of the π* back-bonding reflects the stability of the resulting carbonyls. Generally, the more nucleophilic the CO moiety upon bonding, the higher the stability of the adduct. Positive charges destabilize TMI–CO complexes. The stability of neutral carbonyls, which often appear in the zeolite systems, is intermediate. Apart from this short-range electron interaction, specific long-range electrostatic effects imposed by the zeolite lattice, such as polarization and dispersion forces, must be included when analysing the chemical state of intrazeolite carbonyl adducts.243,244
 | ||
| Fig. 22 Schematic representation of the σ-donation and π-back-donation effects during binding of CO to a transition-metal cation (a). IR spectra of CO adsorption on reduced Cu+-exchanged ZSM5, BEA, MOR, and SSZ-13 zeolites. The consecutive sets of spectra correspond to increasing doses of CO, which lead to predominant formation of mono- (b1), di- (b2), and tricarbonyl species (b3) adapted from ref. 257 with permission from the Royal Society of Chemistry, Copyright 2015. A schematic diagram showing the splitting of the C–O vibration IR bands due to the coupling of two and three CO molecules in CuZSM-5 zeolite (c). The ΔG vs. T and pCO phase diagrams of the isolated Cu+, Cu+(CO), and Cu+(CO)2 species hosted within SSZ-13, ZSM-5, and MOR zeolites, adapted from ref. 244 under the terms of the CC BY 4.0 license, Copyright 2023, published by Elsevier B.V. | ||
Cu–zeolites are well-suited for studying the coordinative unsaturation of the Cu+ cations and binding of carbon monoxide. Exemplary IR spectra of CO sorption at increasing pressure for Cu+–zeolites (ZSM-5, BEA, MOR, and SSZ-13) are shown in Fig. 22b. Depending on the CO pressure and temperature, various copper carbonyl adducts are formed. At room temperature and low pCO, Cu+(CO) monocarbonyls are characterized by a single band observed at 2154–2159 cm−1, Fig. 22b1. Upon introducing more doses of CO, the formation of dicarbonyls Cu+(CO)2 is observed (see Fig. 22b2), as indicated by splitting of the monocarbonyl band into two peaks corresponding to the asymmetric (νasym, 2150–2152 cm−1) and symmetric (νsym, 2178–2180 cm−1) vibrations of the two coupled CO oscillators. In such a case, the Iasym/Isym ratio can be used to estimate the angle the geminal ligands form in the {TMI(CO)2}n adducts, using the Iasym/Isym = tg2(θ/2) equation proposed by Cotton.245 The presence of two bands is indicative of a C2v local symmetry of the dicarbonyl species.
A further increase in pCO (Fig. 22b3) leads to the transformation of dicarbonyls into Cu+(CO)3 species, and the appearance of a new triplet of the IR bands with approximate positions at 2135, 2168, and 2192 cm−1. The scheme of splitting of the carbonyl bands upon increasing the number of CO ligands coordinated by Cu+–zeolite centers is shown in Fig. 22c. This triplet is indicative of a local symmetry lower than C3v. The presence of individual species or the joint occurrence of the mono-, di-, or tricarbonyls is linked to the accessibility of the copper centres and the size of the intrazeolite channels and pockets. The IR spectra shown in Fig. 22b1–b3 reveal that ZSM-5 and BEA zeolites are more apt for the formation of well-defined polycarbonyls Cu+(CO)n (n = 1, 2, 3) than MOR or SSZ-13 zeolites, suggesting CO sensitivity to the speciation of the copper active centres.
The stability of the carbonyl species can be predicted with first-principles thermodynamic calculations (see Chapter 3.1) and compared with spectroscopic observations. The calculated phase diagrams (ΔG vs. T and pCO) shown in Fig. 22d1–d3 delineate the stability regions of [Cu(CO)]+ and [Cu(CO)2]+ adducts and the bare Cu+ centres located in various sites of the SSZ-13, ZSM-5, and MOR zeolites.244 In all cases, formation of the carbonyl adducts is thermodynamically favoured. The ZSM-5 topology exhibits the highest propensity among the described zeolite series for the formation of [Cu(CO)]+ adducts. In contrast, the SSZ-13 framework exhibits the lowest energy difference between the mono- and dicarbonyl species.
The phase diagrams can be used for elucidating the critical conditions for the decomposition of the involved adducts at either a fixed temperature or CO pressure. For instance, at room temperature, transformation between di- and monocarbonyls is irreversible only for the 8-MR sites of the SSZ-13 framework. The decomposition temperature of [Cu(CO)]+ to bare Cu+ species at 10−3 mbar (corresponding to a negligible amount of CO in typical catalytic conditions) in the case of SSZ-13 is much lower (162 °C) than that for the other two frameworks (275 °C and 340 °C for MOR and ZSM-5, respectively), especially for the Cu+ cations located in the 6-MR. This influence of the framework topology was observed experimentally during the TPD experiments for the SSZ-13, ZSM-5, and MOR samples, corroborating the FPT results.244
Similar behaviour was observed for Ni+-exchanged zeolites subjected to CO adsorption. However, since Ni+ centres are paramagnetic, EPR spectroscopy can also be used to elucidate the structure and properties of the resulting carbonyls.80,114,247,248 Yet, the primary identification of the adducts formed is provided by IR spectroscopy.31,239,249 Typical IR spectra are shown in Fig. 23a. The spectral region of the CO vibrations can be separated into two parts, imposed by a band located at 2175 cm−1, which is attributed to the CO molecule interacting with the Brønsted centres. The IR bands located at higher frequencies originate from CO interacting with the oxidized nickel centres (Ni2+, Ni2+-oxo species). In contrast, those of lower frequencies are associated with CO adsorbed on the reduced intrazeolite Ni+ cations.
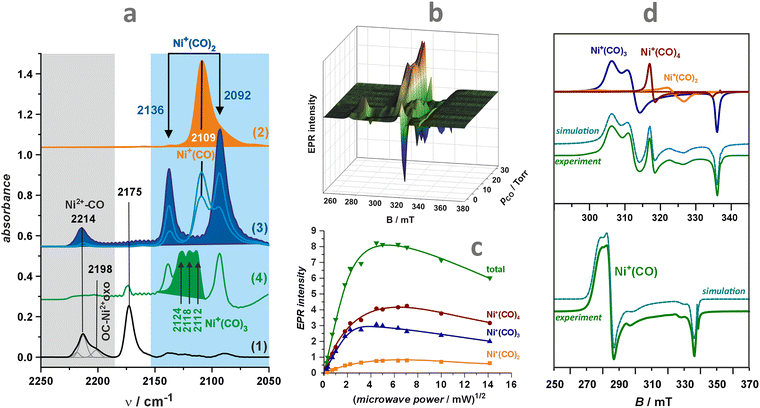 | ||
| Fig. 23 IR and EPR fingerprints for the formation of nickel(I) polycarbonyls in the reduced NiZSM-5. The IR spectra of CO adsorption (a) on thermally activated NiZSM-5 (1), sample reduced in CO and evacuated at 150 °C (2), sorption–desorption equilibrium showing conversion of mono- and dicarbonyls (3), sorption of CO excess (4), adapted from ref. 247 with permission from the American Chemical Society, Copyright 2011. The set of CW-EPR spectra obtained after variable pressure CO sorption (up to 30 Torr) (b). Changes in the intensity of the mono-, di-, tri-, and tetracarbonyl EPR spectra recorded during microwave power saturation experiments (c). Decomposition of the experimental EPR spectra into individual carbonyl signals (d). Panels b, c, and d adapted from ref. 246 with the author's permission. | ||
Briefly, the adsorption of CO at room temperature leads to a band at 2214 cm−1 due to the Ni2+–CO adducts in ZSM-5. At low temperatures, this band reveals a shoulder at 2198 cm−1 associated with the Ni2+-oxo species. After reduction of NiZSM-5 with CO (400 °C), this new band disappears, indicating a reactive character of the adsorption of CO associated with the redox transformation of Ni-oxo species to Ni+. This is accompanied by the development of a new doublet signal characteristic of nickel(I) geminal dicarbonyl adducts, with symmetric (2136 cm−1) and antisymmetric (2092 cm−1) vibrations. Desorption of CO at progressively increasing temperatures (Fig. 23a, spectra (2) and (3)) results in transformation of the Ni+(CO)2 dicarbonyl into the Ni+CO monocarbonyl adducts (see the band at 2109 cm−1). On the other hand, upon increasing the number of CO doses, a set of bands at 2124, 2118, and 2112 cm−1 appears between the symmetric and antisymmetric dicarbonyl bands, which are attributed to the tricarbonyl Ni+(CO)3 species. The corresponding vibrational splitting scheme is similar to that of Cu+(CO)3 (Fig. 22c), although the positions of the bands are different. Therefore, both Cu- and Ni-containing zeolites provide easily accessible, reduced Cu+ and Ni+ centres, capable of forming several polycarbonyl adducts, whose stoichiometry and structure depend on CO pressure and temperature. More accurate measurements of the CO frequencies, and the definite confirmation of the polycarbonyl structures (ligation stoichiometry), can be ascertained using isotopically labelled gas mixtures 12C16O/12C18O/13C16O/12C18O.249,250
Magnetic properties of carbonyl adducts and the binding mechanism. The CO adsorption process can be followed successfully by in situ EPR measurements.80,114,239,248 The advantage of EPR over IR spectroscopy stems from the lack of limitations imposed on the CO pressure, as the high pressures lead to the appearance of excessive CO in the gas phase, obscuring the IR spectra of the surface species. The EPR spectra of Ni+/ZSM-5 (and Ni+/BEA) zeolites, pre-reduced with CO, show dramatic changes upon increasing the pressure of CO (Fig. 23b). CW-EPR measurements at liquid helium temperature with an increasing microwave power allowed to saturate successively the component signals of the individual carbonyl species coexisting upon CO adsorption. Then, using computer simulation, the individual EPR spectra of the adducts [Ni+(CO)n]ZSM-5 with n = 1, 2, 3, 4 (mono-, di-, tri-, and tetra-carbonyl nickel(I)) can be obtained (see Fig. 23c and d). Their magnetic properties have been examined using the DFT calculations of spin-Hamiltonian parameters for model complexes [Ni+(CO)nLm] (n = 1–4, L = H2O, OH−), which can be regarded as discrete, well-defined molecular analogues of the intrazeolite polycarbonyls.251 The molecular nature of the calculated g and 13C hyperfine tensors, when using 13CO, can be interpreted in terms of the nickel coordination state and its local symmetry, providing clear guidelines for justifying their assignment.
Although the DFT calculations of the g and 13C tensors has been restricted to the rudimentary [Ni+(CO)nLm] models, despite missing of the relevant EPR data for such discrete systems, generic categories of the g tensor structure–relationship can be delineated, and associated with the particular magnetophore [Ni+(CO)n] that is embedded in the zeolite matrices. Additionally, the calculated data can be confronted with the available EPR parameters for nickel(I) polycarbonyls that are produced in ZSM-5 zeolites or supported on silica,252,253 as the surface functional groups (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO−, –OH,
SiO−, –OH, ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O–Si(Al)
Si–O–Si(Al)![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ) play the role of mere ligands and can be inserted into the spectrochemical series close to aqua and hydroxyl ligands.254 Additionally, it has been shown that the [Ni+(CO)n] core acts as the proper magnetophore, whose spectroscopic properties are primarily controlled by the spatial arrangement of the CO ligands, being only slightly perturbed by the number and position of the H2O, OH−, or
) play the role of mere ligands and can be inserted into the spectrochemical series close to aqua and hydroxyl ligands.254 Additionally, it has been shown that the [Ni+(CO)n] core acts as the proper magnetophore, whose spectroscopic properties are primarily controlled by the spatial arrangement of the CO ligands, being only slightly perturbed by the number and position of the H2O, OH−, or ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO− co-ligands.
SiO− co-ligands.
The comparison of results obtained from DFT calculations reveals that the polycarbonyl complexes can be divided into two classes with distinct ground states, characterized by distinctive EPR spectra. They are schematically illustrated in Fig. 24a1 and a2 and accompanied by the simulated EPR spectra using the DFT-calculated parameters and typical experimental linewidths. The class of the |3dz2〉 ground state (e.g., T-shaped monocarbonyl, tri- and tetracarbonyls) is characterized by a rhombic EPR spectrum with the gxx, gyy components varying between 2.4 and 2.1 (the actual shift depends on the number of CO ligands), and the smaller gzz value close to ge = 2.023. In the case of the |3dx2−y2〉 ground state, observed for the dicarbonyl complexes, the reversed g-tensor values are expected with one component being larger (2.2–2.13) and two components lying closer to the ge value (2.07–2.01).
 | ||
| Fig. 24 EPR spectra of nickel(I) carbonyls in ZSM-5. Simulated X-band EPR spectra for the generic structural models of Ni+ carbonyl adducts with dominant 3dz2 (a1) or 3dx2−y2 (a2) ground state of the nickel core (depicted structures show SOMO contours, derived from DFT calculations). Experimental X-band EPR spectra of the isotopically labelled carbonyl species, showing hyperfine structures due to the 13CO ligands (hyperfine splitting is shown with stick diagrams) (b1), (b2), (b3). For better comparison of the hyperfine splittings, the spectra are recalculated to the common magnetic field axis and supplemented with the corresponding spin density contours calculated for the identified carbonyl structures. HYSCORE spectra of the monocarbonyl species, including echo-detected EPR spectrum (c1), where the arrows indicate the observer positions at which HYSCORE spectra were recorded, whereas the unit spheres show orientation selectivity connected with the observer positions. Spin density contour of the Ni+CO magnetophore (c2), and HYSCORE spectra recorded at B2 (c3) and B3 (c4) positions in the magnetic field. Adapted from ref. 248 and 251 with permissions from the American Chemical Society, Copyrights 2008 and 2013. | ||
It was found that increasing the number n of CO ligands resulted in smaller Δgii shifts as the energy separation between occupied and virtual spinorbitals increases from 0.8 (n = 1) to 1.6 eV (n = 4). The other reason stems from the fact that the corresponding matrix elements of the g-tensor (see Chapter 2.2) are dominated by the spin–orbit couplings (SOC) of the metal centre and the ligands. Noting the substantial difference in the SOC constants, λNi+ = 565 cm−1 and λC = 30 cm−1, the resulting g tensor shifts become reduced considerably in magnitude, upon passing from the mono- to the tetracarbonyl adducts.251
Direct confirmation of the structure of the [Ni+(CO)n] adducts formed within the channels of ZSM-5 zeolite can be achieved using EPR measurements with an isotopically labelled 13CO. Due to the nuclear spin I = 1/2 of 13C, the labelled carbon monoxide can be used for counting the number of the CO ligands and their possible equivalence, as the EPR spectrum acquires an informative superhyperfine structure (Fig. 24b1–3). Additionally, molecular models of the individual polycarbonyl species, along with the corresponding spin density contours, are also shown in these figures. The 13CO EPR measurements eventually prove the presence of the tri- and tetracarbonyls. In the latter case, almost complete solvation of the Ni+ adsorption centres takes place, leaving a residual attachment of the adduct to the zeolite backbone with one Ni–Oz bond only. Notably, it has been previously observed that nickel undergoes significant migration upon formation of Ni+(CO)n adducts in NiCaX zeolite.255
The EPR measurements are usually performed at cryogenic temperatures. Only mono- and dicarbonyls were observed in the IR spectra at room temperature. Higher polycarbonyls (n > 2) are possibly formed only at cryogenic conditions. Indeed, a comparison of the energies of the successive adsorption steps for the mono- (−42.9 kcal mol−1), di- (−20.2 kcal mol−1), and tricarbonyl species (−5.7 kcal mol−1) with the TΔS term of CO(g) reveals that already above 140 °C, the dicarbonyls are unstable. Therefore, for simple thermodynamic reasons, in most cases, only the monocarbonyl species can be expected at actual catalytic conditions. Thus, their structure and properties have been studied in more detail so far.
The expected hyperfine doublet is not resolved in the [Ni+CO]–ZSM-5 adduct. This issue has been explained elsewhere,251 based on the composition of SOMO and its structural misalignment with the Ni–C bond direction (see Fig. 24c2). To describe the mechanism of CO–Ni+ bond formation, pulse EPR measurements (HYSCORE) are of particular relevance. They allow for the successful determination of the small 13C hyperfine couplings.248 The corresponding echo-detected EPR spectrum and HYSCORE spectra are collated in Fig. 24c1, c3 and c4. The interaction of 13CO with Ni+ZSM-5 under low pCO pressures gives rise to the formation of a monocarbonyl adduct of the trigonal Ni+ with gzz > gyy ≫ gxx > ge, |Ayy| > |Azz| > |Axx|, which is characteristic of the T-shaped conformation (Fig. 24a1). The binding of CO is accompanied by an intrinsic d–d relaxation of the nickel 3d manifold, due to the allied charge and β-spin density relocation between the 3dxz and 3dx2−y2 orbitals, which stabilizes energetically the carbonyl adduct. The resolved spectroscopic parameters (gxx = 2.018, gyy = 2.380, gzz = 2.436, Axx = +1.0 MHz, Ayy = −3.6 MHz, Azz = −1.6 MHz for 13C hyperfine interaction, and e2Qq/h = −13 MHz, η = 0.8 for 27Al quadrupole interaction), reinforced by DFT calculations within the SOMF/B3LYP calculation scheme, provide a suitable background for validation of the T-shaped structure of the NiI–CO intrazeolite adduct.248
Electronic details on the CO bonding mechanism can be deduced from the frontier molecular orbital (FMO) interaction diagram, and NOCV analysis of the interacting CO and Ni+–zeolite model fragments (see Chapter 4.1.1). The resultant orbital overlap correlation diagram of the π(2p) and σ states of the CO ligand with the 3d states of the zeolite [Ni+2cM7]frag fragment is shown in Fig. 25a. The ligation of CO results primarily from the sizable π overlap between low-lying π(2p) CO states with the symmetry-adopted 3dxz and 3dyz orbitals of the nickel core. It is enhanced by a slight contribution owing to the σ-type overlap of σ(2p + 2s) with one of the lobes of the in-plane 3dxz orbital, made possible by an unusual T-shape geometry of the CO–Ni–zeolite entity.
 | ||
| Fig. 25 The molecular energy diagram and electronic structure of the Ni+–CO adduct in ZSM-5 (a) with the corresponding Kohn–Sham frontier orbital interaction diagram, and NOCV deformation density contours (b). For the charge density (α + β) and the spin density (α − β) contours, the corresponding values indicate the interaction energies associated with the individual channels of the orbital σ and π symmetries. Adapted from ref. 248 with permission from the American Chemical Society, Copyright 2013. | ||
The energy levels of the bonding and antibonding π(2p) CO orbitals define the low and high-energy boundaries encompassing the 3d nickel-based states of the [NiI2cM7] fragment. The interaction of 3d orbitals with the corresponding  and
and  MO of the CO ligand gives rise to strong spin polarization, reflected by the pronounced shift of the α and β spin manifolds of the carbonyl adduct. The singly-occupied α-orbital (SOMO) exhibits small delocalization on the CO moiety, which accounts well for the lack of the 13C hyperfine splitting in the CW-EPR spectra. Yet, the residual spin density on the ligand is responsible for a very weak 13C hyperfine interaction, as detected with the HYSCORE technique.
MO of the CO ligand gives rise to strong spin polarization, reflected by the pronounced shift of the α and β spin manifolds of the carbonyl adduct. The singly-occupied α-orbital (SOMO) exhibits small delocalization on the CO moiety, which accounts well for the lack of the 13C hyperfine splitting in the CW-EPR spectra. Yet, the residual spin density on the ligand is responsible for a very weak 13C hyperfine interaction, as detected with the HYSCORE technique.
The delicate balance between the donation and back-donation effects can be quantified using the ETS-NOCV analysis, which enabled the identification and visualization of specific charge and spin flow channels. The main orbital contributions to the α and β electron and spin density flows constituting those channels are shown in Fig. 25b, along with the corresponding energy values. As a result, the analysis enabled the disentanglement of the cooperative σ donation and π back-donation effects involved in the ligation of a CO molecule to Ni+ ions hosted in zeolites.248 The dominant effect is the back-donation along the π channel of a spinless charge transfer. This explains the position of the carbonyl band in the IR spectrum and its bathochromic frequency shift. The spin density redistribution within the CO moiety primarily operates via the 4α and (3α + 4β)σ channels. Due to the substantially uneven contributions of the 3α and 4β components, the ensuing unbalanced spin flow leads to a spin polarization of the carbon sp-hybrid. On the contrary, the 4α channel allows for a direct delocalization onto the carbon 2s orbital. Since the polarization effect prevails, this explains the negative sign of the isotropic constant aiso(13C).248 These two effects virtually cancel each other, resulting in a minute net spin density flow within the σ channel. Because upon the CO attachment the unpaired electron relaxation (1β) is restricted to the 3d-based orbitals of nickel, and the main channels (one σ and two π) of the electron density flow within the Ni+–CO unit involve both α and β spins in a similar manner, the magnetophore of the monocarbonyl adduct is essentially constituted by the metal core. All the discussed effects provide a rational basis for an in-depth molecular interpretation of the IR and EPR parameters in terms of charge and spin flows along the σ and π channels.
Quantification of TMI with CO as an IR molecular probe. The IR spectra of adsorbed CO can be used to explore the nature and content of TMI in zeolites, which primarily relies on the formation and quantification of C-bonded carbonyls. The small kinetic size of the CO and its high affinity to ligation make this molecule well-suited as an effective probe for investigating Lewis and redox sites present inside the channels of zeolites. The vibrational spectrum of the diatomic CO molecule is relatively simple and strongly depends on the nature of the adsorption site. The advantage of CO as a probe molecule lies in its sensitivity to the speciation of TMI due to the subtle balance of electrostatic effects, σ-donation and π-back-donation as well as the static and dynamic interactions between the adsorbed molecules.256,257 As a result, the CO-IR technique can inspect various valence states of TMI and their speciation (bare TMI, isolated TMI–oxo species, oxide nanoclusters). Additionally, it is often possible to selectively detect cations in different valence and coordination states, even when present simultaneously.258 Yet, although CO can serve as a probe for analysing the coordination vacancies of exchangeable cations within zeolites, in some cases, the adsorption of CO is isodesmic, i.e., formation of new TMI–CO bonds occurs at the expense of the TMI–Oz bonds with the zeolite framework, keeping the overall coordination number intact.248 Spectroscopic fingerprints for commonly studied intrazeolite carbonyl adducts of Co, Cu, Fe, and Ni are presented in Table 4.
| Intrazeolite TMI–CO adduct | Frequency/cm−1 | Ref. | |
|---|---|---|---|
| Co/MFI | Co2+–CO | 2204 | 32 |
| (CoO)n–CO | 2194 | ||
| Ni/ZSM-5 | Ni2+–CO | 2220–2180 | 31, 80, 249 and 259 |
| Ni+–CO | 2109 | ||
| Cu/ZSM5 | Cu+–CO | 2157 | 260 |
| Cu0–CO | 2124 | ||
| Cu2+–CO | 2206 | ||
| Fe/MFI | Fe2+–CO | 2196 | 261 and 262 |
| Fe2+–(CO)2 | 2188 | ||
There are certain limitations to using CO as a probe, primarily when reactive CO adsorption occurs, resulting in chemical modification of the TMI centre by the adsorbed species. The typical products of reactive CO adsorption include carbonates, bicarbonates, carboxylates, and even formates. In some instances, CO can also be oxidised to carbon dioxide.263 The undesired reactive CO adsorption can often be mitigated by using low-temperature experiments. These issues should be considered when aiming for a more accurate determination of the oxidation states of TMI ions in zeolites. A more general account of the application of IR spectroscopy in zeolite research can be found in previous works.256,257
After establishing the experimental conditions for generating the monocarbonyl adducts (see the ΔG(p,T) diagrams), IR absorption coefficients can be obtained through careful CO titration under controlled conditions (CO pressure and temperature). The most convenient situation occurs when the specific probe molecule reacts selectively with only one type of adsorption center, and the stoichiometry of this process is well understood. It can be inferred, for instance, from the FPT phase diagrams (Fig. 22d1–d3), which also reveal differences in the formation of monocrbonyls between the zeolite frameworks and TMI localisation within the particular channels.243 In most cases, it is reported that the value of the absorption coefficient for the respective carbonyls is independent of the zeolite structure, despite the observed various CO stretching frequencies.
In the case of cobalt cations accommodated in the pentasil zeolites (e.g., MFI, FER), the CO band at 2204 cm−1 is attributed to Co2+–CO adducts formed with the exchanged Co2+ cations, whereas the bands at 2194 cm−1 and 2179 cm−1 are associated with Co2+ in oxide clusters and segregated CoO, respectively.32 The plot of the intensity of the characteristic monocarbonyl IR band as a function of the amount of CO sorbed is used to determine the absorption coefficient. For the 2204 cm−1 band, the absorption coefficient is equal to 0.123 ± 0.002 cm2 μmol−1, and its value is independent of the zeolite type and the adsorption temperature.32 For the 2194 cm−1 band, a value of 0.129 ± 0.004 cm2 μmol−1 has been reported, based on the intensity (height) of the corresponding IR signal. In addition, the absorption coefficient of the CO–OH band at 2175 cm−1 due to adsorption of CO on Brønsted centres is equal to 0.120 ± 0.003 cm2 μmol−1 (determined for FER zeolite). All these coefficients can be used to evaluate the complete balance of cationic sites in pentasil zeolites from a single IR adsorption measurement.
Coordination of CO to Ni2+ cations leads to the formation of Ni2+–CO monocarbonyl adducts with the IR bands located in two spectral regions: 2220–2180 cm−1 and 2170–2130 cm−1.80,249,259 The low-energy region is characteristic of carbonyls formed on nanosized NiO and mixed oxides. The high-energy band is characteristic of isolated Ni2+ cations present in the exchangeable positions. The absorption coefficient for this band in NiZSM-5 zeolite (2212 cm−1) equals 0.143 ± 0.003 cm2 μmol−1.31 The same value was obtained for NiY, despite slight differences in the CO stretching frequencies of the Ni2+–CO monocarbonyls (2212 and 2220 cm−1 for NiZSM-5 and NiY, respectively). During the reactive adsorption of CO on nickel–oxo compounds, CO acts simultaneously as a reducing agent and as a probe for the generated Ni+ cations.247 The characteristic band of the Ni+–CO adduct is located at 2109 cm−1, and the absorption coefficient is equal to 1.104 ± 0.018 cm2 μmol−1.31 A strong increase in the absorption coefficient of Ni+–CO compared to Ni2+–CO originates from more efficient transfer of the 3d electron density from the Ni+ cation onto the π* antibonding orbital of CO (π-back-donation effect) due to the better energy matching of the overlapping orbitals.249
The interaction of CO with copper sites in thermally treated ZSM-5 zeolite results in the formation of a strong band at 2157 cm−1 due to Cu+–CO monocarbonyls at low CO doses. In contrast, the band at 2130 cm−1 produced when CO was sorbed in higher amounts was attributed to Cu+ ions present in an oxide form.260 Treatment of CuZSM-5 zeolite with H2 results in the appearance of a band at 2124 cm−1, attributed to the monocarbonyls of metallic copper (Cu0–CO). When oxidised with O2, some of the Cu+ cations in exchange positions are transformed into Cu2+ species, which is recognised by the development of a band at 2206 cm−1 due to the Cu2+–CO monocarbonyls. By measuring the intensity (height) of the 2157 cm−1 band corresponding to the sorbed CO, the slope of the resulting linear correlation defines the extinction coefficient, yielding a value of 1.30 cm2 μmol−1. The extinction coefficient of CO interacting with Cu2+ species in zeolite CuZSM-5 was obtained after treatment with oxygen. The intensity of a relatively weak Cu2+–CO band at 2206 cm−1 can be used to calculate the absorption coefficient, which equals 0.11 cm2 μmol−1. Note that this value is similar to other divalent cations hosted in ZSM-5 (see above). The experimental and calculation details can be found elsewhere.260
Iron speciation in zeolites is also extensively studied using IR spectroscopy with a CO probe. For instance, the corresponding carbonyl bands appear at 2200–2194 cm−1 for the zeolites BEA,264 FER,265 and MFI.261 In general, iron species in zeolites prepared from a ferrous solution were found to be mainly in the Fe2+ form. Fe2+–CO monocarbonyls (with the band at 2195 cm−1) convert easily into Fe2+(CO)2 dicarbonyls (2188 cm−1) at low temperatures, but the reaction progress depends on the exchangeable sites within the zeolite. Other identified Fe2+ ions in FER produced exclusively monocarbonyls (band at 2189 cm−1), and in comparison to the previous hosting site, they were easily oxidised to Fe3+ ions in the presence of oxygen (or air). Sorption of CO on FeZSM-5 zeolite resulted in monocarbonyl bands at 2188 and 2200 cm−1, which were attributed to the Fe2+(CO) based on the results of oxidation/reduction reactions with O2 and H2.262 The calculated extinction coefficient based on the integral absorption is equal to 2.52 ± 0.07 cm μmol−1, while the value obtained from the band height measurement drops to 0.11 ± 0.01 cm2 μmol−1.
4.3. Non-innocent molecules – ligation pathways
Non-innocent (ambivalent) ligands such as O2/O2−/O22−, NO/NO+/NO−, NO2/NO2− play an essential role in a large variety of catalytic reactions involving metallozeolite catalysts, including HC (hydrocarbons) oxidation and HC-SCR,17,156,157,266 NH3-SCR,156,188,267,268 deNOx269,270 or oxidation of CH4271–275 and NO172,276,277 in particular. Their ambiguous electronic and magnetic structures, as well as their electronic flexibility upon binding to intrazeolite TMI, pose challenges for the clear assignment of the metal and ligand oxidation states, and therefore, for establishing their distinct roles in the redox mechanisms of the investigated reaction. In contrast to the innocent H2O or NH3 ligands (which are characterised by a well-defined charge that is usually preserved upon ligation, see Chapter 4.2), the non-innocent ligands can change their redox states due to breaching of the Pauli shield, and participate in electron transfer to or from the TMI centres. As a result, the valence and coordination states of non-innocent ligands can change to facilitate the mechanistic redox steps during a catalytic reaction. The non-innocent ligands can play an auxiliary role, meaning that they do not interact directly with the reactants, but alter the redox state of the metal centre (redox functionality tuning), or participate explicitly in the reaction by making and breaking covalent bonds with the captured reactant molecules.172 For instance, the appearance of an unusual 3d9 state of cobalt is made possible upon the coordination of redox-active NO ligands to Co2+ hosted in ZSM-5, which triggers the subsequent capture of olefin molecules by the Co0 centres for driving the HC-SCR reaction efficiently with the involvement of the Co2+/Co0 redox couple.17 An intricate network of NO oxidation172 and NO reduction with ammonia over Cu/CHA and Cu/MFI catalysts199,278,279 or with ethylene over NiSZM-5156 can also be invoked here as illustrations.To circumvent the ambiguity of oxidation state assignments and dichotomy of the electrons division, the Enemark–Feltham notation {XYM}d+π can be used, where XY indicates a diatomic ligand, M – metal, and d + π is the sum of the electrons on d orbitals of M and π orbitals of XY.280 Two alternative coordination situations between a transition metal cation, Mp/p±1/z, and an attached non-innocent ligand, Lq/q±1, involve resonance structures, XYqMp/z ⇌ XYq−δMp+δ/z (redox counterparts281), with the delocalized electrons in a single or double energy minimum. In this notation, p and q represent the charges of the TMI and XY ligand, respectively, whereas δ corresponds to the partial charge shifts. This ambivalence is particularly amplified in the case where the 3d levels of the intrazeolite transition metal cations, such as Co, Ni, or Cu, are intermingled with the 2π* levels of the non-innocent XY ligands (Fig. 26a). The classic ligation dichotomy involves here spin pairing and electron transfer categories.
The alignments of the energy levels shown in Fig. 26a favour electron transfer from Cu+ and Ni+ to O2 and spin-pairing for NO. In the case of Cu2+ and Co2+, since the β-3d manifold is located below the 2π* level, coordination of the donor co-ligands (e.g., NH3) is needed to trigger the MLET (see Chapter 4.3.1). Ligation of open-shell non-innocent XY molecules leads to changes in the overall spin state of the {XYM}d+π unit. Exemplary scenarios collated in Fig. 26b illustrate computational isodesmic pathways of spin addition, spin pairing, and spin crossing coupled with spin pairing upon NO molecule coordination to selected transition metal ions of different spin multiplicity hosted in the MFI matrix (see Chapter 4.3.2. for more details).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 species. The deep four-electron dissociative reduction of O2 on single sites occurs at electron-rich TMI. However, attainment of elevated oxidation states (z ≥ 4) is hindered by high energy costs, particularly for those TMI that are positioned after Mn in the periodic table. Actually, it takes place in a more complex manner, favourably on dimeric centres (1
2 species. The deep four-electron dissociative reduction of O2 on single sites occurs at electron-rich TMI. However, attainment of elevated oxidation states (z ≥ 4) is hindered by high energy costs, particularly for those TMI that are positioned after Mn in the periodic table. Actually, it takes place in a more complex manner, favourably on dimeric centres (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), and can be promoted by coupling with proton relocation (electroprotic route), leading to more stable hydroperoxo M–OOH and hydroxyl M–OH intermediates. Various combinations of these processes, involving the removal of the inert triplet ground state of molecular oxygen (3Σg−) and an apposite stabilisation of the resultant species by coordination to the metal centres, make the activation thermodynamically more favourable and kinetically accessible. Isotopic labelling is widely explored in the elucidation of the O2 binding and activation processes, being particularly useful for identifying activated oxygen species and studying the activation mechanisms, using 18O (IR, RS) and 17O (EPR) labelled dioxygen.
2), and can be promoted by coupling with proton relocation (electroprotic route), leading to more stable hydroperoxo M–OOH and hydroxyl M–OH intermediates. Various combinations of these processes, involving the removal of the inert triplet ground state of molecular oxygen (3Σg−) and an apposite stabilisation of the resultant species by coordination to the metal centres, make the activation thermodynamically more favourable and kinetically accessible. Isotopic labelling is widely explored in the elucidation of the O2 binding and activation processes, being particularly useful for identifying activated oxygen species and studying the activation mechanisms, using 18O (IR, RS) and 17O (EPR) labelled dioxygen.
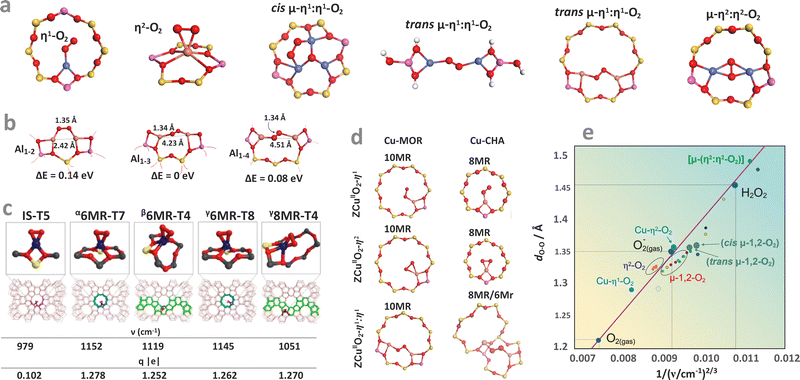 | ||
| Fig. 27 Typical binding modes of oxygen to mono- and dinuclear metal centres hosted in zeolites (a). The influence of Al distribution on the stability of the cis μ-η1:η1-O2 di-copper adducts presented in TON zeolite (b).285 The effect of the zeolite framework on the structure of η2-O2–Co in various sites of the distinct topology of MFI (c), and on the structure of η1-O2–Cu, η2-O2–Cu, and trans μ-η1:η1-O2 di-copper adducts in MOR and CHA zeolites (d).287 The d-O–O vs. 1/(νO–O)2/3 2D correlation diagram for classification of oxygen adducts with the intrazeolite transition metal ions (e). The calculated positions of the reference O2, O2−, H2O2, and bare η1-O2–Cu, η2-O2–Cu and cis, trans μ-η1:η1-O2, μ-η2:η2-O2 species (terminated with –OH) are marked in large circles, whereas the positions of the corresponding adducts of Cu, Co, Fe, hosted in CHA, TON, MFI, MOR zeolites are marked with small circles.286,288 Panels a, b, d, and e based on data from the quoted references. Panel c adapted from ref. 286 with permission from the American Chemical Society, Copyright 2020. | ||
The variety of ways in which single and two adjacent TMI cations (M∪M) can bind an O2 molecule includes a considerable diversity of the resultant structural motifs.282–285 End-on η1-O2 superoxide (Pauling structure), the side-on η2-O2 superoxide or peroxide (Griffith structure), the cis μ-η1:η1 (Yeager structure) and trans μ-η1:η1, side-on μ-η2:η2, μ-η2:η1, as well as the bis(μ-oxo) or η2−ozonide molecular adducts with Fe, Co, Ni, Cu or Zn are the most common in the case of metallozeolites. Their energetic, structural, and spectroscopic characteristics depend on Al location within the rings (Fig. 27b), accommodation locus in the given zeolite framework (Fig. 27c and d), and the framework type (Fig. 27d).285–287 The bridging peroxo species, upon further reductive dissociation, can be converted into highly reactive terminal (such as Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) or bridging (e.g., Cu–O–Cu), mono-oxo species, accomplishing the complete 4e− reduction and splitting of O2, discussed below.
O) or bridging (e.g., Cu–O–Cu), mono-oxo species, accomplishing the complete 4e− reduction and splitting of O2, discussed below.
Dioxygen attachment and activation on single TMI centres. The reductive monodentate (η1) and bidentate (η2) attachment of O2 to single intrazeolite TMI centres can occur through the σ, π and δ-overlap (see Fig. 17c) between the metal donor 3d (or 4s for Zn) and the 2π* acceptor orbitals of dioxygen leading to the formation of paramagnetic superoxide (1e− transfer) or diamagnetic peroxide (2e− transfer) 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 species. However, due to the simultaneous operation of bonding and back-bonding interactions, fractional changes in the charge and spin transfers between the metal and ligand are actually observed. Reasonably, the adducts with the O–O bond length of 1.4–1.5 Å and νO–O 750–930 cm−1 are designated as peroxides, whereas those with 1.2–1.3 Å bond length and νO–O lying in the range of 1050–1200 cm−1 are classified as superoxides.289 Their dinuclear nature can be deduced from the Δ18O shifts (∼50–60 cm−1) in IR spectra, and from the character of 17O hf pattern in the EPR spectra of the paramagnetic superoxide complexes (11 equidistant lines are diagnostic for η2 and up to 36 lines for η1 attachment).290 The correlation between the dO–O bond length and the νO–O vibration frequencies based on empirical Badger relation (dO–O = C/(νO–O)2/3 + b), established previously for homogeneous complexes,289 shows that the vibration frequencies smoothly span the whole range from the superoxide-like to the peroxide-like species (Fig. 27e). As a result, assignment of the discrete (integer) oxidation states of oxygen species has a formal character only. Thus, the covalent communication between the metal centre and the O2 ligand leads to the formation of intrazeolite adducts, which may be regarded as valence hybrids of the limiting superoxide and peroxide extremes.289 In addition to assigning the formal oxidation states to metal and dioxygen moieties, the mode of binding and the orbital overlap responsible for bond formation, as well as the MLET pathway, are of key importance. Especially, recognising the impact of the O2 activation type on the catalytic reactivity with reactant molecules.
1 species. However, due to the simultaneous operation of bonding and back-bonding interactions, fractional changes in the charge and spin transfers between the metal and ligand are actually observed. Reasonably, the adducts with the O–O bond length of 1.4–1.5 Å and νO–O 750–930 cm−1 are designated as peroxides, whereas those with 1.2–1.3 Å bond length and νO–O lying in the range of 1050–1200 cm−1 are classified as superoxides.289 Their dinuclear nature can be deduced from the Δ18O shifts (∼50–60 cm−1) in IR spectra, and from the character of 17O hf pattern in the EPR spectra of the paramagnetic superoxide complexes (11 equidistant lines are diagnostic for η2 and up to 36 lines for η1 attachment).290 The correlation between the dO–O bond length and the νO–O vibration frequencies based on empirical Badger relation (dO–O = C/(νO–O)2/3 + b), established previously for homogeneous complexes,289 shows that the vibration frequencies smoothly span the whole range from the superoxide-like to the peroxide-like species (Fig. 27e). As a result, assignment of the discrete (integer) oxidation states of oxygen species has a formal character only. Thus, the covalent communication between the metal centre and the O2 ligand leads to the formation of intrazeolite adducts, which may be regarded as valence hybrids of the limiting superoxide and peroxide extremes.289 In addition to assigning the formal oxidation states to metal and dioxygen moieties, the mode of binding and the orbital overlap responsible for bond formation, as well as the MLET pathway, are of key importance. Especially, recognising the impact of the O2 activation type on the catalytic reactivity with reactant molecules.The intrazeolite superoxide adducts can then be categorised into the σ, π and δ-type paramagnetic species, exemplified by the [η1-O2−–ZnII]+/MFI,291 [η1-O2−–Co]2+Y292 and [η2-O2−–Ni]+ZSM-564 cage adducts identified univocally by EPR spectroscopy using 17O-labelling.
The Zn+/ZSM-5 (Si/Al = 11.9) species react with O2 (5 mbar, 300 K) with the formation of [O2˙−Zn]+/MFI adducts, as demonstrated by the EPR spectrum with gzz = 2.039, gyy = 2.0108, gxx = 2.0033 (Fig. 28a).78,291 Based on the internuclear bond distance of dO–O = 1.33 Å and νO–O = 115 cm−1 (see Fig. 27e) this adduct has been assigned to top-on [1η-O2˙−–Zn]+/ZSM-5, produced by transfer of the electron density (0.7–0.8) from 4s1 to the in-plane  orbital, via the σ-donation channel that is favourable for the top on ligation (Fig. 28a1). The
orbital, via the σ-donation channel that is favourable for the top on ligation (Fig. 28a1). The  HOMO is mainly responsible for the O2 binding (−150 kJ mol−1), whereas the out-of-plane
HOMO is mainly responsible for the O2 binding (−150 kJ mol−1), whereas the out-of-plane  SOMO is localized essentially on the oxygen moiety, interacting weakly with the Zn ion.
SOMO is localized essentially on the oxygen moiety, interacting weakly with the Zn ion.
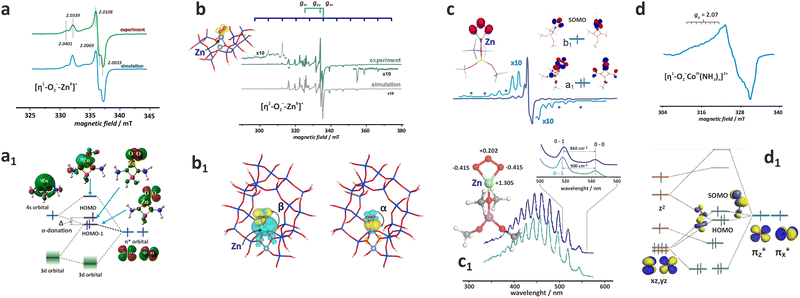 | ||
| Fig. 28 X-band CW-EPR spectrum of the [η1-16O2−–Zn]+/ZSM-5 adduct (a) with the corresponding MO energy diagram (a1) (adapted from ref. 291 with permission from the American Chemical Society, Copyright 2013) and of [η2-17O2−–Zn]+/ZSM-5 (b) with the corresponding NOCV analysis of the spin-polarized MLET along the β-channel and back donation along the α-channel (b1). EPR spectrum (c),293 and UV-vis spectrum (c1) of the [η2-O3−–Ni]+/ZSM-5 adduct (adapted from ref. 294 with permission from the American Chemical Society, Copyright 2021). The EPR spectrum of the cage [η1-O2−–Co(NH3)n]2+/ZSM-5 adduct (d) together with the associated MO diagram of the energy levels (d1).113 Panels b, b1, d, and d1 are inspired by the quoted references. | ||
An alternative η2-attachment of dioxygen, distinct by a higher gzz = 2.061 value (and similar gyy = 2.010, gxx = 2.003), is disclosed by the 17O hyperfine structure with the resolved 11 equidistant lines that are separated by Axx = 7.68 mT (Fig. 28b), observed in the EPR spectrum when 17O2 is contacted with ZnI/ZSM-5 (Si/Al = 140).294 Such 17O hf pattern confirms that both oxygen atoms are magnetically equivalent, which is tantamount to the side-on ligation of dioxygen with ΔEads = −110 kJ mol−1. The internuclear bond distance of dO–O = 1.24 Å is indicative of the superoxide nature of the bound O2. The NOCV analysis reveals that formation of the O2˙− species results from the dominant flow of electron density from the 4s1 to 2π* orbital in the β-channel, which is accompanied by a small back-donation of the α-spin density towards the zinc core (Fig. 28b1). The recognition of both the top-on [η1-O2˙−–Zn]+/MFI (Si/Al = 11.9) and the side-on [η2-O2˙−–Zn]+/MFI (Si/Al = 140) adducts illustrates a subtle role played by the intermolecular electrostatic interactions in supporting the particular binding mode of dioxygen. It is also plausible that the η2 superoxide adduct is actually produced via the η1 intermediate, since the nil overlap between the redox 4s1 to 2π* orbitals in the side-on mode impedes charge flow. In the case of [Zn–O˙−]/MFI species where the spin density is mainly localized on the ligand (characterized by g‖ = 2.37 and g⊥ =1.98 and the UV/vis band at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 cm−1), a room temperature interaction with O2 (pO2 > 0.1 Torr) leads to the reversible formation of a zinc–ozonide adduct, [Zn–O˙−]+/MFI + O2 ↔ [η2- O3˙−Zn]+/MFI, produced by the attack of dioxygen at the O˙− moiety (see Chapter 4.1 and Fig. 17d). It is characterized by gxx = 2.0019, gyy = 2.0106, gzz = 2.0124, Axx = −8.37, Ayy = 0.14, Azz = 0.36 (Fig. 28c), and the nb → π*(O–O–O) band centred at ∼450 nm, which is featured by a well resolved vibronic progression due to the stretching O–O–O oscillations with the 860 and 900 cm−1 splitting for η2-16O3˙−ZnII and η2-18O3˙−ZnII species, respectively (see Fig. 28c1).294 The binding of O2 occurs via an [η1- O3˙−Zn]+ intermediate,293 and a rather small overall energy of this process (96 kJ mol−1), together with low activation barriers (the highest is equal 68 kJ mol−1), accounts well for the experimentally observed complete reversibility of this process. The a1-bonding orbital (labelled in the local C2v symmetry of the zinc–ozonide magnetophore) with the largest overlap between the Zn and O3 counterparts, contributes mainly to the Zn–O3 bond. In contrast, the b1-SOMO is almost entirely localised on the bidentate ozonide moiety. The remaining orbital interactions (a2, b1, and b2 MO) are less important for the strength of the Zn–O3 interaction due to the small overlap. The distinct polarisation of two O–O bonds in the O3 ligand lead to a unique pattern where both side oxygens that are directly bound to Zn2+ become more negatively charged (−0.415|e|). In contrast, the central oxygen acquires surprisingly a partially positive charge (0.202|e|), in comparison to the free ozonide anion (−0.167|e|). The zeolite framework plays a vital role in maintaining the effective charge of the zinc cation at approximately +2, stabilising the highly polarised η2-O3−–Zn2+ bond.
020 cm−1), a room temperature interaction with O2 (pO2 > 0.1 Torr) leads to the reversible formation of a zinc–ozonide adduct, [Zn–O˙−]+/MFI + O2 ↔ [η2- O3˙−Zn]+/MFI, produced by the attack of dioxygen at the O˙− moiety (see Chapter 4.1 and Fig. 17d). It is characterized by gxx = 2.0019, gyy = 2.0106, gzz = 2.0124, Axx = −8.37, Ayy = 0.14, Azz = 0.36 (Fig. 28c), and the nb → π*(O–O–O) band centred at ∼450 nm, which is featured by a well resolved vibronic progression due to the stretching O–O–O oscillations with the 860 and 900 cm−1 splitting for η2-16O3˙−ZnII and η2-18O3˙−ZnII species, respectively (see Fig. 28c1).294 The binding of O2 occurs via an [η1- O3˙−Zn]+ intermediate,293 and a rather small overall energy of this process (96 kJ mol−1), together with low activation barriers (the highest is equal 68 kJ mol−1), accounts well for the experimentally observed complete reversibility of this process. The a1-bonding orbital (labelled in the local C2v symmetry of the zinc–ozonide magnetophore) with the largest overlap between the Zn and O3 counterparts, contributes mainly to the Zn–O3 bond. In contrast, the b1-SOMO is almost entirely localised on the bidentate ozonide moiety. The remaining orbital interactions (a2, b1, and b2 MO) are less important for the strength of the Zn–O3 interaction due to the small overlap. The distinct polarisation of two O–O bonds in the O3 ligand lead to a unique pattern where both side oxygens that are directly bound to Zn2+ become more negatively charged (−0.415|e|). In contrast, the central oxygen acquires surprisingly a partially positive charge (0.202|e|), in comparison to the free ozonide anion (−0.167|e|). The zeolite framework plays a vital role in maintaining the effective charge of the zinc cation at approximately +2, stabilising the highly polarised η2-O3−–Zn2+ bond.
In the case of di-oxo vanadium ↑VO2/BEA, a room temperature contact with dioxygen (2 Torr) leads to the formation of a bent (α = 16°) top-on [η1-O2− VO2+]/BEA complex (gz = 2.0236, gy = 2.113, gx = 2.0054, Az = 0.98, Ay = 0.68, Ax = 0.54 mT) via the MLET, dz2 → 2π*, pathway. The π*-type SOMO is essentially confined to the η1-O2− moiety.295
The π-type adducts are exemplified by superoxide species attached to cage Co2+(NH3)n complexes. The intrazeolite Co2+ (S = 3/2) cations cannot directly activate O2 into the superoxide state due to the inverse energy levels (IEL) of the donor 3d and acceptor 2π* orbitals (see Fig. 26a). However, when boosted by the coordination of stronger σ-donor NH3 co-ligands (which can be allied with an “orthosteric effect”) the resultant [Co(NH3)n]2+ adducts hosted in FAU(Y)292 and ZSM-5 zeolites113 upon exposure to O2 form the corresponding [η1-O2−Co(NH3)n]2+ heteroleptic superoxide complexes identified readily by EPR spectroscopy (Fig. 28d). The reductive binding of O2 is accompanied by a spin crossing in the 3d manifold of the cobalt core (↑↑O2 (S = 1) + ↑↑↑Co2+ (S = 3/2) → ↑O2−–Co3+↑↓ (S = 1/2)), giving rise to the observed doublet state of the superoxide adduct. In an alternative spin pairing process (↑↑O2 (S = 1) + ↑↑↑Co2+ (S = 3/2) → ↑O2−↑↓Co3+↑ (S = 1), the adduct should assume a triplet state. Yet, the g-tensor anisotropy (g1 = 2.084, g2 = 2.01, g3 = 2.00) is diagnostic for the formation of a superoxide species with S = 1/2. The superhyperfine structure (CoA1 = 1.78 mT, CoA2 = 1.2 mT and CoA3 = 1.25 mT)292 can be interpreted in terms of the β-electron density transfer to  formed by the out of plane π-type overlap, and the spin polarization of the close-lying in-plane
formed by the out of plane π-type overlap, and the spin polarization of the close-lying in-plane  of the mixed π/σ character, as discussed elsewhere.296 Such in-plane d/π interactions impart a bent configuration of the Co–O–O moiety and local Cs symmetry of the ensuing magnetophore. A qualitative molecular energy diagram shown in Fig. 28d1 accounts for the reductive coordination of O2 by [Co(NH3)n]2+/ZSM-5 via the MLET mechanism associated with spin crossing.
of the mixed π/σ character, as discussed elsewhere.296 Such in-plane d/π interactions impart a bent configuration of the Co–O–O moiety and local Cs symmetry of the ensuing magnetophore. A qualitative molecular energy diagram shown in Fig. 28d1 accounts for the reductive coordination of O2 by [Co(NH3)n]2+/ZSM-5 via the MLET mechanism associated with spin crossing.
The superoxide η2-species can also be produced in the δ-type MO overlap. This relatively rare binding mode of O2 results from an isodesmic 2Ni+4c/ZSM-5 + 3O2 → [η2-O2−Ni2c]+ZSM-5 process, where the initial coordination number of the nickel cation (Ni+4c) equalled 4, is preserved. The corresponding EPR spectrum obtained for 17O-enriched dioxygen is shown in Fig. 29a. The 11-line pattern proves the side-on attachment of the dioxygen ligand. The diagnostic features of the heteroleptic [η2-O2−Ni4c]+ZSM-5 adduct (ge < gxx(3) = 2.0635 < gyy(2) = 2.0884 < gzz(1) = 2.1675, Ayy(2) (5.67 mT) ≫ Axx(3) (1.0 mT) ∼ Azz(1) (1.3 mT)) with the highest hf splitting along the gyy(2) mid value direction are distinctly different from those observed for the π-type O2− adducts (ge ≈ gxx(3) < gyy(2) < gzz(1), and Azz(1) > Axx(3) ∼ Ayy(2) with the maximum of hf splitting along the highest gzz(1) value). The [η2-O2−Ni]+ZSM-5 complex is best described as a mixed metalloradical with two supporting oxygen donor framework Oz ligands and nearly even spin density repartition between the superoxide moiety and the nickel centre (ρNi = 0.36, ρO(1) = 0.32, ρO(2) = 0.30), as shown in Fig. 29a1. The associated changes in the charge distribution upon O2 attachment (ΔqNi = 0.32, ΔqO = −0.09, ΔqO = −0.11) confirm the MLET mechanism of dioxygen activation with back donation playing a crucial role (see below). Notably, the observed triangle spin density and charge distribution resemble those observed for η2-O3˙−Zn2+ species, where the middle Ni cation and the middle oxygen are both positively charged.
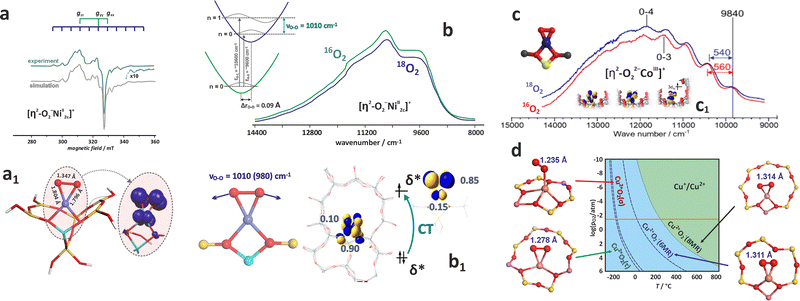 | ||
| Fig. 29 X-band EPR spectrum of [η2-O2−Ni4c]+/ZSM-5 adducts (a), and the structure of the η2-O2Ni moiety with the spin density distribution (a1) adapted from ref. 64 with permission from the American Chemical Society, Copyright 2011. NIR spectra of η2-16O2 and η2-18O2 adducts of nickel (b), and cobalt (c) hosted in MFI zeolite, and the corresponding structures of these species (b1) and (c1), adapted from ref. 286 and 297, with permissions from the American Chemical Society (Copyrights 2020 and 2019, respectively). Thermodynamic stability diagram of η1-O2 and η2-O2 adducts of Cu2+ and Cu+ hosted in CHA (d), based on data from ref. 83. | ||
The SOMO orbital is constituted by a δ overlap between the out-of-plane  MO of dioxygen and the 3dx2−y2 orbital of nickel, whereas LUMO results from the π-type overlap between dzy and in-plane
MO of dioxygen and the 3dx2−y2 orbital of nickel, whereas LUMO results from the π-type overlap between dzy and in-plane  orbitals (see Fig. 30a), following the superoxide nature of the [η2-O2−Ni]+ZSM-5 species. The overall binding energy of dioxygen, equal to −16 kcal mol−1, results from the molecular (−141 kcal mol−1) and electrostatic (−87 kJ mol−1) contributions that are attenuated by a sizable steric repulsion (+212 kJ mol−1).
orbitals (see Fig. 30a), following the superoxide nature of the [η2-O2−Ni]+ZSM-5 species. The overall binding energy of dioxygen, equal to −16 kcal mol−1, results from the molecular (−141 kcal mol−1) and electrostatic (−87 kJ mol−1) contributions that are attenuated by a sizable steric repulsion (+212 kJ mol−1).
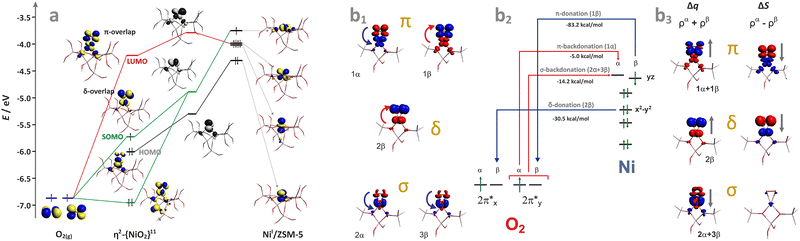 | ||
| Fig. 30 Molecular orbital correlation diagram of O2 binding to Ni+/ZSM-5 (a). The NOCV contours that describe the bonding between the dioxygen and the intrazeolite Ni+ cation (b1), along with the corresponding diagram showing the charge and spin flow channels and the associated energies (b2), together with the orbital channels of the overall charge (Δq) and spin (ΔS) flows (b3). The red and blue contours correspond to loss and gain of the electron and spin density, respectively. Adapted from ref. 64 with permission from the American Chemical Society, Copyright 2011. | ||
The intrazeolite [η2-O2−Ni4c]+/ZSM-5 species exhibit significantly different electronic and magnetic structure than the akin dioxygen adducts with nickel in homogeneous complexes,298,299 where the spin pairing mechanism prevails. The SOMO is then constituted mainly by the 3dz2 orbital, giving rise to gzz ≪ gxx, gyy, and a small 17O hf splitting (which usually remains unresolved). Thus, dissimilar magnetic structures of both types of adducts can be accounted for by the different mechanisms of dioxygen binding, which are based on coupled electron and spin transfer in the case of [η2-O2−Ni4c]+ZSM-5, and a spin pairing model for the homogeneous complexes. The ETS-NOCV analysis of the [η2-O2−Ni4c]+ZSM-5 electronic structure reveals three distinct orbital channels of the congruent and incongruent charge and spin density flows, associated with δ, π, and σ overlap, which contribute jointly to the attachment energy and the reductive activation of the dioxygen ligand (Fig. 30b1 and b2).
The unequal charge and spin density transfers along the π-channel result from the π-donation from 3dyz to  (1β) and the π-backdonation (1α) processes, with highly uneven energetic contributions −83.2 and −5.0 kcal mol−1, respectively. The δ-channel (2β) of a congruent but opposite spin and charge transfer
(1β) and the π-backdonation (1α) processes, with highly uneven energetic contributions −83.2 and −5.0 kcal mol−1, respectively. The δ-channel (2β) of a congruent but opposite spin and charge transfer  contributes to −30.5 kcal mol−1 of the O2–Ni interaction energy, whereas the spinless charge back-donation,
contributes to −30.5 kcal mol−1 of the O2–Ni interaction energy, whereas the spinless charge back-donation,  , through the σ channel (2α + 3β) is associated with a relatively small energy gain of −14.2 kcal mol−1. As a result, the β-spin polarised charge δ-donation, reinforced by the partly counterbalancing β-charge donation and α-polarised back-donation along the π-channel, together with a small charge-only σ-back-donation (Fig. 30b2, and b3) are mainly responsible for the formation of nickel-bound superoxide O2− radical of the (π)2(δ)2(3dz2)2(3dx2−y2)2(3dzy2)2(δ*)1(π*)0 configuration, and its S = 1/2 ground state. This illustrates the inherent complexity of what appears to be a simple process.64
, through the σ channel (2α + 3β) is associated with a relatively small energy gain of −14.2 kcal mol−1. As a result, the β-spin polarised charge δ-donation, reinforced by the partly counterbalancing β-charge donation and α-polarised back-donation along the π-channel, together with a small charge-only σ-back-donation (Fig. 30b2, and b3) are mainly responsible for the formation of nickel-bound superoxide O2− radical of the (π)2(δ)2(3dz2)2(3dx2−y2)2(3dzy2)2(δ*)1(π*)0 configuration, and its S = 1/2 ground state. This illustrates the inherent complexity of what appears to be a simple process.64
The vibronic progression with the O–O stretching frequency of 1010 cm−1 and the isotopic shift, Δ18O = 30 cm−1, associated with the δ → δ* excitation seen in the NIR spectra (Fig. 29b) provides another argument that the δ channel interaction contributes to the formation of the superoxide species.297 The bonding δ orbital is mainly localised on the Ni2+ centre, and the antibonding δ* orbital on the O2− moiety (Fig. 29b1), hence the δ → δ* transition lengthens the O–O bond from 1.308 to 1.405 Å, contributing additionally to dioxygen activation via MLCT. Furthermore, the ionicity of the δ bond has been linked to the abnormal electrophilic reactivity of the unoccupied β-2π* orbital of the superoxide moiety.297
In contrast to the superoxide species produced on Ni+/ZSM-5, the side-on attachment of O2 to Co+ hosted in ZSM-5 leads, via 2e− transfer, to the formation of a peroxo [η2-O22−Co]+/ZSM-5 adduct (Fig. 29c).286 Actually, this species is indirectly produced from a dicarbonyl precursor [Co(CO)2]+ + 2Co2+ + O2 → [Co(O)2]+ + 2[Co(CO)]2+. The positioning of the Al atoms at the interface between the straight and sinusoidal channels of the MFI framework is essential for the successful implementation of this process. In the [η2-O22−Co4c]+/ZSM-5 adduct with S = 1, the Co3+ core is chelated by the peroxo ligand, and supported by two weak donor anionic lattice oxygen atoms, forming a square planar structure (similar to that observed for the superoxide adduct with the intrazeolite Ni2+) with the ground state electronic configuration of (π)2(δ)2(dz2)2(dx2−y2)2(dzy)1(δ*)1(π*)0. This structure of the [η2-O22−Co4c]+/ZSM-5 adduct is ascertained by a distinct NIR absorption band around 9840 cm−1, assigned to the δ → δ* transition in the [Co(O2)]+ moiety (Fig. 29c). The interval between the first and second vibrational fine structure features equal to 560 cm−1 for the 16O2, and the isotopic shift of Δ18O ≈ 20 cm−1 are typical for the symmetric vibrational frequency of the peroxo side-on species (O22−).
The coordination of O2 to Cu+ (d10) cations hosted in zeolites of different topologies (AFI, CHA, TON, MOR, MFI) leads to the formation of stable magnetic, η1, and non-magnetic, η2, adducts with the side-on attachment being energetically more favourable by ∼0.5 eV.285 The η2 adsorption energies are around −1.3 ± 0.1 eV for CHA(8MR), TON(10MR), MFI(10MR), AFI(12MR), dropping to −1.03 eV for MOR(12MR), indicating that the size of the zeolite cavities plays a secondary role in controlling the strength of the Cu–O2 binding. The O–O stretching frequencies varying about 1172–1198 cm−1 are characteristic of superoxide species (CuI/z + O2 → [η2-O2−–CuII]+/z). The thermodynamic stability diagram of η1-O2 and η2-O2 adducts of the Cu2+ and Cu+ cations hosted in the 6MR and 8MR sites of CHA at various temperatures and pO2 pressures (Fig. 29d) shows that O2 is only weakly bound to Cu2+ in both 6MR and 8MR positions, desorbing already below 0 °C under the O2 pressure of 5% (horizontal orange line). This is consistent with a weak activation of dioxygen (dO–O of 1.235 Å is close to the free O2 value of 1.21 Å), primarily due to the formation of inverted energy levels (IEL, see Chapter 4.1 and Fig. 17). The stability of the superoxide [η2-O2−–Cu]+ species hosted in the 6MR and 8MR extends to ∼200 °C, following the sizable charge transfer stabilization of the ligated superoxide moiety. Interestingly, attachment of the ancillary NH3 ligands of stronger donor properties makes the mononuclear [O2–Cu(NH3)2]+ adducts that are solvated in the zeolite cavities unstable (at the DFT calculation level of BEEF-vdW), regardless of the attachment mode.300 Yet, the [η1-O2–Cu(NH3)3]+ species, proposed to be formed upon NH3-induced dissociation of the peroxo diamino dicopper(II) complexes, are apparently stable.301
Dioxygen attachment to dinuclear metal and metal–oxo centres. The binding of O2 by two adjacent TMI cations typically leads to the formation of end-on cis μ-η1:η1, trans μ-η1:η1, the side-on μ-η2:η2, and the bis(μ-oxo)282 species of predominantly peroxo and oxo character, mentioned above (Fig. 27). Notable examples are provided by the bridging oxygen species, produced upon O2 attachment to dimeric Cu+∪Cu+ centres in MOR,285,302 CHA,285,303 BEA,304 MFI285,305,306 and Fe2+∪Fe2+ centres in BEA,307 MOR or FER.308 Other less explored species include trimeric Cu3O3 centres in MOR302 or Co2+∪Ca in FAU(X) zeolites.309 The metal–metal distance and the presence of ancillary ligands (such as common NH3310) play a notable role in controlling the nature of the produced species, as well as the pathways of eventual splitting of the bound O2 moiety.
When the auto-reduced Cu/ZSM-5 is contacted with O2 at room temperature, side-on peroxo dicopper species ([Cu(μ-η2:η2-O22−–Cu]2+) are formed.311 The resonance Raman ν(Cu+,Cu+) band at 269 cm−1, the isotopically sensitive ν(O–O) vibrations at 736 cm−1 (for 16O) and 695 cm−1 (18O), respectively, and the UV-vis peak around 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (assigned to
000 cm−1 (assigned to  ) are their typical diagnostic features (Fig. 31a1 and a2). The [Cu(μ-η2:η2-O22−–Cu]2+ adduct after heating at T > 150 °C transforms into mono-μ-oxo dicopper [Cu(μ-O2−)–Cu]2+ characterized by the UV-vis band at 22
) are their typical diagnostic features (Fig. 31a1 and a2). The [Cu(μ-η2:η2-O22−–Cu]2+ adduct after heating at T > 150 °C transforms into mono-μ-oxo dicopper [Cu(μ-O2−)–Cu]2+ characterized by the UV-vis band at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 and the rR lines at 237 cm−1 (νδ, Δ18O = 3 cm−1), 456 cm−1 (νs, Δ18O = 8 cm−1) and 870 cm−1(νas, Δ18O = 40 cm−1), see Fig. 31a2 and a3. Although the splitting of the O–O bond is an uphill process, a relatively small barrier <0.4 eV (for the SSZ-13 zeolite) makes the subsequent transformation of the μ-η2:η2 peroxo adduct into the bis(μ)oxo descendant quite feasible. Indeed, this process becomes thermodynamically favourable above 200 °C at log(pO2/p0) < 1 (Fig. 31a4). The bis-μ-oxo species are the precursors for mono(μ-oxo)dicopper(II) species,284 which exhibit high activity in C–H bond activation, and are recognised as the active sites for CH4 or benzene hydroxylation.304,311,312
700 cm−1 and the rR lines at 237 cm−1 (νδ, Δ18O = 3 cm−1), 456 cm−1 (νs, Δ18O = 8 cm−1) and 870 cm−1(νas, Δ18O = 40 cm−1), see Fig. 31a2 and a3. Although the splitting of the O–O bond is an uphill process, a relatively small barrier <0.4 eV (for the SSZ-13 zeolite) makes the subsequent transformation of the μ-η2:η2 peroxo adduct into the bis(μ)oxo descendant quite feasible. Indeed, this process becomes thermodynamically favourable above 200 °C at log(pO2/p0) < 1 (Fig. 31a4). The bis-μ-oxo species are the precursors for mono(μ-oxo)dicopper(II) species,284 which exhibit high activity in C–H bond activation, and are recognised as the active sites for CH4 or benzene hydroxylation.304,311,312
 | ||
| Fig. 31 Resonance Raman (a1) and (a3) and UV-vis-NIR (a2) spectra of Cu2+–(O–O)Cu2+ and Cu2+–(O)–Cu2+ species hosted in CHA, together with corresponding FPT diagram (a4).83,311 Influence of copper distance on the nature of oxygen adducts, together with the associated key molecular orbitals responsible for O–O bonding (b1) and (b2).306 Evolution of the dinuclear diamino adducts of O2 with the corresponding energy profile (c).310 Energy profile for dioxygen splitting on Fe/FER catalysts (d), and dependence of the activation energy of O2 dissociation on the zeolite topology (d1). Panels d and d1 are adapted from ref. 308 with permission from the American Chemical Society, Copyright 2021. Panels a–c are based on data form quoted references. | ||
Molecular modelling studies show that the distribution of Al atoms within the cavities/channels and the resultant Cu–Cu distance control to a large extent the nature of the bridging oxygen species. For 2NNAl pairs configuration (dCu–Cu = 2.224 Å) a cis μ-η1:η1-O2 binding mode is preferred, in the case of 3NNAl pairs a μ-η2:η2-O2 (dCu–Cu = 3.397 Å) and a trans μ-η1:η1O2 (dCu–Cu = 3.887 Å) adducts are formed, whereas at larger distances between the Al atoms (4NN) only a trans μ-η1:η1O2 (dCu–Cu = 4.249 Å) can be produced.282 The O–O bond activation gauged by lengthening of the interatomic distance, varies significantly between the adducts.306 In the 2NN configuration, the end-on trans μ-η1:η1O2 complex has the O–O bond of 1.376 Å, whereas for trans μ-η1:η1O2 adducts in 3NN and 4NN environment this bond is shorter (∼1.31 Å). The largest O–O bond length (1.436 Å) is observed for the side-on μ-η2:η2-O2 peroxo species (Fig. 31b1). The corresponding MO energy diagram of these species, shown in Fig. 31b2, reveals a lucid molecular orbital rationale for different extents of dioxygen activation. The antibonding character of the overlap in the HOMO and HOMO−1 orbitals of the O–O moiety for the side-on 3NN adduct is responsible for lengthening of the O–O bond in comparison to 2NN top-on species with only one antibonding HOMO in the frontier orbitals region.282 In the case of the 4NN end-on adduct, HOMO exhibits in-phase overlap, whereas HOMO−1 exhibits out-of-phase overlap of the oxygen orbitals. The cancellation of both effects accounts for the shorter O–O bond in the trans μ-η1:η1O2 4NN in comparison to cis μ-η1:η1O2 2NN species.
The μ-dioxygen adducts are also formed upon reaction of O2 with [(NH3)2Cu]+ complexes, where the parent framework Oz ligands are entirely replaced by the NH3 molecules, which are produced in the reduction half-cycle (RHC) of the SCR reaction.310,313,314 DFT calculations show that the most probable products include trans μ-η1:η1-peroxo and μ-η2:η2-peroxo dicopper(II) adducts with a bidentate attachment of O2, without complete dissociation of the O–O bond, or a bis-μ-oxo dicopper(III) adduct with the split O–O bond (Fig. 31c). Despite that, the corresponding energy profiles are quite sensitive to the calculation scheme, the μ-η2:η2-peroxo dicopper(II) species with the O–O bond retained is favoured.310 It remains in agreement with the experimental UV-vis (a band at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850 cm−1) and EXAFS (Cu–Cu distance of ∼3.4 Å) investigations, which show that the side-on μ-η2:η2 peroxo dicopper(II) complex predominates after O2 interaction with a pair of the cage diamino copper(I) complexes hosted in CHA zeolites (Si/Al = 15, Cu/Al = 0.5) at 200 °C.301
850 cm−1) and EXAFS (Cu–Cu distance of ∼3.4 Å) investigations, which show that the side-on μ-η2:η2 peroxo dicopper(II) complex predominates after O2 interaction with a pair of the cage diamino copper(I) complexes hosted in CHA zeolites (Si/Al = 15, Cu/Al = 0.5) at 200 °C.301
The zeolite FER, MOR, and *BEA frameworks containing iron that exhibit high concentrations of Al atoms (Si/Al < ∼10) with a large part of the Al pairs of apposite spatial organisation are capable of dioxygen capture and subsequent O–O bond splitting. For this purpose, the two cationic sites that form the distant binuclear Fe2+ centres in six rings must face each other in parallel and axial configuration, and the Fe⋯Fe distance should be within a narrow range, from ∼7 to ∼8 Å.308 However, the experimental confirmation of the involved face-to-face configuration of Fe–O species has not been definitive so far. Such active centres are capable of splitting dioxygen to produce, upon dissociation, a pair of ferryl species. The reaction is driven by the cooperative four-electron 2Fe2+ → 2Fe4+ redox cycle, and its primary molecular steps, along with the corresponding energetic profiles, are shown (Fig. 31d1), taking the Fe/FER system as an example. The reaction pathway involves a top-on capture of O2, followed by subsequent transformation of the η1-O2 into more stable η2-O2 species. The trans μ-η1:η1 O2 transition state, located at −0.4 kcal mol−1 to separate reactants, is achieved by returning to the monodentate η1-O2 binding. The dissociation of the dioxygen moiety is energetically slightly favourable by −2.4 kcal mol−1 for the most stable side-on adduct. The activation energy of the O–O bond scission depends on the Fe⋯Fe distance for the iron cations accommodated in the β sites with the Al pairs placed in the para-position, preferably in FER, MOR, and BEA zeolites, with a distinct exception of LTA (where both rings are not parallel), see Fig. 31d2 and a suitable ref. 308.
The properties and distinct chemical reactivity of the coordinated NO are often explained in terms of electron density transfer (ET), resulting in the withdrawal of a single electron from the 2π* orbital to produce a nitrosonium (electrophilic) NOδ+ species, or the addition of an electron to the 2π* orbital, forming a nitroside NOδ− species of nucleophilic character.14,315 Yet, using the Enemark–Feltham notation of the TMI nitrosyl adducts, 2S+1{TMI–NO}n (see Chapter 4.3), the direct attribution of a TMI–NO to nitrosonium (NOδ+) or nitroside (NOδ−) category can be circumvented. The other pathway to NO activation involves an oxygen transfer (OT), resulting in the oxidation of NO to NO2. The occurrence of the elementary ET and OT events depends critically on the nature of the active site. The electron transfer is characteristic of the bare cations,17,247 while oxygen transfer occurs in the case of the various mono or polynuclear oxo-cations.316
The epitomic NO+ and NO− species, which are expected to bind in linear and bent η1-N mode, respectively. But typically observed adducts with the partial charge accumulated on the NO ligand (NOδ−), exemplified by ({2CuNO}11, 2{ZnNO}11), are slightly bent with elongated and polarized N–O bonds. The NOδ+ containing adducts, such as (2{NiNO}9, {3CoNO}8), are also bent with the bonds shortened and polarized.317,318 The NO2−/NO3− oxidation products, which play an essential role in some catalytic processes (e.g., SCR of NO, oxidation of NH3, selective oxidation reactions), are produced along mechanistically more intricate pathways involving the interaction of the activated (bound) NO with O2 or via involvement of elusive HONO species produced upon the interaction of NO with the intrazeolite TMI–OH centres.172
The appearance of nitrosonium and nitroside, or other NOx species can be deduced from the corresponding IR spectra, featured by characteristic position (blue- or red-shifted compared to the bare NO band) and the number of N–O bands.319 For zeolitic systems, such simple discrimination of the nitrosonium vs. nitroside reactivity of NOδ with δ close to +1 or −1, has been rarely observed, and situations with polarisation of the TMI–NO bond rather than formation of ionic adspecies via electron transfer are more common.247,317,320,321
Role of spin and metal electron configuration. The behaviour of the spin density of NO upon binding to TMI can be followed with EPR measurements of in situ NO adsorption. This procedure results in characteristic powder EPR spectra (Fig. 32a–e) attributed to the paramagnetic nitrosyl adducts. Depending on the investigated system (the number of unpaired 3d-electrons of the TMI core), the following processes can be distinguished: (1) spin pairing, (2) spin crossing, and (3) spin addition. The simple spin pairing was observed for VO2 (3d1) species (being indirectly deduced from disappearance of the EPR signal of VO2),295 high-spin 4Co2+ (3d7) centres (leading to the formation of {2Co(NO)2}9 dinitrosyls upon pairing of two odd 3d electrons with two NO molecules),17 and high-spin 3Ni2+ (3d8) cations (formation of the mononitrosyls {2NiNO}9 adducts).247 The reaction of 5Fe2+ (3d6) with NO in ZSM-5 zeolite represents an example of spin pairing combined with spin crossing.322–324 In contrast, the adsorption of NO onto reduced Cu+ (3d10) represents a simple spin addition process to the closed shell Cu+ cation.320 In all five cases, the formation of nitrosyl complex can be rationalized in terms of the spin processes occurring between the spin state of 3d TMI and that of NO (2Π1/2) radical ligand:
 | ||
| Fig. 32 Reactivity of TMI in zeolites toward NO monitored with the CW-EPR spectroscopy. NO adsorption on VO2/SiBEA (a), Co2+/ZSM-5 (b), Ni2+/ZSM-5 (c), reduced Fe2+ZSM-5 (d), reduced Cu+/ZSM-5 (e) metallozeolites. The arrows schematically indicate the number of unpaired electrons involved in the TMI active centre and the resulting nitrosyl adducts. The dotted grey EPR spectra correspond to iron and copper in their parent oxidation states before autoreduction. Figure was based on data from ref. 247, 295, 316 and 322. | ||
(1) 2VO2/SiBEA + NO(g) (2Π1/2) → 1{ON-VO2}2/SiBEA;
(2) 4Co2+/ZSM-5(BEA) + 2NO(g) (2Π1/2) → 2{Co(NO)2}9/ZSM-5(BEA);
(3) 3Ni2+/ZSM-5(BEA) + NO(g) (2Π1/2) → 2{NiNO}9/ZSM-5(BEA);
(4) 5Fe2+/ZSM-5 + NO(g) (2Π1/2) → 3{FeNO}7/ZSM-5;
(5) 1Cu+/ZSM-5 + NO(g) (2Π1/2) → 2{CuNO}11/ZSM-5.
In the case of the 4Co2+ adducts with NO, analysis of the observed cobalt hyperfine splitting indicates that approximately 80% of the spin density (ρ3d ≈ 80%) is localized on the metal centre. This suggests that the magnetic structure of the dinitrosyl intermediates can be represented as NO(↑↓)–↑Co2+–(↓↑)NO, where the unpaired electron resides primarily on the cobalt ion. This adduct, however, undergoes interesting transformation upon thermal treatment, resulting in the reduction of the metal centre to zero-valent cobalt. The latter state was unambiguously confirmed by consecutive adsorption of CO and propene, resulting in EPR spectra characteristic of 3d9 electron configuration of the cobalt cation.17
Similarly, the g-tensor values of Ni2+NO adduct in ZSM-5 zeolite are characteristic of a metal-centred paramagnet with the 3d9 electron configuration.3 This signal has been assigned to the adducts of the type [Ni–NO]2+/ZSM-5 (S = 1/2, 3d9). A similar signal was reported earlier for surface adducts in the Ni–silica systems.325 The [Ni–NO]2+ notation does not reflect the actual redistribution of partial charges that occurs upon NO coordination to Ni2+, and the corresponding shift of the νN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O IR band (1890–1898 cm−1, Fig. 33a) concerning the 1874 cm−1 value of the physisorbed NO. The actual charge redistribution is closer to the Ni(2−δ)+–NOδ+ formulation. The relative position of the
O IR band (1890–1898 cm−1, Fig. 33a) concerning the 1874 cm−1 value of the physisorbed NO. The actual charge redistribution is closer to the Ni(2−δ)+–NOδ+ formulation. The relative position of the  donor level regarding the semi-occupied Ni 3dz2 (σ donation channel) and the position of the occupied 3dxz orbital in comparison to the empty level
donor level regarding the semi-occupied Ni 3dz2 (σ donation channel) and the position of the occupied 3dxz orbital in comparison to the empty level  (π back donation channel), dictate the extent of the actual ligand to metal charge transfer, where the coordinated NO molecule is partially oxidized to NOδ+. This is consistent with the experimentally observed blue shift in the NO stretching frequency in the IR spectrum.247
(π back donation channel), dictate the extent of the actual ligand to metal charge transfer, where the coordinated NO molecule is partially oxidized to NOδ+. This is consistent with the experimentally observed blue shift in the NO stretching frequency in the IR spectrum.247
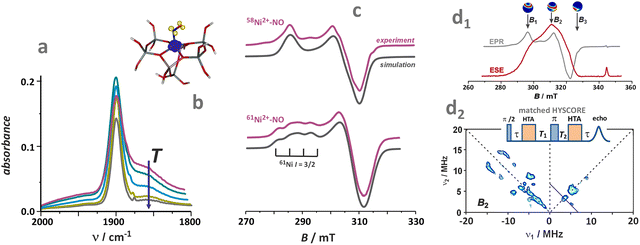 | ||
| Fig. 33 Spectroscopic evidence of the formation of nitrosyl upon NO interaction with Ni2+/ZSM-5. The IR spectra of NO adsorption at various temperatures (a), spin density contour of the [NiNO]2+ adduct in ZSM-5 (b), CW-EPR spectra (77 K) of NO adsorption on Ni and isotopically enriched 61Ni (I = 3/2) hosted in ZSM-5 zeolite (c), electron spin echo detected EPR signal (10 K), the arrows indicate observer positions (B1, B2, B3) at which HYSCORE signals can be measured (d1). HYSCORE spectrum due to the 14N hyperfine interaction recorded at B2 position with the matched pulse sequence (d2). The figure was based on data from ref. 156 and 247. | ||
The EPR results also support such a molecular picture. The g-tensor parameters extracted from the CW-EPR spectrum of {2NiNO}9 adducts in ZSM-5 zeolite (Fig. 33c) are characteristic of a 3d9 electron configuration, which is supported by the presence of 61Ni (I = 3/2) hyperfine splitting when an isotopically-enriched sample was used. At the same time, hyperfine splitting due to 14N (I = 1) is not resolved due to an effective quenching of the spin density at the nitrogen nucleus resulting from the spin pairing ligation. The residual hyperfine structure can be unraveled using HYSCORE spectroscopy, a powerful method for characterizing paramagnetic species in porous materials.95,116,117,156 Electron spin echo (Fig. 33d1) and the HYSCORE spectrum for one selected orientation, corresponding to the maximum amplitude of the echo, is shown in Fig. 33d2 for the {2NiNO}9/ZSM-5 adduct. The characteristic correlation ridges in the so-called strong coupling regime correspond to the following 14N hyperfine parameters Axx = 14.0 MHz, Ayy = 9.0 MHz, Azz = 6.0 MHz, implying that approximately 4% of the total spin density is localised on nitrogen.156
The above observations indicate that nitrosyl adducts are formed via a spin-pairing process, which in the case of Ni2+/ZM-5 involves a one-electron Ni2+(3d8)/Ni+(3d9) couple.247 For the Co2+/ZSM-5 (or BEA) system, adsorption of NO leads to the spontaneous formation of dinitrosyls, engaging a two-electron Co2+(3d7)/Co0(3d9) couple.316
The IR and EPR evidence for the formation of paramagnetic 2{CuNO}11 is shown in Fig. 34a and b. The bonding between the closed-shell Cu+ and NO radical in the channels of ZSM-5 zeolite has been rationalized in terms of the spin addition mechanism and the s/d hybridization of the empty 4s and two occupied 3dσ orbitals (3dz2 and 3dxz) of Cu, which interact with the 2π* MO of NO.320,321,326,327 The empty 3dz2 + 4s acceptor state can overlap more efficiently with the in-plane  of NO. At the same time, the interaction of the NO lone pair is weaker as the latter is situated relatively low in the energy within the 3d manifold (see the MO interaction diagram in Fig. 34c). Such an interaction provides a pathway for the σ-type bond, producing the singly occupied molecular orbital (SOMO). The interaction of the occupied 3dyz orbital with the remaining out-of-plane empty
of NO. At the same time, the interaction of the NO lone pair is weaker as the latter is situated relatively low in the energy within the 3d manifold (see the MO interaction diagram in Fig. 34c). Such an interaction provides a pathway for the σ-type bond, producing the singly occupied molecular orbital (SOMO). The interaction of the occupied 3dyz orbital with the remaining out-of-plane empty  gives rise to the lowest-unoccupied molecular orbital (LUMO). The local Cs symmetry allows for admixing of the Cu 4s state to the 3d manifold. The interaction with the 2π* states of NO results in a charge and spin donation
gives rise to the lowest-unoccupied molecular orbital (LUMO). The local Cs symmetry allows for admixing of the Cu 4s state to the 3d manifold. The interaction with the 2π* states of NO results in a charge and spin donation  , accompanied by a
, accompanied by a  back-donation. SOMO and LUMO are antibonding between Cu+ and NO, exhibiting a mixed 2π*-3d character with a prevailing NO contribution. The redistribution of electronic charge within the Cu–NO unit leads to a partial oxidation of the copper centre and a concurrent reduction of the NO ligand, as evidenced by the red-shift of the N
back-donation. SOMO and LUMO are antibonding between Cu+ and NO, exhibiting a mixed 2π*-3d character with a prevailing NO contribution. The redistribution of electronic charge within the Cu–NO unit leads to a partial oxidation of the copper centre and a concurrent reduction of the NO ligand, as evidenced by the red-shift of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration to 1805 cm−1. In addition, such an orbital picture explains all characteristic features of the EPR spectrum of {2CuNO}11 adducts (Fig. 34b), i.e., monoclinic symmetry, large hyperfine coupling constants (63,65Cu, I = 3/2) due to involvement of Cu 4s in SOMO, and the 14N (I = 1) hyperfine splitting that is typical of ligand-centred nitrosyls radical.320
O stretching vibration to 1805 cm−1. In addition, such an orbital picture explains all characteristic features of the EPR spectrum of {2CuNO}11 adducts (Fig. 34b), i.e., monoclinic symmetry, large hyperfine coupling constants (63,65Cu, I = 3/2) due to involvement of Cu 4s in SOMO, and the 14N (I = 1) hyperfine splitting that is typical of ligand-centred nitrosyls radical.320
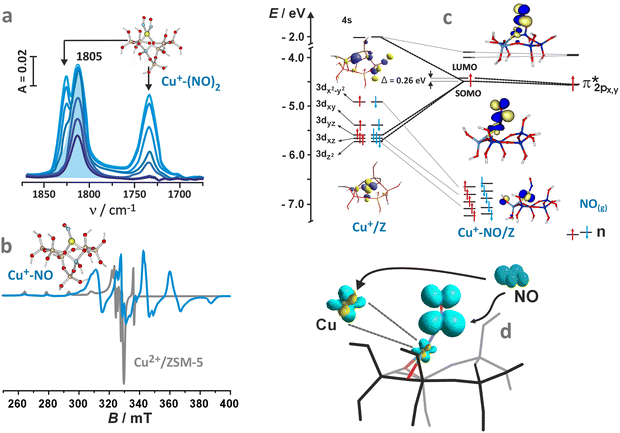 | ||
| Fig. 34 Spectroscopic evidence of the nitrosyl adduct formation upon NO interaction with Cu+/ZSM-5. IR spectra of NO adsorption with the highlighted mononitrosyl band at 1805 cm−1 (a), CW-EPR spectra of the parent Cu2+/ZSM-5 zeolite and the adsorption complex, produced after thermal autoreduction of Cu2+/ZSM-5 and subsequent NO adsorption (b), Kohn–Sham correlation diagram of the {2CuNO}11/ZSM-5 adduct (c), and the corresponding spin density contours of the mononitosyl species (d). Panels a and d adapted from ref. 345 with permission from Elsevier, Copyright 2007. Panel b adapted from ref. 172 under the terms of the CC BY 4.0 license, Copyright 2025, published by American Chemical Society. Panel c adapted from ref. 320 with permission from he American Chemical Society, Copyright 2003. | ||
Beyond the previously discussed  interaction, the primary factor driving the bending of the NO ligand is the enhanced orbital overlap between the
interaction, the primary factor driving the bending of the NO ligand is the enhanced orbital overlap between the  orbital of NO and the 4s orbital of the metal centre. This interaction becomes symmetry-allowed only in a bent geometry, making it inaccessible in the linear coordination mode. The spin density contour shows principal localization on the NO ligand with a sizable Cu contribution, and it is practically confined to the CuNO moiety (Fig. 34d). Thus, the copper nitrosyl in ZSM-5 is a ligand-centred {2CuNO}11 radical for spin classification purposes.
orbital of NO and the 4s orbital of the metal centre. This interaction becomes symmetry-allowed only in a bent geometry, making it inaccessible in the linear coordination mode. The spin density contour shows principal localization on the NO ligand with a sizable Cu contribution, and it is practically confined to the CuNO moiety (Fig. 34d). Thus, the copper nitrosyl in ZSM-5 is a ligand-centred {2CuNO}11 radical for spin classification purposes.
Charge flow during the TMI–NO bond formation and bonding mechanisms. The electronic density flows accompanying the TMI–NO bond formation can be elucidated and quantified using the NOCV method (see Chapter 4.1.1). Since NO is an open-shell ligand, the NOCV analysis should be performed in a spin-resolved (SR) fashion, i.e., separately for the α (↑) and β (↓) spin densities. Moreover, the unpaired electrons on the NO and TMI–zeolite non-interacting fragments should be distributed and coupled consistently with the TMI–NO bond; this is necessary to avoid spurious intra-fragment charge flows that would blur the interpretation of the NOCV results.328
The SR-NOCV method has been applied to a series of increasingly complicated NO interactions with zeolitic TMI, starting from the simplest case of closed-shell Cu+ cations,329,330 through open-shell 3d8 Ni2+ (ref. 156) and 3d9 Cu2+,330 up to the most complex 3d7 Co2+ active centres with NH3 co-ligands40,331 hosted in ZSM-5 zeolite. The SR-NOCV analysis of the NO binding to the Cu+/Cu2+ sites328–330 revealed the following most relevant electron-flow channels: (1) π*-backdonation, (2) donation of an unpaired electron from NO π*, (3) σ-donation from the nitrogen lone pair, (4) covalent Cu–NO contribution. They are illustrated in Fig. 35, using the SR-NOCV results for the representative {CuNO}11, {CuNO}10, and 1{Co(NH3)3(NO)}8 species.
 | ||
| Fig. 35 Dominant SR-NOCV components of the differential density during the NO binding to intrazeolite Cu+, Cu2+ cations and to 1{Co2+(NH3)3} complexes in ZSM-5, along with heuristic assignments of the electron flow channels and the corresponding NOCV eigenvalues. Contour values ±0.001 a.u. Adapted from ref. 40 and 330 with permissions from the Royal Chemical Society (Copyright 2016) and from the Canadian Science Publishing (Copyright 2013), respectively. | ||
The channel (1), which represents backdonation from the doubly occupied Cu 3d⊥ to the empty  MO of NO, increases the population of the 2π* (antibonding) orbital, leading to a nitroside activation of the ligand (NOδ−). The channel (2), which represents the unpaired electron displacement from the initially singly occupied
MO of NO, increases the population of the 2π* (antibonding) orbital, leading to a nitroside activation of the ligand (NOδ−). The channel (2), which represents the unpaired electron displacement from the initially singly occupied  to the Cu–zeolite fragment, acts oppositely. The relative importance of these two channels is sensitive to the oxidation state of Cu and the embedding of zeolite. The 2π*-backdonation channel (1) is most efficient for the zeolitic Cu+ site, consistently with a pronounced red-shift of the NO stretching vibration for the intrazeolite {CuNO}11 systems. The π*-backdonation is considerably diminished in the zeolitic Cu2+ site (cf. Fig. 34). In this case, this channel features strong polarization on NO and involves the electron density transfer from Cu 3d⊥ and nitric oxide O 2p⊥ to the bonding region, rather than straightforward π*-backdonation.330 Moreover, in the Cu2+NO system, the effect of π*-backdonation is effectively cancelled by the opposite effect of the unpaired electron donation from the 2π* SOMO along the channel (2). The net outcome of this competition is the deactivation of NO, which is also reflected by the blue shift of the νN–O stretching frequency.329,330 These results explain why the intrazeolite Cu2+ sites are inefficient in activating NO, although it binds this molecule more strongly than the intrazolite Cu+ centers.330,332
to the Cu–zeolite fragment, acts oppositely. The relative importance of these two channels is sensitive to the oxidation state of Cu and the embedding of zeolite. The 2π*-backdonation channel (1) is most efficient for the zeolitic Cu+ site, consistently with a pronounced red-shift of the NO stretching vibration for the intrazeolite {CuNO}11 systems. The π*-backdonation is considerably diminished in the zeolitic Cu2+ site (cf. Fig. 34). In this case, this channel features strong polarization on NO and involves the electron density transfer from Cu 3d⊥ and nitric oxide O 2p⊥ to the bonding region, rather than straightforward π*-backdonation.330 Moreover, in the Cu2+NO system, the effect of π*-backdonation is effectively cancelled by the opposite effect of the unpaired electron donation from the 2π* SOMO along the channel (2). The net outcome of this competition is the deactivation of NO, which is also reflected by the blue shift of the νN–O stretching frequency.329,330 These results explain why the intrazeolite Cu2+ sites are inefficient in activating NO, although it binds this molecule more strongly than the intrazolite Cu+ centers.330,332
The remaining two electron density flow channels, shown in Fig. 35, are of minor importance for the NO activation and are relatively insensitive to the metal oxidation state and embedding.328 The σ-donation channel (3) appears in all studied models, but hardly influences the strength of the NO bond, as the electron density is donated mainly from the nitrogen lone pair. The covalent Cu–NO channel (4) can be heuristically interpreted as a donation from the NO 2π‖ and Cu 3d‖ orbitals to the bonding region, accompanied by simultaneous intra-NO density redistribution. It may also be understood as the formation of a three-electron bond  , followed by some
, followed by some  mixing in NO. As this channel only exists in the β spin manifold, it contributes to the partial spin transfer from NO to Cu. Spin transfer is also connected with the channel (2), which only exists in the α spin manifold, and channel (1), which exists in both spin manifolds, but its α- and β-spin components are not balanced (compare eigenvalues of 0.37 and 0.25 for the{CuNO}11 adduct in Fig. 35).
mixing in NO. As this channel only exists in the β spin manifold, it contributes to the partial spin transfer from NO to Cu. Spin transfer is also connected with the channel (2), which only exists in the α spin manifold, and channel (1), which exists in both spin manifolds, but its α- and β-spin components are not balanced (compare eigenvalues of 0.37 and 0.25 for the{CuNO}11 adduct in Fig. 35).
In summary, the discussed SR-NOCV results nicely corroborate the spin addition and backdonation mechanisms discussed above for the Cu–NO system, and the interpretation of the EPR experimental data. By showing competition between the two most relevant electron flow channels: (1) π*-backdonation and (2) donation of the 2π* unpaired electron, they rationalize the propensities of different Cu sites to activate NO. Such an insight can hardly be obtained from more popular descriptors, such as atomic charges and spin populations, alone. In particular, the spin density on NO is not a direct indicator of its effective redox state, a conclusion that has also been pointed out in a broader context for other TMI–nitrosyl complexes.50 The fractional charge of the ligated NO is a net result of the opposing electronic flows corresponding to donation and backdonation processes.
DFT studies, supplemented with SR-NOCV analyses, have also been used to elucidate the mechanism of NO bonding to zeolitic Co2+ sites in the presence of ammonia co-ligands.40,331 The experimental studies of mononitrosyl species in Co2+-exchanged MOR and FER zeolites demonstrate that the NO stretching frequency undergoes a blue shift, which changes to a considerable red shift upon NH3 co-adsorption.331 Following the experimental conditions, DFT calculations were conducted on simplified cluster models of the {CoNO}8 species containing none, two, three, or five NH3 co-ligands, which are embedded in a simple one-tetrahedron T1.40,331 The construction of the more realistic zeolitic models is described elsewhere.333,334
The DFT modelling of the (NH3)n{CoNO}8 adducts fully confirmed the electron-donating effect of NH3 lone pairs, leading to enhanced Co 3d → 2π*-backdonation, and explaining the red-shift of the NO stretch in the (NH3)n{CoNO}8 adducts. Interestingly, this electron flow channel turned out to be finely spin-state controlled, i.e., highly more effective in the singlet than in the triplet spin state.331 The relative energies of the two spin states are challenging to predict using the available approximate DFT methods, which is a typical problem for 3d-electron TMI complexes in various coordination environments.53 Yet, the CCSD(T) and CASPT2 results show that the singlet and triplet spin states of the intrazeolite {CoNO}8 species are close in energy, allowing them to coexist in equilibrium under experimental conditions.40 The calculations also reveal that the most substantial red shift of the NO stretching occurs for the complex with three NH3 co-ligands, rather than for the complex with five ligands. While being counterintuitive at first sight (ammonia is a stronger electron donor than zeolitic oxygen groups), this result can be rationalized by invoking the trans effect of the NH3 ligand, present in the pentammine complexes. It leads to elongation of the Co–NO bond, and hereby to the reduction of the π*-backdonation effect in [Co(NH3)5(NO)]2+ as compared with the [Co(NH3)3(NO)]2+ zeolite adduct.328 A similar pattern of complex competition between the binding of strong NH3 co-ligands and preserving the covalent linkages to the zeolite framework, which is an electron-rich, but weaker ligand, has been observed for more realistic zeolite models.334 It is not necessarily full ammonia saturation of the Co2+ site that leads to the highest extent of the NO activation.
According to the SR-NOCV analysis,40 the Co–NO bond formation in the spin singlet {Co(NH3)3(NO)}8 zeolitic species can be best characterized as a combination of (1) spin-pairing between Co2+(3d‖, ↑) and NO ( , ↓) with concomitant (2) π*-backdonation from Co 3d⊥ to NO
, ↓) with concomitant (2) π*-backdonation from Co 3d⊥ to NO  (Fig. 35). The spin pairing channel is consistent with the formation of a covalent σ Co–NO bond (having a significant biradical character – see below). The π*-backdonation channel, which activates the N–O bond, is found in both spin manifolds with the identical eigenvalues, and hence, it does not transmit the spin polarization.
(Fig. 35). The spin pairing channel is consistent with the formation of a covalent σ Co–NO bond (having a significant biradical character – see below). The π*-backdonation channel, which activates the N–O bond, is found in both spin manifolds with the identical eigenvalues, and hence, it does not transmit the spin polarization.
The electronic structure of the discussed 1[Co(NH3)3(NO)]2+ zeolite model (T1) has been described as unpolarized (closed-shell) singlet,40 caused by the application of a pure density functional (BP86). In contrast, hybrid functionals can easily lead to a spin-polarized BS-DFT description, as seen for the intrazeolite {CuNO}10 species discussed earlier. In general, both the existence of a BS solution335 and the distribution of spin density50,51 in the nitrosyl complexes are critically dependent on the choice of the exchange–correlation functional. The BS spin density, although helpful in visualizing the pattern of spin coupling accompanying TMI–NO bond formation, is not expected to accurately reproduce the physical spin density. It merely provides a means of simulating nondynamic correlation effects in the metal–ligand bond, within the limitations of the single-configurational DFT formalism.50,336
A more rigorous description of these effects can be obtained using the multiconfigurational wave function formalism, in which the principal electronic configuration (PEC) is mixed with other configurations, obtained by promoting electron pairs from the bonding to antibonding orbitals. In this way, the antibonding orbital (unoccupied in the PEC) gains fractional occupations, whereas the bonding orbital (doubly occupied in the PEC) reduces its effective occupation below two. Thus, the TMI–NO bond acquires a partial biradical character. In a sense, it is “stretched” or “partially dissociated” already in the equilibrium geometry due to non-optimal overlap between the metal and ligand orbitals.337–339 This effect is most pronounced in first-row TMI due to the small size of their 3d valence orbitals. The ligand cannot approach close enough to achieve the optimum overlap with the 3d orbitals due to Pauli repulsion with the doubly occupied 3s3p outer-core orbitals, which are of approximately the same size as the 3d ones (see Pauli shield in (Fig. 17b)).338 The NO ligand has doubly occupied 2π orbitals in a very similar space region as 2π* ones, giving rise to powerful Pauli repulsion.339 These nondynamic correlation effects exacerbate problems associated with the non-innocent nature of NO, as they influence both the strength of the TMI–NO bond and the effective oxidation state of the NO ligand.
The discussed nondynamic correlation effects can be accounted for by using the CAS method with an active space containing the TMI 3d and NO 2π* orbitals as well as other relevant orbitals, e.g., the additional shell of d orbitals and NO π orbitals, which are needed to achieve a balanced approximation of the electronic wave function in nitrosyl species.40,50,337 The CAS calculations with 13–14 active orbitals have been performed for the intrazeolite 1,3{CoNO}8 adducts with ammonia as co-ligands,40 and for the 2{NiNO}9 complex in ZSM-5 zeolite.156 Based on these results, Fig. 36a shows the pairs of bonding and antibonding orbitals that describe the σ component of the TMI–NO bond.
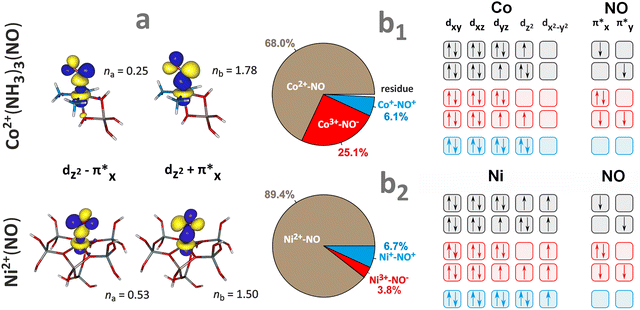 | ||
| Fig. 36 CASSCF natural orbitals with bonding and antibonding character concerning the TMI–NO σ bond, and their fractional occupation numbers for zeolite cluster models hosting (NH3)3{Co(NO)}8 and {NiNO}8 adducts (a) based on results from. Contour values ±0.04 a.u. Breakdown of the contributions from the TMI–NO resonance structures resulting from VB analysis of the CAS wave functions for the (NH3)3{Co(NO)}8 (b1) and {NiNO}9 (b2) adducts into electronic configurations for the individual VB oxidation states. Figure was based on data from ref. 40 and 156 with panel b1 adapted from ref. 328 under the terms of the CC BY license 4.0, Copyright 2021, published by MDPI. | ||
The contributions of TMI and NO fragment orbitals to the bonding and antibonding orbitals are comparable, demonstrating a highly covalent character of the σ-bonds, which is consistent with the spin pairing ligation mechanism.156 The orbitals’ fractional occupation numbers strongly deviate from the ideal integer values (i.e., 2 for the bonding orbital, 0 for the antibonding orbital), indicating considerably reduced bond order, and hence a pronounced biradical character of these bonds. The effective bond order, b = (nb − na)/2, amounts to 0.765 for the intrazeolite {CoNO}8 complex and to 0.485 only for the {NiNO}8/ZSM-5 complex. Thus, the σ-bond in the equilibrium geometry of Ni–NO exhibits a biradical character exceeding 50% (the biradical character is calculated as (1 − b) × 100%).
The spin density of the {NiNO}8/ZSM-5 complex primarily originates from the SOMO, which is predominantly (95%) composed of the Ni 3dxy orbital interacting with lone pairs of the zeolite oxygen atoms. Due to the spin coupling within the Ni–NO bond, the total spin population on Ni increases to +1.22, which is compensated by the negative spin population on NO (−0.17 on N, −0.10 on O) and residual positive spin population on the zeolite oxygens, according to Mulliken spin populations of the CAS wave function.156 Only a minor part of the spin density is retained on the NO ligand (in agreement with the spin-pairing mechanism of ligation), which is consistent with the interpretation of the HYSCORE experimental results discussed above.
Further insight into the multiconfigurational electronic structure of TMI–NO bonds can be gained by analyzing the valence bond (VB) structure of the CAS wavefunction.40,50 In this approach (VB-CAS), the active orbitals undergo a localization procedure, after which each active orbital can be assigned to either the TMI- or NO-fragment. The CAS wave function can be reinterpreted as a superposition of the VB resonance structures with a defined number of electrons assigned to the TMI fragment and the NO ligand (i.e., definite oxidation states of these fragments). The VB-CAS method thus allows circumvention of the limitations of the Feltham–Enemark notation (see Chapter 4.3) by quantifying contributions from the resonance structures belonging to different oxidation states. The technique, initially developed for bioinorganic architectures,50 has been subsequently applied to describe nitrosyl complexes in diverse coordination environments,51,340,341 including intrazeolite TMI–NO adducts.40,156 The VB-CAS method should be clearly distinguished from alternative approaches to assigning oxidation states in nitrosyl complexes, e.g., based on the IUPAC rules (ionic approximation) and/or geometric arguments342,343 and other types of orbital analyses.344
The contributions of the VB-CAS resonance structures for {Co(NH3)3NO}8 are illustrated in Fig. 36b1,40 and for the {NiNO}9 complex in Fig. 36b2.156 The most important individual electronic configurations for a given resonance form are also shown. For both analysed nitrosyl adducts, the CAS wave function is clearly dominated by the resonance form with neutral NO radical, which can be formulated as TMI2+–NO˙ (where TMI = Co or Ni). In the most important configurations of this type, the local spin on NO is antiferromagnetically coupled with the TMI spin. For example, in the {NiNO}9 adduct, 87.3% of the CAS wave function is provided by the Ni2+(SNi = 1)NO˙(SNO = 1/2) resonance structure, with the critical single configuration  constituting 78.5% of the CAS wave function.156 The large contribution of the TMI2+–NO˙ resonance form, particularly in the {NiNO}9 complex, is thus consistent with the above-discussed considerable biradical character of the TMI–NO bonds, and corroborates lucidly the spin-pairing ligation mechanism. The shares of the essential ionic resonance structures, such as M2+–NO− or M+–NO+, are notably different in the two discussed complexes, indicating partial nucleophilic character of NOδ− in the case of 1{CoNO}8 and partial electrophilic character of NOδ+ in 2{NiNO}9. This is consistent with the positions of the NO stretching bands, which are either red-shifted or blue-shifted, in these two cases. Moreover, in the series of {CoNO}8 adducts,40 the relative shares of the Co3+–NO− or Co+–NO+ resonance forms align well with changes of the N–O force constant and the stretching frequency, showing that predictions of the VB-CAS method generally correlate with other descriptors of the NO valence state. Concluding, the VB-CAS shares of the resonance structures appear to be more robust descriptors than the SR-NOCV eigenvalues when comparing complexes with different spin states or geometries.
constituting 78.5% of the CAS wave function.156 The large contribution of the TMI2+–NO˙ resonance form, particularly in the {NiNO}9 complex, is thus consistent with the above-discussed considerable biradical character of the TMI–NO bonds, and corroborates lucidly the spin-pairing ligation mechanism. The shares of the essential ionic resonance structures, such as M2+–NO− or M+–NO+, are notably different in the two discussed complexes, indicating partial nucleophilic character of NOδ− in the case of 1{CoNO}8 and partial electrophilic character of NOδ+ in 2{NiNO}9. This is consistent with the positions of the NO stretching bands, which are either red-shifted or blue-shifted, in these two cases. Moreover, in the series of {CoNO}8 adducts,40 the relative shares of the Co3+–NO− or Co+–NO+ resonance forms align well with changes of the N–O force constant and the stretching frequency, showing that predictions of the VB-CAS method generally correlate with other descriptors of the NO valence state. Concluding, the VB-CAS shares of the resonance structures appear to be more robust descriptors than the SR-NOCV eigenvalues when comparing complexes with different spin states or geometries.
Reactivity of the TMI–NO adducts with NO. The reactivity of nitrosyl adducts is closely related to how the NO molecule is coordinated, and to its electron configuration and spin state. For instance, the chemoselective capture of NO and the formation of mononitrosyl intermediates are pivotal prerequisites for its direct decomposition to N2 and O2 or its reduction into N2 with the aid of hydrocarbons.172,247,316 Since the formation of the N–N bond requires the proximity of two NO molecules, there are two possible pathways along which the adsorption of the second NO molecule can occur. These pathways have been distinguished based on the NO attachment locus (Fig. 37a) and can be termed inner-sphere and outer-sphere attacks. This mechanistic dichotomy determines the regioselective addition of NO to the mononitrosyl intermediate. The inner-sphere addition process leads to the formation of geminal dinitrosyl 2S+1{TMI–(NO)2}d+2 adducts, whereas the outer-sphere pathway results in a dimer bound to the metal centre 2S+1{TMI(N2O2)}d+2.
 | ||
| Fig. 37 The inner- and outer-sphere attack of the second NO molecule on intrazeolite nitrosyl complex (a). Comparison of DFT calculated IR dinitrosyl bands of Cu+(NO)2 species in the attracto and repulso conformations (b), based on data from ref. 345. DFT optimised pathways of the second NO molecule attachment to Cr+–NO (c1) and Zn2+–NO (c2) mononitrosyls, along with the respective spin density repartition that governs the inner- (Cr) or outer-sphere (Zn) direction of the NO attack. DFT-calculated free-energy diagrams at various temperatures for NO decomposition over a mononuclear Cu+ (d1) and vicinal Cu+∪Cu+ dimer (d2) centres hosted in ZSM-5, adapted from ref. 350 with permission from Springer Nature, Copyright 2021. | ||
The formation of dinitrosyl complexes in metallozeolite catalysts is confirmed, mostly by IR spectroscopy.319 The disappearance of the band attributed to the N–O vibration of mononitrosyls and the simultaneous formation of two bands of the collective symmetric and antisymmetric vibrations of the TMI(NO)2 species, provides direct evidence for the formation of dinitrosyl complexes at the expense of the parent mononitrosyl adducts.319,345–347 Similarly, formation of N2O2 dimers, which are diagnostic of the outer-sphere mechanism, has also been observed by IR in the metallozeolites in the spectral range of 1420–1320 cm−1 corresponding to the N–N vibrations.319
Dinitrosyl complexes have often been postulated as intermediates of the NO disproportionation into N2O and NO2, catalysed by transition metal complexes in homogeneous348,349 and zeolitic350 systems. The two dinitrosyl conformations, namely attracto and repulso, are shown in Fig. 37b. According to the classification proposed by Richter and Legzdins,351 the 3d5–10 transition metals prefer an attracto conformation. In this geometry, the bending of both NO groups results in a decrease in the oxygen–oxygen distance (“inward” bending). An “outward” bending, in turn, increases the distance between the oxygen atoms of both NO ligands, with a simultaneous reduction of the distance between the nitrogen atoms (repulso conformation). Such structures have been described in detail for copper(I) centres in zeolites,346,347 and they differ in the respective symmetric and antisymmetric IR bands.345
The interaction pathway of the second NO molecule with a given mononitrosyl complex can be related to the spin repartition within this species. For the first-row paramagnetic TMI–NO/ZSM-5 adducts,317 the spin density is confined almost entirely to the TMI–NO fragment, spreading on the zeolite backbone to a small extent only. Thus, the TMI–NO unit constitutes the magnetophore of the entire TMI–NO/ZSM-5 system (see Chapter 4.1).321 Two examples of the spin density repartition in the 3{CrNO}6 and 2{ZnNO}11 magnetophores hosted in the ZSM-5 framework are shown in Fig. 37c1 and c2. They represent two extreme cases of metal-centered and ligand-centered metallo-radicals, respectively (see Fig. 18e).
The effect of the spin density distribution in TMI–NO on the attachment of the second NO molecule is illustrated by the reaction pathways shown in Fig. 37c1 and c2. For the 3{CrNO}6 magnetophore, the ligation trajectory along which the interaction energy is minimized results in the formation of a dinitrosyl complex 2{Cr(NO)2}7 via an inner-sphere attack. A different scenario occurs for the 2{ZnNO}11 magnetophore. Here, the binding of NO leads to the bond formation directly between the nitrogen atoms, as the incoming NO molecule is repelled from the first coordination sphere of the zinc centre. Therefore, a 3{ZnN2O2}12 complex is formed along the outer-sphere mechanism. Thus, the outer- vs. inner-sphere dichotomy of NO coordination to the paramagnetic mononitrosyl intermediates is essentially controlled by the spin density distribution within the corresponding magnetophores. The inner-sphere attack, which occurs directly at the metal core, is expected for the metal-centered metallo-radicals. In contrast, for the ligand-centered metallo-radicals, the outer-sphere mechanism is preferred. The bent structure of the NO ligand with the associated accumulation of spin density on the nitrogen atom is particularly beneficial for directing the NO attack at the nitrosyl moiety.
The possible mechanisms of NO activation differ depending on the nuclearity of the active centres, as demonstrated for monomeric345 or dimeric copper species350 in zeolites. In the case of mononuclear copper centres, the spin density localisation on the ligand in the Cu–NO magnetophore suggests that the attack of the second NO on the copper nitrosyl intermediate is preferred via an outer-sphere pathway. It occurs with nearly zero activation energy and leads to the direct formation of the N–N bond via the N2O2 intermediate. The latter decomposes into N2O, leaving behind highly reactive intrazeolite CuO/z species (its electronic structure is briefly discussed in Chapter 2.2). It can be brought to the initial state by interacting with the N2O byproduct (CuO/z + N2O → O2 + N2 + Cu/z) or by reduction with auxiliary hydrocarbons (HC-SCR). However, the energy profiles of the reaction pathway (Fig. 37d1) favour the dinitrosyl formation (inner-sphere) rather than the direct NO coupling (outer-sphere).345 Two possible conformers of the dinitrosyl intermediates can be identified using IR spectroscopic signatures (the frequency difference between the symmetric (νsym) and antisymmetric (νasym) components, and the Isym/Iasym intensity ratio).345 Seemingly, only the relative intensities of the stretching vibrations are markedly altered upon changing the conformation, and the IR results confirm an attracto conformation of the copper dinitrosyls in ZSM-5 (see Fig. 37b). Although the attracto conformation brings both oxygen atoms closer to each other, the development of an O–O bond (for initiating direct NO decomposition into O2 and N2) is significantly impeded by the concomitant accumulation of the negative charge on these atoms when they approach. In the alternative repulso conformation, both nitrogen atoms are getting closer to each other. It is beneficial for the incipient N–N bond, and along this mechanistic variant, the NO decomposition takes place. As a result, for direct NO decomposition into N2 and O2, the attracto dinitrosyls are inert, and the repulso conformation favours the reaction initiated by the inner-sphere N–N bond formation. It requires, therefore, an initial transformation of the dinitrosyl intermediates from the attracto into the repulso conformation.345,346 An energy diagram for this transformation is presented in Fig. 37d1. As a result, the mechanistic cycle of the NO direct decomposition on the mononuclear centres of Cu accommodated in zeolite catalysts involves the following steps:
| 1Cu+ + NO(g) → 2{CuNO}11 → cis-1{CuN2O2}12 → trans-1{CuN2O2}12 → 3Cu2+O− + N2O(g). |
It can be accomplished by decomposition of the N2O byproduct on the ensuing copper–oxo centres (see Chapter 4.3.3).350,352 Such a mechanism of direct NO decomposition through the dimeric N2O2 intermediates is substantiated for CuZSM-5 zeolite by spectroscopic evidence.319
Another scenario of NO decomposition occurs over copper dimers and two vicinal single copper centers in ZSM-5 zeolite. The fraction of copper dimers and vicinal Cu centres increases with a decreasing Si/Al ratio and with a rise of the copper site density.350,353,354 Such centres can interconvert from the vicinal Cu+∪Cu+ into the dimer (Cu–O–Cu)2+ species upon interaction with NO, and the corresponding energy profile is shown in Fig. 37d2. The NO decomposition mechanism can be summarized in the following steps:
(1) capture of NO, Cu+∪Cu+ + 2NO → (ON)Cu+∪Cu+(NO), the ensuing mononitrosyls are observed in IR spectra at 1813 cm−1,
(2) N–N bond formation with release of N2O byproduct, (ON)[Cu+∪Cu+](NO) → (Cu–O–Cu)2+ + N2O, formation of (Cu–O–Cu)2+ is confirmed by the band at 1903 cm−1 observed upon subsequent NO adsorption (Cu–O–Cu)2+ + 2NO → (ON)[(Cu–O–Cu)2+](NO),
(3) formation of dinitrogen, Cu+∪Cu+ + N2O → (Cu–O–Cu)2+ + N2.
The latter step is discussed in more detail in Chapter 4.3.3.
Reactivity of TMI–NO with O2 – examples for Cu–zeolites. Recent studies have explored the interaction of NO and O2 with Cu centres of differing nuclearity, in both reduced and oxidized states, focusing on elucidation of the reactivity patterns and thermodynamic stability of intermediates under conditions that closely resemble those of actual SCO and SCR processes. A typical reaction involving nitrosyls as intermediates is the reduction of NO to dinitrogen in the presence of O2, using various reductants, such as hydrocarbons (HC-SCR) or ammonia (NH3-SCR). Since early studies, the redox character of these reactions has been recognized, and Cu-containing zeolites, such as ZSM-5, CHA, have been identified as the most active catalysts.355–360 Although there are several mechanistic proposals of the SCR reaction course,33,277,361,362 their common point is the coexistence of the mutually coupled reduction half-cycle (RHC) and oxidation half-cycle (OHC).214,228,300,363,364 The OHC is associated with the selective catalytic oxidation (SCO) of NO to NO2 and to various charged (nitrates/nitrites) and protonated (HONO) NOx species.33,355–357,364 Spectroscopic IR data support the theoretical and thermodynamic predictions of the formation of Cu2+–NO (1950–1880 cm−1) and Cu+–NO (1810–1800 cm−1) intermediate species. The bands at 1620, 1595, and 1575 cm−1, in turn, correspond to the symmetric stretching modes of bidentate NO3−, whereas the bands at 1500 and 1310 cm−1 come from the antisymmetric and symmetric modes of monodentate NO3− species,214,365,366 overlapping with the antisymmetric and symmetric stretchings of the N-bonded nitrites (NO2−).319 They are typically observed during the NO oxidation and SCR reactions in zeolites by operando IR.278,367,368 The reactivity of NO and O2 toward NO2, NO3−/NO2− formation involves various copper species, such as bare Cu2+/Cu+ and Cu2+–OH−, and dimeric [Cu–O–Cu]2+, which can act as potential active centres for such reactions.369
A valuable thermodynamic insight into NO oxidation over CuSSZ-13 catalyst can be obtained from FPT modelling. The relative stability of the exemplary copper–NOx− species, formed in CHA zeolite after the reaction between NO and O2, at various T and pNO conditions is shown in Fig. 38, for the Cu2+, Cu+, and oxo [Cu–O–Cu]2+ centers. In general, the oxidized isolated Cu2+ centres are unable to capture dioxygen, and the thermodynamic diagrams are dominated by copper(II)–nitrosyls and diverse NOx adducts (x = 1–3) of a radical nature. Under the conditions similar to that of NO SCO, the stability regions of Cu2+NOx, bare Cu2+ and Cu2+NO species are shown in Fig. 38a. In the case of reduced Cu+ (Fig. 38b), which can be generated, i.a., via reduction of Cu2+–OH− with NO producing HONO,95,370 reaction with NO/O2 and charge transfer lead to NO3− dominant anionic species. The complexes formed by the independent capture of NO and O2 are unstable relative to nitrate and nitrite species. Under the experimental SCR/SCO conditions, nitrates decay at approximately 400 °C. For the dimeric active centres, the dinitrate Cu2+–(NO3−)2–Cu2+ adspecies dominate the experimental range of SCR/SCO. The simultaneous adsorption of water and NO is thermodynamically disfavoured, due to the lateral repulsion between H2O and NO ligands. Notably, under the NO–SCO/SCR conditions, several metastable intermediates with comparable thermodynamic profiles can coexist and mutually interconvert. This dynamic equilibrium enhances the functional versatility of bridging copper centres, enabling them to participate in the stoichiometric transformation of nitrates,33 promoting fast SCR through efficient NO2 generation, for instance.278,357
 | ||
| Fig. 38 Thermodynamic ΔG(p,T) diagrams for Cu2+ (a), Cu+ (b) cations, and dual copper centres Cu2+–O2−–Cu2+ (c) in CHA zeolite as a function of temperature (T) and partial pressure of NO (pNO). Thermodynamic profiles for the NO oxidation reaction (NO2 formation) on the isolated copper centres, according to the cationic metal-redox pathway (d). The calculated NO2 production profiles based on the thermodynamic modelling for the isolated copper active centres (e1) and copper dimers (e2). Adapted from ref. 172 under the terms of the CC BY 4.0 license, Copyright 2025, published by the American Chemical Society. | ||
Recently, thermodynamic profiles have been constructed based on DFT/FPT calculations to unravel the course of NO–SCO elementary steps and underly driving forces under different experimental conditions.172 Analysis of such profiles for the typical isolated Cu centres in SSZ-13 reveals the presence of three mechanistic routes of NO oxidation: (1) copper-redox pathway, (2) ligand-redox pathway, and (3) via HONO intermediates. In the case of dimeric Cu species, the NO SCO reaction can proceed (1) via direct NO2 release (thermal decomposition of anionic NOx− adspecies) and (2) via formation of NO2 due to the comproportionation of nitrates with the encaged NO. The corresponding concentration profiles of the involved adspecies and intermediates are shown in Fig. 38d and e.The predicted evolution of the NO2 concentration with reaction temperature, along with the advanced mechanistic tenets, agrees well with the experimental results using isotopically labeled N18O, N16O, and 18O2.172
Intrazeolite coordination of N2O. The N2O molecule is a relatively weak ligand acting as both a σ donor and a π acceptor.374 It is attached most frequently in the top-on monodentate (η1-O and η1-N) way to single TMI cations (Fe, Co, Ni, Cu),373 and in the cis μ-1,3-O,N, μ-1,1-O fashion on bridging M–O–M species.353,375 Rather unique trans μ-1,3-O,N adducts attached to adjacent close-distant Fe cations are proposed in Fe/FER, based on DFT modelling.90 In the case of (N2O)2TMI/Z adducts, η1-O,O, η1-O,N and η1-N,N binding forms, as well as the bidentate η2-O,N attachment of N2O to single TMI have been reported,376 see (Fig. 39a). Since the bis-N2O adducts are observed only at high pN2O pressures and low temperatures, they are not relevant for catalytic considerations.
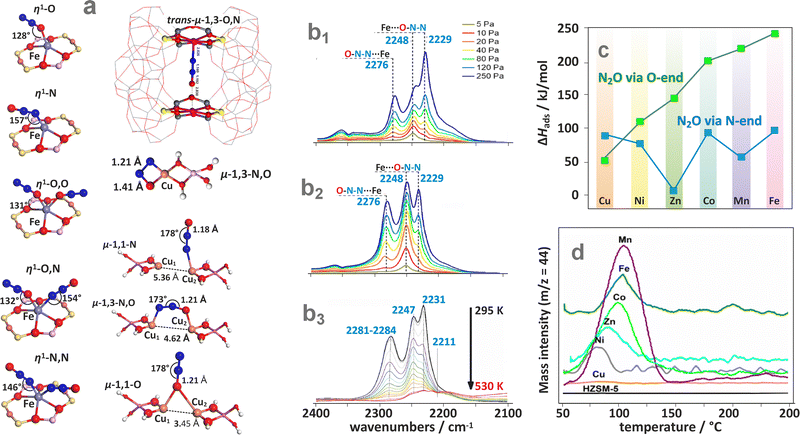 | ||
| Fig. 39 Survey of the coordination modes of N2O to single and dual TMI sites (a), based on data from ref. 20, 353, 371 and 376, with the middle structure adapted from ref. 90 with permission from Elsevier, Copyright 2010. Variable pressure (pN2O = 5–250 Pa) IR spectra of N2O adsorbed at room temperature on Fe, Na-CHA (with Fe predominantly located in 6MR) (b1), and Fe-CHA (with Fe predominantly located in 8MR) zeolites (b2), and variable temperature adsorption of N2O on the Fe/SSZ-13 catalyst followed by IR (b3) adapted from ref. 377 under the terms of the CC BY 4.0 license, Copyright 2024, published by the American Chemical Society. Calculated adsorption energies for η1-O and η1-N binding of N2O to various TMI hosted in the ZSM-5 zeolite (c) together with the corresponding experimental TPD-N2O profiles (d).373 | ||
The variable pressure IR spectra of N2O adsorption recorded at room temperature, shown in Fig. 39b1, indicate that for the Fe/6MR species hosted in the CHA matrix, the IR peak of the η1-N mode dominates, whereas in the case of Fe/8MR the η1-O (2229 cm−1) and η1-N (2276 cm−1) adsorption modes exhibit IR signals of comparable intensities (Fig. 39b2).377 This illustrates directly the influence of the zeolite ring size on the N2O ligation by iron. The 2248 cm−1 band corresponds to Al⋯O–NN species. In the case of Fe/FER zeolites, the η1-N binding is generally stronger than the η1-O one, and significantly depends on the α or β locus, and the particular arrangement of Al atoms in the corresponding rings.90 The temperature dependence of N2O adsorption on Fe/SSZ-13 zeolite indicates that the beneficial η1-O active mode persists till 530 K, whereas the spectator η1-N one is completely depleted at this temperature (Fig. 39b3). The survey of the DFT-calculated N2O adsorption energies for selected 3d TMI hosted in ZSM-5 catalysts, and the related N2O-TPD profiles, are shown in Fig. 39c and d, respectively. The thermal stability of the N2O-TMI adducts does not exceed 150 °C (520 K), and the position of the desorption peaks maxima (Tmax) is linearly correlated with the calculated ΔHads values. The extent of metal-to-ligand charge transfer is the key factor controlling the adsorption strength.373 However, alternatively to desorption, the ligated N2O may react with the TMI centres, dissociating into N2 and leaving the bound oxygen moiety behind (as discussed below).
General mechanistic considerations of N2O activation. A characteristic feature of triatomic molecules like N2O is that bending due to the ν2 vibration (589 cm−1 in the gas phase) or upon interaction with the active sites (TMI) leads to its intrinsic preactivation. This is revealed by a significant buildup of negative charge in the oxygen moiety (qO = −0.2|e|), and the merging of charge at both nitrogen atoms to the same value of qN = 0.1|e|. An elongation of the NN–O bond (by ∼0.3 Å) and a dramatic decrease in the NN–O bond order accompany such changes, making the bent N2O molecule prone to oxygen release (Fig. 40a1). All these features play an important role in the N2O activation process (Fig. 40a2). Furthermore, since the ground state of N2O(1Σ+) is singlet, whereas the ground state of O2(3Σg−) is triplet, the decomposition of N2O into N2 and O2 follows a nonadiabatic reaction coordinate with changing spin multiplicity.
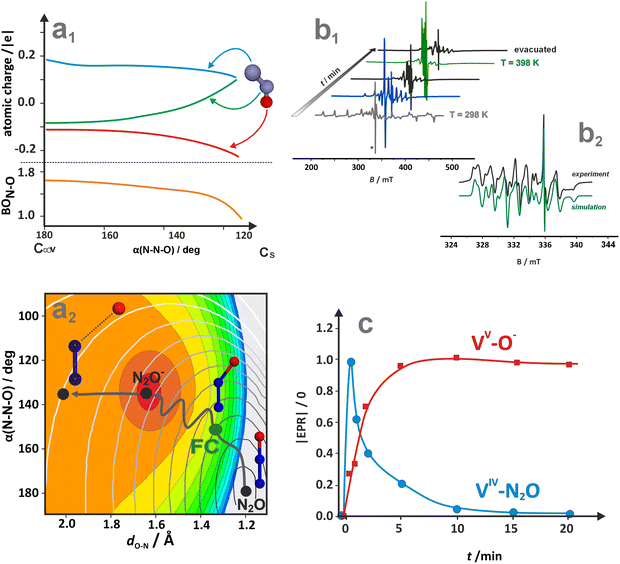 | ||
| Fig. 40 Variation of the charge redistribution and the N–O bond order for the N2O molecule upon bending (a1), and overlay of the potential energy surfaces of N2O (grey iso-energy lines) and N2O− (colour coded areas) with the schematic reaction pathway leading from linear N2O molecule, through bent transition state at Frank–Condon (FC) locus into shallow minimum on the N2O− PES, prompting an eventual dissociation of the N2O− transient (a2). Adapted from ref. 379 under the terms of the CC BY 4.0 license, Copyright 2024, published by the American Chemical Society. Evolution of the EPR spectra recorded during the reaction of N2O with VO2 centres entrapped in BEA zeolite (b1), together with simulation of the EPR signal due to [VO2+]–O˙− species (b2) (adapted from ref. 295 with permission from the Royal Society of Chemistry, Copyright 2016) together with the corresponding plot of gradual transformation of [VO2]–N2O into [VO2+]–O˙− via an electron transfer mechanism (c). | ||
The two generic mechanisms of N2O activation are based on electron transfer (ET) and oxygen atom transfer (OT) scenarios.317 However, in the case of metallozeolite catalysts, any of those occur in the exclusive form. Most N2O dissociation reactions on metallozeolites are initiated by an electron density transfer from the TMI core to the N2O ligand (cationic redox pathway). The extent of the charge transfer, which assists in weakening the N–O bond and promoting transfer of the O-moiety to the TMI core, depends on its nature, location, and the type of zeolite framework. Alternatively, the O-species can also be accommodated on the μ-O2− fragment of the bridging M–O–M centres, producing a peroxo (O22−(1Σg+)) intermediate (defining anionic redox pathway).
Catalytic decomposition of nitrous oxide based on electron transfer (ET) can be formulated in terms of the classic three-step mechanism:
| (1) N2O(1Σ+) + e− → [N2O−]* → O−(2P) + N2(1Σg+), |
| (2) O−(2P) + O−(2P) → O2(3Σg−) + 2e−, |
| (3) O−(2P) + N2O(1Σ+) → O2(3Σg−) + N2(1Σg+) + e−, |
These considerations allow for the formulation of N2O decomposition along the cationic redox mechanism for single Mp+/z centres in the following way:
| (1) N2O(1Σ+) + Mp+/z → [OM]p+/z + N2(1Σg+), |
| (2) N2O(1Σ+) + [OM]p+/z → O2(3Σg−) + N2(1Σg+) + Mp+/z, |
| (3) 2[OM]p+/z → O2(3Σg−) + 2Mp+/z. |
Since the specific charge transfer between the metal centres M and the ligated O-moieties depends on their actual nature, in these general equations only the overall charge “p+” of the involved species is explicitly indicated. For instance, the cationic redox mechanism may involve a single electron transfer producing radical oxyl species O˙−/M, as in the case of 2VO2/BEA, or consecutive two-electron transfer forming oxo-species (α-O), exemplified by 5FeII/BEA.20
The attack of the second N2O molecule can be directed at the terminal oxygen or the metal centre, depending on the chemical characteristics of the accommodation sites imparted by their electronic structure and location in the zeolite matrix.380 In the case of dimeric M–O–M species, the cation M centres or the bridging μ-O2− centres may serve as a possible locus for lodging the O-moieties, forming a peroxo μ-O22− species with a diagnostic band at near 867 cm−1, typically observed by Raman spectroscopy.381
Using the N2O decomposition on Fe/ZSM-5380 as a straight example, the resultant mechanisms can be epitomised as:
| N2O(1Σ+) + [M–μ-O2−–M]p+/z → [O–M–O2−–M]p+/z + N2(1Σg+), |
| [O–M–O2−–M]p+/z → [M––(μ-O2−)2–M]p+/z, |
| N2O(1Σ+) + [M––(μ-O2−)2–M]p+/z → [O–M––(μ-O2−)2–M]p+/z + N2(1Σg+), |
| [O–M–(μ-O2−)2–M]p+/z → [(O22−)M–μ-O2−–M]p+/z → [M–μ-O2−–M]p+/z + O2(3Σg−). |
Actually, by involving both the metal and the bridging oxygen, it exhibits a mixed redox (cationic and anionic) character. The less common anionic redox alternative (attack on μ-O2−) assumes the following sequence:
| N2O(1Σ+) + [M–(μ-O2−)–M]p+/z → [M–(μ-O22−)–M]p+/z + N2(1Σg+), |
| N2O(1Σ+) + [M–(μ-O22−)–M]p+/z → [M–(μ-O2−)–M]p+/z + O2(3Σg−) + N2(1Σg+), |
| 2[M–(μ-O22−)–M]p+/z → 2[M–(μ-O2−)–M]p+/z + O2(3Σg−). |
Herein, the formal oxidation state of M remains essentially intact, whereas for the bridging O2− moiety it changes from −2 to −1 due to the formation of μ-O22− (peroxo) species. Additionally, depending on the N2O coordination energy to the particular intrazeolite TMI and the reaction conditions, adsorption quasi-equilibria such as N2O + Mp+/z ↔ (N2O–M)p+/z, N2O + [OM]p+/z ↔ [OM–N2O]p+/z and O2 + Mp+/z ↔ (O2–M)p+/z have also been taken into account in the microkinetic analysis.20,371,382,383
Exemplary N2O activation pathways on well-defined centres. Investigations documenting N2O activation on metallozeolites induced by a distinct metal-to-ligand electron transfer (MLET) are hardly available in the literature. Nevertheless, a notable example is provided by the VO2(d1) species encaged in the BEA zeolites interacting with N2O.295 The progress of the reaction 2V4+(
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)2 + N2O(1Σ+) → 2[(O
O)2 + N2O(1Σ+) → 2[(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )2V5+–O˙−] + N2(1Σg+) at room temperature followed by EPR is shown in Fig. 40b1, whereas the EPR spectrum of the final 2[(O
)2V5+–O˙−] + N2(1Σg+) at room temperature followed by EPR is shown in Fig. 40b1, whereas the EPR spectrum of the final 2[(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )2V5+–O˙−] product and its simulation are shown in Fig. 40b2. The obtained kinetic profiles of the reactant decay and the product formation (Fig. 40c) are entirely consistent with the MLET-induced dissociation of N2O. A concerted capture of the resulting radical O˙− moiety by the [(O
)2V5+–O˙−] product and its simulation are shown in Fig. 40b2. The obtained kinetic profiles of the reactant decay and the product formation (Fig. 40c) are entirely consistent with the MLET-induced dissociation of N2O. A concerted capture of the resulting radical O˙− moiety by the [(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )2V5+]+ core produces the 2[(O
)2V5+]+ core produces the 2[(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )2V5+–O˙−] species. The EPR parameters (gxx = 2.0202, gyy = 2.0173, gzz = 2.0284 > ge and Azz = 1.65 mT, Ayy = 1.58 Azz = 1.49 mT) are characteristic of the ligand-centred O˙− radical (manifested by the g-tensor features) attached electrostatically to the (O
)2V5+–O˙−] species. The EPR parameters (gxx = 2.0202, gyy = 2.0173, gzz = 2.0284 > ge and Azz = 1.65 mT, Ayy = 1.58 Azz = 1.49 mT) are characteristic of the ligand-centred O˙− radical (manifested by the g-tensor features) attached electrostatically to the (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )2V5+ core (demonstrated by small superhyperfine values due to the coupling with 51V, I = 7/2). This signal disappears (after 30 minutes) upon co-adsorption of CO or propene at ambient temperature, due to the highly reactive character of the O˙− radicals.
)2V5+ core (demonstrated by small superhyperfine values due to the coupling with 51V, I = 7/2). This signal disappears (after 30 minutes) upon co-adsorption of CO or propene at ambient temperature, due to the highly reactive character of the O˙− radicals.The mechanism of N2O activation on cationic centres has been meticulously elaborated by DFT modelling, corroborated to some extent by spectroscopic studies, for the most widely investigated single FeII/z and [FeO]2+/z sites, and dimeric Cu+∪Cu+, Fe2+∪Fe2+, Fe–O–Fe/z and Cu–O–Cu/z centres, accommodated in ZSM-5, BEA, CHA or FER zeolites.20,164,353,380,384 The Co, Mn or Ni zeolites are less frequently examined.385,386
In particular, high activity of dimeric metal centres (Cu+∪Cu+) has been reported for Cu/ZSM-5 zeolites.353 Among the bridging μ-1,1-O and μ-1,3-O,N, and terminal η1-O binding modes of the N2O molecule, only the μ-1,1-O attachment leads to the small activation energy (2 kcal mol−1) that is compatible with the experimental value of 2.5 kcal mol−1. The corresponding energy profile for the singlet and triplet PES indicates that the minimum energy crossing point (MECP) appears after the bent transition state (∠(ONN) = 143°) located on the singlet PES (Fig. 41a1). In the MECP locus, the O–N2 distance is elongated to ∼1.55 Å, and the O–N–N angle decreased to 122°. Moreover, the associated charge and spin flows from both copper sites are distinctly uneven due to the slightly different local environments of the Cu ions (Fig. 41a2 and a3). The most significant changes in spin and charge transfer occur around the MCEP, but not at the TS point, which is a characteristic feature of the nonadiabatic character of N2O dissociation, primarily driven by metal-to-ligand electron transfer.
 | ||
| Fig. 41 N2O decomposition over the bridging Cu+∪Cu+/ZSM-5 (a1)–(a3) and the single Fe2+/*BEA (b1)–(b3) centres. Singlet and triplet potential energy surface for N2O dissociation on the Cu+∪Cu+ centres (a1), and the changes in the charge (a2) and spin (a3) densities along the O–N2 reaction coordinate, adapted from ref. 353 with permission from the American Chemical Society, Copyright 2014. Operando UV-vis-NIR spectra of the Fe2+/*BEA catalyst recorded during N2O adsorption under variable pN2O pressures (0–0.05 atm) at 308 K (b1). Gradual decomposition of the coordinated N2O into [FeO]2+ species and N2 at 373 K in the time interval of 15 min (b2), together with the corresponding energy profile accompanied by the associated molecular orbital structures of the key intermediates (b3), adapted from ref. 20 with permission from Springer Nature, Copyright 2021. | ||
In the case of intrazeolite iron, multiple spectroscopic studies (Mössbauer, VTVH-MCD, UV-vis, IR) corroborated by DFT modelling are available for the definite description of Fe2+/z accommodated in the 6-member rings (β-6MR) present in BEA, MFI, and FER, as high-spin square-planar ferrous species (Fe2+(d6), with S = 2 and D > 0) that are particularly active in N2O decomposition.5 Such centres also appear in the 6MR sites of CHA, where the Cs-symmetric Fe2+ cations are less distorted from the square planar arrangement in comparison to C2-symmetric Fe2+ centres in BEA.147 They are collectively called α-Fe2+ species, and their structural deviations across different zeolites are reflected, among others, in the position of the diagnostic 3dz2 → 3dx2−y2 band appearing at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1 in Fe/BEA, 15
900 cm−1 in Fe/BEA, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1 in Fe/ZSM-5, 16
200 cm−1 in Fe/ZSM-5, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 in Fe/FER, and 13
100 cm−1 in Fe/FER, and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 in Fe/CHA.135,147
000 cm−1 in Fe/CHA.135,147
The remarkable reactivity of the α-Fe2+ centres to N2O activation is realised by transferring formally two electrons from metal to ligand for complete N–O bond cleavage to produce [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ species (α-O) with concomitant N2 release. At moderate temperatures (∼150–250 °C), the reaction occurs quickly with an apparent activation energy of 9–13 kcal mol−1 for Fe/BEA,20 Fe/ZSM-5, and Fe/FER catalysts.5 This process can be followed quantitatively in the UV-vis-NIR operando set-up by observing the gradual transformation of the band at 15
O]2+ species (α-O) with concomitant N2 release. At moderate temperatures (∼150–250 °C), the reaction occurs quickly with an apparent activation energy of 9–13 kcal mol−1 for Fe/BEA,20 Fe/ZSM-5, and Fe/FER catalysts.5 This process can be followed quantitatively in the UV-vis-NIR operando set-up by observing the gradual transformation of the band at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1 into 11
900 cm−1 into 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 with the isosbestic point at 13
500 cm−1 with the isosbestic point at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, which corresponds to the α-Fe2+ + N2O → N2O–α-Fe2+ process (Fig. 41b1). Subsequent transformation of the band at 11
500 cm−1, which corresponds to the α-Fe2+ + N2O → N2O–α-Fe2+ process (Fig. 41b1). Subsequent transformation of the band at 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 into the bands located at 16
500 cm−1 into the bands located at 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1 and 28
900 cm−1 and 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (Fig. 41b2) is diagnostic of the N2O dissociation (N2O–Fe2+ → [α-Fe
000 cm−1 (Fig. 41b2) is diagnostic of the N2O dissociation (N2O–Fe2+ → [α-Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ + N2). The appearance of an isosbestic point at 14
O]2+ + N2). The appearance of an isosbestic point at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 confirms this transformation univocally.20
000 cm−1 confirms this transformation univocally.20
The prime factors governing efficient N2O reduction include the binding of N2O to the active α-Fe2+ site in the η1-O fashion. This promotes the cleavage of the N–O bond, accompanied by the requisite charge redistribution and the formation of a metal–oxo bond. It generates the driving force for the eventual O-atom transfer, without restraining the subsequent evolution of O2 upon capture of the second N2O molecule. A more detailed insight into the reaction coordinate for the oxygen release step on α-Fe/BEA (Fig. 41b3) reveals that this process occurs in two sequential MLET events, with a notable internal rearrangement of electrons within the 3d manifold of the iron core. Upon η1-O attachment, an electron is transferred from the 3dz2 orbital into the 3dyz orbital, which enables an efficient π-back donation from the Fe2+ core into the 3π* LUMO of the N2O ligand.20 The extent of this back-bonding is controlled, among others, by the presence or absence of an axial ligand. At the bent transition state (138°), located at 25 kcal mol−1, the NN–O bond is elongated to 1.45 Å, whereas the Fe–ON2 bond is contracted to 1.83 Å. The TS structure evolves into a highly unstable Fe3+(S = 5/2)↑↓N2O˙− (S = 1/2) species. Once the N–O bond is eventually cleaved, a transient Fe3+–O˙− oxyl is formed with the LUMO composed mainly of the 2px orbital. A second electron transfer converts the oxyl species into the final oxo [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ units with S = 2 (Fig. 41b3).20
O]2+ units with S = 2 (Fig. 41b3).20
The complete energetic profiles of N2O binding, activation and decomposition into elements on different active sites present in the exemplary Fe/ZSM-5 is shown in Fig. 42. They illustrate two mechanistic variants of this reaction for the iron cations, hosted in the β (Al atoms in the T4, T10 position, 4-fold coordination of Fe) and α (Al atoms in the T1, T7 positions, 5-fold coordination of Fe) positions, see Fig. 42a1 and a2, respectively.380
 | ||
| Fig. 42 Mechanistic variants of N2O decomposition over single and bridging Fe–oxo. Energetic profiles for N2O decomposition on Fe2+ cations hosted in the β (a1) and α sites (a2), and dimeric Fe–O–Fe centres (b) hosted in the ZSM-5 zeolite. The reaction energy diagram for the ferro (navy blue) – and antiferromagnetic (green) state of the dimeric iron active centres (c). The figure was based on data from ref. 164 and 380. | ||
The energies of η1-O adsorption of the N2O ligand (−38 kJ mol−1 for α and −39 kJ mol−1 for β sites), the location of the bent transition states TS1 (44 and 41 kJ mol−1), and the N2O dissociation energies with concomitant formation of the [FeO]2+ species (ΔE = −67 and −63 kJ mol−1) are quite similar for both α and β sites Fig. 42a1 and a2. However, the reactivity of the resultant [FeO]2+ units with N2O, which closes the catalytic cycle by releasing O2, evolves along different pathways.
In the case of β-sites, the N2O attack is directed at the metal (Fe) centre with the activation barrier of 167 kJ mol−1 (TS1) and d(Fe–ON2) = 2.065 Å (Fig. 42a1). Upon dissociation of the ligated N2O, the ensuing dioxo-iron intermediate is transformed into dioxygen, and the O2 desorption barrier of 141 kJ mol−1 for S = 2 is decreased to 114 kJ mol−1 for S = 3. For α sites (Fig. 42a2), the N2O attack is directed at the terminal oxo moiety, and the reaction is driven by the formation of an incipient O–O bond in the TS2 state with a relatively high barrier of 243 kJ mol−1. The ensuing η2-O,O intermediate (d(O–O) = 1.345 Å) evolves next into gas phase O2, restoring the Fe2+/α active site. This uphill step costs 141 kJ mol−1 on the quintet (S = 2 + 0) potential energy surface, but is substantially decreased by 53 kJ mol−1 (α) for the septet (S = 2 + 1 = 3) PES, where oxygen is produced in its ground triplet state O2(3Σg−). The corresponding energy profile for S = 3 is marked in blue, indicating that only the last two steps are energetically favoured over the S = 2 pathway (Fig. 42a2).
These differences show that the local coordination environment around the Fe2+ cations and the PES spin multiplicity exhibit a considerable influence on the detailed mechanism and energetics of N2O decomposition, modifying the rate constant via the transmission κ coefficient in the Eyring equation:
 | (8) |
The Landau–Zener transition probabilities PLZ (κ = 2PLZ − PLZ2) between the PES of different spin states, calculated for N2O decomposition on both FeII/ZSM-5 and [FeO]+/ZSM-5 sites, are larger than ∼0.05.21 Such values indicate that without correcting the reaction rates of N2O decomposition for changes in the spin multiplicity, the resultant inaccuracies are equivalent to the activation barrier of ∼4 kcal mol−1 at 700 K. The spin state exhibits substantial influence on the reaction energetics by modifying the electronic structure of the reactants, which is particularly important for attaining the ground triplet state of the O2 product. Owing to the changes in the spin multiplicity, the reaction pathway becomes energetically more favourable.380
A remarkable mechanistic variant of this reaction has been reported for conceivably adjacent Fe centres hosted in the ferrierite matrix.387 The unique short separation of the neighbouring face-to-face β-6MR sites (7.5 Å in FER vs. >9 Å in MFI and BEA), favoured by the suitable location of Al atoms (see Chapter 4.3.1), allows the adjacent α-Fe cations to act cooperatively for efficient N2O activation by forming a trans μ-1,3-O,N bridge between both Fe(II) centres (Fe–NNO⋯Fe → Fe + O–Fe + N2). This finding has been attributed to explaining the superior activity of Fe/FER (∼3 times higher) in comparison to Fe/BEA and Fe/ZSM-5 at 230 °C,90 revealing a distinct synergy between the framework topology and Al distribution. Accordingly, the calculated apparent barrier for the O-atom transfer for trans μ-1,3-O,N bridged intermediates (3–4 kcal mol−1) is smaller for the η1-O species (9–13 kcal mol−1).
For N2O decomposition on dimeric iron–oxo centres ([Fe–(μ-O2−)–Fe]2+/ZSM-5), the minimum energy pathway after spin-state optimisation is shown in Fig. 42. Markedly, the reactivity of such species is dramatically higher in comparison to the isolated Fe2+ and [FeO]+ active sites. It is characterised by the switch of the rate-determining step (RDS) from O2 evolution at low temperatures (400–600 K) to N2O dissociation at high temperatures (T > 600 K). The ferromagnetic vs. antiferromagnetic coupling within the [Fe–(μ-O2−)–Fe]2+ centres exhibits a rather minor influence on the N2O decomposition.164 All the energy differences between the key mechanistic steps are below 5.5 kcal mol−1 (Fig. 42c). For molecular oxygen to desorb in its ground triplet state, the barrier for the PES crossing from the antiferromagnetic singlet to the antiferromagnetic triplet is equal to 7.9 kcal mol−1, whereas for the ferromagnetic coupling it increases to 9.5 kcal mol−1.
Survey of N2O activation and decomposition on various metallozeolite catalysts. The overall reactivity trends in N2O decomposition for the most commonly investigated Fe, Cu, Co, and Ni zeolites are summarised in Table 5. It is rather difficult to establish a definite universal order of the TMI activity variation since incoherent results have been reported. It is caused, most probably, by insufficient control over the speciation of the active sites, differences in the framework topology, and in the Si/Al and M/Al ratio (loading).
| Topology | Si/Al | M/Al | Activity order | Ref. |
|---|---|---|---|---|
| CHA (SSZ-13) | 12 | 0.13–0.32 | Fe ≫ Co > Cu | 371 |
| MFI (ZSM-5) | 25 | 0.5 | Cu ≈ Fe > Co | 388 |
| MFI (ZSM-5) | 18 | 0.73–1.3 | Cu ≫ Co > Fe | 389 |
| MFI (ZSM-5) | 12.5 | 0.02–0.245 | Fe > Co > Ni > Cu | 372 |
| BEA | 15 | 0.11–0.21 | Co > Fe > Cu | 145 |
| BEA | 23–42 | 0.5–1 | Cu > Co > Fe | 385 |
| MOR | 9.2 | 0.64–0.80 | Co > Fe ≫ Ni ∼ 0 | 386 |
The effect of TMI nature and loading on N2O reactivity is illustrated in Fig. 43a1 for Fe, Co, and Cu/SSZ-13 zeolites.371 The reaction rates (Fe ≫ Co > Cu) exhibit appreciably different responses to pN2O (see insert), with considerable deviation from the pseudo-first-order kinetics. The activation energies decrease in the order 141–148 kJ mol−1 (Co) > 111–113 kJ mol−1 (Cu) > 81–85 kJ mol−1 (Fe), whereas the preexponential factors for Fe (12.6–12.8 ([s kP]−1) and Cu (11.8–12.87 [s kP]−1) are quite similar, and significantly lower than that for Co (19.0–19.9 [s kP]−1). On Co/SSZ-13, the N2O decomposition occurs on the isolated Co cations, which tend to enhance the preexponential factor at the cost of a higher activation energy. For iron and copper, this process mainly occurs on dual-oxo centres.371 Thus, the rate constant for Co/SSZ-13 increases proportionally to the Co/Al ratio (Fig. 43a2). In the case of Fe/SSZ-13 catalysts, the rate constant increases till Fe/Al < 0.06 and then levels off, implying that only a fraction of the iron species is active in the N2O decomposition. An exponential activity increase with the Cu/Al ratio suggests, in turn, that dimeric centres are responsible for deN2O reactivity of Cu/SSZ-13, since statistically the number of pairs increases exponentially with copper loading. The same trend of the activity (Fe ≫ Co > Cu) is also observed for BEA zeolites (Fig. 43b).145 However, since the corresponding plots in Fig. 43a2 are derived from relatively small datasets, these conjectures warrant additional validation.
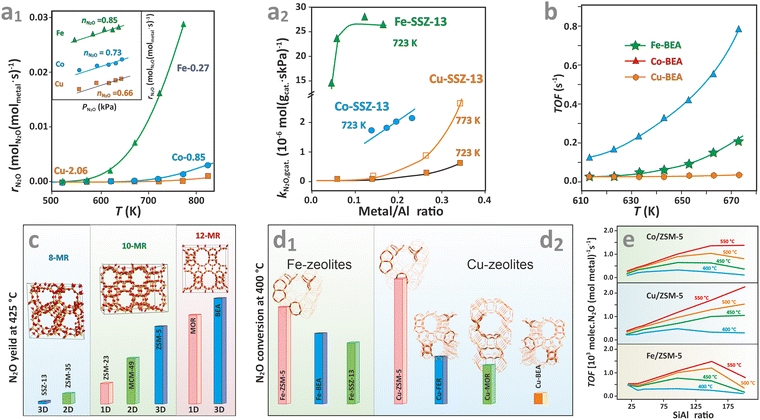 | ||
| Fig. 43 Influence of the transition metal type (Co, Cu, Fe) hosted in CHA zeolites (a1) and the M/Al ratio (a2) on the N2O decomposition performance, together with the apparent rate order (a1, insert). The catalytic performance of Co, Cu, and Fe accommodated in BEA zeolites (b), the influence of the framework type (c) and (d1–2), and the Si/Al ratio for Co/ZSM-5, Cu/ZSM-5, and Fe/ZSM-5 catalysts (e) on the deN2O activity. Figure based on data from ref. 145, 371, 388, 390 and 391. | ||
The influence of zeolite topology on N2O decomposition over various Co/zeolites is illustrated in Fig. 43c, varying as Co/BEA > Co/MOR > Co/ZSM-5 > Co/MCM-49 > Co/ZSM-23 > Co/ZSM-35 > Co/SSZ-13.392 In all cases, the active sites for this reaction are the isolated Co2+ cations. There is a consistent relationship between the self-diffusion coefficient of N2O in different topological zeolites (established by computer simulation) and the N2O conversion (apparently measured under diffusion limitation), revealing that the pore structure of the zeolites (size and dimensionality of the channels) affects the kinetics of the N2O decomposition by influencing the N2O diffusion within the zeolite pores. The three-dimensional pore structure and large pore size of Co/BEA appeared particularly beneficial among the investigated zeolites, leading to the N2O conversion X > 90% at 400 °C. The worst activity of Co/SSZ-13 (X < 10%) is attributed to the blocking of the small-sized pores due to the presence of segregated cobalt oxide entities, which are inactive. The significant influence of the framework topology on N2O decomposition was also observed for Fe/Zeolites (Fig. 43d1). Yet the pore size effect is less pronounced in this case (Fe/ZSM-5 > Fe/BEA > FeSSZ-13).390 The dramatic differences in the activity for the Fe/FER ≫ Fe/BEA > Fe/ZSM-5, in turn, are explained by the presence of unique two face-to-face Fe(II) cations cooperating in the efficient activation of the N2O molecule (discussed above). Notably, in the case of copper, the reactivity decreases as Cu/ZSM-5 > Cu/FER > Cu/MOR (Fig. 43d2),391 implying that the effects of the zeolite framework and the nature of the encaged zeolites are of comparable relevance, and cannot be rigorously separated.
Another parameter that controls N2O activation is the Si/Al ratio388 and the distribution of Al atoms in the T sites of the zeolite framework.377,384 The dependence of TOF values for N2O decomposition on Co/ZSM-5, Cu/ZSM-5 and Fe/ZSM-5 catalysts with various Si/Al ratios at different temperatures for M/Al = 0.5388 is shown in Fig. 43e. Generally, for all cations, the TOF values initially increase until Si/Al ∼ 100–150, and then tend to decline except for Cu/ZSM-5 at T > 475 °C. The drop of TOF for Si/Al > 150 is particularly pronounced in the case of the Fe/ZSM-5 catalyst.
The combined effects of structural heterogeneities in both the encapsulated TMI and the zeolite frameworks (including topology, Si/Al ratio, and Al distribution) on N2O reactivity cannot be rigorously separated. Given the mutual interrelation of these factors, their individual control is insufficient to establish universal reactivity trends for 3d metallozeolites as a function of a selected parameter. The inaccuracies are further emphasised by different conditions of the reaction, and variances resulting from distinct catalyst preparation methods (see Fig. 1).
Conclusions and outlook
After decades of extensive research on metallozeolites and the catalytic chemistry of small molecules, remarkable developments have been made on both fundamental and applied levels. The seemingly simple activation processes occurring in metal–ligand moieties can exhibit a complex nature that can be analyzed in detail by modern computational tools, such as NOCV-ETS, with orbital resolution. For a sensible elucidation of the bonding of non-innocent molecules to transition-metal ions, multireference methods, such as CASSCF or MP2, can provide an adequate treatment of the impact of static and dynamic correlation on the electronic and magnetic structure of the resulting intrazeolite adducts, in close relation to their reactivity. Nevertheless, it is rather difficult to establish definite, universal experimental TMI structure–reactivity trends, as incoherent results have often been reported. This is primarily caused by insufficient control over the speciation of the active sites, as well as by differences in the framework topology and the Si/Al and TMI/Al ratios among the investigated catalysts of nominally the same compositions. Therefore, there is still a need for further advances in the synthesis of metallozeolite materials with atomic precision, their site-specific characterisation, and complex mechanistic studies that benefit from the synergy between modern experimental and theoretical approaches. So far, most efforts have been focused on a few TMI compounds only, being limited essentially to the Cu, Fe, or Co triad, which exhibits the best catalytic performance in many critical catalytic processes, such as SCR, SCO, or C–H bond hydroxylation. However, a deep understanding of the principles of catalytic chemistry of TMI zeolite requires broadening the scope through more comprehensive studies across the periodic table to establish general patterns of bonding, activation, and reactivity, concerning the valence, coordination, and spin states of the encaged cations. These molecular foundations can provide rational tenets for classifying reactivity patterns, optimising existing structures, and predicting new multinuclear and heteronuclear active sites with enhanced reactivity. They may contain not only TMI but also auxiliary non-redox cations (e.g., Ca or Ga) with electronegativities tuned to their purpose. The biocatalysis of small molecules can further inspire the constitution of such multinuclear centres. Additionally, the integration of novel zeolite synthesis and functionalization methods that reduce reliance on poorly controlled Al distribution and minimize unintended TMI speciation is crucial. Equally important is the development of new frameworks that promote deliberately designed supramolecular interactions with reactant molecules, intermediates, and transition states. This may facilitate essential future advancements in the application of metallozeolites in the catalytic chemistry of small molecules.Further experimental progress can be achieved by applying, for example, phase-sensitive detection to enhance the signal-to-noise ratio and time resolution, particularly in operando catalytic studies of metallozeolites under working conditions.393 Insights into the dynamical processes occurring in the cages and channels can be provided, in turn, by pulsed-laser excitations, synchronised with time-resolved spectroscopic detection of the resulting molecular changes on the scale from picoseconds to milliseconds.394 Future research into speciation of active sites can also be inspired by recent advances in TEM imaging techniques, such as iDPC-STEM (integrated differential phase contrast STEM) or ptychography, which are capable of single-atom detection located in microporous channels, proving that TMI species can be directly visualised in beam-sensitive materials such as zeolites.395,396
Finally, many of the topics covered in this review are also relevant to the sister MOF materials functionalized by TMI.397 Due to their unique hybrid structure, they provide even more versatile scaffolds for intentionally tuning the TMI properties, opening new areas of catalytic chemistry where progress is chiefly needed.
Conflicts of interest
There are no conflicts of interest to declare.List of acronyms
| n-MR | n-Member ring |
| ALMO | Absolutely localized molecular orbitals |
| BEA | Beta framework type code |
| BEEF-vdW | Bayesian error estimation functional with van der Waals |
| BS | Broken symmetry |
| CAS | Complete active space |
| CASPT2 | Complete active space with second-order perturbation theory |
| CASSCF | Complete active space self-consistent field |
| CEC | Cation exchange capacity |
| CC | Coupled cluster |
| CCSD(T) | Coupled cluster with single, double, and perturbative triple excitations |
| CHA | Chabazite framework type code |
| COHP | Crystal orbital Hamiltonian population |
| CT | Charge transfer |
| CVD | Chemical vapour deposition |
| DFT | Density functional theory |
| EDE | Dispersion interactions |
| EDX | Energy-dispersive X-ray spectroscopy |
| ENDOR | Electron nuclear double resonance |
| EPR | Electron paramagnetic resonance |
| ESEEM | Electron spin echo envelope modulation |
| ET | Electron transfer |
| ETS-NOCV | Extended-transition-state natural orbitals for chemical valence |
| EXAFS | Extended X-ray absorption fine structure |
| FAU | Faujasite framework type code |
| FC | Franck–Condon |
| FPT | First principles thermodynamics |
| FTIR | Fourier transform infrared spectroscopy |
| HC | High coverage |
| HC-SCR | Hydrocarbon selective catalytic reduction |
| HF | Hartree–Fock |
| HOMO | Highest occupied molecular orbital |
| HSAB | Hard soft acid base |
| HYSCORE | HYperfine sublevel CORrElation spectroscopy |
| iDPC-STEM | (Integrated differential phase contrast STEM) |
| IEL | Inverse/inverted energy levels |
| IZA | International zeolite association |
| LC | Low coverage |
| LMCT | Ligand-to-metal charge transfer |
| LUMO | Lowest unoccupied molecular orbital |
| MAS-NMR | Magic angle spinning nuclear magnetic resonance |
| MD | Molecular dynamics |
| MEL | Mixed energy levels |
| MFI | MFI zeolite framework type code |
| ML | Machine learning |
| MLET | Metal-to-ligand electron transfer |
| MO | Molecular orbital |
| MOR | Mordenite framework type code |
| MP | Möeller–Plesset |
| CN | Coordination number of TMI e.g. Cu4c |
| NEL | Normal energy levels |
| NOCV | Natural orbitals for chemical valence |
| OT | Oxygen transfer |
| PEC | Principal electronic configuration |
| PES | Potential energy surface |
| PL | Photoluminescence |
| rR | Resonance Raman spectroscopy |
| SCO | Selective catalytic oxidation |
| SCR | Selective catalytic reduction |
| SOC | Spin–orbit coupling |
| SOMO | Singly occupied molecular orbital |
| TMI | Transition metal ion |
| TPD | Temperature-programmed desorption |
| UV-Vis | Ultraviolet-visible spectroscopy |
| UV-Vis-NIR | Ultraviolet-visible-near infrared spectroscopy |
| VB | Valence band |
| VB-CAS | Valence bond complete active space |
| VTVH-MCD | Variable-temperature, variable-field magnetic circular dichroism |
| XAFS | X-ray absorption fine structure |
| XANES | X-ray absorption near edge structure |
| X-band CW-EPR | X-band continuous wave electron paramagnetic resonance |
| ZFS | Zero-field splitting |
Data availability
No primary research results, software, or code have been included, and no new data were generated or analysed as part of this review. In a few cases, parts of the compound figures were based on the data available at: https://ruj.uj.edu.pl/entities/publication/2c6d31d7-da08-466d-987d-fcaebbe5db6a, https://ruj.uj.edu.pl/entities/publication/8ae5ec29-e753-4aed-b1e5-1430e36cb24d, https://ruj.uj.edu.pl/entities/publication/d8b1269b-f698-4e80-9051-d96caf48fb52.Acknowledgements
The publication has been supported by the Faculty of Chemistry and the Priority Research Area (SciMat) under the Strategic Programme Excellence Initiative at Jagiellonian University.References
- J. Turkevich, J. Soria and Y. Ono, J. Catal., 1972, 25, 44–54 CrossRef CAS.
- K. Klier, R. Kellerman and P. J. Hutta, J. Chem. Phys., 1974, 61, 4224–4234 CrossRef CAS.
- E. Giamello, D. Murphy, G. Magnacca, C. Morterra, Y. Shioya, T. Nomura and M. Anpo, J. Catal., 1992, 136, 510–520 CrossRef CAS.
- W. Li, Y. Chai, G. Wu and L. Li, J. Phys. Chem. Lett., 2022, 13, 11419–11429 CrossRef CAS PubMed.
- B. E. R. Snyder, M. L. Bols, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Chem. Rev., 2018, 118, 2718–2768 CrossRef CAS PubMed.
- P. Vanelderen, J. Vancauwenbergh, B. F. Sels and R. A. Schoonheydt, Coord. Chem. Rev., 2013, 257, 483–494 CrossRef CAS.
- International Zeolite Association Home Page https://iza-online.org/.
- K. Klier, Langmuir, 1988, 4, 13–25 CrossRef CAS.
- W. Yan, S. Xi, Y. Du, M. K. Schreyer, S. X. Tan, Y. Liu and A. Borgna, ChemCatChem, 2018, 10, 3078–3085 CrossRef CAS.
- J. A. Nasir, J. Guan, T. W. Keal, Y. Lu, A. A. Sokol and C. R. A. Catlow, J. Catal., 2024, 438, 115696 CrossRef.
- B. Ipek, M. J. Wulfers, H. Kim, F. Göltl, I. Hermans, J. P. Smith, K. S. Booksh, C. M. Brown and R. F. Lobo, ACS Catal., 2017, 7, 4291–4303 CrossRef CAS.
- Y. Li and J. Yu, Nat. Rev. Mater., 2021, 6, 1156–1174 CrossRef CAS.
- M. Dusselier and M. E. Davis, Chem. Rev., 2018, 118, 5265–5329 CrossRef CAS PubMed.
- J. A. Nasir, A. M. Beale and C. R. A. Catlow, Chem. Soc. Rev., 2024, 53, 11657–11691 RSC.
- C. Paolucci, J. R. Di Iorio, W. F. Schneider and R. Gounder, Acc. Chem. Res., 2020, 53, 1881–1892 CrossRef CAS PubMed.
- Y. Xu, X. Wang, M. Qin and Q. Li, J. Environ. Chem. Eng., 2022, 10, 107270 CrossRef CAS.
- P. Pietrzyk and Z. Sojka, Chem. Commun., 2007, 1930–1932 RSC.
- M. A. Newton, A. J. Knorpp, V. L. Sushkevich, D. Palagin and J. A. van Bokhoven, Chem. Soc. Rev., 2020, 49, 1449–1486 RSC.
- B. E. R. Snyder, M. L. Bols, H. M. Rhoda, D. Plessers, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Science, 2021, 373, 327–331 CrossRef CAS PubMed.
- M. L. Bols, B. E. R. Snyder, H. M. Rhoda, P. Cnudde, G. Fayad, R. A. Schoonheydt, V. Van Speybroeck, E. I. Solomon and B. F. Sels, Nat. Catal., 2021, 4, 332–340 CrossRef CAS.
- A. Heyden, B. Peters, A. T. Bell and F. J. Kiel, J. Phys. Chem. B, 2005, 109, 1857–1873 CrossRef CAS PubMed.
- W. Loewenstein, Am. Mineral., 1954, 39, 92–96 CAS.
- P. Sazama, K. Mlekodaj, J. Dedecek, V. Pashkova, E. Tabor, P. Klein, M. Urbanova, R. Karcz, S. R. Whittleton, H. M. Thomas, A. V. Fishchuk and S. Sklenak, J. Phys. Chem. C, 2019, 123, 7968–7987 CrossRef.
- S. Dzwigaj and M. Che, J. Phys. Chem. B, 2005, 109, 22167–22174 CrossRef CAS PubMed.
- C. Lamberti, A. Zecchina, E. Groppo and S. Bordiga, Chem. Soc. Rev., 2010, 39, 4951–5001 RSC.
- K. Tarach, J. Sobalska, A. Held, J. Dedecek, E. Tabor and K. Góra-Marek, J. Phys. Chem. C, 2024, 128, 3759–3769 CrossRef CAS.
- K. Sun, F. Fan, H. Xia, Z. Feng, W.-X. Li and C. Li, J. Phys. Chem. C, 2008, 112, 16036–16041 CrossRef CAS.
- S. Dźwigaj, M. Matsuoka, R. Franck, M. Anpo and M. Che, J. Phys. Chem. B, 1998, 102, 6309–6312 CrossRef.
- J. Chen, W. Huang, S. Bao, W. Zhang, T. Liang, S. Zheng, L. Yi, L. Guo and X. Wu, RSC Adv., 2022, 12, 27746–27765 RSC.
- L. Čapek, V. Kreibich, J. Dědeček, T. Grygar, B. Wichterlová, Z. Sobalík, J. A. Martens, R. Brosius and V. Tokarová, Microporous Mesoporous Mater., 2005, 80, 279–289 CrossRef.
- K. Góra-Marek, A. Glanowska and J. Datka, Microporous Mesoporous Mater., 2012, 158, 162–169 CrossRef.
- K. Góra-Marek, B. Gil and J. Datka, Appl. Catal., A, 2009, 353, 117–122 CrossRef.
- M. Fedyna, B. Mozgawa, F. Zasada, K. Góra-Marek, J. Gryboś, W. Piskorz, C. Yin, Z. Zhao, P. Pietrzyk and Z. Sojka, Appl. Catal., B, 2023, 325, 122309 CrossRef CAS.
- S. Zamani, M. Chiesa, V. Meynen, Y. Xiao, B. Prelot, J. Zajac, F. Verpoort, P. Cool and S. Van Doorslaer, J. Phys. Chem. C, 2010, 114, 12966–12975 CrossRef CAS.
- D. Goldfarb and K. Zukerman, Chem. Phys. Lett., 1990, 171, 167–174 CrossRef CAS.
- D. Goldfarb, Phys. Chem. Chem. Phys., 2006, 8, 2325–2343 RSC.
- V. Lagostina, E. Salvadori, M. Chiesa and E. Giamello, J. Catal., 2020, 391, 397–403 CrossRef CAS.
- S. Bordiga, E. Groppo, G. Agostini, J. A. van Bokhoven and C. Lamberti, Chem. Rev., 2013, 113, 1736–1850 CrossRef CAS PubMed.
- S. H. van Vreeswijk and B. M. Weckhuysen, Nat. Sci. Rev., 2022, 9, nwac047 CrossRef CAS PubMed.
- A. Stępniewski, M. Radoń, K. Góra-Marek and E. Broclawik, Phys. Chem. Chem. Phys., 2016, 18, 3716–3729 RSC.
- W. Jeevapong, J. Sittiwong, M. Probst, B. Boekfa, C. Wattanakit, T. Maihom and J. Limtrakul, J. Phys. Chem. C, 2023, 127, 8473–8481 CrossRef CAS.
- J. Klimeš and D. P. Tew, J. Chem. Phys., 2019, 151, 234108 CrossRef PubMed.
- A. M. Teale, T. Helgaker, A. Savin, C. Adamo, B. Aradi, A. V. Arbuznikov, P. W. Ayers, E. J. Baerends, V. Barone, P. Calaminici, E. Cancès, E. A. Carter, P. K. Chattaraj, H. Chermette, I. Ciofini, T. D. Crawford, F. De Proft, J. F. Dobson, C. Draxl, T. Frauenheim, E. Fromager, P. Fuentealba, L. Gagliardi, G. Galli, J. Gao, P. Geerlings, N. Gidopoulos, P. M. W. Gill, P. Gori-Giorgi, A. Görling, T. Gould, S. Grimme, O. Gritsenko, H. J. A. Jensen, E. R. Johnson, R. O. Jones, M. Kaupp, A. M. Köster, L. Kronik, A. I. Krylov, S. Kvaal, A. Laestadius, M. Levy, M. Lewin, S. Liu, P.-F. Loos, N. T. Maitra, F. Neese, J. P. Perdew, K. Pernal, P. Pernot, P. Piecuch, E. Rebolini, L. Reining, P. Romaniello, A. Ruzsinszky, D. R. Salahub, M. Scheffler, P. Schwerdtfeger, V. N. Staroverov, J. Sun, E. Tellgren, D. J. Tozer, S. B. Trickey, C. A. Ullrich, A. Vela, G. Vignale, T. A. Wesolowski, X. Xu and W. Yang, Phys. Chem. Chem. Phys., 2022, 24, 28700–28781 RSC.
- A. M. Teale, P. Verma and D. G. Truhlar, Trends Chem., 2020, 2, 302–318 CrossRef.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2019, 119, 2453–2523 CrossRef CAS PubMed.
- S. Svelle, C. Tuma, X. Rozanska, T. Kerber and J. Sauer, J. Am. Chem. Soc., 2009, 131, 816–825 CrossRef CAS PubMed.
- F. Berger, M. Rybicki and J. Sauer, ACS Catal., 2023, 13, 2011–2024 CrossRef CAS.
- K. Sillar, A. Hofmann and J. Sauer, J. Am. Chem. Soc., 2009, 131, 4143–4150 CrossRef CAS PubMed.
- M. Radoń and K. Pierloot, J. Phys. Chem. A, 2008, 112, 11824–11832 CrossRef PubMed.
- M. Radoń, E. Broclawik and K. Pierloot, J. Phys. Chem. B, 2010, 114, 1518–1528 CrossRef PubMed.
- Q. M. Phung, H. N. Nam and A. Ghosh, Inorg. Chem., 2023, 62, 20496–20505 CrossRef CAS PubMed.
- S. Vancoillie, H. Zhao, M. Radoń and K. Pierloot, J. Chem. Theory Comput., 2010, 6, 576–582 CrossRef CAS PubMed.
- M. Radoń, G. Drabik, M. Hodorowicz and J. Szklarzewicz, Chem. Sci., 2024, 15, 20189 RSC.
- R. K. Carlson, S. O. Odoh, S. J. Tereniak, C. C. Lu and L. Gagliardi, J. Chem. Theory Comput., 2015, 11, 4093–4101 CrossRef CAS PubMed.
- D. A. Pantazis, J. Chem. Theory Comput., 2019, 15, 938–948 CrossRef CAS PubMed.
- Z. A. Alaithan, N. Harrison and G. Sastre, J. Phys. Chem. C, 2021, 125, 19200–19208 CrossRef CAS.
- C. J. Heard, L. Grajciar and A. Erlebach, Nanoscale, 2024, 16, 8108–8118 RSC.
- A. J. Porter and A. J. O’Malley, J. Phys. Chem. C, 2021, 125, 11567–11579 CrossRef CAS.
- V. Van Speybroeck, M. Bocus, P. Cnudde and L. Vanduyfhuys, ACS Catal., 2023, 13, 11455–11493 CrossRef PubMed.
- G. Wang, C. Zhi, Y. Wang and Q. Wang, Comput. Theor. Chem., 2023, 1227, 114228 CrossRef CAS.
- D. J. Hutton, D. H. Lopez and F. Göltl, React. Chem. Eng., 2024, 9, 1685–1695 RSC.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed.
- P. Kozyra, M. Świętek, J. Datka and E. Brocławik, J. Comput. Chem., Jpn., 2013, 12, 30–37 CrossRef CAS.
- P. Pietrzyk, K. Podolska, T. Mazur and Z. Sojka, J. Am. Chem. Soc., 2011, 133, 19931–19943 CrossRef CAS PubMed.
- V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- C. Liu, I. Tranca, R. A. van Santen, E. J. M. Hensen and E. A. Pidko, J. Phys. Chem. C, 2017, 121, 23520–23530 CrossRef CAS PubMed.
- X. Li, H. Han, N. Evangelou, N. J. Wichrowski, P. Lu, W. Xu, S. J. Hwang, W. Zhao, C. Song, X. Guo, A. Bhan, I. G. Kevrekidis and M. Tsapatsis, Nat. Commun., 2023, 14, 3152 CrossRef CAS PubMed.
- S. Ma and Z. P. Liu, Chem. Sci., 2022, 13, 5055–5068 RSC.
- D. Plessers, M. L. Bols, H. M. Rhoda, A. J. Heyer, E. I. Solomon, B. F. Sels and R. A. Schoonheydt, Comprehensive Inorganic Chemistry III, 3rd edn, 2023, pp. 148–164 Search PubMed.
- Q. Zhang, S. Gao and J. Yu, Chem. Rev., 2023, 123, 6039–6106 CrossRef CAS PubMed.
- N. Kosinov, C. Liu, E. J. M. Hensen and E. A. Pidko, Chem. Mater., 2018, 30, 3177–3198 CrossRef CAS PubMed.
- H. M. Rhoda, A. J. Heyer, B. E. R. Snyder, D. Plessers, M. L. Bols, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Chem. Rev., 2022, 122, 12207–12243 CrossRef CAS PubMed.
- Y. Wu, P. Deng, L. Liu, J. Zhang, H. Liu, X. Gao, F.-S. Xiao and L. Wang, Chem. Soc. Rev., 2025, 54, 4745–4762 RSC.
- Y. Li, L. Li and J. Yu, Chem, 2017, 3, 928–949 CAS.
- J. Pérez-Ramírez, C. H. Christensen, K. Egeblad, C. H. Christensen and J. C. Groen, Chem. Soc. Rev., 2008, 37, 2530–2542 RSC.
- C. Chizallet, C. Bouchy, K. Larmier and G. Pirngruber, Chem. Rev., 2023, 123, 6107–6196 CrossRef CAS PubMed.
- C. Cheng, P. Li, X. Yang and R. T. Yang, Catal. Sci. Technol., 2016, 6, 7561–7568 RSC.
- E. Morra, G. Berlier, E. Borfecchia, S. Bordiga, P. Beato and M. Chiesa, J. Phys. Chem. C, 2017, 121, 14238–14245 CrossRef CAS.
- K. A. Chalupka, W. K. Jozwiak, J. Rynkowski, W. Maniukiewicz, S. Casale and S. Dzwigaj, Appl. Catal., B, 2014, 146, 227–236 CrossRef CAS.
- P. Pietrzyk, K. Podolska-Serafin, K. Góra-Marek, A. Krasowska and Z. Sojka, Microporous Mesoporous Mater., 2020, 291, 109692 CrossRef CAS.
- T. Yu, Y. Su, A. Wang, B. M. Weckhuysen and W. Luo, ChemCatChem, 2021, 13, 2766–2770 CrossRef CAS.
- P. J. Smeets, J. S. Woertink, B. F. Sels, E. I. Solomon and R. A. Schoonheydt, Inorg. Chem., 2010, 49, 3573–3583 CrossRef CAS PubMed.
- B. Mozgawa, Copper active sites in chabazite–type zeolites in reactions of selective catalytic reduction of NOx with ammonia – insight into structure and reactivity using spectroscopic methods and DFT modelling, PhD thesis, Jagiellonian University, 2024 Search PubMed.
- J. E. Olszowka, M. Lemishka, K. Mlekodaj, P. Kubat, D. Rutkowska-Żbik, J. Dedecek and E. Tabor, J. Phys. Chem. C, 2021, 125, 9060–9073 CrossRef CAS.
- Z. Sobalik, Z. Tvaruzkova and B. Wichterlova, Microporous Mesoporous Mater., 1998, 25, 225–228 CrossRef CAS.
- E. Broclawik, J. Datka, B. Gil and P. Kozyra, Phys. Chem. Chem. Phys., 2000, 2, 401–405 RSC.
- M. Lemishka, J. Dedecek, K. Mlekodaj, Z. Sobalik, S. Sklenak and E. Tabor, Pure Appl. Chem., 2019, 91, 1721–1732 CrossRef CAS.
- Y. Jangjou, Q. Do, Y. Gu, L.-G. Lim, H. Sun, D. Wang, A. Kumar, J. Li, L. C. Grabow and W. S. Epling, ACS Catal., 2018, 8, 1325–1337 CrossRef CAS.
- B. Wichterlova, J. Dedecek and Z. Sobalik, Single Metal Ions in Host Zeolite Matrices: Structure-Activity-Selectivity-Relationships, in Catalysis by Unique Metal Ion Structures in Solid Matrices, ed. G. Centi, B. Wichterlova and A. T. Bell, 2001, pp. 31–53 Search PubMed.
- S. Sklenak, P. C. Andrikopoulos, B. Boekfa, B. Jansang, J. Nováková, L. Benco, T. Bucko, J. Hafner, J. Dedecek and Z. Sobalík, J. Catal., 2010, 272, 262–274 CrossRef CAS.
- P. J. Carl and S. C. Larsen, J. Phys. Chem. B, 2000, 104, 6568–6575 CrossRef CAS.
- A. Godiksen, P. N. R. Vennestrøm, S. B. Rasmussen and S. Mossin, Top. Catal., 2017, 60, 13–29 CrossRef CAS.
- R. P. Vélez, U. Bentrup, W. Grünert and A. Brückner, Top. Catal., 2017, 60, 1641–1652 CrossRef.
- Z. Sojka, Catal. Rev., 1995, 37, 461–512 CrossRef CAS.
- P. C. Bruzzese, E. Salvadori, S. Jäger, M. Hartman, B. Civalleri, A. Pöppl and M. Chiesa, Nat. Commun., 2021, 12, 4638 CrossRef CAS PubMed.
- V. Nagarajan, D. Rings, L. Moschkowitz, M. Hartmann and A. Pöppl, Chem. Lett., 2005, 34, 1614–1615 CrossRef CAS.
- E. Marceau, L. Bonneviot, S. Dzwigaj, J.-F. Lambert, C. Louis and X. Carrier, J. Catal., 2021, 396, 104–121 CrossRef CAS.
- J. A. Weil, J. R. Bolton and J. E. Wertz, Electron Paramagnetic Resonance Elementary theory and Practical Applications, Wiley, NY, 1994 Search PubMed.
- F. E. Mabbs and D. Collison, Electron Resonance of d Transition Metal Compounds, Elsevier, Amsterdam, 1992 Search PubMed.
- F. Giordanino, P. N. R. Vennestrøm, L. F. Lundegaard, F. N. Stappen, S. Mossin, P. Beato, S. Bordiga and C. Lamberti, Dalton Trans., 2013, 42, 12741–12761 RSC.
- P. Rieger, Coord. Chem. Rev., 1994, 135/136, 203–286 CrossRef CAS.
- F. E. Mabbs and D. Collison, Electron Resonance of d Transition Metal Compounds, Elsevier, Amsterdam, 1992 Search PubMed.
- V. Ovchinnikov and V. N. Konstantinov, J. Magn. Reson., 1979, 32, 179 Search PubMed.
- J. C. Conesa and J. Soria, J. Phys. Chem., 1978, 82, 1575–1578 CrossRef CAS.
- A. Tuel, J. Diab, P. Gelin, M. Dufaux, J.-F. Dutel and Y. B. Taarit, J. Mol. Catal., 1990, 63, 95–102 CrossRef CAS.
- J. Peisach and W. E. Blumberg, Arch. Biochem. Biophys., 1974, 165, 691–708 CrossRef CAS PubMed.
- P. J. Carl and S. C. Larsen, J. Catal., 1999, 182, 208–218 CrossRef CAS.
- E. Morra, E. Giamello and M. Chiesa, Chem. – Eur. J., 2014, 20, 7381–7388 CrossRef CAS PubMed.
- A. Tuel, J. Diab, P. Gelin, M. Dufaux, J.-F. Dutel and Y. B. Taarit, J. Mol. Catal., 1990, 63, 95–102 CrossRef CAS.
- P. Pietrzyk, Z. Sojka, S. Dźwigaj and M. Che, J. Am. Chem. Soc., 2007, 129, 14174–14175 CrossRef CAS PubMed.
- B. M. Weckhuysen and R. A. Schoonheydt, Stud. Surf. Sci. Catal., 1994, 84, 965–972 CrossRef CAS.
- A. M. Volodin, G. M. Zhidomirov, K. A. Dubkov, E. J. M. Hensen and R. A. van Santen, Catal. Today, 2005, 110, 247–254 CrossRef CAS.
- E.-M. El-Malki, D. Werst, P. E. Doan and W. M. H. Sachtler, J. Phys. Chem. B, 2000, 104, 5924–5931 CrossRef CAS.
- K. Podolska-Serafin and P. Pietrzyk, J. Mol. Struct., 2019, 1180, 754–763 CrossRef CAS.
- E. Fernández, M. Moreno-González, M. Moliner, T. Blasco, M. Boronat and A. Corma, Top. Catal., 2018, 61, 810–832 CrossRef.
- P. C. Bruzzese, E. Salvadori, B. Civalleri, S. Jäger, M. Hartmann, A. Pöppl and M. Chiesa, J. Am. Chem. Soc., 2022, 144, 13079–13083 CrossRef CAS PubMed.
- E. Morra, M. Signorile, E. Salvadori, S. Bordiga, E. Giamello and M. Chiesa, Angew. Chem., Int. Ed., 2019, 58, 12398–12403 CrossRef CAS PubMed.
- P. Rzepka, T. Huthwelker, J. Dědeček, E. Tabor, M. Bernauer, S. Sklenák, K. Mlekodaj and J. A. van Bokhoven, Science, 2025, 388, 423–428 CrossRef CAS PubMed.
- J. Krzystek, A. Ozarowski and J. Telser, Coord. Chem. Rev., 2006, 250, 2308–2324 CrossRef CAS.
- B. M. Weckhuysen, A. A. Verberckmoes, M. G. Uytterhoeven, F. E. Mabbs, D. Collison, E. de Boer and R. A. Schoonheydt, J. Phys. Chem. B, 2000, 104, 37–42 CrossRef CAS.
- A. Peng, M. C. Kung, M. O. Ross, B. M. Hofman and H. H. Kung, Top. Catal., 2020, 63, 1708–1716 CrossRef CAS.
- S. A. Bonke, T. Risse, A. Schnegg and A. Brückner, Nat. Rev. Methods Primers, 2021, 1, 33 CrossRef CAS.
- R. Baran, L. Valentin and S. Dźwigaj, Phys. Chem. Chem. Phys., 2016, 18, 12050 RSC.
- D. E. De Vos, B. M. Weckhuysen and T. Bein, J. Am. Chem. Soc., 1996, 118, 9615–9622 CrossRef CAS.
- J. Livage, Materials, 2010, 3, 4175–4195 CrossRef CAS PubMed.
- J. Grand, S. N. Talapaneni, A. Vicente, C. Fernandez, E. Dib, H. A. Aleksandrov, G. N. Vayssilov, R. Retoux, P. Boullay, J. P. Gilson, V. Valtchev and S. Mintova, Nat. Mater., 2017, 16, 1010–1015 CrossRef CAS PubMed.
- D. Zhou, Y. Zhang, H. Zhu, D. Ma and X. Bao, J. Phys. Chem. C, 2007, 111, 2081–2091 CrossRef CAS.
- S. Wannakao, B. Boekfa, P. Khongpracha, M. Probst and J. Limtrakul, ChemPhysChem, 2010, 11, 3432–3438 CrossRef CAS PubMed.
- M. F. Fellah and I. Onal, Phys. Chem. Chem. Phys., 2013, 15, 13969–13997 RSC.
- S. Dźwigaj, M. Matsuoka, M. Anpo and M. Che, J. Phys. Chem. B, 2000, 104, 6012–6020 CrossRef.
- B. E. R. Snyder, L. H. Böttger, M. L. Bols, J. J. Yan, H. M. Rhod, A. B. Jacobs, M. Y. Hu, J. Zhao, E. E. Alp, B. Hedman, K. O. Hodgson, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 4565–4570 CrossRef CAS PubMed.
- J. B. Lim, S. H. Cha and S. B. Hong, Appl. Catal., B, 2019, 243, 750–759 CrossRef CAS.
- M. H. Mahyuddin, Y. Shiota, A. Staykov and K. Yoshizawa, Inorg. Chem., 2017, 56, 10370–10380 CrossRef CAS PubMed.
- A. Oda, T. Ohkubo, T. Yumura, H. Kobayashi and Y. Kuroda, Inorg. Chem., 2019, 58, 327–338 CrossRef CAS PubMed.
- B. E. R. Snyder, P. Vanelderen, M. L. Bols, S. D. Hallaert, L. H. Böttger, L. Ungur, K. Pierloot, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Nature, 2016, 536, 317–321 CrossRef CAS PubMed.
- S. Ye and F. Neese, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1228–1233 CrossRef CAS PubMed.
- Y. Shimoyama and T. Kojima, Inorg. Chem., 2019, 58, 9517–9542 CrossRef CAS PubMed.
- F. Tielens and S. Dźwigaj, Catal. Today, 2010, 152, 66–69 CrossRef CAS.
- M. Matsuoka, S. Higashimoto, H. Yamashita and M. Anpo, Res. Chem. Intermed., 2000, 26, 85–92 CrossRef CAS.
- M. Anpo, T.-H. Kim and M. Matsuoka, Catal. Today, 2009, 142, 114–124 CrossRef CAS.
- S. Higashimoto, M. Matsuoka, H. Yamashita, M. Anpo, O. Kitao, H. Hidaka, M. Che and E. Giamello, J. Phys. Chem. B, 2000, 104, 10288–10292 CrossRef CAS.
- H. S. Lacheen and E. Iglesia, J. Phys. Chem. B, 2006, 110, 5462–5472 CrossRef CAS PubMed.
- M. Smoliło-Utrata, K. A. Tarach, K. Samson, M. Gackowski, E. Madej, J. Korecki, G. Mordarski, M. Śliwa, S. Jarczewski, J. Podobinski, P. Kuśtrowski, J. Datka, D. Rutkowska-Żbik and K. Góra-Marek, Int. J. Mol. Sci., 2022, 23, 5584 CrossRef PubMed.
- M. H. Mahyuddin, A. Staykov, Y. Shiota and K. Yoshizawa, ACS Catal., 2016, 6, 8321–8331 CrossRef CAS.
- N. Liu, R. Zhang, B. Chen, Y. Li and Y. Li, J. Catal., 2012, 294, 99–112 CrossRef CAS.
- J. Gao, Y. Zheng, Y. Tang, J.-M. Jehng, R. Gryboś, J. Handzlik, I. E. Wachs and S. G. Podkolzin, ACS Catal., 2015, 5, 3078–3092 CrossRef CAS.
- M. L. Bols, S. D. Hallaert, B. E. R. Snyder, J. Devos, D. Plessers, H. M. Rhoda, M. Dusselier, R. A. Schoonheydt, K. Pierloot, E. I. Solomon and B. F. Sels, J. Am. Chem. Soc., 2018, 140, 12021–12032 CrossRef CAS PubMed.
- K. Mlekodaj, M. Lemishka, S. Sklenak, J. Dědeček and E. Tabor, Chem. Commun., 2021, 57, 3472–3475 RSC.
- J. Wang, G. Li, X. Ju, H. Xia, F. Fan, J. Wang, Z. Feng and C. Li, J. Catal., 2013, 301, 77–82 CrossRef CAS.
- D. T. Bregante, L. N. Wilcox, C. Liu, C. Paolucci, R. Gounder and D. W. Flaherty, ACS Catal., 2021, 11, 11873–11884 CrossRef CAS.
- T. Ikuno, S. Grundner, A. Jentys, G. Li, E. Pidko, J. Fulton, M. Sanchez-Sanchez and J. A. Lercher, J. Phys. Chem. C, 2019, 123, 8759–8769 CrossRef CAS.
- I. Kurzydym and I. Czekaj, Molecules, 2022, 27, 300 CrossRef CAS PubMed.
- G. Wang, L. Huang, W. Chen, J. Zhou and A. Zheng, Phys. Chem. Chem. Phys., 2018, 20, 26522 RSC.
- G. Li, E. A. Pidko, R. A. van Santen, C. Li and E. J. M. Hensen, J. Phys. Chem. C, 2013, 117, 413–426 CrossRef CAS.
- M. H. Mahyuddin and K. Yoshizawa, Catal. Sci. Technol., 2018, 8, 5875–5885 RSC.
- P. Pietrzyk, K. Góra-Marek, T. Mazur, B. Mozgawa, M. Radoń, M. Chiesa, Z. Zhao and Z. Sojka, J. Catal., 2021, 394, 206–219 CrossRef CAS.
- P. Pietrzyk, C. Dujardin, K. Góra-Marek, P. Granger and Z. Sojka, Phys. Chem. Chem. Phys., 2012, 14, 2203–2215 RSC.
- D. W. Fickel and R. F. Lobo, J. Phys. Chem. C, 2010, 114, 1633–1640 CrossRef CAS.
- A. R. Kulkarni, Z. J. Zhao, S. Siahrostami, J. K. Nørskov and F. Studt, ACS Catal., 2016, 6, 6531–6536 CrossRef CAS.
- G. D. Pirngruber, P. K. Roy and R. Prins, Phys. Chem. Chem. Phys., 2006, 8, 3939–3950 RSC.
- A. J. Heyer, D. Plessers, J. Ma, B. E. R. Snyder, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, J. Am. Chem. Soc., 2024, 146, 6061–6071 CrossRef CAS PubMed.
- L. Noodleman and E. J. Baerends, J. Am. Chem. Soc., 1984, 106, 2316–2327 CrossRef CAS.
- T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223–230 CrossRef CAS.
- N. Hansen, A. Heyden, A. T. Bell and F. J. Keil, J. Phys. Chem. C, 2007, 111, 2092–2101, DOI:10.1021/jp065574q.
- S. Li, Y. Wang, T. Wu and W. F. Schneider, ACS Catal., 2018, 8, 10119–10130 CrossRef CAS.
- G. Li and E. A. Pidko, ChemCatChem, 2019, 11, 134–156 CrossRef CAS.
- C. Liu, G. Li, E. J. M. Hensen and E. A. Pidko, ACS Catal., 2015, 5, 7024–7033 CrossRef CAS.
- G. Li, E. A. Pidko, R. A. van Santen, C. Li and E. J. M. Hensen, J. Phys. Chem. C, 2013, 117, 413–426 CrossRef CAS.
- L. Grajciar, C. J. Heard, A. A. Bondarenko, M. V. Polynski, J. Meeprasert, E. A. Pidko and P. Nachtigall, Chem. Soc. Rev., 2018, 47, 8307–8348 RSC.
- K. Reuter and M. Scheffler, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 65, 035406 CrossRef.
- K. Reuter and M. Scheffler, Phys. Rev. Lett., 2003, 90, 046103 CrossRef PubMed.
- B. Mozgawa, F. Zasada, M. Fedyna, K. Góra-Marek, C. Yin, Z. Zhao, Z. Sojka and P. Pietrzyk, ACS Catal., 2025, 15(4), 2715–2734 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. Grimme, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- K. E. Riley, M. Pitoňák, P. Jurečka and P. Hobza, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS PubMed.
- F. Göltl, A. Grüneis, T. Bučko and J. Hafner, J. Chem. Phys., 2012, 137, 114111 CrossRef PubMed.
- T. Kerber, M. Sierka and J. Sauer, J. Comput. Chem., 2008, 29, 2088–2097 CrossRef CAS PubMed.
- L. Chen, T. V. W. Janssens and H. Grönbeck, Phys. Chem. Chem. Phys., 2019, 21, 10923–10930 RSC.
- M. Fischer, Z. Kristallogr. – Cryst. Mater., 2015, 230, 325–336 CrossRef CAS.
- K. Stanciakova, J. N. Louwen, B. M. Weckhuysen, R. E. Bulo and F. Göltl, J. Phys. Chem. C, 2021, 125, 20261–20274 CrossRef CAS.
- T. Hirano, in MOPAC Manual, ed. J. P. Stewart, 7th edn, 1993 Search PubMed.
- J. A. Greathouse, M. J. Paul, G. Xu and M. D. Powell, Clays Clay Miner., 2023, 71, 54–73 CrossRef CAS.
- G. Pireddu, F. G. Pazzona, P. Demontis and M. A. Załuska-Kotur, J. Chem. Theory Comput., 2019, 15, 6931–6943 CrossRef CAS PubMed.
- G. Piccini and J. Sauer, J. Chem. Theory Comput., 2014, 10, 2479–2487 CrossRef CAS PubMed.
- M. L. Bols, J. Devos, H. M. Rhoda, D. Plessers, E. I. Solomon, R. A. Schoonheydt, B. F. Sels and M. Dusselier, J. Am. Chem. Soc., 2021, 143, 16243–16255 CrossRef CAS PubMed.
- R. Zhang, E. Anderst, K. Groden and J.-S. McEwen, Ind. Eng. Chem. Res., 2018, 57, 13396–13405 CrossRef CAS.
- C. Paolucci, A. A. Parekh, I. Khurana, J. R. Di Iorio, H. Li, J. D. Albarracin Caballero, A. J. Shih, T. Anggara, W. N. Delgass, J. T. Miller, F. H. Ribeiro, R. Gounder and W. F. Schneider, J. Am. Chem. Soc., 2016, 138, 6028–6048 CrossRef CAS PubMed.
- R. Garten, W. Delgass and M. Boudart, J. Catal., 1970, 18, 90–107 CrossRef CAS.
- J. Pérez-Ramírez, G. Mul, F. Kapteijn, J. Moulijn, A. Overweg, A. Doménech, A. Ribera and I. Arends, J. Catal., 2002, 207, 113–126 CrossRef.
- G. Li, P. Vassilev, M. Sanchez-Sanchez, J. A. Lercher, E. J. M. Hensen and E. A. Pidko, J. Catal., 2016, 338, 305–312 CrossRef CAS.
- E. A. Pidko, E. J. M. Hensen and R. A. van Santen, Proc. R. Soc. London, Ser. A, 2012, 468, 2070–2086 CAS.
- E. A. Pidko, E. J. M. Hensen, G. M. Zhidomirov and R. A. van Santen, J. Catal., 2008, 255, 139–143 CrossRef CAS.
- E. A. Pidko, R. A. van Santen and E. J. M. Hensen, Phys. Chem. Chem. Phys., 2009, 11, 2893–2902 RSC.
- S. Wang, C. Li, C. Liu and W. Zhuang, ChemCatChem, 2025, 17, e202401416 CrossRef CAS.
- S. A. Bates, A. A. Verma, C. Paolucci, A. A. Parekh, T. Anggara, A. Yezerets, W. F. Schneider, J. T. Miller, W. N. Delgass and F. H. Ribeiro, J. Catal., 2014, 312, 87–97 CrossRef CAS.
- B. R. Goodman, K. C. Hass, W. F. Schneider and J. B. Adams, Catal. Lett., 2000, 68, 85–93 CrossRef CAS.
- R. J. Deeth, Phys. Chem. Chem. Phys., 2024, 26, 18138–18148 RSC.
- R. Zhang, N. Liu, Z. Lei and B. Chen, Chem. Rev., 2016, 116, 3658–3721 CrossRef CAS PubMed.
- V. Lyaskovskyy and B. de Bruin, ACS Catal., 2012, 2, 270–279 CrossRef CAS.
- M. Mitoraj and A. Michalak, J. Mol. Model., 2007, 13, 347–355 CrossRef CAS PubMed.
- A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933–1939 CrossRef CAS PubMed.
- P. Kozyra, E. Broclawik, M. P. Mitoraj and J. Datka, J. Phys. Chem. C, 2013, 117, 7511–7518 CrossRef CAS.
- F. Sagan and M. P. Mitoraj, Non-covalent interactions in selected transition metal complexes. in Transition Metals in Coordination Environments: Computational Chemistry and Catalysis Viewpoints, ed. E. Broclawik, T. Borowski and M. Radoń, Springer International Publishing, Cham, Switzerland, 2019, pp. 65–89 Search PubMed.
- M. P. Mitoraj, F. Sagan, D. W. Szczepanik, J. H. de Lange, A. L. Ptaszek, D. M. E. van Niekerk and I. Cukrowski, ChemPhysChem, 2020, 21, 494–502 CrossRef CAS PubMed.
- Metal-Ligand Interactions: From Atoms, to Clusters, to Surfaces, ed. D. R. Salahub and N. Russo, Springer, Dordrecht, 1990 Search PubMed.
- B. Zouchoune and A. Saiad, Inorg. Chim. Acta, 2018, 473, 204–215 CrossRef CAS.
- Y. Jing, J. Liu, Z. Ye, J. Su, Y. Liu and Z. Ke, Catal. Sci. Technol., 2021, 11, 7189–7199 RSC.
- Y. Gu, Q. Zhu, Z. Liu, C. Fu, J. Wu, Q. Zhu, Q. Jia and J. Ma, J. Mater. Chem. A, 2022, 10, 14976–14988 RSC.
- A. Delabie, K. Pierloot, M. H. Groothaert, B. M. Weckhuysen and R. A. Schoonheydt, Microporous Mesoporous Mater., 2000, 37, 209–222 CrossRef CAS.
- H. Petitjean, C. Chizallet and D. Berthomieu, Ind. Eng. Chem. Res., 2018, 57, 15982–15990 CrossRef CAS.
- P. Sazama, J. Moravkova, S. Sklenak, A. Vondrova, E. Tabor, G. Sadovska and R. Pilar, ACS Catal., 2020, 10, 3984–4002 CrossRef CAS.
- Y. Mao, H.-F. Wang and P. Hu, Int. J. Quantum Chem., 2015, 115, 618–630 CrossRef CAS.
- T. V. W. Janssens, H. Falsig, L. F. Lundegaard, P. N. R. Vennestrøm, S. B. Rasmussen, P. Georg Moses, F. Giordanino, E. Borfecchia, K. A. Lomachenko, C. Lamberti, S. Bordiga, A. Godiksen, S. Mossin and P. Beato, ACS Catal., 2015, 5, 2832–2845 CrossRef CAS.
- C.-Y. Sung, S. Al Hashimi, A. McCormick, M. Cococcioni and M. Tsapatsis, Microporous Mesoporous Mater., 2013, 172, 7–12 CrossRef CAS.
- R. Z. Khaliullin, A. T. Bell and M. Head-Gordon, J. Chem. Phys., 2008, 128, 184112 CrossRef PubMed.
- R. Z. Khaliullin, E. A. Cobar, R. C. Lochan, A. T. Bell and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 8753–8765 CrossRef CAS PubMed.
- A. Daouli, E. P. Hessou, H. Monnier, M.-A. Dziurla, A. Hasnaoui, G. Maurin and M. Badawi, Phys. Chem. Chem. Phys., 2022, 24, 15565–15578 RSC.
- L. Benco and D. Tunega, Phys. Chem. Miner., 2009, 36, 281–290 CrossRef CAS.
- F. Gao, D. Mei, Y. Wang, J. Szanyi and C. H. Peden, J. Am. Chem. Soc., 2017, 139, 4935–4942 CrossRef CAS PubMed.
- L. N. Wilcox, S. H. Krishna, C. B. Jones and R. Gounder, Catal. Sci. Technol., 2021, 11, 7932–7942 RSC.
- M. Colombo, G. Koltsakis, I. Nova and E. Tronconi, Catal. Today, 2012, 188, 42–52 CrossRef CAS.
- F. Giordanino, E. Borfecchia, K. A. Lomachenko, A. Lazzarini, G. Agostini, E. Gallo, A. V. Soldatov, P. Beato, S. Bordiga and C. Lamberti, J. Phys. Chem. Lett., 2014, 5, 1552–1559 CrossRef CAS PubMed.
- I. Lezcano-Gonzalez, U. Deka, B. Arstad, A. Van Yperen-De Deyne, K. Hemelsoet, M. Waroquier, V. Van Speybroeck, B. M. Weckhuysen and A. M. Beale, Phys. Chem. Chem. Phys., 2014, 16, 1639–1650 RSC.
- L. Chen, T. V. W. Janssens, M. Skoglundh and H. Grönbeck, Top. Catal., 2019, 62, 93–99 CrossRef CAS.
- K. Leistner, K. Xie, A. Kumar, K. Kamasamudram and L. Olsson, Catal. Lett., 2017, 147, 1882–1890 CrossRef CAS.
- B. Mozgawa, F. Zasada, M. Fedyna, K. Góra-Marek, E. Tabor, K. Mlekodaj, J. Dědeček, Z. Zhao, P. Pietrzyk and Z. Sojka, Chem. Soc. Rev., 2021, 50, 17159–17180 Search PubMed.
- C. Paolucci, I. Khurana, A. A. Parekh, S. Li, A. J. Shih, H. Li, J. R. Di Iorio, J. D. Albarracin-Caballero, A. Yezerets and J. T. Miller, Science, 2017, 357, 898–903 CrossRef CAS PubMed.
- R. Millan, P. Cnudde, V. Van Speybroeck and M. Boronat, JACS Au, 2021, 1, 1778–1787 CrossRef CAS PubMed.
- R. Millan, E. Bello-Jurado, M. Moliner, M. Boronat and R. Gomez-Bombarelli, ACS Cent. Sci., 2023, 9, 2044–2056 CrossRef CAS PubMed.
- Y. Fu, W. Ding, H. Lei, Y. Sun, J. Du, Y. Yu, U. Simon, P. Chen, Y. Shan, G. He and H. He, J. Am. Chem. Soc., 2024, 146, 11141–11151 CrossRef CAS PubMed.
- A. Martini, C. Negri, L. Bugarin, G. Deplano, R. K. Abasabadi, K. A. Lomachenko, T. V. W. Janssens, S. Bordiga, G. Berlier and E. Borfecchia, J. Phys. Chem. Lett., 2022, 13, 6164–6170 CrossRef CAS PubMed.
- A. Daouli, J. Rey, E. H. Lahrar, V. Valtchev, M. Badawi and R. Guillet-Nicolas, Langmuir, 2023, 39, 15962–15973 CrossRef CAS PubMed.
- V. Zdravkova, M. Mihaylov and K. Hadjiivanov, J. Phys. Chem. C, 2012, 116, 12706–12711 CrossRef CAS.
- A. Itadani, M. Tanaka, T. Mori, M. Nagao, H. Kobayashi and Y. Kuroda, J. Phys. Chem. C, 2007, 111, 12011–12023 CrossRef CAS.
- G. Spoto, S. Bordiga, G. Ricchiardi, D. Scarano, A. Zecchina and F. Geobaldo, J. Chem. Soc., Faraday Trans., 1995, 91, 3285–3290 RSC.
- Y. Kuroda, Y. Yoshikawa, S.-I. Konno, H. Hamano, H. Maeda, R. Kumashiro and M. Nagao, J. Phys. Chem., 1995, 99, 10621–10628 CrossRef CAS.
- J. Datka, P. Kozyra, E. Kukulska-Zając, M. Szutiak and N. Kumar, Stud. Surf. Sci. Catal., 2004, 154B, 1655–1660 CAS.
- A. I. Serykh and M. D. Amiridis, J. Phys. Chem. C, 2007, 111, 17020–17024 CrossRef CAS.
- S. Morpurgo, G. Moretti and M. Bossa, Phys. Chem. Chem. Phys., 2007, 9, 417–424 RSC.
- V. Zdravkova, N. Drenchev, E. Ivanova, M. Mihaylov and K. Hadjiivanov, J. Phys. Chem. C, 2015, 119, 15292–15302 CrossRef CAS.
- G. Frenking, I. Fernández, N. Holzmann, S. Pan, I. Krossing and M. Zhou, JACS Au, 2021, 1, 623–645 CrossRef CAS PubMed.
- E. Mansoor, J. Van der Mynsbrugge, M. Head-Gordon and A. T. Bell, Catal. Today, 2018, 312, 51–65 CrossRef CAS.
- G. Deplano, M. Signorile, C. Atzori, D. de Salusso, E. Borfecchia, V. Crocella and S. Bordiga, Catal. Today, 2024, 427, 114403 CrossRef CAS.
- F. A. Cotton and G. Wilkinson, Advanced Inorganic Chemistry, Wiley, New York, 1980 Search PubMed.
- K. Podolska, Interaction of nickel ions in zeolites with small molecules: spectroscopic investigations and molecular modeling, PhD thesis, Jagiellonian University, 2011 Search PubMed.
- P. Pietrzyk, K. Podolska and Z. Sojka, J. Phys. Chem. C, 2011, 115, 13008–13015 CrossRef CAS.
- P. Pietrzyk, T. Mazur, K. Podolska-Serafin, M. Chiesa and Z. Sojka, J. Am. Chem. Soc., 2013, 135, 15467–15478 CrossRef CAS PubMed.
- K. Hadjiivanov, H. Knozinger and M. Mihaylov, J. Phys. Chem. B, 2002, 106, 2618–2624 CrossRef CAS.
- M. Mihaylov, O. Lagunov, E. Ivanova and K. Hadjiivanov, Top. Catal., 2011, 54, 308–317 CrossRef CAS.
- P. Pietrzyk, K. Podolska and Z. Sojka, J. Phys. Chem. A, 2008, 112, 12208–12219 CrossRef CAS PubMed.
- L. Bonnevoit, D. Olivier and M. Che, J. Mol. Catal., 1983, 21, 415 CrossRef.
- K. Dyrek and M. Che, Chem. Rev., 1997, 97, 305 CrossRef CAS PubMed.
- M. Che, Stud. Surf. Sci. Catal., 1993, 75, 31–68 CrossRef CAS.
- D. Oliver, M. Richard and M. Che, Chem. Phys. Lett., 1978, 60, 77–80 CrossRef.
- K. I. Hadjiivanov and G. N. Vayssilov, Adv. Catal., 2002, 47, 307–511 CAS.
- S. Bordiga, C. Lamberti, F. Bonino, A. Travert and F. Thibault-Starzyk, Chem. Soc. Rev., 2015, 44, 7262–7341 RSC.
- X. Deng, D. Yang, W. Li, Y. Chai, G. Wu and L. Li, Trends Chem., 2023, 5, 892–905 CrossRef CAS.
- G. Busca, V. Lorenzelli and V. Sanchez-Escribano, Chem. Mater., 1992, 4, 595 CrossRef CAS.
- K. Góra-Marek, A. E. Palomares, A. Glanowska, K. Sadowska and J. Datka, Microporous Mesoporous Mater., 2012, 162, 175–180 CrossRef.
- I. Malpartida, E. Ivanova, M. Mihaylov, K. Hadjiivanov, V. Blasin-Aubé, O. Marie and M. Daturi, Catal. Today, 2010, 149, 295–303 CrossRef CAS.
- K. Góra-Marek, K. Brylewska, K. A. Tarach and M. Choi, Dalton Trans., 2015, 44, 8031–8040 RSC.
- M. I. Shilina, T. N. Rostovshchikova, S. A. Nikolaev and O. V. Udalova, Mater. Chem. Phys., 2019, 223, 287–298 CrossRef CAS.
- S. M. Maier, A. Jentys, E. Metwalli, P. Müller-Buschbaum and J. A. Lercher, J. Phys. Chem. Lett., 2011, 2, 950–955 CrossRef CAS.
- E. Ivanova, M. Mihaylov, K. Hadjiivanov, V. Blasin-Aubé, O. Marie, A. Plesniar and M. Daturi, Appl. Catal., B, 2010, 93, 325–338 CrossRef CAS.
- S. S. Goryashenko, Y. K. Park, D. S. Kim and S.-E. Park, Res. Chem. Intermed., 1998, 24, 933–951 CrossRef CAS.
- M. Saeidi and M. Hamidzadeh, Res. Chem. Intermed., 2017, 43, 2143–2157 CrossRef CAS.
- N. B. Younes, J. Martínez Ortigosa, O. Marie, T. Blasco and M. Mhamdi, Res. Chem. Intermed., 2021, 47, 2003–2028 CrossRef.
- Y. Yokomichi, T. Yamabe, T. Kakumoto, O. Okada, H. Ishikawa, Y. Nakamura, H. Kimura and I. Yasuda, Appl. Catal., B, 2000, 28, 1–12 CrossRef CAS.
- M. Anpo, M. Matsuoka, H. Mishima and H. Yamashita, Res. Chem. Intermed., 1997, 23, 197–217 CrossRef CAS.
- G. Brezicki, J. Zheng, C. Paolucci, R. Schlögl and R. J. Davis, ACS Catal., 2021, 11, 4973–4987 CrossRef CAS.
- W. Kaim and B. Schwederski, Coord. Chem. Rev., 2010, 254, 1580–1588 CrossRef CAS.
- P. Xiao, Y. Wang, Y. Lu, K. Nakamura, N. Ozawa, M. Kubo, H. Gies and T. Yokoi, J. Am. Chem. Soc., 2024, 146, 10014–10022 CrossRef CAS PubMed.
- M. J. Wulfers, S. Teketel, B. Ipek and R. F. Lobo, Chem. Commun., 2015, 51, 4447–4450 RSC.
- A. R. Kulkarni, Z.-J. Zhao, S. Siahrostami, J. K. Nørskov and F. Studt, Catal. Sci. Technol., 2018, 8, 114–123 RSC.
- A. A. Verma, S. A. Bates, T. Anggara, C. Paolucci, A. A. Parekh, K. Kamasamudram, A. Yezerets, J. T. Miller, W. N. Delgass, W. F. Schneider and F. H. Ribeiro, J. Catal., 2014, 312, 179–190 CrossRef CAS.
- M. Moreno-González, R. Millán, P. Concepción, T. Blasco and M. Boronat, ACS Catal., 2019, 9, 2725–2738 CrossRef.
- C. Liu, G. Malta, H. Kubota, T. Toyao, Z. Maeno and K.-I. Shimizu, J. Phys. Chem. C, 2021, 125, 21975–21987 CrossRef CAS.
- X. Guo, R. Zhang, Z. Di, B. Kang, H. Shen, Y. Wei, J. Jia and L. Zheng, Appl. Catal., B, 2024, 343, 123519 CrossRef CAS.
- J. H. Enemark and R. D. Feltham, Coord. Chem. Rev., 1974, 13, 339–406 CrossRef CAS.
- W. Kaim and B. Schwederski, Coord. Chem. Rev., 2010, 254, 1580–1588 CrossRef CAS.
- C. J. Cramer, M. Włoch, P. Piecuch, C. Puzzarini and L. Gagliardi, J. Phys. Chem. A, 2006, 110, 1991–2004 CrossRef CAS PubMed.
- P. Vanelderen, R. G. Hadt, P. J. Smeets, E. I. Solomon, R. A. Schoonheydt and B. F. Sels, J. Catal., 2011, 284, 157–164 CrossRef CAS PubMed.
- J. S. Woertink, P. J. Smeets, M. H. Groothaert, M. A. Vance, B. F. Sels, R. A. Schoonheydt and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18908–18913 CrossRef CAS PubMed.
- L. Vilella and F. Studt, Eur. J. Inorg. Chem., 2016, 1514–1520 CrossRef CAS.
- A. Oda, Y. Mamenari, T. Ohkubo and Y. Kuroda, J. Phys. Chem. C, 2019, 123, 17842–17854 CrossRef CAS.
- I. A. Pankin, A. Martini, K. A. Lomachenko, A. V. Soldatov, S. Bordiga and E. Borfecchia, Catal. Today, 2020, 345, 125–135 CrossRef CAS.
- G. Yang, L. Zhou, X. Liu, X. Han and X. Bao, Catal. Commun., 2007, 8, 1981–1984 CrossRef CAS.
- C. J. Cramer and W. B. Tolman, Acc. Chem. Res., 2007, 40, 601–608 CrossRef CAS PubMed.
- K. Sobańska, A. Krasowska, T. Mazur, K. Podolska-Serafin, P. Pietrzyk and Z. Sojka, Top. Catal., 2015, 58, 796–810 CrossRef.
- A. Oda, H. Torigoe, A. Itadani, T. Ohkubo, T. Yumura, H. Kobayashi and Y. Kuroda, J. Am. Chem. Soc., 2013, 135, 18481–18489 CrossRef CAS PubMed.
- R. F. Howe and J. H. Lunsford, J. Am. Chem. Soc., 1975, 97, 5156–5159 CrossRef CAS.
- A. Oda, T. Ohkubo, T. Yumura, H. Kobayashi and Y. Kuroda, Angew. Chem., Int. Ed., 2017, 56, 9715–9718 CrossRef CAS PubMed.
- A. Oda, J. Kumagai, K. Sawabe, T. Ohkubo, Y. Kuroda and A. Satsuma, J. Phys. Chem. C, 2021, 125, 5136–5145 CrossRef CAS.
- P. Pietrzyk and K. Góra-Marek, Phys. Chem. Chem. Phys., 2016, 18, 9490–9496 RSC.
- Z. Sojka, E. Giamello, M. Che, A. Zecchina and K. Dyrek, J. Phys. Chem., 1988, 92, 1541–1547 CrossRef CAS.
- A. Oda, T. Nanjo, T. Ohkubo and Y. Kuroda, J. Phys. Chem. C, 2020, 124(21), 11544–11557 CrossRef CAS.
- S. Yao, E. Bill, C. Milsmann, K. Wieghardt and M. A. Driess, Angew. Chem., Int. Ed., 2008, 47, 7110–7113 CrossRef CAS PubMed.
- E. Kimura, R. Machida and M. Kodama, J. Am. Chem. Soc., 1984, 106, 5497–5505 CrossRef CAS.
- L. Chen, H. Falsig, T. V. W. Janssens and H. Grönbeck, J. Catal., 2018, 358, 179–186 CrossRef CAS.
- C. Negri, T. Selleri, E. Borfecchia, A. Martini, K. A. Lomachenko, T. V. W. Janssens, M. Cutini, S. Bordiga and G. Berlier, J. Am. Chem. Soc., 2020, 142, 15884–15896 CrossRef CAS PubMed.
- M. H. Mahyuddin, T. Tanaka, A. Staykov, Y. Shiota and K. Yoshizawa, Inorg. Chem., 2018, 57, 10146–10152 CrossRef CAS PubMed.
- H. Li, C. Paolucci, I. Khurana, L. N. Wilcox, F. Göltl, J. D. Albarracin-Caballero, A. J. Shih, F. H. Ribeiro, R. Gounder and W. F. Schneider, Chem. Sci., 2019, 10, 2373–2384 RSC.
- K. Shimizu, R. Maruyama, T. Hatamachi and T. Kodama, J. Phys. Chem. C, 2007, 111, 6440–6446 CrossRef CAS.
- A. B. Ene, M. Bauer, T. Archipova and E. Roduner, Phys. Chem. Chem. Phys., 2010, 12, 6520–6531 RSC.
- T. Yumura, M. Takeuchi, H. Kobayashi and Y. Kuroda, Inorg. Chem., 2009, 48, 508–517 CrossRef CAS PubMed.
- A. Kornas, E. Tabor, D. K. Wierzbicki, J. E. Olszowka, R. Pilar, J. Dedecek, M. Śliwa, H. Jirglova, S. Sklenak, D. Rutkowska-Żbik and K. Mlekodaj, Appl. Catal., B, 2023, 336, 122915 CrossRef CAS.
- E. Tabor, M. Lemishka, J. E. Olszowka, K. Mlekodaj, J. Dedecek, P. C. Andrikopoulosk and S. Sklenak, ACS Catal., 2021, 11, 2340–2355 CrossRef CAS.
- X. Yang, Z. Liu, B. Gao, Z. Chen, K. Yan, S. Wang, Y. Xia, Y. Zhang, L. Wang, X. Xu and Y. Tang, ACS Catal., 2023, 13, 15572–15580 CrossRef CAS.
- T. V. W. Janssens, E. Borfecchia, K. A. Lomachenko, H. Grönbeck and G. Berlier, ChemCatChem, 2024, 16, e202400384 CrossRef CAS.
- P. J. Smeets, R. G. Hadt, J. S. Woertink, P. Vanelderen, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, J. Am. Chem. Soc., 2010, 132, 14736–14738 CrossRef CAS PubMed.
- H. M. Rhoda, A. J. Heyer, B. E. R. Snyder, D. Plessers, M. L. Bols, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Chem. Rev., 2022, 122, 12207–12243 CrossRef CAS PubMed.
- C. Liu, H. Kubota, T. Toyao, Z. Maeno and K. Shimizu, Catal. Sci. Technol., 2020, 10, 3586–3593 RSC.
- H. Lei, D. Chen, J.-Y. Yang, A. Khetan, J. Jiang, B. Peng, U. Simon, D. Ye and P. Chen, Environ. Sci. Technol., 2023, 57, 12465–12475 CrossRef CAS PubMed.
- I. Karamanis, A. Daouli, H. Monnier, M.-A. Dziurla, G. Maurin and M. Badawi, Mol. Syst. Des. Eng., 2023, 8, 1165–1181 RSC.
- P. Pietrzyk, C. Dujardin, K. Góra-Marek, P. Granger and Z. Sojka, Phys. Chem. Chem. Phys., 2012, 14, 2203–2215–144 RSC.
- P. Pietrzyk, F. Zasada, W. Piskorz, A. Kotarba and Z. Sojka, Catal. Today, 2007, 119, 219–227 CrossRef CAS.
- Past and Present in DeNOx Catalysis: From Molecular Modeling to Chemical Engineering, in Stud. Surf. Sci. Catal., ed. P. Granger and V. I. Parvulescu, 2007, vol. 171, pp. 27–65 Search PubMed.
- K. Hadjiivanov, Catal. Rev.:Sci. Eng., 2000, 42, 71–144 CrossRef CAS.
- P. Pietrzyk, W. Piskorz, Z. Sojka and E. Brocławik, J. Phys. Chem. B, 2003, 107, 6105–6113 CrossRef CAS.
- P. Pietrzyk and Z. Sojka, J. Phys. Chem. A, 2005, 109, 10571–10581 CrossRef CAS PubMed.
- A. M. Volodin, K. A. Dubkov and A. Lund, Chem. Phys. Lett., 2001, 333, 41–44 CrossRef CAS.
- R. Pérez Vélez, I. Ellmers, H. Huang, U. Bentrup, V. Schünemann, W. Grünert and A. Brückner, J. Catal., 2014, 316, 103–111 CrossRef.
- S. Malykhin, A. Volodin and G. Zhidomirov, Appl. Magn. Reson., 2008, 33, 153–166 CrossRef CAS.
- Z. Sojka, P. Pietrzyk, G. Martra, M. Kermarec and M. Che, Catal. Today, 2006, 114, 154–161 CrossRef CAS.
- C. W. Bauschlicher Jr., S. R. Langhoff and H. J. Partridge, J. Chem. Phys., 1991, 94, 2068–2072 CrossRef.
- V. Umamaheswari, M. Hartmann and A. Pöppl, J. Phys. Chem. B, 2005, 109, 1537–1546 CrossRef CAS PubMed.
- E. Brocławik, P. Kozyra, M. Mitoraj, M. Radoń and P. Rejmak, Molecules, 2021, 26, 1511 CrossRef PubMed.
- P. Kozyra, M. Radoń, J. Datka and E. Broclawik, Struct. Chem., 2012, 23, 1349–1356 CrossRef CAS.
- M. Radoń, P. Kozyra, A. Stępniewski, J. Datka and E. Broclawik, Can. J. Chem., 2013, 91, 538–543 CrossRef.
- K. Góra-Marek, A. Stępniewski, M. Radoń and E. Brocławik, Phys. Chem. Chem. Phys., 2014, 16, 24089–24098 RSC.
- F. Göltl and J. Hafner, J. Chem. Phys., 2012, 136, 064503 CrossRef PubMed.
- P. Rejmak, E. Broclawik, K. Góra-Marek, M. Radoń and J. Datka, J. Phys. Chem. C, 2008, 112, 17998–18010 CrossRef CAS.
- E. Broclawik, K. Góra-Marek, M. Radoń, M. Bucko and A. Stępniewski, J. Mol. Model., 2017, 23, 160 CrossRef CAS PubMed.
- M. Radoń, Inorg. Chem., 2015, 54, 5634–5645 CrossRef PubMed.
- F. Neese, J. Biol. Inorg. Chem., 2006, 11, 702–711 CrossRef CAS PubMed.
- M. Radoń and E. Broclawik, Electronic properties of iron sites and their active forms in porphyrin-type architectures, in Computational methods to study the structure and dynamics of biomolecules and biomolecular processes – from bioinformatics to molecular quantum mechanics, ed. A. Liwo, Springer International Publishing, Cham, 2019, pp. 755–823 Search PubMed.
- M. Kaupp, J. Comput. Chem., 2007, 28, 320–325 CrossRef CAS PubMed.
- G. Monsch and P. Klüfers, Angew. Chem., Int. Ed., 2019, 58, 8566–8571 CrossRef CAS PubMed.
- N. C. Tomson, M. R. Crimmin, T. Petrenko, L. E. Rosebrugh, S. Sproules, W. C. Boyd, R. G. Bergman, S. DeBeer, F. D. Toste and K. Wieghardt, J. Am. Chem. Soc., 2011, 133, 18785–18801 CrossRef CAS PubMed.
- Q. M. Phung, H. N. Nam, V. Austen, T. Yanai and A. Ghosh, Inorg. Chem., 2025, 64, 1702–1710 CrossRef CAS PubMed.
- P. Karen, Angew. Chem., Int. Ed., 2015, 54, 4716–4726 CrossRef CAS PubMed.
- T. Ampßler, G. Monsch, J. Popp, T. Riggenmann, P. Salvador, D. Schröder and P. Klüfers, Angew. Chem., Int. Ed., 2020, 59, 12381–12386 CrossRef PubMed.
- M. Gimferrer, J. Van der Mynsbrugge, A. T. Bell, P. Salvador and M. Head-Gordon, Inorg. Chem., 2020, 59, 15410–15420 CrossRef CAS PubMed.
- P. Pietrzyk, B. Gil and Z. Sojka, Catal. Today, 2007, 126, 103–111 CrossRef CAS.
- A. Pulido and P. Nachtigall, Phys. Chem. Chem. Phys., 2009, 11, 1447–1458 RSC.
- M. Radoń and E. Bocławik, J. Phys. Chem. A, 2011, 115, 11761–11774 CrossRef PubMed.
- R. Lin and P. J. Farmer, J. Am. Chem. Soc., 2001, 123, 1143–1150 CrossRef CAS PubMed.
- I. M. Wasser, S. de Vries, P. Moënne-Loccoz, I. Schröder and K. D. Karlin, Chem. Rev., 2002, 102, 1201–1234 CrossRef CAS PubMed.
- P. Xie, T. Pu, G. Aranovich, J. Guo, M. Donohue, A. Kulkarni and C. Wang, Nat. Catal., 2021, 4, 144–156 CrossRef CAS.
- G. B. Richter-Addo and P. Legzdins, Metal Nitrosyls, Oxford University Press, New York, 1992 Search PubMed.
- K. M. Farhan and P. K. Sajith, Ind. Eng. Chem. Res., 2025, 64, 5257–5268 CrossRef CAS.
- M.-L. Tsai, R. G. Hadt, P. Vanelderen, B. F. Sels, R. A. Schoonheydt and E. I. Solomon, J. Am. Chem. Soc., 2014, 136, 3522–3529 CrossRef CAS PubMed.
- A. Wijerathne, A. Sawyer, R. Daya and C. Paolucci, J. Am. Chem. Soc. Au, 2024, 4, 197–215 CAS.
- A. R. Fahami, T. Günter, D. E. Doronkin, M. Casapu, D. Zengel, T. H. Vuong, M. Simon, F. Breher, A. V. Kucherov, A. Brückner and J.-D. Grunwaldt, React. Chem. Eng., 2019, 4, 1000–1018 RSC.
- L. Chen, T. V. W. Jansen, P. N. R. Vennestrom, J. Jansson, M. Skoglundh and H. A. Grönbeck, ACS Catal., 2020, 10, 5646–5656 CrossRef CAS.
- M. Bendrich, A. Scheuer, R. E. Hayes and M. Votsmeier, Appl. Catal., B, 2018, 222, 76–87 CrossRef CAS.
- W. Hu, T. Selleri, F. Gramigni, E. Fenes, K. R. Rout, S. Liu, I. Nova, D. Chen, X. Gao and E. Tronconi, Angew. Chem., Int. Ed., 2021, 60, 7197–7204 CrossRef CAS PubMed.
- C. Liu, H. Kubota, T. Amada, K. Kon, T. Toyao, Z. Maeno, K. Ueda, J. Ohyama, A. Satsuma, T. Tanigawa, N. Tsunoji, T. Sano and K.-I. Shimizu, ChemCatChem, 2020, 12, 3050–3059 CrossRef CAS.
- W. Hu, F. Gramigni, N. D. Nasello, N. Usberti, U. Iacobone, S. Liu, I. Nova, X. Gao and E. Tronconi, ACS Catal., 2022, 12, 5263–5274 CrossRef CAS.
- R. Daya, D. Trandal, U. Menon, D. J. Deka, W. P. Partridge and S. Y. Joshi, ACS Catal., 2022, 12, 6418–6433 CrossRef CAS.
- C. Liu, H. Kubota, T. Toyao, Z. Maeno and K.-I. Shimizu, Catal. Sci. Technol., 2020, 10, 3586–3593 RSC.
- A. Oda, H. Shionoya, Y. Hotta, T. Takewaki, K. Sawabe and A. Satsuma, ACS Catal., 2020, 10, 12333–12339 CrossRef CAS.
- C. Paolucci, A. A. Verma, S. A. Bates, V. F. Kispersky, J. T. Miller, R. Gounder, W. N. Delgass, F. H. Ribeiro and W. F. Schneider, Angew. Chem., Int. Ed., 2014, 53, 11828–11833 CrossRef CAS PubMed.
- M. P. Ruggeri, I. Nova, E. Tronconi, J. A. Pihl, T. J. Toops and W. P. Partridge, Appl. Catal., B, 2015, 166–167, 181–192 CrossRef CAS.
- H.-Y. Chen, M. Kollar, Z. Wei, F. Gao, Y. Wang, J. Szanyi and C. H. F. Peden, Catal. Today, 2019, 320, 61–71 CrossRef CAS.
- Y. Zhang, Y. Peng, K. Li, S. Liu, J. Chen, J. Li, F. Gao and C. H. F. Peden, ACS Catal., 2019, 9, 6137–6145 CrossRef CAS.
- L. Negahdar, N. E. Omori, M. G. Quesne, M. D. Frogley, F. Cacho-Nerin, W. Jones, W. T. Price, R. A. Catlow and A. M. Beale, ACS Catal., 2021, 11, 13091–13101 CrossRef CAS.
- F. Gao, E. D. Walter, M. Kollar, Y. L. Wang, J. Szanyi and C. H. F. Peden, J. Catal., 2014, 319, 1–14 CrossRef CAS.
- C. Liu, S. Yasumura, T. Toyao, Z. Maeno and K.-I. Shimizu, J. Phys. Chem. C, 2022, 126, 11594–11601 CrossRef CAS.
- F. Lin, T. Andana, Y. Wu, J. Szanyi, Y. Wanga and F. Gao, J. Catal., 2021, 401, 70–80 CrossRef CAS.
- G. He, B. Zhang, H. He, X. Chen and Y. Shan, Sci. Total Environ., 2019, 673, 266–271 CrossRef CAS PubMed.
- B. Zhang, G. He, Y. Shan and H. He, Catal. Today, 2019, 327, 177–181 CrossRef CAS.
- W. B. Tolman, Angew. Chem., Int. Ed., 2010, 49, 1018–1024 CrossRef CAS PubMed.
- V. I. Avdeev and A. F. Bedilo, Chem. Phys. Lett., 2018, 695, 222–227 CrossRef CAS.
- D. Sengupta, J. B. Adams, W. F. Schneider and K. C. Hass, Catal. Lett., 2001, 74, 193–199 CrossRef CAS.
- P. Xiao, Y. Wang, Y. Lu, K. Nakamura, N. Ozawa, M. Kubo, H. Gies and T. Yokoi, J. Am. Chem. Soc., 2024, 146, 10014–10022 CrossRef CAS PubMed.
- Z. Sojka and M. Che, J. Phys. Chem., 1996, 100, 14776–14785 CrossRef CAS.
- L. Nowakowski, C. Hudy, F. Zasada, J. Gryboś, W. Piskorz, A. Wach, Y. Kayser, J. Szlachetko and Z. Sojka, J. Am. Chem. Soc., 2024, 146, 24450–24466 CrossRef CAS PubMed.
- G. Li, E. A. Pidko, I. A. W. Filot, R. A. van Santen, C. Li and E. J. M. Hensen, J. Catal., 2013, 308, 386–397 CrossRef CAS.
- H. Xia, K. Sun, K. Sun, Z. Feng, W. X. Li and C. Li, J. Phys. Chem. C, 2008, 112, 9001–9005 CrossRef CAS.
- E. V. Kondratenko and J. Perez-Ramırez, J. Phys. Chem. B, 2006, 110, 22586–22595 CrossRef CAS PubMed.
- C. Sang, B. H. Kim and C. R. F. Lund, J. Phys. Chem. B, 2005, 109, 2295–2301 CrossRef CAS PubMed.
- Z. Sobalik, J. Novakova, J. Dedecek, N. K. Sathu, E. Tabor, P. Sazama, P. Stastny and B. Wichterlova, Microporous Mesoporous Mater., 2011, 146, 172–183 CrossRef CAS.
- Z. Piwowarska, E. Micek, M. Rutkowska and L. Chmielarz, Microporous Mesoporous Mater., 2015, 209, 54–65 CrossRef.
- D. Pietrogiacomi, M. C. Campa, L. R. Carbone and M. Occhiuzzi, Appl. Catal., B, 2019, 240, 19–29 CrossRef CAS.
- K. Jíša, J. Nováková, M. Schwarze, A. Vondrová, S. Sklenák and Z. Sobalik, J. Catal., 2009, 262, 27–34 CrossRef.
- B. M. Abu-Zied, W. Schwieger and A. Unger, Appl. Catal., B, 2008, 84, 277–288 CrossRef CAS.
- F. Kapteijn, G. Marban, J. Rodriguez-Mirasol and J. A. Moulijn, J. Catal., 1997, 167, 256–265 CrossRef CAS.
- A. Li, P. Wang, L. Zhang, H. Zhao, M. Jin and L. Lei, Fuel, 2024, 378, 132888 CrossRef CAS.
- P. J. Smeets, M. H. Groothaert, R. M. van Teeffelen, H. Leeman, E. J. M. Hensen and R. A. Schoonheydt, J. Catal., 2007, 245, 358–368 CrossRef CAS.
- B. Kang, R. Zhang, M. Guo, X. Guo, Z. Di, Y. Wei and J. Jia, Energy Fuels, 2023, 37, 18019–18029 CrossRef CAS.
- J. W. A. Fischer, F. Buttignol, A. Brenig, D. Klose, D. Ferri, V. Sushkevich, J. A. van Bokhoven and G. Jeschke, Catal. Today, 2024, 429, 114503 CrossRef CAS.
- A. P. Hawkins, A. E. Edmeades, C. D. M. Hutchison, M. Towrie, R. F. Howe, G. M. Greetham and P. M. Donaldson, Chem. Sci., 2024, 15, 3453–3465 RSC.
- K. Mitsuishi, K. Nakazawa, R. Sagawa, M. Shimizu, H. Matsumoto, H. Shima and T. Takewaki, Sci. Rep., 2023, 13, 316 CrossRef CAS PubMed.
- D. Liu, L. Liu, K. Wu, J. Zhou, Q. Cheng, J. Lv, T. Cao, D. Zhang, F. Lin and Y. Han, J. Phys. Chem. C, 2021, 125, 18952–18960 CrossRef CAS.
- C. H. Hendon, A. J. Rieth, M. D. Korzyński and M. Dinca, ACS Cent. Sci., 2017, 3, 554–563 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |