Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
DPD simulations of anionic surfactant micelles: a critical role for polarisable water models†
Rachel L.
Hendrikse
 *a,
Carlos
Amador
b and
Mark R.
Wilson
*a,
Carlos
Amador
b and
Mark R.
Wilson
 a
a
aDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK. E-mail: rachel.hendrikse@durham.ac.uk
bProcter and Gamble, Newcastle Innovation Centre, Whitley Road, Newcastle upon Tyne, NE12 9BZ, UK
First published on 13th September 2024
Abstract
We investigate the effects of polarisable water models in dissipative particle dynamics (DPD) simulations, focussing on the influence these models have on the aggregation behaviour of sodium dodecyl sulfate solutions. Studies in the literature commonly report that DPD approaches underpredict the micellar aggregation number of ionic surfactants compared to experimental values. One of the proposed reasons for this discrepancy is that existing water models are insufficient to accurately model micellar solutions, as they fail to account for structural changes in water close to micellar surfaces. We show that polarisable DPD water models lead to more realistic counterion behaviour in micellar solutions, including the degree of counterion disassociation. These water models can also accurately reproduce changes in the dielectric constant of surfactant solutions as a function of concentration. We find evidence that polarisable water leads to the formation of more stable micelles at higher aggregation numbers. However, we also show that the choice of water model is not responsible for the underestimated aggregation numbers observed in DPD simulations. This finding addresses a key question in the literature surrounding the importance of water models in DPD simulations of ionic micellar solutions.
1 Introduction
Since its inception, DPD has found widespread use in the simulation of complex and computationally demanding soft matter systems, including polymer and surfactant solutions.1–12 DPD allows for significantly faster equilibration time than traditional molecular dynamics (MD) approaches, making it particularly applicable to systems where spontaneous aggregation occurs: such as micellar solutions,1–6 lyotropic liquid crystals,6,12–15 and chromonic mesophases16,17 or systems where complex molecular self-organisation occurs.18–20 In this paper, we study the aggregation behaviour of the well-known anionic surfactant sodium dodecyl sulfate (SDS) using DPD, and address one of the key weaknesses of standard DPD approaches: the inability to predict the correct dielectric behaviour of aqueous solutions.SDS has been the focus of many experimental studies across literature, due to its widespread use in commercial products, particularly in personal care products. Aqueous SDS solutions are arguably one of the most studied systems in surfactant research. This is particularly true of the micellar phase,21–33 although higher concentration liquid phases have also been extensively characterised.34–36 Much of the literature dedicated to micellar solutions has focused on determining the shape, size, and structure of micelles, as well as looking at the impact of variables such as salt,23–25,27–29 temperature,29–31 and concentration.26–29,31–33 Other research has looked at the impact of mixing surfactants with other components such as other surfactants,22,24,26,30 to understand the changes this may produce in micellar properties. However, despite the abundance of SDS studies in literature, experimental data can often be difficult to interpret as studies can often conflict with each other. In particular, different experimental approaches usually lead to different conclusions surrounding the size and shape of SDS micelles, complicating our understanding of these systems.
Due to the difficulties associated with interpreting experimental data, as highlighted above, SDS has also been the focus of numerous existing theoretical and modelling studies. Such studies can help provide insight where experiments may struggle. Theoretical thermodynamic models have been used to predict the properties of micelle solutions using the free energy of formation of an aggregate in solution.37–40 These models can be used to predict the critical micelle concentration (CMC), and the average expected size and shape of aggregates. Simulation studies range from detailed all-atom MD approaches,41–45 to those using coarse-grained approaches such as DPD.1–5 Here, MD simulations are typically limited to studying very small systems and are often prohibitively computationally expensive for studying systems consisting of multiple micelles, or for studying the aggregation process itself. This makes it desirable to develop accurate DPD modelling techniques to allow one to study far larger systems at longer time scales using a simulation approach. Other approaches to predicting surfactant properties include field-based approaches such as self-consistent field theory.46–48
There are several existing studies using DPD to study SDS solutions. However, most of these studies have taken the traditional DPD approach:4,5i.e., simulations are carried out with an uncharged model in which explicit electrostatic interactions are not included. The first attempt to model SDS with explicit electrostatics was presented by Mao et al.,2 which was followed a few years later by Anderson et al.3 Both models were found to significantly underestimate the aggregation number in comparison to experimental values. Potential reasons proposed by the authors for this discrepancy include equilibration issues,3 inadequate calculation of the short-range repulsion parameters,2,3 and the treatment of charged particles.2
One interesting suggestion made by both sets of authors,2,3 is that underpredicted aggregation numbers may result from the typical treatment of water in DPD. Specifically, coarse-grained simulation techniques such as DPD are typically performed using a constant dielectric constant across the simulation box. This approach may be inadequate for taking into account the structural changes of water near charged surfaces, such as those seen with a charged micelle.49–51 We propose that this may result in the degree of counterion dissociation being artificially inflated, and causing smaller micelle sizes. A change in counterion dissociation is also highly likely to influence micelle-micelle interactions. In this article, we aim to address this suggestion by making use of a polarisable water model.
Very few polarisable water models for DPD have been proposed in the existing literature. Existing models are those presented by Peter and Pivkin,52 Peter et al.,53 Vaiwala et al.54 and, most recently, Chiacchiera et al.55 In this paper, we begin by presenting a study of these existing models for the purpose of applying them to micellar solutions. However, we show that the Peter and Pivkin52 and Peter et al.53 models do not reproduce the dielectric constants that they claim to, and instead produce dielectric constant values for water which are much lower than the experimental values. Therefore, we base our polarisable water model on the work of Vaiwala et al.54 To the best of our knowledge, this is the first attempt at modelling ionic micelles using DPD with a polarisable water model.
2 Dissipative particle dynamics
2.1 Overview of forces
DPD is a coarse-grained simulation method in which groups of atoms are represented by soft ‘beads’. The relative softness of the interbead forces allows for long time steps, enhanced diffusion, and faster equilibration times in comparison to both atomistic and coarse-grained molecular dynamics.The total force acting on bead i can be written as a sum of contributing forces from bonded and non-bonded components:
 | (1) |
 | (2) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = rij/|rij|. The dissipative and random forces are given by the following expressions
ij = rij/|rij|. The dissipative and random forces are given by the following expressionsFDij = −γωD(rij)(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij·vij) ij·vij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (3) |
FRij = σωR(rij)ζij![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ijΔt−1/2, ijΔt−1/2, | (4) |
| ωD = [ωR]2 | (5) |
| σ2 = 2γkBT, | (6) |
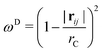 | (7) |
 | (8) |
 | (9) |
The rC parameter serves as a means for converting DPD length scales into real units. A value for rC is usually calculated by matching the density of water simulated to the density of water experimentally at room temperature. This is dependent on the choice of bead density ρD and the degree of coarse graining used for water NC. We take the conventional choice of ρD = 3rC−3, resulting in rC being determined by the expression
 | (10) |
2.2 Electrostatics in DPD
Electrostatics are implemented using smeared charges to avoid artificial ion pair formation. This has become the standard approach for DPD simulations.2,3,54,58 Various forms of the smearing function have been proposed in the literature,59 including a linear charge distribution, where the charge distribution ρ(r) is given as | (11) |
 | (12) |
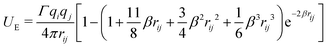 | (13) |
 | (14) |
We base our polarisable water model on the work of Vaiwala et al.,54 who used a linear charge distribution function (with R = 1.6rC, as suggested by Groot58). However, the surfactant models we use were originally tested using the Slater-type charge density distribution. These parameterisations were calculated by Anderson et al.3 (using β = 0.929rC, as suggested by González-Melchor et al.60) and Mao et al.2 (using β = 4rC). The R = 1.6rC and β = 0.929rC choices for the linear and Slater smearing result in nearly identical electrostatic potentials, and in particular the Slater-type potential with β = 0.929rC has been used extensively throughout the literature. Consequently, throughout this work, we chose to use the Slater-type potential with β = 0.929rC. Noting that a slight variation of electrostatic treatment from the original Vaiwala et al. paper may result in very slight differences in results compared to those originally published.
3 Polarisable water model and calculating the dielectric constant
The polarisable water model used is based on the work of Vaiwala et al.54 and is illustrated in Fig. 1. We note in passing the similarity of this model to the polarisable Martini model and variants61–64 that are commonly used in coarse-grained models of biological65,66 and soft-matter systems.64 It is also noted that an interesting alternative is provided by a charged dimer model, such as discussed in the recent work of Chiacchiera.55 In Fig. 1, water particles are treated as Drude oscillators with a central water bead (W) and two attached oppositely charged beads (D). The central bead represents multiple water molecules (2 or 4 waters in this work - see Section 4). It is important to note that beads that are directly bonded do not interact with each other (i.e. the central water bead and Drude beads do not interact with each other through space when they belong to the same particle). Drude beads (D) interact with the Drude beads of another particle via the dissipative, random and electrostatic forces, but do not interact via the conservative force. Central water beads (W) interact via all forces except the electrostatic force. These force interactions are summarised in Table 1.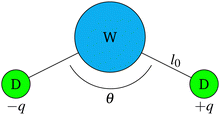 | ||
| Fig. 1 Model for polarisable water particles. Each particle is made up of a central water bead (W) attached to two charged Drude beads (D) possessing charges ±q. | ||
| F C ij | F Dij | F R ij | F E ij | F B ij | F A ij | |
|---|---|---|---|---|---|---|
| W–W | ✓ | ✓ | ✓ | |||
| W–D (intra) | ✓ | ✓ | ||||
| W–D (inter) | ✓ | ✓ | ||||
| D–D (intra) | ✓ | |||||
| D–D (inter) | ✓ | ✓ | ✓ |
The total mass of the water particle is m, where the central water bead has mass 2m/3 and each of the Drude beads has mass m/6. In practice, reduced units are used where the DPD particle mass m = 1. The bond between Drude beads and water beads is controlled by eqn (8), where the length of the bond is set as l0 = 0.35rC, and the strength is set by C = 512kBT/rC2. The angle between the bonded beads (D–W–D angle) is controlled by eqn (9) where the equilibrium bond angle θ0 = 0 and D = 1kBT/rad2. These parameter choices are based on the work of Vaiwala et al.54 It is important to note that although the Drude beads do not interact within their own particle, we observe that there is no effect on the temperature control because of this. All beads are thermalized by collisions in the system, and we find no difference in the temperature of individual beads across the simulation.
The relative permittivity (dielectric constant) of the solvent εr is calculated using classical Fröhlich–Kirkwood theory,67,68 using the fluctuations of the total dipole moment M
 | (15) |
 where q is the Drude charge, NW is the number of water particles, and rk+ and rk− are the positions of the positively and negatively charged Drude beads. Note that in the absence of an external field, we expect that 〈M〉2 = 0.
where q is the Drude charge, NW is the number of water particles, and rk+ and rk− are the positions of the positively and negatively charged Drude beads. Note that in the absence of an external field, we expect that 〈M〉2 = 0.
Similarly to Vaiwala et al.,54 we chose to set εs = 2. Since alkanes tend to possess a dielectric constant value ≈2,69 this choice reasonably reproduces the dielectric screening of the micelle core. Therefore, to reproduce the correct relative permittivity for water, we aim for a target value of εr/εs = 78.3/2 ≈ 39.2.
Vaiwala et al.54 base their water parameterisation on a mapping of four water molecules per DPD bead. The model is parameterised to reproduce the compressibility of water at room temperature and relative dielectric permittivity. The compressibility of the fluid is primarily influenced by the choice of aWW. To reproduce the compressibility of water at room temperature, the conservative repulsion for water beads aWW is typically defined as aWW ≈ 25NCkBT/rC, where NC is the degree of coarse graining. Using this relation, Vaiwala et al.54 choose to set aWW = 100.
The relative dielectric permittivity is largely influenced by the choice of Drude charge q and the equilibrium bond length l0. In the following sections, we discuss surfactant parameterisations based on the use of different values of aWW, and therefore we simulate using the same aWW values that the surfactant parameterisations were based on. In theory, deviating from aWW = 100 also influences the calculated dielectric constant (in addition to l0 and q). However, we will show that the dielectric constant calculated is largely independent of aWW.
4 Surfactant models
We apply the polarisable water model (discussed in the previous section) to solutions containing micelles formed by sodium dodecyl sulfate (SDS). We investigate the effect of the polarisable water on two different parameterisations of SDS. The first of these models was developed by Mao et al.,2 which was also one of the first models of SDS in DPD to explicitly include electrostatic charges. The second of these models is that developed by Anderson et al.3 The coarse graining of SDS used in both of these parameterisation schemes is illustrated in Fig. 2. | ||
| Fig. 2 Coarse-graining used in the (a) Mao et al.2 and (b) Anderson et al.3 parameterisation schemes of SDS. Beads are coloured according to type. | ||
In the scheme developed by Mao et al.,2 the aij interaction values were determined by mapping to experimental values for the solvent compressibility and infinite dilution activity coefficient. Furthermore, the bond parameters were also parameterised via matching to atomistic molecular dynamics calculations. In this scheme, they coarse-grain water beads to four water molecules (NC = 4). In the Anderson et al.3 scheme, the authors vary both the interaction value aij and the bead cut-offs rC in their parameterisation. Their parameters are fit to a combination of mutual solubilities, partition coefficients, and molar volumes (densities). They choose to coarse grain water beads in terms of two water molecules (NC = 2).
While both of these models were found in their original articles to do a reasonably good job of predicting the CMC value, they were also both found to underpredict the aggregation number when compared to experimental data. At a concentration of 7 wt%, the aggregation number calculated by Mao et al.2 is reported as N ≈ 30, while in the Anderson et al.3 scheme they report an aggregation number of N = 47. Both of these are significantly lower than the experimentally predicted value of N ≈ 80.27
A length scale for the system rC can be calculated by matching the density of a water simulation to the experimental density of water at room temperature. Since the surfactant models discussed in this section are based on different coarse-grainings of water, this will result in two different length scale conversations. For the Anderson et al.3 scheme this results in rCNC=2 = 5.65 Å, while for the Mao et al.2 we calculate rCNC=4 = 7.11 Å. The impact of this on the dielectric constant will be discussed in the following section.
It is also important to note that both of these parameterisations were originally developed under the assumption that bonded beads interact with each other, and therefore the models will not produce the correct surfactant behaviour if bonded interactions are turned off. Therefore, we stipulate that while bonded beads do not interact within water particles, they do within our surfactant molecules.
Henceforth in this article, for simplicity, we will refer to Mao et al.2's parameterisation as scheme A, Anderson et al.3's representation as scheme B.
5 Dielectric constant of water and aqueous salt solutions
For scheme A (using NC = 4), the Drude bead charge is set as qNC=4 = 0.6e, based on the work of Vaiwala et al.54 For scheme B (using NC = 2), keeping the same equilibrium bond length l0 = 0.35rC and the same charge q = 0.6e will result in a different value of the dielectric constant, due to the effective shortening of the bond length from changing rC.Therefore, to generate the correct dielectric constant for water, we must in theory alter either the equilibrium bond length or the charge on the Drude bead. Here, we keep the bond length constant in DPD units (l0 = 0.35rC), and tune the Drude charge appropriately.
We note in passing that, within LAMMPS, the charge is set in terms of unit-less quantities (unit style ‘lj’), where the charge is input in reduced units  , which is a result of setting 4πε0 = 1 in this units system. Therefore, eqn (15) tells us that the dielectric constant for scheme B will be the same as scheme A if we maintain the same value of q*. In units of electronic charge (due to the change in rC when the degree of coarse-graining is varied from NC = 4 to NC = 2) this is equivalent to altering the charge on the Drude bead to
, which is a result of setting 4πε0 = 1 in this units system. Therefore, eqn (15) tells us that the dielectric constant for scheme B will be the same as scheme A if we maintain the same value of q*. In units of electronic charge (due to the change in rC when the degree of coarse-graining is varied from NC = 4 to NC = 2) this is equivalent to altering the charge on the Drude bead to 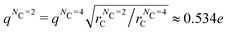 . Further details on the reduced charge can be obtained in the ESI.†
. Further details on the reduced charge can be obtained in the ESI.†
In addition to the Vaiwala water model, we also calculated the dielectric constant produced by models by Peter and Pivkin52 and Peter et al.53 These simulations are performed using 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water particles in a cubic simulation box with periodic boundary conditions and an edge length L = 20. We simulate for an equilibration period of 30
000 water particles in a cubic simulation box with periodic boundary conditions and an edge length L = 20. We simulate for an equilibration period of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps before we begin collecting data. We then run for a further 70
000 time steps before we begin collecting data. We then run for a further 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 timesteps, calculating the dipole moments every 100 timesteps.
000 timesteps, calculating the dipole moments every 100 timesteps.
The differences between the three water models discussed in this article are highlighted in Table 2. However, we find much smaller values for εr than reported in the original articles, finding values εr = 3.2 (Peter and Pivkin52) and εr = 4.3 (Peter et al.53), which greatly differs from the experimental value of εr/εs = 78.3/2 ≈ 39.2. We suggest that the authors in these articles may not allow for the necessary equilibration time of dipole moments before calculating εr (suggested by the relationship the authors present between angle constant D and εr). However, we will show here that the dielectric constant calculated based on Vaiwala's parameters matches the experimental value much more closely.
5.1. Relationship between εr and aWW
As mentioned above, we find that the value for εr is independent of the value of the interaction parameters aWW, which we show in this section. To do this, we perform a parameter sweep over different values of aWW and calculate the dielectric constant, keeping the value of charge and bond length constant. These simulations are performed in the same way as previously (Table 2).Fig. 3 shows the value of εr/εs calculated as a function of the number of time steps. Also presented is the final value of εr/εs over the entire simulation run time, where we see negligible difference between different values of aWW within the expected simulation error. This allows us to apply the polarisable water model described in this article to systems with different degrees of coarse-graining without any concern about how it impacts the dielectric constant.
 | ||
| Fig. 3 Ratio of relative permittivity of the solvent εr to the background permittivity εs for varying values of interaction parameter aWW. | ||
5.2 Aqueous NaCl solutions
Experiments have shown that aqueous salt solutions exhibit a reduction in dielectric constant with increasing salt content,70 which has also been shown to be reproducible in molecular dynamics simulations.71–73 Before we apply the water model to micellar solutions, we test whether the polarisable water model can reproduce dielectric decrement behaviour.We test the polarisable water using both scheme A (Mao et al.2) and scheme B (Anderson et al.3) coarse-graining approaches and set up the simulations in the same manner as described in Section 5.1. The sodium chloride salt is represented as two oppositely charged beads corresponding to hydrated ions, each of which has a charge of magnitude |q| = e. The short-range aij interactions are set as the same as those for water beads.
Fig. 4 presents the impact of varying the salt content in the two different models, compared with experimental data. The polarisable water model correctly predicts the drop in relative permittivity with the addition of ions. There is a small discrepancy between the experimental data and the simulated data, however, the DPD model is shown to be just as accurate as molecular dynamics approaches.71,73
 | ||
| Fig. 4 The ratio of the dielectric of a salt solution εr* to that calculated for pure water εr, shown as a function of NaCl salt content. We show simulated data for both scheme A (Mao et al.2) and scheme B (Anderson et al.3) SDS models. Experimental data taken from Buchner et al.70 | ||
6 Micellar solutions
In this section, we compare the differences in surfactant aggregation behaviour when standard water and polarisable water models are applied. We also compare the effect that polarisable water has on the two different SDS models discussed thus far. In their original papers, both models showed a fairly strong relationship between aggregation number and concentration. Therefore, in each case, calculations are performed at four different concentrations: 2.5, 5, 7.5 and 10 wt% (corresponding to molar concentrations 87, 173, 260 and 346 mM). Each simulation is conducted in a cubic box with edge length L = 20rC, with a total number of beads n = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Details on the number of water and surfactant beads this corresponds to can be found in the ESI.†
000. Details on the number of water and surfactant beads this corresponds to can be found in the ESI.†
6.1 Aggregation number
For each simulation, we calculate a weighted aggregation number, defined as NW = 〈N2〉/〈N〉 where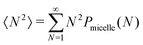 . Here N is the number of monomers in a given molecule, and Pmicelle is the probability of finding a monomer existing in a micelle of size N. The use of the weighted aggregation number, as opposed to simply the aggregation number, better represents polydisperse systems and is also more comparable with the experimental aggregation number. For this calculation, we output trajectory information every 10
. Here N is the number of monomers in a given molecule, and Pmicelle is the probability of finding a monomer existing in a micelle of size N. The use of the weighted aggregation number, as opposed to simply the aggregation number, better represents polydisperse systems and is also more comparable with the experimental aggregation number. For this calculation, we output trajectory information every 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps.
000 time steps.
The instantaneous aggregation number as a function of time step is shown in Fig. 5. We note that the micelles produced by scheme B (Anderson et al.3) are generally larger and more stable than those produced by scheme A (Mao et al.2).
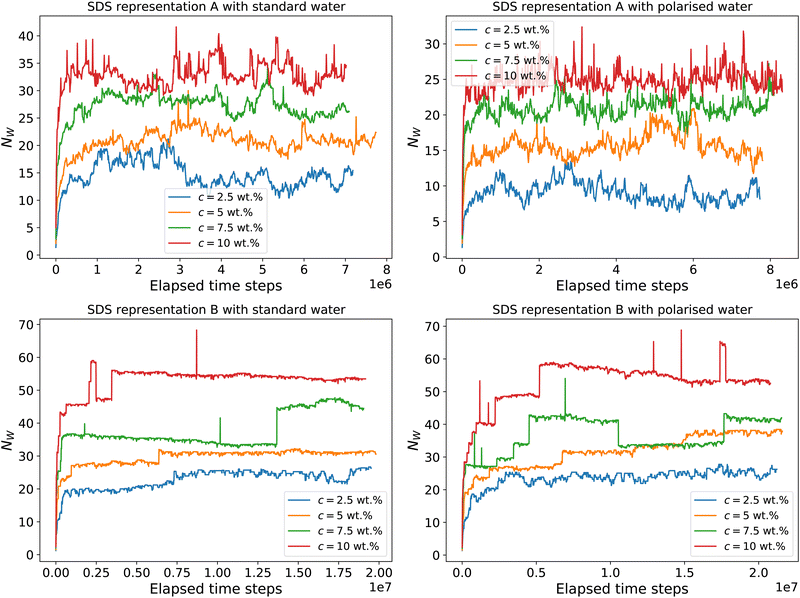 | ||
| Fig. 5 Weighted aggregation number NW as a function of simulated time steps for different concentrations. We simulate using a standard water model and the polarisable water model. We also test two different SDS parameterizations A (Mao et al.2) and B (Anderson et al.3) with water coarse-graining applicable to each model. | ||
We equilibrate our micellar solutions until the final aggregation number no longer appears to be changing with further simulation time steps. Fig. 6 shows the calculated aggregation numbers, where the weighted aggregation number is calculated from the final 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps. This figure shows that we do not see a significant difference between the polarisable and standard water models, at least with regard to the instantaneous aggregation number. The experimental value of the aggregation number varies between different experimental methods but is usually reported as between ≈75–110 in this concentration range.26,27,29,31 As reported in the original DPD studies, the aggregation number is underpredicted in Fig. 6 compared with experimental data. However, we note an increase in the average aggregation number with increasing concentration, which is in line with experimental observations.29
000 time steps. This figure shows that we do not see a significant difference between the polarisable and standard water models, at least with regard to the instantaneous aggregation number. The experimental value of the aggregation number varies between different experimental methods but is usually reported as between ≈75–110 in this concentration range.26,27,29,31 As reported in the original DPD studies, the aggregation number is underpredicted in Fig. 6 compared with experimental data. However, we note an increase in the average aggregation number with increasing concentration, which is in line with experimental observations.29
6.2 Pre-assembled micelles
In Section 6.1 we initialised our simulations with random initial configurations, allowing the surfactant molecules to equilibrate into aggregates. Besides the issue of the dielectric constant, one additional frequently proposed reason that aggregation numbers are underpredicted is related to equilibration issues. Equilibration issues are expected to be more significant for ionic surfactants (than nonionic ones) on account of the strong electrostatic repulsion involved between the surfactant head groups.Therefore, we also study micelles which are pre-formed at aggregation numbers close to the experimentally known values. This allows us to analyse if there is any difference in the behaviour of the polarisable and non-polarisable models at larger aggregation numbers. While other authors have taken the approach of placing micelles in a structured arrangement at the start of a simulation, we take a more practical approach. We initially simulate for a short period during which we apply no electrostatic interactions (effectively turning the counterions and head groups into water beads). We find that in all cases this leads to the relatively quick formation of a single micelle in the simulation box, owing to the lack of head-group repulsion limiting the micelle size. We take this as equivalent to a pre-assembled micelle. Then we simply turn on the electrostatic interactions and equilibrate.
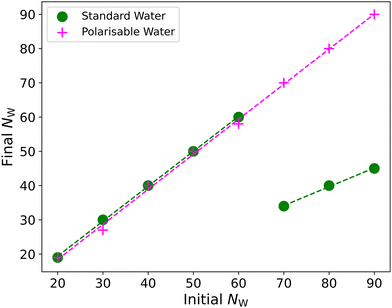
We perform these calculations using SDS scheme B only, conducting simulations in a box with edge length L = 15rC. Fig. 7 shows the final aggregation number after approximately 4.5 × 106 time-steps, relative to the aggregation number the micelle is initialised at. We observe that the micelles in the simulations containing the polarisable water model appear to be significantly more stable than the micelles using standard water. In the case of using standard water, at preassembled aggregation numbers of >60, the micelle breaks down into two different aggregates, while in the polarisable case, the micelle remains a single whole micelle.
Above the upper limit of aggregation numbers shown in Fig. 7 (N > 90), we find that the micelle fragments when the electrostatic interactions are switched on in both water models. However, we also note that the fragmentation becomes somewhat more random for larger initial micelle sizes. For example, a micelle with an initial size N = 100 may fragment into two or three micelles in independent simulations. We find that this is usually related to how evenly the first ‘split’ of the initial micelle is. For example, if the micelle initially fragments into two micelles of approximately equal size (resulting in NW ≈ 50), then it will not divide any further. However, if it initially fragments unevenly, (e.g. N = 20 and N = 80), then the larger micelle may divide again. This behaviour could make it difficult to ascertain an equilibrium aggregation number NW using this approach, due to the randomness in how larger micelles can fragment.
We can quantitatively determine the degree of sphericalness of the micelles in these simulations by calculating the eccentricity e, which we define using the moment of inertia of the micelle:
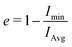 | (16) |
 | ||
| Fig. 8 The eccentricity of micelles (a) using the Anderson et al.3 parameterization as a function of their size N, where the error bar represents the standard deviation over the measurement period. Figure (b) shows two examples of the micelle shape when aggregation number N = 90. Images taken from the same simulation at two different time steps. Note the bead colour indicates the bead type, where: CH3 bead (pink), CH2 bead (blue) and head group (purple). | ||
In both models, the eccentricity value is relatively small, particularly within the range  . This is in good agreement with the experimental measurements discussed above, which indicated relatively spherical micelles. The micelles are most spherical around the size of N ≈ 40, before increasing in eccentricity for larger N. The error bars plotted for large N indicate significant amounts of fluctuation in micelle shape. Fig. 8b highlights the variation in shape for aggregates at sizes N = 90, showing that the micelle varies from nearly completely spherical to almost rod-like (note that more details about the fluctuation of eccentricity over the simulation time can be found in the ESI†). This significant fluctuation in micelle shape has also been observed for SDS in molecular dynamics44 and experimental studies.75 Palazzesi et al. use molecular dynamics to also calculate the eccentricity of an SDS micelle with an aggregation number of N = 60, finding an average value of e = 0.154, which we note is in excellent agreement with our average value using DPD.
. This is in good agreement with the experimental measurements discussed above, which indicated relatively spherical micelles. The micelles are most spherical around the size of N ≈ 40, before increasing in eccentricity for larger N. The error bars plotted for large N indicate significant amounts of fluctuation in micelle shape. Fig. 8b highlights the variation in shape for aggregates at sizes N = 90, showing that the micelle varies from nearly completely spherical to almost rod-like (note that more details about the fluctuation of eccentricity over the simulation time can be found in the ESI†). This significant fluctuation in micelle shape has also been observed for SDS in molecular dynamics44 and experimental studies.75 Palazzesi et al. use molecular dynamics to also calculate the eccentricity of an SDS micelle with an aggregation number of N = 60, finding an average value of e = 0.154, which we note is in excellent agreement with our average value using DPD.
6.3 Dielectric constant
This decrease in relative permittivity has been suggested to arise from a variety of possible origins, including the orientational ordering of water molecules close to the surface78,80,81 and a decrease in the density of water molecules due to the presence of counterions.78,82 We propose that a reduction in ε leads to a reduction in charge screening between the head groups of surfactant molecules. Therefore, a greater number of counterions condense at the micelle surface (in comparison to a case in which there is no reduction) to screen electrostatic interactions between the negatively charged head groups. It is of interest that previous works,41 in which various MD water models and force fields have been investigated for SDS micelles, appear to illustrate a link between counterion condensation and water model. We note that the authors appear to report a higher degree of condensation when models with lower dielectric constants are chosen.
It is nontrivial to calculate the dielectric constant as a function of position in our micellar systems, which would allow us to assess this theory. The dielectric constant is fundamentally a macroscopic property, and it is an open area of research concerning how the relative permittivity can be studied for inhomogeneous systems. While for a bulk material one can use Fröhlich-Kirkwood theory (eqn (15)), in inhomogeneous systems this equation becomes invalid. However, some studies have successfully calculated dielectric profiles for systems in which there is some spatial symmetry, for example in lipid bilayer systems83 or in slab geometries,73 where one has to assume dipole fluctuations in different perpendicular layers are not directly coupled.
In a similar manner, we estimate the variation in the relative permittivity as a function distance from the micelle's surface, by calculating the mean square dipole mB of an inner spherical region of radius R (where R = 0 is the micelle's centre of mass). We estimate
 | (17) |
Fig. 10 shows a plot of ε(R) as a function of R, where we also show the density profiles for the micelle and water. We see that the calculated value of ε(R) increases with distance from the micelle centre, and appears to be particularly tied with the increase in the water density. This suggests that indeed we do see a lower local dielectric constant closer to the micelle surface, which is strongly linked to an excluded volume effect due to the presence of ions.
6.4 Counter-ion behaviour
In this section, we investigate the impact of the water model and SDS model on the degree of disassociation of counterions. The degree of disassociation α potentially plays a role in the transition from spherical to rod-like micelles. The transition to elongated micelles can lead to viscoelastic behaviour, therefore accurate calculations for α are a crucial area of research. However, there exists a wide range of α values in the literature,86–88 resulting from different experimental techniques and a lack of consensus over the definition of ‘dissociated ions’, an issue which has been discussed in literature.87 However, values of around α = 0.3 are most commonly reported.86,87 The calculation ofα from simulations is complicated by the fact that molecular dynamics simulations have shown that the value of α can depend on the choice of force field.41Fig. 11 shows the radial distribution function (RDF) between the SO4 (SO4−) and NA (Na+) beads for different simulation cases. We observe that in the polarisable models, the head group and their counterion are closer than in the standard water case, and are significantly closer in the scheme B surfactant model. This shift in the radial distribution function (between the micelle and counter ions) has also been observed when comparing polarisable and non-polarisable MARTINI force fields.89 While molecular dynamics simulations have reported41 that there are generally two distinct peaks within the first 0.6 nm, corresponding to the first two sodium shells, we only observe a single, broader peak. We attribute this to the coarse graining used in this work, which smears these into a single peak.
 | ||
| Fig. 11 Radial distribution function between the SO4 and NA beads for different simulation cases. All data presented for simulations at 10 wt%. Both SDS parameterisation schemes are shown: A (Mao et al.2) and B (Anderson et al.3). | ||
We calculate the number of ions bound to the micelle β (where bound ions β = 1 − α), defining an ion to be bound if it is within a defined cut-off of one of the surfactant head groups. Molecular dynamics simulations41 report that, depending on the force field used, there exists on average around 60% (range 45–70% for the six force fields tested) of the sodium atoms within 0.6 nm of the RDF shell. We choose our cut-off distance to be RCut = 0.8RC for the scheme A (Mao et al.2) SDS model, and RCut = 1RC for scheme B (Anderson et al.3). Converted into real units, both of these cut-offs are approximately 0.57 nm, allowing for direct comparison with the molecular dynamics data.
Fig. 12 shows the fraction of ions bound to the micelles in each simulation case (note that we only consider ions associated with micelles in this calculation and surfactants which are considered free monomers are not included). The number of bound ions increases with concentration and is consistently higher in the polarisable models compared to standard water. The introduction of the polarisable model also causes the number of bound ions to be more comparable with both molecular dynamics data, and experimental data.
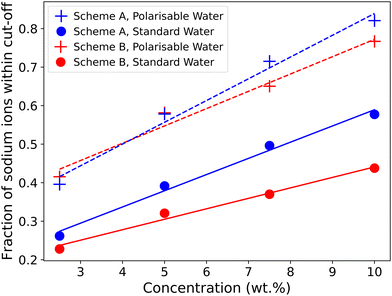 | ||
| Fig. 12 Fraction of sodium ions within a defined cut-off range of head group beads. Cut-off distances of RCut = 1RC in the Anderson et al.3 SDS model, and RCut = 0.8 RC for the Mao et al.2 model. | ||
6.5 Micelle interactions
Finally, we briefly consider the impact of the polarisable water model on micelle–micelle interactions. The interactions between micelles are primarily influenced by the electrostatic interaction, as there is a net long-range force acting on micelles due to their net charge. We focus on scheme B for the surfactant and analyse the trajectories from simulations described earlier in this article (Section 6.1) for the micelles that form at 2.5 wt% SDS. At this concentration, we have three micelles, with an average aggregation number of NW ≈ 25. The radial distribution function g(r) between the COM of micelles is calculated, and shown in Fig. 13 where we can see that there are only minor differences between the predictions from the two models. To further probe differences between the water models, we perform an additional set of simulations for a micellar system with added salt. The aim here was to bring the micelles slightly closer together, as in Fig. 13 it can be observed that they remain reasonably far apart during the whole measurement period. | ||
| Fig. 13 Radial distribution function g(r) between the COM of micelles in an aqueous solvent both with and without added NaCl salt. | ||
We simulate a system consisting of two micelles of sizes N ≈ 64 and N ≈ 48, in a simulation box of size L = 23 which corresponds to a concentration of ≈2.5 wt% (85 mM). There is a small amount of fluctuation in the micelle sizes over the measurement period, but never more than ΔN ± 2. Here we can access larger micelle sizes, due to the enhanced head group screening that the salt provides. We then swap a number of the water particles for salt particles, which are defined in the same way as discussed in Section 5.2. We swap 200 water molecules for 100 sodium and 100 chloride ions, giving a salt concentration of ≈76 mM.
We generate the initial configuration of the two micelles by performing a similar trick to that discussed in Section 6.2, where we initially turn off the electrostatic charges to encourage micelle formation, and then turn them back on again once this has occurred to study their behaviour. In this case, rather than allowing a single micelle to form as before, we pause the simulation at the point where we have our two micelles, allowing us to use this as the starting configuration. Fig. 13 shows the radial distribution function g(r) between the COM of the two micelles. Here, with salt present, we see more variation between the two water models. It appears that, on average, the micelles get closer more often, an indication of the better electrostatic screening provided by the polarisable water model.
The potential of mean force (PMF), W(r), can be obtained from g(r)
W(r) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(r). g(r). | (18) |
 | ||
| Fig. 14 Potential of mean force between micelles, calculated using the RDF in Fig. 13. | ||
Increases in the PMF at shorter distances are expected as the electrostatic repulsion grows as the charged micelles get closer. However, we note that there is a significant region in which W(r) < 0, implying that at larger distances there is an attractive force between the micelles. Interestingly, a description of intermicellar interactions in terms of a balance between a repulsive and an attractive potential has been proposed and discussed from both an experimental90 and theoretical91,92 point of view, but is not always observed in simulations.93
7 Conclusions
We investigated the impact of polarisable water models on the aggregation behaviour of sodium dodecyl sulfate, allowing us to study whether the under-predicted aggregation numbers in DPD simulations can be improved with more complex water modelling. This polarisable water model was tested on simple salt solutions to confirm the correct dielectric behaviour of the model. Following this, the models were applied to the more complex surfactant solution cases.We conclude that the underprediction of aggregate sizes in DPD models cannot alone be attributed to water modelling. However, there is evidence that polarisable water models produce micelles, which are more stable at larger aggregation numbers, and provide more accurate predictions for counterion behaviour. The use of polarisable water significantly increases the number of bound ions to the micelle, resulting in estimates for the number of bound ions much closer to experimental values, as well as being more in line with what is observed in molecular dynamics simulations. The observation that polarisable water leads to more stable micelles implies that equilibration is a key influence in the underprediction of aggregation numbers, particularly when our simulations are initialised with random positions for the surfactant molecules.
Furthermore, we show that the calculated dielectric constant increases as a function of distance from the surface of the micelle, as was initially postulated at the start of this article. This effect is likely due to the presence of counterions surrounding the micellar surface and is a phenomenon that would not normally be reflected in traditional DPD simulations using nonpolarisable water models.
It is possible that there are other simplifications in coarse-grained modelling that influence micelle formation and could be the source of aggregation under-prediction. For example, molecular dynamics94 simulations of SDS micelles in water have shown that water molecules near the headgroup exhibit a distortion of the water–water hydrogen bonding. There have been some efforts to incorporate explicit hydrogen bonding into DPD, via the inclusion of a Morse potential,95 and it would be interesting in future to assess whether models such as this have any impact on aggregation in DPD simulations.
We note that polarisable water models are more computationally demanding than the traditional DPD modelling approaches and therefore may not be appropriate for all systems of interest. However, for systems where counterion behaviour is a key aspect of interest, a polarisable water model is essential. We also note that our polarisable DPD model is still more computationally efficient than traditional fully atomistic approaches. We expect the models described here to find use in a range of diverse situations, including systems with charged surfaces, concentrated electrolyte solutions, and future studies of specific ion effects, as demonstrated, for example, in the Hofmeister series.
Author contributions
RH: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft. CA: project administration, writing – review and editing. MW: funding acquisition, project administration, supervision, writing – review and editing.Data availability
Data supporting this article have been uploaded as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the support of Durham University for the use of its HPC facility, Hamilton. RH would like to acknowledge support through an EPSRC/P&G funded Prosperity Partnership grant EP/V056891/1.Notes and references
- R. L. Hendrikse, C. Amador and M. R. Wilson, Soft Matter, 2024, 20, 6044–6058 RSC
.
- R. Mao, M.-T. Lee, A. Vishnyakov and A. V. Neimark, J. Phys. Chem. B, 2015, 119, 11673–11683 CrossRef CAS PubMed
.
- R. L. Anderson, D. J. Bray, A. Del Regno, M. A. Seaton, A. S. Ferrante and P. B. Warren, J. Chem. Theory Comput., 2018, 14, 2633–2643 CrossRef CAS PubMed
.
- D. Nivón-Ramírez, L. I. Reyes-García, R. Oviedo-Roa, R. Gómez-Balderas, C. Zuriaga-Monroy and J.-M. Martínez-Magadán, Colloids Surf., A, 2022, 645, 128867 CrossRef
.
- Z. Mai, E. Couallier, M. Rakib and B. Rousseau, J. Chem. Phys., 2014, 140, 204902 CrossRef PubMed
.
- R. L. Hendrikse, A. E. Bayly and P. K. Jimack, J. Phys. Chem. B, 2022, 126, 8058–8071 CrossRef CAS PubMed
.
- S. J. Gray, M. Walker, R. Hendrikse and M. R. Wilson, Soft Matter, 2023, 19, 3092–3103 RSC
.
- V. Symeonidis, G. Em Karniadakis and B. Caswell, Phys. Rev. Lett., 2005, 95, 076001 CrossRef PubMed
.
- S. B. Chen, J. Phys. Chem. B, 2022, 126, 7184–7191 CrossRef CAS PubMed
.
- H. Droghetti, I. Pagonabarraga, P. Carbone, P. Asinari and D. Marchisio, J. Chem. Phys., 2018, 149, 184903 CrossRef PubMed
.
- V. Symeonidis, G. E. Karniadakis and B. Caswell, J. Chem. Phys., 2006, 125, 184902 CrossRef PubMed
.
- R. Hendrikse, A. Bayly and P. Jimack, J. Chem. Phys., 2023, 158, 214906 CrossRef CAS PubMed
.
- M. R. Wilson, G. Yu, T. D. Potter, M. Walker, S. J. Gray, J. Li and N. J. Boyd, Crystals, 2022, 12, 685 CrossRef CAS
.
- T. L. Rodgers, O. Mihailova and F. R. Siperstein, J. Phys. Chem. B, 2011, 115, 10218–10227 CrossRef CAS PubMed
.
- M. Lísal and J. K. Brennan, Langmuir, 2007, 23, 4809–4818 CrossRef PubMed
.
- M. Walker, A. J. Masters and M. R. Wilson, Phys. Chem. Chem. Phys., 2014, 16, 23074–23081 RSC
.
- M. Walker and M. R. Wilson, Soft Matter, 2016, 12, 8588–8594 RSC
.
- M. Walker and M. R. Wilson, Soft Matter, 2016, 12, 8876–8883 RSC
.
- M. Bates and M. Walker, Soft Matter, 2009, 5, 346–353 RSC
.
- M. A. Bates and M. Walker, Liq. Cryst., 2011, 38, 1749–1757 CrossRef CAS
.
- B. Cabane, R. Duplessix and T. Zemb, J. Phys., 1985, 46, 2161–2178 CrossRef CAS
.
- M. Bergstrom and J. S. Pedersen, Phys. Chem. Chem. Phys., 1999, 1, 4437–4446 RSC
.
- L. J. Magid, Z. Li and P. D. Butler, Langmuir, 2000, 16, 10028–10036 CrossRef CAS
.
- M. Kakitani, T. Imae and M. Furusaka, J. Phys. Chem., 1995, 99, 16018–16023 CrossRef CAS
.
- S. S. Berr and R. R. M. Jones, Langmuir, 1988, 4, 1247–1251 CrossRef CAS
.
- M. Ludwig, R. Geisler, S. Prévost and R. von Klitzing, Molecules, 2021, 26, 4136 CrossRef CAS PubMed
.
- R. Ranganathan, L. Tran and B. L. Bales, J. Phys. Chem. B, 2000, 104, 2260–2264 CrossRef CAS
.
- B. L. Bales, L. Messina, A. Vidal, M. Peric and O. R. Nascimento, J. Phys. Chem. B, 1998, 102, 10347–10358 CrossRef CAS
.
- B. Hammouda, J. Res. Natl. Inst. Stand. Technol., 2013, 118, 151–167 CrossRef CAS PubMed
.
- S. Khodaparast, W. N. Sharratt, G. Tyagi, R. M. Dalgliesh, E. S. Robles and J. T. Cabral, J. Colloid Interface Sci., 2021, 582, 1116–1127 CrossRef CAS PubMed
.
- V. Y. Bezzobotnov, S. Borbely, L. Cser, B. Farago, I. A. Gladkih, Y. M. Ostanevich and S. Vass, J. Phys. Chem., 1988, 92, 5738–5743 CrossRef CAS
.
- S. L. Gawali, M. Zhang, S. Kumar, D. Ray, M. Basu, V. K. Aswal, D. Danino and P. A. Hassan, Langmuir, 2019, 35, 9867–9877 CrossRef CAS PubMed
.
- Y. Mirgorod, A. Chekadanov and T. Dolenko, Chem. J. Mold., 2019, 14, 107–119 CAS
.
- P. Kékicheff, C. Grabielle-Madelmont and M. Ollivon, J. Colloid Interface Sci., 1989, 131, 112–132 CrossRef
.
- M. P. McDonald and W. E. Peel, J. Chem. Soc., Faraday Trans. 1, 1976, 72, 2274 RSC
.
- J. Bahadur, A. Das and D. Sen, J. Appl. Crystallogr., 2019, 52, 1169–1175 CrossRef CAS
.
- J. Iyer and D. Blankschtein, J. Phys. Chem. B, 2014, 118, 2377–2388 CrossRef CAS PubMed
.
- A. Goldsipe and D. Blankschtein, Langmuir, 2007, 23, 5953–5962 CrossRef CAS PubMed
.
- S. Puvvada and D. Blankschtein, J. Phys. Chem., 1992, 96, 5567–5579 CrossRef CAS
.
- E. A. Iakovleva, P. O. Sorina, E. A. Safonova and A. I. Victorov, Fluid Phase Equilib., 2022, 556, 113376 CrossRef CAS
.
- X. Tang, P. H. Koenig and R. G. Larson, J. Phys. Chem. B, 2014, 118, 3864–3880 CrossRef CAS PubMed
.
- B. J. Chun, J. I. Choi and S. S. Jang, Colloids Surf., A, 2015, 474, 36–43 CrossRef CAS
.
- G. Roussel, C. Michaux and E. A. Perpète, J. Mol. Model., 2014, 20, 2469 CrossRef PubMed
.
- F. Palazzesi, M. Calvaresi and F. Zerbetto, Soft Matter, 2011, 7, 9148–9156 RSC
.
- D. L. Gurina and Y. A. Budkov, Colloids Surf., A, 2023, 676, 132200 CrossRef CAS
.
- F. Leermakers and J. Lyklema, Colloids Surf., 1992, 67, 239–255 CrossRef CAS
.
- V. G. de Bruijn, L. J. P. van den Broeke, F. A. M. Leermakers and J. T. F. Keurentjes, Langmuir, 2002, 18, 10467–10474 CrossRef CAS
.
- Y. Lauw, F. A. M. Leermakers and M. A. Cohen Stuart, J. Phys. Chem. B, 2003, 107, 10912–10918 CrossRef CAS
.
- S. Chanda and K. Ismail, Indian J. Chem., Sect. A: Inorg., Bio-inorg., Phys., Theor. Anal. Chem., 2009, 48, 775–780 Search PubMed
.
- S. Pal, S. Balasubramanian and B. Bagchi, J. Chem. Phys., 2004, 120, 1912–1920 CrossRef CAS PubMed
.
- H. Steinhoff, B. Kramm, G. Hess, C. Owerdieck and A. Redhardt, Biophys. J., 1993, 65, 1486–1495 CrossRef CAS PubMed
.
- E. K. Peter and I. V. Pivkin, J. Chem. Phys., 2014, 141, 164506 CrossRef PubMed
.
- E. K. Peter, K. Lykov and I. V. Pivkin, Phys. Chem. Chem. Phys., 2015, 17, 24452–24461 RSC
.
- R. Vaiwala, S. Jadhav and R. Thaokar, Mol. Simul., 2018, 44, 540–550 CrossRef CAS
.
- S. Chiacchiera, P. B. Warren, A. J. Masters and M. A. Seaton, Polarisable soft solvent models with applications in dissipative particle dynamics, 2024 Search PubMed.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef
.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS
.
- R. D. Groot, J. Chem. Phys., 2003, 118, 11265–11277 CrossRef CAS
.
- P. B. Warren and A. Vlasov, J. Chem. Phys., 2014, 140, 084904 CrossRef PubMed
.
- M. González-Melchor, E. Mayoral, M. E. Velázquez and J. Alejandre, J. Chem. Phys., 2006, 125, 224107 CrossRef PubMed
.
- S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810 CrossRef PubMed
.
- J. Michalowsky, L. V. Schäfer, C. Holm and J. Smiatek, J. Chem. Phys., 2017, 146, 054501 CrossRef PubMed
.
- M. Vögele, C. Holm and J. Smiatek, J. Mol. Liq., 2015, 212, 103–110 CrossRef
.
- J. Song, M. Ma, Y. Dong, M. Wan, W. Fang and L. Gao, J. Chem. Theory Comput., 2023, 19, 1864–1874 CrossRef CAS PubMed
.
- A. Catte, M. R. Wilson, M. Walker and V. S. Oganesyan, Soft Matter, 2018, 14, 2796–2807 RSC
.
-
X. Periole and S.-J. Marrink, in The Martini Coarse-Grained Force Field, ed. L. Monticelli and E. Salonen, Humana Press, Totowa, NJ, 2013, pp. 533–565 Search PubMed
.
- J. G. Kirkwood, J. Chem. Phys., 1939, 7, 911–919 CrossRef CAS
.
-
H. Fröhlich, Theory of dielectrics: dielectrics constant and dielectric loss., Clarendon Press, Oxford, 2nd edn, 1958 Search PubMed
.
- A. D. Sen, V. G. Anicich and T. Arakelian, J. Phys. D: Appl. Phys., 1992, 25, 516 CrossRef CAS PubMed
.
- R. Buchner, G. T. Hefter and P. M. May, J. Phys. Chem. A, 1999, 103, 1–9 CrossRef CAS
.
- S. Seal, K. Doblhoff-Dier and J. Meyer, J. Phys. Chem. B, 2019, 123, 9912–9921 CrossRef CAS PubMed
.
- C. J. Shock, M. J. Stevens, A. L. Frischknecht and I. Nakamura, J. Chem. Phys., 2023, 159, 134507 CrossRef CAS PubMed
.
- P. Zarzycki, J. Colloid Interface Sci., 2023, 645, 752–764 CrossRef CAS PubMed
.
- S. Vass, J. S. Pedersen, J. Pleštil, P. Laggner, E. Rétfalvi, I. Varga and T. Gilányi, Langmuir, 2008, 24, 408–417 CrossRef CAS PubMed
.
- S. Choudhury, P. K. Mondal, V. K. Sharma, S. Mitra, V. G. Sakai, R. Mukhopadhyay and S. K. Pal, J. Phys. Chem. B, 2015, 119, 10849–10857 CrossRef CAS PubMed
.
- D. K. George, A. Charkhesht, O. A. Hull, A. Mishra, D. G. S. Capelluto, K. R. Mitchell-Koch and N. Q. Vinh, J. Phys. Chem. B, 2016, 120, 10757–10767 CrossRef CAS PubMed
.
- P. Fernandez, S. Schrödle, R. Buchner and W. Kunz, ChemPhysChem, 2003, 4, 1065–1072 CrossRef CAS PubMed
.
- E. Gongadze and A. Igli
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) , Bioelectrochemistry, 2012, 87, 199–203 CrossRef CAS PubMed
, Bioelectrochemistry, 2012, 87, 199–203 CrossRef CAS PubMed .
- D. J. Bonthuis, S. Gekle and R. R. Netz, Phys. Rev. Lett., 2011, 107, 166102 CrossRef PubMed
.
- H. Zhu, F. Yang, Y. Zhu, A. Li, W. He, J. Huang and G. Li, RSC Adv., 2020, 10, 8628–8635 RSC
.
- H. Itoh and H. Sakuma, J. Chem. Phys., 2015, 142, 184703 CrossRef PubMed
.
- T. Sato, T. Sasaki, J. Ohnuki, K. Umezawa and M. Takano, Phys. Rev. Lett., 2018, 121, 206002 CrossRef CAS PubMed
.
- F. Zhou and K. Schulten, J. Phys. Chem., 1995, 99, 2194–2207 CrossRef CAS
.
- V. Ballenegger and J.-P. Hansen, J. Chem. Phys., 2005, 122, 114711 CrossRef CAS PubMed
.
- J. Powles, R. Fowler and W. Evans, Chem. Phys. Lett., 1984, 107, 280–283 CrossRef CAS
.
- S. Ikeda, Colloid Polym. Sci., 1991, 269, 49–61 CrossRef CAS
.
- B. L. Bales, J. Phys. Chem. B, 2001, 105, 6798–6804 CrossRef CAS
.
- B. Naskar, A. Dey and S. P. Moulik, J. Surfactants Deterg., 2013, 16, 785–794 CrossRef CAS
.
- A. V. Sangwai and R. Sureshkumar, Langmuir, 2011, 27, 6628–6638 CrossRef CAS PubMed
.
- M. Corti and V. Degiorgio, J. Phys. Chem., 1981, 85, 711–717 CrossRef CAS
.
- I. Sogami and N. Ise, J. Chem. Phys., 1984, 81, 6320–6332 CrossRef
.
- I. Sogami, Phys. Lett. A, 1983, 96, 199–203 CrossRef
.
- S. Kawada, K. Fujimoto, N. Yoshii and S. Okazaki, J. Chem. Phys., 2017, 147, 084903 CrossRef PubMed
.
- C. D. Bruce, S. Senapati, M. L. Berkowitz, L. Perera and M. D. E. Forbes, J. Phys. Chem. B, 2002, 106, 10902–10907 CrossRef CAS
.
- G. Kacar and G. de With, J. Mol. Liq., 2020, 302, 112581 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00873a |
| This journal is © The Royal Society of Chemistry 2024 |