 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Homoleptic hexa- and penta-coordinated gallium(I) amide complexes of ruthenium and molybdenum†
Raphael
Bühler‡
 ,
Richard J. J.
Weininger‡
,
Richard J. J.
Weininger‡
 ,
Johannes
Stephan
,
Johannes
Stephan
 ,
Maximilian
Muhr
,
Balasai M.-T.
Bock
,
Christian
Gemel
and
Roland A.
Fischer
,
Maximilian
Muhr
,
Balasai M.-T.
Bock
,
Christian
Gemel
and
Roland A.
Fischer
 *
*
Chair of Inorganic and Metalorganic Chemistry, Technical University of Munich, School of Natural Sciences, Department of Chemistry, Lichtenbergstraße 4, 85748 Garching, Germany and Catalysis Research Center, Erst-Otto-Fischer-Straße 1, 85748 Garching, Germany. E-mail: roland.fischer@tum.de
First published on 20th April 2024
Abstract
Reaction of neutral olefin complexes of ruthenium and molybdenum with GaTMP (TMP = 2,2,6,6-tetramethylpiperidinyl) by substitution leads to the formation of respective five- and six-coordinated homoleptic products. [Ru(GaTMP)5] (1) and [Mo(GaTMP)6] (2) were isolated and characterized. Core structure geometries were analyzed using continuous shape measure, and the complexes were subjected to DFT calculations unveiling competing π-interactions between the transition metal center and the amido substituent with the unoccupied pπ orbitals of the gallium.
Introduction
Exploring the chemistry of low valent group-13 metallo-ligands ER* (E = Al, Ga, In; R* = sterically demanding protection group) coordinated to d- and f-block metal centers (transition metals, M) has significantly been motivated by the isolobal relationship between ER* and CO. The choice or design of R* has been crucial to allow for preparative access to ER* compounds and utilize them in organometallic coordination chemistry. The first example of a mononuclear homoleptic complex of the general formula [M(ER*)n], namely [Ni(InC(SiMe3)3)4] (R* = C(SiMe3)3), was reported by W. Uhl in 1998,1 followed by P. Jutzi's [Ni(GaCp*)4] in 1999 and our [Ni(AlCp*)4] in 2005 (Cp* = C5(CH3)5).2,3 All these complexes can be viewed as analogues of [Ni(CO)4]. However, there are cases such as the trinuclear, linear [(Cp*In)2Pd(μ-(InCp*))2Pd(μ-(InCp*)2)Pd(InCp*)2],4 which has no analogous metal carbonyl [Mn(CO)m] structure. Other protecting groups, R*, including amides (e.g. N(SiMe3)(2,6-bis-mesityl phenyl)),5 ketoiminates (e.g. DDP = 2-{(2,6-diisopropylphenyl)amino}-4-{(2,6-diisopropylphenyl)-imino}-2-pentene) and amidinates (e.g. [N(Ar)]2CNCy2; Ar = C6H3iPr2-2,6; Cy = cyclohexyl), have been introduced with great success, for example, to yield [Pt(Ga[N(Ar)]2CNCy2)3], as reported by Jones and co-workers.6 Due to the high steric bulk of these types of metallo-ligands ER*, the transition metal coordination number of any of their homoleptic complexes has not exceeded three. We and others have reviewed the development of this chemistry in the past.7–10 Specifically, an updated comprehensive listing of all structurally elucidated homoleptic complexes [Ma(ER*)b], including [Mo(GaCp*)6] as the only example of that series with coordination number cn(M) greater than five, is provided in the ESI.†11The history of heterometallic group-13 metal/transition metal complexes of the more general formula [(LnM)a(ER3−a)] (L = CO, phosphines, etc.; R = any inorganic or organic substituent, i.e. including hydrides or halides) featuring unsupported covalent (donor/acceptor) bonds M–E dates back to the early work of Hieber on [((CO)4Co)3In] in 1942.12,13 The related work since the mid-1990s focused on synthesis, structure and the elucidation of details of the M–E bonding by theoretical approaches applying various computational frameworks.14,15 Herein, we are particularly interested in exploring the transition from discrete heterometallic complexes to the related clusters in which an intermetalloid MaEb core is protected by an all-hydrocarbon shell of R*, i.e. matching with the general formula [MaEb](R*)c, with (a + b) > c.16–18 A recent example of that work is the assignment of individual structures from a preparative inseparable ensemble of Ni/Ga clusters [Ni6+xGa6+y](Cp*)6 = [NixGa6+y](NiCp*)6 (x + y ≤ 2). Notably, in this particular case, protection group transfer (R* = Cp*) occurs from the Ga to the Ni during the synthesis of the clusters from Ni(0) olefin complexes with GaCp* in toluene or mesitylene at elevated temperatures.19,20
A relationship exists between the molecular coordination and cluster chemistry of the solid-state and the materials chemistry of the respective intermetallic M/E (nano) phases and their catalytic properties.21–23 For example, the oligonuclear Ni/Ga hydrido clusters [HxNi3(GaR*)7] (x = 2,4,6; R* = TMP = 2,2,6,6-tetramethylpiperidinyl) are moderately active in alkyne semi-hydrogenation to alkenes, mimicking the surface chemistry of the respective solid-state Ni/Ga (nano) alloys.20 Compared to the other types of R* mentioned in this introduction, considerably few studies have been conducted using R* = TMP as a protecting group, which was mainly introduced by Linti and co-workers. With respect to GaTMP in particular, only the following few complexes are known in the literature: [(CO)5Cr(GaTMP)] and [(CO)3Cr(μ2-GaTMP)3Cr(CO)3] were prepared simultaneously from [Cr(CO)5(cyclooctene)]; [(CO)3Co(μ2-GaTMP)2Co(CO)3] was synthesized from [Co2(CO)8].24 The homoleptic dinuclear [Ni2(GaTMP)7]24 and trinuclear [Ni3(GaTMP)3(μ2-GaTMP)3(μ3-GaTMP)]20 complexes were accessible from [Ni(COD)2] (COD = 1,5-cyclooctadiene). Searching for any compound with the structural element structure TMP-E-M yielded one more entry to the list. [(TMP)2AlFe(Cp)(CO)2] was reported in 1997 by Nöth et al.,25 while Dankert and Hevia published earlier this year the synthesis of [(TMP)2AlZn(Cp*)].26 However, here, the E center (E = Al) is a tri-coordinate and is formally in a higher oxidation state. Thus, these compounds and any related ones are not of immediate concern to our work. Thus, we further investigate the coordination chemistry of GaTMP against d-block metals M with a focus on homoleptic [Ma(GaTMP)b] complexes or clusters [HxMaGab](TMP)c and aim for a more expanded library of such compounds. Herein, we now report the first homoleptic GaTMP complexes of second row transition metals, namely [Ru(GaTMP)5] (1) and [Mo(GaTMP)6] (2).
Results and discussion
[Ru(GaTMP)5] (1, Fig. 1) was obtained as a brown, crystalline solid, suitable for SC-XRD, by reacting [Ru(COD)(COT)] (COD = 1,4-cyclooctadiene; COT = η6–1,3,5-cyclooctatriene) with 1.25 eq. (GaTMP)4 in toluene at 100 °C for 19 h (Fig. 2). After workup, compound 1 was isolated at a yield of 20% (based on Ru).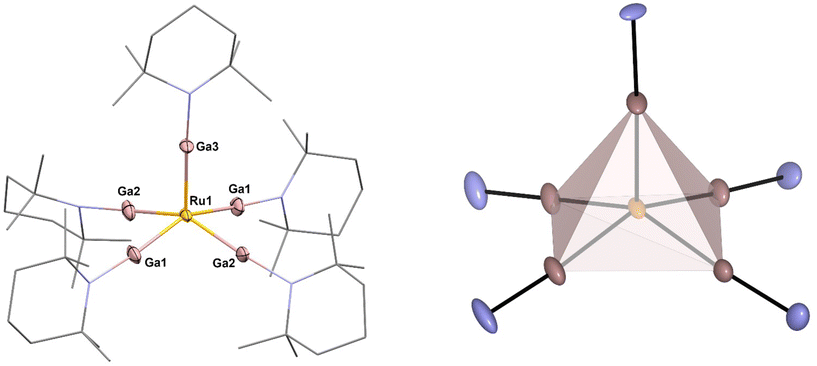 | ||
| Fig. 1 Left: molecular structure of [Ru(GaTMP)5] (1) in the solid state determined by single crystal X-ray diffraction. Ru: yellow, Ga: pink, N: blue and C: grey. Hydrogen atoms and disordered molecule fragments are omitted. C and N are displayed as wireframe. Right: square pyramidal coordination polyhedron calculated from crystal structure data. Thermal ellipsoids are shown at the 50% probability level. Selected bond lengths [Å] and angles [°]: Ru1–Ga3: 2.274(10) Ru1–Ga2#1/Ga2: 2.281(7), Ru1–Ga1#1/Ga1: 2.291(6), Ga3–Ru1–Ga2#1/Ga2: 104.6(2), Ga3–Ru1–Ga1#1/Ga1: 103.0(2), Ga2–Ru1–Ga1: 84.2(3), Ga2–Ru1–Ga1#:1 89.3(2). Note: Ga1/Ga1#1 and Ga2/Ga2#1 are symmetry related. | ||
The C, H and N values of 1 obtained by elemental analysis are within the expected range. The 1H-NMR and 13C-NMR in C6D6 (25 °C; see Fig. S1–3†) indicate the presence of five equivalent TMP groups with only minor shifts of all signals with respect to free (GaTMP)4.27 Trace impurities are almost absent. The presence of only one set of signals for all five GaTMP units indicates a fast fluxional process, which is very common for five-coordinate metal complexes.28 The IR spectrum (see Fig. S8†) does not show absorption bands in the region associated with Ru-H vibrations (ca. 1900 cm−1–1700 cm−1) and all features can be assigned to the TMP groups (see Fig. S10†).29 High-resolution LIFDI-MS (Fig. S11–13†) gives a molecular ion [M]+ signal of 100% rel. intensity at 1151.25 m/z (calcd. m/z 1151.25) and a fragment [M − TMP]+ signal at 1011.11 m/z of 1.6% rel. intensity (calcd. m/z 1011.11). Compound 1 crystallizes in the monoclinic space group C2/c, and the molecular structure in the solid state is shown in Fig. 1 together with a selection of structural parameters (bond lengths and angles).
The molecular unit of 1 exhibits a square pyramidal coordinated Ru center that is slightly distorted along the z-axis, elevating the Ru above the Ga4 plane by 0.545 Å, with Gaax1-Ru–Ga angles in the range of 103.0–104.6°. The Ru–Ga bond lengths show only a slight variance between 2.274 Å (Ru1–Ga3), 2.291 Å (Ru1–Ga1) and 2.281 Å (Ru1–Ga2) but are significantly shortened by 0.10 Å–0.15 Å compared to known Ru–GaCp* complexes.29–36 To quantify the distortion of the [RuGa5] core, the so-called continuous shape measures were calculated.22 Using continuous shape measures (SQ(P)), distortions of molecular structures from reference structures (e.g. ideal polhyhedra) can be quantified (for details and the calculation code see ESI†). In general, SQ(P) = 0 indicates no distortion from the reference, SQ(P) < 1.00 indicates minor distortions and 1.00 < SQ(P) < 3.00 indicates major distortions from the reference shape.22 In the case of 1, SQ(P) = 0.99 was found when compared to an ideal square pyramid with the Ru in the centroid of the polyhedron, while SQ(P) was distinctly higher for a square pyramidal shape when was placed Ru in the center of the basal square plane (SQ(P) = 4.63) or compared to an ideal trigonal bipyramidal shape with the Ru in the centre of the equatorial plane (SQ(P) = 7.63). With respect to the α and β angles (150.72° and 154.11°), a τ5 value of 0.0565 is found. This value is close to the ideal value of a basally distorted square pyramid,37 as demonstrated by the Ruthenium center being 0.545 Å above the square plane.
[Mo(GaTMP)6] (2, Fig. 3) was obtained in an analogous synthesis to 1 by reaction of [Mo(η4-C4H6)3] with 1.5 eq. of (GaTMP)4 in toluene at 110 °C for 22 h. Compound 2 was isolated as a beige, crystalline solid suitable for SC-XRD in a total yield of 42% after workup.
The C, H and N values of 2 obtained by elemental analysis are within the expected range. 1H-NMR and 13C-NMR spectra in toluene-d8 exhibit each set of TMP signals, which are only slightly shifted with respect to the signals of 1 or free (GaTMP)4 (see Fig. S4–6†).27 IR spectroscopy provides data very similar to [Ru(GaTMP)5] (1) and shows no absorption in the range of typical Mo-H vibrations between 1900 cm−1 and 1650 cm−1, indicating the presence of hydrides (see Fig S9†).38,39 High-resolution LIFDI-MS (see Fig. S14–16†) gives a molecular ion [M]+ signal at 1356.32 m/z (calcd. m/z 1356.32) with 100% rel. intensity. The compound crystallizes in the monoclinic space group P21/c, with two crystallographically distinct units per unit cell, both exhibiting six Ga(TMP) ligands coordinating in an octahedral fashion around the Mo centers (Fig. 3). In relation to each other, the two independent octahedral units are rotated along all three axes. The average Mo–Ga bond lengths of the independent units are 2.385 Å and 2.386 Å with minimal deviation. Ga–Mo–Ga angles in both units point to a slight distortion from the ideal octahedral geometry and range between 81.9° and 97.7°. The analogous [Mo(GaCp*)6] molecule shows less angular distortion with Ga–Mo–Ga angles between 85.1° and 94.2° with slightly elongated Mo–Ga bonds (average 2.462 Å; shortest bond: 2.385 Å).11 Comparing 2 (both independent molecules in the elementary cell) to the ideal octahedral geometry yielded only minor deviation, giving SQ(P) = 0.20. Both GaCp* and GaTMP are closely related ligands and formally isolobal to CO but are predominantly σ-donor ligands with notably weak π-backbonding.7,24,27,40 The slightly shortened M–GaTMP distances with respect to the M–GaCp* distances may be taken as an indication of more significant π-backbonding of GaTMP, compared to GaCp*. This effect is more clearly observed when comparing 2 to its homologue [Mo(GaCp*)6] although no such direct comparison is available for 1; however, an indirect comparison to the series of previously reported Ru–GaCp* supports this assignment.11,24,27,29–34,36,40 The same trend towards shortened M–Ga bonds when comparing GaTMP to GaCp* can be found across all known M-GaTMP compounds. Seifert et al. reported the investigation of a series of heteroleptic M-GaTMP compounds also bearing carbonyl ligands that afford additional insight because they allow for the direct comparison of M–CO vs. M–Ga distances. They observed shorter M–Ga and longer M–CO distances for the TMP stabilized gallium(I) ligand, leading to the suggestion of more pronounced π-backbonding for GaTMP compared to GaCp*.24
Although a square pyramidal ligand sphere around a Ru(0) centre is not uncommon,41,42 mononuclear, homoleptic compounds of Ru(0) with this structure are still rare in the literature. The only known examples are Ru(CO)5, Ru(NO)5 and bis(2,3,4,5-tetramethylthiophene)ruthenium.43,44 These compounds, however, rely on ligands with strong π-backbonding, whereas 1 has primarily only σ-donating ligands. To gain more insights into the structure and bonding situation of 1, we performed DFT calculations starting with the experimental square pyramidal (SP) structure of the molecular crystal structure as the input for modelling 1SP and from a hypothetical, ideal trigonal bipyramidal (TB) structure for modelling 1TB. The model structures 1SP and 1TB were optimized at the BP86/TZVPP level of theory (see computational details), and frequency calculations were performed to ascertain that the optimized structure is true energy minima. The trigonal bipyramidal structure 1TB shows a distortion in the equatorial plane with Gaeq–Ru–Gaeq angles of 110°, 118° and 130°, most notable in the outer coordination sphere (Neq–Ru–Neq angles of 104°, 112° and 142°). The axial distortion is also significant with the angles Gaax–Ru–Gaax = 161° and Nax–Ru–Nax = 153°. Although both computed structure models 1SP and 1TB (Fig. S20†) are highly distorted compared to the ideal square pyramidal and trigonal bipyramidal geometries, they are both energy minima structures, as shown by the frequency calculations. On the energetic side, the ΔE and ΔG between 1SP and 1TB are very small (0.9 and 2.0 kcal mol−1 respectively, Table 1) and, with respect to the precision of DFT energies, are not significant. Additionally, the HOMO–LUMO gaps are nearly identical (Table 1), indicating similar electronic structures. The NMR data show only one GaTMP signal group. This indicates a rapid exchange between both structures in the solution, while the observed crystal structure might be favored by the packing effects.
| Complexes | HOMO–LUMO Gap [eV] | ΔE [kcal mol−1] | ΔG [kcal mol−1] |
|---|---|---|---|
| [Ru(GaTMP)5] (1SP) | 2.56 | 0.9 | 2.0 |
| [Ru(GaTMP)5] (1TB) | 2.51 | ||
| [Ru(GaNMe2)5] (1NMe2 SP) | 3.02 | 0.0 | 0.2 |
| [Ru(GaNMe2)5] (1NMe2 TB) | 3.08 | ||
| [Mo(GaTMP)6] (2) | 3.10 | ||
| [Mo(GaNMe2)6] (2NMe2) | 3.15 |
To facilitate a straightforward bonding analysis, a simplified model of 1 based on GaNMe2 model ligands was employed and calculated (1NMe2), and the molecular orbitals were analyzed (Fig. S21†). The primary coordination sphere shows a distortion similar to 1SP and 1TB. Beyond the expected σ-donating properties of the Ga-amide (Fig. S19†), the orbital analysis shows the occupied π orbital of the Ga–N bond to interact with the dyz and dxz orbitals in the HOMO-7 and HOMO-8 (Fig. 4). This behavior of the gallium(I) amide ligand is also observed for the 2NMe2 (Fig. S22†) model complex (HOMO-6, -7 and -8, Fig. 4) and is in line with the bonding model for TM–ER, i.e. competing TM → E π-back-donation and E ← R π-donation when R has at least one occupied pπ-orbital.13
 | ||
| Fig. 4 Occupied molecular orbitals of 1NMe2 (a) and 2NMe2 (b) showing π interactions between the GaNMe2 ligand and the transition metal. | ||
Conclusion
[Ru(GaTMP)5] (1) and [Mo(GaTMP)6] (2) were prepared by ligand substitution from the olefinic precursor compounds. [Ru(GaTMP)5] is a rare example of homoleptic Ru(0) complexes and the first case where the ligand sphere is dominated by σ-donation. [Mo(GaTMP)6] was prepared similarly to [Mo(GaCp*)6] though notably without the need for supporting hydrogenolysis of the butadiene ligands of the Mo(0)-precursor and exhibits the same trends observed in the ruthenium compound. The compounds were characterized using crystallography, 1H and 13C-NMR, IR spectroscopy, high-resolution mass spectrometry and elemental analysis. Bond lengths between the title compounds and previously reported TM–GaCp* compounds were analyzed, and the results were compared to homologous homoleptic and heteroleptic transition metal-GaCp*/GaTMP compounds that have been reported previously. The findings indicate that the Ru–GaTMP bond, though primarily dominated by the σ-donor property of the gallium amide ligand, exhibits competing π interaction between the π-back-bonding of the ruthenium and the π-donation of the amide to the gallium. The precursor complexes and possible intermediates, such as 1 and 2, require a thorough theoretical investigation of their bonding situation. The translation of this difference between GaTMP and GaCp* in ligand properties into synthetic access to novel intermetalloid clusters [MaGab](TMP)c is the subject of ongoing research by our group.Experimental
All manipulations were carried out using standard Schlenk and glovebox techniques under argon atmospheres. Solvents were dried and degassed using an MBraun Solvent Purification System. The final H2O content of all solvents was checked by Karl Fischer titration and was below 5 ppm. Tris(butadiene)-molybdenum was prepared from MoCl5 according to the literature-known procedures and characterized by 1H-NMR (see ESI Fig. S7†).45,46 (GaTMP)4 was prepared from GaCp* according to the literature.20 NMR spectra were recorded using a Bruker Avance III AV400US (25 °C; 1H, 400 MHz; 13C, 101 MHz). Chemical shifts are given relative to trimethylsilane and were referenced to the residual solvent peak as internal standards. Chemical shifts are reported in parts per million, downfield shifted from TMS, and are consecutively reported as position (δH or δC), relative integral, multiplicity (s = singlet, and m = multiplet) and assignment. FTIR spectra were measured with an ATR setup using a Bruker Alpha FTIR spectrometer under an argon atmosphere inside a glovebox. Liquid Injection Field Desorption Ionization Mass Spectrometry (LIFDI-MS) was measured directly from an inert atmosphere glovebox with a Thermo Fisher Scientific Exactive Plus Orbitrap (mass accuracy 3 ppm; external calibration) equipped with an ion source from Linden CMS.47 Reference isotope patterns were calculated using enviPat Web.48Computational details
Computational modelling of the molecular structures was performed using the ORCA5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 software package with the exchange–correlation functional BP86.50 Grimme's Dispersion correction, including Becke–Johnson damping (D3BJ),51,52 was used. The structure optimization and analytical calculations of the Hessian were performed using Ahlrich's def2-TZVPP basis set53 with the auxiliary basis def2/J.54
49 software package with the exchange–correlation functional BP86.50 Grimme's Dispersion correction, including Becke–Johnson damping (D3BJ),51,52 was used. The structure optimization and analytical calculations of the Hessian were performed using Ahlrich's def2-TZVPP basis set53 with the auxiliary basis def2/J.54
Synthesis and analytical data of Ru(GaTMP)5 (1)
A 50 mL Schlenk-tube was loaded with a sample of 49.0 mg [(COD)(COT)Ru] (0.16 mmol, 1.00 eq.), and a sample of 164 mg (GaTMP)4 (0.78 mmol, 1.22 eq.) and the two solids were then dissolved in 5 mL of toluene. The orange-coloured solution was then stirred at 100 °C for 19 h; during this time, a change in colour to dark red occurred. Removing the liquid in vacuo yielded a brown solid, which was extracted with 10 mL n-hexane. The resulting solution was reduced in vacuo to 1/3 volume and cooled to −80 °C overnight. A brown, crystalline product suitable for SC-XRD was isolated from the reddish-brown supernatant solution via filtration at −78 °C and dried in vacuo. This yielded 35.0 mg (30 μmol, 20%) of [Ru(GaTMP)5] (1) as brown crystals. 1H-NMR (C6D6): δ (ppm) = 1.34 [t, 3JHH = 6.05 Hz, 20 H, (CH3)2CCH2], 1.57 [m, 10 H, CH2CH2CH2], 1.71 [s, 60 H, CH3]. 13C-NMR (C6D6): δ (ppm) = 18.9 [CH2CH2CH2], 36.3 [CH3], 41.0 [CH2CH2CH2], 55.2 [C(CH3)2]. C45H90Ga5N5Ru (1150.94): calcd C 46.96, H 7.88, Ga 30.29, N 6.09, Ru 8.78; found C 47.31, H 8.12, N 6.14. LIFDI-MS: m/z 1151.25 [M]+ (calcd. m/z 1151.25).Synthesis and analytical data of [Mo(GaTMP)5] (2)
A 100 mL Schlenk-tube was loaded with a sample of 100 mg [(η4-C4H6)3Mo] (385.8 μmol, 1.00 eq.), and a sample of 485 mg (GaTMP)4 (2.31 mmol, 6.00 eq.) and both solids were dissolved in 30 mL toluene. The solution was stirred at 110 °C for 22 hours. The liquid was removed in vacuo, and the remaining solid was extracted with 5 ml boiling hexane. The resulting solution was set to 0 °C overnight, after which a beige, crystalline product was isolated via filtration and then dried in vacuo, affording 218 mg of [Mo(GaTMP)6] (2) (160.8 μmol, 42%). 1H-NMR (Tol-d8): δ (ppm) = 1.35 [t, 3JHH = 6.11 Hz, 24 H, (CH3)2CCH2], 1.60 [m, 12 H, CH2CH2CH2], 1.73 [s, 72 H, CH3]. 13C-NMR (Tol-d8): δ (ppm) = 18.9 [CH2CH2CH2], 36.6 [CH3], 41.2 [CH2CH2CH2], 55.1 [C(CH3)2]. C54H108Ga6MoN6 (1355.79) Calc: C 47.84; H 8.03; N 6.20; Mo 7.08; Ga 40.86. Found: C 47.40; H 8.07; N 5.98. LIFDI-MS: m/z 1356.32 [M]+ (calcd. m/z 1356.32).Author contributions
R. B. and R. J. J. W. contributed equally. R. B.: experimental work, DFT calculations, data analysis and manuscript preparation. R. J. J. W.: experimental work, data analysis, and manuscript preparation. J. S.: SC XRD data acquisition and structure refinement. M. M.: experimental work. B. M. T. B.: experimental work. C. G.: CSHM calculations, research supervision and manuscript preparation. R. A. F.: research conception and manuscript preparation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the German Research Foundation (DFG) within a Reinhart Koselleck Project (FI-502/44−1). The authors thank Fabrizio Napoli M.Sc. (TUM) for providing IR reference data.References
- W. Uhl, M. Pohlmann and R. Wartchow, Angew. Chem., Int. Ed., 1998, 37, 961–963 CrossRef CAS PubMed.
- P. Jutzi, B. Neumann, L. O. Schebaum, A. Stammler and H.-G. Stammler, Organometallics, 1999, 18, 4462–4464 CrossRef CAS.
- B. Buchin, T. Steinke, C. Gemel, T. Cadenbach and R. A. Fischer, Z. Anorg. Allg. Chem., 2005, 631, 2756–2762 CrossRef CAS.
- T. Steinke, C. Gemel, M. Winter and R. A. Fischer, Angew. Chem., Int. Ed., 2002, 41, 4761–4763 CrossRef CAS PubMed.
- R. J. Wright, M. Brynda, J. C. Fettinger, A. R. Betzer and P. P. Power, J. Am. Chem. Soc., 2006, 128, 12498–12509 CrossRef CAS PubMed.
- S. P. Green, C. Jones and A. Stasch, Inorg. Chem., 2007, 46, 11–13 CrossRef CAS PubMed.
- C. Gemel, T. Steinke, M. Cokoja, A. Kempter and R. A. Fischer, Eur. J. Inorg. Chem., 2004, 2004, 4161–4176 CrossRef.
- S. González-Gallardo, T. Bollermann, R. A. Fischer and R. Murugavel, Chem. Rev., 2012, 112, 3136–3170 CrossRef PubMed.
- C. Jones and A. Stasch, in The Group 13 Metals Aluminium, Gallium, Indium and Thallium: Chemical Patterns and Peculiarities, vol. 285, John Wiley & Sons, 2011 Search PubMed.
- R. A. Fischer and J. Weiß, Angew. Chem., Int. Ed., 1999, 38, 2830–2850 CrossRef PubMed.
- T. Bollermann, T. Cadenbach, C. Gemel, K. Freitag, M. Molon, V. Gwildies and R. A. Fischer, Inorg. Chem., 2011, 50, 5808–5814 CrossRef CAS PubMed.
- W. Hieber and U. Teller, Z. Anorg. Allg. Chem., 1942, 249, 43–57 CrossRef CAS.
- W. R. Robinson and D. P. Schussler, Inorg. Chem., 1973, 12, 848–854 CrossRef CAS.
- J. Uddin and G. Frenking, J. Am. Chem. Soc., 2001, 123, 1683–1693 CrossRef CAS PubMed.
- J. Uddin, C. Boehme and G. Frenking, Organometallics, 2000, 19, 571–582 CrossRef CAS.
- J. Weßing, C. Ganesamoorthy, S. Kahlal, R. Marchal, C. Gemel, O. Cador, A. C. H. Da Silva, J. L. F. Da Silva, J.-Y. Saillard and R. A. Fischer, Angew. Chem., Int. Ed., 2018, 57, 14630–14634 CrossRef PubMed.
- M. Schütz, C. Gemel, M. Muhr, C. Jandl, S. Kahlal, J.-Y. Saillard and R. A. Fischer, Chem. Sci., 2021, 12, 6588–6599 RSC.
- I. Antsiburov, M. Schütz, R. Bühler, M. Muhr, J. Stephan, C. Gemel, W. Klein, S. Kahlal, J.-Y. Saillard and R. A. Fischer, Inorg. Chem., 2024, 63, 3749–3756 CrossRef CAS PubMed.
- M. Muhr, J. Stephan, L. Staiger, K. Hemmer, M. Schütz, P. Heiß, C. Jandl, M. Cokoja, T. Kratky, S. Günther, D. Huber, S. Kahlal, J.-Y. Saillard, O. Cador, A. C. H. Da Silva, J. L. F. Da Silva, J. Mink, C. Gemel and R. A. Fischer, Commun. Chem., 2024, 7, 29 CrossRef CAS PubMed.
- M. Muhr, H. Liang, L. Allmendinger, R. Bühler, F. E. Napoli, D. Ukaj, M. Cokoja, C. Jandl, S. Kahlal, J.-Y. Saillard, C. Gemel and R. A. Fischer, Angew. Chem., Int. Ed., 2023, 62, e202308790 CrossRef CAS PubMed.
- C. Ganesamoorthy, J. Weßing, C. Kroll, R. W. Seidel, C. Gemel and R. A. Fischer, Angew. Chem., Int. Ed., 2014, 53, 7943–7947 CrossRef CAS PubMed.
- M. Molon, C. Gemel, M. von Hopffgarten, G. Frenking and R. A. Fischer, Inorg. Chem., 2011, 50, 12296–12302 CrossRef CAS PubMed.
- T. Cadenbach, T. Bollermann, C. Gemel, M. Tombul, I. Fernandez, M. v. Hopffgarten, G. Frenking and R. A. Fischer, J. Am. Chem. Soc., 2009, 131, 16063–16077 CrossRef CAS PubMed.
- A. Seifert and G. Linti, Inorg. Chem., 2008, 47, 11398–11404 CrossRef CAS PubMed.
- B. N. Anand, I. Krossing and H. Nöth, Inorg. Chem., 1997, 36, 1979–1981 CrossRef CAS PubMed.
- F. Dankert and E. Hevia, Chem. – Eur. J., 2024, 30, e202304336 CrossRef CAS PubMed.
- A. Seifert and G. Linti, Eur. J. Inorg. Chem., 2007, 2007, 5080–5086 CrossRef.
- W. Zou, Y. Tao and E. Kraka, J. Chem. Theory Comput., 2020, 16, 3162–3193 CrossRef CAS PubMed.
- M. Muhr, R. Bühler, H. Liang, J. Gilch, C. Jandl, S. Kahlal, J.-Y. Saillard, C. Gemel and R. A. Fischer, Chem. – Eur. J., 2022, 28, e202200887 CrossRef CAS PubMed.
- T. Steinke, M. Cokoja, C. Gemel, A. Kempter, A. Krapp, G. Frenking, U. Zenneck and R. A. Fischer, Angew. Chem., Int. Ed., 2005, 44, 2943–2946 CrossRef CAS PubMed.
- M. Cokoja, C. Gemel, T. Steinke, F. Schröder and R. A. Fischer, Dalton Trans., 2005, 44–54 RSC.
- B. Buchin, C. Gemel, A. Kempter, T. Cadenbach and R. A. Fischer, Inorg. Chim. Acta, 2006, 359, 4833–4839 CrossRef CAS.
- T. Cadenbach, C. Gemel, T. Bollermann and R. A. Fischer, Inorg. Chem., 2009, 48, 5021–5026 CrossRef CAS PubMed.
- T. Cadenbach, C. Gemel, R. Schmid, M. Halbherr, K. Yusenko, M. Cokoja and R. A. Fischer, Angew. Chem., Int. Ed., 2009, 48, 3872–3876 CrossRef CAS PubMed.
- R. Bühler, M. Muhr, J. Stephan, R. A. Wolf, M. Schütz, C. Gemel and R. A. Fischer, Dalton Trans., 2023, 52, 10905–10910 RSC.
- T. Cadenbach, T. Bollermann, C. Gemel and R. A. Fischer, Dalton Trans., 2009, 322–329 RSC.
- A. G. Blackman, E. B. Schenk, R. E. Jelley, E. H. Krenske and L. R. Gahan, Dalton Trans., 2020, 49, 14798–14806 RSC.
- X. Wang and L. Andrews, J. Phys. Chem. A, 2005, 109, 9021–9027 CrossRef CAS PubMed.
- H.-G. Cho and L. Andrews, J. Am. Chem. Soc., 2005, 127, 8226–8231 CrossRef CAS PubMed.
- P. Jutzi, B. Neumann, G. Reumann and H.-G. Stammler, Organometallics, 1998, 17, 1305–1314 CrossRef CAS.
- M. A. Bennett, M. Bown and D. C. R. Hockless, Aust. J. Chem., 2000, 53, 507–515 CrossRef CAS.
- M. A. Bennett, H. Neumann, A. C. Willis, V. Ballantini, P. Pertici and B. E. Mann, Organometallics, 1997, 16, 2868–2878 CrossRef CAS.
- S. Luo, T. B. Rauchfuss and S. R. Wilson, Organometallics, 1992, 11, 3497–3499 CrossRef CAS.
- W. Manchot and W. J. Manchot, Z. Anorg. Allg. Chem., 1936, 226, 385–415 CrossRef CAS.
- J. R. Dilworth, R. L. Richards, G. J. J. Chen and J. W. McDonald, in Inorg. Synth, 1990, pp. 33–43 Search PubMed.
- W. Gausing and G. Wilke, Angew. Chem., Int. Ed. Engl., 1981, 20, 186–187 CrossRef.
- M. Muhr, P. Heiß, M. Schütz, R. Bühler, C. Gemel, M. H. Linden, H. B. Linden and R. A. Fischer, Dalton Trans., 2021, 50, 9031–9036 RSC.
- M. Loos, C. Gerber, F. Corona, J. Hollender and H. Singer, Anal. Chem., 2015, 87, 5738–5744 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2341048 and 2341049. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00823e |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |


