Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of tuning decision trees in random forest regression on predicting porosity of a hydrocarbon reservoir. A case study: volve oil field, north sea
Kushan
Sandunil
 *a,
Ziad
Bennour
*a,
Ziad
Bennour
 a,
Hisham
Ben Mahmud
a,
Hisham
Ben Mahmud
 b and
Ausama
Giwelli
b and
Ausama
Giwelli
 cd
cd
aCurtin University Malaysia, 98009 Miri, Sarawak, Malaysia. E-mail: kwkushan@postgrad.curtin.edu.my
bUniversiti Teknologi PETRONAS, 32610 Seri Iskandar, Perak Darul Ridzuan, Malaysia
cINPEX, 100 St Georges Terrace, 6000 Perth, WA, Australia
dWASM, Curtin University, Kensington, WA 6151, Australia
First published on 8th August 2024
Abstract
Machine learning (ML) has emerged as a powerful tool in petroleum engineering for automatically interpreting well logs and characterizing reservoir properties such as porosity. As a result, researchers are trying to enhance the performance of ML models further to widen their applicability in the real world. Random forest regression (RFR) is one such widely used ML technique that was developed by combining multiple decision trees. To improve its performance, one of its hyperparameters, the number of trees in the forest (n_estimators), is tuned during model optimization. However, the existing literature lacks in-depth studies on the influence of n_estimators on the RFR model when used for predicting porosity, given that n_estimators is one of the most influential hyperparameters that can be tuned to optimize the RFR algorithm. In this study, the effects of n_estimators on the RFR model in porosity prediction were investigated. Furthermore, n_estimators’ interactions with two other key hyperparameters, namely the number of features considered for the best split (max_features) and the minimum number of samples required to be at a leaf node (min_samples_leaf) were explored. The RFR models were developed using 4 input features, namely, resistivity log (RES), neutron porosity log (NPHI), gamma ray log (GR), and the corresponding depths obtained from the Volve oil field in the North Sea, and calculated porosity was used as the target data. The methodology consisted of 4 approaches. In the first approach, only n_estimators were changed; in the second approach, n_estimators were changed along with max_features; in the third approach, n_estimators were changed along with min_samples_leaf; and in the final approach, all three hyperparameters were tuned. Altogether 24 RFR models were developed, and models were evaluated using adjusted R2 (adj. R2), root mean squared error (RMSE), and their computational times. The obtained results showed that the highest performance with an adj. R2 value of 0.8505 was achieved when n_estimators was 81, max_features was 2 and min_samples_leaf was 1. In approach 2, when n_estimators’ upper limit was increased from 10 to 100, there was a test model performance growth of more than 1.60%, whereas increasing n_estimators’ upper limit from 100 to 1000 showed a performance drop of around 0.4%. Models developed by tuning n_estimators from 1 to 100 in intervals of 10 had healthy test model adj. R2 values and lower computational times, making them the best n_estimators’ range and interval when both performances and computational times were taken into consideration to predict the porosity of the Volve oil field in the North Sea. Thus, it was concluded that by tuning only n_estimators and max_features, the performance of RFR models can be increased significantly.
1. Introduction
Artificial intelligence (AI) has become a popular topic over the past few years due to its immense potential in STEM fields. Machine learning (ML) is a branch of AI where it learns with or without supervision to make predictions. Its abilities to predict or forecast outputs, decrease computational time, and extract features from complex and high-dimensional datasets make it a great tool for working with complex and huge datasets.1–3 The concept of ML was first put forward by Turing.4 Since then, ML has seen a significant improvement with the invention of complex and high-performing algorithms. With the popularity of ML algorithms, like many other engineering sectors, their applicability in reservoir engineering has been tested, especially in porosity prediction. Porosity gives an idea about the fluid storage capacity, and it plays a vital role in the upstream oil and gas industry since it is used in estimating the petroleum initially in place in the reservoir. Core analysis is a reliable and widely accepted approach that is used to estimate porosity. However, this method is expensive and time-consuming. To address these challenges, petroleum engineers and researchers are investigating the applicability of ML in reservoir characterization. Random forest regression (RFR) is one such ML algorithm that has been successfully used to predict porosity. To enhance the performance of ML models, hyperparameter optimization is used. In this research, the effects of one of the main hyperparameters of RFR, the number of decision trees in the forest (n_estimators) when predicting the porosity of a sandstone-dominated section in Volve oilfield have been investigated. Moreover, the behaviours of two other widely used hyperparameters in RFR, the minimum number of samples required to be at a leaf node (min_samples_leaf), and the number of features considered for the best split (max_features) when tuned along with n_estimators, have been studied. Apart from the primary objectives mentioned, this study tested the feasibility of an optimized RFR algorithm in reservoir characterization, specifically porosity prediction, and could be further extended to permeability and saturation predictions in future studies.ML application in reservoir characterization has significantly increased over the last couple of decades due to its ability to tackle regression and classification-type problems.5–7 With the evolution of ML, a notable number of algorithms have been introduced. The artificial neural network (ANN), which uses a parallel processing approach and was developed based on the function of a neuron of a human brain, has been utilized in petrophysical parameter prediction.8,9 Support vector regression (SVR) is another algorithm developed in the initial stages of the ML timeline, and it can handle non-linear relationships between a set of inputs and an output. Moreover, SVR has been utilized widely in reservoir characterization.10–13 The least absolute shrinkage and selection operator (LASSO) regression and Bayesian model averaging (BMA) have also been extensively used in ML-related studies in the literature.14 BMA uses Bayes theorem and LASSO uses residual sums of squares to build a linear relationship between the inputs and the output. BMA and LASSO regressions have been used in permeability modelling in recent studies.5 Apart from petrophysical parameter predictions, ML models have also been used in lithofacies classification.15 Generally, these studies utilized ML approaches to model lithofacies sequences as a function of well-logging data to predict discrete lithofacies distribution at missing intervals.16–18 Besides permeability prediction, water saturation estimation, and lithofacies classification, ML models have been used in reservoir porosity estimation, which is the parameter of focus in this study. ML algorithms, such as ANN, deep learning, and SVR, have been used to predict porosity using logging data, seismic attributes, and drilling parameters.19–21
Apart from the mentioned ML models, the ML approach known as ensemble learning has been applied in many recent studies. Here, ML base models (weaker models) are strategically combined to produce a high-performing and efficient model as shown in Fig. 1. Ensemble ML models have become a popular tool among researchers to predict petrophysical properties due to their ability to reduce overfitting and underfitting.22–26 RFR is one such popular ensemble ML model that was developed by amalgamating multiple decision trees.27
Hyperparameter tuning is a process that is implemented to fine-tune ML algorithms to obtain optimal models.28–30 Several hyperparameters can be controlled in an RFR model, such as n_estimators, max_features, min_samples_leaf, maximum depth of the tree (max_depth), fraction of the original dataset assigned to any individual tree (max_samples), minimum number of samples required to split an internal node (min_samples_split), maximum leaf nodes to restrict the growth of the tree (max_leaf_nodes).
Hyperparameter optimization has been utilized in recent studies related to reservoir characterization. Wang et al. developed an RFR model to predict permeability in the Xishan Coalfield, China.24 Five hyperparameters, n_estimators, max_features, max_depth, min_samples_leaf and min_samples_split, were tuned during hyperparameter optimization. Zou et al. estimated reservoir porosity using a random forest algorithm.31 During the hyperparameter optimization stage, n_estimators, max_features, min_samples_leaf, min_samples_split and max_depth were tuned. Rezaee and Ekundayo tuned n_estimators, min_samples_leaf, min_samples_split, and max_depth during the development of the RFR model used to predict the permeability of precipice sandstone in the Surat Basin, Australia.32
Even though hyperparameters have been tuned during the hyperparameter optimization phase of an ensemble ML model development, the literature lacks studies that specifically focus on the effects of hyperparameter tuning in ensemble learning when predicting petrophysical properties in reservoir characterization. Addressing this research gap, in this study, the authors investigated the influence of one of the most utilized hyperparameters in the literature, namely, the n_estimators of RFR, when predicting the porosity of a hydrocarbon reservoir. Also, the effects of n_estimators were studied along with another two widely used hyperparameters, max_features and min_samples_leaf, when predicting the porosity of the Volve oil field in the North Sea. The study considered a supervised learning regression approach. The workflow of the study consisted of data preprocessing, RFR model development, and model analysis. Several RFR models were developed, including tuning n_estimators, tuning n_estimators along with max_features, tuning n_estimators along with min_samples_leaf, and tuning all three hyperparameters at once under four approaches by integrating grid search optimization and K-fold cross-validation. The models’ performances were evaluated based on the adjusted coefficient of determination (adj. R2), root mean squared error (RMSE), and computational time. Only the three aforementioned hyperparameters were considered due to processing capacity limitations; however, this study is expected to be a solid initiation towards the development of future studies on the effects of hyperparameters in ML algorithms in reservoir characterization.
2. Methodology
The development of an ML model involves multiple steps, namely, data acquisition, data preprocessing, model development, and data analysis.33–35 In this study the abovementioned steps were implemented to develop robust ML models.2.1 Geological setting and dataset
The Volve oil field (Fig. 2) was selected as the study area and the well log data of the field is publicly available. Several ML-related studies have been conducted using the Volve oil field datasets.36–38 It was formed during the Jurassic period by the collapse of adjacent salt ridges. Oil was discovered in the field in 1993 in the middle Jurassic Hugin sandstone formations, identifying it as a clastic reservoir.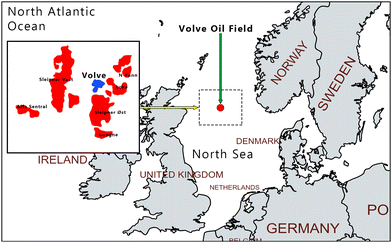 | ||
| Fig. 2 Study area – Volve oil field's location in the North Sea. Adapted from Mapchart.39 | ||
The Hugin Formation is 153 m thick and oil-bearing and was penetrated at 3796.5 m, approximately 60 m deeper than expected. The total oil column in the well was 80 m, but no clear oil–water contact was observed.38,40 The reservoir section was made up of highly variable fine to coarse-grained, well to poorly-sorted subarkosic arenite sandstones with good to excellent reservoir properties. The Hugin Formation of the area consists of a shallow marine shoreface, coastal plain/lagoonal, channel, and possibly mouth bar deposits. The underlying Skagerrak Formation was completely tight due to extensive kaolinite and dolomite cementation. The current study used data from well 15/9-19A. The well was drilled through the Skagerrak Formation and terminated approximately 30 m into the Triassic Smith Bank Formation. To fully utilize the available data, the study considered data from the 3666.59 to 3907.08 m depth interval. This depth interval ran through three formations, namely, Draupne, Heather, and Hugin. The stratigraphic column and description of the vertical facies distribution of the section are shown in Fig. 3.
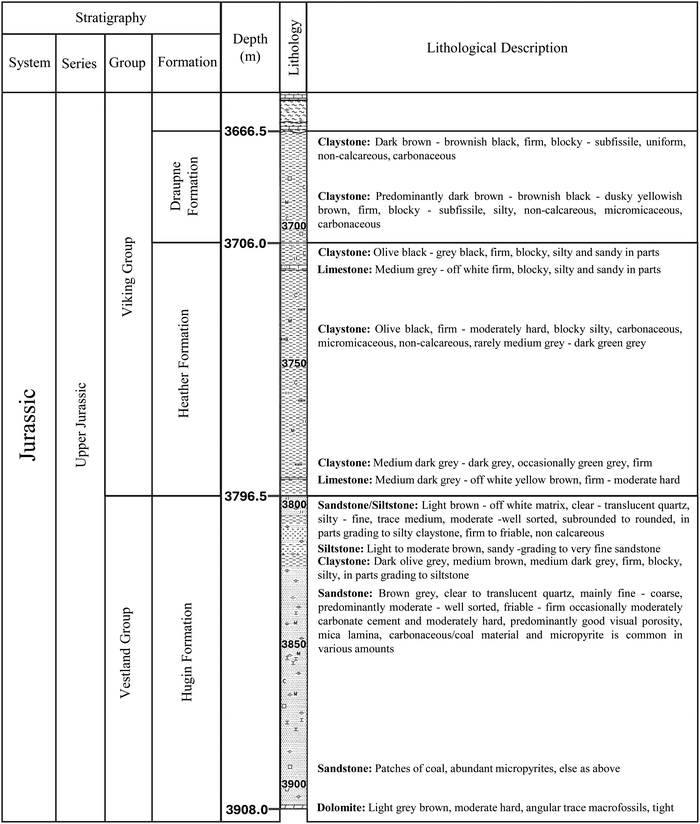 | ||
| Fig. 3 Stratigraphic column and facies description of the considered subsurface section. Adapted from Statoil.41 | ||
The dataset consisted of depth, well log data, and the corresponding calculated porosity values and had a total of 1547 data points. Three well log parameters, namely, resistivity log (RES), neutron porosity log (NPHI), and gamma-ray log (GR) along with corresponding depth were used as input features, and total porosity (PHIF) was used as the target data. PHIF was calculated using porosity from the density log (PHID) and NPHI. PHIF was derived from the density log, which was calibrated to overburden corrected core porosity for wells drilled with either oil-based mud or water-based mud. NPHI was used to correct for varying mud filtrate invasion. Eqn (1) and (2) were used to calculate PHIF and PHID, respectively.
| PHIF = PHID + A × (NPHI − PHID) + B | (1) |
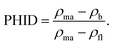 | (2) |
2.2 Data preprocessing
The raw data acquired from the Volve oil field was subjected to data preprocessing before it was used in ML model development. Three main data preprocessing practices, namely, (i) data cleaning, (ii) feature scaling, and (iii) data division, were utilized in this study.42–49 Under data cleaning, missing values and outliers were identified. Missing values were the sections where data points were missing from the dataset. Outliers include the data that were outside of a considered range in each feature. The interquartile range method was used to detect the outliers. Both missing data and outliers were treated by removing them completely from the dataset.50,51Feature scaling is also a common practice implemented during data preprocessing. There are two widely used feature scaling approaches in the literature, namely, normalization and standardization. However, in this study feature scaling was neglected since RFR is a tree-based ML model where splits do not change with any monotonic transformation.52
Data division was carried out by splitting the dataset into 2 parts for training and testing. The training portion was used to train the ML models while the testing portion was used to test the trained models. The train-test ratio was considered as 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, i.e., 80% of the total dataset was allocated for training while the remaining 20% was used for testing.53,54
20, i.e., 80% of the total dataset was allocated for training while the remaining 20% was used for testing.53,54
2.3 Machine learning model development
The RFR model is a combination of multiple decision trees. A typical architecture of an RFR model is shown in Fig. 4. Segal demonstrated the random forest algorithm mathematically as h(x;θr), r = 1,…,R, where x represents the observed input vector associated with the vector X.55X and θr are independent and identically distributed random vectors. For mathematical clarification we define a vector with numerical outcomes Y. Therefore, the training dataset of the RFR can be assumed to be drawn from a joint distribution of (X,Y).For regression, the random forest prediction is the unweighted average over the collection:
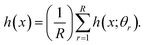 | (3) |
As r → ∞, the Law of Large Numbers ensures
EX,Y(Y − ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) (X))2 → EX,Y(Y − Eθh(X;θ))2. (X))2 → EX,Y(Y − Eθh(X;θ))2. | (4) |
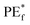 . The convergence in eqn (4) implies that random forests do not overfit.
. The convergence in eqn (4) implies that random forests do not overfit.
Next, we define the average prediction error for an individual tree as h(X;θ)
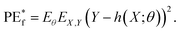 | (5) |
Assuming that for all θ the tree is unbiased, i.e., 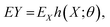 then
then
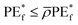 | (6) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) is the weighted correlation between residuals Y − h(X;θ) and Y − h(X;θ′) for independent θ,θ′.
is the weighted correlation between residuals Y − h(X;θ) and Y − h(X;θ′) for independent θ,θ′.
The inequality shown by eqn (6) highlights what is required for accurate RFR, which is having a low correlation between residuals of differing tree members of the forest and low prediction error for the individual trees. The model's performance can be further enhanced by tuning its hyperparameters.
During the study, RFR models were developed using the Python programming language. The cleaned dataset obtained during the data preprocessing stage was loaded into Python, then split into training and testing. The Python-based scikit-learn library's RandomForestRegressor was used to develop the RFR algorithm. The RandomForestRegressor comes with default hyperparameters built into it. Default values assigned to some of the main hyperparameters of RFR in scikit-learn are given in Table 1.
| Hyperparameter | Default value |
|---|---|
| n_estimators | 100 |
| max_features | 1.0 |
| min_samples_leaf | 1 |
| max_depth | None |
| max_samples | None |
| min_samples_split | 2 |
| max_leaf_nodes | None |
However, rather than using the default hyperparameters assigned by the scikit-lean library, to achieve the primary objectives of the study, hyperparameter optimization was implemented. Hyperparameter optimization is a commonly used practice to build robust ML models.56,57 The hyperparameters of RFR were tuned using the grid search optimization (GSO) approach. For this, the GridSearchCV optimization algorithm in the scikit-learn library was used. GSO was considered since it runs through all the possible combinations in the hyperparameter space, thus selecting the best combination of the space.57,58 The hyperparameter space was predefined by including the possible values and it was fed into the GSO algorithm.
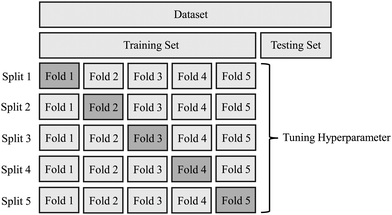
GSO was implemented along with random subsampling cross-validation. An approach known as the K-fold cross-validation was used. During the K-fold cross-validation, the training dataset is divided into K number of same-sized portions (folds), and K − 1 of the portions are used for training and the remainder are used for validation.59,60 This is repeated until each fold gets the chance to be the validation set. For this study, a 5-fold cross-validation was implemented as shown in Fig. 5. Therefore, the training set was divided into five portions and during each split, four portions were used for training and one portion was used for validation.
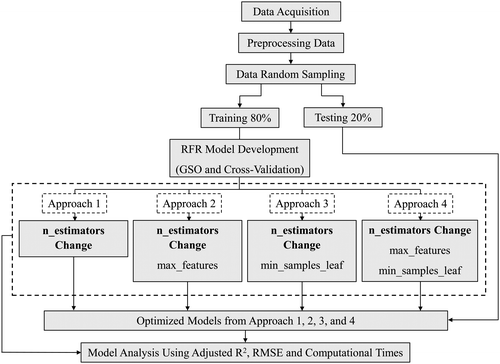
Tuning was done under 4 approaches as shown in Fig. 6 to investigate the effects of the considered hyperparameters. In the first approach, n_estimators was changed from 1 to 10, 1 to 100, and 1 to 1000 in different intervals. The notation used to demonstrate the n_estimators change is shown in Table 2.
| n_estimators change notation | Starting value | Ending value | Increment |
|---|---|---|---|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 10 | 1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 100 | 1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
1 | 100 | 10 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 | 1000 | 1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
1 | 1000 | 10 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1 | 1000 | 100 |
In the second approach, n_estimators was changed from 1 to 1000 in the same way as approach 1 along with max_features. Here, max_features was changed from 10% to 100% of total features in increments of 10%. In the third approach, n_estimators was changed in the same way along with min_samples_leaf. In this case, min_samples_leaf was changed from 1 to 20 in intervals of 1. In the fourth approach, all 3 hyperparameters, i.e., n_estimators, max_features and min_samples_leaf were varied at the same time in the above-mentioned intervals. In each approach, values of all the other hyperparameters of RFR were kept at their default values assigned by the scikit-learn library. The link to the GitHub folder with the developed codes is given in the appendix.
2.4 Results analysis
In the literature, the coefficient of determination (R2) seems to be the go-to statistical parameter to evaluate the performance of the RFR models.61–63 However, an improved version of R2 known as the adjusted coefficient of determination (adj. R2) was used in this study to evaluate the developed models since it takes the number of data points and the number of input features into consideration during evaluation.5 The mathematical equation of R2 is shown in eqn (7). Eqn (8) shows the mathematical equation of adj. R2. The closer the adj. R2 is to 1, the higher the performance of the model.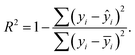 | (7) |
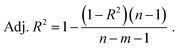 | (8) |
In eqn (7) and (8), yi is the actual value, ŷ is the predicted value, ȳ is the mean value of the distribution, n is the number of data points and m is the number of input features.
Apart from the adj. R2, models were also evaluated using RMSE. The mathematical equation of RMSE is shown in eqn (9).
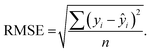 | (9) |
3. Results and discussion
The adj. R2 values obtained using approach 1 of the methodology are tabulated in Table 3. When only n_estimators increased from 1 to 10 in intervals of 1 (keeping all the other hyperparameters at their default values), the model yielded a training adj. R2 of 0.9650, validation adj. R2 of 0.8188 and testing adj. R2 of 0.8024. The training score is higher than the validation (cross-validation) and testing scores as expected since the model is fitted (trained) to the training set and this pattern was observed in all the models developed during the study. In approach 1, when the upper limit of n_estimators value was increased from 10 to 100, the training, validation, and testing scores showed significant increases. The training score had an increase of 1.14%, the validation score had an increase of 2.19%, and the test score had an increase of 2.22%. This rise in performance can be seen in Fig. 7 where the adj. R2 values of the testing models were plotted for each approach.| Model no. | n_estimators change | n_estimators | Adj. R2 | Computational time (s) | ||
|---|---|---|---|---|---|---|
| Training | Validation | Testing | ||||
| M11 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
8 | 0.9650 | 0.8188 | 0.8024 | 0.81 |
| M12 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
51 | 0.9760 | 0.8367 | 0.8202 | 70.25 |
| M13 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
51 | 0.9760 | 0.8367 | 0.8202 | 6.88 |
| M14 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
51 | 0.9760 | 0.8367 | 0.8202 | 6932.55 |
| M15 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
51 | 0.9760 | 0.8367 | 0.8202 | 707.56 |
| M16 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
801 | 0.9799 | 0.8352 | 0.8218 | 65.73 |
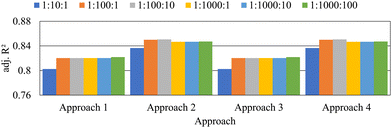 | ||
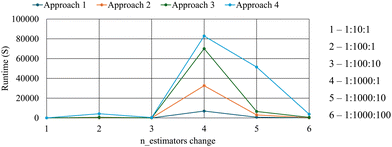
| Fig. 7 Adjusted coefficient of determination values of each approach for different changes in n_estimators. | ||
Interestingly, when the upper limit of the n_estimators range was pushed beyond 100, the performance of the model did not show any noticeable increase in all training validation and testing adj. R2 values. When n_estimators changed from 1 to 100 in intervals 1 and 10 (models M12 and M13) and n_estimators changed from 1 to 1000 in intervals 1 and 10 (models M14 and M15), the models showed the same performance, i.e. a training score of 0.9760, validation score of 0.8367 and a testing score of 0.8202. However, when the n_estimators changed from 1 to 1000 in intervals of 100, the training and testing scores of the M16 model showed a slight increase in performance, yielding an adj. R2 of 0.9799 and 0.8218, respectively. However, the validation score showed a slight decrease, which was negligible.
The highest computational time of 6932.55 seconds was shown by the model M14 where n_estimators changed from 1 to 1000 in increments of 1. The results from approach 1 showed that after a certain n_estimators value, the models’ performances increased drastically and the performance was maintained at a constant value over a certain n_estimators range showing that the performance of the RFR when n_estimators was tuned was efficient within a certain range. Since the range and interval at which the n_estimators values are tuned affect the computational time, an effective range and an interval for n_estimators should be decided upon, taking computational time into account.
In approach 2, max_features were also tuned along with n_estimators. Results obtained using approach 2 of the methodology are tabulated in Table 4. As observed in approach 1, clear spikes in training, validation, and testing adj. R2 values were observed when the upper limit of n_estimators was increased from 10 to 100. The training score had an increase of 1.36%, the validation score had an increase of 1.92%, and the test score had an increase of 1.60%. This clear jump in performance is noticeable in Fig. 7. Interestingly, the performances of the models developed in approach 2 were significantly higher than the performance of the corresponding “n_estimators change” in approach 1. This is quite visible in Fig. 8. Further, going from approach 1 to 2, the average validation score increased by 2.24% and the testing score increased by 3.52%, which was significant. This increase in adj. R2 values is an indication that tuning max_features has a major impact on predicting the porosity using RFR. Model M21, where n_estimators were changed from 1 to 10 in intervals of 1 and max_features were changed from 0.1 to 1 in intervals of 0.1, showed the least performance with a training score of 0.9672, validation score of 0.8381, and a testing score of 0.8366. On the other hand, model M23 showed the highest testing performance with an adj. R2 of 0.8505 where n_estimators changed from 1 to 100 in intervals of 10 and max_features changed from 0.1 to 1 in intervals of 0.1. The model M23 yielded its best test model when n_estimators was 81 and max_features were 0.5. It should be noted that even though model M23 had the highest testing score, the training, and validation scores were not the best out of all the models developed in approach 2. The highest training score of 0.9823 was shown by models M24, M25, and M26. The highest validation scores were shown by models M24 and M25. However, it is more meaningful to select model M23 as the best-performing model since the testing set represents an independent dataset that had never been seen by the model before.
| Model no. | n_estimators change | n_estimators | max_features | Adj. R2 | Computational time (s) | ||
|---|---|---|---|---|---|---|---|
| Training | Validation | Testing | |||||
| M21 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
9 | 0.1 | 0.9672 | 0.8381 | 0.8366 | 3.69 |
| M22 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
79 | 0.5 | 0.9804 | 0.8542 | 0.8500 | 326.56 |
| M23 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
81 | 0.5 | 0.9806 | 0.8541 | 0.8505 | 30.20 |
| M24 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
520 | 0.5 | 0.9823 | 0.8556 | 0.8467 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620.39 620.39 |
| M25 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
521 | 0.5 | 0.9823 | 0.8556 | 0.8467 | 3045.27 |
| M26 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
801 | 0.5 | 0.9823 | 0.8554 | 0.8471 | 284.29 |
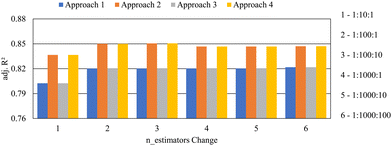 | ||
| Fig. 8 Adjusted coefficient of determination values for each change in n_estimators for different approaches. | ||
The anomaly in the validation score observed when the n_estimators were changed from 1 to 1000 in intervals of 100 in approach 1 was also observable in approach 2. The difference in train–test scores provides an idea about the generalizability of the model. The smaller the train–test difference, the higher the generalizability of the model. Overall, the train–test difference in approach 2 was noticeably less than that of approach 1. The average train–test difference decreased by 15.51% on going from approach 1 to 2. This showed that the generalizability of the models improved when max_features was introduced into the hyperparameter space. Similar to approach 1, the highest runtime was shown when the n_estimators changed from 1 to 1000 in increments of 1.
In approach 3, n_estimators was investigated with the alteration of min_samples_leaf, and the results obtained are tabulated in Table 5. Notably, all the performance results obtained for all the RFR models except the runtimes were the same as that of approach 1, as seen in Fig. 7 and 8. This was because the optimum value selected by the grid search optimization of the min_samples_leaf was the same as the default value assigned by the scikit-learn library for the RFR algorithm, hence the best testing adj. R2 was shown by model M34 when the n_estimators was changed from 1 to 1000 in intervals of 100. Computational times were longer than those obtained in approach 1 since models developed in approach 3 had a larger hyperparameter space as compared to approach 1.
| Model no. | n_estimators change | n_estimators | min_samples_leaf | Adj. R2 | Computational time (s) | ||
|---|---|---|---|---|---|---|---|
| Training | Validation | Testing | |||||
| M31 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
8 | 1 | 0.9650 | 0.8188 | 0.8024 | 7.79 |
| M32 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
51 | 1 | 0.9760 | 0.8367 | 0.8202 | 674.81 |
| M33 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
51 | 1 | 0.9760 | 0.8367 | 0.8202 | 64.96 |
| M34 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
51 | 1 | 0.9760 | 0.8367 | 0.8202 | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 039.55 039.55 |
| M35 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
51 | 1 | 0.9760 | 0.8367 | 0.8202 | 6525.18 |
| M36 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
801 | 1 | 0.9799 | 0.8352 | 0.8218 | 606.28 |
In approach 4, n_estimators was changed along with both max_features and min_samples_leaf. The results in Table 6 show that the performances of the models were the same as that of approach 2. A similar phenomenon caused this performance similarity as observed between approach 1 and approach 3. In this case, the default value for min_samples_leaf was always selected during the tuning process and the max_features selected for the optimum model was similar to that of approach 2. Approach 4 had the longest computational time since 3 hyperparameters had to be tuned simultaneously. The highest runtime for all models was recorded in this approach by model M44, which was 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832.02 seconds. In approach 4, as also observed in approach 2, there was a test model performance increase of 1.60% when the upper limit of n_estimators was increased from 10 to 100. When the upper limit was increased from 100 to 1000, there was a test model performance drop of around 0.4%.
832.02 seconds. In approach 4, as also observed in approach 2, there was a test model performance increase of 1.60% when the upper limit of n_estimators was increased from 10 to 100. When the upper limit was increased from 100 to 1000, there was a test model performance drop of around 0.4%.
| Model no. | n_estimators change | n_estimators | max_features | min_samples_leaf | Adj. R2 | Computational time (s) | ||
|---|---|---|---|---|---|---|---|---|
| Training | Validation | Testing | ||||||
| M41 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
9 | 0.1 | 1 | 0.9672 | 0.8381 | 0.8366 | 56.22 |
| M42 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
79 | 0.5 | 1 | 0.9804 | 0.8542 | 0.8500 | 4242.86 |
| M43 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
81 | 0.5 | 1 | 0.9806 | 0.8541 | 0.8505 | 425.65 |
| M44 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
520 | 0.5 | 1 | 0.9823 | 0.8556 | 0.8467 | 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832.02 832.02 |
| M45 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
521 | 0.5 | 1 | 0.9823 | 0.8556 | 0.8467 | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444.27 444.27 |
| M46 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
801 | 0.5 | 1 | 0.9823 | 0.8554 | 0.8471 | 3796.99 |
Table 7 shows the RMSE values of approaches 1, 2, 3, and 4. While the adj. R2 values give an idea about the correlation between the actual porosities and the predicted porosities, the RMSE values provide an idea about the difference (or the error) between the two. Therefore, RMSE is also an important parameter in ML model performance evaluation. The pattern in which RMSE values fluctuated in the 4 approaches was similar to that of adj. R2. The smallest RMSEs were shown by model M16 with a training model RMSE of 0.9988 and a testing model RMSE of 2.8312. The improvement in the results when max_features was introduced into the hyperparameter space was also evident based on the RMSE values obtained in approach 2. There was a clear decrease in RMSE values in both training and testing models in approaches 2 and 4 where max_features was tuned.
| RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Approach 1 | Approach 2 | Approach 3 | Approach 4 | ||||||||
| Model no. | Training | Testing | Model no. | Training | Testing | Model no. | Training | Testing | Model no. | Training | Testing |
| M11 | 1.2894 | 2.9967 | M21 | 1.2516 | 2.7218 | M31 | 1.2894 | 2.9967 | M41 | 1.2516 | 2.7218 |
| M12 | 1.0817 | 2.8499 | M22 | 0.9835 | 2.5917 | M32 | 1.0817 | 2.8499 | M42 | 0.9835 | 2.5917 |
| M13 | 1.0817 | 2.8499 | M23 | 0.9798 | 2.5875 | M33 | 1.0817 | 2.8499 | M43 | 0.9798 | 2.5880 |
| M14 | 1.0817 | 2.8499 | M24 | 0.9399 | 2.6190 | M34 | 1.0817 | 2.8499 | M44 | 0.9399 | 2.6190 |
| M15 | 1.0817 | 2.8499 | M25 | 0.9396 | 2.6187 | M35 | 1.0817 | 2.8499 | M45 | 0.9396 | 2.6187 |
| M16 | 0.9988 | 2.8312 | M26 | 0.9396 | 2.6148 | M36 | 0.9988 | 2.8312 | M46 | 0.9396 | 2.6148 |
Runtime and grid search combinations had a positive relationship, i.e., when the number of combinations in the grid search space was the largest, the runtime of the model was the highest, and vice versa. Further, it was observed that from approach 1 to approach 3, the increase in computational times was roughly proportional to each other as seen in Fig. 9. However, in approach 4 where n_estimators was changed along with the tuning of max_features and min_samples_leaf, an anomaly was observed when n_estimators was changed from 1 to 1000 in intervals of 10.
Even though the primary objective of the study was to investigate the influences of n_estimators along with max_features and min_samples_leaf on the performance of RFR, having an overall picture of the variation of the actual and predicted porosity and their relationship is important to understand the model's applicability in porosity prediction. To achieve this, depth-porosity graphs and correlation plots were plotted. Fig. 10 shows one such depth-porosity graph and a correlation plot developed for the best-performing RFR test model (model M23) of the study. The depth-porosity plot indicated that most of the time, the predicted porosity followed the pattern of the actual porosity. The correlation plot showed that the majority of the points were scattered around the perfect correlation line, which is an indication of a high correlation between the actual values and the predicted values.
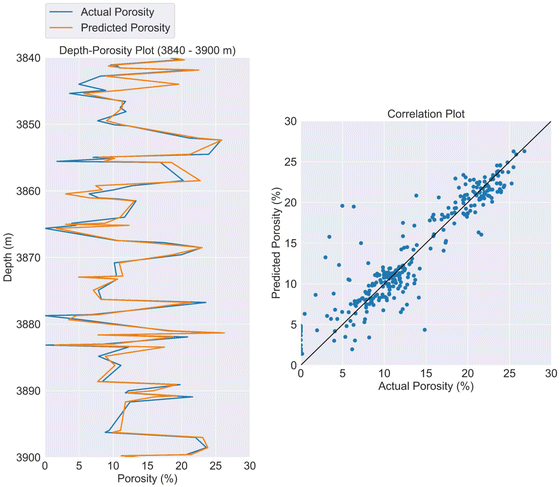 | ||
| Fig. 10 Depth-porosity and correlation plots obtained from the predictions of the best-performing RFR testing model. | ||
4. Conclusions
The aim of this study was to examine the effects of tuning the number of decision trees in the forest (n_estimators) in random forest regression (RFR) for predicting porosity within the Volve oil field in the North Sea. Additionally, the study investigated the influence of n_estimators when tuned with two other commonly used hyperparameters, namely, the number of features to consider when looking for the best split (max_features) and the minimum number of samples required to be at a leaf node (min_samples_leaf). The hyperparameters were tuned using grid search optimization integrating 5-fold cross-validation, and model performances were evaluated based on adj. R2, RMSE, and computational times.• Overall, based on both the performance and computational time, the RFR model with n_estimators at 81 and max_features at 2 (while keeping all the other hyperparameters at their default values), which was developed in approach 2, produced the most effective model for predicting the porosity of the Volve oil field in the North Sea with a testing model adj. R2 of 0.8505, a testing model RMSE of 2.5875, and a computational time of 30.2 seconds.
• There was a notable increase in performance when the upper limit of the n_estimators increased from 10 to 100. On the other hand, the performance of the models did not increase significantly when the upper limit of n_estimators increased from 100 to 1000. This phenomenon indicated that identifying an effective n_estimators range that is not too low (which will make the performance significantly low) and not too high (which will increase the computational time) is important to produce an efficient RFR model during porosity prediction.
• A range of 1 to 100 changed in intervals of 10 can be suggested for n_estimators when developing an RFR model to predict the porosity of the Volve oil field since these models showed higher performances and lower computational times in all four approaches. When the n_estimators range of 1 to 100 was changed in intervals of 10, it always yielded a high adj. R2 value (in approaches 2 and 4, it yielded the highest testing model adj. R2 value) for the model and had the second least computational time.
• When n_estimators was tuned along with max_features in approach 2, the results improved drastically as compared to approach 1 where only n_estimators was tuned. There was an average validation score increase of 2.24% and a testing score increase of 3.52% on going from approach 1 to 2. This improvement of the scores (adj. R2) showed that max_features has a significant influence on the RFR model's performance.
• It was observed that computational time was largely affected by the number of hyperparameters altered, their range, and interval. Of all the approaches, the longest computational time was when n_estimators was tuned from 1 to 1000 in intervals of 1 along with max_features and min_samples_leaf.
Based on the results, only by adjusting n_estimators and max_features can an RFR model be developed with a robust prediction power to estimate the porosity in the Volve oil field.
Recommendations
This study focused on three hyperparameters, namely, n_estimators, max_features and min_samples_leaf. Apart from these hyperparameters, min_samples_split and max_depth are also widely used in the literature during hyperparameter optimization in RFR. Therefore, for future studies, it is recommended that the behaviour of min_samples_split and max_depth along with n_estimators be investigated.Abbreviation
| AI | Artificial intelligence |
| ML | Machine learning |
| RFR | Random forest regression |
| ANN | Artificial neural network |
| SVR | Support vector regression |
| LASSO | Least absolute shrinkage and selection operator |
| BMA | Bayesian model averaging |
| GSO | Grid search optimization |
| RMSE | Root mean squared error |
| R 2 | Coefficient of determination |
| adj. R2 | Adjusted coefficient of determination |
| RES | Resistivity log |
| NPHI | Neutron porosity log |
| GR | Gamma ray log |
| PHIF | Total porosity |
| PHID | Porosity from density log |
| n_estimators | Number of trees in the forest |
| max_features | Number of features considered for the best split |
| min_samples_leaf | Minimum number of samples required to be at a leaf node |
| max_depth | Maximum depth of the tree |
| max_samples | Fraction of the original dataset assigned to any individual tree |
| min_samples_split | Minimum number of samples required to split an internal node |
| max_leaf_nodes | Maximum leaf nodes to restrict the growth of the tree |
| A | A regression coefficient |
| B | A regression coefficient |
| ρ ma | Matrix density |
| ρ b | Measured bulk density |
| ρ fl | Pore fluid density |
| n | Number of datapoints |
| m | Number of input features |
| X | Independent and identically distributed random vector |
| θ r | Independent and identically distributed random vector |
| x | Observed input vector associated with vector X |
| Y | A vector with numerical outcomes |
| y i | Actual value |
| ŷ | Predicted value |
| ȳ | Mean value of the distribution |
Author contributions
Kushan Sandunil: conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization, writing – original draft. Ziad Bennour: conceptualization, methodology, supervision, funding acquisition, resources, writing – review & editing. Hisham Ben Mahmud: supervision, funding acquisition, writing – review & editing. Ausama Giwelli: supervision, writing – review & editing.Data availability
Data for this article, including codes and graphs are available at GitHub at https://github.com/kwkushan/effects-of-tuning-decision-trees-in-random-forest-regression-on-predicting-porosity-kushan-sandunil-. A description about the available files in GitHub repository can be found in the appendix.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Appendix
The authors would like to share open repository folder containing the codes and resources for this study on https://github.com/ and extend an invitation to collaborate through Open Knowledge sharing. In the folder, 4 codes are provided; Code_1 was developed by only tuning n_estimators. Code_2 was developed by tuning n_estimators along with max_features. Code_3 was developed by tuning n_estimators along with min_samples_leaf and the Code_4 was developed by tuning all three hyperparameters, i.e., n_estimators, max_features and min_samples_leaf. The GitHub repository with the developed codes in the study can be accessed via this https://github.com/kwkushan/effects-of-tuning-decision-trees-in-random-forest-regression-on-predicting-porosity-kushan-sandunil-.Acknowledgements
Authors would like to thank Curtin University Malaysia and Curtin Malaysia Postgraduate Research Scholarship (CMPRS) for hosting and allocating the research grant for the study. Further, a special thanks would be given to Equinor and the Volve license partners for making the Volve field dataset available for scientific research (https://discovervolve.com/citation-non-commerciality-clause/).References
- C. Kavuri and S. L. Kokjohn, Exploring the potential of machine learning in reducing the computational time/expense and improving the reliability of engine optimization studies, Int. J. Engine Res., 2020, 21(7), 1251–1270 Search PubMed.
- N. Zhan and J. R. Kitchin, Uncertainty quantification in machine learning and nonlinear least squares regression models, AIChE J., 2022, 68(6), e17516 Search PubMed.
- X. Zhang, Y. Tian, L. Chen, X. Hu and Z. Zhou, Machine learning: a new paradigm in computational electrocatalysis, J. Phys. Chem. Lett., 2022, 13(34), 7920–7930 Search PubMed.
- A. M. Turing, Computing machinery and intelligence, Springer, Netherlands, 2009 Search PubMed.
- W. J. Al-Mudhafar, Bayesian and LASSO regressions for comparative permeability modeling of sandstone reservoirs, Nat. Resour. Res., 2019, 28(1), 47–62 Search PubMed.
- C. Ojukwu, K. Smith, N. Kadkhodayan, M. Leung and K. Baldwin, Reservoir Characterization, Machine Learning and Big Data–An Offshore California Case Study. InSPE Nigeria Annual International Conference and Exhibition 2020 Aug 11 (p. D013S002R005). SPE.
- A. A. Silva, M. W. Tavares, A. Carrasquilla, R. Misságia and M. Ceia, Petrofacies classification using machine learning algorithms, Geophysics., 2020, 85(4), WA101–WA113 Search PubMed.
- M. Amiri, J. Ghiasi-Freez, B. Golkar and A. Hatampour, Improving water saturation estimation in a tight shaly sandstone reservoir using artificial neural network optimized by imperialist competitive algorithm–A case study, J. Pet. Sci. Eng., 2015, 127, 347–358 Search PubMed.
- S. Elkatatny, M. Mahmoud, Z. Tariq and A. Abdulraheem, New insights into the prediction of heterogeneous carbonate reservoir permeability from well logs using artificial intelligence network, Neural Comput. Appl., 2018, 30, 2673–2683 Search PubMed.
- K. O. Akande, T. O. Owolabi, S. O. Olatunji and A. AbdulRaheem, A hybrid particle swarm optimization and support vector regression model for modelling permeability prediction of hydrocarbon reservoir, J. Pet. Sci. Eng., 2017, 150, 43–53 Search PubMed.
- S. Baziar, H. B. Shahripour, M. Tadayoni and M. Nabi-Bidhendi, Prediction of water saturation in a tight gas sandstone reservoir by using four intelligent methods: a comparative study, Neural Comput. Appl., 2018, 30, 1171–1185 Search PubMed.
- F. Anifowose, A. Abdulraheem and A. Al-Shuhail, A parametric study of machine learning techniques in petroleum reservoir permeability prediction by integrating seismic attributes and wireline data, J. Pet. Sci. Eng., 2019, 176, 762–774 Search PubMed.
- M. Z. Kamali, S. Davoodi, H. Ghorbani, D. A. Wood, N. Mohamadian, S. Lajmorak, V. S. Rukavishnikov, F. Taherizade and S. S. Band, Permeability prediction of heterogeneous carbonate gas condensate reservoirs applying group method of data handling, Mar. Pet. Geol., 2022, 139, 105597 Search PubMed.
- W. Al-Mudhafar Integrating bayesian model averaging for uncertainty reduction in permeability modeling. Inoffshore technology conference 2015 May 4 (pp. OTC-25646). OTC.
- G. Wang, Y. Ju, C. Li, T. R. Carr and G. Cheng Application of artificial intelligence on black shale lithofacies prediction in Marcellus Shale, Appalachian Basin. InUnconventional Resources Technology Conference, Denver, Colorado, 25-27 August 2014 2014 Aug 27 (pp. 1970–1980). Society of Exploration Geophysicists, American Association of Petroleum Geologists, Society of Petroleum Engineers.
- W. J. Al-Mudhafar, Integrating well log interpretations for lithofacies classification and permeability modeling through advanced machine learning algorithms, J. Pet. Explor. Prod. Technol., 2017, 7(4), 1023–1033 Search PubMed.
- W. J. Al-Mudhafar, Integrating lithofacies and well logging data into smooth generalized additive model for improved permeability estimation: Zubair formation, South Rumaila oil field, Mar. Geophys. Res., 2019, 40, 315–332 Search PubMed.
- J. Kim, Lithofacies classification integrating conventional approaches and machine learning technique, J. Nat. Gas Sci. Eng., 2022, 100, 104500 Search PubMed.
- S. R. Na’imi, S. R. Shadizadeh, M. A. Riahi and M. Mirzakhanian, Estimation of reservoir porosity and water saturation based on seismic attributes using support vector regression approach, J. Appl. Geophys., 2014, 107, 93–101 Search PubMed.
- A. Al-AbdulJabbar, K. Al-Azani and S. Elkatatny, Estimation of reservoir porosity from drilling parameters using artificial neural networks, Petrophysics, 2020, 61(03), 318–330 Search PubMed.
- W. Chen, L. Yang, B. Zha, M. Zhang and Y. Chen, Deep learning reservoir porosity prediction based on multilayer long short-term memory network, Geophysics, 2020, 85(4), WA213–WA225 Search PubMed.
- F. A. Anifowose Ensemble machine learning: the latest development in computational intelligence for petroleum reservoir characterization. InSPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition 2013 May 19 (pp. SPE-168111). SPE.
- A. Subasi, M. F. El-Amin, T. Darwich and M. Dossary, Permeability prediction of petroleum reservoirs using stochastic gradient boosting regression, J. Ambient Intell. Humaniz. Comput., 2022, 1 Search PubMed.
- J. Wang, W. Yan, Z. Wan, Y. Wang, J. Lv and A. Zhou, Prediction of permeability using random forest and genetic algorithm model, Comput. Model. Eng. Sci., 2020, 125(3), 1135–1157 Search PubMed.
- D. A. Otchere, T. O. Ganat, R. Gholami and M. Lawal, A novel custom ensemble learning model for an improved reservoir permeability and water saturation prediction, J. Nat. Gas Sci. Eng., 2021, 91, 103962 Search PubMed.
- Z. Zhang and Z. Cai, Permeability prediction of carbonate rocks based on digital image analysis and rock typing using random forest algorithm, Energy Fuels, 2021, 35(14), 11271–11284 Search PubMed.
- T. H. Lee, A. Ullah and R. Wang, Bootstrap aggregating and random forest, Macroeconomic forecasting in the era of big data: Theory and practice, 2020, pp. 389–429 Search PubMed.
- M. M. Maher and S. Sakr Smartml: A meta learning-based framework for automated selection and hyperparameter tuning for machine learning algorithms. InEDBT: 22nd International conference on extending database technology 2019 Mar 26.
- L. Yang and A. Shami, On hyperparameter optimization of machine learning algorithms: Theory and practice, Neurocomputing, 2020, 415, 295–316 Search PubMed.
- J. Isabona, A. L. Imoize and Y. Kim, Machine learning-based boosted regression ensemble combined with hyperparameter tuning for optimal adaptive learning, Sensors, 2022, 22(10), 3776 Search PubMed.
- C. Zou, L. Zhao, M. Xu, Y. Chen and J. Geng, Porosity prediction with uncertainty quantification from multiple seismic attributes using random forest, J. Geophys. Res.: Solid Earth, 2021, 126(7), e2021JB021826 Search PubMed.
- R. Rezaee and J. Ekundayo, Permeability prediction using machine learning methods for the CO2 injectivity of the precipice sandstone in Surat Basin, Australia, Energies, 2022, 15(6), 2053 Search PubMed.
- S. García, J. Luengo and F. Herrera, Introduction to data preprocessing, in Data preprocessing in data mining, ed. J. Kacprzyk and L. C. Jain, Springer International Publishing, Cham, Switzerland, 2015, pp. 10–13 Search PubMed.
- V. Gudivada, A. Apon and J. Ding, Data quality considerations for big data and machine learning: Going beyond data cleaning and transformations, Int. J. Adv. Softw., 2017, 10(1), 1–20 Search PubMed.
- K. Maharana, S. Mondal and B. Nemade, A review: Data pre-processing and data augmentation techniques, Global Transit. Proceedings, 2022, 3(1), 91–99 Search PubMed.
- A. Al Ghaithi and M. Prasad Machine learning with artificial neural networks for shear log predictions in the Volve field Norwegian North Sea. InSEG Technical Program Expanded Abstracts 2020 2020 Sep 30 (pp. 450–454). Society of Exploration Geophysicists.
- C. S. Ng, A. J. Ghahfarokhi and M. N. Amar, Well production forecast in Volve field: Application of rigorous machine learning techniques and metaheuristic algorithm, J. Pet. Sci. Eng., 2022, 208, 109468 Search PubMed.
- N. O. Nikitin, I. Revin, A. Hvatov, P. Vychuzhanin and A. V. Kalyuzhnaya, Hybrid and automated machine learning approaches for oil fields development: The case study of Volve field, North Sea, Comput. Geosci., 2022, 161, 105061 Search PubMed.
- Mapchart. World map: simple [Internet]. 2024 [cited 2024 Jul 22]. Available from: https://www.mapchart.net/world.html.
- S. Sen and S. S. Ganguli Estimation of pore pressure and fracture gradient in Volve field, Norwegian North Sea. InSPE Oil and Gas India Conference and Exhibition. 2019 Apr 8 (p. D022S027R002). SPE.
- Statoil. 15/9-19A Well Composite Log, Sleipner, Theta Vest Prospect Structure [Internet]. 1998 [cited 2023 Mar 1]. Available from: https://discovervolve.com/citation-non-commerciality-clause/.
- I. F. Ilyas and X. Chu, Data cleaning, Morgan & Claypool, 2019 Search PubMed.
- A. Jain, H. Patel, L. Nagalapatti, N. Gupta, S. Mehta, S. Guttula, S. Mujumdar, S. Afzal, R. Sharma Mittal and V. Munigala Overview and importance of data quality for machine learning tasks. InProceedings of the 26th ACM SIGKDD international conference on knowledge discovery & data mining 2020 Aug 23 (pp. 3561–3562).
- S. Rawat, A. Rawat, D. Kumar and A. S. Sabitha, Application of machine learning and data visualization techniques for decision support in the insurance sector, Int. J. Inf. Manag. Data Insights, 2021, 1(2), 100012 Search PubMed.
- M. M. Ahamad, S. Aktar, M. Rashed-Al-Mahfuz, S. Uddin, P. Liò, H. Xu, M. A. Summers, J. M. Quinn and M. A. Moni, A machine learning model to identify early stage symptoms of SARS-Cov-2 infected patients, Expert Syst. Appl., 2020, 160, 113661 Search PubMed.
- I. H. Sarker, Y. B. Abushark, F. Alsolami and A. I. Khan, Intrudtree: a machine learning based cyber security intrusion detection model, Symmetry, 2020, 12(5), 754 Search PubMed.
- H. Feizi, H. Apaydin, M. T. Sattari, M. S. Colak and M. Sibtain, Improving reservoir inflow prediction via rolling window and deep learning-based multi-model approach: case study from Ermenek Dam, Turkey, Stoch. Environ. Res. Risk Assess., 2022, 36(10), 3149–3169 Search PubMed.
- J. J. Salazar, L. Garland, J. Ochoa and M. J. Pyrcz, Fair train-test split in machine learning: Mitigating spatial autocorrelation for improved prediction accuracy, J. Pet. Sci. Eng., 2022, 209, 109885 Search PubMed.
- G. M. Mask and X. Wu Deriving New Type Curves through Machine Learning in the Wolfcamp Formation. InSPE Reservoir Characterisation and Simulation Conference and Exhibition. 2023 Jan 24 (p. D011S001R007). SPE.
- T. Emmanuel, T. Maupong, D. Mpoeleng, T. Semong, B. Mphago and O. Tabona, A survey on missing data in machine learning, J. Big Data, 2021, 8, 1–37 Search PubMed.
- M. M. Seliem, HandlingOutlier data as missing values by imputation methods: application of machine learning algorithms, Turk. J. Comput. Math. Educ., 2022, 13(1), 273–286 Search PubMed.
- R. Garcia-Carretero, R. Holgado-Cuadrado and Ó. Barquero-Pérez, Assessment of classification models and relevant features on nonalcoholic steatohepatitis using random forest, Entropy, 2021, 23(6), 763 Search PubMed.
- I. C. Suherman and R. Sarno Implementation of random forest regression for COCOMO II effort estimation. In2020 international seminar on application for technology of information and communication (iSemantic) 2020 Sep 19 (pp. 476–481). IEEE.
- S. Yilmazer and S. Kocaman, A mass appraisal assessment study using machine learning based on multiple regression and random forest, Land use policy, 2020, 99, 104889 Search PubMed.
- M. R. Segal Machine learning benchmarks and random forest regression.
- M. Abbaszadeh, S. Soltani-Mohammadi and A. N. Ahmed, Optimization of support vector machine parameters in modeling of Iju deposit mineralization and alteration zones using particle swarm optimization algorithm and grid search method, Comput. Geosci., 2022, 165, 105140 Search PubMed.
- M. A. Abbas, W. J. Al-Mudhafar and D. A. Wood, Improving permeability prediction in carbonate reservoirs through gradient boosting hyperparameter tuning, Earth Sci. Inform., 2023, 16(4), 3417–3432 Search PubMed.
- K. Sandunil, Z. Bennour, H. Ben Mahmud and A. Giwelli Effects of Tuning Hyperparameters in Random Forest Regression on Reservoir's Porosity Prediction. Case Study: Volve Oil Field, North Sea. InARMA US Rock Mechanics/Geomechanics Symposium 2023 Jun 25 (pp. ARMA-2023). ARMA.
- W. J. Al-Mudhafar Incorporation of bootstrapping and cross-validation for efficient multivariate facies and petrophysical modeling. InSPE Rocky Mountain Petroleum Technology Conference/Low-Permeability Reservoirs Symposium 2016 May 5 (pp. SPE-180277). SPE.
- M. Rahimi and M. A. Riahi, Reservoir facies classification based on random forest and geostatistics methods in an offshore oilfield, J. Appl. Geophys., 2022, 201, 104640 Search PubMed.
- A. A. Mahmoud, S. Elkatatny, W. Chen and A. Abdulraheem, Estimation of oil recovery factor for water drive sandy reservoirs through applications of artificial intelligence, Energies, 2019, 12(19), 3671 Search PubMed.
- H. Al Khalifah, P. W. Glover and P. Lorinczi, Permeability prediction and diagenesis in tight carbonates using machine learning techniques, Mar. Pet. Geol., 2020, 112, 104096 Search PubMed.
- W. M. Ridwan, M. Sapitang, A. Aziz, K. F. Kushiar, A. N. Ahmed and A. El-Shafie, Rainfall forecasting model using machine learning methods: Case study Terengganu, Malaysia, Ain Shams Eng. J., 2021, 12(2), 1651–1663 Search PubMed.
- H. Wang, Z. Lei, X. Zhang, B. Zhou and J. Peng, Machine learning basics, Deep Learning, 2016, 98–164 Search PubMed.
- P. Mehta, M. Bukov, C. H. Wang, A. G. Day, C. Richardson, C. K. Fisher and D. J. Schwab, A high-bias, low-variance introduction to machine learning for physicists, Phys. Rep., 2019, 810, 1–24 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |