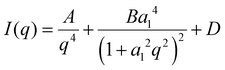The impact of templating and macropores in hard carbons on their properties as negative electrode materials in sodium-ion batteries

Abstract

Due to the abundance of sodium and the comparable working principle to lithium-ion technology, sodium-ion batteries (SIBs) are of high interest as sustainable electochemical energy storage devices. Non-graphitizing (“hard”) carbons are widely investigated as negative electrode materials due to their high sodium storage capacity close to the potential of Na/Na⁺, excellent safety, and simple synthesis pathways from abundant resources. The accumulation of sodium in “closed pores” that are inaccessible to the electrolyte solvent molecules is typically considered as a main source of capacity. While several features such as the microstructure of hard carbons (controllable by e.g. precursors or carbonization conditions) on their electrochemical properties have been widely investigated, the influence of macropores and domain sizes of hard carbons received less research attention. We investigate the use of polystyrene as a sacrificial template to introduce additional internal porosity into glucose-derived hard carbons, in the form of micrometer-sized channels, and the effect on the sodium storage properties and irreversible processes. Despite no significant changes in the microstructure of the hard carbons, pronounced differences in their electrochemical signature can be resolved at working potentials above, but also below 0 V vs. Na/Na⁺ for different polystyrene amounts and thus macropore contents. Carbons with higher polystyrene amount exhibit higher reversible sodium storage capacity, but also suffer from a more pronounced capacity loss due to irreversible reactions in the first cycle(s). Furthermore, their sodium nucleation overpotential is shifted to higher values in capacity limited measurements, which is likely due to the higher electric resistance. The necessary time to achieve full sodiation capacity increases with a lower content of macropores.

---

Introduction

Lithium-ion batteries (LIBs) have emerged as a major state-of-the-art technology for electrochemical energy storage, especially after the commercialisation of the graphite–LiCoO₂ system in the 1990s.^1,2 Due to their high gravimetric and volumetric energy as well as low self-discharge rate, LIBs are nowadays prevalent in portable electronics and in the electric vehicle market.³ Unfortunately, a couple of issues can be foreseen for the expected future growth of the LIB market. The uneven distribution of lithium across the globe causes many political as well as logistical problems. Furthermore, lithium is usually retrieved from brine, which requires a significant amount of water and energy, posing challenges to the water supply of the local population.^4,5 In addition, lithium recycling technology is still in its infancy and highly energy demanding. Hence, the development of technologies with comparable properties but with the utilization of different raw materials is required. Sodium-ion batteries (SIBs) stand out as a promising alternative to LIBs due to the higher abundance and possible economic benefits of sodium. One major advantage of SIBs, compared to other alternative technologies, is that their working mechanism is in large part comparable to LIBs. This will facilitate practical implementation of SIBs as “drop-in technology” in terms of battery production and application.^6,7 Nevertheless, the fact that sodium is a softer ion than lithium due to its larger ion radius at similar charge, changes the cell chemistry especially at the negative electrode. No thermodynamically stable binary intercalation compounds can be formed between sodium and graphite – the commonly applied negative electrode material in LIBs. Studies of sodium ions in a solvation shell of ether electrolyte into graphite, resulting in the formation of ternary graphite intercalation compounds (t-GICs), report about a generally low storage capacity, approximately half of that of LIBs.^8–11

To date, non-graphitizing hard carbon materials (HCs) are the most promising candidates for the use as negative electrode materials in SIBs. HCs have favourable capacities (>300 mA h g⁻¹), a suitable working potential, and a long cycle life. They can be obtained from the pyrolysis of low-cost, abundant, and renewable carbon-rich organic precursors, such as various carbohydrates and biomass.^12,13 In a first approximation, the structure of HC can be explained by the “falling cards model” proposed by Dahn et al.¹⁴ Graphene sheets are stacked randomly, resulting in small, interconnected graphitic domains, with voids formed in between. These so-called “internal pores” or “closed pores” can neither be accessed by most gases in ordinary physisorption measurements, nor by the electrolyte components other than sodium upon cycling.^15,16 Internal pores as well as the spaces between the sheets are both apparently involved in sodium storage, but the detailed mechanism of sodiation in HC is still under discussion. Nowadays, the most accepted mechanism is the “intercalation-micropore filling” suggested by Stevens et al.^17,18 In several small-angle X-ray scattering (SAXS) studies as well as solid-state NMR investigations the sodium clustering inside the closed pores in a quasi-metallic state at potentials around 0 V vs. Na/Na⁺ was observed and discussed as main source of plateau capacity.^19–27

Therefore, in recent years, attention has increasingly turned to obtaining control over the introduction of closed pores in HCs.^28–31 While the contribution of these pores to sodium storage capacity is meanwhile well understood, the effect of their accessibility, that is, of carbon particle sizes and/or larger (open) transport pores on the sodium storage properties of HCs has been less investigated. However, the influence of the length of sodium transport pathways within HC materials of comparable microstructure should play an important role during cycling because sodium transport is considerably slower than electron transport, especially when high uptakes are achieved in the plateau region. For instance, it has been shown that a decrease of the HC particle size by ball-milling prior to electrode fabrication, and the corresponding increase in the external surface area, lead to the opening of closed pores and thus to a decrease of the reversible plateau capacity and an increased contribution of irreversible processes.³² On the other side, it can be generally expected that the decrease of the size of the HC domains (either due to a decrease of the carbon particle size or due to the introduction of additional larger pores into a particle of a given size) decreases the necessary time to achieve the fully available sodium storage capacity. In this regard, there is no systematic knowledge available about the interplay of macroporosity of HCs on the balance between shortening of Na⁺ transport pathways and irreversible capacity loss in the first cycle due to solid electrolyte interphase (SEI) formation on the electrolyte accessible surface area.³³

Polystyrene is possibly a suitable sacrificial template for creating this balance. Since linear polystyrene decomposes completely during carbonization, it can form open and closed voids in HCs, thus contributing to an increase in porosity.³⁴ In this work, polystyrene template particles are applied in order to modify the secondary pore structure and by that the electrochemical properties of HCs for SIB negative electrodes. Through a combined analysis of gas-accessible porosity, total porosity as detected by small-angle X-ray scattering (SAXS), skeletal density, and scanning electron microscopy (SEM) it is shown that the addition of polystyrene alters the structure of HCs by adding extra porosity in a size range suitable to investigate the impact on first-cycle efficiency, the sodium storage capacity as well as the time needed to achieve full sodiation. Moreover, the influence of the template content on the nucleation overpotential of metallic sodium deposition is investigated. For a series of 3 samples with comparable (glucose-derived) HC microstructure but with different macroporosity, it is found that a decreased size of the carbon domains leads to a higher contribution of irreversible processes, but also increases the reversible sodium storage capacity. In contrast, lower macropore content increases the necessary time to achieve full sodiation capacity. The reduced length of sodium transport pathways in more porous carbons come along with an increase of the overpotential needed for the nucleation of bulk sodium, pointing at an increased electric resistance in such materials. Although the structural differences seem to be minor at first glance, they can be resolved with the structural characterization tools, and the underlying structure–property relationships are still found within the electrochemical measurements, which is considered a step towards detailed understanding of structure–property relationships of HC materials when applied as negative electrode materials in SIBs.

Experimental

Materials synthesis

Polystyrene spheres (PS) were synthesized by microemulsion polymerization following the method of Jang et al.³⁵ 3 g of poly-(ethylene oxide)–poly-(propylene oxide)–poly-(ethylene oxide) triblock copolymer Pluronic P65 (EO₂₀PO₃₀EO₂₀, (≥99%, Biosynth Carbosynth)) were dissolved in distilled water (40 mL) and stirred until homogeneity at room temperature. Then 1 g of methyl methacrylate (MMA, Sigma Aldrich,99%) was added to the solution and the mixture was heated to 70 °C. After reaching this temperature, 0.01 g of potassium peroxodisulfate (KPS, Sigma Aldrich, ≥99%) was added. Polymerization of MMA was proceeded at 70 °C by continuously stirring for 2 h. The solution was cooled down to room temperature. After that, styrene (1 g, Sigma Aldrich, stabilised, for synthesis) and divinylbenzene (DVB, 0.1 g, Sigma Aldrich, ≥99%) were added. The system of surfactant/polymethyl methacrylate (PMMA)/styrene solution was heated again to 70 °C and 0.01 g of KPS was added as initiator for the styrene polymerisation. The solution was kept at 70 °C for 2 h at constant stirring. After cooling down to room temperature, the PMMA template and the surfactant were extracted from the solution using dichloromethane (≥99.8%, Sigma Aldrich) and ethanol (≥98%, Sigma Aldrich) as solvents. The solution was left for precipitation of PS particles (24 h) and the precipitated PS spheres were washed with deionized water and dried at room temperature. Inhibitors from MMA, DVB and styrene were removed in advance by the Schlenk-frit technique using basic Al₂O₃ (Sigma Aldrich).

Polystyrene particles were homogeneously dispersed in 20 ml deionized water by an ultrasound homogenizer (Bandelin SONOPULS HD 3400) at 120 W power for 20 minutes. These were then mixed with different amounts of the carbon precursor glucose as described below. The “X” in all sample codes of the different polystyrene-templated hard carbons (PS-HC-X) refer to the mass ratio of glucose : polystyrene. PS-HC-2, for instance, represents the sample prepared with a glucose : PS mass ratio of 2, PS-HC-20 – stands for a glucose : PS mass ratio 20 and HC is a PS-free hard carbon material.

Typically, 4 g D-glucose (≥99%, Sigma Aldrich) and 0.25 ml of concentrated H₂SO₄ (98%, VWR chemicals) were added to the dispersion of the respective amount of PS in water and the mixture was stirred to homogeneity. The mixture was transferred to a porcelain dish, heated in a drying oven (DRY-Line Prime, VWR) to 100 °C and kept at this temperature for 6 h before being heated to 160 °C and held for another 6 h. After this step, the mixture (after grinding in a mortar) was placed in a porcelain-combustion boat, and then pre-carbonized at 600 °C for 1 h under N₂ flow with a heating rate of 10 K min⁻¹ in a horizontal tubular furnace (Carbolite Gero). The final carbonization was carried out in a high temperature oven (LORA, HTM Reetz) at 1700 °C for 1 h under N₂ flow with a heating rate of 7 K min⁻¹.

Characterization of the materials

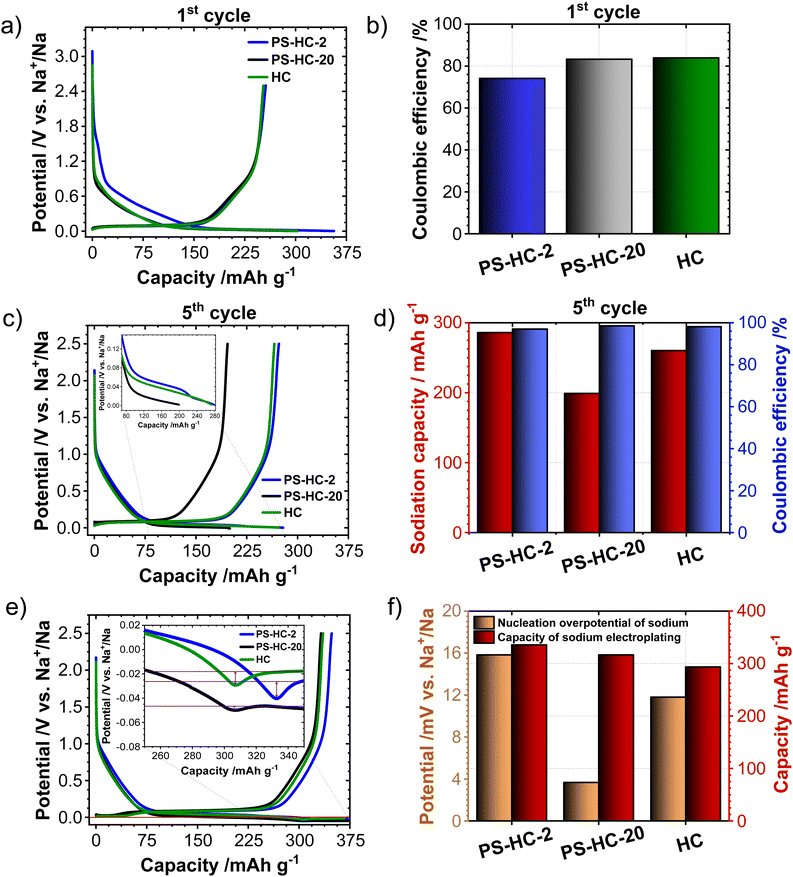
Dynamic light scattering (DLS) measurements of water-dispersed polystyrene spheres (2 mg mL⁻¹) were carried out using a Goniometer (ALV/CGS-3) with a 632.8 nm He–Ne laser at detection angle of 90° at 25 °C. The ALV-7002 FAST Correlator Software was used to calculate the particle size distributions according to the CONTIN algorithm. Thermogravimetric analyses (TGA) were performed on a Netzsch STA 449 in Al₂O₃ crucibles under N₂ in a temperature range from 25 °C to 1000 °C with a heating rate of 10 K min⁻¹. N₂ and CO₂ physisorption measurements were conducted on a gas sorption analyser (Quantachrome Quadrasorb) at −196 °C and 0 °C, respectively. Samples were outgassed at 150 °C under vacuum for 24 h before each physisorption test. For the N₂ physisorption, quenched-solid density functional theory (QSDFT, for N₂ at 77 K on carbon surfaces with slit/cylindrical pores, adsorption branch kernel) was used for the calculation of the specific surface area and pore size distribution (PSD). For the CO₂ isotherms, non-local density functional theory model (NLDFT, for CO₂ at 273 K on carbon, adsorption branch) was used to determine the PSD and ultramicropore volume. H₂O vapor adsorption/desorption isotherms were measured volumetrically using an Autosorb IQ apparatus (Quantachrome Instruments). The analysis temperature was controlled by a circulating-bath temperature controller with an accuracy of 0.1 K. Before the H₂O vapour sorption experiments samples were outgassed at 200 °C under vacuum for 20 h. Density measurements were carried out on a 3P densi 100S gas pycnometer at room temperature using helium as a test gas in a 1 ml measuring cell. The samples were dried for 2 h at 150 °C in a drying oven before measurement. For transmission electron microscopy (TEM) observations of aqueous samples, copper grids were rendered hydrophilic by Ar plasma cleaning for 30 s (Diener Electronics). Sample preparation was carried out by dispersing 4 mg of polystyrene spheres in 2 ml of deionized water. Then 10 μL of the sample was applied to the grid, and excess sample was blotted with a filter paper. TEM-images were acquired with a 200 kV FEI Tecnai G² 20 transmission electron microscope equipped with a 4k × 4k Eagle HS CCD camera and a 1k × 1k Olympus MegaView camera for overview images. In order to obtain transmission electron micrographs of PS-HCs, a suspension of the sample in ethanol was sonicated for 10 minutes and drop-casted on a Cu-grid with a lacey carbon support followed by drying for 15 minutes. The TEM study of PS-HCs was performed using a JEOL JEM-F200 (S)TEM operated at 80 kV and equipped with a field emission gun. TEM images were recorded using a TVIPS TemCam-F216 camera. Scanning electron microscopy (SEM) was performed on a Phenom ProX desktop SEM device using 15 kV acceleration voltage. Elemental analysis (EA) for carbon, hydrogen, and nitrogen (C/H/N) was conducted using a Vario Micro device through combustion analysis. The oxygen content was calculated by subtracting the sum of the obtained amounts of carbon, hydrogen, and nitrogen from 100%. Raman spectra were obtained on a Raman microscope (in Via, Renishaw, 633 nm laser wavelength, 50× LWD objective). Spectra were recorded in the range 500–3600 cm⁻¹ with three accumulations at a laser power was 3.5 mW. The bands were fitted with Lorentz functions in the Origin PRO 2021 software and the I_D/I_G ratios were calculated from the maximum intensities obtained from the fits. Small-angle X-ray scattering (SAXS) patterns were obtained using a Bruker Nanostar 2 instrument with sample-detector distance of 27.70 cm. Cu_Kα radiation (λ = 1.5418 Å) was applied. Generated anode voltage and current were 50 kV and 600 μA, respectively. The focal spot size of the beam was 115 μm in diameter. The samples were filled into borosilicate capillaries with a diameter of 1.5 mm. The intensity calibration was performed as described in the literature.³⁶ Silver behenate was used as calibration material. For analysis of the obtained patterns, the absolute scattering intensity was normalized by the apparent filling density and then fitted with the function of Debye et al.,³⁷ which was used in the work of Stevens and Dahn as scattering intensity from nanopores and macropores.¹⁹
where q is the wavevector, a₁ is the characteristic length over which electron density variations occur, A and B are surface areas of the macro and micro pores, respectively, and D is a constant background term. Powder X-ray diffraction patterns (PXRD) of materials were recorded on a Bruker D2 Phaser in Bragg–Brentano geometry in a 2θ range 10–80° with a step size of 0.02° using Cu_Kα radiation. The anode voltage was 30 kV and the anode current 10 mA. A horizontal silicon single crystal holder was used as a sample holder. In order to determine the 2θ position as well as a full width at half maximum (FWHM) of the obtained reflections, they were separately fitted with a Gaussian function in Origin PRO 2021 software. 2θ positions of the selected reflection corresponded to its centre of gravity. The interlayer distances d₀₀₂ were calculated according to the Bragg equation. The crystallite sizes for (002) and (100) reflections (L_c and L_a, respectively) were calculated using Scherrer equation.

Electrochemical measurements

Before electrode preparation, materials were ground in a mortar and then placed to planetary ball mill Fritsch PULVERISETTE 7 for 15 minutes with 1 reverse repetition at 800 rpm. After that, the powder was passed through an analytical sieve (Retsch) with a mesh size of 56 μm. Then 135 mg of active material was mixed with 7.5 mg of conductive carbon black Super C65 (Imerys Graphite & Carbon) as well as of 375 μL of 20 mg mL⁻¹ water solution of carboxymethylcellulose (CMC, Sigma Aldrich). The mixture was stirred in an impact ball mill Fritsch PULVERISETTE 23 in 50 Hz for 3 minutes, and the obtained slurry was coated onto a carbon covered aluminium foil (MTI Corporation) using a doctor blade at 100 μm wet film thickness at 30 mm s⁻¹. The electrodes were dried 24 hours in a vacuum oven at 70 °C. Discs of 12 mm diameter were punched from the electrode sheets. The areal loading of the electrodes was 1.6–2.4 mg cm⁻², depending mainly on the filling density of the active material. Electrochemical experiments were performed in a two-electrode setup, using Swagelok-type cells and a Biologic MPG-2 potentiostat. The electrolyte was 150 μl of NaPF₆ in 6 : 4 v/v mixture of ethylene carbonate and diethyl carbonate. Sodium metal (Sigma Aldrich) discs were applied as counter and as reference electrode. A combination of a Celgard 2310 PEO membrane (Asahi Kasei Corporation) and a glass fibre filter (Whatman GF/C, GE Healthcare) was used as the separator. Before cycling of each hard carbon/sodium half-cell, the electrochemical impedance spectroscopy (EIS) was measured in a frequency range from 20 kHz to 10 mHz with 11 frequencies per decade at 10 mV amplitude. For galvanostatic charge–discharge measurements (GCPL), the applied current densities were chosen with respect to the theoretical capacity of a Li–graphite anode (C₃₇₂ = 372 mA h g⁻¹). The bulk sodium plating capacity was determined at C/20 (18.6 mA g⁻¹) and C/2 (186 mA g⁻¹), as the capacity at which the crystallization overpotential occurred by intentionally oversodiating the HC electrode after cycling-in in a voltage range of 2.5–0.002 V for 8 cycles.³⁸ For the constant voltage experiments after galvanostatic reduction to 0.002 V, the voltage was maintained at 0.002 V using as a limitation an absolute current of 6.2 mA g⁻¹ (C/60). Stability tests were performed in capacity-limited mode at C/20 for 30 cycles and C/2 for 100 cycles. 90% of the previously determined bulk sodiation capacity value has been used as limitation value. Before transferring to the capacity limited mode, the similar cycling-in procedure over a voltage range 2.5–0.002 V for 8 times at C/20 current density was applied.

Results and discussion

Structural characterization

Dynamic light scattering of the obtained PS spheres was carried out to determine their apparent hydrodynamic radius 〈R_h〉. The average particle radius is 42 nm (Fig. 1(a)). Transmission electron microscopy reveals that larger spheres, with sizes around 200–250 nm, are also locally present (Fig. S1, ESI†). A suitable sacrificial template for porous hard carbons decomposes upon pyrolysis, creating hollow spaces without the need to be removed by additional synthetic steps. Therefore, the decomposition of PS was tracked by means of thermogravimetric analysis under N₂ atmosphere (Fig. 1(b)). A complete mass loss at a temperature of approximately 450 °C indicates the full decomposition of the PS, rendering them as a suitable sacrificial template for HC. Monitoring the mass change of the PS and glucose after the polymerisation step at 160 °C is relevant to obtain information the incorporation of the template and the possibility for complete decomposition (Fig. 1(b)). Reasonably, the residual mass increases with decreasing PS content, approaching the behaviour of the pure glucose sample. The pyrolysis yields, calculated as the ratio of the mass after final carbonisation with respect to the mass of used glucose (Fig. 1(c)), are in the same range irrespective of the PS content. This indicates that only minor carbon residuals might be formed due to decomposition of the sacrificial template and the formed hard carbons mainly consist of the pyrolysis products of glucose.

Fig. 1 (a) Particle size distribution of polystyrene spheres obtained from dynamic light scattering. (b) Thermogravimetric analysis of the carbon polymer from glucose, mixtures of PS with glucose obtained at 160 °C and pure PS under nitrogen atmosphere. (c) Yield of pyrolysis normalized to the glucose content. (d) Density values. (e) Powder X-ray diffraction patterns. (f) Raman spectra of hard carbon materials.

Despite significantly different template contents, the density values of PS-HCs as well as HC (Fig. 1(d)) are all typical for hard carbon materials. This is a first indication that the addition of PS as sacrificial templates does not significantly change the hard carbon microstructure. This is further confirmed by powder X-ray diffraction analysis, which shows, for all samples, patterns typical for hard carbon materials, namely two broad reflections at 25° 2 theta as well as at 44° 2 theta, corresponding to (002) and (100) lattices, respectively (Fig. 1(e)). Positions and intensities of the reflections of all samples are comparable, which is another sign for their comparable carbon microstructure (Fig. S2a and Table S1, ESI†). Moreover, calculated interlayer distances (d₀₀₂) (inset Fig. 1(e)) as well as crystallite stack height L_c and width L_a (Table S2, ESI†) validate the comparability in microstructures of investigated materials. In addition, all patterns show considerable amorphous scattering at smaller angels. This phenomenon typically points towards the presence of open and closed pores in the nm-size regime and was further examined by SAXS as discussed below. Raman spectroscopy helps to understand the chemical binding motifs and the carbonization/graphitization degree of carbonaceous materials.³⁹ Raman spectra of PS-HCs and blank HC (Fig. 1(f)) contain a D- and a G-band, which are characteristic for hard carbon materials. The G-band is related to the bond stretching of all pairs of sp² atoms in rings and chains whereas the D-band represents breathing modes of sp² atoms in rings at defect sites.⁴⁰ Therefore, the intensity ratios between D- and G-peaks (I_D/I_G) as well as the width of the peaks can provide information about the degree of defectiveness and disorder in the investigated carbons. Generally, all samples represent a well-ordered structure leading to sharp Raman peaks, which is expected after thermal treatment at 1700 °C. The A-band originating from amorphous carbon phases located between D- and G-band is of low intensity in all samples (Fig. 1(f) and Fig. S2b, ESI†). The I_D/I_G ratios for all samples (inset Fig. 1(f)) are in a comparable range (1.51–1.68), as well as the I_A/I_G ratios (Table S3, ESI†), and the overtone peaks of D + G and 2D are observable for all samples. TEM enables direct observation of the microstructure of hard carbons. As anticipated, after high-temperature processing, the revealed microstructure is typically composed of disordered domains combined with graphitic stacking (Fig. S3, ESI†). As for PXRD and Raman analyses, it can be concluded that the carbon microstructure in all samples is expectedly comparable after thermal treatment at similar maximum temperature.

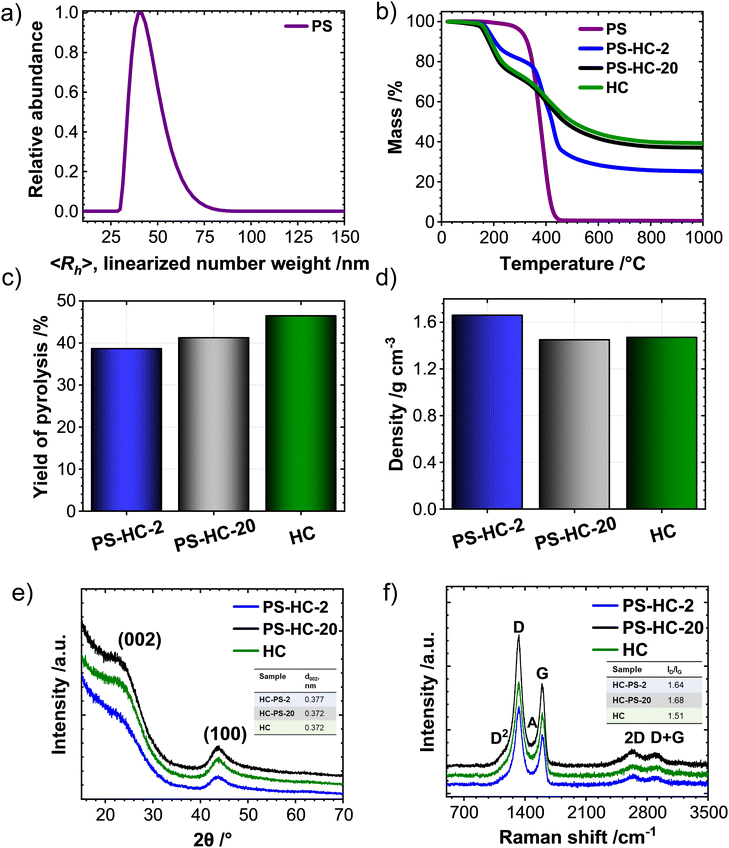
The porosity of the synthesized carbons was investigated by means of N₂, CO₂ as well as vapor H₂O sorption experiments. During SIB cycling, a high open porosity and specific surface area contributes to the decomposition of the electrolyte and by that also to the formation of the solid–electrolyte interphase (SEI). This, in turn, leads to irreversible capacity loss as well as low Coulombic efficiency in the first cycles.^33,41,42 Formed inactive mass has to be added to the battery thus decreasing the energy density on cell level. In contrast, a high degree of internal porosity is anticipated to promote the targeted storage of sodium without excessive contribution to irreversible processes, as sodium clustering exclusively occurs in such voids and thus contributes to a prolonged and stable plateau at low potentials versus Na/Na⁺.⁴³ N₂-physisorption isotherms of the PS-HCs as well as HC (Fig. 2(a)) can be classified as IUPAC type-II,⁴⁴ which is typical for non-porous materials. The specific surface areas determined by the QSDFT method are between 1 and 10 m² g⁻¹ (Table S4, ESI†). While still not considerably a nanoporous carbon material, the porosity values of PS-HC-2 significantly exceed those of the PS-free sample and the one with lower PS content. The gas uptake at higher relative pressures, which is associated with adsorption on external surface area or the presence of larger open pores, also increases with higher PS content. This indicates that the PS are introducing larger pores and possibly also open a few closed pores due to enlargement of the external surface area.³² On the other hand, closed pores as well as ultramicropores (i.e., those pores with diameters smaller than 0.7 nm) are too small to be detected by N₂-physisorption, since nitrogen gas displays limited diffusion at cryogenic temperature.⁴⁵ Due to the enhanced diffusion at elevated temperatures and the slightly smaller kinetic diameter of the adsorbate, CO₂-physisorption at 273 K is a more suitable technique to investigate such ultramicropores.⁴⁶ The CO₂-physisorption isotherms of PS-HCs (Fig. 2(b)) generally display a low gas uptake between 0.6 and 2.7 cm³ g⁻¹ at 1 atm pressure, confirming the lack of open, gas-accessible micro- and mesoporosity in the PS-HCs. However, comparison of CO₂ uptakes as well as pore volume values calculated according to the NLDFT model (Table S4, ESI†) indicate that the addition of external surface area due to higher PS content slightly increases the porosity and pore volume. Thus, the obtained CO₂ isotherms are consistent with the N₂ isotherms and confirm the effect of the presence of PS during carbonization, namely resulting in the contribution of additionally formed or newly accessible open porosity.

Fig. 2 (a) N₂-physisorption isotherms at 77 K. (b) CO₂-physisorption isotherms at 273 K. (c) H₂O-vapour physisorption isotherms at 298 K. (d) Small-angle scattering curves. (e) SEM images of hard carbon materials.

Because of the even smaller kinetic diameter (0.265 nm) as well as higher experiment temperature (298 K) H₂O-vapour physisorption seems to be an even more suitable technique for detecting very small (<0.5 nm) and possibly even closed pores inaccessible for N₂ and CO₂. In principle, the H₂O-isotherms of PS-HCs as well as HC (Fig. 2(c)) can be categorized as type V in the IUPAC classification.⁴⁴ All materials can be characterized as hydrophobic as the adsorption branches demonstrate low vapor uptake at low relative pressures.⁴⁷ It is known, that hydrophobicity/hydrophilicity of the carbonaceous material is strongly linked with oxygen content, since H₂O can be adsorbed by hydrogen bonding on oxygen-containing functional groups.⁴⁸ Confirming this observation, elemental analysis data (Table S5, ESI†), show an almost negligible oxygen content for all carbons. Whilst the water uptakes of HC and PS-HC-20, with rather low PS content, remain small (with a slightly higher uptake for HC) and of comparable shape, PS-HC-2 shows a relatively higher water uptake (Table S6, ESI†), which is in line with the N₂ and CO₂ physisorption results. While the overall water uptake in PS-HC-2 is still rather low, the isotherm resembles the typical shape of microporous carbon materials. H₂O, therefore, seems to be a suitable adsorbent for the detection of closed micro- and small mesopores for this series of samples.

As it is known from the literature, small-angle X-ray scattering is a complementary analysis technique, which allows for the detection of the entire porosity including the closed pores due to a distinct scattering contrast between vacuum and carbon material across the sample.^19,49 The difference between physisorption and SAXS measurements can illuminate the existence of closed porosity in such samples. Generally, all samples yield comparable scattering curves (Fig. 2(d)) and their shape is typical for porous carbon materials. This indicates a widely comparable carbon structure with mostly internal, gas-inaccessible porosity. The low skeletal densities (Fig. 1(d)) are well in line with these observations. The autocorrelation function derived by Debye et al.³⁷ and used by Stevens and Dahn¹⁹ was applied for the calculation of parameters A and B, which are proportional to the total surface areas of the large (macro) and small (micro) pores, respectively. As can be observed (Fig. S4, ESI†), the addition of PS affects surface area of the big pores (A). Particularly, for the material with the highest PS content, the surface area of macropores, A, is the highest, meanwhile, the surface area of micropores, B, is comparable with the other two materials. As a result, the ratio of surface areas of large pores to small ones (A/B) is highest for the material containing the highest amount of polystyrene (inset Fig. 2(d)). Thus, it becomes obvious that at high concentrations, the addition of PS leads to the formation of large pores and a material with a lower filling density. PS-HC-20 exhibits an opposite trend for this parameter and thus has fewer large pores detectable via SAXS, in comparison to HC and PS-HC-2.

SEM measurements (Fig. 2(e)) show distinct differences in the morphologies between the materials, clearly related to the amount of polystyrene. The number of pores in the micrometre range is significantly increased in case of high amounts of polystyrene, which can be correlated to the gas uptake in the higher relative pressure regime in the sorption analyses as well as SAXS results, and indeed proves the presence of an increased external surface area albeit at still comparable sizes of primary HC particles in all samples.

In summary, the structural characterization demonstrates that the addition of polystyrene mainly affects the macroporosity of the resulting materials. While the carbon microstructure such as carbon ordering, interlayer spacing as well as the content of intrinsic porosity remain comparable, a higher content of macropores is found in PS-HC-2. This can lead to the opening of pores, which remain undetected in gas sorption experiments for materials without additional macropores.

Additional analysis of the structure at the intermediate stage (after 600 °C) is beneficial for gaining insight into the contribution of the template at this point.^31,50 Therefore, the external porosity was additionally investigated after the pre-carbonization step (after 600 °C). N₂-physisorption isotherms at 77 K of the PS-HCs-600 as well as HC-600 (Fig. S5a, ESI†) correspond to the IUPAC type-I(a) isotherm, indicating the existence of predominantly narrow micropores with a diameter of less than 2.5 nm. It is proved by pore size distribution data (Fig. S5b, ESI†), obtained from quenched-solid density functional theory (QSDFT, for N₂ at 77 K on carbon surfaces with slit/cylindrical pores, adsorption branch kernel). Generally, the addition of polystyrene contributes to an increase in both surface area as well as pore volume (Table S7, ESI†). CO₂-isotherms of PS-HCs-600 (Fig. S5c, ESI†) and pore size distribution (Fig. S5d, ESI†) obtained from non-local density functional theory model (NLDFT, for CO₂ at 273 K on carbon, adsorption branch) indicate that polystyrene does not contribute to the formation of additional porosity in the ultramicropore range (Table S7, ESI†). SEM images (Fig. S6a, ESI†) verified the differences in morphologies related to the amount of polystyrene, similar to those observed after 1700 °C (Fig. 2(e)). TEM images (Fig. S6b, ESI†) as well as elemental analysis (Table S8, ESI†) highlight the comparability across the microstructure and chemical composition of these intermediate carbons. Upon examination of this data, it can be inferred that the alteration of the template at 600 °C affects only the macroporosity. This contribution follows the same trend observed after the high-temperature treatment.

Electrochemical sodium storage

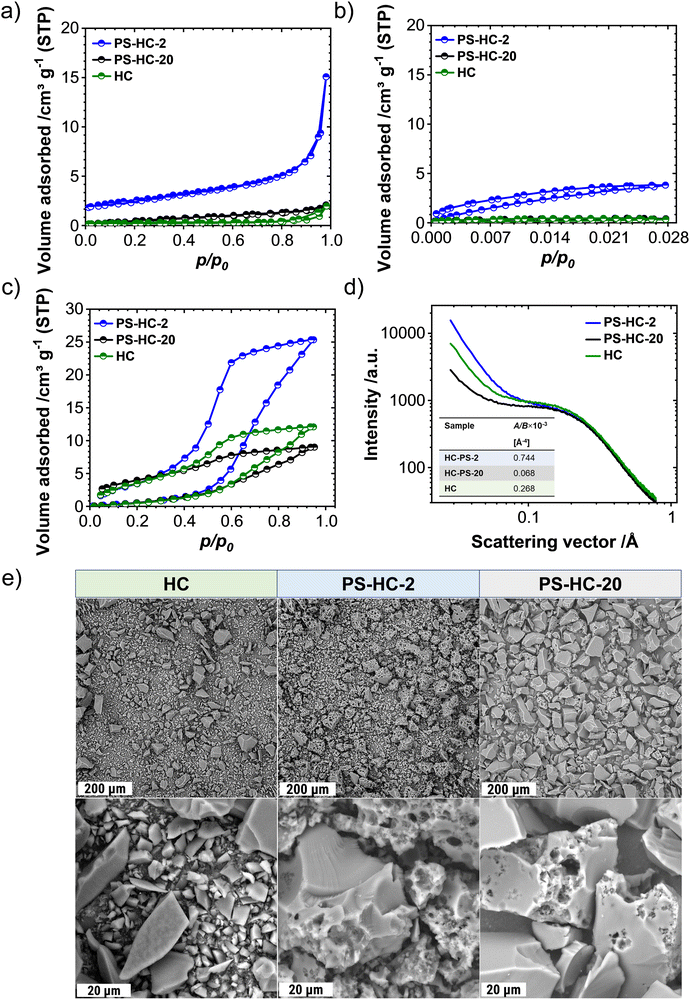
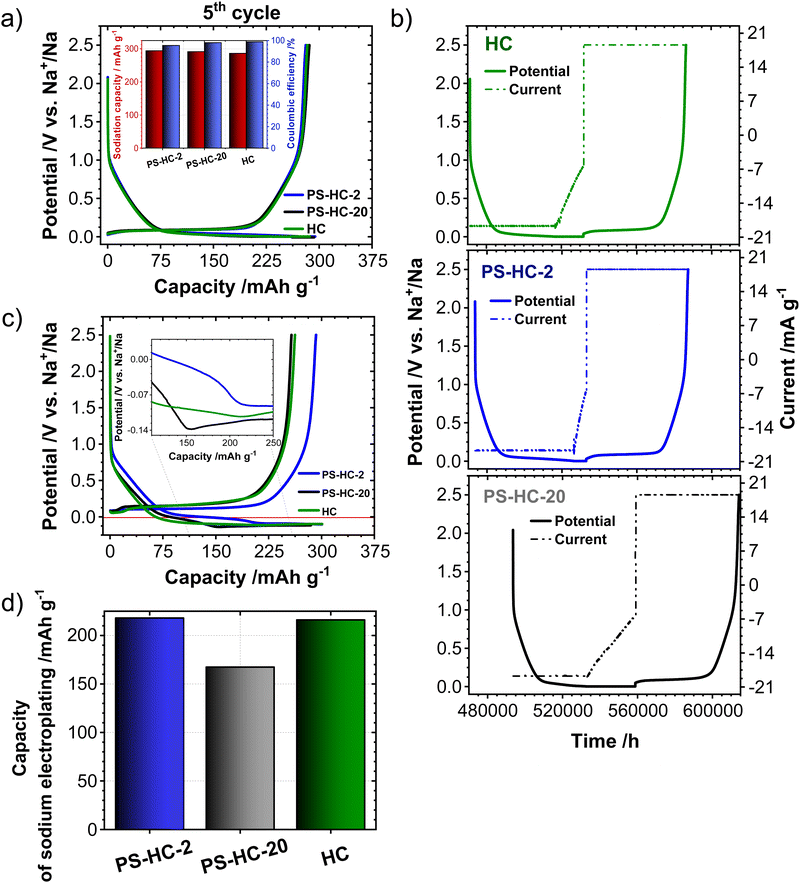
In order to investigate the influence of the structural features on the sodium storage performance of the PS-HCs, galvanostatic charge–discharge measurements with a lower voltage limit of 0.002 V vs. Na/Na⁺ were conducted at first. Moreover, it was recently demonstrated that hard carbons can deliver additional reversible capacity when being charged until the nucleation of sodium starts (e.g. without potential limit), which is mainly governed by the crystallization overpotential at values slightly below 0 V vs. Na/Na⁺. Since the exploitation of this process can contribute additional capacity, capacity limited experiments were conducted in addition to potential limited tests (see experimental details).^22,38,51 Since the construction of the cell can affect cycling results, EIS data obtained before cycling (Fig. S7, ESI†) can provide an insight into how well the cell is assembled.^52,53 The equivalent series resistance (ESR) is observed to be comparable across the materials (Fig. S7b, ESI†). Therefore, the influence of ESR on the differences observed in charge–discharge experiments can be excluded. The galvanostatic charge–discharge curves of PS-HCs (Fig. 3 and Fig. S8, ESI†) have been recorded at low current densities, corresponding to C/20 of a Li/graphite cell i.e. 18.6 mA g⁻¹. Comparing the results from two experiments, it can be observed that in the first cycle (Fig. 3(a) and Fig. S8a, ESI†), the initial coulombic efficiency (ICE) increases as the polystyrene content decreases (Fig. 3(b)). This is probably related to the existence of more accessible sites, caused by the change in morphology through the introduction of micrometre-sized pores. However, all materials represent ICE values above 74% (Fig. 3(b)). Despite the fact that the ICE decreases with templating, it remains within a reasonable range compared to highly porous carbons.^33,38,54 A significant difference in sodiation capacity between templated samples is observed in the voltage limited 5^th cycle (Fig. 3(c) and Fig. S8b, ESI†). PS-HC-2 has a sodiation capacity value almost similar to that of HC from glucose. However, in case of PS-HC-20, which has the lowest PS content, the capacity drop is remarkable (Fig. 3(d)). The loss mainly occurs in plateau capacity, while the slope capacity values remain nearly identical (Fig. S8c, ESI†). If the slope region corresponds to adsorption of sodium on the defects and its intercalation into the graphitic domains, this behaviour is well in line with the observations made in Raman spectroscopy, where the samples exhibited D, G, and A-bands (inset Fig. 1(f) and Table S3, ESI†) of similar height ratios, as well as XRD data, which consisted of broad (100) and (002) reflections of similar 2 Theta positions and FWHMs (Fig. 1(e) and Table S1, ESI†). This points to a comparable degree of graphitization and disorder. Moreover, if the plateau region corresponds to sodium clustering inside the internal pores, it can be directly correlated to sorption analyses as well as SAXS. Despite the comparable values of the micropore surface area, B, with HC, the capacity of PS-HC-20 is 73 mA h g⁻¹ less than that of HC. Nevertheless, PS-HC-20 exhibits the lowest macropore surface area, A, as well as lower vapor H₂O uptake at 298 K (Fig. S4 and Table S6, ESI†). In addition, the plateau potential for PS-HC-20 is the lowest (inset Fig. 3(c)). Therefore, it is likely that the large pores act as diffusion paths that improve the accessibility of the closed pores for sodium. In the case of PS-HC-20, the diffusion might be too slow and the mass transport hindered due to the lack of big pores. This could lead to a decrease in capacity because the sodium does not reach all the pores in the particles where clustering can potentially occur. In addition, Tian et al.⁵⁵ discussed a shift of plateau voltages to higher values as a result of a slower insertion due to smaller interlayer distance of graphitic domains. However, the difference in interlayer distances of PS-HCs and HC is insignificant (inset Fig. 1(e)). PS-HC-20 represents the same interlayer spacing as pure HC, which gives further evidence that the interlayer spacing in these materials does not lead to differences in plateau voltages. A higher volume of macropores results in lower transport resistance, and consequently, a higher plateau voltage might be observed. In the capacity limited cycle (Fig. 3(e)), PS-HCs and HC demonstrate nearly similar values of bulk sodium plating capacity. Nonetheless, the onset potentials of this process are different. The capacity values as well as nucleation overpotentials of sodium (Fig. 3(f)) are calculated as an average from 2 experiments (Fig. S8d, ESI†). The overpotential values were determined by subtracting the minimum from the voltage baseline of sodium plating (inset in Fig. 3(e)).³⁸ PS-HC-2 has the highest value of sodium crystallization overpotential (15.83 mV). As a consequence, observed features of the sodium storage process may be related to the electronic resistance between materials.³² This hypothesis can be confirmed by the increase in the presence of macropores for higher PS ratios, which is observed in sorption measurements, SAXS, and supplemented by SEM (Fig. 2).

Fig. 3 Galvanostatic charge–discharge curves of hard carbon materials recorded at C/20 current density. (a) Voltage limited first cycle. (b) Initial Coulombic efficiency calculated from 2 experiments. (c) Voltage limited stable cycle (5th). (d) Coulombic efficiency of 5th cycle calculated from 2 experiments. (e) Capacity limited cycle. (f) Capacity of sodium electroplating and nucleation overpotential of sodium calculated from 2 experiments.

In order to further investigate the differences in the sodium storage properties caused by different contents of macropores, galvanostatic charge–discharge measurements characteristic with the final constant voltage step at a current density of C/20 were performed. As shown in Fig. 4(a), the material with lowest content of transport pores, PS-HC-20, achieved a sodiation capacity value close to PS-HC-2, as well as reference HC from glucose. However, there is a noticeable difference in the time taken to reach the full capacity (Fig. 4(b) and Fig. S9a, ESI†). This is reflecting that the lowest number of pores responsible for sodium transport is present in PS-HC-20, and underlines the importance of small diffusion paths to achieve full sodium storage capacity within a given timeframe. To further verify the hypothesis of different transport resistances, galvanostatic charge–discharge tests at higher current density (C/2, 186 mA g⁻¹) with capacity limitation were recorded. As demonstrated (inset Fig. 4(c), inset Fig. S9b, ESI† and Fig. 4(d)), PS-HC-2 exhibits the highest values of both sodium electroplating capacity as well as sodium nucleation overpotential. This indicates a difference in the sodium transport pathways among the investigated materials. At higher current densities, faster sodium transfer processes are required, so that the presence of shorter pathways for sodium transport facilitates the occupation of sodium storage sites into the carbon and, as a result, leads to higher capacity in this kind of measurement. Thus, PS-HC-2, which has more macropores and smaller sodium transport domains, exhibits the highest value of plating capacity at high current densities due to faster filling of all sodium storage sites. In order to evaluate the potential application tests of PS-HCs, long-term cycling tests at low (C/20) as well as high (C/2) current densities were conducted using the capacity limited approach (see reference³⁸). After voltage limited cycling at low current density, the templated materials were cycled to 90% of the determined bulk sodiation capacity values at the two different current densities. These experiments directly display the impact of additional macropores, which is a comparable cyclability irrespectively of the applied current density (Fig. S9c and d, ESI†). As expected, even after application of high current density, materials with extreme values of the template amount demonstrated high stability as well as reversibility. The Coulombic efficiency values (Fig. S9c and d, ESI†) are all greater than 99%.

Fig. 4 (a) and (b) Galvanostatic charge–discharge curves of hard carbon materials recorded at C/20 current density with constant voltage step (2 mV) corresponding to 5th cycle. (c) Galvanostatic charge–discharge curves of materials recorded at C/2 current density corresponding to capacity limited cycle. (d) Capacity values of sodium electroplating at C/2 current density calculated from 2 experiments.

Conclusions

Polystyrene particles were applied as a template for hard carbon materials. The impact of the template/precursor ratio on the obtained materials structure was investigated my means of nitrogen, carbon dioxide, water vapor sorptions as well as small-angle X-ray scattering combined with scanning electron microscopy. The results revealed that addition of polystyrene modifies the structure of hard carbons by adding extra macroporosity. This difference in porosity affects the electrochemical storage of sodium. The increased macropore content results in irreversible capacity loss in the first cycle, reduced sodium transport domains, increased the reversible sodium storage capacity in the voltage limited cycles as well as increased electrical resistance in capacity limited cycle. On the contrary, hard carbon with a limited macropore content requires more time to reach full sodiation capacity. At higher current densities, faster sodium transfer processes contributed to the highest capacity value for the most macroporous carbon. Therefore, this work provides insight into the impact of hard carbon macroporosity on the balance between reducing sodium transport pathways and irreversible capacity loss in the first cycle. In addition, the importance of the work is connected to the fact that structural differences that seem insignificant can be resolved by structural characterization and well correlated with electrochemistry. This is a significant step towards a deeper understanding of structure–property relationships of hard carbons as negative electrode materials in SIBs. Furthermore, the revealed difference in accessibility of the closed pores for sodium opens the new perspectives for the development of hard carbons with improved rate capability. In-depth exploration of full cell behavior, reinforced by in situ spectroscopic evidences, could serve as an additional valuable contribution to the investigations of the sodium storage mechanism in such carbons. Further work could also incorporate cyclic voltammetry for extensive understanding the kinetics of sodium ions in such materials. Likewise, electrochemical impedance spectroscopy at different states of charge is considered as an excellent tool to provide kinetic as well as mechanistic insights in such electrochemical systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research was supported by the Federal Ministry of Education and Research (BMBF) within project NATTER under grant number 03XP0525E. S. P. and M. O. acknowledge fruitful scientific discussion with Prof. Markus Antonietti from the Max Planck Institute of Colloids and Interfaces (Department of Colloid Chemistry) in Potsdam-Golm. We thank Dr Nadja Tarakina from the same institute for providing the TEM measurements. Seed funding for this work has been provided by the project “CLUSTERBATT” within the Fraunhofer-MaxPlanck collaboration programme. The German Research Council (DFG) is gratefully acknowledged for financial support (TRR234 “CataLight”, project ID: 364549901, project B05). L. I. K. acknowledges Alexander von Humboldt Foundation for funding.

References

1. A. Manthiram, ACS Cent. Sci., 2017, 3, 1063–1069.
2. D. Saurel, B. Orayech, B. Xiao, D. Carriazo, X. Li and T. Rojo, Adv. Energy Mater., 2018, 8, 1703268.
3. M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561.
4. H. Vikström, S. Davidsson and M. Höök, Appl. Energy, 2013, 110, 252–266.
5. D. Kushnir and B. A. Sandén, Resour. Policy, 2012, 37, 93–103.
6. N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682.
7. P. K. Nayak, L. Yang, W. Brehm and P. Adelhelm, Angew. Chem., Int. Ed., 2018, 57, 102–120.
8. G. Yoon, H. Kim, I. Park and K. Kang, Adv. Energy Mater., 2017, 7, 1601519.
9. M. Goktas, C. Bolli, E. J. Berg, P. Novák, K. Pollok, F. Langenhorst, M. Roeder, O. Lenchuk, D. Mollenhauer, P. Adelhelm, M. Goktas, P. Adelhelm, C. Bolli, E. J. Berg, P. Novák, K. Pollok, F. Langenhorst, M. Roeder, O. Lenchuk and D. Mollenhauer, Adv. Energy Mater., 2018, 1702724.
10. B. Babu, M. Enke, S. Prykhodska, A. Lex-Balducci, U. S. Schubert and A. Balducci, ChemSusChem, 2021, 14, 4836–4845.
11. Y. Liu, B. V. Merinov and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 3735–3739.
12. S. Komaba, W. Murata, T. Ishikawa, N. Yabuuchi, T. Ozeki, T. Nakayama, A. Ogata, K. Gotoh and K. Fujiwara, Adv. Funct. Mater., 2011, 21, 3859–3867.
13. E. Irisarri, A. Ponrouch and M. R. Palacin, J. Electrochem. Soc., 2015, 162, A2476–A2482.
14. J. R. Dahn, W. Xing and Y. Gao, Carbon N. Y., 1997, 35, 825–830.
15. E. R. Buiel, A. E. George and J. R. Dahn, Carbon N. Y., 1999, 37, 1399–1407.
16. J. S. McDonald-Wharry, M. Manley-Harris and K. L. Pickering, Energy Fuels, 2016, 30, 7811–7826.
17. D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 1271.
18. D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2001, 148, A803.
19. D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 4428.
20. D. A. Stevens, PhD Thesis, Dalhousie University, Halifax, Nova Scotia, Canada, 2000.
21. R. Morita, K. Gotoh, K. Kubota, S. Komaba, K. Hashi, T. Shimizu and H. Ishida, Carbon N. Y., 2019, 145, 712–715.
22. Y. Morikawa, S. Nishimura, R. Hashimoto, M. Ohnuma and A. Yamada, Adv. Energy Mater., 2020, 10, 1903176.
23. J. M. Stratford, P. K. Allan, O. Pecher, P. A. Chater and C. P. Grey, Chem. Commun., 2016, 52, 12430–12433.
24. R. Morita, K. Gotoh, M. Fukunishi, K. Kubota, S. Komaba, N. Nishimura, T. Yumura, K. Deguchi, S. Ohki, T. Shimizu and H. Ishida, J. Mater. Chem. A, 2016, 4, 13183–13193.
25. K. Gotoh, T. Yamakami, I. Nishimura, H. Kometani, H. Ando, K. Hashi, T. Shimizu and H. Ishida, J. Mater. Chem. A, 2020, 8, 14472–14481.
26. H. Au, H. Alptekin, A. C. S. Jensen, E. Olsson, C. A. O’Keefe, T. Smith, M. Crespo-Ribadeneyra, T. F. Headen, C. P. Grey, Q. Cai, A. J. Drew and M.-M. Titirici, Energy Environ. Sci., 2020, 13, 3469–3479.
27. E. Šić, K. Schutjajew, U. Haagen, H. Breitzke, M. Oschatz, G. Buntkowsky and T. Gutmann, ChemSusChem, 2023, 2301300.
28. Q. Meng, Y. Lu, F. Ding, Q. Zhang, L. Chen and Y.-S. Hu, ACS Energy Lett., 2019, 4, 2608–2612.
29. K. Schutjajew, P. Giusto, E. Härk and M. Oschatz, Carbon N. Y., 2021, 185, 697–708.
30. T. Morishita, T. Tsumura, M. Toyoda, J. Przepiórski, A. W. Morawski, H. Konno and M. Inagaki, Carbon N. Y., 2010, 48, 2690–2707.
31. A. Kamiyama, K. Kubota, D. Igarashi, Y. Youn, Y. Tateyama, H. Ando, K. Gotoh and S. Komaba, Angew. Chem., Int. Ed., 2021, 60, 5114–5120.
32. I. K. Ilic, K. Schutjajew, W. Zhang and M. Oschatz, Carbon N. Y., 2022, 186, 55–63.
33. H. Alptekin, H. Au, E. Olsson, J. Cottom, A. C. S. Jensen, T. F. Headen, Q. Cai, A. J. Drew, M. Crespo Ribadeneyra and M. M. Titirici, Adv. Mater. Interfaces, 2022, 9, 1–12.
34. F. Xu, H. Han, Y. Qiu, E. Zhang, H. Repich, C. Qu, H. Yu, H. Wang and S. Kaskel, Carbon N. Y., 2020, 167, 896–905.
35. J. Jang and H. K. Ha, Polym. Prepr. (Am. Chem. Soc., Div. Polym. Chem.), 2002, 43, 580–581.
36. C. A. Dreiss, K. S. Jack and A. P. Parker, J. Appl. Crystallogr., 2006, 39, 32–38.
37. P. Debye, H. R. Anderson and H. Brumberger, J. Appl. Phys., 1957, 28, 679–683.
38. K. Schutjajew, J. Pampel, W. Zhang, M. Antonietti and M. Oschatz, Small, 2021, 17, 2006767.
39. M. Oschatz, P. Pré, S. Dörfler, W. Nickel, P. Beaunier, J.-N. Rouzaud, C. Fischer, E. Brunner and S. Kaskel, Carbon N. Y., 2016, 105, 314–322.
40. A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 1–13.
41. H. Kumar, E. Detsi, D. P. Abraham and V. B. Shenoy, Chem. Mater., 2016, 28, 8930–8941.
42. J. Song, B. Xiao, Y. Lin, K. Xu and X. Li, Adv. Energy Mater., 2018, 8, 1–24.
43. X. Dou, I. Hasa, D. Saurel, C. Vaalma, L. Wu, D. Buchholz, D. Bresser, S. Komaba and S. Passerini, Mater. Today, 2019, 23, 87–104.
44. M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069.
45. A. Beda, C. Vaulot and C. Matei Ghimbeu, J. Mater. Chem. A, 2021, 9, 937–943.
46. P. Rallapalli, K. P. Prasanth, D. Patil, R. S. Somani, R. V. Jasra and H. C. Bajaj, J. Porous Mater., 2011, 18, 205–210.
47. L. Liu, S. (Johnathan) Tan, T. Horikawa, D. D. Do, D. Nicholson and J. Liu, Adv. Colloid Interface Sci., 2017, 250, 64–78.
48. C. O. Ania, B. Cabal, J. B. Parra and J. J. Pis, Adsorpt. Sci. Technol., 2007, 25, 155–167.
49. E. Härk, A. Petzold, G. Goerigk, S. Risse, I. Tallo, R. Härmas, E. Lust and M. Ballauff, Carbon N. Y., 2019, 146, 284–292.
50. L. Yu, C. Falco, J. Weber, R. J. White, J. Y. Howe and M. M. Titirici, Langmuir, 2012, 28, 12373–12383.
51. Y. Zheng, Y. Lu, X. Qi, Y. Wang, L. Mu, Y. Li, Q. Ma, J. Li and Y. S. Hu, Energy Storage Mater., 2019, 18, 269–279.
52. A. Eddahech, O. Briat, H. Henry, J.-Y. Delétage, E. Woirgard and J.-M. Vinassa, Microelectron. Reliab., 2011, 51, 1968–1971.
53. M. S. Hosen, R. Gopalakrishnan, T. Kalogiannis, J. Jaguemont, J. Van Mierlo and M. Berecibar, World Electr. Veh. J., 2021, 12, 77.
54. K. Tang, L. Fu, R. J. White, L. Yu, M. Titirici, M. Antonietti and J. Maier, Adv. Energy Mater., 2012, 2, 873–877.
55. Z. Tian, Y. Zhang, J. Zhu, Q. Li, T. Liu and M. Antonietti, Adv. Energy Mater., 2021, 11, 2102489.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00129j

---