 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Significant Joule self-heating pervasive in the emergent thin-film transistor studies†
V.
Bruevich
 *a,
Y.
Patel
*a,
Y.
Patel
 b,
J. P.
Singer
b,
J. P.
Singer
 b and
V.
Podzorov
*a
b and
V.
Podzorov
*a
aDept. of Physics & Astronomy, Rutgers University, 136 Frelinghuysen Rd, Piscataway, NJ 08854, USA. E-mail: bruevich@physics.rutgers.edu; podzorov@physics.rutgers.edu
bDept. of Mechanical & Aerospace Engineering, Rutgers University, 98 Brett Road, Piscataway, NJ 08854, USA
First published on 21st October 2024
Abstract
In this Perspective, recent literature on field-effect transistors based on emergent semiconducting materials, including metal-halide perovskites, conjugated polymers, and small-molecule organic semiconductors, is analyzed in terms of electric power and power density reached in transistors’ channel during their measurements. We used an in situ IR imaging to directly obtain the surface temperature distribution of biased devices under the experimental conditions commonly used in the literature. It is shown that at such conditions, the semiconducting channel would be resistively self-heated to significant temperatures, easily in excess of 150 °C. This implies a non-equilibrium device operation, possible materials’ degradation, parameter drift, and, in the best-case scenario, a non-room-temperature mobility extracted from such measurements. We show that this problem is rather common in various subfields represented in the literature, indicating that paying attention to the biasing conditions in transistor research and monitoring the local temperature of the semiconducting channel are necessary.
Studies of field-effect transistors (FETs) based on emergent semiconducting materials,1–3 including metal-halide perovskites,4–11 organic semiconductors,12–15 layered inorganic materials, such as transition metal dichalcogenides, graphene and others,16–18 nanocrystal arrays and nanowire/tube networks,19,20 as well as metal oxides,21–24 are important for our understanding of the basic charge transport properties of these materials and developing novel applications. However, in a number of studies, rather extreme biasing regimes were exploited in thin-film transistor (TFT) measurements of soft lattice metal-halide perovskites and organic semiconductors without addressing the potential issues related to very high local Joule heating and electric fields generated in the semiconducting channels (for details, see Tsable S1, ESI†).
In this Perspective, we employed an in situ infra-red (IR) imaging of biased resistive thin films to directly address the problem of local Joule heating (a rise of the active material's temperature, T) under some of the typical biasing conditions used in exemplar studies summarized in Table S1 (ESI†). In particular, there is a group of representative papers, in which both Joule power and power density reached in the TFT measurements were very high (lines 1–9 of Table S1, ESI†).25–33 In our tests, we applied the Joule power density on the lower end of the range covered in these representative papers to ensure that we probe the lower bound of the associated temperature rise. To be experimentally specific, we emulated as closely as possible the totality of the experimental conditions (including the sample geometry, resistance, applied power, power density, substrate, etc.) used in a recent study of hybrid perovskite TFTs.25,34 As shown in this Perspective, common issues with device characteristics (nonlinearities, hysteresis, instabilities, fluctuations, etc.) and thus complications with the carrier mobility extraction encountered in the literature (see, e.g., a recent report over a study performed at similar biasing conditions),35 might be partially associated with the run-away heating effects.
Fig. 1 below shows the results of these thermal imaging experiments. The source video of the test is available as a Supplementary movie file (ESI†). In order to reproduce the reported measurement conditions, we used a commercially available thin-film chip resistor (a metal film deposited on a small, flat ceramic substrate, package 0402) of resistance R = 1 kΩ. The area of the resistive film is comparable to the channel area, A, of the reported TFTs (A = channel length × channel width = 0.2 × 1 mm2). In our setup (Fig. 1a or Supplementary video, ESI†), the resistor is firmly glued film-down to a smooth oxide surface of a silicon wafer similar to those used in ref. 25–33 (a 0.6 mm-thick single-crystal Si wafer with a thin layer of thermal SiO2), ensuring a direct thermal contact between the active film and the substrate. Note that the size of the Si substrate (10 × 10 mm2) in our case is much greater than the dimensions of the sample. The resistor is electrically connected to a power source with 44 AWG tin-coated copper wires that are soldered directly to the resistor's contact pads located on the sides of the ceramic chip, such that these contacts do not interfere with making a good physical contact of the resistive film with the wafer. To induce Joule heating of the resistive film not greater than that in the representative papers (lines 1–9 of Table S1, ESI†),25–33 we have applied some of the lowest Pmax among the values reached in those studies, Pmax = 200 W cm−2. In some of the studies we examined, significantly greater Pmax was apparently reached (for detailed parameters, see Table S1, ESI†). Pmax in TFTs is defined as the product of the source–drain voltage, VDS, and the maximum source–drain current, ImaxDS, reached during the recording of a TFT's transfer curve (typically corresponding to the maximum gate voltage, VGS), divided by the channel area, A = L·W:15,36
 | (1) |
 | ||
| Fig. 1 Thermal imaging of a surface temperature distribution of a biased resistive film on a Si wafer closely emulating the experimental conditions of H. Zhu et al.25 (for detailed parameters, see line 1 in Table S1, ESI†). (a) A photograph of a small thin-film resistor chip thermally anchored to a square piece of a large silicon wafer (10 × 10 mm2) and wired to a power source. (b) A screenshot from the thermal video taken right after the device has been powered up (the higher the local temperature, the brighter the color). The full video, recorded with an IR camera, is available as a Supplementary movie file (ESI†). (c) Temporal temperature profiles, T(t), calculated from the thermal video in the three regions outlined with the rectangles in panel (b): the resistive thin-film device itself (black), a small region of the substrate close to the device (red), and a larger region of the substrate far from the device (green). The temperature is averaged over the area of each rectangle. An electric bias, generating some of the lowest power density (200 W cm−2) among the Pmax values reached in the representative TFT studies,25–33 was applied at the time marked by the vertical red dotted line and then turned off at ∼22 s. The sample's prompt heating rate (∼350 °C s−1) was determined by a linear fit of the initial heating region of the black curve (near the red dotted line). | ||
During the test, we imaged our sample from the top with an infrared thermal camera Micro-Epsilon ThermoIMAGER TIM640 (15 degrees, f = 41.5 mm, default emissivity 0.880) capturing a video of the in situ temperature distribution along the surface of the sample and the substrate (all exposed non-metallic surfaces are imaged). Based on the tabulated emissivity of the imaged materials, the accuracy of these temperature measurements is estimated to be about 10%.
Fig. 1b is a screenshot from a video of the surface temperature distribution of the biased device. The detailed temporal profiles, T(t), calculated from the full video (Supplementary movie file, ESI†) are shown in Fig. 1c. The local temperature is calculated by averaging the data in the three regions outlined in Fig. 1b with the rectangles: the device itself (black curve), a small region of the Si/SiO2 substrate close to the device (red curve), and a region of the substrate far from the device (green curve). It can be seen from Fig. 1c or the Supplementary video (ESI†) that right after the excitation current is applied, the resistor heats up very quickly, reaching temperatures well above 100 °C in a fraction of a second (at a rate of ∼350 °C s−1), and then rapidly heating up further, to >150 °C. The temperature of the substrate (Si/SiO2 wafer) also increases rapidly and significantly: its temperature near the sample goes up to ∼80 °C (red curve in Fig. 1c). These observations confirm a good thermal contact between the active film and the Si wafer in our experiment. Importantly, even if we conservatively assume that the thermal contact between the resistive film and the wafer in our test were poor, improving it could only lead to an even higher temperature of the substrate. In this sense, the substrate's temperature in the vicinity of the sample gives the lower bound for the temperature of the sample itself regardless of the quality of thermal contact. Combined with the facts that thermal mass of the substrate in our control experiment is much greater than that of the resistive film, and thermal conductivity of heavily doped Si wafers is very good, we likely underestimate the temperature of the sample. Also, the calculated Joule power and its density are direct consequences of Ohm's and Joule's laws. Therefore, once the few essential experimental parameters, such as VDS, ImaxDS, L and W, are given in a paper, those indicators of a potential overheating of the sample can be unambiguously calculated and become relevant, irrespective of a specific TFT channel material.
Thus, our demonstration unambiguously shows that the Joule heating of the semiconducting films in the TFT measurements under high biases reported in ref. 25–33 must be very significant, with the local temperature of the channel that can easily increase from room temperature all the way to >150 °C. Such measurements certainly cannot be portrayed as room-temperature, continuous (steady-state), reproducible TFT operation. Such conditions would inevitably bring the sample out of thermal equilibrium with the setup/ambient. Interestingly, our results are quantitatively consistent with the temperature rise due to Joule heating estimated in strontium tin oxide thin films using an all-electrical pulsed measurement technique.37 The detrimental effects of heating will be especially harmful in the most important high-current region of TFTs’ transfer curves. Such a biasing regime cannot be considered safe or reliable when studying semiconductors whose properties might be temperature dependent. Furthermore, possible issues with the material degradation, parameter drift, or chemical and structural modifications (due to, e.g., an ionic drift or electro-chemistry), known to occur in perovskites or disordered organic semiconductors under such measurement conditions, could have an impact on the reported results and conclusions. As compared to conventional inorganic semiconductors, emergent soft-lattice electronic materials, including metal-halide perovskites and organic semiconductors,38–41 are not expected to be very stable structurally,42 morphologically,43 or electrically (on bias stressing),27 especially at T > 150 °C. Although some of these materials might be annealed at the fabrication stage, applying a very strong electric bias simultaneously with unintended and uncontrolled heating in TFT measurements could be much more detrimental to these devices than merely thermal annealing. The applied electric bias in TFT measurements in the papers analyzed in Table S1 (ESI†) is indeed very strong. For example, in the study of hybrid perovskite TFTs by H. Zhu et al.,25 an average longitudinal electric field applied during the transfer curve measurements was EDS ≡ VDS/L = 2 kV cm−1 (line 1 of Table S1, ESI†). Given the fact that those are saturation regime measurements, the local electric field in the pinch-off region of the hybrid perovskite channel must have been even higher. The authors explicitly report their measurements as a continuous, steady-state, room-temperature TFT operation. However, it remains unclear how the detrimental effects of self-heating, including the likely material's degradation, were mitigated, as none of these issues were addressed.
It must be noted that, while we have chosen the specific biasing conditions similar to those in a few papers,25,26 the problem we have outlined seems to be pervasive in the TFT literature. Indeed, similarly strong or sometimes even stronger biasing is used with various delicate materials, including conjugated polymers with Pmax ∼ 400–750 W cm−2, small-molecule organic semiconductors with Pmax ∼ 2–7 kW cm−2, and two-dimensional fused aromatic networks with Pmax ∼ 10 kW cm−2 (for details, see Table S1, ESI†). To put these values in perspective, the following comparison might be useful: (a) the working surface of a typical household clothes iron emits about 0.36 W cm−2 during the full-power operation; (b) the integral (over the entire electro-magnetic spectrum) power density emitted by our sun at its surface is Psun ≈ 6.4 kW cm−2;44 and (c) the power density of a CO2 laser beam in industrial laser cutting machines, sufficient to cut (or engrave) thin sheets of plastics, wood or leather, is in the range Plaser![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cutter = 3–10 kW cm−2.45 To make matters worse, besides the extremely high power densities, some of the studies also reach very significant absolute powers, Wmax ≡ |VDS|·|ImaxDS|, in the channel of their TFTs in the range 0.2–0.4 W (Table S1, ESI†), which is very high for small devices based on delicate thin-film materials.
cutter = 3–10 kW cm−2.45 To make matters worse, besides the extremely high power densities, some of the studies also reach very significant absolute powers, Wmax ≡ |VDS|·|ImaxDS|, in the channel of their TFTs in the range 0.2–0.4 W (Table S1, ESI†), which is very high for small devices based on delicate thin-film materials.
Finally, we would like to discuss the limitations of eqn (1) that defines the theoretical maximum power density in a TFT channel, as it assumes zero contact resistance (Rcont = 0). Given the expression for the transistor's source–drain current in the limit of zero contact resistance,  , where σ□ is the sheet conductivity of the channel per square (in Ω−1), eqn (1) leads to:
, where σ□ is the sheet conductivity of the channel per square (in Ω−1), eqn (1) leads to:
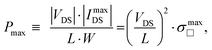 | (2) |
 is the maximum channel conductivity reached at the highest carrier density nmax corresponding to ImaxDS, μ is the charge carrier mobility in the channel, and e is the elementary charge. Thus, in the limit of short-channel devices (L → 0), the above theoretical Pmax diverges as
is the maximum channel conductivity reached at the highest carrier density nmax corresponding to ImaxDS, μ is the charge carrier mobility in the channel, and e is the elementary charge. Thus, in the limit of short-channel devices (L → 0), the above theoretical Pmax diverges as  . The actual (local) Joule power density, Pchmax, generated in the channel does not diverge, because it will inevitably become limited by the contact effects as L → 0. Indeed, when Rcont is not negligible in comparison with the channel resistance,
. The actual (local) Joule power density, Pchmax, generated in the channel does not diverge, because it will inevitably become limited by the contact effects as L → 0. Indeed, when Rcont is not negligible in comparison with the channel resistance, 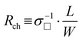 , the actual voltage drop on the semiconducting channel, VDS, should be smaller than
, the actual voltage drop on the semiconducting channel, VDS, should be smaller than  :
: | (3) |
Thus, Pchmax, generated in the channel of such devices can be expressed as:
 | (4) |
The contact effects that typically become relatively more significant in short-channel devices will be limiting the voltage drop along the channel, thus also limiting the local Joule power density generated in the semiconducting film. Nevertheless, because shrinking the device's length inevitably places the contacts in a closer proximity to the semiconducting channel, any heat generated in the resistive contacts can be easily transferred to the channel and vice versa, so that, with L → 0, the net heat (generated by both the channel and the contacts) is released in an increasingly smaller volume of the sample. Thus, parameter Pmax given by the simple eqn (1) is a sufficiently strong indicator for potentially serious problems: high Pmax could mean that the channel has been significantly over-heated during the TFT measurements, unless (a) special measures were undertaken to efficiently cool the devices, or (b) the reported devices were long-channel TFTs with highly resistive contacts. If such unusual long-channel yet contact-dominated TFTs are reported (case b), one has to pay attention to the reported carrier mobility. Indeed, while the local power density, Pchmax, generated in the channel of such devices might be reduced due to the contact effects (Pchmax < Pmax), so should be the two-probe TFT mobility, μ. This suggests that the reported μ in such devices cannot be too high. Hence, publications reporting an unusually high (for a given material) two-probe TFT mobility, in which the power density Pmax estimated by eqn (1) is also very high, are especially concerning. As one can see from Table S1 (ESI†), there are many such reports. In a nutshell, with a high Pmax, one cannot simultaneously have a high two-probe TFT mobility μ, yet argue that the contact effects have prevented overheating of the semiconducting channel.
Given the above considerations, a more direct and physically meaningful parameter is the local temperature, T, of the semiconducting channel that governs the physical properties of the material and largely defines the device characteristics. The local T is the result of a balance between the rates of heat generation and dissipation and thus depends not only on Pmax but also other experimental parameters and conditions, including the type and size of the substrate, the net absolute applied power (in watts), cooling efficiency of the substrate, the lateral channel dimensions in comparison with the substrate's thickness and size, how fast TFT measurements are carried out (the gate voltage sweep rate), etc. In the majority of papers reporting TFT measurements at extreme biasing conditions, including those reaching very high Pmax, the gate voltage sweep rates or device heat management efforts are not mentioned.
For instance, in very short-channel devices (when the channel length is much smaller than the thickness of the substrate, L ≪ d), the TFT channel can be approximately considered to be in contact with a semi-infinite space of the substrate material, which would allow a radial heat dissipation into the substrate in any direction within a solid angle of 2π. On the contrary, for longer channel devices (L ≳ d), the heat must first flow vertically into a thin substrate and then propagate away laterally through it, which would limit the cooling rate. In addition, in short-channel devices, the heat generated in the channel can be more efficiently removed via the metal contacts due to their proximity to the channel, provided that the contacts are sufficiently thick and are well thermally anchored. Thus, the natural heat dissipation in short-channel devices is expected to be somewhat better.46 Therefore, seeing a very high Pmax in normal-to-long channel devices with a high reported TFT mobility is especially alarming. For example, in H. Zhu et al.,25 the TFT channel is not short at all (L ∼ d), meaning that the power density Pmax ≈ 200 W cm−2 estimated viaeqn (1) is close to the actual local power density in the channel.
To conclude, a number of recent studies of transistors based on emerging electronic materials, carrying out measurements under extreme biasing conditions, could have been affected by a significant increase of the local temperature of the semiconducting channel, possibly leading to materials’ degradation, parameter drift, or nonlinearities that in turn could lead to errors in the extracted charge-carrier mobilities. At the very least, the mobilities reported in those studies are most certainly not room-temperature mobilities. We have clearly demonstrated this problem here (using the experimental conditions similar to or milder than those in the representative ref. 25–33) by performing an in situ IR imaging of electrically biased resistive channel, indeed confirming a rapid increase of the local temperature of such devices to well above 150 °C. This Perspective emphasizes the need for restricting the power and power densities applied in TFT measurements, along with a concerted and well-documented effort on device heat management (cooling) and in situ monitoring of the local temperature of devices in such experiments.
Data availability
The data supporting this article, including thermal imaging video and table with the literature analysis, have been included as part of the ESI.†Author contributions
VB fabricated devices; VB, YP, VP and JPS carried out thermal imaging tests; VB and VP analyzed the data and surveyed the literature; VP wrote initial draft of the paper, and all authors contributed to editing the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
VB and VP thank partial support of their research at Rutgers University via the Donald H. Jacobs Chair in Applied Physics. The authors thank Mario Caironi for helpful discussions.References
- B. L. Anderson and R. L. Anderson, Fundamentals of Semiconductor Devices, McGraw-Hill, New York, 1st edn, 2005, ch. 7, p. 385 Search PubMed.
- C. H. Ahn, A. Bhattacharya, M. Di Ventra, J. N. Eckstein, C. D. Frisbie, M. E. Gershenson, A. M. Goldman, I. H. Inoue, J. Mannhart, A. J. Millis, A. F. Morpurgo, D. Natelson and J.-M. Triscone, Rev. Mod. Phys., 2006, 78, 1185–1212 CrossRef CAS.
- S. Z. Bisri, S. Shimizu, M. Nakano and Y. Iwasa, Adv. Mater., 2017, 29, 1607054 CrossRef PubMed.
- C. R. Kagan, D. B. Mitzi and C. D. Dimitrakopoulos, Science, 1999, 286, 945–947 CrossRef CAS PubMed.
- X. Y. Chin, D. Cortecchia, J. Yin, A. Bruno and C. Soci, Nat. Commun., 2015, 6, 7383 CrossRef CAS PubMed.
- J. G. Labram, D. H. Fabini, E. E. Perry, A. J. Lehner, H. Wang, A. M. Glaudell, G. Wu, H. Evans, D. Buck, R. Cotta, L. Echegoyen, F. Wudl, R. Seshadri and M. L. Chabinyc, J. Phys. Chem. Lett., 2015, 6, 3565–3571 CrossRef CAS PubMed.
- Y.-H. Lin, P. Pattanasattayavong and T. D. Anthopoulos, Adv. Mater., 2017, 29, 1702838 CrossRef PubMed.
- X. Liu, D. Yu, X. Song and H. Zeng, Small, 2018, 14, 1801460 CrossRef PubMed.
- Y. Liu, P.-A. Chen and Y. Hu, J. Mater. Chem. C, 2020, 8, 16691–16715 RSC.
- F. Paulus, C. Tyznik, O. D. Jurchescu and Y. Vaynzof, Adv. Funct. Mater., 2021, 31, 2101029 CrossRef CAS.
- V. Bruevich, L. Kasaei, S. Rangan, H. Hijazi, Z. Zhang, T. Emge, E. Y. Andrei, R. A. Bartynski, L. C. Feldman and V. Podzorov, Adv. Mater., 2022, 34, 2205055 CrossRef CAS PubMed.
- G. Horowitz, Adv. Mater., 1998, 10, 365–377 CrossRef CAS.
- V. Podzorov, MRS Bull., 2013, 38, 15–27 CrossRef.
- K. Sakai, Y. Okada, T. Uemura, J. Tsurumi, R. Häusermann, H. Matsui, T. Fukami, H. Ishii, N. Kobayashi, K. Hirose and J. Takeya, NPG Asia Mater., 2016, 8, e252–e252 CrossRef CAS.
- H. H. Choi, K. Cho, C. D. Frisbie, H. Sirringhaus and V. Podzorov, Nat. Mater., 2018, 17, 2–7 CrossRef CAS PubMed.
- V. Podzorov, M. E. Gershenson, C. Kloc, R. Zeis and E. Bucher, Appl. Phys. Lett., 2004, 84, 3301–3303 CrossRef CAS.
- Y. J. Zhang, M. Yoshida, R. Suzuki and Y. Iwasa, 2D Mater., 2015, 2, 044004 CrossRef.
- S. B. Mitta, M. S. Choi, A. Nipane, F. Ali, C. Kim, J. T. Teherani, J. Hone and W. J. Yoo, 2D Mater., 2021, 8, 012002 CrossRef CAS.
- J. Jang, W. Liu, J. S. Son and D. V. Talapin, Nano Lett., 2014, 14, 653–662 CrossRef CAS PubMed.
- A. Molazemhosseini, F. A. Viola, F. J. Berger, N. F. Zorn, J. Zaumseil and M. Caironi, ACS Appl. Electron. Mater., 2021, 3, 3106–3113 CrossRef CAS PubMed.
- K. Ueno, S. Nakamura, H. Shimotani, A. Ohtomo, N. Kimura, T. Nojima, H. Aoki, Y. Iwasa and M. Kawasaki, Nat. Mater., 2008, 7, 855–858 CrossRef CAS PubMed.
- C. Leighton, T. Birol and J. Walter, APL Mater., 2022, 10, 040901 CrossRef CAS.
- H. Wang, J. Walter, K. Ganguly, B. Yu, G. Yu, Z. Zhang, H. Zhou, H. Fu, M. Greven and C. Leighton, Phys. Rev. Mater., 2019, 3, 075001 CrossRef CAS.
- H. T. Yi, B. Gao, W. Xie, S.-W. Cheong and V. Podzorov, Sci. Rep., 2014, 4, 6604 CrossRef CAS PubMed.
- H. Zhu, W. Yang, Y. Reo, G. Zheng, S. Bai, A. Liu and Y.-Y. Noh, Nat. Electron., 2023, 6, 650–657 CrossRef CAS.
- A. Liu, H. Zhu, S. Bai, Y. Reo, T. Zou, M.-G. Kim and Y.-Y. Noh, Nat. Electron., 2022, 5, 78–83 CrossRef CAS.
- W. Yang, K. Zhang, W. Yuan, L. Zhang, C. Qin and H. Wang, Adv. Mater., 2024, 36, 2313461 CrossRef CAS PubMed.
- F. Yang, C. Li, J. Zhang, G. Feng, Z. Wei and W. Li, Org. Electron., 2016, 37, 366–370 CrossRef CAS.
- Y. Ji, C. Xiao, Q. Wang, J. Zhang, C. Li, Y. Wu, Z. Wei, X. Zhan, W. Hu, Z. Wang, R. A. J. Janssen and W. Li, Adv. Mater., 2016, 28, 943–950 CrossRef CAS PubMed.
- Y. Diao, B. C. K. Tee, G. Giri, J. Xu, D. H. Kim, H. A. Becerril, R. M. Stoltenberg, T. H. Lee, G. Xue, S. C. B. Mannsfeld and Z. Bao, Nat. Mater., 2013, 12, 665–671 CrossRef CAS PubMed.
- A. Zhang, C. Xiao, Y. Wu, C. Li, Y. Ji, L. Li, W. Hu, Z. Wang, W. Ma and W. Li, Macromolecules, 2016, 49, 6431–6438 CrossRef CAS.
- J. Lee, A. R. Han, H. Yu, T. J. Shin, C. Yang and J. H. Oh, J. Am. Chem. Soc., 2013, 135, 9540–9547 CrossRef CAS PubMed.
- H.-R. Tseng, L. Ying, B. B. Y. Hsu, L. A. Perez, C. J. Takacs, G. C. Bazan and A. J. Heeger, Nano Lett., 2012, 12, 6353–6357 CrossRef CAS PubMed.
- V. Bruevich and V. Podzorov, Zenodo, 2023 DOI:10.5281/zenodo.10046994.
- V. Podzorov and V. Bruevich, Nat. Electron., 2024, 7, 266–268 CrossRef.
- H. H. Choi, K. Cho, C. D. Frisbie, H. Sirringhaus and V. Podzorov, Zenodo, 2017 DOI:10.5281/zenodo.1050699.
- P. Golani, C. N. Saha, P. P. Sundaram, F. Liu, T. K. Truttmann, V. R. S. K. Chaganti, B. Jalan, U. Singisetti and S. J. Koester, Appl. Phys. Lett., 2022, 121, 162102 CrossRef CAS.
- D. A. Egger, A. Bera, D. Cahen, G. Hodes, T. Kirchartz, L. Kronik, R. Lovrincic, A. M. Rappe, D. R. Reichman and O. Yaffe, Adv. Mater., 2018, 30, 1800691 CrossRef PubMed.
- M. J. Schilcher, D. J. Abramovitch, M. Z. Mayers, L. Z. Tan, D. R. Reichman and D. A. Egger, Phys. Rev. Mater., 2023, 7, L081601 CrossRef CAS.
- A. Troisi and G. Orlandi, Phys. Rev. Lett., 2006, 96, 086601 CrossRef PubMed.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315 CrossRef CAS.
- L. E. Mundt and L. T. Schelhas, Adv. Energy Mater., 2020, 10, 1903074 CrossRef CAS.
- N. K. Tailor, M. Abdi-Jalebi, V. Gupta, H. Hu, M. I. Dar, G. Li and S. Satapathi, J. Mater. Chem. A, 2020, 8, 21356–21386 RSC.
- C. B. Honsberg and S. G. Bowden, Photovoltaics Education Website, 2019, https://www.pveducation.org/pvcdrom/properties-of-sunlight/solar-radiation-in-space, (accessed June 10, 2024).
- Parallax Technology, Inc., 2024, https://www.parallax-tech.com/faq.htm, (accessed June 10, 2024).
- A. Perinot, M. Giorgio, V. Mattoli, D. Natali and M. Caironi, Adv. Sci., 2021, 8, 2001098 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc02612h |
| This journal is © The Royal Society of Chemistry 2024 |
