Open Access Article
Open Access ArticleElucidating the role of physicochemical interactions on gel rheology
Elnaz
Nikoumanesh
 ,
Charles Joseph M.
Jouaneh
,
Charles Joseph M.
Jouaneh
 and
Ryan
Poling-Skutvik
and
Ryan
Poling-Skutvik
 *
*
Department of Chemical Engineering, University of Rhode Island, Kingston, RI 02881, USA. E-mail: ryanps@uri.edu
First published on 25th June 2024
Abstract
Soft materials are characterized by their intricate interplay of structure, dynamics, and rheological properties. This complexity makes it challenging to accurately predict their response to shear stress. Here, we investigate how the nature of bonds – electrostatic attractions, physical entanglements, physical repulsion, and covalent bonds – affects the linear and nonlinear rheology of gels. Specifically, we determine the critical roles these bonds play in the yield transition and thixotropic recovery of gel properties through a combination of linear oscillatory deformations, serial creep divergence measurements, and time-resolved flow sweeps. Different classes of gels are prepared with nearly identical linear rheology but significantly different yield transitions and nonlinear properties post-yielding. These differences are directly related to the kinetics by which the underlying elastic networks rebuild after flow. Gels which exhibit thixotropic hysteresis are able to fully recover their yield stress over time while non-thixotropic gels possess time-independent yielding metrics. This direct comparison between thixotropy and yielding reveals the intimate relationship between these phenomena and their controlling physical mechanisms within soft, amorphous materials.
1 Introduction
Gels are a class of materials characterized by their mechanical properties between those of liquids and solids.1 At rest, gels possess a percolating network that elastically deforms to support small applied stresses and that suppresses relaxations.2 When subjected to a large stress, however, the gel network breaks down to facilitate flow and viscously dissipates energy.3–5 This transition from elastic deformation to viscous flow is known as the yield transition and is most commonly associated with a finite strain or stress.6–8 Even though the yield transition is ubiquitous and critically important for many industrial processes,9,10 there remains significant ambiguity over how to define and quantify “the” yield stress σy or yield strain γy.11Recent insights into this phenomenon reveal that some of the ambiguity arises from the fact that the yield transition is a continuous rather than instantaneous process.12 In this continuous framework, materials accumulate finite plastic strain during deformation, eventually resulting in network failure. Furthermore, as flow develops, shear forces may result in the remodeling and breakdown of the fluid structure. If this structural change is reversible, the elastic network reforms over time once the flow is suppressed, and this reformation is referred to as thixotropy.13,14 Although many yield-stress materials exhibit thixotropy, these phenomena are distinct in their origins with thixotropy being time-dependent while yielding is stress-dependent. Nevertheless, these observations indicate that both yielding and thixotropy are inherently dynamic processes facilitated by the rearrangement of gel constituents coupled with external stresses and deformations. Thus, it becomes essential to understand the nature of the physicochemical bonds connecting these particulates into a cohesive elastic network to predict their yielding and thixotropic properties.15
Broadly, thixotropic yield stress fluids can be prepared from a wide variety of constituent building blocks with varying interparticle potentials and geometries.13 In the case of small aspect ratio particles such as spheres or rods, elastic networks are formed through repulsive or attractive potentials. In a repulsive paradigm, yield stress fluids develop through the jamming of hard or soft particles at high volume fractions so that the particle size and elasticity control elasticity.16–18 This elastic transition can occur at low volume fractions for highly charged species in which long-range electrostatic repulsion facilitates the formation of a Wigner glass.19 By contrast, in an attractive paradigm, an elastic network results from the growth and percolation of fractal clusters either through diffusion-limited or reaction-limited aggregation.20–23 In gels with either attractive or repulsive interactions, the gel strength and elasticity depend strongly on the concentration and strength of the resulting bonds. Particles with specific interactions or patches tend to form more complex structures due to their ability to explore a wider range of energy landscapes during assembly.24,25 Additionally, fibers or polymer chains possess elongated, high aspect ratio conformations that allow the particulates to interpenetrate and develop elasticity through physical entanglements.26,27 Finally, covalent networks can be formed through multifunctional crosslinkers.28 In contrast to other interaction profiles, covalent crosslinking results in an irreversible bond that once broken under flow is not able to reform without additional reactants. Although theories postulate how these different interaction profiles and structural moieties build elasticity, their impact on nonlinear rheology through yield transition and thixotropic recovery remains poorly understood.
Here, we prepare gels possessing different physicochemical interactions – electrostatic attraction, physical entanglement, physical repulsion, and covalent crosslinking – but quantitatively similar linear rheological moduli. Despite their similar linear responses, these gels exhibit vastly different nonlinear properties which we quantify through serial creep divergence (SCD) rheology29 and hysteresis loops in steady shear flow sweeps.30,31 For attractive gels or gels possessing physical entanglements, we observe significant thixotropy and a time-dependent yield stress. For gels possessing physical repulsions and covalent crosslinks, we observe yield transitions characterized by a time-independent yield stress. We attribute the distinct nonlinear rheology of these gels to the different dynamics of constituent building blocks. For thixotropic gels, the time-dependent yield stress arises from the finite time scales associated with the coupled diffusion–aggregation of colloidal clusters or reptative re-entanglement of fibrillar networks. By contrast, time-independent yield stresses emerge for samples exhibiting minimal thixotropy due to either infinitely fast or infinitely slow recoveries for repulsive gels and covalent networks, respectively. These observations demonstrate that yielding and thixotropy are highly related phenomena that emerge from dynamic rearrangements of constitutive building blocks. Additionally, our findings demonstrate that SCD is a sensitive probe of dynamics in thixotropic yield stress fluids but that accurate interpretation of the recovery kinetics requires prior knowledge of dynamic modes.
2 Materials and methods
2.1 Materials
Cellulose nanocrystals (CNCs) were purchased from CelluForce (Montreal, Canada) as a dry powder, potassium chloride (KCl) was purchased from Fisher Scientific, Carbopol 940 was purchased from Lubrizol as a dry white powder, 4-(4,6-dimethoxy-1,3,5-triazin-2-yl)-4-methyl-morpholinium chloride (DMTMM) and hexamethylenediamine (HMDA) were purchased from Sigma-Aldrich, and TEMPO-oxidized cellulose nanofibers (CNFs) were purchased from the University of Maine. All materials were used as received.2.2 Gel preparation
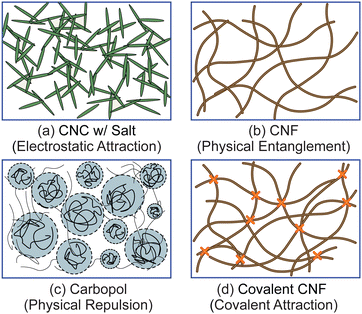
To test the effect of different physicochemical interactions on gel rheology, we prepared four different classes of samples (Fig. 1). First, we prepared electrostatically attractive CNC gels by adding KCl to destabilize the colloidal suspension. Second, we prepared physically entangled CNF gels by evaporating solvent to increase the fibril concentration. Third, we prepared gels with physically repulsive gels by dissolving Carbopol at sufficiently high concentrations. Finally, we crosslinked the carboxylic acid groups on the surface of CNFs with diamines to form a covalently linked gel. Additional details on each sample are provided below.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio to carboxylic acid groups on the CNF, resulting in a 0.8
1 molar ratio to carboxylic acid groups on the CNF, resulting in a 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of COOH
1 molar ratio of COOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NH2 along with sufficient water to prepare a final gel at 1 wt%. All hydrogels were initially prepared by mixing the aforementioned components in a 50 mL beaker and then casting the gel immediately into a 26 mm circular silicone mold.
NH2 along with sufficient water to prepare a final gel at 1 wt%. All hydrogels were initially prepared by mixing the aforementioned components in a 50 mL beaker and then casting the gel immediately into a 26 mm circular silicone mold.
2.3 Rheology
The rheological properties of these gels were assessed through a variety of rheological procedures. Rheological measurements were conducted using a TA Instruments HR20 rheometer. A solvent trap was employed to reduce evaporation during the experiments. To further mitigate evaporation, the edges of the samples were coated with mineral oil. All measurements were conducted at a constant temperature of T = 25 °C.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 100 rad s−1 for 1 minute. This pre-shear disrupted the underlying structural network in the material and erased previous mechanical history. After, we allowed the sample to rest under quiescent conditions for a waiting time tw before imposing a stress σ and measuring the sample compliance. We repeated this procedure for increasing tw and σ.
= 100 rad s−1 for 1 minute. This pre-shear disrupted the underlying structural network in the material and erased previous mechanical history. After, we allowed the sample to rest under quiescent conditions for a waiting time tw before imposing a stress σ and measuring the sample compliance. We repeated this procedure for increasing tw and σ.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) max = 103 s−1 to low
max = 103 s−1 to low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) min = 10−2 s−1 through N = 8 steps per decade with each step lasting for a duration of 3 ≤ δt ≤ 100 s. We then immediately increased the shear rate back from
min = 10−2 s−1 through N = 8 steps per decade with each step lasting for a duration of 3 ≤ δt ≤ 100 s. We then immediately increased the shear rate back from ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) min to the initial value of
min to the initial value of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) max. By controlling the time at each shear rate, the average shear stress reflected changes in the sample structure.
max. By controlling the time at each shear rate, the average shear stress reflected changes in the sample structure.
3 Results and discussion
Because of the variety of rheological protocols used in this work, we provide a quick overview of our results before discussing each finding in detail below. First, using linear frequency sweeps, we verify that the four classes of gels investigated here – electrostatically attractive CNC, physically entangled CNF, physically repulsive Carbopol, and covalently crosslinked CNF – exhibit quantitatively similar viscoelastic relaxations. Second, we identify that each of these gels exhibits the expected yield transition with increasing stress under oscillatory and steady shear deformations. Third, by conducting SCD protocols, we identify that this yield transition depends strongly on shear history for electrostatically attractive CNC and physically entangled CNF gels but is independent of shear history for physically repulsive Carbopol gels. For covalently bonded CNF gels, the yield transition is unique for the first yielding event and then becomes independent of shear history for subsequent yielding. Lastly, we reconcile these different yielding kinetics by quantifying the magnitude of thixotropic hysteresis in time-resolved flow sweeps.3.1 Linear frequency sweeps
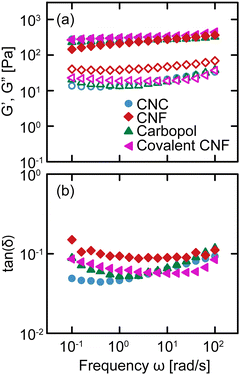
We conduct oscillatory rheology to quantify the linear viscoelastic properties of gels as a function of frequency ω. The linear moduli of gels depend strongly on the concentration of constituent species and effective bond density.35 By varying the concentrations of salt, constituent species, and crosslinker, we prepare gels that exhibit quantitatively similar relaxation spectra despite their different physicochemical compositions, as shown in Fig. 2. For each gel, the storage modulus G′ is nearly independent of frequency, varying by less than an order of magnitude over four decades in frequency, with a value of G′ ≈ 300 Pa. Additionally, the loss modulus G′′ is significantly lower than G′, resulting in tan(δ) = G′′/G′ ≈ 0.1 for all samples without a strong dependence on ω. These results confirm that the various classes of gels are viscoelastic solids with suppressed relaxations. Furthermore, the linear rheology of these gels is nearly indistinguishable across the gel classes, providing us with an ideal comparison to evaluate the role of physicochemical interactions in their nonlinear response.3.2 Yielding response
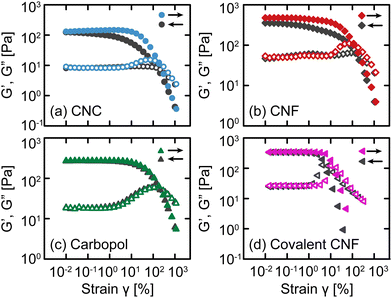
After confirming that these gels exhibit similar linear relaxation spectra, we now assess how different interactions modify their nonlinear response. As an initial test, we apply oscillatory deformations at a fixed frequency (ω = 10 rad s−1) and varying strain γ (Fig. 3). With increasing γ (i.e., an up-sweep), each gel undergoes a yield transition. At small γ, the materials deform linearly with G′ and G′′ that are independent of γ, but at larger γ, G′ decreases rapidly and G′′ experiences an overshoot associated with the accumulation of unrecoverable strain.12,36 These responses confirm that the gels yield under sufficiently high stress to transition from solid-like to liquid-like behavior.After the samples have fully yielded so that G′′ > G′, we continue to apply oscillatory deformations but with decreasing γ (i.e., a down-sweep). For simple viscoelastic materials, the down-sweep and up-sweep measurements should agree because the moduli act as state variables dictated by ω and γ. While this is true for Carbopol gels, confirming that they form simple yield stress fluids,37,38 the amplitude sweeps disagree for the electrostatically attractive CNC, physically entangled CNF, and covalent CNF gels, especially around the G′′ overshoot. For the CNC and entangled CNF gels, the G′′ overshoot is almost completely missing from the down-sweep and G′ is only fully recovered at very small strains. We attribute these differences to the kinetics of colloidal and fibrillar rearrangements from the fluidized state at a high γ to the gel state at a low γ. Once the network fluidizes,39 there is a finite time scale associated with network reformation as CNCs or CNFs diffuse and re-aggregate or re-entangle, respectively. Thus, the difference between up- and down-sweeps reflects the evolving structure of the sample post-yielding.
The covalent CNF gel has similar but qualitatively distinct differences between the up- and down-sweeps; the G′′ overshoot is preserved, and G′ recovers entirely at a relatively high γ. Whereas the CNC and entangled CNF gels possess recoverable bonds, the covalent CNF network can only yield by breaking chemical bonds either along the cellulose backbone or the amide bond formed between the diamine crosslinker and carboxylic acid groups on the CNF surface. Once broken, these bonds cannot reform and therefore the network cannot recover. Surprisingly though, the linear elastic modulus of this covalent network fully recovers after yielding despite the network losing some fraction of bonds during flow. Instead, the weaker network manifests through a decrease in the yield strain γy (and therefore in the the yield stress σy), quantified by the crossover between G′ and G′′. This initial finding suggests that nonlinear properties may be a more sensitive metric to assess gel strength and shear history dependence than the standard linear recovery measurements after step changes in shear strain or rate.40,41
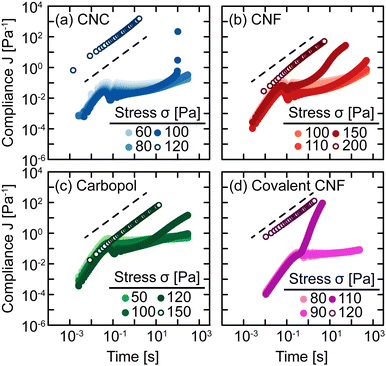
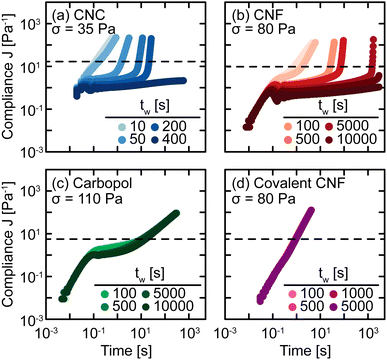
The sensitivity of yielding to shear history is further investigated through creep measurements in which samples are subjected to a constant stress rather than a sinusoidal strain. Whereas strain-controlled oscillatory measurements require the sample to deform a specified magnitude, deformation in creep is accumulated over time as the material responds to the applied stress. Here, we measure the compliance J = γ/σ of freshly prepared gels as a function of time under different values of stress σ spanning the yield stress σy (Fig. 4). Across different gel classes, we observe qualitatively similar behavior. At low σ, gels deform elastically with very weak time dependence consistent with previous measurements on colloidal gels.42 As σ increases, the gel compliance increases more rapidly with time as unrecoverable strain accumulates.12 At a sufficiently high σ, the samples yield under stress with a dramatic increase in their compliance as their elastic structure fluidizes. After the samples have yielded, subsequent creep measurements result in viscous flow in which the compliance scales with time as J = t/η in which η is the effective viscosity of the fluidized gel.43 This viscous flow indicates that the structural network of the gel breaks down during the yield transition.
In addition, this structural change is inferred from the difference in the creep ringing response of gels pre- and post-yielding. Creep ringing refers to the underdamped oscillations observed at small times as a result of the coupling of instrument inertia to material elasticity.44 Oscillations only appear when the material elasticity is sufficiently high relative to the sum of viscous and applied stresses.45,46 For all gels, the oscillations disappear when σ > σy, indicating an overdamped response. For the CNC, entangled CNF, and covalent CNF gels, we attribute this overdamped response to lower gel elasticities resulting from structural breakdown, supported by the significantly higher compliance values measured for post-yielded samples. By contrast, the compliance of Carbopol gels agrees at short times with the pre-yielded samples, indicating that the network elasticity is maintained across the yield transition. The overdamped response thus emerges because the applied stress dominates the material elasticity. These creep measurements thus further suggest that the yield transition is highly sensitive to the structural breakdown and recovery facilitated by physicochemical interactions between constituents and their resulting rearrangements.
3.3 Serial creep divergence (SCD)
To probe the kinetics of structural breakdown and recovery, we conduct SCD measurements.29,34 SCD is a rheological protocol designed to quantify the yield transition in the presence of thixotropy by applying creep deformations as a function of waiting time tw after yielding. Briefly, this procedure consists of pre-shearing the samples to remove shear history effects and to initialize the gel structure. After this pre-shear, the sample is allowed to rest quiescently for a set time period tw. Then, the sample is subjected to a constant stress σ to measure the compliance as a function of time. The yield time Δty is determined as the time at which the compliance J crosses an arbitrary threshold J* that distinguishes between primary creep and viscous flow behaviors. If Δty ≪ tw, the SCD measurement provides quasi-instantaneous characterization of the gel strength. By tracking the evolution of Δty with tw and σ, we build a comprehensive understanding of yielding and structural recovery.SCD measurements are performed on all gel classes, as shown in Fig. 5. At short tw, the gels exhibit a nearly constant power law increase in compliance, indicating that the samples immediately flow through a combination of viscous dissipation, characterized by the scaling J ∼ t, and instrument inertia, characterized by the scaling J ∼ t2. This rapid increase in compliance indicates that while these materials are elastic at rest (Fig. 2), the pre-shear protocol and forced yielding destroy the underlying elastic network with insufficient time for the network to recover. For the Carbopol gel, however, there is an intermediate plateau present even for the shortest tw measured. This difference in short time behavior indicates that the elastic network in Carbopol gels is restored nearly instantaneously after yielding, consistent with the lack of hysteresis in oscillatory amplitude sweeps (Fig. 3) and the agreement observed in the creep ringing regime (Fig. 4).
As tw increases, the CNC and entangled CNF gels begin to exhibit intermediate plateaus in their creep response. These plateaus indicate that the gels temporarily support the applied stress through a partial recovery of their underlying elastic network, consistent with the substantial hysteresis observed for these materials in oscillatory amplitude sweeps (Fig. 4(a and b)). After a long tw, the network sufficiently restructures to fully support σ, resulting in persistent long-time plateaus. For example, the compliances of CNC and entangled CNF gels after tw = 400 s or 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s, respectively, no longer exhibit upturns to cross J*. We observe qualitatively different behavior for Carbopol and covalently crosslinked CNF gels in which there is no significant change in J as a function of tw. For Carbopol, we associate this temporal independence to a nearly instantaneous recovery of elasticity after yielding; because the network is formed by physical repulsion, once the polymeric microgels viscously rearrange during flow, they immediately re-enter a free energy minimum formed by a cage of nearest neighbors.47,48 For covalent CNF networks, we attribute this behavior to the opposite effect in which the structure is permanently destroyed under flow. In contrast to the instantaneous recovery in Carbopol, the breaking of covalent bonds results in effectively infinitely long recovery times unless more reactants and catalysts are present to restore the broken covalent bonds. This picture is supported by the fact that after preshearing, the covalent CNF gels yield and flow at much lower stresses than the neat gel i.e., σ = 80 Pa in SCD but σ ≈ 110 Pa in creep (Fig. 4). Surprisingly, this decrease in the apparent yield stress of the covalent CNF contrasts with the recovery in linear elasticity observed in Fig. 3, suggesting that non-linear rheological metrics are more sensitive to structural changes in the material than linear properties.
000 s, respectively, no longer exhibit upturns to cross J*. We observe qualitatively different behavior for Carbopol and covalently crosslinked CNF gels in which there is no significant change in J as a function of tw. For Carbopol, we associate this temporal independence to a nearly instantaneous recovery of elasticity after yielding; because the network is formed by physical repulsion, once the polymeric microgels viscously rearrange during flow, they immediately re-enter a free energy minimum formed by a cage of nearest neighbors.47,48 For covalent CNF networks, we attribute this behavior to the opposite effect in which the structure is permanently destroyed under flow. In contrast to the instantaneous recovery in Carbopol, the breaking of covalent bonds results in effectively infinitely long recovery times unless more reactants and catalysts are present to restore the broken covalent bonds. This picture is supported by the fact that after preshearing, the covalent CNF gels yield and flow at much lower stresses than the neat gel i.e., σ = 80 Pa in SCD but σ ≈ 110 Pa in creep (Fig. 4). Surprisingly, this decrease in the apparent yield stress of the covalent CNF contrasts with the recovery in linear elasticity observed in Fig. 3, suggesting that non-linear rheological metrics are more sensitive to structural changes in the material than linear properties.
The qualitative changes observed in SCD can be quantified by defining the yield time Δty as the difference between the time at which J(t) = J* and the inertial response of the instrument (see ref. 29 for specifics), which we plot as a function of tw and applied stress σ in Fig. 6. For all samples, we observe a decrease in Δty with respect to σ as higher stress causes the elastic networks to fail more rapidly. This stress-activated failure is commonly observed in associating suspensions49,50 and polymer networks.51,52 Additionally, for CNC and entangled CNF gels, we observe an increase in Δty with tw as the elastic network rebuilds during quiescent rest. Once the elastic networks sufficiently recover, the samples no longer yield on experimental time scales and thus, Δty diverges at a finite tw. By contrast, there is no significant change in Δty for Carbopol and covalent CNF gels, confirming that there is no structural recovery in these systems.
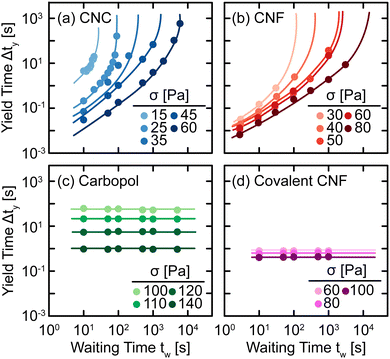 | ||
| Fig. 6 Yield time Δty as a function of waiting time tw under different applied stresses σ for (a) CNC, (b) entangled CNF, (c) Carbopol, and (d) covalent CNF gels. Curves are guides to the eye. | ||
3.4 Restructuring kinetics
The changes observed in SCD demonstrate that there are unique restructuring kinetics across different classes of gels. We gain insight into these kinetics by recognizing that the time tw,∞ at which Δty diverges physically represents the time necessary for the gel constituents to form a network with a yield stress equal to the applied stress σ. Thus, by inverting the relationship and tracking how σ depends on tw,∞, we explicitly quantify the kinetics by which the gel structure rebuilds after yielding (Fig. 7(a)). For both CNC and entangled CNF gels, the kinetics collapse onto separate master curves by normalizing the applied stress by a critical stress σc, which represents the limit of network yield stress,29 and normalizing the divergent yield times by a kinetic timescale τ0, which describes constituent rearrangements. With these normalized variables, we observe an increase in the stress that the CNC and entangled CNF gels can withstand as the waiting time increases. This increase in stress follows the restructuring kinetics of the elastic network after yielding. Furthermore, by combining the results of this study with SCD results from our earlier investigations,29,34 in which we varied constituent concentrations to prepare gels with different critical stresses σc, we show that the normalization time scale τ0 decreases exponentially σc according to τ0 ∼ exp(−σc/στ), where στ = 5.5 ± 0.4 Pa and 26 ± 3 Pa for CNC and CNF gels, respectively (Fig. 7(b)). This decrease in τ0 with σc indicates that stiffer gels recover their yield stress more rapidly.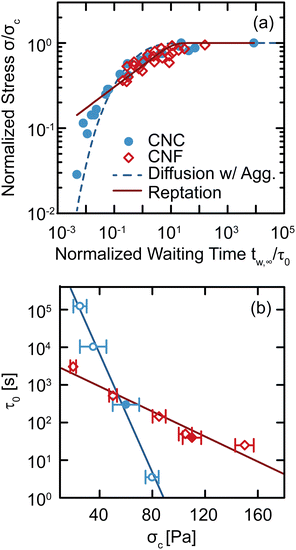 | ||
| Fig. 7 (a) Normalized stress σ/σc as a function of the normalized divergent waiting time tw,∞/τ0 for CNC and entangled CNF gels. The dashed line shows the best fit to the diffusion–aggregation model (eqn (2)) and the solid line is the best fit to the reptation model (eqn (3)). (b) Normalization time scale τ0 as a function of critical stress σc. Solid lines are exponential fits. Closed symbols are from this work and open symbols are from our earlier work on CNC gels29 and entangled CNF gels.34 | ||
Further insight into the physics of this relationship can be gained by modeling the restructuring kinetics according to constituent dynamics. Our kinetic modeling assumes that these thixotropic gels yield by forming shear bands in which the shear stress is localized to a narrow interface between plug-like regions. Shear banding is commonly observed for thixotropic yield stress fluids3,53–57 and is predicted theoretically.58,59 With this assumption, the network should rebuild through the Brownian motion of constituents across this shear band interface and reintegration into the cohesive elastic network preserved within each shear band. Although these models were developed in earlier work, they demonstrate the specific physical mechanisms underlying thixotropy, allowing us to contrast thixotropic kinetics across different physicochemical interactions.
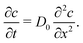 | (1) |
By assuming that these gels fail at a shear band interface and recover through the growth of fractal clusters, we solve this differential equation to get
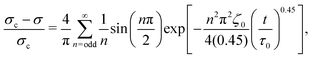 | (2) |
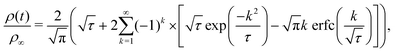 | (3) |
Although these models for the coupled diffusion–aggregation of attractive colloids and reptative re-entanglement of fibers across a shear band interface predict the measured increase in the yield stress of these gels, there are surprisingly small quantitative differences between the kinetics of these two gel classes. For example, for tw,∞/τ0 > 10−1, the measured values and model predictions are nearly indistinguishable (Fig. 7(a)). Significant differences do appear, however, on shorter time scales where reptative re-entanglement predicts an order-of-magnitude larger yield stress than diffusion–aggregation. The similarity between these models demonstrates one limitation of the SCD procedure; it is challenging to isolate the specific restructuring mechanisms unless the constituent interactions and conformations are well understood. Nevertheless, SCD reveals that the attractive CNC and entangled CNF gels undergo nearly complete structural recovery after yielding if given sufficient time.
3.5 Thixotropic recovery
Up to this point, we have attributed changes in the response of gels post-yielding to structural recovery, i.e., thixotropy. We now explicitly test this hypothesis using an established rheological protocol.30,31 Briefly, this protocol consists of conducting flow sweeps from high shear rates![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) to low and back using N = 8 steps per decade and averaging over a time interval δt ranging from 3 s to 100 s per step. This protocol results in flow sweeps with different magnitudes of hysteresis depending on the gel class, as shown in Fig. 8. For the CNC and entangled CNF gels, which show an increase in yield stress with waiting time, we observe significant differences between the flow sweeps in the up and down directions. By contrast, there is no significant difference between the Carbopol and covalent CNF gels, consistent with the time-independent yield stress measured in SCD. Furthermore, the intercepts of these flow curves should correspond to the dynamic yield stress of the gels. This intercept is comparable to σc for Carbopol, consistent with a lack of structural change during flow, but significantly lower than σc for the other gel classes. This suppressed yield stress is consistent with the expected structural breakdown during flow, which is recoverable for CNC and entangled CNF gels but irrecoverable for the covalent CNF gels.
to low and back using N = 8 steps per decade and averaging over a time interval δt ranging from 3 s to 100 s per step. This protocol results in flow sweeps with different magnitudes of hysteresis depending on the gel class, as shown in Fig. 8. For the CNC and entangled CNF gels, which show an increase in yield stress with waiting time, we observe significant differences between the flow sweeps in the up and down directions. By contrast, there is no significant difference between the Carbopol and covalent CNF gels, consistent with the time-independent yield stress measured in SCD. Furthermore, the intercepts of these flow curves should correspond to the dynamic yield stress of the gels. This intercept is comparable to σc for Carbopol, consistent with a lack of structural change during flow, but significantly lower than σc for the other gel classes. This suppressed yield stress is consistent with the expected structural breakdown during flow, which is recoverable for CNC and entangled CNF gels but irrecoverable for the covalent CNF gels.
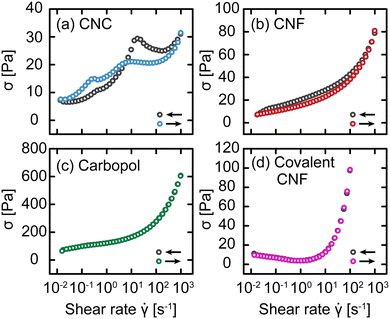 | ||
Fig. 8 Stress σ as a function of shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for (a) CNC, (b) entangled CNF, (c) Carbopol, and (d) covalent CNF gels with decreasing for (a) CNC, (b) entangled CNF, (c) Carbopol, and (d) covalent CNF gels with decreasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (gray) and increasing (gray) and increasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (color) with δt = 10 s. (color) with δt = 10 s. | ||
The magnitude of rheological hysteresis is quantified through the logarithmic area Aσ between the down and up sweeps according to
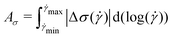 | (4) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = σup(
) = σup(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) − σdown(
) − σdown(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) and larger values of Aσ correspond to higher degrees of thixotropy. This logarithmic integration appropriately weighs contributions from a low and a high
) and larger values of Aσ correspond to higher degrees of thixotropy. This logarithmic integration appropriately weighs contributions from a low and a high ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Consistent with the existing literature,30,31,65 taking the absolute value of Δσ guarantees that any difference in stress contributes to Aσ rather than canceling out, but it does obscure directional dependence. Typically, thixotropic fluids are more structured at a low
. Consistent with the existing literature,30,31,65 taking the absolute value of Δσ guarantees that any difference in stress contributes to Aσ rather than canceling out, but it does obscure directional dependence. Typically, thixotropic fluids are more structured at a low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ,66,67 so stepping up from a low
,66,67 so stepping up from a low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) to a high
to a high ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) should result in a higher σ than stepping down from high to low. Nevertheless, we calculate Aσ using trapezoidal numerical integration as a function of δt (Fig. 9). To compare the magnitude of hysteresis across gel classes, we normalize Aσ by σc. For the Carbopol and covalent CNF gels, we observe minimal hysteresis across all δt and attribute the small values of Aσ/σc to experimental errors. For the CNC and entangled CNF gels, however, we observe significantly larger values of Aσ/σc. Although we do not observe the non-monotonic peaks in Aσ that were identified in earlier investigations of thixotropic yield stress fluids,30,31,65 the high magnitude of hysteresis observed for these samples demonstrates that these gels are indeed thixotropic. Thus, only thixotropic gels possess time-dependent yield stresses while non-thixotropic gels exhibit constant yield stresses.
should result in a higher σ than stepping down from high to low. Nevertheless, we calculate Aσ using trapezoidal numerical integration as a function of δt (Fig. 9). To compare the magnitude of hysteresis across gel classes, we normalize Aσ by σc. For the Carbopol and covalent CNF gels, we observe minimal hysteresis across all δt and attribute the small values of Aσ/σc to experimental errors. For the CNC and entangled CNF gels, however, we observe significantly larger values of Aσ/σc. Although we do not observe the non-monotonic peaks in Aσ that were identified in earlier investigations of thixotropic yield stress fluids,30,31,65 the high magnitude of hysteresis observed for these samples demonstrates that these gels are indeed thixotropic. Thus, only thixotropic gels possess time-dependent yield stresses while non-thixotropic gels exhibit constant yield stresses.
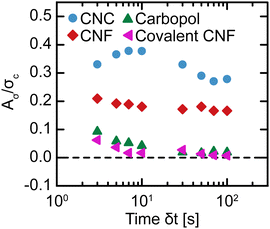 | ||
| Fig. 9 Normalized hysteric area Aσ/σc as a function of the time interval per step δt in flow sweeps for different gel classes. | ||
4 Conclusions
From our nonlinear rheological protocols, we observe various behaviors of gels post-yielding depending on their physicochemical interactions. For physically repulsive Carbopol gels, the elastic network recovers nearly instantaneously after yielding, resulting in negligible hysteresis between up and down sweeps and a time-independent yield stress. For covalent CNF gels, the elastic network is permanently destroyed locally upon yielding, also resulting in negligible hysteresis and a time-independent yield stress but with a significantly weaker yield stress after the first yielding event. For electrostatically attractive CNC and physically entangled CNF gels, we observe significant hysteresis and time-dependent yield stresses. After yielding, these gels dynamically rebuild their elastic structure and recover their yield stress through coupled diffusion–aggregation or reptative re-entanglement, respectively.Through independent measurements of thixotropy and yielding, we demonstrate the intimate relationship between these two phenomena across different classes of gels. The effect of yielding on the linear and nonlinear properties of gels can vary drastically depending on the mechanisms by which the gels form a percolating elastic network. These effects can be best understood by considering the dynamics of the underlying constituents and the kinetics of bond reformation. Furthermore, we demonstrate that the yield stress is a more sensitive metric of network strength than linear properties. Whereas linear viscoelasticity may fully recover after yielding, the stress at which the gel fails may be significantly altered.
Data availability
Raw data for this article, including linear frequency sweeps, oscillation amplitude sweeps, creep compliance measurements, serial creep divergence rheology, and flow sweeps are available at Open Science Foundation at https://doi.org/10.17605/OSF.IO/SYEZK.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the ACS Petroleum Research Fund Doctoral New Investigator Grant No. 65826-DNI9.References
- W. Richtering and B. R. Saunders, Soft Matter, 2014, 10, 3695–3702 RSC.
- H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382 CrossRef CAS.
- J. Colombo and E. Del Gado, J. Rheol., 2014, 58, 1089–1116 CrossRef CAS.
- S. Jamali, G. H. McKinley and R. C. Armstrong, Phys. Rev. Lett., 2017, 118, 048003 CrossRef PubMed.
- A. Kurokawa, V. Vidal, K. Kurita, T. Divoux and S. Manneville, Soft Matter, 2015, 11, 9026–9037 RSC.
- N. J. Balmforth, I. A. Frigaard and G. Ovarlez, Annu. Rev. Fluid Mech., 2014, 46, 121–146 CrossRef.
- A. Malkin, V. Kulichikhin and S. Ilyin, Rheol. Acta, 2017, 56, 177–188 CrossRef CAS.
- D. P. Keane, C. J. Constantine, M. D. Mellor and R. Poling-Skutvik, Langmuir, 2023, 39, 7852–7862 CrossRef CAS PubMed.
- D. Miranda-Nieves and E. L. Chaikof, ACS Biomater. Sci. Eng., 2017, 3, 694–711 CrossRef CAS PubMed.
- R. J. Mondschein, A. Kanitkar, C. B. Williams, S. S. Verbridge and T. E. Long, Biomaterials, 2017, 140, 170–188 CrossRef CAS PubMed.
- H. A. Barnes, J. Non-Newtonian Fluid Mech., 1999, 81, 133–178 CrossRef CAS.
- G. J. Donley, P. K. Singh, A. Shetty and S. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21945–21952 CrossRef CAS PubMed.
- H. A. Barnes, J. Non-Newtonian Fluid Mech., 1997, 70, 1–33 CrossRef CAS.
- J. Mewis and N. J. Wagner, Adv. Colloid Interface Sci., 2009, 147–148, 214–227 CrossRef CAS PubMed.
- Y. Wang and R. H. Ewoldt, J. Rheol., 2023, 67, 1199–1219 CrossRef CAS.
- A. J. Liu and S. R. Nagel, Annu. Rev. Condens. Matter Phys., 2010, 1, 347–369 CrossRef.
- T. K. Haxton, M. Schmiedeberg and A. J. Liu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 031503 CrossRef PubMed.
- F. Khabaz, M. Cloitre and R. T. Bonnecaze, Phys. Rev. Fluids, 2018, 3, 033301 CrossRef.
- D. Bonn, H. Tanaka, G. Wegdam, H. Kellay and J. Meunier, EPL, 1999, 45, 52–57 CrossRef CAS.
- T. Witten and L. Sander, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 5686–5697 CrossRef.
- M. Y. Lin, H. M. Lindsay, D. A. Weitz, R. C. Ball, R. Klein and P. Meakin, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 2005–2020 CrossRef CAS PubMed.
- V. Trappe, V. Prasad, L. Cipelletti, P. N. Segre and D. A. Weitz, Nature, 2001, 411, 772–775 CrossRef CAS PubMed.
- S. Babu, J. C. Gimel and T. Nicolai, Eur. Phys. J. E, 2008, 27, 297–308 CrossRef CAS.
- Z. Gong, T. Hueckel, G.-R. Yi and S. Sacanna, Nature, 2017, 550, 234–238 CrossRef PubMed.
- T. Zhang, D. Lyu, W. Xu, X. Feng, R. Ni and Y. Wang, Nat. Commun., 2023, 14, 8494 CrossRef CAS PubMed.
- R. Everaers, S. K. Sukumaran, G. S. Grest, C. Svaneborg, A. Sivasubramanian and K. Kremer, Science, 2004, 303, 823–826 CrossRef CAS PubMed.
- J. Qin and S. T. Milner, Macromolecules, 2014, 47, 6077–6085 CrossRef CAS.
- F. Chambon and H. Winter, Polym. Bull., 1985, 13, 499–503 CrossRef CAS.
- E. Nikoumanesh and R. Poling-Skutvik, J. Chem. Phys., 2023, 159, 044905 CrossRef CAS PubMed.
- T. Divoux, V. Grenard and S. Manneville, Phys. Rev. Lett., 2013, 110, 018304 CrossRef PubMed.
- R. Radhakrishnan, T. Divoux, S. Manneville and S. M. Fielding, Soft Matter, 2017, 13, 1834–1852 RSC.
- M. Agarwal and Y. M. Joshi, Phys. Fluids, 2019, 31, 063107 CrossRef.
- C. A. Montalbetti and V. Falque, Tetrahedron, 2005, 61, 10827–10852 CrossRef CAS.
- R. Poling-Skutvik, E. McEvoy, V. Shenoy and C. O. Osuji, Phys. Rev. Mater., 2020, 4, 102601 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- K. Kamani, G. J. Donley and S. A. Rogers, Phys. Rev. Lett., 2021, 126, 218002 CrossRef CAS PubMed.
- T. Divoux, C. Barentin and S. Manneville, Soft Matter, 2011, 7, 9335–9349 RSC.
- M. Dinkgreve, M. Fazilati, M. M. Denn and D. Bonn, J. Rheol., 2018, 62, 773–780 CrossRef CAS.
- V. V. Vasisht, G. Roberts and E. Del Gado, Phys. Rev. E, 2020, 102, 010604 CrossRef CAS PubMed.
- M. Zhang, D. Xu, X. Yan, J. Chen, S. Dong, B. Zheng and F. Huang, Angew. Chem., Int. Ed., 2012, 51, 7011–7015 CrossRef CAS PubMed.
- Z. Wei, J. H. Yang, J. Zhou, F. Xu, M. Zrínyi, P. H. Dussault, Y. Osada and Y. M. Chen, Chem. Soc. Rev., 2014, 43, 8114–8131 RSC.
- J. H. Cho and I. Bischofberger, Soft Matter, 2022, 18, 7612–7620 RSC.
- R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, 1999 Search PubMed.
- R. H. Ewoldt and G. H. McKinley, Rheol. Bull., 2007, 76, 4–6 Search PubMed.
- C. Baravian and D. Quemada, Rheol. Acta, 1998, 37, 223–233 CrossRef CAS.
- C. Baravian, G. Benbelkacem and F. Caton, Rheol. Acta, 2007, 46, 577–581 CrossRef CAS.
- Z. Zhou, J. V. Hollingsworth, S. Hong, H. Cheng and C. C. Han, Langmuir, 2014, 30, 5739–5746 CrossRef CAS PubMed.
- N. Koumakis, M. Laurati, A. R. Jacob, K. J. Mutch, A. Abdellali, A. B. Schofield, S. U. Egelhaaf, J. F. Brady and G. Petekidis, J. Rheol., 2016, 60, 603–623 CrossRef CAS.
- C. Ligoure and S. Mora, Rheol. Acta, 2013, 52, 91–114 CrossRef CAS.
- L. C. Johnson, B. J. Landrum and R. N. Zia, Soft Matter, 2018, 14, 5048–5068 RSC.
- L. Vanel, S. Ciliberto, P.-P. Cortet and S. Santucci, J. Phys. Appl. Phys., 2009, 42, 214007 CrossRef.
- P. J. Skrzeszewska, J. Sprakel, F. A. de Wolf, R. Fokkink, M. A. Cohen Stuart and J. van der Gucht, Macromolecules, 2010, 43, 3542–3548 CrossRef CAS.
- T. Divoux, D. Tamarii, C. Barentin and S. Manneville, Phys. Rev. Lett., 2010, 104, 208301 CrossRef PubMed.
- O. Nechyporchuk, M. N. Belgacem and F. Pignon, Carbohydr. Polym., 2014, 112, 432–439 CrossRef CAS PubMed.
- T. Divoux, M. A. Fardin, S. Manneville and S. Lerouge, Annu. Rev. Fluid Mech., 2016, 48, 81–103 CrossRef.
- D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005 CrossRef.
- R. Benzi, T. Divoux, C. Barentin, S. Manneville, M. Sbragaglia and F. Toschi, Phys. Rev. Lett., 2019, 123, 248001 CrossRef CAS PubMed.
- M. L. Manning, E. G. Daub, J. S. Langer and J. M. Carlson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 016110 CrossRef CAS PubMed.
- R. L. Moorcroft and S. M. Fielding, Phys. Rev. Lett., 2013, 110, 086001 CrossRef PubMed.
- S. Prager and M. Tirrell, J. Chem. Phys., 1981, 75, 5194–5198 CrossRef CAS.
- R. P. Wool, B. L. Yuan and O. J. McGarel, Polym. Eng. Sci., 1989, 29, 1340–1367 CrossRef CAS.
- P. G. De Gennes, Tribol. Ser., 1981, 7, 355–367 Search PubMed.
- P. Prentice, Polymer, 1983, 24, 344–350 CrossRef CAS.
- A. A. Griffith, Philos. Trans. R. Soc. Math. Phys. Eng. Sci., 1921, 221, 163–198 Search PubMed.
- S. Jamali, R. C. Armstrong and G. H. McKinley, Phys. Rev. Lett., 2019, 123, 248003 CrossRef PubMed.
- Y. Wei, M. J. Solomon and R. G. Larson, J. Rheol., 2019, 63, 673–675 CrossRef CAS.
- R. G. Larson and Y. Wei, J. Rheol., 2019, 63, 477–501 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |