 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spiers Memorial Lecture: New directions in molecular scattering
George C.
Schatz
 a,
Alec M.
Wodtke
a,
Alec M.
Wodtke
 *bcd and
Xueming
Yang
*bcd and
Xueming
Yang
 ef
ef
aDept of Chemistry, Northwestern University, Evanston, Illinois 60208, USA
bInstitute for Physical Chemistry, Georg August University, Goettingen, Germany
cMax Planck Institute for Multidisciplinary Natural Sciences, Goettingen, Germany. E-mail: alec.wodtke@mpinat.mpg.de
dInternational Center for the Advanced Studies of Energy Conversion, Georg August University, Goettingen, Germany
eDalian Institute for Chemical Physics, Chinese Academy of Sciences, Dalian, China
fDepartment of Chemistry, College of Science, Southern University of Science and Technology, Shenzhen, China
First published on 1st May 2024
Abstract
The field of molecular scattering is reviewed as it pertains to gas–gas as well as gas–surface chemical reaction dynamics. We emphasize the importance of collaboration of experiment and theory, from which new directions of research are being pursued on increasingly complex problems. We review both experimental and theoretical advances that provide the modern toolbox available to molecular-scattering studies. We distinguish between two classes of work. The first involves simple systems and uses experiment to validate theory so that from the validated theory, one may learn far more than could ever be measured in the laboratory. The second class involves problems of great complexity that would be difficult or impossible to understand without a partnership of experiment and theory. Key topics covered in this review include crossed-beams reactive scattering and scattering at extremely low energies, where quantum effects dominate. They also include scattering from surfaces, reactive scattering and kinetics at surfaces, and scattering work done at liquid surfaces. The review closes with thoughts on future promising directions of research.
1. Setting the scene with a little history
The discovery of quantum mechanics1,2 marks the historical starting point for the field of chemical dynamics, especially once Born and Oppenheimer conceived of an approximation for molecules involving an effective potential energy function created by the average field of the electrons.3 Soon, the first potential energy surface (PES) for a chemical reaction was calculated,4,5 the idea of a reaction's transition state was conceived and the first theory of absolute reaction rates was developed.6,7 With the emerging capabilities of computation,8 comparisons of experiment and theory became possible, allowing the new theoretical concepts to be put to the test. Initially, experiments relied on molecular spectroscopy,9–11 made more powerful by the invention of the laser12–14 and the growing use of laser-induced fluorescence (LIF),15–22 which provided nascent quantum-state population distributions produced by chemical reactions.23,24But it was molecular scattering that revolutionized the study of chemical dynamics, first during the so-called “alkali age”,25,26 then as a tool to study ion–molecule chemistry,27,28 and especially with the advent of the universal crossed-molecular-beam method,29 which led to the 1986 Nobel Prize in Chemistry. Experiments were now able to control reactant incidence energy, achieve single-collision conditions and detect product molecules' recoil velocities. Product flux maps gave clear insights into the qualitative nature of a reactions' transition state, allowing direct detection of steric entrance-channel effects, reaction complex formation and, through control of incidence translational energy, the presence of reaction barriers.
In the words of its inventor and chief protagonist: “The idea of crossed molecular beams experiments is in a sense to ‘visualize’ the details of a chemical reaction by tracing the trajectories of the reaction products”.30 Achieving a rigorous “visualization” of a reaction required the application and rapid development of theory. The calculation of PESs evolved from empirical and semi-empirical models, to Hartree–Fock theory,31 and to wavefunction-based methods that include electron–electron correlation, and large basis sets such that nearly exact results are obtained for some reactions. Simulating the atomic motions governed by PESs has also advanced, from classical mechanics,32,33 to time-independent quantum scattering theory,34–36 to time-dependent wave-packet motion.37–39 Classical mechanics remains the workhorse. In parallel, density functional theory (DFT)40 can often perform a balancing act between useful accuracy and affordability and it is increasingly common to see on-the-fly studies that compute the forces as the trajectory proceeds.41
The state of the field in 1987 was described prophetically in the Nobel lecture of Yuan T. Lee, from which we extract one quote, where the laureate made a prediction. “In the near future, ab initio calculations of potential energy surfaces and exact scattering calculations on…simple…systems will likely provide more detailed and accurate information…than one could possibly learn in the laboratory”.30 We will show examples below demonstrating that this prediction has indeed been realized and that from those calculations, astonishing insights can be obtained.
But a second prediction is of even greater significance to this review: “the fruitful interplay of theory and experiment will then extend to more complicated systems, making chemistry a more exact science”.30 One of the most important characteristics of the new directions being established in molecular scattering relies on a fruitful collaboration of experiment and theory that is far more valuable than the sum of its parts. In the same sense that two eyes provide stereoscopic vision, these two windows into nature allow fundamental insights to crystallize. This process of collaboration is bidirectional. Of course, pure theory can guide experiment by making predictions of unexpected behavior; more importantly however, where the current gold is to be found is when theory can be applied to understand what the experimentalist has unambiguously observed, but cannot understand.
This cooperation of experiment and theory represents the current state-of-the-art and provides a framework for new directions and for this review. The review is organized as follows. In Sections 2 and 3, we provide an overview of, respectively, theoretical and experimental advances made in recent years that serve as our scientific tool kit for approaching new problems. Major advances have been made since the 1986 Nobel lecture and it is important to understand the current tools we work with, as well as to examine the problems we hope to solve. In Section 4, we present a few examples of simple gas-phase scattering problems where theory is so powerful that experiment is perhaps no longer necessary, and in Section 5, examples of more complex problems where theory and experiment collaborate to make progress. Sections 6 and 7 present examples in beam surface scattering analogous to those in Sections 4 and 5, respectively. Section 8 concludes with a discussion of future perspectives.
2. Advances in theoretical methods
Theory has become a powerful tool for the quantitative description of both gas-phase and gas–surface collisions. A key factor for this has been the development of methods including machine learning (ML), which enable the representation of full (or at least high)-dimensional potential energy surfaces (PESs), including multiple PESs that interact via spin–orbit or derivative couplings. These surfaces are often derived from a large number of high-quality electronic structure calculations, and they can include all nuclear degrees of freedom for gas-phase systems with 3–8 atoms. For gas–surface systems, only selected degrees of freedom are included. Dynamics calculations are carried out with quantum-dynamics codes that handle the important degrees of freedom (and provide an approximate treatment of other degrees of freedom), and with classical or quasiclassical trajectories as an important alternative for reactions that are outside the ability of quantum calculations. In the following, we describe the potential surface and dynamic method development, as well as methods for describing nonadiabatic effects for bimolecular reactions and gas–surface reactions, focusing on work published mostly in the last 10 years. A discussion of specific systems is provided later, in Sections 4–7. To restrict the scope, we omit studies that did not consider global PESs, and methods concerned primarily with energy transfer and photodissociation rather than with bimolecular and gas–surface reactions.2.1. High-dimensional ground-state PESs
Concerning methods for representing potential surfaces, there is a long history of doing this with analytical functions in combination with least-squares fitting to determine parameters in the functions. In recent work, the combination of analytical functions with machine learning to determine parameters has become quite important. One example of this is the permutationally invariant polynomial (PIP) approach, as recently reviewed by Bowman and coworkers.49–52 These papers describe the development of PIP surfaces via monomial symmetrization. Additionally, a machine-learning kernel-based approach involving Gaussian process regression has been combined with PIP to determine parameters. Bowman has also reviewed the use of a two-level potential fitting process, the so-called Δ-machine-learning approach, in which PIP is used to develop a lower-level surface based on a large number of DFT calculations, and then machine learning (a neural net) is used to describe the difference between the lower-level surface and a higher-level surface obtained from coupled-cluster calculations.53 In another direction with machine-learning potentials, Meuwly has developed surfaces using the reproducing kernel Hilbert space method.54,55 A broader discussion of machine learning for describing global surfaces and many other properties, including the direct determination of rate coefficients, has been presented by Meuwly.56 This paper includes a general discussion of the merits of ML and least-squares-based representations. Another powerful approach that can be used to directly determine rate coefficients from potentials is ring-polymer molecular dynamics (RPMD), as recently implemented by Guo and coworkers for the S(3P) + H2 reaction using potentials that were described using the PIP-NN method.57 However, for that reaction, intersystem crossing dominates the dynamics below 1000 K, which was not included in the RPMD calculation.
For the global PESs, we mention a recent review by Guo, who discusses machine-learning methods for both gas-phase and gas–surface reactions,60 and a paper by Stark et al. that examines hydrogen on metals.61 The Guo paper considers neural-network and Gaussian process regression approaches—as well as the PIP-NN mentioned above, including an application of this approach to gas–surface systems—that incorporate permutational symmetry in the “gas” part, and periodicity in the surface part. If the surface is rigid, this method works well. However, if it is not, an attractive alternative is to use the atomistic NN method of Behler and Parrinello,62–64 in which the PES is expressed as a sum of atomistic contributions, each encoded by mapping functions that describe the local environment. Another useful paper is by Zhang et al. concerning the Shepard interpolation method as applied to molecule–surface systems.65 Here the “Grow” method66 for combining BOMD trajectories that include local Hessians with potential energy interpolation based on the Shepard method is generalized to include periodic boundary conditions, so that the underlying symmetry of the crystalline surface is included. Applications of this method to the H2 molecule interacting with fcc(111) and hcp(0001) metal surfaces were considered.
One difficulty with machine learning arises when training data are limited. Here, the neural network may produce unphysical values of the PES that must be searched for and retrained. An alternative to ML is the use of physically realistic fitting functions, for example effective medium theory, which has been successfully applied to generate full-dimensional potentials for H interacting with metals.67–69 The fitting error is typically larger with this approach, but the PES remains physically constrained. This is analogous to a Lennard-Jones potential for a diatomic molecule, which is less accurate than a spline function, but will not yield unphysical energies.
2.2. High-dimensional quantum dynamics
While most of the methods reviewed above were originally developed long ago, the technology for carrying out scattering calculations continues to be developed. For example, Zhao et al. have described the use of wave packets that start near the transition state of a chemical reaction, but which can be used to calculate state-to-state reaction probabilities,80 and DuPuy et al. have described Smolyak representations with absorbing boundary conditions for use with a reaction-path Hamiltonian model of reactive scattering.81
2.3. Electronically non-adiabatic dynamics
Nonadiabatic effects resulting from the presence of many coupled PESs are very common in gas-phase collision processes, as many of these processes involve atoms or molecules with open-shell character (i.e., that's what makes the species reactive). As a result, the development of PESs and methods for simulating the dynamics has often focused on generating multiple surfaces and on determining their couplings, where the couplings can involve either derivative coupling of adiabatic surfaces, or spin–orbit coupling that leads to intersystem crossing. Among the recent studies in this area is a paper by Kendrick in 2018, concerned with the description of quantum reactive scattering using hyperspherical coordinates that includes many surfaces and nonadiabatic effects.90 Also, Meuwly in 2020 provided an overview of methods for describing dynamics involving multiple PESs,91 including a detailed description of surface-hopping methods for describing nonadiabatic dynamics.Studies on the impact of multi-surface and nonadiabatic effects on the dynamics of gas–surface reactions have mainly been focused on friction models arising when nuclear motions are coupled to a continuum of electronic states that are present when a molecule interacts with a metal surface. Recent work includes studies by Kroes on hot-atom relaxation in the H + Pd(100) system92 and in N2 dissociative chemisorption on Ru(0001).93 Also, Guo has studied frictional effects in H2 scattering from Ag(111).94 The Guo work describes the inclusion of friction effects in terms of a generalized Langevin equation, in which there is an electronic friction tensor that is determined by Fermi's golden rule based on derivative couplings and an empirically chosen delta function to smooth out the k-state interpolation. In addition, the friction tensor is represented as a function of nuclear coordinates using a NN approach, which requires special care because of the dependence of this tensor on the molecular coordinate directions.
In gas–surface interactions, a local density friction approximation is often used;95 this approach often works well for nonadiabatic energy transfer in atom scattering from metals.92,96 Recently, tensorial electronic friction methods have been more extensively elaborated.97,98 Friction tensors can also be represented by neural networks99 and show great promise for describing nonadiabatic interactions of molecules with metal surfaces.100,101
3. Advances in experimental methods
Scattering methods are sensitive probes of the microscopic world, as exemplified by one of the most famous experiments of the modern era of physics, the α-particle scattering from gold foil by Rutherford,102 which helped establish the structure of the atom, thereby laying the foundation for theoretical chemistry. In an analogous way, molecular beam scattering methods have been essential for the study of reaction dynamics in both gas–gas and gas–surface collisions. In such experiments, the kinetic energy and angular distributions of scattered atoms and molecules are measured; these distributions contain detailed dynamical information that can be used to understand chemical reactions in gas-phase or gas–surface interactions. The two key capabilities needed for molecular beam scattering methods are: (1) the production of intense atomic or molecular beams and (2) methods for sensitive detection of atoms and molecules. Over the last few decades, great experimental advances have been achieved, allowing much higher energy and angular resolution and more sensitive detection.Since the development of the original universal crossed-molecular-beams method29—see above—many improvements have been demonstrated. For example, dramatically improved vacuum in the universal detector chamber was achieved using state-of-art vacuum techniques. This further lowered the detector background and thereby enhanced the detection efficiency.103 Further development of the crossed universal beams method has employed different ionization methods, such as tunable VUV synchrotron ionization,104 VUV laser ionization105–107 and soft electron-impact ionization.108 These techniques have provided powerful tools to study the dynamics of both elementary and complex chemical reactions.
Molecular detection based on laser ionization and ion imaging has revolutionized scattering experiments. While resonance-enhanced multiphoton ionization (REMPI) had been developed already in the 60's and the 70's,109–118 it was only in the mid 90's that it was combined with molecular beams to provide product speed and angular distributions.119 Ion imaging was quickly applied to products of both photodissociation120 as well as bimolecular reactions121,122 and became even more attractive when velocity-map imaging (VMI)123 demonstrated enhanced resolution, comparable to that of the Lee style rotating mass spectrometric detector. With the advent of “slice imaging” in 2001,124 symmetry requirements for image data analysis could be circumvented, and over time, this approach has become the method of choice for many problems in chemical dynamics.125–127 Recently, a two-photon near-threshold ionization scheme for H atoms was applied in the H + HD reaction, and high kinetic and angular resolution for hydrogen atom product imaging was achieved.128 The most modern variations of this include covariance imaging129 and pixel imaging mass spectrometry.130 These techniques allow analysis of complex polyatomic dissociation events via the identification of momentum-matched dissociation partners. It is not an exaggeration to say that ion imaging is the most important experimental development since the universal crossed-beams method.
Another important experimental method developed for crossed-molecular-beam scattering study is the H-atom Rydberg tagging time-of-flight (HRTOF) technique, which provides very high kinetic-energy resolution. This technique was developed by Welge and co-workers,131,132 who also employed laser photolysis of HI to produce nearly monoenergetic H atoms with tunable kinetic energy for studying the H + D2 reaction,133 and it has been widely applied in the study of elementary chemical reactions134–139 as well as photodissociation dynamics studies of molecules with H-atom products.140–142 The central scheme of this technique is the two-step excitation of the H-atom product from its ground state to a long-lived high-n Rydberg state without ionization. The Rydberg “tagged” neutral H atoms are not influenced either by space charge or stray fields, and after a certain flight distance, they are easily field-ionized and the time-of-flight (TOF) spectrum is recorded using microchannel plates. The method's unique combination of high resolution and high sensitivity makes it particularly powerful in providing detailed quantum dynamical information on benchmark elementary chemical reactions and it is able to detect subtle quantum phenomena in chemical reactions, such as reaction resonances, spin–orbit dynamics effects, and geometric phase effects.
Great progress has also been made in developing intense and high-quality atomic and molecular beams for crossed-beams scattering experiments and gas–surface scattering experiments. These include, for example, photolytic and discharge radical beam sources of H,143 C,144–146 O(3P,1D),147 F,148 Cl,1491CH2,150 C2,151,152 C3,153 C2H,154 OH,147 CN,155 NCO,156 and CH3 and phenyl radicals.107
Our ability to control the beam's translational energy has also improved enormously. On the low-energy side of things, polar molecules can be brought nearly to a standstill,157 whereas on the high-energy side, fast O-atom sources with speeds of more than 8000 m s−1 can be generated with laser detonation sources.158,159 This wide range of beam speeds allows us to study reaction dynamics at extremely low temperatures near absolute zero or at temperatures of more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000°, extending experimental studies of reaction dynamics to extreme environments, such as the interstellar media and hot rocket plumes.
000°, extending experimental studies of reaction dynamics to extreme environments, such as the interstellar media and hot rocket plumes.
Molecular beams of stable species with vibrational excitation have also been developed, which allows investigation of the effects of vibrational excitation on gas-phase chemical reactions as well as gas–surface reactions.160–164 Oriented molecular beams of NO,165 and aligned methane166,167 and hydrogen (HD) molecules168,169 in vibrationally excited states, can also be prepared for studies of steric effects in reactive scatterings. The optical preparation of small molecules for scattering experiments is in itself a broad field that goes beyond the scope of this paper.
4. Simple systems in gas-phase scattering
In this section, we provide some benchmark examples of crossed-beams scattering studies of both triatomic elementary and complex reactions. Here, the simplicity of the systems is such that essentially exact theoretical calculations are possible; in fact, the experiments are of such high quality that this can be demonstrated. Combining theory and experiment leads to some remarkable conclusions about quantum mechanical reactivity.4.1. The H + H2 reaction: searching for the geometric phase effect
The H + H2 → H2 + H reaction (along with its isotopic variants) has been one of the most important bench-mark systems for studies of quantum dynamics in chemical reactions133,136,170–172 and these reactions have provided a key testing ground for developing a quantum dynamical theory and understanding quantum phenomena in chemical reactions. Experimentally, this reaction has been studied using all three major crossed-molecular-beams scattering methods. Lee and coworkers used the universal crossed-molecular-beams method to obtain differential cross sections for the D + H2 reaction.173 The Rydberg atom-tagging technique has played a particularly important role.132,133,135,137,139,170,174 This reaction system has also been studied using the ion imaging technique.122,175,176 The recent experimental studies on this reaction have provided an accurate reactive-scattering picture of this system for detailed comparisons with quantum-dynamics calculations.Some of the first theories of chemical reactivity were developed based on these reactions, first employing a co-linear model in the 1970s,177 and subsequently, three-dimensional quantum-dynamics calculations were performed.35,178 Since then, many dynamics calculations have been carried out and over the years, and quantitative agreement between theory and experiment has been reached for the dynamics at low collision energies. This laid the foundation for quantitatively understanding the quantum reaction dynamics of this reaction, especially the dynamics of bottleneck transition states in chemical reactions.179,180 Ever-improving scattering experiments and exact quantum-dynamics calculations based on highly accurate potential energy surfaces have driven our understanding of the dynamics of this reaction to new heights.
The interplay between experiment and theory led to the direct observation of the geometric phase (GP) effect in this reaction,181 which describes the quantum influence of the conical intersection on the reaction, i.e., including a vector potential that describes the phase acquired when a quantum state is adiabatically transported around a conical intersection when calculating the overall scattering cross section.182 Great efforts in both theory and experiment have been made in this direction.170,183–188 Accurate quantum-dynamics calculations helped guide experiment, showing that the GP effect is negligible at total energies below 1.6 eV188–193 but could be significant at high collision energies.
In 2018, a high-resolution crossed-beams imaging study on the H + HD → H2 + D reaction was performed at a collision energy of 2.77 eV. This unambiguously revealed evidence of the GP effect, which could be found in the H2 product state-resolved angular distributions.175Fig. 1 shows the experimental image of the D products from this reaction. Comparison to quantum-dynamics calculations showed that the observations could only be quantitatively reproduced when the GP effect was included. The GP effect could be shown to arise from the quantum interference between a direct abstraction channel and an insertion type channel (see Fig. 2) possible at high energy, which is topologically different—that is, it involves a pathway that passes around the conical intersection. The close interplay between theory and experiment was essential, not only to push the understanding of the reaction dynamics to an unprecedented level, but also for the discovery of the geometric phase effect in chemical reactions.
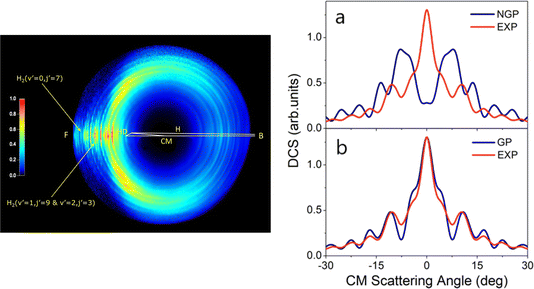 | ||
| Fig. 1 (left panel) Experimental image of the D-atom product from the H + HD → H2 + D reaction at a collision energy of 2.77 eV. “F” and “B” represent the forward (0°) and backward (180°) scattering directions, respectively, for the H2 co-product in the center-of-mass frame relative to the H-atom beam direction. Oscillatory structures in the forward scattering direction are observed for H2 product in specific quantum states—these oscillations reflect interference generated by the geometric phase effect in the reaction. (right panels) Comparisons between the experimental (EXP) and theoretical product angular distributions: (a) NGP, not including the geometric phase effect; (b) GP, including geometric phase effect for the H + HD (v = 0, j = 0) → H2 (v′ = 0, j′ = 7) + D reaction at 2.77 eV. Adapted from ref. 175 and used with permission under lic. no. 5744150372346. | ||
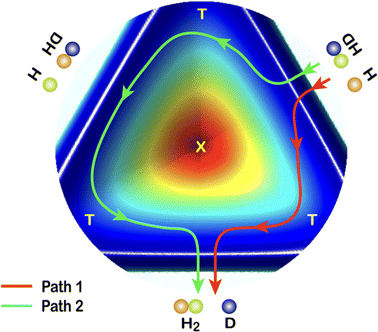 | ||
| Fig. 2 A cut view through the H + HD potential energy surface with transition states (T) and conical interaction (X). Two representative reaction pathways are shown: a one-transition-state reaction path (Path 1) and a two-transition-states reaction path (Path 2). Adapted from ref. 175 and used with permission under lic. no. 5744150372346. | ||
4.2. The F + H2 reaction: probing reaction resonances
The F + H2 → HF + H reaction has also proven to be one of the most important systems for studying quantum mechanical reaction dynamics. In particular, it exhibits reaction resonances, which have attracted great attention over the last forty years. Reaction resonances were first proposed in the quantum-dynamics calculation of the F + H2 reaction based on a collinear model194,195 and the first crossed-molecular-beams study of the F + H2 reaction was performed with product vibrational state resolution in 1984. An unexpected forward-scattering peak for the HF (v′ = 3) product was observed while HF (v′ = 1, 2) products were found to be backward scattered. The forward scattering peak was attributed to a reaction resonance.196 Due to a lack of adequate theory at the time, an unambiguous determination of the physical origin of this forward scattering was not possible.197,198 In 2000, a clear step-like structure was observed in the collision-energy-dependent integral cross section in F + HD → HF + D and assigned to a quasi-bound quantum resonance.199Over the last couple of decades, improved experiments have become possible using the H-atom Rydberg-tagging technique with full product rotational and vibrational state resolution.200–203 These data provide unprecedented detail and require a close collaboration with highly accurate quantum dynamical theory. Through this cooperative approach, a spectroscopically accurate physical picture for reaction resonances has emerged and shows clearly that they reside in the post barrier region. The resonance states are quasi-bound quantum states in the transition-state complex of the vibrationally excited HF molecule bound to an H-atom (see Fig. 3). Excellent agreement was also reached between the crossed-beams scattering experiment and negative-ion photodetachment studies.201,204,205 It is noteworthy to point out that reaction resonances demonstrated so clearly in the F + H2 reaction also exist in many other systems, suggesting that reaction resonance is not a rare phenomenon in chemistry. It is obviously more general than we have realized previously.
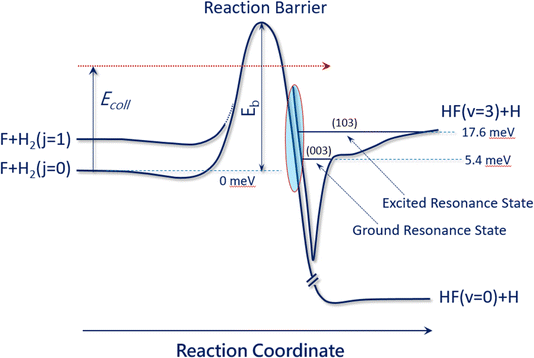 | ||
| Fig. 3 Reaction resonances in the F + H2 reaction. This figure presents the accurate physical picture of the quantum resonances in the F + H2 (j = 0) and F + H2 (j = 1) reactions, resembling a vibrationally excited HF molecule in the presence of an H atom. Two resonance states reside in the exit channel: the ground resonance state (003) at 5.4 meV is mainly responsible for the F + H2 (j = 0) reaction at temperatures below 40 K, while the excited resonance state (103) at 17.6 meV plays a more important role for the F + H2 (j = 0) reaction at temperatures above 40 K (adapted from ref. 200). | ||
The fluorine atom exhibits two spin orbit states, offering an opportunity to investigate the spin–orbit effect on this reaction. Recently, high-resolution velocity-map ion imaging was performed on the F(2P3/2) + HD → HF + D reaction and a peculiar horse-shoe pattern in the scattering differential cross section was observed at a collision energy of 2.10 kcal mol−1.206 This was attributed to quantum interference between spin–orbit split-partial-wave resonances in this reaction, suggesting that spin–orbit interaction has a significant influence on the detailed dynamics of this resonance-mediated chemical reaction.
In this section, we have provided examples of dynamics studies of two important elementary reactions: the H + H2 reaction and the F + H2 reaction. Many more simple elementary reactions like these have also been investigated, for example, Cl + H2,207–209 C(1D) + H2,210 O(3P) + H2,211 O(1D) + H2,212,213 N(2D) + H2,214 and OH + H2 (ref. 134 and 215), to name a few of the most important ones. Experimentally, full differential cross sections of the scattering dynamics of these elementary chemical reactions can be measured over a wide collision energy range with full quantum-state resolution. Theoretically, the advancement of efficient quantum-dynamics methods and rapidly growing computing power now makes accurate calculations of the reactive-scattering dynamics possible. The close interplay between theory and experiment has greatly enhanced our understanding of the quantum dynamics of elementary chemical reactions, especially for reaction resonances and geometric phase effects.
It is now possible to say with confidence that quantum theory of chemical reactions has advanced to a quantitatively accurate level, especially for reactions involving only the ground electronic state. Many simple elementary reactions, like those mentioned above, can in fact be studied using theoretical tools with high accuracy. Precise reactive-scattering experiments are often used as the ultimate testing ground for further developing quantum theory of chemical reactions to even higher levels of accuracy. The successes of quantum theory in elementary chemical reactions give us high confidence to seek quantitative understanding of more complex and challenging problems, to which we now turn.
5. Dynamics of more complex gas-phase reactions
In this section, we describe selected studies on gas–gas collision dynamics where the cooperative interaction of theory and experiment is essential to successful outcomes. This cooperative approach allows much more complex problems to be tackled than ever before, providing quantitative outcomes that in some cases can even be used to support engineering efforts on practical real-world problems.5.1. Crossed-beams scattering
Although initially used to target the simplest reactions, crossed-molecular-beams scattering has proven to be a powerful tool for studies of polyatomic reactions, often providing a deep understanding of the dynamics and mechanisms of complex chemical reactions.108,216 Using sliced velocity-map ion imaging to measure the state-resolved differential cross section for CD3 products from F + CD4 → DF + CD3, Liu and coworkers217,218 demonstrated that vibrational state-resolved, pair-correlated information can be obtained. Striking differences in the correlation between different product state pairs could be detected, indicating the complexity of polyatomic reactions. An interesting reaction resonance phenomenon was also observed.219 Crossed-beams reactive-scattering studies on F + CHD3 → HF + CD3,220,221 F + CH4 → HF + CH3,222 Cl + CH4 → HCl + CH3,223 Cl + SiH4 → HCl + SiH3,224 and F + SiH4 → HF + SiH3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225 have also been carried out and vibrational state pair correlated information could also be acquired. In the study of the H + CD4 reaction, a depression in the reactivity of H + CD4 → HD + CD3 by collision energy was observed.226
225 have also been carried out and vibrational state pair correlated information could also be acquired. In the study of the H + CD4 reaction, a depression in the reactivity of H + CD4 → HD + CD3 by collision energy was observed.226
The power of combining experiment and theory could also been seen in a study on the O(1D) + CHD3 → OH + CD3 reaction.227 This reaction has long been thought to be the prototypical example of collision-complex formation that occurs by direct insertion of the O atom into a C–H bond. Such reactions are expected to exhibit forward–backward symmetry in the center-of-mass angular distributions. It was therefore a puzzle to understand why this reaction exhibited strong forward scattering in state-resolved ion imaging measurements of the CD3 products. Using an accurate full-dimensional PES, quasiclassical trajectories were able to reproduce the forward scattering and demonstrated that the “insertion reaction” is essentially a two-step process where abstraction products (OH + CD3) remain bound to one another long enough to rotate into position to form a C–O bond, thus producing the hot methanol “insertion” complex. The dynamics discovered here were called trapped abstraction and are thought to be important in many reactions currently named insertion reactions.
A major issue in studying the bimolecular chemistry of larger systems is evaluating the branching between the many possible product channels and understanding the dynamical mechanisms that produce them. An excellent example is the reaction of O(1D) with CH4 studied using an improved universal crossed-molecular-beams apparatus with an ultrahigh-vacuum detector (∼1 × 10−12 torr).228 Three different reaction channels have been detected: the OH + CH3 channel, the CH2OH/CH3O + H channel and the H2CO/HCOH + H2 channel. Note that the crossed-molecular-beams method does not necessarily yield information about which product isomers are formed. Interestingly, the dynamics of the three channels appear to be quite distinctive. The OH + CH3 products appear to be forward scattered, and the CH2OH/CH3O + H channel is slightly backward scattered, while the H2CO/HCOH + H2 product angular distribution is almost isotropic. It is interesting to see that the three channels in the same reaction appear to have quite different dynamical behaviors.
As the reactions involve more and more atoms, the crossed-beams method has been augmented with important experimental improvements. For example, using low-energy electrons for electron-impact soft ionization, dissociative ionization can be suppressed. When this is successful, each measured mass-to-charge ratio indicates the mass of the detected product. This has proven to be a powerful tool for analyzing more complex reactions. For example, five different reaction channels have been detected and studied in the reaction of O(3P) with C2H2.229
In the even more complex reaction of O(3P) + C3H4 (allene), this approach has been able to identify and quantify four reaction channels forming C2H4 + CO, C2H2 + H2CO, C2H3 + HCO, CH2CCHO + H, and CH2CO + CH2. Because some of the observed products can only be formed via intersystem crossing (ISC) from triplet to singlet potential energy surfaces, the breakdown of spin conservation in this reaction could be inferred. The product branching ratios indicate that fully 90% of the reactive events proceed through ISC.231 ISC has since then been identified as an important aspect of the mechanisms of the reactions of O3P with ethene,230 pyridine232 and 1,3-butadiene.233 In the simplest of these (see Fig. 4) surface-hopping trajectory calculations could be performed using two full-dimensional PESs (singlet and triplet) to investigate the ISC dynamics more directly. Excellent agreement between experiment and theory demonstrated theory's ability to describe complex multichannel nonadiabatic reactions.
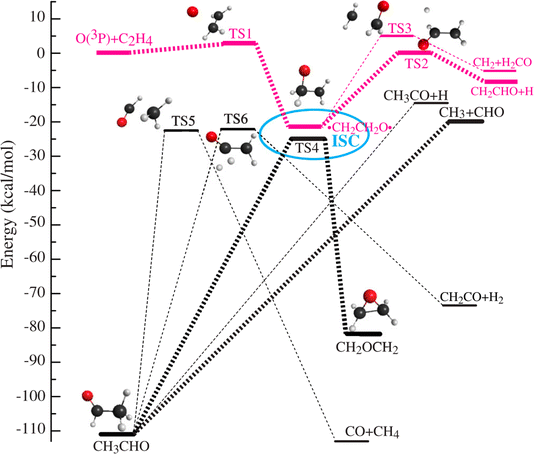 | ||
Fig. 4 Simplified schematic of triplet (red) and singlet (black) potentials of the O(3P) + C2H4 reaction. The electrophilic oxygen atom attacks the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond through a very low barrier of about 3 kcal mol−1 and forms an energetic triplet biradical, ˙CH2CH2O˙. The biradical region, enclosed by the ellipse, is where intersystem crossing (ISC) takes place with the greatest probability. ISC competes with fragmentation and rearrangement. The corresponding singlet biradical can isomerize to acetaldehyde (CH3CHO), which subsequently dissociates because of its high energy content. The triplet biradical can dissociate to H + CH2CHO or to CH2 + H2CO. The singlet biradical can also isomerize to oxirane via oxygen migration and ring-closure. The oxirane will finally isomerize to CH3CHO and further dissociate from CH3CHO into various products, CH3 + HCO, and H + CH3CO. Adapted from ref. 230. C bond through a very low barrier of about 3 kcal mol−1 and forms an energetic triplet biradical, ˙CH2CH2O˙. The biradical region, enclosed by the ellipse, is where intersystem crossing (ISC) takes place with the greatest probability. ISC competes with fragmentation and rearrangement. The corresponding singlet biradical can isomerize to acetaldehyde (CH3CHO), which subsequently dissociates because of its high energy content. The triplet biradical can dissociate to H + CH2CHO or to CH2 + H2CO. The singlet biradical can also isomerize to oxirane via oxygen migration and ring-closure. The oxirane will finally isomerize to CH3CHO and further dissociate from CH3CHO into various products, CH3 + HCO, and H + CH3CO. Adapted from ref. 230. | ||
In general, the application of theory in combination with crossed-molecular-beams experiments has led to fundamental understanding of quite complex reactions.234–251 The impact of modern scattering on real systems can be exemplified in the studies of O(3P) + C6H6 (benzene). Here, a theoretical statistical approach could be validated by comparison to the crossed-molecular-beam results and subsequently used to compute channel-specific rate constants as a function of temperature and pressure.252 Such rate constants are essential to microkinetic models of combustion and atmospheric chemistry.
Crossed molecular beam scattering experiments have also been applied to problems in interstellar and planetary chemistry.146,253–258 An excellent example of this is the reaction of N(2D) with benzene.259 Theory shows that the atom adds to the benzene ring and after isomerization can form several cyclic and linear intermediates, which undergo unimolecular decomposition. With the help of theory, it could be clearly shown that the dominant channel forms the ring-contracted C5H5 cyclic radical along with HCN and that formation of HNC is negligible. Note that the experiment is incapable of distinguishing HCN from HNC, as only the mass-to-charge ratio is determined.
Crossed molecular beam studies of reactions of transition-metal atoms with hydrocarbons is another exciting area of modern scattering research, providing mechanistic and dynamical information about inorganic reactions.260–277 This has been made possible by laser vaporization sources for transition-metal atom beams that have been developed for, among others, Mo, Y, Zr, Nb, and Al.260–265 State-selected and electronically excited Mo atoms can be produced by laser excitation followed by radiative relaxation, resulting in the reaction Mo(5S2) + CH4 → MoCH2 + H2.265 The competition between C–C and C–H bond insertion was studied with experiment and theory for cyclopropane270,271 and propene271 and four butene isomers,272 as well as alkynes.272 When methane was vibrationally excited with a laser, yttrium atom insertion into the C–H bond was enhanced by at least a factor of two.274
5.2. Ions and electrons in crossed-beams experiments
The crossed molecular beams method using ion imaging has also been applied to ion–molecule reactions, providing great insights into textbook reaction mechanisms.278 For example, the SN2 mechanisms for ion exchange could be studied in the reaction of F− + C2H5Cl → Cl− + C2H5F. Measured angle- and velocity-differential scattering cross sections were compared with quasiclassical trajectory simulations carried out on a full-dimensional PES, and quantitative agreement was found. The anti-E2 pathway turned out to be most important, but the SN2 substitution pathway became more relevant at higher collision energy.279Another interesting direction uses ion imaging to study electron–molecule collisions. Electron bombardment ionization has long been one of the most important detection techniques for molecules, yet the underlying physical chemistry has not been thoroughly understood. Recently, this process has been studied using ion imaging in a crossed-beams geometry.280–285 The use of pixel imaging mass spectrometry and covariance imaging allows identification of fragments arising from the same parent ions and detection of doubly charged ions on a large background of singly charged ions.281 This is particularly useful when analyzing the fragmentation patterns of larger polyatomic molecules and provides accurate observations of the decomposition channels that occur in the violent ionization event.
5.3. Cold collisions
In 1997 a rather overlooked paper appeared, describing calculations of the motion of a dipolar molecule within an electrostatic trap.286 The calculations were based on precisely measured Stark shifts in fields up to 140 kV cm−1 for the doubly degenerate (v = 0, J = 1) level of metastable CO (ã3Π). This paper described the basic physics that launched the emerging field of cold collisions.287–291 What the authors had realized and demonstrated with their model calculations was that it was possible to manipulate the velocities of molecules with external electric fields, especially if one concentrated on slow-moving dipolar molecules with near-degenerate low-field-seeking states; that is, those exhibiting a 1st order Stark effect. This was the secret-sauce added to the original recipe of Auerbach and Wharton, who had, years earlier, developed ideas to use the Stark effect to accelerate molecules.292 In a breathtakingly short span of time, deceleration of molecules was demonstrated in the laboratory,293 as was phase-stable confinement in a travelling trap,294 and a storage ring was built and characterized.295 These extraordinary new tools were followed by additional inventions, like a molecular synchrotron296 and a trap on a chip.297 Meanwhile, other methods for decelerating and trapping atoms and molecules were being developed, like the coherent paddle,298 the magnetic coil gun298,299 and the Zeeman decelerator.300,301 The lesson had been learned. If one were to choose specific states of atoms and molecules that exhibited optimal magnetic or electric properties, one might exploit those properties to produce decelerated beams with tunable velocities. Such states could be found as the ground state of a few molecules, but with discharges and laser excitation, even more possibilities came into view in the form of excited states.It was clear from the outset that these new techniques would be important for molecular scattering, promising to reveal subtle nuclear quantum effects that had never before been seen. Putting Stark decelerated molecules to work for this purpose was accomplished early on, in a crossed-beams configuration for OH scattering from Xe,302 D2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 303 and Ar.304 Considerations about how to achieve optimized energy resolution, with an eye toward seeing collision resonances, were also reported.305 Another innovation was the merging of two nearly perfectly co-propagating molecular beams and 3D printing methods were developed to help fabricate the complex structures needed for the electrodes.306 Merged beams allowed extraordinarily low incidence energies and high energy resolution to be achieved in collisions. The energy resolution was, in fact, now so high that optimized VMI detection needed to be developed to take full advantage of it.307
303 and Ar.304 Considerations about how to achieve optimized energy resolution, with an eye toward seeing collision resonances, were also reported.305 Another innovation was the merging of two nearly perfectly co-propagating molecular beams and 3D printing methods were developed to help fabricate the complex structures needed for the electrodes.306 Merged beams allowed extraordinarily low incidence energies and high energy resolution to be achieved in collisions. The energy resolution was, in fact, now so high that optimized VMI detection needed to be developed to take full advantage of it.307
With all of these wonderful tools in place, new observations were guaranteed. By scanning the collision energy, reaction resonances were detected for Penning ionization308–311 and rotationally inelastic collisions.312 A key element of these observations followed the pioneering work on F + H2 reaction resonances seen at much higher energies;202,313 as in that work, by obtaining the incidence-energy dependence of a small angular fraction of the differential scattering angular distribution, the resonances could be directly seen. While this was not the first observation of resonance behavior in molecular scattering, these new methods allowed resonance line shapes to be measured with unprecedented (∼1 cm−1) energy resolution, from which resonance lifetimes could be experimentally derived.314 With the help of theory and by comparing integral to differential scattering cross sections, the contributions of individual scattering waves could be determined.315 In analogous work, HD rotational energy transfer with H2 and D2 was examined at low collision energy with bond axis orientation and evidence of resonances sensitive to the anisotropic interaction between molecules was found.316 First-principles simulations of these experiments identified the L = 2 partial wave engaging in a shape resonance as being responsible for the observations.317 This showed once again how valuable it can be to resolve partial waves when searching for evidence of scattering resonances.
Other fascinating quantum phenomena have since been observed in molecular scattering. This includes diffraction scattering318–320 and the transition at low incidence energies from Langevin capture scattering to Wigner scattering.321 Taking advantage of the high energy resolution, quantum-state correlated scattering could also be achieved.320 Illustrating the analogy to high-precision molecular spectroscopy, experimental and theoretical comparisons for NO scattering with H2 were able to validate one PES versus another, even though the binding energies between the two differed by only 2 cm−1.322
5.4. Low-temperature kinetics
The inspired ideas of this field also led to a creative new approach to study ion–molecule chemistry at extraordinarily low temperatures, where the reaction is observed within the orbit of a Rydberg electron.323 Using external fields, the Rydberg atom's velocity could be controlled324 and when matched to the speed of another merged beam, reaction conditions that simulate a temperature near 0 K could be achieved. This provided a special approach to studying state-resolved capture probabilities. In one example, reactions of He+ + CH3F forming CH2+ and CHF+ were observed and a large enhancement of the reaction probability was seen below a collision energy of 1 K. This was explained by a state-resolved capture model involving low-field-seeking states of the CH3F molecule becoming favorably oriented for reaction within the electric field of the He+.323 This reaction model was also able to explain the more complex behavior exhibited by the reaction of He+ with NH3 forming NH2+ and NH+.325 Using isotopic labeling, it could be shown that the reactivity of high-field-seeking states of ammonia exhibiting a 1st-order Stark effect increased dramatically at low collision energy. High-field-seeking states with a 2nd-order Stark effect were less strongly reactive, while the reactivity of low-field-seeking states became suppressed. State-resolved electrostatic influences on the reaction He+ + CO → He + C+ + O were also seen; here, CO's negative quadrupole moment suppresses reaction at low collision energy.326 Other interesting insights were derived from studies of the reactions of He+ with CH4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 and N2
327 and N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 328 and NO.329
328 and NO.329
Understanding quantum effects in chemistry has importance far beyond the field of cold-collision physics. For example, quantum mechanical tunneling can be important in astrochemistry taking place in cold dense interstellar clouds.330 This conclusion now supersedes the traditional viewpoint that reactions are unimportant in astrochemistry if they possess significant activation barriers. This is due to the fact that barriers can be overcome by tunneling, especially when gas-phase collisions first lead to reactant complexes bound by even weak van der Waals forces, as was shown first to be the case for the reaction OH + CH3OH → H2O + CH3O331 and later for many other reactions.330 Here, Laval nozzle expansions are ideal for producing low-temperature thermal conditions.332
For ion–molecule reactions, other methods are required—for example the tunneling contribution to the reaction of H2 + D− → H− + HD could be determined via rate measurements at 10 K in a cryogenic 22-pole ion trap.333 These are some of the smallest reaction rates ever measured and comparison to theory was essential to the conclusions of the work. It is however unusual that such accurate calculations of tunneling rates can be performed. Normally one relies on the observation of unusually large kinetic isotope effects to identify tunneling. Recently, it has been pointed out that more accurate multi-dimensional tunneling334 and resonance enhancement335 models of tunneling are needed to accurately characterize quantum mechanical rates in condensed phases.
This concludes our review of new directions in gas-phase molecular scattering. In the remainder of the review, we turn to a very different research area involving gas–surface scattering. Beam–surface scattering has been pursued nearly as long as beam–beam scattering. However, it has only been in recent years that challenges associated with instrumental complexity and the physical phenomena themselves have been slowly overcome. Here again, cooperation of theory with experiment is essential. Before entering into this broad and fascinating field, we note several prior reviews on gas–surface scattering dynamics.336–347
6. Simple systems in scattering from surfaces
Applications of ab initio dynamical theory to problems in surface scattering are nearly always subject to severe approximations, as has been outlined in Section 2. One is normally restricted to the use of DFT-GGA, and there are many atoms (degrees of freedom) involved, requiring the dynamics to be computed on high-dimensional PESs under the classical approximation. This means that in scattering from surfaces, the number of systems is small where the information gleaned from ab initio dynamical theory surpasses that obtained from experiment. Such systems do however exist.6.1. H-atom scattering from simple surfaces
In comparison to other possible choices, H-atom scattering is simple and provides perhaps the best chance for current theoretical methods to be implemented with the fewest possible approximations and with the highest accuracy. This motivated construction of a novel instrument, where nearly mono-energetic H atoms could be scattered from clean and well-defined surfaces held in an ultrahigh vacuum and the incidence and scattering angle-dependent energy loss distributions could be measured with high resolution.349 The experimental challenges involved in the execution of such an experiment are the production of near monoenergetic H atoms—achieved by laser photolysis of molecular beam cooled hydrogen halide molecules—and achieving high-resolution energy loss distributions, which is accomplished using Rydberg atom tagging as described in Section 3. Fortunately, these techniques had been previously worked out for gas-phase problems133—it was only necessary to adapt them to a UHV set-up.A diagram of the H-atom surface scattering set-up is shown in Fig. 5;349 work performed with this instrument has been recently reviewed.348 H scattering has been performed from solid surfaces composed of metals,350–355 adsorbate-modified metals,356 semiconductors357,358 and graphene359,360 grown on a number of substrates.
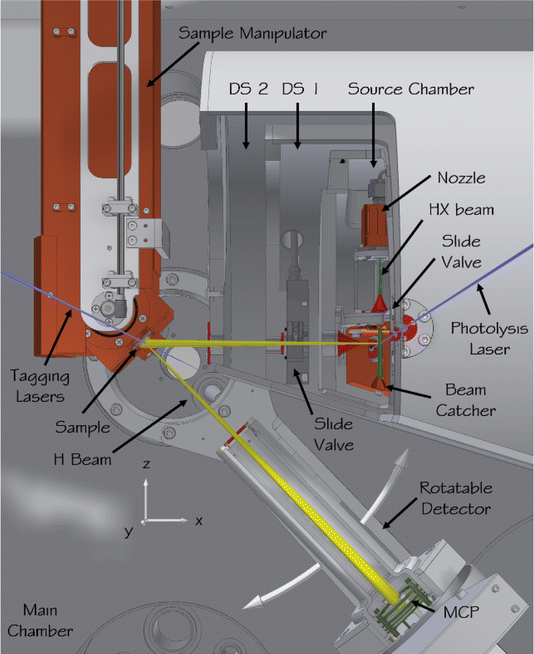 | ||
| Fig. 5 Apparatus for scattering H atoms from pristine surfaces. In the source chamber, a hydrogen halide molecular beam (green) is formed in a supersonic expansion from a pulsed nozzle, passes a skimmer (red), and is intersected by the photolysis laser (blue) before it hits a liquid-nitrogen-cooled beam catcher. Some of the generated H atoms (yellow) leave the source chamber through a second skimmer, pass two differential pumping stages, and enter the main chamber where they collide with the sample surface. The sample is mounted on a six-axis manipulator allowing the incidence polar and azimuthal angles to be varied. The surface temperature can also be varied. The scattered H atoms are excited to a metastable Rydberg state by the tagging lasers, pass an aperture defining the angular resolution of the detector, and after a 250 mm flight path are field ionized and the ions are detected by a microchannel plate detector. The detector is mounted on a rotatable arm to enable variation of the scattering angle. The ultimate pressure in the scattering chamber can be reduced to below 1 × 10−10 torr. Adapted from ref. 348. | ||
The simplest example so far studied with this instrument is that of H scattering from a cryogenic Xe solid surface at an incidence energy of 2.76 eV.361 Here, classical molecular dynamics simulations performed on a full-dimensional PES constructed from DFT-GGA data perfectly reproduce experimental observations, when using an effective medium theory to fit DFT data.68 See Fig. 6. This allowed the simulations to be “unpacked”, providing more information than one could imagine obtaining from experiment alone.
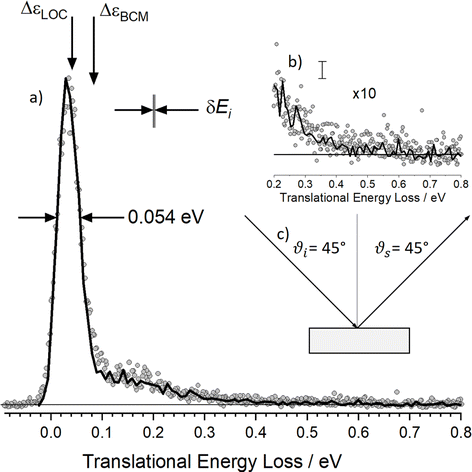 | ||
| Fig. 6 Energy-loss spectrum for H scattering from solid Xe. (a) Rydberg tagging experiment (circles) and MD simulation (solid line). The sharp peak dominating the energy distribution results from single-bounce line-of-centers scattering and “weak double-bounce scattering”. The shoulder spanning 0.1–0.5 eV results from strong double-bounce and multibounce collisions including subsurface scattering. The inset (b) shows a zoomed in view of the data with the largest inelasticity and an estimate of the statistical noise in the MD trajectories. (c) Experimental conditions: Ei = 2.76 eV, ϑi = 45°, ϑs = 45° and φi = 0° and TS = 45 K. The spread in the H atoms' incidence energy δEi is also shown. Adapted from ref. 361. | ||
In fact, it was possible to determine the number of collisions. Here, it is important to recall that a collision is an ambiguous quantity—for example, high impact-parameter collisions that lead to an infinitesimal deflection are, in principle, collisions; but they result in a negligible energy-loss. Using a definition of weak and strong collisions that was based on the distance of closest approach during the trajectory, it was shown that double-bounce trajectories are more important than single-bounce events, even for specular scattering, where one might think single-bounce events would dominate. The tendency of each bounce to direct H atoms out of the plane of detection means that two bounces can compensate out-of-plane momentum such that the trajectory remains in the detection plane. These weak double-bounce events exhibit nearly the same energy loss as that predicted by the single-bounce line-of-centers model.
A large fraction of the observed scattering results from trajectories that visit regions of space below the first layer of Xe atoms (sub-surface multibounce scattering) before returning to the gas phase. See Fig. 7. Overall, these multibounce and subsurface scattering dynamics allow as much as 0.5 eV of the incident 2.76 eV energy to be lost from the H atoms colliding with a solid Xe surface, far exceeding the predicted energy loss of the binary collision model (0.082 eV) normally considered the largest energy loss possible. Subsurface penetration is also responsible for sticking of the H atom, which was computed to occur for 15% of the trajectories.
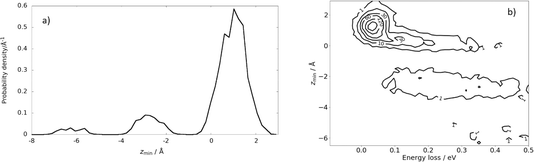 | ||
| Fig. 7 Subsurface scattering: (a) probability density distribution of the scattering trajectories as a function of distance of closest approach to the surface, zmin. The equilibrium positions of the Xe surface atoms define zmin = 0. (b) Probability correlation distribution comparing the depth of penetration and energy-loss. The numbers on the contour lines indicate the numbers of MD trajectories. Ei = 2.76 eV, ϑi = 45°, ϑs = 45°, and φi = 0° and TS = 45 K. Adapted from ref. 361. | ||
6.2. H-atom scattering from metals
These studies could be extended to H scattering from Au (111), where electronically adiabatic MD simulations failed dramatically.353 However, energy loss measurements were in good agreement with classical MD simulations with electronic friction applied on a full-dimensional PES.68 See Fig. 8. Here, Effective Medium Theory (EMT) was fitted to the DFT data68 and a local density electronic friction approximation was employed.95,362,363 In the meantime, the EMT formula (originally derived for fcc metals) was derived for bcc metals as well.67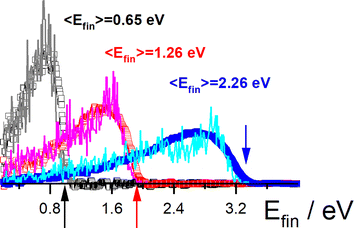 | ||
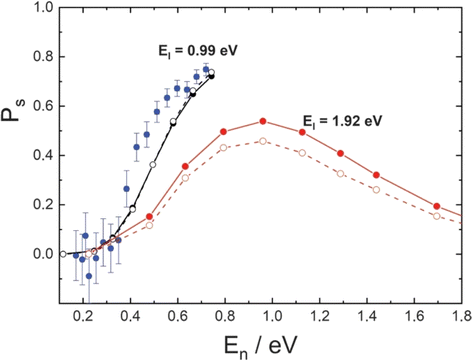
Fig. 8 H scattering from Au(111) at three incidence energies Ein. Experimental results (open squares) are compared to theory (solid lines): Ein = 3.33 eV (blue), 1.92 eV (red), and 0.99 eV (black). Colored arrows mark the three incidence energies. Also shown are the average final translational energies, 〈Efin〉. The scattering angles are ϑi = 45°, ϑs = 45° and φi = 0° with respect to the [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction. Adapted from ref. 353 and used with permission under lic. no. 574300005425. ] direction. Adapted from ref. 353 and used with permission under lic. no. 574300005425. | ||
The theoretical simulations are thought to provide accurate sticking probabilities, which are difficult to measure experimentally. The theory also reveals a novel sticking mechanism for H atoms, where (as in the Xe case) sub-surface penetration occurs. The electronic friction is so strong in the subsurface region that the H atoms resurface within 100 femtoseconds and thermalize to the most stable binding sites.353 Similar results were found on six metals350–352 and on different surface facets,354 suggesting the generality of the behavior originally seen for Au(111). This allowed a generalization and determination of a quantitative formula for computing the incidence angle and energy-dependent sticking probability of H and D on metals.351,352 The isotope effect is small350 and theory could explain this as a compensation effect. Lighter H atoms more effectively excited electron–hole pairs, but D atoms more effectively excited phonons.364 Theoretical simulations of these scattering experiments were also capable of explaining the isotope effect seen in chemicurrent experiments.364
6.3. H-atom scattering from graphene
Advancing in complexity, we next consider the H scattering from graphene. H scattering from graphene grown on Pt was carried out as described above in the discussion of Fig. 8. When grown on Pt, the graphene layer is polycrystalline with two rotational domains and is physisorbed to the metal. The scattering distributions are bimodal with a quasi-elastic component and another that exhibits a large energy loss due to the formation of a transient covalent C–H bond.360 The transient bond formation channel increases in importance as the incidence angle is scanned from a glancing to a normal direction to the surface, which is evidence that a barrier to forming the C–H bond must be overcome. These dynamics were investigated from a theoretical perspective using DFT calculations on a free-standing model of the system and fitting with REBO360 or NN.365 Classical trajectory calculations also showed bimodal behavior in the energy-loss distributions. Analysis of the trajectories showed that the large energy loss was made possible by the re-hybridization of the C-atom involved in the transient bond, which exerts strong forces on neighboring C-atoms as the delocalized π-bonding network is broken up. In this way, C-atom motion, parallel to the surface, was excited within about 10 femtoseconds, whereas out-of-plane C atom motion was only seen after about 20–30 femtoseconds.Sticking probabilities (Fig. 9) could be derived from the experiment over a limited range of the normal component of the incidence energy. MD simulations on a full-dimensional PES were in good agreement with those values. Theoretical predictions of the sticking probabilities at higher energies were also made and there is no reason to doubt that they are reliable, although they remain unconfirmed by experiment. RPMD trajectories were run to simulate the ZPE and tunneling, but quantum effects were found to be small. Strictly speaking, RPMD is only valid under thermal conditions and its use in this way is not rigorously correct. To what degree RPMD can be trusted for such applications, would rely on making comparisons to better quantum-dynamics simulations. Very recently, MCTDH calculations on H scattering from graphene with 75 dimensions and using a NN PES have been demonstrated and compared to experiment.87 These calculations confirmed that quantum effects are small for incidence energies of 1.96 eV, but a marked increase in sticking probability was seen at 0.96 eV incidence energy, due to the influence of quantum effects.
 | ||
| Fig. 9 H-atom sticking probabilities at graphene. Experimentally derived (blue) and theoretically predicted (black) sticking probabilities for EI = 0.99 eV plotted against the normal component of the incidence energy (En). Theoretically predicted sticking probabilities for EI = 1.92 eV are shown in red. Theoretical simulations used a full-dimensional EMFT-REBO PES that includes the influence of the Pt substrate with classical molecular dynamics (solid symbols) or ring polymer molecular dynamics (open symbols). Adapted from ref. 360 and used with permission under lic. no. 5743000308890. | ||
6.4. H-atom scattering from germanium
Most recently, H-atom scattering has been extended to the case of semiconductor surfaces. Again, the interplay between experiment and theory has been crucial. Reminiscent of the H scattering from graphene, for collisions of H-atoms at a Ge (111)-c(2 × 8) surface, a quasi-elastic peak was seen, as well as a channel exhibiting a large energy loss.357 Interestingly, the threshold of the high-energy-loss channel was coincident with the surface bandgap,357 suggesting the cause of the bimodal behavior is very different than in the case of graphene. Molecular dynamics simulations were carried out using a high-dimensional NN PES computed with DFT within the Born–Oppenheimer approximation. The calculations matched the quasielastic channel within the uncertainty of the measurements; however, there was no sign of a high-energy-loss channel. This strongly suggested that the high-energy-loss channel does not arise from transient chemical bond formation, but rather is due to promotion of an electron from the valence band to the conduction band. The high-energy-loss channel also increased in importance with increasing translational energy of the H-atom beam, a typical sign of Born-Oppenheimer Approximation failure. The authors concluded that the high-energy H-atom collisions at the surface of the Ge semiconductor were able to efficiently excite electrons from the valence band to the conduction band.357 The isotope effect was later taken as evidence of a site-specific transition that is related to the electronic structure of the adatoms and rest atoms present on the surface reconstruction.3587. More complex systems for molecule–surface scattering
One of the great successes of gas-phase crossed molecular beams scattering arises from the single-collision conditions afforded by the method. In these experiments, two continuous beams cross one another, each with a density ρ ∼ 1011 cm−3. The crossing volume of the two beams V ∼ 0.03 cm3, as well as the relative velocity vrel ∼ 105 cm s−1 and the collision cross-section σcoll ∼ 10−14 cm2 can be combined in eqn (1) below to calculate the rate of collisions.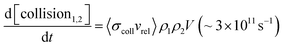 | (1) |
When comparing this to the incident flux of one of the beams at the collision zone, 1015 s−1, one quickly appreciates that in this experiment, the probability for a single condition is on the order one in a thousand. Hence, the probability that two collisions occur is on the order of one in a million. For reactive processes of complex polyatomic molecules, the single-collision conditions provide an enormous simplification, allowing scientists to observe all of the initially formed reaction products—that is, the results of the first collision—and characterize them quantitatively. See for example ref. 232, 233, 252, 259 and 366.
There is no applicable analogous experiment in surface chemistry, as single-collision conditions are rarely obtained. It is as if we perform a crossed-beams scattering experiment where one beam possesses an atomic density of 1022 cm−3. While this simple statement glosses over a great deal, the H-atom scattering from Xe presented above confirms the assertion that it is unlikely that incident atoms and molecules experience a single collision upon encountering a solid or liquid surface.361 Even more catastrophic to the idea of single-collision surface chemistry is the fact that when a surface reaction is initiated by an incident molecular beam, it is typical that these molecules first adsorb and thermalize with the surface, possibly while also dissociating to form the first reaction intermediates. Products are then formed only after these intermediates diffuse—possibly, they may also isomerize—and react to final products. Often this involves reaction with other pre-adsorbed molecules. Another key difference is that—unlike the pristine homogeneity of a vacuum—surfaces are heterogeneous. Hence, diffusion of intermediates to especially reactive sites of the surface is often essential to the mechanism. This is even true when carrying out experiments with nearly perfect single-crystal surfaces.
Despite these critical differences, experimental methods for reactive scattering on surfaces using molecular beams have advanced dramatically in recent years. The usefulness of molecular beams for reactive scattering at surfaces can be seen in the recently obtained results using the “isothermal pulsed molecular beams” method.367,368 In this approach, molecular beams deposit reactants at a catalytic surface within the well-controlled conditions of an ultra-high-vacuum chamber. Desorbing products are then detected by electron bombardment ionization quadrupole mass spectrometry. Adsorbates are simultaneously detected using infrared absorption spectroscopy (IRAS). An apparatus for applying this method has been described.369 This approach has quite important advantages over the well-known temperature programmed reaction (TPR) method, where reactants are deposited at low temperature and desorbing products are detected while a linear temperature ramp is applied to the surface. Most importantly, the reactions important to the catalysis can be studied at controlled and variable temperatures in an isothermal experiment.
This method has been applied to answer a variety of interesting questions in catalysis. Surface accessibility of subsurface hydrogen in palladium nanoparticles was investigated, and it was shown that diffusion between the surface and bulk is strongly altered by C atoms that can bind near low-valence step-edges.370 In other work, hydrogen recombination371 as well as reaction of hydrogen with adsorbed 2-butene372 was found to involve subsurface hydrogen. The “spectator effect”, which is closely related to ligand-directed hydrogenation,373 was studied in selective partial hydrogenation of acrolein.374,375 Here, the influence of surface crowding by nonreactive molecules could be shown to have a profound impact on the chemistry. In another study, it could be shown that the adsorption of butanal is accompanied by keto–enol isomerization to form three adsorbed intermediates,376,377 whose chemistry controls the product formation.
Also using this method, methanol oxidation to methyl formate was observed on Au (332).378–380 Nanoporous gold is an important catalyst for this reaction—its high surface area and the ability of Ag impurities in this material to activate oxygen are crucial.381 Despite the many potential differences to the nanoporous catalyst, very similar reactivity was observed on single-crystal Au (111) and (332). For these pure gold catalysts, the oxygen was introduced as gas-phase atoms from an effusive molecular beam. The experiments clearly showed the efficient formation of the desired methylformate product and, using IRAS, the buildup of adsorbed bidentate formate, which slowly poisoned the catalyst. Due to the well-controlled conditions of these experiments, insights into the reaction mechanism could be obtained. A previously proposed mechanism for methylformate formation involving recombination of two adsorbed methoxy intermediates382,383 could be confirmed. Over-oxidation of the methylformate to undesired side products was also seen and conditions could be found where it could be suppressed. A special adsorbed oxygen species was inferred that is capable of oxidizing methylformate.380
7.1. Kinetics of reactions at surfaces
These experiments give a glimpse of the power of reactive molecular beam scattering in surface chemistry, a power that can be amplified when combined with quantitative measurements of reaction rates. Such experiments were first developed in the early 1970's, with the advent of the molecular beam relaxation spectroscopy.384,385 This method employed a modulated molecular beam to dose the surface and an electron bombardment ionization mass spectrometer to detect products. The temperature-dependent phase shift could be used to gain information on the reaction kinetics. In one of the successes of this technique, it could be seen that CO oxidation on a stepped platinum surface proceeds via a Langmuir–Hinshelwood and not an Eley–Rideal mechanism.386More recently, a family of related techniques have become possible that take advantage of modern pulsed molecular beams and pulsed lasers as well as ion imaging. The velocity-resolved kinetics (VRK) methods387–389 now make the experimental determination of reaction rates much more quantitative. Discovered serendipitously while performing state-to-state time-of-flight measurements involving molecular beams scattering from Pt,390 VRK relies on laser methods that simultaneously obtain the densities and velocities of molecules, allowing accurate determinations of molecular flux. To appreciate this point, consider the units involved in the simple desorption reaction expressed by the following kinetic eqn (2):
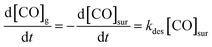 | (2) |
Because the concentration of CO at the surface [CO]sur is in units of surface density and because kdes is a 1st-order rate constant with units of inverse time, the rate of production of gas-phase CO has units of flux. Hence, monitoring the reaction rate via detection of gas-phase CO requires methods to measure flux, which as just mentioned may be accomplished via a simultaneous measurement of density and velocity. An additional advantage of measuring molecular velocities arises as it becomes possible to accurately calculate when the molecule left the surface on its way toward the detection laser beam. Hence, by using short pulsed molecular beams to initiate the reaction, the reaction time at the surface can be determined with less than ∼10 μs uncertainty.
These simple insights, along with the remarkably high signal-to-noise ratio afforded by VRK, permitted the first bi-exponential desorption traces to be observed,390 from which the role of terraces and steps could be discerned. See Fig. 10. Here, a rather cumbersome two-laser scheme was employed that relied on a detailed knowledge of the spectroscopy of CO.
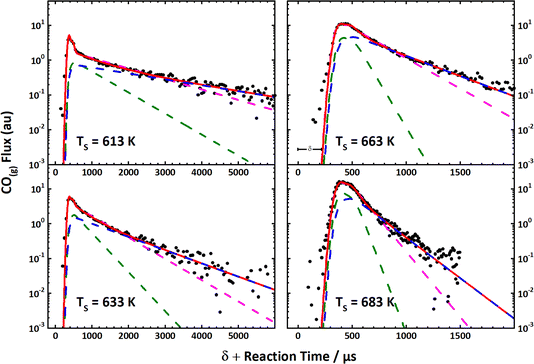 | ||
Fig. 10 The first velocity-resolved kinetic data. In this experiment, a short-pulsed CO molecular beam was incident at a Pt (111) surface at time δ, determined in a separate experiment. The CO molecules leaving the surface were excited to the metastable ã3Π state <1 mm away from the surface. The metastable molecules were subsequently ionized ∼12 mm from the surface using 1 + 1 REMPI via the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 3Σ+ state. The delay between the two laser pulses was fixed, defining the velocity of the molecules being detected. The timing of the pulsed molecular beam was then varied with respect to both laser pulses to observe the residence time of the molecules on the surface. Bi-exponential kinetics (solid black circles) can be clearly seen. The two components are related to (1) desorption from terrace sites (green dashed line) and (2) diffusion from steps to terraces followed by desorption (magenta dashed line). The sum of the two components (blue dashed line) matches the data well. Note the vertical axes are logarithmic. Adapted from ref. 390. 3Σ+ state. The delay between the two laser pulses was fixed, defining the velocity of the molecules being detected. The timing of the pulsed molecular beam was then varied with respect to both laser pulses to observe the residence time of the molecules on the surface. Bi-exponential kinetics (solid black circles) can be clearly seen. The two components are related to (1) desorption from terrace sites (green dashed line) and (2) diffusion from steps to terraces followed by desorption (magenta dashed line). The sum of the two components (blue dashed line) matches the data well. Note the vertical axes are logarithmic. Adapted from ref. 390. | ||
This approach to the kinetics of surface reactions was made more general by employing non-resonant multiphoton ionization (MPI) in concert with slice ion imaging.124 Here, non-resonant MPI was performed by focusing the output of a titanium–sapphire laser—available with ∼1 mJ pulse energies and a 35 fs pulse duration operating at a 1000 kHz repetition rate. This allows experiments with many molecules not normally considered suitable for laser detection. For example, both H2O391 and CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 387 products from H2 and CO oxidation on Pt, respectively, could be studied with VRK, as could formic acid (HCOOH),392 NH3,393 H2,394,395 CO387 and NO.396 Detection of many other molecules is also possible with this method.
387 products from H2 and CO oxidation on Pt, respectively, could be studied with VRK, as could formic acid (HCOOH),392 NH3,393 H2,394,395 CO387 and NO.396 Detection of many other molecules is also possible with this method.
Accurate desorption rate constants obtained using VRK contain valuable information on molecule–surface interactions, adsorbate binding energies and diffusion barriers, which can be derived using transition-state theory (TST). For example, NO desorption rate constants from Pd(111) and (332) provided accurate NO binding energies (1.766 ± 0.024 eV) and diffusion barriers (0.29 ± 0.11 eV).396 Similar results were obtained from VRK measurements of NH3 desorption from Pt(111) and (332). Here, the NH3 binding energy to Pt(111) (1.13 ± 0.02 eV) and the diffusion barrier (0.71 ± 0.04 eV) could be accurately derived. In addition, NH3's binding-energy preference for steps over terraces on Pt (0.23 ± 0.03 eV) was obtained. The influence of co-adsorbed oxygen on the NH3-binding energy—it increases by 0.15 eV—and diffusion barrier—it increases by 0.39 eV—was also found.397 Formic acid desorption rates measured with VRK also yielded an accurate desorption energy (0.639 ± 0.008 eV) from Pd(111) as well as the diffusion barrier (0.37 ± 0.13 eV) across 111 terraces. In other VRK measurements of the recombinative desorption rates of hydrogen from Pd, the dissociative adsorption energy of H2 and its isotopic variants to Pd were obtained. In fact, the kinetic data were even sensitive to hydrogen diffusion between the surface and the bulk; hence, the bulk absorption energy could also be obtained.394 Where comparison is possible, the binding energies obtained above compare well with results from single-crystal adsorption micro-calorimetry.398,399
One advantage of VRK (or for that matter any accurate desorption kinetics measurement) is that, in addition to binding energies, accurate diffusion barriers can be derived. This is because a TST rate constant has both an energetic term—the energy needed to reach the transition state—and an entropic term, which mainly influence the pre-factor. The experiment provides information on both and since the entropy of the adsorbate is strongly influenced by its propensity to diffuse, desorption rate constants also reflect the barriers to diffusion. The three examples above are instructive in several ways. For example, the ratio of the diffusion barrier to desorption energy in all three was much larger than the commonly used 12% rule.400 For ammonia in particular, accurate binding energies and diffusion barriers have significant implications for engineering models of the Ostwald process, where ammonia is oxidized to NO. Specifically, it was possible to understand why established rate models of the Ostwald process incorrectly predict low selectivity and yields of NO under typical reactor operating conditions. These errors are likely due to a failure of the assumption of mean-field kinetics, used in those models.393
Perhaps the most important impact of VRK stems from its high accuracy and precision. The accuracy of the rate constants derived from VRK could be demonstrated using the principle of detailed balance. When desorption rate-constants were directly computed from sticking probabilities and other experimentally available quantities and compared to VRK rates, agreement was within the signal-to-noise of the VRK experiments—see Fig. 11.395 Note that this required no adjustable parameters. This not only provides a striking example of the power of the principle of detailed balance, it also reveals the strengths and weaknesses of commonly applied approximations used in TST for surface reactions. This work helped show that for this reaction, quantum effects are large even at high temperature. Beyond zero-point energy effects, which are well known, the wave nature of the light adsorbed atom produces a quantum delocalization and concomitant high entropy that dramatically reduces its recombination rate constant.395 The H-atom's spin degeneracy also contributes a factor of four reduction in the rate, as combining H atoms to form the ground electronic state of H2 is only possible for one of the four spin combinations.
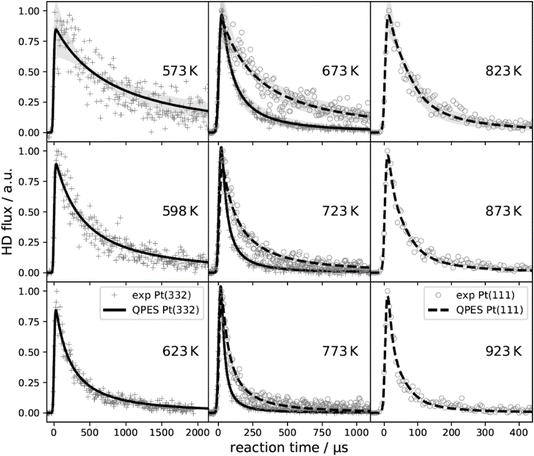 | ||
| Fig. 11 Velocity resolved kinetics (VRK) of hydrogen atom recombination on Pt (111) and Pt (332). Measured reaction rates for Pt (111) (∘) and Pt (332) (+) are compared to the results of a quantum rate model based on the principle of detailed balance and experimentally derived dissociative sticking coefficients (dashed and solid lines). The temperature dependence and the transient rate of the measurements is quantitatively captured by the quantum rate model for both facets. The shaded regions of the top three panels indicate the 2σ-uncertainty. Excellent agreement was achieved without adjustable parameters. Adapted from ref. 395 and used with permission under lic. no. 5743000493441. | ||
The high accuracy demonstrated for VRK provides some of the first experimentally derived thermal rate constants that are accurate enough to provide benchmarks for first-principles rate theories for surface chemistry. The VRK benchmarks were exploited in a recent theoretical study. Using a 6D PES generated with machine learning from DFT data obtained at the GGA level, Ring Polymer Molecular Dynamics (RPMD) was used to directly obtain thermal rate constants.88 The derived rate constants, which exhibited large quantum effects, were (only) a factor of two lower than those from experiment when the PBEα-vdW-DF2 functional was used.
Surface site-specific rate constants for reactive processes like CO oxidation on Pt can also be obtained with VRK.387 These experiments revealed another advantage of measuring product velocity—when reactions occur via different mechanisms, they may lead to products with different speed distributions—see Fig. 12. In this case, CO oxidation at terraces produced hyperthermal speed distributions of CO2, whereas the dominant reaction occurring at steps led to CO2 products with thermal speed distributions. Subsequent theoretical calculations showed that CO2 is bound more strongly at steps than at terraces, due to charge transfer forming a bent CO2−-like adsorbate.401
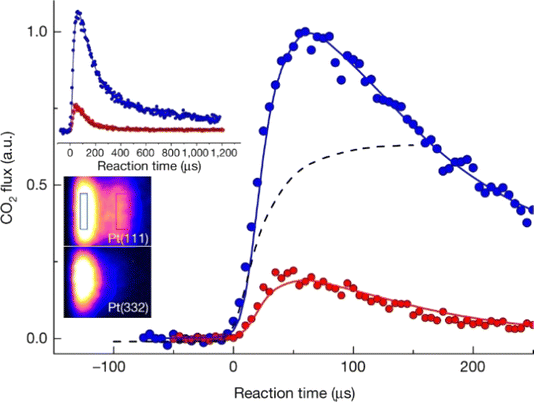 | ||
| Fig. 12 Velocity-resolved kinetics of CO2 from CO oxidation at a Pt surface. The lower left inset shows an ion image with velocity-space integration windows for a hyperthermal (red rectangle; 1280–1610 m s−1) and a thermal (blue rectangle; 420–590 m s−1) channel. The kinetics of the two velocity groups are shown as blue and red circles in the upper inset and in the main figure. The thermal velocity products result from reaction at steps, whereas the hyperthermal velocities arise from reaction at terraces; note that the hyperthermal channel is visible for the (111) surface only. The solid red and blue lines are fits using a kinetic model involving two reactions at steps and one at terraces. The dashed black line represents the measured CO dosing function. The surface temperature was 593 K. Adapted from ref. 387. | ||
Combining kinetic data with product velocity distributions can provide additional information on a surface reaction's energy landscape, as was shown in a VRK study of the decomposition of formic acid to CO2 on Pt (111). Here, the rate limiting reaction is decomposition of the bidentate formate intermediately formed after O–H bond dissociation at the Pt surface.
| HCO*O* → H* + CO2(g) | (3) |
The asterisks in the chemical eqn (3) indicate the atoms bound to the metal in the formate intermediate. Temperature-dependent VRK data was analyzed to obtain the forward reaction's activation energy, which was taken as a measure of the barrier to the forward reaction, while the maximum measured CO2 translational energy was taken as a measure of the barrier height for the reverse reaction.402 The difference between these two barrier heights gave an independent measure of the heat of formation of the bidentate formate bound to Pt (111), which was in good agreement with single-crystal adsorption calorimetry.403 This procedure could be repeated as a function of oxygen surface coverage on both Pt (111) and (332), providing information on the reaction pathway. While this investigation made measurements of the decomposition of formate, from the derived energy diagrams it was also possible to conclude what a Pt catalyst requires for optimal functionalization of CO2 with hydrogen. The results of this work clearly showed that CO2 could be most easily activated to a formate adsorbate on a Pt surface with a high defect density and oxygen-lean or oxygen-free conditions.
Perhaps of greatest future significance, VRK of surface reactions can be used to identify reaction intermediates, providing critical information on reaction mechanisms in catalysis (https://doi.org/10.1039/D3FD00174A). In another paper appearing in this Faraday Discussion, formic acid decomposition on palladium exhibited a “fast” and a “slow” kinetic channel for CO2 production. These channels are well-resolved—see Fig. 13—by VRK and the branching between them is easily measured and, moreover, strongly dependent upon isotopic substitution (https://doi.org/10.1039/D3FD00174A). Here, theoretical examination of measured kinetic isotope effects makes it possible to assign the fast and slow channels to decomposition of two reaction intermediates—carboxyl and bidentate formate, respectively.
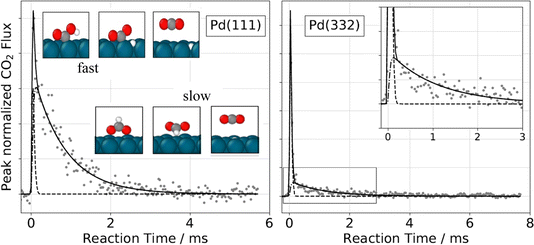 | ||
| Fig. 13 Observation of two temporally resolved CO2 formation channels in formic acid decomposition on Pd. Typical peak-normalized kinetic traces of CO2 on Pd(111) (left) and Pd(332) (right) at 403 K using HCOOH. The solid lines are a kinetic fit (see https://doi.org/10.1039/D3FD00174A). The inset in the right panel shows an enlarged view of the slow component, which decays over several milliseconds at this temperature, whereas the fast component exhibits a time dependence similar to that of the incident pulsed molecular beam (dashed line). The insets in the left panel show the reactant, transition state, and product structures computed from DFT for the fast and slow channels on Pd(111). | ||
Since these studies were reported, additional variants of VRK have been reported. A high-repetition-rate version of VRK drastically reduces measurement time and may be useful for following nonstationary catalysts, for example, undergoing poisoning or activation.388 Laser-induced desorption VRK provides possibilities to directly detect reaction intermediates. Here, a femtosecond pulse of laser light is used to desorb reaction intermediates via a DIMET (desorption induced by multiple electronic transitions) process. These hyperthermal desorbates are then detected in the gas phase via laser ionization.389
7.2. Hot beams
An important opportunity for both gas-phase and gas–surface experiments has been pursued by Minton and others through the development of hyperthermal sources of atomic species like O, N, F, and Ar using a laser detonation source.159 This source can produce translational energies in the several-eV range that are important in upper atmospheric chemistry and space science. It has been demonstrated for O atoms that only the electronic ground state has significant population in these sources, which makes it possible to study reactive collisions involving high barriers and endothermic processes with the reaction dynamics theories described earlier. This has been demonstrated both for crossed-beams studies, such as for the O + H2 reaction,404 and for beam-surface experiments, such as O + graphite147,345 and O + ionic liquids.405 Recent gas-phase reactions have focused on reactions that are important in hypersonics, including N + O2 (ref. 406) and O + NO,407 where it is possible to use the results to validate reaction dynamics calculations with high-quality PESs, and then the calculations can be used to generate rate coefficients that are crucial for atmospheric modelers. The gas–surface hyperthermal beam studies have also been used to provide insights about the structure of ionic-liquid interfaces,408,409 and about processes that are important for degradation of hypersonic and space vehicle components.410,4117.3. Molecular scattering from liquid surfaces
The scattering of atoms and molecules from liquid surfaces became popular after the advent of the scraped rotating-wheel method, originally developed by Fenn to measure evaporation rates from liquid surfaces.412 Here, a molecular beam is incident upon a low-vapor-pressure liquid that forms a film on a rotating disk within a vacuum chamber. A metal or Teflon scraper ensures that the surface remains clean. Scattered molecules are detected under collision-free conditions; hence, the observations reflect the fundamental interactions experienced by the molecule at the vacuum–liquid interface. Pioneering work from the labs of Gil Nathanson413,414 used neutral time-of-flight (TOF) mass spectrometry to obtain velocity and angular distributions of scattered molecules.413,414 Other labs have since employed laser-based methods including LIF,415 infrared416 and UV-vis417 absorption spectroscopy. Two excellent reviews appeared in 2016,86,347 outlining many of the common observations seen in this field. Initially, inelastic scattering was the focus of the field; here, two channels—trapping followed by desorption as well as direct inelastic scattering—are often seen. This is not only true for inert systems like rare-gas atom scattering from liquid surfaces, but also for radical scattering.418More recently, attention has turned to reactions of incident atoms and molecules at liquid surfaces. This has proven useful, for example, to gain an understanding of the structure of liquid surfaces, an idea that has been demonstrated for pure molecular liquids, for salty solutions, and especially for ionic liquids. For example, Al atom beams could probe the surface content of fluorine in ionic liquids through a reaction forming hyper-thermal AlF, which could be detected by LIF.419 Similar ideas were exploited for OH reactive scattering from ionic liquids, where the surface structure of several ionic liquids was found to be independent of the ionic head group and rather dominated by the alkane side chain.420 Reactions of solvated electrons initiated by Na atom adsorption at a glycerol surface were also reported.421
The cylindrical, liquid micro-jet of Faubel, Schlemmer and Toennies422 is an innovation that has raised the ambitions of this field and, since its invention, efforts have intensified to study the vacuum/water interface. For example, with the ability to introduce liquid water into a vacuum chamber, photoelectron spectroscopy became possible, for example using core-level photoelectron spectroscopy423 to measure work functions of liquid-water surfaces.424
However, methods for scattering molecules from surfaces of high-vapor-pressure liquids like water are not yet fully mature. A recent review discusses many of the “lessons learned” in developing liquid microjets for scattering experiments.346 Here, an important potential pitfall must be attended to; rapid evaporation from the surface of liquid microjets is a stark reality of introducing a high-vapor-pressure liquid to a vacuum. There is a danger that molecules scattered from the surface of liquid water may be re-scattered by gas-phase water molecules evaporating from the jet. The evaporation rate depends on the radius of the cylindrical microjet; the smaller the radius, the less dense the vapor sheath around the liquid.347 Salts and/or surfactants may also be introduced to further lower the vapor pressure of the liquid. In addition, water evaporation is strong enough that the liquid's temperature drops with distance from the nozzle, an effect that of course also lowers the evaporation rate. The temperature of the liquid can be determined from the velocity distribution of evaporating Ar that has been pre-dissolved in the water. This distribution is then fitted to a Maxwell–Boltzmann function and a temperature is obtained. Of course, this relies on an assumption that the sticking probability of Ar to cold liquid-water surfaces is velocity-independent.
While the technical challenges are formidable, the future appears promising, especially for reactive scattering from aqueous surfaces. Reactions of solvated electrons at a water interface (similar to those described above for glycerol) have been demonstrated.425 Uptake of gas-phase molecules has also been studied by comparing scattering from the glass nozzle to that from the aqueous surface. It could be shown, for example, that HCl is efficiently taken up by the solution and experiments with DCl showed no isotope exchange, strongly suggesting that only the molecules that undergo direct inelastic scattering fail to dissolve.426 In another example of the potential of this approach, Br2 was found to emerge back to the gas phase after a beam of N2O5 collided with an aqueous microjet with a large concentration of dissolved LiBr.427 These experiments reflect chemistry thought to be important in sea-water aerosol droplets.
One specific problem with cylindrical microjets that may ultimately limit their usefulness is their small size—they are typically on the order of 30 μm in diameter. Direct comparison of scattering signals from rotating-wheel and cylindrical-microjet geometries shows at least a two-order of magnitude loss of scattering signal when using the microjet.429 It would, of course, be a tremendous practical advantage to develop flat liquid jets. In fact, it has been known since the 1960's that colliding cylindrical jets of water form flat leaf-like structures, which may be many mm in size—see Fig. 14.428
 | ||
| Fig. 14 Planar sheets of water are formed by collisions of cylindrical jets. Such leaf-like structures can be many mm in extent. This is an original figure based on a figure from ref. 428. | ||
Inspired by this, molecular beam scattering from flat liquid jets has been recently achieved for dodecane,430,431 which has a vapor pressure about 1% that of water. Extending these successes to aqueous interfaces will doubtless still be challenging, in particular because the flat-jet geometry is markedly less favorable for the formation of a gas-sheath than is the cylindrical jet. Furthermore, flat jets exhibit temperature gradients;432 however, this does not appear to be an insurmountable problem. There is every reason to believe that this approach will bear fruit in the near future.
8. Perspectives
The purpose of this review has been to present highlights of recent work using molecular scattering for the study of basic chemical reactivity in the gas phase and at surfaces. We have emphasized emerging laboratory methods that allow new types of measurements to be made and the fruitful cooperation between experiment and theory. In this final section, we claim an ability to see the future and point out new directions that we deem to be especially ripe for study. Unfortunately, this section may read like a laundry list of half-baked research proposals, which it is. Nevertheless, we hope that it may still provide value by inspiring readers to think more deeply along certain lines that lead them to concrete new work.The study of nonadiabatic processes is becoming more and more common in both gas-phase and gas–surface collision processes, with a broader and broader range of processes being considered, including species that are generated in highly excited states and that have many possible product channels and electronic states. At the most fundamental level, full quantum calculations are performed. These are primarily restricted to gas-phase processes, but provide valuable insight concerning quantum interference, including the geometric phase effect, and concerning spin-forbidden processes that can sometimes be crucial, even if they are rare. Trajectory surface hopping is gradually becoming available in public-domain codes (along with the ability to calculate nonadiabatic couplings), and has already proven important in studying a variety of gas-phase and gas–surface processes. It will be important to carry out further theory development in this field, as well as to extend the range of problems that can be studied.
For experimental crossed molecular beams scattering studies, the development of new atomic and molecular beams and detection methods is essential. Development of high-quality atomic and molecular beams, especially highly intense beams with narrow velocity spread, are important in the study of reactive-scattering experiments. This allows us to measure detailed differential cross sections for reaction products at specific quantum states, providing most thorough dynamics information for a specific chemical reaction. New laser photolysis techniques and other methods, such as discharge and thermal dissociation, etc., can be applied to generate high-quality atomic and radical beams for future crossed-beams scattering studies.
In addition to new atomic and molecular beams, development of low-background, more universal and highly sensitive detection methods are certainly desirable. For neutral reactive-scattering experiments, an efficient ionization detection scheme is the key. Therefore, a better ionization scheme, especially efficient soft VUV ionization, is important for further development of crossed-beams methods. One promising direction is the VUV ionization detection based on free electron laser (FEL) light sources, such as the Dalian Coherent Light Source, which can provide intense VUV laser light. Direct VUV FEL ionization can provide universal and efficient detection schemes for atomic and molecular species. Higher-repetition VUV FELs, which are based on superconducting accelerator technology, will certainly become a more powerful tool for universal detection of reactive-scattering products for complex chemical reactions.
More powerful and accurate quantum-dynamics calculation methods will be further developed; thus, the dynamics of more complex reactions can be investigated accurately, especially when accurate potential energy surfaces for complex reactions become available. This will enable us to acquire more accurate dynamics and kinetics information for both elementary and complex chemical reactions. Further development of dynamics theory, in concert with the development of advanced crossed-beams scattering experimental methods, will surely drive the field of chemical reaction dynamics to become a more exact science. Looking to the future, accurate calculations and predictions of both dynamics and kinetics for all chemical reactions may soon be a reality, with the help of AI technologies.
For gas–surface dynamics, there has been an explosion of interest in adding friction-based methods to incorporate energy transfer involving degrees of freedom that are not explicitly included in the dynamics. We expect this to continue, such that friction will become a standard feature in dynamics calculations, enabling the connection between dynamics and reaction-kinetics studies.
The field of cold collisions also provides new vistas for exploring quantum phenomena. Although the possibility that reactive bimolecular collisions at very low temperatures might access the regime where Wigner tunneling might be important, which was appreciated long ago and calculations using quantum scattering have been available for some time,433 experimental studies within this regime have primarily been a recent phenomenon due to interest in Bose-Einstein condensates involving diatomic molecules, and in interstellar kinetics. This will stimulate further work, both experiment and theory, to explore the consequences of reactions in this regime. We also note the attractive possibilities of using ions in cold collisions, for example creating cold plasma by combining negative and positive ions.
Growing interest in hypersonic flight and in vehicle reentry from lunar missions and beyond will continue to stimulate interest in future studies of hyperthermal reaction dynamics. This regime can be effectively studied using quasi-classical trajectory methods, but with significant challenges in the treatment of multiple electronic states and their couplings.406
The future of surface chemistry involves understanding reaction mechanisms under the high temperature and pressure conditions where real catalysis takes place; both theoretical and experimental reaction kinetics will be essential (https://doi.org/10.1039/D3FD00174A). Micro-kinetic modeling forms the underlying mathematical framework of catalysis, and to establish a fundamental foundation, existing rate theories must be improved395 and new ones must be developed. The aim is to accurately predict reaction rates from theory. Comparison of experiment and theory at the level of elementary reaction rates is an activity that is rarely undertaken.88 Much more of this will be needed in the future. Experimental methods for following the kinetics of reactions have been improving, but we will also need methods to follow the time-dependent concentrations of reaction intermediates. This calls for new means for sensitive and specific, yet universal, detection of adsorbates. Laser-induced desorption followed by gas-phase ionization389 has the potential to provide mass-spectrometric-like signatures of intermediates, if it can be combined with a universal means of detection (e.g., electron bombardment ionization or soft VUV ionization). Multi-mass imaging130 and covariance imaging129 are two other excellent experimental methods that are likely to find application in problems of reactive scattering from surfaces.
Real catalytic conditions give rise to dynamic changes in structures at the interface434 that may produce transient reactive configurations. Identifying these reactive configurations is one of the most important goals for future work. Time-resolved microscopies and other experimental methods promise such observations, but it remains highly challenging to link observations of reacting systems under real conditions to fundamental quantities that might allow non-empirical models to be developed. This is where theoretical discovery of reaction mechanisms in surface chemistry may become much more important. The structure of such “theoretical discovery” of mechanisms has already been demonstrated for gas-phase reactions.435,436 It is reasonable to forecast that such methods will be automated437 and enhanced with machine-learning algorithms and eventually become useful for surface chemistry and heterogeneous catalysis.
Machine learning has great potential for future creative applications; we believe we have so far just seen the tip of the iceberg. For example, it has recently been shown that electronic Hamiltonian matrices can be machine learned.438 This holds out the possibility that machine learning could lead to predictive models, or at least be much more transferable between related systems.
Quantum dynamics is another frontier; while, especially for surface chemistry, it is rarely used, here, we acknowledge its common ad hoc use when it is incorporated into transition-state theory. High-dimensional calculations have recently been demonstrated with 75 nuclear degrees of freedom using MCTDH methods.87 Future application of these methods will lead to a deeper understanding of tunneling and reaction resonances as well as the influence of nuclear and electron exchange symmetry on surface chemistry.395
The molecular-scattering methods reviewed in this paper have proven to be extremely useful in revealing the basic principles of gas-phase chemistry, surface chemistry and even reactivity in liquids. The major opportunity afforded by these methods, which is not as easily exploited in other types of experiments, is that it can be combined with first-principles theory and in so doing, much deeper insight becomes possible. The major reason for this arises from the fact that molecular-scattering experiments deliver many qualitative and especially quantitative observables. These include not only the elementary reaction products’ identity, but also their quantitative scattering properties like recoil angle, speed and quantum-state population distributions. This large diversity of accurately determined observations places extreme pressure on theory to come up with the right answers for the right reasons. Once this high standard has been reached, the theory may be unpacked to learn aspects of reactivity that cannot be directly seen in the laboratory. New directions in molecular scattering exploit the fruitful collaboration of experiment and theory using the improving tools developed by experimentalists and theorists. While it is unlikely that we will ever reach a point where everything can be computed from theory, we see an extremely bright future, where few problems remain intractable, when the creative spirit is applied to, on the one hand, develop and perfect new measurement methods that make new observations and, on the other, exploit the advance of computational science to explain them.
Conflicts of interest
There are no conflicts of Interest amongst the authors.Acknowledgements
GCS was supported by ONR MURI Award N00014-22-1-2661. Open Access funding provided by the Max Planck Society.References
- M. Born, W. Heisenberg and P. Jordan, Z. Phys., 1926, 35, 557–615 CrossRef CAS.
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1929, 123, 714–733 CAS.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457–484 CrossRef.
- H. Eyring and M. Polanyi, Z. Phys. Chem., 1931, 12, 279–311 CAS.
- H. Eyring and M. Polanyi, Z. Phys. Chem., 2013, 227, 1221–1245 CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- H. Eyring, Trans. Faraday Soc., 1938, 34, 0041–0048 RSC.
- F. T. Wall, L. A. Hiller and J. Mazur, J. Chem. Phys., 1958, 29, 255–263 CrossRef CAS.
- N. Basco and R. G. W. Norrish, Can. J. Chem., 1960, 38, 1769–1779 CrossRef CAS.
- A. B. Meinel, Astrophys. J., 1950, 111, 555 CrossRef.
- J. D. McKinley, D. Garvin and M. J. Boudart, J. Chem. Phys., 1955, 23, 784–786 CrossRef CAS.
- A. L. Schawlow and C. H. Townes, Phys. Rev., 1958, 112, 1940–1949 CrossRef CAS.
- T. H. Maiman, Nature, 1960, 187, 493–494 CrossRef.
- J. V. V. Kasper and G. C. Pimentel, Phys. Rev. Lett., 1965, 14, 352 CrossRef CAS.
- R. N. Zare, Annu. Rev. Anal. Chem., 2012, 5, 1–14 CrossRef CAS PubMed.
- L. O. Hocker, M. A. Kovacs, C. K. Rhodes, G. W. Flynn and A. Javan, Phys. Rev. Lett., 1966, 17, 233 CrossRef CAS.
- J. T. Yardley and C. B. Moore, J. Chem. Phys., 1966, 45, 1066 CrossRef CAS.
- A. M. Ronn, J. Chem. Phys., 1968, 48, 511 CrossRef CAS.
- W. J. Tango, J. K. Link and R. N. Zare, J. Chem. Phys., 1968, 49, 4264 CrossRef CAS.
- K. Sakurai and H. P. Broida, J. Chem. Phys., 1969, 50, 2404 CrossRef CAS.
- F. P. Schäfer, W. Schmidt and J. Volze, Appl. Phys. Lett., 1966, 9, 306–309 CrossRef.
- P. P. Sorokin, J. R. Lankard, E. C. Hammond and V. L. Moruzzi, IBM J. Res. Dev., 1967, 11, 130–148 CAS.
- J. C. Polanyi, Acc. Chem. Res., 1972, 5, 161 CrossRef CAS.
- J. C. Polanyi, Angew. Chem., Int. Ed., 1987, 26, 952–971 CrossRef.
- E. H. Taylor and S. Datz, J. Chem. Phys., 1955, 23, 1711–1718 CrossRef CAS.
- D. Herschbach, G. H. Kwei and J. A. Norris, J. Chem. Phys., 1961, 34, 1842 CrossRef CAS.
- Z. Herman, J. D. Kerstetter, T. L. Rose and R. Wolfgang, J. Chem. Phys., 1967, 46, 2844 CrossRef CAS.
- W. R. Gentry, E. A. Gislason, Y. T. Lee, B. H. Mahan and C. W. Tsao, Discuss. Faraday Soc., 1967, 137, 137–145 RSC.
- Y. T. Lee, J. D. McDonald, P. R. Lebreton and D. R. Herschbach, Rev. Sci. Instrum., 1969, 40, 1402 CrossRef CAS.
- Y. T. Lee, Angew. Chem., Int. Ed., 1987, 26, 939–951 CrossRef.
- C. C. J. Roothaan, Rev. Mod. Phys., 1951, 23, 69–89 CrossRef CAS.
- N. C. Blais and D. L. Bunker, J. Chem. Phys., 1962, 37, 2713 CrossRef CAS.
- M. Karplus, R. D. Sharma and R. N. Porter, J. Chem. Phys., 1964, 40, 2033 CrossRef CAS.
- D. G. Truhlar and A. Kuppermann, J. Chem. Phys., 1970, 52, 3841 CrossRef CAS.
- A. Kuppermann and G. C. Schatz, J. Chem. Phys., 1975, 62, 2502–2504 CrossRef CAS.
- A. B. Elkowitz and R. E. Wyatt, J. Chem. Phys., 1975, 62, 2504–2506 CrossRef CAS.
- E. A. McCullough and R. E. Wyatt, J. Chem. Phys., 1971, 54, 3578 CrossRef CAS.
- E. J. Heller, J. Chem. Phys., 1975, 62, 1544–1555 CrossRef CAS.
- H. D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 CrossRef CAS PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- J. Chen, Z. G. Sun and D. H. Zhang, J. Chem. Phys., 2015, 142, 024303 CrossRef PubMed.
- Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26–34 CrossRef CAS PubMed.
- J. M. Bowman, G. Czako and B. N. Fu, Phys. Chem. Chem. Phys., 2011, 13, 8094–8111 RSC.
- C. Qu, Q. Yu and J. M. Bowman, Annu. Rev. Phys. Chem., 2018, 69, 151–175 CrossRef CAS PubMed.
- C. Qu, Q. Yu, B. L. Van Hoozen, J. M. Bowman and R. A. Vargas-Hernandez, J. Chem. Theory Comput., 2018, 14, 3381–3396 CrossRef CAS PubMed.
- A. Nandi, C. Qu, P. L. Houston, R. Conte and J. M. Bowman, J. Chem. Phys., 2021, 154, 051102 CrossRef CAS PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Inf. Model., 2017, 57, 1923–1931 CrossRef CAS PubMed.
- D. Koner, J. C. S. Veliz, R. J. Bemish and M. Meuwly, Phys. Chem. Chem. Phys., 2020, 22, 18488–18498 RSC.
- M. Meuwly, Chem. Rev., 2021, 121, 10218–10239 CrossRef CAS PubMed.
- K. M. Thompson, Y. D. Gao, P. Marshall, H. Wang, L. S. Zhou, Y. L. Li and H. Guo, J. Chem. Phys., 2017, 147, 134302 CrossRef PubMed.
- S. Mallikarjun Sharada, T. Bligaard, A. C. Luntz, G.-J. Kroes and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 19807–19815 CrossRef CAS.
- T. Tchakoua, T. Jansen, Y. van Nies, R. F. A. van den Elshout, B. A. B. van Boxmeer, S. P. Poort, M. G. Ackermans, G. S. Beltrao, S. A. Hildebrand, S. E. J. Beekman, T. van der Drift, S. Kaart, A. Santic, E. E. Spuijbroek, N. Gerrits, M. F. Somers and G.-J. Kroes, J. Phys. Chem. A, 2023, 127, 10481–10498 CrossRef CAS PubMed.
- B. Jiang, J. Li and H. Guo, J. Phys. Chem. Lett., 2020, 11, 5120–5131 CrossRef CAS PubMed.
- W. G. Stark, J. Westermayr, O. A. Douglas-Gallardo, J. Gardner, S. Habershon and R. J. Maurer, J. Phys. Chem. C, 2023, 127, 24168–24182 CrossRef CAS PubMed.
- J. Behler, Angew. Chem., Int. Ed., 2017, 56, 12828–12840 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- T. J. Frankcombe, M. A. Collins and D. H. Zhang, J. Chem. Phys., 2012, 137, 144701 CrossRef PubMed.
- R. P. A. Bettens and M. A. Collins, J. Chem. Phys., 1999, 111, 816–826 CrossRef CAS.
- N. Hertl, A. Kandratsenka and A. M. Wodtke, Phys. Chem. Chem. Phys., 2022, 24, 8738–8748 RSC.
- S. M. Janke, D. J. Auerbach, A. M. Wodtke and A. Kandratsenka, J. Chem. Phys., 2015, 143, 124708 CrossRef PubMed.
- M. Kammler, S. M. Janke, A. Kandratsenka and A. M. Wodtke, Chem. Phys. Lett., 2017, 683, 286–290 CrossRef CAS.
- D. H. Zhang and H. Guo, Annu. Rev. Phys. Chem., 2016, 67, 135–158 CrossRef CAS PubMed.
- B. Fu and D. H. Zhang, J. Chem. Theory Comput., 2018, 14, 2289–2303 CrossRef CAS PubMed.
- Z. G. Sun and D. H. Zhang, Prog. Chem., 2012, 24, 1153–1165 CAS.
- Z. G. Sun, W. T. Yang and D. H. Zhang, Phys. Chem. Chem. Phys., 2012, 14, 1827–1845 RSC.
- G. G. Balint-Kurti, Theor. Chem. Acc., 2010, 127, 1–17 Search PubMed.
- Z. G. Sun, H. Guo and D. H. Zhang, J. Chem. Phys., 2010, 132, 084112 CrossRef PubMed.
- H. L. Zhao, X. X. Hu, D. Q. Xie and Z. G. Sun, J. Chem. Phys., 2018, 149, 174103 CrossRef PubMed.
- D. C. Clary, Faraday Discuss., 2018, 212, 9–32 RSC.
- H. D. Meyer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 351–374 CAS.
- U. Manthe, J. Phys.: Condens.Matter, 2017, 29, 253001 CrossRef PubMed.
- B. Zhao, Z. G. Sun and H. Guo, J. Chem. Phys., 2014, 140, 234110 CrossRef PubMed.
- L. Dupuy, D. Lauvergnat and Y. Scribano, Chem. Phys. Lett., 2022, 787, 139241 CrossRef CAS.
- G. J. Kroes, Phys. Chem. Chem. Phys., 2012, 14, 14966–14981 RSC.
- G. J. Kroes, Phys. Chem. Chem. Phys., 2021, 23, 8962–9048 RSC.
- G.-J. Kroes and C. Díaz, Chem. Soc. Rev., 2016, 45, 3658–3700 RSC.
- J. W. Lu, B. S. Day, L. R. Fiegland, E. D. Davis, W. A. Alexander, D. Troya and J. R. Morris, Prog. Surf. Sci., 2012, 87, 221–252 CrossRef CAS.
- M. A. Tesa-Serrate, E. J. Smoll, T. K. Minton and K. G. McKendrick, Annu. Rev. Phys. Chem., 2016, 67, 515–540 CrossRef CAS PubMed.
- L. Shi, M. Schröder, H.-D. Meyer, D. Peláez, A. M. Wodtke, K. Golibrzuch, A.-M. Schönemann, A. Kandratsenka and F. Gatti, J. Chem. Phys., 2023, 159, 194102 CrossRef CAS PubMed.
- L. Zhang, J. Zuo, Y. V. V. Suleimanov and H. Guo, J. Phys. Chem. Lett., 2023, 14, 7118–7125 CrossRef CAS PubMed.
- C. Li, Y. Li and B. Jiang, Chem. Sci., 2023, 14, 5087–5098 RSC.
- B. K. Kendrick, J. Chem. Phys., 2018, 148, 069902 CrossRef PubMed.
- D. Koner, R. J. Bemish and M. Meuwly, J. Phys. Chem. A, 2020, 124, 6255–6269 CrossRef CAS PubMed.
- M. Blanco-Rey, J. I. Juaristi, R. Díez Muiño, H. F. Busnengo, G. J. Kroes and M. Alducin, Phys. Rev. Lett., 2014, 112, 103203 CrossRef CAS PubMed.
- P. Spiering, K. Shakouri, J. Behler, G.-J. Kroes and J. Meyer, J. Phys. Chem. Lett., 2019, 10, 2957–2962 CrossRef CAS PubMed.
- Y. L. Zhang, R. J. Maurer, H. Guo and B. Jiang, Chem. Sci., 2019, 10, 1089–1097 RSC.
- J. I. Juaristi, M. Alducin, R. D. Muiño, H. F. Busnengo and A. Salin, Phys. Rev. Lett., 2008, 100, 116102 CrossRef CAS PubMed.
- M. Pavanello, D. J. Auerbach, A. M. Wodtke, M. Blanco-Rey, M. Alducin and G. J. Kroes, J. Phys. Chem. Lett., 2013, 4, 3735–3740 CrossRef CAS.
- M. Askerka, R. J. Maurer, V. S. Batista and J. C. Tully, Phys. Rev. Lett., 2016, 116, 217601 CrossRef PubMed.
- R. J. Maurer, M. Askerka, V. S. Batista and J. C. Tully, Phys. Rev. B, 2016, 94, 115432 CrossRef.
- Y. L. Zhang, R. J. Maurer and B. Jiang, J. Phys. Chem. C, 2020, 124, 186–195 CrossRef CAS.
- C. L. Box, Y. Zhang, R. Yin, B. Jiang and R. J. Maurer, JACS Au, 2021, 1, 164–173 CrossRef CAS PubMed.
- Y. Zhang, C. L. Box, T. Schaefer, A. Kandratsenka, A. M. Wodtke, R. J. Maurer and B. Jiang, Phys. Chem. Chem. Phys., 2022, 24, 19753–19760 RSC.
- E. Rutherford, Philos. Mag., 1911, 21, 669–688 CAS.
- J. J. Lin, D. W. Hwang, S. Harich, Y. T. Lee and X. M. Yang, Rev. Sci. Instrum., 1998, 69, 1642–1646 CrossRef CAS.
- X. Yang, J. Lin, Y. T. Lee, D. A. Blank, A. G. Suits and A. M. Wodtke, Rev. Sci. Instrum., 1997, 68, 3317–3326 CrossRef CAS.
- P. A. Willis, H. U. Stauffer, R. Z. Hinrichs and H. F. Davis, Rev. Sci. Instrum., 1999, 70, 2606–2614 CrossRef CAS.
- D. R. Albert and H. F. Davis, Phys. Chem. Chem. Phys., 2013, 15, 14566–14580 RSC.
- D. R. Albert, M. A. Todt and H. F. Davis, J. Phys. Chem. A, 2013, 117, 13967–13975 CrossRef CAS PubMed.
- N. Balucani, G. Capozza, F. Leonori, E. Segoloni and P. Casavecchia, Int. Rev. Phys. Chem., 2006, 25, 109–163 Search PubMed.
- J. L. Hall, E. J. Robinson and L. M. Branscomb, Phys. Rev. Lett., 1965, 14, 1013 CrossRef CAS.
- R. A. Fox, R. M. Kogan and E. J. Robinson, Phys. Rev. Lett., 1971, 26, 1416 CrossRef CAS.
- B. Held, C. Manus, G. Mainfray and J. Morellec, Phys. Rev. Lett., 1972, 28, 130 CrossRef CAS.
- B. Held, G. Mainfray, C. Manus, J. Morellec and F. Sanchez, Phys. Rev. Lett., 1973, 30, 423–426 CrossRef.
- W. C. Lineberger and T. A. Patterson, Chem. Phys. Lett., 1972, 13, 40 CrossRef CAS.
- C. B. Collins, B. W. Johnson, D. Popescu, G. Musa, M. L. Pascu and I. Popescu, Phys. Rev. A, 1973, 8, 2197–2201 CrossRef.
- P. M. Johnson, M. R. Berman and D. Zakheim, J. Chem. Phys., 1975, 62, 2500–2502 CrossRef CAS.
- G. Petty, C. Tai and F. W. Dalby, Phys. Rev. Lett., 1975, 34, 1207–1209 CrossRef CAS.
- P. M. Johnson, J. Chem. Phys., 1976, 64, 4143–4148 CrossRef CAS.
- D. H. Parker, S. J. Sheng and M. A. El-Sayed, J. Chem. Phys., 1976, 65, 5534–5535 CrossRef CAS.
- A. J. R. Heck and D. W. Chandler, Annu. Rev. Phys. Chem., 1995, 46, 335–372 CrossRef CAS PubMed.
- D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445–1447 CrossRef CAS.
- M. A. Buntine, D. P. Baldwin, R. N. Zare and D. W. Chandler, J. Chem. Phys., 1991, 94, 4672–4675 CrossRef CAS.
- T. N. Kitsopoulos, M. A. Buntine, D. P. Baldwin, R. N. Zare and D. W. Chandler, Science, 1993, 260, 1605–1610 CrossRef CAS PubMed.
- A. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- C. R. Gebhardt, T. P. Rakitzis, P. C. Samartzis, V. Ladopoulos and T. N. Kitsopoulos, Rev. Sci. Instrum., 2001, 72, 3848–3853 CrossRef CAS.
- D. Townsend, M. P. Minitti and A. G. Suits, Rev. Sci. Instrum., 2003, 74, 2530–2539 CrossRef CAS.
- J. J. Lin, J. G. Zhou, W. C. Shiu and K. P. Liu, Rev. Sci. Instrum., 2003, 74, 2495–2500 CrossRef CAS.
- M. N. R. Ashfold, N. H. Nahler, A. J. Orr-Ewing, O. P. J. Vieuxmaire, R. L. Toomes, T. N. Kitsopoulos, I. A. Garcia, D. A. Chestakov, S. M. Wu and D. H. Parker, Phys. Chem. Chem. Phys., 2006, 8, 26–53 RSC.
- D. Yuan, W. Chen, C. Luo, Y. Tan, S. Li, Y. Huang, Z. Sun, X. Yang and X. Wang, J. Phys. Chem. Lett., 2020, 11, 1222–1227 CrossRef CAS PubMed.
- C. S. Slater, S. Blake, M. Brouard, A. Lauer, C. Vallance, J. J. John, R. Turchetta, A. Nomerotski, L. Christensen, J. H. Nielsen, M. P. Johansson and H. Stapelfeldt, Phys. Rev. A, 2014, 89, 011401 CrossRef.
- A. Nomerotski, M. Brouard, E. Campbell, A. Clark, J. Crooks, J. Fopma, J. J. John, A. J. Johnsen, C. Slater, R. Turchetta, C. Vallance, E. Wilman and W. H. Yuen, J. Instrum., 2010, 5, C07007 Search PubMed.
- L. Schnieder, W. Meier, K. H. Welge, M. N. R. Ashfold and C. M. Western, J. Chem. Phys., 1990, 92, 7027–7037 CrossRef CAS.
- L. Schnieder, K. Seekamprahn, J. Borkowski, E. Wrede, K. H. Welge, F. J. Aoiz, L. Banares, M. J. Dmello, V. J. Herrero, V. S. Rabanos and R. E. Wyatt, Science, 1995, 269, 207–210 CrossRef CAS PubMed.
- L. Schnieder, K. SeekampRahn, E. Wrede and K. H. Welge, J. Chem. Phys., 1997, 107, 6175–6195 CrossRef CAS.
- B. R. Strazisar, C. Lin and H. F. Davis, Science, 2000, 290, 958–961 CrossRef CAS PubMed.
- S. D. Chao, S. A. Harich, D. X. Dai, C. C. Wang, X. M. Yang and R. T. Skodje, J. Chem. Phys., 2002, 117, 8341–8361 CrossRef CAS.
- S. A. Harich, D. Dai, X. M. Yang, S. D. Chao and R. T. Skodje, J. Chem. Phys., 2002, 116, 4769–4772 CrossRef CAS.
- D. X. Dai, C. C. Wang, S. A. Harich, X. Y. Wang, X. M. Yang, S. D. Chao and R. T. Skodje, Science, 2003, 300, 1730–1734 CrossRef CAS PubMed.
- M. H. Qiu, L. Che, Z. F. Ren, D. X. Dai, X. Y. Wang and X. M. Yang, Rev. Sci. Instrum., 2005, 76, 083107 CrossRef.
- J. Y. Zhang, D. X. Dai, C. C. Wang, S. A. Harich, X. Y. Wang, X. M. Yang, M. Gustafsson and R. T. Skodje, Phys. Rev. Lett., 2006, 96, 093201 CrossRef PubMed.
- R. N. Dixon, D. W. Hwang, X. F. Yang, S. Harich, J. J. Lin and X. Yang, Science, 1999, 285, 1249–1253 CrossRef CAS PubMed.
- M. N. R. Ashfold, B. Cronin, A. L. Devine, R. N. Dixon and M. G. D. Nix, Science, 2006, 312, 1637–1640 CrossRef CAS PubMed.
- G. Sun, X. F. Zheng, K. S. Xu, Y. Song and J. S. Zhang, J. Phys. Chem. A, 2021, 125, 8882–8890 CrossRef CAS PubMed.
- Y. Nagaya, H. Nakatsu, S. Ogura, K. Shimazaki, H. Ueta, K. Takeyasu and K. Fukutani, J. Chem. Phys., 2021, 155, 194201 CrossRef CAS PubMed.
- R. I. Kaiser, C. Ochsenfeld, M. Head-Gordon, Y. T. Lee and A. G. Suits, Science, 1996, 274, 1508–1511 CrossRef CAS PubMed.
- R. I. Kaiser and A. M. Mebel, Int. Rev. Phys. Chem., 2002, 21, 307–356 Search PubMed.
- R. I. Kaiser, D. S. N. Parker and A. M. Mebel, Annu. Rev. Phys. Chem., 2015, 66, 43–67 CrossRef CAS PubMed.
- Z. Zhao, Y. Wang, X. Yang, J. Quan, B. C. Krueger, P. Stoicescu, R. Nieman, D. J. Auerbach, A. M. Wodtke, H. Guo and G. B. Park, Nat. Chem., 2023, 15, 1006–1011 CrossRef CAS PubMed.
- Z. F. Ren, M. H. Qiu, L. Che, D. X. Dai, X. Y. Wang and X. M. Yang, Rev. Sci. Instrum., 2006, 77, 016102 CrossRef.
- J. J. Valentini, M. J. Coggiola and Y. T. Lee, Rev. Sci. Instrum., 1977, 48, 58–63 CrossRef CAS.
- H. F. Davis, J. Shu, D. S. Peterka and M. Ahmed, J. Chem. Phys., 2004, 121, 6254–6257 CrossRef PubMed.
- R. I. Kaiser, N. Balucani, D. O. Charkin and A. M. Mebel, Chem. Phys. Lett., 2003, 382, 112–119 CrossRef CAS.
- S.-H. Lee, W.-J. Huang, Y.-C. Lin and C.-H. Chin, Astrophys. J., 2012, 759, 75–84 CrossRef.
- W.-J. Huang, Y.-L. Sun, C.-H. Chin and S.-H. Lee, J. Chem. Phys., 2014, 141, 124314 CrossRef PubMed.
- F. Stahl, P. von Ragué Schleyer, H. F. Bettinger, R. I. Kaiser, Y. T. Lee and H. F. Schaefer III, J. Chem. Phys., 2001, 114, 3476–3487 CrossRef CAS.
- R. G. Macdonald, K. P. Liu, D. M. Sonnenfroh and D. J. Liu, Can. J. Chem., 1994, 72, 660–672 CrossRef CAS.
- R. G. Macdonald and K. P. Liu, J. Phys. Chem., 1991, 95, 9630–9633 CrossRef CAS.
- S. Y. T. van de Meerakker, N. Vanhaecke, M. P. J. van der Loo, G. C. Groenenboom and G. Meijer, Phys. Rev. Lett., 2005, 95, 013003 CrossRef PubMed.
- T. K. Minton, K. P. Giapis and T. Moore, J. Phys. Chem. A, 1997, 101, 6549–6555 CrossRef CAS.
- J. M. Zhang, D. J. Garton and T. K. Minton, J. Chem. Phys., 2002, 117, 6239–6251 CrossRef CAS.
- N. Bartels, T. Schäfer, J. Huhnert, R. W. Field and A. M. Wodtke, J. Chem. Phys., 2012, 136, 214201 CrossRef PubMed.
- N. Bartels, B. C. Krüger, S. Meyer, A. M. Wodtke and T. Schäfer, J. Phys. Chem. Lett., 2013, 4, 2367–2370 CrossRef CAS.
- P. R. Shirhatti, I. Rahinov, K. Golibrzuch, J. Werdecker, J. Geweke, J. Altschaffel, S. Kumar, D. J. Auerbach, C. Bartels and A. M. Wodtke, Nat. Chem., 2018, 10, 592–598 CrossRef CAS PubMed.
- J. Geweke, P. R. Shirhatti, I. Rahinov, C. Bartels and A. M. Wodtke, J. Chem. Phys., 2016, 145, 054709 CrossRef PubMed.
- I. Rahinov, R. Cooper, C. Yuan, X. M. Yang, D. J. Auerbach and A. M. Wodtke, J. Chem. Phys., 2008, 129, 214708 CrossRef PubMed.
- T. Schäfer, N. Bartels, N. Hocke, X. M. Yang and A. M. Wodtke, Chem. Phys. Lett., 2012, 535, 1–11 CrossRef.
- B. L. Yoder, R. Bisson, P. M. Hundt and R. D. Beck, J. Chem. Phys., 2011, 135, 224703 CrossRef PubMed.
- K. Liu, Annu. Rev. Phys. Chem., 2016, 67, 91–111 CrossRef CAS PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, J. Chem. Phys., 2019, 150, 174301 CrossRef PubMed.
- Y. Wang, J. Huang, W. Wang, T. Du, Y. Xie, Y. Ma, C. Xiao, Z. Zhaojun, D. H. Zhang and X. Yang, Science, 2023, 379, 191–195 CrossRef CAS PubMed.
- E. Wrede, L. Schnieder, K. H. Welge, F. J. Aoiz, L. Banares, J. F. Castillo, B. Martinez-Haya and V. J. Herrero, J. Chem. Phys., 1999, 110, 9971–9981 CrossRef CAS.
- J. Jankunas, M. Sneha, R. N. Zare, F. Bouakline and S. C. Althorpe, J. Chem. Phys., 2013, 139, 144316 CrossRef PubMed.
- H. Gao, M. Sneha, F. Bouakline, S. C. Althorpe and R. N. Zare, J. Phys. Chem. A, 2015, 119, 12036–12042 CrossRef CAS PubMed.
- R. E. Continetti, B. A. Balko and Y. T. Lee, J. Chem. Phys., 1990, 93, 5719–5740 CrossRef CAS.
- S. A. Harich, D. X. Dai, C. C. Wang, X. M. Yang, S. D. Chao and R. T. Skodje, Nature, 2002, 419, 281–284 CrossRef CAS PubMed.
- D. Yuan, Y. Guan, W. Chen, H. Zhao, S. Yu, C. Luo, Y. Tan, T. Xie, X. Wang, Z. Sun, D. H. Zhang and X. Yang, Science, 2018, 362, 1289 CrossRef CAS PubMed.
- D. F. Yuan, S. R. Yu, W. T. Chen, J. W. Sang, C. Luo, T. Wang, X. Xu, P. Casavecchia, X. A. Wang, Z. G. Sun, D. H. Zhang and X. M. Yang, Nat. Chem., 2018, 10, 653–658 CrossRef CAS PubMed.
- G. C. Schatz and A. Kuppermann, J. Chem. Phys., 1973, 59, 964–965 CrossRef CAS.
- J. Z. H. Zhang, S. I. Chu and W. H. Miller, J. Chem. Phys., 1988, 88, 6233–6239 CrossRef CAS.
- R. T. Skodje and X. M. Yang, Int. Rev. Phys. Chem., 2004, 23, 253–287 Search PubMed.
- D. C. Chatfield, S. L. Mielke, T. C. Allison and D. G. Truhlar, J. Chem. Phys., 2000, 112, 8387–8408 CrossRef CAS.
- C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1979, 70, 2284–2296 CrossRef CAS.
- D. F. Yuan, Y. Huang, W. T. Chen, H. L. Zhao, S. R. Yu, C. Luo, Y. X. Tan, S. W. Wang, X. G. Wang, Z. G. Sun and X. M. Yang, Nat. Commun., 2020, 11, 7 CrossRef PubMed.
- B. Lepetit, Z. Peng and A. Kuppermann, Chem. Phys. Lett., 1990, 166, 572–580 CrossRef CAS.
- Y. S. M. Wu, A. Kuppermann and B. Lepetit, Chem. Phys. Lett., 1991, 186, 319–328 CrossRef CAS.
- E. Wrede and L. Schnieder, J. Chem. Phys., 1997, 107, 786–790 CrossRef CAS.
- M. P. de Miranda, D. C. Clary, J. F. Castillo and D. E. Manolopoulos, J. Chem. Phys., 1998, 108, 3142–3153 CrossRef CAS.
- B. K. Kendrick, J. Chem. Phys., 2000, 112, 5679–5704 CrossRef CAS.
- J. C. Juanes-Marcos and S. C. Althorpe, J. Chem. Phys., 2005, 122, 204324 CrossRef PubMed.
- B. K. Kendrick, J. Phys. Chem. A, 2003, 107, 6739–6756 CrossRef CAS.
- J. C. Juanes-Marcos, S. C. Althorpe and E. Wrede, Science, 2005, 309, 1227–1230 CrossRef CAS PubMed.
- S. C. Althorpe, J. Chem. Phys., 2006, 124, 084105 CrossRef PubMed.
- F. Bouakline, S. C. Althorpe and D. P. Ruiz, J. Chem. Phys., 2008, 128, 124322 CrossRef PubMed.
- B. K. Kendrick, J. Hazra and N. Balakrishnan, Phys. Rev. Lett., 2015, 115, 153201 CrossRef CAS PubMed.
- S. F. Wu, B.R. Johnson and R. D. Levine, Mol. Phys., 1973, 25, 839–856 CrossRef CAS.
- G. C. Schatz, J. M. Bowman and A. Kuppermann, J. Chem. Phys., 1973, 58, 4023–4025 CrossRef CAS.
- D. M. Neumark, A. M. Wodtke, G. N. Robinson, C. C. Hayden and Y. T. Lee, Phys. Rev. Lett., 1984, 53, 226–229 CrossRef CAS.
- F. J. Aoiz, L. Banares, V. J. Herrero, V. S. Rabanos, K. Stark and H. J. Werner, Chem. Phys. Lett., 1994, 223, 215–226 CrossRef CAS.
- J. F. Castillo, D. E. Manolopoulos, K. Stark and H. J. Werner, J. Chem. Phys., 1996, 104, 6531–6546 CrossRef CAS.
- R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S. H. Lee, F. Dong and K. P. Liu, Phys. Rev. Lett., 2000, 85, 1206–1209 CrossRef CAS PubMed.
- T. G. Yang, L. Huang, C. L. Xiao, J. Chen, T. Wang, D. X. Dai, F. Lique, M. H. Alexander, Z. G. Sun, D. H. Zhang, X. M. Yang and D. M. Neumark, Nat. Chem., 2019, 11, 744–749 CrossRef CAS PubMed.
- D. E. Manolopoulos, K. Stark, H. J. Werner, D. W. Arnold, S. E. Bradforth and D. M. Neumark, Science, 1993, 262, 1852–1855 CrossRef CAS PubMed.
- M. H. Qiu, Z. F. Ren, L. Che, D. X. Dai, S. A. Harich, X. Y. Wang, X. M. Yang, C. X. Xu, D. Q. Xie, M. Gustafsson, R. T. Skodje, Z. G. Sun and D. H. Zhang, Science, 2006, 311, 1440–1443 CrossRef CAS PubMed.
- Z. F. Ren, L. Che, M. H. Qiu, X. A. Wang, W. R. Dong, D. X. Dai, X. Y. Wang, X. M. Yang, Z. G. Sun, B. Fu, S. Y. Lee, X. Xu and D. H. Zhang, Proc. Natl. Acad. Sci. U.S.A., 2008, 105, 12662–12666 CrossRef CAS PubMed.
- J. B. Kim, M. L. Weichman, T. F. Sjolander, D. M. Neumark, J. Klos, M. H. Alexander and D. E. Manolopoulos, Science, 2015, 349, 510–513 CrossRef CAS PubMed.
- T. Wang, T. G. Yang, C. L. Xiao, Z. G. Sun, D. H. Zhang, X. M. Yang, M. L. Weichman and D. M. Neumark, Chem. Soc. Rev., 2018, 47, 6744–6763 RSC.
- W. R. Dong, C. L. Xiao, T. Wang, D. X. Dai, X. M. Yang and D. H. Zhang, Science, 2010, 327, 1501–1502 CrossRef CAS PubMed.
- M. Alagia, N. Balucani, L. Cartechini, P. Casavecchia, G. G. Volpi, F. J. Aoiz, L. Bañares, T. C. Allison, S. L. Mielke and D. G. Truhlar, Phys. Chem. Chem. Phys., 2000, 2, 599–612 RSC.
- M. Alagia, N. Balucani, L. Cartechini, P. Casavecchia, E. H. vanKleef, G. G. Volpi, F. J. Aoiz, L. Banares, D. W. Schwenke, T. C. Allison, S. L. Mielke and D. G. Truhlar, Science, 1996, 273, 1519–1522 CrossRef CAS.
- X. G. Wang, W. R. Dong, C. L. Xiao, L. Che, Z. F. Ren, D. X. Dai, X. Y. Wang, P. Casavecchia, X. M. Yang, B. Jiang, D. Q. Xie, Z. G. Sun, S. Y. Lee, D. H. Zhang, H. J. Werner and M. H. Alexander, Science, 2008, 322, 573–576 CrossRef CAS PubMed.
- N. Balucani, G. Capozza, E. Segoloni, A. Russo, R. Bobbenkamp, P. Casavecchia, T. Gonzalez-Lezana, E. J. Rackham, L. Bañares and F. J. Aoiz, J. Chem. Phys., 2005, 122, 234309 CrossRef PubMed.
- S. A. Lahankar, J. M. Zhang, K. G. McKendrick and T. K. Minton, Nat. Chem., 2013, 5, 315–319 CrossRef CAS PubMed.
- M. Alagia, N. Balucani, L. Cartechini, P. Casavecchia, E. H. van Kleef, G. G. Volpi, P. J. Kuntz and J. J. Sloan, J. Chem. Phys., 1998, 108, 6698–6708 CrossRef CAS.
- X. H. Liu, J. J. Lin, S. Harich, G. C. Schatz and X. M. Yang, Science, 2000, 289, 1536–1538 CrossRef CAS PubMed.
- M. Alagia, N. Balucani, L. Cartechini, P. Casavecchia, G. G. Volpi, L. A. Pederson, G. C. Schatz, G. Lendvay, L. B. Harding, T. Hollebeek, T. S. Ho and H. Rabitz, J. Chem. Phys., 1999, 110, 8857–8860 CrossRef CAS.
- C. L. Xiao, X. Xu, S. Liu, T. Wang, W. R. Dong, T. G. Yang, Z. G. Sun, D. X. Dai, X. Xu, D. H. Zhang and X. M. Yang, Science, 2011, 333, 440–442 CrossRef CAS PubMed.
- P. Casavecchia, F. Leonori and N. Balucani, Int. Rev. Phys. Chem., 2015, 34, 161–204 Search PubMed.
- J. J. Lin, J. G. Zhou, W. C. Shiu and K. P. Liu, Science, 2003, 300, 966–969 CrossRef CAS PubMed.
- J. G. Zhou, J. J. Lin, W. C. Shiu and K. P. Liu, J. Chem. Phys., 2003, 119, 4997–5000 CrossRef CAS.
- W. Shiu, J. J. Lin and K. P. Liu, Phys. Rev. Lett., 2004, 92, 103201 CrossRef PubMed.
- J. G. Zhou, J. J. Lin and K. P. Liu, J. Chem. Phys., 2003, 119, 8289–8296 CrossRef CAS.
- J. Y. Yang, D. Zhang, B. Jiang, D. X. Dai, G. R. Wu, D. H. Zhang and X. M. Yang, J. Phys. Chem. Lett., 2014, 5, 1790–1794 CrossRef CAS PubMed.
- W. Shiu, J. J. Lin, K. P. Liu, M. Wu and D. H. Parker, J. Chem. Phys., 2004, 120, 117–122 CrossRef CAS PubMed.
- Z. Chen, J. Chen, R. J. Chen, T. Xie, X. G. Wang, S. Liu, G. R. Wu, D. X. Dai, X. M. Yang and D. H. Zhang, Proc. Natl. Acad. Sci. U.S.A., 2020, 117, 9202–9207 CrossRef CAS PubMed.
- G. R. Wu, W. Q. Zhang, H. L. Pan, Q. A. Shuai, J. Y. Yang, B. Jiang, D. X. Dai and X. M. Yang, Phys. Chem. Chem. Phys., 2010, 12, 9469–9474 RSC.
- W. Q. Zhang, G. R. Wu, H. L. Pan, Q. Shuai, B. Jiang, D. X. Dai and X. M. Yang, J. Phys. Chem. A, 2009, 113, 4652–4657 CrossRef CAS PubMed.
- W. Q. Zhang, Y. Zhou, G. R. Wu, Y. P. Lu, H. L. Pan, B. N. Fu, Q. A. Shuai, L. Liu, S. Liu, L. L. Zhang, B. Jiang, D. X. Dai, S. Y. Lee, Z. Xie, B. J. Braams, J. M. Bowman, M. A. Collins, D. H. Zhang and X. M. Yang, Proc. Natl. Acad. Sci. U.S.A., 2010, 107, 12782–12785 CrossRef CAS PubMed.
- J. Y. Yang, K. J. Shao, D. Zhang, Q. Shuai, B. N. Fu, D. H. Zhang and X. M. Yang, J. Phys. Chem. Lett., 2014, 5, 3106–3111 CrossRef CAS PubMed.
- J. J. Lin, J. Shu, Y. T. Lee and X. Yang, J. Chem. Phys., 2000, 113, 5287–5301 CrossRef CAS.
- P. Casavecchia, G. Capozza, E. Segoloni, F. Leonori, N. Balucani and G. G. Volpi, J. Phys. Chem. A, 2005, 109, 3527–3530 CrossRef CAS PubMed.
- B. N. Fu, Y. C. Han, J. M. Bowman, L. Angelucci, N. Balucani, F. Leonori and P. Casavecchia, Proc. Natl. Acad. Sci. U.S.A., 2012, 109, 9733–9738 CrossRef CAS PubMed.
- F. Leonori, A. Occhiogrosso, N. Balucani, A. Bucci, R. Petrucci and P. Casavecchia, J. Phys. Chem. Lett., 2012, 3, 75–80 CrossRef CAS.
- P. Recio, S. Alessandrini, G. Vanuzzo, G. Pannacci, A. Baggioli, D. Marchione, A. Caracciolo, V. J. Murray, P. Casavecchia, N. Balucani, C. Cavallotti, C. Puzzarini and V. Barone, Nat. Chem., 2022, 14, 1405–1412 CrossRef CAS PubMed.
- C. Cavallotti, A. Della Libera, C. W. Zhou, P. Recio, A. Caracciolo, N. Balucani and P. Casavecchia, Faraday Discuss., 2022, 238, 161–182 RSC.
- B. B. Dangi, D. S. N. Parker, R. I. Kaiser, D. Belisario-Lara and A. M. Mebel, Chem. Phys. Lett., 2014, 607, 92–99 CrossRef CAS.
- D. S. N. Parker, S. Maity, B. B. Dangi, R. I. Kaiser, A. Landera and A. M. Mebel, Phys. Chem. Chem. Phys., 2014, 16, 12150–12163 RSC.
- D. S. N. Parker, T. Yang, R. I. Kaiser, A. Landera and A. M. Mebel, Chem. Phys. Lett., 2014, 595–596, 230–236 CrossRef CAS.
- T. Yang, B. B. Dangi, D. S. N. Parker, R. I. Kaiser, Y. An and A. H. H. Chang, Phys. Chem. Chem. Phys., 2014, 16, 17580–17587 RSC.
- T. Yang, B. B. Dangi, P. Maksyutenko, R. I. Kaiser, L. W. Bertels and M. Head-Gordon, J. Phys. Chem. A, 2015, 119, 12562–12578 CrossRef CAS PubMed.
- T. Yang, B. B. Dangi, R. I. Kaiser, L. W. Bertels and M. Head-Gordon, J. Phys. Chem. A, 2016, 120, 4872–4883 CrossRef CAS PubMed.
- M. Lucas, A. M. Thomas, R. I. Kaiser, E. K. Bashkirov, V. N. Azyazov and A. M. Mebel, J. Phys. Chem. A, 2018, 122, 3128–3139 CrossRef CAS PubMed.
- A. M. Thomas, M. Lucas, L. Zhao, J. Liddiard, R. I. Kaiser and A. M. Mebel, Phys. Chem. Chem. Phys., 2018, 20, 10906–10925 RSC.
- C. He, L. Zhao, A. M. Thomas, G. R. Galimova, A. M. Mebel and R. I. Kaiser, Phys. Chem. Chem. Phys., 2019, 21, 22308–22319 RSC.
- C. He, L. Zhao, A. M. Thomas, A. N. Morozov, A. M. Mebel and R. I. Kaiser, J. Phys. Chem. A, 2019, 123, 5446–5462 CrossRef CAS PubMed.
- C. He, G. R. Galimova, Y. Luo, L. Zhao, A. K. Eckhardt, R. Sun, A. M. Mebel and R. I. Kaiser, Proc. Natl. Acad. Sci. U.S.A., 2020, 117, 30142–30150 CrossRef CAS PubMed.
- C. He, S. J. Goettl, Z. Yang, S. Doddipatla, R. I. Kaiser, M. X. Silva and B. R. L. Galvao, Phys. Chem. Chem. Phys., 2021, 23, 18506–18516 RSC.
- Z. Yang, C. He, S. Goettl and R. I. Kaiser, J. Phys. Chem. A, 2021, 125, 5040–5047 CrossRef CAS PubMed.
- G. R. Galimova, A. M. Mebel, S. J. Goettl, Z. Yang and R. I. Kaiser, Phys. Chem. Chem. Phys., 2022, 24, 22453–22463 RSC.
- S. J. Goettl, C. He, D. Paul, A. A. Nikolayev, V. N. Azyazov, A. M. Mebel and R. I. Kaiser, J. Phys. Chem. A, 2022, 126, 1889–1898 CrossRef CAS PubMed.
- C. He, S. J. Goettl, Z. Yang, R. I. Kaiser, A. A. Nikolayev, V. N. Azyazov and A. M. Mebel, J. Phys. Chem. Lett., 2022, 13, 4589–4597 CrossRef CAS PubMed.
- C. He, Z. Yang, S. Doddipatla, A. M. Thomas, R. I. Kaiser, G. R. Galimova, A. M. Mebel, K. Fujioka and R. Sun, Phys. Chem. Chem. Phys., 2022, 24, 26499–26510 RSC.
- L. B. Tuli, S. J. Goettl, A. M. Turner, A. H. Howlader, P. Hemberger, S. F. Wnuk, T. Guo, A. M. Mebel and R. I. Kaiser, Nat. Commun., 2023, 14, 1527 CrossRef CAS PubMed.
- G. Vanuzzo, A. Caracciolo, T. K. Minton, N. Balucani, P. Casavecchia, C. de Falco, A. Baggioli and C. Cavallotti, J. Phys. Chem. A, 2021, 125, 8434–8453 CrossRef CAS PubMed.
- A. V. Wilson, D. S. N. Parker, F. T. Zhang and R. I. Kaiser, Phys. Chem. Chem. Phys., 2012, 14, 477–481 RSC.
- F. T. Zhang, P. Maksyutenko and R. I. Kaiser, Phys. Chem. Chem. Phys., 2012, 14, 529–537 RSC.
- N. Balucani, Chem. Soc. Rev., 2012, 41, 5473–5483 RSC.
- T. Yang, L. Bertels, B. B. Dangi, X. Li, M. Head-Gordon and R. I. Kaiser, Proc. Natl. Acad. Sci. U.S.A., 2019, 116, 14471–14478 CrossRef CAS PubMed.
- Z. Yang, S. Doddipatla, R. I. Kaiser, A. A. Nikolayev, V. N. Azyazov and A. M. Mebel, Astrophys. J. Lett., 2021, 908, L40 CrossRef CAS.
- L. Zhao, S. Doddipatla, R. I. Kaiser, W. Lu, O. Kostko, M. Ahmed, L. B. Tuli, A. N. Morozov, A. H. Howlader, S. F. Wnuk, A. M. Mebel, V. N. Azyazov, R. K. Mohamedf and F. R. Fischer, Phys. Chem. Chem. Phys., 2021, 23, 5740–5749 RSC.
- N. Balucani, A. Caracciolo, G. Vanuzzo, D. Skouteris, M. Rosi, L. Pacifici, P. Casavecchia, K. M. Hickson, J. C. Loison and M. Dobrijevic, Faraday Discuss., 2023, 245, 327–351 RSC.
- P. A. Willis, H. U. Stauffer, R. Z. Hinrichs and H. F. Davis, J. Phys. Chem. A, 1999, 103, 3706–3720 CrossRef CAS.
- H. U. Stauffer, R. Z. Hinrichs, J. J. Schroden and H. F. Davis, J. Phys. Chem. A, 2000, 104, 1107–1116 CrossRef CAS.
- F. F. Li, C. W. Dong, J. Chen, J. X. Liu, F. Y. Wang and X. Xu, Chem. Sci., 2018, 9, 488–494 RSC.
- C. W. Dong, J. X. Liu, F. F. Li and F. Y. Wang, Chin. J. Chem. Phys., 2016, 29, 99–104 CrossRef CAS.
- D. Yan, Y. J. Ma, F. F. Li, J. X. Liu, G. J. Wang and F. Y. Wang, Chin. J. Chem. Phys., 2020, 33, 239–242 CrossRef CAS.
- P. A. Willis, H. U. Stauffer, R. Z. Hinrichs and H. F. Davis, J. Chem. Phys., 1998, 108, 2665–2668 CrossRef CAS.
- H. U. Stauffer, R. Z. Hinrichs, J. J. Schroden and H. F. Davis, J. Chem. Phys., 1999, 111, 10758–10761 CrossRef CAS.
- H. U. Stauffer, R. Z. Hinrichs, P. A. Willis and H. F. Davis, J. Chem. Phys., 1999, 111, 4101–4112 CrossRef CAS.
- R. Z. Hinrichs, P. A. Willis, H. U. Stauffer, J. J. Schroden and H. F. Davis, J. Chem. Phys., 2000, 112, 4634–4643 CrossRef CAS.
- J. J. Schroden, M. Teo and H. F. Davis, J. Chem. Phys., 2002, 117, 9258–9265 CrossRef CAS.
- R. Z. Hinrichs, J. J. Schroden and H. F. Davis, J. Am. Chem. Soc., 2003, 125, 860–861 CrossRef CAS PubMed.
- R. Z. Hinrichs, J. J. Schroden and H. F. Davis, J. Phys. Chem. A, 2003, 107, 9284–9294 CrossRef CAS.
- J. J. Schroden, C. C. Wang and H. F. Davis, J. Phys. Chem. A, 2003, 107, 9295–9300 CrossRef CAS.
- R. Z. Hinrichs, J. J. Schroden and H. F. Davis, J. Phys. Chem. A, 2008, 112, 3010–3019 CrossRef CAS PubMed.
- D. L. Proctor and H. F. Davis, Proc. Natl. Acad. Sci. U.S.A., 2008, 105, 12673–12677 CrossRef CAS PubMed.
- F. F. Li, Y. J. Ma, D. Yan, A. Xu, J. X. Liu and F. Y. Wang, J. Phys. Chem. Lett., 2022, 13, 11630–11635 CrossRef CAS PubMed.
- M. Oana, Y. Nakatsuka, D. R. Albert and H. F. Davis, J. Phys. Chem. A, 2012, 116, 5039–5044 CrossRef CAS PubMed.
- J. J. Schroden and H. F. Davis, J. Phys. Chem. A, 2012, 116, 3508–3513 CrossRef CAS PubMed.
- J. Meyer and R. Wester, Annu. Rev. Phys. Chem., 2017, 68, 333–353 CrossRef CAS PubMed.
- J. Meyer, V. Tajti, E. Carrascosa, T. Győri, M. Stei, T. Michaelsen, B. Bastian, G. Czakó and R. Wester, Nat. Chem., 2021, 13, 977–981 CrossRef CAS PubMed.
- P. A. Robertson, D. Heathcote, D. Milesevic and C. Vallance, J. Phys. Chem. A, 2022, 126, 7221–7229 CrossRef CAS PubMed.
- D. Heathcote, P. A. Robertson, A. A. Butler, C. Ridley, J. Lomas, M. M. Buffett, M. Bell and C. Vallance, Faraday Discuss., 2022, 238, 682–699 RSC.
- H. Kockert, D. Heathcote, J. W. L. Lee and C. Vallance, Mol. Phys., 2021, 119, e1811909 CrossRef.
- J. N. Bull, J. W. L. Lee and C. Vallance, Phys. Rev. A, 2017, 96, 042704 CrossRef.
- J. N. Bull, J. W. L. Lee and C. Vallance, Phys. Rev. A, 2015, 91, 022704 CrossRef.
- J. N. Bull, M. Bart, C. Vallance and P. W. Harland, Phys. Rev. A, 2013, 88, 062710 CrossRef.
- R. T. Jongma, G. von Helden, G. Berden and G. Meijer, Chem. Phys. Lett., 1997, 270, 304–308 CrossRef CAS.
- E. Narevicius and M. G. Raizen, Chem. Rev., 2012, 112, 4879–4889 CrossRef CAS PubMed.
- S. Y. T. van de Meerakker, H. L. Bethlem, N. Vanhaecke and G. Meijer, Chem. Rev., 2012, 112, 4828–4878 CrossRef CAS PubMed.
- P. Jansen and F. Merkt, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 120–121, 118–148 CrossRef CAS PubMed.
- J. Onvlee, S. N. Vogels, A. von Zastrow, D. H. Parker and S. Y. T. van de Meerakker, Phys. Chem. Chem. Phys., 2014, 16, 15768–15779 RSC.
- J. Onvlee, S. N. Vogels and S. Y. T. van de Meerakker, ChemPhysChem, 2016, 17, 3583–3595 CrossRef CAS PubMed.
- D. Auerbach, E. E. A. Bromberg and L. Wharton, J. Chem. Phys., 1966, 45, 2160–2166 CrossRef CAS.
- H. L. Bethlem, G. Berden and G. Meijer, Phys. Rev. Lett., 1999, 83, 1558–1561 CrossRef CAS.
- H. L. Bethlem, G. Berden, A. J. A. van Roij, F. M. H. Crompvoets and G. Meijer, Phys. Rev. Lett., 2000, 84, 5744–5747 CrossRef CAS PubMed.
- F. M. H. Crompvoets, H. L. Bethlem, R. T. Jongma and G. Meijer, Nature, 2001, 411, 174–176 CrossRef CAS PubMed.
- C. E. Heiner, D. Carty, G. Meijer and H. L. Bethlem, Nat. Phys., 2007, 3, 115–118 Search PubMed.
- S. A. Meek, H. L. Bethlem, H. Conrad and G. Meijer, Phys. Rev. Lett., 2008, 100, 153003 CrossRef PubMed.
- E. Narevicius, A. Libson, M. F. Riedel, C. G. Parthey, I. Chavez, U. Even and M. G. Raizen, Phys. Rev. Lett., 2007, 98, 103201 CrossRef CAS PubMed.
- E. Narevicius, A. Libson, C. G. Parthey, I. Chavez, J. Narevicius, U. Even and M. G. Raizen, Phys. Rev. Lett., 2008, 100, 093003 CrossRef PubMed.
- S. D. Hogan, D. Sprecher, M. Andrist, N. Vanhaecke and F. Merkt, Phys. Rev. A, 2007, 76, 023412 CrossRef.
- S. D. Hogan, A. W. Wiederkehr, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2008, 101, 143001 CrossRef CAS PubMed.
- J. J. Gilijamse, S. Hoekstra, S. Y. T. van de Meerakker, G. C. Groenenboom and G. Meijer, Science, 2006, 313, 1617–1620 CrossRef CAS PubMed.
- M. Kirste, L. Scharfenberg, J. Klos, F. Lique, M. H. Alexander, G. Meijer and S. Y. T. van de Meerakker, Phys. Rev. A, 2010, 82, 042717 CrossRef.
- L. Scharfenberg, J. Klos, P. J. Dagdigian, M. H. Alexander, G. Meijer and S. Y. T. van de Meerakker, Phys. Chem. Chem. Phys., 2010, 12, 10660–10670 RSC.
- L. Scharfenberg, S. Y. T. van de Meerakker and G. Meijer, Phys. Chem. Chem. Phys., 2011, 13, 8448–8456 RSC.
- S. D. S. Gordon and A. Osterwalder, Phys. Rev. Appl., 2017, 7, 044022 CrossRef.
- V. Plomp, Z. Gao and S. Y. T. van de Meerakker, Mol. Phys., 2021, 119, e1814437 CrossRef.
- A. B. Henson, S. Gersten, Y. Shagam, J. Narevicius and E. Narevicius, Science, 2012, 338, 234–238 CrossRef CAS PubMed.
- J. Jankunas, K. Jachymski, M. Hapka and A. Osterwalder, J. Chem. Phys., 2015, 142, 164305 CrossRef PubMed.
- A. Klein, Y. Shagam, W. Skomorowski, P. S. Zuchowski, M. Pawlak, L. M. C. Janssen, N. Moiseyev, S. Y. T. van de Meerakker, A. van der Avoird, C. P. Koch and E. Narevicius, Nat. Phys., 2017, 13, 35–38 Search PubMed.
- B. Margulis, P. Paliwal, W. Skomorowski, M. Pawlak, P. S. Zuchowski and E. Narevicius, Phys. Rev. Res., 2022, 4, 043042 Search PubMed.
- Q. Ma, A. van der Avoird, J. Loreau, M. H. Alexander, S. Y. T. van de Meerakker and P. J. Dagdigian, J. Chem. Phys., 2015, 143, 044312 CrossRef PubMed.
- X. M. Yang and D. H. Zhang, Acc. Chem. Res., 2008, 41, 981–989 CrossRef CAS PubMed.
- P. Paliwal, A. Blech, C. P. Koch and E. Narevicius, Nat. Commun., 2021, 12, 7249 CrossRef CAS PubMed.
- T. De Jongh, M. Besemer, Q. Shuai, T. Karman, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2020, 368, 626–630 CrossRef CAS PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Nat. Chem., 2018, 10, 561–567 CrossRef CAS PubMed.
- J. F. E. Croft, N. Balakrishnan, M. Huang and H. Guo, Phys. Rev. Lett., 2018, 121, 113401 CrossRef CAS PubMed.
- S. N. Vogels, J. Onvlee, A. von Zastrow, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meerakker, Phys. Rev. Lett., 2014, 113, 263202 CrossRef PubMed.
- A. von Zastrow, J. Onvlee, S. N. Vogels, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meerakker, Nat. Chem., 2014, 6, 216–221 CrossRef CAS PubMed.
- V. Plomp, Z. Gao, T. Cremers, M. Besemer and S. Y. T. van de Meerakker, J. Chem. Phys., 2020, 152, 091103 CrossRef CAS PubMed.
- G. Tang, M. Besemer, S. Kuijpers, G. C. Groenenboom, A. van der Avoird, T. Karman and S. Y. T. van de Meerakker, Science, 2023, 379, 1031–1036 CrossRef CAS PubMed.
- Q. Shuai, T. de Jongh, M. Besemer, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, J. Chem. Phys., 2020, 153, 244302 CrossRef CAS PubMed.
- V. Zhelyazkova, F. B. V. Martins, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2020, 125, 263401 CrossRef CAS PubMed.
- S. D. Hogan, P. Allmendinger, H. Sassmannshausen, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2012, 108, 063008 CrossRef CAS PubMed.
- V. Zhelyazkova, F. B. V. Martins, J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 21606–21622 RSC.
- F. B. V. Martins, V. Zhelyazkova and F. Merkt, New J. Phys., 2022, 24, 113003 CrossRef CAS.
- V. Zhelyazkova, F. B. V. Martins and F. Merkt, Phys. Chem. Chem. Phys., 2022, 24, 16360–16373 RSC.
- V. Zhelyazkova, F. B. V. Martins, M. Zesko and F. Merkt, Phys. Chem. Chem. Phys., 2022, 24, 2843–2858 RSC.
- V. Zhelyazkova, F. B. V. Martins, S. Schilling and F. Merkt, J. Phys. Chem. A, 2023, 127, 1458–1468 CrossRef CAS PubMed.
- D. E. Heard, Acc. Chem. Res., 2018, 51, 2620–2627 CrossRef CAS PubMed.
- R. J. Shannon, M. A. Blitz, A. Goddard and D. E. Heard, Nat. Chem., 2013, 5, 745–749 CrossRef CAS PubMed.
- A. Potapov, A. Canosa, E. Jiménez and B. Rowe, Angew. Chem., Int. Ed., 2017, 56, 8618–8640 CrossRef CAS PubMed.
- R. Wild, M. Notzold, M. Simpson, T. D. Tran and R. Wester, Nature, 2023, 615, 425–429 CrossRef CAS PubMed.
- E. X. Han, W. Fang, M. Stamatakis, J. O. Richardson and J. Chen, J. Phys. Chem. Lett., 2022, 13, 3173–3181 CrossRef CAS PubMed.
- A. Choudhury, J. A. A. DeVine, S. Sinha, J. A. A. Lau, A. Kandratsenka, D. Schwarzer, P. Saalfrank and A. M. M. Wodtke, Nature, 2022, 612, 691–696 CrossRef CAS PubMed.
- A. M. Wodtke, Chem. Soc. Rev., 2016, 45, 3641–3657 RSC.
- A. M. Wodtke, J. C. Tully and D. J. Auerbach, Int. Rev. Phys. Chem., 2004, 23, 513–539 Search PubMed.
- G. B. Park, B. C. Krüger, D. Borodin, T. N. Kitsopoulos and A. M. Wodtke, Rep. Prog. Phys., 2019, 82, 096401 CrossRef CAS PubMed.
- H. Chadwick and R. D. Beck, Annu. Rev. Phys. Chem., 2017, 68, 39–61 CrossRef CAS PubMed.
- H. Chadwick and R. D. Beck, Chem. Soc. Rev., 2016, 45, 3576–3594 RSC.
- A. L. Utz, Curr. Opin. Solid State Mater. Sci., 2009, 13, 4–12 CrossRef CAS.
- J. C. Tully, Annu. Rev. Phys. Chem., 2000, 51, 153–178 CrossRef CAS PubMed.
- J. C. Tully, Acc. Chem. Res., 1981, 14, 188–194 CrossRef CAS.
- G. B. Park, T. N. Kitsopoulos, D. Borodin, K. Golibrzuch, J. Neugebohren, D. J. Auerbach, C. T. Campbell and A. M. Wodtke, Nat. Rev. Chem, 2019, 3, 723–732 CrossRef.
- J. T. Paci, T. K. Minton and G. C. Schatz, Acc. Chem. Res., 2012, 45, 1973–1981 CrossRef CAS PubMed.
- X.-F. Gao and G. M. Nathanson, Acc. Chem. Res., 2022, 55, 3294–3302 CrossRef CAS PubMed.
- J. A. Faust and G. M. Nathanson, Chem. Soc. Rev., 2016, 45, 3609–3620 RSC.
- O. Bünermann, A. Kandratsenka and A. M. Wodtke, J. Phys. Chem. A, 2021, 125, 3059–3076 CrossRef PubMed.
- O. Bünermann, H. Y. Jiang, Y. Dorenkamp, D. J. Auerbach and A. M. Wodtke, Rev. Sci. Instrum., 2018, 89, 094101 CrossRef PubMed.
- H. Y. Jiang, Y. Dorenkamp, K. Krüger and O. Bünermann, J. Chem. Phys., 2019, 150, 184704 CrossRef PubMed.
- Y. Dorenkamp, H. Jiang, H. Koeckert, N. Hertl, M. Kammler, S. M. Janke, A. Kandratsenka, A. M. Wodtke and O. Bünermann, J. Chem. Phys., 2019, 150, 099901 CrossRef PubMed.
- Y. Dorenkamp, H. Jiang, H. Kockert, N. Hertl, M. Kammler, S. M. Janke, A. Kandratsenka, A. M. Wodtke and O. Bünermann, J. Chem. Phys., 2018, 148, 034706 CrossRef PubMed.
- O. Bünermann, H. Y. Jiang, Y. Dorenkamp, A. Kandratsenka, S. M. Janke, D. J. Auerbach and A. M. Wodtke, Science, 2015, 350, 1346–1349 CrossRef PubMed.
- N. Hertl, K. Krüger and O. Bünermann, Langmuir, 2022, 38, 14162–14171 CrossRef CAS PubMed.
- R. Martin-Barrios, N. Hertl, O. Galparsoro, A. Kandratsenka, A. M. Wodtke and P. Larregaray, Phys. Chem. Chem. Phys., 2022, 24, 20813–20819 RSC.
- L. Lecroart, N. Hertl, Y. Dorenkamp, H. Jiang, T. N. Kitsopoulos, A. Kandratsenka, O. Bünermann and A. M. Wodtke, J. Chem. Phys., 2021, 155, 034702 CrossRef CAS PubMed.
- K. Krüger, Y. Wang, S. Tödter, F. Debbeler, A. Matveenko, N. Hertl, X. Zhou, B. Jiang, H. Guo, A. M. Wodtke and O. Bünermann, Nat. Chem., 2023, 15, 326–334 CrossRef PubMed.
- K. Krüger, Y. Wang, L. Zhu, B. Jiang, H. Guo, A. M. Wodtke and O. Bünermann, Nat. Sci., 2023, e20230019 Search PubMed.
- H. Y. Jiang, X. C. Tao, M. Kammler, F. Z. Ding, A. M. Wodtke, A. Kandratsenka, T. F. Miller and O. Bünermann, J. Phys. Chem. Lett., 2021, 12, 1991–1996 CrossRef CAS PubMed.
- H. Y. Jiang, M. Kammler, F. Z. Ding, Y. Dorenkamp, F. R. Manby, A. M. Wodtke, T. F. Miller, A. Kandratsenka and O. Bünermann, Science, 2019, 364, 379 CrossRef CAS PubMed.
- N. Hertl, A. Kandratsenka, O. Bünermann and A. M. Wodtke, J. Phys. Chem. A, 2021, 125, 5745–5752 CrossRef CAS PubMed.
- Y. G. Li and G. Wahnström, Phys. Rev. Lett., 1992, 68, 3444–3447 CrossRef CAS PubMed.
- Y. G. Li and G. Wahnström, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 14528–14542 CrossRef CAS PubMed.
- A. Kandratsenka, H. Y. Jiang, Y. Dorenkamp, S. M. Janke, M. Kammler, A. M. Wodtke and O. Bünermann, Proc. Natl. Acad. Sci. U.S.A., 2018, 115, 680–684 CrossRef CAS PubMed.
- S. Wille, H. Jiang, O. Bünermann, A. M. Wodtke, J. Behler and A. Kandratsenka, Phys. Chem. Chem. Phys., 2020, 22, 26113–26120 RSC.
- P. Liang, E. V. F. De Aragão, G. Pannacci, G. Vanuzzo, A. Giustini, D. Marchione, P. Recio, F. Ferlin, D. Stranges, N. F. Lago, M. Rosi, P. Casavecchia and N. Balucani, J. Phys. Chem. A, 2023, 127, 685–703 CrossRef CAS PubMed.
- S. Schauermann, N. Nilius, S. Shaikhutdinov and H.-J. Freund, Acc. Chem. Res., 2013, 46, 1673–1681 CrossRef CAS PubMed.
- S. Schauermann and H.-J. Freund, Acc. Chem. Res., 2015, 48, 2775–2782 CrossRef CAS PubMed.
- S. Attia, E. J. Spadafora, J. Hartmann, H.-J. Freund and S. Schauermann, Rev. Sci. Instrum., 2019, 90, 053903 CrossRef PubMed.
- W. Ludwig, A. Savara, R. J. Madix, S. Schauermann and H.-J. Freund, J. Phys. Chem. C, 2012, 116, 3539–3544 CrossRef CAS.
- A. Savara, W. Ludwig and S. Schauermann, ChemPhysChem, 2013, 14, 1686–1695 CrossRef CAS PubMed.
- A. Savara, W. Ludwig, K.-H. Dostert and S. Schauermann, J. Mol. Catal. A: Chem., 2013, 377, 137–142 CrossRef CAS.
- C. Schroeder, A.-K. Baumann, M. C. Schmidt, J. Smyczek, P. A. Haugg, O.-C. Graap and S. Schauermann, J. Phys. Chem. C, 2022, 126, 4907–4920 CrossRef CAS.
- K.-H. Dostert, C. P. O'Brien, F. Mirabella, F. Ivars-Barcelo, S. Attia, E. Spadafora, S. Schauermann and H.-J. Freund, ACS Catal., 2017, 7, 5523–5533 CrossRef CAS.
- K.-H. Dostert, C. P. O'Brien, F. Ivars-Barcelo, S. Schauermann and H.-J. Freund, J. Am. Chem. Soc., 2015, 137, 13496–13502 CrossRef CAS PubMed.
- J. Wulfes, A.-K. Baumann, T. Melchert, C. Schroeder and S. Schauermann, Phys. Chem. Chem. Phys., 2022, 24, 29480–29494 RSC.
- J. Wulfes, A.-K. Baumann, M. Cieminski, C. Schroeder and S. Schauermann, J. Catal., 2024, 429, 115213 CrossRef CAS.
- C. D. Feldt, T. Kirschbaum, J. L. Low, W. Riedel and T. Risse, Catal. Sci. Technol., 2022, 12, 1418–1428 RSC.
- C. D. Feldt, T. Gimm, R. Moreira, W. Riedel and T. Risse, Phys. Chem. Chem. Phys., 2021, 23, 21599–21605 RSC.
- C. D. Feldt, P. A. Albrecht, S. Eltayeb, W. Riedel and T. Risse, Chem. Commun., 2022, 58, 4336–4339 RSC.
- G. Wittstock, M. Baeumer, W. Dononelli, T. Kluener, L. Luehrs, C. Mahr, L. V. Moskaleva, M. Oezaslan, T. Risse, A. Rosenauer, A. Staubitz, J. Weissmueller and A. Wittstock, Chem. Rev., 2023, 123, 6716–6792 CrossRef CAS PubMed.
- B. Xu, R. J. Madix and C. M. Friend, Acc. Chem. Res., 2014, 47, 761–772 CrossRef CAS PubMed.
- B. J. Xu, X. Y. Liu, J. Haubrich, R. J. Madix and C. M. Friend, Angew. Chem., Int. Ed., 2009, 48, 4206–4209 CrossRef CAS PubMed.
- J. A. Schwarz and R. J. Madix, Surf. Sci., 1974, 46, 317–341 CrossRef CAS.
- M. P. D'Evelyn and R. J. Madix, Surf. Sci. Rep., 1983, 3, 413–495 CrossRef.
- J. A. Fair and R. J. Madix, J. Chem. Phys., 1980, 73, 3486 CrossRef CAS.
- J. Neugebohren, D. Borodin, H. W. Hahn, J. Altschaffel, A. Kandratsenka, D. J. Auerbach, C. T. Campbell, D. Schwarzer, D. J. Harding, A. M. Wodtke and T. N. Kitsopoulos, Nature, 2018, 558, 280 CrossRef CAS PubMed.
- D. Borodin, K. Golibrzuch, M. Schwarzer, J. Fingerhut, G. Skoulatakis, D. Schwarzer, T. Seelemann, T. Kitsopoulos and A. M. Wodtke, ACS Catal., 2020, 10, 14056–14066 CrossRef CAS PubMed.
- K. Papendorf, K. Golibrzuch, T. Zhong, S. Schwabe, T. N. Kitsopoulos and A. M. Wodtke, Chem.: Methods, 2022, 2, e202200017 CAS.
- K. Golibrzuch, P. R. Shirhatti, J. Geweke, J. Werdecker, A. Kandratsenka, D. J. Auerbach, A. M. Wodtke and C. Bartels, J. Am. Chem. Soc., 2015, 137, 1465–1475 CrossRef CAS PubMed.
- D. Borodin, M. Schwarzer, H. W. Hahn, J. Fingerhut, Y. Wang, D. J. Auerbach, H. Guo, J. Schroeder, T. N. Kitsopoulos and A. M. Wodtke, Mol. Phys., 2021, 119, e1966533 CrossRef.
- J. Fingerhut, D. Borodin, L. Lecroart, M. Schwarzer, S. Hoerandl, A. Kandratsenka, D. J. Auerbach, A. M. Wodtke and T. N. Kitsopoulos, J. Phys. Chem. A, 2023, 127, 142–152 CrossRef CAS PubMed.
- D. Borodin, I. Rahinov, O. Galparsoro, J. Fingerhut, M. Schwarzer, K. Golibrzuch, G. Skoulatakis, D. J. Auerbach, A. Kandratsenka, D. Schwarzer, T. N. Kitsopoulos and A. M. Wodtke, J. Am. Chem. Soc., 2021, 143, 18305–18316 CrossRef CAS PubMed.
- M. Schwarzer, N. Hertl, F. Nitz, D. Borodin, J. Fingerhut, T. N. Kitsopoulos and A. M. Wodtke, J. Phys. Chem. C, 2022, 126, 14500–14508 CrossRef CAS PubMed.
- D. Borodin, N. Hertl, G. B. Park, M. Schwarzer, J. Fingerhut, Y. Wang, J. Zuo, F. Nitz, G. Skoulatakis, A. Kandratsenka, D. J. Auerbach, D. Schwarzer, H. Guo, T. N. Kitsopoulos and A. M. Wodtke, Science, 2022, 377, 394–398 CrossRef CAS PubMed.
- D. Borodin, I. Rahinov, J. Fingerhut, M. Schwarzer, S. Hörandl, G. Skoulatakis, D. Schwarzer, T. N. Kitsopoulos and A. M. Wodtke, J. Phys. Chem. C, 2021, 125, 11773–11781 CrossRef CAS PubMed.
- D. Borodin, O. Galparsoro, I. Rahinov, J. Fingerhut, M. Schwarzer, S. Horandl, D. J. Auerbach, A. Kandratsenka, D. Schwarzer, T. N. Kitsopoulos and A. M. Wodtke, J. Am. Chem. Soc., 2022, 144, 21791–21799 CrossRef CAS PubMed.
- C. T. Campbell, Acc. Chem. Res., 2019, 52, 984–993 CrossRef CAS PubMed.
- T. L. Silbaugh and C. T. Campbell, J. Phys. Chem. C, 2016, 120, 25161–25172 CrossRef CAS.
- A. U. Nilekar, J. Greeley and M. Mavrikakis, Angew. Chem., Int. Ed., 2006, 45, 7046–7049 CrossRef CAS PubMed.
- L. Zhou, A. Kandratsenka, C. T. Campbell, A. Wodtke and H. Guo, Angew. Chem., Int. Ed., 2019, 58, 6916–6920 CrossRef CAS PubMed.
- J. Fingerhut, D. Borodin, M. Schwarzer, G. Skoulatakis, D. J. Auerbach, A. M. Wodtke and T. N. Kitsopoulos, J. Phys. Chem. A, 2021, 125, 7396–7405 CrossRef CAS PubMed.
- T. L. Silbaugh, E. M. Karp and C. T. Campbell, J. Am. Chem. Soc., 2014, 136, 3964–3971 CrossRef CAS PubMed.
- D. J. Garton, A. L. Brunsvold, T. K. Minton, D. Troya, B. Maiti and G. C. Schatz, J. Phys. Chem. A, 2006, 110, 1327–1341 CrossRef CAS PubMed.
- B. H. Wu, J. M. Zhang, T. K. Minton, K. G. McKendrick, J. M. Slattery, S. Yockel and G. C. Schatz, J. Phys. Chem. C, 2010, 114, 4015–4027 CrossRef CAS.
- A. Caracciolo, J. C. S. Veliz, D. D. Lu, H. Guo, M. Meuwly and T. K. Minton, J. Phys. Chem. A, 2023, 127, 8834–8848 CrossRef CAS PubMed.
- A. Caracciolo, J. M. Zhang, S. A. Lahankar and T. K. Minton, J. Phys. Chem. A, 2022, 126, 2091–2102 CrossRef CAS PubMed.
- E. J. Smoll, M. A. Tesa-Serrate, S. M. Purcell, L. D'Andrea, D. W. Bruce, J. M. Slattery, M. L. Costen, T. K. Minton and K. G. McKendrick, Faraday Discuss., 2018, 206, 497–522 RSC.
- S. M. Purcell, P. D. Lane, L. D'Andrea, N. S. Elstone, D. W. Bruce, J. M. Slattery, E. J. Smoll, S. J. Greaves, M. L. Costen, T. K. Minton and K. G. McKendrick, J. Phys. Chem. B, 2022, 126, 1962–1979 CrossRef CAS PubMed.
- R. Nieman, M. Sands, Y. Q. Wang, T. K. Minton, E. E. Mussoni, J. Engerer and H. Guo, Phys. Chem. Chem. Phys., 2023, 25, 15479–15489 RSC.
- J. S. Wright, A. Jones, B. Farmer, D. L. Rodman and T. K. Minton, CEAS Space J., 2021, 13, 399–413 CrossRef.
- S. L. Lednovich and J. B. Fenn, AICHE J., 1977, 23, 454–459 CrossRef CAS.
- M. E. Saecker, S. T. Govoni, D. V. Kowalski, M. E. King and G. M. Nathanson, Science, 1991, 252, 1421–1424 CrossRef CAS PubMed.
- G. M. Nathanson, Annu. Rev. Phys. Chem., 2004, 55, 231–255 CrossRef CAS PubMed.
- A. G. Knight, C. S. Olivares, M. J. Roman, D. R. Moon, P. D. Lane, M. L. Costen and K. G. McKendrick, J. Chem. Phys., 2023, 158, 244705 CrossRef CAS PubMed.
- D. J. Nesbitt, A. M. Zolot, J. R. Roscioli and M. Ryazanov, Acc. Chem. Res., 2023, 56, 700–711 CrossRef CAS PubMed.
- P. D. Lane, K. E. Moncrieff, S. J. Greaves, K. G. McKendrick and M. L. Costen, J. Phys. Chem. C, 2020, 124, 16439–16448 CrossRef CAS.
- M. J. Roman, A. G. Knight, D. R. Moon, P. D. Lane, S. J. Greaves, M. L. Costen and K. G. McKendrick, J. Chem. Phys., 2023, 158, 244704 CrossRef CAS PubMed.
- P. D. Lane, T. Gstir, S. M. Purcell, M. Swierczewski, N. S. Elstone, D. W. Bruce, J. M. Slattery, M. L. Costen and K. G. McKendrick, J. Phys. Chem. A, 2023, 127, 5580–5590 CrossRef CAS PubMed.
- M. A. Tesa-Serrate, E. J. Smoll Jr, L. D'Andrea, S. M. Purcell, M. L. Costen, D. W. Bruce, J. M. Slattery, T. K. Minton and K. G. McKendrick, J. Phys. Chem. C, 2016, 120, 27369–27379 CrossRef CAS.
- W. A. Alexander, J. P. Wiens, T. K. Minton and G. M. Nathanson, Science, 2012, 335, 1072–1075 CrossRef CAS PubMed.
- M. Faubel, S. Schlemmer and J. P. Toennies, Z. Med. Phys., 1988, 10, 269–277 CAS.
- R. Dupuy, S. Thurmer, C. Richter, T. Buttersack, F. Trinter, B. Winter and H. Bluhm, Acc. Chem. Res., 2023, 56, 215–223 CrossRef CAS PubMed.
- B. Winter, S. Thürmer and I. Wilkinson, Acc. Chem. Res., 2023, 56, 77–85 CrossRef CAS PubMed.
- X. F. Gao, D. J. Hood, X. Y. Zhao and G. M. Nathanson, J. Am. Chem. Soc., 2023, 145, 10987–10990 CrossRef CAS PubMed.
- J. A. Faust, T. B. Sobyra and G. M. Nathanson, J. Phys. Chem. Lett., 2016, 7, 730–735 CrossRef CAS PubMed.
- T. B. Sobyra, H. Pliszka, T. H. Bertram and G. M. Nathanson, J. Phys. Chem. A, 2019, 123, 8942–8953 CrossRef CAS PubMed.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1960, 259, 1–17 CAS.
- D. K. Lancaster, A. M. Johnson, D. K. Burden, J. P. Wiens and G. M. Nathanson, J. Phys. Chem. Lett., 2013, 4, 3045–3049 CrossRef CAS.
- C. Lee, M. N. Pohl, I. A. Ramphal, W. Yang, B. Winter, B. Abel and D. M. Neumark, J. Phys. Chem. A, 2022, 126, 3373–3383 CrossRef CAS PubMed.
- W. Yang, C. Lee, S. Saric, M. N. Pohl and D. M. Neumark, J. Chem. Phys., 2023, 159, 054704 CrossRef CAS PubMed.
- T. Buttersack, H. Haak, H. Bluhm, U. Hergenhahn, G. Meijer and B. Winter, Struct. Dyn., 2023, 10, 034901 CrossRef CAS PubMed.
- T. Takayanagi, N. Masaki, K. Nakamura, M. Okamoto, S. Sato and G. C. Schatz, J. Chem. Phys., 1987, 86, 6133–6139 CrossRef CAS.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045433 CrossRef.
- L.-P. Wang, A. Titov, R. McGibbon, F. Liu, V. S. Pande and T. J. Martinez, Nat. Chem., 2014, 6, 1044–1048 CrossRef CAS PubMed.
- C. A. Grambow, A. Jamal, Y.-P. Li, W. H. Green, J. Zador and Y. V. Suleimanov, J. Am. Chem. Soc., 2018, 140, 1035–1048 CrossRef CAS PubMed.
- R. van de Vijver and J. Zador, Comput. Phys. Commun., 2020, 248, 106947 CrossRef CAS.
- K. T. Schuett, M. Gastegger, A. Tkatchenko, K. R. Mueller and R. J. Maurer, Nat. Commun., 2019, 10, 5024 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |
