Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Automated monitoring of electrocatalyst corrosion as a function of electrochemical history and electrolyte formulation†
Ken J.
Jenewein
 *abc,
Kevin
Kan
*abc,
Kevin
Kan
 cd,
Dan
Guevarra
cd,
Ryan J. R.
Jones
cd,
Dan
Guevarra
cd,
Ryan J. R.
Jones
 cd,
Yungchieh
Lai
cd,
Santosh K.
Suram
cd,
Yungchieh
Lai
cd,
Santosh K.
Suram
 e,
Joel A.
Haber
e,
Joel A.
Haber
 cd,
Serhiy
Cherevko
cd,
Serhiy
Cherevko
 a and
John M.
Gregoire
a and
John M.
Gregoire
 *cd
*cd
aHelmholtz-Institute Erlangen-Nürnberg for Renewable Energy (IET-2), Forschungszentrum Jülich, Cauerstrasse 1, 91058 Erlangen, Germany. E-mail: k.jenewein@fz-juelich.de
bDepartment of Chemical and Biological Engineering, Friedrich-Alexander-Universität Erlangen-Nürnberg, Egerlandstrasse 3, 91058 Erlangen, Germany
cDivision of Engineering and Applied Science, California Institute of Technology, Pasadena, CA, USA. E-mail: gregoire@caltech.edu
dLiquid Sunlight Alliance, California Institute of Technology, Pasadena, CA, USA
eToyota Research Institute, Los Altos, CA 94022, USA
First published on 5th August 2024
Abstract
Automated platforms assessing the stability of electrocatalysts are key to accelerate the deployment of clean energy technologies. Here, we present a robust system that allows the study of corrosion behavior in conjunction with the electrochemical protocol and electrolyte composition over many individual electrodes. Oxygen reduction reaction on Pt is used as a proof-of-concept platform, where the influence of the potential window and phosphoric acid (PA) addition on Pt dissolution is probed. A total of 72 hours of automated operation was realized with actions including liquid management, cell cleaning, aliquoting, PA injection, and bubble detection and removal, demonstrating further advancements in automated stability testing for electrocatalysts.
Guaranteeing the long-term operational stability of catalysts is pivotal to satisfy industrial requirements for electrocatalytic energy conversion devices such as fuel cells or electrolyzers. Stability can be influenced by potential fluctuation or pH, which are the basis for Pourbaix diagrams based on thermodynamics.1 The kinetics of corrosion and electrocatalysis can also be strongly modulated by the presence of adatoms or other electrolyte components.2,3 The traditional assessment of electrocatalyst degradation via activity loss tends to lack the necessary sophistication to decipher degradation mechanisms, for which in situ analytics are more useful.4 In this light, tracking metal dissolution is a particularly effective proxy for assessing catalyst stability.5
Catalyst dissolution is known to vary with operating conditions, which are difficult to account for using modern computational methods.6 The impact of external parameters like potential, pH, or electrolyte are often studied to understand how to circumvent such degradation. Due to the dimensionality of the parameter space, and the requirement to monitor dissolution beyond transient behavior, mapping the relationship between dissolution and experimental conditions is inherently time-consuming. As a result, the dissolution behavior of electrocatalysts is largely unknown, decelerating efforts to discover novel, more stable catalysts. Hence, high-throughput (HT) methods using automated experiments can shorten the knowledge feedback and, ultimately, the time-to-market for new materials in clean energy technologies. Respecting the multi-objective nature of electrocatalysis by studying dissolution already in the early stages of accelerated catalyst developments helps to gain a holistic picture of the material beyond just activity.7 Advancing automation in electrochemical labs can also tackle poor reproducibility and the demand for stricter electrochemical reporting requirements.8
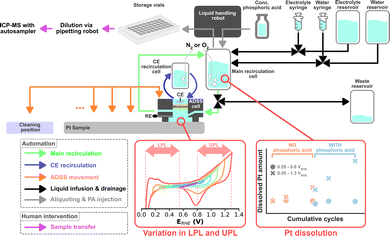
Automated HT dissolution studies based on flow-through systems using on-line analytics have been established.9,10 However, such systems have not implemented a method to monitor the equilibration of the electrode and the electrolyte or to perturb the electrolyte formulation to study the influence of electrolyte composition on catalyst dissolution in an automated fashion. Recently, Kan et al. introduced an accelerated durability screening system (ADSS) using a recirculating electrolyte.11 Here, an automated liquid handling robot takes scheduled aliquots that are analyzed for their dissolved metal content using an inductively coupled plasma with mass spectrometry (ICP-MS).
The same liquid handling robot, in principle, can be used to perform scheduled injections of a poisoning agent to systematically study the dissolution during such perturbations. Thus, in this study, we upgraded ADSS by introducing another variable into possible dissolution studies, namely electrolyte composition. Furthermore, the robustness of the system was enhanced to enable the automatic assessment of multiple samples. A simplified schematic of the ADSS campaign is shown in Fig. 1. Oxygen reduction reaction (ORR) on magnetron sputtered Pt with a nominal thickness of 100 nm was chosen as a proof-of-concept platform. Magnetron sputter synthesis was chosen to promote uniformity and reproducibility across different samples and enable a systematic study of the role of operational conditions.
Pt dissolution was studied with regard to two factors. First is the potential window, which is crucial to prolong the lifetime of Pt-based catalysts.12 Second is the introduction of phosphoric acid (PA). The possible impact of banning per- and polyfluorinated substances (PFAS) on current proton-exchange membrane (PEM) technologies like PEM fuel cells has given rise to the accelerated development of high-temperature fuel cells based on PFAS-free membranes such as PA-doped polybenzimidazole (PBI) and poly (2,5-benzimidazole) (ABPBI) membranes.13
It is known from literature that PA can act as a poisoning agent for Pt by decreasing the electrochemical active surface area (ECSA) and/or specific catalyst activity.14,15 However, there are only a few PA-related Pt dissolution studies,16–18 while a systematic assessment is lacking, making such an investigation highly relevant to understand whether PA increases or decreases catalyst dissolution.
The electrochemical testing protocol was based on cyclic voltammograms (CVs), as shown in Fig. S1 (ESI†), where all potentials are references to the reversible hydrogen electrode (RHE). A detailed listing of the ADSS sequence can be found in the ESI.† All protocols start with a 10 min N2 purging followed by 20 cleaning CVs with a fixed potential window of 0.05–1.5 VRHE recorded at 200 mV s−1. Every following CV was recorded at 100 mV s−1. Cleaning CVs are proceeded by 5 CVs with a varying lower potential limit (LPL) between 0.05–0.55 VRHE and upper potential limit (UPL) between 0.8–1.3 VRHE per sample, which is used for the rest of the protocol. The LPL and UPL are varied in 0.1 V steps for every sample. An aliquot of 100 μL is taken by the robotic liquid handler using a syringe to determine the starting Pt concentration within the recirculating system before starting the main dissolution study. The electrolyte is then saturated with O2 for 6 min, which is followed by 5, 25, and 50 CVs, where a 100 μL aliquot is taken after each set. After the last aliquot, the liquid handling robot injects 90 μL of concentrated PA into the recirculation system, targeting a final PA concentration of ca. 0.2 M in the electrolyte. The electrolyte is homogenized by recirculating it for one minute, after which the same 5, 25, and 50 CVs with aliquots are executed. After the final aliquot, the system is saturated with N2 again for 15 min before recording 5 CVs once more. The syringe used for liquid retrieval and injection is always cleaned with 200 μL of water after every use. Between each sample, the ADSS cell moves to a cleaning position and is subjected to a cleaning procedure, after which it moves to a new sample that will be measured with a different LPL-UPL combination. Each aliquot was further diluted 10× with 2% HNO3 using an external pipetting robot. The diluted samples were then analyzed with an autosampler connected to ICP-MS.
The campaign screens for 6 LPLs (0.05, 0.15, 0.25, 0.35, 0.45, 0.55 VRHE) and 6 UPLs (0.8, 0.9, 1.0, 1.1, 1.2, 1.3 VRHE), totaling 36 experiments. This translates into a total ADSS automation time of about 72 hours, necessitating robust automation with minimal intervention. Two essential hardware and software upgrades were undertaken. First is the automated refilling of the syringe pumps used to infuse the electrolyte and water. Each syringe has a volume of 50 mL and each experiment consumes 7 mL of electrolyte and 18 mL of water, which would allow only two experiments per syringe fill. This motivated the development of an automated syringe refilling procedure where the syringes were connected to a larger reservoir and the recirculation cell via a 3-port valve. As soon as the syringes infuse a given amount of liquid into the main recirculation cell, the same amount is automatically aspired from the reservoir. The second upgrade involves an improved bubble management. Bubbles can be detrimental when working in a micro- or macro-fluidic regime, which is the case for many flow cells applied in electrocatalysis research. Bubbles can be introduced during, e.g., the electrolyte filling processes, where they cut the electric path, causing overloads, and ultimately impeding electrochemical measurements. Thus, a bubble removal procedure was implemented, which was triggered based on an on-the-fly analysis of open circuit potential (OCP) measurements (see ESI† for a detailed explanation of the bubble removal process).
The ADSS was orchestrated using the hierarchical experimental laboratory automation and orchestration (HELAO) framework.19
To generally understand how PA addition affects the electrochemical features of Pt, the last CV of the 5 CVs recorded in N2 with and without PA addition were superimposed and plotted in Fig. S3 (ESI†). As the potential window is varied, different Pt features are accessed, such as the hydrogen under potential deposition (HUPD) around 0.05–0.3 VRHE, Pt oxide formation at around 0.9 VRHE, and Pt oxide reduction at approximately 0.7 VRHE. Looking at the last two columns, it is apparent that the Pt oxide formation and subsequent reduction are getting suppressed as the LPL increased from 0.05 to 0.55 VRHE after adding PA. The dependence of applied potential on phosphate coverage has been discussed in previous reports, and it could be argued that cycling down to 0.05 VRHE replaces more adsorbed phosphates with protons,20,21 freeing Pt sites that become available for oxidation and reduction again.
The Hupd region is shifted more to reductive currents for the final CV (in blue) with lower UPLs. A possibility of residual O2 in the electrolyte cannot be excluded, which, however, would imply that the same degree of reductive shift should be present for all LPL-UPL combinations. This is not the case, as higher UPLs are less shifted than lower UPLs. Again, an effect of the adsorbed PA and its retention depending on the potential windows, is plausible. Examining the kinetic region of the anodic sweeps of each ORR CV (see Fig. S4, ESI†) reveals a dependence of the cycling stability on the potential window and the addition of a poisoning agent. The change in the kinetic current is less pronounced when combining a high UPL with a low LPL compared to when combining a low UPL with a high LPL. Additionally, a general lowering in activity is observed when introducing PA into the electrolyte, highlighted by the increased overpotential to reach the same current density. Such a deactivation phenomenon is in agreement with previous reports.15
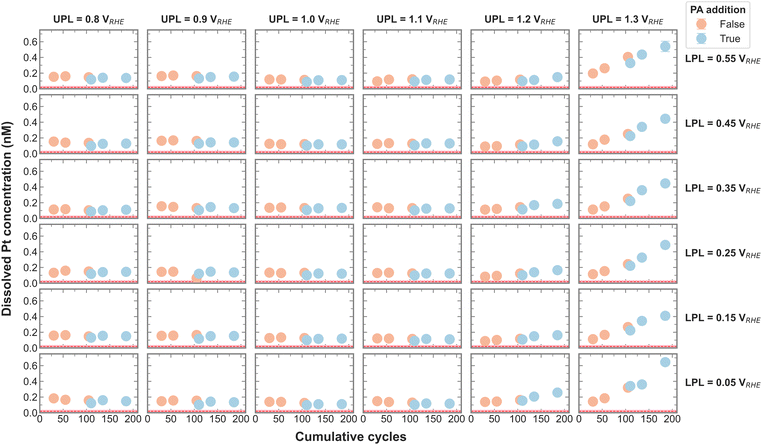
Dissolution is an important aspect of catalyst stability, and the measured Pt dissolution across the entire campaign is shown in Fig. 2. The continuously decreasing electrolyte volume with each aliquot is accounted for by normalizing the Pt concentrations by the current recirculation volume. The red line signifies the Pt concentration in the electrolyte before any electrochemistry was executed, which was deduced from control experiments. It is apparent that Pt dissolution is detected with UPLs above 1.1 VRHE. Cherevko et al. have shown that the main Pt dissolution mechanism is tied to Pt-redox processes.22 An anodic dissolution is encountered around 1.1 VRHE coming from surface oxidation and oxide place exchange. A more severe cathodic dissolution is encountered around 1 VRHE when reducing the surface again. The amount of Pt dissolution seems less affected by the change in LPL between 0.05 and 0.55 VRHE and is in agreement with on-line dissolution studies. This makes sense, as all LPLs are low enough to reduce any surface oxide.22
Upon close inspection, it appears that the dissolved amount of Pt increases steeper after PA addition, meaning the dissolution rate increases with the poisoning agent. The effect of different anions on Pt dissolution was previously reported, where strongly adsorbing anions such as SO42− were shown to trigger more Pt dissolution on single crystals than less adsorbing anions.23 A definitive explanation for this observation has yet to be found. The authors hypothesize a delayed onset of oxide place exchange with stronger adsorption, favoring more dissolution. Although PO43− was not included in the above-mentioned study, we presume that a similar effect is causing the increase in Pt dissolution rate in the present study.
In order to visualize the change in Pt dissolution rate more clearly, the slope of the three Pt concentrations before and after PA addition was calculated and plotted in Fig. S5 (ESI†). Indeed, it seems that the dissolution rate increases with the presence of PA, an accelerated dissolution that is exacerbated by a UPL above 1.1 VRHE.
To test for a statistically significant dissolution rate change, a box plot is plotted in Fig. 3 based on the data shown in Fig. S5 (ESI†). Only UPLs of 1.2 and 1.3 VRHE are shown, since those generated significant Pt dissolution. The data for different LPLs was aggregated since the LPL had only negligible influence on Pt dissolution. The general trend persists, namely, the addition of PA into the electrolyte increases the Pt dissolution rate, where the rate increases slightly with 1.2 VRHE and significantly more with 1.3 VRHE as UPL.
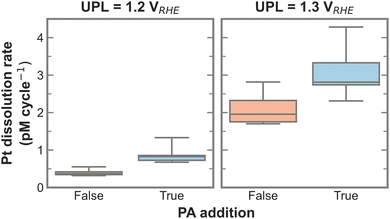 | ||
| Fig. 3 Box plot of Pt dissolution rate in relation to PA addition for 1.2 and 1.3 VRHE as UPL based on data shown in Fig. S5 (ESI†). | ||
Lastly, two repeat measurements were conducted using the widest LPL-UPL range (0.05–1.3 VRHE) to verify the repeatability of the obtained Pt dissolution and dissolution rates. As shown in Fig. S6 and S7 (ESI†), the experiments are quite reproducible, which is attributed to the high degree of automation applied during this study. All repeat measurements show the same observation as before, where PA increases the Pt dissolution rate. Interestingly, recalculating the dissolution rate before PA addition gives 1.66 ng cm−2 cycle−1, which is very close to previously reported values based on on-line Pt dissolution studies where the authors found 2.5 ng cm−2 cycle−1 for the same potential range and electrolyte.22 The slight difference might stem from a lowered corrosion rate due to the presence of dissolved Pt in the recirculating electrolyte, which is absent for the flow-through system utilized in the cited reference.
Herein, we build upon the ADSS system for measuring electrode–electrolyte equilibration, automating (i) exchange of electrodes, (ii) robotic modification of electrolyte during electrochemical operation, (iii) experiment orchestration to enable unattended operation and recovery from failure (i.e., bubble management and syringe refilling), and (iv) data analysis and visualization workflow from the unprecedented data streams. These advancements enabled a cumulative 72-hour procedure to study the Pt dissolution during ORR in relation to varying potential windows and PA addition. The automated campaign revealed that UPLs must pass above 1.1 VRHE to detect electrochemical Pt dissolution beyond that of initial levels from the establishment of an electrode–electrolyte interface and cleaning. The presence of PA generally increases the Pt dissolution rate, posing an opportunity to discover catalysts that mitigate PA-mediated corrosion, per the vision of PBI-based fuel cells. We envision using this system to study multinary alloys combined with active learning guidance that autonomously chooses the electrocatalyst composition, electrochemical protocol, and schedule of poisoning agent injection to map out composition–operation–dissolution relations much faster than simple grid search approaches.
The development of the ADSS was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award DE-SC0023139. The Pt dissolution study was supported by Toyota Research Institute. We acknowledge the support of Debasish Benarjee, Hongfei Jia, Honghong Lin, Chip Roberts, Gauhua Zhu from Toyota Research Institute of North America for providing insight on the role of phosphoric acid for fuel cell applications. Additionally, the authors thank the German Academic Exchange Service for supporting K. J. J.'s involvement in this work.
Data availability
The data supporting this study are openly available at https://doi.org/10.22002/z0w1x-mfq28.Conflicts of interest
J. M. G. is engaged in industrial research on catalyst discovery.Notes and references
- M. Pourbaix, Atlas of Electrochemical Equlibria in Aqueous Solutions, NACE International, 1974.
- S. Geiger, S. Cherevko and K. J. J. Mayrhofer, Electrochim. Acta, 2015, 179, 24–31 CrossRef CAS.
- X. Chen, L. P. Granda-Marulanda, I. T. McCrum and M. T. M. Koper, Nat. Commun., 2022, 13, 38 CrossRef CAS PubMed.
- R. Frydendal, E. A. Paoli, B. P. Knudsen, B. Wickman, P. Malacrida, I. E. L. Stephens and I. Chorkendorff, ChemElectroChem, 2014, 1, 2075–2081 CrossRef CAS.
- S. Cherevko, Curr. Opin. Electrochem., 2018, 8, 118–125 CrossRef CAS.
- S. Cherevko, N. Kulyk and K. J. J. Mayrhofer, Nano Energy, 2016, 29, 275–298 CrossRef CAS.
- A. Kormányos, K. J. Jenewein and S. Cherevko, Trends Chem., 2022, 4, 475–478 CrossRef.
- S. Minteer, J. Chen, S. Lin, C. Crudden, S. Dehnen, P. V. Kamat, M. Kozlowski, G. Masson and S. J. Miller, J. Org. Chem., 2023, 88, 4036–4037 CrossRef CAS PubMed.
- K. J. Jenewein, G. D. Akkoc, A. Kormányos and S. Cherevko, Chem. Catal., 2022, 2, 2778–2794 CrossRef CAS.
- K. J. Jenewein, S. Thienhaus, A. Kormanyos, A. Ludwig and S. Cherevko, Chem. Sci., 2022, 13, 13774–13781 RSC.
- K. Kan, D. Guevarra, L. Zhou, R. J. R. Jones, Y. Lai, M. Richter and J. M. Gregoire, ChemCatChem, 2024, 16, e202301300 CrossRef CAS.
- T. Dukic, L. J. Moriau, I. Klofutar, M. Sala, L. Pavko, F. J. Gonzalez Lopez, F. Ruiz-Zepeda, A. Pavlisic, M. Hotko, M. Gatalo and N. Hodnik, ACS Catal., 2024, 14, 4303–4317 CrossRef PubMed.
- R. Haider, Y. Wen, Z. F. Ma, D. P. Wilkinson, L. Zhang, X. Yuan, S. Song and J. Zhang, Chem. Soc. Rev., 2021, 50, 1138–1187 RSC.
- Q. He, X. Yang, W. Chen, S. Mukerjee, B. Koel and S. Chen, Phys. Chem. Chem. Phys., 2010, 12, 12544–12555 RSC.
- H. Lin, Z. Hu, K. H. Lim, S. Wang, L. Q. Zhou, L. Wang, G. Zhu, K. Okubo, C. Ling, Y. S. Kim and H. Jia, ACS Catal., 2023, 13, 5635–5642 CrossRef CAS.
- M. S. Kondratenko, M. O. Gallyamov, O. A. Tyutyunnik, I. V. Kubrakova, A. V. Chertovich, E. K. Malinkina and G. A. Tsirlina, J. Electrochem. Soc., 2015, 162, F587–F595 CrossRef CAS.
- T. Søndergaard, L. N. Cleemann, L. Zhong, H. Becker, T. Steenberg, H. A. Hjuler, L. Seerup, Q. Li and J. O. Jensen, Electrocatalysis, 2017, 9, 302–313 CrossRef.
- P. Bindra, S. J. Clouser and E. Yeager, J. Electrochem. Soc., 1979, 126, 1631–1632 CrossRef CAS.
- D. Guevarra, K. Kan, Y. Lai, R. J. R. Jones, L. Zhou, P. Donnelly, M. Richter, H. S. Stein and J. M. Gregoire, Digital Discovery, 2023, 2, 1806–1812 RSC.
- B. F. Gomes, M. Prokop, T. Bystron, R. Loukrakpam, C. M. S. Lobo, M. Kutter, T. E. Günther, M. Fink, K. Bouzek and C. Roth, J. Electroanal. Chem., 2022, 918, 116450 CrossRef CAS.
- S. Kaserer, K. M. Caldwell, D. E. Ramaker and C. Roth, J. Phys. Chem. C, 2013, 117, 6210–6217 CrossRef CAS.
- A. A. Topalov, S. Cherevko, A. R. Zeradjanin, J. C. Meier, I. Katsounaros and K. J. J. Mayrhofer, Chem. Sci., 2014, 5, 631–638 RSC.
- V. Briega-Martos, T. Fuchs, J. Drnec, O. M. Magnussen and S. Cherevko, ChemElectroChem, 2024, 11, e202300554 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cc02906b |
| This journal is © The Royal Society of Chemistry 2024 |