Open Access Article
Open Access ArticleBand gap tuning through cation and halide alloying in mechanochemically synthesized Cs3(Sb1−xBix)2Br9 and Cs3Sb2(I1−xBrx)9 solid solutions†
Giulia
Giovilli
a,
Benedetta
Albini
 b,
Virginia
Grisci
c,
Sara
Bonomi
a,
Marco
Moroni
a,
Edoardo
Mosconi
b,
Virginia
Grisci
c,
Sara
Bonomi
a,
Marco
Moroni
a,
Edoardo
Mosconi
 d,
Waldemar
Kaiser
d,
Waldemar
Kaiser
 d,
Filippo
De Angelis
cdef,
Pietro
Galinetto
b and
Lorenzo
Malavasi
d,
Filippo
De Angelis
cdef,
Pietro
Galinetto
b and
Lorenzo
Malavasi
 *a
*a
aDepartment of Chemistry and INSTM, University of Pavia, Via Taramelli 16, Pavia 27100, Italy
bDepartment of Physics, University of Pavia, Via Bassi 6, Pavia 27100, Italy. E-mail: lorenzo.malavasi@unipv.it; Tel: +39 382 987921
cDepartment of Chemistry, Biology and Biotechnology, University of Perugia and INSTM, Via Elce di Sotto 8, Perugia 06123, Italy
dComputational Laboratory for Hybrid/Organic Photovoltaics (CLHYO), Istituto CNR di Scienze e Tecnologie Chimiche “Giulio Natta” (CNR-SCITEC), Via Elce di Sotto 8, Perugia 06123, Italy
eDepartment of Mechanical Engineering, College of Engineering, Prince Mohammad Bin Fahd University, P.O. Box 1664, Al Khobar 31952, Saudi Arabia
fSKKU Institute of Energy Science and Technology (SIEST) Sungkyunkwan University, Suwon, 440-746, Korea
First published on 5th June 2023
Abstract
Modulation of the optical properties of lead-free defective perovskites can contribute to the design of optimized materials for several applications ranging from photodetection to photocatalysis. Here, we explored two novel alloying strategies in Cs3Sb2Br9 by preparing, through mechanochemical synthesis, Sb/Bi and Br/I mixed systems. An unexpected band gap bowing has been observed in alloyed Sb/Bi compositions, showing lower absorption edges with respect to pure compounds. Such behavior has been computationally modelled suggesting the presence of local aggregates as the source of such a reduction of the band gap. Further modulation of the optical properties has been achieved by halide alloying showing a progressive red-shift by increasing the iodide content. In both cases, full solubility at the solid state has been determined by means of diffraction and Raman spectroscopy. Overall, this study proposes and rationalizes doping strategies in the Cs3Sb2Br9 defective perovskite, achieved through the use of a sustainable synthetic procedure such as mechanochemistry.
Introduction
In the last decade, metal-halide perovskites (MHPs) have grown to be the most promising material class for future photovoltaic (PV) devices. While their huge potential is out of the question, recent experimental and computational research expands beyond the class of lead-halide perovskites exploring chemical and structural phase spaces of MHPs and perovskite derivatives.1 Several structually diverse systems are now under investigation, including, for example, 3D, 2D, and double perovskites, targeting applications beyond PV, e.g. photodetection and photocatalysis.2–11The expansion of the discovered material space of MHPs has recently moved towards the investigation of lead-free systems in order to overcome the concerns related to Pb-toxicity. While effective alternatives for PV applications rely mostly on tin-based compositions, several other phases containing different metals such as Bi, Sb, Cu, and Ge have been discovered and investigated.12–19 In many cases, such perovskites result ill-suited for PV devices but possess very appealing optoelectronic properties, which can be exploited in other applications. Among these systems, bismuth- and antimony-based perovskite derivatives of general formula Cs3M2X9 (M = Bi, Sb; X = Br, I) have shown strong technological potential, in particular in the area of photocatalysis (both for solar fuel generation and organic synthesis) and photodetection.20–36
Bismuth-based defect-ordered perovskites have been an object of more intense studies compared to the corresponding Sb systems, notwithstanding their appealing optoelectronic properties such as high carrier mobility, low trap density, and long diffusion length. As a matter of fact, Cs3Sb2Br9 millimeter-sized single crystals and nanoflakes have been applied in the fabrication of photodetectors with excellent performance in terms of responsivity and detectvity.37,38 Good photodetectors based on Cs3Sb2Br9 have also been prepared by means of a chemical vapor deposition technique.39 Cs3Sb2Br9 and Cs3Sb2I9 were also revealed to be suitable candidates for photocatalytic applications and in this respect have been, for example, applied in photocatalytic carbon dioxide reduction, water splitting, and aromatic C-H bond activation.40–44 Some efforts have also been made towards the possible use of these defect-ordered perovskites in the manufacturing of solar cells. Cs3Sb2I9 has been preferentially used for PV due to its suitable band gap of around 2 eV, providing good stability but relatively low efficiencies of around 2–3%.45–47
While there is clearly a relevant interest in Sb-based materials, many of their fundamental features still need to be explored: for example synthetic procedures, band gap tuning by metal or halide alloying, and their electronic structure. Considering the structural and optoelectronic similarity with Bi-based analogues, which have been more deeply investigated, it appears that some tuning strategies of the photophysical properties of Sb materials should be clarified to enlarge the plethora of lead-free perovskite derivatives. For example, the preparation of mixed Sb/Bi phases of vacancy ordered perovskites has not been reported in the current literature but there is a strong motivation to investigate such a system. Indeed, a recent work on the Cs2Ag(SbxBi1−x)Br6 double perovskite solid solution has demonstrated a nonlinear trend of the band gap value as a function of x, providing mixed compositions with lower values with respect to Cs2AgBiBr6 and Cs2AgSbBr6.48 However, the possibility of successfully preparing a continuous solid solution within the vacancy-ordered Cs3(Sb1−xBix)2Br9 system is still to be verified. The choice of a suitable synthetic route for these Sb/Bi materials is critical due to the low solubility of halide precursors posing strong limitations for traditional synthesis procedures applied to MHPs. A viable choice could be the use of mechanochemistry which has been recently applied to Bi-based systems but never to Sb-containing perovskites or mixed compositions. Finally, the halide alloying strategy to modulate the optical properties of perovskites is still to be investigated in Sb vacancy-ordered materials.
Based on the above considerations, in this work we carried out the mechanochemical synthesis of the Cs3(Sb1−xBix)2Br9 and Cs3Sb2(I1−xBrx)9 systems (0 ≤ x ≤ 1) to understand the effect of Sb/Bi and I/Br alloying on the structural and optical properties. For both alloying routes, we employ mechanochemistry as the main preparation technique to verify its suitability for Sb-based systems and its ability to provide phase-pure mixed compositions.
Results and discussion
Cs3(Sb1−xBix)2Br9 system
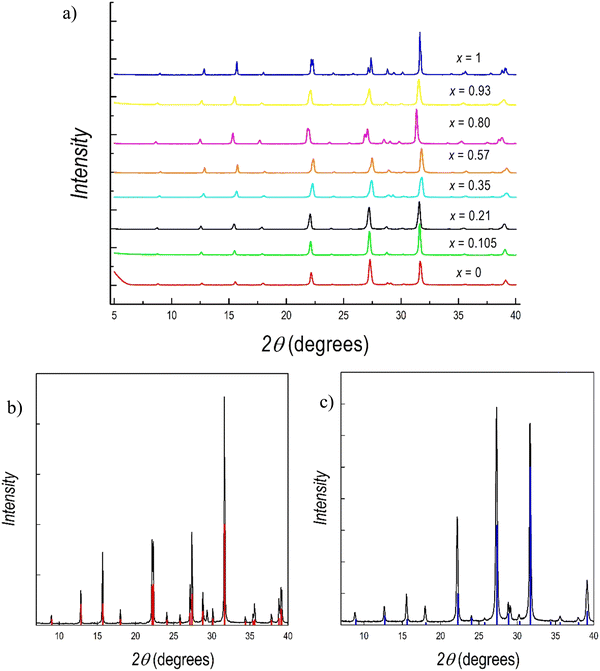
Powdered samples of the Cs3(Sb1−xBix)2Br9 system for x = 0, 0.1, 0.2, 0.4, 0.6, 0.8, 0.9, and 1 have been prepared using a planetary ball miller according to the experimental conditions reported in the Experimental section (see the ESI†). Fig. 1 shows the appearance of the eight samples prepared from Cs3Sb2Br9 (left) to Cs3Bi2Br9 (right).
Fig. 2 presents the room temperature (RT) X-ray diffraction (XRD) patterns collected for all the samples reported in Fig. 1. Samples have been measured both with Cu-K radiation (Fig. 1) and with Mo-K radiation (Fig. S1a and b, ESI†) to provide the most reliable structural results on these novel samples. Compositions (expressed as x) in Fig. 1 refer to the effective stoichiometries determined by microprobe analysis (see later in the text). All the samples are single phase and in agreement with the hexagonal symmetry of P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1, the space group that describes the two end members, namely Cs3Sb2Br9 and Cs3Bi2Br9. A superposition of the reference structure model for these last two samples and the experimental patterns are shown in Fig. 2b and c, respectively.
m1, the space group that describes the two end members, namely Cs3Sb2Br9 and Cs3Bi2Br9. A superposition of the reference structure model for these last two samples and the experimental patterns are shown in Fig. 2b and c, respectively.
According to these results, the mechanochemical synthetic procedure was effective in preparing single-phase materials for both of the two stoichiometric compositions, Cs3Sb2Br9 and Cs3Bi2Br9, and for the mixed Sb/Bi samples. A green and sustainable synthetic approach such as this has never been applied to Sb-based defective perovskites nor to B-site mixed compositions, while a previous report on its effective use for the preparation of Cs3Bi2Br9 is reported in the current literature.49
The morphology and chemical composition of the samples has been determined by means of scanning electron microscopy (SEM) and microprobe analysis. Images of the sample morphology are provided in Fig. S2 (ESI†). As a consequence of the mechanochemical synthesis, the samples do not possess a well-defined morphology, as occurs in solution-chemistry synthesis, and grains with various shapes and dimensions (in the micron and sub-micron range) are observed. Elemental analysis by energy dispersive spectroscopy (EDS) confirmed a good agreement with the nominal compositions (see Table 1). In the rest of the paper, we will make use of the effective compositions instead of the nominal ones when discussing the experimental results.
| Nominal (x) | Effective (x) | a = b (Å) | c (Å) | Volume (Å3) | Direct BG (eV) | Indirect BG (eV) |
|---|---|---|---|---|---|---|
| 0 | 0 | 7.9015(3) | 9.7119(4) | 525.12(4) | 2.50 | 2.31 |
| 0.1 | 0.105 | 7.9065(3) | 9.7227(4) | 526.37(4) | 2.34 | 2.07 |
| 0.2 | 0.21 | 7.9090(3) | 9.7284(4) | 527.01(4) | 2.31 | 2.03 |
| 0.4 | 0.35 | 7.9126(3) | 9.7523(4) | 528.79(4) | 2.33 | 2.04 |
| 0.6 | 0.57 | 7.9326(3) | 9.7907(4) | 533.55(4) | 2.34 | 2.11 |
| 0.8 | 0.80 | 7.9502(3) | 9.8261(4) | 537.86(4) | 2.39 | 2.12 |
| 0.9 | 0.93 | 7.9580(3) | 9.8382(4) | 539.58(4) | 2.43 | 2.17 |
| 1 | 1 | 7.9666(3) | 9.8422(4) | 540.97(4) | 2.58 | 2.46 |
The XRD patterns have been refined using the Rietveld method. The lattice parameters determined are reported in Table 1, while Fig. 3a and b show their trend together with lattice volume as a function of x (Bi-content).
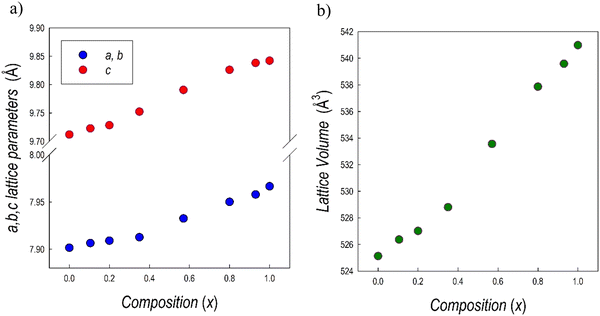 | ||
| Fig. 3 Trend of (a) a = b and c lattice parameters, (b) cell volume for the samples of the Cs3(Sb1−xBix)2Br9 solid solution as a function of x. | ||
The linear trend of the lattice volume reported in Fig. 3c agrees with Vegard's law for solid solution, confirming the complete solubility of Sb/Bi in the lattice. This result could be anticipated based on the similar ionic radii between Sb3+ and Bi3+ ions and the same crystal structure of the two end-members.
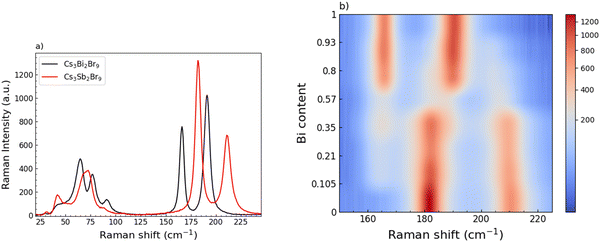
A Raman investigation has been performed, focusing on the low energy part of the Raman activity, i.e. in the range 25–250 cm−1. At a first glance, the single-phase of the end-members samples is confirmed, as reported in Fig. 4a. Indeed, the Raman spectrum of the Cs3Bi2Br9 sample clearly shows the characteristic modes at 165 and 190 cm−1, due to the bond vibrations inside the octahedral cage, BiBr6, as already described in our previous work.36
In analogy with Cs3Bi2Br9, Cs3Sb2Br9 Raman response presents, qualitatively, the same spectral fingerprints: a broadened structure centered at about 70 cm−1, clearly resulting from the overlapping of different modes, and two sharp and symmetric mode peaks at 182 and 210 cm−1, resulting from the Sb-Br bond vibrations in the octahedral unit SbBr6. The proper assignment of the mode symmetry seems to be controversial.
Indeed, in ref. 50, the mode at 210 cm−1 is given an A1g symmetry and the one at 182 cm−1 an E1g one, while in ref. 37, the opposite is given.37,50 However, besides this discrepancy, the two vibrational modes foresee the displacement of both Sb and Br atoms, as it is for the Cs3Bi2Br9 sample.50 The Raman spectra collected for the whole set of samples, moving from Cs3Bi2Br9 to Cs3Sb2Br9, in the region between 25 and 280 cm−1 are reported in Fig. S3 (ESI†). It's clear that the progressive substitution of Sb atoms with heavier Bi ones highly affects the modes above 150 cm−1. From these data we derived a color map (Fig. 4b) showing the energy changes experienced by the A1g and Eg modes by gradually varying the relative abundance of Sb and Bi. The energy changes of the main Raman bands indicate a clear two-mode behavior where, for a small amount of Bi, the peculiar modes of the Cs3Bi2Br9 sample already affect the collected spectra, with a constant increase of their intensities as the number of BiBr6 units progressively replace the SbBr6 ones. The increasing in Bi amount causes a redshift of the Raman bands, particularly pronounced for the mode at 210 cm−1, in agreement with a progressive cell expansion and resulting increase of the interatomic distance, as pointed out by the XRD measurements.
The crossover between Bi-rich and Sb-rich systems is also well evidenced in Fig. S4a (ESI†) where the intensity of the mode at about 165 cm−1 characteristic of Cs3Bi2Br9 and the one at 210 cm−1 of Cs3Sb2Br9 are plotted as a function of Bi content: as the former increases, the latter decreases. In Fig. S4b (ESI†), the spectrum for the x = 0.57 sample is reported together with the result from the best-fitting procedure using four Lorentzian curves according to the above mentioned two-mode behavior.
Fig. 5a reports the UV-Vis reflectance spectra collected for the whole series of samples of the Cs3(Sb1−xBix)2Br9 solid solution. It can be seen that the absorption edges of the two stoichiometric compounds, i.e. the red spectrum for Cs3Sb2Br9 and the blue spectrum for Cs3Bi2Br9, are blue-shifted with respect to all the mixed compositions. Bi-and Sb-based defective perovskites present a dual direct–indirect transition, which has been previously observed and also described from a computational point of view.51,52 The direct band gap transition derives from the promotion of electrons from the valence band (VB) to the conduction band (CB) followed by the excited electrons relaxing to the CB minimum and recombining with the holes in the VB maximum. If this process occurs with the assistance of phonons, an indirect band gap transitions occurs. The values of the direct and indirect band gaps, determined from the Tauc plots (reported in Fig. S5, ESI†), are shown in Fig. 5b as a function of x.
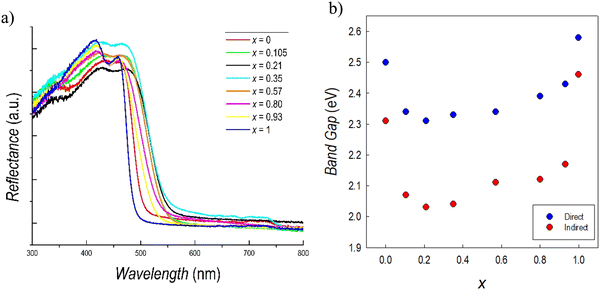 | ||
| Fig. 5 (a) Reflectance spectra and (b) trend of the band gaps of the Cs3(Sb1−xBix)2Br9 solid solution. | ||
The values of direct and indirect band gaps for Cs3Sb2Br9 and Cs3Bi2Br9 are in agreement with those previously reported in current literature.34,36,39,51 By looking at Fig. 5b, a significant bowing of the band gap in mixed compositions is observed. This result is unexpected since, in general, metal ion replacement in solid solution provides a scaling of the band gap obeying Vegard's law. The reduction of the band gap (direct) in mixed compositions is relevant, reaching a minimum value of about 2.35 eV when x is around 0.2–0.4. The same trend of band gap bowing is observed for the indirect band gap. Such a trend has never been observed before in any defective perovskite, but has been reported for the double perovskite system Cs2AgSb(1−x)BixBr6 and attributed to chemical rather than structural effects.48 In our case, we cannot exclude a synergistic effect due to the coexistence of mass disorder and microscopic strain, as it is expected in a two-mode scenario evidenced by Raman data.48 The present results corroborate the strategy of band gap tuning by Sb/Bi mixing, which seems to be general, considering the structural difference between defective perovskite and double perovskites, and therefore related to the peculiar electronic properties of antimony and bismuth in mixed compositions.
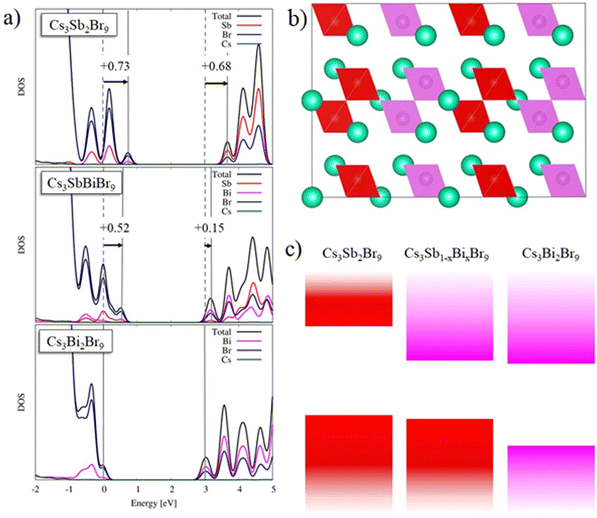
To understand the unexpected change in band gap, density functional theory (DFT) calculations have been performed for the reference systems Cs3Sb2Br9 and Cs3Bi2Br9 as well as for mixed Cs3(Sb0.5Bi0.5)2Br9. Ionic positions of the three systems were obtained by PBE+D3 geometry optimization, followed by refined electronic structure calculations using the hybrid HSE06 functional including spin–orbit coupling (see the ESI† for computational details). The indirect bandgap and first direct transition of Cs3Bi2Br9 (Cs3Sb2Br9) were calculated to be 2.97 (2.91) and 3.10 (2.96) eV, respectively (see Table 2). Previous GW-BSE calculations showed large exciton binding energies of ∼300 meV, which are not captured in our DFT calculations.53 Correcting our DFT results by the large exciton binding energies results in a fair agreement with the experimental band gap values.
| Cs3Sb2Br9 | Cs3(Sb0.5Bi0.5)2Br9 | Cs3Bi2Br9 | |
|---|---|---|---|
| D/I | I | I | I |
| BG direct | 2.96 | 2.71 | 3.10 |
| BG indirect | 2.91 | 2.59 | 2.97 |
| Exp. direct | 2.50 | 2.34 | 2.58 |
| Exp. indirect | 2.31 | 2.11 | 2.46 |
For the pure Sb and Bi species, the contribution of valence band is primarily given from bromine 4p orbitals with slight metal contribution, while the conduction band is mainly due to the metal cation (for Sb 5p orbitals and Bi 6p orbitals) and its interaction with bromine 4p orbitals, see Fig. 6a. Moving to the mixed Bi/Sb material, we observe substantial differences depending on the arrangement of the metal ions. The fully mixed system, with alternating SbBr6 and BiBr6 octahedra, interestingly shows a negligible difference in band gaps, with indirect and direct bandgaps of 2.90 and 3.00 eV, compared to the pure Sb and Bi species, see Fig. S6 (ESI†). When we consider aggregates of Sb and Bi, see Fig. 6b, we observe a decrease to 2.59 and 2.71 eV of the indirect and direct band gaps, respectively (cf.Fig. 6a). In terms of stability, the two models show the same energy, suggesting that both appear equally in the crystal structure. This clearly suggests that the band-gap decrease found experimentally for the mixed Sb/Bi material is associated with the presence of this kind of aggregate. As a matter of fact, considering the energy alignment in the density of states (Fig. 6a), we found, moving from Cs3Bi2Br9 to Cs3SbBiBr9, an upshift in the VB and CB of 0.52 eV and of 0.15 eV, respectively. In contrast, the VB is nicely aligned with the Cs3Bi2Br9 compound, showing a shift of only 0.21 eV, compared to a large CB shift of 0.53 eV. The DOS of mixed Cs3SbBiBr9 shows that the VB is mainly associated with Br alongside a slight Sb contribution, while the CB is made up of Bi and Br states in a similar ratio. Consequently, we can explain the drop in band gap upon Sb/Bi alloying by the formation of SbBr6 and BiBr6 aggregates, which dominate the VB and the CB, respectively, as schematically shown in Fig. 6c. This is the first report of such an effect in this Sb/Bi vacancy ordered perovskite alloys, while an analogous trend was found for the double perovskite system Cs2AgSbxBi(1−x)Br6.48
Band gap bowing of mixed metal perovskites has been observed in Pb/Sn perovskites and attributed to a chemical effect: mismatch in energy between s and p atomic orbitals of the two metals.54 A similar interpretation also holds for the present Cs3(Sb1−xBix)2Br9 solid solution where a mismatch in energy between s and p atomic orbitals of Sb and Bi is found. It is of relevance to report here this novel tuning strategy for defective perovskites which allows achieving significantly lower band gap values through metal alloying instead of the usual halide mixing, known to be the main strategy for modulating the absorption edge in these systems.25,26,36
Cs3Sb2(Br1−xIx)9 system
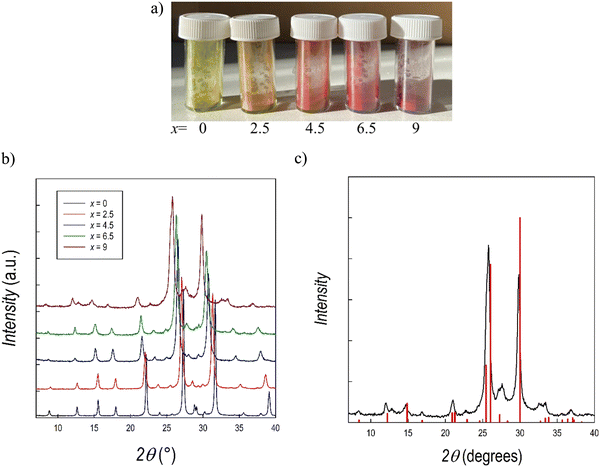
We further explored alloying strategies by tuning the halide content Br/I of the Cs3Sb2Br9 perovskite. While such a strategy has been explored for the Bi analogue, no studies are reported for the Sb-based composition.25,36 For this purpose, samples of the Cs3Sb2Br9−xIx system with x = 0 (also reported above), 2.5, 4.5, 6.5, and 9 have been synthesized by means of mechanochemistry according to the experimental conditions reported in the ESI.† Photographs of the five samples are displayed in Fig. 7a. XRD patterns for the whole series are shown in Fig. 7b. For the Cs3Sb2I9 perovskite two different polymorphs have been previously reported, namely the layered modification with e.g. (space group) P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (analogous to Cs3Sb2Br9, see above) and the dimer modification with the space group P63/mmc, featuring SbI6 octahedra fused into Sb2I93− dimers through sharing of their triangular faces.55 According to the literature, the dimer form is synthesized from solution using a polar solvent, whereas the layered form is obtained from a solid state reaction.56 However, the present synthetic approach has never been reported before for Cs3Sb2I9, and additional information on the stability of the different polymorphs has been obtained. According to Fig. 7c, reporting the XRD patterns of Cs3Sb2I9 perovskite against the expected structure for the P
m1 (analogous to Cs3Sb2Br9, see above) and the dimer modification with the space group P63/mmc, featuring SbI6 octahedra fused into Sb2I93− dimers through sharing of their triangular faces.55 According to the literature, the dimer form is synthesized from solution using a polar solvent, whereas the layered form is obtained from a solid state reaction.56 However, the present synthetic approach has never been reported before for Cs3Sb2I9, and additional information on the stability of the different polymorphs has been obtained. According to Fig. 7c, reporting the XRD patterns of Cs3Sb2I9 perovskite against the expected structure for the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 space group, we could obtain the layered modification through mechanochemistry. Nonetheless, this was possible after optimizing the synthesis approach in terms of milling cycles and time. By way of an example, Fig. S7 (ESI†) presents the pattern of Cs3Sb2I9 obtained at 400 rpm with 6 milling cycles which shows a mixed sample composed of the two polymorphs. The present results show the first successful synthesis of layered Cs3Sb2I9 by means of a mechanochemistry approach.
m1 space group, we could obtain the layered modification through mechanochemistry. Nonetheless, this was possible after optimizing the synthesis approach in terms of milling cycles and time. By way of an example, Fig. S7 (ESI†) presents the pattern of Cs3Sb2I9 obtained at 400 rpm with 6 milling cycles which shows a mixed sample composed of the two polymorphs. The present results show the first successful synthesis of layered Cs3Sb2I9 by means of a mechanochemistry approach.
Fig. 7b presents the RT Cu-K XRD patterns of all the samples of the Cs3Sb2Br9−xIx system, all in agreement with the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 e.g. A clear shift of all the peaks towards lower angles is evident by increasing the iodide content (x), in agreement with the unit-cell volume increase. All the samples result in being single-phase and the patterns have been refined using the Rietveld method: lattice parameters and cell volume trend as a function of x are shown in Fig. 8 and listed in Table 3. Microprobe analysis resulted in a perfect agreement (within the e.s.d.) between nominal and effective halide contents.
m1 e.g. A clear shift of all the peaks towards lower angles is evident by increasing the iodide content (x), in agreement with the unit-cell volume increase. All the samples result in being single-phase and the patterns have been refined using the Rietveld method: lattice parameters and cell volume trend as a function of x are shown in Fig. 8 and listed in Table 3. Microprobe analysis resulted in a perfect agreement (within the e.s.d.) between nominal and effective halide contents.
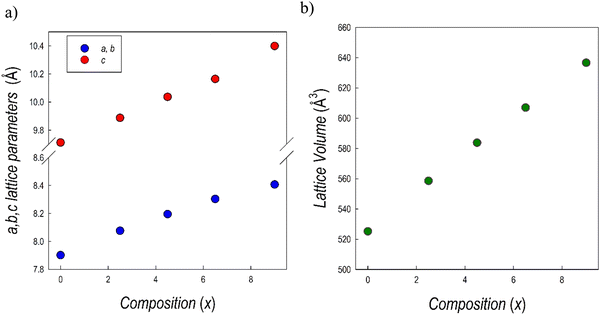 | ||
| Fig. 8 Trend of (a) a = b and c lattice parameter, and (b) cell volume for the samples of the Cs3Sb2Br9−xIx solid solution as a function of x. | ||
| X | a = b (Å) | c (Å) | Volume (Å3) | Direct BG (eV) | Indirect BG (eV) |
|---|---|---|---|---|---|
| 0 | 7.9015(3) | 9.7119(4) | 525.12(4) | 2.50 | 2.31 |
| 2.5 | 8.0760(3) | 9.8875(4) | 558.49(4) | 2.21 | 1.87 |
| 4.5 | 8.1950(3) | 10.0368(4) | 583.74(4) | 2.02 | 1.71 |
| 6.5 | 8.3037(3) | 10.1642(4) | 606.95(4) | 1.98 | 1.70 |
| 9 | 8.4074(3) | 10.3995(4) | 636.61(4) | 1.95 | 1.67 |
All the data follow a linear trend as a function of the iodide content, according to Vegard's law, confirming the formation of a continuous solid solution in this system, as with the analogous Bi-based system.25,36
The observed unit-cell expansion together with the progressive substitution of Br atoms with a heavier one leads again to a clear redshift of the Raman modes, more pronounced with respect to what is observed when Bi/Sb are replaced at the B sites, as described above. From Fig. 9 this behavior is particularly evident for the mode at 210 cm−1 characteristic of the Cs3Sb2Br9 structure: its center shifts up to 185 cm−1 for the x = 6.5 sample, then it completely disappears in the Cs3Sb2I9 compound.
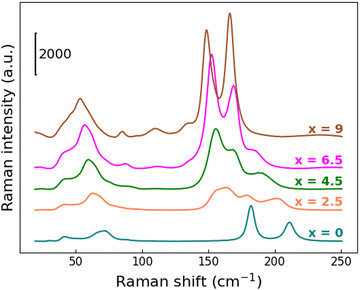 | ||
| Fig. 9 RT Raman spectra in the region between 25 and 250 cm−1 for Cs3Sb2Br9−xIx solid solutions as a function of x. | ||
Moving from one end-member to the other, gradual changes are observed, but it's harder to recognize a two-mode behavior, probably as a result of higher disorder in the chemical distribution related to the specific site involved in the substitution. Moreover, as a consequence of the later-discussed bandgap redshift, the Raman intensity of the x = 4.5, 6.5 and 9 samples are strongly increased: indeed, these three samples start absorbing at 638 nm, namely the incident laser wavelength used to perform the characterization.
Finally, the Raman activity of the Cs3Sb2I9 sample is consistent with the literature.52,57 The spectrum is dominated by two intense features at 148.9 and 166.3 cm−1, once again assigned to the A1g and Eg vibrational modes, involving both I and Sb atoms in the octahedral unit. Other less pronounced modes at 135.2 cm−1, 110.1 cm−1 and 85.3 cm−1, together with a broad feature at about 50 cm−1, are present in the spectrum. According to ref. 50 and 56, the lowest frequency modes, 85.3 cm−1 and the structure at 50 cm−1, are assigned to Sb–I bending and Sb–I–Sb interactions, respectively.
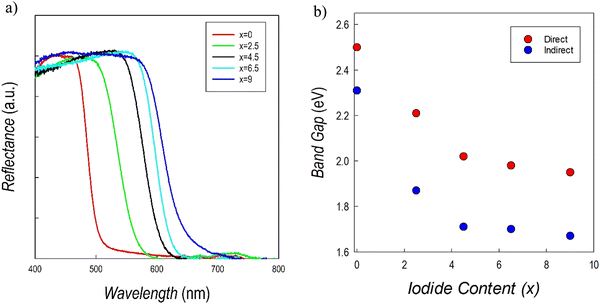
UV-vis absorption spectroscopy measurements on the Cs3Sb2Br9−xIx system are reported in Fig. 10a. There is a clear red shift obtained by increasing the amount of iodide, with a more pronounced effect up to x = 4.5. The trend of direct and indirect band gap values as a function of iodide content is shown in Fig. 10b.
The values for the two end members are in agreement with those reported in current literature.41,43 On the other hand, no previously reported data for Br/I mixed samples are available. Data in Fig. 10b show a relevant initial reduction of the (direct) band gap from about 2.5 to 2.1 eV (at 50% of Br and I), followed by a smoother reduction of the band gap up to about 2.0 eV, showing again a bowing of the Eg. A similar alloying strategy was investigated for the Cs3Bi2Br9−xIx defective perovskites showing as well a degree of band-gap bowing which is, however, less pronounced than the present Sb-based perovskites.25,36
Conclusions
In the present work we explored two novel alloying strategies for the Cs3Sb2Br9 defective perovskites, namely Sb/Bi and Br/I mixing. All the samples have been prepared for the first time (for these systems) following a mechanochemistry route, indicating its suitability in providing single-phase materials and in preserving the stoichiometry (for both stoichiometric and alloyed samples). The variation of cell parameters for Cs3(Sb1−xBix)2Br9 follows Vegard's law indicating the formation of a continuous solid solution. On the other hand, the trend of both direct and indirect band gaps shows a significant bowing and reduction for mixed Sb/Bi compositions, allowing access to band gap values lower than the two end-members, namely Cs3Sb2Br9 and Cs3Bi2Br9. This behavior has been modelled by DFT indicating that, for mixed systems, Sb and Bi aggregates control different regions of the electronic structure, showing a Sb-like valence band edge and a Bi-like conduction band edge, causing the drop in the band gap at all mixing ratios.For the Cs3Sb2Br9−xIx system we reported the first successful mechanochemical synthesis of the layered polymorph of the Cs3Sb2I9 perovskite, previously obtained only via a conventional solid state reaction. The Br/I alloying resulted in a linear expansion of the unit cell by increasing the I content, also confirming, in this case, a full solubility of the two halides in the lattice. Absorption spectroscopy indicates a progressive red-shift by increasing x, with a pronounced bowing of the band gap from x = 4.5 to x = 9.
For both Cs3(Sb1−xBix)2Br9 and Cs3Sb2Br9−xIx the Raman inspection allowed confirming the single-phase structure of all the end-members. Moreover, the reported results, confirmed by XRD evidence, point out a redshift of the modes as a consequence of the cell expansion and the substitution of heavier ions that enlarged the reduced mass of the vibrational unit. The Raman features of the mixed samples are consistent with a two-mode behavior and the mixed phonon landscape, which can, in turn, play an active role in the electronic response.
The present results provide a novel sustainable synthetic route for the preparation of Sb-based defective perovskites and, more importantly, two alloying strategies which allow tuning the band gap in most of the visible spectrum, also providing the first evidence of band gap reduction by metal mixing (Sb/Bi) in a defective perovskite structure. Such an effect has been previously observed only in double perovskites (Cs2AgSbxBi(1−x)Br6), suggesting its possible universal character which is worth of further exploration in other related systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
LM acknowledges support from the Ministero dell’Università e della Ricerca (MUR) and the University of Pavia through the program “Dipartimenti di Eccellenza 2023–2027.” EM and WK wish to thank project Ricerca@CNR PHOTOCAT (CUP B93C21000060006) and the POR H2 project, L.A.1.1.35 (CUP B93C22000630006). This work has been further funded by the European Union – NextGenerationEU under the Italian Ministry of University and Research (MUR) National Innovation Ecosystem grant ECS00000041 – VITALITY. F. D. A. acknowledges the Università degli Studi di Perugia and MUR for support within the project Vitality.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- B.-M. Bresolin, Y. Park and D. W. Bahnemann, Catalysts, 2020, 10, 709 CrossRef CAS.
- W. Zhang, G. E. Eperon and H. J. Snaith, Nat. Energy, 2016, 1, 16048 CrossRef CAS.
- X.-K. Liu, W. Xu, S. Bai, Y. Jin, J. Wang, R. H. Friend and F. Gao, Nat. Mater., 2021, 20, 10–21 CrossRef CAS PubMed.
- H. Huang, B. Pradhan, J. Hofkens, M. B. J. Roeffaers and J. A. Steele, ACS Energy Lett., 2020, 5, 1107–1123 CrossRef CAS.
- K. Ren, S. Yue, C. Li, Z. Fang, K. A. M. Gasem, J. Leszczynski, S. Qu, Z. Wang and M. Fan, J. Mater. Chem. A, 2022, 10, 407–429 RSC.
- L. Romani and L. Malavasi, ACS Omega, 2020, 5, 25511–25519 CrossRef CAS PubMed.
- M. Corti, S. Bonomi, R. Chiara, L. Romani, P. Quadrelli and L. Malavasi, Inorganics, 2021, 9, 56 CrossRef CAS.
- R. Dong, C. Lan, F. Li, S. Yip and J. C. Ho, Nanoscale Horiz., 2019, 4, 1342–1352 RSC.
- W.-G. Li, X.-D. Wang, J.-F. Liao, Y. Jiang and D.-B. Kuang, Adv. Funct. Mater., 2020, 30, 1909701 CrossRef CAS.
- D. Ricciarelli, W. Kaiser, E. Mosconi, J. Wiktor, M. W. Ashraf, L. Malavasi, F. Ambrosio and F. De Angelis, ACS Energy Lett., 2022, 1308–1315 CrossRef CAS.
- J. Cao and F. Yan, Energy Environ. Sci., 2021, 14, 1286–1325 RSC.
- M. Chen, M.-G. Ju, H. F. Garces, A. D. Carl, L. K. Ono, Z. Hawash, Y. Zhang, T. Shen, Y. Qi, R. L. Grimm, D. Pacifici, X. C. Zeng, Y. Zhou and N. P. Padture, Nat. Commun., 2019, 10, 16 CrossRef CAS PubMed.
- P. Cheng, T. Wu, J. Liu, W.-Q. Deng and K. Han, J. Phys. Chem. Lett., 2018, 9, 2518–2522 CrossRef CAS PubMed.
- A. Abate, Joule, 2017, 1, 659–664 CrossRef CAS.
- J. Li, H.-L. Cao, W.-B. Jiao, Q. Wang, M. Wei, I. Cantone, J. Lü and A. Abate, Nat. Commun., 2020, 11, 310 CrossRef CAS PubMed.
- N. K. Noel, S. D. Stranks, A. Abate, C. Wehrenfennig, S. Guarnera, A.-A. Haghighirad, A. Sadhanala, G. E. Eperon, S. K. Pathak, M. B. Johnston, A. Petrozza, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 3061–3068 RSC.
- C. Ponti, G. Nasti, D. Di Girolamo, I. Cantone, F. A. Alharthi and A. Abate, Trends Ecol. Evol., 2022, 37, 281–283 CrossRef CAS PubMed.
- A. Weis, P. Ganswindt, W. Kaiser, H. Illner, C. Maheu, N. Glück, P. Dörflinger, M. Armer, V. Dyakonov, J. P. Hofmann, E. Mosconi, F. De Angelis and T. Bein, J. Phys. Chem. C, 2022, 126, 21040–21049 CrossRef CAS.
- Z. Jin, Z. Zhang, J. Xiu, H. Song, T. Gatti and Z. He, J. Mater. Chem. A, 2020, 8, 16166–16188 RSC.
- B.-B. Yu, M. Liao, J. Yang, W. Chen, Y. Zhu, X. Zhang, T. Duan, W. Yao, S.-H. Wei and Z. He, J. Mater. Chem. A, 2019, 7, 8818–8825 RSC.
- R. Waykar, A. Bhorde, S. Nair, S. Pandharkar, B. Gabhale, R. Aher, S. Rondiya, A. Waghmare, V. Doiphode, A. Punde, P. Vairale, M. Prasad and S. Jadkar, J. Phys. Chem. Solids, 2020, 146, 109608 CrossRef CAS.
- M. Pazoki, M. B. Johansson, H. Zhu, P. Broqvist, T. Edvinsson, G. Boschloo and E. M. J. Johansson, J. Phys. Chem. C, 2016, 120, 29039–29046 CrossRef CAS.
- D. Liu, B.-B. Yu, M. Liao, Z. Jin, L. Zhou, X. Zhang, F. Wang, H. He, T. Gatti and Z. He, ACS Appl. Mater. Interfaces, 2020, 12, 30530–30537 CrossRef CAS PubMed.
- S. Ghosh, S. Mukhopadhyay, S. Paul, B. Pradhan and S. K. De, ACS Appl. Nano Mater., 2020, 3, 11107–11117 CrossRef CAS.
- G. Chen, P. Wang, Y. Wu, Q. Zhang, Q. Wu, Z. Wang, Z. Zheng, Y. Liu, Y. Dai and B. Huang, Adv. Mater., 2020, 32, 2001344 CrossRef CAS PubMed.
- Y. Dai, C. Poidevin, C. Ochoa-Hernández, A. A. Auer and H. Tüysüz, Angew. Chem., Int. Ed., 2020, 59, 5788–5796 CrossRef CAS PubMed.
- J. S. Han, Q. V. Le, H. Kim, Y. J. Lee, D. E. Lee, I. H. Im, M. K. Lee, S. J. Kim, J. Kim, K. J. Kwak, M.-J. Choi, S. A. Lee, K. Hong, S. Y. Kim and H. W. Jang, Small, 2020, 16, 2003225 CrossRef CAS PubMed.
- S. S. Bhosale, A. K. Kharade, E. Jokar, A. Fathi, S. Chang and E. W.-G. Diau, J. Am. Chem. Soc., 2019, 141, 20434–20442 CrossRef CAS PubMed.
- Y. Dai and H. Tüysüz, ChemSusChem, 2019, 12, 2587–2592 CrossRef CAS PubMed.
- L. Romani, A. Speltini, C. N. Dibenedetto, A. Listorti, F. Ambrosio, E. Mosconi, A. Simbula, M. Saba, A. Profumo, P. Quadrelli, F. De Angelis and L. Malavasi, Adv. Funct. Mater., 2021, 31, 2104428 CrossRef CAS.
- C. Tedesco and L. Malavasi, Molecules, 2023, 28, 339 CrossRef CAS PubMed.
- M. Medina-Llamas, A. Speltini, A. Profumo, F. Panzarea, A. Milella, F. Fracassi, A. Listorti and L. Malavasi, Nanomaterials, 2023, 13, 263 CrossRef CAS PubMed.
- A. Pradhan, M. K. Jena and S. L. Samal, ACS Appl. Energy Mater., 2022, 5, 6952–6961 CrossRef CAS.
- Z. Ma, Z. Shi, D. Yang, F. Zhang, S. Li, L. Wang, D. Wu, Y. Zhang, G. Na, L. Zhang, X. Li, Y. Zhang and C. Shan, ACS Energy Lett., 2020, 5, 385–394 CrossRef CAS.
- S. Bonomi, P. Galinetto, M. Patrini, L. Romani and L. Malavasi, Inorg. Chem., 2021, 60, 14142–14150 CrossRef CAS PubMed.
- P. Liu, Y. Liu, S. Zhang, J. Li, C. Wang, C. Zhao, P. Nie, Y. Dong, X. Zhang, S. Zhao and G. Wei, Adv. Opt. Mater., 2020, 8, 2001072 CrossRef CAS.
- Z. Zheng, Q. Hu, H. Zhou, P. Luo, A. Nie, H. Zhu, L. Gan, F. Zhuge, Y. Ma, H. Song and T. Zhai, Nanoscale Horiz., 2019, 4, 1372–1379 RSC.
- S. K. Shil, F. Wang, K. O. Egbo, Z. Lai, Y. Wang, Y. Wang, D. Zhao, S.-W. Tsang, J. C. Ho and K. M. Yu, ACS Appl. Mater. Interfaces, 2021, 13, 35930–35940 CrossRef CAS PubMed.
- H.-H. Zhang, Z.-C. Zhou, Y.-J. Dong, L. Zhang, H.-Y. Chen and D.-B. Kuang, Sol. RRL, 2021, 5, 2100559 CrossRef CAS.
- C. Lu, D. S. Itanze, A. G. Aragon, X. Ma, H. Li, K. B. Ucer, C. Hewitt, D. L. Carroll, R. T. Williams, Y. Qiu and S. M. Geyer, Nanoscale, 2020, 12, 2987–2991 RSC.
- Y. Hai, W. Huang, Z. Li, D. Wu, Q. Huang and X. Tang, ACS Appl. Energy Mater., 2021, 4, 5913–5917 CrossRef CAS.
- Y. Wang, Q. Zhou, Y. Zhu and D. Xu, Appl. Catal., B, 2021, 294, 120236 CrossRef CAS.
- H. Wang, B. Zhou and W. Li, Phys. Chem. Chem. Phys., 2023, 25, 486–493 RSC.
- K. M. Boopathi, P. Karuppuswamy, A. Singh, C. Hanmandlu, L. Lin, S. A. Abbas, C. C. Chang, P. C. Wang, G. Li and C. W. Chu, J. Mater. Chem. A, 2017, 5, 20843–20850 RSC.
- A. Singh, S. Najman, A. Mohapatra, Y.-J. Lu, C. Hanmandlu, C.-W. Pao, Y.-F. Chen, C. S. Lai and C.-W. Chu, ACS Appl. Mater. Interfaces, 2020, 12, 32649–32657 CrossRef CAS PubMed.
- K. Ahmad, P. Kumar and S. M. Mobin, Chem. – Asian J., 2020, 15, 2859–2863 CrossRef CAS PubMed.
- Z. Li, S. R. Kavanagh, M. Napari, R. G. Palgrave, M. Abdi-Jalebi, Z. Andaji-Garmaroudi, D. W. Davies, M. Laitinen, J. Julin, M. A. Isaacs, R. H. Friend, D. O. Scanlon, A. Walsh and R. L. Z. Hoye, J. Mater. Chem. A, 2020, 8, 21780–21788 RSC.
- Y. El Ajjouri, V. S. Chirvony, N. Vassilyeva, M. Sessolo, F. Palazon and H. J. Bolink, J. Mater. Chem. C, 2019, 7, 6236–6240 RSC.
- D. Samanta, S. P. Chaudhary, B. Ghosh, S. Bhattacharyya, G. Shukla and G. D. Mukherjee, Phys. Rev. B, 2022, 105, 104103 CrossRef CAS.
- Y. Zhang, J. Yin, M. R. Parida, G. H. Ahmed, J. Pan, O. M. Bakr, J.-L. Brédas and O. F. Mohammed, J. Phys. Chem. Lett., 2017, 8, 3173–3177 CrossRef CAS PubMed.
- J. Gu, G. Yan, Y. Lian, Q. Mu, H. Jin, Z. Zhang, Z. Deng and Y. Peng, RSC Adv., 2018, 8, 25802–25807 RSC.
- S. Rieger, B. J. Bohn, M. Döblinger, A. F. Richter, Y. Tong, K. Wang, P. Müller-Buschbaum, L. Polavarapu, L. Leppert, J. K. Stolarczyk and J. Feldmann, Phys. Rev. B, 2019, 100, 201404 CrossRef CAS.
- A. Goyal, S. McKechnie, D. Pashov, W. Tumas, M. Van Schilfgaarde and V. Stevanovic, Chem. Mater., 2018, 30, 3920–3928 CrossRef CAS.
- B. Saparov, F. Hong, J.-P. Sun, H.-S. Duan, W. Meng, S. Cameron, I. G. Hill, Y. Yan and D. B. Mitzi, Chem. Mater., 2015, 27, 5622–5632 CrossRef CAS.
- K. Yamada, H. Sera, S. Sawada, H. Tada, T. Okuda and H. Tanaka, J. Solid State Chem., 1997, 134, 319–325 CrossRef CAS.
- K. M. McCall, C. C. Stoumpos, S. S. Kostina, M. G. Kanatzidis and B. W. Wessels, Chem. Mater., 2017, 29, 4129–4145 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental conditions, SEM images, additional XRD patterns, and computational details. See DOI: https://doi.org/10.1039/d3tc01492d |
| This journal is © The Royal Society of Chemistry 2023 |